Abstract
The novel hyphenation of electrospray-differential mobility analysis with single particle-inductively coupled plasma mass spectrometry (ES-DMA-spICP-MS) was demonstrated with the capacity for real-time size, mass and concentration measurement of nanoparticles (NPs) on a particle-to-particle basis. In this proof-of-concept study, the feasibility of this technique was validated through both concentration and mass calibration using NIST gold NP reference materials. A detection limit of 105 NPs mL−1 was determined under current experimental conditions, which is about four orders of magnitude lower in comparison to a traditional ES-DMA setup using a condensation particle counter as detector. Furthermore, independent and simultaneous quantification of both size and mass of NPs provides information regarding NP aggregation states. Two demonstrative applications include gold NP mixtures with a broad size range (30 nm to 100 nm), and aggregated gold NPs with a primary size of 40 nm. Finally, this technique was shown to be potentially useful for real-world samples with high ionic background due to its ability to remove dissolved ions from the background.
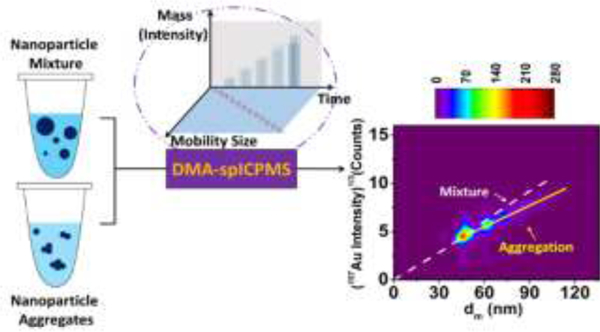
Overall, we demonstrate the capacity of this new hyphenated technique for: (1) Clearly resolving NP populations from a mixture containing a broad size range; (2) Accurately measures a linear relationship which should inherently exist between mobility size and one-third power of ICP-MS intensity for spherical NPs; (3) Monitoring propagation of NP aggregation with well characterized oligomers; and (4) Differentiating aggregated NPs and non-aggregated states based on the “apparent density” derived from both DMA size and spICP-MS mass.
Graphical Abstract
1. INTRODUCTION
Engineered nanoparticles (NPs) in colloidal form have found a wide range of commercial applications.1–4 However, when released into the environment, they are unlikely to remain in their pristine manufactured state throughout their lifecycle. Their transport properties and potential interaction with living organisms are highly dependent on their state of aggregation, complexation and dissolution.5–7 In order to evaluate the potential impact of nanotechnology on environmental and biological systems, validated analytical tools are critically needed which address challenges posed by real-world samples. This includes the analysis of environmentally relevant concentrations in the μg L−1 to mg L−1 range8 and different NP states, including size polydispersity, aggregation and adsorption of coatings. Ultimately, the ability to distinguish between naturally occurring and engineered NPs would be highly beneficial.
In this regard, no single analytical tool is available that can fulfill the wide range of characterization needs. One method that has featured prominently in the area of environmental systems is inductively coupled plasma mass spectrometry (ICP-MS). ICP-MS provides rapid and quantitative elemental analysis, and low limit of detection (LOD). More recently, single particle-ICP-MS (spICP-MS) has emerged as a powerful technique to quantify NPs on a particle-to-particle mass basis and to differentiate between dissolved and particulate forms. The potential of using spICP-MS for simultaneous particle sizing, mass measurement, and particle number quantification at environmentally relevant concentrations has been demonstrated, and further method development and validation are ongoing.9–12 Though promising, the technique has some significant limitations. First, ICP-MS is a mass based analytical tool, thus unless chemical composition, density and shape are known a priori, the size of NPs cannot be accurately determined. Additionally, spICP-MS, without further size information, cannot be employed to distinguish between complex NP states, such as aggregate forms, heteroaggregates or particles with coatings (such as proteins). In this respect, an upstream separation tool hyphenated with spICP-MS to pre-sort constituents in a complex sample has the potential to address such limitations by providing independent size information.
While chromatographic pre-separation has been suggested, to our knowledge, the only method directly coupled to spICP-MS to-date is hydrodynamic chromatography (HDC). Pergantis et al.13 utilized HDC online with spICP-MS for the detection and characterization of metal-containing NPs in terms of number concentration, size and metal content. Subsequent work by Rakcheev et al.14 explored HDC-spICP-MS to investigate morphology and temporal behavior of aggregation. While HDC has a very low LOD (≈ ng L−1) and can be applied to heterogeneous and complex samples, its resolution (the capacity to resolve multiple populations) was found to be insufficient to separate a mixture of NPs ((5, 20, 50 and 100) nm); Efforts must be made to improve resolution by, for example, optimization of flow rates and column length. Furthermore, to obtain size from retention time in HDC requires the calibration with standards, and the influence of surface coatings on retention time complicates the accuracy for size determination.15 Finally, we are aware of on-going efforts to hyphenate asymmetric flow field-flow fractionation with spICP-MS, but to-date published literature is limited to off-line analysis of collected fractions.16
In the present work, we employ electrospray-differential mobility analysis (ES-DMA) as an ion-mobility based size discrimination technique, coupled to spICP-MS. The DMA has been routinely used to characterize NPs across a broad size range from ≈ 3nm to a few hundred nm, and was one of the primary analytical techniques for size value assignment of NIST gold NP reference materials. DMA has the advantage of superb resolution (capable of differentiating a 1% difference in mobility), fast measurement times (of order minutes) and size selectivity.17 Furthermore, due to the ability to classify and separate ionic species from NPs by DMA, it shows great potential for reducing ionic background for real-world samples where high background is an issue for analytical aspects (i.e. spICP-MS). Prior work with ES-DMA has demonstrated its ability to separate discrete NP aggregates, characterize coating densities, and measure non-spherical geometries.18–20 Recently, ES-DMA was hyphenated on-line with ICP-MS operating in conventional-mode (i.e., non-single particle mode) for size differentiated elemental analysis21,22 and quantification of surface complexed cisplatin anti-tumor drug.23 In this approach an independent measurement of number concentration was necessary to obtain the size distribution and a condensation particle counter (CPC) was employed for this purpose.
In this proof-of-concept study, which is the follow up of our previous work cited above, we have demonstrated, for the first time, the capabilities and advantages of coupling ES-DMA directly to ICP-MS operated in time-resolved single particle analysis mode (i.e., spICP-MS), for characterizing NP size, mass, and number concentration at environmentally relevant concentrations and on a particle-by-particle basis. The simultaneous and independent measurement of NP mass and size makes this coupled approach valuable for studying aggregation process as well as differentiating between mixtures of various size NPs vs. aggregations of NPs.
2. EXPERIMENTAL
2.1. Chemicals
Gold NPs (AuNPs) were used as a test bed in this study as they can be readily obtained in a variety of monodisperse sizes, and are available as NIST reference materials. A series of AuNPs were employed in this study including NIST reference materials with nominal diameters of 30 nm and 60 nm (RM 8012 and RM 8013, respectively), and AuNP suspensions with nominal diameters of 40 nm, 80 nm and 100 nm obtained from Ted Pella (Redding, CA, U.S.A.).¶ The sizes of AuNPs were validated by mobility measurement using a customized ES-DMA-CPC system and compared with reference values (Table S-1, Supporting Information, SI). Ammonium acetate (AmAc - Sigma, 99.9%) was used for preparation of buffer solutions for electrospray and for inducing AuNP aggregation. The DMA was calibrated with NIST standard reference material polystyrene spheres (SRM 1963a) with a certified mobility diameter of (101.8 ± 1.1) nm. High purity filtered deionized (DI) water was used to prepare all solutions and suspensions. Formation of AuNP aggregates consisting of primary 40 nm monomers was induced by adjusting the ionic strength through addition of aqueous AmAc (for details refer to the SI).
2.2. Instrumentation
2.2.1. Principles of Differential Mobility Analysis (DMA)
The electrical mobility of a particle is defined as:
| (1) |
where is the drift velocity of a charged NP under the electric field with magnitude . By balancing electric and drag forces on the particle with charge , electrical mobility is also given by:
| (2) |
where (a function of ) is the Cunningham slip factor, which corrects for the non-slip boundary condition,24 is the viscosity of the carrier gas, is the electrical mobility diameter and is the elementary electric charge. For a spherical NP with 1e, is equal to the geometric diameter, while for a non-spherical NP, is the equivalent diameter of a sphere having the same drag force.20
DMA classifies NPs based on mobility (i.e., ). In a cylindrical DMA, the inner electrode is maintained at a high voltage and the outer cylinder is grounded (Fig. 1 c). A flow of polydisperse aerosol (called aerosol flow, ) and a laminar sheath flow () enter the DMA, and the charged NPs traverse radially with velocity , described by Eqs. (1) and (2) and are classified by mobility , under a given applied voltage , such that:
| (3) |
Figure 1.
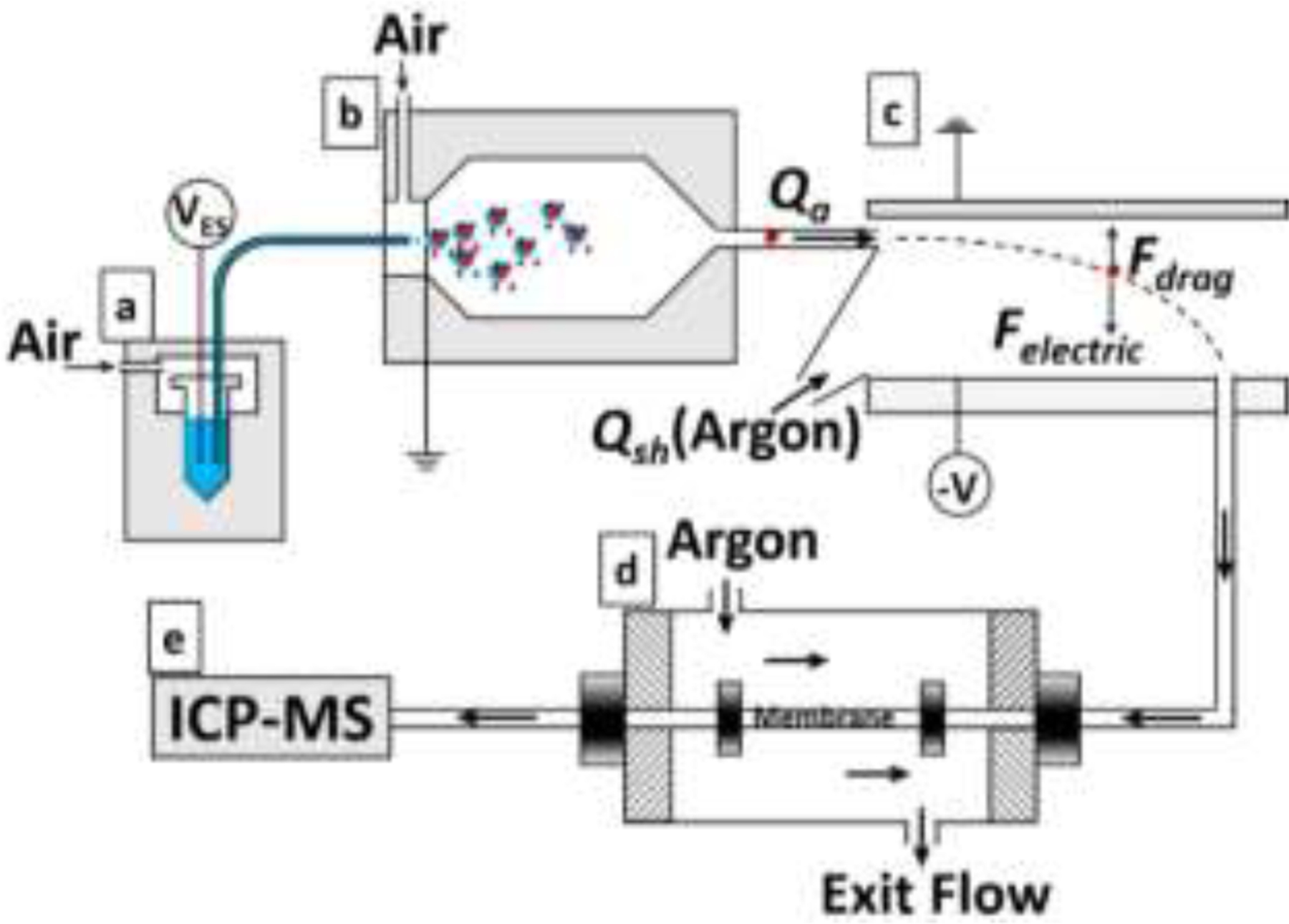
Experimental configuration for ES-DMA-spICP-MS: (a) electrospray unit, (b) 210Po neutralizer chamber, (c) differential mobility analyzer column, (d) gas exchange device to exchange air with argon for ICP-MS compatibility, (e) ICP-MS detector.
Therefore, at a fixed sheath flow and DMA configuration, is strictly a function of applied voltage, and NPs of given mobility are selected by controlling the voltage. DMA is an aerosol technique, and therefore the analysis of colloidal suspensions is achieved by applying an electrospray process prior to DMA classification.
2.2.2. ES-DMA-spICP-MS
A schematic of the instrumentation is shown in Fig. 1, and is composed of four major components: ((a)-(b)) ES and neutralizer for aerosolizing colloidal nanoparticles, (c) DMA for particle mobility classification, (d) a gas exchange device (GED) to exchange air to ICP compatible argon - this requirement arises because the ES nominally requires some quantity of an electronegative gas (e.g., O2) for stable operation, and (e) the ICP-MS for elemental-specific particle counting and mass quantification.
The electrosprayed droplets were charge-reduced with a 210Po neutralizer such that the aerosolized particles carry a known Boltzmann charge distribution (predominantly +1, 0 and −1 charges). Multiple charging is a concern for larger particles > 50 nm, but are otherwise easily identified and excluded from analysis. Although only charged particles are size selected, with a known Boltzmann charge distribution, the total number of particles can be obtained after performing a “charge correction” (see “Calculation of Number Concentration” in the SI).17 The DMA was operated with an aerosol flow of 1 L min−1 in air and a sheath flow of 10 L min−1 in argon, for a theoretic resolution factor of 10.25 This corresponds to a capacity for DMA to differentiate a 10 % change in mobility and thus about 5 % in diameter. The particles exiting the DMA (1 L min−1) pass through the GED with 3 L min−1 of argon passing countercurrent to the direction of the particle-air flow, to exchange air with argon sufficient to sustain the plasma. The ICP-MS was operated in time resolved mode in order to monitor single particle signal intensity as DMA voltage was stepped up with respect to time, allowing a stream of single particles characterized by a specific to exit the DMA at the selected voltage, ionize as single events in the plasma, and be detected by the mass spectrometer.
Unlike many liquid-based fractionation methods or chromatographic separations, the DMA offers flexibility in operation: enabling an arbitrarily chosen mobility size for a pre-determined time by choosing voltage and DMA step time accordingly. And with the fixed voltage, the DMA operates as a band filter to allow one specific size of NPs to exit (see Fig. S-2 in the SI)
2.3. Data Acquisition and Processing
2.3.1. Distinguishing Particle Events
In spICP-MS, 197Au was recorded with dwell time, , defining the measurement window for particle events. With an appropriately chosen , a single intensity pulse represents a single particle event. In the present study, 10 ms was chosen to minimize both particle splitting (a single particle event split over two adjacent dwell periods) and coincidence (more than one particle event occurring within a single dwell period). A five-sigma criterion (5σ) was applied to distinguish particle events from background9 (for details refer to the SI). The Au background signal with DMA hyphenation is lower relative to direct analysis of aqueous NP suspensions (particularly in the presence of dissolved ionic forms). This is because there is no interference arising from dissolved ions in solution (Au3+), as they form “salt” particles after electrospray process and will be separated based on size by DMA from the NP of interest therefore leaving a clean background for ICPMS detection of NP.. Therefore, the hyphenation of DMA with spICP-MS offers the advantage of reduced background and better detection of NP populations relative to conventional stand-alone spICP-MS. This is true for any kind of NPs where the dissolved ions/molecules are of the same content as NP which are concerns for spICPM-MS detection due to elevated dissolved background. The size of “salt” particles are directly dependent on the concentration of dissolved ions/molecules and the droplet size from electrospray process. However, under our experimental condition, 6.5mg L−1 of dissolved Au3+ still separate well from the NP signal of interest. (see SI, Fig. S-3, S-4)
2.3.2. Particle Mobility Size Determination
In our experiments, by stepping the applied voltage, the DMA is operated in a step-wise mode with respect to DMA scanning time, , so that singly charged NPs are selected as shown on the y-axis in Fig. 2 incet. Operationally, a mobility step size, , and a step time, , are fixed. The lag time for NPs exiting the DMA to reach the ICP-MS interface was determined to be approximately 15 s (see Fig. S-5 in the SI). Although recorded continuously by ICP-MS with respect to , this transit time of 15 s has to be subtracted from 31 s yielding 16 s for actual data analysis for an individual step, as indicated by the dashed zone in Fig. 2 incet. With a spICP-MS dwell time of 10 ms, about 1600 measurements can be performed at each selected mobility size using the current experimental setup. Therefore for the singly charged state is correlated with DMA scanning time (i.e., spICP-MS recording time) by Eq. 4:
| (4) |
where is the spherical equivalent mobility diameter of NPs selected by the DMA at , is the initial stepped diameter at . The bracket in Eq. 4 represents the greatest integer function such that the DMA selects particle size in a step-wise mode (the greatest integer function rounds to the nearest smaller whole number). For a nonspherical particle (e.g., clusters of NPs), is the equivalent spherical mobility diameter with the same drag force as the measured particle.
Figure 2.
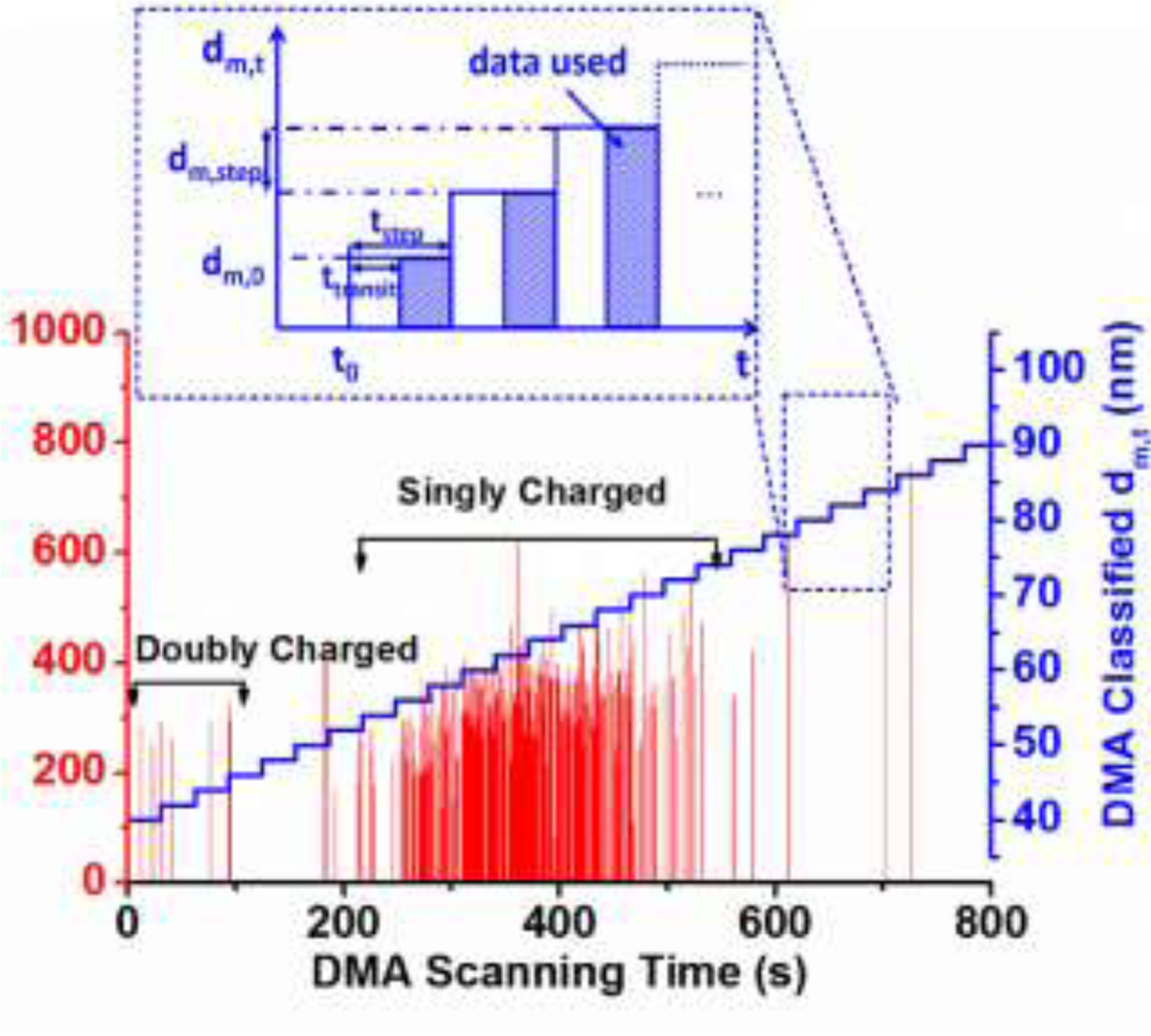
spICP-MS intensity spectrum as a function of DMA scanning time for 60 nm AuNPs. Single particle events are presented as red spikes. The selected by the DMA with respect to time is represented by the stepped blue line following Eq. 4 (, , and ). Two major populations representing singly and doubly charged 60 nm AuNPs are highlighted by the black brackets. Inset shows operational features of DMA-spICP-MS relevant to data acquisition (Eq. 4).
3. RESULTS AND DISCUSSION
3.1. The ES-DMA-spICP-MS spectrum
A typical time-resolved intensity (197Au) spectrum for nominal 60 nm AuNPs obtained by DMA-spICP-MS is presented in Fig. 2 (raw data before removing background). The detection by spICP-MS yields element-specific intensity spikes, each representing a single particle event generating an ion plume in the plasma. Thus each spike should be directly relatable to the mass of a specific element in one particle. In our case, since the particles comprise single component Au, the spike represents the total mass of the metallic core (excluding citrate capping agent). Unlike raw intensity spectra obtained in stand-alone spICP-MS, time on the x-axis is the DMA scanning time, which corresponds to the selected mobility size for singly charged particles (step-mode following Eq. 4: blue line in Fig. 2). Therefore, a correlated size and mass measurement is achieved by the coupling of DMA to spICP-MS. Closer examination of the spectrum shows that the majority of event spikes are narrowly distributed between 200 s and 600 s, which corresponds to a mobility size ranging from 50 nm to 75 nm (i.e., the singly charged nominal 60 nm AuNP population). The doubly charged states of this population have a greater mobility, corresponding to a theoretical mobility diameter from 35 nm to 52 nm. Hence the small number of single particle events below 100 s is attributed to doubly charged particles. As expected, the nominal intensity of the single particle events are of similar magnitude, with average of 280 counts, regardless of the charged state of the particle.
Overall, there are three independent types of information that can be extracted from the spectrum: particle mobility size determined by DMA, intensity of each event spike and frequency of spikes. In the following section, we establish two calibration curves that correlate (1) the intensity to the NP mass, and (2) the frequency of spikes to the NP number concentration. The two calibration curves combined with the known DMA classified size can be used for simultaneous determination of NP mass, size and particle concentration for unknown samples.
3.2. Proof of concept studies
3.2.1. Measurement of number concentration
In order to explore the capacity of DMA-spICP-MS to measure NP concentration and its sensitivity range, we utilized 60 nm AuNPs, serially diluted to yield a final number concentration ranging from (3.1 × 106 to 7.9 × 107) mL−1 (mass concentration of 6 μg L−1 to 160 μg L−1). The number concentration was calculated based on the mass concentration (51.86 μg g−1) given on the RM certificate combined with an assumption of spherical shape with a Gaussian fit DMA measured diameter. Fig. 3(a) illustrates a linear relationship between the number of particles in the aerosol phase detected by spICP-MS and the concentration of NPs in solution (i.e., NspICP-MS and [NP] respectively in “Calculation of Number Concentration”, SI) with a R2 value of 0.99999, indicating a high degree of linearity. This demonstrates the capacity of DMA-spICP-MS to quantitatively measure NP concentration in solution for unknown samples with appropriate calibration. For our ES-DMA-spICP-MS system and acquisition parameters we find that the upper range of concentration for which single particle events are statistically meaningful without significant (< 5 %) particle coincidence is ≈ 108 mL−1. A LOD of 3.7 x 105 NPs mL−1 was determined under our experimental conditions from the calibration curve: Y(NspICP-MS) =2.6×10−5X ([AuNP 60nm]) + 46.4 (LOD=3.3σ/S, where σ = standard deviation of y-intercept from regression line, S = slope of the calibration curve).26 This leads to a mass LOD of 0.8 μg L−1 for 60 nm AuNPs. In comparison, the LOD for stand-alone spICP-MS was reported to be 102 NPs mL−1 in theory 27 and 103 NPs mL−1 in practice. 28 Around 3 orders higher in LOD for hyphenation of ES-DMA-spICP-MS relative to stand-alone spICP-MS is primarily due to lower liquid from ES (≈400nL min−1, in comparison to ≈500mL min−1 for stand-alone spICP-MS). The slope of the calibration curve represents the transport efficiency, which takes into account particle loss channels associated within ES, DMA and ICP-MS (including GED). (see in “Calculation of Number Concentration”, SI). We evaluated and concluded that the total particle transport efficiency is 12 % (i.e. 88% total particle loss) with the majority loss associated with front-end ES-DMA (accounted for 94% of the total particle loss).
Figure 3.
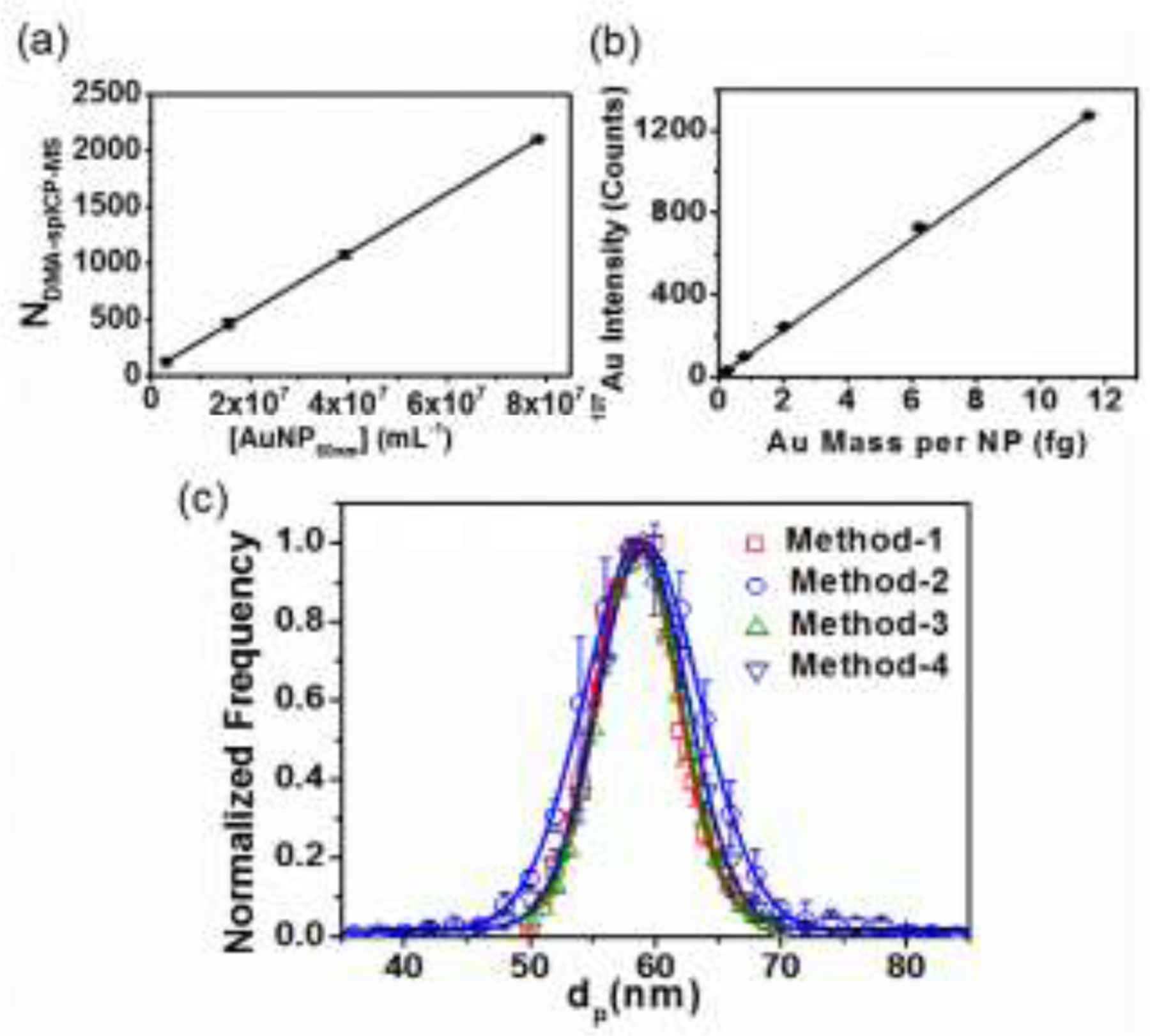
(a) Number concentration calibration curve (60 nm AuNP). (b) Mass calibration curve based on AuNPs of various sizes (30 nm, 60 nm, and 40 nm, 80 nm and 100 nm AuNPs). Au mass per NP was calculated based on DMA mobility equivalent spherical size. (c) Comparison of PSD for 60 nm AuNPs measured by DMA-spICP-MS and other conventional methods: Method-1: by summation of particle spikes over each DMA step by DMA-spICP-MS; Method-2: by single particle event intensity from DMA-spICP-MS; Method-3: by conventional DMA-CPC; Method-4: by single particle event intensity from conventional stand-alone spICP-MS. Lines represent Gaussian fits applied to each set of data. Error bars, if not visually apparent, are smaller than the symbols and are based on one standard deviation from at least two replicate runs.
3.2.2. Measurement of Nanoparticle Mass
In order to demonstrate the capability for accurate mass measurement, NPs of different nominal diameters: 30 nm, 40 nm, 60 nm, 80 nm and 100 nm were utilized. The mass of each NP was calculated by assuming that AuNPs have a density equal to bulk gold (19.3 g cm−3) and are spherical in shape. The geometric diameter (equivalent to mobility diameter for spheres) was obtained by a Gaussian peak fit to the particle size distribution measured by DMA-CPC (see Table S-1 in SI). The reader should keep in mind that because the DMA resolution is much higher than the width of the size distribution for these nominally monodisperse AuNPs, the DMA must be scanned / stepped over the entire size distribution to obtain a full representation of the population by event spikes. AuNPs of different sizes were measured and the averaged intensities of each size were used to construct a mass calibration curve versus the mass of a NP calculated from the diameter.
Within the size range studied, a linear relationship is demonstrated between the averaged 197Au intensity, and the Au mass per AuNP as shown in Fig. 3(b): Y (197Au Intensity) = 110.5X (Au mass per NP) + 3.3; R2= 0.99995 This mass calibration curve demonstrates the capacity for the determination of metal mass of unknown NPs from detected spike intensity of an appropriate element. From the calibration curve, a LOD of 0.1 fg (4×1035 Au atoms) is obtained, which converts to a AuNP size of about 23 nm. This detection limit (dependent on sensitivity to noise of the ICP-MS instrument) is comparable to the smallest detectable size of 15 nm for AuNPs reported by Hu et al.29 and the theoretical calculated size of 13 nm obtained by Lee et al..30
3.2.3. Measurement of particle size distributions
Next we compare the particle size distribution (PSD) of 60 nm AuNPs obtained by DMA-spICP-MS with that obtained from the standard ES-DMA-CPC method. The latter technique was applied as one of the primary tools for development of traceable NIST AuNP reference materials.31 The CPC detects particles by light scattering from droplets that nucleate and grow on the particles themselves and the LOD for ES-DMA-CPC is reported to be >109 NPs mL−1.32
Using the raw data obtained by DMA-spICP-MS (Fig. 2), the spikes representing particle events were first resolved from the background based on a 5σ criteria as discussed previously. Then two different methods were applied to obtain particle size distributions. In one approach, where the ICP-MS was used exclusively as a particle counter, the number of particle spikes occurring over the step time of a mobility size were summed, and this process was repeated for each size step to yield a number-based PSD as shown in Fig. 3(c) (designated as “Method-1”). In the second method, the intensities of all particle spikes were converted to mass using the mass calibration curve (Fig. 3(b)). Based on spherical geometry and the density of Au, the mass was converted to size and the distribution was obtained and designated as “Method-2”, in Fig. 3(c). The PSDs obtained from DMA-spICP-MS, either by counting NP frequency at a specific size, or by converting NP mass to diameter, are internally consistent and consistent with the PSD obtained by the traditional ES-DMA-CPC (“Method-3”, in Fig. 3(c)). This clearly demonstrates that for a near monodisperse PSD of the NPs type examined here, the mass resolution and counting ability of the DMA-spICP-MS yields accurate size distributions.
The FWHM (Full Width at Half Maximum) was calculated for the Gaussian fits. The FWHM (7.7) for the PSD obtained by counting single particle event spikes (Method-1) was essentially equivalent to that (7.8) obtained by DMA-CPC (Method-3). This is reasonable, since in the case of single particle event counting, the size binning is determined by the DMA; in this case the spICP-MS is utilized as an ultra-sensitive particle counter, and thus functionally similar to a CPC. The PSD obtained based on DMA-spICP-MS particle intensity (Method-2) has a slightly wider breadth (FWHM=10.8) in comparison to the other two methods (Method-1 and Method-3). The FWHM in PSD obtained from the single particle intensity by conventional stand-alone spICP-MS (Method-4) is 8.6, which is intermediate between the DMA-size based (Method-1 and Method-3) and Method-2.
Results indicate that the nature of determining size (either by DMA or by conversion from spICP-MS particle intensity) has an influence in the resulting width of the PSD. For the case examined here, DMA yields a narrower PSD in comparison to a single particle intensity based method (i.e., better resolution). The reason for the difference in FWHM, comparing Method-2 to Method-4, is not clear at this point. One likely attribution is the different operating condition in ICP-MS, which influences single particle intensity for each event (e.g., gas introduction for DMA-spICP-MS in comparison to liquid introduction for conventional stand-alone spICP-MS). Considering the error bars (precision) from the PSD, the PSDs with the exception of Method-2 are essentially indistinguishable. The upper size limit for our study is around 150 nm, which is primarily limited by the breakdown voltage of argon used as sheath flow in the DMA. An improvement in efficiency for the GED would permit the use of air (with higher breakdown voltage) as the sheath flow, and thereby expand the applicability to sizes of several hundred nm.
3.3. Resolving mixed populations
In order to evaluate the robustness of DMA-spICP-MS, we turn to a problem of more practical relevance, that of particle mixtures, using a 5-component AuNP sample with sizes ranging from 30 nm to 100 nm. For these experiments the number concentration of NPs of various sizes were adjusted to a nominally equivalent basis, based on independent spICP-MS measurements. Fig. 4(a) is a 3-D contour map and heat map showing simultaneously the measurement of NP mobility size, NP mass (intensity per NP) and NP concentration (frequency of NPs). Populations of AuNPs of different sizes are clearly distinguishable from each other, demonstrating the superb resolution obtained by coupling DMA with spICP-MS.
Figure 4.
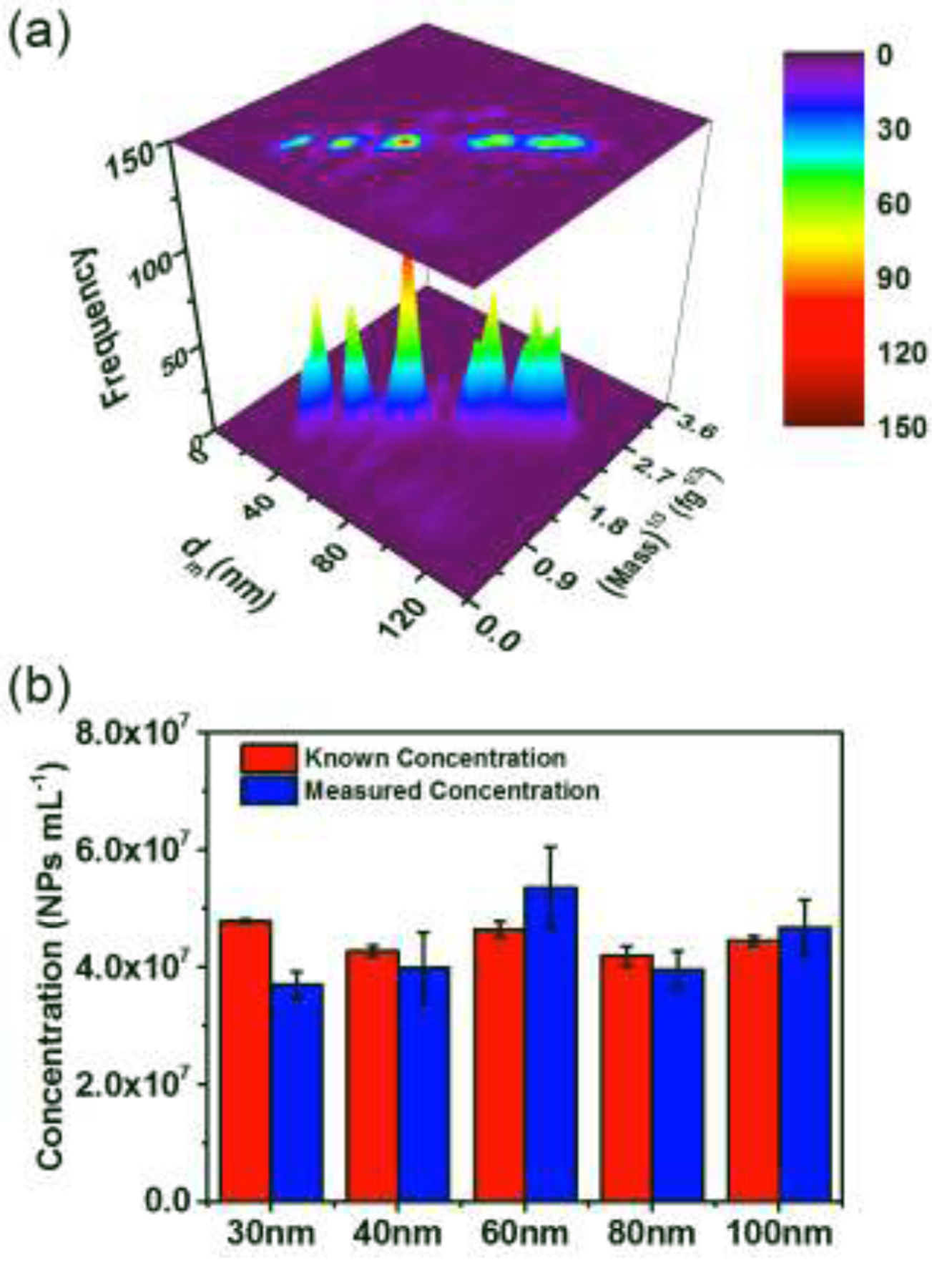
(a) Plot of size, mass1/3 and concentration (frequency of NPs) for mixtures containing five sizes of AuNPs as obtained by ES-DMA-spICP-MS. (b) Comparison between measured and known NP concentration initially mixed for five different sizes. Error bars represent one standard deviation for three replicate measurements. The known concentration initially mixed was based on independent relative number concentration measurement for all five different sizes by stand-alone spICP-MS and normalized to known 60 nm AuNPs concentration from certificate.
For spheres one would predict a linear relationship between mobility diameter and 1/3 power of 197Au intensity (mass1/3). This is clearly apparent in the heat map of Fig. 4(a), as the five NP populations lie on a diagonal. The off-diagonal populations, which are obviously fewer in number, located above the diagonal correspond to doubly charged NPs, while the populations below the diagonal are indications of split particle events.
This pattern if obtained for an unknown sample should also indicate that the particles in the mixture are largely spherical and in an unaggregated state (as will be shown in section 3.4–3.5). Furthermore, the diagonal also implies that there is no significant coating on the particle, because otherwise, the coating would bias particles of the same 197Au mass toward a larger mobility size and would appear below the diagonal line. Therefore, independent and simultaneous quantification of both size and mass provides rich information regarding the NP state (e.g., shape, state of aggregation, and coating information), which is not possible using stand-alone spICP-MS. Utilizing 60 nm AuNPs for single-point calibration of concentration, the measured particle number concentration for all five populations are consistent with the known concentration initially in the mixture (Fig. 4(b)). This implies high fidelity of the system in measuring number concentration, size, and mass simultaneously as well as providing NP states information.
3.4. Analysis of discrete aggregates
Here, we examine a fundamental issue frequently encountered in colloidal systems, that of particle aggregation and the ability to quantify both the process and the products. In Fig. 5, we present results clearly demonstrating the capacity of DMA-spICP-MS to differentiate discrete aggregates, and track aggregation temporally, in this case over a 9 d period. As singlet primary 40 nm AuNPs aggregate, the mass for -mers (discrete aggregates composed of primary particles) increases linearly with ; similarly, for DMA the mobility size will increase, but will follow a non-linear function of (i.e., independent confirmation of aggregate number is required).
Figure 5.
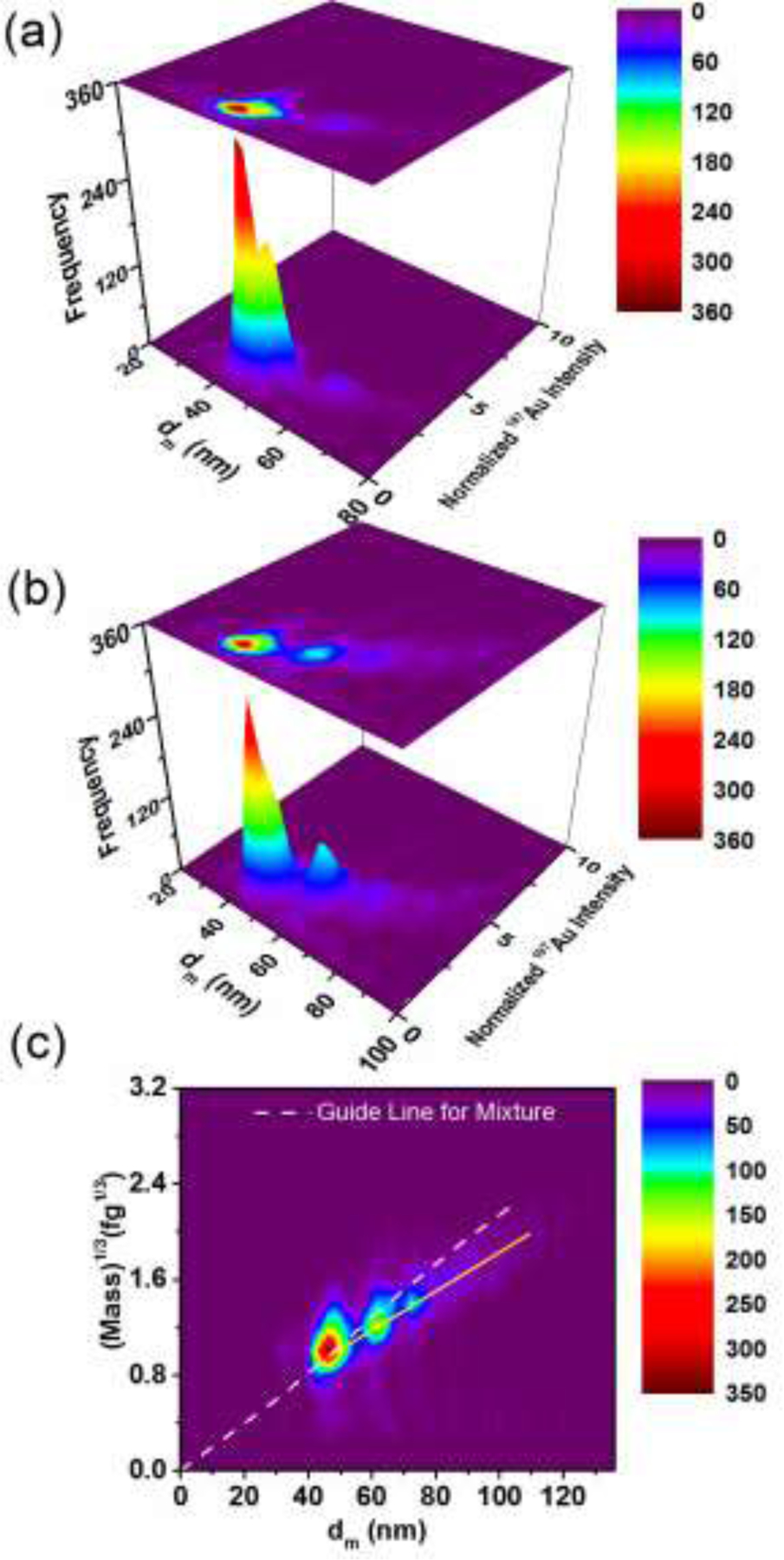
Heat map showing aggregation of 40 nm AuNPs occurring over 9 d ((a). day 1 and (b). day 9); 197Au intensity was normalized to that of the first monomer peak. (c) Comparison of discrete aggregates with the expected results for a mixture of solid spheres.
Distinguishable populations of NP oligomers are presented as islands (heat map) associated with the peaks in Fig. 5. For day 1 after initiation of aggregation, two populations are clearly resolved and distinguished from each other (Fig. 5(a)). As the aggregation process propagates, aggregates with larger size and mass appear, forming a continuum of discrete aggregation states in solution. In Fig. 5(b), three peaks are clearly resolved on day 9 of aggregation, while two additional low height peaks appear at larger sizes forming a tail (see Fig. S-6 in the SI). The first (smallest size) peak (in bin 44 nm to 46 nm) with maximum height is identified as the monomer 40 nm AuNPs (, see Table S-1 in the SI). In order to assign the remaining peaks, each spike intensity contributing to the peak was normalized to the intensity of 40 nm monomers, resulting in normalized intensities of 1, 2, 3, 4 and 5. In other words, the normalized intensities correspond to monomers, dimers, trimers, tetramers and pentamers of the aggregating AuNPs, since intensity (correlating to particle mass) linearly increases with the number of primary NPs associated with a given aggregate. In these studies the samples were first diluted to appropriate concentration to avoid particle coincidence. However, as aggregation proceeds number concentration decreases, and thus by day 9, the dilution employed was 8x lower than day 1 so as to obtain similar spICP-MS spike frequency. This difference in dilution factor would need to be accounted for if the objective were quantitative kinetic information.
A more challenging test of DMA-spICP-MS is to explore its suitability to differentiate NP aggregates from mixtures of solid spherical NPs that vary in size. This is a substantial challenge for either stand-alone spICP-MS or DMA. However, due to the fact that DMA-spICP-MS offers an independent measurement of both mass and size (i.e., density), the approach offers a unique capability to differentiate NP states. As mentioned previously, the mixture of spherical NPs lies diagonally on a graph of (197Au) 1/3 versus . In contrast, the aggregated sample clearly exhibits a deviation from the diagonal (indicated by the dashed white line in Fig. 5(c)). More specifically, the peak trail in the heat map for the aggregated sample lies below the diagonal for mixtures of spheres, indicating that for particles with the same mass as spheres, a larger is observed. This is due to the fact that the non-spherical and less compact structure of aggregates presents a larger drag force relative to a sphere of equivalent mass.
These results show that the hyphenation of DMA with spICP-MS can be used to track aggregation temporally, resolve aggregate distributions and distinguish solid spheres from aggregates. The following section will demonstrate quantitative differentiation of aggregates and spheres by defining an apparent density parameter.
3.5. Apparent Density for Aggregates
One can also apply a more quantitative approach by defining a “mobility-based apparent density” to characterize the state of aggregation:
| (5) |
where represents the mass of NP aggregates measured by spICP-MS intensity for each particle event calibrated using spherical 60 nm AuNPs. is the measured mobility diameter as previously defined, and the function represents the volume of a sphere that has the same mobility as the aggregate. Eq. 5 represents an apparent density for the measured particle. Thus for a particle with an apparent density less than the theoretical solid bulk density, we conclude that this particle must be an aggregate. Fig. 6(a) shows apparent density for a mixture of different size spherical solid AuNPs. Five distinct populations are clearly resolved with similar apparent density centered just below 20 g cm−3, which is close to the expected density based on the known bulk density of Au (19.3 g cm−3). By contrast, Fig. 6(b) shows a decreasing apparent density with respect to size for aggregates of primary 40 nm AuNPs. As aggregates form, the apparent density decreases from just less than 20 g cm−3 for spherical monomers to approximately 12.5 g cm−3 for discrete aggregate states. The decreasing apparent density results from the formation of less compact NP aggregates. A decreasing relative density for agglomerates has been observed using hyphenation of HDC with spICP-MS.14 However that work presents the results as an average over the whole distribution, while in this work we are able to both identify aggregates, and assign an apparent density to each oligomer state. In this way ES-DMA-spICP-MS offers the opportunity to quantitatively assess the state of aggregation and the aggregation number of discrete populations. Besides, the apparent density would also be useful in getting some complimentary information about unknown particles, such as porosity or coating, and even be able to distinguish these two with other complimentary techniques.
Figure 6.
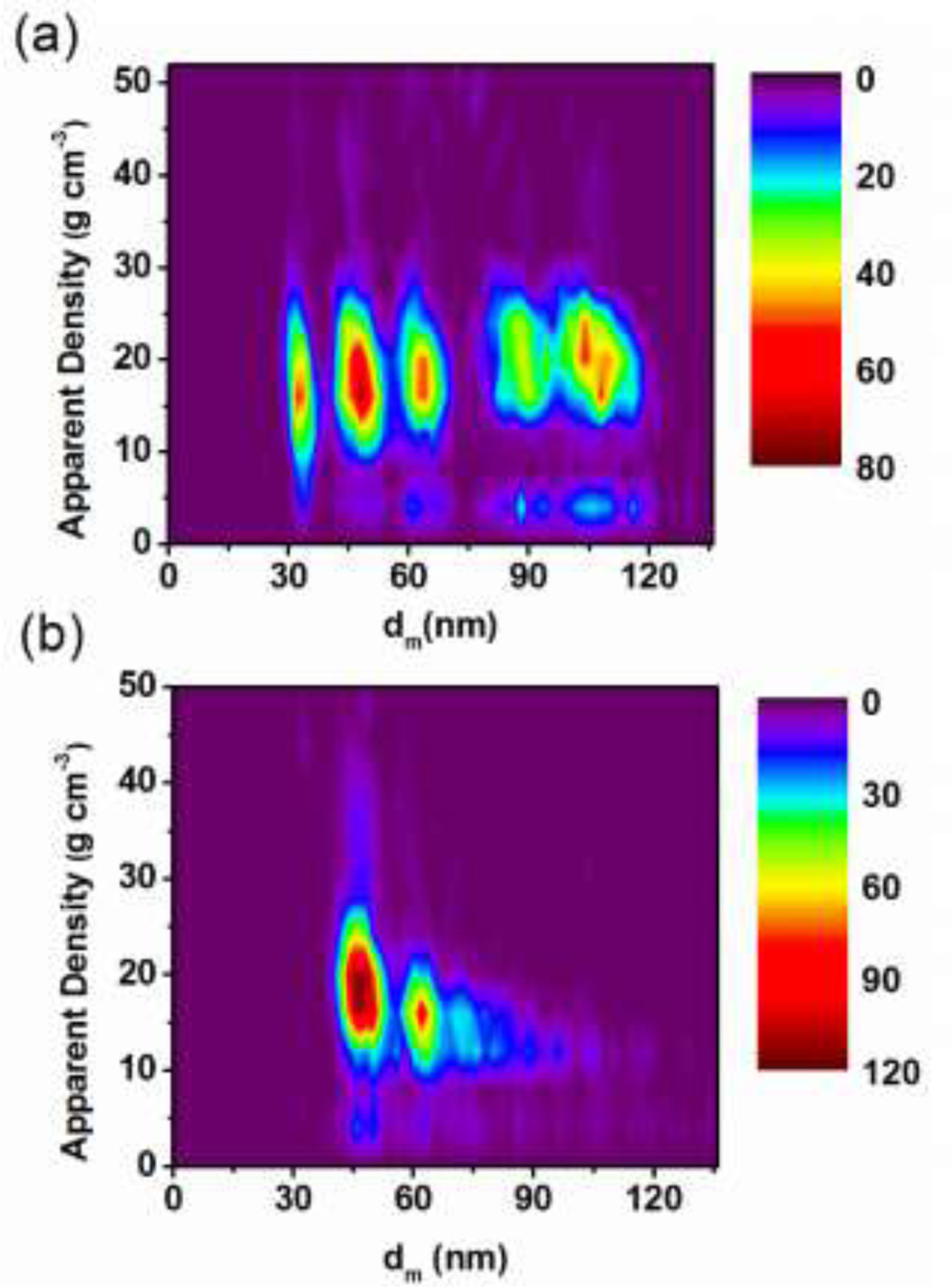
Heat maps for mobility-based apparent density: (a) NP mixtures containing 30 nm, 40 nm, 60 nm, 80 nm and 100 nm AuNPs. (b) Aggregates consisting of 40 nm primary AuNPs. The map indicates a small population with apparent density of 40 g cm−3, which we attribute to particle coincidence and that around 4 g cm−3are due to particle splitting.
4. CONCLUSIONS
The capacity of ES-DMA-spICP-MS for simultaneous determination of NP size, mass and concentration, and the analysis of complex mixtures and aggregated samples was demonstrated using AuNPs. The high size resolution and tunability associated with DMA, combined with the low LOD, single particle detection and elemental specificity of spICP-MS permits not only resolution of different NP populations, but also enables the detection of different aggregate states (oligomers) with a defined apparent density at environmentally relevant concentrations. Meanwhile the operational flexibility of ES-DMA allows for selection of a specific particle size and step time, both simplifying and expanding the capabilities of stand-alone spICP-MS as it has been implemented to-date. The concurrent improvements in the spICP-MS technique (both data processing and hardware capabilities), leading to increased sensitivity and faster acquisition, is pushing the lower size limit downward and improving the overall statistical quality of data. Overall the coupling of mobility analysis with spICP-MS offers what we believe to be a substantial and novel advancement in the characterization of NP populations.
Supplementary Material
ACKNOWLEDGEMENTS
The authors would like to thank De-Hao Tsai (National Tsing Hua University) and John M. Pettibone (NIST) for their thorough reviews and comments on the manuscript, and Karen E. Murphy (NIST) for helpful discussions. Funding for this research was in part provided by the nanoEHS initiative at NIST, coordinated by Dr. Debra Kaiser, Materials Measurement Laboratory.
Footnotes
ASSOCIATED CONTENT
Supporting Information
Additional information as noted in the text. This material is available free of charge via the Internet at http://pubs.acs.org.
The authors declare no competing financial interest.
The identification of any commercial product or trade name does not imply endorsement or recommendation by the National Institute of Standards and Technology.
REFERENCES
- (1).Contado C Nanomaterials in consumer products: a challenging analytical problem. Frontiers in chemistry 2015, 3, 48. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (2).Duncan TV Applications of nanotechnology in food packaging and food safety: barrier materials, antimicrobials and sensors. Journal of colloid and interface science 2011, 363, 1–24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (3).Vance ME; Kuiken T; Vejerano EP; McGinnis SP; Hochella MF; Rejeski D; Hull MS Nanotechnology in the real world: Redeveloping the nanomaterial consumer products inventory. Beilstein journal of nanotechnology 2015, 6, 1769–1780. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (4).de Dios AS; Diaz-Garcia ME Multifunctional nanoparticles: Analytical prospects. Anal Chim Acta 2010, 666, 1–22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (5).Levard C; Hotze EM; Lowry GV; Brown GE Environmental Transformations of Silver Nanoparticles: Impact on Stability and Toxicity. Environ Sci Technol 2012, 46, 6900–6914. [DOI] [PubMed] [Google Scholar]
- (6).Reidy B; Haase A; Luch A; Dawson KA; Lynch I Mechanisms of Silver Nanoparticle Release, Transformation and Toxicity: A Critical Review of Current Knowledge and Recommendations for Future Studies and Applications. Materials 2013, 6, 2295–2350. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (7).Lowry GV; Gregory KB; Apte SC; Lead JR Transformations of Nanomaterials in the Environment. Environ Sci Technol 2012, 46, 6893–6899. [DOI] [PubMed] [Google Scholar]
- (8).Maurer-Jones MA; Gunsolus IL; Murphy CJ; Haynes CL Toxicity of Engineered Nanoparticles in the Environment. Anal Chem 2013, 85, 3036–3049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (9).Tuoriniemi J; Cornelis G; Hassellov M Size Discrimination and Detection Capabilities of Single-Particle ICPMS for Environmental Analysis of Silver Nanoparticles. Anal Chem 2012, 84, 3965–3972. [DOI] [PubMed] [Google Scholar]
- (10).Pace HE; Rogers NJ; Jarolimek C; Coleman VA; Gray EP; Higgins CP; Ranville JF Single particle inductively coupled plasma-mass spectrometry: a performance evaluation and method comparison in the determination of nanoparticle size. Environ Sci Technol 2012, 46, 12272–12280. [DOI] [PubMed] [Google Scholar]
- (11).Pace HE; Rogers NJ; Jarolimek C; Coleman VA; Higgins CP; Ranville JF Determining transport efficiency for the purpose of counting and sizing nanoparticles via single particle inductively coupled plasma mass spectrometry. Anal Chem 2011, 83, 9361–9369. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (12).Mitrano DM; Lesher EK; Bednar A; Monserud J; Higgins CP; Ranville JF Detecting nanoparticulate silver using single-particle inductively coupled plasma-mass spectrometry. Environ Toxicol Chem 2012, 31, 115–121. [DOI] [PubMed] [Google Scholar]
- (13).Pergantis SA; Jones-Lepp TL; Heithmar EM Hydrodynamic chromatography online with single particle-inductively coupled plasma mass spectrometry for ultratrace detection of metal-containing nanoparticles. Anal Chem 2012, 84, 6454–6462. [DOI] [PubMed] [Google Scholar]
- (14).Rakcheev D; Philippe A; Schaumann GE Hydrodynamic Chromatography Coupled with Single Particle-Inductively Coupled Plasma Mass Spectrometry for Investigating Nanoparticles Agglomerates. Anal Chem 2013, 85, 10643–10647. [DOI] [PubMed] [Google Scholar]
- (15).Gray EP; Bruton TA; Higgins CP; Halden RU; Westerhoff P; Ranville JF Analysis of gold nanoparticle mixtures: a comparison of hydrodynamic chromatography (HDC) and asymmetrical flow field-flow fractionation (AF4) coupled to ICP-MS. J Anal Atom Spectrom 2012, 27, 1532–1539. [Google Scholar]
- (16).Loeschner K; Navratilova J; Kobler C; Molhave K; Wagner S; von der Kammer F; Larsen EH Detection and characterization of silver nanoparticles in chicken meat by asymmetric flow field flow fractionation with detection by conventional or single particle ICP-MS. Anal Bioanal Chem 2013, 405, 8185–8195. [DOI] [PubMed] [Google Scholar]
- (17).Guha S; Li M; Tarlov MJ; Zachariah MR Electrospray-differential mobility analysis of bionanoparticles. Trends Biotechnol 2012, 30, 291–300. [DOI] [PubMed] [Google Scholar]
- (18).Tsai DH; Pease LF; Zangmeister RA; Tarlov MJ; Zachariah MR Aggregation Kinetics of Colloidal Particles Measured by Gas-Phase Differential Mobility Analysis. Langmuir 2009, 25, 140–146. [DOI] [PubMed] [Google Scholar]
- (19).Tsai DH; DelRio FW; MacCuspie RI; Cho TJ; Zachariah MR; Hackley VA Competitive Adsorption of Thiolated Polyethylene Glycol and Mercaptopropionic Acid on Gold Nanoparticles Measured by Physical Characterization Methods. Langmuir 2010, 26, 10325–10333. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (20).Li MD; You R; Mulholland GW; Zachariah MR Development of a Pulsed-Field Differential Mobility Analyzer: A Method for Measuring Shape Parameters for Nonspherical Particles. Aerosol Sci Tech 2014, 48, 22–30. [Google Scholar]
- (21).Okada Y; Yabumoto J; Takeuchi K Aerosol spectrometer for size and composition analysis of nanoparticles. J Aerosol Sci 2002, 33, 961–965. [Google Scholar]
- (22).Elzey S; Tsai DH; Yu LL; Winchester MR; Kelley ME; Hackley VA Real-time size discrimination and elemental analysis of gold nanoparticles using ES-DMA coupled to ICP-MS. Anal Bioanal Chem 2013, 405, 2279–2288. [DOI] [PubMed] [Google Scholar]
- (23).Tsai DH; Cho TJ; Elzey SR; Gigault JC; Hackley VA Quantitative analysis of dendron-conjugated cisplatin-complexed gold nanoparticles using scanning particle mobility mass spectrometry. Nanoscale 2013, 5, 5390–5395. [DOI] [PubMed] [Google Scholar]
- (24).Allen MD; Raabe OG Slip Correction Measurements of Spherical Solid Aerosol-Particles in an Improved Millikan Apparatus. Aerosol Sci Tech 1985, 4, 269–286. [Google Scholar]
- (25).Flagan RC On differential mobility analyzer resolution. Aerosol Sci Tech 1999, 30, 556–570. [Google Scholar]
- (26).Group IEW: Validation of analytical procedures: text and methodology Q2(R1). In International Conference on Harmonisation of Technical requirements for Registration of Pharmaceuticals for Human use, 2005. [Google Scholar]
- (27).Laborda F; Jimenez-Lamana J; Bolea E; Castillo JR Critical considerations for the determination of nanoparticle number concentrations, size and number size distributions by single particle ICP-MS. J Anal Atom Spectrom 2013, 28, 1220–1232. [Google Scholar]
- (28).Mitrano DM; Barber A; Bednar A; Westerhoff P; Higgins CP; Ranville JF Silver nanoparticle characterization using single particle ICP-MS (SP-ICP-MS) and asymmetrical flow field flow fractionation ICP-MS (AF4-ICP-MS). J. Anal. At. Spectrom. 2012, 27, 1131–1142. [Google Scholar]
- (29).Hu SH; Liu R; Zhang SC; Huang Z; Xing Z; Zhang XR A New Strategy for Highly Sensitive Immunoassay Based on Single-Particle Mode Detection by Inductively Coupled Plasma Mass Spectrometry. J Am Soc Mass Spectr 2009, 20, 1096–1103. [DOI] [PubMed] [Google Scholar]
- (30).Lee S; Bi XY; Reed RB; Ranville JF; Herckes P; Westerhoff P Nanoparticle Size Detection Limits by Single Particle ICP-MS for 40 Elements. Environ Sci Technol 2014, 48, 10291–10300. [DOI] [PubMed] [Google Scholar]
- (31).Hackley V Gold Nanoparticles, Nominal 60 nm Diameter for NIST2015. [Google Scholar]
- (32).Guha S; Pease LF; Brorson KA; Tarlov MJ; Zachariah MR Evaluation of electrospray differential mobility analysis for virus particle analysis: Potential applications for biomanufacturing. J Virol Methods 2011, 178, 201–208. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


