Identification of spatial homogeneous regions in tissues with concordex

Abstract

Spatial homogeneous regions (SHRs) in tissues are domains that are homogeneous with respect to cell type composition. We present a method for identifying SHRs using spatial transcriptomics data, and demonstrate that it is efficient and effective at finding SHRs for a wide variety of tissue types. The method is implemented in a tool called concordex, which relies on analysis of k-nearest-neighbor (kNN) graphs. The concordex tool is also useful for analysis of non-spatial transcriptomics data, and can elucidate the extent of concordance between partitions of cells derived from clustering algorithms, and transcriptomic similarity as represented in kNN graphs.

Introduction

Spatially resolved transcriptomics (SRT) have enabled highly multiplexed molecular profiling of cells within a tissue, with current technologies presenting a range of tradeoffs in approach and resolution (1). Broadly, in-situ hybridization based methods, such as seqFISH (2, 3), seqFISH+ (4), and MERFISH (5), offer cellular or sub-cellular resolution for capture of hundreds to thousands of genes, while methods that rely on spatial barcoding and sequencing (e.g. Visium, Slide-Seq (6), Slide-SeqV2 (7)) offer near-cellular resolution and measure the expression of genes across the entire transcriptome.

A major goal of spatial trancriptomics data analysis is the partitioning of assayed tissues into regions that constitute domains of functional or compositional homogeneity. This task first relies on abstracting transcriptomic expression into notions of cell type, whereby cells of the same type have similar transcriptomic profiles, but can be morphologically or functionally distinct. The concept of a spatial region introduces another layer of abstraction and requires aggregation of cell types into domains with distinct cell type composition. The cells in these regions are characterized by their local cellular environments, and have neighborhoods with similar proportions of cell types, which can be a mixture of cell types or a single type. We therefore refer to regions with this property as spatial homogeneous regions (SHRs).

Several algorithms have been proposed for identifying spatial or tissue domains defined by coherent gene expression, yet in principle, these domains can consist of various cell types with different expression profiles (8–13). The result is that these methods implicitly identify SHRs. Broadly, these approaches rely on neural networks, hidden Markov random fields (HMRFs), or spatial smoothing to encode spatial dependence. For example, Giotto (11) and BayesSpace (13) infer domain assignment using an HMRF and rely on the expression of a cell or spot and its neighbors. BANKSY (8) uses spatial kernels to encode spatial dependence in the local and extended environment around a tissue. GASTON (12) relies on a neural network to represent gene expression and spatial information as a one-dimensional gradient. SpaGCN (10) and STAGATE (9) use graph convolutional neural networks to integrate gene expression with spatial and/or histology information. Although many of these methods consider local gene expression, their criteria for aggregating cells into a spatial domain remains ambiguous, and regions are often defined by the procedure used to generate them rather than the underlying interpretation of their relationship to the tissue architecture. In some cases, methods generate cell type labels rather than explicitly defining spatial regions, thus obfuscating the question of what it should mean to partition tissues into spatial regions. The question of how to best identify SHRs in spatially distinct regions of a tissue remains open.

In non-spatial transcriptomics data analysis, the k-nearest-neighbor (kNN) graph has become a widely used data structure for representing similarities between cells. kNN graphs are used in many clustering algorithms (14, 15) and for visualization (16). We show that the kNN graph representation of transcriptomics data is useful for answering questions about spatial homogeneity in SRT data and develop an approach using spatial kNN graphs to identify SHRs. The key to our approach is a method we develop for assessing the neighborhood composition of nodes in a kNN graph built from spatial or non-spatial attributes, which we implement in a tool called concordex. We show that concordex can efficiently and effectively identify SHRs in spatial transcriptomics data, and also that it is a useful tool for assessing concordance between partitions of cells derived from clustering and kNN graphs in non-spatial transcriptomics data. We demonstrate the utility of concordex in many contexts with both simulated and publicly available biological datasets that encompass a range of technologies.

Results

Neighborhood consolidation with concordex.

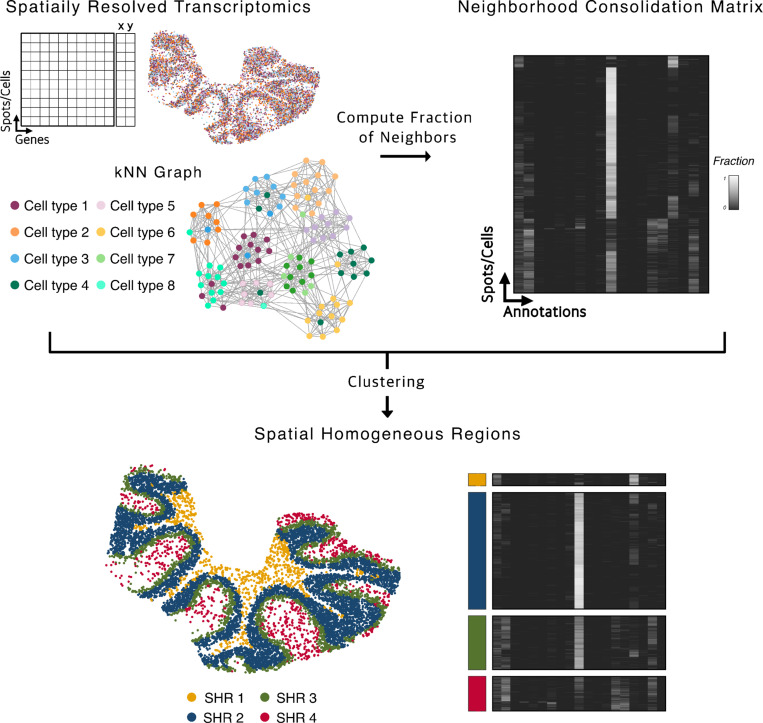
The concordex framework can be used to interrogate the neighborhood composition of the nodes of a kNN graph, $G=(V,E)$, where $V$ is a set of cells and $E$ is the set of edges in the graph. The edges of the graph are determined by some metric on $V$, usually by computation of transcriptomic or spatial distance, and the nodes are assigned predetermined discrete or continuous labels. When discrete labels are available, assessment with concordex proceeds first by computation of the neighborhood consolidation matrix $K$, with one row for each cell $i$ and one column for each label $j$ (Figure 1). The entries $K_{ij}$ can be interpreted as the fraction of neighbors of cell $i$ that are assigned label $j$.

Fig. 1.

The concordex workflow: A kNN graph is constructed from spatial coordinates and associated annotations. For each cell or spot, the entries in the neighborhood consolidation matrix represent the fraction of neighbors that have the label indicated on the column. SHRs are defined by clustering the neighborhood similarity matrix.

The neighborhood consolidation matrix provides a starting point for identification of SHRs and revealing within-region heterogeneity. When $K$ is built from a spatial adjacency graph, the rows describe the local neighborhood composition around a spatial location. Clustering the rows in $K$ assembles cells into SHRs, where cells within a region can be thought of as having similar neighborhood composition. In the non-spatial context, the matrix $K$ can reveal cells with non-homogeneous neighborhoods, thereby identifying sub-populations that can be important to follow-up on. Assessing cluster boundaries is straightforward and proceeds with computation of the $d\times d$ similarity matrix, $S$, by aggregating the rows of $K$. The similarity matrix is obtained by grouping cells with the same label and averaging the fractions down the columns of each sub-matrix. Qualitative assessment of the similarity matrix provide direct visualization of between-cluster relationships and within-cluster heterogeneity.

In the sections below, we apply concordex in spatial contexts to identify SHRs, and in non-spatial contexts to assess clustering results and validate data integration methods on simulated and real data. By default, we use k-means clustering to identify SHRs in the spatial context, but similar results can be obtained from graph-based clustering algorithms such as Leiden (14) or Louvain (15).

Prediction of periportal and pericentral regions in the mouse liver.

We evaluated the ability of concordex to partition a dataset into biologically meaningful SHRs. We used data from the Vizgen MERFISH mouse liver map which measured the expression of 347 genes in more than 300,000 cells across 1,791 fields of view (17). MERFISH profiles gene expression at subcellular resolution and relies on highly multiplexed in situ hybridization to target a limited set of genes. The cell type labels were obtained from a companion analysis published by Vizgen which emphasized organization of cells around the portal and central blood vessels (17). The intervening tissue is composed of regions of functional hepatocytes and immune related cells. We use concordex to identify these broad regions and compared the results to the known architecture of the tissue.

The periportal and pericentral blood vessel regions can be readily identified by concordex (Figure 2A). As in the Vizgen tutorial, these regions are composed mostly of hepatocytes and there is a stark imbalance between the hepatocyte clusters that localize to either region. We used the expression of the genes Aldh1b1 and Cyp1a2 to identify periportal and pericentral hepatocytes, respectively. The expression of these genes decreases with increasing distance from the blood vessel which is consistent with these genes marking the region nearest to the vessel. Figure 2B shows that the expression of these genes correlates strongly with SHR regions identified by concordex (Figure 2A). The periportal and pericentral regions are largely composed of hepatocyte clusters 0 and 6, similar to the results from the Vizgen analysis.

Fig. 2.

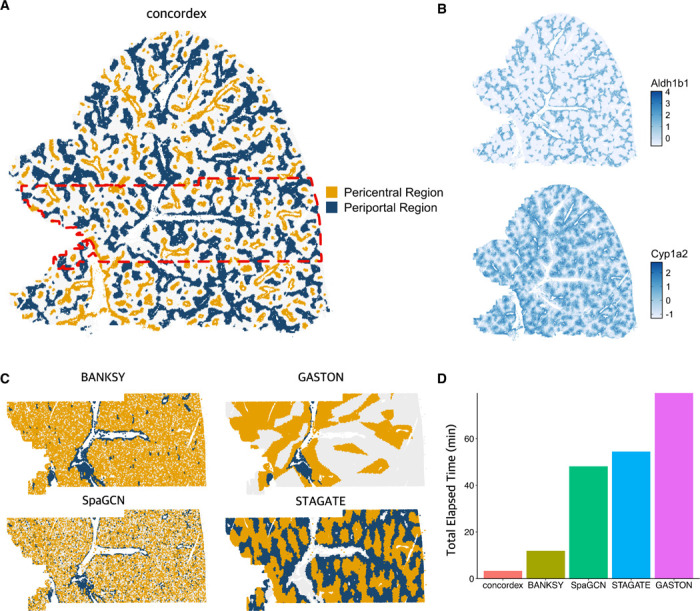
Evaluation of methods on mouse liver. A) Results of concordex displaying partioining of mouse liver into spatially homogeneous regions corresponding to pericentral and periportal regions. B) Expression of two marker genes for pericentral (Cyp1a2) and periportal (A1dh1b1) regions. C) Performance of Banksy, GASTON, SpaGCN, and STAGATE on a portion of the mouse liver (red rectangle in panel A. D) Runtime of methods on the mouse liver portion shown in panel C.

Given the size of the dataset and for ease of comparison to other tools, we focused on a limited number of fields of view around the central portal blood vessel. With the exception of GASTON, all methods can identify the periportal and pericentral regions around the vessels (Figure 2C). The results from GASTON do not seem to correspond to known organization of the tissue. Additionally, we found that other methods require significant time to complete on a machine with 260 GB RAM and using default parameter settings. In contrast, concordex is much faster, taking only a few minutes with the longest step typically being computation of the adjacency matrix (Figure 2D).

Architecture of the mouse cerebellum.

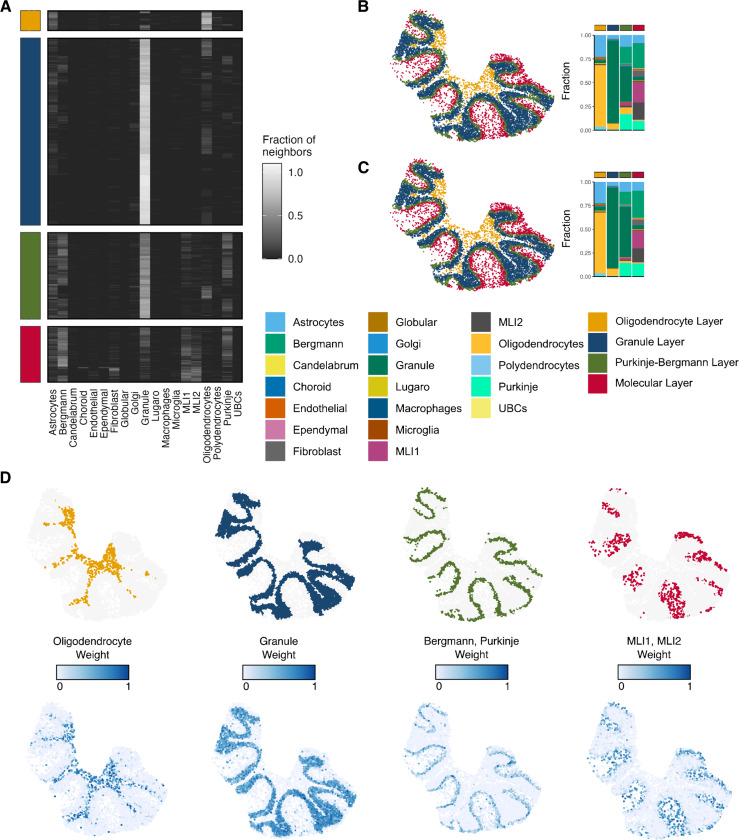
We next applied the method to mouse cerebellum data that was generated using Slide-Seq V2 (7). Though this method has near cellular resolution (10μm), spatial capture spots can contain information from more than one cell. We therefore used the cell type labels that were published with the original manuscript and determined by the spot deconvolution method RCTD (18). This tissue is known to contain well-defined domains (18) namely the molecular, Purkinje-Bergmann, Granule, and white matter layers. Since these regions also have distinct cell type composition, we reasoned that concordex should be able to detect the boundaries between each layer.

Inspection of the neighborhood consolidation matrix highlights that SHRs do not need to be dominated by a single cell type (Figure 3A). Qualitative assessment of the predicted SHRs show agreement with the expected morphology of the tissue and contain cell types in proportions similar to canonical expectations (Figure 3B). Notably, the performance of concordex is comparable to more complex methods that rely on neural networks (Supplementary Figure S1). In each SHR, we compared the prediction to the RCTD weights of the most dominant cell types in the region (Figure 3D). All regions predicted by concordex correspond strongly to the cell type localization, even in areas of low cell density.

Fig. 3.

Results of concordex on a slice of mouse cerebellum. A) A heatmap showing for each cell in each region, the fraction of neighbors of each cell types. B) Identification of spatial homogeneous regions with concordex based on cell type annotations. C) Identification of spatial homogeneous regions with concordex based on 50-dimensional PCA coordinates. D) Comparison of RCTD weights to distinct concordex spatial homogeneous regions.

The SHRs predicted by concordex share the most agreement with the regions predicted by GASTON (Supplementary Figure S1). Visual inspection of the regions predicted by STAGATE and SpaGCN visually resemble the expected arrangement in the cerebellum, but inspection of the cell type proportions in each region reveals a failure to resolve the canonical layers (Supplementary Figure S1). In particular, STAGATE does not distinguish between the molecular and Purkinje layers. This is most evident in the bar graphs showing the cell type composition of each layer where there is little difference between the composition predicted Purkinje and molecular cell layers.

To demonstrate that concordex can produce meaningful results when discrete labels are not available, we used the top 50 PC loadings to label each spot. We averaged the loadings of the neighbors of each cell to create the neighborhood consolidation matrix and used this as input to clustering algorithms as above. Using this labelling approach, each row of the matrix is a spot, each column is a PC, and the entries are the average loadings of the PCs across neighbors. The resulting SHRs are qualitatively similar to the results using discrete labels (Figure 3C) and most spots receive the same assignment with either labeling scheme.

Since concordex should only aggregate spots into a SHR if they share similar neighborhood composition, we tested whether concordex could detect manipulations to the cell type identity of a subset of spots. We chose a subset of spots in the molecular layer and randomly reassigned their cellular identity by swapping cell labels (Supplementary Figure S2). This created an artificial, heterogeneous region that was distinct from the organized layers in the remaining tissue (Supplementary Figure S2). We observed that concordex was able to distinguish the heterogeneous region from the remaining molecular layer and the organization of the unaltered tissue remained largely unchanged. Notably, this alteration significantly altered the regions predicted by GASTON (Supplementary Figure S2), resulting in an organization that did not correspond to the known tissue structure. Altogether, these results reveal that concordex is sensitive to varying cell type composition and can reliably distinguish regional differences in a tissue.

Identification of Spatially Homogeneous Regions in Simulated Data Using concordex.

To better understand the utility of our approach, we simulated control datasets in various patterns. First, we designed a synthetic dataset containing two cell types and distributed the cells on a checkerboard grid in different proportions (Figure 4A, Methods). This scenario is useful because it allows analysis of whether a method can detect regions of varying cell type composition, even when a cell type is present throughout the entire spatial field of view. We assessed whether region prediction methods BANKSY (8), Giotto (11), and neural network (NN)-based methods SpaGCN (10), STAGATE (9), and GASTON (12) could perform the same region segmentation task. Ideally, methods should detect the checkerboard as a macropattern rather than the exact positions of the individual cell types.

Fig. 4.

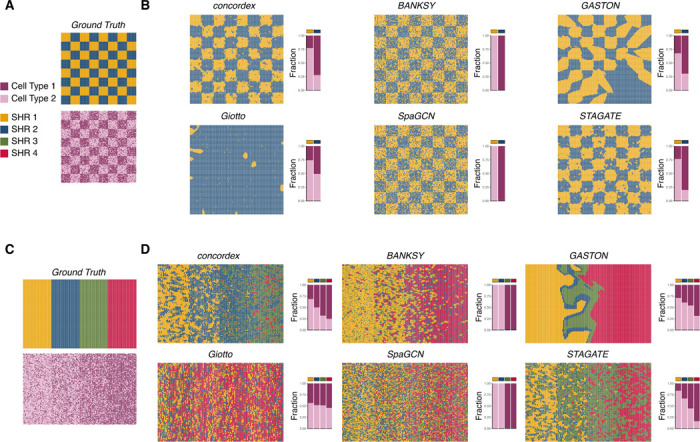
Evaluation of methods on synthetic datasets. A) A control experiment in which a chessboard pattern consists of two regions, each comprising two cell types, one with 80% of one cell type, and 20% of another, and the other region with a 20% / 80% mix. B) Performance of concordex and five other methods on the control experiment from panel A. C) A control experiment consisting of a gradient of regions, each with two cell types, and with increasing proportion of one cell type across the gradient. D) Performance of concordex and five other methods on the control experiment from panel C.

We find that concordex is able to effectively represent the distinct checkerboard squares (Figure 4B), and moreover, each detected region contains the expected proportion of the simulated cell types. The concordex predictions were most similar to STAGATE, with both methods producing recognizable checkerboards and correctly assigning grid points with high accuracy. Conversely, other methods failed to perform this task in notable ways. Two methods, BANKSY and SpaGCN, reproduced the cell type assignment rather than aggregating the points into regions even when using parameters that should prefer region identification over cell type identification. On the other hand, Giotto and GASTON do not produce a recognizable checkerboard (Figure 4B). This result highlights that concordex specifically aggregates locations with similar neighborhood composition and also does not require similar regions to be spatially contiguous.

We also arranged the simulated cell types in sequential layers and used concordex to predict the layers (Figure 4C). This simulation produced results consistent with the checkerboard simulation. The predicted SHRs from concordex reveal a continuous gradient along the field of view (Figure 4D). Again, BANKSY and SpaGCN failed to identify distinct regions. Both methods identify cell types, but do not imply boundaries between regions (Figure 4D). Predicted regions from GASTON and Giotto neither reveal the cell type distribution nor the layer pattern in the simulated data (Figure 4D). Importantly, concordex captures the expected organization of the simulated tissue across an array of gene expression patterns and relies on compositional changes, not expression, to determine regional boundaries.

Using concordex to Evaluate Cell type Clustering and Integration Effects.

We also evaluated the ability of concordex to assess the fidelity of cell type clustering and dataset integration on data generated from in-utero and ex-utero mouse embryos at the E10.5 developmental stage (19). We evaluated the data in the 15-dimensional PCA space and 2-dimensional UMAP embedding by computing the neighborhood consolidation and similarity matrices using cell type or growth condition as the label.

Using cell type labels, we found that the concordex similarity matrix can readily visualize distinct clusters in both the PCA and UMAP embeddings. In the log-normalized PCA data, concordex suggests an relationship between some cell type clusters (Supplementary Figure 3A). For example, the neighborhoods of cells in cluster 0 are composed of cells from clusters 5, 7, 10, and 13. We observed that simply changing the random state improves the qualitative appearance of the cluster separation in the UMAP embedding, reflecting the arbitrary nature of otherwise equivalent embeddings. While tuning the hyperparameters can alter how well the UMAP embedding preserves the structure of the PCA space, concordex directly visualizes the cluster relationships in the PCA-embedded data and reduces the need to embed the data in fewer dimensions.

Consistent with (20), we observed that the UMAP embedding can be a poor representation of the kNN graph in general. For example, inspection of the clusters in the scaled-stabilized data UMAP embedding indicates a close relationship between several clusters even though this structure is not apparent in the kNN graph generated from the PCA-embedded data (Supplementary Figure 3B). The neighborhood consolidation matrix allows for the assessment of the degree to which clusters overlap; e.g., it can show which cluster has the greatest number of cells where more than half of their neighbors have a different label. We found that the number of cells with mixed neighborhoods is often greater in the UMAP embedding (Supplementary Figure 4), showing that clusters are more mixed in the UMAP embedding than they are in the PCA space. These relationships are especially difficult to glean from the UMAP embedding alone, where overlapping clusters can appear indistinguishable, whereas concordex provides an exact assessment of the extent of mixing between clusters. Moreoover, the concordex similarity matrix is sufficient to visualize the global structure of the kNN graph when combined with the concordex measures.

Discussion

Efforts to characterize the expression and functional similarities of cells in their tissue context rely on accurate methods to identify regions with compositional similarity. We developed concordex to explicitly aggregate cells into regions based on the compositional similarity of their local neighborhoods. This approach enables long-range identification of regions and broad characterization of tissues. Our method is fast and flexible, leveraging research that has resulted in optimized algorithms for computing the kNN graph. On simulated data, concordex readily identifies global organization, even when the same cell types are represented throughout the spatial field. Using concordex, we were able to identify the well-described laminar structure of the mouse cerebellum and regions of functional importance in the mouse liver.

Importantly, we have demonstrated the utility of using local neighborhood compositional similarity as a marker of SHRs. Other methods aim to detect regions within a tissue where gene expression is consistent. The assumption is that the organization of tissues is related to the spatial dependence of gene expression. However, this approach for region identification often overlooks the cell type heterogeneity within a region and confounds the biological interpretation of spatial domains with the procedure used to generate them. For example, the notion of a ‘tissue domain’ in the Banksy paper (8), is defined as the result obtained when ‘building aggregates with neighborhood kernel[s] and spatial yadstick[s]’. Similarly, in the GASTON paper (12), ‘spatial domains’ are described in terms of topographic maps, that result from isodepth which the GASTON method infers. Again, the notion of a ‘spatial’ or ‘tissue’ domain is tautological with the algorithm used to produce it. In the concordex framework, we prioritize the biological definition of spatial homogeneous regions, and our approach to identify SHRs follows from the definition, not the other way around. Thus, while other methods can, at times, produce similar results to concordex, concordex reliably distinguishes between cell type and region assignment and is particularly adept at identifying SHRs that recur in spatially distant parts of the tissue.

Many SRT studies aim to identify the relative position of cell types in space. Implicit in these analyses is that cell types are organized into SHRs, and efforts to identify region-specific variation largely rely on alignment to previously characterized anatomical structures (21). On the other hand, computational approaches for identifying SHRs vary in their scalability and interpretability. Spatial smoothing approaches often increase the dimension of SRT data, usually by concatenating information from spatial neighbors into a single matrix as input to dimension reduction and clustering algorithms (8, 22). These approaches are computationally burdensome as $k$ (the number of neighbors) and $n$ (the number of observations) becomes large, and can be intractable even for current datasets. As spatial transcriptomics technologies continue to improve, not only in terms of resolution, but also throughput, computational efficiency will become increasingly important.

Aggregation of cells and spots into neighborhoods based on the compositional similarity of their local neighborhoods enables long-range SHR identification of regions and broad characterization of the tissue. As we showed in simulation, existing methods that are based on gene expression or attributes derived from gene expression can fail to differentiate cell type variation from regional variation. By using information about cell neighborhoods, concordex naturally allows for cells of the same type to be assigned to different regions. When cell type labels are used with concordex, one possible limitation is that densely populated cells with identical neighborhoods may be identified as a single SHR, which may not correspond to a histological feature. We believe that this result is important for what it reveals about the tissue organization, such as varying cell density and type homogeneity.

We also demonstrated that concordex has non-spatial applications when the neighborhood consolidation matrix is constructed from principal components or expression vectors. A typical use case of concordex in this context includes assessing the existence of and relationships between predefined groups or clusters. In contrast to UMAP, the similarity matrix can be used to visualize distinct clusters without distorting the global relationships between them. The neighborhood consolidation matrix is especially useful for estimating the proximity of clusters and presents a more natural interpretation of the biological relationship between them. Given that UMAP plots are also used to visualize gene expression data within a cluster, we note that gene expression can be readily plotted as a heatmap grouped by pre-defined clusters without loss of information present in the UMAP visualization.

In summary, concordex provides an accurate and efficient framework for identifying SHRs across a variety of spatial scales and technologies, furthering the understanding of complex spatial regionalization patterns. Future work should focus on identifying genes with regionally restricted expression and distinguishing this pattern from cell type localization. We believe that the SHRs identified by concordex can offer substantial insight in future analyses and will facilitate further efforts to characterize complex tissues.

Methods

concordex: k-nearest neighbor concordance index.

The k-nearest neighbor (kNN) graph $G=(V,E)$ can be generated from a scRNA-seq or SRT dataset where $V$, the set of cells or spots, and $E$, the set of edges, are determined according to some metric on $V$. The number of cells in the dataset is denoted $|V|=n$.

The concordex workflow requires coloring the nodes of $G$ from a finite set $C$ with $|V|=j$ distinct labels. The colored graph is used to create the $n\times j$ neighborhood consolidation matrix, $K$. In the scRNA-seq or SRT context these labels can represent quantities such as cluster assignment or batch. However, these quantities are not always available and can instead be replaced by continuous vectors such as principal components projections. We conceptualize the case for continuous labels by considering the $k$ nearest-neighbors of a node as a $(k-1)$-simplex whose vertices can be described in ${ℝ}^m$ for $m\ge k$.

When continuous vectors are used to color the nodes in $G$, this amounts to assigning those vectors to the vertices of the neighborhood simplex. This approach is easily amenable to discrete labels, where each discrete label is assigned to a unique element of a vector in ${ℝ}^m$. The vertices can then be mapped to the standard vectors in ${ℝ}^m$. In either case, the $n$ rows of $K$ can be interpreted as the center of mass of each simplex. The columns of $K$ represent each of discrete labels or the non-zero elements of the vectors in ${ℝ}^m$. For discrete labels, the entries $K_{ij}$ can be interpreted further and represent the fraction of neighbors of cell $i$ that are assigned label $j$.

To assemble cells or spots into spatial homogeneous regions (SHRs), we use the matrix $K$ and the k-means clustering algorithm when there is prior information for the expected number of domains. However, when the number of SHRs is not known, unsupervised clustering algorithms such as Leiden (14) can be used to generate assignments. In discrete cases, we define a concordex metric by generating a $j\times j$ similarity matrix, $\mathbf{S}$. Since the rows of $K$ can be mapped to a distinct label, we average the fraction of neighbors in each cell down the rows of the same color and so that the rows and columns are in the same order.

The concordex metric is computed by averaging the fractions on the main diagonal of $\mathbf{K}$. That is,

$$\text{concordex}=\frac{1}{j}\sum _{i=1}^j{\mathbf{S}}_{ii}.$$

Datasets and pre-processing.

Slide-Seq V2 Mouse Cerebellum.

We downloaded the count matrix, spatial locations, and cell type labels for replicate 1 from reference (18). The dataset contains counts for 11,626 spatial locations and 23,096 genes. The pixels were filtered to include only spots with a minimum of 100 UMIs detected and those that were not labeled ‘reject’. This left a total of 9,985 pixels available for analysis. A detailed description of the preprocessing steps is available (18).

MERFISH Mouse Liver.

For the mouse liver dataset, we downloaded the gene count matrix, spatial cell metadata, and cell boundary polygons from the Vizgen data portal. We processed the data from a single replicate (“Liver1Slice1”) according to the example Colab notebook provided from (17).

As in the tutorial, “Blank” genes were removed from the count matrix. Each cell was normalized by the total count over all remaining genes and counts were log-transformed with a pseudocount of 1. After processing, there were a total of 347 genes, 367,335 cells, and 1,791 fields of view (FOVs) remaining in the dataset. The mean-centered, normalized count matrix was used to compute the first 50 principal components. Cell types were identified with leiden clustering using a resolution of 1.5.

Where indicated, we subsetted the dataset to include only FOVs 500 to 1000 leaving 100,742 cells and 347 genes for analysis. For the runtime comparisons, we used the subsetted dataset and default parameter values for each method.

10x Chromium Mouse Ex-Utero Embryo.

The datasets used in this study were derived from reference (19). A detailed description of the pre-processing steps are described else-where (20). Briefly, two transformed count matrices were provided by the authors. The ‘Log-Normalized’ dataset consisted of log-transformed counts and the ‘Stabilized-Scaled’ dataset had been variance stabilized using Seurat and subsequently mean-centered and scaled. Both datasets were integrated using Seurat. The count matrices were mean-centered and scaled before principal component analysis (PCA). PCA analysis was performed using sklearn TruncatedSVD to 15 dimensions to agree with the analysis performed by the original authors. We used the findkNN function from the Bioc-Neighbors package in R to find the exact 30 nearest neighbors for each cell in the dataset.

The UMAP algorithm was applied to the 15-dimensional PCA embeddings with default settings except where noted. The subsequent visualizations were colored using labels provided by the authors.

Simulated Datasets.

For the checkerboard simulation in Figure 4A, we created a square lattice with 120 rows and columns. Each individual checker box had a dimension of 15 rows and columns so that the grid resembled a true checkerboard. Each square in the lattice represents a ‘cell’ for a total of 14,400 cells.

We used the splatter simulation software (23) to generate a count matrix containing 14,400 cells and 10,000 genes. We updated the ‘group.prob’ parameter to generate 2 cell types with distinct gene expression profiles. All other parameters were kept at their default settings. A total of [number] cells were labeled ‘Type 1’ and the remaining cells were labeled ‘Type 2’. In the white regions of the checkerboard, we assigned 80% of the squares ‘Type 1’ and in the black regions, 20% of the squares were assigned ‘Type 1’.

For the results in Figure 4D, we generated a laminar pattern in the grid by grouping squares every 30 columns to create 4 layers. In the layered configuration, each stripe had approximately 25%, 40%, 60%, and 75% of the locations within the group assigned to ‘Type 1’, respectively.

Data availability

Data and code to reproduce the figures in this manuscript are available at the following Github repository: https://github.com/pachterlab/JBMMCKP_2023/