Transformation of spatial representations along hippocampal circuits

Bérénice Gandit; Lorenzo Posani; Chun-Lei Zhang; Soham Saha; Cantin Ortiz; Manuela Allegra; Christoph Schmidt-Hieber

doi:10.1016/j.isci.2024.110361

. 2024 Jun 24;27(7):110361. doi: 10.1016/j.isci.2024.110361

Transformation of spatial representations along hippocampal circuits

Bérénice Gandit ^1,², Lorenzo Posani ³, Chun-Lei Zhang ¹, Soham Saha ^1,⁵, Cantin Ortiz ^1,², Manuela Allegra ^1,^6,^∗, Christoph Schmidt-Hieber ^1,^4,^7,^∗∗

PMCID: PMC11277690 PMID: 39071886

Summary

The hippocampus is thought to provide the brain with a cognitive map of the external world by processing various types of spatial information. To understand how essential spatial variables such as direction, position, and distance are transformed along its circuits to construct this global map, we perform single-photon widefield microendoscope calcium imaging in the dentate gyrus and CA3 of mice freely navigating along a narrow corridor. We find that spatial activity maps in the dentate gyrus, but not in CA3, are correlated after aligning them to the running directions, suggesting that they represent the distance traveled along the track in egocentric coordinates. Together with population activity decoding, our data suggest that while spatial representations in the dentate gyrus and CA3 are anchored in both egocentric and allocentric coordinates, egocentric distance coding is more prevalent in the dentate gyrus than in CA3, providing insights into the assembly of the cognitive map.

Subject areas: Neuroscience, Behavioral neuroscience, Sensory neuroscience

Graphical abstract

Highlights

•
Spatial activity in the dentate gyrus and CA3 is modulated by the direction of motion
•
The dentate gyrus and CA3 show conjunctive coding of ego- and allocentric information
•
The dentate gyrus shows a higher prevalence of egocentric representations
•
CA3 shows a higher prevalence of allocentric representations

Neuroscience; Behavioral neuroscience; Sensory neuroscience

Introduction

Neuronal activity in the hippocampus is thought to provide the brain with a cognitive map of its spatial surroundings. This map is constructed from the collective firing of spatially modulated neurons that fire spikes at one or more specific locations in the environment.¹ What type of spatial information is required to build this cognitive map? During navigation, the spatial firing of place cells is anchored in a global, “allocentric” coordinate system centered in the outside world.² The allocentric representation of an environment can be modulated by its boundaries: for example, when the environment is narrowed from open 2-dimensional surroundings to a linear track, the presence and location of place fields become increasingly dependent on the running direction.³^,⁴ However, to make use of visually identified spatial landmarks, additional information about their position relative to a body-centred, egocentric coordinate system is required to compute one’s own position in world-centred coordinates.⁵^,⁶

Egocentric and allocentric information is thought to be conveyed to the hippocampus by distinct input sources.⁷ The lateral entorhinal cortex (LEC) represents information relative to external cues in egocentric coordinates, whereas the medial entorhinal cortex (MEC) processes information about self-motion in an allocentric coordinate system.⁸^,⁹ While both LEC and MEC project to the dentate gyrus and CA3, individual layers of the entorhinal cortex show specific projection patterns to hippocampal subregions, such that these information streams will be differentially available along the hippocampal circuit.¹⁰ It is therefore conceivable that ego- and allocentric coordinates are differentially processed and represented within hippocampal subregions.

This view is consistent with the parallel map theory, which posits that the cognitive map is constructed from distinct contributions from different hippocampal subregions, with the dentate gyrus using navigation-relevant landmarks and downstream subregions processing information relative to local positional cues.¹⁰ Recent work has shown that ego- and allocentric coordinates are both processed in CA1 to build spatial representations with allocentric coordinates prevailing in a familiar environment.¹¹ However, how ego- and allocentric information is processed upstream of CA1 is poorly understood.

To address this question, we perform single-photon widefield microendoscope calcium imaging from hippocampal subregions of mice freely navigating along a narrow linear track, and compare neuronal activity between the dentate gyrus and CA3. In both the dentate gyrus and CA3, spatial activity maps are decorrelated in different running directions, indicating that spatial representations in both subregions depend on the direction of travel. Spatial representations in the dentate gyrus, but not in CA3, are highly correlated after aligning them to the direction of travel, suggesting that distance covered on the track is represented in egocentric coordinates in this subregion. Together with the decoding of population activity, our results indicate that while spatial representations in the dentate gyrus and CA3 are anchored in both egocentric and allocentric coordinates, they evolve from conjunctive coding with a higher prevalence of egocentric representations in the dentate gyrus to a higher contribution of allocentric coding in CA3.

Results

Single-photon microendoscope calcium imaging from the dentate gyrus and CA3 of freely navigating mice

To explore how the hippocampus constructs a representation of space, we recorded neuronal activity from the dentate gyrus or the CA3 region using microendoscope single-photon calcium imaging in freely navigating mice (Figures 1A–1C). We first implanted a gradient-index (GRIN) lens above the dentate gyrus (Figures 1D–1F and S1) or CA3 (Figures 1G–1I and S2). We then recorded neuronal population activity as the mice spontaneously navigated back and forth along a linear track during 10-min sessions over multiple days (Figure 1C). The 60-cm linear track was enriched with visual cues (e.g., playing cards) on the walls and Lego bricks at both ends of the track (Figure 1C). This approach allowed us to record neuronal activity from the dentate gyrus and CA3 in freely navigating animals (Figures 1F and 1I) and the bidirectional nature of the animals’ movements allowed us to disentangle allocentric and egocentric representations in hippocampal neurons.

Experimental approach for *in vivo* Ca²⁺ imaging in the dentate gyrus and CA3 in freely moving mice

(A) Schematic of the microendoscope (Doric lenses, efocus) allowing electronic focusing.

(B) Schematic of a mouse implanted with a microendoscope to perform *in vivo* Ca²⁺ imaging through a GRIN lens.

(C) (top) Schematic of the experimental setup illustrating a mouse freely navigating along a linear corridor in outbound (OUT) and inbound (IN) running directions. (bottom) Trajectory of an example mouse along the 60-cm linear track.

(D) Schematic of the implant of the 0.5 mm diameter GRIN lens in the dentate gyrus.

(E) Representative confocal image of the GRIN lens position above GCaMP6f-expressing neurons in the dentate gyrus. The dotted lines indicate the GRIN lens position and the imaged region. gcl: granule cell layer.

(F) Representative maximum projection of GCaMP6f-expressing granule cells during an *in vivo* recording session. FOV: field of view.

(G) Same as D but for CA3.

(H) Same as E but for CA3. pyr: pyramidal layer.

(I) Same as F but for CA3.

Spatial representations are modulated by the direction of motion and built using distance coding in the dentate gyrus

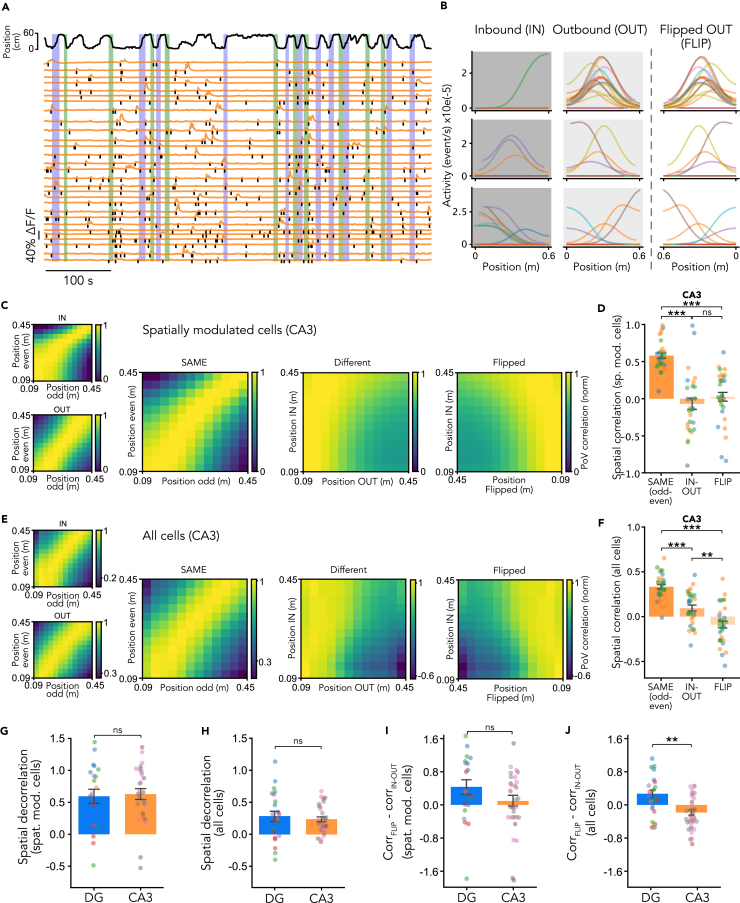
To determine how spatial activity is modulated by the running direction, we split the neuronal activity according to the direction of the animal’s movement (Figures 2A, 2B, S3, S4, and S8–S10). We compared spatial activity maps for the same running directions by splitting laps into odd and even traversals and computing map correlations between even and odd laps for a given direction (IN (odd-even) and OUT (odd-even); Figures 2C and S9). The dentate gyrus showed a pronounced correlation for spatial activity maps in the same direction (between IN (odd-even) and OUT (odd-even); Figure 2D). We then computed correlations between spatial activity maps for traversals in the same direction and spatial activity maps for traversals in opposite directions and found a lower correlation in opposite directions (Figure 2D; p < 0.01). Comparable results were found whether we included only spatially modulated cells (Figures 2C and 2D) or all cells (Figures 2E and 2F). These findings indicate directional discrimination in the dentate gyrus, as the spatial activity maps for the two opposite running directions were almost completely decorrelated.

While spatial representations were decorrelated between different running directions, we found that population vector correlations were high when one of the running directions was reversed (Figures 2A, 2C, and 2E). This observation suggests that space is represented relative to the starting point of a track traversal, indicating that spatial activity is tuned to the distance covered by the animal rather than to allocentric positional coordinates. To quantify this observation, we measured correlations between spatial activity maps for traversals in opposite directions after reversing the order (“flipping”) of the maps for the outbound direction. We found that the dentate gyrus showed substantial correlations between flipped maps that were comparable to the correlations observed between maps for the same running direction (Figure 2D; p > 0.05). The same result was obtained when all cells, both spatially modulated and unmodulated, were included (Figure 2F; correlation value: p > 0.05). This finding is consistent with the notion that neuronal activity in the dentate gyrus encodes the distance traveled along the track in either running direction.

Spatial representations are modulated by the running direction in CA3 and are built using position coding

To investigate whether spatial representations are also modulated by the running direction in downstream hippocampal subregions, we recorded neuronal activity from CA3 under the same experimental conditions as for the dentate gyrus (Figures 3A, 3B, and S4). We first compared spatial activity maps for the same running directions. Similar to the dentate gyrus, CA3 showed a pronounced correlation for spatial activity maps in the same direction (between IN (odd-even) and OUT (odd-even); Figures 3C and 3D). We then computed correlations between spatial activity maps for traversals in the same direction and spatial activity maps for traversals in opposite directions and found a lower correlation for traversals in opposite directions (Figure 3D; p < 0.01). Comparable results were found for both spatially modulated and unmodulated cells (Figures 3C–3F).

Spatial representations are modulated by the running directions in CA3 and are built using position coding

(A) Representative imaging session showing animal speed and motion direction along the linear track, and representative fluorescence traces extracted from regions of interest (ROIs) of an example recording session in CA3. The black tick marks indicate detected activity events during running periods. The purple and green vertically shaded regions highlight inbound or outbound running directions.

(B) Spatial activity maps for three example cells across laps in inbound (left), outbound (middle) and flipped outbound running directions (right). Each colored line refers to the spatial activity map of the example cell for a single lap crossing.

(C) Left: Spatial population vector (PoV) correlation matrices for inbound (top) and outbound (bottom) running directions in CA3. PoV correlations were computed for each spatial bin in the even lap crossings (x axis) with each bin in the odd lap crossings (y axis), including only spatially modulated cells. Right: Spatial PoV correlation matrices for same (left, SAME odd-even), different (right, IN-OUT) running directions and flipped outbound running direction in CA3, including only spatially modulated cells.

(D) Correlations between mean spatial activity maps across recording sessions within the same direction (SAME even-odd), different directions (IN-OUT) and between inbound and flipped outbound directions in CA3, including only spatially modulated cells (left, spatial correlation: SAME even-odd, 0.581 ± 0.037; IN-OUT, −0.070 ± 0.073; FLIP, 0.025 ± 0.064; Mann Whitney U test: SAME odd-even vs. IN-OUT, p = 3.926e-08; IN-OUT vs. FLIP, p = 2.752e-01; SAME odd-even vs. FLIP, p = 5.074e-09; Kruskal Wallis test with Bonferroni correction, p = 5.863e-11).

(E) Same as C but including all cells.

(F) Same as D but including all cells (spatial correlation: SAME even-odd, 0.333 ± 0.025_; IN-OUT, 0.095 ± 0.033; FLIP, −0.090 ± 0.039; Mann Whitney U test: SAME odd-even vs. IN-OUT, p = 5.849e-06; IN-OUT vs. FLIP, p = 3.111e-03; SAME odd-even vs. FLIP, p = 6.012e-09; Kruskal Wallis test with Bonferroni correction, p = 1.198e-10).

(G) Spatial decorrelation, quantified as the difference between spatial correlations within the same direction (even-odd) and between different directions (inbound and outbound) in the DG (0.595 ± 0.110) and CA3 (0.629 ± 0.087), including only spatially modulated cells. No differences have been found between the two hippocampal subregions (DG vs. CA3: Mann Whitney U test, p = 0.739).

(H) Same as F but including all cells: DG (0.287 ± 0.079) and CA3 (0.239 ± 0.038). No differences have been found between the two hippocampal subregions (DG vs. CA3: Mann Whitney U test, p = 0.624).

(I) Quantification of the difference between spatial correlations within the flipped (inbound-flipped outbound, FLIP) and different (inbound-outbound, IN-OUT) directions in the DG (0.436 ± 0.174) and CA3 (0.096 ± 0.134), including only spatially modulated cells. No statistically significant differences were found between the two hippocampal subregions (Mann Whitney U test, p = 0.106).

(J) Same as H but including all cells in the DG (0.271 ± 0.100) and CA3 (−0.185 ± 0.069). The difference between the spatial correlations within flipped (FLIP) and opposite (IN-OUT) directions was significantly higher in DG than in CA3 (Mann Whitney U test, p = 0.001). Bars represent mean ± SEM. Dots indicate the mean correlation value for all cells in a recording session colour-coded by animal (DG, spatially modulated cells, n = 21 sessions from 5 animals, including 99 cells; all cells, n = 23 sessions from 5 animals, including 365 cells. CA3, all cells, n = 31 sessions from 3 animals, including 527 cells; spatially modulated cells, for D, I n = 30 sessions from 3 animals, including 156 cells, for G, n = 27 sessions from 3 animals, including 152 cells). ns, not significant; ∗, p < 0.05; ∗∗, p < 0.01; ∗∗∗, p < 0.001.

To determine how directional spatial representations evolve from the dentate gyrus to CA3, we directly compared the two hippocampal subregions by first measuring the spatial decorrelation (i.e., the reduction in correlation). No significant difference was observed between the dentate gyrus and CA3, regardless of whether only spatially modulated cells (Figure 3G) or all cells (Figure 3H) were included. Moreover, we quantified the proportion of spatially modulated cells, which was similar in both subregions (Figure S6A). Overall, these results indicate that both the dentate gyrus and CA3 show directional spatial representations of the linear track.

Finally, we measured correlations between spatial activity maps for traversals in opposite directions after reversing the order (“flipping”) of the maps for the outbound direction. In contrast to the dentate gyrus, the correlation of the flipped maps in CA3 was lower than the correlation in the same direction, regardless of whether only spatially modulated cells (Figure 3D) or all cells (Figure 3F) were included in the analysis (p < 0.01 in both cases). We then defined a measure of distance coding by subtracting the correlation value of the maps in opposite directions from the correlation values of the flipped maps and found that when only spatially modulated cells were selected, the measure of distance coding was not significantly different between the two hippocampal subregions (Figure 3I; p > 0.05). However, when all cells were selected, the measure of distance coding was significantly more pronounced in the dentate gyrus than in CA3 (Figure 3J; p < 0.05). Taken together, these results indicate that, at the single-cell level, spatial activity in the dentate gyrus, but not in CA3, appears at equivalent locations in egocentric coordinates during track crossings of a linear track in different directions, suggesting that they represent the distance covered by the animal from its starting point.

Dentate gyrus and CA3 are selective for running direction

Activity in the dentate gyrus has been reported to be highly selective for the environmental context.¹²^,¹³ We wondered whether such selectivity would also be reflected by overall changes in activity across running directions. We first quantified the activity levels and found that they were comparable between the dentate gyrus and CA3 (Figure S5A; p > 0.05). To assess whether the dentate gyrus and CA3 show selective activity for different running directions within the same environment, we quantified the relative differences in event rates during runs in one direction vs. the other, without accounting for the spatial modulation of individual neurons. We found that directional selectivity was comparable in both hippocampal subregions (Figure S5B; p > 0.05). To explore whether directional selectivity within each subregion was higher than chance, we computed the expected selectivity from a shuffled version of the experimental dataset (bootstrap). We found that in both the dentate gyrus and CA3, the selectivity from the experimental dataset was higher than the expected shuffled selectivity (Figure S5C; p < 0.05). Overall, similar to the directional modulation of spatial representations in the dentate gyrus and CA3 (Figures 2 and 3), these results reveal that both hippocampal subregions are selective for running direction based on overall changes in activity.

Transformation of population codes for distance and position from dentate gyrus to CA3

Our analysis of spatial correlations of “flipped” maps indicates that in the dentate gyrus, but not in CA3, individual neurons produce spatial maps consistent with an egocentric spatial representation, encoding the distance that the animal has traveled from its starting point rather than its allocentric position along the track. However, despite a low egocentric map correlation at the single-cell level in CA3, traveled distance could still be represented in activity as these neuronal populations could employ different encoding schemes to jointly represent position and distance traveled. For example, separate coding schemes could be used to encode traveled distance in different running directions, resulting in low spatial “flip” correlations despite a high discriminability of different running distances.

To evaluate the extent to which egocentric and allocentric coordinates are represented in the two hippocampal subregions, we isolated population activity vectors from the first and the last third of the track and labeled them according to both position and distance traveled (Figure 4A). We then used a linear decoder to predict the value of these labels from the population activity in a cross-validated decoding scheme.¹⁴ To ensure that the two variables were independently assessed, the decoder for one variable was run on a balanced training set that did not favor either value of the second variable. To do so, the position decoder (divided into two conditions labeled as 0 and 1) was trained on a balanced mix of distance conditions (labeled as start and end) for each of the two position values: (0-start + 0-end) vs. (1-start + 1-end) - and vice versa for the distance decoding analysis (Figure 4A). Our decoding analysis revealed that information about both egocentric distance and allocentric position were decodable in the dentate gyrus, with a higher decoding performance for egocentric information, consistent with the findings on single-cell spatial directional remapping (Figures S5 and 4B; p < 0.05). Interestingly, despite the low flipped spatial correlation in CA3, we found that CA3 neuronal activity represented both variables, with a preference for the allocentric position coordinate (Figure 4B; p < 0.01). To qualitatively compare the two hippocampal subregions, we also measured the Delta decoding performance by computing the difference between egocentric and allocentric variables (Figure 4C). Our decoding results suggest that on a linear track, the dentate gyrus and CA3 encode both egocentric distance and allocentric position information, with a higher decoding performance for egocentric distance information in the dentate gyrus and a higher decoding performance for allocentric information in CA3. Furthermore, while egocentric representations are absent in CA3 at the single-cell level, egocentric information can be decoded at the population level suggesting that the dentate gyrus and CA3 employ different coding strategies for egocentric distance.

Transformation of conjunctive population codes from more egocentric coding in the dentate gyrus to more allocentric coding in CA3

(A) Schematic of the different labeling of the neural data used for the decoding analysis of allocentric position (left) and egocentric traveled distance (right). In the two cases, the neural data is the same but the label is changed according to different behavioral correlates.

(B) Decoding performance obtained by the analysis in A for activity in the two recorded regions (mean decoding performance: DG, egocentric distance, 0.60 ± 0.02 SEM; allocentric position, 0.54 ± 0.015 SEM; p = 0.015; CA3, egocentric distance, 0.64 ± 0.012 SEM; allocentric position, 0.68 ± 0.014 SEM; Mann-Whitney U test, p = 0.009).

(C) Delta decoding performance (difference between egocentric and allocentric variables) in the dentate gyrus and CA3 (DG, p = 0.015; CA3, t-test, p = 0.009).

Bars represent mean ± SEM. Dots represent the mean value for all cells in a recording session colour-coded by animal (DG, n = 26 sessions from 5 animals, including 302 cells; CA3, n = 31 sessions from 3 animals, including 467 cells). Individual significance levels of allo and ego populations in Figure 4B are computed with one-sample t-test against chance levels of 0.5. ∗, p < 0.05; ∗∗, p < 0.01; ∗∗∗, p < 0.001.

Discussion

In this study, we explore how dentate gyrus neurons represent spatial position, running direction, and distance, and how this information evolves in the downstream subregion CA3, providing one of the first descriptions of these representations in two of the major hippocampal subregions under the same task conditions in freely moving animals. Using single-photon calcium imaging in mice spontaneously running back and forth along a linear track, we find directionality in dentate gyrus activity, with spatial activity maps for the two opposite running directions being almost completely uncorrelated. Similar to the dentate gyrus, CA3 shows decorrelated spatial activity maps for running direction. This directional modulation of spatial activity is also reflected in the overall changes in activity across running directions in the two hippocampal subregions. Furthermore, activity in the dentate gyrus, but not in CA3, shows pronounced correlations of spatial activity maps after aligning them to the running direction, indicating that the dentate gyrus encodes the distance covered on the linear track in egocentric coordinates. Consistently, decoding of population responses suggests that hippocampal representations encode both egocentric and allocentric information and evolve from conjunctive coding with a higher contribution of egocentric representations in the dentate gyrus to more allocentric representations in CA3.

Directional modulation of spatial activity and selectivity in the dentate gyrus and CA3

We measured the ability of neuronal populations to discriminate distinct environments by quantifying the correlations of spatial activity maps across running directions. To promote directional representations, we make use of a narrow linear track, where directional modulation is known to be particularly pronounced.³^,⁴ We find that spatial activity maps in the dentate gyrus and CA3 are modulated by the direction of running of the animal (outbound and inbound), consistent with previous reports.⁴^,¹⁵^,¹⁶ Our data indicate that the directional spatial modulation is implemented by changes in the location of the spatial activity, a process known as “global remapping”.

To assess directional discrimination independently of the spatial modulation of individual neurons, we quantified “directional selectivity” as the relative difference in activity between the two running directions. Our findings show that this directional selectivity is comparable in the two hippocampal subregions (Figure S5). This observation is consistent with previous reports of high selectivity for running direction in both the dentate gyrus and CA3.¹⁵^,¹⁶ We show that in both the dentate gyrus and CA3, selectivity is significantly different from that expected from a bootstrap dataset, suggesting that both the dentate gyrus and CA3 are selective for running direction based on changes in activity.

Hippocampal neurons are known to change the location of their spatial firing fields to represent a novel environment or contextual changes within a given environment.³^,⁴^,¹⁷^,¹⁸ During locomotion along a stereotyped trajectory, experience modulates spatial representations by shifting place field locations according to direction as the environment becomes familiar.⁴ Here, only recording sessions in a familiar environment were analyzed and it is conceivable that the spatial representations produced by dentate gyrus and CA3 became directional as the environment became familiar.

Sources of directional signals

One possible source of directionally tuned inputs to the hippocampus might be head-direction cells that are located in the MEC.¹⁹ Alternatively, directionally tuned inputs to the hippocampus might be provided by grid cells. Although grid cells are not tuned to a single direction, they show modulation by head direction in a location-dependent manner.²⁰ Grid cells are most abundant in layer II of the MEC, and while they represent only a minority of MEC neurons (10–20%) that project to the hippocampus,¹⁹^,²¹^,²²^,²³ the MEC II projects strongly to the dentate gyrus and might be the main source of EC inputs to CA3.²⁴^,²⁵^,²⁶ A second type of grid cells might also provide directionally tuned inputs to the hippocampus: a majority of grid cells located in MEC III and V show conjunctive coding of position and direction.¹⁹ In contrast to the dentate gyrus, the source of directionally tuned inputs to CA3 remains to be elucidated, as the connectivity patterns between the EC and CA3 vary across species.²⁴^,²⁷^,²⁸^,²⁹^,³⁰ It is possible that hippocampal neurons receive multiple sources of inputs, such that the dentate gyrus receives directionally tuned inputs from grid cells in MEC II and CA3 receives directionally tuned inputs from conjunctive coding grid cells in MEC III.

In contrast to head-direction cells in other brain subregions, directional tuning is thought not to be a fundamental firing property of hippocampal neurons, but to arise from experience-dependent learning. This notion is based on the variability of directional firing in hippocampal neurons,³^,⁴^,¹⁶^,³¹ the modulation of directional firing by different factors such as experience³^,⁴^,¹⁶ and the availability of local cues.³² Directional tuning of hippocampal neurons may therefore arise from inhomogeneous distributions of head direction signals caused by differences in the positions visited at different head directions, which may then lead to preferential firing in the most frequently encountered running directions.³¹ Related theoretical work has proposed that directional firing can be interpreted as a predictive code arising from repeated visits to the same running direction.³³ Thus, directionality might also arise de novo in hippocampal neurons during experience, without necessarily requiring a precomputed directional signal as input.

Distance coding in the dentate gyrus

Our finding that spatial activity maps are decorrelated for different running directions in the two hippocampal subregions indicates that the familiar environment is not represented in a single, allocentric reference frame when encountered in different running directions. However, we find that spatial activity maps for the dentate gyrus show substantial correlations after aligning them to the direction of running, on the order of the correlations observed between maps for the same running direction. This finding indicates that the dentate gyrus encodes the distance covered along the linear track. Notably, this observation is made when all recorded cells are included, but not when only spatially modulated cells are selected, indicating that neurons that are not apparently spatially modulated play an important role in encoding distance run along the track to construct spatial representations. Contrary to the dentate gyrus, egocentric distance coding was observed in CA3 at the population level but not at the single cell level. In addition, our decoding of population activity indicates that the dentate gyrus encodes both egocentric distance and allocentric position information, with a higher prevalence for egocentric distance information. These results are consistent with previous reports of mixed selectivity and multiplexed coding in the dentate gyrus.¹⁴^,³⁴^,³⁵^,³⁶

At first sight, high directional selectivity and distance coding appear to be contradictory, as distance coding requires neuronal activity at equivalent distances in both directions of running and would therefore counteract directionally selective firing. We hypothesize that the two observations can be reconciled by rate changes of the distance-coding, “flipped” firing fields - i.e., the firing fields appear at equivalent distances but with different firing rates. Thus, a combination of “flipped” rate change signals along with a population of purely directional neurons would allow the dentate gyrus to reconcile high directional selectivity with distance coding.

Some features of spatial representations in the dentate gyrus and CA3 might also indicate a differential response to local and distal cues. While the spatial activity of individual neurons does not show any obvious association to particular locations, we observe strong and wide-spread correlations in the spatial activity of the dentate gyrus at the extremities of the track (Figures 2C and 2E) suggesting that a different spatial code might build a spatial representation at these locations, possibly relying on distal cues. It is conceivable that the presence of the visual cues on the walls in our experimental paradigm might result in them being perceived as distal cues. This would be consistent with previous work indicating that dentate gyrus granule cells show less remapping following changes in the same environment than across distinct environments, probably due to its encoding of distal cues that remain identical in the same environment.³⁷ Further experiments allowing changes in the availability of local and distal cues are needed to shed light on the roles of spatial cues, egocentric and allocentric spatial information in building spatial representations in the dentate gyrus and CA3.

Lack of distance coding in CA3

In contrast to the dentate gyrus, we found a lack of correlations of spatial activity maps in CA3 neurons after aligning the maps to the running direction, suggesting that CA3 does not encode egocentric distance at the single-cell level. However, our decoding of population activity indicates that CA3 encodes both distance traveled in different running directions and position information at the population level, with a higher prevalence for position encoding. This is consistent with previous work showing that spatial representations in CA3 are more stable than those of the dentate gyrus.³⁸ CA1 is known to produce a conjunctive code of egocentric and allocentric information with a higher degree of allocentric coding observed in familiar environments.¹¹ It is therefore conceivable that the high prevalence of allocentric coding observed in CA3 might be due to the familiar nature of the environment.

Despite a low egocentric map correlation at the single cell level, our results suggest that CA3 might implement changes in firing activity at the population level to encode distance traveled in different running directions that were not detected when spatial map correlations of individual neurons were analyzed.¹⁶ Notably, rate remapping would not have been captured by Pearson correlations that we used to quantify spatial map correlations at the single-cell level. Consequently, the absence of allocentric coding in the dentate gyrus and CA3 as measured with single-neuron spatial map correlations does not rule out rate remapping of allocentric activity. It is also conceivable that an allocentric representation was formed upon the first exposure to the linear track and became directional as the environment became familiar, consistent with previous work.⁴ This representation might have included shifted spatial fields that would have been detected by our decoder of population activity but might have been missed by the single-cell spatial correlations.³²

While egocentric representations have been observed in extrahippocampal structures and egocentric to allocentric transformation is thought to occur upstream of the hippocampus, our results indicate that at least part of this transformation is carried out within the hippocampus. Our findings would suggest that the dentate gyrus is the first station along the hippocampal circuits to encode unique episodic traces while maintaining the integrity of the spatial code for locations.

What is the source of information about distance and position?

While directional signals to the hippocampus might be provided by the MEC, where does information about distance and position originate? Our results indicate that the dentate gyrus and CA3 may use different coordinate systems to generate a spatial representation of the environment. This might be explained by the distinct projection patterns that the two hippocampal subregions directly receive from the LEC and MEC,³⁹^,⁴⁰ which process both types of information. LEC neurons show egocentric coding of objects⁸ and might convey this information to the dentate gyrus via the lateral perforant path. In addition, projections from the MEC to the dentate gyrus might also contribute to egocentric coding in the dentate gyrus since MEC neurons are tuned to distance traveled ⁴¹ and generate a dynamic representation of the animal’s position during navigation using self-motion information.⁴²^,⁴³^,⁴⁴ MEC neurons are also sensitive to the distance separating an animal from an object, leading to the classification of a subpopulation of MEC neurons as “object-vector cells”.⁴⁵ Consistent with the notion that distance signals are transmitted from the MEC to the dentate gyrus, the MECII-dentate gyrus pathway has been shown to generate a persistent representation of the behavioral task performed by the animal suggesting that the MECII-dentate gyrus pathway plays a critical role in the representation of non-allocentric information.⁴⁶^,⁴⁷

Entorhinal cortical projection patterns to CA3 vary across species²⁴^,²⁷^,²⁸ and the mouse CA3 might receive projections from either EC II³⁰ or EC III.²⁹^,³⁰ Thus, it is possible that the mouse CA3 receives egocentric information via inputs from the LEC III and allocentric information via inputs from MEC III, possibly from grid cells that exhibit highly dynamic spatial representations and mixed selectivity.⁴⁸ The duality of these input sources might explain the difference in the relative prevalence of egocentric and allocentric coding in the dentate gyrus and CA3. Alternatively, CA3 might receive inputs from EC II, whereby egocentric information would be conveyed via LEC II and allocentric information via MEC II, possibly via grid cells, which are thought to convey positional information the hippocampus.⁹^,⁴⁹ CA3 also receives projections from the dentate gyrus, which might also convey distance and position coding information to CA3.⁴⁰ The multiplicity of input sources to CA3, which also receives back projections from CA1,⁵⁰^,⁵¹ might foster the integration of positional and self-motion information and might also explain the difference in the relative prevalence of egocentric and allocentric coding in the dentate gyrus and CA3.

While conjunctive coding of allocentric and egocentric information in the dentate gyrus and CA3 results from dual inputs conveying both types of information to each region,¹¹ changes in synaptic plasticity might also contribute to egocentric and allocentric coding in the two subregions. Previous work has shown that behavioral timescale synaptic plasticity changes the prevalence of egocentric and allocentric coding in CA1 by adjusting synaptic weights.¹¹^,⁵²^,⁵³ Therefore, it is conceivable that this form of synaptic plasticity might also play a role in changing the prevalence of egocentric and allocentric coding in the dentate gyrus and CA3. The dentate gyrus and CA3 show distinct synaptic input organizations such that in the dentate gyrus, the lateral perforant path terminates in the outer one-third of the molecular layer and the medial perforant path terminates in the middle one-third of the molecular layer, while in CA3 the medial and lateral perforant path both terminate in the stratum lacunosum-moleculare. As a result, behavioral timescale synaptic plasticity might modulate perforant path inputs differently in the two regions, and might underlie the difference in relative prevalence of ego- and allocentric information in the two subregions.

Bearing versus sketch maps: The parallel map theory

Our findings provide direct experimental evidence for several theories of how the hippocampus constructs the cognitive map along its circuits. First, our finding that the dentate gyrus shows a higher prevalence for distance coding supports the view that it is required to align internally generated spatial representations with external landmarks, as suggested by lesion experiments.⁵⁴ Second, our finding that CA3 uses a separate coding strategy to the dentate gyrus to represent distance traveled is compatible with theoretical models in which the place cell population generates a cognitive map by the parallel integration of two different input streams of allocentric and egocentric information.⁵⁵^,⁵⁶ Finally, our experimental data revise the parallel map theory, which predicts that hippocampal subregions contribute differentially to the cognitive map, with the dentate gyrus constructing primarily a “bearing map” from self-motion and directional cues, whereas downstream subregions construct a “sketch map” from local positional cues.¹⁰ Our results add to this theory by providing direct evidence for the distinct roles of the two hippocampal subregions in representing space, with the dentate gyrus providing conjunctive coding with a higher contribution of egocentric representations, whereas CA3 provides more allocentric representations and then transmits them to CA1, where a global map of space is generated.

Limitations of the study

Some limitations to our study arise from the difficulty in targeting specific cell populations using single-photon widefield in vivo calcium imaging. To distinguish granule cells from other dentate gyrus cell types, such as inhibitory interneurons or mossy cells, during the manual verification of the segmentation of the field of view into regions of interest (ROIs) we only selected ROIs consistent with the small and densely packed cell bodies of granule cells. We cannot rule out that some neurons are adult-born granule cells. However, adult-born neurons represent a very small proportion of the dentate gyrus neuronal population.⁵⁷ Moreover, it has been recently demonstrated that adult-born neurons were difficult to target with direct AAV injections into the dentate gyrus.⁵⁸ Therefore we do not expect that the activity of adult-born granule cells substantially contributes to our results and conclusions.

In CA3, a lack of specificity in targeting the neuronal population of interest might arise as a result of the placement of the GRIN lens. CA3 is part of a continuous cell layer and is adjacent to CA2. Although the location of CA2 is more dorsal than CA3, the two subregions can only be formally distinguished through the expression of specific AAV serotypes in CA2. The position of the lens in our CA3 animals suggests that we are recording from CA3 neurons, but the possibility of a contribution from CA2 cannot be ruled out (Figure S2).

The presence of rewards during a navigation task modulates hippocampal spatial activity through the activation of the dopaminergic circuit.⁵⁹ Here, we chose a spontaneous navigation task to explore spatial activity without the reward-driven activation of the dopaminergic system. The absence of rewards during a navigation task has been shown to decrease the reliability of CA1 place fields and their stability over time,⁵⁹^,⁶⁰ which might explain why the spatial correlation values that we obtained are lower than those reported in previous studies.⁶¹^,⁶² To obtain stable spatial representations with our experimental paradigm, we discarded the sessions where mice were first exposed to an environment, since previous studies report that spatial representations become more stable as an environment becomes familiar.⁶¹^,⁶² Also, while there is evidence of reward-coding in the dentate gyrus⁶³ and CA1,⁵⁹ the evidence for reward-coding in CA3 is scarce, and the disruption of the ventral tegmental area modulates CA1 but not CA3 activity⁶⁴ suggesting that the reward-related dopaminergic modulation of CA3 is only weak. Overall, while the spatial correlations we obtained might have been higher using a rewarded spatial navigation task, our study provides rare insights into the representation of space in both the dentate gyrus and CA3 during spontaneous exploration without the reward-driven activation of the dopaminergic system.

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Bacterial and virus strains

pAAV.Syn.GCaMP6f.WPRE.SV40	Addgene	100837-AAV1
pENN-AAV-CamKII-GCaMP6f-WRPE-SV40	Addgene	100834-AAV1

Deposited data

Analyzed data	This paper	Available upon request

Experimental models: Organisms/strains

Mouse: C57BL/6J	Janvier labs	SC-C57J-M4S

Software and algorithms

Suite2p	https://github.com/MouseLand/suite2p	Pachitariu et al., 2017⁶⁵; https://doi.org/10.1101/061507
Custom Python code	https://github.com/neurodroid/haussmeister	https://doi.org/10.5281/zenodo.10366829

Open in a new tab

Resource availability

Lead contact

Further information and requests for resources should be directed to and will be fulfilled by the lead contact Christoph Schmidt-Hieber (christoph.schmidt-hieber@uni-jena.de).

Materials availability

This study did not generate new unique reagents.

Data and code availability

•
Processed and raw data reported in this paper are available from the lead contact upon request.
•
Analysis code is available from https://github.com/neurodroid/haussmeister. A snapshot has been deposited under Zenodo: https://doi.org/10.5281/zenodo.10366829. The analysis software suite2p⁶⁵ is available from https://github.com/MouseLand/suite2p.
•
Any additional information required to reanalyse the data reported in this paper is available from the lead contact upon request.

Experimental model and study participant details

Mice

All procedures were performed in accordance with European and French guidelines on the ethical use of animals for experimentation (EU Directive 2010/63/EU) after approval by the Institut Pasteur Ethics Committee (CETEA protocol number 160066). Wild-type male C57BL/6J mice from Janvier labs aged 6 to 39 weeks were used for all experiments. They were housed collectively or individually in a room maintained at 21C with a 12 h inverted light/dark cycle, in polycarbonate individually ventilated cages, enriched with running wheels, and ad libitum access to food and water. A total of 8 mice were used in this study.

Method details

Surgical procedures

Surgery was performed at least 7 days after the arrival of the mice at the animal facility, and was carried out using a stereotaxic apparatus (Kopf instruments). The mice were anesthetised with isoflurane throughout the surgery (3–4% during induction and 1–2% during the remainder of the surgery; 2 L/minO2 and 0.2–0.5 L/minO2 respectively). An analgesic solution (buprenorphine, 0.05 mg/kg i.p., Vetergesic) was administered at least 30 min before surgery. The incision sites were infiltrated with lidocaine at the start of the procedure. A second analgesic solution consisting of meloxicam (10 mg/kg s.c., Metacam) was administered before the end of the surgery. The body temperature of the mice was maintained at 36°C using a heating pad, and their eyes were protected using a hydrating eye gel (Ocrygel). A postoperative analgesic solution (meloxicam 5 mg/kg) was administered orally in combination with a surgical recovery diet (Dietgel, ClearH2O) for 2 days. Recovery of the mice was monitored for 72h.

Stereotaxic injections of viral vectors

The skin was first covered with Providone-iodine (Betadine) and then cut using a scalpel blade. A small craniotomy was made over the right dorsal hippocampus (1.5mm lateral and 1.9mm posterior to Bregma). An injection of AAV1.Syn.GCaMP6f.WPRE.SV4 (500 nL; 3.4x10¹² TU/mL, Addgene) was given to n = 5 animals with DG implants, n = 1 animal with a CA3 implant and an injection of AAV-CamKII-GCaMP6f-WRPE-SV40 (500 nL; ≥1×10¹² vg/mL, Addgene) was given to n = 2 animals with CA3 implants. Mean event rates were slightly higher in mice implanted with hSyn than in mice implanted with CamKII (Figure S6B). The injection was carried out using an oil injection pump and a glass micropipette at the injection site defined by the following stereotaxic coordinates: DG: 1.9 mm posterior from Bregma, 1.5 mm lateral from the midline and at 1.7 mm depth from the dural surface; CA3: 1.9 mm posterior from Bregma, 2.0 mm lateral from the midline and at 2.1 mm depth from the dural surface. Viral vector injection and GRIN lens implantation were performed either simultaneously or separately to allow expression of the genetically encoded calcium indicator and implantation under visual control. In instances where the injection and implant were carried out separately, the mice were allowed to recover from the injection for at least 1 day before undergoing subsequent procedures.

Chronic GRIN lens implantation

To perform in vivo calcium imaging from the dentate gyrus, a Gradient Refractive Index Lens (GRIN lens) was implanted above the granule cell layer of the dentate gyrus or the pyramidal cell layer of CA3 (Figures 1A, 1B, and 1D-1I). GRIN lens implants were performed either simultaneously with or up to three weeks after virus injection. Mice were anesthetized (see surgical procedure), and the head position and angle were closely monitored to target the subregion of interest. Following application of Betadine to the skin surface and local analgesia, the skin covering the skull was cut with scissors and removed. Following cleaning of the exposed skull with saline solution, all overlying connective tissue was removed by applying a green and a red activator (Super-bond C&B, Sun Medical) to the exposed skull for 1 min and 30 s each. A craniotomy was performed (600–900 μm diameter) and the dura mater was removed. First, a stainless steel needle (500 μm diameter, custom-made, Phymep) was lowered down to 1.9 mm for DG and 2.15 mm for CA3, at a rate of 400 μm/min. Second, the imaging cannula was slowly lowered at a rate of 100 μm/min into the implant site at the following target coordinates: DG: 1.9 mm posterior from Bregma, 1.5 mm lateral from the midline and at 1.9 mm depth from the dural surface; CA3: 1.9 mm posterior from Bregma, 2.0 mm lateral from the midline and at 2.15 mm depth from the dural surface. The procedure was performed blindly in n = 1 animal with a DG implant (using 0.5 mm diameter SICL_D_500_80 Snap-in Imaging Cannula, Model L-D Depth range: 0mm–3.46 mm from Doric lenses) or under visual control of the microendoscope to increase the success rate of the implant in n = 4 animals with DG implants and n = 3 animals with CA3 implants (using eSICL_D_500_80 Snap-in Imaging Cannula, eFocus, Model L-D Depth range: 0 mm–3.46 mm from Doric lenses; Figures 1D–1I). In n = 2 animals with DG implants and n = 2 animals with CA3 implants, a focusing ring was screwed around the metal head post attached to the lens to calibrate the implant depth and increase adhesion to the skull. Metal screws were used to stabilise the position of the GRIN lens in n = 2 animals with CA3 implants. The lens and protruding metal head post were then stabilised with opaque dental cement (Super-bond C&B, Sun Medical) in all animals.

To minimize tissue damage caused by optical imaging, we used a GRIN lens with a small diameter (0.5 mm). We found that our values of activity rates in the dentate gyrus (mean event rate of 0.025 events per second) and CA3 (mean event rate of 0.029 events per second) were consistent with published work that recorded hippocampal activity using imaging techniques.¹³^,¹⁴^,³⁸^,⁶⁶^,⁶⁷ However, the authors cannot exclude that some of the tissue damage caused by the lens as well as variability in the lens position (Figures S1-S2) might affect some of the measured parameters.

Behavioral paradigm

Single-photon microendoscope widefield calcium imaging

During the imaging sessions, the microscope head was clipped to the metal ring protruding from the imaging cannula (Snap-in Surface Fluorescence Microscope Body-L, SFMB_L_458, Doric Lenses in n = 1 animal with a DG implant or eFocus Snap-In Fluorescence Microscope Body-L, eSFMB_L_458, Doric lenses in n = 4 animals with DG implants and n = 3 animals with CA3 implants). A fiber optic patch cord transmitting LED light and an HDMI cable collecting the digital signal connected the mouse to the microscope (Fluorescence microscope driver, FMD_L, Doric Lenses). The cable lengths were optimised to allow unrestricted movement of the mouse. To obtain a high spatial sampling of the physical environment, we chose to expose the animals to a linear track, similar to previous studies.⁶⁸ The mice navigated freely in a 60 cm-long, 6 cm-wide and 31 cm-high linear track made of PVC and enriched with visual cues: 3 playing cards placed on one wall and a sheet of paper placed on the opposing wall, pieces of Lego and drawings positioned at each end of the linear track constituted the visual cues. A plexiglass lid with a linear opening to allow the microscope cables to pass through was placed on top of the linear track. Imaging was performed using Doric Neuroscience studio software and the animal’s behavior was recorded using a camera (Doric, Sony IMX290 sensor) to allow tracking of the animal’s trajectory. The software triggered the behavioral camera by sending a TTL signal for each frame to synchronise the two recordings. The exposure duration was 50 ms (20Hz) for 7 mice and 40 ms (25Hz) for one dentate gyrus mouse, and the illumination power setting was optimised for each animal and imaging subregion, and maintained throughout the experiments.

The imaging field of view (FOV) was first inspected 2–3 weeks following the implant to check for the presence of fluorescent neurons. If fluorescent signals were observed in the FOV, the mice were handled daily during the week prior to the start of recordings to reduce the animals’ stress during the experiments (Figures 1F–1I).

Navigation on the linear track

The activity of hippocampal neurons was recorded while the mouse navigated back and forth in opposite directions along a linear track (length: 60 cm). Mice were exposed to the linear track for 4 consecutive days: the first session was considered to be novel and was excluded from the analysis; subsequent exposures were considered to be familiar and were included in the analysis. During the recording sessions, mice were exposed to the linear track and recorded for 10 min. Mice explored the environment spontaneously without any reward. Cells that were recorded in different sessions from the same animals may be the same cells, the sessions are therefore not independent.

During imaging sessions, mice completed 14.0 ± 1.6 (n = 26 sessions from DG implants) and 15.7 ± 1.3 (n = 31 sessions from CA3 implants) continuous runs (“laps” as defined below) across the linear track (Figure S7A). The running speed was comparable across the three groups of implanted animals (Figure S7B; DG, 7.893 ± 0.205 cm/s; CA3, 8.117 ± 0.159 cm/s). The duration of the imaging sessions was also comparable between DG-implanted and CA3-implanted mice (Figure S7C; DG, 609.182 ± 10.262 s; CA3, 607.118 ± 6.130 s).

Post-hoc analysis

At the end of the experiments, the animals were perfused with 4% formaldehyde (Sigma) after lethal injection of pentobarbital (150 mg/kg). The brain tissue was harvested and sectioned at 60 μm thick sections using a vibratome (Leica). Cell bodies were stained with Hoechst 33342, Trihydrochloride, Trihydrate - FluoroPure Grade. Confocal microscopy was used to image the position of the lens in the tissue and the viral injection sites (Zeiss; Figures 1F-1I).

Quantification and statistical analysis

Behavioral analysis

Analysis of behavioral and imaging data was performed using established procedures in the laboratory,¹³^,⁶⁹^,⁷⁰ with some adaptations to account for the specific characteristics of single-photon widefield imaging as detailed below.

To track the position of the animal, the mice were filmed along the linear track using a camera (Doric, Sony IMX 290 sensor) operating at the same frame rate as the microscope sensor (typically 20Hz). For each frame captured by the microscope sensor, the acquisition software emitted a TTL pulse to trigger a corresponding frame capture by the behavior camera. Animal motion was analyzed using the markerless pose estimation software DeepLabCut (Mathis et al., 2018). 4 labels (snout tip, left and right ear, tail base) were identified across all captured frames. The position of the animal was computed as the mean of the coordinates of the 4 labels. “Laps”, i.e., continuous runs at a speed of >0.5 cm/s in a single direction along the linear track, were identified after low-pass filtering position data at f_c = 0.5Hz. Lap definitions were stringent and included only periods of active running to exclude large synchronous patterns of population activity observed prior to movement onset in the dentate gyrus, consistent with previous findings.⁷¹ Only uninterrupted runs in one direction that covered at least 70% of the total length of the track were considered as a quantifiable lap. Neuronal activity data were assigned to one of two directions (“IN” or “OUT”). Neuronal activity data outside of quantifiable laps, including resting periods, were not included in the analysis.

Imaging data processing

Recordings of neural activity were first motion-corrected in the xy plane to account for artifacts caused by animal movement using an algorithm built into the Doric Neuroscience Studio software. Segmentation into ROIs was performed using a singular value decomposition algorithm built into the suite2p software.⁶⁵ The fluorescent signal from the neuropil was subtracted from the extracted fluorescence using the suite2p software. Quantification of neuronal activity was consistent with previously reported methods.⁷² ‘Events’ were defined as regions in the normalised fluorescence changes (dF/F) exceeding a threshold of mean ± 1.0 standard deviations of the overall dF/F signal, a minimum duration above threshold of 300 ms (which corresponds approximately to the GCaMP6f half decay time⁷³), and an integral of 50 dF/F x 1s. Visual inspection of the event detection result confirmed these parameters.¹³

Identification of spatially modulated cells

Spatial activity maps were computed using data from continuous running periods. The linear track was divided into 20 spatial bins (3 cm bin width). The sum of events in each spatial bin was divided by the occupancy of the animal in that bin; spatial maps were smoothed with a Gaussian filter (sigma = 4 bins).

Spatially modulated neurons were defined as cells that consistently fired at the same location of the linear track across lap crossings in the same running direction. We identified spatially modulated cells by computing the mean pairwise Pearson’s correlation (r) between spatial maps across lap crossings. Outbound and inbound lap crossings were analyzed separately. To obtain a null model for the mean correlation and selectivity, we dissociated the activity for each neuron and spatial position by shuffling the recorded position in blocks of 300 ms and repeated this bootstrap procedure 10 times. Neurons whose mean correlation value exceeded the bootstrap with a Z score greater than 1.0 in at least one running direction were identified as spatially modulated cells. This approach accounts for both coherence and stability of spatially modulated cells, as it will not identify a cell as spatially modulated if it fires in a single lap (low stability), or if it fires in different locations across laps (low coherence), or if it fires sparsely yielding a high mean pairwise correlation by chance (low stability, giving low Z score from the bootstrap procedure).

Spatial correlations and decorrelations

To quantify session-wise correlations between spatial activity maps in the running direction (IN/IN or OUT/OUT), we split the data into two groups that we defined as “even” and “odd” lap crossings in the same direction of motion. We first computed spatial activity maps for each cell for even-numbered (“even”) and odd-numbered (“odd”) laps. We then computed the correlation (Pearson’s r) between spatial activity maps for even and odd laps for each cell. Finally, we computed the mean of individual correlation values for each session, for either all or only neurons that were spatially modulated (see above). To quantify session-wise correlations (Pearson’s r) between inbound and outbound spatial activity maps, we computed correlations as described above using inbound and outbound laps instead of “even” and “odd” laps. To quantify distance coding, we measured correlations (Pearson’s r) between spatial activity maps for lap crossings in opposite directions after reversing the order (“flipping”) of the maps for the outbound direction. Decorrelation was computed by subtracting the correlation of different running directions (OUT vs. IN) from the mean of the correlations of the same direction (IN and OUT).

Population vector (PoV) analysis

Population vectors (PoVs) were defined as the collection of event rates of either the population of all spatially modulated neurons or all cells (including non-spatially modulated cells) measured in a spatial bin. PoV correlations were obtained by computing Pearson’s R between corresponding PoVs of different running directions (OUT vs. IN) or of the same running direction divided into even and odd lap crossings. PoV correlation matrices show colour-coded PoV correlations between all spatial bins in one condition and all spatial bins in the other condition. The PoV correlation matrices were normalised using a convolutional filter using a filter size of 3 pixels. The filter takes 3 values from around the pixel of interest on a row-by-row basis and then multiplies the values by the corresponding value in the kernel matrix. For illustration purposes only, we performed a normalisation to the maximum value across each row and discarded 3 and 5 pixels (0.03 cm each) at the beginning and end of the track, respectively. This was done to increase the contrast of the PoV correlation matrix display.

Rate vector and selectivity

To compute direction selectivity, the event rate for the i-th cell r_i was defined as the number of neural events of a cell divided by the amount of running time in a given direction. For each recording session, the selectivity of the i-th neuron was defined as the normalised difference of the event rates r of this neuron, computed during inbound and outbound running: |r_i^I – r_i^O|/(r_i^I + r_i^O).

For each recording session, the average selectivity index was computed across all neurons to obtain an individual value for the recorded population. Selectivity is strongly affected by sparsity: neurons that fire very sparsely in time (few events) have a higher chance of being highly selective. In order to compute the significance of our selectivity values taking into account the different levels of sparsity of the analyzed cell types (pyramidal neurons in CA3 and granule cells in the DG), we compared the selectivity values obtained from the data with the mean selectivity values obtained from a null model that keeps the activity intact but breaks the direction selectivity by randomly shuffling the inbound and outbound labels of individual trials. The null model distribution was estimated for each individual session by iteratively shuffling the labels 20 times and computing the selectivity index, as defined above, at each iteration for all cells recorded in that session. Following the iterations, we calculated the mean of the null model values to determine an “expected” mean selectivity value of individual neurons from that session. We then compared the difference between the experimentally determined directional selectivity (for DG and CA3) and the expected selectivity of the cell types.

Decoding of position and distance from population responses

For the decoding analysis, we used custom-written Python scripts and the scikit-learn SVC implementation.⁷⁴ The neural decoder algorithm was based on linear classifiers trained on pseudo-simultaneous population activity generated by combining 100 ms-binned neural patterns recorded from different animals performing the same behavioral task. The decoding algorithm was cross-validated and tested against a null model with shuffled trial condition labels.

Data labeling

For each session, we labeled the recorded neural data according to the animal’s position along the track (denoted as position) and according to the egocentric distance traveled in the run event (denoted as distance). For each variable, we defined two classes that were used to train and test the decoding algorithm. Being L the length of the track, we labeled the data as follows.

Position:

•
(0): = position <0.2 L
•
(1): = position >0.8 L

Distance:

•
(start): = distance <0.2 L
•
(end): = distance >0.8 L

To avoid the two variables confounding each other, we balanced the data so that the four combined classes (0-start, 0-end, 1-start, 1-end) contained the same amount of data. Position decoding was therefore performed by training and testing a decoder to discriminate a balanced mixture of distance values in the two position classes: (0-start, 0-end) vs. (1-start, 1 end). Similarly, distance decoding was performed on a balanced mix of positional values: (0-start, 1-start) vs. (0-end + 1-end). Only data with at least n = 1 neurons showing activity were included in the decoding analysis.

Cross-validation

All performance assessments were performed using n = 10 cross validation (CV) folds. For each CV fold, we randomly selected 80% of the time bins of each condition and used them to build pseudo-simultaneous (PS) activity (see below), which was used to train a Support Vector Machine (SVM) with a linear kernel to classify PS patterns into one of the two conditions. Similarly, the remaining 20% of the trials were used to generate PS activity, which was used to test the trained SVM. Where a single value was presented, the decoding performance was then assessed as the mean accuracy on the test set over the CV folds.

Pseudo-population

To construct pseudo-populations, we randomly selected 100 ms binned neural patterns from the training and testing trials of all animals and concatenated them to form a larger pseudo-simultaneous neural pattern. To obtain the training and testing datasets used in the cross-validation scheme, this procedure was repeated 2N times per condition, where N is the total number of neurons. To increase the signal-to-noise ratio of the decoder, we used a procedure where the decoder is trained to classify groups of n=3 time bins (n = 1 corresponds to standard single time bin decoding). In practice, this was done at the time of pseudo-population activity generation by sampling and concatenating 3 random time bins for each individual animal, effectively creating pseudo-population vectors of 3N neurons, where N is the total number of recorded neurons across animals.

Null model and p-value

All decoding performance values were tested against a null model created by shuffling the condition labels of individual trials. After each shuffle of the labels, the exact same 10-fold cross-validated decoding procedure described above was repeated on the shuffled data. The p-value of the decoding performance was computing the Z score of the performance of the data compared to the distribution of performances obtained by 20 repetitions of the shuffling procedure.

Statistics

Data are presented as mean ± SEM across sessions unless stated otherwise. Statistical significance was assessed with the appropriate statistical test as described in individual figure captions. Information relative to the number of recording sessions, animals and cell numbers included in the analysis are presented in Table S1 and additional information relative to statistics is presented in Table S2.

Acknowledgments

We thank Yaniv Ziv for comments and discussions on an earlier version of this article, Lucile Le Chevalier Sontag and Claire Lecestre for technical assistance. B.G. is part of the Pasteur-Paris University (PPU) International PhD Program. This project has received funding from the European Union (ERC StG 678790 NEWRON to C.S.-H., ERC MSCA 800027 FindMEMO to M.A., and innovation program under the Marie Sklodowska-Curie grant agreement No 665807 to B.G.), the Pasteur Weizmann Council (to C.S.-H.), the Fondation pour la Recherche Médicale (grant number FDT202001010897 to B.G. and FDT202304016565 to C.O.), the INCEPTION program (Investissement d’Avenir grant ANR-16-CONV-0005 to C.O.), and the Agence Nationale de la Recherche (ANR-22-CE16-0005-01 MEMNET to C.S.-H.).

Author contributions

C.S.-H. conceived the project. C.S.-H. and B.G. designed experiments with inputs from C.Z. B.G. performed experiments with contributions from M.A. B.G., C.S.-H., S.S, C.O., and L.P. analyzed the experimental data. C.S.-H. supervised the project. B.G., M.A., and C.S.-H. wrote the article with inputs from L.P.

Declaration of interests

Soham Saha is a co-founder of MedInsights SAS, Paris.

Published: June 24, 2024

Footnotes

Supplemental information can be found online at https://doi.org/10.1016/j.isci.2024.110361.

Contributor Information

Manuela Allegra, Email: manuela.allegra@unipd.it.

Christoph Schmidt-Hieber, Email: christoph.schmidt-hieber@uni-jena.de.

Supplemental information

Document S1. Figures S1–S10 and Tables S1 and S2

mmc1.pdf^{(3.7MB, pdf)}

References

1.O’Keefe J., Dostrovsky J. The hippocampus as a spatial map. Preliminary evidence from unit activity in the freely-moving rat. Brain Res. 1971;34:171–175. doi: 10.1016/0006-8993(71)90358-1. [DOI] [PubMed] [Google Scholar]
2.O’Keefe J., Nadel L. Clarendon Press; 1978. The Hippocampus as a Cognitive Map. [Google Scholar]
3.McNaughton B.L., Barnes C.A., O’Keefe J. The contributions of position, direction, and velocity to single unit activity in the hippocampus of freely-moving rats. Exp. Brain Res. 1983;52:41–49. doi: 10.1007/BF00237147. [DOI] [PubMed] [Google Scholar]
4.Navratilova Z., Hoang L.T., Schwindel C.D., Tatsuno M., McNaughton B.L. Experience-dependent firing rate remapping generates directional selectivity in hippocampal place cells. Front. Neural Circuits. 2012;6:6. doi: 10.3389/fncir.2012.00006. [DOI] [PMC free article] [PubMed] [Google Scholar]
5.Mittelstaedt M.-L., Mittelstaedt H. Homing by path integration in a mammal. Naturwissenschaften. 1980;67:566–567. [Google Scholar]
6.McNaughton B.L., Battaglia F.P., Jensen O., Moser E.I., Moser M.-B. Path integration and the neural basis of the “cognitive map.”. Nat. Rev. Neurosci. 2006;7:663–678. doi: 10.1038/nrn1932. [DOI] [PubMed] [Google Scholar]
7.Lisman J.E. Role of the dual entorhinal inputs to hippocampus: a hypothesis based on cue/action (non-self/self) couplets. Prog. Brain Res. 2007;163:615–625. doi: 10.1016/S0079-6123(07)63033-7. [DOI] [PubMed] [Google Scholar]
8.Wang C., Chen X., Lee H., Deshmukh S.S., Yoganarasimha D., Savelli F., Knierim J.J. Egocentric coding of external items in the lateral entorhinal cortex. Science. 2018;362:945–949. doi: 10.1126/science.aau4940. [DOI] [PMC free article] [PubMed] [Google Scholar]
9.Hafting T., Fyhn M., Molden S., Moser M.-B., Moser E.I. Microstructure of a spatial map in the entorhinal cortex. Nature. 2005;436:801–806. doi: 10.1038/nature03721. [DOI] [PubMed] [Google Scholar]
10.Jacobs L.F., Schenk F. Unpacking the cognitive map: the parallel map theory of hippocampal function. Psychol. Rev. 2003;110:285–315. doi: 10.1037/0033-295x.110.2.285. [DOI] [PubMed] [Google Scholar]
11.Qian F.K., Li Y., Magee J.C. Experience-dependent place-cell referencing in hippocampal area CA1. bioRxiv. 2023 doi: 10.1101/2023.11.23.568469. Preprint at. [DOI] [Google Scholar]
12.Neunuebel J.P., Knierim J.J. CA3 retrieves coherent representations from degraded input: direct evidence for CA3 pattern completion and dentate gyrus pattern separation. Neuron. 2014;81:416–427. doi: 10.1016/j.neuron.2013.11.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
13.Allegra M., Posani L., Gómez-Ocádiz R., Schmidt-Hieber C. Differential Relation between Neuronal and Behavioral Discrimination during Hippocampal Memory Encoding. Neuron. 2020;108:1103–1112.e6. doi: 10.1016/j.neuron.2020.09.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
14.Stefanini F., Kushnir L., Jimenez J.C., Jennings J.H., Woods N.I., Stuber G.D., Kheirbek M.A., Hen R., Fusi S. A Distributed Neural Code in the Dentate Gyrus and in CA1. Neuron. 2020;107:703–716.e4. doi: 10.1016/j.neuron.2020.05.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
15.Jung M.W., McNaughton B.L. Spatial selectivity of unit activity in the hippocampal granular layer. Hippocampus. 1993;3:165–182. doi: 10.1002/hipo.450030209. [DOI] [PubMed] [Google Scholar]
16.Schwindel C.D., Navratilova Z., Ali K., Tatsuno M., McNaughton B.L. Reactivation of Rate Remapping in CA3. J. Neurosci. 2016;36:9342–9350. doi: 10.1523/JNEUROSCI.1678-15.2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
17.Anderson M.I., Jeffery K.J. Heterogeneous modulation of place cell firing by changes in context. J. Neurosci. 2003;23:8827–8835. doi: 10.1523/JNEUROSCI.23-26-08827.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
18.Muller R.U., Kubie J.L. The effects of changes in the environment on the spatial firing of hippocampal complex-spike cells. J. Neurosci. 1987;7:1951–1968. doi: 10.1523/JNEUROSCI.07-07-01951.1987. [DOI] [PMC free article] [PubMed] [Google Scholar]
19.Sargolini F., Fyhn M., Hafting T., McNaughton B.L., Witter M.P., Moser M.B., Moser E.I. Conjunctive representation of position, direction, and velocity in entorhinal cortex. Science. 2006;312:758–762. doi: 10.1126/science.1125572. [DOI] [PubMed] [Google Scholar]
20.Gerlei K., Passlack J., Hawes I., Vandrey B., Stevens H., Papastathopoulos I., Nolan M.F. Grid cells are modulated by local head direction. Nat. Commun. 2020;11:4228. doi: 10.1038/s41467-020-17500-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
21.Diehl G.W., Hon O.J., Leutgeb S., Leutgeb J.K. Grid and Nongrid Cells in Medial Entorhinal Cortex Represent Spatial Location and Environmental Features with Complementary Coding Schemes. Neuron. 2017;94:83–92.e6. doi: 10.1016/j.neuron.2017.03.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
22.Zhang S.-J., Ye J., Miao C., Tsao A., Cerniauskas I., Ledergerber D., Moser M.B., Moser E.I. Optogenetic dissection of entorhinal-hippocampal functional connectivity. Science. 2013;340 doi: 10.1126/science.1232627. [DOI] [PubMed] [Google Scholar]
23.Kitamura T., Sun C., Martin J., Kitch L.J., Schnitzer M.J., Tonegawa S. Entorhinal Cortical Ocean Cells Encode Specific Contexts and Drive Context-Specific Fear Memory. Neuron. 2015;87:1317–1331. doi: 10.1016/j.neuron.2015.08.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
24.Kerr K.M., Agster K.L., Furtak S.C., Burwell R.D. Functional neuroanatomy of the parahippocampal region: the lateral and medial entorhinal areas. Hippocampus. 2007;17:697–708. doi: 10.1002/hipo.20315. [DOI] [PubMed] [Google Scholar]
25.Witter M.P., Amaral D.G. Entorhinal cortex of the monkey: V. Projections to the dentate gyrus, hippocampus, and subicular complex. J. Comp. Neurol. 1991;307:437–459. doi: 10.1002/cne.903070308. [DOI] [PubMed] [Google Scholar]
26.Witter M.P., Naber P.A., van Haeften T., Machielsen W.C., Rombouts S.A., Barkhof F., Scheltens P., Lopes da Silva F.H. Cortico-hippocampal communication by way of parallel parahippocampal-subicular pathways. Hippocampus. 2000;10:398–410. doi: 10.1002/1098-1063(2000)10:4<398::AID-HIPO6>3.0.CO;2-K. [DOI] [PubMed] [Google Scholar]
27.Dolorfo C.L., Amaral D.G. Entorhinal cortex of the rat: topographic organization of the cells of origin of the perforant path projection to the dentate gyrus. J. Comp. Neurol. 1998;398:25–48. [PubMed] [Google Scholar]
28.Steward O. Topographic organization of the projections from the entorhinal area to the hippocampal formation of the rat. J. Comp. Neurol. 1976;167:285–314. doi: 10.1002/cne.901670303. [DOI] [PubMed] [Google Scholar]
29.van Groen T., Miettinen P., Kadish I. The entorhinal cortex of the mouse: organization of the projection to the hippocampal formation. Hippocampus. 2003;13:133–149. doi: 10.1002/hipo.10037. [DOI] [PubMed] [Google Scholar]
30.Suh J., Rivest A.J., Nakashiba T., Tominaga T., Tonegawa S. Entorhinal cortex layer III input to the hippocampus is crucial for temporal association memory. Science. 2011;334:1415–1420. doi: 10.1126/science.1210125. [DOI] [PubMed] [Google Scholar]
31.Muller R.U., Bostock E., Taube J.S., Kubie J.L. On the directional firing properties of hippocampal place cells. J. Neurosci. 1994;14:7235–7251. doi: 10.1523/JNEUROSCI.14-12-07235.1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
32.Battaglia F.P., Sutherland G.R., McNaughton B.L. Local sensory cues and place cell directionality: additional evidence of prospective coding in the hippocampus. J. Neurosci. 2004;24:4541–4550. doi: 10.1523/JNEUROSCI.4896-03.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
33.Stachenfeld K.L., Botvinick M.M., Gershman S.J. The hippocampus as a predictive map. Nat. Neurosci. 2017;20:1643–1653. doi: 10.1038/nn.4650. [DOI] [PubMed] [Google Scholar]
34.Morris A.M., Weeden C.S., Churchwell J.C., Kesner R.P. The role of the dentate gyrus in the formation of contextual representations. Hippocampus. 2013;23:162–168. doi: 10.1002/hipo.22078. [DOI] [PubMed] [Google Scholar]
35.Morris A.M., Curtis B.J., Churchwell J.C., Maasberg D.W., Kesner R.P. Temporal associations for spatial events: the role of the dentate gyrus. Behav. Brain Res. 2013;256:250–256. doi: 10.1016/j.bbr.2013.08.021. [DOI] [PubMed] [Google Scholar]
36.Murano T., Nakajima R., Nakao A., Hirata N., Amemori S., Murakami A., Kamitani Y., Yamamoto J., Miyakawa T. Multiple types of navigational information are independently encoded in the population activities of the dentate gyrus neurons. Proc. Natl. Acad. Sci. USA. 2022;119 doi: 10.1073/pnas.2106830119. [DOI] [PMC free article] [PubMed] [Google Scholar]
37.Senzai Y., Buzsáki G. Physiological Properties and Behavioral Correlates of Hippocampal Granule Cells and Mossy Cells. Neuron. 2017;93:691–704.e5. doi: 10.1016/j.neuron.2016.12.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
38.Sheintuch L., Geva N., Deitch D., Rubin A., Ziv Y. Organization of hippocampal CA3 into correlated cell assemblies supports a stable spatial code. Cell Rep. 2023;42 doi: 10.1016/j.celrep.2023.112119. [DOI] [PMC free article] [PubMed] [Google Scholar]
39.Witter M.P. Intrinsic and extrinsic wiring of CA3: indications for connectional heterogeneity. Learn. Mem. 2007;14:705–713. doi: 10.1101/lm.725207. [DOI] [PubMed] [Google Scholar]
40.Amaral D.G., Scharfman H.E., Lavenex P. The dentate gyrus: fundamental neuroanatomical organization (dentate gyrus for dummies) Prog. Brain Res. 2007;163:3–22. doi: 10.1016/S0079-6123(07)63001-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
41.Campbell M.G., Attinger A., Ocko S.A., Ganguli S., Giocomo L.M. Distance-tuned neurons drive specialized path integration calculations in medial entorhinal cortex. Cell Rep. 2021;36 doi: 10.1016/j.celrep.2021.109669. [DOI] [PMC free article] [PubMed] [Google Scholar]
42.Solstad T., Boccara C.N., Kropff E., Moser M.-B., Moser E.I. Representation of geometric borders in the entorhinal cortex. Science. 2008;322:1865–1868. doi: 10.1126/science.1166466. [DOI] [PubMed] [Google Scholar]
43.Savelli F., Yoganarasimha D., Knierim J.J. Influence of boundary removal on the spatial representations of the medial entorhinal cortex. Hippocampus. 2008;18:1270–1282. doi: 10.1002/hipo.20511. [DOI] [PMC free article] [PubMed] [Google Scholar]
44.Campbell M.G., Ocko S.A., Mallory C.S., Low I.I.C., Ganguli S., Giocomo L.M. Principles governing the integration of landmark and self-motion cues in entorhinal cortical codes for navigation. Nat. Neurosci. 2018;21:1096–1106. doi: 10.1038/s41593-018-0189-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
45.Høydal Ø.A., Skytøen E.R., Andersson S.O., Moser M.-B., Moser E.I. Object-vector coding in the medial entorhinal cortex. Nature. 2019;568:400–404. doi: 10.1038/s41586-019-1077-7. [DOI] [PubMed] [Google Scholar]
46.Cholvin T., Hainmueller T., Bartos M. The hippocampus converts dynamic entorhinal inputs into stable spatial maps. Neuron. 2021;109:3135–3148.e7. doi: 10.1016/j.neuron.2021.09.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
47.Qin H., Fu L., Hu B., Liao X., Lu J., He W., Liang S., Zhang K., Li R., Yao J., et al. A Visual-Cue-Dependent Memory Circuit for Place Navigation. Neuron. 2018;99:47–55.e4. doi: 10.1016/j.neuron.2018.05.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
48.Hardcastle K., Ganguli S., Giocomo L.M. Cell types for our sense of location: where we are and where we are going. Nat. Neurosci. 2017;20:1474–1482. doi: 10.1038/nn.4654. [DOI] [PMC free article] [PubMed] [Google Scholar]
49.Fyhn M., Hafting T., Treves A., Moser M.-B., Moser E.I. Hippocampal remapping and grid realignment in entorhinal cortex. Nature. 2007;446:190–194. doi: 10.1038/nature05601. [DOI] [PubMed] [Google Scholar]
50.Lin X., Amalraj M., Blanton C., Avila B., Holmes T.C., Nitz D.A., Xu X. Noncanonical projections to the hippocampal CA3 regulate spatial learning and memory by modulating the feedforward hippocampal trisynaptic pathway. PLoS Biol. 2021;19 doi: 10.1371/journal.pbio.3001127. [DOI] [PMC free article] [PubMed] [Google Scholar]
51.Sik A., Ylinen A., Penttonen M., Buzsáki G. Inhibitory CA1-CA3-hilar region feedback in the hippocampus. Science. 1994;265:1722–1724. doi: 10.1126/science.8085161. [DOI] [PubMed] [Google Scholar]
52.Grienberger C., Magee J.C. Entorhinal cortex directs learning-related changes in CA1 representations. Nature. 2022;611:554–562. doi: 10.1038/s41586-022-05378-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
53.Priestley J.B., Bowler J.C., Rolotti S.V., Fusi S., Losonczy A. Signatures of rapid plasticity in hippocampal CA1 representations during novel experiences. Neuron. 2022;110:1978–1992.e6. doi: 10.1016/j.neuron.2022.03.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
54.Lee J.W., Kim W.R., Sun W., Jung M.W. Disruption of Dentate Gyrus Blocks Effect of Visual Input on Spatial Firing of CA1 Neurons. J. Neurosci. 2012;32:12999–13003. doi: 10.1523/JNEUROSCI.2608-12.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
55.Laptev D., Burgess N. Neural Dynamics Indicate Parallel Integration of Environmental and Self-Motion Information by Place and Grid Cells. Front. Neural Circuits. 2019;13:59. doi: 10.3389/fncir.2019.00059. [DOI] [PMC free article] [PubMed] [Google Scholar]
56.Posani L., Cocco S., Monasson R. Integration and multiplexing of positional and contextual information by the hippocampal network. PLoS Comput. Biol. 2018;14 doi: 10.1371/journal.pcbi.1006320. [DOI] [PMC free article] [PubMed] [Google Scholar]
57.Cameron H.A., McKay R.D. Adult neurogenesis produces a large pool of new granule cells in the dentate gyrus. J. Comp. Neurol. 2001;435:406–417. doi: 10.1002/cne.1040. [DOI] [PubMed] [Google Scholar]
58.Johnston S., Parylak S.L., Kim S., Mac N., Lim C., Gallina I., Bloyd C., Newberry A., Saavedra C.D., Novak O., et al. AAV ablates neurogenesis in the adult murine hippocampus. Elife. 2021;10 doi: 10.7554/eLife.59291. [DOI] [PMC free article] [PubMed] [Google Scholar]
59.Krishnan S., Heer C., Cherian C., Sheffield M.E.J. Reward expectation extinction restructures and degrades CA1 spatial maps through loss of a dopaminergic reward proximity signal. Nat. Commun. 2022;13:6662. doi: 10.1038/s41467-022-34465-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
60.Kentros C.G., Agnihotri N.T., Streater S., Hawkins R.D., Kandel E.R. Increased attention to spatial context increases both place field stability and spatial memory. Neuron. 2004;42:283–295. doi: 10.1016/s0896-6273(04)00192-8. [DOI] [PubMed] [Google Scholar]
61.Hainmueller T., Bartos M. Parallel emergence of stable and dynamic memory engrams in the hippocampus. Nature. 2018;558:292–296. doi: 10.1038/s41586-018-0191-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
62.Dong C., Madar A.D., Sheffield M.E.J. Distinct place cell dynamics in CA1 and CA3 encode experience in new environments. Nat. Commun. 2021;12:2977. doi: 10.1038/s41467-021-23260-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
63.Shen J., Yao P.-T., Ge S., Xiong Q. Dentate granule cells encode auditory decisions after reinforcement learning in rats. Sci. Rep. 2021;11 doi: 10.1038/s41598-021-93721-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
64.Martig A.K., Mizumori S.J.Y. Ventral tegmental area disruption selectively affects CA1/CA2 but not CA3 place fields during a differential reward working memory task. Hippocampus. 2011;21:172–184. doi: 10.1002/hipo.20734. [DOI] [PMC free article] [PubMed] [Google Scholar]
65.Pachitariu M., Stringer C., Dipoppa M., Schröder S., Rossi L.F., Dalgleish H., Carandini M., Harris K.D. Suite2p: beyond 10,000 neurons with standard two-photon microscopy. bioRxiv. 2016 doi: 10.1101/061507. Preprint at. [DOI] [Google Scholar]
66.Schoenfeld G., Carta S., Rupprecht P., Ayaz A., Helmchen F. In Vivo Calcium Imaging of CA3 Pyramidal Neuron Populations in Adult Mouse Hippocampus. eNeuro. 2021;8 doi: 10.1523/ENEURO.0023-21.2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
67.Danielson N.B., Kaifosh P., Zaremba J.D., Lovett-Barron M., Tsai J., Denny C.A., Balough E.M., Goldberg A.R., Drew L.J., Hen R., et al. Distinct Contribution of Adult-Born Hippocampal Granule Cells to Context Encoding. Neuron. 2016;90:101–112. doi: 10.1016/j.neuron.2016.02.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
68.Ziv Y., Burns L.D., Cocker E.D., Hamel E.O., Ghosh K.K., Kitch L.J., El Gamal A., Schnitzer M.J. Long-term dynamics of CA1 hippocampal place codes. Nat. Neurosci. 2013;16:264–266. doi: 10.1038/nn.3329. [DOI] [PMC free article] [PubMed] [Google Scholar]
69.Zhang C.-L., Koukouli F., Allegra M., Ortiz C., Kao H.L., Maskos U., Changeux J.P., Schmidt-Hieber C. Inhibitory control of synaptic signals preceding locomotion in mouse frontal cortex. Cell Rep. 2021;37 doi: 10.1016/j.celrep.2021.110035. [DOI] [PMC free article] [PubMed] [Google Scholar]
70.Gómez-Ocádiz R., Trippa M., Zhang C.L., Posani L., Cocco S., Monasson R., Schmidt-Hieber C. A synaptic signal for novelty processing in the hippocampus. Nat. Commun. 2022;13:4122. doi: 10.1038/s41467-022-31775-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
71.Pofahl M., Nikbakht N., Haubrich A.N., Nguyen T., Masala N., Distler F., Braganza O., Macke J.H., Ewell L.A., Golcuk K., Beck H. Synchronous activity patterns in the dentate gyrus during immobility. Elife. 2021;10 doi: 10.7554/eLife.65786. [DOI] [PMC free article] [PubMed] [Google Scholar]
72.Dombeck D.A., Harvey C.D., Tian L., Looger L.L., Tank D.W. Functional imaging of hippocampal place cells at cellular resolution during virtual navigation. Nat. Neurosci. 2010;13:1433–1440. doi: 10.1038/nn.2648. [DOI] [PMC free article] [PubMed] [Google Scholar]
73.Dana H., Sun Y., Mohar B., Hulse B.K., Kerlin A.M., Hasseman J.P., Tsegaye G., Tsang A., Wong A., Patel R., et al. High-performance calcium sensors for imaging activity in neuronal populations and microcompartments. Nat. Methods. 2019;16:649–657. doi: 10.1038/s41592-019-0435-6. [DOI] [PubMed] [Google Scholar]
74.Pedregosa F., Varoquaux G., Gramfort A., Michel V., Thirion B., Grisel O., Blondel M., Prettenhofer P., Weiss R., Dubourg V., et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011;12:2825–2830. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Document S1. Figures S1–S10 and Tables S1 and S2

mmc1.pdf^{(3.7MB, pdf)}

Data Availability Statement

•
Processed and raw data reported in this paper are available from the lead contact upon request.
•
Analysis code is available from https://github.com/neurodroid/haussmeister. A snapshot has been deposited under Zenodo: https://doi.org/10.5281/zenodo.10366829. The analysis software suite2p⁶⁵ is available from https://github.com/MouseLand/suite2p.
•
Any additional information required to reanalyse the data reported in this paper is available from the lead contact upon request.

[bib1] 1.O’Keefe J., Dostrovsky J. The hippocampus as a spatial map. Preliminary evidence from unit activity in the freely-moving rat. Brain Res. 1971;34:171–175. doi: 10.1016/0006-8993(71)90358-1. [DOI] [PubMed] [Google Scholar]

[bib2] 2.O’Keefe J., Nadel L. Clarendon Press; 1978. The Hippocampus as a Cognitive Map. [Google Scholar]

[bib3] 3.McNaughton B.L., Barnes C.A., O’Keefe J. The contributions of position, direction, and velocity to single unit activity in the hippocampus of freely-moving rats. Exp. Brain Res. 1983;52:41–49. doi: 10.1007/BF00237147. [DOI] [PubMed] [Google Scholar]

[bib4] 4.Navratilova Z., Hoang L.T., Schwindel C.D., Tatsuno M., McNaughton B.L. Experience-dependent firing rate remapping generates directional selectivity in hippocampal place cells. Front. Neural Circuits. 2012;6:6. doi: 10.3389/fncir.2012.00006. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib5] 5.Mittelstaedt M.-L., Mittelstaedt H. Homing by path integration in a mammal. Naturwissenschaften. 1980;67:566–567. [Google Scholar]

[bib6] 6.McNaughton B.L., Battaglia F.P., Jensen O., Moser E.I., Moser M.-B. Path integration and the neural basis of the “cognitive map.”. Nat. Rev. Neurosci. 2006;7:663–678. doi: 10.1038/nrn1932. [DOI] [PubMed] [Google Scholar]

[bib7] 7.Lisman J.E. Role of the dual entorhinal inputs to hippocampus: a hypothesis based on cue/action (non-self/self) couplets. Prog. Brain Res. 2007;163:615–625. doi: 10.1016/S0079-6123(07)63033-7. [DOI] [PubMed] [Google Scholar]

[bib8] 8.Wang C., Chen X., Lee H., Deshmukh S.S., Yoganarasimha D., Savelli F., Knierim J.J. Egocentric coding of external items in the lateral entorhinal cortex. Science. 2018;362:945–949. doi: 10.1126/science.aau4940. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib9] 9.Hafting T., Fyhn M., Molden S., Moser M.-B., Moser E.I. Microstructure of a spatial map in the entorhinal cortex. Nature. 2005;436:801–806. doi: 10.1038/nature03721. [DOI] [PubMed] [Google Scholar]

[bib10] 10.Jacobs L.F., Schenk F. Unpacking the cognitive map: the parallel map theory of hippocampal function. Psychol. Rev. 2003;110:285–315. doi: 10.1037/0033-295x.110.2.285. [DOI] [PubMed] [Google Scholar]

[bib11] 11.Qian F.K., Li Y., Magee J.C. Experience-dependent place-cell referencing in hippocampal area CA1. bioRxiv. 2023 doi: 10.1101/2023.11.23.568469. Preprint at. [DOI] [Google Scholar]

[bib12] 12.Neunuebel J.P., Knierim J.J. CA3 retrieves coherent representations from degraded input: direct evidence for CA3 pattern completion and dentate gyrus pattern separation. Neuron. 2014;81:416–427. doi: 10.1016/j.neuron.2013.11.017. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib13] 13.Allegra M., Posani L., Gómez-Ocádiz R., Schmidt-Hieber C. Differential Relation between Neuronal and Behavioral Discrimination during Hippocampal Memory Encoding. Neuron. 2020;108:1103–1112.e6. doi: 10.1016/j.neuron.2020.09.032. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib14] 14.Stefanini F., Kushnir L., Jimenez J.C., Jennings J.H., Woods N.I., Stuber G.D., Kheirbek M.A., Hen R., Fusi S. A Distributed Neural Code in the Dentate Gyrus and in CA1. Neuron. 2020;107:703–716.e4. doi: 10.1016/j.neuron.2020.05.022. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib15] 15.Jung M.W., McNaughton B.L. Spatial selectivity of unit activity in the hippocampal granular layer. Hippocampus. 1993;3:165–182. doi: 10.1002/hipo.450030209. [DOI] [PubMed] [Google Scholar]

[bib16] 16.Schwindel C.D., Navratilova Z., Ali K., Tatsuno M., McNaughton B.L. Reactivation of Rate Remapping in CA3. J. Neurosci. 2016;36:9342–9350. doi: 10.1523/JNEUROSCI.1678-15.2016. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib17] 17.Anderson M.I., Jeffery K.J. Heterogeneous modulation of place cell firing by changes in context. J. Neurosci. 2003;23:8827–8835. doi: 10.1523/JNEUROSCI.23-26-08827.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib18] 18.Muller R.U., Kubie J.L. The effects of changes in the environment on the spatial firing of hippocampal complex-spike cells. J. Neurosci. 1987;7:1951–1968. doi: 10.1523/JNEUROSCI.07-07-01951.1987. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib19] 19.Sargolini F., Fyhn M., Hafting T., McNaughton B.L., Witter M.P., Moser M.B., Moser E.I. Conjunctive representation of position, direction, and velocity in entorhinal cortex. Science. 2006;312:758–762. doi: 10.1126/science.1125572. [DOI] [PubMed] [Google Scholar]

[bib20] 20.Gerlei K., Passlack J., Hawes I., Vandrey B., Stevens H., Papastathopoulos I., Nolan M.F. Grid cells are modulated by local head direction. Nat. Commun. 2020;11:4228. doi: 10.1038/s41467-020-17500-1. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib21] 21.Diehl G.W., Hon O.J., Leutgeb S., Leutgeb J.K. Grid and Nongrid Cells in Medial Entorhinal Cortex Represent Spatial Location and Environmental Features with Complementary Coding Schemes. Neuron. 2017;94:83–92.e6. doi: 10.1016/j.neuron.2017.03.004. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib22] 22.Zhang S.-J., Ye J., Miao C., Tsao A., Cerniauskas I., Ledergerber D., Moser M.B., Moser E.I. Optogenetic dissection of entorhinal-hippocampal functional connectivity. Science. 2013;340 doi: 10.1126/science.1232627. [DOI] [PubMed] [Google Scholar]

[bib23] 23.Kitamura T., Sun C., Martin J., Kitch L.J., Schnitzer M.J., Tonegawa S. Entorhinal Cortical Ocean Cells Encode Specific Contexts and Drive Context-Specific Fear Memory. Neuron. 2015;87:1317–1331. doi: 10.1016/j.neuron.2015.08.036. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib24] 24.Kerr K.M., Agster K.L., Furtak S.C., Burwell R.D. Functional neuroanatomy of the parahippocampal region: the lateral and medial entorhinal areas. Hippocampus. 2007;17:697–708. doi: 10.1002/hipo.20315. [DOI] [PubMed] [Google Scholar]

[bib25] 25.Witter M.P., Amaral D.G. Entorhinal cortex of the monkey: V. Projections to the dentate gyrus, hippocampus, and subicular complex. J. Comp. Neurol. 1991;307:437–459. doi: 10.1002/cne.903070308. [DOI] [PubMed] [Google Scholar]

[bib26] 26.Witter M.P., Naber P.A., van Haeften T., Machielsen W.C., Rombouts S.A., Barkhof F., Scheltens P., Lopes da Silva F.H. Cortico-hippocampal communication by way of parallel parahippocampal-subicular pathways. Hippocampus. 2000;10:398–410. doi: 10.1002/1098-1063(2000)10:4<398::AID-HIPO6>3.0.CO;2-K. [DOI] [PubMed] [Google Scholar]

[bib27] 27.Dolorfo C.L., Amaral D.G. Entorhinal cortex of the rat: topographic organization of the cells of origin of the perforant path projection to the dentate gyrus. J. Comp. Neurol. 1998;398:25–48. [PubMed] [Google Scholar]

[bib28] 28.Steward O. Topographic organization of the projections from the entorhinal area to the hippocampal formation of the rat. J. Comp. Neurol. 1976;167:285–314. doi: 10.1002/cne.901670303. [DOI] [PubMed] [Google Scholar]

[bib29] 29.van Groen T., Miettinen P., Kadish I. The entorhinal cortex of the mouse: organization of the projection to the hippocampal formation. Hippocampus. 2003;13:133–149. doi: 10.1002/hipo.10037. [DOI] [PubMed] [Google Scholar]

[bib30] 30.Suh J., Rivest A.J., Nakashiba T., Tominaga T., Tonegawa S. Entorhinal cortex layer III input to the hippocampus is crucial for temporal association memory. Science. 2011;334:1415–1420. doi: 10.1126/science.1210125. [DOI] [PubMed] [Google Scholar]

[bib31] 31.Muller R.U., Bostock E., Taube J.S., Kubie J.L. On the directional firing properties of hippocampal place cells. J. Neurosci. 1994;14:7235–7251. doi: 10.1523/JNEUROSCI.14-12-07235.1994. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib32] 32.Battaglia F.P., Sutherland G.R., McNaughton B.L. Local sensory cues and place cell directionality: additional evidence of prospective coding in the hippocampus. J. Neurosci. 2004;24:4541–4550. doi: 10.1523/JNEUROSCI.4896-03.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib33] 33.Stachenfeld K.L., Botvinick M.M., Gershman S.J. The hippocampus as a predictive map. Nat. Neurosci. 2017;20:1643–1653. doi: 10.1038/nn.4650. [DOI] [PubMed] [Google Scholar]

[bib34] 34.Morris A.M., Weeden C.S., Churchwell J.C., Kesner R.P. The role of the dentate gyrus in the formation of contextual representations. Hippocampus. 2013;23:162–168. doi: 10.1002/hipo.22078. [DOI] [PubMed] [Google Scholar]

[bib35] 35.Morris A.M., Curtis B.J., Churchwell J.C., Maasberg D.W., Kesner R.P. Temporal associations for spatial events: the role of the dentate gyrus. Behav. Brain Res. 2013;256:250–256. doi: 10.1016/j.bbr.2013.08.021. [DOI] [PubMed] [Google Scholar]

[bib36] 36.Murano T., Nakajima R., Nakao A., Hirata N., Amemori S., Murakami A., Kamitani Y., Yamamoto J., Miyakawa T. Multiple types of navigational information are independently encoded in the population activities of the dentate gyrus neurons. Proc. Natl. Acad. Sci. USA. 2022;119 doi: 10.1073/pnas.2106830119. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib37] 37.Senzai Y., Buzsáki G. Physiological Properties and Behavioral Correlates of Hippocampal Granule Cells and Mossy Cells. Neuron. 2017;93:691–704.e5. doi: 10.1016/j.neuron.2016.12.011. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib38] 38.Sheintuch L., Geva N., Deitch D., Rubin A., Ziv Y. Organization of hippocampal CA3 into correlated cell assemblies supports a stable spatial code. Cell Rep. 2023;42 doi: 10.1016/j.celrep.2023.112119. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib39] 39.Witter M.P. Intrinsic and extrinsic wiring of CA3: indications for connectional heterogeneity. Learn. Mem. 2007;14:705–713. doi: 10.1101/lm.725207. [DOI] [PubMed] [Google Scholar]

[bib40] 40.Amaral D.G., Scharfman H.E., Lavenex P. The dentate gyrus: fundamental neuroanatomical organization (dentate gyrus for dummies) Prog. Brain Res. 2007;163:3–22. doi: 10.1016/S0079-6123(07)63001-5. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib41] 41.Campbell M.G., Attinger A., Ocko S.A., Ganguli S., Giocomo L.M. Distance-tuned neurons drive specialized path integration calculations in medial entorhinal cortex. Cell Rep. 2021;36 doi: 10.1016/j.celrep.2021.109669. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib42] 42.Solstad T., Boccara C.N., Kropff E., Moser M.-B., Moser E.I. Representation of geometric borders in the entorhinal cortex. Science. 2008;322:1865–1868. doi: 10.1126/science.1166466. [DOI] [PubMed] [Google Scholar]

[bib43] 43.Savelli F., Yoganarasimha D., Knierim J.J. Influence of boundary removal on the spatial representations of the medial entorhinal cortex. Hippocampus. 2008;18:1270–1282. doi: 10.1002/hipo.20511. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib44] 44.Campbell M.G., Ocko S.A., Mallory C.S., Low I.I.C., Ganguli S., Giocomo L.M. Principles governing the integration of landmark and self-motion cues in entorhinal cortical codes for navigation. Nat. Neurosci. 2018;21:1096–1106. doi: 10.1038/s41593-018-0189-y. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib45] 45.Høydal Ø.A., Skytøen E.R., Andersson S.O., Moser M.-B., Moser E.I. Object-vector coding in the medial entorhinal cortex. Nature. 2019;568:400–404. doi: 10.1038/s41586-019-1077-7. [DOI] [PubMed] [Google Scholar]

[bib46] 46.Cholvin T., Hainmueller T., Bartos M. The hippocampus converts dynamic entorhinal inputs into stable spatial maps. Neuron. 2021;109:3135–3148.e7. doi: 10.1016/j.neuron.2021.09.019. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib47] 47.Qin H., Fu L., Hu B., Liao X., Lu J., He W., Liang S., Zhang K., Li R., Yao J., et al. A Visual-Cue-Dependent Memory Circuit for Place Navigation. Neuron. 2018;99:47–55.e4. doi: 10.1016/j.neuron.2018.05.021. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib48] 48.Hardcastle K., Ganguli S., Giocomo L.M. Cell types for our sense of location: where we are and where we are going. Nat. Neurosci. 2017;20:1474–1482. doi: 10.1038/nn.4654. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib49] 49.Fyhn M., Hafting T., Treves A., Moser M.-B., Moser E.I. Hippocampal remapping and grid realignment in entorhinal cortex. Nature. 2007;446:190–194. doi: 10.1038/nature05601. [DOI] [PubMed] [Google Scholar]

[bib50] 50.Lin X., Amalraj M., Blanton C., Avila B., Holmes T.C., Nitz D.A., Xu X. Noncanonical projections to the hippocampal CA3 regulate spatial learning and memory by modulating the feedforward hippocampal trisynaptic pathway. PLoS Biol. 2021;19 doi: 10.1371/journal.pbio.3001127. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib51] 51.Sik A., Ylinen A., Penttonen M., Buzsáki G. Inhibitory CA1-CA3-hilar region feedback in the hippocampus. Science. 1994;265:1722–1724. doi: 10.1126/science.8085161. [DOI] [PubMed] [Google Scholar]

[bib52] 52.Grienberger C., Magee J.C. Entorhinal cortex directs learning-related changes in CA1 representations. Nature. 2022;611:554–562. doi: 10.1038/s41586-022-05378-6. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib53] 53.Priestley J.B., Bowler J.C., Rolotti S.V., Fusi S., Losonczy A. Signatures of rapid plasticity in hippocampal CA1 representations during novel experiences. Neuron. 2022;110:1978–1992.e6. doi: 10.1016/j.neuron.2022.03.026. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib54] 54.Lee J.W., Kim W.R., Sun W., Jung M.W. Disruption of Dentate Gyrus Blocks Effect of Visual Input on Spatial Firing of CA1 Neurons. J. Neurosci. 2012;32:12999–13003. doi: 10.1523/JNEUROSCI.2608-12.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib55] 55.Laptev D., Burgess N. Neural Dynamics Indicate Parallel Integration of Environmental and Self-Motion Information by Place and Grid Cells. Front. Neural Circuits. 2019;13:59. doi: 10.3389/fncir.2019.00059. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib56] 56.Posani L., Cocco S., Monasson R. Integration and multiplexing of positional and contextual information by the hippocampal network. PLoS Comput. Biol. 2018;14 doi: 10.1371/journal.pcbi.1006320. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib57] 57.Cameron H.A., McKay R.D. Adult neurogenesis produces a large pool of new granule cells in the dentate gyrus. J. Comp. Neurol. 2001;435:406–417. doi: 10.1002/cne.1040. [DOI] [PubMed] [Google Scholar]

[bib58] 58.Johnston S., Parylak S.L., Kim S., Mac N., Lim C., Gallina I., Bloyd C., Newberry A., Saavedra C.D., Novak O., et al. AAV ablates neurogenesis in the adult murine hippocampus. Elife. 2021;10 doi: 10.7554/eLife.59291. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib59] 59.Krishnan S., Heer C., Cherian C., Sheffield M.E.J. Reward expectation extinction restructures and degrades CA1 spatial maps through loss of a dopaminergic reward proximity signal. Nat. Commun. 2022;13:6662. doi: 10.1038/s41467-022-34465-5. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib60] 60.Kentros C.G., Agnihotri N.T., Streater S., Hawkins R.D., Kandel E.R. Increased attention to spatial context increases both place field stability and spatial memory. Neuron. 2004;42:283–295. doi: 10.1016/s0896-6273(04)00192-8. [DOI] [PubMed] [Google Scholar]

[bib61] 61.Hainmueller T., Bartos M. Parallel emergence of stable and dynamic memory engrams in the hippocampus. Nature. 2018;558:292–296. doi: 10.1038/s41586-018-0191-2. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib62] 62.Dong C., Madar A.D., Sheffield M.E.J. Distinct place cell dynamics in CA1 and CA3 encode experience in new environments. Nat. Commun. 2021;12:2977. doi: 10.1038/s41467-021-23260-3. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib63] 63.Shen J., Yao P.-T., Ge S., Xiong Q. Dentate granule cells encode auditory decisions after reinforcement learning in rats. Sci. Rep. 2021;11 doi: 10.1038/s41598-021-93721-8. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib64] 64.Martig A.K., Mizumori S.J.Y. Ventral tegmental area disruption selectively affects CA1/CA2 but not CA3 place fields during a differential reward working memory task. Hippocampus. 2011;21:172–184. doi: 10.1002/hipo.20734. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib65] 65.Pachitariu M., Stringer C., Dipoppa M., Schröder S., Rossi L.F., Dalgleish H., Carandini M., Harris K.D. Suite2p: beyond 10,000 neurons with standard two-photon microscopy. bioRxiv. 2016 doi: 10.1101/061507. Preprint at. [DOI] [Google Scholar]

[bib66] 66.Schoenfeld G., Carta S., Rupprecht P., Ayaz A., Helmchen F. In Vivo Calcium Imaging of CA3 Pyramidal Neuron Populations in Adult Mouse Hippocampus. eNeuro. 2021;8 doi: 10.1523/ENEURO.0023-21.2021. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib67] 67.Danielson N.B., Kaifosh P., Zaremba J.D., Lovett-Barron M., Tsai J., Denny C.A., Balough E.M., Goldberg A.R., Drew L.J., Hen R., et al. Distinct Contribution of Adult-Born Hippocampal Granule Cells to Context Encoding. Neuron. 2016;90:101–112. doi: 10.1016/j.neuron.2016.02.019. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib68] 68.Ziv Y., Burns L.D., Cocker E.D., Hamel E.O., Ghosh K.K., Kitch L.J., El Gamal A., Schnitzer M.J. Long-term dynamics of CA1 hippocampal place codes. Nat. Neurosci. 2013;16:264–266. doi: 10.1038/nn.3329. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib69] 69.Zhang C.-L., Koukouli F., Allegra M., Ortiz C., Kao H.L., Maskos U., Changeux J.P., Schmidt-Hieber C. Inhibitory control of synaptic signals preceding locomotion in mouse frontal cortex. Cell Rep. 2021;37 doi: 10.1016/j.celrep.2021.110035. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib70] 70.Gómez-Ocádiz R., Trippa M., Zhang C.L., Posani L., Cocco S., Monasson R., Schmidt-Hieber C. A synaptic signal for novelty processing in the hippocampus. Nat. Commun. 2022;13:4122. doi: 10.1038/s41467-022-31775-6. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib71] 71.Pofahl M., Nikbakht N., Haubrich A.N., Nguyen T., Masala N., Distler F., Braganza O., Macke J.H., Ewell L.A., Golcuk K., Beck H. Synchronous activity patterns in the dentate gyrus during immobility. Elife. 2021;10 doi: 10.7554/eLife.65786. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib72] 72.Dombeck D.A., Harvey C.D., Tian L., Looger L.L., Tank D.W. Functional imaging of hippocampal place cells at cellular resolution during virtual navigation. Nat. Neurosci. 2010;13:1433–1440. doi: 10.1038/nn.2648. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib73] 73.Dana H., Sun Y., Mohar B., Hulse B.K., Kerlin A.M., Hasseman J.P., Tsegaye G., Tsang A., Wong A., Patel R., et al. High-performance calcium sensors for imaging activity in neuronal populations and microcompartments. Nat. Methods. 2019;16:649–657. doi: 10.1038/s41592-019-0435-6. [DOI] [PubMed] [Google Scholar]

[bib74] 74.Pedregosa F., Varoquaux G., Gramfort A., Michel V., Thirion B., Grisel O., Blondel M., Prettenhofer P., Weiss R., Dubourg V., et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011;12:2825–2830. [Google Scholar]

PERMALINK

Transformation of spatial representations along hippocampal circuits

Bérénice Gandit

Lorenzo Posani

Chun-Lei Zhang

Soham Saha

Cantin Ortiz

Manuela Allegra

Christoph Schmidt-Hieber

Summary

Graphical abstract

Highlights

Introduction

Results

Single-photon microendoscope calcium imaging from the dentate gyrus and CA3 of freely navigating mice

Figure 1.

Spatial representations are modulated by the direction of motion and built using distance coding in the dentate gyrus

Figure 2.

Spatial representations are modulated by the running direction in CA3 and are built using position coding

Figure 3.

Dentate gyrus and CA3 are selective for running direction

Transformation of population codes for distance and position from dentate gyrus to CA3

Figure 4.

Discussion

Directional modulation of spatial activity and selectivity in the dentate gyrus and CA3

Sources of directional signals

Distance coding in the dentate gyrus

Lack of distance coding in CA3

What is the source of information about distance and position?

Bearing versus sketch maps: The parallel map theory

Limitations of the study

STAR★Methods

Key resources table

Resource availability

Lead contact

Materials availability

Data and code availability

Experimental model and study participant details

Mice

Method details

Surgical procedures

Stereotaxic injections of viral vectors

Chronic GRIN lens implantation

Behavioral paradigm

Single-photon microendoscope widefield calcium imaging

Navigation on the linear track

Post-hoc analysis

Quantification and statistical analysis

Behavioral analysis

Imaging data processing

Identification of spatially modulated cells

Spatial correlations and decorrelations

Population vector (PoV) analysis

Rate vector and selectivity

Decoding of position and distance from population responses

Data labeling

Cross-validation

Pseudo-population

Null model and p-value

Statistics

Acknowledgments

Author contributions

Declaration of interests

Footnotes

Contributor Information

Supplemental information

References

Associated Data

Supplementary Materials

Data Availability Statement

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases