Significance analysis for clustering with single-cell RNA-sequencing data

Abstract

Unsupervised clustering of single-cell RNA-sequencing data enables the identification of distinct cell populations. However, the most widely used clustering algorithms are heuristic and do not formally account for statistical uncertainty. We find that not addressing known sources of variability in a statistically rigorous manner can lead to overconfidence in the discovery of novel cell types. Here we extend a previous method, significance of hierarchical clustering, to propose a model-based hypothesis testing approach that incorporates significance analysis into the clustering algorithm and permits statistical evaluation of clusters as distinct cell populations. We also adapt this approach to permit statistical assessment on the clusters reported by any algorithm. Finally, we extend these approaches to account for batch structure. We benchmarked our approach against popular clustering workflows, demonstrating improved performance. To show practical utility, we applied our approach to the Human Lung Cell Atlas and an atlas of the mouse cerebellar cortex, identifying several cases of over-clustering and recapitulating experimentally validated cell type definitions.

Unsupervised clustering is widely applied in single-cell RNA-sequencing (scRNA-seq) workflows. The goal is to detect distinct cell populations that can be annotated as known cell types or discovered as novel ones. A common claim from applying these workflows is that new cell subtypes or states have been discovered because a clustering algorithm divided a population associated with a known cell type into more than one group. But how do we know if this partition could have happened by chance, even with only one cell population being present? Current approaches do not consider this question. Furthermore, because the most popular clustering algorithms are heuristic and do not rely on underlying generative models, they are simply not designed for statistical inference.

As an example, consider the Louvain and Leiden algorithms¹ as implemented by the widely used Seurat toolkit². A standard procedure is to (1) apply principal component analysis to the log-transformed and normalized counts, (2) compute the Euclidean distance between the first 30 principal components of each pair of cells, (3) find the 20 nearest neighbors for each cell, (4) specify a weight for each pair of cells based on the number of neighbors in common and use this to define weighted edges in a network, and (5) divide the network into clusters that maximize modularity¹. The number of clusters found is related to a tuning parameter called the resolution, the best value of which is typically selected by manual inspection of the clusters or by maximizing criteria related to clustering stability^3–6. Note that an underlying generative model is not provided to motivate any of these steps nor to assess how much the results can change due to natural uninteresting random variation. Hence, these and other similar algorithms do not examine the statistical possibility of under- or over-clustering, which leads to the failure to detect rare populations or the false discovery of novel populations, respectively.

Over-clustering can be particularly insidious because clustering algorithms will partition data even in cases where there is only uninteresting random variation present⁷. Moreover, due to the data snooping bias, also known as double-dipping, cells that have been incorrectly clustered into two groups can have genes that appear to be differentially expressed with spuriously small $P$ values⁸. This is because, for example, if we force a single population into two clusters, the algorithm will assign cells that are more similar to each other to the same group, but the statistical test does not take this selection into account when considering the null hypothesis. As a result, if one does not account for this statistical reality, over-clustered output can appear to show convincing differences.

Statistical inference frameworks for clustering have been introduced in contexts other than cell population discovery with scRNA-seq data^9,10. These assume an underlying parametric distribution for the data, specifically Gaussian distributions, where distinct populations have different centers. A given set of clusters can then be assessed in a formal and statistically rigorous manner by asking whether or not these clusters could have plausibly arisen under data from a single Gaussian distribution. If so, then the set of clusters probably indicates over-clustering. However, a limitation of many of these approaches in the context of scRNA-seq cell population discovery is that one can compare only one versus two clusters, rather than any number of clusters, and clustering cannot be done in a hierarchical fashion. Significance of hierarchical clustering (SHC)¹¹ addresses this limitation by incorporating hypothesis testing within the hierarchical procedure. However, SHC is not directly applicable to scRNA-seq data due to the Gaussian distributional assumption, which is inappropriate for these sparse count data^12,13.

In this Article, we extend the SHC approach to propose a model-based hypothesis testing framework embedded in hierarchical clustering for scRNA-seq data. Motivated by previous exploratory analyses¹³, we defined a parametric distribution to represent cell populations, and developed an approach implemented in two ways. First, like SHC, our approach can perform hierarchical clustering with built-in hypothesis testing to automatically identify clusters representing distinct populations. We refer to this self-contained method as single-cell SHC (sc-SHC). To permit significance analysis for datasets that have already been clustered, we developed a version that can be applied to any provided set of clusters. Our approach corrects for multiple, sequential hypothesis testing and controls the family-wise error rate (FWER), with interpretable summaries of clustering uncertainty. We also extend our approach to the setting with batch labels. We motivate the need for statistical inference in scRNA-seq clustering pipelines, describe the mathematical details of our approach, benchmark our approach on real data against popular clustering workflows, and finally demonstrate the advantages with both in the Human Lung Cell Atlas and a mouse cerebellum dataset.

Results

Current clustering workflows over-cluster

To assess the performance of the clustering stability approach applied in current workflows to avoid over-clustering, we simulated scRNA-seq data from a single distribution representing one cell population (Fig. 1a). Because typical clustering workflows only consider a subset of high-variance genes, we simulated 5,000 cells with 1,000 genes each, intended to represent expressed genes, using a previously published model¹³ (‘Simulated study’ in Methods). The expression counts for each cell were drawn from the samejoint distribution over all 1,000 genes, and thus an algorithm that reports more than one cluster in these data is over-clustering.

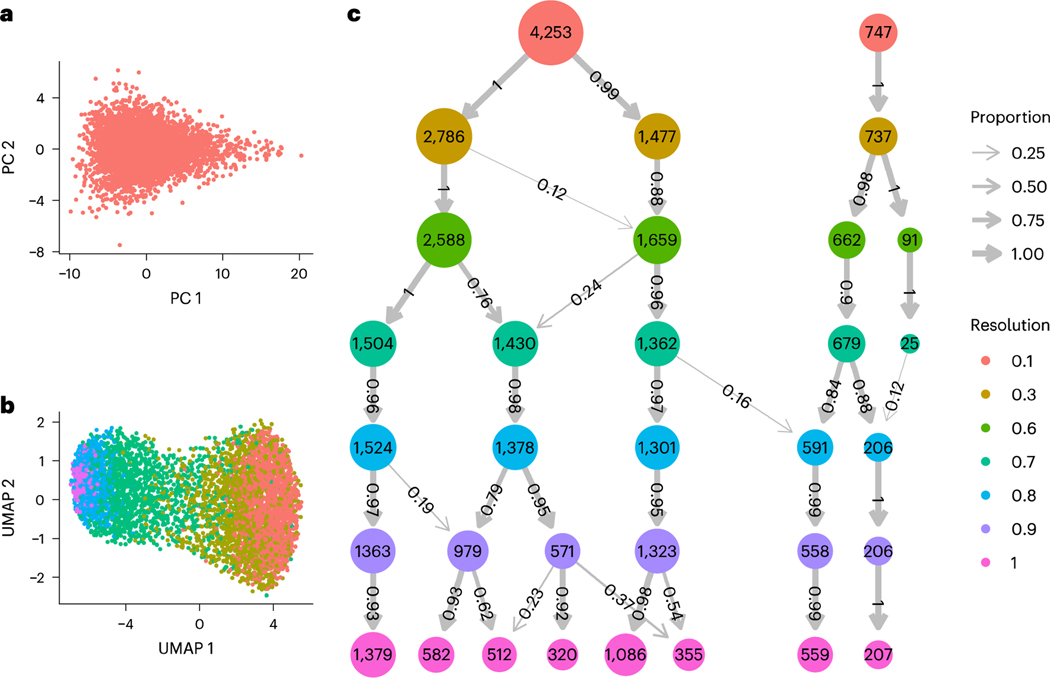
Fig. 1|. Clustering results for applying Seurat’s implementation of the Louvain algorithm to simulated data representing one cell population.

a, PCA plot of 5,000 cells generated from the same joint distribution over 1,000 genes, b, UMAP plot colored by cluster membership when using the default resolution parameter of 0.8. c, A modified clustree visualization of the resulting clusters using Seurat’s implementation of the Louvain algorithm at different resolution parameters, denoted by row. The number of circles in each row represents the number of clusters found with the respective resolution parameter, with the circle’s label and area denoting the number of cells in the cluster. The arrow widths and labels denote what proportion of the cells in each cluster came from the clusters at the previous resolution parameter.

We clustered these simulated expression counts using the most popular clustering algorithm, Seurat’s implementation of the Louvain algorithm² (for details, see ‘Simulated study’ in Methods). We compared results obtained using different resolution parameters used to control the final number of clusters. The number of clusters found varied from two to eight, with the default resolution parameter resulting in five clusters, demonstrating substantial over-clustering (Fig. 1b). Furthermore, as the resolution parameter increased, most clusters represented increasing subdivisions of previous cluster output, indicating a high degree of stability (Fig. 1c). This demonstrates that clustering stability does not necessarily provide a useful statistical assessment. Moreover, applying the standard approach of visualizing the clusters with uniform manifold approximation and projection (UMAP) plots provided further confirmation bias (Fig. 1b). The current approach is therefore prone to over-clustering with no tools provided for detecting the problem.

Significance analysis can both identify and assess clusters

We introduce a model-based hypothesis testing framework that can be applied to any provided set of clusters to determine which, if any, should be merged due to over-clustering. The approach can also be built into hierarchical clustering¹¹ to produce a self-contained clustering pipeline that identifies clusters with statistical evidence that they represent distinct populations. The key idea is to define a realistic parametric distribution to represent a cell population, and then assess whether a separation into two clusters, proposed by the algorithm, could have arisen by chance from cells belonging to only one population. We use a parametric joint distribution that takes into account natural and technical variability, as well as correlation between genes (details in Methods).

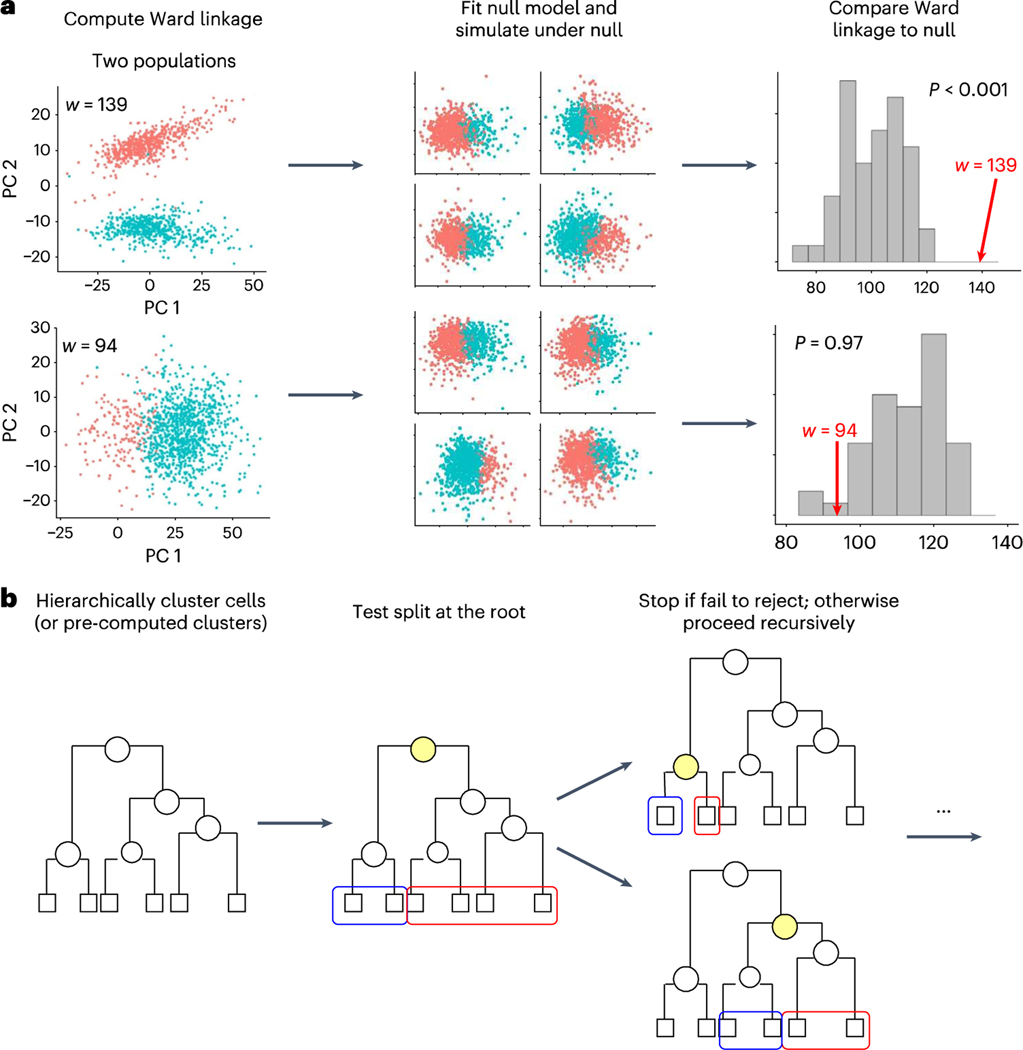
To illustrate the foundational concepts of our framework, we first describe the simplest case. Suppose we have a dataset that has been clustered into two groups, and we want to evaluate whether these two clusters should be just one. Specifically, we want to evaluate whether the clustering algorithm could have found such clustering structure, by chance, from data generated by a single distribution. To answer this question, we first computed a quality assessment metric for the clusters, specifically the Ward linkage¹⁴, which we denote with $w$. The Ward linkage finds the difference between the expected sum of squares of the data when the two clusters are merged, and the expected sum of squares when the two clusters are separate. Hence, larger values suggest greater separation of the two clusters. We then fit our parametric model, assuming just one population, to the data to obtain a null model. We used this model to perform a parametric bootstrap procedure¹⁰ (Fig. 2a) and form a null distribution for the Ward linkage. With a null distribution in place, we can estimate a $P$ value: the probability of observing a Ward linkage for two clusters as high as or higher than $w$ when only one population is present.

Fig. 2 |. Schematic illustrating our approach to significance analysis for clustering.

a, Schematic of the test used by our approach to decide whether a proposed two-way split is significant. We show two examples, one in which two distinct populations were simulated (top) and one in which only one population was simulated (bottom). The schematics show how we use hierarchical clustering to divide the data into two, fit a single parametric model to the data, simulate 100 datasets under that model, and cluster each simulated dataset and compute the Ward linkage. We then compare the Ward linkage of the observed clusters to this empirical null distribution to decide whether to reject the null hypothesis, b, Schematic of our approach. We hierarchically cluster all the cells (or pre-computed clusters), and carry out significance analysis to decide whether to split the root node into the two clusters denoted by blue and red. We stop if we fail to reject the null hypothesis, and otherwise recursively continue performing tests to decide if we split each node or not.

To develop a clustering pipeline, we extended SHC¹¹ for scRNA-seq. Specifically, we applied hierarchical clustering to distances computed using a method developed for scRNA-seq (Methods). This resulted in a tree where the root node divided the cells into two groups, and each successive node encoded a further two-way split, all the way down to leaf nodes representing the individual cells. Note that we can obtain several different clustering results by merging branches¹⁵). To decide what branches to merge, we recursively applied the statistical test, described above, at each node, adjusting the significance threshold each time to control the FWER. After running this full procedure, we had a final set of clusters that have been determined by hypothesis testing to represent cells from distinct distributions (Fig. 2b). We also provide a useful uncertainty summary for each cluster by adapting the concept of an adjusted $P$ value. Specifically, we run the pipeline using a FWER considered to be the highest tolerable false positive rate, then, for each split in the tree, we define an adjusted $P$ value as the infimum of FWER thresholds that would have permitted this particular split to be considered statistically significant. Full details are in the Methods.

To apply our significance analysis framework to any given set of pre-computed clusters produced by any algorithm, we modified our approach as follows. We first hierarchically clustered the centers of the provided clusters, such that each leaf of the tree represents one of the original clusters, and then again recursively applied our statistical test at each node. After running this procedure, we obtained a final, possibly merged set of clusters to correct for any potential over-clustering. Full details are in the Methods.

Finally, when the data have known batch structure, we altered our approach in two ways. First, the batch effects were accounted for in the distance computation (‘Accounting for batch effects’ in Methods). Second, when evaluating each tree split, we computed the test statistic separately for each batch and reported the median of these values, and correspondingly fit and simulated the null model separately for each batch. Further details are in the Methods.

Significance analysis improves current clustering approaches

To benchmark our method against current clustering workflows, we constructed three datasets with known ground truth: a one-population dataset, a five-populations dataset and a five-similar-populations dataset. Specifically, we constructed our datasets using 2,885 cells from the 293T cell line¹⁶. Because these cells are all from the same cell line, they represent a single, well-defined population. The one-population dataset consists of these 2,885 cells, completely unaltered. The five-populations dataset consists of these same 2,885 cells, but modified to create five different populations of equal size, with up to 100 genes permuted to create differing gene expression levels across populations. Finally, the five-similar-populations dataset was modified in the same way except that the fourth and fifth populations differ by only 10 genes, instead of 100 (for details, see ‘Benchmark data’ in Methods).

We ran our clustering pipeline on each of these three datasets, as well as four popular existing clustering workflows for comparison: Seurat’s implementation of the Louvain algorithm (denoted here as Seurat-Louvain), Seurat’s implementation of the Leiden algorithm (denoted here as Seurat-Leiden)², Monocle’s cluster_cells function¹⁷ and SC3’s consensus clustering algorithm¹⁸. Both Monocle and SC3 have built-in mechanisms to choose the number of clusters, but both Seurat-Louvain and Seurat-Leiden require the user to specify the resolution parameter, which is related to the number of clusters. We thus ran these latter algorithms in two ways: using the default resolution parameter, and using clustree to guide the choice of resolution parameter (‘Benchmark data’ in Methods). We then also applied our significance analysis to the clustering outputs produced by each of these methods.

For each approach and dataset, we reported the number of clusters found and the Adjusted Rand Index (ARI), a metric of cluster accuracy where values closer to 1 indicate higher accuracy¹⁹. To compute the ARI, we compared the outputted cluster labels to the ground-truth population labels. In the one-population dataset, our clustering pipeline was the only method that correctly found just one cluster; other approaches found anywhere from 2 to 15 clusters. While applying stability analysis (clustree) resulted in much improved performance compared to default parameters, these other algorithms still overestimated the number of clusters. However, applying our significance analysis improved the performance of all other algorithms and correctly combined all outputs into a single cluster (Table 1).

Table 1 |.

Number of clusters $(k)$ and ARI, comparing outputted cluster labels to the ground-truth population labels, when our clustering pipeline, sc-SHC, as well as existing methods, are applied to three datasets. We also applied our significance analysis on top of each existing method

	One-population				Five-populations				Five-similar-populations
	Original		With significance analysis		Original		With significance analysis		Original		With significance analysis
	$k$	ARI	$k$	ARI	$k$	ARI	$k$	ARI	$k$	ARI	$k$	ARI
sc-SHC	1	1.00	N/A	N/A	5	1.00	N/A	N/A	5	0.99	N/A	N/A
Seurat-Louvain-Clustree	6	0.00	1	1.00	5	0.99	5	0.99	4	0.78	4	0.78
Seurat-Louvain-Default	9	0.00	1	1.00	7	0.89	5	0.99	8	0.67	4	0.78
Seurat-Leiden-Clustree	4	0.00	1	1.00	8	0.88	6	0.93	4	0.78	4	0.78
Seurat-Leiden-Default	9	0.00	1	1.00	8	0.88	6	0.93	10	0.59	4	0.78
Monocle	2	0.00	1	1.00	6	0.96	6	0.96	4	0.74	4	0.74
SC3	15	0.00	1	1.00	11	0.91	8	0.96	11	0.91	7	0.97

In the five-populations dataset, our approach again found the correct number of clusters (five) with perfect correspondence to the ground-truth labels. Seurat-Louvain with clustree also found the correct number of clusters, with just seven cells incorrectly partitioned. All other approaches found between 6 and 11 clusters. Applying significance analysis improved the performance of these methods. Specifically, the output of Seurat-Louvain under the default settings was merged into five clusters with near-perfect correspondence to the ground-truth labels, limited only by mistakes from the original clustering. Both Seurat-Leiden outputs were pruned from eight to six clusters, with an increase in ARI from 0.88 to 0.93. In each case, the sixth cluster consisted of eight cells across four of the ground-truth populations, and hence could not be correctly merged with any of the other clusters. For Monocle, no clusters were merged. As with the Seurat-Leiden outputs, the Monocle cluster outputs were not perfectly subdivided from the ground-truth labels, and further merges from the six-cluster solution would have mixed together cells from different populations. Finally, the output of SC3 was pruned from 11 to 8 clusters, improving the ARI from 0.91 to 0.96, although it would have been technically possible to prune down to 6 without making mistakes (Table 1). Thus, in all but one case, significance analysis merged the clustering outputs as much as possible without creating additional clustering errors.

In the five-similar-populations dataset, our approach once again found the correct number of clusters (five), with an ARI of 0.99. No other approach found the correct number of clusters, and instead found either too few (4) or too many (between 8 and 11). Regardless of the number of clusters, all except SC3 combined the two similar populations into one. Applying significance analysis pruned SC3’s 11-cluster output down to 7 clusters with an ARI of 0.97. For all other methods, significance analysis resulted in a four-cluster solution, either by maintaining the original output or pruning down, which represents the best that could have been found from those outputs (Table 1).

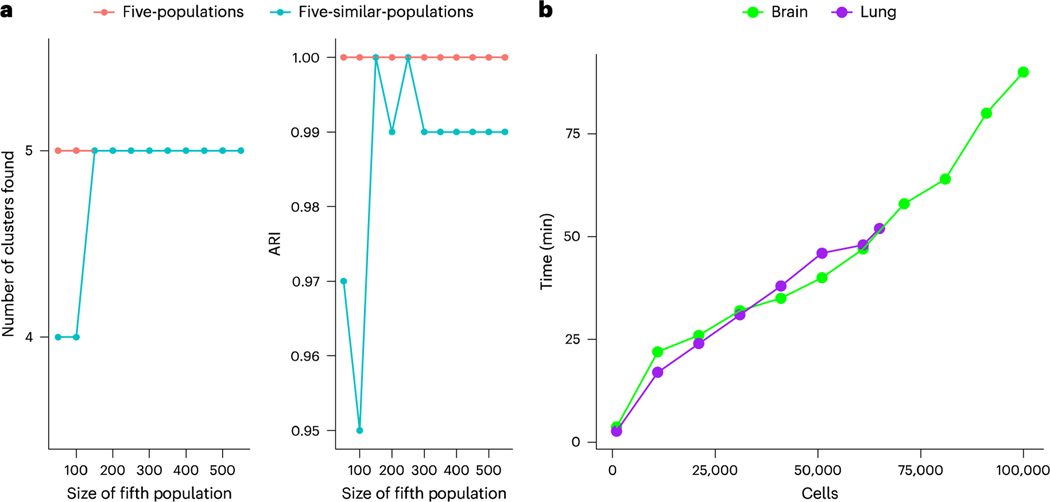
To assess our approach’s ability to detect clusters in settings with uneven cluster sizes, for example in the presence of rare cell populations, we created additional versions of the five-populations and the five-similar-populations dataset in which the size of the fifth population was varied from 50 to 550 cells (Fig. 3). Under the five-populations dataset, the correct number of clusters and maximum possible ARI were found in all cases. Under the five-similar-populations dataset, the fifth population was combined with the fourth at the two smallest sizes (50 and 100 cells), but then the correct solution was found at all other sizes.

Fig. 3 |. Additional benchmarks of our approach.

a, The number of clusters and ARI found under our approach when the size of the fifth population is varied from 50 to 550 cells in the five-populations and five-similar-populations dataset, b, The computational time of sc-SHC on subsets of a mouse cerebellum dataset (brain) ranging from 1,000 to 100,000 cells, and the computational time of our significance analysis on pre-computed clusters for subsets of the Human Lung Cell Atlas (lung), ranging from 1,000 to 65,000 cells.

Finally, we assessed the computational time of sc-SHC on subsets of a mouse cerebellum dataset²⁰ ranging from 1,000 cells to 100,000 cells, and the computational time of our significance analysis on pre-computed clusters for subsets of 1,000 to 65,000 cells in the Human Lung Cell Atlas²¹ (Fig. 3). Each subset was sampled at random from the full dataset, so that each represents approximately the same amount of data complexity (that is, number of ground-truth cell types). We analyze results on the full versions of these data in ‘Our method corrects over-clustering in Human Lung Cell Atlas’ and ‘Our method identifies populations in the mouse cerebellum’ in Results. Each of these subsets was run using two cores; greater speed is possible with more. We find that computational timing scales roughly linearly with the number of cells in our dataset. For example, datasets of around 1,000 cells take about 3 min; 30,000 cells take about 30 min; and 100,000 cells take about 90 min.

Our method corrects over-clustering in Human Lung Cell Atlas

To demonstrate how our approach provides different results in real-world data, we applied our significance analysis to clusters reported by the Human Lung Cell Atlas²¹. This atlas consists of 65,662 cells from 3 patients; we treated patient labels as batch effects, as described in the Methods. The original study identified 57 clusters, some of which were interpreted as novel cell types. Our approach merged these clusters into 45, indicating over-clustering in the original project. Specifically, 38 of the 45 clusters found to be statistically significant corresponded exactly to 38 of the original clusters. The remaining 7 were combinations of 2 to 4 of the originally reported clusters.

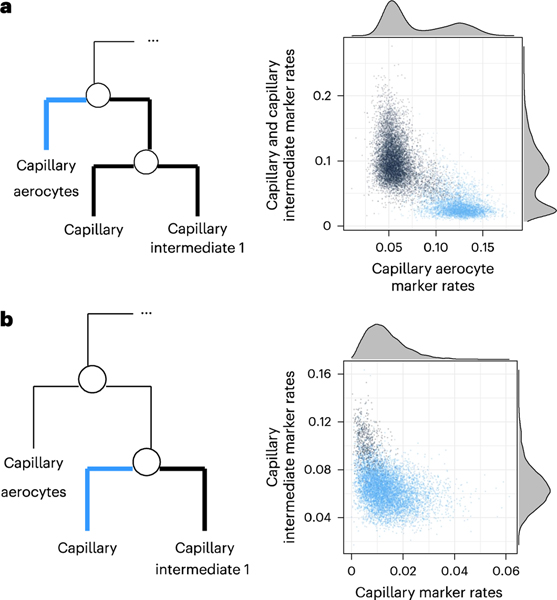
To illustrate one of the examples of over-clustering, we consider what the original study reported as three clusters: capillary aerocytes, capillary and capillary intermediate 1. Applying significance analysis did not find evidence of the presence of the capillary intermediate 1 subpopulation and merged it with the capillary cluster, while the capillary aerocytes were found to be a distinct population. An scRNA-seq gating plot (described in ‘scRNA-seq gating plots’ in Methods), comparing cells in the capillary aerocyte cluster to cells reported to be in the other two, shows strong evidence of two distinct modes, which was consistent with capillary aerocytes being a distinct population (Fig. 4a). However, an scRNA-seq gating plot comparing the reported capillary and capillary intermediate 1 clusters did not show evidence of two distinct populations (Fig. 4b).

Fig. 4 |. Applying significance analysis to clusters reported by the Human Lung Cell Atlas.

a, scRNA-seq gating plot for the proposed split between capillary aerocytes, and capillary and capillary intermediate 1 cells. We compare the proportion of UMIs in each cell representing significantly more highly expressed genes in capillary and capillary intermediate 1 cells to the proportion of UMIs representing significantly more highly expressed genes in capillary aerocytes. b, scRNA-seq gating plot for the proposed split between capillary and capillary intermediate 1 cells.

Many of the other clusters that were merged were similar examples where gating plots did not show evidence of more than one mode. Like the capillary and capillary intermediate 1 clusters, these were often subpopulations that might be interpreted as belonging to a trajectory. For example, the alveolar epithelial type 2 cluster and signaling alveolar epithelial type 2 cluster were merged, as were the ciliated and proximal ciliated clusters, and the macrophage and proliferating macrophage clusters. One of the largest merges combined the basal, differentiating basal, proliferating basal and proximal basal clusters together. By contrast, there were other instances in which related subpopulations were still found to belong to distinct clusters and represent multiple modes, such as the myeloid dendritic type 1 and myeloid dendritic type 2 clusters, or the classical monocyte and OLR1+ classical monocyte clusters. Examples of these clustering results are visualized in Supplementary Fig. 1 to show the contrast between the original clusters and those obtained after significance analysis.

Our method identifies populations in the mouse cerebellum

We also applied our clustering pipeline to a mouse cerebellum dataset²⁰. In particular, we examined 133,858 nongranule cells from six mouse cerebellar cortices, treating the mouse labels as batch effects, and found a total of 23 clusters. The original study clustered and annotated the data in an iterative process using both Seurat’s implementation of the Louvain algorithm² and LIGER²². They reported the resulting annotations at two levels of granularity—high-level major cell types, of which there are 17, and finer-level subclusters, of which there are 46. The ARI comparing our reported clusters with the major cell type level was 0.95, and the ARI with the subcluster level was 0.70, demonstrating that our clustering approach recovered overall similar structure as the original study. These results are visualized in Supplementary Fig. 2 to compare the high-level cell types, finer-level subclusters and our pipeline’s results.

The original study examined two cases in greater detail to determine whether particular subpopulations represent discrete or continuously varying subtypes, using an extensive combination of both computational and experimental techniques. First, they examined unipolar brush cells, which their initial clustering suggested can be divided into three clusters. They performed a post hoc analysis of trajectories of differentially expressed genes across these clusters, as well as a set of experiments to functionally characterize unipolar brush cells through glutamate-evoked currents. On the basis of these analyses, they concluded that there is evidence unipolar brush cells actually exist along a continuum, rather than as discrete subpopulations. Our clustering results recapitulated this finding by yielding a single cluster of unipolar brush cells, notably without requiring any extra post hoc analyses. The adjusted $P$ value for splitting this cluster was 1, indicating that our approach finds a high degree of certainty that these cells all belong to one cluster rather than more.

Second, the original study looked at molecular layer interneuron cells, which are conventionally considered to belong to a continuum. Their initial clustering results found three subpopulations of molecular layer interneuron cells, but after extensive computational and experimental analysis, the authors found evidence for two discrete subtypes (one of which combines two of the initial clusters). Their computational analysis examined gene expression trajectories and marker genes, and their experimental analysis included single-molecule fluorescence in situ hybridization to confirm mutually exclusive marker genes, as well as measurements of electrical characteristics to show binary differences in properties. Our clustering results again were highly consistent with these findings: we yielded two separate clusters corresponding to the two molecular layer interneuron subtypes reported by the authors, with requiring any extra steps or analyses. The adjusted $P$ values for both were also 1, indicating high certainty that neither of these clusters should be further split.

Discussion

Clustering analysis is an integral part of numerous scRNA-seq analysis pipelines. scRNA-seq data are affected by natural and technical random variability, yet the most popular pipelines do not account for statistical uncertainty. As a result, over-clustering is common, and overconfident interpretations can lead to flawed cell-type annotations and incorrect claims of discoveries of novel subtypes. To address this problem, we proposed a significance analysis framework that integrates algorithmic clustering with a probabilistic model. By assuming an underlying parametric model of gene expression, we built on previously developed statistical methodology to create a parametric bootstrap procedure that evaluates whether observed clustering structure can arise even when only one population is present. In particular, we presented two ways of applying this idea: a self-contained approach (sc-SHC) that builds hypothesis testing into hierarchical clustering to automatically identify clusters corresponding to distinct cell populations, and a post hoc approach that can evaluate any provided set of clusters for possible over-clustering. We further extended these approaches to accommodate more complex datasets with batch effects, for example due to multi-sample structure.

Using a simulation study built from experimental data, we demonstrated the substantial improvements provided by our approach when clustering with scRNA-seq data. In particular, we showed that current approaches are prone to over-clustering data and that performing significance analysis improves this by correctly merging spurious clusters. While stability analyses such as clustree yield notable improvement, they do not completely alleviate the problem of over-clustering. By contrast, in our simulations, sc-SHC found the correct number of clusters, with ARIs above 0.99. We also showed that our approach prevented over-clustering without being overly conservative—even when two distinct populations differed only by the expression of ten genes, our approach still correctly separated them. Our post hoc approach also performed favorably, reducing over-clustering in nearly every instance. However, we note that this post hoc approach is limited by the accuracy of the original clustering: our approach can improve other methods only in reducing over-clustering, not in fixing incorrect annotations.

Finally, to demonstrate that our approach makes a difference on published datasets, we applied this framework to the Human Lung Cell Atlas and a mouse cerebellum dataset, explicitly accounting for the multi-sample structure, to correct over-clustering. In the Human Lung Cell Atlas, we found 12 fewer clusters than were originally reported. Reducing over-clustering can prevent incorrectly interpreting certain clusters as novel cell types, and can also improve power in differential expression analyses by not unnecessarily over-partitioning the data. In addition, several sets of clusters that our approach merged appear to indicate continuous, rather than discrete, cell states, the determination of which can inform the appropriate downstream analyses to apply. In the mouse cerebellum dataset, our results demonstrate how our approach can immediately, directly and rigorously obtain clusters that required substantial additional post hoc, downstream computational and experimental analyses in the original study.

A limitation of model-based approaches is that the definition of a distinct population depends on the appropriateness of the parametric model assumed to describe gene expression. Although extensive data exploration indicates that the model we used does in fact describe observed data from distinct populations, scenarios in which it is not appropriate should be considered. For example, we assumed a unimodal marginal distribution for gene expression within a population. This implies that, for cell populations in which some gene expression follows multi-modal distributions, our approach might also result in over-clustering as the incorrect assumption may lead to incorrectly rejecting the one population null hypothesis. Also note that, like all clustering algorithms, our approach identifies discrete populations of cells. Our model-based approach associates these discrete populations with different unimodal probability distributions. However, this does not preclude the presence of biologically meaningful variation within these populations. For example, a continuously varying gene expression level might be associated with different stages within a cell cycle. However, methods that partition cells into distinct groups, such as clustering, are not an appropriate tool for statistically describing these important sources of variability, although model-based approaches such as ours can be adapted to quantify this variation through a continuous parameter in the model. Finally, we note that as with all statistical approaches, any potentially novel discoveries from our method should still be carefully considered and explored before being accepted as fact.

Online content

Any methods, additional references. Nature Portfolio reporting summaries, source data, extended data, supplementary information, acknowledgements, peer review information; details of author contributions and competing interests; and statements of data and code availability are available at https://doi.org/10.1038/s41592-023-01933-9.

Methods

Significance hierarchical clustering for scRNA-seq

Our approach takes raw unique molecular identifier (UMI) counts as input. The first step in hierarchical clustering is computing a distance between each pair of cells. Because scRNA-seq data are characterized by small counts and high dimensionality, computing Euclidean distance is not appropriate nor computationally convenient. We therefore computed Euclidean distance on the latent variables estimated by the approximate generalized linear model–principal components analysis (GLM-PCA) procedure¹², that is, PCA on the Poisson deviance residuals, using the $G=2,500$ genes with the largest deviance under a multinomial null model¹². We computed Euclidean distance on the first 30 latent variables to produce an $N\times N$ distance matrix $D$, with entries $d_{i,j}$ representing the distance between cells $i$ and $j$ and $N$ the number of cells. We then applied hierarchical clustering to $D$ using Ward’s criterion¹⁴.

To identify clusters corresponding to distinct populations from this tree, we followed a procedure similar to SHC¹¹. We first decide on a desired FWER of the entire procedure, referred to as $\alpha$. For the results presented here, we used $\alpha =0.05$ in the simulations and $\alpha =0.25$ for the real data applications. We then proceeded to go down the tree, deciding which splits to keep and which to merge. We began at the root node, which can be interpreted as splitting all $N$ cells into two clusters. We then decided whether or not to keep this split via hypothesis testing. First, we defined the Ward linkage¹⁴ as a test statistic, denoted as $w$ and defined in detail in ‘Quantifying clustering quality with the Ward linkage’ in Methods. Note that the better two clusters match the data, the higher the value of this statistic. Next, we estimated a null distribution for this statistic. To do this, we defined and fit a null parametric model $\mathcal{F}$, described in detail in ‘Parametric model of gene expression’ in Methods‘, and then used parametric bootstrap (generating the maximum of 1,000 cells or the total number of cells in the two clusters) to estimate a null distribution. Data exploration indicated that this null distribution can be approximated with a normal distribution, which permitted the use of fewer bootstrap samples to obtain a precise estimate of this distribution. With this estimate in place, we computed a $P$ value for $w$. Note that this assumption of normality can be avoided by obtaining more bootstrap samples and calculating the $P$ value from the resulting empirical distribution of bootstrapped $w$ values. To control computational time, we first estimated the $P$ value using 10 bootstrap samples, and then computed 40 more only if this first estimate was between $0.1\alpha$ and $10\alpha$.

If the $P$ value was greater than or equal to $\alpha$, we failed to reject the null hypothesis, and concluded that all the data should belong to one cluster. Otherwise, we rejected the null hypothesis, split the data into the two proposed clusters, and continued recursively down the tree. Specifically, in the next step, we examined the next highest nodes, which propose further binary splits within each of these two newly formed clusters. We applied the same hypothesis test as above to each of these proposed splits. Because these proposed splits, unlike the split at the root node, pertain to subsets of the total cells, we made two modifications to the test. First, we re-applied the dimension reduction procedure to the relevant cells and computed an updated distance matrix for the test statistic calculation. Second, to maintain the FWER at level a, we accounted for the multiple, nested nature of this hypothesis testing by comparing the $P$ value at a given node to $\frac{N_k-1}{N-1}\alpha$, with $N_k$ the number of cells below that node. This approach to FWER control was first proposed by ref. 23 in the context of hierarchical variable selection, and was used by ref. 11 in SHC.

When we failed to reject the null hypothesis at any given node, we did not test any further nodes on that branch. Instead, the cells below that node are all considered to belong to one cluster. Otherwise, if we did reject the null hypothesis, we continued testing at subsequent nodes. By the end of the procedure, we had a set of nodes where we failed to reject the null hypothesis, which corresponds to the final set of clusters.

Parametric model of gene expression

Define the $G\times N$ UMI counts matrix as $\mathit{Y}$. Motivated by previous work¹³, we assumed each gene $g$ belongs to one of two latent states: unexpressed or expressed. If $J_0$ is the set of indices corresponding to unexpressed genes and $J_1$ is the set of indices corresponding to expressed genes, then

$${\mathit{Y}}_{J_0,n}\sim \prod _{g\in J_0}\text{Poisson}\left({\mu }_g\right).$$

This implies that unexpressed genes are described by independent Poisson distributions with means ${\mu }_g$. The expressed genes were assumed to follow a Poisson log-MVN distribution:

$${\mathit{Y}}_{J_1,n}\sim \text{Poisson log-MVN}(\mathit{\mu },\mathbf{\Sigma }),$$

with mean vector $\mathit{\mu }$ of length $\left|J_1\right|$ and $\left|J_1\right|\times \left|J_1\right|$ covariance matrix $\mathbf{\Sigma }$, for all cells $n=1,\dots ,N$. When considering all $G$ genes, this forms a joint distribution for the cell population, which we refer to as $\mathcal{F}$.

Given observed $\mathit{Y}$, we can fit $\mathcal{F}$ in a computationally efficient way using Method of Moments. First, we determined which genes belong to which latent state by testing for overdispersion. Specifically, we computed the dispersion parameter $\alpha$ for each gene, then tested the one-sided hypothesis $\alpha =0$ versus $\alpha >0$ at level 0.05. Genes that are overdispersed, which corresponds to rejecting this null hypothesis, were assumed to be expressed, and otherwise they were assumed to be unexpressed.

Next, we estimated the parameters of $\mathcal{F}$ using expressions derived from the moment equations. For each unexpressed gene $g$, we set

$${\widehat{\mu }}_g=\frac{1}{N}\sum _{n=1}^N{Y}_{g,n}.$$

For each expressed gene $g$, we set

$${\widehat{\text{Σ}}}_{g,g}=\log \left(\frac{v_g-m_g}{m_g^2}+1\right)$$

and

$${\widehat{\mu }}_g=\log m_g-\frac{1}{2}{\widehat{\text{Σ}}}_{g,g},$$

where $m_g$ and $v_g$ are the sample mean and variance, respectively, for gene $g$. Then for any two genes $g_1$, $g_2$ such that $g_1\ne g_2$, we set

$${\widehat{\text{Σ}}}_{g_1,g_2}=\log \left(\frac{{\sigma }_{g_1{g}_2}}{\exp \left({\widehat{\mu }}_{g_1}+{\widehat{\mu }}_{g_2}+\frac{1}{2}\left({\widehat{\text{Σ}}}_{g_1,g_1}+{\widehat{\text{Σ}}}_{g_2,g_2}\right)\right)}+1\right),$$

where ${\sigma }_{g_1{g}_2}$ is the sample covariance between genes $g_1$ and $g_2$. Finally, because the resulting covariance matrix was not guaranteed to be positive definite, we approximated $\widehat{\text{Σ}}$ by a close positive definite matrix. This was done by substituting any undefined values with a constant, reconstructing the matrix with only those eigenvectors with positive eigenvalues, fixing the variances to their previously computed values, and finally replacing any remaining negative or near-zero eigenvalues with small positive values as implemented in ref. 24.

Quantifying clustering quality with the Wald linkage

Given two clusters, we quantified the clustering quality by computing the Ward linkage¹⁴, which is found as follows. If $C_1$ and $C_2$ denote the indices for the cells belonging to clusters 1 and 2, respectively, and if ${\mathit{x}}_i$ represents the coordinates of cell $i$ in principal component (PC) space, we compute

$$\text{ESS}\left(C_1\right)=\sum _{i\in C_1}{\Vert {\mathit{x}}_i-\frac{1}{\left|C_1\right|}\sum _{i\in C_1}{\mathit{x}}_i\Vert }^2$$

$$\text{ESS}\left(C_2\right)=\sum _{i\in C_2}{\Vert {\mathit{x}}_i-\frac{1}{\left|C_2\right|}\sum _{i\in C_2}{\mathit{x}}_i\Vert }^2$$

$$\text{ESS}\left(C_1,C_2\right)=\sum _{i\in C_1\cup C_2}{\Vert {\mathit{x}}_i-\frac{1}{\left|C_1\right|+\left|C_2\right|}\sum _{i\in C_1\cup C_2}{\mathit{x}}_i\Vert }^2.$$

The Ward linkage is then found as $\text{ESS}\left(C_1,C_2\right)-\left(\text{ESS}\left(C_1\right)+\text{ESS}\left(C_2\right)\right)$ We normalize this value by the total number of cells $\left|C_1\right|+\left|C_2\right|$, and the result is reported as our test statistic. Note that larger values correspond to a greater increase in variance if the two clusters were merged, and hence indicate better clustering quality for the two clusters.

Quantifying uncertainty

We summarized the uncertainty for each split in the hierarchical cluster using the adjusted $P$-value metric. Specifically, at each split, we can report the infimum of FWER thresholds such that the split would have been found to be statistically significant. Suppose the $P$ value at node $k$ is $p_k$. To find the split statistically significant while controlling the FWER to level $\alpha$, we require

$$p_k<\frac{N_k-1}{N-1}\alpha ,$$

with $N_k$ the number of cells below the node $k$ and $N$ the total number of cells, as described in ‘Significance hierarchical clustering for scRNA-seq” in Methods. Hence, we would achieve significance at any $\alpha$ belonging to the set

$$\left\{\alpha :\alpha >\frac{N-1}{N_k-1}{p}_k\right\},$$

and we thus report the adjusted $P$ value as the infimum of this set, that is, $\frac{N-1}{N_k-1}{p}_k$.

Significance analysis for pre-computed clusters

Although the pre-computed clusters can arise from any algorithm after any processing pipeline, we again require the raw UMI counts as input. We started by computing a tree-like hierarchy for any given set of clusters. Specifically, for each of $K$ clusters, we computed the average expression for an informative subset of genes. These can either be the set of genes used in the clustering algorithm, if available, or they can be chosen as the $G=\mathrm{2,500}$ genes with the largest deviance under a multinomial null model¹². Because there are many cells per cluster and we have reduced our feature space to an informative subset of genes, the data are no longer small counts for these centers, and we applied Euclidean distance to obtain a $K\times K$ distance matrix. This created a tree whose leaves are the cluster labels, and we followed a similar procedure as before.

In particular, we began at the root node and considered the two-way split dividing ail cells into two clusters. As before, we applied the approximate GLM-PCA transformation, computed Euclidean distance using 30 latent factors, and computed the Ward linkage $w$. We then fit the parametric model to the data and performed parametric bootstrap to generate counts for each cell under the null hypothesis. Because we rarely have access to the exact clustering algorithm used to produce the original clusters, we assigned the randomly generated cells to a cluster by first transforming them with the same GLM-PCA transformation applied to the observed data, computing a distance between each observed cell and each bootstrapped cell, and, for each bootstrapped cell, using majority voting from the $k$-nearest neighbor observed cells for $k=15$. This provided cluster assignments for each bootstrapped sample, which in turn permitted us to compute a null distribution and proceed as in ‘Significance hierarchical clustering for scRNA-seq’ in Methods. If this $k$-nearest neighbor procedure only returned one cluster (which may happen if, for example, one of the original clusters is very tiny and/or highly dispersed), we instead used the clustering procedure in ‘Significance hierarchical clustering for scRNA-seq’ in Methods to cluster the bootstrapped cells. We then continued down the tree as before, considering at each node the cells belonging to the cluster labels of the leaves below that node. If we reached a leaf, we stopped and did not consider further splits within that cluster.

Accounting for batch effects

If the data contain batch effects, this can result in spurious clusters in which the same cell type is split by batch label. In settings where batch labels are known, we made several modifications to our procedure in order to mitigate these effects and ensure the null model accurately represents the data. First, when performing the approximate GLM-PCA procedure, we computed Poisson deviance residuals separately for each batch, and then applied PCA. Second, when testing a split of the clustering tree, we separately computed the Wald linkage for each batch, and reported the final test statistic as the median of these values. Analogously, to obtain the null distribution of test statistics, we fit the null model and generated data for each batch, again computed the Wald linkage in each case, and took the median of these values. Note that, by performing each of these steps within each batch, we avoid making any assumptions, for example linearity, on the parametric form of the batch effects. If a given batch was only minimally represented in a split being tested, specifically if it had fewer than 20 cells in at least one of the clusters, we excluded the cells of that batch from consideration. If this resulted in no cells remaining (for example, if the split perfectly separates by batch), then we automatically considered all cells under this split as belonging to one cluster.

scRNA-seq gating plots

To visualize differences at proposed splits in hierarchical clustering, we introduced scRNA-seq gating plots, inspired by the dot plots used in flow cytometry. At any given node, we first identified differentially expressed genes between cells in the two clusters in question. We used the findMarkers function implemented by scran²⁵ and considered the set of genes with false discovery rate <0.05 and absolute log fold change greater than 0.5. We split these genes into two sets: those that were more highly expressed in the first cluster and those that were more highly expressed in the second cluster. For each cell, we then computed the proportion of UMIs attributed to each of these two sets of genes. The scRNA-seq gating plots compare these two quantities for all cells, colored by cluster label, with density plots on the margins. If the two clusters in fact represent distinct populations, one should be able to visually see at least two clusters in this plot.

Simulated study

To investigate over-clustering in current clustering workflows, we simulated scRNA-seq data from a single distribution to represent one cell population. In particular, we simulated 5,000 cells with 1,000 genes each, representing expressed genes. Previous exploratory analyses found the Poisson log-normal distribution to be appropriate for expressed genes¹³, so counts for gene $g$, where $g=1,\dots ,1,000$, were drawn from a Poisson log-normal $\left({\mu }_g,3\right)$ distribution. The parameters ${\mu }_g$ were set by sampling from a Normal(0,2) distribution and then fixing those values for all cells.

These data were clustered using Seurat’s implementation of the Louvain algorithm². We applied a standard workflow consisting of the following Seurat functions: NormalizeData, ScaleData, RunPCA, RunUMAP, FindNeighbors and Findclusters. All functions were run using default parameters, except for Findclusters, which we ran ten separate times with resolution parameters varying from 0.1 to 1, with intervals of 0.1. Note that the default resolution parameter is 0.8. We then used a popular clustering stability analysis, clustree⁶, to visualize the results across these different parameter choices.

Benchmark data

To construct data for benchmarking, we used 2,885 cells from the 293T cell line¹⁶. The one-population dataset consisted of these 2,885 cells with no changes. To construct the five-populations dataset, the first 20% of the cells were unaltered. Then, distinct permutations over a set of 100 genes, representing the 50 highest-expressing and 50 lowest-expressing genes, were applied to each successive 20% of the cells. The five-similar-populations dataset was created using this same process, except the permutation for the last 20% of the cells differs by only ten genes from the permutation used for the previous 20% of the cells.

When applying the Louvain and Leiden algorithms as implemented by Seurat, we ran these algorithms in two ways. First, we used the default resolution parameter of 0.8. Second, we used clustree to pick the optimal resolution parameter. This was done by varying the resolution parameter from 0.1 to 1 at intervals of 0.1, then choosing the largest parameter such that none of the clusters from the next resolution overlap by more than 25% of cells with two different clusters from the resulting output.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.

Data availability

The datasets used in this work are publicly available and can be found as follows. The 293T cells are available at https://www,10xgenomics.com/resources/datasets/293-t-cells-l-standard-l-l-0. The Human Lung Cell Atlas is available at https://hlca.ds.czbiohub.org/. The mouse cerebellum atlas is available at the Broad Institute Single Cell Portal with study ID SCP795.

Code availability

The software developed in this work is publicly available as an Rpackage at https://github.com/igrabski/sc-SHC ref. 26.