Abstract
Background:
Polygenic risk scores (PRS) are linear combinations of genetic markers weighted by effect size that are commonly used to predict disease risk. For complex heritable diseases such as late-onset Alzheimer’s disease (LOAD), PRS models fail to capture much of the heritability. Additionally, PRS models are highly dependent on the population structure of the data on which effect sizes are assessed and have poor generalizability to new data.
Objective:
The goal of this study is to construct a paragenic risk score that, in addition to single genetic marker data used in PRS, incorporates epistatic interaction features and machine learning methods to predict risk for LOAD.
Methods:
We construct a new state-of-the-art genetic model for risk of Alzheimer’s disease. Our approach innovates over PRS models in two ways: First, by directly incorporating epistatic interactions between SNP loci using an evolutionary algorithm guided by shared pathway information; and second, by estimating risk via an ensemble of non-linear machine learning models rather than a single linear model. We compare the paragenic model to several PRS models from the literature trained on the same dataset.
Results:
The paragenic model is significantly more accurate than the PRS models under 10-fold cross-validation, obtaining an AUC of 83% and near-clinically significant matched sensitivity/specificity of 75%. It remains significantly more accurate when evaluated on an independent holdout dataset and maintains accuracy within APOE genotype strata.
Conclusions:
Paragenic models show potential for improving disease risk prediction for complex heritable diseases such as LOAD over PRS models.
Keywords: Alzheimer’s disease, data mining, deep learning, epistasis, machine learning, predictive genetic testing
INTRODUCTION
Alzheimer’s disease (AD) is the most common cause of dementia, affects millions of Americans, and is the only disease among the leading causes of death in the US for which no effective prevention or cure exists [1]. The FDA recently drafted a set of industry guidelines for clinical trials of AD treatments targeting the earliest stages of disease [2], indicating increasing focus on and investment in presymptomatic intervention. However, trials aimed at averting the underlying causes of disease have proven difficult because pathological changes in AD happen well in advance of cognitive decline. While changes in levels of transient biomarkers, such as amyloid-β (Aβ) and tau in cerebrospinal fluid (CSF) [3] and even blood [4] can be seen prior to onset of symptoms, these changes indicate that pathogenic processes have already begun. Furthermore, a transient biomarker test administered too far in advance of symptom onset may not indicate future risk of developing AD. An accurate genetic test for AD, on the other hand, could be used at any point in life to identify individuals at high risk for developing the disease before changes in biomarkers can be detected.
Development of such a test is complicated by the complex genetic structure of the more common, late-onset form of AD (LOAD). The strongest risk factor for LOAD, the Apolipoprotein E (APOE) ε4 allele, increases risk of developing LOAD ~15 fold for those with 2 copies of the ε4 allele and ~3 fold for those with 1 copy [5]; however, it only accounts for ~9.3% of phenotypic variance [6]. Many additional genetic risk factors have since been identified, all having much smaller effect sizes.
Recent genetic risk prediction models for LOAD have attempted to capture this complexity using polygenic risk scores (PRS), in which an individual’s risk is assessed via an additive model of single nucleotide polymorphism (SNP) markers. The simplest form of PRS (p-value based thresholding, or P + T for short), is calculated by summing the total number of risk alleles across multiple markers, weighted by effect size determined from a genome wide association study (GWAS). PRS models for LOAD have reported area under the receiver operator characteristic curve (AUC) ranging from 0.62–0.78 for clinically diagnosed LOAD [7] and 0.82 in pathologically confirmed cases [8]. P + T models implicitly assume independence between SNP markers, and accordingly prune the set of candidate markers to minimize linkage disequilibrium (LD). Several methods have been proposed to correct for LD architecture without pruning potentially meaningful markers. PRS-SBayesR [9] and PRS-CS [10] both use a Bayesian framework to correct prior effect sizes from a GWAS by accommodating for LD architecture through an external reference panel; PRS-SBayesR employs Bayesian multiple regression whereas PRS-CS employs a continuous shrinkage method.
These models focus only on the additive effects of SNPs, leaving a significant amount of heritability unexplained. Of the ~63% estimated heritability of LOAD [11], only 28–39% is explained by additive genetic components [12]; PRS models capture only 11.4% of the estimated heritability [13].
One possible source of missing heritability is non-additive, or epistatic, interactions between SNPs. Epistatic interactions have been discovered involving genes that are independently associated with LOAD, as well as between genes that are not significantly associated with LOAD on their own [14].
This has led to an increased interest in incorporating epistatic interactions into PRS-like models. A recent study [15] constructed a LOAD genetic risk prediction model for AD combining epistatic risk with polygenic risk and achieved an AUC of 0.67. Although this was lower than other reported PRS models for AD, it was an improvement over their model using only PRS scores in the same dataset. Genome-wide epistasis studies are often limited to two-way interactions between SNPs; the large number of SNPs means that the number of possible genotype combinations for higher order interactions is practically infinite.
In [16], the authors develop a high-order interactions-aware PRS (hiPRS) by combining frequent itemsets mining with a mutual information-based interaction selection algorithm to construct an interpretable weighted PRS-like model. When used to predict mortality of stage II-III colon-rectal cancer patients treated with oxaliplatin, they were able to construct a model with an AUC of 0.72. In [17], SNPs occurring frequently in cases are partitioned into risk and protective sets and a portion from each is selected through an odds ratio criterion between cases and controls. The full model is then trained on the proportion of protective and risk SNP sets in each study participant’s genome. With this model, the authors obtained AUCs ranging from 0.63–0.78 for a variety of toxicity endpoints in prostate cancer radiotherapy patients.
Several authors have explored epistatic effects in AD through multifactor dimensionality reduction (MDR) [18] and variations thereof. In its most basic form, MDR designates a combination of alleles as “high risk” or “low risk”, depending on the proportion of cases to controls possessing that genotype. In [15] the authors develop an epistatic risk score (ERS) for AD inspired by MDR to capture interaction terms in an additive model. This ERS is combined with a traditional (P + T) PRS as a weighted sum, with weighting factor chosen to maximize model AUC. A similar approach is pursued in [19], wherein an additive ERS model is constructed with effect sizes provided by Model-Based MDR. When [15] is applied to clinical AD diagnosis, this model obtains an AUC of 0.714.
In this paper, we use Crush-MDR [20], a machine learning algorithm that combines multifactor dimensionality reduction with an evolutionary search algorithm, to identify epistatic interactions in LOAD. Crush-MDR stochastically explores the interaction space, allowing for the discovery of rare interactions and significant interactions whose individual markers may have only nominal effect1. These interactions are included with single SNPs and PRS values to produce a non-linear, state-of-the-art LOAD risk prediction model. We term our model a paragenic risk model as it incorporates genetic markers beyond individual SNPs and is an ensemble of machine learning models together with a PRS model.
To validate our model, we compare its performance to P + T, PRS-CS, and hiPRS PRS models. The paragenic risk model shows significant improvement over PRS-based models or gradient boosting machines alone, obtaining a mean 10-fold cross-validated area under the receiver operator characteristic curve (AUC) of 0.83 (95% CI [0.82, 0.84]) in predicting LOAD in clinically diagnosed cases. Additionally, our paragenic model maintains high AUC within APOE genotype strata, unlike PRS models.
MATERIALS AND METHODS
Participants
The dataset used for modeling consisted of data from the Alzheimer’s Disease Neuroimaging Initiative (ADNI), the National Alzheimer’s Coordinating Center and the Alzheimer’s Disease Genetics Consortium (NACC/ADGC), the Framingham Heart Study (FHS), the Knight-ADRC at Washington University in St. Louis (Knight-ADRC), and Emory University. Phenotypes and covariates (case/control status, age, APOE genotypes, and education level) were not defined consistently across studies and were re-categorized to be as consistent as possible (Supplementary Methods). Individuals under the age of 55, the minimum age for inclusion in ADNI, were excluded from the dataset, resulting in an initial dataset consisting of 9,767 individuals, 3,879 (39.7%) of which were cases.
Participants with non-European ancestry were excluded from this study, in keeping with the methodology followed by previously-published PRS models, in which the GWAS summary statistics [21] were computed only on individuals of European ancestry. Removing population structure is a nearly universally-followed best practice for genetics research, as not doing so can result in false positive and false negative association results. Moreover, the subsample of non-European participants was prohibitively small (n = 172) to perform a cross-ancestry assessment. Genetic ancestry was determined by genomic principal components analysis (PCA), computed with regards to an independent reference population taken from Phase 3 of the 1000 Genomes Project [22] (see the Supplementary Material for more details). After removing non-European individuals, we were left with a final dataset consisting of 9,595 individuals, 3,818 (39.8%) of whom were cases (Table 1).
Table 1.
Overview of study participants. Age and Education are presented as mean and standard deviation in years, sex as number of males, and APOE as count for 0, 1, and 2 alleles
| Covariate | Cross-validation |
Holdout (ADNI3) |
||
|---|---|---|---|---|
| Cases (n = 3,879, 40%) | Controls (n = 5,888, 60%) | Cases (n = 28, 11%) | Controls (n = 238, 89%) | |
|
| ||||
| Age | 78.0 (8.8) | 74.0 (8.8) | 74.0 (8.9) | 72.3 (6.3) |
| Sex | 1,937 (50%) | 2,436 (41%) | 17 (61%) | 91 (38%) |
| APOE ε2 | 3,588, 285, 6 | 5,039, 821, 28 | 27, 1, 0 | 214, 24, 0 |
| APOE ε4 | 1,583, 1,804, 492 | 4,291, 1,465, 132 | 9, 14, 5 | 157, 73, 8 |
| Education | 15.1 (3.1) | 15.8 (2.6) | 15.6 (2.8) | 16.9 (2.2) |
The ADNI3 dataset was held out as an independent validation set. Diagnosis was made in the same way as the previous ADNI phases. After removing individuals related to or included in the main dataset, the ADNI3 data consisted of 316 individuals, assessed at multiple ages, for a total of 681 records. There were 28 unique cases and 238 unique controls. There were 50 unique instances of mild cognitive impairment (MCI), which were excluded from modeling.
Data collection
For data collected on the Emory University cohort, all research participants provided informed consent for blood and CSF collection and allowed clinical and biospecimen data to be repurposed under protocols approved by the Institutional Review Board of Emory University. A clinical diagnosis using standard clinical research criteria was assigned by a neurologist with subspecialty training in behavioral neurology. Genotyping was performed using the Affymetrix Precision Medicine Array using DNA extracted from the buffy coat by the Qiagen GenePure kit following the manufacturer’s recommended protocol.
Genotyping
Different genotyping chips were used across studies; therefore, genotypes from all studies were imputed to the Haplotype Reference Consortium (HRCr1.1) panel using the Michigan Imputation Server [23]. All files were prepared for imputation using the provided perl script (HRC-1000G-checkbim.pl). The imputed genotypes were filtered to biallelic SNPs with R-squared>0.8 in all cohorts. SNPs with large differences in minor allele frequency (MAF) across studies or with potential strand flips were also removed. KING [24] was used to identify duplicate participants that were then removed from the dataset. Variants were then filtered to include those with MAF>0.1 using PLINK (v. 1.90), resulting in a final dataset containing ~3.7M individual SNPs.
Model overview
Throughout this work, we will use the following terminology to refer to different models trained to predict AD status:
Baseline model: a gradient boosting machines (GBM) model trained on age, sex, and APOE genotype.
PRS model: a linear model in which a PRS is combined with the above covariates. We consider the P + T, PRS-CS, and hiPRS polygenic models.
Epistatic model: any model trained on mined epistatic features along with individual SNP markers and other covariates. We used two separate epistatic models trained on the same set of features—one using GBM and one using a neural network.
Ensemble model: any model trained on the predictions of other models.
Paragenic model: any ensemble model containing a PRS model and at least one epistatic model.
The paragenic modeling pipeline consists of three main phases: 1) feature engineering and selection, in which impactful SNP variants and interaction terms are discovered; 2) component modeling, in which individual models are trained on (possibly subsets of) the engineered features to predict LOAD risk; and 3) ensemble modeling in which the predictions of the component models are used to train a final LOAD risk model (Fig. 1). We now provide an overview of each of these steps, leaving the details to the subsequent sections.
Fig. 1.
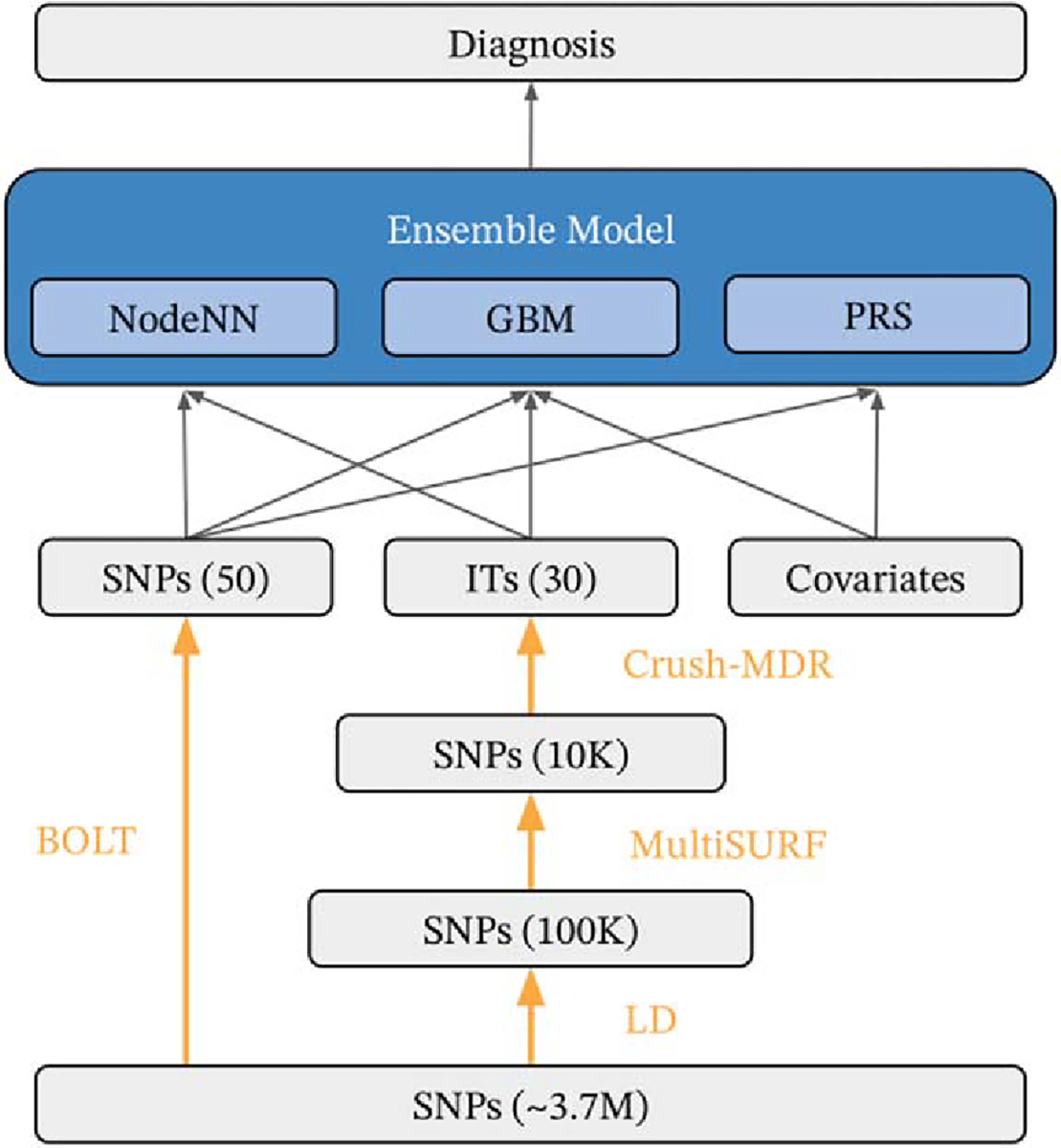
Schematic of mining and modeling procedure. Data is labeled in gray, mining steps in orange, and models in blue. Black arrows indicate which features go into which models. Association testing was performed using BOLT, and the top scoring SNPs were directly used as model features. Interaction features were mined by LD pruning to ~100K variants, further reduced to ~10K variants using MultiSURF, and 30 interaction features were found with Crush-MDR. An ensemble of neural network (NodeNN), Gradient boosting (GBM), and logistic regression PRS models (PRS) were trained on case/control status.
Phase 1. Three types of features were used in the modeling: covariates (age, sex, APOE genotype, education level, and ancestral principal components), single SNP markers, and interaction features. Association testing was performed on the candidate SNPs to determine a significantly smaller set of individual SNP features. Interaction features were mined with the following pipeline: First, LD pruning was performed to reduce the set of candidate SNPs under consideration for interaction testing to ~100 K variants. This set of SNPs was further reduced using the MultiSURF algorithm to ~10 K variants. Finally, the Crush-MDR algorithm was used on this SNP candidate pool to mine for association with case/control status.
Phase 2. Three separate component models were then trained. A GBM model and a neural network (NN) model were trained on the above features. A logistic regression model was trained on the set of covariate features together with a P + T PRS.
Phase 3. Finally, the probabilities predicted by the component models were used to train a final logistic regression classifier.
All model assessment was performed using 10-fold nested cross-validation, and the same cross-validation fold partitions were used for each individual model.
Epistatic models
Feature engineering and association testing pipelines were run both to select individual SNPs as well as interactions between SNPs for inclusion in the individual epistatic models (details below). The selected features, along with covariates (age, sex, APOE, education level, and the first 20 genomic principal components) were used to independently train and validate GBM and neural network models predicting case/control status. We chose XGBoost [25] as the GBM due to its ability to handle missing features, and NODEnn [26] for the NN model.
Individual SNP selection
Individual SNPs were selected by linear mixed modeling (LMM) association with case/control status using BOLT [27]. The participants were randomly partitioned into 10 cross-validation folds. Related individuals were detected using KING [24] and assigned to the same fold for the LMM step, after which the maximum unrelated set for each family group was computed and retained. This procedure for handling relatedness resulted in slight variability between folds of the sizes of the training/test sets. Training sets (each consisting of 9 folds) had a mean of 3374 (sd 18.9) cases and 4851 (sd 23.5) controls, and the test sets (1-fold) had a mean of 375 (sd 18.9) cases and 539 (sd 23.5) controls.
In preliminary studies, we found there to be diminishing returns in terms of model complexity and computational requirements with regards to the number of single SNP features included (see Supplementary Figure 1). Thus, the top 50 SNPs as ranked by log odds ratio were included as features in the modeling step, which empirically had a good tradeoff between model performance and complexity/computability.
Epistatic interaction feature engineering
Epistatic interaction terms were selected using Crush-MDR [20]. This algorithm uses an evolutionary algorithm guided by “expert knowledge” to mine the space of SNP interactions using MDR [18]. In the context of evolutionary algorithms, expert knowledge refers to an external source of data used to either encourage or discourage the stochastic evolution to include particular SNPs with the other SNPs in a candidate interaction. Candidate SNPs for interaction mining were selected within each training set of unrelated individuals.
To reduce the dataset to a size that could fit in memory, we performed LD pruning using PLINK to downsample to approximately 100K SNPs. Empirically, a downsampling r2 > 0.11 resulted in the desired number of SNPs. Within each pair of SNPs in LD, the SNP with the higher IGAP effect size was retained. The dataset was further reduced using the MultiSURF algorithm [28] and the top 10,000 SNPs associated with disease status were retained. MultiSURF was run on an Amazon Web Services (AWS) Elastic Compute Cloud (EC2) cluster. Crush-MDR was constrained to mine for combinations of 2 or 3 SNPs, resulting in an interaction space consisting of ~167 billion possible interactions.
MultiSURF is a Relief-based algorithm, which uses a nearest neighbor approach to estimate the quality of each feature in the context of other features. In our context, this means that it can identify SNPs that are involved in interactions but may not have an individual association. Crush is an evolutionary algorithm that distributes calculations across a large number of compute nodes, providing an efficient way to search a space that is too large to exhaust. Each interaction is tested for its association with the phenotype using one or more objective functions, and Crush evolves the interactions in promising directions to intelligently search the massive space of possible interactions. For this work, two objectives were calculated for each interaction: MDR balanced accuracy and mean cartesian entropy between all pairs of SNPs in the interaction (see [20]). Crush then used multiobjective optimization to select optimal interactions using Pareto optimization. The evolution was guided using expert knowledge in the form of the number of shared pathways between each pair of SNPs as well as pairwise mutual information conditioned on case/control status. There is still a significant stochastic component to Crush’s evolution, but using expert knowledge means that interactions with shared pathways and/or high mutual information are more likely to be evolved to and subsequently examined.
Shared pathways were computed using annotations from the Gene Ontology (GO) database [29, 30]. Each SNP was associated with the gene closest in distance to it, or containing it if there was such a gene. The number of shared pathways between two SNPs was defined as the number of unique GO terms shared by both genes. GO terms from all three aspects (molecular function, cellular component, biological process) and at any point in the hierarchy were considered. The interactions on the Pareto front were selected as features for downstream modeling.
MDR’s association calculation is based on converting each interaction into a set of high-risk and low-risk genotype combinations, rather than the interactions themselves. Therefore, the interaction terms were represented for each individual as whether they had a low-risk or high-risk genotype combination, based on the relative proportion of cases and controls with that genotype combination in the training set. Genotype combinations that were not found in the training set were coded as missing.
Gradient boosting model
A GBM was trained on the variants, epistatic terms, and covariates selected above using R (version 3.6) and the XGBoost library (version 1.3.0) [25]. Within each cross-validation training fold, the hyperparameters were tuned in an inner cross-validation loop using Origin [31], a distributed implementation of the nondominated sorting genetic algorithm II (NSGA II) [32], run on a cluster of AWS spot instances. Hyperparameters were tuned using the following two step procedure. First, the learning rate was set to 0.1 and the number of trees to 1000 while the eta, max_depth, min_child_weight, subsample, and gamma parameters were tuned. The values for these parameters were then fixed, the learning rate set to 0.05, and the number of trees then tuned, bound between 500 and 10,000 trees.
Neural network model
The NODEnn architecture does not support missing feature values; therefore, only variants and epistatic terms were included in the modeling as there was no way to meaningfully impute the environmental covariates. Imputed genotype dosage values were used in place of allele counts for single SNPs to minimize missing values; any remaining missing values were imputed using k-nearest neighbors (k = 5) imputation on the training set. After imputation, the dosage and epistatic features were normalized to be between 0 and 1.
The NODEnn model was trained in Python 3.9 using the PyTorch implementation2 provided by the original authors [26] running on an NVIDIA Titan RTX GPU. Our network consisted of two blocks, each consisting of 1024 neural trees with depth = 6 and dimension = 3 and quasi-hyperbolic Adam [33] with the recommended hyperparameter settings of v0 = 0.7, v1 = 1.0, β0 = 0.95and β1 = 0.998astheoptimizer. The NODEnn model was regularized using early stopping. On each fold, 10% of the training set was held out as a validation set; training was stopped when the model failed to improve after 5 epochs.
Calculation of PRS model
We compare our model to several PRS and PRS-like models: a P + T model in which candidate SNPs are determined using p-value based clumping and thresholding [34], the PRS-CS model [10], and the hiPRS model [16]. In brief, the participants were partitioned into a discovery set, on which SNPs were selected and other model fitting steps were performed (e.g., fitting the posterior effect sizes in PRS-CS), and a test set on which the PRS model was evaluated. The same cross-validation folds as the epistatic model were used: the training sets were used as discovery sets in the PRS models and the test sets were used for validation.
Standard quality control procedures were applied: only SNPs having MAF≥0.01, Hardy–Weinberg equilibrium χ2 test p-value>10−6 and genotyping call rate ≥ 0.9 were included in the discovery set [35]. Individuals with genotype missingness ≥ 0.1 were removed and related individuals as determined with a kinship coefficient cutoff of 0.125 were randomly pruned. The PRS scores were incorporated with APOE ε2, ε4 genotype, age, and sex into a predictive model under logistic regression using the StatsModels package (version 0.13.1) [36].
The P + T model was computed as a linear combination of the discovery set SNPs, weighted by the effect sizes from the IGAP study[21]3.We performed random LD pruning and intelligent pruning with the–clump option in PLINK using r2 > 0.2 and a physical distancing threshold of 1Mb to be consistent with [34]. In addition to doing SNP selection through discovery sets as above, we also experimented with selecting SNPs based directly off of the IGAP p-values. The resulting model obtained an AUC lower than those with SNP selection performed on the discovery sets above, and thus was excluded from further analysis.
Markers were selected using p-value thresholds ranging from 0.05 to 1.0; the model with significance threshold p = 0.6 resulted in the PRS model with the highest AUC and was used for comparative analysis.
The PRS-CS model [10] was run with the default parameter settings (gamma-gamma prior parameters a = 1, b = 0.5; ϕ automatically inferred from the data, and 1000 Markov chain Monte Carlo iterations with 500 burn-in iterations) and the provided LD reference panel of European samples from Phase 3 of the 1000 Genomes Project [22]. Prior effect sizes were taken from the IGAP study [21].
The hiPRS model [16] was computed with 10 interaction terms and default threshold parameter (δ = 0.1). For computational feasibility, we used a smaller set of validated SNPs from a different GWAS [37]. After QC, 30 SNPs remained for modeling.
Paragenic and ensemble models
To train the ensemble models, within-training-set predictions were computed on each fold for the GBM and NN epistatic models as well as the P + T PRS model. For each training fold, these predictions were provided as features to train an ensemble model by stacking [38] with logistic regression as a meta model using Scikit-Learn (version 1.1.1) [39]. Predictions for the stacked model were then computed on the test set for each fold and used for final ensemble model evaluation. We also trained and evaluated an ensemble model for each of the various combinations of individual GBM, NN, and PRS models. Figure 2 and Supplementary Table 1 summarize the selected features.
Fig. 2.
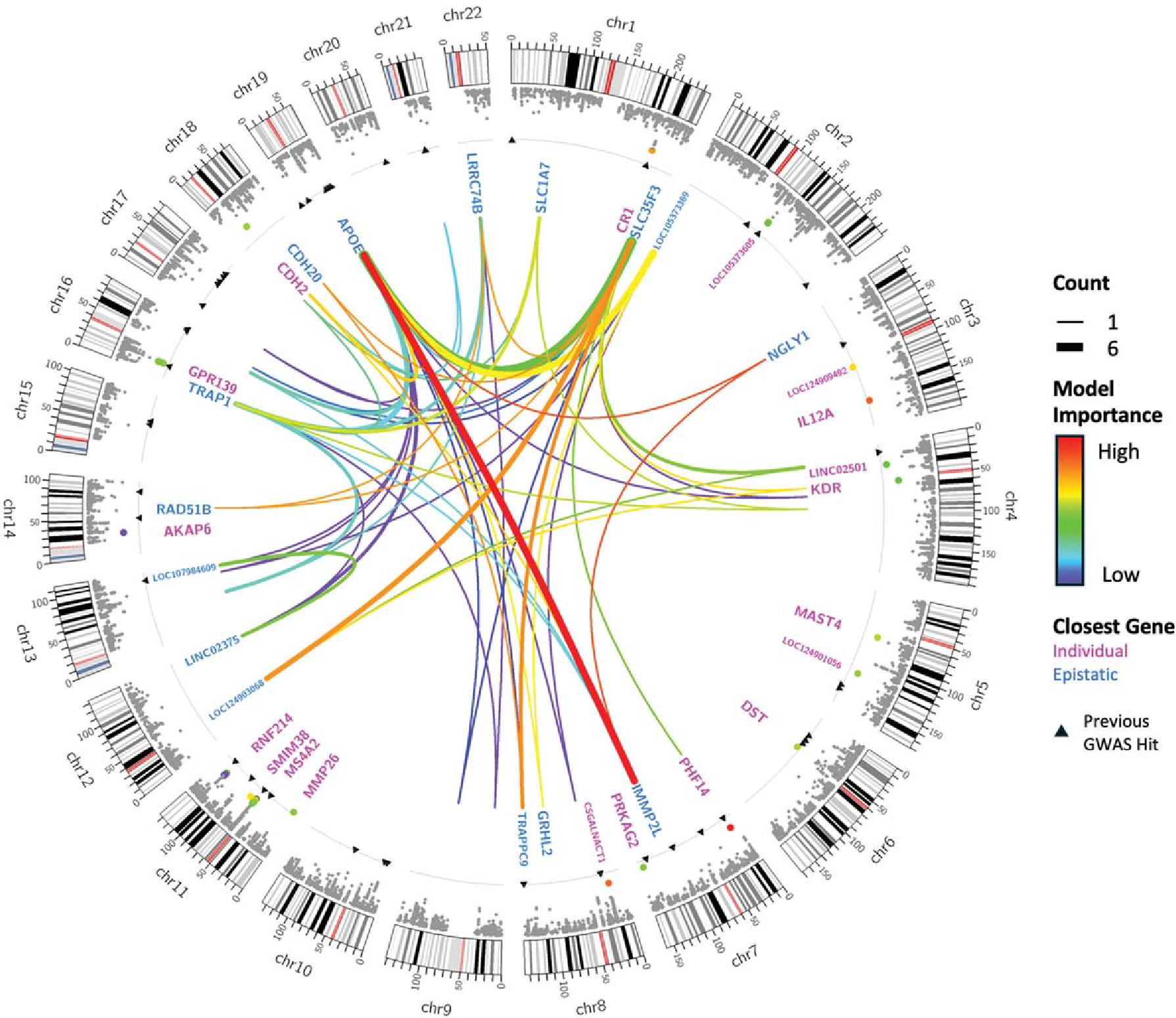
Feature selection results. Along each chromosome, a Manhattan plot shows the −log(p) for each SNP, with the 50 SNPs included in the model highlighted and colored according to their relative feature importance in the XGBoost model. Black triangles indicate the positions of GWAS hits associated with late-onset AD at a p-value ≤ 5 × 10−8 in the GWAS Catalog [40]. The gray line shows the genome-wide significance threshold of 5 × 10−8. In the center, the 30 epistatic interactions on the Pareto front are shown. Line thickness is proportional to the number of times each pair of SNPs appeared on the Pareto front, and they are also colored according to feature importance in the model. Names of closest genes are given for SNPs selected individually (magenta) or as part of important epistatic interactions (blue). Plot created using Circos [41].
RESULTS
The paragenic ensemble models were compared to their individual component models and PRS models, as well as combinations of the individual components of the model ensemble. A baseline GBM model on age, sex, and number of APOE ε2 and ε4 alleles was included as well. Model efficacy was measured by area under the receiver operator characteristic curve (ROC AUC or just AUC), specificity, and sensitivity. Models were evaluated both by cross-validation performance and in the independent holdout set of ADNI3 participants. Multiple testing correction was performed with the Bonferroni method.
Model performance
Models were first assessed using the test set predictions from 10-fold cross-validation. Model AUC, sensitivity, and specificity was calculated for each test set (Table 2). Probability thresholds maximizing the sum of sensitivity and specificity were computed in the training sets for each fold and then applied to the test sets; confidence intervals of sensitivity and specificity statistics were computed using bootstrap sampling. (Model analysis including all participants, including those of non-European descent, can be found in Supplementary Table 2.)
Table 2.
Comparison of individual models and ensembles on cross-validation, calculated as mean and 95% confidence intervals across folds
| Model | ROC AUC | Specificity | Sensitivity |
|---|---|---|---|
|
| |||
| Baseline (age + sex + APOE) | 0.749 (0.739, 0.759) | 0.735 (0.723, 0.747) | 0.641 (0.626, 0.657) |
| PRS | 0.796 (0.786, 0.805) | 0.757 (0.746, 0.769) | 0.698 (0.683, 0.712) |
| PRS-CS | 0.787 (0.777, 0.796) | 0.723 (0.711, 0.735) | 0.718 (0.704, 0.733) |
| HiPRS | 0.746 (0.736, 0.756) | 0.688 (0.676, 0.700) | 0.676 (0.661, 0.691) |
| GBM | 0.804 (0.795, 0.813) | 0.707 (0.695, 0.719) | 0.746 (0.732, 0.759) |
| NN | 0.727 (0.716, 0.737) | 0.687 (0.675, 0.699) | 0.648 (0.632, 0.664) |
| PRS + GBM | 0.829 (0.820, 0.837) | 0.758 (0.745, 0.769) | 0.741 (0.726, 0.755) |
| GBM + NN | 0.803 (0.794, 0.812) | 0.711 (0.699, 0.722) | 0.740 (0.725, 0.753) |
| PRS + NN | 0.801 (0.792, 0.810) | 0.726 (0.714, 0.737) | 0.738 (0.724, 0.752) |
| PRS + GBM + NN | 0.829 (0.821, 0.838) | 0.761 (0.750, 0.772) | 0.736 (0.722, 0.749) |
The paragenic model on PRS + GBM + NN significantly outperformed all individual models (DeLong test statistic Z = −3.2555, p-value=0.0006 between the paragenic model and the model with the next highest AUC). Across the board, the addition of GBM or PRS to a model resulted in significantly improved cross-validation performance.
Models were then trained on the entire dataset and predictions were made on the ADNI3 holdout set. Again, the maximized sum of sensitivity and specificity probability threshold was computed on the training set, and sensitivity and specificity confidence intervals were computed via bootstrapping in the holdout set (Table 3). Comparison of ROC curves in the cross-validation and ADNI3 sets are shown in Fig. 3.
Table 3.
Comparison of individual models and ensembles on holdout dataset (ADNI3)
| Model | ROC AUC | Specificity | Sensitivity |
|---|---|---|---|
|
| |||
| Baseline (age + sex + APOE) | 0.743 (0.628, 0.843) | 0.668 (0.610, 0.728) | 0.655 (0.464, 0.826) |
| PRS | 0.720 (0.608, 0.823) | 0.704 (0.643, 0.764) | 0.678 (0.500, 0.846) |
| PRS-CS | 0.719 (0.599, 0.824) | 0.734 (0.676, 0.791) | 0.609 (0.414, 0.800) |
| HiPRS | 0.756 (0.648, 0.847) | 0.782 (0.724, 0.833) | 0.607 (0.423, 0.778) |
| GBM | 0.810 (0.731, 0.874) | 0.743 (0.688, 0.799) | 0.759 (0.579, 0.920) |
| NN | 0.766 (0.674, 0.849) | 0.590 (0.531, 0.654) | 0.826 (0.675, 0.957) |
| PRS + GBM | 0.788 (0.694, 0.869) | 0.689 (0.631, 0.750) | 0.750 (0.556, 0.903) |
| GBM + NN | 0.808 (0.730, 0.878) | 0.692 (0.637, 0.749) | 0.786 (0.615, 0.929) |
| PRS + NN | 0.750 (0.650, 0.854) | 0.638 (0.576, 0.697) | 0.792 (0.625, 0.926) |
| PRS + GBM + NN | 0.782 (0.691, 0.867) | 0.699 (0.636, 0.754) | 0.714 (0.538, 0.870) |
Fig. 3.
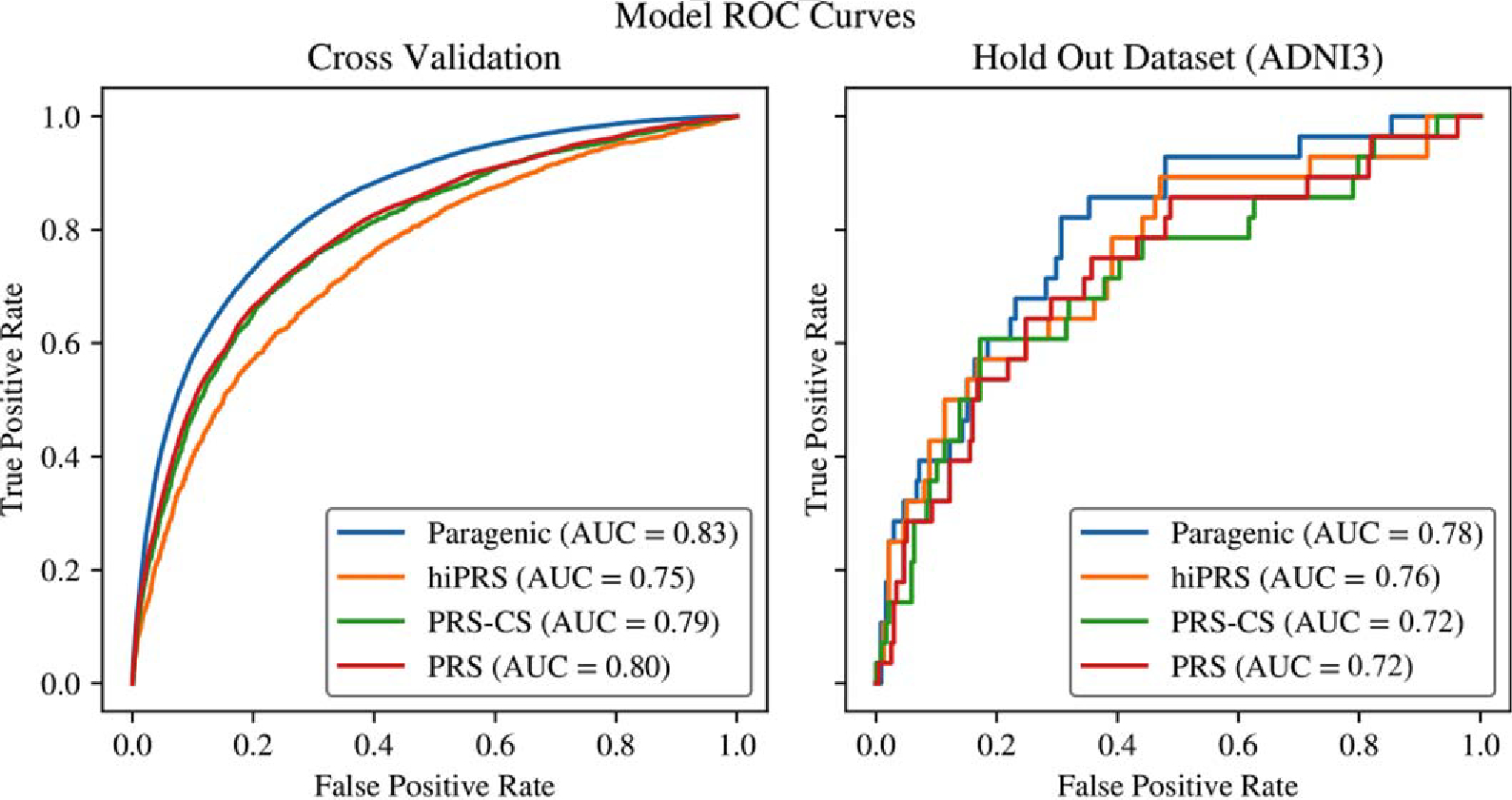
Comparison of ROC curves between PRS and Paragenic models on cross-validation and hold out data (ADNI3).
The GBM and GBM+NN models outperformed all other models in the holdout set in terms of AUC, although the difference is only significant relative to PRS and PRS-CS (Z = −2.0857 – −2.1220, p-value = 0.01692 – 0.01850). Interestingly, contrary to the cross-validation results, inclusion of PRS in an ensemble was generally detrimental to performance on the holdout set.
Model performance by APOE genotype
The full paragenic model (PRS + GBM + NN) showed strong AUC performance within all APOE genotypes in the cross-validation dataset, significantly outperforming PRS within all APOE genotypes except for ε4/ε4 (Fig. 4). The paragenic model performed consistently well within each stratum, staying within 4% points of the unstratified AUC for all genotypes except ε4/ε4. The PRS model largely performed much poorer within each stratum compared to the unstratified AUC, generally 6–7% lower with the exception of the ε2/ε4 stratum. Both models had AUCs on the ε2/ε4 stratum on par with their respective unstratified AUCs. The ε2/ε2 genotype was not well-represented in our data and so was discarded from this analysis.
Fig. 4.
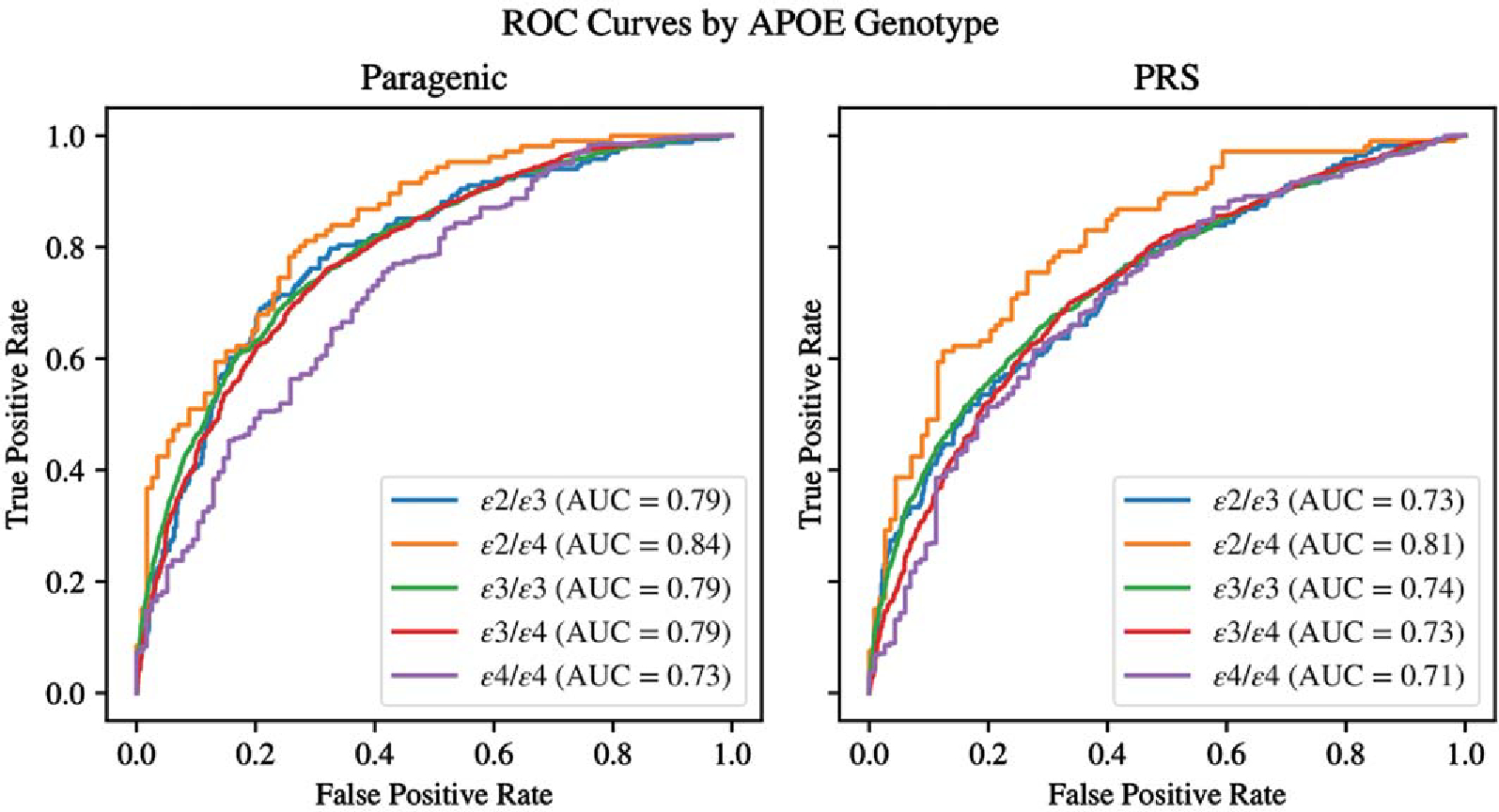
Comparison of ROC curves between PRS and Paragenic models between APOE genotypes on cross-validation data.
Risk prediction by age
To assess age-dependent risk, the Kaplan–Meier survival curve was estimated on the cross-validation dataset within each score quantile of the full paragenic model using the lifelines package (version 0.26.4) in Python 3.9 [42]. The resulting curve showed significant discrimination for LOAD risk at different ages (Fig. 5). The logrank p-values between Q1 and Q2, Q2 and Q3, Q3 and Q4 were 0.0016,<10−14, and<10−17 respectively.
Fig. 5.
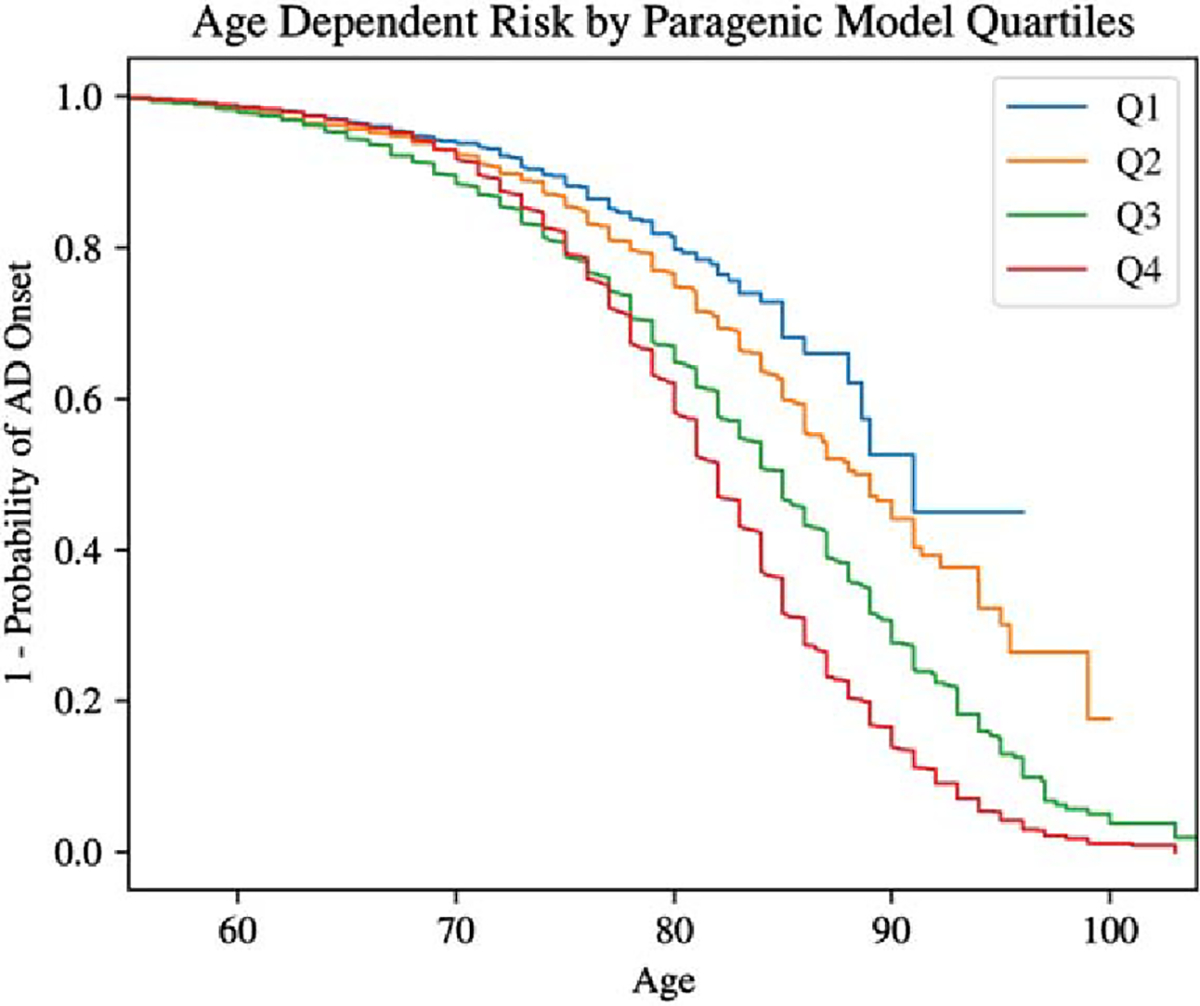
Kaplan–Meier survival curves for paragenic model score quartiles.
Clinical utility
To assess our model for clinical utility, we analyzed the positive and negative predictive values (PPV and NPV) in Python. Following [34], we computed adjusted PPV and NPV values assuming varying LOAD population prevalences of 17% (overall lifetime risk) and 32% (risk for ages 85 + [43]). The results for cross-validation are presented in Table 4.
Table 4.
Comparison of positive and negative predictive value of individual models and ensembles on cross-validation data
| Model | Negative predictive value |
Positive predictive value |
||
|---|---|---|---|---|
| 17% prevalence | 32% prevalence | 17% prevalence | 32% prevalence | |
|
| ||||
| Baseline (age + sex + APOE) | 0.915 (0.911, 0.919) | 0.824 (0.817, 0.832) | 0.301 (0.288, 0.315) | 0.495 (0.476, 0.516) |
| PRS | 0.928 (0.925, 0.932) | 0.849 (0.842, 0.856) | 0.353 (0.338, 0.370) | 0.557 (0.535, 0.578) |
| PRS-CS | 0.926 (0.922, 0.930) | 0.845 (0.838, 0.852) | 0.349 (0.334, 0.366) | 0.553 (0.533, 0.575) |
| hiPRS | 0.912 (0.908, 0.916) | 0.819 (0.811, 0.826) | 0.313 (0.300, 0.328) | 0.514 (0.494, 0.534) |
| GBM | 0.928 (0.925, 0.932) | 0.849 (0.842, 0.855) | 0.357 (0.341, 0.374) | 0.563 (0.543, 0.584) |
| NN | 0.910 (0.906, 0.914) | 0.815 (0.807, 0.823) | 0.266 (0.254, 0.278) | 0.446 (0.429, 0.465) |
| PRS + GBM | 0.935 (0.932, 0.939) | 0.863 (0.856, 0.869) | 0.386 (0.369, 0.403) | 0.593 (0.572, 0.615) |
| GBM + NN | 0.927 (0.923, 0.930) | 0.847 (0.839, 0.854) | 0.358 (0.342, 0.376) | 0.565 (0.544, 0.586) |
| PRS + NN | 0.932 (0.929, 0.936) | 0.857 (0.850, 0.864) | 0.342 (0.327, 0.359) | 0.539 (0.519, 0.559) |
| PRS + GBM + NN | 0.935 (0.932, 0.939) | 0.863 (0.856, 0.869) | 0.386 (0.370, 0.405) | 0.594 (0.574, 0.616) |
The full paragenic model and the paragenic GBM + PRS model had nearly identical predictive value, and both were significantly better than the next closest contender.
The predictive values on the holdout set are consistent with the analysis on the cross-validation dataset. The full paragenic model had the strongest PPV at both prevalences analyzed, but poorer NPV than the purely epistatic models (GBM and NN) (Table 5).
Table 5.
Comparison of positive and negative predictive value of individual models and ensembles on holdout data (ADNI3)
| Model | Negative predictive value |
Positive predictive value |
||
|---|---|---|---|---|
| 17% prevalence | 32% prevalence | 17% prevalence | 32% prevalence | |
|
| ||||
| Baseline (age + sex + APOE) | 0.913 (0.883, 0.944) | 0.820 (0.764, 0.878) | 0.274 (0.232, 0.324) | 0.455 (0.391, 0.535) |
| PRS | 0.919 (0.889, 0.949) | 0.831 (0.773, 0.894) | 0.286 (0.241, 0.337) | 0.471 (0.402, 0.550) |
| PRS-CS | 0.905 (0.874, 0.936) | 0.807 (0.752, 0.864) | 0.286 (0.242, 0.339) | 0.480 (0.411, 0.564) |
| HiPRS | 0.898 (0.852, 0.945) | 0.793 (0.708, 0.886) | 0.271 (0.214, 0.341) | 0.459 (0.370, 0.584) |
| GBM | 0.950 (0.925, 0.975) | 0.893 (0.840, 0.946) | 0.341 (0.290, 0.402) | 0.524 (0.456, 0.608) |
| NN | 0.937 (0.902, 0.969) | 0.866 (0.802, 0.929) | 0.188 (0.159, 0.222) | 0.319 (0.278, 0.370) |
| PRS + GBM | 0.933 (0.905, 0.960) | 0.861 (0.808, 0.915) | 0.354 (0.301, 0.415) | 0.550 (0.479, 0.641) |
| GBM + NN | 0.951 (0.924, 0.975) | 0.892 (0.840, 0.945) | 0.347 (0.296, 0.405) | 0.532 (0.462, 0.616) |
| PRS + NN | 0.935 (0.905, 0.964) | 0.863 (0.803, 0.920) | 0.263 (0.225, 0.312) | 0.427 (0.370, 0.493) |
| PRS + GBM + NN | 0.935 (0.907, 0.961) | 0.864 (0.810, 0.917) | 0.383 (0.325, 0.452) | 0.593 (0.511, 0.690) |
DISCUSSION
In this study, we built a genetic risk prediction model for LOAD using machine learning techniques with the goal of improving upon existing PRS models. Though PRS models have successfully captured the additive genetic components of disease, they do not capture more complex genetic structure such as epistatic interactions. We constructed a PRS model on our dataset and additionally mined the data for epistatic features to include with single SNPs in machine learning models. The final paragenic risk model, an ensemble of a logistic PRS model, a NN epistatic model (NODEnn), and a GBM epistatic model (XGBoost), achieved an AUC of 0.829 in cross-fold validation. This performance is significantly higher than published PRS models (Figs. 3 and 4). While other machine learning models have reported comparable or higher AUCs [44], they performed feature engineering in-sample, which can lead to overestimation of expected performance on real-world (out-of-sample) data [45].
The GBM epistatic model and paragenic models outperformed all variants of PRS in terms of ROC AUC, sensitivity, and specificity both in cross-validation and in an independent holdout set. Ensembling PRS and epistatic models generally improved the modeling over the individual component models across all metrics. As expected, most types of models performed less well on the held-out dataset than in cross-validation. The exceptions were hiPRS, GBM, NN, and GBM + NN, which actually performed slightly better in the holdout set. Ensembling of epistatic models with P + T did not give the same improvement in the holdout set as was observed in the cross-validation analysis, likely because the P + T model performed poorly on the holdout dataset in general. We suspect this is due to the well-known difficulties in applying PRS models trained on one dataset to another [46]. However, ensembling with a P + T model did improve positive predictive value on the holdout set. This issue was not apparent in the cross-validation study, likely because the folds were partitioned without stratification by data source, resulting in test/train splits comprising similar populations. Moreover, the holdout dataset had a significantly smaller proportion of cases, leading to poorer performance of the paragenic models in terms of specificity and NPV.
Importantly, the paragenic model showed improved discriminative ability over the PRS models regardless of APOE genotype. Although the ε4/ε4 genotype is a strong single marker predictor of LOAD, only 9.6% of people with AD carry this genotype and the prevalence is heterogeneous among populations [47]. Thus, predicting AD risk even in the absence of ε4 alleles, and conversely predicting which ε4/ε4 carriers will not develop AD, is necessary. Interestingly, the genotype within which the paragenic model had the lowest ROC AUC was ε4/ε4. This may be due to the lower number of participants in this group and could possibly be improved through modeling within APOE genotypes, or synthetically increasing the prevalence of ε4/ε4 through oversampling.
There are a few limitations of this study. We specifically chose a P + T PRS methodology to be incorporated in our model ensemble as it was simple to implement and had previously been directly applied to LOAD prediction. Additionally, the PRS-CS and hiPRS models likely would have benefited from tuning their various parameters, instead of defaults being used. We had to exclude several SNPs from the GWAS study used in the hiPRS model, due to low quality in our data; this model may have improved with the inclusion of these SNPs. It should be noted that the goal of this study was high predictive accuracy rather than interpretability or to provide insights into the etiology of LOAD. As such, feature significance was not explored in depth. Markers included in the model may be informative in predicting disease without being the true causative factor. Further improvements can likely be made through inclusion of environmental and lifestyle covariates [48]. We found that the differences across studies in data collection methods and completeness for these factors resulted in informative missingness, and thus we were not able to use them in modeling. Inclusion of these factors in a personal risk prediction test would allow users to see how lifestyle changes can reduce their risk of developing disease. Additionally, as with the many published Alzheimer’s PRS models that have been developed in European subjects, this study was conducted on individuals of European ancestry only and thus the prediction accuracy applies only to individuals who fall within the ancestry thresholds used to filter the training and test sets. Accordingly, such models are not yet ready for clinical application, as they cannot currently be equitably applied. The paragenic model and the PRS models that preceded it are each a step along the research path toward a predictive model that is usable in the clinic. Modeling on diverse populations is required in order to extend risk prediction to individuals of all ancestries, and this will be a focus of future work.
To the best of our knowledge, the paragenic model has the highest out-of-sample AUC of any genetic risk prediction model for clinically diagnosed LOAD to date and can serve as a baseline for future models able to identify individuals at high and low risk of developing disease for stratification in clinical trials as well as for personal use.
Supplementary Material
ACKNOWLEDGMENTS
We acknowledge the generous donations made by research volunteers at the Goizueta Alzheimer’s Disease Research Center at Emory University.
The recruitment and clinical characterization of research participants at the Knight-ADRC at Washington University were supported by NIH P30AG066444 (JCM), P01AG03991(JCM), and P01AG026276(JCM). This work was supported by grants from the National Institutes of Health (R01AG044546 (CC), P01AG003991(CC, JCM), RF1AG053303 (CC), RF1AG058501 (CC), U01AG058922 (CC), RF1AG074007 (YJS)), the Chan Zuckerberg Initiative (CZI), the Michael J. Fox Foundation (CC), the Department of Defense (LI- W81XWH2010849), and the Alzheimer’s Association Zenith Fellows Award (ZEN-22–848604, awarded to CC).
This work was supported by access to equipment made possible by the Hope Center for Neurological Disorders, the NeuroGenomics and Informatics Center (https://neurogenomics.wustl.edu/) and the Departments of Neurology and Psychiatry at Washington University School of Medicine.
Data collection and sharing for this project was funded by the Alzheimer’s Disease Neuroimaging Initiative (ADNI) (National Institutes of Health Grant U01 AG024904) and DOD ADNI (Department of Defense award number W81XWH-12-2-0012). ADNI is funded by the National Institute on Aging, the National Institute of Biomedical Imaging and Bioengineering, and through generous contributions from the following: AbbVie, Alzheimer’s Association; Alzheimer’s Drug Discovery Foundation; Araclon Biotech; BioClinica, Inc.; Biogen; Bristol-Myers Squibb Company; CereSpir, Inc.; Cogstate; Eisai Inc.; Elan Pharmaceuticals, Inc.; Eli Lilly and Company; EuroImmun; F. Hoffmann-La Roche Ltd and its affiliated company Genentech, Inc.; Fujirebio; GE Healthcare; IXICO Ltd.; Janssen Alzheimer Immunotherapy Research & Development, LLC.; Johnson & Johnson Pharmaceutical Research & Development LLC.; Lumosity; Lundbeck; Merck & Co., Inc.; Meso Scale Diagnostics, LLC.; NeuroRx Research; Neurotrack Technologies; Novartis Pharmaceuticals Corporation; Pfizer Inc.; Piramal Imaging; Servier; Takeda Pharmaceutical Company; and Transition Therapeutics. The Canadian Institutes of Health Research is providing funds to support ADNI clinical sites in Canada. Private sector contributions are facilitated by the Foundation for the National Institutes of Health (http://www.fnih.org). The grantee organization is the Northern California Institute for Research and Education, and the study is coordinated by the Alzheimer’s Therapeutic Research Institute at the University of Southern California. ADNI data are disseminated by the Laboratory for Neuro Imaging at the University of Southern California.
The NACC database is funded by NIA/NIH Grant U24 AG072122 and the NACC data are contributed by the NIA-funded ADRCs: P30 AG062429 (PI James Brewer, MD, PhD), P30 AG066468 (PI Oscar Lopez, MD), P30 AG062421 (PI Bradley Hyman, MD, PhD), P30 AG066509 (PI Thomas Grabowski, MD), P30 AG066514 (PI Mary Sano, PhD), P30 AG066530 (PI Helena Chui, MD), P30 AG066507 (PI Marilyn Albert, PhD), P30 AG066444 (PI John Morris, MD), P30 AG066518 (PI Jeffrey Kaye, MD), P30 AG066512 (PI Thomas Wisniewski, MD), P30 AG066462 (PI Scott Small, MD), P30 AG072979 (PI David Wolk, MD), P30 AG072972 (PI Charles DeCarli, MD), P30 AG072976 (PI Andrew Saykin, PsyD), P30 AG072975 (PI David Bennett, MD), P30 AG072978 (PI Neil Kowall, MD), P30 AG072977 (PI Robert Vassar, PhD), P30 AG066519 (PI Frank LaFerla, PhD), P30 AG062677 (PI Ronald Petersen, MD, PhD), P30 AG079280 (PI Eric Reiman, MD), P30 AG062422 (PI Gil Rabinovici, MD), P30 AG066511 (PI Allan Levey, MD, PhD), P30 AG072946 (PI Linda Van Eldik, PhD), P30 AG062715 (PI Sanjay Asthana, MD, FRCP), P30 AG072973 (PI Russell Swerdlow, MD), P30 AG066506 (PI Todd Golde, MD, PhD), P30 AG066508 (PI Stephen Strittmatter, MD, PhD), P30 AG066515 (PI Victor Henderson, MD, MS), P30 AG072947 (PI Suzanne Craft, PhD), P30 AG072931 (PI Henry Paulson, MD, PhD), P30 AG066546 (PI Sudha Seshadri, MD), P20 AG068024 (PI Erik Roberson, MD, PhD), P20 AG068053 (PI Justin Miller, PhD), P20 AG068077 (PI Gary Rosenberg, MD), P20 AG068082 (PI Angela Jefferson, PhD), P30 AG072958 (PI Heather Whitson, MD), P30 AG072959 (PI James Leverenz, MD). The Alzheimer’s Disease Genetic Consortium (ADGC), is funded by NIA/NIH Grant U01 AG032984.
From the Framingham Heart Study of the National Heart Lung and Blood Institute of the National Institutes of Health and Boston University School of Medicine. This project has been funded in whole or in part with Federal funds from the National Heart, Lung, and Blood Institute, National Institutes of Health, Department of Health and Human Services, under Contract No. 75N92019D00031.
Funding for SHARe Affymetrix genotyping was provided by NHLBI Contract N02-HL- 64278. SHARe Illumina genotyping was provided under an agreement between Illumina and Boston University. Funding for Affymetrix genotyping of the FHS Omni cohorts was provided by Intramural NHLBI funds from Andrew D. Johnson and Christopher J. O’Donnell.
Funding for CARe genotyping was provided by NHLBI Contract N01-HC-65226.
This study is part of the Building on GWAS for NHLBI-diseases: the U.S. CHARGE consortium (CHARGE-S). Funding for CHARGE-S was provided by NHLBI grant 5RC2HL102419 through the American Recovery and Reinvestment Act of 2009 (ARRA). Data for the Building on GWAS for NHLBI-diseases: the U.S. CHARGE consortium was provided by Eric Boerwinkle on behalf of the Atherosclerosis Risk in Communities (ARIC) Study, L. Adrienne Cupples, principal investigator for the Framingham Heart Study, and Bruce Psaty, principal investigator for the Cardiovascular Health Study. A portion of this research was conducted using the Linux Cluster for Genetic Analysis (LinGA-II) funded by the Robert Dawson Evans Endowment of the Department of Medicine at Boston University School of Medicine and Boston Medical Center. The CHARGE-S investigators request that publications resulting from these data cite their original publication: Psaty BM, O’Donnell CJ, Gudnason V, Lunetta KL, Folsom AR, Rotter JI, Uitterlinden AG, Harris TB, Witteman JC, Boerwinkle E; CHARGE Consortium. Cohorts for Heart and Aging Research in Genomic Epidemiology (CHARGE) Consortium: Design of prospective meta-analyses of genome-wide association studies from five cohorts. Circ Cardiovasc Genet 2:73– 80, 2009.
Funding support for the Framingham Dementia Flag Based on Neurology Exam for Participants in the Original and Offspring Cohorts dataset, the Framingham Dementia Flag From the Neuropsychological Test Battery for Participants in the Original and Offspring Cohorts dataset, and the Framingham Incident cognitive impairment in Original and Offspring cohorts dataset was provided by NIH/NIA grants R01AG08122, R01NS17950, R01AG 033193.
Funding support for the Framingham Neuropsychological Battery Education Questions dataset was provided by NIH/NIA grant R01 #AG16496.
FUNDING
Research reported in this publication was supported by the National Institute on Aging of the National Institutes of Health under award number 2R44AG050366-02. Participant recruitment at Emory was supported in part by awards P30 AG066511 and R01 AG070937.
Footnotes
CONFLICT OF INTEREST
SH, JC, SA, JO, SCH, and EG are employees of Parabon NanoLabs, Inc. CC has received research support from: GSK and EISAI. The funders of the study had no role in the collection, analysis, or interpretation of data; in the writing of the report; or in the decision to submit the paper for publication. CC is a member of the advisory board of Vivid Genomics and Circular Genomics. TW is a co-founder of revXon.
SUPPLEMENTARY MATERIAL
The supplementary material is available in the electronic version of this article: https://dx.doi.org/10.3233/JAD-230236.
The interaction space we consider consists of pairs and triples of SNPs taken from a large candidate pool (~100 K individual SNPs). In [15], the candidate pool of SNPs is filtered to ~36,860 and [19] uses simulated data with 10 individual markers. Both papers only consider pairwise interactions and individual markers.
We note that additional GWAS studies on AD of larger scale than the IGAP study have been published since the research presented here was performed.
DATA AVAILABILITY
The data supporting the findings of this study are available from their original sources: ADNI, dgGaP, and NACC/NIAGADS. Emory data can be requested at the following site: https://alzheimers.emory.edu/research/for-researchers/data-request-form.html. WashU data is available from NIAGADS: https://www.niagads.org/knight-adrc-collection. The data are not publicly available due to privacy or ethical restrictions.
REFERENCES
- [1].Alzheimer’s Association (2022) 2022 Alzheimer’s disease facts and figures. Alzheimers Dement 18, 700–789. [DOI] [PubMed] [Google Scholar]
- [2].Sabbagh MN, Hendrix S, Harrison JE (2019) FDA position statement “Early Alzheimer’s disease: Developing drugs for treatment, Guidance for Industry.” Alzheimers Dement (NY) 5, 13–19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Wolk D, Salloway S, Dickerson B (2019) Putting the new Alzheimer disease amyloid, tau, neurodegeneration (AT [N]) diagnostic system to the test. JAMA 321, 2289–2291. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].West T, Kirmess KM, Meyer MR, Holubasch MS, Knapik SS, Hu Y, Contois JH, Jackson EN, Harpstrite SE, Bateman RJ, others (2021) A blood-based diagnostic test incorporating plasma Aβ42/40 ratio, ApoE proteotype, and age accurately identifies brain amyloid status: Findings from a multi cohort validity analysis. Mol Neurodegener 16, 30. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Neuner SM, Julia T, Goate AM (2020) Genetic architecture of Alzheimer’s disease. Neurobiol Dis 143, 104976. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Ridge PG, Mukherjee S, Crane PK, Kauwe JS, Alzheimer’s Disease Genetics Consortium (2013) Alzheimer’s disease: Analyzing the missing heritability. PLoS One 8, e79771. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Harrison JR, Mistry S, Muskett N, Escott-Price V (2020) From polygenic scores to precision medicine in Alzheimer’s disease: A systematic review. J Alzheimers Dis 74, 1271–1283. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Escott-Price V, Myers AJ, Huentelman M, Hardy J (2017) Polygenic risk score analysis of pathologically confirmed Alzheimer disease. Ann Neurol 82, 311–314. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Lloyd-Jones LR, Zeng J, Sidorenko J, Yengo L, Moser G, Kemper KE, Wang H, Zheng Z, Magi R, Esko T, others (2019) Improved polygenic prediction by Bayesian multiple regression on summary statistics. Nat Commun 10, 5086. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Ge T, Chen C-Y, Ni Y, Feng Y-CA, Smoller JW (2019) Polygenic prediction via Bayesian regression and continuous shrinkage priors. Nat Commun 10, 1776. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Polderman TJ, Benyamin B, De Leeuw CA, Sullivan PF, Van Bochoven A, Visscher PM, Posthuma D (2015) Meta-analysis of the heritability of human traits based on fifty years of twin studies. Nat Genet 47, 702–709. [DOI] [PubMed] [Google Scholar]
- [12].Nazarian A, Kulminski AM (2019) Evaluation of the genetic variance of Alzheimer’s disease explained by the disease-associated chromosomal regions. J Alzheimers Dis 70, 907–915. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Karlsson IK, Escott-Price V, Gatz M, Hardy J, Pedersen NL, Shoai M, Reynolds CA (2022) Measuring heritable contributions to Alzheimer’s disease: Polygenic risk score analysis with twins. Brain Commun 4, fcab308. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Raghavan N, Tosto G (2017) Genetics of Alzheimer’s disease: The importance of polygenic and epistatic components. Curr Neurol Neurosci Rep 17, 78. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Wang H, Bennett DA, De Jager PL, Zhang Q-Y, Zhang H-Y (2021) Genome-wide epistasis analysis for Alzheimer’s disease and implications for genetic risk prediction. Alzheimers Res Ther 13, 55. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Massi MC, Franco NR, Manzoni A, Paganoni AM, Park HA, Hoffmeister M, Brenner H, Chang-Claude J, Ieva F, Zunino P (2023) Learning high-order interactions for polygenic risk prediction. PLoS One 18, e0281618. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Franco NR, Massi MC, Ieva F, Manzoni A, Paganoni AM, Zunino P, Veldeman L, Ost P, Fonteyne V, Talbot CJ, others (2021) Development of a method for generating SNP interaction-aware polygenic risk scores for radiotherapy toxicity. Radiother Oncol 159, 241–248. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Ritchie MD, Hahn LW, Roodi N, Bailey LR, Dupont WD, Parl FF, Moore JH (2001) Multifactor-dimensionality reduction reveals high-order interactions among estrogen-metabolism genes in sporadic breast cancer. Am J Hum Genet 69, 138–147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Le TT, Gong H, Orzechowski P, Manduchi E, Moore JH (2020) Expanding polygenic risk scores to include automatic genotype encodings and gene-gene interactions. Proceedings of the 13th International Joint Conference on Biomedical Engineering Systems and Technologies- Volume 3: BIOSTEC, Valletta, Malta, pp. 79–84. [Google Scholar]
- [20].Moore JH, Andrews PC, Olson RS, Carlson SE, Larock CR, Bulhoes MJ, O’Connor JP, Greytak EM, Armentrout SL (2017) Grid-based stochastic search for hierarchical gene-gene interactions in population-based genetic studies of common human diseases. BioData Min 10, 19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Lambert J-C, Ibrahim-Verbaas CA, Harold D, Naj AC, Sims R, Bellenguez C, Jun G, Destefano AL, Bis JC, Beecham GW, Grenier-Boley B, Russo G, Thornton-Wells TA, Jones N, Smith AV, Chouraki V, Thomas C, Ikram MA, Zelenika D, Vardarajan BN, Kamatani Y, Lin C-F, Gerrish A, Schmidt H, Kunkle B, Dunstan ML, Ruiz A, Bihoreau M-T, Choi S-H, Reitz C, Pasquier F, Hollingworth P, Ramirez A, Hanon O, Fitzpatrick AL, Buxbaum JD, Campion D, Crane PK, Baldwin C, Becker T, Gudnason V, Cruchaga C, Craig D, Amin N, Berr C, Lopez OL, De Jager PL, Deramecourt V, Johnston JA, Evans D, Lovestone S, Letenneur L, Morón FJ, Rubinsztein DC, Eiriksdottir G, Sleegers K, Goate AM, Fiévet N, Huentelman MJ, Gill M, Brown K, Kamboh MI, Keller L, Barberger-Gateau P, McGuinness B, Larson EB, Green R, Myers AJ, Dufouil C, Todd S, Wallon D, Love S, Rogaeva E, Gallacher J, St George-Hyslop P, Clarimon J, Lleo A, Bayer A, Tsuang DW, Yu L, Tsolaki M, Bossù P, Spalletta G, Proitsi P, Collinge J, Sorbi S, Sanchez-Garcia F, Fox NC, Hardy J, Naranjo MCD, Bosco P, Clarke R, Brayne C, Galimberti D, Mancuso M, Matthews F, Moebus S, Mecocci P, Del Zompo M, Maier W, Hampel H, Pilotto A, Bullido M, Panza F, Caffarra P, Nacmias B, Gilbert JR, Mayhaus M, Lannfelt L, Hakonarson H, Pichler S, Carrasquillo MM, Ingelsson M, Beekly D, Alvarez V, Zou F, Valladares O, Younkin SG, Coto E, Hamilton-Nelson KL, Gu W, Razquin C, Pastor P, Mateo I, Owen MJ, Faber KM, Jonsson PV, Combarros O, O’Donovan MC, Cantwell LB, Soininen H, Blacker D, Mead S, Mosley TH, Bennett DA, Harris TB, Fratiglioni L, Holmes C, de Bruijn RFAG, Passmore P, Montine TJ, Bettens K, Rotter JI, Brice A, Morgan K, Foroud TM, Kukull WA, Hannequin D, Powell JF, Nalls MA, Ritchie K, Lunetta KL, Kauwe JSK, Boerwinkle E, Riemenschneider M, Boada M, Hiltunen M, Martin ER, Schmidt R, Rujescu D, Wang L-S, Dartigues J-F, Mayeux R, Tzourio C, Hofman A, Nöthen MM, Graff C, Psaty BM, Jones L, Haines JL, Holmans PA, Lathrop M, Pericak-Vance MA, Launer LJ, Farrer LA, van Duijn CM, Van Broeckhoven C, Moskvina V, Seshadri S, Williams J, Schellenberg GD, Amouyel P (2013) Meta-analysis of 74,046 individuals identifies11newsusceptibilitylociforAlzheimer’sdisease. Nat Genet 45, 1452–1458. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Sudmant PH, Rausch T, Gardner EJ, Handsaker RE, Abyzov A, Huddleston J, Zhang Y, Ye K, Jun G, Hsi-Yang Fritz M, Konkel MK, Malhotra A, Stütz AM, Shi X, Paolo Casale F, Chen J, Hormozdiari F, Dayama G, Chen K, Malig M, Chaisson MJP, Walter K, Meiers S, Kashin S, Garrison E, Auton A, Lam HYK, Jasmine Mu X, Alkan C, Antaki D, Bae T, Cerveira E, Chines P, Chong Z, Clarke L, Dal E, Ding L, Emery S, Fan X, Gujral M, Kahveci F, Kidd JM, Kong Y, Lameijer E-W, McCarthy S, Flicek P, Gibbs RA, Marth G, Mason CE, Menelaou A, Muzny DM, Nelson BJ, Noor A, Parrish NF, Pendleton M, Quitadamo A, Raeder B, Schadt EE, Romanovitch M, Schlattl A, Sebra R, Shabalin AA, Untergasser A, Walker JA, Wang M, Yu F, Zhang C, Zhang J, Zheng-Bradley X, Zhou W, Zichner T, Sebat J, Batzer MA, McCarroll SA, Mills RE, Gerstein MB, Bashir A, Stegle O, Devine SE, Lee C, Eichler EE, Korbel JO, The 1000 Genomes Project Consortium (2015) An integrated mapofstructuralvariationin2,504humangenomes.Nature 526, 75–81.26432246 [Google Scholar]
- [23].Das S, Forer L, Schönherr S, Sidore C, Locke AE, Kwong A, Vrieze SI, Chew EY, Levy S, McGue M, Schlessinger D, Stambolian D, Loh P-R, Iacono WG, Swaroop A, Scott LJ, Cucca F, Kronenberg F, Boehnke M, Abecasis GR, Fuchsberger C (2016) Next-generation genotype imputation service and methods. Nat Genet 48, 1284–1287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Manichaikul A, Mychaleckyj JC, Rich SS, Daly K, Sale M, Chen W-M (2010) Robust relationship inference in genome-wide association studies. Bioinformatics 26, 2867–73. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Chen T, Guestrin C (2016) XGBoost: A scalable tree boosting system. KDD ’16: Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, pp. 785–794. [Google Scholar]
- [26].Popov S, Morozov S, Babenko A (2019) Neural oblivious decision ensembles for deep learning on tabular data. arXiv, doi: 10.48550/arXiv.1909.06312 [Preprint]. Posted Sep 13, 2019. [DOI] [Google Scholar]
- [27].Loh P-R, Tucker G, Bulik-Sullivan BK, Vilhjálmsson BJ, Finucane HK, Salem RM, Chasman DI, Ridker PM, Neale BM, Berger B, Patterson N, Price AL (2015) Efficient Bayesian mixed-model analysis increases association power in large cohorts. Nat Genet 47, 284–290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Urbanowicz RJ, Olson RS, Schmitt P, Meeker M, Moore JH (2018) Benchmarking relief-based feature selection methods for bioinformatics data mining. J Biomed Inf 85, 168–188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].Ashburner M, Ball CA, Blake JA, Botstein D, Butler H, Cherry JM, Davis AP, Dolinski K, Dwight SS, Eppig JT, Harris MA, Hill DP, Issel-Tarver L, Kasarskis A, Lewis S, Matese JC, Richardson JE, Ringwald M, Rubin GM, Sherlock G (2000) Gene Ontology: Tool for the unification of biology. Nat Genet 25, 25–29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30].The Gene Ontology Consortium (2021) The Gene Ontology resource: Enriching a GOld mine. Nucleic Acids Res 49, D325–D334. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].Sullivan K, Luke S, Larock C, Cier S, Armentrout S (2008) Opportunistic evolution: Efficient evolutionary computation on large-scale computational grids. GECCO ‘08: Proceedings of the 10th annual conference companion on Genetic and evolutionary computation, pp. 2227–2232. [Google Scholar]
- [32].Deb K, Pratap A, Agarwal S, Meyarivan T (2002) A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans Evol Comp 6, 182–197. [Google Scholar]
- [33].Ma J, Yarats D (2018) Quasi-hyperbolic momentum and Adam for deep learning. arXiv, doi: 10.48550/arXiv.1810.06801 [Preprint]. Posted Oct 16, 2018. [DOI] [Google Scholar]
- [34].Escott-Price V, Sims R, Bannister C, Harold D, Vronskaya M, Majounie E, Badarinarayan N, GERAD/PERADES, IGAP Consortia, Morgan K, Passmore P, Holmes C, Powell J, Brayne C, Gill M, Mead S, Goate A, Cruchaga C, Lambert JC, Van Duijn C, Maier W, Ramirez A, Holmans P, Jones L, Hardy J, Seshadri S, Schellenberg GD, Amouyel P, Williams J (2015) Common polygenic variation enhances risk prediction for Alzheimer’s disease. Brain 138, 3673–3684. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35].Choi SW, Mak TS-H, O’Reilly PF (2020) Tutorial: A guide to performing polygenic risk score analyses. Nat Prot 15, 2759–2772. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36].Seabold S, Perktold J (2010) Statsmodels: Econometric and statistical modeling with Python. 9th Python in Science Conference, Austin, 28 June-3 July, pp. 57–61. [Google Scholar]
- [37].Bellenguez C, Küçükali F, Jansen IE, Kleineidam L, Moreno-Grau S, Amin N, Naj AC, Campos-Martin R, Grenier-Boley B, Andrade V, et al. (2022) New insights into the genetic etiology of Alzheimer’s disease and related dementias. Nat Genet 54, 412–436. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38].Wolpert DH (1992) Stacked generalization. Neural Netw 5, 241–259. [Google Scholar]
- [39].Pedregosa F, Varoquaux G, Gramfort A, Michel V, Thirion B, Grisel O, Blondel M, Prettenhofer P, Weiss R, Dubourg V, Vanderplas J, Passos A, Cournapeau D, Brucher M, Perrot M, Duchesnay É (2011) Scikit-learn: Machine learning in Python. J Mach Learn Res 12, 2825–2830. [Google Scholar]
- [40].Sollis E, Mosaku A, Abid A, Buniello A, Cerezo M, Gil L, Groza T, Güneş O, Hall P, Hayhurst J, Ibrahim A, Ji Y, John S, Lewis E, MacArthur JAL, McMahon A, Osumi-Sutherland D, Panoutsopoulou K, Pendlington Z, Ramachandran S, Stefancsik R, Stewart J, Whetzel P, Wilson R, Hindorff L, Cunningham F, Lambert SA, Inouye M, Parkinson H, Harris LW (2022) The NHGRI-EBI GWAS Catalog: Knowledgebase and deposition resource. Nucleic Acids Res 51, D977–D985. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [41].Krzywinski MI, Schein JE, Birol I, Connors J, Gascoyne R, Horsman D, Jones SJ, Marra MA (2009) Circos: An information aesthetic for comparative genomics. Genome Res 19, 1639–1645. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [42].Davidson-Pilon C (2019) Lifelines: Survival analysis in Python. J Open Source Softw 4, 1317. [Google Scholar]
- [43].Hebert LE, Weuve J, Scherr PA, Evans DA (2013) Alzheimer disease in the United States (2010–2050) estimated using the 2010 census. Neurology 80, 1778–1783. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [44].Jo T, Nho K, Bice P, Saykin AJ, For the Alzheimer’s Disease Neuroimaging Initiative (2022) Deep learning-based identification of genetic variants: Application to Alzheimer’s disease classification. Brief Bioinform 23, bbac022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [45].Osipowicz M, Wilczynski B, Machnicka MA, for the Alzheimer’s Disease Neuroimaging Initiative (2021) Careful feature selection is key in classification of Alzheimer’s disease patients based on whole-genome sequencing data. NAR Genomics Bioinform 3, lqab069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [46].Clifton L, Collister JA, Liu X, Littlejohns TJ, Hunter DJ (2022) Assessing agreement between different polygenic risk scores in the UK Biobank. Sci Rep 12, 12812. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [47].Ward A, Crean S, Mercaldi CJ, Collins JM, Boyd D, Cook MN, Arrighi HM (2012) Prevalence of apolipoprotein E4 genotype and homozygotes (APOE e4/4) among patients diagnosed with Alzheimer’s disease: A systematic review and meta-analysis. Neuroepidemiology 38, 1–17. [DOI] [PubMed] [Google Scholar]
- [48].Eid A, Mhatre I, Richardson JR (2019) Gene-environment interactions in Alzheimer’s disease: A potential path to precision medicine. Pharmacol Ther 199, 173–187. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The data supporting the findings of this study are available from their original sources: ADNI, dgGaP, and NACC/NIAGADS. Emory data can be requested at the following site: https://alzheimers.emory.edu/research/for-researchers/data-request-form.html. WashU data is available from NIAGADS: https://www.niagads.org/knight-adrc-collection. The data are not publicly available due to privacy or ethical restrictions.


