Abstract
Nature uses bottom-up self-assembly to build structures with remarkable complexity and functionality. Understanding how molecular-scale interactions translate to macroscopic properties remains a major challenge and requires systems that effectively bridge these two scales. Here, we generate DNA and RNA liquids with exquisite programmability in their material properties. Nucleic acids are negatively charged, and in the presence of polycations, they may condense to a liquid-like state. Within these liquids, DNA and RNA retain sequence-specific hybridization abilities. We show that intermolecular hybridization in the condensed phase cross-links molecules and slows down chain dynamics. This reduced chain mobility is mirrored in the macroscopic properties of the condensates. Molecular diffusivity and material viscosity scale with the intermolecular hybridization energy, enabling precise sequence-based modulation of condensate properties over orders of magnitude. Our work offers a robust platform to create self-assembling programmable fluids and may help advance our understanding of liquid-like compartments in cells.
Keywords: DNA/RNA nanotechnology, programmable materials, complex coacervates, associative polymers, liquid-liquid phase separation, biomolecular condensates
Introduction:
The sequence-specific binding properties of nucleic acids form the basis for life, providing the chemical foundation for the replication of genetic material, its decoding by the protein translation apparatus, and for molecular targeting such as by guiding RNA processing1. Nucleic acid hybridization is well-characterized both theoretically as well as experimentally2–4. This sequence-specificity of DNA bonding has been harnessed to generate a variety of self-assembling programmable materials5. These include nanometer-scale structures with precise control of DNA topology such as in DNA origami6,7 to mesoscale soft materials such as hydrogels8,9. In most of these applications, the negative charge on the phosphodiester backbone is neutralized by low valence counterions, and the desired molecular arrangement is achieved by the sequence-programmablity of DNA bonding.
Due to their charge, nucleic acids can also form electrostatic interaction-driven assemblies10,11. When solutions of oppositely charged polymers are mixed, they can undergo associative phase separation, called complex coacervation, resulting in a polymer-rich phase and a dilute supernatant phase12,13. DNA and RNA readily undergo complex coacervation in the presence of cationic polymers11,14. Complex coacervates concentrate nucleic acids without a membrane and this process may have parallels in the origin of life scenarios15,16. Eukaryotic cells also contain numerous membraneless organelles such as nucleoli and stress granules, and complex coacervation of RNA and proteins is implicated in the formation of these bodies17–19. Electrostatic interaction-mediated complexation is also the dominant approach used to assemble nucleic acids for delivering foreign genetic material to cells20,21.
Our previous work indicated that single-stranded DNA and RNA in complex coacervates retain their sequence-specific hybridization properties22. We hypothesized that we could harness this sequence specificity of nucleic acid hybridization in complex coacervates to generate new programmable materials. We were inspired by self-associative polymers that are designed to exhibit reversible associations between polymer chains23,24. These reversible inter-chain cross-links allow reconfiguration of the polymer network and manifest properties that are not accessible to conventional polymer materials with static cross-links, such as self-healing and stimuli-responsive material transformation24. These macroscopic properties depend on the lifetime, densities, and positions of the cross-links between polymer chains25. Precise engineering of these features in synthetic polymers is difficult, and the exquisite programmability of nucleic acid bonding could help overcome these challenges.
Here we generate DNA and RNA liquids with precise control over their viscoelastic properties. We engineered DNA oligonucleotides with short hybridization patches interspersed by single stranded regions (Fig. 1). Polyvalent cations induce complex coacervation resulting in DNA-rich liquids. Within the condensed phase, the DNA concentration is above the overlap concentration facilitating inter-chain hybridization. Such inter-chain hybridizations transiently cross link DNA molecules and slow down their diffusion. DNA mobility and the material properties of the condensed phase scale linearly with the life-time of DNA-DNA cross-links. By engineering the sequence, we can precisely program the hybridization energy and thus tune the properties of these liquids. Similar rules apply to condensates of RNA with cationic peptides. This system may pave the way for a new class of programmable nucleic acid-based materials. It may provide insights on the physics of polyelectrolyte complexation and may help uncover the rules underlying the formation of liquid-like RNA granules in the cell.
Figure 1: Scheme for generating condensates with sequence programmable properties.
(A) Single stranded nucleic acids undergo associative phase separation in the presence of polyvalent cations and produce a polymer rich coacervate phase and a dilute supernatant phase. (B) Representative fluorescent micrographs showing complex coacervates of non-base pairing T-90 DNA in the presence of spermine. Scale bar, 30 μm. (C) We incorporated multiple weak hybridization patches in the DNA/RNA sequence. Inter-molecular hybridization at these sites transiently cross-links two or more strands and impedes their molecular mobility within coacervates. (D) Molecular diffusivity (Dself) and viscosity (η) of these coacervates depend on the lifetime of inter-molecular cross-links (τbond), and can be programmed by modulating the DNA sequence.
Results:
Design of nucleic acids with self-associative patches.
We used a 90-nucleotide long deoxythymidine (T-90) oligonucleotide as a chassis to build self-associative DNA (Fig. 1A–B, Fig. S1A). T-90 does not form appreciable secondary structure at room temperature and provides a benign scaffold to engineer base-pairing sites. To incorporate associative sites, we replaced a subset of T-bases in T-90 with short palindromic interaction patches (Fig. 1C–D, Table S1). These patches provide sites for intra- and inter-strand DNA hybridization while the total charge along the phosphodiester backbone is unchanged. The patch sequences were chosen such that the DNA transiently hybridize at room temperature (hybridization energy, ε = −ΔG/(kbTNA), between 0 and 20, where ΔG is the theoretical predicted free energy of hybridization from nearest neighbor calculations26, kb is the Boltzmann constant, T is the temperature and NA is the Avogadro constant, see Supplementary text S1 for additional notes on patch design). Successive patches were separated by ≥15 non-hybridizing T bases in order to minimize the cooperativity in hybridization between adjacent sites27,28. By changing the patch sequence or temperature, we can program the hybridization energy of the associative patch (Table S1 and S2) and varying the number of patches per DNA allows us to tune the hybridization valency. We refer to these self-associating single-stranded DNA oligonucleotides as patchyDNA drawing parallels to colloids with multiple interaction sites29.
As a polycation, we chose spermine, a cellular metabolite and a tetravalent cation at pH 7.0 (pKa for the four amine groups ≥ 7.9)30. Addition of spermine induced complex coacervation and produced two coexisting aqueous phases: a DNA-poor supernatant phase and a DNA-rich, condensed phase (Fig. 1B, Fig. S1). A small amount (< 1%) of fluorescently labeled DNA was doped to facilitate condensate visualization. The patchyDNA condensates exhibited liquid-like properties (Fig. S1B–E): they were spherical, and upon contact, two or more droplets coalesced and relaxed to a spherical geometry (Fig. S1E). Nearly 90% of DNA partitioned in the condensed phase (Fig. S2), and DNA partitioning and coacervate yield was comparable for the various sequences examined (Fig. S2).
Previous work has shown that the complex coacervate phase can be envisioned as a semi-dilute solution, i.e., within the condensed phase, the polymer concentration is comparable to the overlap concentration, making inter-chain interactions as likely as intra-chain interactions31,32. Consistent with this notion, the DNA concentration in the patchyDNA coacervates (Cdense ~ 1–10 mM, Fig. S2) was comparable to the estimated overlap concentration (Coverlap, for a 90-mer ssDNA ~1 mM) (see Supporting text S2). We also used fluorescence resonance energy transfer (FRET) to directly estimate the mean inter-molecular distance between DNA in the coacervate and dilute phases. We labeled patchyDNA with either a fluorescence donor (Cy3) or an acceptor (Cy5) dye (Table S3). In the condensate, we observed substantial FRET between the two dyes (Fig. S3), indicating that the distance between DNA molecules is comparable to the molecular length scales (Forster radius for Cy3 and Cy5 dye pair ≈ 5 nm33; radius of gyration for 90-mer ssDNA, ≈ 5 nm34). In contrast, no measurable FRET signal was observed in the solution phase indicating that the hybridization patches do not induce stable DNA dimerization (Fig. S3).
As additional evidence for inter-molecular hybridization in the condensed phase, we examined the effect of base-pairing interactions on the phase stability. Complex coacervation is driven by a combination of attractive electrostatic interactions and entropically favorable molecular rearrangements. The loss in configurational entropy upon polyelectrolyte complexation is counterbalanced by the entropy gain upon the release of low-valence counter-ions that were bound to the polyelectrolytes12,13,35. High concentrations of low valence counter ions diminish the relative entropic gain upon polyelectrolyte complexation and inhibit complex coacervation35. Short-range intermolecular interactions such as hydrogen bonding and base stacking may stabilize complex coacervates against salt-mediated dissolution36. Consistent with this expectation, DNA-spermine coacervates were susceptible to NaCl mediated dissolution and the critical salt concentration for coacervate dissolution (C*) increased progressively with the patch hybridization energy (C* = 30 mM for ε = 0, 130 mM for ε = 20.2, Fig. S4). In summation, these results demonstrate that patchyDNA molecules are densely packed in complex coacervates and may form intermolecular base-pairs.
Base-pairing modulates chain dynamics in patchyDNA condensates.
Inter-molecular base-pairing would cross-link DNA strands and impede their mobility. To examine the effect of inter-strand cross-linking on chain dynamics, we used fluorescence recovery after photobleaching (FRAP). In these experiments, a small region of a DNA droplet is photobleached and the recovery is tracked over time. The fraction of fluorescence recovery reports on the proportion of DNA that is mobile within the droplet, while the recovery timescales reported on the molecular diffusivity. For the sequences examined (ε ≤ 20.2) (Fig. 2A, B), the patchyDNA coacervates exhibited near-complete (≥ 80%) fluorescence recovery upon partial photobleaching (Fig. 2C–D, Fig. S5A), indicating that the DNA in the condensed phase is mobile. However, the characteristic fluorescence recovery time, τFRAP, progressively increased with ε, indicating that DNA mobility is reduced as the hybridization energy increases (Fig. 2C–D, Fig. S5A–B). τFRAP can be used to estimate the apparent self-diffusion coefficient, Dself (see Methods)37,38. Dself for the non-base-pairing T-90 was 0.32 ± 0.16 μm2/s (mean ± standard deviation, n = 16). As the hybridization energy of the patch was increased, Dself progressively decreased by nearly three orders of magnitude (Dself = (3.6 ± 1.3) × 10−4 μm2/s at ε = 20.2, mean ± standard deviation, n = 18, Fig. S5C). Base-pairing is temperature sensitive, and besides changing the DNA sequence, ε can also be modulated by changing the temperature (Table S2). For a given interaction patch, Dself could be modulated by nearly 5-fold as the temperature was increased from 20°C to 45°C (for patch sequence GGATCC, Dself = (2.6 ± 0. 3) × 10−3 μm2/s at 20°C, ε = 16.1, versus (17 ± 2) × 10−3 μm2/s at 45°C, ε = 10.8) (Fig. 2E, Fig. S6D). We did not observe any measurable change in Dself for T-90 with temperature, indicating that the DNA-spermine electrostatic interaction is not substantially affected in this temperature range (Fig. S6A and S7).
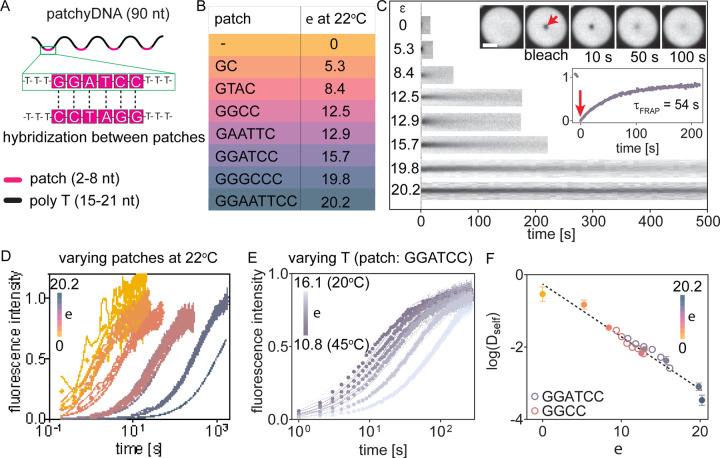
Figure 2: Base-pairing interactions modulate chain dynamics in patchyDNA condensates.
(A) Schematic showing the design of self-associative patchyDNA. The hybridization patches are 2–8 nucleotide long palindromic sequences, and successive patches are separated by ≥15 T bases. (B) Representative patch sequences and the corresponding hybridization energies, ε, at 22°C. (C) Kymographs depicting fluorescence recovery upon partial photobleaching of patchyDNA condensates with the indicated ε. Inset: representative fluorescence micrographs and corresponding fluorescence time trace for DNA with the patch sequence GGATCC. The arrow indicates the point of photobleaching. (D, E) Fluorescence recovery time traces for patchyDNA condensates, where ε was changed either by varying the patch sequence (measurements conducted at 22°C) (D) or by varying the temperature for a given sequence (E). Each data point denotes mean ± SD, n ≥ 5 droplets. (F) Plot showing that logarithm of DNA self-diffusion coefficient (Dself) scales linearly with ε. The dotted line is the least square fit between log(Dself) and ε (slope = −0.14 ± 0.01, R2 = 0.90). The solid and open symbols in (F) denote that ε was varied by changing the patch sequence or by changing the temperature respectively. The color bars in D, E and F denote the range of ε. Scale bar in C is 5 μm.
Interestingly, all of our Dself measurements across various patch sequences and temperatures, when plotted against ε, converged on a single line on the semi-log plot, indicating that Dself scales exponentially with ε (Fig. 2F). This exponential scaling between Dself and ε is reminiscent of the dynamics of unentangled self-associative neutral polymers in the semi-dilute regime25,39. According to this model (referred to as the sticky Rouse model), associative polymers in a network diffuse by breaking inter-molecular cross-links on one site and re-forming at another25,40. Thus, polymer diffusion is inversely related to the lifetime of intermolecular cross-links, τbond39,40. The bond lifetime is determined by the interaction energy and is given by τbond ~ e−Ea/kbT, where Ea is the association energy, and kbT is the normalization for thermal energy. While we do not know the exact solvent environment in the condensed phase, these results indicate that the theoretically estimated hybridization energy provides a reasonable proxy for the association energy and demonstrate that DNA diffusion in the coacervate phase can be precisely programmed by engineering the hybridization patch sequence.
Inter-chain hybridization modulates material properties of DNA coacervates.
We next examined the viscoelastic properties of coacervates using particle tracking microrheology41. In these experiments, fluorescent microspheres are embedded in the material and their movement over time reports on the material’s viscoelastic behavior41,42. Beads trapped in the DNA coacervates exhibited random fluctuations that are effectively described by a Gaussian probability distribution (Fig. 3A–B, Fig. S8). The mean squared displacement (MSD) of beads followed a power law relation with time (t), MSD ~ tα, with diffusion exponent α ≈ 1, across the various patch sequences examined (Fig. 3C–D). This linear relationship between bead MSD and time indicates that the patchyDNA coacervates behave like viscous fluids with minimal elastic behavior and aligns with our observations from fluorescence photobleaching experiments described above.
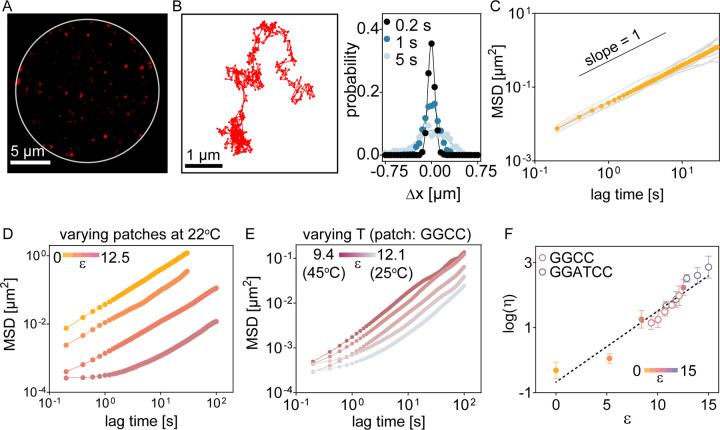
Figure 3: Base-pairing interactions modulate viscosity of patchyDNA condensates.
(A) Representative fluorescence micrograph showing passivated beads (radius = 50 nm) embedded in a patchyDNA coacervate (white circle). (B) Representative time trajectory of a single bead (left) and probability distribution of bead displacement at three different lag times (right) in T-90 coacervates at 22°C. Distributions are well-described by a Gaussian function (solid lines). (C) Mean squared displacement (MSD) with lag time for beads embedded in T-90 condensates at 22°C. Grey lines show the data from individual beads. Mean values are in yellow. Black solid line is provided as a guide for slope = 1. (D) MSD tracks of beads (n > 5, mean) in various patchyDNA condensates at 22°C. (E) Similar to (D) but for beads in GGCC coacervates at different temperatures. (F) Plot showing the logarithm of viscosity (η) versus ε. The solid and open symbols denote ε was varied by changing the patch sequence or by changing the temperature respectively. The dotted line is a linear fit between log(η) and ε (slope = 0.22 ± 0.01, R2 = 0.88). The color bars in D, E and F denote the range of ε.
The bead fluctuations can be used to calculate its diffusion coefficient, Dprobe, using the relationship, MSD ≈ 4·Dprobe t + NF, where NF is the noise floor (see Methods, Fig. S9). Since these coacervates behave like viscous liquids and knowing the size of the bead (see Methods), we can use Stokes-Einstein relation to estimate the material’s dynamic viscosity (η). η increased with ε, increasing from 0.56 ± 0.32 Pa.s (for T-90, ε = 0; mean ± standard deviation, n = 7) to 191 ± 97 Pa.s (for patch sequence GGCC, ε = 12.53; mean ± standard deviation, n = 6). Likewise, for a given DNA sequence, η increased when ε was increased by varying the temperature (Fig. 3E, Fig. S10). Similar to our observations with Dself, η scaled exponentially with ε (Fig. 3F), indicating that the macroscopic properties of the condensates can be programmed by the DNA sequence. We limited our microrheology experiments to DNA with ε ≈ 15 as beyond this regime, the bead diffusion approached the measurement noise floor (Fig. S9).
When two liquid droplets fuse, interfacial tension drives them to minimize the surface area by relaxing to a spherical shape, while viscosity opposes this relaxation. For droplets of a viscous fluid suspended in a lower viscosity medium, the timescales of fusion (τfusion) are proportional to the droplet viscosity (η) and its size (l), and inversely proportional to the interfacial tension (γ)43,44. Consistent with their liquid-like behavior, patchyDNA droplets fused with one another (Fig. 4A). For a given patchyDNA sequence, τfusion increased linearly with the droplet size, l, and the slope of this line provided an estimate of the ratio, η/γ, also knowns as the inverse capillary velocity (Fig. 4B–D and Fig. S11A). We estimated η/γ for the various patchyDNA sequences by examining multiple coalescence events across a range of droplet sizes and found that η/γ increased by 6 orders of magnitude as ε was varied from 0 to 20.2 (Fig. 4E). The droplet coalescence rates, in conjunction with direct viscosity measurements, allowed us to estimate the droplet interfacial tension. Interfacial tension for patchyDNA coacervates was between 400 –1200 μN/m, about two orders of magnitude smaller than that for air-water interface at 22°C (≈ 70 mN/m)45 (Fig. S11B). This ultra-low interfacial tension is comparable to that for condensates of other polymers of similar molecular dimensions46,47. Within the constraints of our experiments, γ did not appreciably change with ε (Fig. S11B). The fusion experiments allowed us to extract η/γ for a larger spectrum of patchyDNA, and in conjunction with our observation that γ exhibits a weak dependence on ε, these results indicate that η scales exponentially with ε, and can be modulated over 6 orders of magnitude as ε varies from 0 to 20.2 (η/γ ≈ 5.2 × 10−4 sμm−1 for ε = 0, ≈ 2.9 × 102 sμm−1 for ε = 20.2). Altogether, our data demonstrate that by programming the sequence of the DNA patch, we can tune the life-time of the DNA-DNA cross-link in complex coacervates and this interchain interaction is reflected in the molecular diffusion and macroscopic properties of the condensed phase.
Figure 4: Base-pairing tunes the fusion dynamics of patchyDNA condensates.
(A) Representative fluorescence micrographs showing fusion between complex coacervates of patchyDNAs with the indicated ε at 22°C. Fusion rates are slower for DNA with higher ε. Scale bar, 10 μm. (B) The characteristic fusion time (τfusion) can be obtained from fitting single exponential (dotted line) to the aspect ratio of the fusing droplets of roughly similar size (l). The plot in (B) corresponds to ε = 15.7 in (A). (C) τfusion linearly increased with the droplet size (l). Representative data from patchyDNA coacervates with patch sequence GGATCC, ε = 15.7. (D) τfusion for various patchyDNA coacervates increases linearly (solid lines) with l. The color bar indicates ε at 22°C. (E) Plot showing that the logarithm of inverse capillary velocity (η/γ) scales linearly with ε (dotted line, slope = 0.28 ± 0.02, R2 = 0.92). The color bars in D and E show the corresponding range of ε.
Heterotypic interactions enable design of stimuli-responsive condensates.
The DNA in the coacervates can also be potentially cross-linked via heterotypic interactions. Such heterotypic associations could allow one to tune the coacervate properties in response to a trigger strand that potentiates inter-molecular cross-linking (Fig. 5A, S12A). As a proof of concept, we designed two sets of patchyDNAs: a primary strand and an actuator secondary strand (Fig. 5A). The patches on these DNAs individually do not self-associate, but they can hybridize to each other (Fig. 5A–B). The coacervates produced from the primary strand alone (patch sequence, CTCCTC) exhibited dynamics and material properties similar to those from T-90 DNA, as expected (Fig. S12B). Upon addition of the cross-linking secondary DNA (patch sequence, GAGGAG), the self-diffusivity of the primary strand diminished (Fig. S12C). The apparent self-diffusion coefficient, Dself, was lowest when the two strands were mixed at equimolar ratio and increased when either strand was in excess (Fig. S12C).
Figure 5: Heterotypic base-pairing modulates molecular dynamics and viscosity of patchyDNA condensates.
(A) Schematic showing design of a primary patchyDNA with inducible inter-molecular cross-linking. The primary strand forms complex coacervates with spermine but this sequence does not contain self-associative hybridization sites (left). Addition of an appropriate secondary patchyDNA strand may cross-link the two DNAs (right). (B) Estimated hybridization energy for heterotypic cross-links (εheterotypic) with the indicated secondary patch sequence. Patch sequence for primary strand is CTCCTC. (C, D) Fluorescence recovery after photobleaching for the primary patchyDNA and (F, G) MSD of embedded beads with lag time, where εheterotypic was modulated either by varying the secondary patchyDNA (C, F) or by varying the temperature for the indicated secondary patchyDNA (D, G). Data depict mean ± SD, n ≥ 5 and mean, n ≥ 5 for (C, D) and (F, G), respectively. (E, H) Plots showing that the logarithm of self-diffusivity (E) and viscosity (H) of the primary patchyDNA scales linearly with εheterotypic. Dotted line denotes the least square fit (slope = −0.34 ± 0.01, R2 = 0.92 and 0.33 ± 0.02, R2 = 0.83, for E and H respectively). The solid and open symbols indicate that εheterotypic was varied by changing the secondary patchyDNA or by changing the temperature, respectively. The color bars in C, D, F, G indicate the range of εheterotypic.
This ability to harness heterotypic interactions allowed us to tune the properties of the coacervates produced from the same primary patchyDNA but in response to distinct cross-linking secondary DNAs as triggers. We examined four distinct secondary sequences that could each hybridize with the same primary patchyDNA but with different hybridization energies (Fig. 5B). Similar to our observations with self-associative patches, both Dself and η scaled exponentially with the inter-molecular hybridization energy, εheterotypic, when the two strands were mixed at stoichiometric ratios (Fig. 5C–H). These results, in conjunction with the findings from previous sections, reinforce that the material properties of DNA complex coacervates can be predictably tuned by modulating hybridization-based cross-links, including in response to an external input.
Inter-molecular hybridization modulates the material properties of RNA-peptide condensates.
Eukaryotic cells are compartmentalized by numerous RNA-containing condensates such as nucleoli, nuclear speckles, and stress granules, that exhibit liquid-like properties17,48. The protein constituents of these condensates often contain charged disordered domains49. In vitro, many of these proteins forms condensates in the presence of RNA18,50. The choice of RNA sequence affects condensate properties37,51 but the role of RNA-RNA interactions in these bodies remains poorly characterized52. Equipped with our biophysical framework, we examined how inter-molecular RNA-RNA hybridization affects the properties of RNA condensates produced with cationic peptides.
We used a 60-nucleotide long polyU (rU-60) RNA and incorporated 4 associative patches that are expected to reversibly hybridize at room temperature (Fig. 6A). rU-60 does not form appreciable secondary structure at or above room temperature (22°C)11. As a cationic peptide, we used poly-l-lysine (K10). The pKa of the lysine side chain is 10.5, and this peptide is expected to be fully protonated at the neutral pH53. The K10 peptide induced RNA complex coacervation (Fig. 6A). These coacervates exhibited liquid-like behavior and upon fusion of two or more droplets, they rapidly relaxed to a spherical geometry (Fig. S13A). The fusion timescales, τfusion, increased linearly with the droplet size, indicating that these coacervates behave like simple viscous liquids (Fig. S13A). The measured viscosity, η, for rU-60/K10 complex coacervates was 4.4 ± 1.6 Pa.s (mean ± standard deviation, n = 5) and increased progressively by about three orders of magnitude to 476 ± 96 Pa.s (mean ± standard deviation, n = 5) as the hybridization energy, εRNA, was increased to 9.5, by either modulating the patch sequence (Fig. 6B) or by changing temperature (Fig. 6C, Fig. S14). The interfacial tension for RNA-peptide coacervates was ~1 mN/s and only modestly varied with εRNA (Fig. S14B). Like patchyDNA, all measured values of η and η/γ across various perturbations could be described by a single exponential relationship (Fig. 6D–E). This exponential scaling between η and εRNA demonstrates that the dynamics of these droplets scale with the lifetime of RNA-RNA bonds and reinforces that the macroscopic properties of these RNA-containing condensates are tuned by inter-strand RNA hybridization.
Figure 6: Inter-molecular base-pairing modulates the properties of RNA-peptide condensates.
(A) Top: representative micrographs showing that non-base-pairing U-60 RNA forms complex coacervates with poly-l-lysine (K10). Scale bar, 10 μm. Bottom: schematic depicting the design of a 60-nucleotide long patchyRNA with four hybridization patches. Table shows hybridization energy of patches (εRNA) at 22°C. (B, C) MSD of passivated beads in patchyRNA/K10 condensates, where εRNA was modulated either by varying the patch sequence (B) or by temperature (C). The color bars represent the range of εRNA. Each datapoint is mean of n ≥5 beads. (D, E) The logarithm of viscosity (η) (D), and inverse-capillary velocity (η/γ) (E) scales linearly with εRNA (dotted line, slope = −0.22 ± 0.01, R2 = 0.85 and 0.25 ± 0.03, R2 = 0.98, respectively). The solid and open symbols in (D) denote εRNA was varied by changing the patch sequence or by temperature respectively.
Discussion:
We harnessed the two fundamental properties of nucleic acids, the negative charge and the sequence programmability of their bonding, to generate liquid-like materials with exquisite control over their physical properties. Nucleic acids in complex coacervates form electrostatic interaction mediated network, and super-imposing base-pairing interactions allowed us to modulate the chain dynamics. By engineering the sequence, we can program the lifetime of inter-strand cross-links, and these molecular scale interactions are reflected in the macroscopic properties of the condensates. We demonstrate programmability over orders of magnitude in chain mobility and condensate viscosity. The material properties scale exponentially with the predicted hybridization energy and allow us to exert striking control over the bulk properties by manipulating the sequence. This ability to tune material properties of DNA and RNA complex coacervates, in conjunction with their inherent stability and biocompatibility, may inspire a new class of nucleic acid-based self-assembling materials.
Polymer networks with dynamic and reversible associations exhibit properties that are not achieved in conventional polymers with static cross-links, and offer new functionalities such as ease of degradation, responsiveness to stimuli, and self-healing23,24. Given these desirable properties, there is considerable interest in generating new polymers with reversible associations, but it remains challenging to precisely engineer the strength and positioning of these interactions in synthetic polymers. Employing DNA hybridization for inter-chain interactions provides exceptional control over the engineerability of these association sites. Advances in DNA synthesis scales54 and development of chimeric DNA-conjugated polymers55 may provide a route to produce bulk-scale materials with precise control over material properties. There is also tremendous interest in understanding the physics of associative polymers, but limitations in the production of synthetic polymers with desired molecular patterns, interactions, and lengths, have hampered experimental examination. Our system may provide a facile platform to overcome these challenges and advance our fundamental understanding of associative polymer systems.
Our work also has implications towards understanding the assembly of biomolecular condensates in the cell. RNA provides scaffold for the formation of numerous biomolecular condensates but how the sequence-specific physicochemical properties of RNA affect its condensation is only beginning to be uncovered52. Previous works have shown that single-stranded and double-stranded nucleic acids, that differ in stiffness and charge density, yield coacervates with distinct properties10,51. We show that besides stable duplexes, transient sequence-specific inter-molecular base-pairing between RNA may profoundly alter condensate properties. These transient interactions impede molecular diffusion and may tune reaction rates. Analogous to the molecular grammar of condensate-associated proteins56, our work may lay the foundation for uncovering the RNA grammar in condensates. Mutations in condensate-associated proteins that alter the viscoelastic properties of condensates are observed in neurodegenerative diseases57. For example, ALS-causative mutations in FUS and TDP-43 reduce stress granules dynamics58. Our work shows that like proteins, RNA sequence and base-pairing interactions can have a profound effect on condensate properties and may potentially harbor disease causative mutations. In particular, GC-rich repeptitive sequences (such as tandem CAG and GGGGCC repeats) that are associated with neurodegenerative disorders produce elastic coacervates with minimal RNA mobility22. Our synthetic nucleic acid coacervate system may help uncover the principles that govern the formation and function of RNA granules in the cell and may be potentially used to create synthetic membraneless organelles in cells.
Methods
M1. Chemicals
Single-stranded DNA and RNA oligonucleotides were purchased from IDT, USA. Spermine tetrahydrochloride and poly-l-lysine hydrochloride (MW 1600 Da) were purchased from Millipore Sigma, USA (S2876), and Alamanda Polymers, USA (26124-78-7), respectively. Nuclease-free water (AM9939) and Tris buffers (pH 7.0, AM9850G and pH 8.0, AM9855G) were obtained from Thermo Fisher Scientific, USA. IDTE pH 7.5 was purchased from IDT, USA (11-05-01-15). DNA was resuspended at a concentration of 250 μM in TE buffer (10 mM Tris, pH 8.0, 0.1 mM EDTA). RNA was resuspended at a concentration of 200 μM in IDTE pH 7.5. Stock solutions of spermine hydrochloride (100 mM) and poly-l-lysine hydrochloride (25 mM) were prepared in nuclease-free water. Stock solutions were aliquoted and stored at −20°C and thawed immediately before use.
M2. In vitro complex coacervation
DNA complex coacervates were prepared by sequentially adding the reagents to a PCR tube in the following order to the indicated concentrations: nuclease-free water, Tris buffer (pH 7.0, 10 mM), DNA solution (10 μM), labeled DNA (40 nM), spermine (4 mM), and NaCl (0–160 mM). The components were thoroughly mixed by pipetting. Immediately after mixing, the solution became turbid indicative of phase separation. The mixture was transferred onto a passivated glass surface for visualization under a microscope. For examining heterotypic interactions, the stock solutions of two DNA species were first mixed at the desired stoichiometric ratio, and complex coacervation was induced as described above. The resulting complex coacervates of DNA mixtures were heat denatured at 70°C for 3 minutes, and cooled down to room temperature before characterization. RNA coacervates were prepared by mixing RNA (16 μM) and poly-l-lysine (0.5 mM) in 10 mM Tris (pH 7.0).
M3. Glass passivation
Glass-bottom 384-well plates (Brooks, MatriPlate MGB101-1-2-LG-L) and cover glass (VWR, USA, 48393-251) were passivated with PEG-silane (MW = 5 kD, Laysan bio, MPEG-SIL-5000-1g). Briefly, the glass surface was first activated with a 0.5 M NaOH (Millipore Sigma, USA, 1310-73-2) solution for 20 minutes at 40°C. This solution was removed, and the glass surface was rinsed three times using Milli-Q water and dried at 40°C for an additional 30 minutes. Subsequently, the glass surface was treated with 5% (w/v) PEG-silane in anhydrous ethanol and incubated at room temperature (22°C) for 20 minutes. After removing the PEG-silane solution, the glass surface was washed three times with Milli-Q water and dried using a gentle flow of dry air. The passivated glasses were used immediately or stored at 4°C.
M4. Microsphere passivation
Red-fluorescent carboxy-coated polystyrene beads (diameter = 100 nm, Invitrogen™ FluoSpheres™ F8801) were passivated with amine-terminated methoxy-PEG (mPEG-NH2; MW 750 Da; Millipore Sigma 07964) following the protocol described by Valentine, M. T. et al. (2004)59. Briefly, beads were diluted to 4 × 1012 particles/ml and tip-sonicated (10% amplitude, 5 seconds on, 5 seconds off, 30 seconds total time) to minimize inter-bead adhesion. The diluted bead solution was dialyzed into 100 mM 2-(N-morpholino)ethanesulfonic acid (MES, 150x volume, Millipore Sigma M3671) at pH 6.0 for 2.5 hours. The dialysis bag was rinsed with deionized water and transferred to a solution mixture of 100 mM MES, 15 mM 1-[3-(dimethylamino)propyl]-3-ethylcarbodiimide (Millipore Sigma E6383), 5 mM N-hydroxysuccinimide (NHS) (Millipore Sigma 130672), and a 10x excess of mPEG-NH2. After 40 minutes of reaction, the dialysis bag was transferred to borate buffer (50 mM boric acid, Millipore Sigma B0394, 36 mM sodium tetraborate, Millipore Sigma 221732) at pH 8.5 containing 5 mM NHS and a 10x excess of mPEG-NH2 and dialyzed for at least 8 hours. This dialysis protocol was repeated two more times before transferring the dialysis cassette to pure borate buffer, where dialysis continued for another 4 hours. Upon completion of dialysis, the bead solution was removed from the dialysis cassette, diluted (50x volume) into 10 mM Tris (Millipore Sigma 93352) pH 7.0 buffer, and stored at 4 °C for future use.
M5. Microscopy
Complex coacervates were visualized using an Andor Dragonfly 500 spinning disk confocal system (Oxford Instruments, USA) mounted on a Nikon TE2000E inverted microscope using a 100x Nikon oil immersion objective (NA 1.45). Images were acquired an Andor iXon EM-CCD or an Andor Zyla sCMOS (Oxford Instruments, USA). Images were captured using 561 nm (for Cy3 labeled DNA), and 637 nm (for Cy5 labeled DNA) excitation lasers. The imaging scan speed was varied between 200 and 0.1 Hz, depending on the dynamics (FRAP recovery rates, MSD of microspheres, and fusion of coacervates) of the samples. Imaging data were processed and analyzed using ImageJ.
Temperature-controlled experiments were conducted using a CherryTemp setup (Cherry Biotech, France) and captured using the spinning disk confocal system described above. In each experiment, a freshly prepared solution was deposited onto a passivated cover glass, and a thermalization chip was positioned on top of the slide following the manufacturer’s protocol. The glass slide and the chip were separated by 500 μm liquid silicone spacers. Temperature was varied between 20°C and 45°C with a precision of 0.1°C. After each heating or cooling step, the system was allowed to equilibrate for 2 minutes before acquiring the images.
M6. FRAP
Fluorescence recovery after photobleaching (FRAP) measurements were conducted using a Micro Point pulsed nitrogen-pumped dye laser (405 nm) from Andor Technologies, integrated with the spinning disk confocal microscope. For each experiment, a circular spot with a diameter of ~1 μm at the center of the complex coacervates was bleached. For experiments involving partial photobleaching, we selected droplets with a minimum diameter of ~10 μm. Fluorescence recovery was recorded at different frame rates for the various patchyDNA sequences in order to account for their different mobility and to minimize the effects of photobleaching during imaging. For rapidly recovering T-90, GC, and GATC coacervates, movies were acquired at 10 fps (frames per second) (30 s total), while GGCC, GAATTC, and GGATCC coacervates were imaged at 1 fps (300 s total). For GGGCCC and GGAATTCC coacervates, we used 0.1 fps frame rate (30 min total). Temperature-dependent FRAP experiments were conducted using the CherryTemp setup described above.
To determine the characteristic recovery time, the mean fluorescence intensity of the circular bleached region (, 1 μm diameter) and mean intensity at the center of an unbleached coacervate (, 1 μm diameter) were monitored before and after photobleaching. The background noise during this imaging was measured by monitoring a circular area (1 μm diameter) in the solution phase, outside of the droplet. The normalized intensity at the bleach spot, , was calculated using the following relation:
| (1) |
Here, , , and are mean pre-bleach intensities averaged over 5 frames. The recovery data were double-normalized to account for lost signal due to the bleaching pulse and photobleaching during imaging. The characteristic FRAP recovery time, , was calculated by fitting vs. with the following equation:
| (2) |
where is the total recovery fraction. The self-diffusion coefficient of DNA within the coacervates was estimated using the following relation:
| (3) |
where is the radius of the bleached spot (0.5 μm)
M7. Condensate fusion
Spontaneous fusion events were manually identified in movies of condensates recorded using either an Andor iXon EM-CCD (for movies at < 20 fps) or an Andor Zyla sCMOS (for movies at > 20 fps). Fusion events for T-90 and GC coacervates were recorded at 200 fps, while coacervates of the other patchyDNA were recorded at rates ranging from 10 to 0.1 fps. The characteristic fusion time, , was calculated from the temporal evolution of the aspect ratio of a coacervate after contact using the following relation:
| (4) |
We chose fusion events between droplets of roughly similar size. In a typical fusion event, and relaxes to ~1 over time. For each patchyDNA, we examined fusion events across a range of droplet sizes. The inverse capillary velocity for was then calculated using the following relation:
| (5) |
Where is the size of the coacervate after fusion, defined as:
| (6) |
Here, and are the long and short axes of the coacervate, respectively. Coacervate fusion experiments were performed on freshly passivated 384-well plates to minimize effects of surface adsorption on fusion dynamics.
M8. Single particle tracking
The viscosity of coacervates was calculated by tracking trajectories of passivated fluorescent polystyrene beads (diameter = 100 nm, Thermo Fisher, USA) embedded in coacervates. Bead trajectories were imaged using Andor iXon EMCCD with a 561 nm excitation laser at 5 fps and analyzed using the Trackmate plugin in ImageJ60.
The diffusion coefficient of beads was calculated from the mean squared displacement using the following relation:
| (7) |
Here, is the diffusion exponent, and NF is the noise floor, estimated by tracking beads stuck at the bottom of the coacervates. Coacervates viscosity was estimated using the Stokes-Einstein relation:
| (8) |
Here,. For all MSD experiments, beads diffusing far away from the coacervate-solution interface were examined in order to minimize any surface effects on bead trajectories. Where indicated, the temperature was modulated using the CherryTemp instrument, as described above, and for each temperature, NF was determined independently.
M9. FRET
To determine FRET efficiency within complex coacervates, we used a method similar to that was used by Nott et. al.61 In brief, three fluorescent images:, and at a fixed z-plane are captured. Here DD = donor emission after donor excitation; DA (FRET signal) = acceptor emission after donor excitation and AA = acceptor emission after acceptor excitation. The FRET efficiency at a given region of interest is then given by,
The donor (Cy3) and acceptor (Cy5) fluorophores were incorporated either at the 5’ terminus or internally in the DNA sequence (see Supplementary info for sequences). Cy3 and Cy5 were excited by 561 nm and 637 nm lasers respectively and their emissions were collected using 600–50 nm and 700–75 nm bandpass filters respectively. To correct for spectral overlap, we calculated corrected FRET efficiency by using three sets of samples: sample containing (a) both Cy3-Cy5 (DDCy3-Cy5, DACy3-Cy5, AACy3-Cy5), (b) only Cy3 (DDCy3, DACy3, AACy3) and (c) only Cy5 (DDCy5, DACy5, AACy5). The corrected FRET efficiency, Fcorr for each pixel within the region of interest was calculated by following the relation,
where and
Low intensity values corresponding to DDCy5 and AACy5 confirmed that signal bleedthrough between channels was minimal. All images were background corrected before processing.
Supplementary Material
Acknowledgements:
We thank Ofer Kimchi, Ella King, Daniel Stein, Alexander Alfredo Alexander-Katz, and members of Jain lab for helpful discussions. This work was supported by grants from the NIH (R35GM151111), David and Lucile Packard Foundation, and the Pew Biomedical Trust.
References:
- 1.Nucleic acids in chemistry and biology. (Royal Society of Chemistry, 2022). [Google Scholar]
- 2.SantaLucia J. A unified view of polymer, dumbbell, and oligonucleotide DNA nearest-neighbor thermodynamics. Proc Natl Acad Sci U S A 95, 1460–1465 (1998). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.SantaLucia J. & Hicks D. The thermodynamics of DNA structural motifs. Annu Rev Biophys Biomol Struct 33, 415–440 (2004). [DOI] [PubMed] [Google Scholar]
- 4.Zuker M. & Stiegler P. Optimal computer folding of large RNA sequences using thermodynamics and auxiliary information. Nucleic Acids Res 9, 133–148 (1981). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Jones M. R., Seeman N. C. & Mirkin C. A. Programmable materials and the nature of the DNA bond. Science 347, 1260901 (2015). [DOI] [PubMed] [Google Scholar]
- 6.Dey S. et al. DNA origami. Nat Rev Methods Primers 1, 13 (2021). [Google Scholar]
- 7.Han D. et al. Single-stranded DNA and RNA origami. Science 358, eaao2648 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Um S. H. et al. Enzyme-catalysed assembly of DNA hydrogel. Nat Mater 5, 797–801 (2006). [DOI] [PubMed] [Google Scholar]
- 9.Udono H., Gong J., Sato Y. & Takinoue M. DNA Droplets: Intelligent, Dynamic Fluid. Adv Biol (Weinh) 7, e2200180 (2023). [DOI] [PubMed] [Google Scholar]
- 10.Vieregg J. R. et al. Oligonucleotide-peptide complexes: Phase control by hybridization. Journal of the American Chemical Society 140, 1632–1638 (2018). [DOI] [PubMed] [Google Scholar]
- 11.Aumiller W. M., Pir Cakmak F., Davis B. W. & Keating C. D. RNA-Based Coacervates as a Model for Membraneless Organelles: Formation, Properties, and Interfacial Liposome Assembly. Langmuir 32, 10042–10053 (2016). [DOI] [PubMed] [Google Scholar]
- 12.Rumyantsev A. M., Jackson N. E. & De Pablo J. J. Polyelectrolyte Complex Coacervates: Recent Developments and New Frontiers. Annu. Rev. Condens. Matter Phys. 12, 155–176 (2021). [Google Scholar]
- 13.Sing C. E. & Perry S. L. Recent progress in the science of complex coacervation. Soft Matter 16, 2885–2914 (2020). [DOI] [PubMed] [Google Scholar]
- 14.King J. T. & Shakya A. Phase separation of DNA: From past to present. Biophys J 120, 1139–1149 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Oparin A. I. The origin of life and the origin of enzymes. Adv Enzymol Relat Areas Mol Biol 27, 347–380 (1965). [DOI] [PubMed] [Google Scholar]
- 16.Drobot B. et al. Compartmentalised RNA catalysis in membrane-free coacervate protocells. Nat Commun 9, 3643 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Banani S. F., Lee H. O., Hyman A. A. & Rosen M. K. Biomolecular condensates: organizers of cellular biochemistry. Nat. Rev. Mol. Cell Biol. 18, 285–298 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Brangwynne C. P., Tompa P. & Pappu R. V. Polymer physics of intracellular phase transitions. Nature Phys 11, 899–904 (2015). [Google Scholar]
- 19.Aumiller W. M. & Keating C. D. Phosphorylation-mediated RNA/peptide complex coacervation as a model for intracellular liquid organelles. Nat Chem 8, 129–137 (2016). [DOI] [PubMed] [Google Scholar]
- 20.Luo D. & Saltzman W. M. Synthetic DNA delivery systems. Nat Biotechnol 18, 33–37 (2000). [DOI] [PubMed] [Google Scholar]
- 21.Paunovska K., Loughrey D. & Dahlman J. E. Drug delivery systems for RNA therapeutics. Nat Rev Genet 23, 265–280 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Jain A. & Vale R. D. RNA phase transitions in repeat expansion disorders. Nature 546, 243–247 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Zhang Z., Chen Q. & Colby R. H. Dynamics of associative polymers. Soft Matter 14, 2961–2977 (2018). [DOI] [PubMed] [Google Scholar]
- 24.Webber M. J. & Tibbitt M. W. Dynamic and reconfigurable materials from reversible network interactions. Nat Rev Mater 7, 541–556 (2022). [Google Scholar]
- 25.Semenov A. N. & Rubinstein M. Thermoreversible gelation in solutions of associative polymers. 1. Statics. Macromolecules 31, 1373–1385 (1998). [Google Scholar]
- 26.Zadeh J. N. et al. NUPACK: Analysis and design of nucleic acid systems. J Comput Chem 32, 170–173 (2011). [DOI] [PubMed] [Google Scholar]
- 27.Zeng Y., Montrichok A. & Zocchi G. Bubble nucleation and cooperativity in DNA melting. J Mol Biol 339, 67–75 (2004). [DOI] [PubMed] [Google Scholar]
- 28.Ares S., Voulgarakis N. K., Rasmussen K. Ø. & Bishop A. R. Bubble Nucleation and Cooperativity in DNA Melting. Phys. Rev. Lett. 94, 035504 (2005). [DOI] [PubMed] [Google Scholar]
- 29.Bianchi E., Blaak R. & Likos C. N. Patchy colloids: state of the art and perspectives. Phys Chem Chem Phys 13, 6397–6410 (2011). [DOI] [PubMed] [Google Scholar]
- 30.Blagbrough I. S., Metwally A. A. & Geall A. J. Measurement of polyamine pKa values. Methods Mol Biol 720, 493–503 (2011). [DOI] [PubMed] [Google Scholar]
- 31.Spruijt E. et al. Structure and dynamics of polyelectrolyte complex coacervates studied by scattering of neutrons, X-rays, and light. Macromolecules 46, 4596–4605 (2013). [Google Scholar]
- 32.Muthukumar M. A Perspective on Polyelectrolyte Solutions. Macromolecules 50, 9528–9560 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Sabanayagam C. R., Eid J. S. & Meller A. Using fluorescence resonance energy transfer to measure distances along individual DNA molecules: corrections due to nonideal transfer. J Chem Phys 122, 061103 (2005). [DOI] [PubMed] [Google Scholar]
- 34.Sim A. Y. L., Lipfert J., Herschlag D. & Doniach S. Salt dependence of the radius of gyration and flexibility of single-stranded DNA in solution probed by small-angle x-ray scattering. Phys Rev E 86, 021901 (2012). [DOI] [PubMed] [Google Scholar]
- 35.Fu J. & Schlenoff J. B. Driving Forces for Oppositely Charged Polyion Association in Aqueous Solutions: Enthalpic, Entropic, but Not Electrostatic. J Am Chem Soc 138, 980–990 (2016). [DOI] [PubMed] [Google Scholar]
- 36.Wang L. et al. Hydrogen bonding enhances the electrostatic complex coacervation between κ-carrageenan and gelatin. Colloids and Surfaces A: Physicochemical and Engineering Aspects 482, 604–610 (2015). [Google Scholar]
- 37.Zhang H. et al. RNA Controls PolyQ Protein Phase Transitions. Molecular Cell 60, 220–230 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Taylor N. O., Wei M. T., Stone H. A. & Brangwynne C. P. Quantifying Dynamics in Phase-Separated Condensates Using Fluorescence Recovery after Photobleaching. Biophysical Journal 117, 1285–1300 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Rubinstein M. & Semenov A. N. Dynamics of entangled solutions of associating polymers. Macromolecules 34, 1058–1068 (2001). [Google Scholar]
- 40.Baxandall L. G. Dynamics of reversibly crosslinked chains. Macromolecules 22, 1982–1988 (1989). [Google Scholar]
- 41.Mason T. G. & Weitz D. A. Linear Viscoelasticity of Colloidal Hard Sphere Suspensions near the Glass Transition. Phys. Rev. Lett. 75, 2770–2773 (1995). [DOI] [PubMed] [Google Scholar]
- 42.Elbaum-Garfinkle S. et al. The disordered P granule protein LAF-1 drives phase separation into droplets with tunable viscosity and dynamics. Proc. Natl. Acad. Sci. U.S.A. 112, 7189–7194 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Eggers J., Lister J. R. & Stone H. A. Coalescence of liquid drops. J. Fluid Mech. 401, 293–310 (1999). [Google Scholar]
- 44.Brangwynne C. P., Mitchison T. J. & Hyman A. A. Active liquid-like behavior of nucleoli determines their size and shape in Xenopus laevis oocytes. Proc Natl Acad Sci U S A 108, 4334–4339 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Soft colloids. (Elsevier Academic Press, 2005). [Google Scholar]
- 46.Aarts D. G. A. L., Schmidt M. & Lekkerkerker H. N. W. Direct visual observation of thermal capillary waves. Science 304, 847–850 (2004). [DOI] [PubMed] [Google Scholar]
- 47.Spruijt E., Sprakel J., Cohen Stuart M. A. & Van Der Gucht J. Interfacial tension between a complex coacervate phase and its coexisting aqueous phase. Soft Matter 6, 172–178 (2010). [Google Scholar]
- 48.Rhine K., Vidaurre V. & Myong S. RNA Droplets. Annu. Rev. Biophys. 49, 247–265 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Choi J.-M., Holehouse A. S. & Pappu R. V. Physical Principles Underlying the Complex Biology of Intracellular Phase Transitions. Annu. Rev. Biophys. 49, 107–133 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Lin Y., Protter D. S. W., Rosen M. K. & Parker R. Formation and Maturation of Phase-Separated Liquid Droplets by RNA-Binding Proteins. Molecular Cell 60, 208–219 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Choi S., Meyer M. O., Bevilacqua P. C. & Keating C. D. Phase-specific RNA accumulation and duplex thermodynamics in multiphase coacervate models for membraneless organelles. Nat Chem 14, 1110–1117 (2022). [DOI] [PubMed] [Google Scholar]
- 52.Roden C. & Gladfelter A. S. RNA contributions to the form and function of biomolecular condensates. Nat Rev Mol Cell Biol 22, 183–195 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Mirtič A. & Grdadolnik J. The structure of poly-l-lysine in different solvents. Biophysical Chemistry 175–176, 47–53 (2013). [DOI] [PubMed] [Google Scholar]
- 54.Praetorius F. et al. Biotechnological mass production of DNA origami. Nature 552, 84–87 (2017). [DOI] [PubMed] [Google Scholar]
- 55.Cangialosi A. et al. DNA sequence–directed shape change of photopatterned hydrogels via high-degree swelling. Science 357, 1126–1130 (2017). [DOI] [PubMed] [Google Scholar]
- 56.Martin E. W. et al. Valence and patterning of aromatic residues determine the phase behavior of prion-like domains. Science 367, 694–699 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Zhou X. et al. Mutations linked to neurological disease enhance self-association of low-complexity protein sequences. Science 377, eabn5582 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Li Y. R., King O. D., Shorter J. & Gitler A. D. Stress granules as crucibles of ALS pathogenesis. Journal of Cell Biology 201, 361–372 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Valentine M. T. et al. Colloid surface chemistry critically affects multiple particle tracking measurements of biomaterials. Biophys. J. 86, 4004–4014 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Ershov D. et al. TrackMate 7: integrating state-of-the-art segmentation algorithms into tracking pipelines. Nat. Methods 19, 829–832 (2022). [DOI] [PubMed] [Google Scholar]
- 61.Nott T. J., Craggs T. D. & Baldwin A. J. Membraneless organelles can melt nucleic acid duplexes and act as biomolecular filters. Nat. Chem. 8, 569–575 (2016). [DOI] [PubMed] [Google Scholar]
- 62.Pierre-Gilles de Gennes. Scaling Concepts in Polymer Physics. (Cornell University Press, 1979). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.