Population genetics meets ecology: a guide to individual-based simulations in continuous landscapes

Abstract

Individual-based simulation has become an increasingly crucial tool for many fields of population biology. However, implementing realistic and stable simulations in continuous space presents a variety of difficulties, from modeling choices to computational efficiency. This paper aims to be a practical guide to spatial simulation, helping researchers to implement realistic and efficient spatial, individual-based simulations and avoid common pitfalls. To do this, we delve into mechanisms of mating, reproduction, density-dependent feedback, and dispersal, all of which may vary across the landscape, discuss how these affect population dynamics, and describe how to parameterize simulations in convenient ways (for instance, to achieve a desired population density). We also demonstrate how to implement these models using the current version of the individual-based simulator, SLiM. Since SLiM has the capacity to simulate genomes, we also discuss natural selection – in particular, how genetic variation can affect demographic processes. Finally, we provide four short vignettes: simulations of pikas that shift their range up a mountain as temperatures rise; mosquitoes that live in rivers as juveniles and experience seasonally changing habitat; cane toads that expand across Australia, reaching 120 million individuals; and monarch butterflies whose populations are regulated by an explicitly modeled resource (milkweed).

Introduction

Explicit spatial models are indispensable for understanding how species live, interact, and evolve across geographic landscapes. However, the process of formulating sensible models of demography in continuous space is fraught with pitfalls and choices that are unfamiliar to many researchers interested spatial modeling. For instance, one of the more commonly used non-spatial models is the Wright–Fisher model, in which the number of individuals is fixed – directly specified as a parameter. However, as we describe below, in spatial models with locally defined dynamics the number of individuals is a stochastic, emergent property of the dynamics and it takes some expertise to arrange a model that produces a desired equilibrium size. Even fundamental population genetics concepts such as selection coefficients cease to have a single obvious interpretation in a spatial context.

Implementation of an individual-based simulation requires great specificity – choices must be made regarding a large number of mechanisms and parameters. Simulated organisms must separately give birth and die, unlike in more abstract theory such as the Wright–Fisher model, where often only the net effects of birth minus death enter (e.g., Cantrell and Cosner, 2004). Here we review various aspects of space that must be modeled, covering both spatial movement and spatial interactions. Spatial movement, such as dispersal, is familiar to population geneticists, but spatial interactions may not be, even though some sort of negative feedback between population density and net reproductive rate is necessary to avoid unbounded growth.

This paper is targeted at researchers who wish to produce simulations that are – at least roughly – modeled on concrete empirical systems. At least parts of this guide will be useful to: empirical researchers wanting to explore plausibility of hypotheses or power of study designs; methods developers who want to test their methods on realistic spatial models; theoreticians wishing to explore spatial models; or managers wishing to explore alternative scenarios. So, we aim to make it easy to build a model starting from those quantities that we generally have good estimates of for particular organisms. This differs from the modeling philosophy in much theoretical work, which often begins from a “simplest possible” model. For instance, population genetics theory often uses the Wright–Fisher model, with the justification that the effects of small fluctuations in population size may be absorbed into the effective population size parameter. Similarly, both evolutionary and ecological theory often rely on (partial) differential equation models that do not explicitly represent individuals, and so rely on various statistical approximations.

Why individual-based simulations, and why in continuous space? Since real individuals are discrete, and live in continuous space, such simulations can in principle more accurately model real-world situations. Some phenomena simply require individual-based simulations (e.g., locally adaptive genotypes). Non-individual-based models can be more computationally efficient, but at an often unknown cost to accuracy (Stillman et al., 2015). For instance, commonly-used discretized spatial landscapes can scale to much larger populations, but such discretized landscapes do not provide a consistent approximation to certain aspects of continuous-space dynamics (in two or more dimensions, Barton et al., 2002^; Battey et al., 2020), and so it is difficult to understand which predictions apply to real-world situations. An even more practical consideration is that developing individual-based simulations in continuous space often requires less time and modeling expertise. This is because it is usually relatively easy to quickly come up with order-of-magnitude estimates of the various aspects of an organism’s life cycle. On the other hand, more abstracted modeling frameworks usually involve analytical approximations, compound parameters, and other technicalities that require careful checking and mathematical experience. For instance, how does one translate “offspring disperse around 100m” to a migration rate between adjacent grid cells in a discretized landscape? (There are good answers to this question, but these are less straightforward than directly inputting a mean dispersal of 100m.) This assumes the modeler has a particular organism in mind, while simulations with fewer choices might feel more general for theoretical work or methods development. However, this can be a false generality, as more work is required after the fact to determine which real-world organisms a given result or method is applicable to.

Explicit individual-based population models are not new to ecology (DeAngelis and Yurek, 2017; Grimm, 1999). Furthermore, a great deal of ecological work has sought to quantify the effects of density-dependent demographic feedback – how demographic processes lead to stability of a population. For a single species, some sort of negative feedback between population density and growth rate is necessary to avoid the population growing without bound, although there are a great many ways to set this up in practice (De Wit, 1960; Beverton and Holt, 1957; Ellner et al., 2016). Demographers have a deep understanding of how to describe and parameterize the statistical properties of birth and death, and what the emergent consequences are for population growth, lifespan, age distribution, and long-term fitness (Tuljapurkar, 2013). Although temporal stochasticity is relatively well-understood in demography (Tuljapurkar, 1989), the consequences of spatial heterogeneity – particularly outside of metapopulation models (Hanski, 1997) – have received less attention.

Geography can have strong effects on patterns of genetic variation (Wright, 1943; Malécot, 1969; Rousset, 2000; Charlesworth et al., 2003; Battey et al., 2020; Min et al., 2022) and on evolutionary processes (Felsenstein, 1976; Uecker et al., 2014; Savolainen et al., 2007). Genetic differentiation is shaped by the movement of individuals, and hence distance and geographical features, as well as the spatio-temporal history of the species (Hewitt, 2011; Rosenberg et al., 2005; Ramachandran et al., 2005). Geography is therefore not only important but also provides a relatively untapped source of information to inform inference (Bradburd and Ralph, 2019). However, it is difficult to obtain analytical predictions from spatial population-genetics models (Felsenstein, 1975; Barton et al., 2002). Most spatial work in population genetics uses partial differential equations that do not represent genetic differentiation (Slatkin, 1973; Barton, 1979; Sedghifar et al., 2016; Etheridge et al., 2024), or specifically look at the fronts of population expansions (Paulose et al., 2019; Nullmeier and Hallatschek, 2013; Etheridge and Penington, 2022).

Simulation has long been a useful tool in the study of populations (Grimm, 1999; DeAngelis and Yurek, 2017), particularly for the purposes of prediction (for example, for population viability analysis, see Dunning Jr et al., 1995) – even predating common usage of digital computers (Pearson, 1960). Simulations are also useful for inference, ranging from exploratory simulations to training for deep learning. The possible uses depend a great deal on the cost of a single simulation: for instance, many modern machine learning methods are only feasible with relatively fast simulations. Introducing geographic space increases computational complexity, making the task of producing sufficient training data more difficult (but see Smith et al., 2023; Champer et al., 2021).

This paper is intended as a guide to the territory of spatial modeling, with a focus on simulating individual-based models. We focus on discrete-time models of continuous geographical space, in which interactions and (usually) dispersal are local. The paper has two main parts: conceptual discussion of practical aspects of spatial simulation, followed by some biologically-motivated examples. The first topic is population regulation, as this is the topic which in our experience is the greatest barrier to new modelers. Next, we discuss spatial movement and mate choice, highlighting some interesting challenges. Subsequently, we discuss implementation of spatial heterogeneity and natural selection. Within each topic we provide examples chosen to demonstrate a particular technique or opportunity, with accompanying code snippets. Last, we demonstrate several complete, biologically-motivated simulations that incorporate many of the ideas presented earlier. We are particularly motivated by the simulation framework provided by SLiM (Haller and Messer, 2023), a flexible and powerful individual-based eco-evolutionary simulator that now includes a full set of tools for modeling interactions between multiple species across geographical landscapes. A minimal but complete SLiM script is provided in Appendix A, and our main text is accompanied by boxes that describe how to implement the spatial models we describe here in SLiM. This paper also serves to describe new capabilities in the newly-released SLiM v4.2. Code for all models below is available at https://github.com/kr-colab/spatial_sims_standard. We recommend that readers open these recipes in SLiM’s GUI to experiment with while reading.

Population dynamics and density

We start by describing how to maintain a stable population. An extremely simple spatial simulation might be as follows: organisms are asexual, and do not move during their lifespan. Each time step, each adult gives birth to a $\mathrm{P}\mathrm{o}\mathrm{i}\mathrm{s}\mathrm{s}\mathrm{o}\mathrm{n}\left(f\right)$ number of offspring, which each disperse to a random location, where displacement from their offspring-bearing parent’s location is drawn from a Normal distribution with mean zero and standard deviation ${\sigma }_D$. Then, each individual, independently, dies with a given probability $\mu$.

Were we to simulate such a model, its flaw would be immediately apparent as it runs: either all individuals rapidly disappear (if $f\le \mu$), or the computer grinds to a halt as the number of individuals explodes (if $f>\mu$). For this reason, we need some kind of density-dependent feedback to maintain a stable population that can be simulated for any reasonable length of time – in other words, we need the net population growth rate to change from positive to negative as the population density grows past some point. To achieve that, either birth rates need to decrease or death rates need to increase with local population density.

To provide density-dependent feedback, we first need a notion of “population density” at a point in space, a measure of the number of individuals nearby per unit area. Let $K$ denote the desired equilibrium population density (in individuals per unit area). A general way to define $n\left(\mathit{x}\right)$, the population density around a location $\mathit{x}$, is to specify an interaction kernel, $\rho \left(\mathit{x}\right)$, which is a nonnegative function with $\int \rho \left(\mathit{x}\right)\mathit{d}\mathit{x}=1$; an interaction scale ${\sigma }_X$; and then if the locations of the individuals in the population are ${\mathit{x}}_1,\dots ,{\mathit{x}}_{\mathit{n}}$, define $n\left(\mathit{x}\right)$ by

$$n\left(\mathit{x}\right)=\frac{1}{{\sigma }_X^2}\sum _i\rho \left(\frac{\mathit{x}-{\mathit{x}}_i}{{\sigma }_X}\right).$$ (1)

(This is in two dimensions; in one dimension we would divide by ${\sigma }_X$ instead of ${\sigma }_X^2$.) Since $\int \rho \left(\mathit{x}/{\sigma }_X\right)\mathit{d}\mathit{x}={\sigma }_X^2$, the value of $n\left(\mathit{x}\right)$ is in units of individuals per unit area. A common choice for $\rho \left(\mathit{x}\right)$ is the Gaussian density function. One concrete interpretation is that if $\rho \left((\mathit{x}-\mathit{y})/{\sigma }_X\right)$ gives the proportion of time that an individual at $\mathit{y}$ spends near $\mathit{x}$, then $n\left(\mathit{x}\right)$ is proportional to the time spent by all individuals near $\mathit{x}$. (More concretely, ${\int }_{A}n\left(\mathit{x}\right)\mathit{d}\mathit{x}$ is the total amount of time spent by all individuals in the region $A$.)

Now suppose that in each time step of the model, first each individual produces a random number of offspring; for an individual at $\mathit{x}$ the mean number of offspring is $f\left(n\right(\mathit{x})/K)$ where $f$ is the birth rate or fecundity, and each juvenile disperses to a nearby location whose displacement from $\mathit{x}$ is chosen from a given probability distribution. Then, all individuals (including those just born) survive with probability $1-\mu \left(n\right(\mathit{x})/K)$, making $\mu \left(u\right)$ the mortality rate at scaled density $u$. As written, each rate depends on spatial location $\mathit{x}$ only through the smoothed population density $n\left(\mathit{x}\right)$ at that location, scaled by a parameter $K$ that controls the equilibrium density. For simplicity, in this model all individuals reproduce (as hermaphrodites), there is no consequence of aging, and we do not explicitly model the movement of an individual during its lifespan (but see subsequent sections).

Equilibrium population density

Will this model stabilize, and if so, to what density? We expect an equilibrium when births balance deaths. If we define the local per capita net reproductive rate (the expected increase due to birth minus the decrease due to death, per individual) to be

$$F\left(u\right)=f\left(u\right)(1-\mu (u\left)\right)-\mu \left(u\right),$$ (2)

then we expect an equilibrium at a density of $n_{\mathrm{*}}$ solving $F\left(n_{\mathrm{*}}/K\right)=0$. For this reason, it is convenient to choose the functional forms of $f$ and $\mu$ so that $F\left(1\right)=0$, in which case we expect the equilibrium $n_{\mathrm{*}}$ to be roughly equal to $K$. (However, we will see below that often $K$ is not exactly the equilibrium density.) In addition to $F\left(1\right)=0$, for the population to be stable we also need $F^{\prime }\left(1\right)<0$ so that the net reproductive rate decreases with density near to the equilibrium. The argument $u$ in $f\left(u\right),\mu \left(u\right)$, and $F\left(u\right)$ is the scaled population density $u=n\left(\mathit{x}\right)/K$, written this way so that it is easy to control the equilibrium population density by simply changing $K$, independently of other factors.

A brief note on what we have done here: it might seem most natural to set up a simulation using fecundity and mortality rates based on empirical observation. If so, then mean population density would be an emergent property of the simulation – in other words, our script would not have a parameter $K$ that we could directly adjust. However, to do this we need empirical estimates of how fecundity and mortality depend on local density, which are very difficult to obtain. A much more common situation is to have estimates of fecundity and mortality rates and population density at equilibrium. The parameterization we outline here, in which $K$ is a directly tunable rather than emergent parameter, is designed to make this use case natural. (Fecundity and mortality rates at equilibrium are also naturally introduced into the functional forms for $f\left(u\right)$ and $\mu \left(u\right)$.)

Functional forms

The next question is: what forms should we use for the functions $f\left(u\right)$ and/or $\mu \left(u\right)$? There is surprisingly little guidance from the theoretical or empirical literature. Population models mostly come in two flavors: “phenomenological” (or “top-down”) models that only consider the net reproductive rate, $F\left(u\right)$; and “mechanistic” (or “bottom-up”) models that explicitly consider birth and death separately (Geritz and Kisdi, 2012). We need a mechanistic model, since our approach here is individual-based, but most literature on density dependence uses phenomenological models (a notable exception, see Coulson et al. (2008), or integral projection models Ellner et al. (2016)). Matrix population models (Caswell, 2000) are (mostly) mechanistic and widely used for management, but rarely incorporate density dependence (for a good reason: management questions are often concerned with short-term predictions, for which linear models are good enough). Furthermore, empirical estimation of functional forms for density dependence is a logistically and statistically daunting task, even without considering environmental variation. Modelers using simulation may therefore wish to simply choose a mathematically convenient form, reducing the problem to estimating parameters given that functional form. Perhaps the most obvious strategy is to multiply the base fecundity or survival by function of $n$ that decreases for sufficiently large $n$. For instance, if we set $\mu$ to a constant and $f\left(n\right)=f_0{e}^{-n}$, then the equilibrium is at $n_{\mathrm{*}}=K\mathrm{l}\mathrm{o}\mathrm{g}\left(\mu /f_0\right)$; setting $f_0=\mu$, this model would conveniently reach equilibrium near $K$. Appendix C summarizes various familiar functional forms for $F\left(u\right)$ from the literature, and works through examples.

Regulation by mortality

Suppose we would like to use density-dependent feedback only on mortality. In this case, the average number of offspring is constant: we may say $f\left(u\right)=f$. Recall that $F\left(u\right)=(1-\mu (u\left)\right)f-\mu \left(u\right)$, and so the survival probability at scaled density $u$ is

$$1-\mu (u)=\frac{1+F(u)}{1+f}.$$ (3)

The Beverton–Holt form for the net effects of density (Beverton and Holt, 1957) would have that $F(u)$ is proportional to $(1+a)/(1+au)-1$, for some constant $a$ that controls the strength of the density-dependent feedback. So, to set up the model to have “Beverton–Holt” feedback, we plug in $F(u)=(1+a)/(1+au)-1$ and obtain that

$$1-\mu (u)=\frac{1+a}{(1+f)(1+au)}\text{if}a\le f.$$ (4)

The leftmost plot in Figure 1 visualizes Equations 3 and 4, and the others will be discussed later in Density dependence, life history, and stochasticity. This is also demonstrated in Box 1, and most of the examples in this paper use this model with $a=f$. The condition that $a\le f$ is so that this gives us a valid probability: otherwise, the survival probability can be negative. In practice, it could be better to reparameterize with $s_0$, the survival probability at low density, so that $a=s_0(1+f)+1$. Note that the strategy used here cannot work with the discrete logistic: since $F(u)=1-u$ can get arbitrarily negative, eventually random density fluctuations will lead to negative probabilities, and errors in the simulation.

Figure 1:

Three example models with “Beverton–Holt” regulation of population density. The relationship between scaled local population density and vital rates: mean fecundity $(f(u))$, probability of death $(\mu (u))$, and net reproduction rate $(F(u)=f(u)-\mu (u))$. In each, the horizontal axis is shown in units of K, the parameter controlling equilibrium density (“carrying capacity”). The models are: mortality from equation (4), fecundity from equation (5), and both from equation (6).

Box 1: Regulating mortality and fecundity in SLiM.

The Wright–Fisher model is a population model with a fixed population size. A spatial Wright–Fisher model, therefore, has global population regulation – individuals are affected by others arbitrarily far away, resulting in counter-intuitive, unrealistic consequences (Felsenstein, 1975). SLiM’s default model is the Wright-Fisher model (“WF”). In this study, our goal is to model particular species in realistic ways, so we use only SLiM’s non-Wright-Fisher (“nonWF”) model, which requires explicitly choosing how births and deaths occur.

In a SLiM nonWF model, the “fitness” attribute of an individual is the probability of survival until the next time step. So, controlling mortality in SLiM is simply a matter of setting individuals’ fitness. To compute local density, we use the localPopulationDensity() function, which computes density just as described in equation (1) (with options for the choice of kernel). To do this we need to first (during setup) define an InteractionType object, here using a Normal kernel with a scale of SX and a maximum distance of SX * 3):

initializeInteractionType(1, “xy”, maxDistance=SX * 3);
i1.setInteractionFunction(“n”, 1.0, SX);

Now, to use Beverton–Holt regulation on mortality as described around equation 4 (setting $a=1$ in equation 4 and with $K$ defined elsewhere), in each time step, we use this interaction type to set survival probabilities:

inds = p1.individuals;
density = i1.localPopulationDensity(inds);
u = density / ((1 + f) * K);
inds.fitnessScaling = 1 / (1 + f * u);

Note that the local population density is measured after reproduction and before death $(N_t^{+}$ in Appendix B), so we divide by $1+f$ as well as $K$ when converting it to scaled population density $u$ from the equation (1), so it reflects density before reproduction.

On the other hand, offspring are produced by a “reproduction() callback”, a chunk of code that is executed each time step for each individual, and produces any desired new offspring for the focal individual. For instance, if we would like to use Ricker regulation on fecundity (see equation 19 with $\alpha =1$ and $\beta =0)$, we might for efficiency pre-compute each individual’s number of offspring:

inds.tag = rpois(length(inds), lambda=exp(−density/K));

and then in the “reproduction() callback produce the offspring:

p1.addCrossed(individual, mate, count=individual.tag);

This example has been simplistic in many ways. Of course, there are many other possible ways to set up $f(u)$ and $\mu (u)$ that result in the same net form of density dependence (see Density dependence, life history, and stochasticity for further discussion). We also discuss there how stochasticity alters the realized equilibrium density. Finally, if there are two sexes and only one sex can bear offspring, then $f$ should not be the total number of offspring, but rather the number of offspring of the offspring-bearing sex (e.g., if females are the offspring-bearing sex, half the total assuming equal numbers of male and female offspring, representing just the female offspring). More generally, if vital rates depend on any aspect of the individual (for example, only adults can reproduce, or mortality is age-dependent), then the equivalent calculations must be done with a matrix population model (Caswell, 2000) or an integral projection model (Ellner et al., 2016). Our examples mostly ignore such complications, although several models in later sections have distinct life stages.

Context and connections

This section reviews wider connections to population modeling, and can be safely skipped by readers not familiar with that literature.

Historically, most spatial population models were either based on partial differential equations and so did not explicitly represent individuals (Skellam, 1951; Beverton and Holt, 1957; Cantrell and Cosner, 2004), used an array of randomly mating populations (i.e., metapopulation models, Hanski, 1997), or had individuals living on a regular grid (Epperson, 2003). Although there are use cases for these, the main reason that individual-based continuous-space models are not more common may simply be convenience, both for mathematical analysis and software programming. The continuous-space formulation we use was introduced by Pacala (1986) and Bolker and Pacala (1997), and has been used in many theoretical studies (Dieckmann and Law, 1999; Snyder and Chesson, 2004; Etheridge et al., 2024).

A more modern extension to matrix population models, integral projection models, more commonly incorporate density dependence (Ellner et al., 2016), and may even estimate functional forms – see for example Adler et al. (2010). Much of the remaining literature on density dependence only considers the form of $F(u)$, rather than separating out the effects of density on different life history components (reviewed in Caswell, 2000^; Eskola and Geritz, 2007). There are a wide variety of methods to infer $F(u)$ from time series data (Lande et al., 2003), but statistical issues make the problem difficult (Freckleton et al., 2006). However, the “$F(u)$” thus inferred is not necessarily the same as ours – many of these methods assume no demographic stochasticity, and hence an infinite population size. In other words, the $F(u)$ that these infer is a landscape-scale relationship, averaging the net effects of birth and death over thousands or millions of individuals. Our $F(u)$, on the other hand, is local, and describes how a single individual is affected by having a few more or less neighbors. These are related, but need not have the same functional forms. In particular, the behavior of $F(u)$ for very large or small values of $u$ is usually much more important when applied to an individual, because the local density around an individual might be proportionally much larger or smaller than average, due to random fluctuations, than the total population size across a landscape. These can have a strong effect - for instance, increasing population density can have a positive effect on population growth (for at least low enough densities), a dynamic which can have interesting and important effects (Courchamp et al., 2008).

Furthermore, effects of density dependence are often mediated (at least in part) through interactions with other species, and the nature of these interactions may depend on environmental context. These interactions are often modeled as the net result of pairwise interactions, and various methods are used to estimate these potentially numerous and environmentally-dependent effects (for recent examples, see Weiss-Lehman et al., 2022; Bimler et al., 2023). It is beyond the scope of this article to review the full range of approaches and possibilities – but, note that there is no obstacle to simulation of multiple species whose interactions vary across space and/or time in SLiM (Haller and Messer, 2023).

Huge amounts of observational effort have gone into detailed estimates of the demography of particular species, especially those of conservation or management concern. However, such observations by necessity describe a snapshot of demographic rates in particular conditions (or, averaged over a particular range of conditions). Estimating the functional responses to density necessary to describe long-term dynamics is much more difficult, although methodological progress has been made, for instance, by incorporating many sources of information with “integrated population models” (Zipkin et al., 2023). A great deal of ecological work has also sought to quantify the effects of density-dependent demographic feedback. In a spatial model, this population density is usually measured locally – around the individual in question – yielding concepts such as the “competition kernel” (Bolker and Pacala, 1997) or “crowding index” (Pacala and Silander, 1985). Density-dependent feedback has a key place in the theory of coexistence between species: the Janzen-Connell hypothesis suggests that stronger intra- than inter-specific negative density-dependent effects could provide a mechanism for species coexistence (Janzen, 1970; Connell, 1971; Terborgh, 2012; Hülsmann et al., 2021). A substantial number of studies across a variety of organisms (mostly plants) have quantified these effects, both within species (e.g., Weiner, 1982^; Silander, Jr and Pacala, 1985^; Specht and Arnold, 2018^; Spotswood et al., 2017) and between (e.g., Mack and Harper, 1977^; Song et al., 2021^; Zaiats et al., 2021). Estimation of density-dependent interactions strengths between many species in a community is challenging, but important for understanding community assembly (e.g., Weiss-Lehman et al., 2022^; Bimler et al., 2023). Adding to this complexity, the effects likely often depend strongly on age (Richardson et al., 2024).

Researchers in plant ecology have made the most progress towards empirical understanding of the mechanistic underpinnings of the sort of local density dependence we require. In practice there are a great many possible ways to quantify the cumulative effect of the neighbors of a single individual (Weigelt and Jolliffe, 2003). Our formulation here treats all individuals equivalently, but in practice one could include the effects of age or size. For instance, a common method in forestry modeling defines a “neighborhood competition index” for a given tree as the sum over all neighbors of their diameter (to some power) divided by distance (to another power) (Bella, 1971; Daniels, 1976; Canham et al., 2004). Empirical studies have estimated these kernels in a variety of situations: for instance, Teller et al. (2016) and Adler et al. (2018) use spline methods to flexibly estimate the effects of total area of nearby plants on a target plant’s growth and survival.

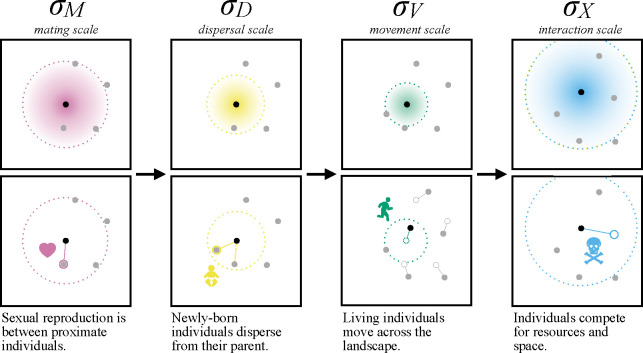
Spatial scales and neighborhood sizes

Now that we understand how to obtain stable simulations, we can move on to a more spatial topic: that of spatial scale. It is convenient to parameterize a spatial model using the following quantities, depicted in Figure 2: (i) interaction scale, ${\sigma }_X$, the typical distance over which individuals affect each other ecologically; (ii) dispersal scale, ${\sigma }_D$, which is a typical distance between parent and offspring; (iii) mate choice scale, ${\sigma }_M$, which is a typical distance between mates; and (iv) movement scale, ${\sigma }_V$, the typical distance over which an individual moves each time step. Note that ${\sigma }_D$ is typically referred to as the “dispersal distance”, but here we use “dispersal scale” for consistency with the other spatial scales. We have already met ${\sigma }_X$, and will discuss the remaining ones in subsequent sections.

Figure 2:

Spatial processes act over spatial scales defined by the σ parameters (radii of dotted circles). In one simulation time step, mate choice, offspring dispersal, adult movement and inter-individual interaction (columns) all take place. (The order of these events is shown here as performed in SLiM.) The scale over which these processes occur are parameterized by ${\sigma }_M$, ${\sigma }_D$, ${\sigma }_V$, and ${\sigma }_X$, respectively; they can be used to calculate neighborhood sizes, to define the scale of the kernels used to draw movement or dispersal vectors (see Movement and dispersal) and to estimate local population density (see Mating and other pairwise interactions).

Each spatial scale parameter determines how many other individuals typically exist in an individual’s “neighborhood”, and so to describe the general behavior of a model it is helpful to look at a few “neighborhood sizes”. First, the mating neighborhood size, $N_M=\pi {\sigma }_M^{2}K$ and the interaction neighborhood size, $N_X=\pi {\sigma }_X^{2}K$, measure, respectively, the typical number of other individuals in a circle of radius ${\sigma }_M$ or ${\sigma }_X$ at equilibrium. Note that these measures are only intended to be order-of-magnitude diagnostics: for instance, depending on the mating kernel, individuals out to $2{\sigma }_M$ or $3{\sigma }_M$ are probably also available to mate. These can be useful diagnostics: for instance, $N_M$ should be the same order of magnitude as the number of potential mates, so if it is small then mate limitation may be a problem (as discussed below in Mating and other pairwise interactions). Less obvious but equally important is $N_X$, which measures the typical number of other individuals that will factor into the local density of a given individual, and hence may affect their demographic rates (such as their survival probability, as in Box 1). $N_X$ provides a measure of the individualto-individual variability in local density: roughly speaking, a larger $N_X$ means that local density is obtained by averaging over a larger area, and is thus less noisy. More concretely, suppose the number of neighbors of an individual within distance ${\sigma }_X$ is $P$. Birth and death rates depend on local density divided by $K$, which is roughly $P/N_X$ – so, if the standard deviation of $P/N_X$ is small, all individuals experience very similar local densities. The distribution of $P$ depends on the details, but we might expect the standard deviation of $P$ to be around $\sqrt{N_X}$ (if it is Poisson, for example), so the standard deviation of $P/N_X$ is proportional to $1/\sqrt{N_X}$. In other words, if $N_X$ is 100 then density should only vary by 10% or so; while if $N_X$ is around 10, then we expect some individuals to experience substantially lower and higher densities. Further discussion of how $N_X$ and $N_M$ can help diagnose odd model behaviour is given in the Appendix (section B).

Another “neighborhood size” that should be introduced here is a classical one: Wright’s neighborhood size, which is $N_W=\pi {\sigma }_{\text{eff}}^{2}K$, where ${\sigma }_{\text{eff}}^2$ is the (squared) effective dispersal distance, the variance of the displacement between parent and offspring along any axis looking back along a lineage (that is, along a chain of parent–offspring relationships). This quantity appears frequently in work on continuous spatial models in population genetics (Wright, 1943, 1946; Barton et al., 2002; Rousset, 1997; Robledo-Arnuncio and Rousset, 2010), and is clearly affected by ${\sigma }_D$, ${\sigma }_V$, and ${\sigma }_M$, as well as the mean generation time, but no explicit expression for ${\sigma }_{\text{eff}}$ from these parameters is known. $N_W$ gives, roughly, the number of “potential parents” of a given individual, and so is a measure of the rate of local genetic drift – if $N_W$ is small, then local inbreeding (and spatial structure more generally) will be stronger.

Practical considerations

Although we encourage basing modeling decisions on empirical understanding, this is not always feasible. For instance, suppose one is simulating a species of fairly common shrub that lives widely across a landscape. In practice its local density is determined by local habitat (perhaps it lives on steeper slopes) and complex local interactions with other species. Any concrete estimate of the interaction scale for a plant is probably quite small – the effect of one shrub on another more than a few meters away is (in the short term at least) necessarily quite small. However, implementing a spatial model with an interaction scale of only a few meters (and no other species) will likely lead to a population size that is much too large. One option is to somehow include other species and fine-scale habitat suitability, but doing this in a realistic and efficient way can be a major challenge. A simpler option is to set the interaction scale to be on the order of the mean inter-individual spacing, and adjust the form of density dependence to roughly match the observed population density. The simulated population will probably be more evenly spread out across space than in reality, but it is hopefully at least a better approximation than a nonspatial model. More work is needed to develop appropriate modeling strategies for such situations, and to understand the consequences of these strategies.

Movement and dispersal

The distance and timing with which individuals move across the landscape influences their spatial distribution, as well as the degree of relatedness expected for nearby individuals. Parent–offspring dispersal and the movement of (adult) organisms during their lifetime are sometimes separated, but can be implemented in similar ways. Clobert et al. (2012) reviews many aspects of dispersal, from parameterization and estimation to implications for ecology and evolution (see also Saastamoinen et al., 2018^; Edelaar and Bolnick, 2012). (Clobert et al. (2012) also defined “dispersal” to be any spatial movement that leads to gene flow; this includes the movement of gametes, which we discuss below.) Besides the overall scale of movement, the next most important choice is the shape of the dispersal distribution, or kernel.

Practical considerations

The easiest way to implement dispersal in two dimensions is simply to say that an individual at $(x,y)$ will produce an offspring that lives at $\left(x+{\sigma }_{D}X,y+{\sigma }_{D}Y\right)$, where $X$ and $Y$ are independent and Gaussian (with standard deviation 1). Most simulations in this paper were done in this way, for familiarity rather than any particular reason. How, then, to draw from a different dispersal kernel? The first guess – choose $X$ and $Y$ from a different distribution – does not work: the result will not be rotationally symmetric, and dispersal will tend to unrealistically align with the axes. Options are to either move a random distance at a uniformly chosen angle (which is simpler), or to multiply a bivariate Gaussian by a random scaling factor (which has other advantages). What to call a given two-dimensional kernel is not standard – for instance, would a “Student’s $t$ kernel” have a $t$-distributed distance? Or, a $t$-shaped cross-section? In simulations below we use the latter convention, as described in Box 3, and discuss these choices more in Appendix D.

Box 3: Random dispersal and displacement.

Perturbing a spatial location by adding a displacement drawn from a given kernel is a common operation in simulations – for instance, to choose offspring locations. To do this, SLiM provides the pointDeviated() method, which also needs to know the shape of the kernel, the type of boundary condition, and other parameters. For instance, the following code:

locs = subpop.pointDeviated(nOff, individual.spatialPosition, “reprising”, INF, “t”
, DF, SD);
offsprings = subpop.addCrossed(individual, mate, count=nOff);
offsprings.setSpatialPosition(locs);

creates nOff offspring, and sets each offspring’s position to a randomly sampled location near the location of the parent (individual). The random displacement is drawn with density $f(x)\propto (1+{\left.\parallel x/\mathrm{S}\mathrm{D}{\parallel }^2/\mathrm{D}\mathrm{F}\right)}^{-(\mathrm{D}\mathrm{F}+1)/2}$, i.e., from the kernel whose density is formed by rotating the $t$ distribution with scale SD and DF degrees of freedom about the origin. The result on falling within the spatial bounds of the simulation.

Movement in practice often depends on the environment, of course: organisms tend to move within particular habitats, and barriers are ubiquitous on all scales. Small-scale heterogeneity may be averaged out across the time scale simulated, and so incorporated (implicitly) in the movement kernel. However, large-scale heterogeneity can be important. Movement on a heterogeneous landscape still relies on some way of randomly choosing nearby points, and hence a movement kernel. One way to incorporate this is discussed in Box 5.

Box 5: Defining and manipulating maps.

The mechanism that SLiM provides extensive support for defining and manipulating spatial maps. We can begin by reading the values for a spatial map (say, of elevation) from a CSV file containing a rectangular grid of values using the code below:

mapValues = readCSV (“ elevation . csv”). asMatrix ();
map = p1. defineSpatialMap (“ elevation “, “xy”, mapValues );

(Images can also be read in as PNG files.) If this is a low-resolution raster then we may wish to smoothly interpolate it to higher resolution, done below with bicubic interpolation:

map . interpolate ( factor =20 , “ cubic “);

Once we have this map, we can extract the values of the map at arbitrary locations – for instance, the elevations at which individuals live:

elevs = map . mapValue ( inds . spatialPosition );

Further operations are available, including blurring and algebraic manipulations of the values. The dispersal method in Box 3 allowed individuals to move equally well in any direction. To guide movement with a map – for instance, to induce a preference for moving uphill, for this example where map values indicate elevation – we can use the map.sampleNearbyPoint() method:

inds = p1. individuals ;
pos = map . sampleNearbyPoint ( inds . spatialPosition , INF , “n”, SM);
inds . setSpatialPosition ( pos );

This will move each individual to a new location sampled nearby and weighted by map value: if the original location is $\mathit{x}$, $\rho ()$ is a Gaussian kernel (specified as type “n”) of width SM, and the value of the map at location $y$ is $m(y)$, then the new location is chosen with density proportional to $m(\mathit{y})\rho ((\mathit{y}-\mathit{x})/{\sigma }_M)$.

Context and connections

The concept of a dispersal distribution is perhaps most well-defined for plants, which (mostly) have only one opportunity to move during their lifetime, as a seed or other propagule. Seeds and pollen can be moved by gravity, wind (Nurminiemi et al., 1998), water (Murray, 2012), or animals (Morales and Morán López, 2022; Pons and Pausas, 2007), and complex models for these have been developed and estimated from empirical data (Neubert et al., 1995; Tufto et al., 1997; Austerlitz et al., 2004; Katul et al., 2005). Of course, many animals have relatively stable locations as well, perhaps depending on the season: for instance, Paradis et al. (1998) review estimates of post-natal and breeding dispersal in many bird species. The combination of these various processes (which often happen across many different spatial scales) has been referred to as the “total dispersal kernel” (Rogers et al., 2019), and can easily lead to “long-tailed” distributions (Cain et al., 2000; Edwards et al., 2007) in which rare, long-distance events are important. Dispersal is notoriously hard to estimate, as it often requires observing rare events, but has been done in a variety of organisms including kangaroo rats (French et al., 1968), mosquitoes (Estep et al., 2014), Drosophila (Dobzhansky and Wright, 1943), Prunus shrubs (Robledo-Arnuncio and García, 2007), pine pollen (Robledo-Arnuncio and Gil, 2005), and butterflies (Suchan et al., 2024). Dispersal can of course also depend on density (Harman et al., 2020) (for example, if individuals preferentially disperse out of crowded areas).

Clumping and movement

In many species reproduction is local, and so tends to produce clumps which are spread out by movement and dispersal. This balance can lead to either smoothly uniform populations, or strikingly uneven landscapes of high and low density on various scales: Figure 3 shows two examples. Such patterns can be intriguing or puzzling, and have real consequences for demography and genetic variation.

Figure 3:

(A, B) Examples of simulations showing clumping (B) and not (A). (C) Dispersal kernel and movement type affects magnitude and spatial scale of clumping. Pair correlation functions (main panel) show density of pairs of individuals found a particular distance apart, relative to distances expected under a Poisson process (1.0; grey dotted line). Curves show the average across 50 independent time steps. Probability density functions (inset) for dispersal scales under the three dispersal kernels used: $t$-distribution with 3 degrees of freedom, $t$-distribution with 5 degrees of freedom, and Gaussian. The scale of $t$-distributions is equal to the standard deviation of the normal distribution $({\sigma }_D=0.3)$. The “adult movement” scenario uses the Gaussian for dispersal as well as for movement at each time step. (D) Fat-tailed dispersal and adult movement flatten genetic isolation-by-distance. Plots show mean genetic distance between pairs of individuals at increasing geographic distance, averaged across ten independent replicates.

Although the scale of movement most strongly affects spatial patterns, the shape of the kernel is also important, and can have surprising effects: even very rare long-range movement can have strong effects on the speed of a range expansion (Mollison, 1972; Paulose et al., 2019) or the relationship between genetic and geographic distances (Smith and Weissman, 2023). For most models in this paper we use a Gaussian distribution for movement, mostly for the sake of familiarity. To see the effects of rare, long-range movement, a convenient “fat-tailed” kernel is the Student’s $t$: the smaller the degrees of freedom parameter, the more likely are extremely long movements. Appendix D has more discussion, including how we define the kernel in more than one dimension.

Spatial clumpiness is sometimes visually obvious (as in Figure 3B), but more generally the clumping tendency of individuals can be measured by spatial correlations. One informative measure of clumping tendency is the pair correlation function, which shows for each distance $x$ how likely an individual is to have a neighbor at that distance relative to the average density (see Baddeley et al., 2015, for discussion and other useful descriptors of point data). Concretely, the pair correlation function estimates the mean density at distance $x$ away from an individual divided by the overall mean density, averaged across individuals; if the points are independently placed, it is constant at 1.0. Figure 3C shows pair correlation functions for simulations in which adults do not move and dispersal follows either a $t$ or a Gaussian distribution, or in which both dispersal and adult movement are Gaussian (with ${\sigma }_D={\sigma }_V)$. Otherwise, simulations are Beverton–Holt regulated on mortality.

Figures 3C shows that individuals are more likely to be around a distance of ${\sigma }_D$ from each other than otherwise, but this tendency is reduced with more long-distance dispersal $(t$ dispersal with lower degrees of freedom). In other words, a little long-range dispersal reduces clumping. Note, however, that in these examples the scale of clumping is quite narrow: correlations only extend out to 2 or 3 multiples of ${\sigma }_D$; for another visualization of this relatively subtle clumping, see Figure S3. Adding adult movement to a dispersal-only model unsurprisingly reduces correlations as well.

In spatial models neighbors tend to be more related to each other than to distant individuals, a pattern known as “isolation by distance” (Wright, 1943). The scale at which this correlation appears is determined by how far individuals move, and is also affected by the shape of the dispersal kernel: Figures 3C&D show that simulations with more long-range movement – but with comparable mean dispersal scale – tend to have a weaker relationship between geographic and genetic distance (see also Smith and Weissman, 2023).

Mating and other pairwise interactions

Mating is a crucial interaction for biological simulations, and there are numerous aspects and choices to consider. We probably don’t want to simulate the detailed movement of individual pollen grains or the meanderings of a male moth seeking a female, and instead would like to skip to the realized outcome, i.e., “choose a mate nearby”. (We follow the literature on mating systems in calling this “mating”, even when referring to plants or broadcast spawners.) As with dispersal, it is easiest to specify what “nearby” means with a kernel: roughly, an individual can be chosen with probability proportional to the kernel. More concretely, if the kernel is $\rho$ and the mating scale is ${\sigma }_M$, then an individual at $\mathit{x}$ would assign weight $w_i=\rho \left(\left({\mathit{x}}_{\mathit{i}}-\mathit{x}\right)/{\sigma }_M\right)$ to another individual at location ${\mathit{x}}_{\mathit{i}}$, and then the probability individual $i$ is chosen is equal to $w_i$ divided by the sum of weights across all (nearby) individuals. This same method can be used for other individual-to-individual interactions, such as predators choosing prey individuals.

So, we can adjust the typical distance between mates with the mating scale, ${\sigma }_M$, which is directly analogous to parameters used to describe interaction $\left({\sigma }_X\right)$ and dispersal $\left({\sigma }_D\right)$, although each uses an underlying kernel in slightly different ways. Of course, the criteria determining potential mates for a given individual differ widely among species (Shuster, 2003). Relevant questions about the mating system include: How often does selfing occur, and in what circumstances? Are sexes separate (dioecy/gonochory) or not (monoecy/hermaphrodity)? Are there distinct mating types or self-incompatibility systems? An important note is that for dioecious species, calculations to determine stability of population density are easiest if done using only the reproducing sex.

Sex-specific spatial structure

The combination of density dependence and mating system can have surprising consequences: for instance, in the dioecious simulations above, clustering is dependent on sex. To see this, Figure 4 shows the mark connection function (Baddeley et al., 2015, §14.6.4.2) for female/male, female/female, and male/male neighbors, which shows the proportion of pairs of points at distance r that are one female and one male, two females, or two males, respectively. Curiously, we see that the probability that an individual’s neighbor is of the other sex does not depend on that neighbor’s distance. However, the probability of having a same-sex neighbor does change with distance. As shown in Figure 4, within $3{\sigma }_D$ neighbors of a female are more likely than expected to be female, and nearby neighbors of a male are less likely to be male than expected.

Figure 4:

Dioecy generates female underdispersion, male overdispersion. Each panel shows the proportion of pairs of individuals at the distance shown on the horizontal axis that are either (left) a female and a male (middle) both female, or (right) both male. Average and standard deviation of 50 independent simulation ticks are shown. Red dashed lines indicate expectation if individuals’ locations were chosen uniformly. Note that the “Male–Female” proportion is be identical to the “Female–Male” proportion, so that twice the left panel plus the other two panels is equal to 1.

Why does this happen? A simple reason is that we are modeling a dioecious scenario with no adult movement and where offspring are only generated by females and placed nearby. Local density-dependent mortality means that all individuals tend to kill their neighbors, but only females can replace them. Correspondingly, the spatial range of a dioecious system where offspring disperse from a particular sex is determined by the range of that sex – others on the periphery cannot extend the range because offspring do not disperse from them. This is a disadvantage for colonizing new areas (Obbard et al., 2006), and may explain the spatial distribution of dioecious individuals away from a range front (Mirski et al., 2017).

Indeed, Shuster (2003) showed that female aggregation (as observed in Figure 4) is a universal consequence in mating systems with female choice (Shuster, 2003, ch. 2). Other aspects of the simulation may differ by sex: for instance, sex-biased dispersal is pervasive (Trochet et al., 2016) and generates detectable spatial patterns of genetic relatedness between sexes (Aguillon et al., 2017; Broquet and Petit, 2009; Laporte and Charlesworth, 2002). Social mating structures can induce sex-biased dispersal and thereby create similar patterns (Pusey and Packer, 1987; Hammond et al., 2005).

Maps: spatial heterogeneity

Most real populations are far from uniformly distributed in space, and in most cases, the underlying cause is thought to be environmental heterogeneity. Until this point, we have considered simulations of homogeneous landscapes only. Such “flat” landscapes are useful for developing models and/or theory, but incorporating aspects of real landscapes can make simulations better match the complicated real world. Spatial heterogeneity can be introduced simply by making some parameter of the model, such as fecundity or mortality, vary across space – in which case we can visualize the parameter as a map. Such maps might represent specific environmental conditions, habitat boundaries, or abstract habitat quality.

Practical considerations

Raster-based images provide a convenient way to introduce a map of spatial heterogeneity into a simulation framework such as SLiM that cannot directly read geospatial data formats. As demonstrated in Box 5, values can be read directly from a CSV file. Alternatively, a monochrome PNG file consists of a rectangular grid of pixels with integer values between 0 and 255; however, the values then need to be shifted and scaled to lie in the desired range after being read in. In the simple example shown in Figure 5, the map could represent the altitude of a (conical) mountain, with darker shades indicating higher elevation. High-resolution maps are publicly available from various sources, including NASA’s Earthdata platform (2024)^, ESA’s Earth System Data Lab (2024), or PRISM Climate Group. Open-source tools for processing remote sensing data are also available (see Montero et al., 2023).

Figure 5:

A spatial simulation using a heterogeneous map of carrying capacity and the reprising boundary condition. (A) A representative time step during the simulation, with each of the roughly 1500 individuals shown as points and the map of carrying capacity, $K(\mathit{x})$, shown in the background. (B) A map of realized density, averaged over 10⁴ time steps. (C) Comparison of realized density to carrying capacity from three different runs using different dispersal scales: each point shows the realized density in one of the pixels of the map shown in (B) plotted against the value of $K(\mathit{x})$ in the center of the pixel, for three values of ${\sigma }_D$ (labeled “SD” in the legend). The dimensions of the map are 25 × 20, and the interaction scale is ${\sigma }_X=0.3$. The simulation has Ricker regulation of fecundity: the expected number of offspring of an individual at location $\mathit{x}$ is $\mathrm{e}\mathrm{x}\mathrm{p}(-\frac{n(\mathit{x})}{K(\mathit{x})}-1)\mu /(1-\mu )$, where $\mu$ is the (fixed) probability of survival, $n(\mathit{x})$ is the local density at $\mathit{x}$, and $K(\mathit{x})$ is obtained from the value of the image at $\mathit{x}$.

To use a raster-based image, we must decide how the bounds of the image map onto geographic space. In general we match the (rectangular) image with the (rectangular) spatial area to be simulated. Although the image is represented as discrete pixels, we will need to obtain values of the map at arbitrary locations (not just at the center each raster pixel). This can be done, for instance, by either associating each pixel’s value with the rectangle it would visually cover (as seen in Box 2), or associating each pixel’s value with the corresponding cell’s midpoint and interpolating between.

Box 2: Summarizing the state of the population.

An extremely useful feature in SLiM is its GUI, which lets the user visualize the simulated individuals. Such visualization can, for instance, let one easily see areas of higher fecundity, differences in age structure, or even local adaptation. One way to do this is by setting the color of each individual: by default, individuals are colored by fitness (i.e., probability of survival), but this code snippet will set the color to reflect the sex of the individual:

females = p1.subsetIndividuals(sex = “F”);
females.color = “white”;
males = p1.subsetIndividuals(sex = “M”);
males.color = “red”;

It can also be helpful to summarize the state of the population as a map. This can be done with great flexibility with the summarizeIndividuals() function, which creates a rasterized map for which the value of each pixel is some summary of the individuals within that pixel. For instance, the map of density shown as the background for the screenshot here was made using the following code:

density = summarizeIndividuals(p1.
  individuals,
  c(25, 25), p1.spatialBounds,
  operation=“individuals.size();”,
  empty=0.0, perUnitArea=T);
p1.defineSpatialMap(“density”,
  “xy”, density, T, c(O,K),
  colors(20, “viridis”));

In this close-up screenshot of a dioecious simulation, there tend to be more females (white points) where the local density is higher (yellow background); and there tend to be more males (red points) where the density is lower (blue background). We discuss the heterogeneous spatial patterns generated in dioecious simulations below, in “Mating and other pairwise interactions”. See below, for instance, in Box 5, for more use of defineSpatialMap(). Furthermore, SLiM’s GUI provides built-in support for various diagnostic plots, such as the age distribution, population size over time, and allele frequency trajectories, and allows you to make your own custom plots as well.

Figure 5 shows results from simulations in which organisms living higher on a simulated mountain are more likely to survive. This is implemented by setting the local carrying capacity, $K(x)$, to be given by the value of the map at $x$.

Figure 5C shows realized densities at various elevations (averaged over 1,000 time steps) with different values of dispersal scale $({\sigma }_D)$. The first thing we notice, either from a bird’s-eye view of the simulation (Figure 5A) or from an empirical map of realized long-term average density (Figure 5B), is that population density at least roughly matches the underlying map (the background in Figure 5A). A more precise comparison (Figure 5C) shows that the local density at $\mathit{x}$ is not exactly $K(\mathit{x})$, and the amount of deviation can depend on various other factors (colors show three choices of ${\sigma }_D)$. In most situations, the equilibrium density is below $K(\mathit{x})$. This is probably for two reasons: first, stochasticity usually reduces equilibrium density (see Appendix B); and second, since the mountain is conical, each location is adjacent to less higher-density area than to lower-density area, and so the net flux of migrants is negative. At the lowest dispersal $({\sigma }_D=0.25$, black points), areas with carrying capacity below about 5 individuals per unit area are not self-sustaining (see Appendix B for more discussion). On the other hand, at the highest dispersal $({\sigma }_D=4$, green points), the overall relationship between density and carrying capacity is flattened as offspring from high-fecundity areas end up across the entire range – however, most offspring are still produced near the top of the mountain, and lower elevations are maintained by source-sink dynamics. Finally, even with the higher carrying capacity, the curves are generally lower than $y=x$ line: we explain why in Appendix B.

Density dependence, life history, and stochasticity

Above we introduced a model of “Beverton–Holt density-dependent feedback on mortality”. We next give some other examples that have the same Beverton–Holt form for the net effect of density on population regulation, but differ in other ways.

Fecundity regulation

The Beverton–Holt density-dependent regulation of equation (4) has the probability of death increase with local density while fecundity stays constant. Alternatively, we can set the probability of death to a constant: $\mu (u)={\mu }_0$, and then solve for $f(u)$ to obtain the Beverton–Holt form $F(u)=\alpha ((1+a)/(1+au)-1)$ (it turns out we will need the scaling factor $0<\alpha <1$ to make a model with positive birth rates and death probabilities between 0 and 1). Then, fecundity should depend on scaled density u as follows:

$$f\left(u\right)=\frac{1}{\left(1-{\mu }_0\right)}\left(\alpha \frac{\left(1+a\right)}{\left(1+au\right)}+\left({\mu }_0-\alpha \right)\right).$$ (5)

This is shown in the middle panel of Figure 1.

Compensatory regulation on juvenile and adult mortality

Although the effect of density on net reproductive rate must be negative to have a stable population, the effect on individual demographic components can go the other way, as long as it is compensated by other components. For instance, the probability of survival $1-\mu (u)$ can increase with density as long as fecundity $f(u)$ decreases faster. One way to do this is to set

$$\begin{array}{l}f(u)=\frac{f_0}{1+bu}\text{and}\\ 1-\mu (u)=\frac{1+F(u)}{1+f(u)},\end{array}$$ (6)

where $F(u)=\alpha ((1+a)/(1+au)-1)$, i.e., the Beverton–Holt form again. This produces valid survival probabilities if $f_0\ge a\alpha$. Depending on the choice of the parameters, $f(u)$ may increase or decrease with $u$, and is not necessarily monotone. One choice is shown in the rightmost panel of Figure 1.

Beverton–Holt models?

In summary, these three examples (4), (5), and (6) might all be reasonably called “Beverton–Holt” models, although they differ substantially in the underlying mechanism, and could show very different demographic patterns (e.g., age distributions). The three models of equations (4), (5), and (6) are shown in Figure 1. Although they have similar behavior around the equilibrium density, they have quite different life history implications. Most strikingly, in the first model, mortality increases with density, in the second mortality is constant, while in the third, mortality decreases with density. There are corresponding differences in age structure among the models, as shown in Figure S6, although the population dynamics (in terms of total population size) are similar. More examples along these lines are given in Appendix C.

Stochastic effects

Despite all this theory, in practice equilibrium density is usually not $K$ – it is often lower. (See Figures 5 and S7, for instance.) This is due, effectively, to various forms of stochasticity.

One is random lack of mates (when $N_M$ is small); another is local extinction by fluctuations (when $N_X$ is small). These effects can be quite troublesome when setting up computational experiments across a range of parameters, especially if we want constant total population size.

Apart from those issues, the most common reasons for significant discrepancy between the observed density and the “desired” density (set by $K)$ have to do with when and how density is measured. First: at what stage is density measured? In each time step, density increases after birth and decreases after death; $K$ can match at most one of these times. Second: where is density measured? We naturally look at total population size divided by total area; however, individuals (useful, but) necessarily experience on average a higher density, since they themselves count towards their density. So, the correct comparison is of $K$ to local population density averaged across the location of all individuals. Since this over-samples areas of higher density, this density will be higher than “total population size divided by area”.

All these issues are discussed in much greater detail in Appendix B. For practical reasons it often suffices to simply be aware that population density is fundamentally an emergent property, determined in complex ways by nearly all parts of the life cycle. If a precise total population size is desired in a particular simulation, a simple solution is to adjust some parameter (e.g., the birth rate) until the desired value is achieved (see Box 6), but of course that will (unavoidably) alter the dynamics of the simulation in other respects.

Box 6: Adaptive empirical tuning for emergent parameters.

We often want a simulation to match a given estimated or observed density. However, this is not as simple as setting the value of $K$ in the code, because population density is an emergent quantity – a complex consequence of births, deaths, movement, and local interactions. Fortunately, even matching emergent quantities can be quite simple in SLiM. The code here matches population density to a desired value, but it demonstrates a general technique that may be applied to match other quantities such as mean age or degree of clustering.

We first define a global parameter ADJ that will be adjusted:

defineGlobal (“ ADJ “, 1.0) ;

Then we modify the code from Box 1 so that this parameter adjusts the carrying capacity:

inds = p1. individuals ;
density = 11. localPopulationDensity ( inds );
u = density / ((1 + f) * K);
inds . fitnessScaling = 1 / (1 + ADJ * f * u);

Then, each timestep ADJ is updated by a factor $\mathrm{e}\mathrm{x}\mathrm{p}[\alpha (Y-K)]$ where $Y$ is global population density (population size divided by total area) and α is an update rate (e.g., $\alpha =0.01)$:

obsDensity = p1. individualCount / ( WIDTH * HEIGHT );
defineGlobal (“ ADJ “, ADJ * exp (( obsDensity - K) * ALPHA ));

If $Y>K$, we want the density to be lowered in the next cycle, so we decrease carrying capacity by increasing ADJ. On the other hand, if $Y<K$, ADJ is decreased so that we get a higher $Y$ in the next cycle.

This tuning should stop after an initial “burn-in” period, or the appropriate value for ADJ, once found, should be hard-coded into the final model. This is particularly important because if changes occur in the simulation that affect population size (e.g., a reduction in habitat), this adaptive code will force the density back to the chosen value, which is generally not desirable – the population size should, in fact, change in response to such changes in the simulated conditions.

Natural selection

Evolutionary simulations of course need natural selection; it turns out that there are many different ways to implement selection in an individual-based simulation that all map to the same abstract models from population genetics, and yet produce distinct outcomes. We demonstrate this by comparing mortality- and fecundity-based selection. How do we think quantitatively about natural selection? Much of population-genetics theory is expressed in terms of the “selection coefficient” of a variant, usually denoted s, which is usually defined in the context of a Wright–Fisher model to be a change in relative probability of being “selected” to provide offspring to the next generation. Implementing natural selection in spatial models, even for the simplest case of a single variant, requires deciding where and how the variant affects the life cycle – for instance, the variant may affect mortality, fecundity, or both. Intuitively, one may achieve the same increase in “fitness” by increasing fecundity or decreasing mortality appropriately. However, these choices are known to produce differences in nonspatial models (Bodmer, 1965; Nagylaki and Crow, 1974), and so analogies between such the dynamics of such alleles and those of a selected allele in a Wright–Fisher model are necessarily approximate. This is important when attempting to match simulation results to theory: just because a variable that affects survival or fecundity is named s does not mean that using its value in expressions derived from the Wright–Fisher model correctly predicts the probability of establishment, mean frequency, or other classical quantities, even in a non-spatial simulation. Below, we parameterize and simulate from two models, in which selection acts on mortality or fecundity, in each choosing s so that variant’s frequency changes on average by a factor of $1+hs$ per time step, when rare, where $h$ is the dominance coefficient. (This may not be the best definition for use with classical formulas, which often measure change per generation.) For a historical and philosophical review of definitions and measures of selection see Endler (1986). Implementation in SLiM is described in Box 7.

Box 7: Selection.

In the nonWF SLiM models we use, the “fitness” of an individual as calculated by SLiM is the probability that the individual survives to the next time step. So, to make it so that each mutation affects survival by a factor of S_MORT, we simply declare it so:

initializeMutationType (“m1”, 0.5 , “f”, S_MORT );

(The factor of 0.5 is the dominance coefficient: heterozygotes will have fitness multiplied by 1 + S_MORT*0.5, and homozygotes by 1 + S_MORT.) To have the same type of mutations also affect fecundity with selection coefficient S FEC, we just need to account for genotype when setting up offspring numbers (as in Box 1):

indiv_s = 2* S_FEC * inds . countOfMutationsOfType (m1) / 2;
inds . tag = rpois ( length ( inds ), mean = FECUN * (1 + indiv_s ) + indiv_s );

(As written, the effects of any mutation of type m1 on fecundity are additive across loci and copies; other arrangements are possible.)

Parameterization of selection

Recall that $f(u)$ and $\mu (u)$ are, respectively, the per-capita mean number of offspring and probability of death per time step when at scaled density $u$. Now, these can depend on the individual’s genotype – so, let $f_k(u)$ be the mean fecundity of an individual with $k$ copies of a focal allele when at scaled density $u$, and similarly ${\mu }_k(u)$ the probability of death. We’ll assume the focal allele is rare, so that most of the population is homozygous (and so use $f_0(u)$ and ${\mu }_0(u))$, but a few individuals are heterozygous (and so use $f_1(u)$ and ${\mu }_1(u))$. If so, then the per capita rate at which the number of focal alleles grows when at scaled density u in an outcrossing species is

$$G(u)=\left(1-{\mu }_1\left(u\right)\right)\left(1+\left(f_0\left(u\right)+f_1\left(u\right)\right)/2\right)-1.$$ (7)

(This is almost the same as the expression for $F(u)$, the expected change in the number of individuals in equation (2), except that the fecundity term is $\left(f_0(u)+f_1(u)\right)/2$; this is because the offspring of a heterozygous parent will only inherit the focal allele from that parent half the time.)

First let’s suppose an additive allele (so that $h=1/2)$ simply increases survival by $s/2$ per allele, so that

$$1-{\mu }_k(u)=(1-\mu (u))(1+ks/2).$$ (8)

If the allele doesn’t affect fecundity (so that $f_k(u)=f(u)$), then

$$G(u)=(1-\mu (u))(1+f(u))(1+s/2)-1.$$ (9)

We’ve set things up here so that $s$ means what we want – the growth rate when the new allele is rare, at the population’s equilibrium density $(u=1)$, is $G(1)=s/2$.

Suppose instead that the allele increases fecundity. To make this allele have the same growth rate when rare as the allele that increases survival, we will set up $f_k(u)$ so that $G(u)$ has the same form. To do this, we can define

$$f_k(u)=(1+f(u))(1+ks)-1.$$ (10)

With this form for fecundity selection, the growth rate when rare at density $u$ is also given by $G(u)$ in equation (9), and so at equilibrium, the per-capita growth rate of the number of alleles is again $s/2$. Roughly speaking, each allele increases fecundity by $s$, rather than the $s/2$ in equation (8) for mortality selection, because here the effects of fecundity are only affecting half of the parents (the offspring-bearing ones).

That’s the theory – how’s it work in practice?

Above we laid out deterministic, large-population-size theory that suggests that a variant that affects survivorship as in (8) or fecundity as in (10) might sweep in similar ways. Although the resulting dynamics are similar, there are substantial differences. Figure 7 shows selective sweeps in spatial and nonspatial simulations, with selection acting on either fecundity or mortality. All simulations use density-dependent feedback on mortality, as in equation 4, and with either probability of survival or mean fecundity adjusted based on the genotype of the individual as in equations (8) and (10). The nonspatial simulations work the same, except that the global density (total number of individuals divided by total area) is substituted for local density when computing the probability of survival.

Figure 7:

Allele frequency (A), population size (B), and average individual age (C) over time in spatial and nonspatial non-WF simulations. Lines end at the time the selected allele fixed (indicated by dotted vertical lines).

Figure 7A shows the allele frequency trajectories of the sweeping alleles: de novo mutations that either increase fecundity (red) or decrease mortality (blue). Comparing the allele-frequency trajectories between mortality- and fecundity-based selection, the speed of both spatial and nonspatial sweeps is unchanged, as predicted (i.e., $G(u)$ is the same for both). We also see the well-known observation that selective sweeps progress more slowly in spatially structured populations.

However, we also see that sweeping populations behave differently in other ways. Figure 7B shows that the equilibrium population density increases as the beneficial allele fixes (as expected, since the selected alleles increase net fecundity minus mortality), but it increases by a greater amount under fecundity-based selection. Furthermore, Figure 7C shows that as the allele increases in frequency, the mean age drops with fecundity-, but not mortality-based selection. The reduction in mean age under fecundity-based selection once the beneficial allele becomes common is intuitive: population size increases as the sweep progresses, but because the beneficial allele does not confer protection against mortality, individuals are subject to the negative effects of increased population density. However, why fecundity-based selection results in a greater increase in population size is less clear.

To understand why this is, consider the population after the fixation of the focal allele: the mean per-capita change in population size, is now equal to zero. In these simulations, density dependence uses the Beverton–Holt model with $a=f_0$, le., $f(u)=f_0$ and $1-\mu (u)=1/\left(1+f_{0}u\right)$. The new scaled equilibrium after flxation occurs at $u$ solving $\left(1-{\mu }_2(u)\right)\left(1+f_2(u)\right)=1$; for mortality-based selection this is at $u_{\mu }=1+s\left(1+\frac{1}{f_0}\right)$, while for fecundity-based selection this is at $u_f=1+2s\left(1+\frac{1}{f_0}\right)$. In other words, the increase in equilibrium density for fecundity-based selection should be roughly twice that of the increase in mortality-based selection.

There are further differences between the spatial and non-spatial simulations, that are likely due to the spatial-density regulation processes that cause realized population sizes in spatial simulations to be smaller than in their nonspatial counterparts (as discussed in the previous section).

Case Studies

How can we combine all the strategies we have seen thus far into a useful model of a living system? Here we illustrate how the preceding spatial modeling concepts can be used to model complex scenarios such as (1) temporal change, (2) complex life cycles, (3) continental-scale systems, and (4) competition for resources.

We motivate each scenario with an organism. The vignettes are not intended to be complete or accurate models of the population biology of these organisms; they are meant to illustrate how to apply the concepts presented in this paper to a study system. Additional methodological information for each vignette can be found in Appendix E and our code example repository https://github.com/kr-colab/spatial_sims_standard.

Changes over time: pikas and environmental change

Modeling spatial heterogeneity (as introduced in section Maps: spatial heterogeneity) makes simulations more realistic and informative, but sometimes temporal change in landscape variables is just as important. With this example, we explore how both seasonal fluctuation and globally rising temperatures affect population dynamics of an alpine organism: the pika.

Pikas (Ochotona daurica) are adapted to mountainous habitat at relatively high elevation, and they cannot survive in extreme heat (or cold), as would be encountered at lower (or higher) elevations (Beever et al., 2010). Such ecology makes pikas potentially vulnerable as global temperatures are expected to increase over time.

Modeling approach

We incorporate three types of temporal change in temperature: (1) within-year seasonal change, (2) random, autoregressive fluctuations between years, and (3) steady global temperature rise. Because temperature varies with elevation and elevation varies dramatically in mountainous regions, we model temperature as a function of elevation. A topographic map for a region (40.40363°N to 40.53856°N; 105.7326°W to 105.5977°W) of Rocky Mountain National Park in Colorado was obtained using the elevatr package in R (with the WGS84 projection) and subsequently used to calculate the temperature at each point in space and time.

We connect temperature to fitness simply by killing offspring that are exposed to temperatures beyond the minimum (−5°C) or maximum (28°C) sustained by pikas (Beever et al., 2010). Each tick of our simulation represents one year. To account for within-year seasonal variation (i.e., winter cold and summer heat), we narrow the viability range by the yearly variation in temperature $(V_S)$, defining the probability of survival of a pika at location $x$ in year $t$ to be

$$1-\mu (\mathit{x},t)=\left\{\begin{array}{ll}0,& \text{if}T(\mathit{x},t)<\left(-5+V_S/2\right)\\ 0,& \text{if}T(\mathit{x},t)>\left(28-V_S/2\right)\\ \frac{1}{1+f_u(\mathit{x})},& \text{otherwise}\end{array}\right.$$

where the last term is our usual Beverton–Holt mortality regulation with local scaled density $u(\mathit{x})=n(\mathit{x})/K$ (see equation 4). In this equation, $T(\mathit{x},t)$ represents the midpoint of seasonal temperatures in year $t$, defined below, and the within-year variability $V_S$ broadens the temperatures experienced by the pikas around that midpoint. For example, if $T(\mathit{x},t)$ were −4°C (inside the viability range), but seasonal temperatures varied by 4°C, the winter would be −6°C – cold enough to kill.

Between-year temperature changes are modeled by the temperature function $T(\mathit{x},t)=T^{\text{elev}}(\mathit{x})+T^{\text{fluct}}(t)+0.016t$, where $T^{\text{elev}}(x)$ is calculated from the elevation map following fltted models from ColladosLara et al. (2020), and an autoregressive term: $T^{\text{fluct}}(0)=0$ and for $t\ge 1$,

$$T^{\text{fluct}}(t)=p^{\text{fluct}}T(t-1)+ϵ(t),$$

where $ϵ(t)$ is Normally distributed with mean zero and standard deviation $s^{\text{fluct}})$. The parameters $p^{\text{fluct}}$ and $s^{\text{fluct}}$ are known as persistence and shock, respectively, and determine how correlated the noise is between years. Finally, we increase the global temperature over time by adding 0.016°C per year (Foster and Rahmstorf, 2011).

Observations and extensions

The resulting simulation is a habitat suitability model in which the population’s geographic distribution moves toward higher elevation as the global temperature increases (Figure 8).

Figure 8:

Pika simulation. (top) Screenshots of individual spatial positions (black) at different time points. The background image shows elevation, where blue and white correspond to lower and higher elevation, respectively. (bottom) The blue line shows population size over time; the red line shows the proportion of habitable space before the addition of random noise.

We found that if the magnitude of random variation around the expected annual temperature is large – e.g., standard deviation 5°C – the probability of extinction increases significantly, particularly for early generations. In other words, one or a few bad years could be devastating for pika populations. This result may provide a useful lesson: even if a species appears to be thriving, the long-term success of the species is not guaranteed.

Surprisingly, simulated population size increased in the intermediate-term future, since for the first few hundred years, habitat losses at lower elevation were more than compensated for by habitat gains at higher elevation. This illustrates that results from simulation on a specific map may not be generalizable.

Here, we use an empirically-informed linear trend with Gaussian noise as our global temperature change schedule. An alternative strategy for simulating temperature changes would be to pre-process multiple temperature maps reflecting different years, for example, and continually feed the simulation new maps over time. Such maps could perhaps even be generated directly from a climate model, rather than temperature being assumed to be a direct function of elevation.

Life cycle stages: mosquitos in Burkina Faso

So far, our models have not taken life cycle stages into account; individuals have been able to mate immediately after they are born, and their survival has not been age-dependent. However, for many organisms their patterns of mobility, competition for resources, and mating capability are age-dependent. In this vignette, we demonstrate how to simulate a population with distinct juvenile and adult phases. Specifically, we set up a simulation of mosquitos in Burkina Faso in West Africa, inspired by North et al. (2019).

Modeling approach

In this model, individuals begin life as juveniles, and mature into adults after a fixed time span. Population regulation and individual behavior depends on the life stage. For adults, survival is independent of the landscape map; adults have a constant survival probability of 0.875 per day (the model takes one time step per day). The population is regulated by density-dependent survival of larvae, that varies across a map. Following the model in North et al. (2019), we set the carrying capacity of larvae based on water availability. Larval carrying capacity was only non-zero at the outlines of water features extracted from GIS data of inland water in Burkina Faso. There, the carrying capacity fluctuated seasonally to mimic rainy and dry seasons. That is, $K(x,y,t)=K_{\text{base}}(x,y)+K_{\text{rain}}(t)$, where $K_{\text{base}}(x,y)$ is obtained from the map of inland water, and $K_{\text{rain}}(t)$ is a sinusoidal function with a period of 365 days and a minimum value of 0. We then use a Beverton-Holt form for the survival probability of larvae. Since there are ten age classes for larvae (and survival of each depends on the total number across all ages), parameterizing the model so that local density is (roughly) $K$ involves solving a system of equations (it is a matrix model), described in Appendix E.2.

A female adult mosquito mates with an adult male within the maximum mating distance, and lays eggs for larvae by sampling a location within the dispersal radius weighted by carrying capacity. Each day, adult mosquitos move by a random displacement sampled from a Gaussian distribution, whereas larvae do not move from their original location until they mature.

Observations and extensions

This model simulates a mosquito population with structured life history. The population size of larvae and adults fluctuate periodically, following precipitation levels with a slight lag (Figure 9). Recall that adult mortality is simply constant, so the periodic fluctuations of adults are mediated through larval carrying-capacity dynamics.

Figure 9:

(left) Adults (blue) and larvae (red) population on the river map of Burkina Faso, at two time points during the year: in the dry season (e.g., top, day 350), larvae can only survive in bodies of water, while in the wet season (e.g., bottom, day 600), larvae can survive in many places. (right) Adults (blue) and larvae (red) population sizes oscillate with the seasonal cycle. Vertical lines indicate the time points when the distribution of the juvenile and adult populations are plotted on the left.

We envision a few immediate extensions to our simulation. Here, we did not distinguish between perennial and fluctuating water sources. Simulating water sources that appear and disappear (adding a $t$ argument to $K_{\text{base}}(x,y)$ could result in extinction dynamics such as those observed in the pika example above. Similarly, the amount and duration of rainfall could be location-dependent (adding $x$, $y$ arguments to $K_{\text{rain}}(t)$).

We set the maximum of the $K_{\text{base}}$ and $K_{\text{rain}}$ functions to 0.002 individuals per square meter, which is probably much lower than in nature, to keep the memory usage of our simulation low. To run a simulation with a realistic (huge) number of mosquitoes we would need to make some efficiency improvements. Fortunately, an example of the necessary techniques follows.

Continental-scale systems: invasion of the cane toads

It is often thought that individual-based spatial models are intrinsically so slow that they are quite limited in the population size that can be modeled. Our goal with this vignette is to demonstrate that this is not necessarily the case, by showing how to model large-scale populations and landscapes with relative ease and efficiency.

Cane toads (Bufo marinus or Rhinella marina) are native to Central and South America, and were intentionally introduced to the Northeast coast of Australia in 1935 as a pest-control measure. Since their introduction, cane toads have experienced explosive population growth, with hundreds of millions of individuals spreading over several million square kilometers, resulting in considerable negative economic and ecological impacts (Shine, 2010; Urban et al., 2008).

Modeling approach

We parameterized the simulation model using information about the biology of cane toads when available. Toad population densities in established populations have been estimated around 8000 per square kilometer (Freeland, 1986). Based on this, and then tailored heuristically over several trial runs to produce the most realistic pattern of range expansion, we settled upon a local carrying capacity of 1000 per square kilometer. Telemetry data shows cane toads can travel up to 0.2 km per day (Shine et al., 2021). In order to interpret simulation time steps roughly as years, we set the spatial scale parameters ${\sigma }_D,{\sigma }_X$, and ${\sigma }_M$ to 20 km. For dispersal, we used a Student’s $t$-distribution, which provided more rare long-range dispersal events than a Gaussian kernel would (See Fig 3).

We chose to model survival probability as a function of precipitation due to its visually similar distribution to the empirical occurrence data, which seems reasonable given cane toads’ known sensitivity to moisture conditions (Child et al., 2009; Cohen and Alford, 1996). Specifically, we multiplied our typical density-dependent survival probability $n(\mathit{x})/K$ by $1/(1+\mathrm{e}\mathrm{x}\mathrm{p}(-(\alpha +\beta P(\mathit{x})))$, where $\alpha$ and $\beta$ are parameters controlling the intercept and slope of the fitness curve, and $P(\mathit{x})$ is the value of precipitation at location $\mathit{x}$ in kg/m²/year. Mating and interaction neighborhoods were large, which led to prohibitively long runtimes, so we used the fast map-based methods for local density estimation described in Box 8 and for mate choice described in Box 9.

Box 8: Using maps for faster spatial interactions.

In Box 1, we estimated the local population density for each individual with equation (1), via the localPopulationDensity() method. For each individual, this method sums the “interaction strength” (i.e., kernel density) for every other individual within the provided maximum distance. So, if the total number of individuals is $T$ and the typical number of “neighbors” (other individuals no more than the maximum distance away) is $N_X$, then the complexity of this operation is ${TN}_X$. If each individual has a large number of neighbors, this can be quite costly. However, if the number of neighbors is large, it should work just as well to (a) create a (discretized) map of local density, and (b) look up the value of the local density experienced by each individual on that map. Map lookup is quick, so if the cost of creating the map is smaller than ${TN}_X$, we will have a more efficient model.

We can create a map whose value at $\mathit{x}$ is (approximately) given by equation (1) in two steps: (1) use summarizeIndividuals() to measure the number of individuals per unit area in each cell in a grid (see Box 2), and (2) smooth() this map using the appropriate kernel, so that the density value at a given point in the resulting map depends upon an appropriate weighted average of the individuals per unit area across nearby cells of the grid. Using the same kernel as in Box 1:

grid_dims = ceil (2 * p1. spatialBounds / SX);
raw = summarizeIndividuals (p1. individuals , grid_dims , p1. spatialBounds ,
    operation =“ individuals . size ();”, perUnitArea =T);
density_map = p1. defineSpatialMap (“ density “, “xy”, raw);
density_map . smooth (SX * 3, “n”, SX);
defineGlobal (“ DENSITY “, density_map );

Then, we can modify the code of Box 1 to use the map instead:

inds = p1. individuals ;
density = p1. spatialMapValue ( DENSITY , inds . spatialPosition );
u = density / ((1 + f) * K);
inds . fitnessScaling = 1 / (1 + f * u);

This obtains (nearly) the same value as would localPopulationDensity() if the resolution of the map should be finer than the scale over which the kernel changes. In this example, that scale is SX, so we have ensured that the map has cells of size smaller than SX/2. The approximation is examined in Appendix F.

Box 9: Using maps for faster mate choice.

A similar problem as in Box 8 arises when choosing mates: even though only one mate needs to be chosen, the underlying operation is of order $T{N}_M$. The same map of density can be used to solve this problem as well: instead of choosing an individual with probability proportional to a kernel, it is (nearly) equivalent to: (1) choose a point in space nearby, with probability proportional to the map multiplied by the kernel, and then (2) take the individual closest to that point. Recall the number of possible mate scales as $N_M={\sigma }_M^{2}K$ from Section Spatial scales and neighborhood sizes. This implies that the number of neighbors grows linearly with $K$. Thus, we can keep the number of potential mate roughly constant regardless of how large local density is by rescaling the maximum distance in the InteractionType used for mate choice by $1/\sqrt{K}$ from the code in Box 4:

initializeInteractionType (2, “xy”, maxDistance =5/ sqrt (K), sexSegregation = “FM”);
i2. setInteractionFunction (“f”, 1.0) ;

We’ve set the maximum distance in the interaction kernel to be a value that should give us around 25 neighbors for each individual; however, if density varies significantly across the landscape, this may make some individuals in low density areas fail to mate. Then, we choose the mate as follows:

mate_location = DENSITY . sampleNearbyPoint ( individual . spatialPosition , 3*SM , “n”, SM);
mate = i2. nearestNeighborsOfPoint ( mate_location , p1 , 1);

Here the specification of a Gaussian mate-choice kernel with standard deviation SM has moved from the definition of the InteractionType to the sampleNearbyPoint call: given a location $x$, a map with value $m(y)$ at $y$, and a kernel $\rho ()$, this returns a random point $z$ sampled with probability proportional to $m(z)\rho (z)$. We then choose the mate as the individual nearest to that point. The approximation is examined in Appendix F.

We initiated the invasion with 10,000 individuals, though the number of individuals actually released in 1935 was likely greater (Shine et al., 2020). We chose the starting locations of the simulated toads by randomly sampling locations from the first four years of the observed occurrence data.

To make the simulation more efficient, we followed the approach described in Box 8, modified to measure the local density of individuals per unit of habitable area.

Observations and extensions

We were able to approach the true spatial and population scale of the cane-toad invasion, with a final census size of about 120 million individuals, nearing the estimated modern census size of Australian cane toads (Australia, 2019), after running for about 5 days using 200 GB of RAM at maximum. We visually compared empirical occurrence data for cane toads to our simulations, with and without annual precipitation’s effect on survival (Figure 10). While there are obvious differences in densities and locations between the simulated and observed data, it is clear that modeling annual precipitation’s effect on survival greatly improves the likeness.

Figure 10:

Simulating the cane toad invasion with and without and effect of annual precipitation on survival. (A) Map of Australia shaded by Annual Precipitation (kg m⁻² year⁻¹). (B) Observed distribution of cane toads from Global Biodiversity Information Facility (GBIF) (C) Simulation of cane toad invasion without Annual Precipitation effecting fitness. (D) Simulation of cane toad invasion with Annual Precipitation effecting fitness with all else being equal to (C).

The approach described here is similar to classical niche modeling (Peterson, 2001), which has been used extensively to model cane-toad distributions (Shine, 2010), but is somewhat simplified by only using one environmental variable. (This would be straightforward to extend; multiple environmental variables could be combined into a single habitability map for use in the model, with no impact on runtime performance.) The benefit of this vignette’s approach over previous approaches is the way that it combines information from the explicit individual-based simulation and environmental data, producing a simulation at a realistic scale with respect to both landscape size and population size.

Resource-explicit competition: monarchs and milkweed

In the preceding examples we have regulated populations through competitive interactions between individuals, either explicitly, as in Box 1, or in a space-averaged manner, as in Box 8. Population regulation in this model is managed quite differently. This is a “resource-explicit” model, wherein the population is extrinsically regulated by the availability of an external resource (Champer et al., 2024), as outlined in Box 10.

Box 10: Resource-explicit foraging and mortality.

In this box, we outline the “resource-explicit” modeling approach described more fully in Champer et al. (2024). This approach implements density-dependent population regulation that is mediated indirectly through the availability of a resource, rather than directly through competitive interactions between individuals. A simple resource-explicit simulation contains two species in a multi-species SLiM model: the focal species, in subpopulation p1, and a species representing the resource, in subpopulation p2 , in which individuals represent patches of the modeled resource.

During their foraging phase, individuals collect resources from nearby patches. Each patch can each support a certain number of individuals per time step. If a patch can support 10 individuals, but there are 100 individuals nearby at a given time step, each individual will receive a resource amount of 1/10 the amount necessary to guarantee survival (but might also forage from other nearby patches). The amount of resource that each individual collects over their foraging phase is stored in their tagF property.

i1. evaluate (c(p1 , p2));
for ( patch in p2. individuals ) {
    customers = i1. nearestNeighbors (patch , p1. individualCount , p1);
    customers . tagF = customers . tagF + inds_fed_per_patch / size ( customers );
}

After their foraging phase, individuals that have not consumed enough resources are killed. In the code example below, this occurs when individuals reach age 2.

at_risk_indivs = p1. subsetIndividuals ( minAge =2) ;
mortality_indices = runif ( size ( at_risk_indivs )) > at_risk_indivs . tagF ;
dead = at_risk_indivs [ mortality_indices ];
species . killIndividuals ( dead );

If an individual collected at least one unit of the resource, its survival to the next time step is guaranteed. Otherwise, it survives with a probability equal to the total amount it collected. See Appendix F for discussion of the relationship to the method of Box 8.

We simulate monarch butterflies (Danaus plexippus) and the milkweed (Asclepias spp.) plants on which they lay their eggs. Though adult monarchs feed on nectar from numerous types of plants, monarch caterpillars are specialists that eat only milkweed (Oberhauser et al., 2004).

Modeling approach

Monarchs in the model progress through three life-cycle stages: caterpillar, pupa, and butterfly. Mortality is modeled differently in each stage. The food resource, milkweed, is directly included in the model as a second species.

During the first two weeks of their lives (time steps 0 and 1), caterpillars interact with nearby milkweed plants and accumulate resources. The amount of resources collected from a milkweed plant each week is inversely proportional to the number of competing caterpillars within a given interaction scale $({\sigma }_X)$ of that plant. This means that a plant fed upon by more caterpillars will be depleted more quickly. When individuals reach their third week, they enter the pupa phase. At this time, survival is proportional to the amount of milkweed eaten as a caterpillar. (The survival probability is calculated only once when it becomes a pupa.) Surviving pupae become butterflies during their fifth week. Butterflies disperse, reproduce, and experience mortality at an age-dependent rate. Mortality is not density-dependent during this life cycle stage. Figure 11 shows a snapshot of the simulation, highlighting the dispersal and reproduction of individuals across the landscape.

Figure 11:

A portion of the landscape with butterflies (orange) and milkweed (green). There are about 40,000 caterpillars and 400 milkweed plants in this area. Each plant provides sufficient resources to allow an average of two caterpillars to survive to adulthood per week. A total of 2,680 butterflies are present in this area. The life history of a single individual is tracked from its origin on a particular milkweed plant, with black lines depicting dispersal, and teal lines showing where this individual laid eggs.

Reproduction also involves a resource-explicit interaction, since monarchs only lay their eggs on milkweed. To accomplish this, a spatial interaction is evaluated between adult males and milkweed (with a much longer range than the interaction between caterpillars and milkweed); each milkweed caches a list of nearby males from that interaction. Next, a similar spatial interaction is evaluated between adult females and milkweed; females are iterated through, with each female selecting a mate from the males cached at the milkweed plants within the female’s interaction range. Finally, the females randomly distribute their eggs at the plants where matings occurred.

Observations and extensions

In addition to reflecting the life history of monarch butterflies, the resource-explicit modeling approach is highly performant. Each female monarch can lay several hundred eggs, very few of which go on to reach adulthood. As a result, the number of caterpillars in the model far exceeds the number of milkweed plants. Thus, regulating the size of the caterpillar population by evaluating a spatial interaction between caterpillars and plants is far more efficient than regulating the population by evaluating an interaction directly between caterpillars.

Conclusion

Individual-based simulations are a powerful method for studying how demographic and population-genetic processes operate over continuous geographic space. Modelers must design rules for how individuals in the simulation interact with others nearby, and how forces such as selection operate. Individual-based simulations are well-suited to this problem, since they are very flexible, and can be tailored to a specific research system. However, flexibility can be both a blessing and a curse: it is easy to design a simulation with unstable population dynamics or unrealistic life-history traits. Similarly, stochasticity can cause a population that is intended to equilibrate to instead die out. Such problems likely reveal a flaw in our understanding of the system being modeled. Here, we provide guidance and connections to the ecological literature for researchers interested in designing stable, efficient, and interpretable spatial simulations. Interpretability is a key advantage to spatial, individual-based simulations, since it can take substantial effort to translate the results of more abstracted models back to the domain of interest.

Realism is not a goal of our case studies, but each illustrates the degree of realism that can be obtained from SLiM without serious effort. Increasing computational efficiency and flexibility of simulation engines are bringing individual-based simulations closer to realistic models of the ecology of specific systems. Careful implementation of ecologically realistic evolutionary models will be important to many applied fields, such as understanding and predicting how climate change affects organisms’ ranges, predicting the consequences of a gene-drive release in the wild, and rescuing species close to extinction. As the scale and specificity of in silico models improves, individual-based simulations will become valuable tools beyond academic research for management professionals in conservation, management, and public health.

Modeling density dependence

Setting out to write this paper, we hoped to provide a comprehensive yet simple guide to best practices in implementing density-dependent population regulation. Although we have provided one or two paths forward and elucidated many of the issues (see in particular Appendix B), careful empirical practitioners will soon encounter additional questions. What are some flexible and robust families of functional forms, and what aspects of these matter in practice? How can these be parameterized so that parameters naturally correspond to observable/interpretable quantities? How can these be fit to data? How should local habitat quality and density interact? At first, we imagined that the answers would be found in familiar names, and so the relationship between local density and fitness would be described as logistic, Beverton–Holt, Ricker, et cetera. However, we quickly found that these models were developed to describe population-level net changes, and so not only do not account for individual-level stochasticity, but furthermore do not separate birth from death. This is an area of active work – see, for instance, Aoyama et al. (2022) and Adler et al. (2018) for recent good examples. Full exploration of these questions was too much for this paper.

Spatial data and niche modeling

Several of our case studies use environmental variables to specify where on the simulated landscape organisms are most likely to live. The explosion in remote-sensing data provides many potential data sources for modeling spatial heterogeneity. However, what is often needed in a model is a composite proxy for “suitability” that can be incorporated into local demographics. The process of predicting where a species might or does live is known as Ecological (or, Environmental) Niche Modeling (Booth et al., 1988; Peterson, 2001). This can be done in a variety of ways; for instance, one might model either the potential or the realized niche, and predict probabilities of occurrence or population densities (reviewed in Sillero, 2011). Environmental niche models are often used to predict suitable habitat either in other locations or other time periods (Werkowska et al., 2017; Yates et al., 2018), but resulting estimates can vary widely in quality and there are a number of statistical pitfalls (Sillero and Barbosa, 2021) that simulation testing could diagnose and simulation-based inference could potentially help avoid.

While ecological niche modeling uses observation data to predict where organisms might live, a collection of landscape-genetics tools try to use genetic relatedness to predict where organisms move. The methods generate a map of “landscape resistance” that aims to describe how easily individuals move over different parts of the landscape (McRae et al., 2008). However, resistance models rely on correlating genetic distance to an abstract notion motivated by electrical circuits (reviewed in Peterson et al., 2019^; Cruzan and Hendrickson, 2020). They lack an underlying mechanistic model, so estimates can be problematic in practice (Cushman et al., 2013; Graves et al., 2013), and are expected to mislead in plausible situations such as biased dispersal (Lundgren and Ralph, 2019). Again, simulation-based inference provides a promising route forward (Smith et al., 2023, 2024), since it does not rely on explicit likelihoods or other mathematical descriptions.

Sampling

Any simulation study that wishes to make comparisons to real data needs to also consider the sampling effort that led to those data, and realistic simulation of many sampling schemes can be daunting. In practice, sampling can strongly affect results (for an example in population genetics, see Battey et al., 2020). However, it is relatively easy to assess the robustness of results to variations in sampling scheme. Furthermore, it is often possible to “over-sample” simulations: as done for instance in Smith et al. (2023), many simulated datasets can be obtained from each costly spatial simulation, simply by repeating the sampling effort (however, if sufficient simulations are not done, model performance will be poor). It would be useful to develop a standard set of tools that implement various sampling schemes for simulated spatial populations.

The future

Although the spatial simulations we present here incorporate many more aspects of real organisms’ lives than does the Wright–Fisher model, there are many things that we have not tried to explicitly model, such as seasonal migration, herding or flocking, territoriality, foraging strategies, microhabitat variation, broadcast spawning, resource storing, pollination, predation, facilitation, and other inter-species interactions. Any of these can be modeled in SLiM with more or less effort, and indeed many are described in the SLiM manual (Haller and Messer, 2024). The decision of which aspects of biology to model is in practice made by prioritizing those aspects expected to substantially affect the question being studied. We are excited to see the wide variety of simulations that researchers develop in the future, as we explore these questions and build on each other’s work.

Figure 6:

Density dependence of mortality (red lines) and fecundity (blue lines) described in equations (8) and (10), with $s=0.25$. Line types show the mortality or fecundity for the different genotypes, i.e., for individuals carrying $k=0,1$, or 2 copies of the focal allele. The mean growth rate of the focal allele when rare (black line; $G(u)$ from equation (7)) is the same for both types of selection, at all densities. The vertical dotted line is at scaled density $u=1$. Other parameters are as in Figure 1.

Box 4: Interactions, and mating.

The mechanism that SLiM uses to mediate most effects that some individuals have on others is called an “interaction type” (see Box 1). We used a symmetric interaction type in Box 1 to compute local density: every individual affected every other. Some interactions are not symmetric: we might, for instance, want each female to be able to find nearby males. To do this, we first set up a sex-specific interaction (again using a Gaussian kernel, with standard deviation SM):

initializeInteractionType(2, “xy”, maxDistance=SM * 3, sexSegregation = “FM”);
i2.setInteractionFunction(“n”, 1.0, SM);

The sexSegregation parameter value of “FM” means that females will receive the interaction and males will exert the interaction; it is asymmetric. Then, we can use the interaction in a reproduction(NULL, “F”) block as follows (the NULL and ‘ $\mathrm{F}$ ‘‘ arguments imply that it applies to all females) to produce a single offspring:

mate = i2.drawByStrength(individual, 1);
subpop.addCrossed(individual, mate, count=1);

This chooses a male mate from among the neighbors of the focal female, individual, with probability proportional to a Gaussian kernel with standard deviation SM, as described in the text. The interaction type itself guarantees that the chosen mate will be male. It is possible to set up other constraints on interaction types as well, such as a minimum and/or maximum age, to represent other constraints on the reproductive eligibility of individuals.

Appendix A. Example SLiM script

Here is a complete SLiM script for a spatial simulation with local Beverton-Holt regulation on mortality.

initialize() {
  initializeSLiMModelType(“nonWF”);
  initializeSLiMOptions(dimensionality=“xy”);
    defineConstant(“SD”, 0.3);   // sigma_D, dispersal scale
    defineConstant(“SX”, 0.3);   // sigma_X, interaction scale for measuring local density
    defineConstant(“SM”, 0.3);   // sigma_M, mate choice scale
    defineConstant(“K”, 5);      // carrying capacity per unit area
    defineConstant(“FECUN”, 0.25); // mean number of offspring per time step
    defineConstant(“WIDTH”, 25.0); // width of the simulated area
    defineConstant(“HEIGHT”, 25.0); // height of the simulated area
    defineConstant(“RUNTIME”, 200); // total number of ticks to run the simulation for
  // Set up constants that depend on externally defined parameters
  defineConstant(“RHO”, FECUN / ((1 + FECUN) * K));
  // basic neutral genetics
  initializeMutationRate(1e-8);
  initializeMutationType(“m1”, 0.5, “f”, 0.0);
  initializeGenomicElementType(“g1”, m1, 1.0);
  initializeGenomicElement(g1, 0, 1e8–1);
  initializeRecombinationRate(1e-8);
  // spatial interaction for local density measurement
  initializeInteractionType(1, “xy”, reciprocal=T, maxDistance=3 * SX);
  i1.setInteractionFunction(“n”, 1, SX);
  // spatial interaction for mate choice
  initializeInteractionType(2, “xy”, reciprocal=T, maxDistance=3 * SM);
  i2.setInteractionFunction(“n”, 1, SM);
}
1 first() {
  sim.addSubpop(“p1”, asInteger(K * WIDTH * HEIGHT));
  p1.setSpatialBounds(c(0, 0, WIDTH, HEIGHT));
  p1.individuals.setSpatialPosition(p1.pointUniform(p1.individualCount));
}
first() {
  // preparation for the reproduction() callback
  i2.evaluate(p1);
}
reproduction() {
  mate = i2.drawByStrength(individual, 1);
  if (mate.size())
    subpop.addCrossed(individual, mate, count=rpois(1, FECUN));
}
early() {
  // Disperse offspring
  offspring = p1.subsetIndividuals(maxAge=0);
  p1.deviatePositions(offspring, “reprising”, INF, “n”, SD);
  // Measure local density and use it for density regulation
  i1.evaluate(p1);
  inds = p1.individuals;
  competition = i1.localPopulationDensity(inds);
  inds.fitnessScaling = 1 / (1 + RHO * competition);
}
late() {
  if (p1.individualCount == 0) {
    catn(“Population went extinct! Ending the simulation.”);
    sim.simulationFinished();
  }
}
RUNTIME late() {
  catn(“End of simulation (run time reached)”);
  // code for output might go here
  sim.simulationFinished();
}

Appendix B. Pitfalls

Even after carefully parameterizing a simulation to equilibrate near a given population density, it is fairly easy in practice to end up with a spatial simulation that mysteriously dies out or behaves oddly in other ways. A less dramatic annoyance is that usually the realized population size is not equal to the desired density, $K$, multiplied by the total area. This section describes the root causes of these issues and ways to diagnose them. The discussion gets into the weeds, so here is a summary of what to check if density is not what you expect (details below):

1. Visualize the simulation to check for odd dynamics or spatial patterns, such as a regular array of clumps.

2. Make sure the neighborhood sizes $N_X$, $N_M$, and $N_D$ are not too small (if in doubt, observe the effects of increasing ${\sigma }_X$, ${\sigma }_M$ and/or ${\sigma }_D)$.

3. Look at the mean density experienced by individuals, not the total density across the landscape. If you want instead to set the total population size, you’ll need a post-hoc adjustment to $K$ as in Box 6.

4. Make sure the stage you’re measuring density in agrees with the theoretical calculations (i.e., between birth and death or between death and birth).

5. Consider stochasticity: density varies randomly across the landscape, making the realized mean density differ from $K$.

Although it is natural to expect that the realized density of a simulation will be exactly the specified value of $K$, it is important to remember in practice that having a density different from $K$ is not necessarily a “problem”: instead, it may reflect the natural biological consequences of the chosen model.

Why are there weird regular clumps?

At its most extreme, a dispersal scale much smaller than the interaction scale can lead to strange, regular arrays of clumps. (Clumps may appear for many other reasons, but here we’re talking about a regular, hexagonal grid of clumps.) Examples are shown in Figure S9. Although such regular patterns formed by this mechanism rare in nature, they are easy to accidentally produce in simulation (and are one reason it is important to visualize the simulation, as in Box 2). For discussion of this strange phenomenon, see Sasaki (1997), Etheridge et al. (2024), or the “Spatial competition and spatial mate choice in a nonWF model” section of the SLiM manual (Haller and Messer, 2024). These are probably an indication that the dispersal or interaction scale are not well-chosen, but may indicate something more interesting.

Why does my simulation run so slowly?

The runtime of an individual-based simulation is at least proportional to the total number of individuals. However, it is common for the runtime of spatial simulations to grow more than linearly in the number of individuals, because of spatial dynamics that involve a large number of pairwise comparisons or interactions (such as spatial mate choice and spatial competition). Performance problems resulting from this can often be diagnosed by looking for large neighborhood sizes: if $N_X$ (the interaction neighborhood size) or $N_M$ (the mating neighborhood size) are large, one may encounter slow run times. Happily, there are solutions that can often be applied.

Perhaps the most obvious solutions are to directly reduce the number of pairwise interactions. One way is to shrink the neighborhood sizes of the model, by reducing ${\sigma }_M$ and/or ${\sigma }_X$. However, that will often noticeably change the behavior of the model and sacrifice biological realism. Another way is to shrink the neighborhood size is to cut off the spatial kernel at a shorter distance, with little loss of exactitude; for a Gaussian spatial kernel, for example, cutting off at two standard deviations rather than three can reduce runtime with (perhaps) little change in dynamics, since interacting individuals 2–3 standard deviations from the focal individual interacted with that individual quite weakly anyway. However, this cannot cut runtime by more than about half, so for most models with large neighborhood sizes, another strategy is needed.

A second option is to use a “resource node” approach, as demonstrated in the “monarchs” example, which effectively mediates the many possible individual-individual interactions with a smaller number of interactions between each individual and a nearby node (representing a localized amount of resources). The approach is discussed more fully in Champer et al. (2024).

A third option is to use spatial map operations to approximate the pairwise interactions more efficiently. Effectively, we can pre-compute a smoothed version of the map of density in each tick of the model, then use that map to look up the density for each individual as a summary of all of the pairwise interactions it receives (Box 8). It turns out the same method can be used to efficiently pick nearby mates as well (Box 9). This option is in fact equivalent to using a regular grid of resource nodes, and can be proven to be a good approximation: see Appendix F.

Figure S1 shows that using the map-based approximation methods described in Boxes 8 and 9 makes it much easier to scale simulations to much higher neighborhood sizes. A naive implementation of pairwise interactions would result in runtimes that are quadratic in total population size, and hence totally infeasible for all but very small populations. Standard pairwise interactions in SLiM use efficient data structures $(k$-d trees) and a maximum cutoff (here, of $3\sigma )$, but still compute all pairwise interactions out to the maximum distance, and so are quadratic instead in neighborhood size $(N_X$ or $N_M)$, shown as solid lines in Figure S1. The spatial map-based methods, on the other hand, scale linearly with neighborhood size. These faster methods are approximate, but correspond closely, especially at high densities, as shown in Figure S2.

All three options have pros and cons, and may alter the behavior of the model. If the natural dynamics of the species are mediated through discrete locations (e.g., feeding or locations or mating sites), then adapting the resource node method is probably the most natural method. (In fact, it has been suggested that uncommon insects gather in discrete locations to find mates for not dissimilar reasons (Alcock, 1987).) If not – and so implementing resource nodes would require inventing new aspects of the model – it may be more natural to use the map-based methods to implement the existing model. Finally, it may be necessary (especially for development purposes!) to simply model a smaller landscape.

Why does my simulation die out?

There are a variety of reasons why a simulation might die out (or have far fewer individuals than you expect). For instance, this can happen if ${\sigma }_M$, ${\sigma }_X$, or ${\sigma }_D$ are too small. In all cases, “too small” can be diagnosed by looking at the relevant neighborhood sizes: for example, if $N_M=K\pi {\sigma }_M^2$ is small (less than about 1), there may be a problem related to ${\sigma }_M$. This problem manifests as individuals being unable to reproduce because they cannot find a mate. This is particularly likely to happen if the mating scale has been made smaller to reduce runtime (see the previous section for discussion). Solutions might be either to increase ${\sigma }_M$, to allow selfing, or to increase the fecundity of those individuals that do reproduce, depending upon the biology of the system being modeled. The result also depends on the mating scheme, as shown in Figure S7.

The reasons that small ${\sigma }_X$ can be a problem are more subtle. Since ${\sigma }_X$ determines the range over which density is computed, and each focal individual itself counts towards its local population density, then if ${\sigma }_X$ is sufficiently small even a single isolated individual can have “local density” greater than the carrying capacity. This effect is demonstrated in Figure S8, in which the population dies out for small ${\sigma }_X$. The effect also appears in Figure S7, in which selfing simulations die out at low $K$ (and hence low $N_X)$ – since they self, they are not dying out due to small $N_M$. Conceptually, this happens if the simulated individuals cannot range over a large enough area to obtain sufficient resources for survival, even in the absence of competition. Since the density of a single individual calculated by equation (1) is $\rho (0)/{\sigma }_X^2$, then this will occur if $\rho (0)/{\sigma }_X^2$ is close to or greater than $K$, i.e., roughly if ${\sigma }_X\le 1/\sqrt{K}$. This could be avoided by excluding the focal individual from the calculation of local density; however, this leads to the opposite problem: densities can get much larger than $K$. This happens because if ${\sigma }_X\le 1/\sqrt{K}$, a single neighbor within scale ${\sigma }_X$ will lead to a “local density” of more than $K$ – but further away neighbors are unaffected. If local density increases mortality, a cartoon version of the situation is that an individual with a neighbor within distance ${\sigma }_X$ is killed, but neighbors further away than this are ignored; as a result, the density equilibrates to around $1/{\sigma }_X^2$, rather than $K$. (The above discussion is in two dimensions; in a one-dimensional model the equilibrium density would be around $1/{\sigma }_X$.)

The population can die out if ${\sigma }_D$ (and/or ${\sigma }_V)$ is too small for similar reasons: conceptually, if offspring do not disperse far enough from their parents and local competition is strong, then families reduce their own fitness. For a simple example, suppose that the probability that a new offspring with local density $n$ survives is $e^{-n/K}$ and ${\sigma }_D$ is much less than ${\sigma }_X$. Then, a group of $m$ siblings form a clump of $m+1$ individuals with their parent, with density at least $(m+1)\rho (0)/{\sigma }_X^2$; so, the expected number of surviving offspring is smaller – at most $m\mathrm{e}\mathrm{x}\mathrm{p}\left(-(m+1)\rho (0)/{\sigma }_X^2\right)$ – and the smaller number should be used in calculations of net reproductive output. However, if new individuals move sufficiently far (with ${\sigma }_V)$ before local density effects, then the effect may be avoided.

The effects of changing ${\sigma }_X$, ${\sigma }_D$, and removing the focal individual from density calculations are shown in an example in Figure S10.

Why is the realized density not equal to $\mathit{K}$?

We’ve carefully set things up so that the equilibrium density in a neutral, spatially homogeneous simulation “should be” equal to $K$. If the realized density is very different (e.g., zero) then the problem is probably one of the pitfalls described above. But even if $N_X$, $N_M$, and $N_V$ are not small, realized density still often differs from $K$ by 20% or 30%. Perhaps the simplest reason is “edge effects”, but we assume the range is large enough these are unimportant (and, in practice SLiM computes local population density in such a way that local density is unaffected by edges). Another simple reason could be that density differs at different points in the life cycle – see below for more discussion of this.

First, we need to consider: which realized population density should we compare to $K$? The first answer that might spring to mind is “number of individuals divided by total area”; however, what matters for equilibrium is the density experienced by individuals. In other words, to see theoretical predictions playing out, we should measure local population density for each individual, and average that across individuals – that is after all the density that matters to the dynamics. This is seen in Figure S8, where mean density around individuals is shown in blue and number of individuals divided by area is shown in red, as well as in Figure S7, where mean density around individuals is shown in dotted lines and number of individuals divided by area in solid. Conceptually, if at equilibrium the simulation is very patchy (so individuals tend to be bunched up), then the mean density experienced by individuals could be much higher than the number of individuals divided by total area. In fact, the mean density around individuals is almost always be higher than the number of individuals divided by total area.

This line of reasoning leads to the second point: across individuals, local population density is a distribution, not a single value. It turns out that this stochasticity can also be important. Conceptually, the decrease in net reproduction of individuals with higher than average density may not be balanced by those individuals with lower density; how this happens depends on the shape of $F(u)$ and the shape of the distribution of densities. Below, we work through both these issues in more detail.

Mean density around individuals

Why is the density experienced by individuals higher than the number of individuals divided by total area? Concretely, suppose that $u_i=n\left(x_i\right)/K$ is the scaled local density for individual $i$; the expected change in population size is zero if ${\sum }_{i}F\left(u_i\right)=0$. Equivalently, if $U$ is the scaled local density for a randomly chosen individual, equilibrium occurs if $\mathbb{E}[F(U)]=0$. Suppose instead that we look at the distribution of local densities across space instead of across individuals. Heuristically, suppose that we divide the landscape up into many small regions, each of area $ϵ$, and let $v_j$ be the scaled density in region $j$ (i.e., $n\left(y_j\right)/K$ for some point $y_j$ in region $j$, and the regions are small enough that density is constant within each). The number of individuals in region $j$ is $ϵK{v}_j$, and so the net contribution to the next step’s population size from region $j$ is $ϵK{v}_{j}F\left(v_j\right)$. This equilibrium occurs if ${\sum }_j{v}_{j}F\left(v_j\right)=0$. Equivalently, if we let $V$ denote the local density around a uniformly chosen point on the landscape, then equilibrium occurs if $\mathbb{E}[VF(V)]=0$. In fact, the relationship between $U$ and $V$ is that $U$ is a size-biased draw from $V$; the relationship between the two is that $\mathbb{E}[f(U)]=\mathbb{E}[Vf(V)]/\mathbb{E}\left[V\right]$ for any function $f$. In particular, $\mathbb{E}\left[U\right]=\mathbb{E}\left[V^2\right]/\mathbb{E}\left[V\right]>\mathbb{E}\left[V\right]$ (by Jensen’s inequality), and $\mathbb{E}\left[V\right]$ is just the total number of individuals divided by the total area (except for some edge effects).

Sharp-eyed readers of this and the next section will notice that we are sweeping something under the rug: when we measure density using equation (1), we do not include the focal individual. Taking this into account properly when defining $V$ is much less clean, so for illustrative purposes we have omitted this. In fact, if individual locations are independent and uniformly distributed, then mean density around individuals (measured without the focal individual!) is equal to the number of individuals divided by total area. Nonetheless, we think the calculations are informative.

Stochasticity

Now we can immediately see how stochasticity interacts with nonlinearity in density dependence to increase or decrease equilibrium density. First suppose that $F$ is convex and decreasing, i.e., $F^{\prime \prime }(u)>0$ and $F^{\prime }(u)\le 0$ for all $u$. Then by Jensen’s inequality, $\mathbb{E}[F(U)]>F(\mathbb{E}[U])$, and since at equilibrium, $\mathbb{E}[F(U)]=0$, we have that $F(\mathbb{E}[U])<0$. Since we’ve assumed that $F(1)=0$ and $F$ is decreasing, this implies that $\mathbb{E}\left[U\right]>1$, i.e., a convex $F$ increases the equilibrium mean density experienced by individuals above $K$. By the same argument if $F$ is concave, $\mathbb{E}\left[U\right]<1$.

We can make the same argument for the total density, $V$: if $G(v)=vF(v)$ is convex, then $\mathbb{E}\left[V\right]>1$, while if $G$ is concave then $\mathbb{E}\left[V\right]<1$. This at first seems odd: if $F(u)$ is convex and $uF(u)$ is concave, then the mean density experienced by individuals is higher than $K$, while the total density is lower than $K$. However, this is perfectly possible, and in fact seen in Figure S8.

A Taylor expansion lets us estimate more precisely the deviation of equilibrium size from $K$. Taylor expanding $F(u)$ about $u=1$, we get that

$$\begin{array}{l}0=\mathbb{E}[F(U)]\approx \mathbb{E}\left[F(1)+(U-1)F^{\prime }(1)+\frac{1}{2}(U-1{)}^2{F}^{\prime \prime }(1)\right]\\ & =(\mathbb{E}[U]-1)F^{\prime }(1)+\frac{1}{2}\mathrm{v}\mathrm{a}\mathrm{r}[U]F^{\prime \prime }(1)+\frac{1}{2}(\mathbb{E}[U]-1{)}^2{F}^{\prime \prime }(1).\end{array}$$

If the deviation is small (i.e., $\left.|\mathbb{E}[U]-1|\ll \left|F^{\prime }(U)/F^{\prime \prime }(U)\right|,(\mathbb{E}[U]-1{)}^2\ll \mathrm{v}\mathrm{a}\mathrm{r}[U]\right)$, the second order term is negligible. Thus, we can write:

$$\mathrm{E}[U]\approx 1-\frac{1}{2}\mathrm{v}\mathrm{a}\mathrm{r}[U]\frac{F^{\prime \prime }(1)}{F^{\prime }(1)},$$ (11)

when $\frac{1}{2}\mathrm{v}\mathrm{a}\mathrm{r}[U]\ll {\left(\frac{F^{\prime }(1)}{F^{\prime \prime }(1)}\right)}^2$. Since $F^{\prime }(1)$ is negative, agrees with the argument above. Figure S11 shows that this prediction bears out well in practice (in two non-spatial models), as long as the population does not go extinct.

Similarly,

$$\begin{array}{l}0=\mathbb{E}[F(U)]=\mathbb{E}[VF(V)]\\ & \approx \mathbb{E}\left[1F(1)+(V-1)\left(F(1)+1F^{\prime }(1)\right)+\frac{1}{2}(V-1{)}^2\left(2F^{\prime }(1)+1F^{\prime \prime }(1)\right)\right]\\ & \approx (\mathbb{E}[V]-1)F^{\prime }(1)+\frac{1}{2}\mathrm{v}\mathrm{a}\mathrm{r}[V]\left(2F^{\prime }(1)+F^{\prime \prime }(1)\right),\end{array}$$

and hence

$$\mathbb{E}[V]\approx 1-\mathrm{v}\mathrm{a}\mathrm{r}[V]\left(1+\frac{F^{\prime \prime }(1)}{2F^{\prime }(1)}\right),$$

which is smaller than $\mathbb{E}[U]$, and further away from 1, except in extreme circumstances.

What determines the strength of stochasticity? Since this has to do with random variation in “experienced” density across the landscape, stochasticity goes down as interaction neighborhood size $N_X$ increases. In other words, if ${\sigma }_X$ is larger, then we measure density averaging over larger areas, which is therefore less variable. As in equation (11), stochasticity affects equilibrium by a factor proportional to var$[U]$. If $Y$ is the number of individuals within distance ${\sigma }_X$ of a random individual, then $\mathbb{E}[Y]$ is around $N_X$, and if noise is Poisson then also $\mathrm{v}\mathrm{a}\mathrm{r}[Y]\approx N_X$. Since $U$ is obtained by dividing $n(x)$ (from equation (1)) by $K$, and $n(x)$ is roughly $Y/\pi {\sigma }_X^2$, we expect $\mathrm{v}\mathrm{a}\mathrm{r}[U]$ to be of order $\mathrm{v}\mathrm{a}\mathrm{r}[Y]/{\left(\pi {\sigma }_X^{2}K\right)}^2=N_X/N_X^2=1/N_X$. So, we expect the deviation of realized density from $K$ to be of order $1/N_X$. Again, this is seen in Figure S8: the form of density dependence has a convex $F(u)$, and so for smaller values of ${\sigma }_X$, the value of $\mathbb{E}[U]$ (blue line) is above $K$. Conversely, the function $uF(u)$ is concave, and so $\mathbb{E}[V]$ (red line) is increasing, but is well below $K$ for other reasons.

The difference between the mean density around individuals $(\mathbb{E}[U])$ and the mean density by area $(\mathbb{E}[V]$, or total population size divided by total area) is well-known: the ratio $\mathbb{E}[U]/\mathbb{E}[V]$ is a scale-dependent measure of clustering known as mean crowding (Lloyd, 1967) that increases the more clustered individuals are on the scale used to measure local density.

Density measurement timing

The other thing to consider is: when is density being measured? In each time step there are some births and some deaths; we follow SLiM in taking births first in the time step, but since the two alternate, this choice seems arbitrary. However, having density effects or movement occur in one or the other stage can affect the model (e.g., Taylor, 2010). Following SLiM as we do, the most common “population size” is at the end of the time step, i.e., after deaths (or equivalently, before births). However, population size may also be measured (and used!) between births and deaths.

Concretely, suppose that $N_t$ is the population size at the start of time step $t$, and $N_t^{+}$ is the population size after births in time step $t$. Above, we did calculations like this: if the mean fecundity in time step $t$ is $f_t$, and the mean probability of survival is $1-{\mu }_t$, then

$$\mathbb{E}\left[N_t^{+}\right]=N_t\left(1+f_t\right)$$ (12)

$$\mathbb{E}\left[N_{t+1}\right]=N_t^{+}\left(1-{\mu }_t\right)$$ (13)

$$=N_t\left(1+f_t\right)\left(1-{\mu }_t\right).$$ (14)

Which density is used to determine $f_t$ and ${\mu }_t$? Naturally, $f_t$ can’t depend on the number of births, so it will use $N_t$ (i.e., the density at the start of the time step). However, should the density dependence for ${\mu }_t$ use $N_t$ or $N_t^{+}$? If the newborn individuals contribute to density, then ${\mu }_t$ should depend on $N_t^{+}$, i.e., density computed using the offspring as well. However, this will be larger than the density at the start of the time step by a factor of $1+f$, and so the equation for the local net per capita reproductive rate analogous to equation (2) is

$$F^{+}(u)=(1+f(u))(1-\mu (u(1+f(u))))-1.$$ (15)

As before, equilibrium would be around density $n_{\mathrm{*}}$ solving $F^{+}\left(n_{\mathrm{*}}/K\right)=0$, and so to arrange as before for the equilibrium density to be around $K$ we’d like to set up the functional forms so that $F^{+}(1)=0$. One way to do this is to start with functional forms for $f(u)$ and $\mu (u)$ so that $F(u)=(1+f(u))(1-\mu (u))-1$ satisfies $F(1)=0$ (i.e., formulated for measuring density between death and birth), and then define the survival probability to be $1-{\mu }^{+}(u)=1-\mu (u/(1+f(1)))$. Then $F^{+}(u)$ defined using ${\mu }^{+}(u)$ satisfies $F^{+}(1)$. This is the approach taken by Battey et al. (2020). Another approach is to compute a density map, as in Box 8, at the start of each time step, and use that map to determine density for juveniles as well.

Appendix C. Parameterization of density dependence

If one wants to use a familiar phenomenological model as the basis for density dependence, there are several popular choices for the function form of $F(u)$. Here, we summarize these, parameterized so that $F(1)=0$ (and so will have an equilibrium near $n_{\mathrm{*}}=K$:

• $F(n)\propto 1-n$, (Discrete-logistic model)

• $F(n)\propto \frac{1+a}{1+an}-1$, (Beverton–Holt model)

• $F(n)\propto \frac{(1+a{)}^{\mathrm{c}}}{(1+an{)}^{\mathrm{c}}}-1$, (Hassell model)

• $F(n)\propto e^{r(1-n)}-1$. (Ricker model)

(Here, $\propto$ indicates that each can be scaled by a constant, reflecting an overall time scaling.)

Using each one still requires a number of choices. Next, we work through in more detail the steps involved in arranging birth and death rates so that the net birth rate, $F$, has a particular functional form, and give a number of examples that help to show the issues involved. Suppose here that each time step has birth followed by death; death applies in the same way to individuals just born as those previously alive; the mean fecundity of an individual with local density $N$ is $f(N/K)$; and the probability of death of an individual with local density $N$ is $\mu (N/K)$.

Roughly, the net change in population size when at scaled density $u=N/K$ is $F(u)=f(u)(1-\mu (u))-\mu (u)$. However, this is not not necessarily right, since it depends when the densities are measured: if the density for mortality is measured after birth, then the density passed to $\mu$ will be different than that passed to $f$. So, we’ll always define $F(u)$ to be the mean per-capita change in population size across one step when starting at scaled population size $u$. However, which point in the time step (i.e., after birth and before death or vice-versa) is the reference point will depend on the situation. Our goal is to figure out how to arrive at a given functional form for $F$ in various scenarios.

Fecundity regulation:

If death probability is constant: $\mu (u)={\mu }_0$, then taking $u$ to be the scaled population density before birth, simply

$$F(u)=f(u)\left(1-{\mu }_0\right)-{\mu }_0,$$

and so

$$f(u)=\frac{F(u)+{\mu }_0}{1-{\mu }_0}.$$

Since $0\le f<\infty$, for this to make sense we need ${\mu }_0>0$ and $F\ge -{\mu }_0$.

Beverton–Holt fecundity regulation:

With $\mathit{F}(\mathit{u})=\mathit{\alpha }((1+\mathit{a})/(1+\mathit{a}\mathit{n})-1)$, this is

$$f(u)=\frac{1}{\left(1-{\mu }_0\right)}\left(\alpha \frac{(1+a)}{(1+au)}+\left({\mu }_0-\alpha \right)\right),$$ (16)

and we need $\alpha \le {\mu }_0$.

Ricker fecundity regulation:

With $\mathit{F}(\mathit{u})=\mathit{\alpha }\left({\mathit{e}}^{\mathit{r}(1-\mathit{u})}-1\right)$, this is

$$f(u)=\frac{1}{1-{\mu }_0}\left(\alpha e^{r(1-u)}+\left({\mu }_0-\alpha \right)\right),$$

and we again need $\alpha \le {\mu }_0$.

Mortality regulation:

Suppose instead that fecundity is constant: $f(u)=f_0$, and that we measure density for mortality after birth (so it includes the new births). Then

$$F(u)=f_0-\mu (u)\left(1+f_0\right),$$

and so the survival probability is

$$1-\mu (u)=\frac{1+F(u)}{1+f_0}.$$

Since we must have $0\le \mu \le 1$, we require that $-1\le F\le f_0$. Note that in this model (regardless of the form of $F)$, the death probability at the stationary point $(u=1$, since $F(1)=0)$ is $\mu (1)=1/\left(1+f_0\right)$; and so the mean lifetime is $1+f_0$. Also note that this produces an equilibrium density of $K$ before death (as opposed to before birth, in the previous models); the density will be lower after death.

Beverton–Holt mortality regulation:

With $\mathit{F}(\mathit{u})=\mathit{\alpha }((1+\mathit{a})/(1+\mathit{a}\mathit{u})-1)$, this is

$$1-\mu (u)=\frac{1}{\left(1+f_0\right)}\left(\alpha \frac{(1+a)}{(1+au)}+(1-\alpha )\right),$$ (17)

and we need $\alpha a\le f_0$.

Ricker mortality regulation:

With $\mathit{F}(\mathit{u})=\mathit{\alpha }\left({\mathit{e}}^{\mathit{r}(1-\mathit{u})}-1\right)$, this is

$$1-\mu (u)=\frac{1}{1+f_0}\left(\alpha e^{r(1-u)}+(1-\alpha )\right),$$

and we need $\alpha \left(e^r-1\right)\le f_0$.

Mortality and fecundity:

Suppose now we’d like both mortality and fecundity to change with density. So that there’s only one density, let’s say again that is measured after birth and before death. If the density at this time is $N$, then the mean number of individuals in the next time step is

$$N(1-\mu (N/K))(1+f(N/K)),$$

so that the mean net change is

$$F(u)=(1-\mu (u))(1+f(u))-1.$$

Given a desired functional form for $F(u)$ and $\mu (u)$ we would then define

$$f(u)=\frac{F\left(u\right)+1}{1-\mu \left(u\right)}-1.$$

Note that for fecundity to remain finite, we need $\mu (u)$ to be bounded away from zero. On the other hand, if we have $f(u)$ then

$$1-\mu \left(u\right)=\frac{F\left(u\right)+1}{1+f\left(u\right)}.$$

Mixed Beverton–Holt:

Suppose we set $f(u)=f_0/(1+bu)$ and would like $F(u)=\alpha ((1+a)/(1+au)-1)$ for some constants $b$ and $\alpha$. Then, we would set

$$1-\mu (u)=\frac{\alpha (1+a)/(1+au)+(1-\alpha )}{f_0/(1+bu)+1},$$ (18)

and we need $\alpha a<f_0$.

Mixed Ricker:

Now suppose that we set $1-\mu (u)=\left(1-{\mu }_0\right)e^{-su}+{\mu }_{\mathrm{\infty }}\left(1-e^{-su}\right)$ and would like $F(u)=\alpha \left(e^{r(1-u)}-1\right.)$. (The extra parameters are not unnecessary complications: we will need $\alpha <1$ and ${\mu }_{\mathrm{\infty }}>0$ for the following to work out.) Then, we would set

$$f(u)=\frac{\alpha e^{r(1-u)}+(1-\alpha )}{\left(1-{\mu }_0\right)e^{-su}+{\mu }_{\mathrm{\infty }}\left(1-e^{-su}\right)}-1,$$

and we need $s\le r$ for this to remain positive. This has $f(0)=\left(\alpha \left(e^r-1\right)+1\right)/\left(1-{\mu }_0\right)-1$, which is positive if $r>0$ (already a requirement). Also, $f(\mathrm{\infty })=(1-\alpha )/{\mu }_{\mathrm{\infty }}-1$, so we also need $1-\alpha >{\mu }_{\mathrm{\infty }}$.

Hassell with mortality regulation

Let’s set up the Hassell, which is $\left.F(u)=b((1+a)/(1+au){)}^c-1\right)$. Note that $F(0)=b\left((1+a{)}^c-1\right),F(\mathrm{\infty })=-b$, and $F^{\prime }(1)=cab(1+a{)}^c$. Setting fecundity to be constant at $f_0$ and plugging in to the expression for mortality regulation above,

$$\mu (0)=\frac{f_0-b\left((1+a{)}^c-1\right)}{1+f_0}$$

and

$$\mu \left(\mathrm{\infty }\right)=\frac{f_0+b}{1+f_0}.$$

So, if we’d like to fix $\mu (0)={\mu }_0$ and ${\mu }_{\mathrm{\infty }}=\mu (\mathrm{\infty })$, then these determine $a$ and $b$:

$$\begin{array}{ll}& b={\mu }_{\mathrm{\infty }}\left(1+f_0\right)-f_0\\ & a={\left(\frac{f_0-{\mu }_0\left(1+f_0\right)}{{\mu }_{\mathrm{\infty }}\left(1+f_0\right)-f_0}+1\right)}^{1/c}-1.\end{array}$$

This leaves us with a parameterization in terms of the mean fecundity, $f_0$, the death rate at low density, ${\mu }_0$, the death rate at high density, ${\mu }_{\mathrm{\infty }}$, and the exponent $c$ that controls how steep the curve is between. (We could reparameterize $c$ so we have a parameter that is exactly $F^{\prime }(1)$, but this is less compelling.)

Ricker parameterization with fecundity regulation If $\mu (u)={\mu }_0$ and we want $F(u)=C\left(e^{\mathit{r}(1-u)}-1\right)$, then

$$f(u)=\alpha e^{-ru}+\beta ,$$ (19)

where letting $\alpha =C{e}^r/\left(1-{\mu }_0\right)$ and $\beta =\left({\mu }_0-C\right)/\left(1-{\mu }_0\right)$. So, $f(0)=\alpha +\beta$ and $f(\mathrm{\infty })=\beta$. If we set $C={\mu }_0$ then this is $\beta =0$ and $\alpha ={\mu }_0{e}^r/\left(1-{\mu }_0\right)$, and so $f(u)={\mu }_0{e}^{-r(u-1)}/\left(1-{\mu }_0\right)$.

Regulation by juvenile mortality

Now suppose that adult death rate and fecundity are constant (so, $f(u)=f$ and $\mu (u)=\mu )$, but that the probability of survival of juveniles is density-dependent. (Perhaps density dependence only affects the species during seedling recruitment.) So, if we call $r(u)$ the probability of survival in the first year at scaled density $u$, the net per capita reproduction function is $F(u)=r(u)f-\mu$. To make this proportional to the Beverton–Holt form, we can set

$$r(u)=\frac{\mu (1+a)}{f(1+au)},$$ (20)

which results in $F(u)=\mu ((1+a)/(1+au)-1)$ – i.e., the Beverton–Holt form, scaled by $\mu$.

Density regulation of both juvenile and adult mortality

Now suppose that the probability of survival of juveniles (i.e., to their first year) is $r(n/K)$, not $1-\mu (n/K)$. In this case,

$$F(u)=r(u)f(u)-\mu (u),$$

and so if we fix $f(u)=f$ then we have, for instance,

$$fr(u)=F(u)+\mu (u).$$

Suppose we want $F(u)=(1+a)/(1+au)-1$ and $\mu (u)=bu/(1+bu)$; then we would have

$$\begin{gathered} fr(u)=\frac{(1+a)}{(1+au)}+\frac{bu}{(1+bu)}-1 \\ =\frac{(1+a)}{(1+au)}-\frac{1}{(1+bu)} \\ =\frac{a}{(1+au)}+\frac{(b-a)u}{(1+au)(1+bu)} \end{gathered}$$

With this definition, $r(0)=a/f$ and $r(\infty )=(b-a)/((b+a)f)$, so we need $a\le \mathrm{m}\mathrm{a}\mathrm{x}(b,f)$ (and some other conditions). Note that $r(\infty )>r(0)$ (i.e., increasing recruitment with density) if $b-a>a(a+b)$: for instance, take $f=1$ and $a=1/4$ and $b=3/4$.

Appendix D. Parameterization and sampling for dispersal kernels

When sampling a new random vector for displacement or dispersal, it is simplest to think in Cartesian coordinates: to draw the displacement as $(X,Y)$ where $X$ and $Y$ are independent draws from some distribution. This works well if $X$ and $Y$ are Gaussian, but plotting the resulting bivariate distribution quickly shows oddities: dispersers will tend to fall on either around the axes or around the diagonals, depending on the distribution chosen. In fact, displacements in orthogonal directions are independent only for the Gaussian distribution. To obtain a rotationally symmetric dispersal kernel, it helps to think in polar/spherical coordinates. This also brings up an issue of terminology: what do we call a given rotationally symmetric bivariate distribution? Natural choices are to name it after the shape of either (a) the profile, $X$, or (b) the distance, $R=\sqrt{X^2+Y^2}$. These agree only in one dimension. We work through some examples below to make the underlying issues clear.

Gaussian (and Rayleigh)

Imagine displacements along the $x$ and $y$ axes are sampled from the same Normal distribution with zero mean and variance of ${\sigma }^2$. The displacement in $x$, $y$ then has the multivariate normal density

$$p\left(x,y\right)=\frac{1}{2\pi {\sigma }^2}\exp \left(-\frac{x^2+y^2}{2{\sigma }^2}\right).$$

In polar coordinates,

$$p(r,\theta )=\frac{1}{2\pi {\sigma }^2}\mathrm{e}\mathrm{x}\mathrm{p}\left(-\frac{r^2}{2{\sigma }^2}\right),$$

i.e., the density only depends on $r$, and so the kernel is radially symmetric.

To find the distribution of $R$, we can find the cumulative distribution, $\mathbb{P}(r<R)$, and differentiate. The CDF can be found by integrating $p(x,y)$ over rings of circumference $2\pi r$ and infinitesimal width of $dr$:

$$\mathbb{P}\{R<s\}=2\pi {\int }_0^{s}p(x,y)rdr,$$ (21)

$$={\int }_0^s\frac{r}{{\sigma }^2}\mathrm{e}\mathrm{x}\mathrm{p}\left(-\frac{r^2}{2{\sigma }^2}\right)dr$$ (22)

Thus, the PDF of $R$ is $p(r)=\frac{r}{{\sigma }^2}\mathrm{e}\mathrm{x}\mathrm{p}\left(-\frac{r^2}{2{\sigma }^2}\right)$, which is a Rayleigh distribution. In summary,

$$X,Y\sim N\left(0,{\sigma }^2\right)$$ (23)

is equivalent to

$$\theta \sim \mathrm{U}\mathrm{n}\mathrm{i}\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{m}(0,2\pi ),R\sim \text{Rayleigh}(\sigma )$$ (24)

By the same argument, in three dimensions the angular part would be uniformly distributed on the sphere, and $R$ has density proportional to $r^2\mathrm{e}\mathrm{x}\mathrm{p}\left(r^2/2{\sigma }^2\right)$.

Student’s

$t$ We can do something similar with the Student’s $t$ distribution, but it will be clear that we need to be careful with generalizing it to a higher dimension.

First, what is the Student’s $t$ distribution? In one dimension, it is the distribution with density

$$p(x)=\frac{\mathrm{\Gamma }\left(\frac{\nu +1}{2}\right)}{\sqrt{\nu \pi {\sigma }^2}\mathrm{\Gamma }\left(\frac{\nu }{2}\right)}{\left(1+\frac{x^2}{\nu {\sigma }^2}\right)}^{-(\nu +1)/2},$$ (25)

where $\nu$ is the “degrees of freedom” and $\sigma$ is a scale parameter. If $\nu =1$, it is a Cauchy distribution, and if $\nu \to \infty$, the distribution converges to a standard Normal distribution. The Student’s $t$ distribution is a heavy tailed distribution: all moments of order $\nu$ or higher are not defined.

Now suppose we want to “use the Student’s $t$” in two dimensions. A wrong way to do this is to sample $x$ and $y$ independently from the same $t$ distribution. If you do that, the joint distribution $p(x,y)$ is $p(x)p(y)$ due to independence, and it looks like

$$p\left(x,y\right)=\frac{\mathrm{\Gamma }{\left(\frac{\nu +1}{2}\right)}^2}{\nu \pi {\sigma }^2\mathrm{\Gamma }{\left(\frac{\nu }{2}\right)}^2}{\left(\left(1+\frac{x^2}{\nu {\sigma }^2}\right)\left(1+\frac{y^2}{\nu {\sigma }^2}\right)\right)}^{-(\nu +1)/2}.$$ (26)

If we plug in $x=r\mathrm{c}\mathrm{o}\mathrm{s}\theta$ and $y=r\mathrm{s}\mathrm{i}\mathrm{n}\theta$ as we did before with the Normal distribution, we realize that $p(x,y)$ depend on both $r$ and $\theta !$ In other words, the distribution of $R$ depends on the angle, $\theta$: long distances will be more common in some directions than others.

It turns out that although there are many ways to generalize the t distribution to more than one dimension, there is not a single standard way (Kotz and Nadarajah, 2004). Here are three possibilities for how we might choose a radially symmetric bivariate kernel $p(x,y)$:

1. The distribution of the distance, $R$, is Student’s $t$.

2. The distribution of the distance along an arbitrary axis, $X$, is Student’s $t$.

3. The shape of the kernel taken along a line through the origin is the Student’s $t$ density.

These conditions are, equivalently, that (1) $p(r,\theta )\propto r^{-1}{\left(1+r^2\right)}^{-(\nu +1)/2}$ (where $p(r,\theta )$ is $p(x,y)$ is radial coordinates); (2) $\int p(x,y)dy\propto {\left(1+x^2\right)}^{-(\nu +1)/2}$; and (3) $p(x,0)\propto {\left(1+x^2\right)}^{-(\nu +1)/2}$. If we chose the first option, then we’d be compelled to call the bivariate Gaussian the “bivariate Rayleigh” distribution, so for consistency with the Gaussian, we’ll discard that option. Although option (2) is perhaps more elegant, figuring out what the actual density is for an arbitrary kernel shape is more involved, so we have chosen to go with option (3) (both here and in SLiM).

So: to make a radially symmetric Student’s $t$ kernel, we’d like a bivariate kernel $p(x,y)$ proportional to $p\left(\sqrt{x^2+y^2}\right)$, where the second $p()$ is the univariate Student’s $t$. With the normalization factor, for $\nu >1$ this is

$$p(x,y)=\frac{(\nu -1)}{4\pi \nu {\sigma }^2}{\left(1+\frac{x^2+y^2}{\nu {\sigma }^2}\right)}^{-(\nu +1)/2}.$$ (27)

The density of $R$, the displacement distance, is equal to $2\pi rp(r,0)$.

$$p_R(r)\propto \frac{r}{\sigma }{\left(1+\frac{r^2}{\nu {\sigma }^2}\right)}^{-(\nu +1)/2}.$$ (28)

Note that if $\nu =1$ (i.e., the Cauchy distribution), the integral ${\int }_0^{\mathrm{\infty }}{p}_R(r)dr$ does not converge. This means $\nu =1$ gives an invalid probability distribution, and so in two dimensional space, the number of degrees of freedom should be greater than 1. (More generally, in $d$ dimensions we’ll need $\nu >d-1$.)

General kernels

To generalize this, begin with a univariate probability distribution with density $f(x)$. Then, we define another distribution for $r$ by $p_R(r)\propto r^{d-1}f(r)$ if in $d$ dimensions. This is equivalent in two dimensions to defining a joint distribution of $x,y$ by $p(x,y)=f\left(\sqrt{x^2+y^2}\right)$. To sample a random variable $(X,Y)$ in two dimension, we sample $R$ from $p_R(r)$, sample $\theta$ from the uniform distribution on $(0,2\pi )$, and set $X=R\mathrm{c}\mathrm{o}\mathrm{s}\theta$ and $Y=R\mathrm{s}\mathrm{i}\mathrm{n}\theta$. (More generally, we would choose the radial component to be uniform on the $d$-sphere; the easiest way to do that is to let $\left(X_1,\dots ,X_d\right)=R\left(Z_1,\dots ,Z_d\right)/\sqrt{Z_1^2+\cdots +Z_d^2}$, where $Z_1,\dots ,Z_d$ are independent standard Normal.) This is how the function pointDeviated() in SLiM returns a displaced locations from various rotationally symmetric kernel.

D.1. Sampling from kernels with a covariance matrix

The multivariate Normal is not necessarily rotationally symmetric: it allows a general covariance matrix; if the covariance matrix is not a multiple of the identity, then the contours of the density are ellipses, not circles. How might we introduce covariance matrices to multivariate dispersal? The most convenient way to do this is to use scale mixtures of Normals, i.e., just multiply a given multivariate Normal distribution (with some covariance matrix) by a random scaling, choosing the distribution of the random scaling appropriately. For instance, if we’d like a fat-tailed dispersal kernel whose level sets are ellipses rotated by an angle $\theta$ counterclockwise, we can write:

U = rgamma (1, NU /2, NU /2);
  dxprime = rnorm (1, 0, SD_X ) / sqrt (U);
  dyprime = rnorm (1, 0, SD_Y ) / sqrt (U);
pos = individual . spatialPosition + c( dxprime * cos ( THETA ) - dyprime * sin ( THETA ),
          dxprime * sin ( THETA ) + dyprime * cos ( THETA ));
if (p1. pointInBounds ( pos )) {
   offspring = subpop . addCrossed ( individual , mate );
   offspring . setSpatialPosition (pos);
}

Note that we use pointInBounds() to check boundary condition, and so the boundary is absorbing. Here we’ve generated a scale mixture of Normals, by dividing our (correlated) multivariate Gaussian by $\sqrt{U}$, where $U$ is Gamma $(\nu /2,\nu /2)$ distributed. This is in fact another (and arguably better) common definition of the “multivariate Student’s $t$” (Kotz and Nadarajah, 2004).

Appendix E. Additional methodological details for case studies

E.1. Temporal change: pikas

For computational efficiency, we focus on a 266 km² region of Rocky Mountain National Park (RMNP) in Colorado. This is a consequential choice: by simulating a restricted area of the species range, we could for example overestimate the probability of extinction by missing larger spatial scale population dynamics. In addition, the resulting genetic variation will certainly be affected by modeling a smaller, narrowly distributed population.

To regulate the population we at first aim for a uniform density of 250 individuals per km² throughout the habitat. This value is informed by the number of pika scat piles observed by Erb et al. (2014) in sites in the Rocky Mountains. For the expected lifetime we use 3.25 years, as reported by Smith (1974). Thus, we set $K=250$ and fecundity equal to $\frac{1}{3.25}$.

We did not find a published value for competitive interaction distance for pikas, nor for mating distance. Therefore, we decided to use the same value for the spatial scales of competition, parent-offspring dispersal, and mating (i.e., ${\sigma }_I={\sigma }_D={\sigma }_M)$. Our assumption will introduce error if the competitive interaction scale in pikas is different than the dispersal scale, or if the mating scale varies from the other two values, which are both likely to be true. There is no adult movement in the pika model.

This simplifying assumption might be accurate, as pikas are territorial (Smith, 1974). To choose a value for ${\sigma }_X$ (and the other, shared interaction scales) we use as a starting point the value of 300 m from Smith (1974) which was the maximum reported distance traveled by juveniles. Assuming that parent-offspring dispersal is Gaussian distributed in each dimension, we calculated a ${\sigma }_X$ such that three standard deviations from the mean, Euclidean distance is $300=\sqrt{\frac{\pi }{2}}{\sigma }_X+3\sqrt{\left(2-\frac{\pi }{2}\right)}{\sigma }_X$ (using formulas for mean and standard deviation of the Rayleigh distribution).

E.2. Complex life cycles: mosquitoes

In our model of mosquitoes, we assume that only the juveniles’ viability is affected by local density, while adult population size is regulated only through a constant mortality. Due to this detail, if we want to control the juvenile density to match carrying capacity, we need to modify the density control function (such as Beverton–Holt model) to reflect the life cycle.

To start our derivation, let’s say density of juveniles with age $i$ is $a_i$ with $i=1,\dots ,m-1$ where $m$ is maturation age. Let’s also define density of adults as $a_m$. The adults have a fixed survival probability, $1-{\mu }_a$. We use a variation of Beverton–Holt model where survival probability of juvenile population is a local population density factor, $\frac{1}{1+\rho u}$, multiplied by the baseline survival probability $1-{\mu }_j$, where ${\mu }_j$ is the baseline mortality of juveniles. (here $u$ is population density of juveniles, i.e., ${\sum }_{i=1}^{m-1}{a}_i)$. Our goal is to find $\rho$.

Then we get a system of $m$ equations for $\mathbf{a}$ (left-hand-side is the $a$ in the next time step, but there is no time dependence by definition of equilibrium.):

$$a_1=\frac{a_{m}FEC/2\cdot \left(1-{\mu }_j\right)}{1+\rho \left(\sum _{i=1}^{m-1}{a}_i+FEC/2\cdot a_m\right)}$$ (29)

$$a_k=\frac{a_{k-1}\left(1-{\mu }_j\right)}{1+\rho \left(\sum _{i=1}^{m-1}{a}_i+FEC/2\cdot a_m\right)}$$ (30)

$$a_m=\frac{a_{m-1}\left(1-{\mu }_j\right)}{1+\rho \left(\sum _{i=1}^{m-1}{a}_i+FEC/2\cdot a_m\right)}+a_m\left(1-{\mu }_a\right),$$ (31)

where $k=2,...,m-1$. Notice that we have a factor of 2 for fecundity, FEC, because only female adults (assumed to be half of total adult population) produces FEC new individuals. $\rho$ controls where the equilibrium density is for juveniles, and it is an unknown for now. We want $\rho$ to make $\sum a_{i=1}^{m-1}=K$, where $K$ is carrying capacity of larvae.

Due to recursive relation between $a_i$ ‘s, we can simplify the system of $m+1$ equations for $m+1$ unknowns $(a_i$ ‘s and $\rho )$ to two equations with two unknowns, $a_m$ and $\rho$.

To make it a little clear, let’s define,

$$r\equiv \frac{1-{\mu }_j}{1+\rho \left(\sum _{i=1}^{m-1}{a}_i+FEC/2\cdot a_m\right)}=\frac{1-{\mu }_j}{1+\rho \left(K+FEC/2\cdot a_m\right)}$$ (32)

Now we start from the first equation of $a_1$,

$$a_1=a_{m}FEC/2\cdot r$$ (33)

and plug it into the next one to find $a_2$.

$$a_2=a_{m}FEC/2\cdot r^2$$ (34)

and keep going to $a_{m-1}$. We see that $a_i=a_{m}FEC/2\cdot r^m$, a nice geometric series. (This makes sense because we tend to see exponential distributed age-structure in simulations.) This is nice because the sum can be simplified very nicely

$$\sum _{i=1}^{m-1}{a}_i=a_m\cdot FEC/2\cdot r\cdot \frac{1-r^{m-1}}{1-r}=K.$$ (35)

This is one of two equations we will need. The second one comes from plugging in $a_{m-1}$ to the original equation for $a_m$.

$$a_m=a_m\left(1-{\mu }_a\right)+a_{m}FEC/2\cdot r^m.$$ (36)

Dividing both sides by $a_m$, and rearranging terms, we get

$$r={\left(\frac{{\mu }_a}{FEC/2}\right)}^{1/m}.$$ (37)

Plugging this into the first equation, we get $a_m$! And we can find $\rho$ by plugging it into the equation we used to define $r$. Finally, we get $a_m$ and $\rho$ as a function of $a_m$ that we have in our simulation model:

$$a_m=K\frac{1-{\left(\frac{{\mu }_a}{FEC/2}\right)}^{1/m}}{1-{\left(\frac{{\mu }_a}{FEC/2}\right)}^{1-1/m}}\cdot {\mu }_a^{-1/m}(FEC/2{)}^{1-1/m}$$ (38)

$$\rho =\frac{\frac{\left(1-{\mu }_j\right)(FEC/2{)}^{1/m}}{{\mu }_a^{1/m}}-1}{K+a_m\cdot FEC/2}$$ (39)

In Figure S12 we compare the expected adults to juveniles ratio from the equation above to the simulated value. Even though we didn’t consider other factors like spatial aspects (finding mates, migrations, heterogeneity of the river map) and seasonal fluctuation, the simulated ratio stay pretty close to theoretical expectation. In addition, I also plot the average local population density that juveniles measure around themselves through an interaction kernel with width $SX=20.0$ in Figure S13. The density closely follows the rain factor which is a sinusoidal function added everywhere on the map to set the baseline carrying capacity, except for when the rain factor is close to zero. During the “dry season”, we see increase of density because we programmed the adult females to disperse offspring to the locations where carrying capacity is high within the maximum dispersal distance.

E.3. Continental-scale systems: cane toads

Note that there has already been considerable effort to simulate the Australian cane toad invasion (Kearney et al., 2008), including simulations that incorporate genetic information to infer many biological parameters (Estoup et al., 2010).

Toads were simulated to have a juvenile state of 1 year. Individuals that were at least one year old were allowed to disperse once each year over their entire lifetime. Toads were randomly assigned to be male or female. Offspring initial locations were set to their mother’s locations.

Previous studies have shown that the spread rate and distribution of cane toads has been influenced by environmental heterogeneity (Urban et al., 2008). We initially used a homogeneous landscape to model the cane toad invasion, which resulted in glaring discrepancies between the simulated and observed distributions. In efforts to increase the likeness of simulated distributions to the observed data, we incorporated environmental heterogeneity across space.

The kernels controlling competition and mate choice were kept as Gaussians.

The pipeline for downloading the complete data is available (https://github.com/kr-colab/spatial_sims/blob/main/silas/range_expansion/pipelines/get_data.smk), and is described here briefly. We downloaded cane toad occurrence data was from the Global Biodiversity Information Facility (https://doi.org/10.15468/dl.8pukaa), bioclimatic variables from WorldClim (https://www.worldclim.org/data/bioclim.html (Fick and Hijmans, 2017)), and a shapefile for the geographic perimeter of Australia from the Australian Bureau of Statistics (https://www.abs.gov.au/). We converted the locations from latitude and longitude values to km using using GeoPandas (Jordahl et al., 2020) (see notebook/vignette for further details), and set the origin of the map to the earliest location in the occurrence data.

Extensions

Our approach could be extended to use multiple environmental maps along with a multivariate fitness function over each environmental dimension.

If desired, the simulations could be extended to include the ability to use and compare genetic information between observed and simulated data. SLiM’s ability to model explicit genomes could also allow for more complexity and realism, such as a heritable component for dispersal ability to model assortative mating for dispersal ability, as well as gene surfing, where deleterious alleles are maintained at the range edge (Miller et al., 2020; Shine et al., 2021). Additional complexity could be incorporated into the life history traits as well. For example, cannibalism has been observed in cane toads (DeVore et al., 2021). This and other modifications could be made related to changes age related competition, fecundity, mortality, and establishment.

E.4. Resource competition: monarchs

The milkweed is only minimally simulated within this model. A number of patch centroids are randomly spread across an area of the model, and a number of milkweed plants are scattered around each centroid according to a Gaussian distribution. During each year of the model, after the monarchs have migrated south for the winter, the locations of the patch centroids and plants are re-randomized.

Appendix F. Map-based approximations to density

In this section, we provide a formal argument showing that the approximation scheme of Box 8 converges to the local density for a fine enough grid. Conceptually, this works because the approximation effectively computes density as if all points were at the node of the region they are in. Since all the regions are small, this does not change things much. The argument applies to a “resource node” scheme as well, as long as the nodes are sufficiently dense.

Suppose that the positions of individuals on the landscape are recorded as a collection of points ${\left\{x_i\right\}}_{i=1}^N$. It will be helpful for notation to represent the state of the population as a point measure, $\mathrm{\Lambda }={\sum }_i{\delta }_{x_i}$. For simplicity in this section, suppose that distances are measured in units of the interaction scale, i.e., ${\sigma }_X=1$. The density we would like to compute from equation (1) is then

$$n(x)=\sum _i\rho \left(x-x_i\right),$$

the convolution of $\mathrm{\Lambda }$ with the kernel $\rho$. Now suppose that we placed a discrete set of nodes on the landscape at locations $\left\{y_j\right\}$, and for each $j$ let $A_j$ denote the portion of space that is closer to $y_j$ than to any other node. In other words, $\left\{A_j\right\}$ is the Voronoi tesselation associated with $\left\{y_j\right\}$; and suppose we assign the boundaries between regions in some sensible way. Suppose that the diameters of all $A_j$ are less than; we will show that using these nodes we can approximate $n(x)$ well to within an error that is proportional – so, finer meshes of nodes will make better approximations.

Suppose that we’re evaluating density at the location of node $y_j$. The approximation outlined in Box 8 seeks to approximate $n\left(y_j\right)$ by

$$\hat{n}\left(y_j\right)=\sum _k\rho \left(y_j-y_k\right)\mathrm{\Lambda }\left(A_k\right),$$

where $\mathrm{\Lambda }\left(A_k\right)$ is the number of individuals within the region $A_k$, which we may write as $\mathrm{\Lambda }\left(A_k\right)={\sum }_i{1}_{A_k}\left(x_i\right)$. So, we can write

$$\begin{array}{l}n(y_j)-\widehat{n}(y_j)=\sum _i(\rho (y_j-x_i)-\sum _k\rho (y_j-y_k)1_{A_k}(x_i))\\ =\sum _k\sum _{i:x_i\in A_k}(\rho (y_j-x_i)-\rho (y_j-y_k)).\end{array}$$ (40)

Now note that by the intermediate value theorem and the fundamental theorem of calculus,

$$\rho \left(y_j-x\right)-\rho \left(y_j-y_k\right)=\left(x-y_k\right){\rho }^{\prime }\left(y_j-y_k+\alpha \left(y_k-x\right)\right)$$

for some $0\le \alpha \le 1$. Now, $\rho (x)\to 0$ as $x\to \mathrm{\infty }$, so for any $\delta$ we may pick $R$ so that

$${\int }_{\left|x-y_j\right|>R-ϵ}{\rho }^{\prime }(x)dx<1/N.$$

Write $N_R=\#\left\{i:\left|x_i-y_j\right|\le R\right\}$ for the number of points closer than $R$. Furthermore, suppose the derivative of $\rho$ is bounded above by $C$, i.e., $∥{\rho }^{\prime }(x)∥\le C$. If $\left|x-y_k\right|\le ϵ$, then

$$\left|\rho \left(y_j-x\right)-\rho \left(y_j-y_k\right)\right|\le ϵC.$$

Since for $x_i\in A_k$, by definition $\left|x_i-y_k\right|\le ϵ$, plugging this into equation (40), and splitting the sum into regions with nodes further than $R$ away and from $y_j$ and not,

$$\left|n\left(y_j\right)-\hat{n}\left(y_j\right)\right|\le ϵ\left(1+C{N}_R\right).$$

Since $C$ and $N_R$ are fixed, this goes to zero as $ϵ\to 0$. This shows that $n\left(y_j\right)\approx \hat{n}\left(y_j\right)$; since $\hat{n}(x)$ is defined for arbitrary $x$ by interpolation, $n(x)\approx \hat{n}(x)$ as well.

Data availability

SLiM scripts suitable for re-use of all simulations used in this paper are at https://github.com/kr-colab/spatial_sims_standard (for SLiM v4.2 Haller and Messer, 2023). Scripts to produce the figures in this manuscript are available at at https://github.com/kr-colab/spatial_sims.