Abstract
Through the previously reported the quantum-identity, the light-model, and the T(temperature)S(entropy) energy, the implied meaning of temperature and entropy, respectively, which it was difficult to intuitively recognize, was clearly defined. In order to minimize possible errors at this time, the interrelationship of the SI base unit, which is the smallest unit, and the T(temperature)S(entropy) unit integration was used. In the process of converting to Planck units, each unit (criterion) for entropy and temperature was calculated, and their physical and chemical meanings were compared and reinterpreted. Thus, the unit of entropy is related to the Boltzmann constant, and the temperature is the oscillation of pure mass units. Therefore, the intuitive recognition of physical and chemical factors based on the unit of meter(m)-time(s) is considered sufficient as an initiator to move closer to new science beyond the current limited application.
Subject terms: Chemistry, Physics
Introduction
To develop an objective and quantitative understanding of physicochemical concepts, it is necessary to consistently use the same dimensions as fundamental units.
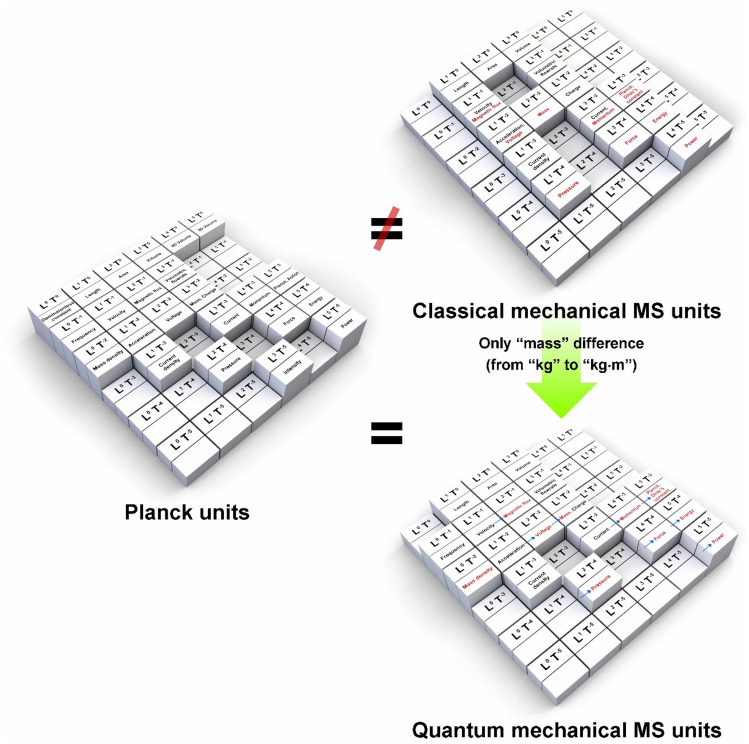
Recent works have taken steps in this direction by considering the base units of the SI system (which are in m, kg, s, A, K, mol, and cd)1 as the fundamental criteria and using this to reinterpret quantum mechanics, which has traditionally been viewed via probabilistic models, through the perspective of classical mechanics, which has been studied using a deterministic approach2–6. To arrive at a clear, objective understanding of what causes the difference between classical and quantum mechanics, differences between the concepts of mass in the bulk and quantum states were studied (Fig. 1). The nature of bulk mass is completely unaffected by its surroundings (Fig. 1a), while quantum mass is affected by an external sphere of influence (Fig. 1b–e), whose effect mimics that of a Lorentz force (represented by = q( + × , where , q, , , and are the Lorentz force, electric charge, electric field, velocity of the charged particle, and magnetic field, respectively)7 (Fig. 1d,e). Therefore, if the difference of external influences on the mass of quantum particles is accounted for, the concept of mass in classical and quantum mechanics, when expressed in metre-second (MS) units, matched exactly without any errors6 (Fig. 2).
Figure 1.
Comparison of the concept of mass from the perspectives of classical and quantum mechanics: (a) In classical mechanics, there is hardly any region outside of a mass that affects it. (b–e) In quantum mechanics, the electromagnetic fields resulting from a given mass exert an external sphere of influence over it like the Lorentz force. Mass in classical and quantum mechanics is intuitively distinguished by the presence or absence of these regions. When these factors are corrected, the two concepts can be unified.
Figure 2.
Planck's unit conversion table showing the process of equalization when the mass “kg (m2/s2)” in classical mechanics is considered as the “mass (m⋅kg)” in quantum mechanics.
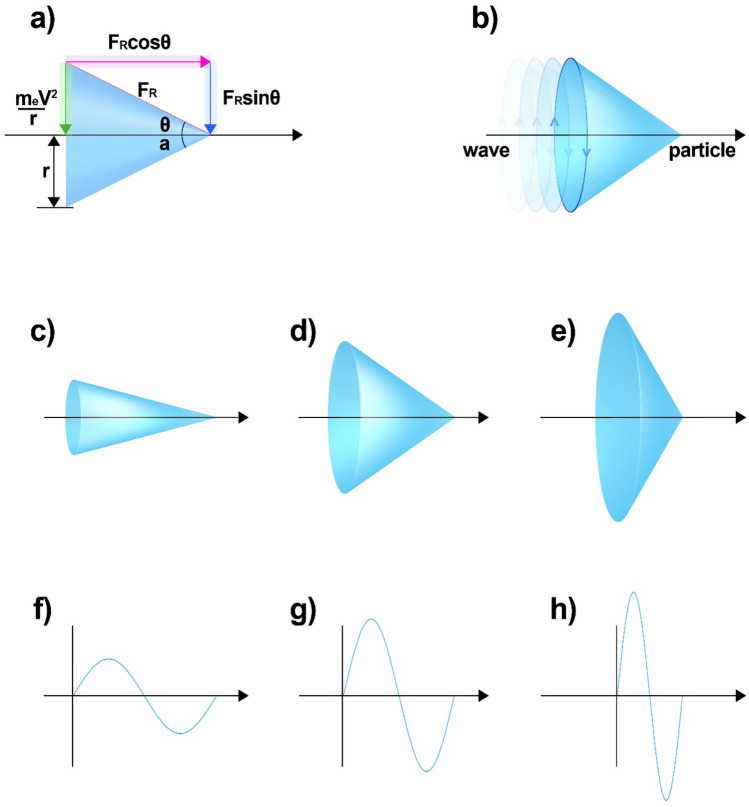
Extending the necessity to have the same dimensions as the fundamental units, a cone-shaped unit of light was proposed to explain the duality (i.e., that attribute by which it simultaneously exhibits the properties of both particles and waves8–13) of light14 (Fig. 3a). The motion of this cone has two components: linear motion at the velocity of light along the direction of its propagation, which is characteristic of particles, and circular motion in the transverse direction at a speed below the velocity of light, which is indicative of wave nature (Fig. 3b). As the energy of the rear portion of the wave gradually increases with its rotational speed, the apex angle of the cone gradually increases (Fig. 3c–e). Its wavelength is long at low rotational velocities and shortens as the rotational velocity increases and approaches the velocity of light (Fig. 3f–h). However, regardless of the difference between these wavelengths, all of these units exhibit mass properties like dots (photons)15 at the front, and periodic properties like a certain area at the rear of the unit (Supplementary Information (SI.), Note S1).
Figure 3.
Conical units of light, exhibiting both mass and wave properties. (a) Parameters of the light unit and their relationship. (b) A typical light unit that, with propagation, exhibits properties of mass at its front and waves at its rear. (c–e) Changes in the magnitude and apex angle of light units with increase in energy. (f–h) Variations in wavelength with increase in energy.
While several scientific phenomena (such as quantum reality and the duality of light) have been sufficiently explained with empirical evidence, there do exist other quantities—such as temperature16,17 and entropy18–21—whose identities are still ambiguous because their dimensions are yet to be clearly defined. Since these two quantities are not uniquely represented by a physical entity, they are usually studied indirectly in terms of the relative energy change before and after a chemical reaction, expressed as the product of temperature (T) and entropy (S)22–25. We have already reported in a previous study26 that depicting energy in terms of TS can create a mismatch between the rates of change of temperature and entropy, leading to a possible hysteresis of these quantities creating an unbalanced, unstable state. However, since it is still difficult to wholly conceptualise temperature and entropy, there exists a limit to accurately grasping the identity of each factor and effectively utilising it.
Therefore, in this study, we attempt to further our intuitive understanding of temperature and entropy by reporting a process in which they are expressed in m2/s3 and m3/s, respectively, in the Planck system of units27. In this process, we also aim to demonstrate that the unit of temperature (K), expressed separately in the base SI unit, can be integrated into the MS system and that the smallest unit of entropy is the Boltzmann constant. While these approaches might, at first glance, seem completely different from existing ones (our suggestions6,14 that both classical and quantum mechanics, much like the particle and wave nature of light, are one and the same), they are a bottom-up approach to presenting a unified dimension28. It is clearly distinguished from existing top-down methods29 that analyse the original cause from experimental results or natural phenomena. In other words, since the dimensions are clearly presented beforehand and their mutual relationship explains the phenomenon in question, the bottom-up method has the advantage of presenting a one-to-one relationship between cause and effect. However, top-down methods present a one-to-many correspondence since multiple microscopic causes could produce the same result. Therefore, this study is an attempt to uncover the identities of temperature and entropy by relating theories that try to find the physicochemical dimensions, forming a larger and more detailed framework. Conversely, this large framework provided a boundary that prevented the occurrence of scientific errors in each theory. This double-checking gives reason to expect a more objective and efficient identification of temperature and entropy.
Results and discussions
Classification into mass and periodic motions
To arrive at a clear and insightful physicochemical interpretation of the varied complex movements and phenomena observed in nature, a simplification that retains only the most relevant features (while boldly removing the rest) is required. Therefore, we will only consider those concepts that inspired the advent of the fields of classical and quantum mechanics—mass and periodic motion. In addition, all types of motion can be expressed as a combination of linear and rotational motions, which characterise mass and periodic motion, respectively. The light unit14, capable of both linear and rotational motion, is an excellent example of this. Moreover, in a previous study that reveals the identity of quantum6, we have reported classical and quantum mechanics to be integrated concepts that are not separate from each other. From a dimensional perspective, this means that the mass expressed in classical mechanics (like in the mass-energy equivalence of Einstein’s theory of relativity, quantified by E = mc2, where E, m, and c are the energy and mass of a particle and the velocity of light, respectively)30 also has a period, while the waves expressed in quantum mechanics (like in the equation E = , where E, c, λ, and h, are the energy, velocity, and wavelength of light and the Planck constant, respectively)31 can also be expressed in units of mass. Therefore, mass and wave periods are reasonable and accessible dimensions for the analysis of unknown phenomena.
To prove the mass-wave equivalence (which, by extension, translates to an equivalence between classical and quantum mechanics), we started with the assumption that the formation of a unit of mass can be traced to a biaxial revolution of a quantum particle at the velocity of light; the physical and chemical identicality6 of the meanings of the unit conversion for the Planck unit system27 is proof of the validity of this assumption. This means that in the equation E = mc2, “c2” represents the unit of mass, while “m” denotes the numerical quantity of these units. This enables a more intuitive understanding of temperature and entropy by converting their dimensions into the MS units corresponding to the Planck measurement system in a way that matches their physicochemical significance. This is simplified to retain only linear and rotational motion and, on further analysis, becomes a process of investigating which factors will remain and what significance they have when progressively evaluated till its root cause at the quantum level.
Visualising the quantum states of a proton and an electron
Like the previous report on quantum particles6, the initial factor causing the unit of mass formed from the revolution of two different axes, determined to be the velocity of light, as shown in Fig. 4, was derived through the following sequential steps.
Figure 4.
Sequence of steps representing the derivation of the Boltzmann constant as a unit of entropy: (a) pure mass formed by biaxial revolution, (b) movement after removing the revolution around one of the two axes, (c) movement of one rotation during repeated revolutions, (d) visualisation of a proton as the quantum particle, (e) quantity of charge on a proton, (f) rotations involved in a single revolution, (g) movement of one rotation during repetitive rotation, (h) physical significance of considering an electron, (i) Boltzmann constant and its magnitude.
First, as shown in Eqs. (1)–(2), the first-order partial derivative of energy with respect to the velocity of light eliminates revolution along one of the two axes (Fig. 4a,b).
| 1 |
| 2 |
However, periodic revolution is still retained along the other axis. Therefore, to obtain information corresponding to the period of a single revolution, Eq. (2) is divided by the frequency (f1) as shown in Eq. (3) below (Fig. 4c):
| 3 |
Since the frequency at this point does not represent any fixed value, it should be replaced with the number of protonic rotations (nf1) that exist in the corresponding time period. Directly substituting the mass of a proton32 in Eq. (3) yields Eq. (4). At this point, if the final calculated value of () is substituted by αcv, then the frequency can always be erased along with the number of rotations to yield a constant value of as shown in Eq. (5), regardless of the value of nf1. Interestingly, this coincides with the magnitude of electric charge (C) of a single proton; its units, expressed in terms of “m⋅kg”, can be considered to signify the effect (m) of one electric charge (kg) on its surroundings (Fig. 4d,e).
| 4 |
| 5 |
From our first assumption (kg ≡ m2/s2), Eq. (5) can be finally expressed in MS units as:
| 6 |
Substituting the mass of the proton with that of the electron33 makes for a considerable departure from Eqs. (3)–(6). This is because in the case of electrons (Fig. 4f), the rotational motion corresponding to spin34,35 must also be considered, which was not required while substituting for the mass of a proton. Therefore, Eq. (3) must be divided once more by the frequency (f2) as shown in Eq. (7) below (Fig. 4g). In other words, since the number of rotations is already included in Eq. (5) when considering the proton, it is sufficient to additionally account only for electronic frequency (f2) when considering electrons. However, like in Eqs. (4)–(6), the frequency in this case does not represent a fixed value; therefore, it is replaced with the number of electronic rotations (nf2) during the corresponding time period. Directly substituting the mass of the electron33 in place of m in Eq. (7), at this point, if the final calculated value () is substituted with , then the frequency can always be erased along with the number of rotations to yield a constant value as shown in Eq. (8), regardless of the value of nf2.
| 7 |
| 8 |
As above, substituting our assumption (kg ≡ m2/s2) into Eq. (8), it can finally be expressed in terms of MS units, as shown in Eq. (9) (Fig. 4h):
| 9 |
Just as the value calculated from the mass of the proton is numerically equal to the charge on the proton, the value calculated above from the mass and spin of the electron is numerically equal to the Boltzmann constant36 (Fig. 4i). The final result here can be said to be the state of a pure electronic unit in which electrons rotate only once, and this is the meaning of the Boltzmann constant. Although exactly, is only the same magnitude, the meaning can be approximated based on the Planck unit conversion25. Since the Boltzmann constant has the same dimensions as the volumetric flow rate6, it is estimated to be about the smallest unit of electromagnetic wave (light with almost linear motion and almost no wavelength)37 that can flow per unit time.
Significance of the Boltzmann constant
Since we approximated the Boltzmann constant as a form of “light with almost linear motion and no wavelength”, it has to be verified to determine its applicability elsewhere. Therefore, its consistency was examined when applied to a light model14 that includes the behaviour of electromagnetic waves. For this, a model featuring a cone-shaped unit of light that embodies all of the duality of light—with a mass corresponding to a particle at its front and a period corresponding to a rotation at its rear—was first proposed (Fig. 3b). The energy corresponding to each part of this unit can be visualised as a cone-shaped structure (Fig. 3a) and quantified as shown in Eq. (10)14, where me and mp are the masses of an electron and a photon, respectively.
| 10 |
However, since electrons rotate in addition to their revolution, this model accounts for a state of motion in which the electrons simultaneously rotate and revolve (Fig. 4f). Additionally, light moves simultaneously in two directions (Fig. 5a)—one being that of its propagation, along which it reaches the velocity of light, and the other in the transverse direction, along which it does not reach the velocity of light (Fig. 5a,b)—with its energy accounting for the effect it has on its surroundings. If the unit movement along the transverse axis also attains the velocity of light, then it embodies mass (kg = c2 = m2/s2, where c, m, and s denote the velocity of light and the units of metre and second, respectively) (Fig. 5c).
Figure 5.
Various cases where the Boltzmann constant was applied as an electromagnetic wave unit to the model of light: (a) a typical model of light rotating along two axes, of which only one reaches the velocity of light, (b) the model of light when the velocity of rotation along the other axis also approaches that of light, (c) mass unit formed when rotation along both axes reaches the velocity of light, (d) typical wavelength in a general light model such as (a), (e) wavelength on one of the axes approaching the velocity of light, (f) wavelength when the velocity of the other axis increases, (g) wavelength at which the velocity of the other axis nearly reaches the speed of light, (h) mass unit formed by c2 as in (c).
When this process is described sequentially, the steps are as follows.
First, the wavelength is represented as displayed in Fig. 5d. The shorter the wavelength, the shorter the distance travelled by the wave (as shown in Fig. 5f), and the denser it becomes. Therefore, when the wavelength reaches its limiting value as the velocity of the wave approaches that of light, it can be regarded as an area (Fig. 5e,g). At this point, Fig. 5e is the velocity of light from the beginning in the horizontal direction of light, whereas Fig. 5g depicts a scenario where the velocity of the wave has not yet reached that of light; Fig. 5a,b, on the other hand, depict cases where it gradually increases to approach that limit in the transverse direction. Therefore, when the revolution of the particle around both axes has completely reached the velocity of light, the mass is made up of a closed curve, as shown in Fig. 5h.
However, the electrons that make up light simultaneously revolve in a screw-like motion (representative of its electrical properties) along the direction of propagation of light and rotate in a spin-like motion (representative of its magnetic properties) in the transverse direction38–40. Therefore, it is believed that the rotation and revolution of an electron are representative of its electrical and magnetic properties; however, since these two motions occur simultaneously, electricity and magnetism, too, are concurrent phenomena and can be treated as a unified electromagnetic phenomenon.
As already mentioned above, we were able to deduce the exact magnitude of the Boltzmann constant (in units of m3/s) while considering the dual influence of electronic rotation and revolution. This implies that after conversion to the Planck system of unit27, the entropy (J/K) can be expressed in terms of m3/s. Therefore, if the concept of entropy is applied to the light model, an increase in entropy can be inferred from a corresponding increase in the number of Boltzmann constants or in the rotation of the rear part of the light unit.
Geometric significance of temperature
Even though the complete meaning of the currently existing concept of temperature cannot be accurately grasped, we can express it in MS by the Planck unit conversion27. As mentioned in our previous report26, there exists the possibility of temperature (T) and entropy (S) being related to each other by means of a hysteresis loop, specifically in terms of energy expressed as TS—in order to increase energy, only either one (but not both) of T or S may be increased at a given time. However, since the identity of S is not clear, there has been little use for it, due to which it has been common to increase the phenomenologically detectable T41–43 alone in most cases.
This means that in the relationship of E = TS, when energy (E, in units of m5/s4) is divided by entropy (m3/s), temperature can be expressed as m2/s3, as shown in Eq. (11) below:
| 11 |
While the equivalent extended MS system of units (Fig. 6)6 assigns temperature with the same dimensions as magnetic field strength and dynamic viscosity, it is still difficult to recognise the intuitive concept of temperature. To make it easier, as shown in Eq. (12) below, the MS unit needs to be considered by dividing it into its constituents of pure mass (in terms of kg ≡ m2/s2)—i.e., mass without any external influence, as shown in SI, Fig. S1a—and frequency.
| 12 |
Figure 6.
Extended MS unit system including various physical meanings.
Equation (12) can be regarded as a representation of a unit of mass vibrating and propagating around (SI, Fig. S1b). Thus, the temperature indicates when a unit of mass begins to vibrate, and any increase in temperature means that these vibrations go correspondingly farther (SI, Fig. S1c).
This geometric perspective seems to dovetail well with established concepts, meaning that our proposed approach to identify quantum particles, light, and TS energy is very likely to be a fundamental principle rather than a long shot. Therefore, by intuitively recognising these principles, we have successfully presented a basis to further expand the range of applications of temperature and entropy.
Conclusions
Established scientific concepts of temperature and entropy are not wholly clear, due to which these quantities are often approached only in terms of their definition. In order to develop an intuitive understanding of these quantities, we proposed in this paper an approach involving the fundamental units and their relationships. To this end, we borrowed the physicochemical meanings of previously reported models of quantum particles and light to demonstrate that the unit of entropy was equivalent to the smallest electromagnetic wave (m3/s) resulting from the rotation and revolution of electrons; the result was, interestingly, in exact agreement with the Boltzmann constant. In addition, temperature could be clearly recognised as the vibrations of pure mass (m2/s2). Therefore, our interpretations of temperature and entropy are likely to facilitate not only a more thorough understanding of the concepts, but also a more robust design of related engineering applications.
Supplementary Information
Acknowledgements
This research was supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (RS-2023-00243422 and NRF-2019R1A6A1A11055660). This study has been conducted with the support of the Korea Institute of Industrial Technology as "Development of precision multi-layer direct bonding process using semiconductor tray(1/1)(kitech JF-24-0090)". We are grateful to Jiye Kim and Baro Jin for their cordiality and hospitality during the course of this research.
Author contributions
Han Gil Na: Conceptualization, Investigation, Visualization, Data curation, Methodology Sangwoo Kim: Investigation, Visualization, Data curation, Supervision, Project administration, Methodology Changhyun Jin: Conceptualization, Investigation, Visualization, Data curation, Supervision, Project administration, Methodology, Writing—original draft, Writing—review and editing.
Data availability
All the data are available from the corresponding author on reasonable request.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
These authors contributed equally: Han Gil Na and Sangwoo Kim.
Supplementary Information
The online version contains supplementary material available at 10.1038/s41598-024-68673-4.
References
- 1.Gobel, E., Mills, I. M. & Wallard, A. J. The International System of Units (SI) (International Bureau of Weights and Measures, 2006). [Google Scholar]
- 2.Norsen, T. Foundations of Quantum Mechanics (Springer, 2017). [Google Scholar]
- 3.Laloë, F. Do We Really Understand Quantum Mechanics? (Cambridge University Press, 2019). [Google Scholar]
- 4.Benacquista, M. J. & Romano, J. D. Classical Mechanics (Springer, 2018). [Google Scholar]
- 5.Helliwell, T. M. & Sahakian, V. V. Modern Classical Mechanics (Cambridge University Press, 2020). [Google Scholar]
- 6.Jin, C. Intuitive distinction between classical mechanics and quantum mechanics separated from the perspective of SI base units. MRS Commun.13, 507 (2023). 10.1557/s43579-023-00370-1 [DOI] [Google Scholar]
- 7.Sawada, K. & Nagaosa, N. Optical magnetoelectric effect in multiferroic materials: Evidence for a Lorentz force acting on a ray of light. Phys. Rev. Lett.95, 237402 (2005). 10.1103/PhysRevLett.95.237402 [DOI] [PubMed] [Google Scholar]
- 8.Klevgard, P. A. Is the photon really a particle?. Optik237, 166679 (2021). 10.1016/j.ijleo.2021.166679 [DOI] [Google Scholar]
- 9.Ninno, G. D. et al. Photoelectric effect with a twist. Nat. Photonics14, 554 (2020). 10.1038/s41566-020-0669-y [DOI] [Google Scholar]
- 10.Dahan, R. et al. Resonant phase-matching between a light wave and a free-electron wavefunction. Nat. Phys.16, 1123 (2020). 10.1038/s41567-020-01042-w [DOI] [Google Scholar]
- 11.Inoue, T. et al. Resonance control of a graphene drum resonator in a nonlinear regime by a standing wave of light. ACS Omega2, 5792 (2017). 10.1021/acsomega.7b00699 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Constantin, M. Light and Vacuum: The Wave-Particle Nature of the Light and the Quantum Vacuum. Electromagnetic Theory and Quantum Electrodynamics Beyond the Standard Model (World Scientific, 2017). [Google Scholar]
- 13.Zhang, W. et al. Wave-particle superposition of distinct atomic spin excitations. Phys. Rev. A98, 063829 (2018). 10.1103/PhysRevA.98.063829 [DOI] [Google Scholar]
- 14.Na, H. G. & Jin, C. Mass-energy equivalence in wave–particle duality of light: Integrated quantum and classical mechanics. Optik188, 71–77 (2019). 10.1016/j.ijleo.2019.05.042 [DOI] [Google Scholar]
- 15.Roychoudhuri, C., Kracklauer, A. F. & Creath, K. The Nature of Light: What is a Photon? (CRC Press, 2017). [Google Scholar]
- 16.Lu, C. X. et al. Temperature effect on performance of triboelectric nanogenerator. Adv. Eng. Mater.19, 1700275 (2017). 10.1002/adem.201700275 [DOI] [Google Scholar]
- 17.Jung, H., Pham, T.-T. & Shin, E. W. Interactions between ZnO nanoparticles and amorphous g-C3N4 nanosheets in thermal formation of g-C3N4/ZnO composite materials: The annealing temperature effect. Appl. Surf. Sci.458, 369 (2018). 10.1016/j.apsusc.2018.07.048 [DOI] [Google Scholar]
- 18.Huang, E.-W. et al. Element effects on high-entropy alloy vacancy and heterogeneous lattice distortion subjected to quasi-equilibrium heating. Sci Rep.9, 14788 (2019). 10.1038/s41598-019-51297-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Chen, S. Y. et al. Phase transformations of HfNbTaTiZr high-entropy alloy at intermediate temperatures. Scr. Mater.158, 50 (2019). 10.1016/j.scriptamat.2018.08.032 [DOI] [Google Scholar]
- 20.Starikov, E. B. How many laws has thermodynamics? What is the sense of the entropy notion? Implications for molecular physical chemistry. Monatsh. Chemie Chem. Mon.152, 871 (2021). 10.1007/s00706-021-02803-w [DOI] [Google Scholar]
- 21.Engelbrektsson, N., Franzen, K. & Starikov, E. B. The basic features of thermodynamics. Monatsh. Chemie Chem. Mon.152, 1437 (2021). 10.1007/s00706-021-02837-0 [DOI] [Google Scholar]
- 22.Gaskell, D. R. Introduction to the Thermodynamics of Materials (CRC Press, 2008). [Google Scholar]
- 23.Bejan, A. Advanced Engineering Thermodynamics (Wiley, 2016). [Google Scholar]
- 24.Li, C.-H. et al. Synthesis, crystal structure and thermodynamic properties of a new praseodymium Schiff-base complex. Thermochim. Acta581, 118 (2014). 10.1016/j.tca.2014.02.021 [DOI] [Google Scholar]
- 25.Spera, D. Z. & Liebman, J. F. Paradigms and paradoxes: Hess’ law and the thermodynamic validity of Jolly’s method for estimating bond dissociation energies. Struct. Chem.29, 1589 (2018). 10.1007/s11224-018-1195-0 [DOI] [Google Scholar]
- 26.Na, H. G., Byoun, Y., Park, S., Choi, M. S. & Jin, C. Experimental study of superheating of tin powders. Sci. Rep.10, 19026 (2020). 10.1038/s41598-020-76223-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Petley, B. W. & Flowers, J. L. Planck, units, and modern metrology. Ann. Phys. Berlin17, 101–114 (2008). [Google Scholar]
- 28.Behroudj, A., Geiger, D. & Strehle, S. Epitaxial bottom-up growth of silicon nanowires on oxidized silicon by alloy-catalyzed gas-phase synthesis. Nano Lett.19, 7895 (2019). 10.1021/acs.nanolett.9b02950 [DOI] [PubMed] [Google Scholar]
- 29.Choi, J., Cho, K. & Kim, S. Flexible thermoelectric generators composed of n-and p-type silicon nanowires fabricated by top-down method. Adv. Energy Mater.7, 1602138 (2017). 10.1002/aenm.201602138 [DOI] [Google Scholar]
- 30.Okun, L. B. Energy and Mass in Relativity Theory (World Scientific Publishing Company, 2009). [Google Scholar]
- 31.Pontes, M. S. et al. In vitro and in vivo impact assessment of eco-designed CuO nanoparticles on non-target aquatic photoautotrophic organisms. J. Hazard. Mater.396, 122484 (2020). 10.1016/j.jhazmat.2020.122484 [DOI] [PubMed] [Google Scholar]
- 32.Taylor, B. N. & Mohr, P. J. The NIST Reference on Constants, Units, and Uncertainty (US National Institute of Standards and Technology, 2015). [Google Scholar]
- 33.Mohr, P. J., Newell, D. B. & Taylor, B. N. CODATA recommended values of the fundamental physical constants: 2014. Rev. Mod. Phys.88, 035009 (2016). 10.1103/RevModPhys.88.035009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Zajac, D. M. et al. Resonantly driven CNOT gate for electron spins. Science359, 439 (2018). 10.1126/science.aao5965 [DOI] [PubMed] [Google Scholar]
- 35.Borjans, F., Groot, X. G., Mi, X., Gullans, M. J. & Petta, J. R. Resonant microwave-mediated interactions between distant electron spins. Nature577, 195 (2020). 10.1038/s41586-019-1867-y [DOI] [PubMed] [Google Scholar]
- 36.Gaiser, C. et al. Final determination of the Boltzmann constant by dielectric-constant gas thermometry. Metrologia54, 280 (2017). 10.1088/1681-7575/aa62e3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Someda, C. G. Electromagnetic Waves (CRC Press, 2017). [Google Scholar]
- 38.Lv, G. et al. Synthesis of birnessite with adjustable electron spin magnetic moments for the degradation of tetracycline under microwave induction. Chem. Eng. J.326, 329 (2017). 10.1016/j.cej.2017.05.123 [DOI] [PubMed] [Google Scholar]
- 39.Liu, F. et al. Transfer channel of photoinduced holes on a TiO2 surface as revealed by solid-state nuclear magnetic resonance and electron spin resonance spectroscopy. J. Am. Chem. Soc.139, 10020 (2017). 10.1021/jacs.7b04877 [DOI] [PubMed] [Google Scholar]
- 40.Belykh, V. V., Yakovlev, D. R. & Bayer, M. Optical detection of electron spin dynamics driven by fast variations of a magnetic field: A simple method to measure T1, T2, and T2* in semiconductors. Sci. Rep.10, 13155 (2020). 10.1038/s41598-020-70036-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Mahdi, J. M., Lohrasbi, S. & Nsofor, E. C. Hybrid heat transfer enhancement for latent-heat thermal energy storage systems: A review. Int. J. Heat Mass Transf.137, 630 (2019). 10.1016/j.ijheatmasstransfer.2019.03.111 [DOI] [Google Scholar]
- 42.Khan, M. M. A. et al. Evaluation of solar collector designs with integrated latent heat thermal energy storage: A review. Sol. Energy166, 334 (2018). 10.1016/j.solener.2018.03.014 [DOI] [Google Scholar]
- 43.Zhang, N. et al. Latent heat thermal energy storage systems with solid–liquid phase change materials: A review. Adv. Eng. Mater.20, 1700753 (2018). 10.1002/adem.201700753 [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All the data are available from the corresponding author on reasonable request.