Extraordinary phase transition revealed in a van der Waals antiferromagnet

Abstract

While the surface-bulk correspondence has been ubiquitously shown in topological phases, the relationship between surface and bulk in Landau-like phases is much less explored. Theoretical investigations since 1970s for semi-infinite systems have predicted the possibility of the surface order emerging at a higher temperature than the bulk, clearly illustrating a counterintuitive situation and greatly enriching phase transitions. But experimental realizations of this prediction remain missing. Here, we demonstrate the higher-temperature surface and lower-temperature bulk phase transitions in CrSBr, a van der Waals (vdW) layered antiferromagnet. We leverage the surface sensitivity of electric dipole second harmonic generation (SHG) to resolve surface magnetism, the bulk nature of electric quadrupole SHG to probe bulk spin correlations, and their interference to capture the two magnetic domain states. Our density functional theory calculations show the suppression of ferromagnetic-antiferromagnetic competition at the surface is responsible for this enhanced surface magnetism. Our results not only show counterintuitive, richer phase transitions in vdW magnets, but also provide viable ways to enhance magnetism in their 2D form.

Surface magnetic order could precede bulk order, but detecting such a separation necessitates experimental probes sensitive to both surface and bulk phase transitions. Here, using second harmonic generation, the authors propose that this situation is realized in a van der Waals antiferromagnet CrSBr.

Introduction

Surfaces are always present in practical materials. Even in macroscopic materials, the presence of surfaces has the potential to enrich their phase diagrams of spontaneous symmetry breaking phases^1–4. Taking magnets as an example, in the temperature (T) versus surface-to-bulk relative exchange interaction ($J_{\mathrm{s}}/J_{\mathrm{b}}$) phase diagram shown in Fig. 1a, three distinct phase transitions were theoretically identified, namely “ordinary”, “surface”, and “extraordinary” transitions. The typical transition, where the surface and the bulk order simultaneously, is called “ordinary”, and the one when the surface orders, but the bulk does not, is a “surface” transition. The transition establishing the bulk order in the presence of the surface order is called “extraordinary”. The point where three different phases meet is a “special point”. In the “ordinary” case when $J_{\mathrm{s}}$ is much weaker than $J_{\mathrm{b}}$, the bulk order generates an effective field to induce a finite order at the surface, and thus the system undergoes only a single phase transition. Conversely, in the “surface” and “extraordinary” cases with $J_{\mathrm{s}}$ much greater than $J_{\mathrm{b}}$, the surface order cannot provide a notable effective field deep in the inner bulk, and thus, the bulk undergoes a separate “extraordinary” phase transition, leading to the split into two phase transitions.

Fig. 1. vdW materials are promising platforms for hosting surface and extraordinary phase transitions.

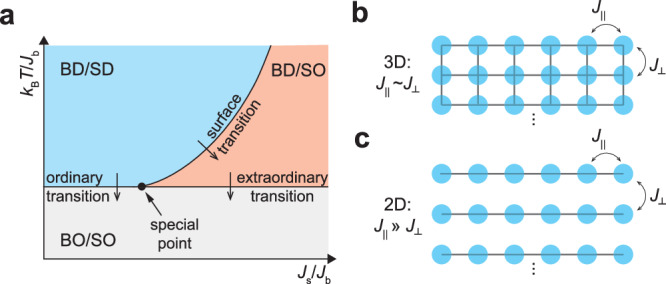
a phase diagram illustrating ordinary, surface and extraordinary phase transitions and the special point. BD bulk disordered, SD surface disordered, SO surface ordered, BO bulk ordered. J_s, mean-field surface interaction, J_b, mean-field bulk interaction. b, c illustrations of intralayer and interlayer interactions strengths, $J_{\parallel }$ and $J_{\perp }$, in b 3D ionic crystals and c quasi-2D van der Waals crystals.

Separation of an ordinary phase transition into surface and extraordinary ones is highly uncommon, and requires that interactions responsible for the ordering are enhanced at the surface compared to the bulk. In three dimensional (3D) magnetic materials where the interaction between sites within the plane (intralayer interaction $J_{\mid \mid }$) is comparable to that for sites between the neighboring planes (interlayer interaction $J_{\perp }$), the mean-field coupling at the surface ($J_{\mathrm{s}}$), being the sum of all interactions, is expected to be smaller than the one inside the bulk ($J_{\mathrm{b}}$) because of the loss of a $J_{\perp }$ contribution from a neighboring layer (Fig. 1b). For such 3D materials, it is unlikely that any minor surface modifications could compensate for the missing $J_{\perp }$ that is of similar strength as $J_{\mid \mid }$. On the other hand, in quasi-two-dimensional (2D) materials where $J_{\mid \mid }$ is much larger than $J_{\perp }$ (Fig. 1c), it becomes possible that small changes in the surface layers could make up for the very weak missing $J_{\perp }$, or even push its mean-field coupling strength beyond the bulk one to overcome the reduction due to stronger fluctuations at the surface. Therefore, quasi-2D materials, such as van der Waals (vdW) materials, are potential material platforms for realizing split surface-extraordinary phase transitions. Yet, the research on vdW and 2D materials in the past couple of decades hardly revealed any viable candidates for such splitting.

One major challenge for detecting surface and extraordinary phase transitions is the lack of experimental tools sensitive to phase transitions both at the surface and inside the bulk. The leading order electric dipole (ED) contribution to second harmonic generation (SHG) is known as an excellent probe for the broken spatial inversion symmetry and has been used extensively to investigate surface properties^5–9. Very recently, the next order electric quadrupole (EQ) and magnetic dipole (MD) contributions to SHG have been successfully detected in many spatial-inversion-symmetric materials^10–13 and further emerged as an important tool for revealing centrosymmetric bulk phase transitions^14–19. The combination of ED and EQ/MD contributions to SHG is a suitable tool for an experimental discovery of surface and extraordinary phase transitions.

The material candidate selected for this study is CrSBr, a vdW layered crystal with an orthorhombic point group ($mmm$). The structural primitive cell contains two edge-sharing distorted octahedra, with Cr at the center and S/Br at the vertices, forming an in-plane (ab-plane) orthorhombic network and stacking vertically along the out-of-plane (c-axis) direction^20,21. Bulk CrSBr exhibits four characteristic temperatures: T* = 185 K²² and T** = 155 K^21–24 for two crossovers for the enhanced local dynamic spin correlations, T_N = 132 K for the onset of bulk layered antiferromagnetic (AFM) order^20–27, and T_F = 30–40 K for the formation of a possible ferromagnetic (FM) state with debated origins^24,26,28. The layered AFM features a FM spin alignment along the b-axis within each atomic layer and an AFM coupling between adjacent layers along the c-axis. The magnetic point group is $mmm1\prime$ for the bulk AFM order where the c-axis translational symmetry is present and $m^{\prime }m{2}^{\prime }$ for the surface order where the out-of-plane translational symmetry is absent. Interestingly, the onset of layered AFM occurs at different temperatures for CrSBr of different thicknesses: 138 K for six-layer CrSBr, 140 K for bilayer CrSBr and the FM order onsets at possibly 146 K for monolayer CrSBr²¹. This monotonic increase of the magnetic onset temperature with the decreasing thickness in CrSBr starkly contrasts with nearly all known vdW magnets, such as CrI₃^29,30, Cr₂Ge₂Te₆³¹, Fe₃GeTe₂³², NiPS₃³³, FePS₃^34,35, MnPSe₃³⁶, etc., where the magnetic onset temperature in few-layer samples is either lower or equal to that of the bulk crystals.

Figure 2a summarizes the magnetic characteristic temperatures in CrSBr of different thicknesses that are probed by different experimental techniques. It can be seen that eliminating all neighboring layers, i.e., transitioning from bulk to monolayer, leads to an increase in the critical temperature by possibly about 14 K, and that keeping only one neighboring layer, i.e., going from bulk to bilayer, results in an increment of 8 K, close to half of the 14 K increment above. In addition, the Néel temperature of 138 K for six-layer CrSBr is comparable to the average temperature of two bilayers and four bulk layers, i.e., $\left(2T_{\mathrm{N}}^{\mathrm{bilayer}}+4T_{\mathrm{N}}^{\mathrm{bulk}}\right)/6=$135 K. Such considerations motivate us to investigate the surface of bulk CrSBr, closely resembling the bilayer case with only one neighboring layer, to search for the extraordinary and surface phase transitions.

Fig. 2. STEM, heat capacity, and SHG characterizations of CrSBr bulk crystals.

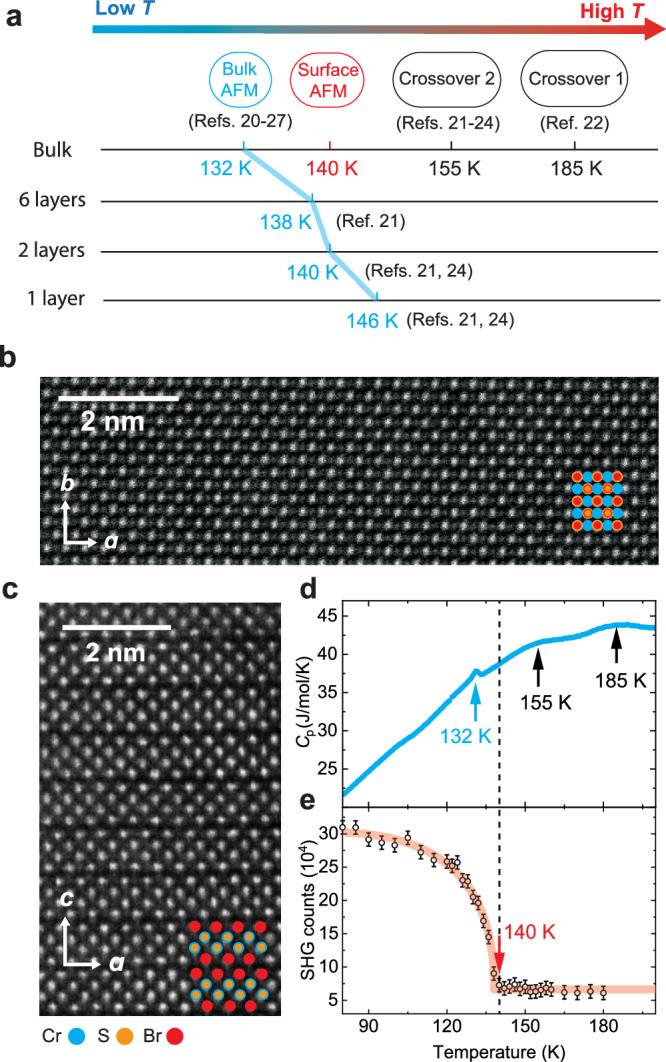
a summary of magnetic phases and corresponding characteristic temperatures in bulk and few-layer CrSBr from the literature. b plan- and c side-view atomically resolved HAADF-STEM images of the CrSBr crystal, confirming the scarcity of atomic and stacking defects. d temperature dependent specific heat result showing the three reported characteristic temperatures, T* = 185 K, T** = 155 K, and T_N = 132 K. e temperature dependent SHG intensity in the S_in-S_out channel at the angle $\varphi =40^{\circ }$ revealing an onset at 140 K for 3D bulk CrSBr, different from the bulk T_N = 132 K. The red curve serves as a guide to the eyes. Error bars indicate the noise level of each SHG measurement.

In this work, using temperature-dependent oblique incidence SHG rotation anisotropy (RA), we reveal a higher-temperature surface and a lower-temperature bulk “extraordinary” phase transition in 3D CrSBr single crystals.

Results

STEM, transport, and SHG charaterizations of 3D CrSBr crystals

vdW materials often suffer from atomic defects and stacking faults that potentially affect their electronic and magnetic properties^37–40. To assess the crystallographic quality of our bulk CrSBr, we performed high-angle annular dark-field scanning transmission electron microscopy (HAADF-STEM) measurements in both plan-view and cross-section-view configurations (see Methods). Figure 2b shows the atomic structure of CrSBr within the ab-plane, with the Br/S column appearing to be the brightest, followed by a dimmer Cr column. Across multiple sites and samples of various thicknesses, atomic defects were rarely observed in the plan-view STEM images of CrSBr. Figure 2c displays the layered structure of CrSBr viewed in the ac-plane, with the vdW gaps showing up as the darker space between atomic layers. We further confirm that the overlying interlayer stacking is the sole preferred stacking geometry for CrSBr and barely any stacking faults were observed across multiple sites (see Supplementary Note 1). This scarcity of atomic defects and stacking faults confirms the high crystalline quality of our CrSBr samples (see Methods for growth method). Our atomic force microscopy measurements also show that our freshly cleaved surfaces exhibit highly flat surfaces with a low density of atomic steps (see Supplementary Note 2).

The temperature-dependent heat capacity for single-crystalline CrSBr samples clearly reproduces the three temperature scales reported in the literature, T* = 185 K, T** = 155 K, and T_N = 132 K (Fig. 2d), whereas T_F = 30 K is revealed by the magnetization measurement (see Supplementary Note 3). Intriguingly, the temperature dependence of the SHG intensity from the same CrSBr batch exhibits a clear order-parameter-like upturn at 140 K (Fig. 2e), a temperature that is hidden to many bulk-sensitive measurements for 3D CrSBr single crystals, for example, heat capacity^21,22, magnetic susceptibility^{20,22,24,26–28}, neutron single crystal diffraction²³, and zero-field $\mu$SR²⁶. We note that, first, unlike T_N = 132 K for 3D CrSBr single crystals, neutron diffraction experiments on CrSBr powders that have a substantial surface to bulk ratio²⁶ showed T_N = 140 K and, second, SHG revealed T_N = 140 K for bilayer CrSBr whose composing layers miss the neighboring layer on one side²¹. The occurrence of the same critical temperature 140 K in bulk single crystals of this study, together with the surface sensitivity of the ED SHG probe^5–9,41,42, indicates that this 140 K onset in bulk CrSBr crystals is likely the surface ordering temperature T_S = 140 K, which is higher than the bulk Néel temperature, T_N = 132 K, but lower than the crossover temperature, T** = 155 K (Fig. 2a).

Oblique incident SHG RA tracking phase transitions in 3D CrSBr crystals

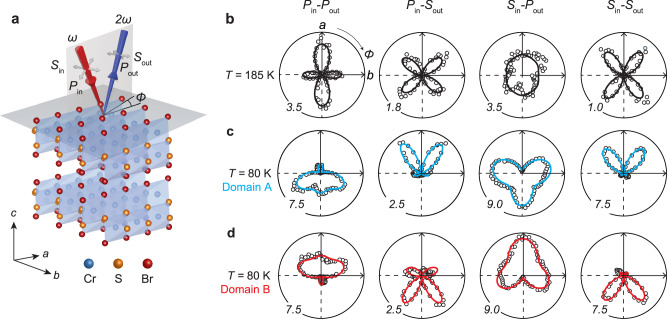
To analyze further the magnetic phase transitions in bulk CrSBr crystals, we performed the rotation anisotropy (RA) measurements of SHG at an oblique incident angle $\theta$, to capture the symmetry evolution across the critical temperatures. In a SHG RA measurement (Fig. 3a), the intensity of reflected SHG light is recorded as a function of the azimuthal angle $\varphi$ between the crystal axis a and the light scattering plane in one of the four polarization channels, P/S_in-P/S_out, with P/S_in/out standing for the incident/outgoing light polarization selected to be parallel/perpendicular to the light scattering plane. We start by showing SHG RA data taken at high temperatures (T $\ge$ T*), specifically at 185 K (Fig. 3b) and 295 K (see Supplementary Note 4), that are nearly identical in both the RA patterns and the SHG intensity in all four polarization channels. The four SHG RA polar plots in Fig. 3b are two-fold rotational symmetric about the c-axis (C_2c) and mirror symmetric with mirrors normal to the a- and b-axis (m_a and m_b). They are well fitted by the EQ contribution to the SHG under the centrosymmetric point group $mmm$. We exclude the surface ED, bulk MD, and electric field-induced SH contributions as primary sources, even if present, for our SHG RA data at T $\ge$ T* (Supplementary Note 4).

Fig. 3. SHG RA revealing two degenerate magnetic domain states.

a schematic of the oblique incidence SHG RA measurement taken on a bulk CrSBr crystal. Red arrow: incident fundamental light, blue arrow: outgoing SHG light, gray arrows: light polarizations, $\omega$, frequency of the incident light. b–d SHG RA polar plots in four channels (P/S_in-P/S_out) at b 185 K, c 80 K from domain A and d 80 K from domain B. Experiment data (circles) are fitted by functional forms simulated based on group theory analysis (solid curves). Numbers at the corners indicate the scales of the polar plots, with 1.0 corresponding to 1 fW.

Upon cooling to low temperatures (T < T_N), we observe two, and only two distinct types of SHG RA data at 80 K through measurements across multiple thermal cycles and in different samples, as shown in Fig. 3c, d. Contrary to the RA patterns at 185 K, the SHG RA patterns at 80 K evidently break the C_2c and m_a symmetries but retain the m_b symmetry. The comparison between Fig. 3c, d demonstrates that the two types of SHG RA data are related by either a C_2c or a m_a operation, which are the symmetries broken below T_N, and therefore, confirms that they correspond to the two degenerate magnetic domain states, $\leftarrow \to \leftarrow \to \dots$ (Domain A) and $\to \leftarrow \to \leftarrow \dots$ (Domain B), where $\leftarrow$/$\to$ represents the spins within individual layers aligning along the negative/positive direction of the b-axis. A real-space survey of SHG RA across a CrSBr single crystal surface shows that the domain size extends up to 500 μm (see Supplementary Note 5), and a survey conducted over several thermal cycles demonstrated the random selection of domain states in individual thermal cycles (see Supplementary Note 5).

To model and fit the SHG RA data at low temperatures, we need to identify the SHG radiation sources and their corresponding point groups. Firstly, due to the absence of reported structural transitions for CrSBr within our temperature range of interest (80–295 K)²⁶, the EQ contribution to SHG based on the structural point group $mmm$ (${\chi }_{ijkl}^{\mathrm{EQ},\mathrm{s}}$) should be present at all temperatures. Secondly, due to the centrosymmetric and time-invariant bulk layered AFM order that sets in below T_N = 132 K, the EQ contribution to SHG from the magnetic point group $mmm{1}^{\prime }$ (${\chi }_{ijkl}^{\mathrm{EQ},\mathrm{bAFM}}$) should be considered at temperatures below T_N. We notice that the symmetry constraints are the same for the structural point group $mmm$ and the magnetic point group $mmm{1}^{\prime }$, resulting in that ${\chi }_{ijkl}^{\mathrm{EQ},\mathrm{s}}$ is of the same form as ${\chi }_{ijkl}^{\mathrm{EQ},\mathrm{bAFM}}$. Hence, from this point onward, we use ${\chi }_{ijkl}^{\mathrm{EQ}}$ to represent the combined contributions from the structure and the bulk AFM. Thirdly, the surface layered AFM breaks the spatial inversion and time reversal (TR) symmetries, and as a result, the ED contribution to SHG from the surface magnetic point group $m^{\prime }m{2}^{\prime }$ (${\chi }_{ijk}^{\mathrm{ED}}$) should be included at low temperatures T < T_S. Therefore, the SHG RA data at 80 K should be modeled by a coherent superposition of the EQ and the ED contributions (see Supplementary Note 6 and Methods) and thus, is capable of probing the magnetic phase transition at the surface. The fitted results based on this model are depicted in Fig. 3c, d, and the interference between the EQ and ED contributions is illustrated for the S_in-S_out polarization channel in Fig. 4. Moreover, the thickness dependent SHG RA measurements below T_N show an increasing trend of the EQ SHG contribution, but a constant level of the ED SHG contribution with increasing sample thickness, which is consistent with their assigned bulk and surface origins, respectively (see Supplementary Note 7).

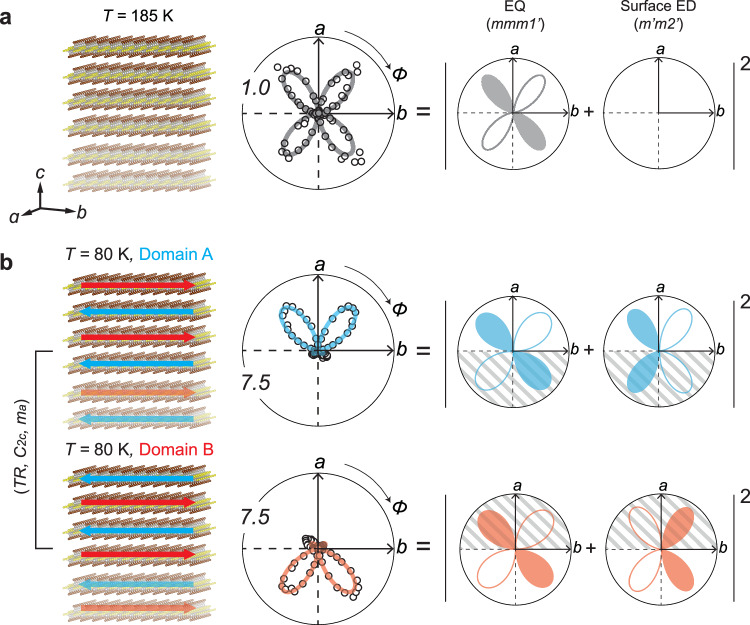
Fig. 4. Interference between bulk EQ and surface ED leading to distinct SHG RA patterns for the two domain states.

a left: schematic of the layered crystal structure at 185 K. Right: SHG RA pattern in the S_in-S_out channel with only the EQ contribution. b left: schematic of the layered crystal structure overlaid with the spin texture in domain states A and B, related by the time-reversal operation (TR), two-fold rotation along the c-axis (C_2c) and mirror operation perpendicular to the a-axis (m_a). Right: SHG RA patterns in the S_in-S_out channel, resulting from the interference between the bulk EQ and the surface ED contributions. The colored shaded areas of the SHG RA patterns indicate a $\pi$ phase shift of the SHG electric field from the white shaded areas. Stripped shaded areas indicate destructive interference. Numbers at the corners indicate the scales of the polar plots, with 1.0 corresponding to 1 fW. EQ electric quadrupole, ED electric dipole.

Figure 4a confirms the sole presence of the EQ contribution to SHG at T = 185 K. More interesting is that Fig. 4b shows distinct consequences between the two domain states from the interference of the bulk EQ and the surface ED contributions: constructive interference in the top half and destructive interference in the bottom half for Domain A, and the exact opposite way for Domain B. The bulk AFM order preserves all the symmetry operations in the structural point group and the TR operation, resulting in ${\chi }_{ijkl}^{\mathrm{EQ}}$(Domain A) = ${\chi }_{ijkl}^{\mathrm{EQ}}$ (Domain B). The surface AFM order however breaks C_2c, m_a, and TR symmetries that relate the two domain states, leading to ${\chi }_{ijk}^{\mathrm{ED}}$(Domain A) = ${-\chi }_{ijk}^{\mathrm{ED}}$(Domain B) (see Supplementary Note 6). This opposite sign relationship between the EQ and ED SHG susceptibilities for the two domain states explains the distinct interference behaviors observed in Fig. 4b.

Our next step is to track the magnetic phase transitions by performing careful temperature dependent SHG RA measurements, paired with magnetization measurements on the same CrSBr crystal. During SHG measurements, we ensure our system is in thermal equilibrium by keeping a slow heating rate, waiting for additional time after the temperature is stabilized (see Methods), and noticing no SHG pattern change as a function of time (see Supplementary Note 8 for SHG RA patterns measured in sequence of time). Figure 5a shows a color map of SHG intensity taken in the S_in-S_out channel as functions of the azimuthal angle $\varphi$ and the temperature T. A horizontal linecut at a fixed ${\varphi }_0$ yields the temperature-dependent SHG intensity, such as the trace shown in Fig. 2e, whereas the vertical linecut at a selected T gives the SHG RA pattern, such as the polar plots shown in Fig. 4. To better visualize the evolution of the SHG RA data as the temperature decreases, we present polar plots at four representative temperatures in the inset of Fig. 5a: T = 185 K (around T*), 146 K (between T** and T_S), 138 K (between T_S and T_N), and 80 K (below T_N). A clear trend can be observed: the RA pattern first increases in the SHG intensity but retains the pattern shape of four even lobes until T_S. It then exhibits two pairs of uneven lobes while further amplifying the intensity of the larger and reducing the intensity of the smaller pair below T_S. As the temperature decreases below T_N, a more pronounced contrast in the SHG intensity between the larger and smaller pairs of lobes is developed.

Fig. 5. Temperature-dependent SHG RA revealing the surface and the extraordinary phase transitions.

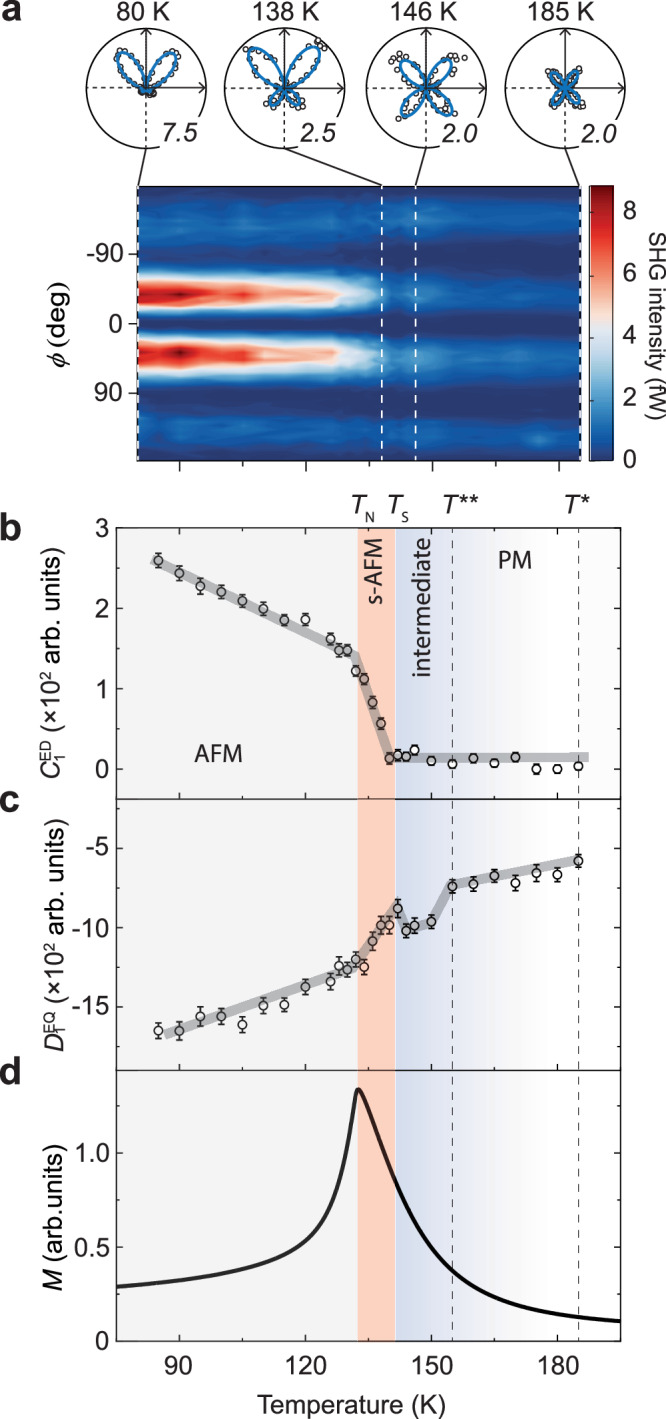
a lower: contour plot of the SHG RA in the S_in-S_out channel as a function of temperature. Upper: SHG RA polar plots in the S_in-S_out channel at four selected temperatures. b The electric dipole (ED) coefficient $C_1^{ED}$ and (c) the electric quadrupole (EQ) coefficient $D_1^{EQ}$ as a function of temperature. Gray curves serve as guides to the eyes. The temperature dependent SHG data were collected during the warming up cycle. d magnetization as a function of temperature measured under 1000 Oe magnetic field along the b-axis. The regions of paramagnetism (PM), intermediate magnetic crossover (intermediate), surface antiferromagnetism (s-AFM) and bulk antiferromagnetism (AFM) are shaded in different colors, with their characteristic temperatures marked. Error bars indicate the standard deviation from the fitting.

The SHG RA pattern at every temperature in Fig. 5a is fitted by the coherent superposition of the surface ED and the bulk EQ contributions to extract the temperature dependence of their sources (see Methods for the fitting procedure). For the S_in-S_out channel, the fitted results include two independent parameters for the surface ED source, $C_1^{\mathrm{ED}}={\chi }_{xyy}^{\mathrm{ED}}+2{\chi }_{yxy}^{\mathrm{ED}}$, and $C_2^{\mathrm{ED}}={\chi }_{xxx}^{\mathrm{ED}}$, and another two for the bulk EQ one, $D_1^{\mathrm{EQ}}={\chi }_{xxxx}^{\mathrm{EQ}}-2{\chi }_{xxyy}^{\mathrm{EQ}}-{\chi }_{yxyx}^{\mathrm{EQ}}$, and $D_2^{\mathrm{EQ}}={\chi }_{xyxy}^{\mathrm{EQ}}+2{\chi }_{yyxx}^{\mathrm{EQ}}-{\chi }_{yyyy}^{\mathrm{EQ}}$. Because ${\chi }_{ijk}^{\mathrm{ED}}$ is variant and ${\chi }_{ijkl}^{\mathrm{EQ}}$ is invariant under the TR operation, we know that ${\chi }_{ijk}^{\mathrm{ED}}$ is proportional to the odd powers of the Néel vector ($\mathbf{N}$) and ${\chi }_{ijkl}^{\mathrm{EQ}}$ scales with the even powers of $\mathbf{N}$. Under the leading-order approximation, ${\chi }_{ijk}^{\mathrm{ED}}\propto \mathbf{N}$ and ${\chi }_{ijkl}^{\mathrm{EQ}}\propto \mathrm{constant}+\mathbf{N}\cdot \mathbf{N}$, and as a result, $C_{1,2}^{\mathrm{ED}}\propto \mathbf{N}$ and $D_{1,2}^{\mathrm{EQ}}\propto \mathrm{constant}+\mathbf{N}\cdot \mathbf{N}$. Figure 5b, c shows the temperature dependence of $C_1^{\mathrm{ED}}$ and $D_1^{\mathrm{EQ}}$ (see $C_2^{\mathrm{ED}}$ and $D_2^{\mathrm{EQ}}$ in Supplementary Note 9), and Fig. 5d displays the temperature dependence of the bulk magnetization of the same CrSBr crystal. The bulk magnetization M clearly shows a divergent behavior at T_N = 132 K, as expected for a bulk CrSBr crystal^20–27. Three important temperature scales are captured in the temperature dependence of ED and EQ contributions, T** = 155 K, T_S = 140 K, and T_N = 132 K that are discussed in-depth below (see Supplementary Note 10 for data from another sample). The surface ED contribution $C_1^{\mathrm{ED}}\left(T\right)$, which is proportional to $\mathbf{N}$, shows an order-parameter-like onset at T_S = 140 ± 0.2 K and then an observable kink at T_N = 132 K. This observation confirms that the surface orders antiferromagnetically at a higher temperature than the bulk, providing definitive evidence for a surface phase transition in bulk CrSBr. The kink behavior at T_N = 132 K reflects the impact of the bulk extraordinary phase transition on the surface order, which is consistent with the theoretical prediction of an $\beta >1$ critical exponent for the surface order parameter at the extraordinary phase transition temperature^4,43. The EQ part $D_1^{\mathrm{EQ}}\left(T\right)$, which scales with $\mathbf{N}\cdot \mathbf{N}$ after a constant offset from the structural contribution, initially experiences a steady but slow increase below T* = 185 K until T** = 155 K. Subsequently, it increases steeply across T**, exhibits a notable peak at T_S = 140 K, and ultimately a kink at T_N = 132 K. Note that the EQ SHG probes CrSBr within the light penetration depth, which includes and goes beyond the surface depth. Provided its sensitivity to the spin correlation via the term $\mathbf{N}\cdot \mathbf{N}$, it shows a weak divergence, i.e., the peak, at T_S, as well as the slope change across T**.

To understand these three observed temperature scales, we compare them with the literature reported ones for CrSBr of bulk, powder, and film forms. First, our bulk AFM order onset temperature, T_N = 132 K, is consistent with that of bulk CrSBr single crystals measured by single crystal neutron diffraction, $\mu$SR, heat capacity, and magnetic susceptibility^20–27. Second, our surface AFM order onset temperature, T_S = 140 ± 0.2 K, coincides with the magnetic critical temperature reported for powder CrSBr measured with powder neutron diffraction²⁶ and bilayer CrSBr with SHG²¹. For powder CrSBr, the surface-to-bulk ratio is significantly increased from that of single crystal CrSBr, and thus, it might be possible that the powder neutron diffraction is sensitive to the surface magnetism. For bilayer CrSBr, it resembles the surface magnetism in 3D CrSBr in the way that they both miss neighboring layers on one side. Therefore, our detection of T_S = 140 ± 0.2 K for the surface magnetic order in 3D CrSBr offers potential explanations for the variation in the magnetic critical temperature of CrSBr. Finally, the temperature scale of T** = 155 K was previously assigned to the onset of an intermediate c-axis incoherent ferromagnetic state, where the spins align ferromagnetically within individual ab-planes but randomly between adjacent ab-planes throughout the bulk of 3D CrSBr^21–24. However, it is thermodynamically unlikely to achieve a phase transition from this intermediate order without c-axis coherence to the layered AFM order at T_N = 132 K for 3D bulk CrSBr, because the energy change scales with volume but the entropy change is proportional to the thickness, leading to a divergent (infinite) critical temperature for this phase transition. As a result, we revise the interpretation of T** = 155 K to be a crossover temperature scale below which the spins form fluctuating, short-ranged patches both within and between ab-planes. Within individual patches, the spins on average align more along the b-axis, making the b-axis more different from the a-axis and thus resulting in the EQ SHG change across T** (see Supplementary Note 11 for detailed explanations).

First-principle calculations explaining surface and extraordinary phase transitions

To understand the increase in the surface magnetism onset temperature in CrSBr despite the stronger fluctuation expected at the surface, we refer to the formula^44–47:

$$T_{\mathrm{N}}\approx \frac{T_{\mathrm{CW}}}{A+\log \left(J_{\mathrm{\mid \mid }}/J^{\prime }\right)}.$$ 1

Here, T_CW denotes the mean-field Curie–Weiss temperature for monolayer CrSBr; A is a constant of the order of 3–5; $J_{\mid \mid }$ is the average characteristic intralayer exchange coupling; $J^{\prime }$ represents a properly-defined combination of the interlayer coupling $J_{\perp }$ and the intralayer Ising anisotropy D, which arises from both the single site anisotropy and the Ising exchange –in a previous study⁴⁸, $J^{\prime }$ was estimated as $J^{\prime }=D+J_{\perp }+\sqrt{{\left(D+J_{\perp }\right)}^2-D^2}$. Note that it is the small but nonzero intralayer anisotropy D that maintains T_N finite for monolayer CrSBr^21,24. Within the mean-field theory, $T_{\mathrm{CW}}$ is directly related to the intralayer exchange coupling strengths:

$$T_{CW}=-\frac{1}{3}S\left(S+1\right)\left(2J_1+4J_2+2J_3+4J_4+4J_5+2J_6+4J_7\right)$$ 2

where $S=3/2$ and $J_{1-7}$ are the intralayer exchange couplings up to the 7th nearest neighbor. From Eq. (1) and Eq. (2), we can see that the change in intralayer exchange coupling (J_1-7) will impact T_N on a linear scale whereas the change in the intralayer anisotropy and interlayer coupling (included in J’) will influence T_N on a logarithmical scale. Thus, the leading order contribution to the enhanced T_N at the surface should be the change in the intralayer exchange coupling from bulk to surface.

To this effect, we performed first-principle density function theory (DFT) calculations to compute $T_{\mathrm{CW}}$ based on the calculated $J_{1-7}$ from an isotropic Heisenberg spin Hamiltonian (Methods), and under four structural configurations (S1–4, discussed below). We have chosen an isotropic Heisenberg spin Hamiltonian for our DFT calculations, because the biaxial anisotropy of CrSBr has  been shown to be at least 2–3 orders of magnitudes smaller than the intralayer exchange coupling, both through first-principle calculations^49,50 and experiments^23,51, and should have minor effects on $T_{\mathrm{CW}}$ and $T_{\mathrm{N}}$. The four strongest intralayer exchange couplings are found to be $J_1$, $J_2$, and $J_3$ that are FM, and $J_6$ that is AFM, as marked in Fig. 6a, whereas the remaining $J_4$, $J_5$, and $J_7$ are negligibly small (see Supplementary Note 12). The four considered structures include bulk CrSBr (S1), rigid monolayer CrSBr that retains the atomic structure within the layer from the bulk (S2), fixed ab monolayer CrSBr that is derived from the intra-unit cell lattice relaxation while keeping the lattice constant same as the bulk (S3), and free monolayer CrSBr after the full lattice relaxation (S4). We vary the Hubbard U across a wide range to verify the consistent and robust trend of $T_{\mathrm{CW}}$ for the four scenarios: $T_{\mathrm{CW}}$ increases from the bulk to the rigid monolayer, further enhances in the fixed ab monolayer, but decreases a bit in the free monolayer, as shown in Fig. 6b. This observed trend suggests two important factors that lead to the increase of $T_{\mathrm{CW}}$: first, the absence of neighboring layers, and second, the intra-unit cell lattice relaxation. Following Eq. (1), both factors will contribute to the enhanced $T_{\mathrm{N}}$ at the surface of CrSBr.

Fig. 6. DFT calculations explaining the origin of a higher transition temperature at the surface.

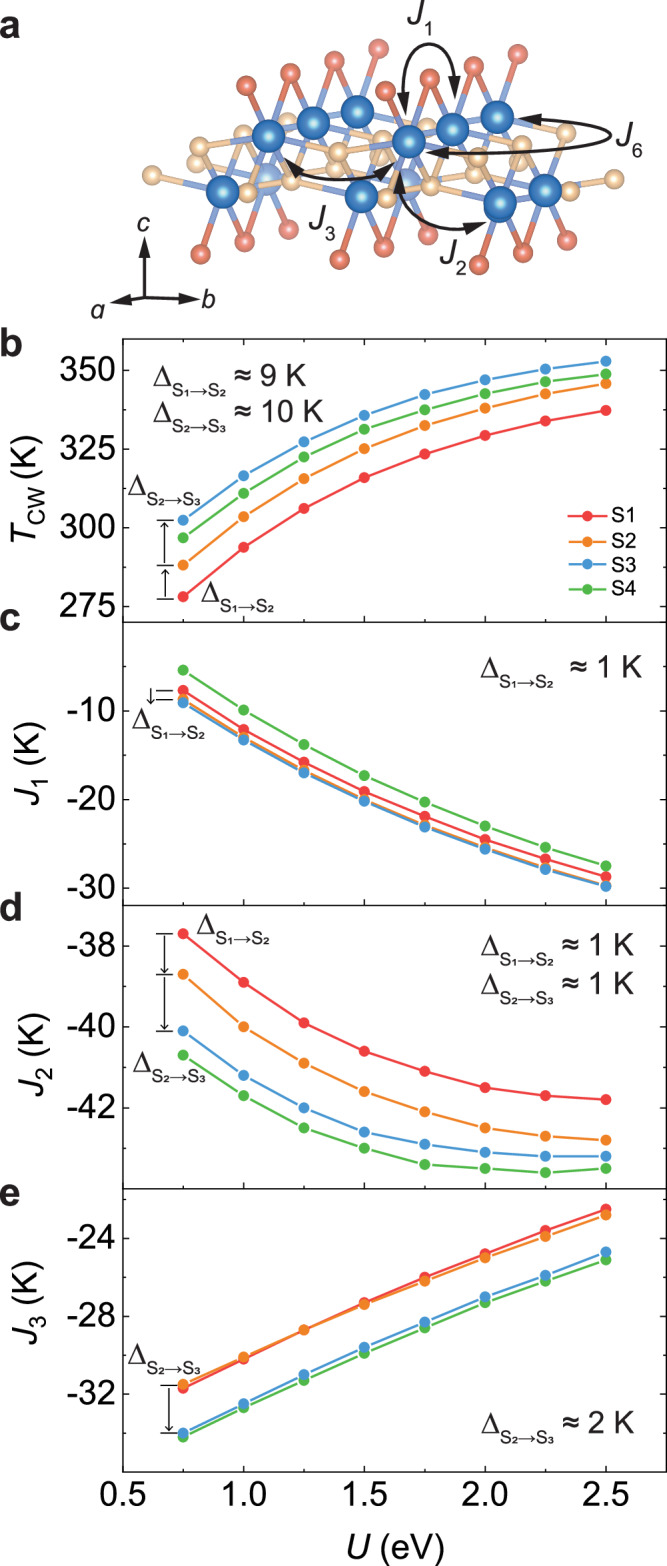
a exchange pathways for J₁, J₂, J₃ and J₆, overlaid on the CrSBr crystal structure. U-dependence of b, T_CW c, J₁ d, J₂, and e, J₃ for S1: bulk CrSBr (red), S2: rigid monolayer (orange), S3: fixed ab monolayer (blue) and S4: free monolayer (green). ${\mathrm{\Delta }}_{\mathrm{S}1\to \mathrm{S}2}$: change in T_CW and corresponding J from bulk to rigid monolayer. ${\mathrm{\Delta }}_{\mathrm{S}2\to \mathrm{S}3}$: change in T_CW and corresponding J from rigid monolayer to fixed ab monolayer.

A close look into the evolution of the intralayer exchange coupling ($J_{1-7}$) across the four structures (S1–4) provides further insights into the two identified factors for the enhanced $T_{\mathrm{CW}}$. The calculated $J_{1-3}$ show noticeable variations for S1 – 4, for a wide range of U, as shown in Fig. 6c–e, whereas $J_{4-7}$ remain unchanged across S1 – 4 structures (see Supplementary Note 12). For the first factor, the absence of neighboring layers leads to a substantial increase in both $J_1$ and $J_2$, i.e., ${\mathrm{\Delta }}_{\mathrm{S}1\to \mathrm{S}2}=~1\mathrm{K}$ shown in Fig. 6c, d. This increase in FM $J_1$ and $J_2$ by simply removing the neighboring layers is likely due to the suppression of a hopping path between the in-plane nearest ($J_1$) and second nearest ($J_2$) neighboring Cr sites going through neighboring layers that contributes an AFM intralayer exchange coupling to $J_1$ and $J_2$. For the second factor, the intra-unit cell lattice relaxation results in an increase in $J_2$ and $J_3$ by about 1 K and 2 K, respectively, i.e., ${\mathrm{\Delta }}_{\mathrm{S}2\to \mathrm{S}3}=~1$ K and $~2$ K shown in Fig. 6d, e. The enhancement in $J_2$ is likely to arise from the increase of Cr-S-Cr angle between the two Cr sites within the unit cell (i.e., between the second nearest neighboring Cr sites), whereas the increase for $J_3$ mainly originates from the decrease of the Cr-S-Cr angle along the b axis (i.e., between the third nearest neighboring Cr sites). The strong dependence of the intralayer exchange coupling on the lattice structure has also been seen in strain-engineered CrSBr^52–54. We further comment that while our calculations successfully explain the enhanced T_N at the surface of 3D CrSBr, they are not intended to, and also cannot, provide the precise values of T_N at the surface and inside the bulk of 3D CrSBr to match the experimental ones.

To summarize, we have successfully demonstrated the presence of surface and extraordinary phase transitions in a vdW AFM, bulk CrSBr, using the combination of bulk single-crystal EQ SHG and surface ED SHG. A clear temperature separation of 8 K is detected between the surface magnetism onset temperature, T_S = 140 ± 0.2 K, and the bulk Néel temperature, T_N = 132 K, showing a counterintuitive enhancement of the critical temperature at the surface. DFT calculations suggest two key factors for the increase of magnetic critical temperature at the CrSBr surface, namely, the absence of neighboring layer and the intra-unit cell lattice relaxation. Our results suggest multiple future research opportunities in vdW and 2D magnetism research. First, vdW magnets are a viable platform for realizing the parameter regime required for split surface and extraordinary phase transitions. In addition to CrSBr, immediate candidates include chromium chalcogenide halides^55,56 and chromium oxyhalides⁵⁷ that have similar magnetic properties to CrSBr, and VI₃⁵⁸, which exhibits a similar thickness dependence of critical temperature; namely, the onset temperature is higher in the few-layer samples than in the bulk. Second, static strain^52–54,59 and dynamic nonlinear phononics^60,61 are promising ways to tune the magnetism or enhance the magnetic critical temperature of CrSBr, thanks to its extreme sensitivity of intralayer exchange coupling to the intra-unit cell atomic arrangement. It is quite likely that a large pool of vdW magnets exhibit a similar exchange coupling dependence on lattice structure as CrSBr and therefore can be candidates for strain and light engineering of magnetism. Third, moiré superlattice of CrSBr can be fundamentally distinct from that of CrI₃^62–66 and offer a new platform for exploring moiré magnetism. On the one hand, the intralayer exchange coupling in CrSBr is shown in this work to significantly depend on the presence of the neighboring layers, which can lead to periodical modulations of intralayer exchange coupling in twisted CrSBr superlattices. This is in contrast to twisted CrI₃ superlattices where only modulations in interlayer exchange coupling are considered. On the other hand, CrSBr has an orthorhombic crystal lattice with one-dimensional electronic properties^67,68. This highly anisotropic electronic property is in sharp contrast to the nearly isotropic electronic structure in CrI₃, and can offer unique moiré electronic and magnetic properties in twisted CrSBr.

Methods

Crystal growth and sample preparations

CrSBr single crystal is naturally grown using direct solid-vapor method through a box furnace. Cr powder (Alfa Aesar, 99.97%) and S powder (Alfa Aesar,99.5%) are accurately weighted inside the Ar-glovebox with total oxygen and moisture level less than 1 ppm. To facilitate the loading of bromide, the bromide liquid (99.8%) is initially solidified with the assist of liquid nitrogen. Cr powders, S powders and solid Br₂ are loaded into a clean quartz ampoule with the mole ratio of 1: 1.1: 1.2. Subsequently, the ampoule was sealed under vacuum using liquid nitrogen trap. We found out the extra amount of the S and Br created positive vapor pressure which effectively reduces the defects in the grown crystals and meanwhile promotes the larger size growth of single crystals. The quartz ampoule was heated up to 930 °C very slowly, stayed at this temperature for 20 h and followed by slowly cooling down to 750 °C (1°/h). The assembly is then quenched down to room temperature. Large size CrSBr will grow naturally at the bottom of the ampoule. A small amount of CrBr₃ is also found at the top of the quartz ampoule and can be easily separated from the CrSBr crystals. The thickness of the sample for SHG RA is about 0.2 mm. The thickness of the samples for the heat capacity and magnetization measurements is between 0.2 mm and 0.5 mm. The thickness of the samples for the TEM measurements is about ten layers for the in-plane measurement and a few nm for the cross-sectional measurement.

Scanning transmission electron microscopy (STEM)

Plan-view specimens were prepared by exfoliating bulk CrSBr flakes on to polydimethylsiloxane (PDMS) gel stamps, which was transferred onto Norcada SiN TEM window grids with 2 µm holes. Cross-sectional specimens were prepared using the standard focus ion beam (FIB) lift-out method on Thermo Fisher Nova 200. HAADF-STEM was performed on JEOL 3100R05 (300 keV, 22 mrad) and Thermo Fisher Spectra 300 (300 keV, 21.4mrad) for plan-view and cross-section-view.

Second harmonic generation

The incident ultrafast light source was of 50 fs pulse duration and 200 kHz repetition rate with a center wavelength 800 nm. It was focused down to a 15 μm diameter spot on the sample with an oblique incidence angle $\theta$ = 11.2° and a power of 850 μW. The polarizations of the incident and reflected light could be selected to be either parallel or perpendicular to each other, with the azimuthal angle $\varphi$ changing correspondingly. The intensity of the reflected SHG signal with 400 nm wavelength was detected by a charge-coupled device (CCD). The temperature dependent SHG was performed during the warming up cycle with a heating rate 0.5 K/min. Additional wait time of 5 min ensures the stability of the temperature. The SHG RA data has been taken at a temperature with a temperature stability of 0.005 K.

Extraction of temperature dependent ${\mathit{C}}^{\mathit{ED}}$ and ${\mathit{D}}^{\mathit{EQ}}$

the electric field in the S_in-S_out channel from the surface magnetic ED SHG under $m’m2’$ is simulated to be

$$E^{\mathrm{SS},\mathrm{surface\; ED}}\left(\varphi \right)=\left({\chi }_{\mathrm{xyy}}+2{\chi }_{\mathrm{yxy}}\right){\mathrm{Cos}\left[\varphi \right]}^2\mathrm{Sin}\left[\varphi \right]+{\chi }_{\mathrm{xxx}}{\mathrm{Sin}\left[\varphi \right]}^3.$$ 3

That from bulk EQ SHG under $mmm$ or $mmm1’$ is

$$E^{\mathrm{SS},\mathrm{bulk}\mathrm{EQ}}\left(\varphi \right)=-\mathrm{Sin}\left[\theta \right]\left(\left({\chi }_{\mathrm{xyxy}}+2{\chi }_{\mathrm{yyxx}}-{\chi }_{\mathrm{yyyy}}\right){\mathrm{Cos}\left[\varphi \right]}^3\mathrm{Sin}\left[\varphi \right]+\left({\chi }_{\mathrm{xxxx}}-2{\chi }_{\mathrm{xxyy}}-{\chi }_{\mathrm{yxyx}}\right)\mathrm{Cos}\left[\varphi \right]{\mathrm{Sin}\left[\varphi \right]}^3\right).$$ 4

We then constructed the functional form of the interfered SHG intensity through

$$I^{\mathrm{SS}}\left(\varphi \right)={\left(E^{\mathrm{SS},\mathrm{surface}\mathrm{ED}}+E^{\mathrm{SS},\mathrm{bulk}\mathrm{EQ}}\right)}^2={\left(\left({\chi }_{\mathrm{xyy}}+2{\chi }_{\mathrm{yxy}}\right)\mathrm{Cos}{\left[\varphi \right]}^2\mathrm{Sin}\left[\varphi \right]+{\chi }_{\mathrm{xxx}}\mathrm{Sin}{\left[\varphi \right]}^3-\mathrm{Sin}\left[\theta \right]\left(\left({\chi }_{\mathrm{xyxy}}+2{\chi }_{\mathrm{yyxx}}-{\chi }_{\mathrm{yyyy}}\right)\mathrm{Cos}{\left[\varphi \right]}^3\mathrm{Sin}\left[\varphi \right]+\left({\chi }_{\mathrm{xxxx}}-2{\chi }_{\mathrm{xxyy}}-{\chi }_{\mathrm{yxyx}}\right)\mathrm{Cos}\left[\varphi \right]\mathrm{Sin}{\left[\varphi \right]}^3\right)\right)}^2.$$ 5

Through the fitting, four coefficients can be extracted: $C_1^{\mathrm{ED}}={\chi }_{xyy}^{\mathrm{ED}}+2{\chi }_{yxy}^{\mathrm{ED}}$ and $C_2^{\mathrm{ED}}={\chi }_{xxx}^{\mathrm{ED}}$ from the ED contribution, $D_1^{\mathrm{EQ}}={\chi }_{xyxy}^{\mathrm{EQ}}+2{\chi }_{yyxx}^{\mathrm{EQ}}-{\chi }_{yyyy}^{\mathrm{EQ}}$ and $D_2^{\mathrm{EQ}}={\chi }_{xxxx}^{\mathrm{EQ}}-2{\chi }_{xxyy}^{\mathrm{EQ}}-{\chi }_{yxyx}^{\mathrm{EQ}}$ from the EQ contribution. Consequently, our fitting can separate out the ED and EQ, and thus, surface and bulk unambiguously.

First-principle calculations

The structure relaxation of CrSBr bulk and monolayers was performed using the Vienna ab initio simulation package (VASP)^69–71. The projector augmented wave (PAW) potentials with the generalized gradient approximation (GGA) exchange-correlation potential in the Perdew-Burke-Ernzerhof variant (PBE)⁷² were used. For the bulk relaxation, we use a $\mathrm{\Gamma }$-centered $6\times 6\times 4k$ mesh, for monolayers a $7\times 7\times 1k$ mesh and an energy cutoff of 900 eV. The convergence criterion is that all forces are smaller than 3 mV/Å. Then, we performed all electron density functional theory calculations using the full potential local orbital (FPLO) code⁷³. We used the non-local optB88-vdW functional to correct for dispersive interactions^74,75. Energy mapping: We use DFT energy mapping^76,77 to determine the Heisenberg Hamiltonian parameters. For this purpose, we use a specially prepared 8-fold supercell of CrSBr with 16 symmetry inequivalent Cr sites. This allows us to determine the first seven in-plane exchange interactions $J_1$ to $J_7$. We use the GGA + U exchange correlation functional with fully-localized limit double counting scheme, for eight different values of U and $J_H$ = 0.72 eV fixed following ref. ⁷⁸. They were then fitted to the Heisenberg Hamiltonian of the form

$$H={\sum }_{i<j}{J}_{ij}{\mathit{S}}_i\cdot {\mathit{S}}_j$$ 6

with Cr³⁺ spin operators ${\mathit{S}}_i,\mid {\mathit{S}}_i\mid$ = 3/2. The Curie-Weiss temperature for this Hamiltonian is given by Eq. (2). Figure 6a was generated using VESTA software⁷⁹.

Author contributions

X.G. and L.Z. conceived the project. X.G. performed the SHG measurements and data analysis under the supervision of L.Z., H.D. and K.S. W.L., A.L.N.K. and B.L. provided the CrSBr single crystals. J.S., S.H.S. and R.H. performed the HAADF-STEM measurements. W.L., D.Z., L.L. and B.L. performed the heat capacity and magnetization measurements. M.S., H.O.J. and I.I.M. performed and interpreted the DFT calculations. X.G. and L.Z. wrote the manuscript. All authors discussed the results.

Peer review

Peer review information

Nature Communications thanks the anonymous reviewers for their contribution to the peer review of this work. A peer review file is available.

Data availability

All data that support the finding of this work are included as main text and Supplementary Figs. Raw data and other data of this study are available from the corresponding author upon request. Source data are provided with this paper.

Competing interests

The authors declare no competing interests.

Supplementary information

The online version contains supplementary material available at 10.1038/s41467-024-50900-1.