Abstract
This paper investigates the soliton solutions and dynamical analysis of (2+1)-dimensional Heisenberg ferro-magnetic spin chains model with beta fractional derivative, which is transformed into the ordinary differential equation. By using the second-order complete discriminant system, the soliton solutions are presented. By utilizing the theory of planar dynamical system, the phase portraits of the dynamical system and its disturbance system are drawn. Moreover, three-dimensional, two-dimensional, and contour plots of soliton solutions for (2+1)-dimensional Heisenberg ferro-magnetic spin chains model with beta fractional derivative have also been plotted.
Keywords: (2+1)-dimensional Heisenberg ferro-magnetic spin chains model, Beta fractional derivative, Soliton solution, Complete discriminant system
Subject terms: Nonlinear phenomena, Information theory and computation
Introduction
Nonlinear partial differential equation (NLPDE)1–13 plays a very important role in the fields of natural science and engineering technology. In the study of NLPDEs, the construction of soliton solutions and the study of dynamic behavior are currently hot topics. Many experts and scholars are committed to this research, and many very important methods have been proposed. For example, the extended the -expansion method14,15, the Hirota bilinear method16, the extended Kudryashov’s method17, the Sine-Gordon expansion method18, the Khater II method19.
With the maturity of fractional calculus theory, fractional partial differential equations(FPDEs)20–24 can better describe mathematical models with memory and genetic properties in the field of natural sciences. The research on FPDEs mainly focuses on numerical solution25, soliton solution26 and qualitative analysis27. This type of FPDE is a (2+1)-dimensional Heisenberg ferro-magnetic spin chains model with beta fractional derivative, which usually is described as follows28
| 1 |
where is an unknown function. , and are real numbers. is the M-fractional derivative. Equation (1) is commonly applied in fluid mechanics, nonlinear optical system and biological molecular system. In Ref.28, Khatun and his collaborators studied the solion solutions of Eq. (1) by using the extended simple method. However, research on the dynamic behavior of such equations has not yet been reported. Moreover, more general Jacobian function solutions are still under study.
The remaining sections of research are as follows. In “Soliton solutions of Eq. (1)” section, Eq. (1) is transformed into the ordinary differential equation. Moreover, the soliton solutions of Eq. (1) are presented by using the second-order complete discriminant system. In “Dynamical analysis” section, the dynamical analysis of dynamical system and its disturbance systems are studied. In “Conclusion” section, a brief conclusion is given.
Soliton solutions of Eq. (1)
Mathematical derivation
In this section, we consider the complex envelope wave structure (see Refs.28,29)
| 2 |
Plugging wave transformation (2) into Eq. (1) and splitting the imaginary and real parts yield
| 3 |
From the second equation of Eq. (3), we have
From the first equation of Eq. (3), we obtain
| 4 |
where , .
Soliton solutions of Eq. (1)
Multiplying two sides of Eq. (4) by , we obtain
| 5 |
where is an integral constant.
Next, we make some assumptions
| 6 |
Substituting Eq. (6) into Eq. (5), we have
| 7 |
and its integral expression is
| 8 |
here, the complete discriminant system30 for Eq. (8) is
| 9 |
Next, we assume that .
Case I ,
If , we obtain the solution of Eq. (1)
| 10 |
| 11 |
If , we have the solution of Eq. (1)
| 12 |
If , we obtain the solution of Eq. (1)
| 13 |
Case II ,
If , , we obtain the solution of Eq. (1)
| 14 |
| 15 |
If , we obtain the solution of Eq. (1)
| 16 |
Case III ,
If and , we obtain the solution of Eq. (1)
| 17 |
If , we obtain the solution of Eq. (1)
| 18 |
where .
Case iv
If , we obtain the solution of Eq. (1)
| 19 |
where .
Numerical simulation
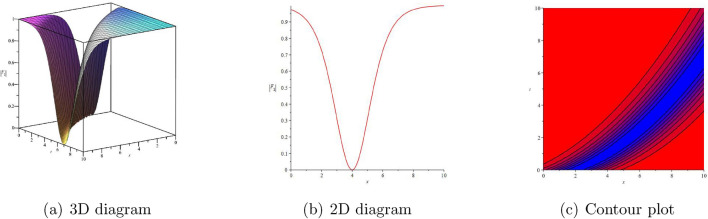
In this section, we use mathematical software of Maple 2022 to draw three-dimensional, two-dimensional, and contour plots of the modulus of solutions and of Eq. (1) when we choose different parameters. From Figs. 1 and 2, it can be seen that the mode length diagrams of these solutions are all dark soliton solutions.
Figure 1.
The solution of (1) with .
Figure 2.
The solution of (1) with .
Dynamical analysis
In this section, the two-dimensional dynamic system (4)31,32 can be described as
| 20 |
its first integral is
| 21 |
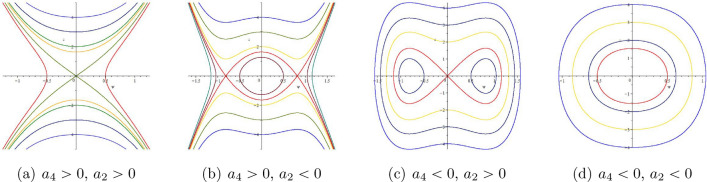
where h is the constant. In this section, we plotted the phase diagram of the system (20) under given parameter conditions as shown in Fig. 3.
Figure 3.
2D phase portraits of (20).
Next, in system (20), we add a small disturbance
| 22 |
By using mathematical software, we can draw the phase diagrams of (22) when considering different initial values and parameters as shown in Figs. 4 and 5.
Figure 4.
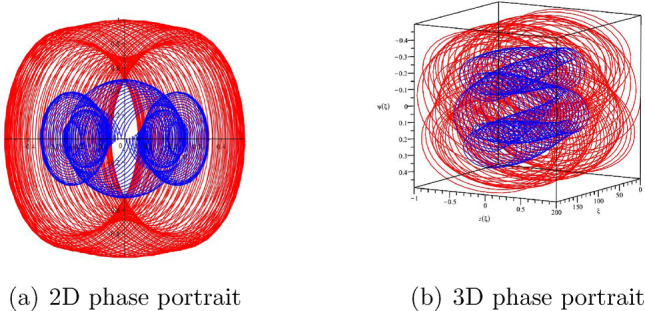
Phase portraits of (22) when , .
Figure 5.
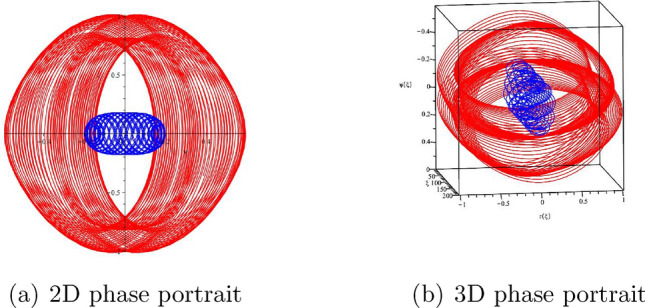
Phase portraits of (22) when , .
Conclusion
In this article, we study the dynamical analysis and the soliton solutions of Eq. (1), respectively. On the one hand, we obtained the soliton solution of Eq. (1). On the other hand, the phase portrait of (20) and its disturbance system was drawn by using mathematical software and dynamic system analysis theory. What’s more, we use mathematical software to draw three-dimensional, two-dimensional, and contour plots of the modulus of solutions and of Eq. (1) when we choose different parameters. Compared with reference28, we not only obtained the dynamic behavior of Eq. (1), but also constructed a more general Jacobian function solution. In future research, we will still study soliton solutions and dynamics of FPDEs.
Author contributions
All authors reviewed the manuscript.
Data availability
The datasets used and/or analyzed during the current study available from the corresponding author on reasonable request.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Majid, S. Z., Asjad, M. I. & Faridi, M. A. Formation of solitary waves solutions and dynamic visualization of the nonlinear Schrödinger equation with efficient techniques. Phys. Scr.99, 065255 (2024). 10.1088/1402-4896/ad4b10 [DOI] [Google Scholar]
- 2.Faridi, W. A. et al. The Lie point symmetry criteria and formation of exact analytical solutions for Kairat-II equation: Paul–Painlevé approach. Chaos Soliton Fract.182, 114745 (2024). 10.1016/j.chaos.2024.114745 [DOI] [Google Scholar]
- 3.Aliyu, A. I. et al. Solitons and complexitons to the (2+1)-dimensional Heisenberg ferromagnetic spin chain model. Int. J. Mod. Phys. B33, 1950368 (2019). 10.1142/S0217979219503685 [DOI] [Google Scholar]
- 4.Aliyu, A. I. et al. Invariant investigation and exact solutions of some differential equations with conformable derivatives. J. Adv. Phys.7, 336–341 (2018). 10.1166/jap.2018.1444 [DOI] [Google Scholar]
- 5.Boakye, G. et al. Some models of solitary wave propagation in optical fibers involving Kerr and parabolic laws. Opt. Quantum Electron.56, 345 (2023). 10.1007/s11082-023-05903-5 [DOI] [Google Scholar]
- 6.Hosseini, K. et al. A generalized nonlinear Schrödinger equation with logarithmic nonlinearity and its Gaussian solitary wave. Opt. Quantum Electron.56, 929 (2024). 10.1007/s11082-024-06831-8 [DOI] [Google Scholar]
- 7.Wu, J. & Huang, Y. H. Boundedness of solutions for an attraction–repulsion model with indirect signal production. Mathematics12, 1143 (2024). 10.3390/math12081143 [DOI] [Google Scholar]
- 8.Li, Z. & Hussain, E. Qualitative analysis and optical solitons for the (1+1)-dimensional Biswas–Milovic equation with parabolic law and nonlocal nonlinearity. Results Phys.56, 107304 (2024). 10.1016/j.rinp.2023.107304 [DOI] [Google Scholar]
- 9.Liu, C. Y. & Li, Z. The dynamical behavior analysis of the fractional perturbed Gerdjikov–Ivanov equation. Results Phys.59, 107537 (2024). 10.1016/j.rinp.2024.107537 [DOI] [Google Scholar]
- 10.Wu, J. & Yang, Z. Global existence and boundedness of chemotaxis-fluid equations to the coupled Solow–Swan model. AIMS Math.8, 17914–17942 (2023). 10.3934/math.2023912 [DOI] [Google Scholar]
- 11.Liu, C. Y. & Li, Z. The dynamical behavior analysis and the traveling wave solutions of the stochastic Sasa–Satsuma Equation. Qual. Theory Dyn. Syst.23, 157 (2024). 10.1007/s12346-024-01022-y [DOI] [Google Scholar]
- 12.Gu, M. S., Peng, C. & Li, Z. Traveling wave solution of (3+1)-dimensional negative-order KdV–Calogero–Bogoyavlenskii–Schiff equation. AIMS Math.9, 6699–6708 (2024). 10.3934/math.2024326 [DOI] [Google Scholar]
- 13.Aliyu, A. I., Li, Y. J. & Baleanu, D. Single and combined optical solitons, and conservation laws in (2+1)-dimensions with Kundu–Mukherjee–Naskar equation. Chin. J. Phys.63, 410–418 (2020). 10.1016/j.cjph.2019.11.001 [DOI] [Google Scholar]
-
14.Mohanty, S. K. M. et al. The exact solutions of the-dimensional Kadomtsev–Petviashvili equation with variable coefficients by extended generalized
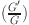 -expansion method. J. King Saud Univ. SCI.35, 102358 (2023). 10.1016/j.jksus.2022.102358 [DOI] [Google Scholar]
-expansion method. J. King Saud Univ. SCI.35, 102358 (2023). 10.1016/j.jksus.2022.102358 [DOI] [Google Scholar] -
15.Ali, R. & Tag-eldin, E. A comparative analysis of generalized and extended
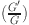 -expansion methods for travelling wave solutions of fractional Maccari’s system with complex structure. Alexdr. Eng. J.799, 508–530 (2023). 10.1016/j.aej.2023.08.007 [DOI] [Google Scholar]
-expansion methods for travelling wave solutions of fractional Maccari’s system with complex structure. Alexdr. Eng. J.799, 508–530 (2023). 10.1016/j.aej.2023.08.007 [DOI] [Google Scholar] - 16.Li, Y., Yao, R. X. & Lou, S. Y. An extended Hirota bilinear method and new wave structures of (2+1)-dimensional Sawada–Kotera equation. Appl. Math. Lett.145, 108760 (2023). 10.1016/j.aml.2023.108760 [DOI] [Google Scholar]
- 17.Zayed, E. M. E. et al. Optical solitons in fiber Bragg gratings having Kerr law of refractive index with extended Kudryashov’s method and new extended auxiliary equation approach. Chin. J. Phys.66, 187–205 (2020). 10.1016/j.cjph.2020.04.003 [DOI] [Google Scholar]
- 18.Das, P. K. et al. A comparative study between obtained solutions of the coupled Fokas–Lenells equations by Sine–Gordon expansion method and rapidly convergent approximation method. Optik283, 170888 (2023). 10.1016/j.ijleo.2023.170888 [DOI] [Google Scholar]
- 19.Khater, M. M. A. & Alfalqi, S. H. Solitary wave solutions for the (1+1)-dimensional nonlinear Kakutani–Matsuuchi model of internal gravity waves. Results Phys.59, 107615 (2024). 10.1016/j.rinp.2024.107615 [DOI] [Google Scholar]
- 20.Rafiq, M. N. et al. New traveling wave solutions for space-time fractional modified equal width equation with beta derivative. Phys. Lett. A446, 128281 (2022). 10.1016/j.physleta.2022.128281 [DOI] [Google Scholar]
- 21.Donfack, E. F., Nguenang, J. P. & Nana, L. On the traveling waves in nonlinear electrical transmission lines with intrinsic fractional-order using discrete tanh method. Chaos Soliton Fract.131, 109486 (2020). 10.1016/j.chaos.2019.109486 [DOI] [Google Scholar]
- 22.Feng, Q. H. A new analytical method for seeking traveling wave solutions of space-time fractional partial differential equations arising in mathematical physics. Optik130, 310–323 (2017). 10.1016/j.ijleo.2016.10.106 [DOI] [Google Scholar]
- 23.Wang, J. & Li, Z. A dynamical analysis and new traveling wave solution of the fractional coupled Konopelchenko–Dubrovsky model. Fract. Fract.8, 341 (2024). 10.3390/fractalfract8060341 [DOI] [Google Scholar]
- 24.Odabasi, M. A new analytical method for seeking traveling wave solutions of space-time fractional partial differential equations arising in mathematical physics. Chin. J. Phys.64, 194–202 (2020). 10.1016/j.cjph.2019.11.003 [DOI] [Google Scholar]
- 25.Ali, K. K. et al. The kink solitary wave and numerical solutions for conformable non-linear space-time fractional differential equations. Results Phys.58, 107423 (2024). 10.1016/j.rinp.2024.107423 [DOI] [Google Scholar]
- 26.Wang, H. L. et al. Propagation of three-dimensional optical solitons in fractional complex Ginzburg–Landau model. Phys. Lett. A498, 129357 (2024). 10.1016/j.physleta.2024.129357 [DOI] [Google Scholar]
-
27.Rahul Kumar, R. et al. Symmetry reductions and qualitative analysis of time fractional
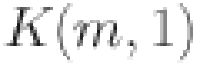 equation. Part. Differ. Equ. Appl. Math.9, 100603 (2024). [Google Scholar]
equation. Part. Differ. Equ. Appl. Math.9, 100603 (2024). [Google Scholar] - 28.Khatun, S., Hoque, F. & Ali, M. Z. Spin dynamic soliton in ferromagnetic materials over the (2+1)-dimensional beta fractional HFSC model. Results Phys.59, 107534 (2024). 10.1016/j.rinp.2024.107534 [DOI] [Google Scholar]
- 29.Abdon, A., Dumitru, B. & Ahmed, A. Analysis of time-fractional Hunter–Saxton equation: A model of neumatic liquid crystal. Open Phys.14, 145 (2016). 10.1515/phys-2016-0010 [DOI] [Google Scholar]
- 30.Liu, C. S. Applications of complete discrimination system for polynomial for classifications of traveling wave solutions to nonlinear differential equations. Comput. Phys. Commun.181, 317–324 (2010). 10.1016/j.cpc.2009.10.006 [DOI] [Google Scholar]
- 31.Iqbal, M. et al. Extraction of newly soliton wave structure to the nonlinear damped Korteweg-de Vries dynamical equation through a computational technique. Opt. Quantum Electron.56, 1189 (2024). 10.1007/s11082-024-06880-z [DOI] [Google Scholar]
- 32.Iqbal, M. et al. Dynamical study of optical soliton structure to the nonlinear Landau–Ginzburg–Higgs equation through computational simulation. Opt. Quantum Electron.56, 1192 (2024). 10.1007/s11082-024-06401-y [DOI] [Google Scholar]
- 33.Hosseini, K. et al. Lie symmetries, bifurcation analysis, and Jacobi elliptic function solutions to the nonlinear Kodama equation. Results Phys.54, 107129 (2023). 10.1016/j.rinp.2023.107129 [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The datasets used and/or analyzed during the current study available from the corresponding author on reasonable request.