Stable organic radical qubits and their applications in quantum information science

Abstract

The past century has witnessed the flourishing of organic radical chemistry. Stable organic radicals are highly valuable for quantum technologies thanks to their inherent room temperature quantum coherence, atomic-level designability, and fine tunability. In this comprehensive review, we highlight the potential of stable organic radicals as high-temperature qubits and explore their applications in quantum information science, which remain largely underexplored. Firstly, we summarize known spin dynamic properties of stable organic radicals and examine factors that influence their electron spin relaxation and decoherence times. This examination reveals their design principles and optimal operating conditions. We further discuss their integration in solid-state materials and surface structures, and present their state-of-the-art applications in quantum computing, quantum memory, and quantum sensing. Finally, we analyze the primary challenges associated with stable organic radical qubits and provide tentative insights to future research directions.

Graphical abstract

Public summary

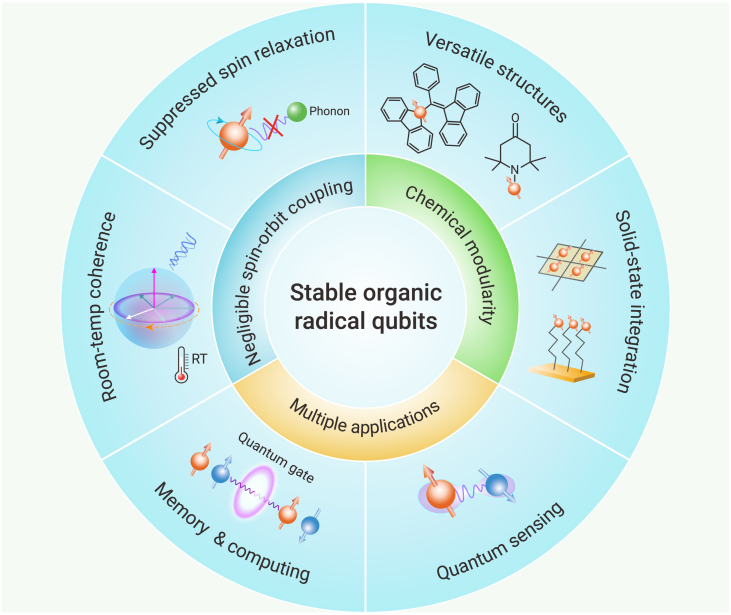
• •Stable organic radicals behave as tunable electron spin qubits with room-temperature quantum coherence.
• •Molecular structures, environment, and operation conditions affect electron spin dynamics of radical qubits.
• •Radical qubits could be integrated into polymers, microporous frameworks, and thin films.
• •Radical qubits enable quantum computing, quantum memory, and quantum sensing.

Introduction

Quantum information science (QIS) takes advantage of unique features of quantum mechanics—superposition and entanglement—for information processing, enabling revolutionary technologies including quantum computing, quantum communication, and quantum sensing.^1,2,3,4 The development of QIS has led to quantum computers that outperform classical supercomputers in specific tasks,^5,6 eavesdropping-free communication between a satellite and a ground station,^7,8 and in vivo metrology of magnetic field and temperature with unprecedented sensitivity and spatial resolution.^9,10 According to the DiVincenzo’s criteria, physical implementation of the basic unit of quantum information, i.e., qubit, requires two-level quantum systems that are coherent, initializable, controllable, measurable, and scalable.¹¹ These criteria have inspired extensive investigations on a myriad of qubit candidates, spanning superconducting circuits,¹² semiconductor quantum dots,¹³ trapped ions,¹⁴ neutral atoms,¹⁵ nuclear spins,^16,17 solid-state electron spin defects,^18,19,20 photons,² Majorana zero modes,²¹ etc. However, none of them is perfect for all QIS technologies—the physical nature of each candidate determines its applicability and limitation.²² For instance, superconducting circuits are highly scalable thanks to their compatibility with concurrent semiconductor technologies, making them ideal building blocks for large-scale quantum computers, yet the ultralow operation temperature (tens of millikelvin) restricts their utility in ambient conditions.¹² Therefore, with the growing interests in applying QIS in various scenarios, such as chemical-specific quantum sensing in biological systems, there is a high demand for new types of qubits.

With atomic-level designability and tunability, molecular electron spin qubits, i.e., molecules with unpaired electrons, hold the promise for new opportunities of QIS.^{23,24,25,26,27} For instance, chemical-recognizing functional groups can be incorporated for highly selective quantum sensing,^28,29,30 and multi-level spin states can be engineered to simplify the implementation of quantum algorithms.³¹ Recent studies have revealed design principles for molecular electron spin qubits with long-lived quantum coherence,³² high operating temperature,^33,34 and optical addressability.^{35,36,37,38,39,40} The removal of environmental nuclear spins improves the decoherence time of a vanadium-based coordination complex approaching 1 ms at cryogenic temperature,³² the suppression of orbital angular momentum gives rise to room temperature coherence of an yttrium-based organometallic molecule,⁴¹ and tailor-designed triplet states enable optical initialization and readout of chromium-based and vanadium-based coordination complexes.^38,42,43 Furthermore, coherent addressing of single-molecular electron spin qubits has been achieved with state-of-the-art single-molecule spectroscopy,^35,36,37 scanning tunneling microscopy,^44,45 atomic force microscopy,⁴⁶ and quantum metrology using a nitrogen-vacancy center in diamond.⁴⁷ These advancements have led to prototype demonstrations of molecular QIS technologies, such as a universal two-qubit quantum logic gate with a radical pair,^48,49 quantum error correction with an endohedral fullerene qudit,³¹ quantum sensing of ¹H and ²H with a Cu²⁺-containing metal-organic framework (MOF),⁵⁰ and intramolecular quantum teleportation with a donor-acceptor molecule.⁵¹ So far, these studies have been focused on coordination complexes^27,52 and photo-generated radicals,⁵³ which typically suffer from low operating temperature and/or short lifetimes, compromising their applications in ambient conditions. Herein, we sought to revisit stable organic radicals, whose electron spin dynamics has been extensively studied over two decades, yet whose applications in QIS remain underexplored.⁵⁴

Organic radicals are open-shell molecules with one or more unpaired electrons, which generally exhibit short lifetimes and high reactivity.⁵⁵ Delocalization and steric hindrance could stabilize organic radicals so that they retain unpaired electrons in ambient conditions.^56,57 Moreover, they could be modified with functional groups to inherit optical,^58,59 electrochemical,^60,61 and magnetic properties,⁶² as well as recognition capabilities.^63,64,65 Their stability and versatile functionalities enable applications in synthesis,^66,67 sensing,⁶⁸ optoelectronics,⁶⁹ spintronics,⁷⁰ and biology.⁷¹ Stable organic radicals also display advantageous spin dynamic properties: they are composed of light elements (C, H, N, O, P, S, etc.) with negligible spin-orbit coupling,^72,73,74 which give rise to quantum coherence at room temperature and in complex chemical environments. Hence, stable organic radicals have been widely used as spin labels for protein structure determination and as polarizing agents for dynamic nuclear polarization.^75,76,77

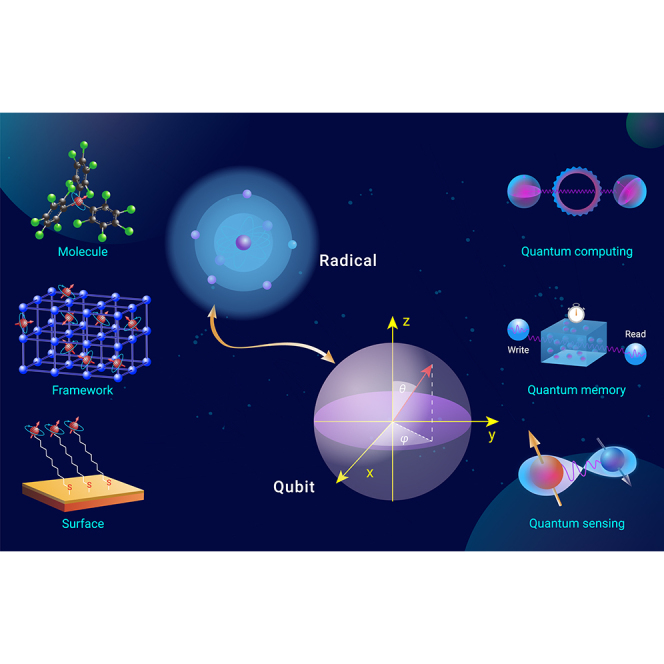
In this review, we highlight the great potential of stable organic radical qubits in QIS applications (Figure 1), which has attracted little attention so far. Following a summary of known stable organic radical qubits, we introduce their electron spin dynamic properties, i.e., figure of merits of qubit performance, with the emphasis on their mechanisms and optimization strategies. We then summarize trials of integrating stable organic radical qubits into solid-state systems and present prototype applications in various quantum information technologies. Finally, although coordination complexes,^27,52 endohedral fullerenes,^31,78,79,80 photo-generated radicals,^53,81,82,83 and injected radicals in devices^84,85 are beyond our scope, we suggest that interested readers explore these alternative molecular qubit systems through additional literature.

Figure 1.

Introduction to stable organic radical qubits

Stable organic radical qubits

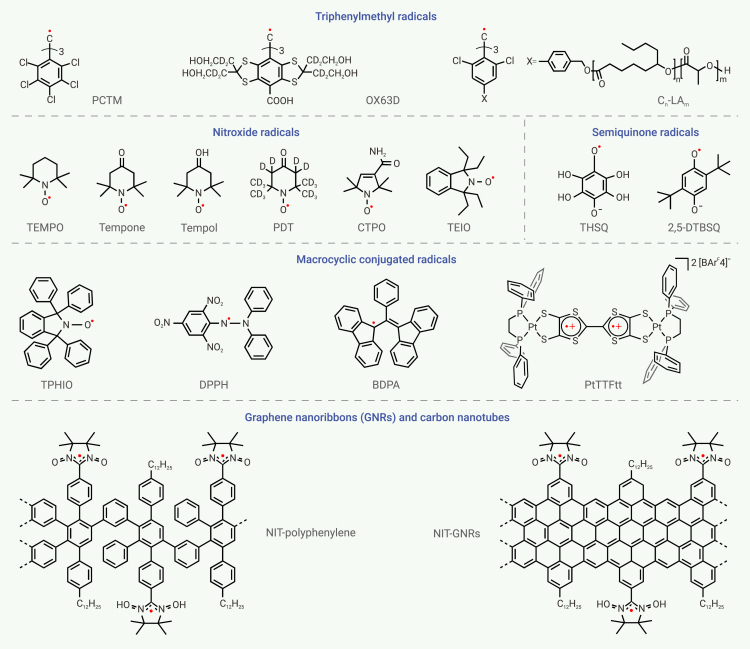
Tens of stable organic radicals have been experimentally demonstrated to be qubits, which are summarized in Figures 2 and S1−S4. These include radicals based on triphenylmethyl, nitroxide, semiquinone, and conjugated macrocyclic structural motifs. The triphenylmethyl radical and its derivatives host an electron spin on the central carbon atom, whose stability stems from large steric hindrance and conjugation pathways provided by the surrounding benzene rings.⁸⁶ The nitroxide radicals, such as (2,2,6,6-tetramethylpiperidin-1-yl)oxyl (TEMPO), possess an unpaired electron residing on the N-O site and stabilized by delocalization effects.^87,88 o-Phenols and p-phenols can be oxidized to form semiquinone radicals whose electron spins are concentrated on oxygen atoms and stabilized by delocalization.⁸⁹ Other radicals, such as tetrathiafulvalene (TTF), 1,3-bisdiphenylene-2-phenylallyl (BDPA), and 2,2-diphenyl-1-picrylhydrazyl, possess unpaired electrons on highly conjugated and sterically hindered backbones.^90,91 In addition, graphene nanoribbons (GNRs)^92,93,94 and carbon nanotubes⁹⁵ could also host stable radicals via chemical modification. All these stable radicals are potential candidates as qubits as they exhibit decent spin dynamic properties and coherent addressability. In this review, we refer to stable organic radical qubits as radical qubits for simplicity.

Figure 2.

Schemes of selected stable organic radical qubits

Electron spin dynamics

QIS applications require qubits to maintain coherence during quantum manipulation and readout.¹¹ Regarding the radical qubit, this demand translates to long electron spin relaxation time (T₁) and decoherence time (T₂).²³ T₁ describes the time that an electron spin takes to relax from a nonequilibrium state to thermodynamic equilibrium (Figure S5A). T₂ describes the time spanned for the electron spin to lose its phase coherence (Figure S5B). In the literature of radical qubits, T₂ is often referred to as the dephasing time or phase memory time (T_m), which encompasses all dephasing processes. For consistency, we use T_m exclusively in this review. Another criterion of the qubit is the ability to manipulate its quantum state through single-qubit quantum logic gates, i.e., arbitrary rotation on the Bloch sphere (Figure S5C), which could be demonstrated via Rabi oscillations. Both T₁ and T_m need to exceed the duration of a quantum gate operation, which is typically tens of nanoseconds.^54,96 The T₁, T_m, and manipulability of a radical qubit are typically characterized by pulse electron paramagnetic resonance (EPR) spectroscopy with specifically designed microwave pulse sequences (Figure S6; see details in the supplemental information).

The spin relaxation and decoherence mechanisms have been summarized in previous reviews, which are highly recommended to interested readers.^54,96 Here, we briefly introduce core concepts of electron spin dynamics. The spin relaxation is induced by exchanging energy of the spin with environment through spin-spin interaction and spin-lattice coupling. The former, namely the cross-relaxation, takes place through flip-flop of nearby electron spins and nuclear spins. The latter is associated with absorption and/or emission of phonons (lattice vibrations) through various processes including direct, Raman, Orbach, local-mode, thermally activated, and tumbling-dependent processes, which are summarized in Table S1. In the direct process, the spin relaxes by emitting a phonon whose energy is equal to the Zeeman splitting; hence, it is a one-phonon relaxation process. The spin may also undergo two-phonon relaxation, where it transitions to a virtual energy level (Raman process) or a low-lying excited state (Orbach process) by absorbing a phonon and relaxing to its ground state by emitting another phonon. The local-mode process is caused by the localized molecular vibration instead of the lattice vibration. The thermally activated process involves a motion, such as rotation of a methyl group or hydrogen hopping within a hydrogen bond, whose rate is comparable with the Larmor frequency of the spin. Moreover, for molecules in a solution, the tumbling causes spin rotation and modulation of anisotropic interactions, introducing an additional source of relaxation. Finally, electron spins in semiconductors may encounter additional relaxation mechanisms, such as Elliott-Yafet mechanism and D’yakonov-Perel’ mechanism, which are beyond the scope of this review.⁹⁷

The spin relaxation induces decoherence as well—T₁ sets the upper limit of T_m with T_m ≤ 2T₁.^98,99,100 Nonetheless, in most radicals, the decoherence is mainly caused by environmental magnetic noise that modifies Larmor frequencies of electron spins and accordingly reduces the phase coherence of their quantum states. Such a decoherence effect manifests itself in two types of processes: instantaneous diffusion and spectral diffusion.^54,96 The instantaneous diffusion takes place if the electron spin of interest and a nearby electron spin display similar Larmor frequencies. In this case, applying a resonant pulse simultaneously rotates both spins. The rotation of the latter instantaneously alters the magnetic field experienced by the former, which causes decoherence. The spectral diffusion is caused by nuclear spins, electron spins, and rotary functional groups (e.g., methyl and phenyl groups), etc. These species may introduce stochastic magnetic noise that leads to decoherence of the electron spin of interest during the free evolution time. In addition, for electron spins with anisotropic g-factors or anisotropic hyperfine interactions, molecular tumbling in solution effectively acts as magnetic noise by modulating the anisotropy, thus it also results in decoherence.^54,96

In Tables 1 and S2, we have compiled a summary of experimentally demonstrated radical qubits, along with their corresponding spin dynamic properties, to the best of our knowledge. The majority of radical qubits exhibit coherence at room temperature with T₁ consistently surpassing T_m. At room temperature, most radicals exhibit T₁ values on the order of tens of microseconds, whereas their T_m values are mostly on the order of microseconds or hundreds of nanoseconds. Notably, several radicals based on GNRs could display exceptionally long T₁ at room temperature, approaching nearly 1 ms when dissolved in d₁₄-o-terphenyl.^92,93 Moreover, identical radical qubits may display remarkably different values for T₁ and T_m when characterized under different conditions. Even under the same condition, subtle adjustments to the structure of radicals and choice of solvents can induce significant variations. Therefore, spin relaxation and decoherence processes of a radical qubit could be tweaked by molecular design and environmental engineering. Herein, we discuss the influence of molecular structure, temperature, solvent, Larmor frequency, radical concentration, and pulse sequence on the spin relaxation and decoherence processes, aiming at providing a framework of designing radical qubits and interpreting their spin dynamic properties.

Table 1.

T₁ and T_m of selected stable organic radical qubits

Radicala	Concentration / mmol·L−1	Frequency / GHz	Solvent	Temperature / K	T1 / μs	Tm / μs	Reference
OX63D	1	9.5	H2O: glycerol = 4:6	77	3334a	NAb	Chen et al.101
		95			5000a
OX63D	NAb	9.5	MeOH	300	16.5	5.8	Kuzhelev et al.102
		34			15.6	1.8
OX63D	NAb	9.5	H2O	300	16.0	7.3	Kuzhelev et al.102
		34			15.3	2.2
OX63D	NAb	9.5	D2O	300	16.1	7.6	Kuzhelev et al.102
		34			16.1	2.0
OX63D	NAb	9.5	CHCl3	300	11.4	9.1	Kuzhelev et al.102
		34			11.2	5.4
BDPA	0.0007	9.5	Toluene	Ambient	12c	9.8c	Meyer et al.103
DPPH	0.012	9.5	Toluene	Ambient	2.0c	1.3c	Meyer et al.103
PDT	0.25	9.5	H2O	Ambient	0.56	0.59	Meyer et al.103
2,5-DTBSQ	0.3	9.5	Ethanol	Ambient	7.8c	3.2c	Elajaili et al.104
TEMPO	1.0	9.5	H2O: glycerol = 1:1	295a	2.00c	NAb	Sato et al.105
Tempone	0.3	9.5	H2O: glycerol = 1:1	100	100c	5c	Nakagawa et al.106
Tempol	3	9.5	Sucrose octaacetate	298a	19.95c	NAb	Sato et al.107
DTBN	3	9.5	Sucrose octaacetate	250a	5.6c	0.40c	Sato et al.107
TEIO	3	9.5	Sucrose octaacetate	300a	25.12c	0.63c	Sato et al.107
PCTM	0.2-0.5	9.5	Toluene : CHCl3 = 4:1	298	10c	NAb	Kathirvelu et al.108
PtTTFtt	0.05	9.5	DCM	298	1.44c	0.34c	McNamara et al.109
NIT-polyphenylene	NAb	9.4	Powder	300a	1.43c	0.6c	Slota et al.92
NIT-GNRs	NAb	9.4	Powder	300a	1.43c	0.2c	Slota et al.92
C50-LA90	1%d,e	9.73	NAb	30	2102	0.186	Hou et al.110
		9.65		298	25.02	0.148
C50-LA140	0.7%d,e	9.73	NAb	30	3522	0.300	Hou et al.110
		9.65		298	29.62	0.213
C50-LA400	0.4%d,e	9.73	NAb	30	5173	0.377	Hou et al.110
		9.65		298	29.23	0.318
MgHOTP	0.66%e	9.4	NAb	296	10.55	0.153	Sun et al.111
				296	21.61f	0.202f
TAPPy-NDI	0.01%e	9.4	NAb	100	790	1.26	Oanta et al.112
				296	30.2	0.49
Ni-HATI_iPr	1%e	9.7	NAb	100	3c	0.09c	Lu et al.113
PTCM	0.1%e	9.26	NAb	100	150c	1.5c	Dai et al.114
				298	35.6	1.08
TEMPO SAM	NAb	9.47	NAb	10	9200	13.53	Tesi et al.115
BTEV-BTR	1%e	9	NAb	80	386	4.39	Poryvaev et al.116

See the full collection of data in Table S2.

^aAbbreviations are consistent with those in Figures S1-S4.

^bNot available.

^cValue estimated from a figure in the reference.

^dvalue estimated from the synthetic condition.

^eMolar percentage of the radical.

^fMgHOTP soaked in THF.

Molecular structure

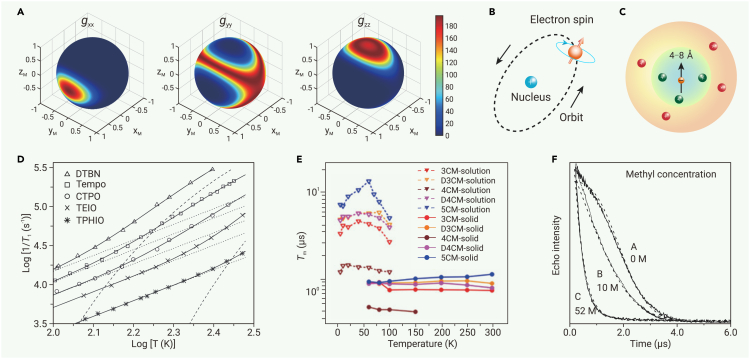
The structure of a molecule determines intrinsic properties of its electron spin (g-anisotropy, spin multiplicity, etc.), contributes to the phononic and magnetic environment, and dictates their interactions. The spin relaxation is mainly affected by spin-orbit coupling and molecular rigidity.⁹⁹ A strong spin-orbit coupling facilitates spin relaxation because it allows the motion of an electron (e.g., vibration) to affect its spin state (Figure 3B). It also gives rise to g-anisotropy that intensifies the tumbling-induced relaxation in solution (Figure 3A).¹¹⁷ As the strength of spin-orbit coupling decreases with decreasing atomic number, radical qubits that consist of only light elements exhibit weak spin-orbit coupling and in turn suppressed spin relaxation.^72,73,74 Therefore, they could maintain microsecond-scale T₁ even at room temperature (Tables 1 and S2), which is difficult for metal-based molecular qubits with only a few exceptions.^{33,34,41,118,119,120} Another strategy to slow down spin relaxation is to reduce the density of states of low-frequency phonons that couple strongly to the electron spin.^{121,122,123,124,125,126,127,128} This often translates to a rigid structure enforced by conjugation and steric hindrance. For instance, improving the degree of conjugation of and introducing bulky groups into nitroxide radicals consistently increase T₁ across a wide range of temperature (Figure 3D),¹⁰⁷ and incorporating radicals onto GNRs, i.e., hydrocarbons with extended conjugation, gives rise to T₁ up to 1 s at 5 K.^92,93

Figure 3.

Influence of molecular structures on spin dynamics

(A) g-Anisotropy mapped on a Bloch sphere calculated with EasySpin.¹²⁹

(B) Illustration of spin-orbit coupling.

(C) Illustration of spin diffusion barrier (inner circle). Green nuclei are within the spin diffusion barrier, and the red ones are out of it.

(D) Influence of conjugation and steric hindrance on T₁ of various nitroxide radicals dissolved in sucrose octaacetate. Dotted and dashed lines represent contributions from the Raman process and thermally activated process, respectively, and solid lines represent their sums. Reproduced from Sato et al.¹⁰⁷ with permission from Taylor & Francis, copyright 2007.

(E) Influence of the number of chlorine atoms substituted on triphenylmethyl radicals on their T_m values. The triphenylmethyl radical was either dissolved in d₈-toluene solution or diluted in powders of hydrogenated diamagnetic analogues. 5CM is the same as PCTM (Figure 2). Reproduced from Dai et al.¹¹⁴ with permission from John Wiley & Sons, copyright 2018.

(F) Influence of concentration of methyl groups in solution on the T_m of tempone radical. Reproduced from Zecevic et al.¹³⁰ with permission from Taylor & Francis, copyright 1998.

The major sources of electron spin decoherence are nearby nuclear spins.⁹⁶ The influence of a nuclear spin depends on its distance from the electron spin and its magnetic moment. When the nuclear spin resides within a certain radius (typically 4−8 Å depending on the magnetic moment) of the electron spin, a distance called the spin-diffusion barrier, they are strongly coupled by hyperfine/superhyperfine interactions (Figure 3C).^96,131,132 This detunes the nuclear spin to other more distant nuclei in the bath, reducing its participation in nuclear flip-flop events. As a result, the nuclear spin within the spin-diffusion barrier exerts little contribution to decoherence. In contrast, when the nuclear spin is beyond the spin-diffusion barrier, it tends to reduce T_m of the electron spin and its decoherence effect scales with the magnetic moment.¹³¹ Therefore, a useful design strategy for improving coherence is to reduce the number of nuclear spins beyond the spin-diffusion barrier. For radicals that can rarely avoid hydrogen atoms, deuteration could significantly improve T_m because ²H has a much smaller magnetic moment than ¹H. Besides ²H, ³⁵Cl and ³⁷Cl have low nuclear gyromagnetic ratios, offering viable alternatives to ¹H for extending T_m. For instance, substituting chlorine for hydrogen onto aromatic rings of the triphenylmethyl radical significantly enhances its T_m as showcased in the recent investigation by Dai et al. (Figure 3E).¹¹⁴ Besides nuclear spins, motions of functional groups, e.g., rotation of methyl groups and liberation of phenyl groups, could also generate magnetic noise that causes decoherence.⁵⁴ Zecevic et al. systematically examined the impact of methyl groups on the T_m of the tempone radical. They deliberately mixed various solvents to maintain a relatively constant total proton concentration while tuning the ratio of methyl to non-methyl protons. They observed that an elevated concentration of methyl protons expedites decoherence (Figure 3F).¹³⁰ Thus, it is advised to avoid rotary groups through molecular design to improve T_m.

Temperature

Temperature affects the harmonicity and excitation of phonon modes of a radical, which in turn influences its spin-lattice coupling. Depending on the coupling mechanism, spin relaxation processes exhibit different temperature dependencies (Figure 4A; Table S1) and dominate in different temperature regions. Cross-relaxation is typically temperature independent.^133,134 The direct relaxation rate (1/T₁) is linear to temperature and is typically salient at low temperatures (mostly below 10 K). The Raman process is significant at higher temperature. Its relaxation rate often exhibits exponential dependence on temperature.^135,136 The exponent may be 7−9 if only acoustic phonons are involved in spin-lattice coupling and may appear as 3−5 if optical phonons are involved as well. Moreover, the exponent is close to 2 in the high-temperature limit where the thermal energy well exceeds the energies of phonons participating in spin-lattice coupling. At even higher temperature, thermally activated and local-mode processes may dominate the spin relaxation. The thermally activated relaxation rate levels off when the thermal energy is well above the activation energy, whereas the local-mode processes become faster as temperature increases. The relaxation rate of the Orbach process also increases with increasing temperature, and its contribution is especially significant when the thermal energy exceeds the excitation energy. In addition, in fluid solutions, the tumbling process is typically dominant, and the temperature dependence of the tumbling relaxation rate is correlated to that of the solvent viscosity, which is discussed in the next sub-section.^54,96

Figure 4.

Influence of temperature on spin dynamics

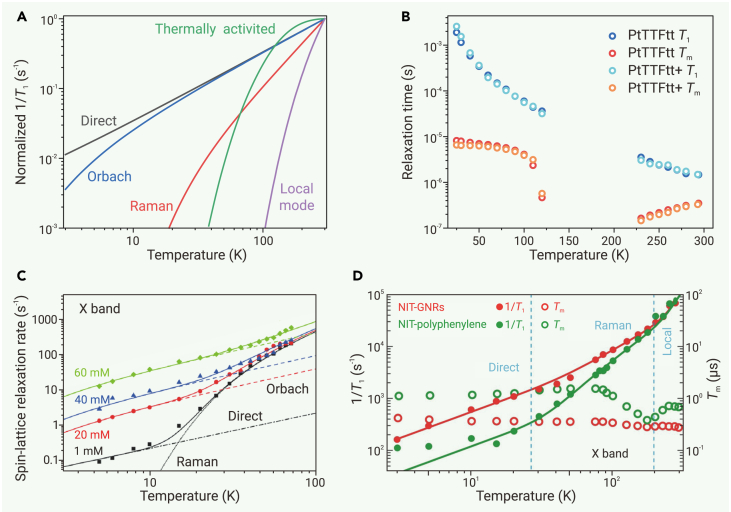
(A) Temperature dependence of spin-lattice relaxation rate under various relaxation processes normalized to the 1/T₁ at 300 K. Simulations were performed based on corresponding equations in Table S1, and simulation parameters of Orbach, Raman, thermally activated, and local-mode processes are arbitrary.

(B) Temperature dependence of T₁ and T_m for PtTTFtt and PtTTFtt+. Reproduced from McNamara et al.¹⁰⁹ ©The Authors, some rights reserved; distributed under CC-BY-NC-ND 4.0 (http://creativecommons.org/licenses/by-nc-nd/4.0/).

(C) Temperature dependence of spin-lattice relaxation rate for d₂₄-OX063 with various concentrations. Reproduced from Chen et al.¹⁰¹ with permission from Royal Society of Chemistry, copyright 2016.

(D) Temperature dependence of 1/T₁ and T_m for NIT-GNRs and NIT-polyphenylene. Reproduced from Slota et al.⁹² with permission from Springer Nature, copyright 2018.

Fitting the temperature dependence of T₁ with the formulae summarized in Table S1 could reveal processes involved in spin relaxation at certain temperature, and it can offer valuable insights into spin dynamics, including spin-phonon coupling strengths, Debye temperatures, activation energies of specific intramolecular motions, molecular vibrations strongly coupled to the spin, and low-lying excited spin states, among other factors. For instance, fitting the T₁ of d₂₄-OX063 collected at 5−100 K with the abovementioned spin relaxation mechanisms shows that the direct process dominates below 10 K, whereas the Raman and Orbach processes play major roles above 10 K (Figure 4C).¹⁰¹ The fitting further revealed the Debye temperature of 135 K and an excitation energy of 0.3 meV. This information is critical to understand the spin dynamics of this radical and its performance in dynamic nuclear polarization. Similarly, in polyphenylene and GNR modified by nitronyl nitroxide radicals (NIT-polyphenylene and NIT-GNR, respectively), fitting variable-temperature T₁ reveals direct, Raman, and local mode processes dominating below 25 K, between 25 and 200 K, and above 200 K, respectively (Figure 4D).⁹² The local mode process is associated with a characteristic energy of 1,354 cm⁻¹, which indicates a dominant contribution from the stretch of the N-O bond to the spin relaxation.

The temperature dependence of T_m is mainly determined by nuclear spin diffusion, motional effects, molecular tumbling processes, and spin relaxation.^54,96 They dominate at different temperature regions. At low temperature, intramolecular motions are quenched, solvent is frozen, and spin relaxation is slow, so the decoherence is mainly caused by nuclear spin diffusion. T_m is independent of temperature in this regime, which has been observed in trityl-CH₃ and trityl-CD₃ radicals.¹³⁷ As temperature increases, motions, e.g., rotation of methyl groups, become active, which causes decoherence and significantly reduces T_m. In frozen solutions, as the temperature approaches the glass transition temperature of the solvent, the complex motion of the solvent molecules can shorten the T_m strongly to make coherence undetectable. In contrast, when the temperature further increases well above the solvent’s melting point, the rapid molecular tumbling tends to average out the g-anisotropy and mitigate the impact of the surrounding environment, leading to an increase in T_m with increasing temperature. Finally, in both fluid solution and solid state, T₁ becomes short at high temperature, providing the upper limit of T_m. These temperature dependencies of T_m manifest themselves in two TTF-based coordination complexes, mono-radicaloid PtTTFtt+ and diradicaloid PtTTFtt, dissolved in a mixture of dichloromethane and toluene.¹⁰⁹ The T_m of each complex exhibits a small variation within the temperature range of 20–90 K, declines sharply as the temperature further increases, and becomes unmeasurable at 130–220 K (melting points of toluene and dichloromethane are 178.1 and 176.5 K, respectively). Above 220 K, where the solution is fluid, T_m increases with increasing temperature (Figure 4B).

Solvent and Larmor frequency

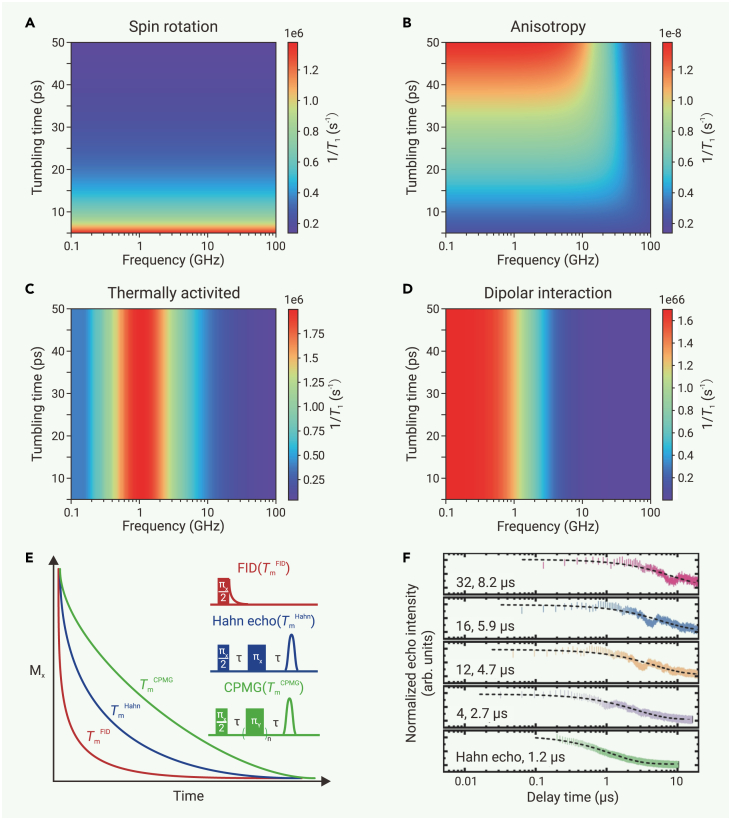
The impact of solvent on spin relaxation mainly stems from its viscosity and protons (hydrogen atoms). In fluid solution, spin relaxation processes mainly include tumbling-induced spin rotation and modulation of anisotropic interactions comprising g-anisotropy, A-anisotropy, and dipolar coupling with solvent nuclei (Figures 5A–5D).⁵⁴ An increase in viscosity enhances collisions between spin centers and solvent molecules, intensifying the effects of g-anisotropy and A-anisotropy that reduce T₁ and T_m. In addition, the tumbling correlation time, ${\tau }_R$, increases with increasing viscosity, which may alter the spin relaxation mechanism as well as the dependence of T₁ on the Larmor frequency of electron spin ($\omega$).¹³⁸ As exemplified in solutions of the PDT radical,¹¹⁷ when ${\left(\omega {\tau }_R\right)}^2\ll 1$, the tumbling is fast, which effectively averages out the g-anisotropy and A-anisotropy, rendering the spin system isotropic. As a result, T₁ is governed by the spin rotation that is frequency independent. When ${\left(\omega {\tau }_R\right)}^2$ is non-negligible, the modulation of anisotropic interaction is significant, and T₁ becomes frequency dependent—T₁ increases with increasing ω. (The frequency dependencies of T₁ and T_m remain underexplored likely due to limited availability of multi-band EPR spectrometers; see further discussions in the supplemental information.).

Figure 5.

Influence of Larmor frequency and pulse sequence on spin dynamics

(A−D) Spin relaxation driven by (A) spin rotation, (B) modulation of g-anisotropy and A-anisotropy, (C) thermally activated process, and (D) dipolar interaction, respectively, with solvent nuclei under various tumbling times and Larmor frequencies. Simulations were performed based on the corresponding equations in Table S1, and simulation parameters are arbitrary.

(E) FID, Hahn echo, and CPMG decay curves. Reproduced from Mirzoyan et al.¹³⁹ with permission from John Wiley & Sons, copyright 2021.

(F) Echo decay curves acquired by Hahn echo or CPMG sequences with various numbers of π_Y pulses for chemically modified carbon nanotubes. Reproduced from Chen et al.⁹⁵; distributed under CC-BY 4.0 (http://creativecommons.org/licenses/by/4.0/).

Protons in solvent molecules typically facilitate spin relaxation and decoherence. Their nuclear spins act as environmental magnetic noise that weakly couples to electron spins through superhyperfine interaction, reducing both T₁ and T_m via spectral diffusion. Deuteration helps relieve this problem because the nuclear magnetic moment of deuterium is six times less than that of the proton. For instance, at 250 MHz and room temperature, the trityl-CD₃ exhibits T₁ and T_m of 12.2 and 11 μs in H₂O, respectively, while these values become 16.4 and 14 μs in D₂O.¹³⁸ Furthermore, N- and O-based radicals readily form hydrogen bonds with protons of polar solvent molecules, which facilitates spin relaxation through proton hopping within the hydrogen bonds, a thermally activated process. This phenomenon is evident in the study on semiquinone radicals dissolved in alcoholic solvent.^54,96 Replacing OH with OD in the solvent approximately halves the relaxation rate.¹⁰⁴ Complete deuteration of the solvent further improves T₁ and almost eliminates its frequency dependence, indicating that thermally activated proton hopping dominates spin relaxation in this system (Figure S7).

Radical concentration

The radical concentration determines spin-spin interaction, which induces both spin relaxation and decoherence. For a radical in solution, its concentration dependence of T₁ depends on the charge state. T₁ of a positively or negatively charged radical remains concentration independent at relatively high concentration because the radicals tend to repel each other to keep long spin-spin distance and in turn weak spin-spin interaction. For instance, semiquinone radicals, which hold negative charges, exhibit negligible concentration dependence of T₁ up to 1 mmol/L.^140,141 In contrast, neutral radicals, e.g., nitroxide radicals, lack Coulombic repulsion and could get close to each other transiently, leading to strong dipolar interaction and significant concentration dependence of T₁. On the other hand, the influence of charge is not salient for radicals in solids where they cannot easily move, as exemplified by radicals embedded in a covalent organic framework (COF).¹¹²

The rate of instantaneous diffusion linearly scales with the radical concentration, so the T_m decreases with increasing radical concentration, as exemplified by tempol.¹⁴² When the radical concentration is high, instantaneous diffusion dominates the spin decoherence.^54,96 As a result, the influences of nuclear spin diffusion and motional groups are not salient, and T_m tends to be temperature independent. At low radical concentration, instantaneous diffusion is suppressed, nuclear modulations of the electron spin precession become significant, and T_m shows temperature dependence. Because spin-spin interaction induces severe decoherence, it is necessary to dilute the radical to achieve a long T_m.

Pulse sequence

A pulse sequence can be considered as a noise filter that partially eliminates environmental noise.¹⁴³ As both T₁ and T_m are sensitive to such noise, they are dependent on pulse sequences used for their characterization. T₁ is typically characterized by saturation recovery and inversion recovery pulse sequences (Figure S6). Saturation recovery involves applying either a strong, long pulse or a series of π/2 pulses, known as a “picket fence,” to achieve saturation, resulting in the equal partition of spins between the ground state and the excited state. The long time of this saturation process effectively averages out the influence of spectral diffusion, so this pulse sequence approaches the intrinsic T₁.^142,144 In contrast, the inversion recovery uses a short π pulse to flip the spin to its excited state, so it is prone to spectral diffusion and usually gives rise to shorter T₁ compared with that acquired by the saturation recovery—$T_1^{\mathrm{IR}}<T_1^{\mathrm{SR}}$.¹⁴⁵

T_m could be measured by free induction decay (FID) as well as Hahn echo decay, Carr-Purcell-Meiboom-Gill (CPMG), and more advanced dynamical decoupling pulse sequences. The FID reflects the decoherence effect encompassing all influencing factors.¹⁴² The Hahn echo decay pulse sequence exerts a refocusing π pulse (Figure S6) that suppresses the decoherence caused by static non-uniformity in the magnetic environment, but it is difficult to completely eliminate spectral diffusion because a single π pulse gives rise to a wide noise window.⁵⁴ The CPMG pulse sequence applies a train of spin-locking π pulses that further suppresses spectral diffusion and improve coherence by filtering out environmental noise efficiently.^{146,147,148,149} Thus, T_m generally increases with an increasing number of π pulses applied—$T_{\mathrm{m}}^{\mathrm{FID}}<T_{\mathrm{m}}^{\mathrm{Hahn}}<T_{\mathrm{m}}^{\mathrm{CPMG}}$ (Figure 5E).¹³⁹ For example, for radicals trapped on chemically modified carbon nanotubes, Hahn echo gives rise to a T_m = 1.2 μs at 5 K, whereas CPMG significantly improves T_m, reaching 8.2 μs with 32 π pulses (Figure 5F).⁹⁵ Sometimes, a long CPMG pulse sequence could improve T_m toward T₁.¹⁴⁶

In addition, the pulse itself could also influence T₁ and T_m. First, instrumental artifacts, e.g., the instability and imprecision of the microwave source and amplifier as well as the pulse generator, could introduce pulse errors that cause relaxation and decoherence and shorten both T₁ and T_m. As pulse errors accumulate with an increasing number of pulses, the abovementioned coherence enhancement of the CPMG pulse sequence tends to saturate at a certain sequence length. More advanced dynamical decoupling sequences, such as XY8, could be applied to eliminate pulse errors and improve T_m.^150,151,152 Second, given a certain spin rotation angle, a longer pulse shows a narrower excitation bandwidth that excludes more environmental noise. Thus, the long pulse tends to improve both T₁ and T_m.^153,154 Similarly, as the pulse shape also influences the excitation bandwidth, e.g., a chirped pulse exhibits much wider excitation bandwidth than a rectangular pulse, it should alter T₁ and T_m as well.¹⁵⁵

Overall, the experimentally observed T₁ and T_m values are highly influenced by the methods used for their characterization. Therefore, when acquiring the spin dynamics of even the same spin system at various conditions (temperature, radical concentration, etc.), it is necessary to maintain consistent pulse sequences and pulse parameters to ensure comparability.

Guidelines for improving T₁ and T_m

The above discussions point out the following guidelines for improving T₁ and T_m of radical qubits through optimization of molecular structures, environmental conditions, and operational parameters.

• a)Improve structural rigidity: a rigid structure reduces low-energy phonons/vibrational modes, thereby enhancing T₁. The structural rigidity can be designed by introducing steric hindrance and conjugation.
• b)Eliminate nuclear spins: nuclear spin diffusion is the major source of decoherence at low temperature, so reducing the number of surrounding nuclear spins improves T_m. The most efficient strategy is to construct radical qubits with nearly nuclear-spin-free elements including C, O, and S. If hydrogen atoms are unavoidable, they should be positioned within the nuclear spin diffusion barrier or be replaced by deuterium or chlorine atoms. Similarly, the solvent should also be free of nuclear spins (e.g., CS₂) or be deuterated.
• c)Avoid rotary groups: rotary groups such as methyl, phenyl, and amino groups act as environmental magnetic noise that reduces both T₁ and T_m. They should be eliminated from the radical by molecular design and from the solvent by avoiding toluene, N,N-dimethylformamide, dimethyl sulfoxide, acetonitrile, etc.
• d)Reduce temperature: low temperature helps improve both T₁ and T_m. This is viable for quantum computing and quantum memory but may not be feasible for quantum sensing that ideally operates at room temperature.
• e)Reduce radical concentration: spin-spin interaction causes instantaneous diffusion that facilitates both spin relaxation and decoherence. Therefore, given sufficient spins for EPR detection, the radical concentration should be as low as possible to improve T₁ and T_m.
• f)Use long pulses: a long pulse helps improve both T₁ and T_m. Practically, as the spin loses coherence during the pulse, the pulse length should be much shorter than the T_m.
• g)Apply dynamical decoupling: dynamical decoupling pulse sequences could eliminate spectral diffusion, instantaneous diffusion, and decoherence caused by pulse errors, so they can greatly improve T_m.

Solid-state integration

Integration of radical qubits into solid-state materials and architectures can combine qubit behaviors with versatile functionalities and processabilities, opening the possibility of integrating QIS with well-established technologies, such as organic electronics, spintronics, optoelectronics, and chemical sensing. Although there have been extensive studies on polymers,^156,157 COFs,^158,159 MOFs,^160,161,162 thin films,^163,164,165 self-assembled monolayers (SAMs),^166,167,168 and functionalized nanoparticles¹¹⁶ consisting of stable organic radicals, the spin dynamics in these solid-state structures has rarely been investigated. Compared with small molecules, polymers and framework materials have soft backbones and modular structures. These characteristics impart tunable phonon modes and designable spatial distribution of radicals,^169,170,171 thereby creating additional platforms to modulate spin-lattice relaxation and decoherence, respectively. Meanwhile, substrates of thin films and SAMs could also affect spin dynamics by providing a vastly different phononic, electrical, and/or magnetic environment.^172,173,174 Therefore, it is critical to articulate structure-spin dynamics relationships of radical qubits in solid state to optimize their performance in practical applications. We summarize recent advances in solid-state-integrated radical qubits and list their spin dynamic properties in Table S3.

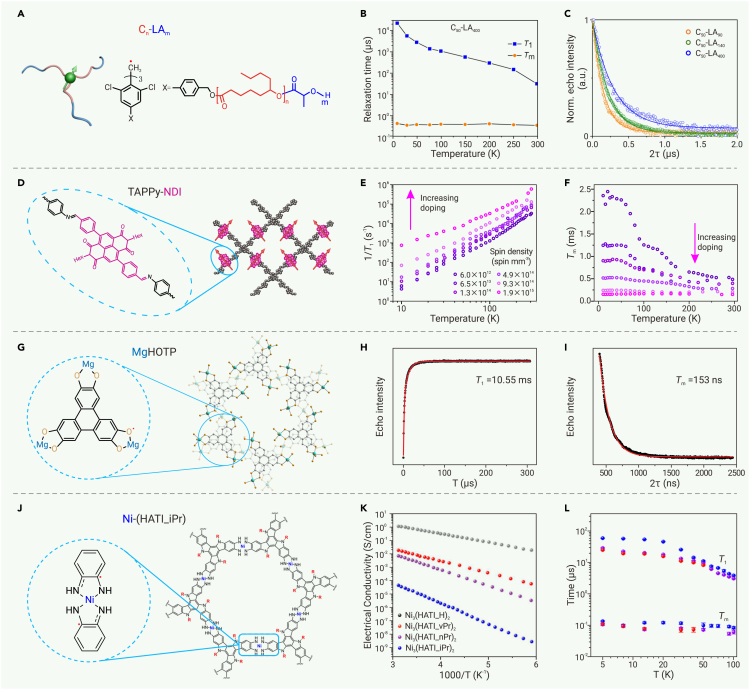
Organic polymers could integrate radicals as monomers. The spatial distribution of radicals could be designed by side-chain engineering or block copolymer self-assembly. Hou et al. integrated chlorine-substituted triphenylmethyl radicals into a series of block copolymers with diblock polyesters (Figure 6A).¹¹⁰ The processability of these block copolymers allows easy preparation of thin films. Annealing-induced phase separation leads to self-assemblies with various morphologies, including sphere, lamellae, cylinder, and gyroid. These morphologies are determined by the structures and lengths of polyesters. This morphological control allows for the tuning of spin-spin distances, which in turn affects spin dynamics. Both T₁ and T_m increase with the length of the polyesters (Figure 6C). Importantly, some of these films show room temperature coherence, with one example (C₅₀-LA₄₀₀) exhibiting T₁ = 29.23 μs and T_m = 0.318 μs at 298 K (Figure 6B). Therefore, these thin films of block copolymers behave as tunable qubits.

Figure 6.

Integration of radical qubits in polymers and microporous materials

(A–C) (A) Structures, (B) variable-temperature T₁ and T_m, and (C) Hahn echo decay curves (298 K) of C_n-LA_m block copolymers. Reproduced from Hou et al.¹¹⁰ with permission from John Wiley & Sons, copyright 2024.

(D–F) (D) Structure of TAPPy-NDI, and (E and F) concentration and temperature dependencies of its T₁ and T_m. Reproduced from Oanta et al.¹¹² with permission from American Chemical Society, copyright 2023.

(G–I) (G) Structure, (H) inversion recovery curve (296 K), and (I) Hahn echo decay curve (296 K) of MgHOTP. Reproduced from Sun et al.¹¹¹ with permission from American Chemical Society, copyright 2022.

(J–L) (J) Structure, (K) variable-temperature electrical conductivity, and (L) variable-temperature T₁ and T_m of Ni₃(HATI_X)₂. Reproduced from Lu et al.¹¹³ with permission from American Chemical Society, copyright 2024.

Different from organic polymers that are mostly amorphous, MOFs and COFs are crystalline microporous materials with designable structures through reticular chemistry. MOFs are composed of inorganic nodes connected by organic linkers through coordination bonds, whereas COFs consist of purely organic monomers with covalent linkages.^175,176 By using stable radicals as building blocks, one can construct ordered arrays of qubits with predefined spin-spin distances and orientations. The modular lattices enable precise control over frequencies and density of states of phonons.^177,178 Moreover, the microporosity facilitates post-synthetic modification of radical concentration with redox chemistry.¹⁷⁹ These enable fine-tuning of spin-spin interaction and spin-phonon coupling, offering opportunities for systematic investigation of the structure-spin dynamics relationship, which provides guidelines for optimizing the T₁ and T_m of radical qubits in framework materials.

As a proof of concept, Oanta et al. synthesized a layered COF (TAPPy-NDI) containing naphthalene diimide (NDI), which can be post-synthetically reduced by cobaltocene to generate NDI^·− radicals (Figure 6D).¹¹² Controlling the stoichiometry between NDI and cobaltocene gives rise to a wide range of spin concentrations spanning from 6.0 × 10¹² to 1.9 × 10¹⁵ mm⁻³. Both T₁ and T_m increase with decreasing spin concentration from 10 to 296 K, indicating that the spin-spin interaction plays a key role in both spin relaxation and decoherence (Figures 6E and 6F). In addition, the spin concentration strongly tweaks the decoherence mechanism. When it is low, the temperature dependence of T_m from 10 to 296 K exhibits various plateaus and declines, indicating that the decoherence is caused by spectral diffusion from nuclear spins, rotary functional groups, and spin relaxation at different temperature regions (Figure 6F). As the spin concentration increases, the temperature dependence of T_m gradually diminishes and eventually disappears, indicating that instantaneous diffusion becomes the dominant factor. Indeed, the spin concentration controls both spin dynamics and electrical conductivity of this COF,¹⁸⁰ rendering it a material that can be fine-tuned by guest molecules and potentially controlled by a gate.

MOFs utilize metal ions as building blocks, resulting in versatile structures and functionalities. However, these metal ions may also introduce additional sources of decoherence due to their electron and nuclear spins. Metal ions should be diamagnetic and should possess few nuclear spins. Choices include Mg²⁺, Ca²⁺, Ti⁴⁺, Zn²⁺, Zr⁴⁺, octahedrally coordinated low-spin Fe²⁺, square-planarly coordinated Ni²⁺, etc. The combination of these metal ions with stable radicals, such as TEMPO and TTF, has led to the synthesis of several MOFs that exhibit electron spin signatures in their continuous wave EPR spectra.^160,162,181 However, studies on their electron spin dynamics are only beginning to emerge. In 2022, Sun et al. reported the spin dynamics of a MOF, MgHOTP, integrating Mg²⁺ and 2,3,6,7,10,11-hexaoxytriphenylene (HOTP), the latter of which is spontaneously oxidized in air to form a semiquinone-like radical (Figure 6G).¹¹¹ The powder of this material exhibits T₁ = 10.55 μs (Figure 6H) and T_m = 153 ns at 296 K (Figure 6I), demonstrating the qubit behavior of HOTP-based radicals. Soaking it in tetrahydrofuran (THF) enhances the T₁ to 21.61 μs and the T_m to 202 ns, further demonstrating the guest-tunability of spin dynamics.

Recently, Lu et al. investigated the spin dynamics in a series of layered MOFs, Ni₃(HATI_X)₂, consisting of square-planarly coordinated Ni²⁺ and substituted 2,3,7,8,12,13-hexaiminotriindole (HATI_X) (Figure 6J), where X represents hydrogen (H), allyl (vPr), n-propyl (nPr), or isopropyl (iPr) groups.¹¹³ The substituents interfere with interlayer π-stacking, resulting in an enlarged interlayer distance and dislocated packing. On the one hand, this hampers charge transport and reduces electrical conductivity (Figure 6K); on the other hand, it suppresses phonons and in turn spin-lattice relaxation. Meanwhile, the spin decoherence seems to be governed by the local nuclear and electron spin bath. As a result, Ni₃(HATI_iPr)₂ shows higher T₁ than Ni₃(HATI_vPr)₂ and Ni₃(HATI_nPr)₂ at 5–100 K, yet the T_m values of these three MOFs are almost identical (Figure 6L). Notably, the most conductive analog, Ni₃(HATI_H)₂, does not exhibit electron spin coherence even at 5 K, indicating fast spin relaxation caused by phonon scattering of itinerant electrons through the Elliott-Yafet relaxation mechanism. Thus, this work shows that electron delocalization may deteriorate spin coherence, posing demands on balancing charge transport and spin dynamics in MOFs.

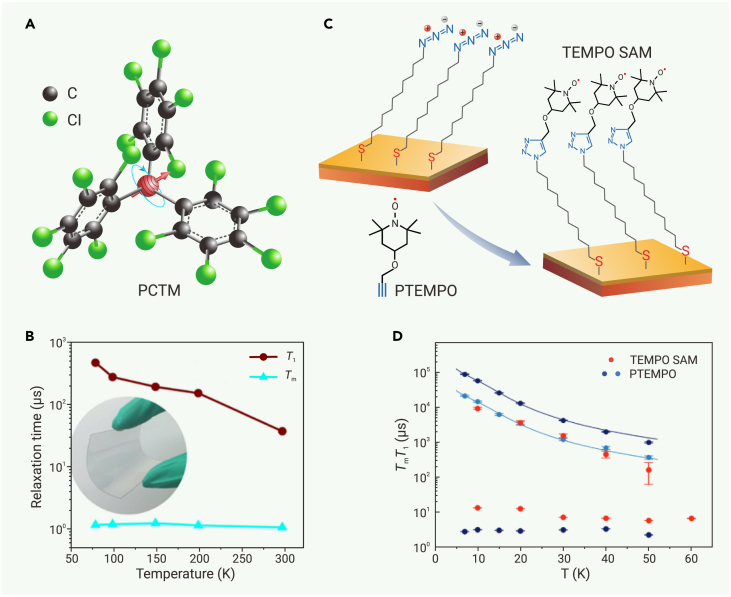
Thin film and surface integration of radical qubits are prerequisites for many device-related applications. The key challenge in fabricating thin films of radical qubits is to suppress decoherence caused by spin-spin interaction. This could be done by diluting the radical with its diamagnetic analog. Dai et al. prepared thin films of a mixture of perchlorinated triphenylmethyl radical (PCTM) and its diamagnetic hydrogenated analog at a molar ratio of 1:1,000 (Figure 7A). These films were deposited onto quartz and polyethylene terephthalate substrates via vapor deposition and spin coating.¹¹⁴ The PCTM in a film of 200 nm thickness exhibits T₁ = 35.6 μs and T_m = 1.08 μs at 298 K (Figure 7B), which are nearly identical to the values observed for the powder of this molecule, indicating that the substrate does not interfere with spin dynamics in the film. An alternative dilution method is to separate radical qubits by polymers. For instance, dispersing BDPA radicals within polymethyl methacrylate generates thin films exhibiting T₁ = 20–40 ms and T_m ≈ 0.6 μs at 7 K,¹⁸² and, as discussed above, incorporating chlorine-substituted triphenylmethyl radicals into block copolymers enables further control of film morphology and spatial distribution of radicals. This approach results in tunable quantum coherence at room temperature.¹¹⁰

Figure 7.

Integration of radical qubits in thin films and SAMs

(A and B) (A) Structure and (B) variable-temperature T₁ and T_m of thin films of the PCTM radical. Reproduced from Dai et al.¹¹⁴ with permission from John Wiley & Sons, copyright 2018.

(C) Fabrication of TEMPO SAM on a gold surface.

(D) Temperature dependencies of T₁ and T_m for the TEMPO SAM and a dilute solution of TEMPO (PTEMPO). (C and D) Reproduced from Tesi et al.¹¹⁵ distributed under CC-BY 4.0 (http://creativecommons.org/licenses/by/4.0/).

SAM is a useful strategy to integrate functional molecules onto the surface of substrates.¹⁶⁸ Tesi et al. developed a bottom-up method to arrange radical qubits as functional groups of SAMs onto the surface of gold.¹¹⁵ This method includes two steps: first, an azide-modified alkanethiolate SAM is grown on gold; second, an alkyne-modified TEMPO radical reacts with azide groups via a click reaction, functionalizing the SAM with radical qubits (Figure 7C). A Fabry-Pérot resonator operating at the Q-band frequency was used to characterize spin dynamics of monolayer radicals, revealing T₁ = 9.2 ms and T_m = 13.53 μs at 10 K (Figure 7D). This T_m value exceeds that observed for a dilute solution of TEMPO radicals (PTEMPO) at the same temperature (T_m = 3.23 μs at 10 K) (Figure 7D), verifying that the substrate does not reduce the coherence. The modularity of this method points out opportunities for further functionalization of the SAM, which might open the door for SAM-based QIS applications.

Applications in quantum information science

In this section, we summarize proof-of-concept QIS applications of radical qubits reported so far, including quantum computing, quantum memory, and quantum sensing.

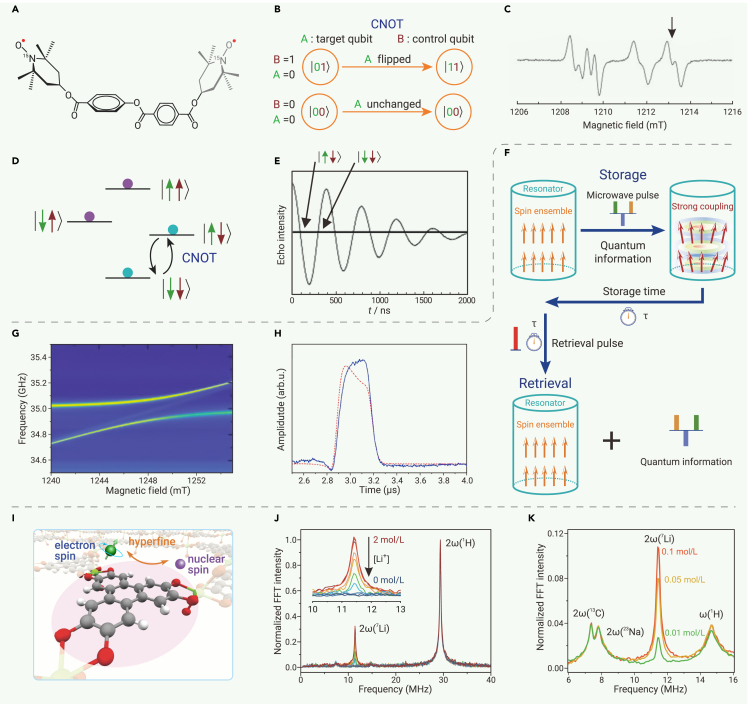
Quantum computing runs quantum algorithms capable of solving problems that are practically unsolvable for classical computers, such as factoring large numbers.^183,184 The implementation of quantum algorithms can be decomposed into a set of single-qubit and two-qubit universal quantum logic gates.¹⁸⁵ The latter, e.g., CNOT and iSWAP gates, require quantum entanglement between qubits, which could be established by qubit-qubit interaction.^186,187 To this end, two radical qubits can be integrated into a single molecule with a designated spin-spin interaction by sophisticated molecular design. Their weak spin-orbit coupling and hyperfine coupling give rise to narrow resonant linewidths that facilitate implementation of two-qubit quantum logic gates. Nakazawa et al. designed a molecule containing two TEMPO radicals separated by 2 nm (Figure 8A) and realized the CNOT gate with this molecule.⁴⁸ The TEMPO moieties are enriched with the isotopes by ¹⁵N and ²H to simplify the hyperfine structures and narrow the EPR spectrum linewidths. The z axes of g-tensors of the two radicals and the spin dipolar tensor are not co-linear due to the non-linear molecular structure. These features enable implementation of the CNOT gate with this two-qubit molecule (Figure 8B). With a specific orientation of a single crystal mounted in a Q-band pulse EPR spectrometer, the transition frequencies of $|\downarrow \downarrow ⟩\Rightarrow |\uparrow \downarrow ⟩$ and $|\downarrow \uparrow ⟩\Rightarrow |\uparrow \uparrow ⟩$ differ by 9.5 MHz, which exceeds their linewidths (Figure 8C). Thus, when the magnetic field is tuned resonant with the first transition, the first spin can be flipped only when the second spin is in the $|\downarrow ⟩$ state (Figure 8D). With the second spin as the control qubit and the first spin as the target qubit, a π pulse of 200 ns achieves the CNOT gate operation (Figures 8B and 8E). Although a rigorous benchmarking of the CNOT gate remains to be conducted, this demonstration shows the potential of tailor-design multi-qubit molecules for implementing quantum logic gates, which is a cornerstone for molecular quantum computing.

Figure 8.

QIS applications of radical qubits

(A–E) Molecular quantum logic gate. (A) The molecule containing two ¹⁵N- and ²H-substituted TEMPO radicals used for the CNOT gate implementation. (B) Schematic illustration of the CNOT gate. (C) Continuous wave (CW) EPR spectrum of the biradical molecule. The arrow points to the resonance field at which the CNOT gate is implemented. (D) Schematic energy diagram of four zero-field split electron spin states of the biradical molecule. (E) Manifestation of the CNOT gate through the Rabi oscillation. (C–E) reproduced from Nakazawa et al.⁴⁸ with permission from John Wiley & Sons, copyright 2021.

(F–H) Molecular quantum memory. (F) Conceptual illustration of quantum memory. (G) Avoided crossing in a 2D CW EPR spectrum of BDPA·Bz radicals showing the strong coupling between electron spins and the microwave cavity. (H) A spin echo that shows the retrieval of quantum information stored in the quantum memory for 1.4 μs. Reproduced from Lenz et al.¹⁸⁸ distributed under CC-BY 4.0 (http://creativecommons.org/licenses/by/4.0/).

(I–K) Molecular quantum sensing. (I) Conceptual illustration of quantum sensing harnessing hyperfine interaction between MOF-integrated radicals and nuclear spins of adsorbed ions. (J) CP-ESEEM spectra of MgHOTP in THF solutions with various concentrations of Li⁺. (K) CP-ESEEM spectra of MgHOTP in THF solutions consisting of both Li⁺ and Na⁺. Reproduced from Sun et al.¹¹¹ with permission from American Chemical Society, copyright 2022.

Quantum memories allow for the storage and retrieval of quantum information (Figure 8F), which is essential for quantum computing and long-distance quantum communication.^{189,190,191,192,193,194} Lenz et al. fabricated a quantum memory with an ensemble of a stable organic radical (benzene complex of BDPA, BDPA·Bz) coupled with a three-dimensional Fabry-Pérot microwave resonator.¹⁸⁸ The large number of spins (6 × 10¹⁸ spins) dramatically improves the spin-photon coupling strength that surpasses both the spin decoherence rate and the cavity dissipation rate, establishing strong coupling between the spin ensemble and the cavity (Figure 8G). Such strong coupling improves the T_m of the radical even at room temperature thanks to the cavity protection effect and enables spin-photon entanglement. At 7 K, a weak microwave pulse can transfer the quantum information conveyed by the microwave photons to the spin ensemble. This quantum information can be stored for 1.4 μs and then retrieved to microwave photons by a strong microwave pulse (Figure 8H). Thus, these results demonstrate that the spin-ensemble-resonator hybrid system can be used as a quantum memory.

Quantum sensing harnesses a quantum system, a quantum property, or a quantum phenomenon to measure a physical quantity, such as magnetic field, temperature, and frequency.¹⁴³ Radical qubits can be used to detect nuclear spins at relatively high temperature via quantum sensing: when a nuclear spin is weakly coupled to the electron spin, it not only causes spin relaxation and decoherence of the radical but also modulates its Larmor precession. The modulation frequency is related to the Larmor frequency of the nuclear spin and the modulation intensity scales with the number of nuclear spins surrounding the radical, enabling both identification and quantification of the nuclear spin. Driven by this idea, Sun et al. designed a MOF, MgHOTP, containing semiquinone-like radicals (Figure 6G) and demonstrated quantum sensing of Li⁺ at room temperature in THF solution.¹¹¹ The microporosity of this material allows diffusion of Li⁺ into the nanometer-size pores, enforcing close contact and weak hyperfine interaction between radicals and Li⁺ (Figure 8I). Relaxometry shows decreasing T₁ and T_m with increasing concentration of Li⁺ in the range of 0.5–2 mol/L. Hyperfine spectroscopy (combination-peak electron spin echo envelope modulation, CP-ESEEM) reveals a modulation frequency corresponding to the Larmor frequency of Li⁺. The modulation intensity increases with the concentration of Li⁺ in the range of 5 × 10⁻³ to 0.5 mol/L (Figure 8J). Furthermore, because many nuclear spins exhibit unique Larmor frequencies, the hyperfine spectroscopy can detect multiple nuclear spins simultaneously and unambiguously, exemplified by Li⁺ and Na⁺ in this work (Figure 8K). Thus, radical qubits hold the promise for chemical-specific quantum sensing in complex environments and at room temperature.

Beyond nuclear spins, radical qubits could also be used for quantum sensing of magnetic field. Bonizzoni et al. integrated BDPA radicals into a coplanar microwave resonator, developed quantum sensing protocols based on dynamical decoupling pulse sequences, and performed echo detection to sense alternative-current magnetic field with a sensitivity reaching 10⁻⁹ T/Hz^1/2.¹⁹⁵ In addition, radical-based quantum superposition and quantum sensing have been hypothesized to be essential for bird navigation.¹⁹⁶ For example, it is proposed that the illumination of cryptochromes in birds’ eyes produces FAD^·− (FAD, flavin adenine dinucleotide) radical pairs with strong and anisotropic hyperfine coupling with ¹⁴N. Acting as magnetic orientation sensors, these radical pairs might allow birds to detect the Earth’s magnetic field and keep them oriented during migration.^197,198,199

Summary and outlooks

In this review, we summarize spin dynamic properties, mechanisms, and their optimization strategies of stable organic radicals, present their integration into solid-state materials and surface structures, and enumerate their prototypical applications in quantum computing, quantum memory, and quantum sensing. Besides the room temperature quantum coherence and versatile integrability that have been discussed extensively above, radical qubits distinguish from other types of qubits by their atomic-level rational designability. Their bottom-up synthesis allows for precise control over the structural rigidity as well as the type, amount, and spatial distribution of nuclear spins and functional groups surrounding the electron spin. This precise control is crucial for prolonging both the T₁ and T_m. Such synthetic versatility also facilitates rational design of radical qubits for QIS: multiple radical qubits could be incorporated into one molecule with prescribed inter-qubit interactions to implement specific quantum logic gates, luminescent radical qubits may introduce spin-optical interfaces that are essential for quantum communication,^58,200 and radical qubits functionalized by molecular/ionic recognition groups may enable highly selective quantum sensing, and their integration with photo-excited triplets may lead to complex molecular qubit systems with versatile functionalities.^201,202 Thanks to these unique advantages, stable organic radical qubits could promote the development of quantum information technologies that demand compatibility with room temperature and complex chemical environments. This would facilitate QIS applications in biological systems, energy storage devices, electronics, environmental monitoring, and more.

With their great potential in QIS applications, stable organic radical qubits pose many opportunities and challenges for future research. First, besides the radical qubits listed in Tables 1 and S2, many others remain to be characterized from the QIS perspective, such as 7,7,8,8-tetracyanoquinonedimethane mono-anion radical, perylene cation radical, dithiophenalenyl radical and their derivatives, among others. Second, spin dynamics of radical qubits need to be investigated in various application-related scenarios. Integration of radical qubits into microporous materials, thin films, and devices necessitates in-depth examination of spin relaxation and decoherence mechanisms because these structures introduce complex phononic, magnetic, and electrical environments. Third, to take full advantage of radical qubits for QIS, strategies need to be developed to achieve high-fidelity initialization, manipulation, and readout of single radical qubits in mild conditions. This is technically difficult because thermal initialization requires a strong magnetic field and ultralow temperature, while conventional EPR-based spin state readout only works for ensembles.²⁰² To this end, we could learn from the addressing strategies of other types of qubits. Optical pumping and spin injection may be implemented to initialize radicals.^15,203,204 Optical,^35,36,37 electrical,^44,45,205 scanning probe microscopic,⁴⁶ and quantum metrological strategies^47,206 could be sufficiently sensitive to detect single electron spins. In addition, recent studies of the chirality-induced spin selectivity effect may offer an ultimate solution to initialize and readout single electron spins with chiral moieties embedded in radicals.²⁰⁷ Finally, efforts should be paid to improve scalability of radical qubits, which requires coherent addressing of each qubit in a system. This is challenging for conventional EPR as most radicals exhibit similar g-factors (close to 2.0023) and can hardly be spectrally distinguished. Implementing radical qubits into single-molecule spintronic devices may enable spatial addressing of individual qubits, leading to fabrication of universal molecular quantum computers.

Published Online: June 21, 2024

Lead contact website

https://sunlei.lab.westlake.edu.cn/.