The form and evolution of international migration networks, 1990–2015

Abstract

Presently, there is no agreed upon data-driven approach for identifying the geographic boundaries of migration networks that international migration systems are ultimately manifested in. Drawing from research on community detection methods, we introduce and apply the Information Theoretic Community Detection Algorithm for identifying and studying the geographic boundaries of migration networks. Using a new set of estimates of country-to-country migration flows every 5 years from 1990 to 1995 to 2010–2015, we trace the form and evolution of international migration networks over the past 25 years. Consistent with the concept of dynamic stability, we show that the number, size and internal country compositions of international migration networks have been remarkably stable over time; however, we also document many short-term fluctuations. We conclude by reflecting on the spirit of our work in this paper, which is to promote consensus around tools and best practices for identifying and studying international migration networks.

1 |. INTRODUCTION

A persistent problem in research on international migration systems is how to detect the boundaries of the ‘identifiable geographic structure [s]’ that systems are ultimately manifested in Massey et al. (1998:61; see also Bakewell, 2014; Kritz & Zlotnik, 1992; Mabogunje, 1970). Presently, aside from a generic set of guiding ‘general principles’ (Zlotnik, 1992:20), there is no agreed upon data-driven approach for systematically identifying these structures, or what Kritz and Zlotnik (1992:15) called migration ‘network[s]’ consisting of sets of countries that are connected to one another by migration flows in patterned ways. Accordingly, in this paper, drawing from research on community detection methods, we introduce and apply the Information Theoretic Community Detection Algorithm (Rosvall & Bergstrom, 2008), for identifying and studying the geographic boundaries of migration networks. Using a new set of estimates of country-to-country migration flows every 5 years from 1990 to 1995 to 2010–2015 based on a method recently developed by Azose and Raftery (2019), we trace the form and evolution of international migration networks over the past 25 years. Consistent with the concept of dynamic stability (Kilduff, Tsai, & Hanke, 2006; see also Rogers, Raymer, & Willekens, 2002), we show that the number, size and internal country compositions of international migration networks have been remarkably stable over time; however, we also document many short-term fluctuations. We conclude by discussing the contribution of this paper against the backdrop of the continued need for tools and best practices for identifying and studying international migration networks.

2 |. BACKGROUND

2.1 |. Migration systems

Research on migration and migration systems often invokes Mabogunje’s (1970) work on rural–urban migration in Africa (Bakewell, 2014). Mabogunje (1970:3) defined a migration system as ‘a complex of interacting elements, together with their attributes and relationships’. Unpacking this definition, the elements comprising a migration system take many forms, ranging from individuals and households to places such as nation-states and international bodies like the United Nations. Elements are characterized by unique sets of demographic, economic, geopolitical and sociocultural attributes (e.g., interests, motivations and other defining features and characteristics), with recent studies also stressing the importance of environmental characteristics (Black, Bennett, Thomas, & Beddington, 2011; Curtis, Fussell, & DeWaard, 2015; Hunter, Luna, & Norton, 2015). Finally, elements engage in relationships, or connections or exchanges, with one another. These take many forms, and might include, for example, flows of ideas and information, financial capital and goods and services (Fawcett, 1989).

2.2 |. The geographic boundaries of migration networks

According to Massey et al. (1998:61), ‘[t]he end result is a set of relatively stable exchanges of people between [places] … yielding an identifiable geographic structure that persists across space and time’. In other words, although migration systems are ‘emergent social entities’ that are actively and continually created and sustained by unique sets of elements and exchanges at different spatial and temporal scales (Bakewell, 2014:301; see also Bakewell, Engbersen, Fonseca, & Horst, 2016), they are ultimately manifested in, but not synonymous with, ‘network[s]’ of places that are connected to one another by migration flows in patterned ways (Kritz & Zlotnik, 1992:15; see also DeWaard & Ha, 2019).¹ As the focus of this paper is on international migration networks, our concern going forward is with sets of countries that are connected to one another by country-to-country migration flows.

A persistent problem in research on international migration networks is how to identify their geographic boundaries (Bakewell, 2014; Mabogunje, 1970; Zlotnik, 1992). One a priori approach is to do so by considering why and how certain countries, and not others, are ‘linked by large migration flows’ (Kritz & Zlotnik, 1992:3). For example, scholars routinely reference a ‘European migration [network]’ (Favell, 2008:711), the origins of which Massey et al. (1998) trace to the 1957 signing of the Treaty of Rome, which established the European Economic Community. Similarly, Martin (2013:4; see also Massey, Durand, & Malone, 2002) and others refer to a ‘North American migration [network]’ that revolves around immigration to the United States and Canada. Although, on the surface, there seems nothing problematic with these sorts of designations, upon closer inspection, they lack a uniform set of criteria and methods for making these designations that can be applied across cases.

This problem led Zlotnik (1992:20) to propose five ‘general principles’ to guide empirical efforts to identify international migration networks. To paraphrase, these principles include (1) focusing on ‘interacting nation-states’, (2) analyzing available migration data, (3) identifying other relevant linkages (for example; ‘comparable levels of development’, ‘cultural affinity’) shared by migrant-sending and migrant-receiving countries, (4) examining the characteristics of migrant-sending countries, and (5) examining the characteristics of migrant-receiving countries to see what those in each group have in common (e.g., ‘coherence in policies’). Zlotnik (1992) used these principles to identify and study international migration networks in the Americas and Western Europe. DeWaard, Kim, and Raymer (2012) subsequently applied these principles to identify three migration networks in the European Union (EU) and Norway, followed by studying the key determinants of these migration flows (see also Nogle, 1994).

The importance of Zlotnik’s (1992) work notwithstanding, as DeWaard et al. (2012) noted at the conclusion of their paper, it is not exactly clear how to go about putting the above five principles into practice. For example, in discussing her second principle, Zlotnik (1992:20) suggested that discrete migration networks might be identified by locating ‘threshold[s]’ in ‘matrices of inflows, outflows, and net flows between all countries as they evolved through time.’ However, no guidance is provided on exactly how to go about doing this. Accordingly, as a place to start, DeWaard et al. (2012) used average linkage clustering to partition nearly 4000 annual migration flows among EU countries and Norway over a 5-year period between 2003 and 2007 into three migration networks.

Perhaps as a consequence of the lack of a clear and uniform set of criteria and methods that can be used to identify international migration networks in practice, research in this area has failed to keep pace with substantive developments in other complementary areas (Bakewell, 2014). One example is research on the ‘globalization of migration’ (Castles, de Haas, & Miller, 2014:16; see also Czaika & de Haas, 2014), which refers to ‘the tendency for more and more countries to be significantly affected by international migration.’ While providing little guidance on how to operationalize the idea in practice, Zlotnik (1992:19) alluded to a process of consolidation involving the emergence of one ‘all-encompassing’ international migration network over time. The origins of this idea can be found in world systems theory (Wallerstein, 1974, 1980) and world polity theory (Meyer, Boli, Thomas, & Ramirez, 1997; Thomas & Meyer, 1984), which emphasize the long-run historical progression of global capitalist expansion, exploitation and inequality driven by competition for [cheap] land, raw materials and labor (Castles et al., 2014). In the process, trade, transportation and military linkages were established and expanded (Massey et al., 1998). This has continued to the present day, as has the proliferation of ideas and identities aided in no small part by media and communications technologies in an increasingly transnational world (Ali & Hartmann, 2015; Nobles, 2013; Portes, 2001; Schiller, Basch, & Blanc, 1995).

At the other end of this continuum of the globalization of migration is the idea that multiple ‘geographically discrete’ international migration networks come to coexist alongside one another over time (Salt, 2001:31). This dynamic is set into motion by historical linkages and legacies of colonialism (e.g., Algeria and France) and military intervention (the United States in Latin America and Southeast Asia) and is reinforced by policies and practices that are specific to particular places (such as the EU or the African Economic Community) and populations (such as guest workers or refugees fleeing communism after World War II). In the process, migration flows are increasingly confined to, or ‘channelized’ among (Jones, 1982:76), smaller groups of migrant-sending and migrant-receiving countries (IOM, 2018). As a result, multiple migration networks (versus an all-encompassing one) emerge and crystalize over time.

Although there are other configurations of the globalization of migration—for example, the concept of ‘dynamic stability’ emphasizes long-run consistency in the number of migration networks while acknowledging short-term fluctuations (Kilduff et al., 2006; see also Rogers et al., 2002)—the broader argument of this paper is that research on international migration systems and networks has not kept pace with these developments, perhaps due in part to the lack of a clear and uniform set of criteria and methods that can be used to empirically identify and study migration networks. To help fill this gap, the aim of this paper is to introduce and apply one such empirical tool—the Information Theoretic Community Detection Algorithm (Rosvall & Bergstrom, 2008)—for identifying and studying the form and evolution of international migration networks. In our case, we seek to identify communities that take the form of networks of countries that are connected to one another by migration flows in patterned ways.

3 |. APPROACH

3.1 |. Migration flow data

We use estimates of country-to-country migration flows from Abel and Cohen (2019) based on a method developed by Azose and Raftery (2019). These estimates cover 200 countries every 5 years from 1990 to 1995 to 2010–2015 and use the most recent input data on migrant stocks and demographic change from the United Nations (the estimates in the original Azose and Raftery, 2019, use older versions). The method used to produce these estimates builds on prior research by Abel (2013, 2018). Estimates of global country-to-country migration flows have received considerable attention in both scholarly and popular circles (Abel & Sander, 2014; Ali & Hartmann, 2015; Mingels, 2016; Sander, Abel, Bauer, & Schmidt, 2014; Sorrel, 2016; Stockton, 2014).

The starting point for developing the above estimates is data on country-level migrant stocks, disaggregated by country of birth, taken from national censuses and other administrative sources (United Nations, 2019a). Through the demographic balancing equation, any change in country-level migrant stocks between two consecutive periods must be the product of component changes in fertility, mortality and migration. After accounting for fertility and mortality using data from the United Nations (2019b), it is possible to estimate country-to-country migration flows every 5 years over the past several decades.

Given the strict assumptions in his approach, Abel’s (2013) estimation procedure yields minimum counts of country-to-country migration flows that are required to match the aforementioned country-level migrant stock data in consecutive periods. This means that some or perhaps all country-to-country migration flows are under-estimated. Azoze and Raftery (2019:116) developed pseudo-Bayes variation of the estimation method of Abel (2013) that more closely approximate reported levels of country-to-country migration using a weighted sum of minimum and maximum counts of country-to-country flows required to match migrant stock data in consecutive periods.

One limitation of any of the flow estimates based on changes in migrant stock data (such as those of Azose & Raftery, 2019) is that the estimates do not reconcile the often-discrepant migration reports of migrant-sending and migrant-receiving countries. It is well-documented that international migration data (such as those collated by international organizations, e.g., the United Nations or Eurostat) suffer from problems of availability, quality and cross-national comparability due to different data collection, processing, and reporting infrastructures, as well as different definitions (e.g., of ‘migration’ or ‘migrant’) and timing criteria (such as three, six or 12 months) employed (Bilsborrow, Hugo, Oberai, & Zlotnik, 1997; Levine, Hill, & Warren, 1985; Poulain, Perrin, & Singleton, 2006; Willekens, Massey, Raymer, & Beauchemin, 2016; Zlotnik, 1987). Rather than tackling these issues (e.g., see Raymer, Wiśniowski, Forster, Smith, & Bijak, 2013), estimates of global bilateral flows from changes in migrant stocks can be viewed more pragmatically insofar as they effectively force country-to-country migration flows to map onto each country’s (idiosyncratic) report of migrant stocks. Clearly, one downside of this pragmatism is that estimates such as those in Abel and Cohen (2019) do not contribute to substantive debates about the availability, quality and cross-national comparability of data on international migration, which is an unfortunate, but again unavoidable, limitation given growing calls for an analytically tractable definition and timing criterion that can and should be used in migration research (Bilsborrow, 2016; United Nations, 1998; Willekens et al., 2016).

The above said, relative to other sources of data on migration flows, the estimation of global country-to-country migration flows from changes in bilateral migrant stock data provide a far greater geographically and temporally encompassing set of information on country-to-country migration flows among 200 countries over the past 25 years. The estimates from the method of Azose and Raftery (2019) provide a comparatively closer match to available reported sending and receiving migration flows than other alternative estimation methods as illustrated using a set of validation measures by Abel and Cohen (2019).

3.2 |. The information theoretic community detection algorithm

We use estimates of country-to-country migration flows every 5 years from 1990 to 1995 to 2010–2015 from the Abel and Cohen (2019) data (based on the Azose and Raftery’s, 2019, method), in conjunction with the Information Theoretic Community Detection Algorithm (ITCDA; Rosvall & Bergstrom, 2008), to identify and study the geographic boundaries of international migration networks over the past 25 years. Although there are many community detection algorithms, and several recent papers that have used some of these algorithms to study international migration networks using migrant stock data (Danchev & Porter, 2018; Fagiolo & Mastrorillo, 2013; Peres, Xu, & Wu, 2016; Tatem and Smith (2010); Tranos, Gheasi, & Nijkamp, 2015; Windzio, 2018), we use the ITCDA for two reasons.

First, for the sake of consistency with prior theoretical and empirical research on migration systems (Bakewell, 2014; DeWaard et al., 2012; Kritz & Zlotnik, 1992; Mabogunje, 1970; Massey et al., 1998; Zlotnik, 1992), we seek to identify ‘geographically discrete’ migration networks (Salt, 2001:31). In contrast to community detection algorithms that identify overlapping, or fuzzy, networks (Devi & Poovammal, 2016; Xie, Kelley, & Szymanski, 2013), the ITCDA identifies discrete networks. In our case, these discrete networks can be viewed straightforwardly as the most dominant migration network to which each country belongs.

Second, despite the abundance of community detection algorithms (Danon, Díaz-Guilera, Duch, & Areanas, 2005; Fortunanto, 2010; Gates, Henry, Steinley, & Fair, 2016; Liu, Sui, Kang, & Gao, 2014; Pons & Latapy, 2006; Yang, Algesheimer, & Tessone, 2016), most algorithms are designed for networks consisting of, what are referred to in social network analysis and network science as, undirected edges among a set of nodes in a graph (Borgatti, Mehra, Brass, & Labianca, 2009; Wasserman & Faust, 1994). An example of an undirected edge is a road connecting two places (i.e., the nodes), Places A and B. In this example, the edge is undirected because the road, or relationship, between Places A and B is symmetric. In contrast, the ITCDA is well suited to identify and study networks consisting of directed edges characterized by asymmetric relationships. An example of a directed edge is the migration flow from Places A to B, where the size of the flow corresponds to the weight of the edge, or the edge weight. Another example of a directed edge is the migration flow from Places B to A. The goal of the ITCDA is find an efficient description of (weighted) directed edges in a graph.

We apply the ITCDA to identify and study international migration networks every 5 years from 1990 to 1995 to 2010–2015. In our case, countries correspond to nodes and country-to-country migration flows correspond to edges. We define the edge weights as the probability of country-to-country migration. These weights are calculated by dividing the size of the migration flow from sending country $i$ to receiving country $j$ in a given 5-year period by the population of $i$ at the beginning of the period. Using a given set of 5-year probabilities of country-to-country migration flows (hereafter, flows), the ITCDA searches for groups of countries, which correspond here to international migration networks, wherein flows move easily within, but not between, networks.

The ITCDA treats the process of identifying a set of migration networks by treating the world as a single network, which can be subsequently be decomposed into a set of discrete subnetworks. This is achieved by assuming that the country-to-country migration probabilities, detailed above, can be used to approximate the probability of individual migration from one country to another over the single world network. This permits treating the flow of migrants and the identification of a set of migration networks as a data compression problem. Formally, this obtained by finding the equilibrium state of the single world network by decomposing it into the most efficient set of sub-networks $m$. Based on information theory, this can be done by maximizing entropy, $k\sum p_{i}log{p}_i$, where $k$ is a normalizing constant and $p_i$ is the probability of an event—in our case, migration—occurring (Gray, 2011). Maximizing this equation can be a challenging optimization problem. To solve this problem, Rosvall and Bergstrom (2008) proposed setting the initial state of the optimization through a simple greedy search (Merz & Freisleben, 2000) and then employing simulated annealing (Van Laarhoven & Aarts, 1987) to find the optimal $m$, $k$, and $p_i$. Specifically, ITCDA defines modules, $M$, over the entire set of country-to-country flows such that $n$ countries are initially placed into $m$ networks with no overlapping countries. To formalize the entropy equation to be optimized, Rosvall and Bergstrom (2008) defined a modified entropy equation, which is the objective function to be optimized:

$$L(M)=q_{\curvearrowright }H(Q)+{\sum }_{i=1}^m{p}_{\curvearrowright }^{i}H\left(P^i\right),$$ (1)

Equation 1 consists of two terms that summarize the entropy between migration networks and within migration networks. The first term, $q_{\curvearrowright }H\left(Q\right)$, expresses the entropy between networks, where $q$ is the per step probability that a person goes from one network to another. The second term, ${\sum }_{i=1}^m{p}_{\curvearrowright }^{i}H\left(P^i\right)$, expresses the weighted entropy of the probability within networks, where $p^i$ is the per step probability within each network. These quantities are estimated using a random walk algorithm (Ribeiro & Towsley, 2010). The initial number of networks is selected by the greedy algorithm, which works by selecting two networks and merging them together, recalculating the function in Equation 1, and then repeating this process until Equation 1 is optimized. The ITCDA then uses simulated annealing, a probabilistic approach for calculating the global optimum of a function, to approximate the true global maximum of the entropy equations. The ITCDA is available in the igraph package in R, developed by Csárdi and Nepusz (2006). Our analysis was performed by passing directed network graph objects based on the period specific country-to-country flows to the cluster_infomap function (Csárdi, 2020).

4 |. RESULTS

4.1 |. International migration networks by period

We begin by displaying counts of the number of international migration networks identified by the ITCDA in each period in Table 1, as well as the number of countries in each network. Focusing on the first period, 1990–1995, the ITCDA identified 17 migration networks, which are indexed in Table 1 from largest (1) to smallest (17). As is evident, the number of countries in each migration network ranged from two countries to 45 countries. The three largest migration networks contain more than one-half of all countries, and the five largest networks contain about two-thirds of all countries. At the other end of the spectrum, one migration network is a triad consisting of three countries. Two migration networks consist of two countries, which are sometimes referred to as migration channels or corridors (IOM, 2018; Jones, 1982).

TABLE 1.

Number and size of international migration networks, 1990–1995 to 2010–2015

	Period A: 1990–1995	Period B: 1995–2000	Period C: 2000–2005	Period D: 2005–2010	Period E: 2010–2015
Number of networks	17	17	15	17	15
Number of countries in network
Network 01	45	41	50	49	50
Network 02	39	38	33	36	40
Network 03	17	22	23	17	22
Network 04	14	17	23	16	17
Network 05	14	14	17	15	11
Network 06	11	11	13	11	10
Network 07	9	9	8	9	9
Network 08	9	9	7	9	9
Network 09	8	7	5	8	8
Network 10	8	7	5	6	6
Network 11	6	6	5	5	5
Network 12	5	5	4	5	4
Network 13	4	4	3	4	4
Network 14	4	4	2	4	3
Network 15	3	3	2	2	2
Network 16	2	2		2
Network 17	2	2		2

Note. For reference here and in some subsequent figures, periods are indexed (A, B, …, E), as are networks (01, 02, …, N), which are also ordered by size starting with the largest network (01).

Examining the results for the remaining four periods displayed in Table 1, there is remarkable consistency in the number of international migration networks—ranging from 15 to 17—identified by the ITCDA in each period. There are also five relatively large migration networks in each period that consistency contain about two-thirds of all countries. Finally, in each period, there is a set of small migration networks consisting of pairs or small handful of countries.

To put the figures in Table 1 into geographic context, we display a map of the 17 international migration networks that were identified by the ITCDA in the 1990–1995 period in Figure 1. These migration networks are color-coded such that the 45 countries in the largest network in 1990–1995 are displayed in mauve, the 39 countries in the second largest network are displayed in red, and so on. Taking stock of these results, at least two observations stand out. First, the results seem consistent with prior research on migration systems and networks. For example, recalling the work of Massey et al. (2002) on ‘the Mexico-U.S. migration system’, the United States and Mexico occupy the same migration network, as does every other country in Central America, most countries in the Caribbean, and several countries in South America. This is not surprising. After all, the United States has long history of political and military interventions in these regions, accompanied by policy developments at home (such as the 1965 Immigration and Nationality Act or the 1997 Nicaraguan Adjustment and Central American Relief Act), that strongly incentivized and buttressed ‘South–North’ migration over past half century (Durand & Massey, 2010:10–14; see also Alvarado & Massey, 2010; DeWaard, Nobles, & Donato, 2018; Riosmena, 2010).

FIGURE 1.

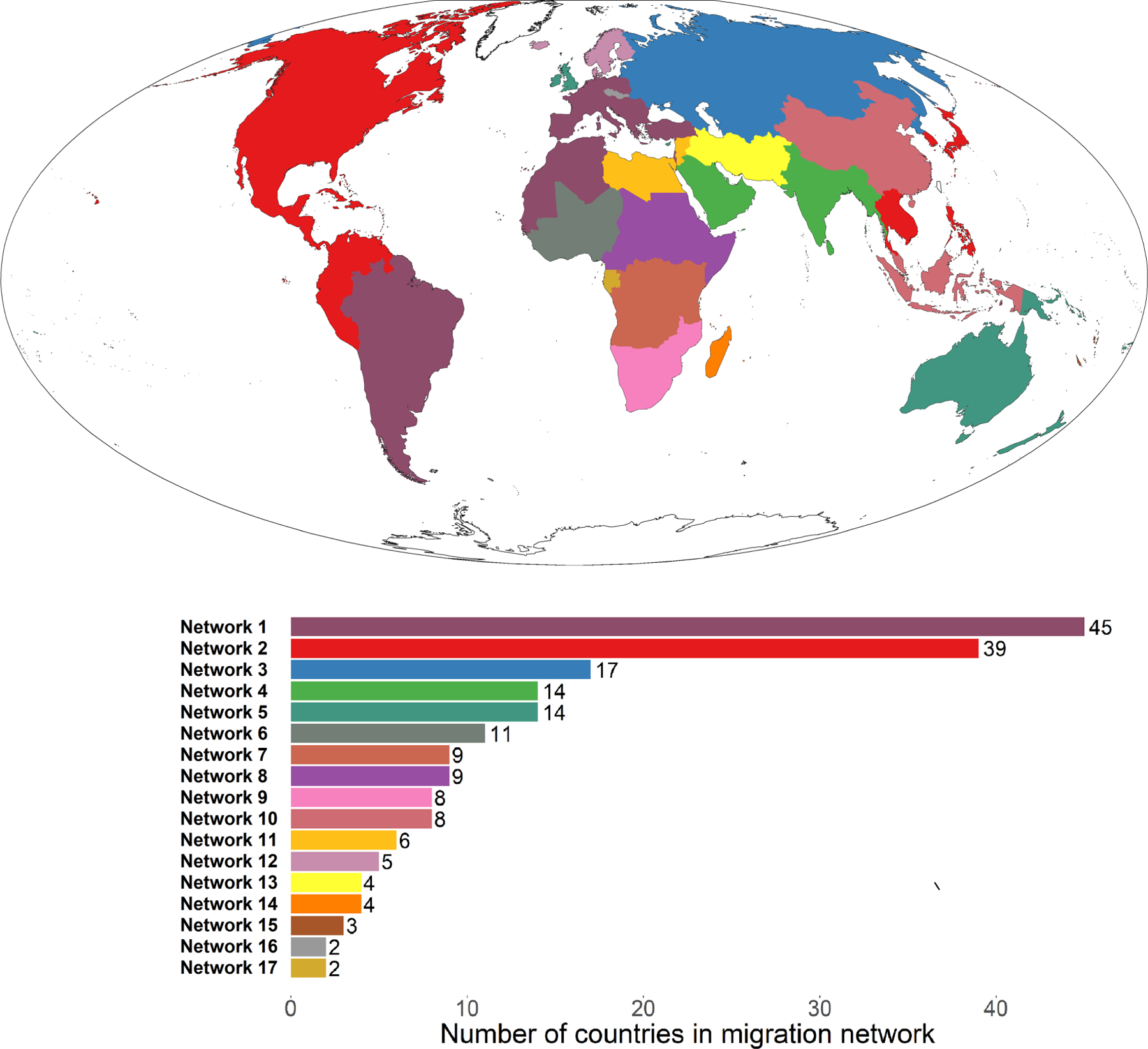
International migration networks: 1990–1995.

Source: Authors’ calculations using data from Abel and Cohen (2019). World map is graphed using the Mollweide projection

Second, consistent with the previous observation, most international migration networks are highly regional phenomena. For example, Durand and Massey (2010:8–10) described patterns of ‘intraregional’ migration in Latin America characterized by (1) short distance and temporary moves following seasonal harvests, (2) ethnic migration, particularly by those in ethnic groups located near or straddling national boundaries and (3) labor migration to urban areas. Similarly, as noted by Bakewell et al. (2009:23; see also Bakewell & de Haas, 2007; Sander & Maimbo, 2003) in his discussion of South–South migration, the majority of African migration is intracontinental and intraregional, with ‘several migration sub-systems centered on continental migration poles’ like Libya, Côte d’Ivoire and Ghana and South Africa. In addition to past and post-colonial influences, Bakewell, de Haas, Castles, Vezzoli, and Jónsson (2009) attributed the prevalence of intracontinental and intraregional migration in Africa in recent decades to increasing labor migration and refugee flows.

Similar maps of the international migration networks identified by the ITCDA in each of the remaining four periods are displayed Figures 2–5. A similar color-coding scheme is retained across the periods to make it easier to follow specific networks overtime, for instance, the red color code does not change in the 2010–2015 period when the second largest network (in red) from previous periods become the largest network. In general, the two previous observations about our results being consistent with prior research and the highly regional nature of international migration networks appear to hold in each of the remaining periods. There are also some noticeable differences. For example, starting in the 2000–2005 period, the Czech Republic and Slovakia, which entered the European Union (EU) in 2004, became part of a larger migration network consisting countries in continental Europe, as well as countries in North Africa, South America, and elsewhere. Of course, the United Kingdom and Sweden, which are long-time EU members, are not part of this migration system. Sweden, for example, has consistently been part of a migration system with Denmark, Iceland, Finland and Norway. Each of these countries is a member of the Nordic Passport Union, which permits the free movement of citizens.

FIGURE 2.

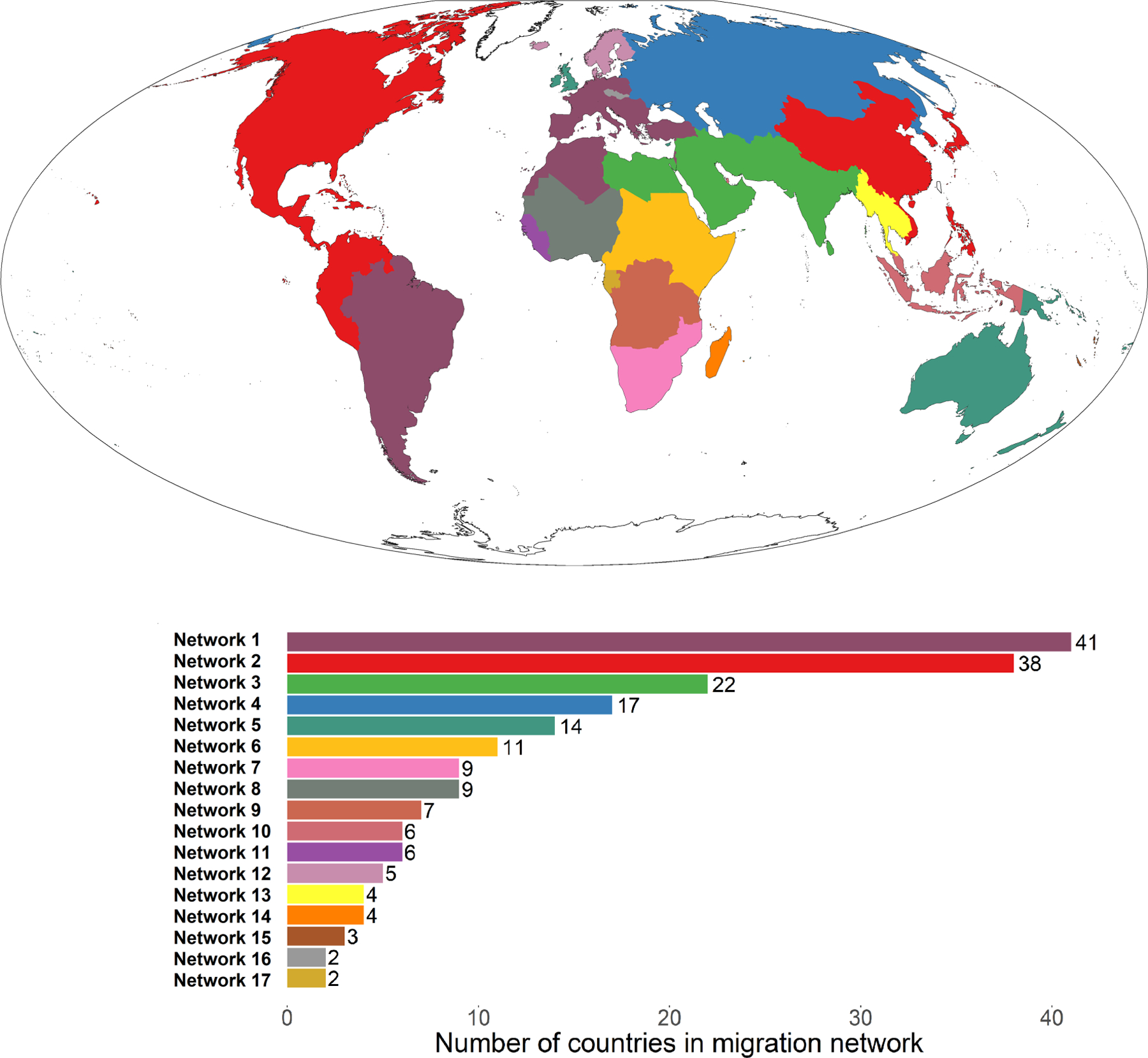
International migration networks: 1995–2000.

Source: Authors’ calculations using data from Abel and Cohen (2019). World map is graphed using the Mollweide projection

FIGURE 5.

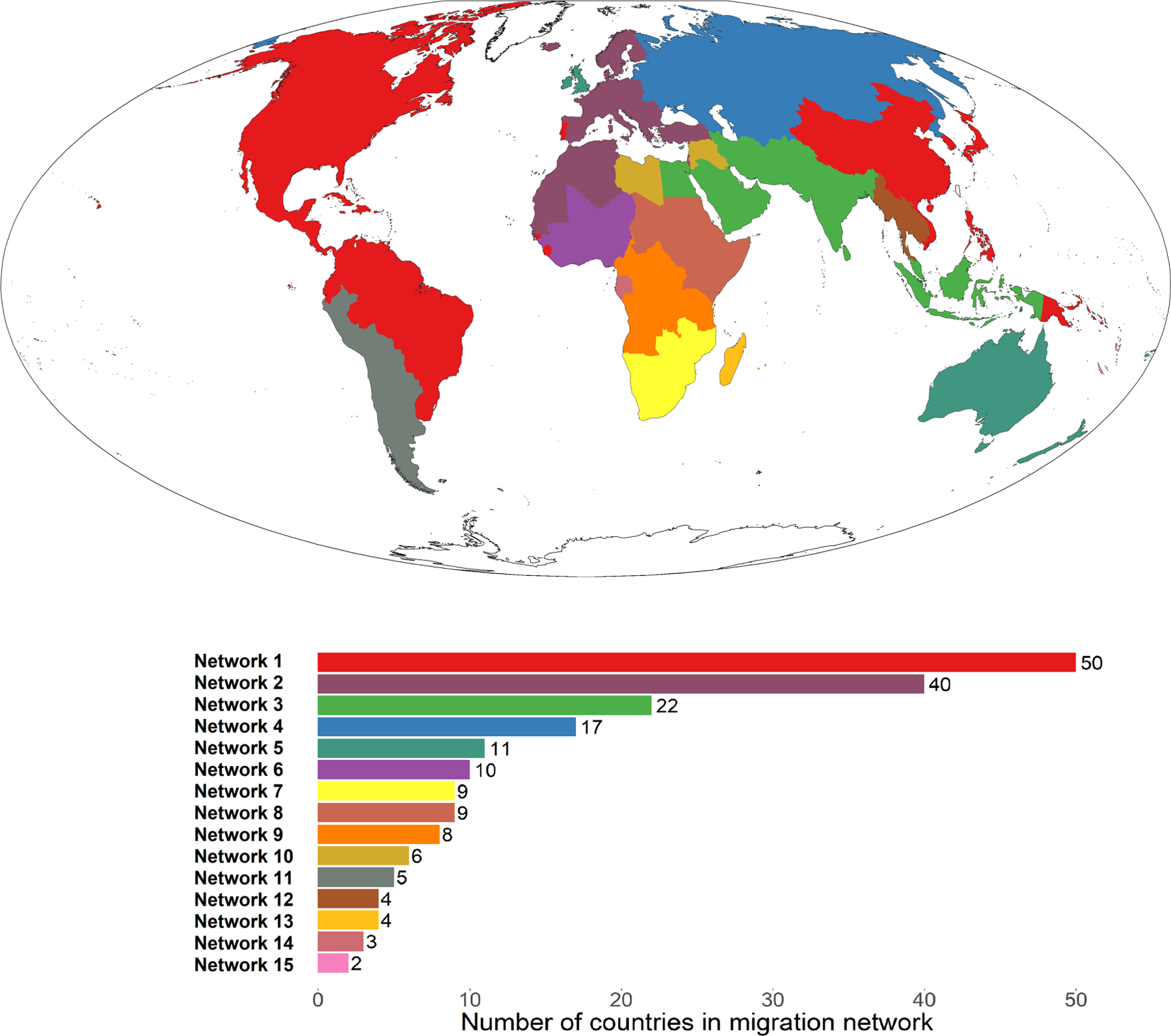
International migration networks: 2010–2015.

Source: Authors’ calculations using data from Abel and Cohen (2019). World map is graphed using the Mollweide projection

Given the different geographic sizes of international migration networks and of countries, it is can be difficult to see the country compositions of the migration networks identified by the ITCDA in Figures 1–5. Accordingly, in Figure 6, we display a tile plot which shows the unique country compositions of each migration network in each period. Countries are organized by world region, and three-character country codes. The corresponding full country names for each country code are provided in the online supporting information file country_codes.csv. We further use numbers (1, 2, …, N) to index the migration networks and retain the same color-coding scheme as the maps displayed in Figures 1–5 to enhance readability of the Figure.

FIGURE 6.

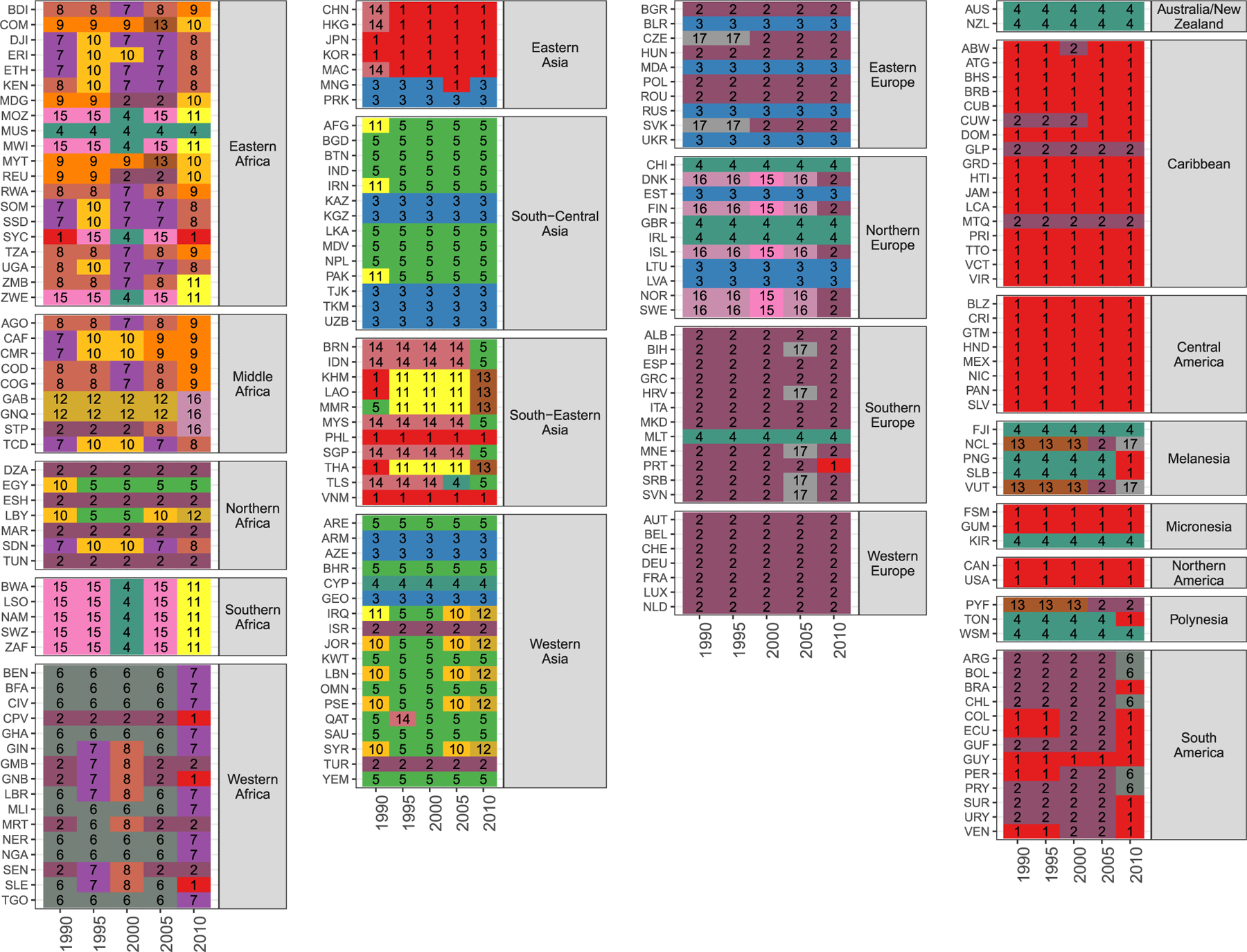
Country composition of international migration networks, 1990–1995 to 2010–2015. Please refer to online supporting information file country_codes.csv for corresponding full country names corresponding to the ISO-3 country codes used in the plot. Colors and numbers used to distinguish international migration networks

Focusing on geographically smaller countries, take the examples of the small island states of New Caledonia (NCL) and Vanuatu (VUT). Located in Melanesia and approximately 600 km from one another, these two countries have consistently been part of the same migration system over the past 25 years. The same is true for other many other countries such as Gabon (GAB) and Equatorial Guinea (GNQ) in Middle Africa, as well as Japan (JPN) and Korea (KOR) in Eastern Asia. These results are nice illustrations of Tobler’s (1970:236) first law of geography—namely, that ‘near things are more related than distant things’. Also, consistent with prior theoretical and empirical research on migration systems, they reinforce the point raised earlier that a migration system, which consists of a set of an underlying set of actors and their relationships at different scales, is ultimately manifested in an ‘identifiable geographic structure’, or a migration network, ‘that persists across space and time’ (Massey et al., 1998:61). Indeed, the internal compositions of the migration networks in and across each period displayed in Figure 6 seemingly reflect underlying demographic, economic, geopolitical and sociocultural characteristics and relationships.

4.2 |. International migration networks over time

Moving away from a period-by-period account, and thinking more fluidly about change over time in the number, size and composition of international migration networks, we display a Sankey diagram in Figure 7. This diagram combines two pieces of information that were provided and discussed in the previous subsection—the number of migration networks identified in each period and the corresponding size of each network—with the transitions of individual countries and groups of countries from one network to another between consecutive periods. This figure helps to visualize two different features that have characterized the form and evolution of migration networks over the past 25 years and that are best summed up as ‘dynamic stability’ (Kilduff et al., 2006; see also Rogers et al., 2002). Specifically, the number and size of migration networks has been remarkably stable over the past 25 years, as have the internal compositions of these networks to a lesser extent. At the same time, our results also reveal short-term fluctuations in the number, size and internal compositions of migration networks over time. Consequently, we can dispense with the idea of a single ‘all-encompassing international migration network over time (Zlotnik, 1992:19). And, although our results are consistent with idea that multiple ‘geographically discrete’ migration networks come to coexist alongside one another (Salt, 2001:31), they also suggest significant continued shuffling over time.

FIGURE 7.

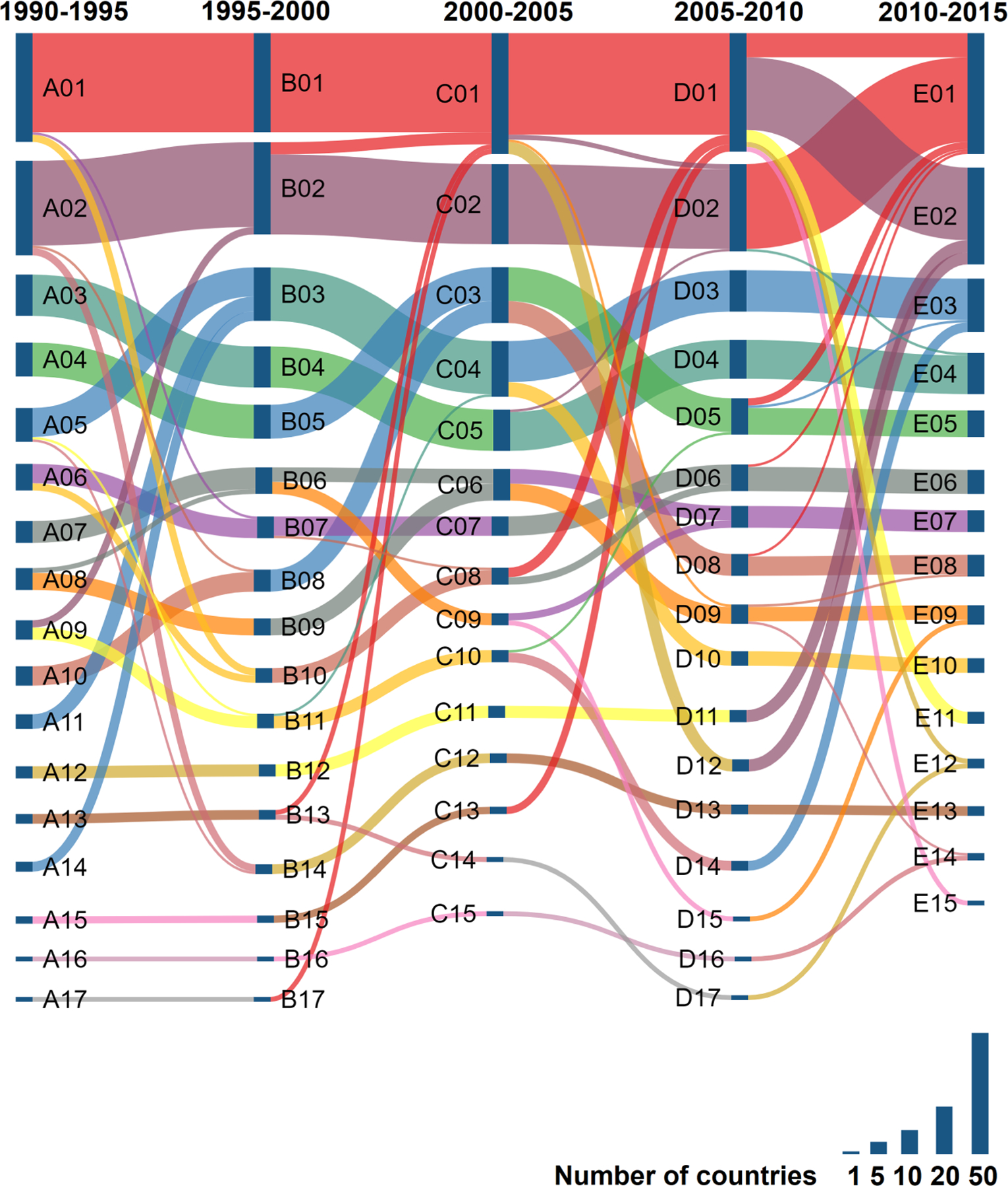
Change in international migration networks, 1990–1995 to 2010–2015. Darkened vertical bars indicate the number of international migration networks in each 5-year period. The size of each bar indicates the number of countries composing the migration network. Curved colored bars indicate transitions of countries from one migration network to another between consecutive periods. Please refer to online supporting information file country_membership. csv for corresponding network memberships of each county in each period

The final step of our analysis is to further integrate the period results and provide portrait of international migration networks over the entire 25-year period. To do this, we constructed a joint probability matrix of country-to-country migration, $\text{M}\left(1990–2015\right)$, wherein each element denotes the probability of migrating from migrant-sending country $i$ to migrant-receiving country $j$ over the entire from 1990 to 1995 to 2010–2015:

$$\mathbf{\text{M}}(\mathbf{1990}-\mathbf{2015})={\prod }_{\text{p}=1990-1995}^{2010-2015}\mathbf{\text{M}}(\mathbf{\text{p}}).$$ (2)

We used the joint migration probabilities in Equation 2 as weights in the ITCDA. In Figure 8, we display a map of the resulting 16 international migration networks that were identified. Consistent with our results and discussion above, with few exceptions, these migration networks are strongly geographically clustered and highly regional phenomena.

FIGURE 8.

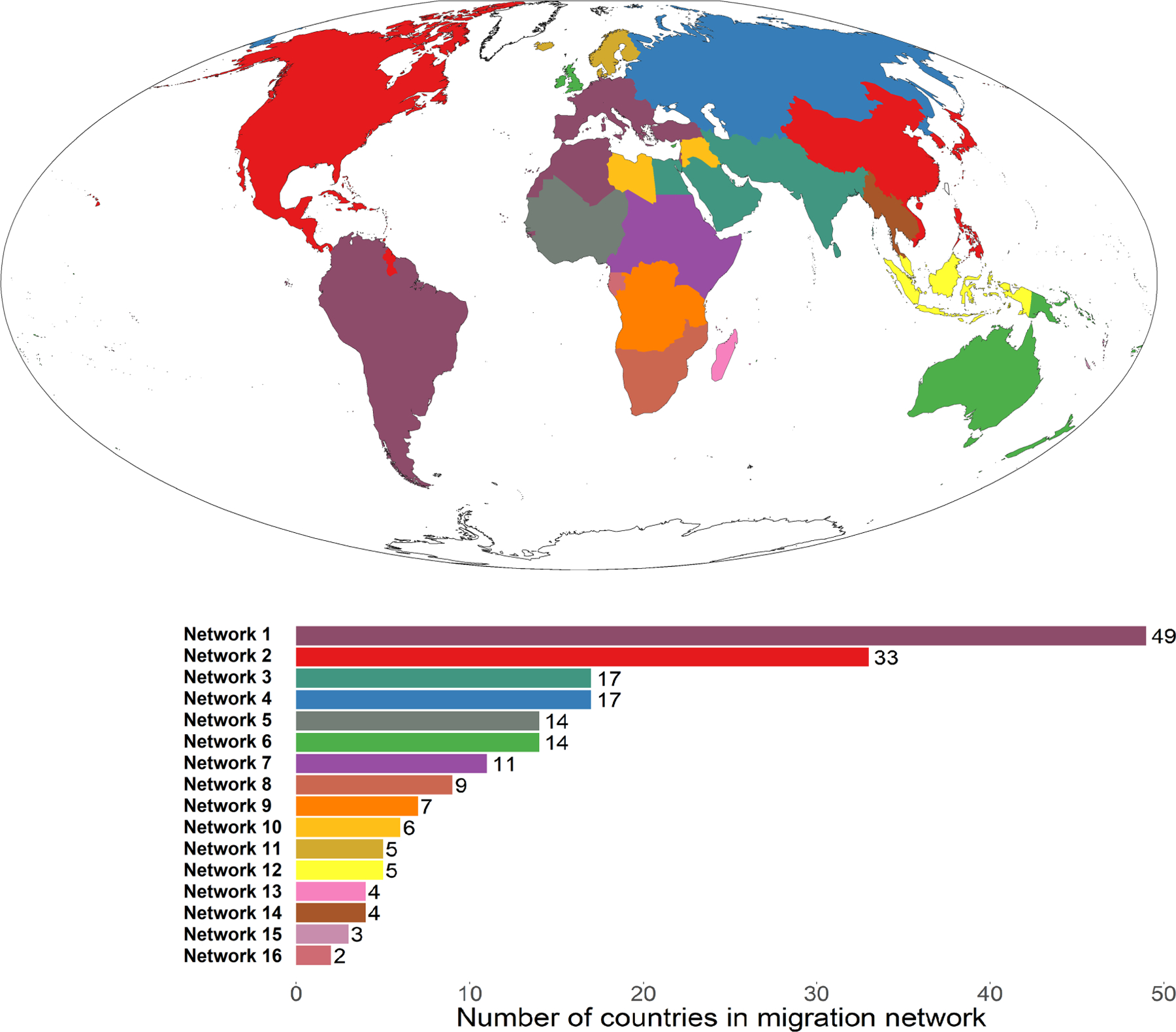
International migration networks: 1990–1995 to 2010–2015.

Source: Authors’ calculations using data from Abel and Cohen (2019). Notes: Generating this map, which displays the number and size of international migration networks over the entire 25-year period, requires a constant number of countries in each 5-year period. Accordingly, the number of countries is constant in each 5-year period using 2010–15 country boundaries. World map is graphed using the Mollweide projection

5 |. DISCUSSION

Informed by prior theoretical and empirical research on international migration systems, our work in this paper was motivated by the lack of a clear and uniform set of criteria and methods to identify and study the migration networks that systems are ultimately manifested in (Bakewell, 2014; Kritz & Zlotnik, 1992; Mabogunje, 1970; Massey et al., 1998; Zlotnik, 1992), which, we and others have argued, has resulted in research on migration systems and networks not keeping pace with substantive developments in other complementary areas (Bakewell, 2014). Drawing from research on community detection methods, we therefore introduced and applied the ITCDA to identify and study international migration networks over the past 25 years (Rosvall & Bergstrom, 2008). Unlike other community detection algorithms, the ITCDA is uniquely suited for this task because, consistent with prior research on international migration systems and networks, it identifies ‘geographically discrete’ networks (Salt, 2001:31). The ITCDA is also explicitly designed to handle data consisting of directed edges characterized by asymmetric relationships (e.g., migration from Places A to B and migration in the opposite direction from Places B to A).

The results generated are consistent with prior theoretical and empirical research on international migration systems and networks (Bakewell et al., 2009; Durand & Massey, 2010; Massey et al., 2002; Zlotnik, 1992). They also reveal two key findings. First, the number, size and internal country compositions of international migration networks have been remarkably stable over time. Second, this stability has been accompanied by many short-term fluctuations. As we noted at the end of the previous section, one of the substantive contributions of our work is that it can help to adjudicate between competing conceptualizations of the form and evolution of international migration systems. Specifically, our results do not support the idea of a single ‘all-encompassing’ international migration network (Zlotnik, 1992:19). Instead, our results point to the existence and evolution of multiple migration networks, the number, size and internal country compositions of which are slightly and continually changing over time. Our findings are therefore more in line with the concept of dynamic stability, which emphasizes long-run consistency in the number of migration networks while also acknowledging short-term fluctuations over time (Kilduff et al., 2006; see also Rogers et al., 2002).

The second contribution of this paper was to introduce and demonstrate the ITCDA as a potentially valuable tool that can be used researchers to study migration systems and networks, both international and domestic. In doing so, our hope is that researchers eventually come to some consensus about best practices in this area that can and should be implemented uniformly across studies and cases (see Willekens et al., 2016). In this vein, the spirit of our work in this paper is no different than that of, for example, Lutz, Goujon, Kc, Stonawski, and Stiliankis (2018) to identify and formalize future scenarios of international migration, Abel (2013, 2018), Dennett (2016) and Azose and Raftery (2019) in developing a specific approach for estimating country-to-country migration flows, the work of Raymer et al. (2013) who proposed a Bayesian framework to harmonize publicly available data on international migration, and the efforts of Bell et al. (2002; see also Bell et al., 2015) and Bernard (2017) in advocating for particular period and cohort measures of migration, respectively.

Previous research on network analyses of global migration (Danchev & Porter, 2018; Fagiolo & Mastrorillo, 2013; Peres et al., 2016; Tatem & Smith, 2010; Tranos et al., 2015; Windzio, 2018) has been distinguished by one or both of two common characteristics: (1) the use of migrant stock data and (2) the use of an undirected walktrap algorithm to detect network communities. In this paper, we deviated from both these traits and utilized migration flow data, rather than migrant stock data, as they provide a direct measure of movement patterns during a given period. We also adopted the use of the directional ITCDA for detecting network communities. We believe that both of these features are better suited for analyzing migration networks in comparison to previous research efforts. Future research on the application of community detection methods in studying migration might entail further exploration of existing or new directed algorithms as they become available. For example, at the time of writing, a directed version of the walktrap algorithm does not currently exist in igraph.²

As for the limitations of this paper, there are many. First, as we noted earlier, migrant stock data used to estimating country-to-country migration flows are not harmonized across countries, which means the flow estimates we used reflect countries’ (idiosyncratic) reports of migrant stocks. This is an unavoidable limitation with these estimates, but one that we think is substantially outweighed by their geographic and temporal scope. Second, recalling Zlotnik’s (1992:20) ‘general principles’, there are other types of linkages (such as ‘comparable levels of development’ or ‘cultural affinity’) shared by migrant-sending and migrant-receiving countries that we did not and cannot consider given the mechanics of the ITCDA that we introduced here. Third, although the ITCDA identifies ‘geographically discrete’ migration networks (Salt, 2001:31), which is consistent with Zlotnik’s (1992:20) approach, future research might also wish to consider the use of community detection algorithms that allow for countries to belong to multiple, overlapping networks (see Devi & Poovammal, 2016; Xie et al., 2013). However, to our knowledge, no such algorithms of this type currently exist that can handle data consisting of directed edges characterized by asymmetric relationships. Finally, as is the case with any research paper, especially those with such an expansive geographic and temporal scope, a persistent challenge is to distill the information down in ways that are digestible and substantively relevant and meaningful to diverse audiences.

In closing, our work stands to inform theoretical and empirical research on international migration networks and their underlying migration systems. Going forward, the insights from and tools used in this paper can and should be applied to examine regional migration networks, both international and domestic. Future research might also seek to take a more event-centered approach and document the form and evolution of a given migration network before, during, and after a specific shock or set of shocks (e.g., see Fix et al., 2009; Fussell, Curtis, & DeWaard, 2014). Finally, as new and disaggregated estimates of country-to-country migration flows become available, future research might use the ITCDA algorithm to identify international migration networks by, for example, age and other characteristics. One potential starting point here is Abel’s (2018) set of estimates of country-to-country migration flows by sex; however, like Abel’s (2013) previous estimates, these are minimum counts of country-to-country migration flows that are required to match the aforementioned country-level migrant stock data by sex in consecutive periods.

FIGURE 3.

International migration networks: 2000–2005.

Source: Authors’ calculations using data from Abel and Cohen (2019). World map is graphed using the Mollweide projection

FIGURE 4.

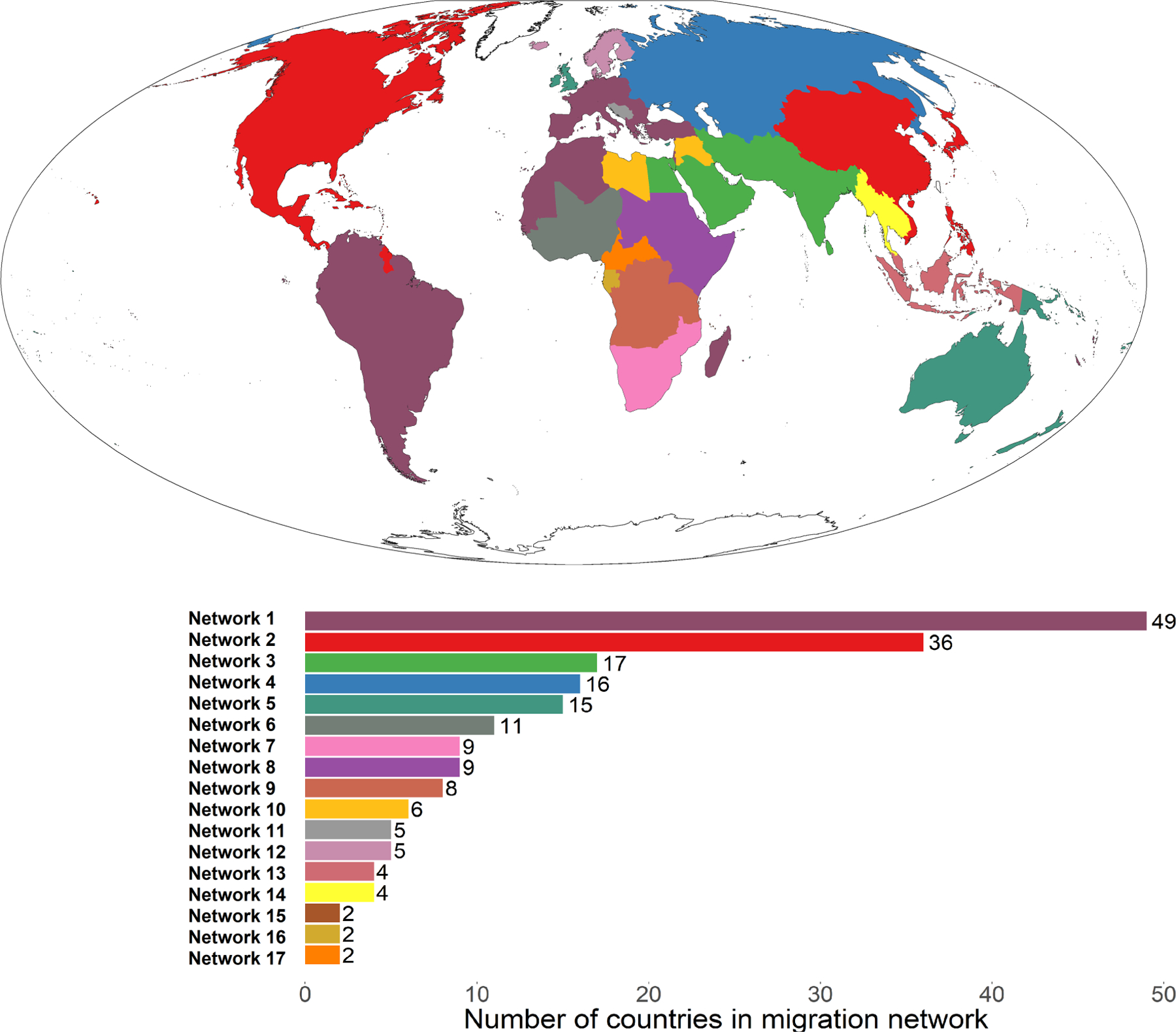
International migration networks: 2005–2010.

Source: Authors’ calculations using data from Abel and Cohen (2019). World map is graphed using the Mollweide projection

DATA AVAILABILITY STATEMENT

Data are available in the supporting information.