Detection of fluorescent protein mechanical switching in cellulo

Summary

The ability of cells to sense and respond to mechanical forces is critical in many physiological and pathological processes. However, determining the mechanisms by which forces affect protein function inside cells remains challenging. Motivated by in vitro demonstrations of fluorescent proteins (FPs) undergoing reversible mechanical switching of fluorescence, we investigated whether force-sensitive changes in FP function could be visualized in cells. Guided by a computational model of FP mechanical switching, we develop a formalism for its detection in Förster resonance energy transfer (FRET)-based biosensors and demonstrate its occurrence in cellulo within a synthetic actin crosslinker and the mechanical linker protein vinculin. We find that in cellulo mechanical switching is reversible and altered by manipulation of cell force generation, external stiffness, and force-sensitive bond dynamics of the biosensor. This work describes a framework for assessing FP mechanical stability and provides a means of probing force-sensitive protein function inside cells.

Graphical abstract

Highlights

• •An approach to probe the effect of cellular forces on fluorescent protein (FP) function
• •FP function is sensitive to load magnitude and dynamics (e.g., duration)
• •FP function in biosensors is affected by bond dynamics and substrate stiffness
• •Force-induced changes in FP function can be used to indirectly probe mechanosensing

Motivation

Cells sense mechanical cues via force-induced alterations in protein structure and function, but elucidation of the molecular mechanisms is hindered by the lack of approaches to probe the effect of forces on protein structure and function inside cells. Motivated by in vitro observations of reversible fluorescent protein mechanical switching, we developed an approach for detecting fluorescent protein mechanical switching in cellulo. This enables the visualization of force-sensitive protein function inside living cells.

Shoyer et al. develop an approach to probe how mechanical forces affect the function of fluorescent proteins inside living cells and leverage it to study mechanosensitive molecular processes. Fluorescent protein mechanical switching is manipulated by perturbations to force-activate bonds and substrate stiffness, consistent with its sensitivity to protein loading dynamics.

Introduction

The ability of cells to sense and respond to mechanical forces is critical in many developmental and physiological processes, and its dysregulation is involved in the progression of several disease states, including fibrosis and cancer.¹ To sense mechanical stimuli, cells must convert forces into biochemically detectable signals, which occurs through a multi-step molecular process.^1,2,3,4 Forces are first transmitted across specific proteins (termed mechanotransmission). This results in force-induced changes in protein structure and function (termed mechanosensing), such as the unfolding of a domain to expose a cryptic binding site.³ Such protein conformational changes are then recognized biochemically (termed mechanotransduction), often through the binding/unbinding of transducer proteins. These new protein complexes drive downstream alterations in cell signaling and gene expression (termed mechanoresponse).³ Despite significant progress in our understanding of the initial and final steps of this process, elucidating the molecular mechanisms of mechanosensing and mechanotransduction remains challenging.^1,5

In vitro single-molecule techniques have provided a physical understanding of mechanosensitive molecular mechanisms. Using these techniques, the extension and unfolding of mechanosensitive protein domains, such as those in talin and α-catenin, as well as the subsequent binding of transducer proteins, such as vinculin, have been directly characterized.^6,7,8 However, determining where, when, and in which proteins these processes occur in cells is still challenging. Increased understanding of the spatiotemporal regulation of mechanosensitive processes inside cells has largely come from the emergence of imaging techniques.⁹ The development of molecular tension sensors (MTSs) to visualize loads across specific proteins inside cells has advanced our understanding of mechanotransmission, elucidating which proteins transmit loads and how these loads vary across biological contexts.¹⁰ Progress in mechanosensing has been enabled by techniques to label unfolded protein domains via the binding of secondary probes, including antibodies that recognize the extended conformations of p130Cas or α-catenin,^11,12 and STReTCh (sensing tension by reactive tag characterization), which operates by the force-induced exposure of SpyTag and subsequent covalent binding of SpyCatcher.¹³ Likewise, advances in mechanotransduction have been made by monitoring the localization of endogenous transducer proteins in response to molecular tension across a load-bearing protein.¹⁴ However, labeling could affect protein function or compete with the binding of endogenous mechanotransducers, and these tools are often limited to fixation and/or depend on target protein-specific reagents that can be difficult to develop. Furthermore, these in cellulo techniques are based on the binding of a secondary probe (a synthetic marker or a labeled natural protein) to force-exposed domains, which conflates the steps of mechanotransduction and mechanosensing. Currently, there are no approaches analogous to in vitro techniques that can report mechanosensing (i.e., force-induced conformation changes in protein domains) inside cells.

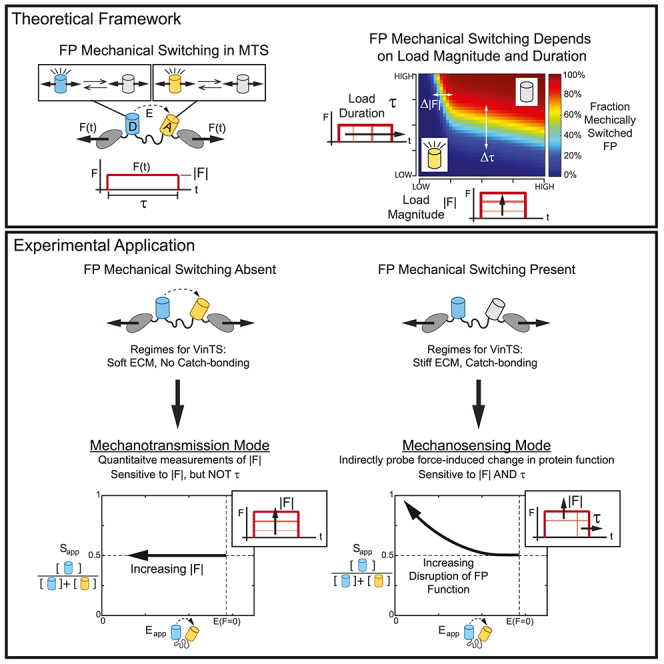
To begin to address this technological gap, we asked whether the function of MTSs could be extended. MTSs were designed to measure the magnitude of loads on proteins (i.e., mechanotransmission). The largest class of MTSs used in cells are genetically encoded Förster resonance energy transfer (FRET)-based MTSs.^10,15 They consist of two fluorescent proteins (FPs) separated by an extensible linker domain.¹⁶ Load across the MTS deforms the extensible linker domain, altering the distance between the FPs and the FRET efficiency. The FPs inside MTSs are also subject to loading, but their photophysical properties have been assumed to be force insensitive. However, recent in vitro experiments have demonstrated that GFP fluorescence can be switched on and off by cycles of mechanical loading.¹⁷ This process is reversible and associated with an intermediate transition that is distinct from the complete unfolding or denaturation of the FP.^17,18 Therefore, FP mechanical switching is a reversible, force-sensitive transition between two structural/functional states. Additionally, FP mechanical switching is a kinetic process that inherently depends on both the magnitude and dynamics of loading (e.g., load duration or rate). This is important because both the magnitude and the dynamics of mechanical forces are known to drive mechanosensing by endogenous protein domains,^5,8,19,20,21 as well as cell-level responses to mechanical stimuli.^3,4 A properly functioning sensor of mechanotransmission will never accurately report the presence of mechanosensing. This is because the linker extends on a nearly instantaneous timescale, rendering the sensor’s signals independent of load duration/dynamics. In contrast, FP mechanical switching, like force-induced conformational changes in mechanosensitive domains, responds to a combination of load magnitude and load duration/dynamics. We thus hypothesized that FP mechanical switching within an FRET-based MTS for a protein of interest could be used to indirectly probe if, when, and where mechanically similar domains within the protein of interest undergo force-induced conformational changes, without the need for fixation or secondary probe binding. At the same time, we also reasoned that the continued use and design of MTSs to measure mechanotransmission requires an understanding of FP mechanical switching.

Here, we investigated whether FP mechanical switching occurs inside cells. To create a physical framework, we first developed a kinetic model of FP mechanical switching in the context of FRET-based MTSs and then simulated expected experimental readouts. This revealed the effect of FP mechanical switching on FRET-based MTSs and predicted unique data signatures for the detection of FP mechanical switching in cellulo. Guided by this framework, we found that a synthetic actin-binding domain tension sensor (ABDTS) exhibited strong signatures of FP mechanical switching. The effect was reverted by pharmacological disruption of F-actin, indicating the reversibility of FP mechanical switching in cellulo. We also found less, but detectable, FP mechanical switching in a tension sensor for the mechanical linker protein vinculin (VinTS). FP mechanical switching in vinculin was sensitive to both manipulations of the vinculin-actin catch bond and mechanical stiffness of the external microenvironment. Together, this work describes an experimental paradigm for detecting the effect of mechanical loads on FP function in cells. This enables the visualization of force-dependent changes in FP structure/function, which can be leveraged to indirectly probe mechanosensitive processes in cellulo independent of secondary probe binding.

Results

Development of a framework to assess FP mechanical switching in cellulo

To investigate FP mechanical switching in the context of fusion proteins in cells, we first considered a single FP within a load-bearing protein (Figure S1; Note S1, section II). Specifically, we modeled a load-bearing protein with a single FP in the line of loading subject to dynamic loading parameterized by a load magnitude $F$ and a characteristic load duration $\tau$. The load duration is governed by unbinding from the loading source with rate constant $k_{unbind}$ (where $\tau \equiv 1/k_{unbind}$) (Figure S1A). The FP can reversibly switch between functional and non-functional states in a force-sensitive manner. Informed by single-molecule studies on the response of GFP to mechanical loading, FP mechanical switching is modeled as a two-step, sequential process (Figure S1B; Note S1, section II.A; Equation S1; and Table S1). The first step is a fast, near-equilibrium transition at a characteristic force,²² which is permissive for the second step. The second step is a transition to a non-fluorescent state, which is described by a Bell model force-dependent rate constant.¹⁷ The kinetics of this second step are expected to be slower and a potential source of non-equilibrium effects (e.g., loading rate or load duration dependence). As a large number of FPs with different structures, photophysical properties, and mechanical stabilities exist, and the integration of FPs into fusion proteins in the cellular environment can alter these properties, we assessed the extent of FP mechanical switching over a large parameter space.^16,22,23,24 The model identified regions of the mechanical switching parameter space where FP mechanical switching was likely or unlikely to occur as a function of the load magnitudes and durations estimated for protein loading in cells^10,25 (Figures S1C–S1O; Note S1, section II.B). These analyses indicate that FP mechanical switching is sensitive to changes in both load magnitude and load duration, suggesting that mechanical switching of an FP inside a load-bearing protein could, in principle, be suitable for indirectly probing if, when, and where the protein of interest supports mechanosensing.

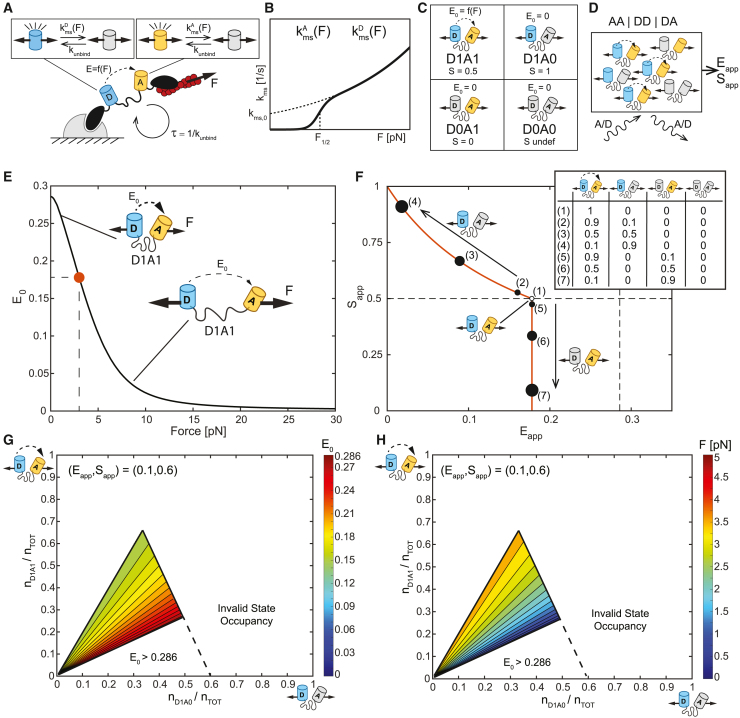
To investigate the detection of FP mechanical switching in FRET-based MTSs, we had to extend the model of FP mechanical switching to an MTS, specify an imaging modality, and establish a framework for displaying the data. To mediate FRET, two FPs must have distinct photophysical properties, where one FP (the donor) can non-radiatively transfer energy to the other FP (the acceptor).²⁶ In our model, MTSs are subject to dynamic loading parameterized by a load magnitude $F$ and a characteristic load duration $\tau$, during which the acceptor and donor FP can reversibly switch between functional and non-functional states in force-sensitive manners (Figures 1A, 1B, and S2; Note S1, sections III.A.1–III.A2; Equations S4 and S5; Table S2). Therefore, within a population of MTSs, each sensor exists in one of four states: D1A1, D1A0, D0A1, and D0A0, where “D” represents the donor FP, “A” represents the acceptor FP, and “0” or “1” indicates whether an FP is in the non-fluorescent or fluorescent state, respectively (Figure 1C).

Figure 1.

Framework for FP mechanical switching in FRET-based MTSs

(A and B) (A) Model of FP mechanical switching in MTSs. MTSs are subject to dynamic loading parameterized by a load magnitude $F$ and a characteristic load duration $\tau$, which is governed by unbinding from the loading source with rate constant $k_{unbind}$. Donor and acceptor FPs are in the line of loading and undergo FP mechanical switching with force-dependent rate constants $k_{MS}^D\left(F\right)$ and $k_{MS}^A\left(F\right)$. $k_{MS}^D\left(F\right)$ and $k_{MS}^A\left(F\right)$ have the same functional form, shown in (B), but different parameters.

(C) Four possible MTS states based on the status of the donor and acceptor FP. For each state, the FRET efficiency, $E_0$, and FP stoichiometry, $S$, are indicated.

(D) Schematic of 3-channel FRET measurements of a simulated population of MTSs.

(E) FRET efficiency-force calibration, $E_0=f\left(F\right)$, for an MTS in the D1A1 state, with dot indicating $F$ of 3 pN.

(F) Plot of $S_{app}$ versus $E_{app}$ containing the ($E_{app}$, $S_{app}$) curve for MTS populations subject to constant loading at magnitude $F$ of 3 pN for cases of acceptor-only mechanical switching (varying amounts of D1A1 and D1A0 states) or donor-only mechanical switching (varying amounts of D1A1 and D0A1 states). The fraction of sensors in each state is indicated in the key.

(G) Contour plot of $E_0$ on the (fraction of sensors in D1A0 state, fraction of sensors in D1A1 state) plane demonstrating all $E_0$ values consistent with the single point ($E_{app}$, $S_{app}$) of (0.1, 0.6). White indicates regions with invalid state occupancies and/or $E_0$ values.

(H) Corresponding contour plot of $F$ using the $E_0=f\left(F\right)$ calibration in (E). Levels are in increments of 0.01 for (F) and 0.025 for (H).

The plots in (F)–(H) relate to Equations 3 and 4.

See also Note S1 and Figures S1–S4.

To understand how mechanical switching affects FRET measurements, we needed to select an imaging modality. As sensitized emission is the most widely used imaging modality for measuring FRET-based sensors in cellulo, we chose to focus on it.^27,28,29 In this approach, FRET-based sensors are imaged in three channels (DD: donor excitation, donor emission; DA: donor excitation, acceptor emission; AA: acceptor excitation, acceptor emission). Using calibration methods, the apparent FRET efficiency, $E_{app}$, and FP stoichiometry (abundance of donor relative to total FPs), $S_{app}$, can be computed from these images^27,28,29 (Figure 1D; Note S1, section III.A.3). $E_{app}$ and $S_{app}$ are calculated using the following equations²⁹:

$$E_{app}=\frac{I_{DA,corr}}{I_{DA,corr}+{\gamma }^M·I_{DD}}$$ (Equation 1)

$$S_{app}=\frac{I_{DA,corr}+{\gamma }^M·I_{DD}}{I_{DA,corr}+{\gamma }^M·I_{DD}+I_{AA}/{\beta }^X}$$ (Equation 2)

where $I_{DD}$ is the intensity in the DD-channel, $I_{AA}$ is the intensity in the AA-channel, $I_{DA,corr}$ is the intensity in the DA-channel corrected for donor bleedthrough and acceptor direct excitation, and ${\gamma }^M$ and ${\beta }^X$ are constants for calibrated measurements of three-channel FRET^27,28,29 (see Note S1, section III.A.3 and STAR Methods).

A framework for displaying FRET data based on two-dimensional histograms of $E_{app}$ and $S_{app}$ was recently developed to visualize and understand the effect of FP stoichiometry on three-channel FRET measurements.²⁹ For one-piece intramolecular FRET sensors, the ES-histogram framework provides a data quality control, as sensors with one donor and one acceptor FP should, by design, exhibit $S_{app}=0.5$. Deviations indicate a lack of FP function due to photobleaching, maturation, or other processes. To investigate the detection and effects of FP mechanical switching in MTSs, we extended the ES-histogram framework to include the force-sensitive, continuously variable FRET signal of FRET-based MTSs and the mechanical switching of acceptor and donor FPs (Figures S3 and S4; Note S1, section III.B.1). Sensors in the D1A1 state (both FPs in the functional state) undergo intramolecular FRET with a FRET efficiency ($E_0$), which depends on the magnitude of molecular tension across the MTS, $F$, according to the FRET efficiency-force calibration, $E_0=f\left(F\right)$, of the tension sensor module.^16,30 Here, the previously determined FRET efficiency-force calibration for the original tension sensor module (TSMod) (mTFP1-(GPGGA)₈-mVenus) was used to facilitate comparisons to experimental data in this work^16,30 (Figure 1E). To simulate three-channel FRET measurements analogous to experimental data, we considered the three-channel FRET signal contribution from each of the four states to determine $E_{app}$ and $S_{app}$ for a population of MTSs containing a specified number of sensors in each state ($n_{D1A1},n_{D1A0},n_{D0A1},n_{D0A0}$) (Note S1, section III.A.3; Tables S3 and S4; Equations S12–S19).

To build intuition, we derived simplified expressions for an MTS population containing a specified number of sensors in each state in which all sensors are subject to constant loading at a magnitude, $F$:

$$E_{app}=\frac{E_0}{1+\left(\frac{n_{D1A0}}{n_{D1A1}}\right)}$$ (Equation 3)

$$S_{app}=\frac{n_{D1A1}+n_{D1A0}}{\left(n_{D1A1}+n_{D1A0}\right)+\left(n_{D1A1}+n_{D0A1}\right)}$$ (Equation 4)

where $E_0=f\left(F\right)$ is the FRET efficiency-force calibration for sensors in the D1A1 state, and a non-zero number of sensors in the D1A1 state ($n_{D1A1}>0)$ is assumed. Equations 3 and 4 indicate how FP mechanical switching should affect three-channel FRET measurements of MTSs and quantitative estimates of molecular tension magnitude. In the absence of FP mechanical switching, all MTSs exist in the D1A1 state ($n_{D1A0}=n_{D0A1}=n_{D0A0}=0$), so $E_{app}=E_0$ and $S_{app}=0.5$. The resulting relationship $E_{app}=E_0$ indicates that quantitative measurements of molecular tension magnitude using the $E_0=f\left(F\right)$ calibration are valid in the absence of FP mechanical switching. In the presence of FP mechanical switching, ($E_{app}$, $S_{app}$) curves can be constructed for MTS populations subject to the same load magnitude, $F$, and having variable amounts of acceptor-only (some D1A0) or donor-only (some D0A1) mechanical switching (referred to as tension isoclines; Figures 1F, S4C, and S4D; Note S1, section III.B.1). Increasing levels of acceptor mechanical switching move the data up/left with decreasing $E_{app}$ coupled to increasing $S_{app}$. Increasing levels of donor mechanical switching move the data directly downward with decreasing $S_{app}$. These trends are consistent with the known effects of excess donors and acceptors, respectively, in other force-insensitive FRET-based biosensors.²⁹ In the presence of FP mechanical switching, quantitative measurements of molecular tension magnitude are not possible for two reasons. The first reason is, because both the acceptor and donor FPs can undergo mechanical switching, the actual occupancy of sensors in each of the possible four states (D1A1, D1A0, D0A1, and D0A0) cannot be uniquely determined from the experimentally measurable quantities ($E_{app}$ and $S_{app}$). In the presence of FP mechanical switching, a single $\left(E_{app},S_{app}\right)$ data point is consistent with many possible values of $E_0$, and hence, $F$ (demonstrated for an example data point in Figures 1G and 1H). Therefore, $E_{app}\ne E_0$, and quantitative measurements of molecular tension magnitude are invalidated. We note that formalisms assuming donor-only or acceptor-only mechanical switching would reduce the number of unknowns, but we are hesitant to utilize such approaches at this time. It is challenging to experimentally eliminate the possibility of donor mechanical switching in the presence of acceptor mechanical switching (or vice versa) because sensors harboring two non-fluorescent FPs are not optically detectable. The second reason is that FP mechanical switching is more likely at higher versus lower tension magnitudes, which could bias measurements of tension magnitude distributions (Note S1, section VI). Overall, $E_{app}=E_0$, which is required for quantitative measurements of molecular tension magnitude, can only be assumed in the absence of both acceptor and donor mechanical switching, which is confirmed via the ES-histogram by confirming that $S_{app}\sim 0.5$ across the full range of $E_{app}$ values.

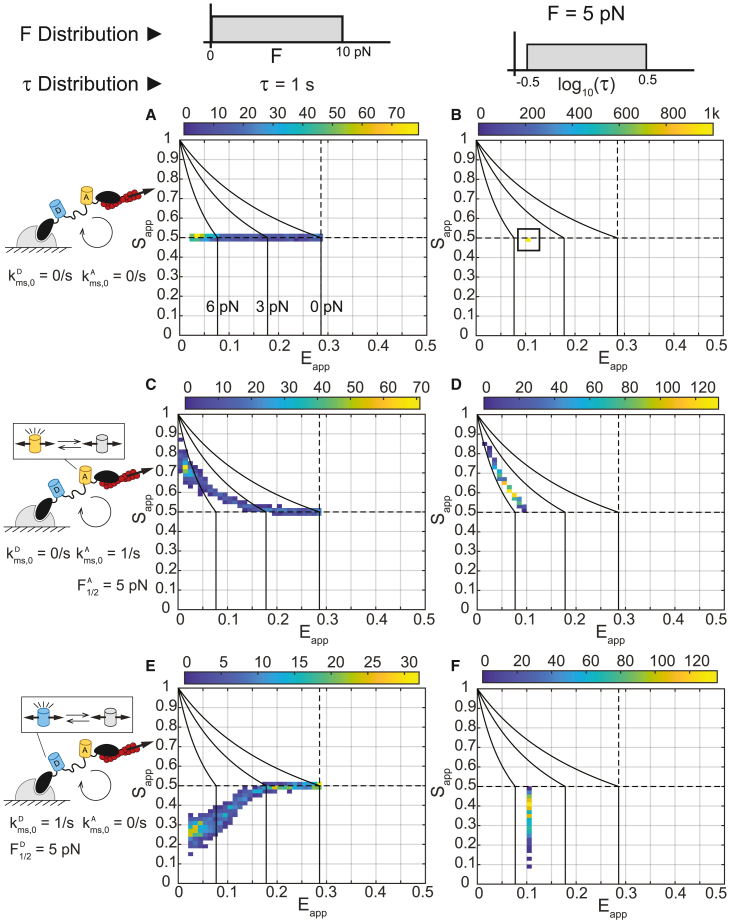
We next assessed the suitability of the ES-histogram framework for detecting FP mechanical switching in MTSs that undergo dynamic binding, loading, and unbinding (Note S1, sections III.B.2–III.B.5 and IV). We first asked how the three-channel FRET signals for MTSs with FP mechanical switching responded to variations in load magnitude at constant load duration or variations in load duration at constant load magnitude. To do so, we simulated three-channel FRET measurements for populations of MTSs subject to variations in load magnitude $F$ or load duration $\tau$ with no (Figures 2A and 2B), acceptor-only (Figures 2C and 2D), or donor-only mechanical switching (Figures 2E and 2F). In the absence of FP mechanical switching, the MTS responds only to variations in load magnitude (Figure 2A) and is not sensitive to variations in load duration (Figure 2B). Therefore, in the absence of mechanical switching, an MTS functions according to the original design intention—in other words, as a quantitative probe for mechanotransmission ($E_{app}=E_0$) due to the extension of the deformable linker domain within the tension sensor module. In the presence of acceptor or donor mechanical switching, the sensor now responds to both variations in load magnitude (Figures 2C, 2E, S7C, and S7D; Note S1, section III.B.4) and load duration (Figures 2D, 2F, S7A, and S7B; Note S1, section III.B.4). Therefore, the ES-histogram provides additional information, indicating force-sensitive changes in FP structure/function resulting from the loading dynamics of the protein of interest that contains the MTS. However, contributions from load magnitude and duration cannot be decoupled from the ES-histogram (Figures S7 and S9; Note S1, sections III.B.4 and IV), and quantitative measurements of molecular tension magnitude are no longer possible ($E_{app}\ne E_0$).

Figure 2.

Response of MTSs to variation in load magnitude or load duration

(A–F) ES-histograms for 1,000 simulated populations of MTSs subject to a (A, C, and E) load magnitude ($F$) drawn from a uniform distribution between 0 and 10 pN and a characteristic load duration ($\tau$) of 1 s, or (B, D, and F) $F$ of 5 pN and $\tau$ drawn from a log-uniform distribution from 10^−0.5 to 10^0.5 s for cases of (A and B) no FP mechanical switching, (C and D) acceptor mechanical switching only, or (E and F) donor mechanical switching only, according to base model parameters given in Note S1 and Table S2. Each MTS population comprises 50 sensors having the same FP parameters, $F$ values, and $\tau$ values. The color bars indicate bin counts. In all plots, reference black lines are tension isoclines for acceptor-only or donor-only mechanical switching at $F$ of 0, 3, and 6 pN (from right to left).

See also Note S1 and Figures S5–S12.

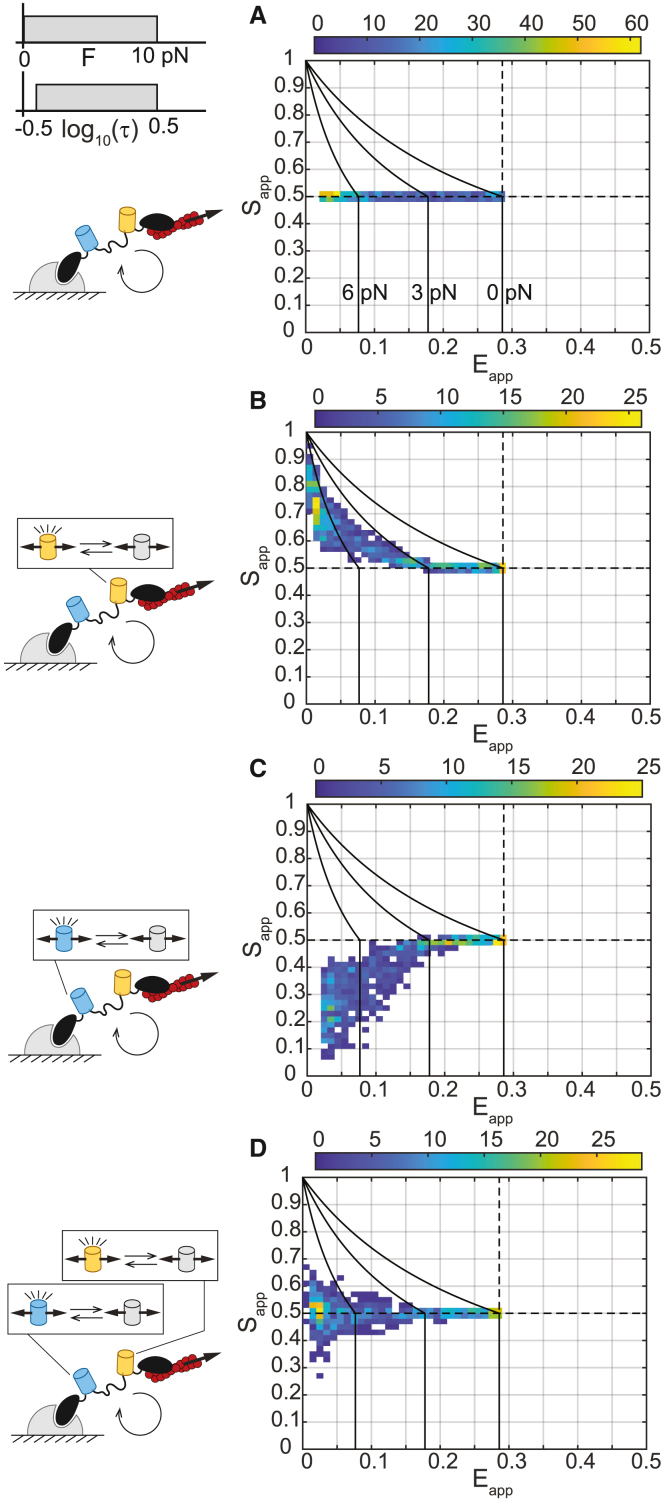
Lastly, we generated signatures for all cases of FP mechanical switching that would be analogous to experimental data, where both the load magnitudes and durations vary. To do so, we simulated three-channel FRET measurements for populations of MTSs subject to variations in both load magnitude $F$ and characteristic load duration $\tau$ that exhibit no (Figure 3A), acceptor-only (Figure 3B), donor-only (Figure 3C), or both donor and acceptor (Figure 3D) mechanical switching. In the absence of FP mechanical switching, both acceptor and donor FPs are functional (D1A1 state), and the data are distributed along $S_{app}=0.5$ and $E_{app}=E_0$ (Figure 3A). Thus, the spread in $E_{app}$ is solely due to the extension of the deformable linker domain within the tension sensor module, and load magnitudes can be accurately inferred. FP mechanical switching results in deviations in $S_{app}$ from 0.5. Increased acceptor mechanical switching increases $S_{app}$ and decreases $E_{app}$, resulting in an up/left-slanting data signature (Figure 3B). This trend is observed for a wide range of FP mechanical switching parameters and is distinct from constitutive acceptor loss of function (e.g., due to photobleaching or large differences in FP maturation time [Figure S5; Note S1, section III.B.2]). Increased donor mechanical switching decreases $S_{app}$, with larger effects at lower $E_{app}$ values, resulting in a down/left-slanting data signature (Figure 3C). This trend is conserved for a wide range of FP parameters and is distinct from constitutive donor loss of function (e.g., due to photobleaching or large differences in FP maturation time [Figure S6; Note S1, section III.B.3]). Lastly, we considered when both acceptor and donor FPs undergo mechanical switching. If the acceptor and donor exhibit identical FP mechanical switching kinetics, then $S_{app}$ values deviate from 0.5 positively and negatively (Figure 3D), producing a signature that is distinct from cases where one or both FPs lack mechanical switching. In the case where both FPs undergo mechanical switching but with non-identical parameters, dominant mechanical switching of acceptor or donor remains detectable in the presence of lower levels of mechanical switching in the other species (Figure S8; Note S1, section III.B.5). Therefore, we conclude that minor and substantial FP mechanical switching in either donor and/or acceptor FPs in response to diverse aspects of mechanical loading are detectable using the ES-histogram framework.

Figure 3.

Data signatures of FP mechanical switching in MTSs

(A–D) ES-histograms for 1,000 simulated populations of MTSs subject to a load magnitude ($F$) drawn from a uniform distribution between 0 and 10 pN and a characteristic load duration ($\tau$) drawn from a log-uniform distribution from 10^−0.5 to 10^0.5 s for cases of (A) no FP mechanical switching, (B) acceptor mechanical switching only, (C) donor mechanical switching only, or (D) identical acceptor and donor mechanical switching, according to base model parameters given in Note S1 and Table S2. Each MTS population comprises 50 sensors having the same FP parameters, $F\text{values}$, and $\tau$ values. The color bars indicate bin counts. In all plots, reference black lines are tension isoclines for acceptor-only or donor-only mechanical switching at $F$ of 0, 3, and 6 pN (from right to left).

See also Note S1 and Figures S5–S12.

Taken together, these analyses demonstrate the effect of FP mechanical switching on three-channel FRET measurements of MTSs, predict unique data signatures for the detection of FP mechanical switching in cellulo, and indicate that additional information related to loading dynamics/duration can be obtained from FP mechanical switching in MTSs.

Synthetic actin-binding tension sensor exhibits FP mechanical switching in cellulo

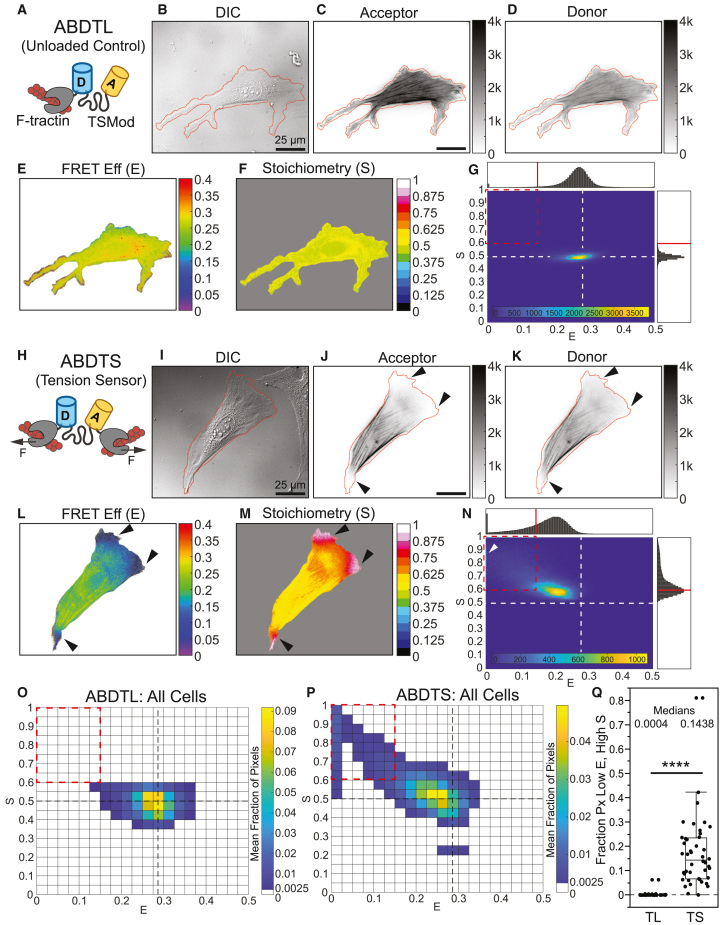
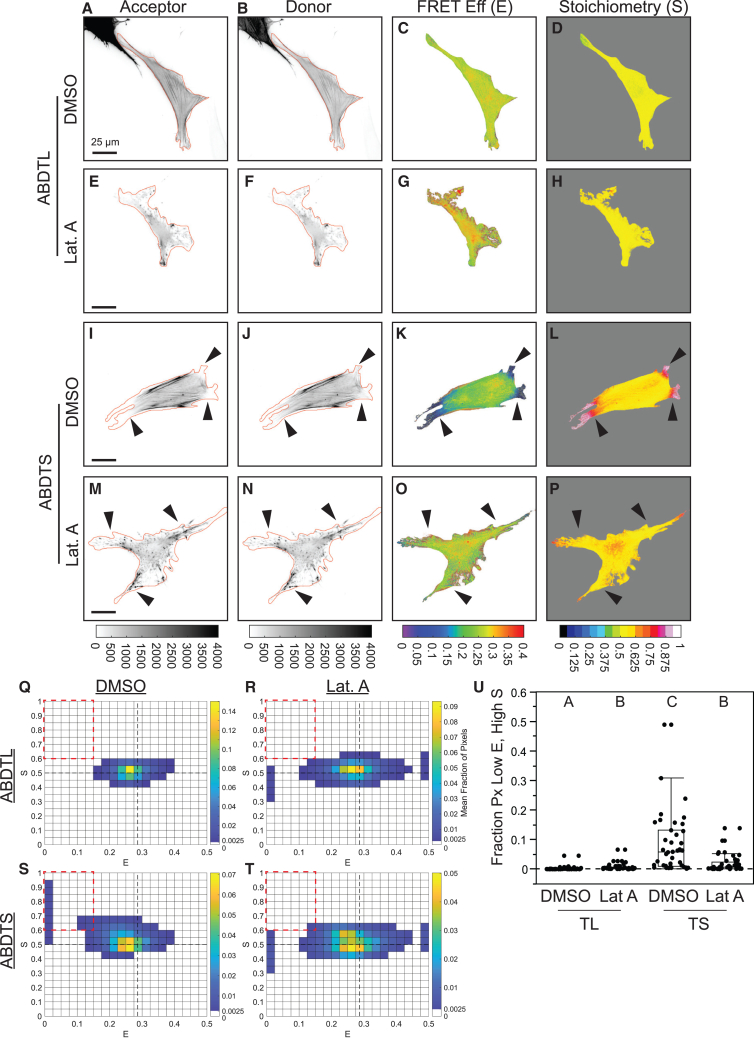
Next, we investigated whether FP mechanical switching could be detected in cellulo. To begin, we sought to assess this with a structurally simple MTS that is loaded directly by the actin cytoskeleton and is not subject to biochemical regulation. Therefore, we created the synthetic ABDTS by attaching the F-actin binding domain F-tractin^31,32 to both ends of the original TSMod,³⁰ which is composed of mTFP1-(GPGGA)₈-mVenus (Figure 4H). This sensor is anticipated to act like an actin cross-linking protein and report forces that promote the relative translocation of two cross-linked F-actin filaments. As an unloaded control, we used a version containing a single F-tractin domain (ABDTL, actin-binding domain tailless control) (Figure 4A). We performed three-channel FRET imaging of these constructs in NIH3T3 cells. F-tractin reversibly binds filamentous actin (F-actin), while having a low affinity for monomeric actin.^31,33 F-tractin has been shown to localize to F-actin networks in the lamellipod, lamellum, and cortex, and to stress fibers in many cell types.³² Consistent with this, both constructs localized to stress fibers and F-actin networks at the cell edge in NIH3T3 cells (Figures 4B–4D and 4I–4K). However, it should be noted that the acceptor signal can only provide a quantitative estimate of sensor concentration in the absence of acceptor mechanical switching, which can only be assumed by design for ABDTL.

Figure 4.

Synthetic actin-binding tension sensor exhibits FP mechanical switching in cellulo

(A) Schematic of ABDTL.

(B–G) Representative NIH3T3 cell expressing ABDTL, showing images of differential interference contrast (DIC) used to create cell outline, acceptor and donor intensities with cell outline overlaid in red, FRET efficiency and stoichiometry in cell mask, and ES-histogram of pixels in the cell.

(H) Schematic of ABDTS.

(I–N) Images and histogram for a representative NIH3T3 cell expressing ABDTS, analogous to those in (B)–(G). For single-cell ES-histograms in (G) and (N), the color bars indicate pixel counts.

(O and P) ES-histograms for whole-cell populations of ABDTL (O) and ABDTS (P), where color bars indicate the cell-averaged fraction of pixels in each bin (N = 38/44 cells for ABDTL/ABDTS over 5 experimental days).

(Q) Boxplot of fraction of pixels in each cell in the low $E$, high $S$ bin ($E<0.15,S>0.60$) for ABDTL and ABDTS. The difference between the groups was detected using the Wilcoxon rank-sum test; ∗∗∗∗p < 0.0001. p values are given in Note S3.

See also Figures S13–S15.

ABDTL exhibited a spatially uniform FRET efficiency of ∼0.285, corresponding to the unloaded value for TSMod,²⁸ and stoichiometry of ∼0.5 (Figures 4E, 4F, S13A, and S13B; note that all experimental FRET measurements are inherently apparent FRET efficiency and FP stoichiometry, but are indicated as $E$ and $S$ without the subscript to match previous conventions^16,27,28,34). Both $E$ and $S$ had no dependence on acceptor intensity, an estimate of ABDTL concentration, and $E$ did not exceed the unloaded value for TSMod across the full concentration range (Figures S14A, S14C, and S14E), supporting an absence of intermolecular FRET due to the bystander effect in the actin-binding sensor system at the expression levels used here. ES-histograms of single cells expressing ABDTL and the whole-cell population contained a single major density centered on $E\sim 0.285$ and $S\sim 0.5$ (Figures 4G and 4O), resembling the predicted signature for an unloaded MTS with no FP mechanical switching from the model (Figure S4B). The increased spread in the ABDTL data (Figures 4G and 4O) compared to the theoretical prediction (Figure S4B) likely arises from experimental noise in live cells, such as due to height variations, local differences in index of refraction, different pHs in various sub-cellular compartments, or small differences in $E_{app}$ and $S_{app}$ as the protein is produced/degraded. Additionally, the imaging and FRET correction process introduce and propagate noise in the system. This variation is common in FRET imaging data,^16,26,28,29 and similar variations have been reported previously for the unloaded cytoplasmic TSMod.²⁸ Together, these data confirmed proper function of ABDTL as an unloaded control.

ABDTS exhibited regions of lower FRET efficiency ($E<0.285$) and higher stoichiometry ($S>0.5$) (Figures 4L–4M), consistent with the presence of acceptor mechanical switching. Regions of low $E$ and high $S$ were consistently near the cell edge in areas of positive curvature. $E$ was closer to 0.285 and $S$ was closer to 0.5 in the center of the cells and within stress fibers (Figures S13C and S13D). This suggests that loading and FP mechanical switching in ABDTS occurs most strongly in lamellar actin networks, where actin filaments may be more likely to move relative to one another. The lack of loading in stress fibers is possibly due to differences in the density, alignment, or relative motion of F-actin in these structures^35,36 and/or issues related to the size of the sensor. At the edge of the cell, we observed that the acceptor signal was nearly completely lost, while the donor signal was only partially reduced (Figures S13E–S13H). We verified that these patterns were not due to an ABDTS-induced alteration in, or loss of, F-actin in these regions by fixing and labeling ABDTL- and ABDTS-expressing cells with phalloidin (Figures S15A–S15J). We also assessed the relationship between $E$ or $S$ and acceptor intensity, analogous to the analysis we performed on ABDTL (Figure S14). Importantly, in the presence of FP mechanical switching, the acceptor intensity is no longer an estimate of sensor concentration. At the lowest acceptor intensities, $E$ was lowest and $S$ was highest, further supporting that regions of low $E$ and high $S$ were due to acceptor mechanical switching (Figures S14B, S14D, and S14F). ES-histograms of a single cell (Figure 4N) and the whole-cell population (Figure 4P) contained a major up/left-slanting density extending to lower FRET efficiencies ($E<0.285$) and higher stoichiometries ($S>0.5$). These data resemble the predicted signature of a loaded MTS with dominant acceptor mechanical switching from the model (Figure 3B). The spread in the ABDTS experimental data (Figures 4N and 4P) compared to the theoretical prediction (Figure 3B) likely arises from the increased complexity of a cellular environment (e.g., unknown and spatially variable load magnitudes, loading durations, and load rates) as well as experimental noise, which is inherent in FRET imaging data.^16,26,28,29 Furthermore, at the lowest FRET efficiency values ($E$ ∼0–0.025, coming mainly from pixels at the very edge of the cell), the ES-histogram had a wider range of $S$ spanning between 0.5 and 1. This resembles the biphasic trends observed in the model for two different mechanisms: (1) acceptor mechanical switching with a lower force threshold combined with donor mechanical switching with a higher force threshold (Figure S8C; Note S1, section III.B.5), or (2) acceptor mechanical switching with force-induced unbinding (Figures S10H and S10K; Note S1, section V.B.1). Our observation of partial loss of donor signal (in addition to near-complete loss of acceptor signal) at the very edge of ABDTS- but not ABDTL-containing cells (Figures S13E–S13H) supports the first explanation. To quantitatively compare ABDTS versus ABDTL, we computed the fraction of pixels in each cell in a low $E$, high $S$ bin ($E<0.15,S>0.60$; cutoffs indicated by the red dashed box in Figures 4G and 4N–4P) and found that ABDTS had a significantly higher fraction of pixels than ABDTL (Figure 4Q). The trends in $E$ and $S$ for ABDTL and ABDTS were also not altered by fixation (Figures S15K–S15M). Together, these data indicate that FP mechanical switching occurs in ABDTS, with mechanical switching of mVenus (acceptor) being dominant over mTFP1 (donor).

To test the feasibility of mVenus and mTFP1 having different mechanical stabilities, we performed steered molecular dynamics (SMD) simulations on the two FPs, an approach previously applied to GFP.¹⁸ In agreement with our experimental observations, we found that mTFP1 had a higher mechanical stability than mVenus in the SMD simulations (Figures S16–S18; Note S2; Videos S1, S2, and S3). This is broadly consistent with previous single-molecule experimental work showing that even FPs derived from the same species, GFP and enhanced yellow FP, have different mechanical stabilities in vitro.^22,23

Video S1. Time-lapse of SMD simulation of α-GFP, related to Figures 4 and S16

Timelapse showing unfolding of alpha-GFP at a pulling speed of 1 nm/ns (left) and a force vs. time plot from the same simulation (right). Grid ticks in the timelapse correspond to 0.1 nm. The N-terminal handle of the FP is colored blue, while the first beta-strand is colored purple and the remainder of the FP is colored green. The simulation timepoint is indicated via a vertical dashed line in the force vs. time plot. Black translucent circles in the force vs. time plot show the raw data, while the blue circles show the force vs. time plot smoothed by 250 points. A red circle shows the maximum force value before the pullout of the beta strand, which coincides with the transition from the Δα state to the Δαβ state.

Video S2. Time-lapse of SMD simulation of mTFP1, related to Figures 4 and S17

Timelapse showing unfolding of mTFP1 at a pulling speed of 1 nm/ns (left) and a force vs. time plot from the same simulation (right). Grid ticks in the timelapse correspond to 0.1 nm. The N-terminal handle of the FP is colored blue, while the first beta-strand is colored red and the remainder of the FP is colored teal. The simulation timepoint is indicated via a vertical dashed line in the force vs. time plot. Black translucent circles in the force vs. time plot show the raw data, while the blue circles show the force vs. time plot smoothed by 250 points. A red circle shows the maximum force value before the pullout of the beta strand, which coincides with the transition from the Δα state to the Δαβ state.

Video S3. Time-lapse of SMD simulation of mVenus, related to Figures 4 and S17

Timelapse showing unfolding of mVenus at a pulling speed of 1 nm/ns (left) and a force vs. time plot from the same simulation (right). Grid ticks in the timelapse correspond to 0.1 nm. The N-terminal handle of the FP is colored blue, while the first beta-strand is colored red and the remainder of the FP is colored yellow. The simulation timepoint is indicated via a vertical dashed line in the force vs. time plot. Black translucent circles in the force vs. time plot show the raw data, while the blue circles show the force vs. time plot smoothed by 250 points. A red circle shows the maximum force value before the pullout of the beta strand, which coincides with the transition from the Δα state to the Δαβ state.

To determine whether acceptor mechanical switching in ABDTS was manipulable, we used latrunculin A to disrupt the actin cytoskeleton of fully spread cells containing ADBTL or ABDTS (Figure 5). Latrunculin A treatment caused no changes in ABDTL-expressing cells in comparison to the vehicle control (Figures 5A–5H), and the ES-histograms for vehicle versus latrunculin A treatment were similar for ABDTL-expressing cells (Figures 5Q and 5R). In comparison to vehicle treatment, latrunculin A treatment of ABDTS-expressing cells caused an increase in $E$ toward 0.285 and a decrease in $S$ toward 0.5 within the regions at the edge of the cell, indicating a reduction in acceptor mechanical switching (Figures 5I–5P). Comparisons of ES-histograms for vehicle versus latrunculin A-treated cells revealed that actin disruption caused a loss of density at low $E$, high $S$ for ABDTS-expressing cells (Figures 5S and 5T). Furthermore, ES-histograms for latrunculin A-treated ABDTS-expressing cells resembled those for vehicle and latrunculin A-treated ABDTL-expressing cells (Figures 5Q, 5R, and 5T). Quantification revealed that latrunculin A-treated ABDTS-expressing cells had a significant reduction in the fraction of pixels in the low $E$, high $S$ bin compared to vehicle exposed ABDTS-expressing cells and were not statistically different from latrunculin A-treated ABDTL-expressing cells (Figure 5U). Taken together, these data demonstrate the presence of reversible FP mechanical switching in a synthetic actin-binding sensor in living cells.

Figure 5.

Pharmacological disruption of actin reverses FP mechanical switching in ABDTS

(A–D) Representative NIH3T3 cells expressing ABDTL with vehicle control, (E–H) ABDTL treated with latrunculin A (Lat. A), (I–L) ABDTS with vehicle control, or (M–P) ADBTS treated with latrunculin A. Images are acceptor and donor intensities, with cell outline overlaid in red and FRET efficiency and stoichiometry in cell mask.

(Q–T) ES-histograms for whole-cell populations of ABDTL with vehicle control (Q, N = 43 cells), ABDTL treated with latrunculin A (R, N = 40 cells), ABDTS with vehicle control (S, N = 39 cells), and ADBTS treated with latrunculin A (T, N = 40 cells) over 3 experimental days, where color bars indicate the cell-averaged fraction of pixels in each bin.

(U) Boxplot of fraction of pixels in each cell in the low $E$, high $S$ bin ($E<0.15,S>0.60$) for the indicated conditions. Differences between groups were detected using the Steel-Dwass test. Levels not connected by the same letter are significantly different at p < 0.05. p values are given in Note S3.

FP mechanical switching is detectable in vinculin tension sensor and is sensitive to force-activated bond dynamics and external stiffness

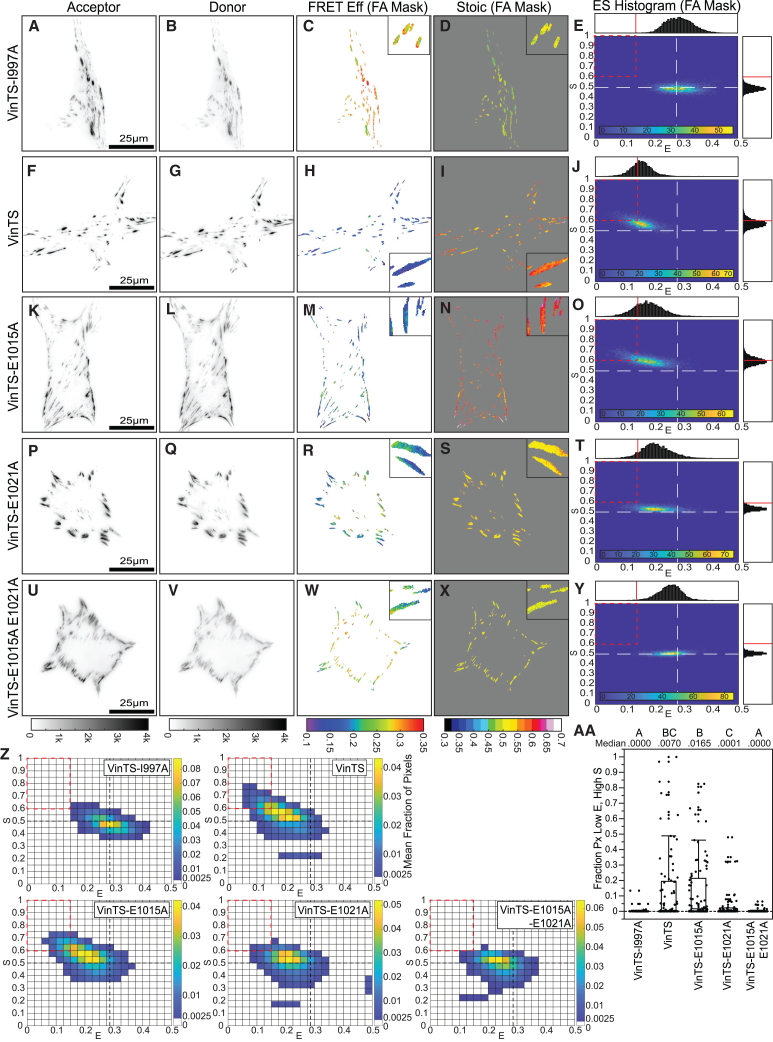
We next asked whether FP mechanical switching could be detected in an MTS within a naturally occurring protein. We focused on the mechanical linker protein vinculin, which couples the actin cytoskeleton to focal adhesions (FAs) to mediate adhesion reinforcement and stiffness sensing.^30,37,38 We focused on vinculin because it has been widely studied with an existing tension sensor (VinTS),^{2,10,14,16,39,40} and VinTS variants that unload vinculin^38,41 as well as progressively disrupt vinculin-actin catch-bonding³⁹ have been developed recently. Applying our framework, we re-analyzed existing datasets of VinTS and these mutants expressed in vinculin^−/− mouse embryonic fibroblasts (MEFs).^38,39 As the tension-insensitive control, we used VinTS-I997A, which contains a point mutation that disrupts vinculin’s binding to actin and has been shown to unload vinculin.^38,41 VinTS-I997A in FAs showed $E$ corresponding to unloaded TSMod and $S$ corresponding to no FP mechanical switching at both the single-cell (Figures 6A–6E and S19A–S19E) and cell population levels (Figure 6Z), as expected for a tension-insensitive control. In contrast, VinTS in FAs exhibited a spectrum of behaviors. At one end of this spectrum, VinTS in the FAs of some cells exhibited lower FRET efficiency ($E<0.285$) with no apparent FP mechanical switching ($S\sim 0.5$) (Figures S19F–S19J), matching the model prediction for MTS loading without FP mechanical switching (Figure 3A). At the other end of this spectrum, VinTS in the FAs of other cells exhibited both a lower FRET efficiency ($E<0.285$) and a higher stoichiometry ($S>0.5$) with an up/left-sloping ES-histogram shape (Figures 6F–6J and S19K–S19O). This matches the prediction for MTS loading with acceptor mechanical switching (Figure 3B). Despite the cell-to-cell heterogeneity, the presence of mechanical switching in VinTS is also apparent at the cell population level (Figure 6Z). To quantify this, we again looked at the fraction of pixels in each cell in a low $E$, high $S$ bin ($E<0.15,S>0.60$), indicating a significant difference between VinTS and VinTS-I997A (Figure 6AA). This is consistent with acceptor mechanical switching in VinTS but not in the unloaded VinTS-I997A.

Figure 6.

FP mechanical switching in VinTS is sensitive to manipulation of the vinculin-actin catch bond

(A–Y) Representative vinculin^−/− MEFs expressing VinTS-I997A (A–E), VinTS (F–J), VinTS-E1015A (K–O), VinTS- E1021A (P–T), or VinTS-E1015A-E1021A (U–Y) on FN-coated glass, showing images of acceptor intensity, donor intensity, FRET efficiency in the FA mask, stoichiometry in the FA mask, and an ES-histogram of FA-masked pixels for the cell. For single-cell ES-histograms in (E), (J), (O), (T), and (Y), the color bars indicate pixel counts.

(Z) ES-histograms for whole-cell populations (N = 59/89/92/88/101 cells over 2/4/3/3/3 experimental days for VinTS-I997A/VinTS/VinTS-E1015A/VinTS-E1021A/VinTS-E1015A-E1021A), where color bars indicate the cell-averaged fraction of FA-masked pixels in each bin.

(AA) Boxplot of fraction of pixels in each cell in the low $E$, high $S$ bin ($E<0.15,S>0.60$) for each construct. Differences between groups were detected using the Steel-Dwass test. Levels not connected by the same letter are significantly different at p < 0.05. p values are given in Note S3.

The data are a new analysis of the 3-channel FRET images from an experiment in a previous publication.³⁹

See also Figures S19–S21.

To attempt to discern the origin of the heterogeneous responses in the VinTS data, we assessed whether acceptor mechanical switching in VinTS correlated with aspects of cell or FA morphology (Figure S20). We found no significant correlations with any of 10 distinct metrics, suggesting that individual aspects of cell or FA morphology do not explain the observed cell-to-cell variability. The heterogeneity could be due to cell-to-cell variability in vinculin phosphorylation levels, which have been shown to affect the ability of vinculin to bear loads and the turnover dynamics of vinculin as measured by FRAP,^37,40,42,43 but further work will be required to determine the basis of the heterogeneous responses in VinTS.

To probe the subcellular relationship between $E$ and $S$, we examined large FAs that we previously reported to exhibit gradients in VinTS FRET efficiency.¹⁶ We find that gradients in $E$ along single FAs (lower at cell edge) were accompanied by gradients in $S$ (higher at cell edge) (Figure S21). This indicates a gradient in acceptor mechanical switching in VinTS along single FAs (higher at cell edge). Thus, the previously reported¹⁶ gradients in vinculin tension are more precisely described as gradients in vinculin tension magnitude and/or duration.

Force-activated bond dynamics play an important role in mechanosensitive processes at FAs,^2,4 and vinculin is known to form a strong catch bond with F-actin, whose duration increases with force up to a certain point.⁴⁴ Our modeling indicated that FP mechanical switching can be sensitive to changes in load duration (Figures 2, S1, and S7), as well as alterations to force-sensitive bond dynamics of the MTS (Figures S10 and S11; Note S1, section V). To assess whether manipulating vinculin catch-bonding affects FP mechanical switching, we re-analyzed the data of VinTS harboring single (VinTS-E1015A and VinTS-E1021A; Figures 6K–6T) and double (VinTS-E1015A-E1021A; Figures 6U–6Y) point mutations that were previously shown to progressively disrupt vinculin catch-bonding while retaining other key aspects of vinculin function.³⁹ The ES-histograms at both single-cell and cell population levels demonstrate that the acceptor mechanical switching signature of VinTS was partially reduced in the single mutants and completely eliminated in the double mutant, which is thought to greatly reduce or eliminate vinculin catch-bonding³⁹ (Figure 6Z). The fraction of pixels in the low $E$, high $S$ bin ($E<0.15,S>0.60$) for VinTS-E1015A-E1021A was significantly lower than that for VinTS and was similar to VinTS-I997A (Figure 6AA), indicating an elimination of acceptor mechanical switching in the double mutant. However, while both VinTS-E1015A-E1021A and VinTS-I997A had no apparent FP mechanical switching ($S\sim 0.5$), the ES-histogram of VinTS-E1015A-E1021A was shifted to a slightly lower $E$ than VinTS-I997A (Figure 6Z), consistent with the VinTS-E1015A-E1021A double mutant remaining partially loaded, as previously reported.³⁹ We also found that the double mutant (VinTS-E1015A-E1021A) exhibited a small $E$ gradient along single FAs (lower at cell edge) but no $S$ gradient (Figures 6W and 6X). This demonstrates the existence of tension magnitude gradients independent of mechanical switching. Together, these analyses indicate that FP mechanical switching occurs in VinTS and requires vinculin catch-bonding, suggesting that variations in S are a biologically relevant readout.

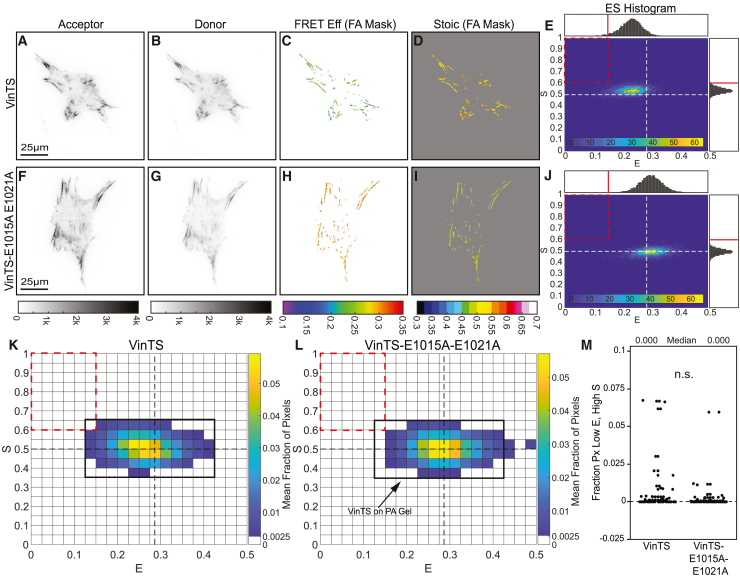
We lastly sought to determine whether FP mechanical switching in VinTS responds to alterations in mechanical stimuli. Altering ECM stiffness is thought to affect the loading dynamics of mechanical proteins within FAs.^2,4 In molecular clutch models of the FA, substrate stiffness is a major determinant of protein loading rate, with lower loading rates typically occurring on softer substrates.⁴ In the context of our model, the degree of FP mechanical switching in MTSs was also predicted to respond to changes in loading rates (Figure S12; Note S1, section V). Therefore, we experimentally tested the hypothesis that changing the stiffness of the substrate that cells were plated on would alter FP mechanical switching in vinculin. To do so, we seeded vinculin^−/− MEFs stably expressing VinTS or VinTS-E1015A-E1021A on fibronectin (FN)-coated polyacrylamide (PA) gels (Figure 7). Previous work indicated that the $E$ of VinTS did not change on 10 kPa gels compared to glass, but did not assess $S$¹⁶. Therefore, we chose a softer gel (of approximately 3.5 kPa stiffness; Figure S22) and directly assessed $E$ and $S$. In VinTS-expressing cells plated on PA gels, we observed changes in the ES-histogram shape consistent with a loss of FP mechanical switching (Figures 7A–7E and 7K). In contrast, the ES-histogram shapes for VinTS-E1015A-E1021A expressing cells on PA gels and glass were similar and consistent with little to no FP mechanical switching (Figures 7F–7J and 7L). Furthermore, we found no statistical difference in the fraction of pixels in the low $E$, high $S$ bin between the two constructs in cells plated on 3.5-kPa PA gels (Figure 7M), suggesting that the soft substrate eliminated acceptor mechanical switching in vinculin.

Figure 7.

Acceptor mechanical switching in VinTS is eliminated on soft substrates

(A–J) Representative vinculin^−/− MEFs expressing VinTS (A–E) or VinTS-E1015A-E1021A (F–J) on FN-coated PA gels, showing images of acceptor intensity, donor intensity, FRET efficiency in the FA mask, stoichiometry in the FA mask, and an ES-histogram of FA-masked pixels for the cell. For single-cell ES-histograms in (E) and (J), the color bars indicate pixel counts.

(K and L) ES-histograms for whole-cell populations of vinculin^−/− MEFs expressing VinTS or VinTS-E1015A-E1021A on PA gels (N = 87/92 cells over 3 experimental days for VinTS/VinTS-E1015A-E1021A), where color bars indicate the cell-averaged fraction of FA-masked pixels in each bin. The black outline for VinTS from (K) is overlaid on the histogram for VinTS-E1015A-E1021A in (L) as a guide for the eye.

(M) Boxplot of fraction of FA-masked pixels in each cell in the low $E$, high $S$ bin ($E<0.15,S>0.60$). The difference between the groups was detected using the Wilcoxon rank-sum test; n.s., not significant. p values are given in Note S3.

See also Figure S22.

Taken together, these results demonstrate that FP mechanical switching occurs in an MTS within a naturally occurring mechanical linker protein, vinculin, and is sensitive to key cell-intrinsic (force-activated bond dynamics) and cell-extrinsic (substrate stiffness) factors underlying mechanosensitive processes at FAs.

Discussion

Uncovering the molecular mechanisms of mechanosensitive signaling requires characterizing multiple steps: mechanotransmission, mechanosensing, mechanotransduction, and mechanoresponse.³ A current challenge is understanding the spatiotemporal regulation of these steps. Progress has been limited by the lack of tools to probe the various steps inside cells, especially mechanosensing (force-induced changes in protein structure and function). Motivated by in vitro experiments demonstrating that FPs undergo reversible, force-induced changes in their structure/function in response to mechanical loading,¹⁷ we hypothesized that FP mechanical switching within an FRET-based MTS for a protein of interest could be used to indirectly probe if, when, and where mechanically similar domains within the protein of interest could mediate mechanosensing. We also reasoned that the continued use and design of MTSs to measure mechanotransmission requires an understanding of FP mechanical switching. Therefore, we use computational modeling to develop a formalism to detect FP mechanical switching in FRET-based biosensors in cellulo by three-channel imaging of sensitized emission. Guided by this formalism, we demonstrate that FP mechanical switching occurs in cellulo in both a synthetic actin cross-linking protein and the mechanical linker protein vinculin. In cellulo mechanical switching is reversible and sensitive to manipulations of cell-generated forces, force-sensitive bond dynamics of the biosensor, and external mechanical stiffness. Together, this work describes an experimental paradigm for detecting the effect of mechanical loads on FPs in cells.

These findings demonstrate that genetically encoded FRET-based MTSs can operate in two modes. The first is measuring mechanotransmission (i.e., the original design intention of MTSs), which requires the absence of FP mechanical switching. In the mechanotransmission mode, quantitative measurements of molecular tension magnitude using the FRET efficiency-force relationship $E_0=f\left(F\right)$ for calibrated MTSs^10,15 are possible because $E_{app}=E_0$ in the absence of FP mechanical switching. In the presence of FP mechanical switching, the calibration becomes inaccurate ($E_{app}\ne E_0$), and alterations in $E_{app}$ due to load magnitude or load duration cannot be decoupled.

To use an MTS in mechanotransmission mode, the framework developed here should be used to ensure the absence of FP mechanical switching in the MTS. Specifically, it should be shown using the ES-histogram that the MTS maintains $S_{app}\sim 0.5$ across the full range of $E_{app}$ values. The absence of FP mechanical switching ensures the accuracy of quantitative measurements of load magnitude using the FRET efficiency-force calibration. However, we note that in the presence of most deviations in $S_{app}$, a reduction in $E_{app}$ is still indicative of loading, meaning relative comparisons between loaded and unloaded states are still possible, even though the effects of load magnitude and load duration cannot be separated. Additionally, the existing guidelines for force-insensitive FRET-based biosensors established by Coullomb et al. (i.e., the unloaded control should have $S_{app}$ of approximately 0.5 and $E_{app}$ of approximately the unloaded $E_0$ value for the tension sensor module) should also be applied to the unloaded control to rule out factors not related to FP mechanical switching.²⁹

Additionally, we posited that in the presence of substantial FP mechanical switching, MTSs can also operate in a mechanosensing mode. In this mode, the MTS provides a readout of force-induced changes in FP function in response to the load magnitude and load dynamics across the protein of interest. Conceptually, this resembles the force-induced conformational changes of mechanosensing domains that are thought to mediate mechanosensing.^5,6,7,8,45 We note that, like some mechanosensing domains, FP mechanical switching depends on both the load magnitude and load dynamics (e.g., load duration or rate), which is evidenced by the kinetics of GFP mechanical switching from in vitro experiments.¹⁷ Thus, FP mechanical switching is not another means to measure load magnitude. Instead, it is an approach to assess whether certain force-induced conformation changes are occurring in a specific load-bearing protein and biological context. Compared to other imaging-based techniques for mechanosensing,^11,12,13 which rely on labeling unfolded protein domains with secondary binding probes, our approach based on FP mechanical switching has the advantage of being independent of secondary probe binding. Additionally, our approach is suited for measurements of mechanosensing in live cells. The main disadvantage is that the readout is of an FP in the line of loading within the protein of interest and not of endogenous domains. Thus, our approach is an indirect measurement of the capability of the protein of interest to support mechanosensing. To be biologically relevant, the FP undergoing mechanical switching and the mechanosensing domain of interest must have similar mechanical properties. The relevance of mVenus mechanical switching to the force-induced conformational changes of mechanosensitive protein domains characterized previously at the single molecule level is currently unclear. Therefore, we consider this first demonstration of the mechanosensing mode to be analogous to the first examples of uncalibrated MTSs used in mechanotransmission mode,⁴⁶ in that these measurements were indicative of loading but the magnitudes were not known. We do note that, excitingly, mechanical switching of mVenus in VinTS responded to a variety of biologically interesting manipulations, such as manipulation of catch-bonding and the stiffness of the substrate. Determining the relationships between FP mechanical switching and force-sensitive conformational changes in endogenous mechanosensitive domains will be a key topic for the future.

A broad consequence of this work is that the identity of FPs (and thus mechanical properties), as well as their placement (with respect to the line of loading), are critical design elements of any probe or biosensor for a load-bearing protein. Even when different FPs or placements are tolerated biologically, altering either aspect could have unintended consequences on the performance of the sensor or probe when it is placed under mechanical load. Therefore, unless the lack of mechanical switching has been demonstrated in both systems, results from MTSs for the same protein but with different FPs may not be directly comparable even when using FRET efficiency measurements. This is one potential explanation for discrepancies in sets of vinculin^38,47 or E-cadherin^48,49 tension measurements, each based on MTSs with two different FP pairs. Additionally, the consequences of FP identity and placement apply to other probes and sensors that put FPs in the line of mechanical loading but were not explicitly designed to be force sensitive. One example is synthetic cross-linkers harboring a single FP between binding domains, such as the membrane-actin cortex linkers that have been previously used to image membrane proximal actin or manipulate membrane-cortex adhesion.^50,51 Another example is conformation sensors that were designed for reporting the relief of head-tail inhibition (also commonly referred to as autoinhibition), which is often found in load-bearing proteins.⁵² This includes the vinculin conformation sensor (VinCS), in which one FP is inserted in the line of force between the head and tail and the other is outside the line of force at the C terminus. For instance, multiple versions of VinCS exist that use different FP FRET pairs and change if the donor or acceptor FP is placed in the loaded versus unloaded positions in the sensor,^30,53,54 suggesting that each version could be affected by FP mechanical switching differently.

An important future direction suggested by this work is the screening and engineering of FPs with different mechanical switching properties. Here, we found that mVenus mechanical switching was dominant over mTFP1, indicating that FPs can have different mechanical switching sensitivities in cellulo. To our knowledge, GFP is the only FP to have its in vitro mechanical switching properties characterized.¹⁷ However, our experimental data, combined with modeling of a wide set of FP mechanical switching parameters (Figures S1 and S5; Note S1, section VII), suggest that mVenus undergoes mechanical switching in cellulo at lower load magnitudes and/or durations than would be expected for GFP in vitro. This suggests differences in the mechanical switching properties of GFP versus mVenus and/or differences in mechanical switching for single FPs in vitro versus FPs inside sensors in cellulo. For MTSs in mechanotransmission mode and other probes and sensors with FPs in the line of loading, proper sensor function requires the use of mechanically stable FPs. It was previously shown in vitro that YPet and mCherry can be subjected to considerable load magnitudes and durations (e.g., 24 pN for >5 min) without unfolding.⁵⁵ This suggests that these FPs could be well suited for sensors requiring mechanically stable FPs, like MTSs in mechanotransmission mode. However, we suggest that their mechanical switching properties be verified in cellulo when used in biosensors. However, the development of future MTSs in mechanosensing mode will require finding FPs with desired mechanical switching properties to enable sensors that function as indirect detectors of mechanosensing in response to a plethora of dynamic loading conditions and for pairing with specific endogenous mechanosensitive domains.

This work describes a framework for assessing FP mechanical stability and provides a means of probing force-sensitive protein function in cellulo. First, it provides quality control that will immediately improve the development and application of genetically encoded FRET-based MTSs designed to quantitatively measure the first step in mechanosensitive signaling, mechanotransmission. Second, it provides an approach leveraging FP mechanical switching inside MTSs to indirectly probe another key step in mechanosensitive signaling, mechanosensing. Together, these and existing tools form an overlapping continuum for probing the multi-step molecular mechanisms of mechanosensitive signaling.

Limitations of the study

When applying our framework and experimental methodology for detecting FP mechanical switching in cellulo, the following limitations of the study should be considered.

First, in our mathematical model, we made assumptions about the effect of FP mechanical switching on the photophysical properties of FPs to determine the signal contribution for each sensor state in three-channel FRET measurements. To our knowledge, forced-induced changes in the excitation or emission wavelengths of FPs have not been described. Therefore, we assumed that donor FPs that have undergone mechanical switching cannot be excited by any excitation light in the optical system, and that acceptor FPs that have undergone mechanical switching cannot be excited by any excitation light in the optical system and also cannot accept energy from donor FPs. If this assumption is not met, then a substantially more complex formalism is needed. Other, less critical assumptions associated with the mathematical model are detailed in Note S1, section VI.

Second, we focused on sensitized emissions for the FRET imaging modality because both the acceptor and donor are readily observable, its ease of use and low-cost, standard calibration methodologies to measure FRET efficiency, and, most important, existing frameworks for analyzing FP stoichiometry.^27,28,29 The framework we developed is not immediately adaptable to other FRET modalities, such as fluorescence lifetime imaging and spectral imaging-based FRET, which are also used to image MTSs.^55,56 However, we suggest that sensitized emission FRET can be used for the quality control of existing and future MTSs designed for mechanotransmission mode before using them in other imaging modalities.

Third, we applied our framework to TSMod,³⁰ which contains a calibrated unstructured tension sensing element. The framework here can be applied immediately to TSMod in other endogenous and synthetic proteins. By modifying the eff-force relationship, the framework can be readily applied to other calibrated tension sensing elements whose eff-force relationships are loading rate independent and have no hysteresis, such as unstructured repeats of GGSGGS¹⁰ and domains with rapid unfolding transition like HP35 and HP35st.¹⁵ In contrast, the framework is not readily modifiable for structured tension sensing elements exhibiting loading rate dependence or hysteresis.

Lastly, FP mechanical switching is not a direct readout for force-induced changes of mechanosensitive domains within the protein of interest. A greater understanding of the mechanical behavior of FPs will be needed to use FP mechanical switching as a proxy/indirect readout for specific mechanosensitive domains.

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Bacterial and virus strains
NEB 5-alpha competent E. coli	New England Biolabs	C2987U
Chemicals, peptides, and recombinant proteins
Fibronectin	Thermo Fisher	33016015
Phalloidin-AF647	Thermo Fisher	A22287
Latrunculin A	Sigma-Aldrich	L5163
DMEMgfp-2 live cell visualization media	Sapphire North America	MC102
Lipofectamine 2000	Thermo Fisher	11668019
OptiMEM	Thermo Fisher	31985070
EcoRI-HF	New England Biolabs	R3101S
NotI-HF	New England Biolabs	R3189S
BamHI-HF	New England Biolabs	R3136S
T4 DNA Ligase	New England Biolabs	M0202S
Critical commercial assays
Gibson Assembly Master Mix	New England Biolabs	E2611S
Experimental models: Cell lines
NIH/3T3 cells	ATCC	Cat# CRL-1658; RRID:CVCL_0594
Vinculin −/− mouse embryonic fibroblasts	Gift from Dr. Ben Fabry and Dr. Wolfgang H. Goldmann, Friedrich-Alexander-Universität Erlangen-Nürnberg; Mierke et al. 201057	N/A
Oligonucleotides
Primer (forward) used in construction of ABDTS, specifically for the generation of fragment containing F-tractin and Linker 1 by PCR using pEGFP-C1 F-tractin-EGFP: CCACTAGTCCAGTGTGGTGGA TGGCGCGACCACGGGGC	Integrated DNA Technologies	N/A
Primer (reverse) used in construction of ABDTS, specifically for the generation of fragment containing F-tractin and Linker 1 by PCR using pEGFP-C1 F-tractin-EGFP: TGCTCACCATCATGGTGGCGA CCGGTAGCG	Integrated DNA Technologies	N/A
Primer (forward) used in construction of ABDTS, specifically for the generation of the fragment containing TSmod by PCR using pcDNA3.1-TSMod: CGCCACCATGATGGTGAGCAAGGGCGAG	Integrated DNA Technologies	N/A
Primer (reverse) used in construction of ABDTS, specifically for the generation of the fragment containing TSmod by PCR using pcDNA3.1-TSMod: CGCTGCCGCCCTTGTACAGCTCGTCCATGC	Integrated DNA Technologies	N/A
Primer (forward) used in construction of ABDTS, specifically for the generation of the fragment containing Linker 2 and F-tractin by PCR using pEGFP-C1 F-tractin-EGFP: GCTGTACAAGGGCGGCAGCGGCAGCGATCCCCC CGTGGCCACCATGGCGCGACCACGGGGC	Integrated DNA Technologies	N/A
Primer (reverse) used in construction of ABDTS, specifically for the generation of the fragment containing Linker 2 and F-tractin by PCR using pEGFP-C1 F-tractin-EGFP: CGGGCCCTCTAGACTCGAGCTTACCCTGCGGCCGCTGC	Integrated DNA Technologies	N/A
Recombinant DNA
pcDNA3.1-VinTS	Grashoff et al. 201030	Addgene 26019
pcDNA3.1-VinTS-I997A	Rothenberg et al. 201838	Addgene 111828
pcDNA3.1-VinTS-E1015A	Chirasani et al. 202439	Addgene 213415
pcDNA3.1-VinTS-E1021A	Chirasani et al. 202439	Addgene 213416
pcDNA3.1-VinTS-E1015A-E1021A	Chirasani et al. 202439	Addgene 213417
pRRL-VinTS	Rothenberg et al. 201838	Addgene 111830
pRRL-VinTS-E1015A-E1021A	Chirasani et al. 202439	Addgene 213411
pcDNA3.1-ABDTS	This paper	Addgene 215368
pcDNA3.1-ABDTL	This paper	Addgene 215371
Software and algorithms
MATLAB	Mathworks	N/A
MATLAB Code, Image Pre-processing	LaCroix et al. 201816	Zenodo: https://doi.org/10.5281/zenodo.11625595 Also see Gitlab: https://gitlab.oit.duke.edu/HoffmanLab-Public/image-preprocessing
MATLAB Code, Three-Channel FRET Image Analysis	LaCroix et al. 201816	Zenodo: https://doi.org/10.5281/zenodo.11625634 Also see Gitlab: https://gitlab.oit.duke.edu/HoffmanLab-Public/fret-analysis
MATLAB Code, Simulation and Analysis of Mathematical Models of FP Mechanical Switching in MTSs	This paper	Zenodo: Also see Gitlab: https://gitlab.oit.duke.edu/HoffmanLab-Public/fpmechanicalswitchinmts_model
JMP Pro	SAS	N/A

Resource availability

Lead contact

Further information and requests for resources and reagents should be directed to and will be fulfilled by the lead contact, Brenton D. Hoffman (brenton.hoffman@duke.edu).

Materials availability

All plasmids generated in this study will be made publicly available on Addgene.

Data and code availability

• •All data reported in this paper will be shared by the lead contact upon request.
• •MATLAB codes used to perform image pre-processing (https://gitlab.oit.duke.edu/HoffmanLab-Public/image-preprocessing), perform three channel sensitized emission FRET image analysis (https://gitlab.oit.duke.edu/HoffmanLab-Public/fret-analysis), and analyze and simulate the mathematical models of FP mechanical switching in MTSs (https://gitlab.oit.duke.edu/HoffmanLab-Public/fpmechanicalswitchinmts_model) are publicly available on GitLab. Archival DOIs are listed in the key resources table.
• •Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.

Experimental model and study participant details

Cell culture and expression of DNA constructs

Vinculin −/− MEFs (kindly provided by Dr. Ben Fabry and Dr. Wolfgang H. Goldmann, Friedrich-Alexander-Universität Erlangen-Nürnberg)⁵⁷ were maintained at 37°C in a humidified 5% CO₂ atmosphere in Dulbecco′s Modified Eagle′s Medium (DMEM) high glucose with sodium pyruvate (D6429; Sigma Aldrich, St. Louis, MO) supplemented with 10% FBS (HyClone SH30071.03; Cytivia, Marlborough, MA), 1% v/v non-essential amino acids (11140050; Thermo Fisher Scientific, Waltham, MA), and 1% v/v penicillin-streptomycin solution (15140122; Thermo Fisher). The generation of cell lines stably expressing VinTS and VinTS-E1015A-E1021A via lentiviral transduction were described previously.^38,39,58 NIH3T3cells were obtained from ATCC (CRL-1658) and maintained in the same conditions, using the same media formulation except for the omission of non-essential amino acids. For transient expression of ABDTS or ABDTL, NIH 3T3s were transfected at 50–75% confluence in 6-well tissue culture plates (25–105; Genesee Scientific, El Cajon, CA) using Lipofectamine 2000 (11668019; Thermo Fisher) and OptiMEM (31985070; Thermo Fisher) following the manufacturer’s instructions.

Method details

Generation of DNA constructs

Construction of pcDNA3.1-VinTS, pcDNA3.1-VinTS-I997A, pcDNA3.1-VinTS-E1015A, pcDNA3.1-VinTS-E1021A, pcDNA3.1-VinTS-E1015A-E1021A, pRRL-VinTS, and pRRL-VinTS-E1015A-E1021A have been described previously.^30,38,39 ABDTS is comprised of F-tractin (actin-binding peptide from rat neuronal inositol 1,4,5-triphosphate 3-kinase A), followed by a 9 amino acid linker (GLALPVATM, hereafter called “Linker 1”), the original TSMod, an 11 amino acid linker (GGSGSDPPVAT, hereafter called “Linker 2”), and a second F-tractin. F-tractin and Linker 1 were derived from pEGFP-C1 F-tractin-EGFP (Addgene Plasmid #58473).³² The original TSMod was derived from pcDNA3.1-TSMod (Addgene Plasmid #26021).³⁰ Linker 2 (GGSGSDPPVAT) was used previously in another construct containing F-tractin.³³ Gibson Assembly (with Gibson Assembly Master Mix, E2611S; NEB, Ipswich, MA) was used to generate pcDNA3.1-ABDTS from pcDNA3.1 vector digested with EcoRI-HF (Cat #: R3101S; NEB)/NotI-HF (Cat #: R3189S; NEB) and the following three fragments containing complementary regions: (1) F-tractin and Linker 1, (2) TSMod, and (3) Linker 2 and F-tractin. The fragment containing F-tractin and Linker 1 was generated by Polymerase Chain Reaction (PCR) using pEGFP-C1 F-tractin-EGFP and the oligonucleotide primer sequences (5′ to 3′) CCACTAGTCCAGTGTGGTGGATGGCGCGACCACGGGGC (forward) and TGCTCACCATCATGGTGGCGACCGGTAGCG (reverse). The fragment containing TSmod was generated by PCR using pcDNA3.1-TSMod and the oligonucleotide primer sequences (5′ to 3′) CGCCACCATGATGGTGAGCAAGGGCGAG (forward) and CGCTGCCGCCCTTGTACAGCTCGTCCATGC (reverse). The fragment containing Linker 2 and F-tractin was generated by PCR using pEGFP-C1 F-tractin-EGFP and the oligonucleotide primer sequences (5′ to 3′) GCTGTACAAGGGCGGCAGCGGCAGCGATCCCCCCGTGGCCACCATGGCGCGACCACGGGGC (forward) and CGGGCCCTCTAGACTCGAGCTTACCCTGCGGCCGCTGC (reverse). ABDTL is comprised of F-tractin, Linker 1, and the original TSMod, i.e., only the part of ABDTS before Linker 2 and the second F-tractin. pcDNA3.1-ABDTL was generated via PCR from pcDNA3.1-ABDTS and inserted into pcDNA3.1 via BamHI-HF (Cat #: R3136S; NEB)/EcoRI-HF (Cat #: R3101S; NEB) digestion and subsequent ligation (Cat #: M0202S; NEB). All newly generated constructs were verified by DNA sequencing (GENEWIZ from Azenta).

Cell seeding

For imaging, glass bottom dishes with no. 1.5 coverslips (FD35-100; World Precision Instruments, Sarasota, FL) or no. 1.5 glass coverslips mounted in reusable metal dishes (30-1313-03192; Bioptechs, Butler, PA) were incubated with 10 μg/mL fibronectin (33016015; Thermo Fisher) in PBS at room temperature for 1 h and rinsed once with PBS. Approximately 3000 cells/cm² were plated on the dishes. Cells were incubated for 4 h to enable sufficient spreading.

Analysis of previous VinTS datasets

Analyses were conducted on previously obtained three-channel FRET images of Vinculin −/− MEFs expressing VinTS or VinTS-I997A on FN-coated glass that were part of the data in the study by Rothenberg et al.,³⁸ and the three-channel FRET images of Vinculin −/− MEFs expressing VinTS, VinTS-I997A, VinTS-E1015A, VinTS-E1021A, or VinTS-E1015A-E1021A on FN-coated glass that were part of the data in the study by Chirasani, Khan, Malavade et al.³⁹

Fixation & phalloidin labeling of actin

For fixation, cells were washed twice with PBS, fixed with 4% v/v EM-grade paraformaldehyde (Cat #: 15700; Electron Microscopy Sciences, Hatfield, PA) in PBS for 10 min and then rinsed with PBS. To label actin, cells were permeabilized with 0.1% Triton X- in PBS for 5 min, blocked with 2% bovine serum albumin (BSA, A7906-100G; Sigma-Aldrich) in PBS for 30 min, treated with Alexa Fluor 647-conjugated phalloidin (A22287; Thermo Fisher) at a 1:100 dilution for 60 min, and then rinsed three times with PBS. Cells were imaged in PBS.

Pharmacological Inhibitors

Cells were seeded on fibronectin-coated glass coverslips as described above. A solution of 1 μM Latrunculin A (L5163; Sigma-Aldrich) were prepared from a 2 mM stock solution in DMSO (D2650; Sigma-Aldrich) by dilution in complete growth medium. Vehicle only controls were conducted with DMSO in complete growth medium. Cells were treated for 15 min at 37°C prior to fixation.

Imaging of FRET-based sensors and Immunofluorescence

An Olympus inverted fluorescent microscope (IX83; Olympus, Tokyo, Japan) was used to image samples as described previously.³⁸ Images were acquired at 60x magnification (UPlanSApo 60X/NA1.35 Objective, Olympus) and illuminated by a Lambda LS equipped with a 300W ozone-free xenon bulb (Sutter Instrument, Novato, CA). The images were captured using a sCMOS ORCA-Flash4.0 V2 camera (Hamamatsu Photonics, Hamamatsu, Japan). The FRET images were acquired using a custom filter set comprised of an mTFP1 excitation filter (ET450/30x; Chroma Technology Corp, Bellows Falls, VT), mTFP1 emission filter (FF02-485/20–25, Semrock, Rochester, NY), Venus excitation filter (ET514/10x; Chroma Technology Corp), Venus emission filter (FF01-571/72; Semrock), and dichroic mirror (T450/514rpc; Chroma Technology Corp). For sensitized emission FRET microscopy, three images are acquired to calculate FRET efficiency.⁵⁸ These include imaging the acceptor (I_AA, Venus excitation, Venus emission), FRET (I_DA, mTFP1 excitation, Venus emission), and donor (I_DD, mTFP1 excitation, mTFP1 emission). For immunofluorescent imaging, we utilized the DA/FI/TR/Cy5-4X4 M-C Brightline Sedat filter set (Semrock) and the associated dichroic mirror (FF410/504/582/669-Di01). The motorized filter wheels (Lambda 10-3; Sutter Instrument), automated stage (H117EIX3; Prior Scientific, Rockland, MA), and image acquisition were controlled through MetaMorph Advanced software (Molecular Devices, San Jose, CA). Differential interference contrast (DIC) images were acquired at 60x magnification using a polarizer (IX-LWPO, Olympus) mounted above the condenser, an adjustable DIC slider (U-DICT, Olympus) containing one of the Nomarski prisms, and a mirror unit equipped with the analyzer (IX3-FDICT, Olympus). The Nomarski prism within the DIC slider was adjusted to achieve optimum contrast prior to each experiment.

For live cell imaging of NIH3T3cells, growth media was replaced with DMEMgfp-2 live cell visualization media (MC102; Sapphire North America, Ann Arbor, MI), supplemented with 10% FBS, 30 min before imaging. For live cell imaging of MEFs, growth media was replaced with the same live cell visualization media and supplemented with 10% FBS and 1% NEAA, 30 min before imaging. A constant temperature was maintained across the sample using an objective heater (Objective Heater Medium 150819-13; Bioptechs, Butler, PA) in conjunction with a stage and lid heater (Stable Z System 403–1926; Bioptechs). A humidified CO₂ perfusion system (130708; Bioptechs) was used to maintain a stable pH. All components were brought to thermal equilibrium prior to imaging.

Preparation of methacrylated coverslips and hydrophobic glass substrate

18x18 No. 2 glass coverslips (48368-040; VWR, Radnor, PA) were exposed to air plasma for 5 min. Immediately before addition to glass coverslips, 500 μL of glacial acetic acid (ACROS Organics AC124040010; Thermo Fisher) was added to a solution of 3-(Trimethoxysilyl) propyl methacrylate (M6514-25ML; Sigma-Aldrich) in ethanol (E7023-500ML; Sigma-Aldrich; 30 μL in 9.5 mL). This solution was applied to the coverslips and incubated for 5 min. The coverslips were then washed twice with ethanol and dried via compressed air. Coverslips were prepared < 1h before fabrication of polyacrylamide gels.

A hydrophobic glass substrate was prepared using by first rinsing with DI H₂O, then 70% ethanol in DI H₂O (Sigma-Aldrich), and finally 100% isopropyl-alcohol (BDH-11334LP; VWR International). This was dried via compressed air. Rain-X Original Glass Water Repellent (ITW Global Brands, Houston, TX) was applied to the pre-cleaned glass substrate according to the manufacturer’s instructions.

Preparation, imaging, and mechanical testing of PA gels

Polyacrylamide (PA) gels were fabricated using a methodology to improve ECM protein attachment described previously.⁵⁹ PA gels of the 5% acrylamide/0.08% bis-acrylamide formulation were prepared using 375 μL of 40% acrylamide solution (1610140; Bio-Rad, Hercules, CA), 120 μL of 2% bis-acrylamide solution (1610142; Bio-Rad), and 2475 μL of DI H₂O. This solution was de-gassed for 10 min via sonication under vacuum. The de-gassed solution was mixed with a 1.5M solution of 2-aminoethyl methacrylate (516155-5G; Sigma-Aldrich) in DI H₂O at a ratio of 1:100. This solution was passed through a 0.2 μm syringe filter (VWR) to remove any particulate. This solution was mixed with a 100 mg/mL solution of Irgacure-2959 (410896-10G; Sigma-Aldrich) in methanol (VWR) at a ratio of 1:100. 240 μL of this solution was pipetted onto a hydrophobic glass substrate (see above). A methacrylated coverslip (see above) was inverted onto the droplet of PA solution and exposed to UV light for 15 min. Following polymerization, the glass substrate was flooded with PBS and the gel-attached coverslips were gently removed. Gels were placed in a 6-well plate and washed twice with PBS. Following washing, a working solution of 0.83 mg/mL solution of sulfosuccinimidyl 6-(4′-azido-2′-nitrophenylamino)hexanoate (sulfo-SANPAH, 22589; Thermo Fisher) in PBS was prepared from a stock solution of 83 mg/mL sulfo-SANPAH in DMSO (Sigma-Aldrich). The working solution was pipetted onto the surface of each gel, ensuring complete coverage. The gels were then exposed to UV light for 5 min. The gels were rinsed twice with PBS and covered with a 10 μg/mL solution of fibronectin in PBS (for gels to be used for cell attachment) or 10 μg/mL BSA in PBS (to reduce non-specific adhesion for gels to be used in mechanical testing) prior to incubation overnight at 4°C.

For imaging, gels were kept in a 6-well dish. The fibronectin in PBS solution was changed to full MEF growth media prior to seeding cells. MEFs (stably expressing VinTS or VinTS-E1015A-E1021A) were seeded at approximately 5700 cells/cm² and allowed to adhere for 24h prior to fixation. Following fixation, the gels were stored in PBS until imaging. No. 1.5 glass coverslips were mounted in reusable metal dishes (Bioptechs, Butler, PA). A 50 μL droplet of PBS was added to the coverslip and the gel was carefully inverted onto the droplet. Imaging was performed in this configuration.

Mechanical testing of PA gels was performed via atomic force microscopy (Asylum Research MFP 3D, Santa Barbara, CA). Hydrogels were immersed in PBS and indented with a spherical cantilever (10 μm radius, borosilicate glass, Novascan Technologies, Ames, IA) with a spring constant of 188.39 pN/nm at an indentation speed of 0.8 μm/s. Young’s modulus was determined via Hertzian model fit. The Young’s modulus for the PA gel formulation used in this study was determined to be 3.5 kPa (Figure S22).

Mathematical models of FP mechanical switching in MTS

The formulation and implementation of the mathematical models of FP mechanical switching in load-bearing proteins and MTSs are provided in Note S1.

Steered molecular dynamics simulations of FPs

The methods for SMD simulations of FPs are provided in Note S2.

Quantification and statistical analysis

Calculation of FRET efficiency and stoichiometry from sensitized emission

FRET was detected through measurement of sensitized emission²⁷ and calculated using custom written code in MATLAB (Mathworks).⁵⁸ All analyses were conducted on a pixel-by-pixel basis. Prior to FRET calculations, all images were first corrected for dark current, uneven illumination, background intensity, and three-dimensional offsets caused by chromatic aberrations and minute hardware misalignments (registration) as previously described.²⁸ Spectral bleedthrough coefficients were determined through FRET-imaging of cells expressing only donor or only acceptor FPs. The donor bleedthrough coefficient ($dbt$) was calculated for mTFP1 as:

$$dbt=⟨\frac{I_{DA}}{I_{DD}}⟩$$

where $I_{DA}$ is the intensity in the FRET-channel, $I_{DD}$ is the intensity in the donor-channel, and data were binned by donor-channel intensity. Similarly, the acceptor bleedthrough coefficient ($abt$) was calculated for Venus (A206K) as:

$$abt=⟨\frac{I_{DA}}{I_{AA}}⟩$$

where $I_{AA}$ is the intensity in the acceptor-channel, and data were binned by acceptor-channel intensity. For the mTFP1-Venus (A206K) FP pair on our microscope setup, the cross-talk between donor and acceptor channels (signal from donor in acceptor channel and vice-versa) was determined to be negligeable. To correct for spectral bleedthrough in experimental data, pixel-by-pixel FRET corrections were performed according to the equation:

$$I_{DA,corr}=I_{DA}-{dbt·I}_{DD}-{abt·I}_{AA}$$

where $I_{DA,corr}$ is the corrected FRET intensity (also defined in the literature as $F_c$). After bleedthrough correction, FRET efficiency was calculated. Through imaging donor-acceptor fusion constructs of differing, but constant, FRET efficiencies, it is possible to calculate two proportionality constants that enable the calculation of FRET efficiencies for a given FRET pair.²⁷ These proportionality constants are $G$:

$$G=-\frac{\Delta \left(\frac{I_{DA,corr}}{I_{AA}}\right)}{\Delta \left(\frac{I_{DD}}{I_{AA}}\right)}$$

where Δ indicates the change between two donor-acceptor fusion proteins, and $k$:

$$k=\frac{I_{DD}+\frac{I_{DA,corr}}{G}}{I_{AA}}$$

Using published methods,²⁸ the calibration factors were experimentally determined for mTFP1 and Venus (A206K). With these two proportionality constants, it is possible to calculate both the apparent FRET efficiency ($E_{app}$):

$$E_{app}=\frac{I_{DA,corr}}{I_{DA,corr}+G·I_{DD}}$$

and FP stoichiometry²⁹ ( $S_{app}$):

$$S_{app}=\frac{I_{DA,corr}+G·I_{DD}}{I_{DA,corr}+G·I_{DD}+G·k·I_{AA}}$$

The calibration constants $G$ and $k$ were monitored over the course of this work to control for changes in lamp and filter performance. Note, these formulas are equivalent to the formulas from Coulomb et al.²⁹ with ${\alpha }^{BT}=dbt$, ${\delta }^{DE}=abt$, ${\gamma }^M=G$, and ${\beta }^X=\frac{1}{G·k}$:

$$I_{DA,corr}=I_{DA}-{{\alpha }_{BT}·I}_{DD}-{{\delta }_{DE}·I}_{AA}$$

$$E_{app}=\frac{I_{DA,corr}}{I_{DA,corr}+{\gamma }^M·I_{DD}}$$

$$S_{app}=\frac{I_{DA,corr}+{\gamma }^M·I_{DD}}{I_{DA,corr}+{\gamma }^M·I_{DD}+\frac{I_{AA}}{{\beta }^X}}$$

Note that all experimental FRET measurements are inherently apparent FRET efficiency ($E_{app}$) and FP stoichiometry ( $S_{app}$), but are indicated for experimental data in this work using $E$ and $S$ without the subscript to match previous conventions.^16,27,28,34

To analyze $E$ and $S$, the following approaches were used to generate analysis masks. For ABDTS and ABDTL, analysis masks were constructed for whole cells. Cell masks were manually drawn using DIC images (for live imaging) or phalloidin-labeled actin images (for fixed imaging). Cell masks were refined by excluding pixels in which the intensity of both $I_{AA}$ and $I_{DD}$ was below a small threshold value (exclude px if $I_{AA}<50$ and $I_{DD}<50$). This condition preserves regions containing signal from both or a single FP. For VinTS variants, analysis masks contained all pixels in the FAs of single cells. Segmentation of FAs was done as previously reported using a water-based algorithm.⁵⁸ Segmentation and manual cell mask generation for VinTS variants were performed using the acceptor channel, which is independent of FRET, as previously described.³⁸

For ES-histogram analyses, all pixels in the above-described analysis mask were used. $E$ outside [0.000, 0.500] and $S$ outside [0.000, 1.000] were set to the nearest limit. ES-histograms were constructed with fixed bin widths. For single cells, pixel counts were plotted, and bin widths of 0.005 for $E$ and 0.010 for $S$ were used. For cell populations, histograms show the average of the relative fraction of each bin across cells in the indicated group, which gives each cell in the population an equal waiting regardless of its size (number of pixels in analysis mask). Here, bin widths of 0.025 for $E$ and 0.050 for $S$ were used. To quantitatively compare the extent of acceptor FP mechanical switching between groups or conditions, the fraction of pixels in a larger bin containing low $E$ values and high $S$ values was quantified for each cell. Specifically, we quantified the fraction of pixels in each cell with $E<0.15$ and $S>0.60$.

Computation of cell and FA morphology metrics

Cell and FA morphology was analyzed for the VinTS dataset. Cell masks were used to compute cell morphology metrics. FA masks were used to compute FA morphology metrics. All morphology metrics were computed using the MATLAB “regionprops” function. The following cell morphology metrics were used: cell area ($A$), cell perimeter ($P$), cell form factor ($4\pi A/P^2$), cell eccentricity (ratio of the distance between the center and one foci to the length of the semi-major axis for the fitted ellipse), and cell solidity ($A/\left[ConvexHullArea\right]$). The following FA morphology metrics were used: number of FAs in the cell, mean area of FAs in the cell, standard deviation of area of FAs in the cell, mean eccentricity of FAs in the cell, and standard deviation of eccentricity of FAs in the cell. For all analyses, FAs smaller than 16 px or 0.1866 μm² were discarded as done previously.¹⁴

Statistical analysis

Statistical analyses were performed using JMP Pro (SAS, Cary, NC) software. Normality of each dataset was assessed using Q-Q plots and Shapiro-Wilks test. For normal datasets, comparisons of data with equal variances, as determined with Levene’s test, were analyzed with an ANOVA and, if necessary, Tukey’s Honest Significant Difference (HSD) tests. Datasets with unequal variances were analyzed with a non-parametric Welch’s ANOVA and, if necessary, the Steel-Dwass multiple comparisons test. For non-normal datasets, comparisons of data were analyzed with a Kruskal-Wallis test and, if necessary, Steel-Dwass multiple comparisons test. A p value of p < 0.05 was considered statistically significant. In figures, a single asterisk (∗), double asterisk (∗∗), triple asterisk (∗∗∗), and quadruple asterisk (∗∗∗∗) indicate p-values less than 0.05, 0.01, 0.001, and 0.0001, respectively, and ns indicates a p-value greater than or equal to 0.05. Cells were treated as independent observations. Sample sizes for each experiment can be found in the figure legends. Where used, standard boxplots were created using JMP Pro, where the bottom and top of the box indicate the first and third quartiles, respectively, the middle line indicates the median, the whiskers extend to the outermost data points below the first quartile and above the third quartile that are within 1.5 times the interquartile range, and data outside the whiskers are indicated as points.

Published: July 9, 2024