Skip to main content
PMC home page
Radiology: Artificial Intelligence logoLink to Radiology: Artificial Intelligence
. 2024 May 8;6(4):e230275. doi: 10.1148/ryai.230275

Improving Automated Hemorrhage Detection at Sparse-View CT via U-Net–based Artifact Reduction

Johannes Thalhammer 1,✉, Manuel Schultheiß 1, Tina Dorosti 1, Tobias Lasser 1, Franz Pfeiffer 1, Daniela Pfeiffer 1, Florian Schaff 1
PMCID: PMC11294955  PMID: 38717293

Abstract

Purpose

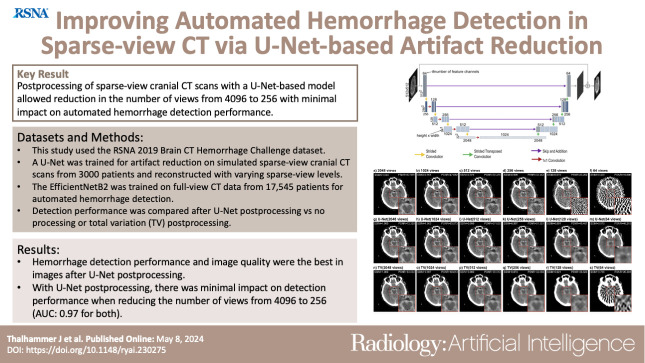
To explore the potential benefits of deep learning–based artifact reduction in sparse-view cranial CT scans and its impact on automated hemorrhage detection.

Materials and Methods

In this retrospective study, a U-Net was trained for artifact reduction on simulated sparse-view cranial CT scans in 3000 patients, obtained from a public dataset and reconstructed with varying sparse-view levels. Additionally, EfficientNet-B2 was trained on full-view CT data from 17 545 patients for automated hemorrhage detection. Detection performance was evaluated using the area under the receiver operating characteristic curve (AUC), with differences assessed using the DeLong test, along with confusion matrices. A total variation (TV) postprocessing approach, commonly applied to sparse-view CT, served as the basis for comparison. A Bonferroni-corrected significance level of .001/6 = .00017 was used to accommodate for multiple hypotheses testing.

Results

Images with U-Net postprocessing were better than unprocessed and TV-processed images with respect to image quality and automated hemorrhage detection. With U-Net postprocessing, the number of views could be reduced from 4096 (AUC: 0.97 [95% CI: 0.97, 0.98]) to 512 (0.97 [95% CI: 0.97, 0.98], P < .00017) and to 256 views (0.97 [95% CI: 0.96, 0.97], P < .00017) with a minimal decrease in hemorrhage detection performance. This was accompanied by mean structural similarity index measure increases of 0.0210 (95% CI: 0.0210, 0.0211) and 0.0560 (95% CI: 0.0559, 0.0560) relative to unprocessed images.

Conclusion

U-Net–based artifact reduction substantially enhanced automated hemorrhage detection in sparse-view cranial CT scans.

Keywords: CT, Head/Neck, Hemorrhage, Diagnosis, Supervised Learning

Supplemental material is available for this article.

© RSNA, 2024

Keywords: CT, Head/Neck, Hemorrhage, Diagnosis, Supervised Learning

graphic file with name ryai.230275.VA.jpg

Open in a new tab

Summary

Postprocessing of sparse-view cranial CT scans with a U-Net–based model allowed a reduction in the number of views, from 4096 to 256, with minimal impact on automated hemorrhage detection performance.

Key Points

  • ■ Reducing artifacts in sparse-view cranial CT scans improved automated hemorrhage detection across all investigated subtypes, evidenced by the area under the receiver operating characteristic curve (AUC) values for reconstructions using 512 or fewer views (P < .001).

  • ■ Comparison of a U-Net– and total variation–based approach for artifact reduction in sparse-view cranial CT scans showed that the convolutional neural network–based approach achieved superior performance regarding artifact reduction, image quality parameters, and subsequent automated hemorrhage detection in terms of structural similarity index and AUC values across all investigated subtypes for reconstructions using 512 or fewer views (P < .001).

Introduction

Intracranial hemorrhage is a potentially life-threatening disease with a 30-day fatality rate of 40.4%, accounting for 10%–30% of annual strokes (1,2). Prompt and accurate diagnosis is vital for optimal treatment, typically achieved through cranial CT scans (3). However, the increased use of medical CT scans, including cranial scans, raises concerns about radiation-related health risks (4,5). A routine head CT scan exposes patients to a median effective dose of 2 mSv, similar to natural radiation accumulated per year. This affects not only the brain but also nearby areas (5,6).

Besides lowering the tube current, sparse-view CT is a promising approach to reducing radiation dose by decreasing the number of views. However, this reduction causes artifacts in the filtered back projection (FBP)–reconstructed images. To restore image quality for accurate diagnosis, suitable processing methods are needed. In the past, compressed sensing and iterative reconstruction approaches have been widely investigated, which generally minimize a compressed sensing–based regularization term as well as a data-fidelity term to ensure data consistency (7–9). These approaches have been proven to yield good results in terms of reducing image noise and artifacts. However, they are also computationally demanding due to the repeated update steps during iterative optimization. Additionally, these methods require parameter optimization and can alter image texture.

Recently, machine learning approaches using deep neural networks have gained substantial attention. In the context of artifact reduction at sparse-view CT, it has been shown that convolutional neural networks (CNNs) are able to achieve excellent results with comparably low computational effort during inference (10–12). Approaches that combine deep learning and iterative techniques for sparse-view artifact reduction can also be found in the literature (13,14).

In parallel, extensive research has been conducted on the application of deep learning techniques for automated detection and classification of pathologic features in CT images, and many systems are already U.S. Food and Drug Administration approved and Conformité Européenne certified (15–17). Typically, these algorithms are trained on standard-dose data, which restricts their applicability to dose-reduced or sparse-view data. This is because the additional noise and artifacts in sparse-view data are expected to negatively impact the reliability of these systems.

Therefore, the aim of the current study is twofold. First, we aim to explore the potential benefits of deep learning–based artifact reduction in sparse-view cranial CT scans. Second, we assess whether this approach can enhance the performance of automated hemorrhage detection.

Materials and Methods

This retrospective study was exempt from institutional review board review due to the use of publicly available data. The code is available at: https://github.com/J-3TO/Sparse-View-Cranial-CT-Reconstruction.

Network Architectures

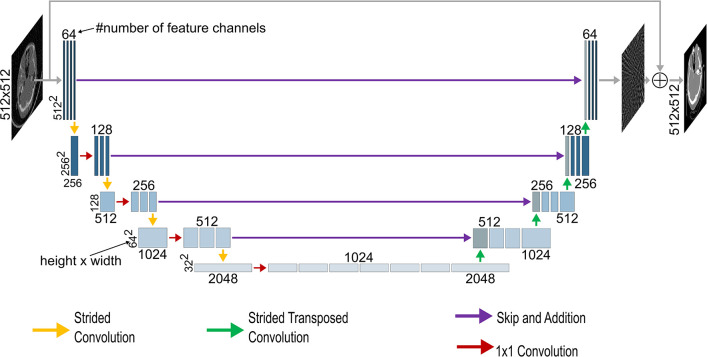
Given the parallel-beam geometry of our dataset, where streak artifacts are expected to be contained within the individual two-dimensional sections without extending into neighboring ones, we opted for a two-dimensional U-Net architecture in our experiments, considering it the most efficient option. Figure 1 illustrates the U-Net architecture for artifact reduction for a 512 × 512 input (18). The initial input is downsampled by encoder blocks consisting of convolutional layers and strided convolutions, decreasing the spatial resolution down to the size of the bottleneck feature maps. The subsequent upsampling is performed through encoder blocks, consisting of, again, convolutional layers and transposed strided convolutions, which were adapted from Guo et al (19). Skip connections connect the encoder and decoder parts. The final network output is generated by summing the initial input image with the output of the last decoder block. In-depth details about the architecture can be found in the legend of Figure 1. The model was initialized with random weights. For hemorrhage detection, EfficientNet-B2 was used, initialized with ImageNet pretrained weights (20). Both models were implemented in Keras (version 2.0.4) (21).

Figure 1:

The architecture of the U-Net used in this study for a 512 × 512 input. If not stated otherwise, each block of feature channels is connected to the previous one by a 3 × 3 convolution. The vertical numbers represent the resolution of the feature channels at each level, while the horizontal numbers indicate the number of feature channels in each block. Initially, the input undergoes processing through a block of four convolutional layers with 64 feature channels, followed by four encoding blocks. In each encoding block, the input is downsampled using a strided convolution, with a 2 × 2 stride and a 1 × 1 convolution, followed by three convolutional layers with kernel size 3 × 3. After the four encoding blocks, a bottleneck feature map of size 32 × 32 with 1024 feature channels is obtained. The feature maps then undergo expansion through four decoding blocks. In each block, the input is processed by three convolutional layers with kernel size 3 × 3, followed by upsampling using a strided transposed convolution with a stride of 2 × 2. This upsampling approach was adapted from Guo et al (19). The feature maps are then added with the corresponding feature maps from the encoding path. Following the decoding blocks, three 3 × 3 convolutional layers with 64 output channels and one convolutional layer with one output channel are applied. The final output is obtained by adding the initial input to this feature map.

Open in a new tab

The architecture of the U-Net used in this study for a 512 × 512 input. If not stated otherwise, each block of feature channels is connected to the previous one by a 3 × 3 convolution. The vertical numbers represent the resolution of the feature channels at each level, while the horizontal numbers indicate the number of feature channels in each block. Initially, the input undergoes processing through a block of four convolutional layers with 64 feature channels, followed by four encoding blocks. In each encoding block, the input is downsampled using a strided convolution, with a 2 × 2 stride and a 1 × 1 convolution, followed by three convolutional layers with kernel size 3 × 3. After the four encoding blocks, a bottleneck feature map of size 32 × 32 with 1024 feature channels is obtained. The feature maps then undergo expansion through four decoding blocks. In each block, the input is processed by three convolutional layers with kernel size 3 × 3, followed by upsampling using a strided transposed convolution with a stride of 2 × 2. This upsampling approach was adapted from Guo et al (19). The feature maps are then added with the corresponding feature maps from the encoding path. Following the decoding blocks, three 3 × 3 convolutional layers with 64 output channels and one convolutional layer with one output channel are applied. The final output is obtained by adding the initial input to this feature map.

Datasets

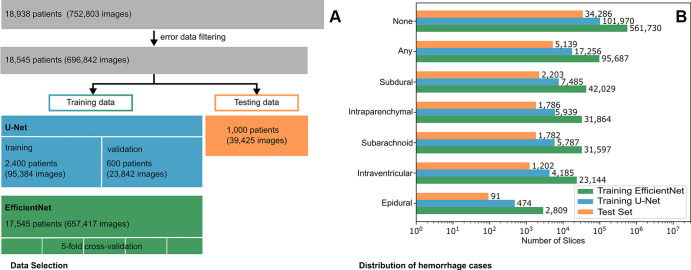
This study used the Radiological Society of North America (RSNA) 2019 Brain CT Hemorrhage Challenge dataset, with each CT image annotated for hemorrhage presence and subtype (subarachnoid, intraventricular, subdural, epidural, and intraparenchymal) (22,23). The dataset consists of CT scans in 18 938 different patients. After filtering out images that either did not have a resolution of 512 × 512 pixels or that led to various errors during data generation, the dataset was narrowed down to 18 545 patients. The list of patients was randomly shuffled via the Fisher-Yates algorithm, implemented in Python's built-in random module (Python version 3.8.10) (24). The first 1000 patients were then selected for testing and excluded from all further training.

For U-Net training, the next 3000 patients were selected from the patient list. Prior experiments have indicated that this number is sufficient to effectively train the U-Net without experiencing overfitting problems (10,12). The first 2400 patients (80%) served as training data and the remaining 600 patients (20%) as validation data. The CT pixel values of the dataset were encoded as either 12-bit or 16-bit unsigned integers. To create sparse-view CT images, we clipped the 16-bit images to the potential 12-bit image range of [0–4095] and divided all images by 4095 to normalize them to range [0–1]. Sinograms with 4096 views were created under parallel-beam geometry from the CT dataset using the Astra Toolbox (version 2.1.0) (25). Reference standard images were reconstructed from 4096 views using FBP. Six sparse-view subsets were generated using FBP with 64, 128, 256, 512, 1024, and 2048 views, respectively.

Due to overfitting concerns, the remainder of the dataset, except the test split, was used for training the EfficientNet-B2 (17 545 patients). Individual images were scaled to Hounsfield units and clipped to the diagnostically relevant brain window [0–80] HU. To meet the requirements of the pretrained ImageNet, images were rescaled to [0–255], resized to 260 × 260 pixels by bilinear resizing, and transformed to three-channel images by concatenating three neighboring CT images (26).

Figure 2 depicts the data selection process and the distribution of the labeled hemorrhage subtypes.

Figure 2:

(A) Flowchart of the data selection process. (B) Distribution of the labeled hemorrhage subtypes in the used data split of the EfficientNet-B2, the U-Net, and the test set. Note the logarithmic scaling of the x-axis.

Open in a new tab

(A) Flowchart of the data selection process. (B) Distribution of the labeled hemorrhage subtypes in the used data split of the EfficientNet-B2, the U-Net, and the test set. Note the logarithmic scaling of the x-axis.

For external testing, the CQ500 dataset (mean age, 48.13 years [range, 7–95 years]; 36.25% [178] female, 63.75% [313] male) derived from the Centre for Advanced Research in Imaging, Neurosciences and Genomics (ie, CARING) in New Delhi, India, was used (27). The file list was shuffled using the Fisher-Yates algorithm, and the first 10 000 images were selected. These images were preprocessed in the same manner as the RSNA dataset.

Training

The U-Net was trained separately for each sparse-view subset, using sparse-view images as input and full-view images as reference standard. It was trained with mean squared error loss for 75 epochs with a mini-batch size of 32. Randomly selected 256 × 256 patches from the images were rotated by 0°, 90°, 180°, or 270°. The learning rate was lr = 10−4/(epoch + 1). Hyperparameters were selected based on a trial-and-error approach, ensuring that the loss curves exhibited fast convergence. The EfficientNet-B2 was trained with fivefold cross-validation and binary cross-entropy loss with a mini-batch size of 32 for 15 epochs. The learning rate followed a cosine annealing schedule with warm restarts after epochs one, three, and seven with an initial learning rate of 5 · 10−4 and minimal learning rate of 10−5. The model with the lowest validation loss was selected for each split. The final predictions for each image were obtained by calculating the arithmetic mean of each class from the outputs of the five different splits.

Total Variation

In this work, we used the isotropic total variation (TV) method by Chambolle (28) for artifact reduction (scikit-image version 0.19.3) (29). The optimal weight for each sparse-view subset was determined by randomly sampling 1000 images from the U-Net training set and iterating through weights ranging from 0.001 to 1.000 in 0.001 increments. We identified a global maximum within this weight range for each subset, suggesting the range was reasonable. The weights that yielded the best score for the structural similarity index measure (SSIM) were selected to calculate the metrics on the test set (30). We also explored using the peak signal-to-noise ratio (PSNR) as an optimization metric. The resulting images, however, exhibited substantial visual degradation compared with SSIM optimization.

Saliency Maps

The saliency maps were obtained by computing the gradient of the class score with respect to the input image, as described in Simonyan et al (31). To quantify the saliency maps, we shuffled (Fisher-Yates) the test set images containing intraparenchymal hemorrhages and selected the first 100. The hemorrhage regions were manually segmented and verified by a board-certified radiologist (D.P.) who has 16 years of experience. For the selected images, we then calculated the saliency map for each sparse-view level with and without U-Net postprocessing, respectively. The segmented masks were used to compute the ratio of the sum of saliency map values within the mask to the sum of values outside the mask.

Statistical Analysis

Image quality of the different postprocessing methods was compared using SSIMs, PSNRs, and SNRs (scikit-image version 0.19.3) (29). To ensure a focus on diagnostically relevant pixels while excluding potentially distorting background pixels, both metrics were applied within a mask of the intracranial region. This mask was generated using the CNN developed and trained by Cai et al (32). A Shapiro-Wilk test showed that the metrics did not follow a normal distribution. Subsequently, 95% CIs of the mean were calculated using bootstrapping with 1000 resamples. The Wilcoxon signed rank test was performed to examine significant differences between no postprocessing and TV or U-Net postprocessing. A Bonferroni-corrected significance level to account for the multiple hypothesis tests of .00033 (.001/3) was used for the P values (33).

To assess inference speed, 100 images from each sparse-view subset were selected from the test set, and the individual inference times for TV and U-Net postprocessing were measured on an NVIDIA GeForce RTX 3090 with 24-GB VRAM. This process was repeated 50 times, and 95% CIs were calculated using bootstrapping with 1000 resamples.

To quantify hemorrhage detection performance, empirical area under the receiver operating characteristic curve (AUC) values, including 95% CIs, were estimated as described by DeLong et al (34). Thereby, the algorithmic implementation by Sun and Xu adapted to Python version 3.8.10 was used (35). Statistical differences in AUCs between sparse-view and full-view datasets, as well as between different postprocessing methods, were evaluated using the DeLong two-sided test. Again, Bonferroni correction was applied, leading to a significance level of P = .00017 (.001/6) for comparing the six sparse-view subsets with the full-view data and a significance level of P = .00033 (.001/3) for comparing raw FBP, TV postprocessing, and U-Net postprocessing. Confusion matrices were generated with Scikit-learn (version 1.1.3); the discrimination thresholds were selected for each subset to maximize the geometric mean of the true-positive and true-negative rates (36). The saliency map ratios with and without U-Net postprocessing were compared in the same manner as the SSIM and PSNR values by using the Wilcoxon signed rank test and calculating 95% CIs of the mean by bootstrapping with 1000 resamples. If not stated otherwise, SciPy version 1.4.1 was used for the statistical analysis (37).

Results

Artifact Reduction

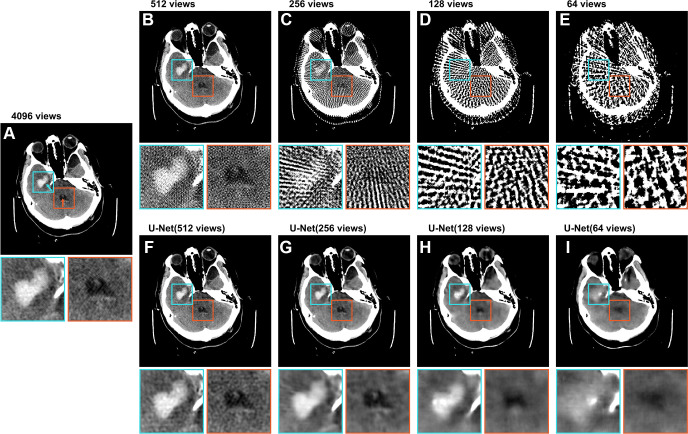
Figure 3A–3E shows a CT image from the test set, reconstructed with varying numbers of views. The full-view (4096 views) image showed a clearly visible intraparenchymal hemorrhage. The intraventricular subtype was also discernible, although it was more challenging to detect. The image reconstructed from 512 views showed decreased image quality and the presence of artifacts, but the hemorrhages could still be identified. In the image reconstructed from 256 views, streak artifacts become pronounced, making it challenging to distinguish small features. Although the intraparenchymal subtype was still discernible, the intraventricular subtype was barely recognizable. Images reconstructed from 128 and 64 views show severe streak artifacts and distortion of the brain tissue. The hemorrhages could not be identified. Figure 3F–3I shows the U-Net predictions of the sparse-view images, revealing a clear reduction in streak artifacts compared with the respective input images (Fig 3B–3E). With increasingly sparse-sampled input, the prediction also tended to become smoother (ie, sharp image features were not retained). However, image quality of the sparse-view CT scans still improved, and the similarity between predictions and full-view images increased. The contours of the hemorrhage can be recognized until the 256-view and 128-view predictions for intraparenchymal and intraventricular subtypes, respectively.

Figure 3:

Axial CT image (512 × 512 pixels) from the test set labeled with an intraparenchymal (cyan arrow) and an intraventricular (orange arrow) hemorrhage. The top row displays raw images, and the bottom row demonstrates artifact reduction by the U-Net. The labeled intraparenchymal and intraventricular hemorrhages are shown in detail in the zoomed-in extracts. (A) Image shows the image reconstructed from 4096 views. (B–E) Images show the same image reconstructed from 512, 256, 128, and 64 views, respectively. (F–I) Images show the U-Net predictions of the corresponding sparse-view images in the upper row. All images are presented in the brain window ranging from 0 HU to 80 HU. Both inserts are 80 × 80 pixels.

Open in a new tab

Axial CT image (512 × 512 pixels) from the test set labeled with an intraparenchymal (cyan arrow) and an intraventricular (orange arrow) hemorrhage. The top row displays raw images, and the bottom row demonstrates artifact reduction by the U-Net. The labeled intraparenchymal and intraventricular hemorrhages are shown in detail in the zoomed-in extracts. (A) Image shows the image reconstructed from 4096 views. (B–E) Images show the same image reconstructed from 512, 256, 128, and 64 views, respectively. (F–I) Images show the U-Net predictions of the corresponding sparse-view images in the upper row. All images are presented in the brain window ranging from 0 HU to 80 HU. Both inserts are 80 × 80 pixels.

Comparison with TV

For comparison, we also implemented TV-based artifact reduction, which is commonly used to address undersampling (38,39). Figure 4A–4F displays results of an image labeled “healthy” from the test set, reconstructed from a varying number of views. In the 2048-view reconstruction, no artifacts were visible. When the number of views was further reduced, the image quality deteriorated with only the skull shape discriminable in the 64-view reconstruction. Figure 4G–4L shows the respective U-Net predictions of the sparse-view CT images. Consistent with Figure 3, the U-Net reduced the artifacts considerably. Again, the resulting images were increasingly smoothed as the number of views decreased. In Figure 4M–4R, the results of TV postprocessing are depicted, which could reduce the artifacts well down to 256 views with sparse sampling. However, the results for 128- and 64-sparse view data were inferior compared with the results from U-Net postprocessing. An additional example is presented in Figure 5, showing images labeled with a subarachnoid hemorrhage.

Figure 4:

Axial CT image (512 × 512 pixels) from the test set labeled as “healthy.” (A–F) Images show the filtered back projection reconstruction from 2048, 1024, 512, 256, 128, and 64 views, respectively. (G–L) Images show the U-Net predictions of the respective images in the upper row, and (M–R) images show the results of the total variation (TV)–based method. The presented structural similarity index measure (SSIM) and peak signal-to-noise ratio (PSNR) values were calculated over the entire CT image scaled to [0–1] from the full Hounsfield unit range (−1024 to 3071 HU) with respect to the 4096-view reconstruction. All images are presented in the brain window ranging from 0 HU to 80 HU. The insert is 100 × 100 pixels; the entire image is 512 × 512 pixels.

Open in a new tab

Axial CT image (512 × 512 pixels) from the test set labeled as “healthy.” (A–F) Images show the filtered back projection reconstruction from 2048, 1024, 512, 256, 128, and 64 views, respectively. (G–L) Images show the U-Net predictions of the respective images in the upper row, and (M–R) images show the results of the total variation (TV)–based method. The presented structural similarity index measure (SSIM) and peak signal-to-noise ratio (PSNR) values were calculated over the entire CT image scaled to [0–1] from the full Hounsfield unit range (−1024 to 3071 HU) with respect to the 4096-view reconstruction. All images are presented in the brain window ranging from 0 HU to 80 HU. The insert is 100 × 100 pixels; the entire image is 512 × 512 pixels.

Figure 5:

Axial CT image (512 × 512 pixels) from the test set labeled with a subarachnoid hemorrhage. (A–F) Images show the filtered back projection reconstruction from 2048, 1024, 512, 256, 128, and 64 views, respectively. (G–L) Images show the U-Net predictions of the respective images in the upper row, and (M–R) images show the results of the total variation (TV)–based method. The presented structural similarity index measure (SSIM) and peak signal-to-noise ratio (PSNR) values were calculated over the entire CT image scaled to [0–1] from the full Hounsfield unit range (−1024 to 3071 HU) with respect to the 4096-view reconstruction. All images are presented in the brain window ranging from 0 HU to 80 HU. The insert is 100 × 100 pixels; the entire image is 512 × 512 pixels.

Open in a new tab

Axial CT image (512 × 512 pixels) from the test set labeled with a subarachnoid hemorrhage. (A–F) Images show the filtered back projection reconstruction from 2048, 1024, 512, 256, 128, and 64 views, respectively. (G–L) Images show the U-Net predictions of the respective images in the upper row, and (M–R) images show the results of the total variation (TV)–based method. The presented structural similarity index measure (SSIM) and peak signal-to-noise ratio (PSNR) values were calculated over the entire CT image scaled to [0–1] from the full Hounsfield unit range (−1024 to 3071 HU) with respect to the 4096-view reconstruction. All images are presented in the brain window ranging from 0 HU to 80 HU. The insert is 100 × 100 pixels; the entire image is 512 × 512 pixels.

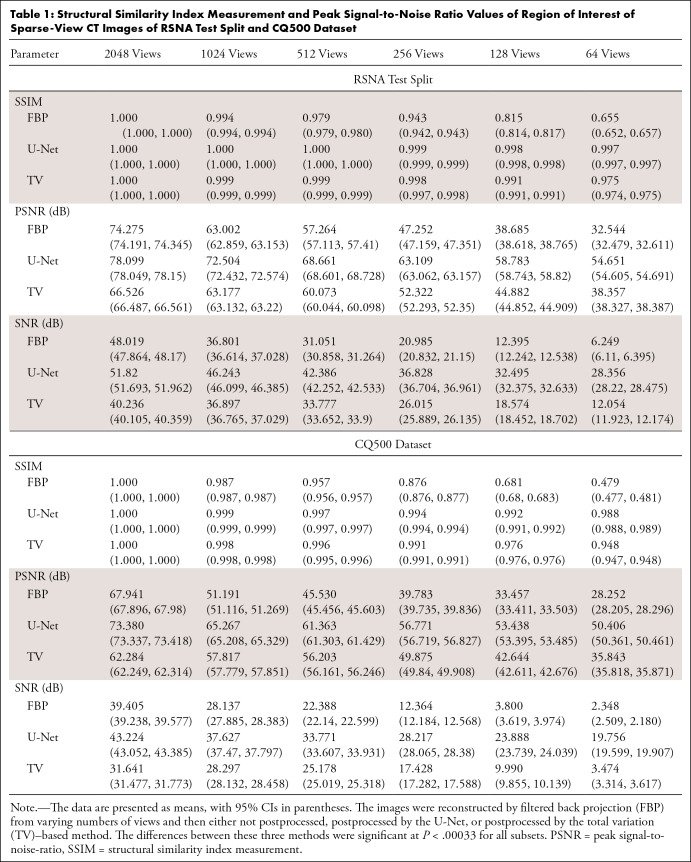
Table 1 presents the mean SSIM, PSNR, and SNR values of the reconstructed images calculated on the RSNA test set and the CQ500 dataset, with individual values calculated in reference to the 4096-view images. Both U-Net and the TV postprocessing quantitatively increased the SSIM by reducing streak artifacts, compared with raw FBP reconstructions. This aligns with the visual results in Figures 3–5. U-Net postprocessing also enhanced PSNR values, whereas TV processing resulted in decreased PSNR values for specific subsets, specifically down to and including the 512-view subset for the RSNA test split and the 2048-view subset of the CQ500 dataset, when compared with the respective raw FBP images. The PSNR values of the remaining subsets improved after TV processing. Direct comparison revealed U-Net's stronger performance in all cases, with statistically significant differences between postprocessing for each subset (P < .00033).

Table 1:

Structural Similarity Index Measurement and Peak Signal-to-Noise Ratio Values of Region of Interest of Sparse-View CT Images of RSNA Test Split and CQ500 Dataset

graphic file with name ryai.230275.tbl1.jpg

Open in a new tab

The mean inference speed of the TV method and the U-Net were also compared for 100 images per sparse-view subset. For the 64-, 128-, 256-, 512-, 1024-, and 2048-view data, the U-Net took 2.254 (95% CI: 2.249, 2.258), 2.244 (95% CI: 2.24, 2.249), 2.209 (95% CI: 2.206, 2.214), 2.206 (95% CI: 2.203, 2.211), and 2.213 (95% CI: 2.205, 2.244) seconds, and the TV algorithm took 46.886 (95% CI: 46.595, 47.19), 30.84 (95% CI: 30.704, 30.99), 17.091 (95% CI: 17.02, 17.16), 7.393 (95% CI: 7.343, 7.449), 7.237 (95% CI: 7.196, 7.275), and 5.096 (95% CI: 5.069, 5.129) seconds, respectively.

Detection of Hemorrhage Subtypes

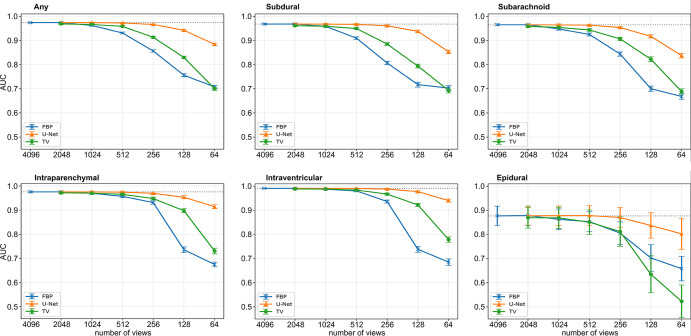
Finally, we evaluated the impact of artifact reduction on automated hemorrhage detection by examining the outcomes of the EfficientNet-B2 hemorrhage detection network. Figure 6 demonstrates the AUC values for the raw images (blue) and the images postprocessed by either TV (green) or the U-Net (orange) for varying levels of subsampling for each subtype. If not stated otherwise, the given AUC values in the following text refer to the predicted “any” class, stating if a hemorrhage was present in the image, regardless of subtype. Overall, detection performance decreased as the number of views used for the reconstruction decreased. When reducing the number of views from 4096 (AUC = 0.97 [95% CI: 0.97, 0.98]) to 1024 (AUC = 0.96 [95% CI: 0.96, 0.97]), there was a slight decrease in performance (P = .01 for epidural, P < .00017 for other subtypes), which further decreased with fewer views. In TV-postprocessed images, the AUC values slightly decreased until 512 views (AUC = 0.96 [95% CI: 0.96, 0.96], P = .00033 for epidural, P < .00017 for other subtypes) and decreased significantly for fewer views (256 views: AUC = 0.91 [95% CI: 0.91, 0.92], P < .00017). With the U-Net, there was a minimal decrease in detection performance as the number of views reduced from 4096 views to 512 views (AUC = 0.97 [95% CI: 0.97, 0.98], P = .62 for epidural, P < .00017 for other subtypes) and to 256 views (AUC = 0.97 [95% CI: 0.96, 0.97], P = .17 for epidural, P < .00017 for other subtypes). Below 256 views, a noticeable decline is visible (128 views: AUC = 0.94 [95% CI: 0.94, 0.95], P < .00017). For all the cases reconstructed with 1024 views or fewer, except the epidural subtype, the AUC values obtained from U-Net postprocessed images surpass those of TV-processed and raw sparse-view images significantly (P < .0003). For the epidural subtype, a significant difference is only observable for 512 views or fewer (512 views: U-Net: AUC = 0.88 [95% CI: 0.84, 0.92], TV: AUC = 0.85 [95% CI: 0.80, 0.90]). Notably, the detection of epidural hemorrhages is generally poorer compared with other subtypes. The individual AUC values of all subtypes and the corresponding ROC curves are given in Table S1 and Figure S1, respectively. All the individual P values can be found in Table S2.

Figure 6:

Results of the EfficientNet-B2 detection network. Graphs depict the mean area under the receiver operator characteristic curve (AUC) values with 95% CIs associated with the any, subdural, subarachnoid, intraparenchymal, intraventricular, and epidural classes, respectively. The 95% CIs are indicated by the error bars around each data point. The individual P values among the different values can be found in Table S2. FBP = filtered back projection, TV = total variation.

Open in a new tab

Results of the EfficientNet-B2 detection network. Graphs depict the mean area under the receiver operator characteristic curve (AUC) values with 95% CIs associated with the any, subdural, subarachnoid, intraparenchymal, intraventricular, and epidural classes, respectively. The 95% CIs are indicated by the error bars around each data point. The individual P values among the different values can be found in Table S2. FBP = filtered back projection, TV = total variation.

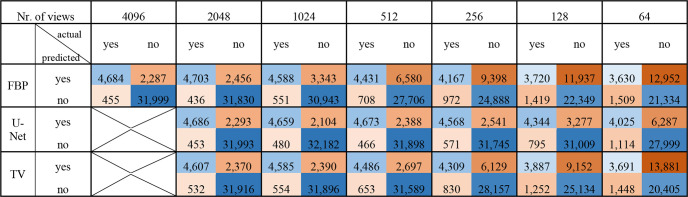
Figure 7 shows the confusion matrices for the any class of CT images reconstructed with varying numbers of views, without postprocessing (FBP) and with either TV or U-Net postprocessing. The decrease in detection performance and the impact of postprocessing agree with the results in Figure 6. The confusion matrices for all classes can be found in Figure S2.

Figure 7:

Confusion matrices for hemorrhage detection performance of full-view images and reconstructed images with varying numbers of views without postprocessing and postprocessing with either U-Net or TV. Images were reconstructed with FBP from 2048 to 64 views. Each 4 × 4 field represents an individual confusion matrix corresponding to one sparse-view dataset and one processing method. FBP = filtered back projection, TV = total variation.

Open in a new tab

Confusion matrices for hemorrhage detection performance of full-view images and reconstructed images with varying numbers of views without postprocessing and postprocessing with either U-Net or TV. Images were reconstructed with FBP from 2048 to 64 views. Each 4 × 4 field represents an individual confusion matrix corresponding to one sparse-view dataset and one processing method. FBP = filtered back projection, TV = total variation.

Examples of individual image detection results are depicted in Figure 8. The presence of an intraparenchymal hemorrhage remained undetected in the sparse-view reconstructions, despite U-Net or TV postprocessing. However, for the subarachnoid hemorrhage, TV postprocessing, and for the intraventricular hemorrhage, U-Net postprocessing, yielded correct detection results. For the first healthy case, both sparse-view and postprocessed images were erroneously classified as positive for hemorrhage. Nevertheless, for the second healthy case, TV postprocessing resulted in a true-negative detection, while U-Net postprocessing lead to a true-negative detection in the third healthy case presented.

Figure 8:

Examples of detection results of individual axial sections by the EfficientNet-B2 network. Each column displays a full-view image, followed by its corresponding sparse-view reconstruction, and then the sparse-view image postprocessed, either by the U-Net or the total variation (TV) algorithm. The first three columns depict images labeled with intraparenchymal, subarachnoid, and intraventricular hemorrhages, respectively, while the last three columns show images labeled as healthy. In the upper left corner of each image, it is indicated whether the images were correctly classified (true positive [TP] or true negative [TN]) or not (false negative [FN] or false positive [FP]), utilizing the same thresholds as for the confusion matrices in Figure 7. All images are presented in the brain window ranging from 0 HU to 80 HU.

Open in a new tab

Examples of detection results of individual axial sections by the EfficientNet-B2 network. Each column displays a full-view image, followed by its corresponding sparse-view reconstruction, and then the sparse-view image postprocessed, either by the U-Net or the total variation (TV) algorithm. The first three columns depict images labeled with intraparenchymal, subarachnoid, and intraventricular hemorrhages, respectively, while the last three columns show images labeled as healthy. In the upper left corner of each image, it is indicated whether the images were correctly classified (true positive [TP] or true negative [TN]) or not (false negative [FN] or false positive [FP]), utilizing the same thresholds as for the confusion matrices in Figure 7. All images are presented in the brain window ranging from 0 HU to 80 HU.

Saliency Maps

Figure 9 shows the saliency maps for the images of Figure 3 with regard to the any class. The rectangles are positioned identically to those in Figure 3, indicating the location of the hemorrhages. For images reconstructed down to and including 256-view sparse-sampling (Fig 3A–3C), the network primarily focused on the area of the intraparenchymal hemorrhage for its prediction. However, for reconstructions with fewer views (Fig 3D, 3F), such a focused area was no longer discernible. Conversely, for the U-Net postprocessed images (Fig 3F–3I), all the saliency maps focused on the subarachnoid hemorrhage area.

Figure 9:

Saliency maps by the EfficientNet-B2 model of the CT images of Figure 3 with regard to the “any” class. (A) Image shows the saliency map of the full-view image. (B–E) Images show the saliency maps of the images reconstructed from 512, 256, 128, and 64 views, respectively. (F–H) Images show the saliency maps of the images postprocessed by the U-Net of the corresponding sparse-view images. All maps were normalized via min-max normalization to range [0–1]. The rectangles are at the same position as in Figure 3, indicating the location of the present hemorrhages. Note: Saliency maps were generated by analyzing the gradients of the EfficientNet-B2 model with respect to the input. High values indicate that changes to those pixels have a substantial impact on the model's output, and therefore, those pixels are most important for the prediction.

Open in a new tab

Saliency maps by the EfficientNet-B2 model of the CT images of Figure 3 with regard to the “any” class. (A) Image shows the saliency map of the full-view image. (B–E) Images show the saliency maps of the images reconstructed from 512, 256, 128, and 64 views, respectively. (F–H) Images show the saliency maps of the images postprocessed by the U-Net of the corresponding sparse-view images. All maps were normalized via min-max normalization to range [0–1]. The rectangles are at the same position as in Figure 3, indicating the location of the present hemorrhages. Note: Saliency maps were generated by analyzing the gradients of the EfficientNet-B2 model with respect to the input. High values indicate that changes to those pixels have a substantial impact on the model's output, and therefore, those pixels are most important for the prediction.

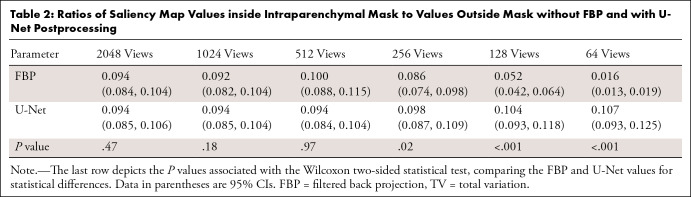
The results of the quantitative saliency map analysis are displayed in Table 2. When using 128 views or fewer, a significant difference was discernible between raw FBP reconstructions and U-Net postprocessed ones (P < .001). This agrees with the results shown in Figure 6D and Figure 9.

Table 2:

Ratios of Saliency Map Values inside Intraparenchymal Mask to Values Outside Mask without FBP and with U-Net Postprocessing

graphic file with name ryai.230275.tbl2.jpg

Open in a new tab

Discussion

In this work, we investigated CNN-based artifact reduction in sparse-view cranial CT scans and the subsequent impact on automated hemorrhage detection. We demonstrated that a deep CNN, specifically a U-Net architecture, leads to substantial improvements in the visual quality of sparse-view cranial CT scans. Evaluation using the SNR, PSNR, and SSIM metrics quantitatively confirmed the enhanced image quality achieved by the network. Furthermore, we trained a hemorrhage detection network on full-view CT images and applied it to sparse-view images with and without postprocessing by the U-Net. The results showed that the U-Net enabled a reduction in views from 4096 to 512 with minimal impact on detection performance and to 256 views with only a slight performance decrease. Compared with the 4096-view image, this would correspond to a respective dose reduction of 87.5% (1–512 of 4096) and 93.75% (1–256 of 4096). However, even without postprocessing, a meaningful decline in detection performance was observed for subsets using fewer than 2048 views. This suggests that using fewer views for the full-view image would also be sufficient, subsequently mitigating the stated dose reduction. In comparison, Prasad et al (40) demonstrated a 50% reduction in radiation dose for low-dose chest CT scans and Wu et al (41) a 46% dose reduction for cranial CT scans, while maintaining diagnostic integrity. Additionally, we compared the results of the U-Net with an analytical approach based on TV. The U-Net had superior performance compared with TV postprocessing with respect to image quality parameters, inference speed, and automated hemorrhage detection.

We selected the U-Net architecture for its multiscale encoder-decoder structure with skip connections, allowing it to efficiently solve image-to-image problems without requiring complex training optimizations. The excellent results with U-Net–based approaches in sparse-view artifact reduction, exemplified by studies such as those conducted by Han and Ye (10), Jin et al (11), or Genzel et al (42), whose method notably secured first place in the American Association of Physicists in Medicine DL-sparse-view CT Challenge, further motivated our adaption of this architecture. The artifact reduction performance of our network was on par with these reported methods. For instance, the U-Net proposed by Jin et al (11) was a U-Net with an additional skip connection from input to output and reported SNR improvements of 15.31 dB and 11.18 dB for 50 views and 143 views, respectively, compared with raw FBP reconstructions on their “biomedical dataset.” We observed SNR improvements of 22.11 dB and 20.1 dB for the 64-view and 128-view images, respectively, compared with raw FBP reconstructions for the RSNA test split. Han and Ye (10) extended the U-Net architecture to satisfy the frame condition and reported PSNR improvements of 11.57 dB and 9.97 dB for 60 views and 120 views, respectively. In comparison, we observed PSNR improvements of 22.11 dB and 20.01 dB for our 64-view and 128-view reconstructions, respectively. It is essential to note that drawing conclusions about method superiority from these values is difficult given the differences in training datasets and data preprocessing methods, which can substantially influence the results. The success of these architectures, including our U-Net, can be attributed to their multiresolution feature. The exponentially large receptive field due to the pooling and unpooling layers makes it possible to handle streak artifacts that occur at sparse-view CT and typically spread over a large portion of the image. We chose a two-dimensional approach due to the parallel-beam geometry of our data. In cases with different geometries, such as cone beam, it might be worthwhile to explore a computationally more expensive three-dimensional U-Net variant in future works.

The U-Net demonstrated robustness by substantially improving image quality across all investigated levels of subsampling on both the RSNA dataset and the external CQ500 dataset. This was evidenced by the calculated PSNR and SSIM values. The TV approach was also able to significantly improve the SSIM values of the sparse-view data. Interestingly, no clear trend in the PSNR values could be identified for TV processing. This is most likely because the weights for the TV method were set to optimize the SSIM, rather than PSNR, as described in the Total Variation section. The results of automated hemorrhage detection further validated the importance of artifact reduction, with substantial improvements observed in AUC values and confusion matrices. Saliency maps provided additional support to these findings by revealing that pronounced artifacts in sparse-view images disrupted the detection process, leading to increased false-positive and false-negative results. By reducing these artifacts through postprocessing, these effects can be mitigated and the detection performance can be maintained, without the need for specific training on subsampled data.

It is important to acknowledge some limitations of this study. The sparse-view data used in our study were retrospectively generated under simplified conditions from CT volumes, which may not fully capture the complexity of real-world scenarios. Additionally, the training dataset had imbalances in terms of negative cases and not all hemorrhage subtypes were represented equally. This might explain the relatively poor performance in classifying the epidural subtype compared with the other subtypes. Furthermore, analyzing the patient demographics across data splits was not possible due to the unavailability of such information in the RSNA dataset.

In summary, our findings highlight the importance of employing appropriate postprocessing techniques to achieve optimal image quality and diagnostic accuracy while minimizing radiation dose. Furthermore, our study demonstrates that leveraging deep learning methods for artifact reduction can lead to substantial improvements in hemorrhage detection on sparse-view cranial CT scans. This has promising implications for rapid automated hemorrhage detection on sparse-view cranial CT data to assist radiologists in routine clinical practice. Subsequent studies focused on evaluating U-Net–based artifact reduction using clinically measured sparse-view data are essential for the successful integration of this approach into clinical practice.

Supported by the Federal Ministry of Education and Research (BMBF) and the Free State of Bavaria under the Excellence Strategy of the Federal Government and the Länder, the German Research Foundation (GRK2274), as well as by the Technical University of Munich–Institute for Advanced Study.

Disclosures of conflicts of interest: J.T. No relevant relationships. M.S. Currently Siemens Healthineers employee but was not affiliated with the company during the research and preparation of this manuscript. T.D. No relevant relationships. T.L. No relevant relationships. F.P. No relevant relationships. D.P. Funded by the Federal Ministry of Education and Research (BMBF) and the Free State of Bavaria under the Excellence Strategy of the Federal Government and the Länder, the German Research Foundation (GRK2274), as well as by the Technical University of Munich–Institute for Advanced Study. F.S. No relevant relationships.

Abbreviations:

AUC
area under the receiver operating characteristic curve
CNN
convolutional neural network
FBP
filtered back projection
PSNR
peak signal-to-noise ratio
RSNA
Radiological Society of North America
SSIM
structural similarity index
TV
total variation

References

  • 1. van Asch CJ , Luitse MJ , Rinkel GJ , van der Tweel I , Algra A , Klijn CJ . Incidence, case fatality, and functional outcome of intracerebral haemorrhage over time, according to age, sex, and ethnic origin: a systematic review and meta-analysis . Lancet Neurol 2010. ; 9 ( 2 ): 167 – 176 . [DOI] [PubMed] [Google Scholar]
  • 2. Feigin VL , Lawes CM , Bennett DA , Barker-Collo SL , Parag V . Worldwide stroke incidence and early case fatality reported in 56 population-based studies: a systematic review . Lancet Neurol 2009. ; 8 ( 4 ): 355 – 369 . [DOI] [PubMed] [Google Scholar]
  • 3. Currie S , Saleem N , Straiton JA , Macmullen-Price J , Warren DJ , Craven IJ . Imaging assessment of traumatic brain injury . Postgrad Med J 2016. ; 92 ( 1083 ): 41 – 50 . [DOI] [PubMed] [Google Scholar]
  • 4. Brenner DJ , Hall EJ . Computed tomography--an increasing source of radiation exposure . N Engl J Med 2007. ; 357 ( 22 ): 2277 – 2284 . [DOI] [PubMed] [Google Scholar]
  • 5. Smith-Bindman R , Lipson J , Marcus R , et al . Radiation dose associated with common computed tomography examinations and the associated lifetime attributable risk of cancer . Arch Intern Med 2009. ; 169 ( 22 ): 2078 – 2086 . [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 6. Poon R , Badawy MK . Radiation dose and risk to the lens of the eye during CT examinations of the brain . J Med Imaging Radiat Oncol 2019. ; 63 ( 6 ): 786 – 794 . [DOI] [PubMed] [Google Scholar]
  • 7. Hu Z , Gao J , Zhang N , et al . An improved statistical iterative algorithm for sparse-view and limited-angle CT image reconstruction . Sci Rep 2017. ; 7 ( 1 ): 10747 . [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 8. Ritschl L , Bergner F , Fleischmann C , Kachelriess M . Improved total variation-based CT image reconstruction applied to clinical data . Phys Med Biol 2011. ; 56 ( 6 ): 1545 – 1561 . [DOI] [PubMed] [Google Scholar]
  • 9. Lauzier PT , Chen G-H . Characterization of statistical prior image constrained compressed sensing (PICCS): II. Application to dose reduction . Med Phys 2013. ; 40 ( 2 ): 021902 . [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 10. Han Y , Ye JC . Framing U-Net via Deep Convolutional Framelets: Application to Sparse-View CT . IEEE Trans Med Imaging 2018. ; 37 ( 6 ): 1418 – 1429 . [DOI] [PubMed] [Google Scholar]
  • 11. Jin KH , McCann MT , Froustey E , Unser M . Deep Convolutional Neural Network for Inverse Problems in Imaging . IEEE Trans Image Process 2017. ; 26 ( 9 ): 4509 – 4522 . [DOI] [PubMed] [Google Scholar]
  • 12. Cheslerean-Boghiu T , Hofmann FC , Schulthei M , Pfeiffer F , Pfeiffer D , Lasser T . WNet: A Data-Driven Dual-Domain Denoising Model for Sparse-View Computed Tomography With a Trainable Reconstruction Layer . IEEE Trans Comput Imaging 2023. ; 9 : 120 – 132 . [Google Scholar]
  • 13. Wu W , Hu D , Niu C , Yu H , Vardhanabhuti V , Wang G . DRONE: Dual-Domain Residual-based Optimization NEtwork for Sparse-View CT Reconstruction . IEEE Trans Med Imaging 2021. ; 40 ( 11 ): 3002 – 3014 . [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 14. Chen G , Zhao Y , Huang Q , Gao H . 4D-AirNet: a temporally-resolved CBCT slice reconstruction method synergizing analytical and iterative method with deep learning . Phys Med Biol 2020. ; 65 ( 17 ): 175020 . [DOI] [PubMed] [Google Scholar]
  • 15. Wang X , Shen T , Yang S , et al . A deep learning algorithm for automatic detection and classification of acute intracranial hemorrhages in head CT scans . Neuroimage Clin 2021. ; 32 : 102785 . [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 16. Artificial Intelligence and Machine Learning (AI/ML)-Enabled Medical Devices . U.S. Food & Drug Administration Web site. https://www.fda.gov/medical-devices/software-medical-device-samd/artificial-intelligence-and-machine-learning-aiml-enabled-medical-devices. Updated October 19, 2023. Accessed July 10, 2023.
  • 17. Detected lesions . BrainScan Web Site. https://brainscan.ai/examples.html. Accessed July 10, 2023.
  • 18. Ronneberger O , Fischer P , Brox T . U-Net: Convolutional Networks for Biomedical Image Segmentation . In: Navab N , Hornegger J , Wells WM , Frangi AF , eds. Medical Image Computing and Computer-Assisted Intervention – MICCAI 2015. MICCAI 2015. Lecture Notes in Computer Science , vol 9351 . Springer; , 2015. ; 234 – 241 . [Google Scholar]
  • 19. Guo S , Yan Z , Zhang K , Zuo W , Zhang L . Toward Convolutional Blind Denoising of Real Photographs . In: 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) . IEEE; , 2019. ; 1712 – 1722 . [Google Scholar]
  • 20. Tan M , Le QV . EfficientNet: Rethinking Model Scaling for Convolutional Neural Networks . arXiv 1905.11946 [preprint] https://arxiv.org/abs/1905.11946. Posted May 28, 2019. Accessed July 20, 2023. [Google Scholar]
  • 21. Keras Web site. https://keras.io. Published 2015. Accessed July 20, 2023.
  • 22. RSNA Intracranial Hemorrhage Detection Challenge (2019) . RSNA Web site. https://www.rsna.org/rsnai/ai-image-challenge/rsna-intracranial-hemorrhage-detection-challenge-2019. Accessed July 20, 2023.
  • 23. Flanders AE , Prevedello LM , Shih G , et al . Construction of a Machine Learning Dataset through Collaboration: The RSNA 2019 Brain CT Hemorrhage Challenge . Radiol Artif Intell 2020. ; 2 ( 3 ): e190211 . [Published correction appears in Radiol Artif Intell 2020;2(4):e209002.] [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 24. Fisher NI . Statistical analysis of circular data . Cambridge University Press; , 1993. . [Google Scholar]
  • 25. Palenstijn WJ , Batenburg KJ , Sijbers J . Performance improvements for iterative electron tomography reconstruction using graphics processing units (GPUs) . J Struct Biol 2011. ; 176 ( 2 ): 250 – 253 . [DOI] [PubMed] [Google Scholar]
  • 26. Abadi M , Agarwal A , Barham P , et al . TensorFlow: Large-Scale Machine Learning on Heterogeneous Distributed Systems . arXiv 1603.04467 [preprint] https://arxiv.org/abs/1603.04467. Posted March 14, 2016. Accessed July 20, 2023. [Google Scholar]
  • 27. Chilamkurthy S , Ghosh R , Tanamala S , et al . Deep learning algorithms for detection of critical findings in head CT scans: a retrospective study . Lancet 2018. ; 392 ( 10162 ): 2388 – 2396 . [DOI] [PubMed] [Google Scholar]
  • 28. Chambolle A . An Algorithm for Total Variation Minimization and Applications . J Math Imaging Vis 2004. ; 20 : 89 – 97 . [Google Scholar]
  • 29. van der Walt S , Schönberger JL , Nunez-Iglesias J , et al . scikit-image: image processing in Python . PeerJ 2014. ; 2 : e453 . [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 30. Wang Z , Bovik AC , Sheikh HR , Simoncelli EP . Image quality assessment: from error visibility to structural similarity . IEEE Trans Image Process 2004. ; 13 ( 4 ): 600 – 612 . [DOI] [PubMed] [Google Scholar]
  • 31. Simonyan K , Vedaldi A , Zisserman A . Deep Inside Convolutional Networks: Visualising Image Classification Models and Saliency Maps . arXiv 1312.6034 [preprint] https://arxiv.org/abs/1312.6034. Posted December 20, 2013. Accessed July 20, 2023. [Google Scholar]
  • 32. Cai JC , Akkus Z , Philbrick KA , et al . Fully automated segmentation of head CT neuroanatomy using deep learning . Radiol Artif Intell 2020. ; 2 ( 5 ): e190183 . [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 33. Dunn OJ . Multiple Comparisons among Means . J Am Stat Assoc 1961. ; 56 ( 293 ): 52 – 64 . [Google Scholar]
  • 34. DeLong ER , DeLong DM , Clarke-Pearson DL . Comparing the areas under two or more correlated receiver operating characteristic curves: a nonparametric approach . Biometrics 1988. ; 44 ( 3 ): 837 – 845 . [PubMed] [Google Scholar]
  • 35. Sun X , Xu W . Fast implementation of DeLong's algorithm for comparing the areas under correlated receiver operating characteristic curves . IEEE Signal Process Lett 2014. ; 21 ( 11 ): 1389 – 1393 . [Google Scholar]
  • 36. Pedregosa F , Varoquaux G , Gramfort A , et al . Scikit-learn: Machine Learning in Python . J Mach Learn Res 2011. ; 12 : 2825 – 2830 . [Google Scholar]
  • 37. Virtanen P , Gommers R , Oliphant TE , et al . SciPy 1.0: fundamental algorithms for scientific computing in Python . Nat Methods 2020. ; 17 ( 3 ): 261 – 272 . [Published correction appears in Nat Methods 2020;17(3):352.] [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 38. Sidky EY , Pan X . Image reconstruction in circular cone-beam computed tomography by constrained, total-variation minimization . Phys Med Biol 2008. ; 53 ( 17 ): 4777 – 4807 . [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 39. Zhang Y , Zhang W , Lei Y , Zhou J . Few-view image reconstruction with fractional-order total variation . J Opt Soc Am A Opt Image Sci Vis 2014. ; 31 ( 5 ): 981 – 995 . [DOI] [PubMed] [Google Scholar]
  • 40. Prasad SR , Wittram C , Shepard JA , McLoud T , Rhea J . Standard-dose and 50%-reduced-dose chest CT: comparing the effect on image quality . AJR Am J Roentgenol 2002. ; 179 ( 2 ): 461 – 465 . [DOI] [PubMed] [Google Scholar]
  • 41. Wu D , Wang G , Bian B , Liu Z , Li D . Benefits of Low-Dose CT Scan of Head for Patients With Intracranial Hemorrhage . Dose Response 2020. ; 19 ( 1 ): 1559325820909778 . [Published correction appears in Dose Response 2021;19(1):15593258211002755.] [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 42. Genzel M , Gühring I , Macdonald J , März M . Near-Exact Recovery for Tomographic Inverse Problems via Deep Learning . arXiv 2206.07050 [preprint] https://arxiv.org/abs/2206.07050 Posted June 14, 2022. Accessed July 20, 2023. [Google Scholar]

Articles from Radiology: Artificial Intelligence are provided here courtesy of Radiological Society of North America

RESOURCES