Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2024 Jul 22;18(30):19732–19741. doi: 10.1021/acsnano.4c05251

Structure and Formation Mechanisms in Tantalum and Niobium Oxides in Superconducting Quantum Circuits

Jin-Su Oh †, Rahim Zaman ‡, Akshay A Murthy §, Mustafa Bal §, Francesco Crisa §, Shaojiang Zhu §, Carlos G Torres-Castanedo ∥, Cameron J Kopas ⊥, Joshua Y Mutus ⊥, Dapeng Jing #, John Zasadzinski ∇, Anna Grassellino §, Alex Romanenko §, Mark C Hersam ∥, Michael J Bedzyk ∥, Matt Kramer †, Bi-Cheng Zhou ‡, Lin Zhou †,○,*
PMCID: PMC11295204  PMID: 39034612

Abstract

graphic file with name nn4c05251_0007.jpg

Improving the qubit’s lifetime (T1) is crucial for fault-tolerant quantum computing. Recent advancements have shown that replacing niobium (Nb) with tantalum (Ta) as the base metal significantly increases T1, likely due to a less lossy native surface oxide. However, understanding the formation mechanism and nature of both surface oxides is still limited. Using aberration-corrected transmission electron microscopy and electron energy loss spectroscopy, we found that Ta surface oxide has fewer suboxides than Nb oxide. We observed an abrupt oxidation state transition from Ta2O5 to Ta, as opposed to the gradual shift from Nb2O5, NbO2, and NbO to Nb, consistent with thermodynamic modeling. Additionally, amorphous Ta2O5 exhibits a closer-to-crystalline bonding nature than Nb2O5, potentially hindering H atomic diffusion toward the oxide/metal interface. Finally, we propose a loss mechanism arising from the transition between two states within the distorted octahedron in an amorphous structure, potentially causing two-level system loss. Our findings offer a deeper understanding of the differences between native amorphous Ta and Nb oxides, providing valuable insights for advancing superconducting qubits through surface oxide engineering.

Keywords: superconducting qubits, surface encapsulation, tantalum oxides, niobium oxides, STEM-EELS, CALPHAD

Quantum information processing holds the potential to surpass traditional computers in various aspects,1,2 including quantum physics, chemistry simulations,3,4 and optimization algorithms.5 Among the diverse materials considered for quantum computing, superconducting materials offer significant possibilities for solid-state platforms.6,7 Their fabrication utilizes well-established semiconductor methodologies,8 such as thin film deposition and lithography, which place a superconducting quantum bit (qubit) at the forefront of quantum computing technology.9 Over the last two decades, the advancement of superconducting qubits has primarily stemmed from optimizing the design of the quantum circuit.10−14 However, it is widely acknowledged that intricate processing methodologies can introduce defects at the interfaces and surfaces of the superconducting quantum circuits, thereby introducing decoherence sources.15−18 Therefore, a precise understanding of how the material’s structure and defects contribute to decoherence is essential for enhancing the performance of superconducting qubits. This understanding is particularly crucial for the Josephson junction (JJ) and resonators, which serve as fundamental components in the superconducting quantum circuits.19

Niobium (Nb)-based superconducting quantum devices have dominated the field for an extended period as this material offers cost advantages, flexibility in deposition methodologies, and compatibility with industrial-scale processes.20,21 Nonetheless, as the T1 of two-dimensional transmon qubits composed of Nb has long plateaued around 100 μs, it has become clear that alternative materials approaches are needed.22 Recent work highlights Nb surface oxides’ critical role in limiting T1.23 As a result, encapsulating the surface of niobium with various metals and dielectrics allows for significant improvements, with 2–5× longer T1 achievable compared to bare Nb. Through this approach, Bal et al. achieved a maximum T1 of 602 μs, with a tantalum (Ta) capping layer on Nb.23 This demonstrates that Ta oxide is less lossy than Nb oxide and explains why other groups have previously been able to achieve max T1 values of 360 μs (Place et al.,24 reported Ta-based qubits) and 503 μs (Wang et al.,25 demonstrated a further improvement through the implementation of a dry-etch process) with Ta. This improvement has been attributed to factors such as a thinner total surface oxide thickness,26 a reduced number or absence of stable suboxides on the Ta surface,21,25−27 or the abrupt transition from higher oxidation states to lower ones.21,26 However, Bal et al.23 suggest no clear correlation between oxide thickness and overall loss. Instead, they propose that this loss may arise from variations in the chemical stoichiometry (i.e., the presence of stable suboxides in the Nb oxide). Other potential factors include variations in the local crystallinity and the presence of impurities. Despite these extensive studies, the reasons for forming fewer suboxides in Ta and their lower dissipative nature in terms of dielectric loss remain unclear. Furthermore, as niobium pentoxide is the most detrimental part of qubit’s coherence,17,28,29 the low-loss characteristics of tantalum pentoxide may be another reason for performance enhancement. Thus, a direct comparison between the Ta and Nb pentoxides should be carried out thoroughly.

We systematically compare microstructure and device performance fabricated from two superconducting thin films, as discussed by Bal et al.:23 (1) an uncapped Nb thin film on a silicon (Si) substrate (later called the uncapped film) and (2) Ta-capped Nb thin film on Si. Our results suggest that Ta oxide is less lossy than Nb oxide due not only to the formation of less complicated oxides but also to a closer-to-crystalline nature of the oxide bonding. Our results offer valuable insights for advancing superconducting qubits through surface oxide engineering.

Results and Discussion

As discussed, Ta capping of Nb leads to a 2–5× improvement in the qubit T1.23 This enhanced T1 suggests that the notable systematic improvements are intricately linked to the metal-air (M-A) interface rather than the superconducting metal itself.23 To evaluate the origin of the differences in loss between Ta and Nb oxides, we performed a detailed comparison of the M-A interface for both the Nb and Ta-capped Nb films.

Overall, the surface morphologies are nearly identical between the two samples. Figure 1 shows the atomic force microscopy (AFM) images of the Nb- and Ta-capped samples. The film’s root-mean-square (RMS) roughness is less than 1 nm, exhibiting a similar value between the bare Nb and Ta-capped Nb thin films.

Figure 1.

Figure 1

Open in a new tab

AFM surface images of Nb/Si and Ta/Nb/Si samples.

Cross-sectional transmission electron microscopy (TEM) micrographs in Figure 2 show that both samples exhibit columnar grain structures, with the Nb thin films measuring approximately 200 nm thick and the Ta capping layers at around 10 nm. Notably, there is a thickness difference in the amorphous surface oxide layer between the two samples. The native amorphous surface oxide layer on the uncapped Nb film is approximately 4 nm. In comparison, the surface oxide layer on the Ta capping layer is approximately 5.5 nm (Figure 2b,g). In addition, the Ta-capped film’s surface appears to follow the uncapped film’s surface morphology, which aligns with the AFM analysis in Figure 1. Energy-dispersive X-ray spectroscopy (EDS) elemental distribution maps highlight these features, as depicted in Figure 2c–e,h–j. Atomic-resolution high-angle annular dark-field (HAADF)-scanning TEM (STEM) micrograph confirms the epitaxial growth of Ta on Nb due to its almost identical lattice constant, as shown in Figure 2k. The grain boundary of the Ta capping layer follows that of the Nb film, as indicated by a yellow dashed line in Figure 2k, which indicates that the Ta capping layer exhibits the same lateral grain size as the Nb thin film.

Figure 2.

Figure 2

Open in a new tab

Cross-sectional TEM images of bare Nb and Ta-capped Nb thin films. a, Cross-sectional bright-field TEM image and b, high-resolution TEM image of the bare Nb thin film on Si. c, HAADF-STEM image and d, e, the corresponding EDS elemental distribution maps of Nb and O at the NbOx-Nb interface. f, Cross-sectional bright-field TEM image and g, high-resolution TEM image of the Ta-capped Nb thin film on Si. h, HAADF-STEM image and i, j, the corresponding EDS elemental distribution map of Ta and O at the TaOx-Ta-Nb interface. k, Atomic-resolution HAADF-STEM showing epitaxial growth of Ta on Nb.

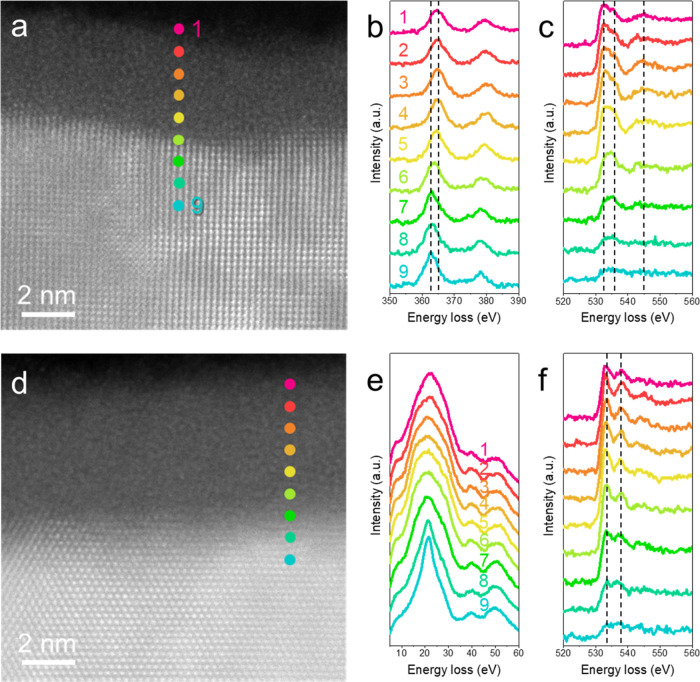
We further compared the oxygen states of Nb and Ta across the M-A interface. Figure 3 shows spatially resolved electron energy loss spectroscopy (EELS) results to elucidate the chemistry of the amorphous oxide layer. A gradual oxidation state transition is observed across the M-A interface for the amorphous Nb oxide layer. Cross-sectional HAADF-STEM images at the M-A interface indicate the spot position for spatially resolved EELS, where the distance between adjacent spots is 0.83 nm. Figure 3b displays the energy-loss near-edge structure (ELNES) of the Nb M23 edge, confirming a transition from +5 to +0, indicated by two dashed lines at 365 and 363 eV, respectively. According to the Nb M23 edge,30 the outermost four spots (1–4) correspond to the Nb2O5, followed by NbO2 at spot 5. This gradual transition in the oxidation state is further supported by ELNES of the O K edge (Figure 3c), where the first two dominant peaks (indicated by dashed lines at 532.5 and 535.5 eV) with a third peak at 545 eV represent higher oxidation states (+4 and +5).30 The intensity ratio of the first two peaks changes slightly at spot 5, indicating a decrease in oxidation state to +4, i.e., NbO2.30 This is consistent with our previous study31 and reveals a gradual transition in the amorphous oxide layer from Nb2O5 to NbO2 and finally NbO (spot 6) at the interface between the amorphous surface oxide layer and Nb metal.

Figure 3.

Figure 3

Open in a new tab

EELS line profiles of surface oxides on Nb and Ta. a, HAADF-STEM micrograph of the NbOx-Nb interface of the bare Nb thin film. Colored spots denote the positions in which EEL spectra are taken. b, c, Corresponding spatially resolved EEL spectra showing ELNESs of Nb M23 edge and O K edge. d, HAADF-STEM micrograph of the TaOx-Ta interface of Ta-capped Nb thin film. Colored spots denote the positions in which EEL spectra are acquired. e, f, Corresponding spatially resolved EEL spectra showing ELNESs of Ta O23 edge and O K edge. The distance between adjacent spots is 0.83 nm.

In contrast, the Ta surface exhibits a relatively abrupt transition from Ta2O5 to Ta. Unlike Nb, Ta lacks a core-loss edges fingerprint to track the oxidation states. However, the plasmon peaks in the low-loss energy region show an abrupt transition from spot 7 to spot 8 (Figure 3e), where spots 8 and 9 exhibit sharp plasmon peaks corresponding to metallic Ta, and spots 1 to 7 show bell-shaped plasmon peaks. The O K edge further confirms this abrupt transition, with two well-separated dominant peaks at 533.5 and 537 eV, denoted by dashed lines in Figure 3f, indicating Ta2O5 for spots 1 to 7.32,33 Therefore, based on the ELNES study across the Ta oxide layer, spot 8 may correspond to either suboxide species or a mixture of metallic Ta and some Ta2O5. To corroborate this, we performed principal component analysis (PCA). However, the PCA result did not show clear evidence of suboxide species at the Ta-TaOx interface (details in the Supporting Information). In general, it is evident that Ta exhibits a thinner transition layer with an upper limit of 0.8 nm and undergoes a more abrupt transition from +5 to +0 states compared to Nb (within about 0.8–1.6 nm). This observation holds true, whether conservatively or radically determined, despite the total thickness of the amorphous Ta surface oxide layer being greater than its Nb counterpart, aligning well with previous works.23,25,26

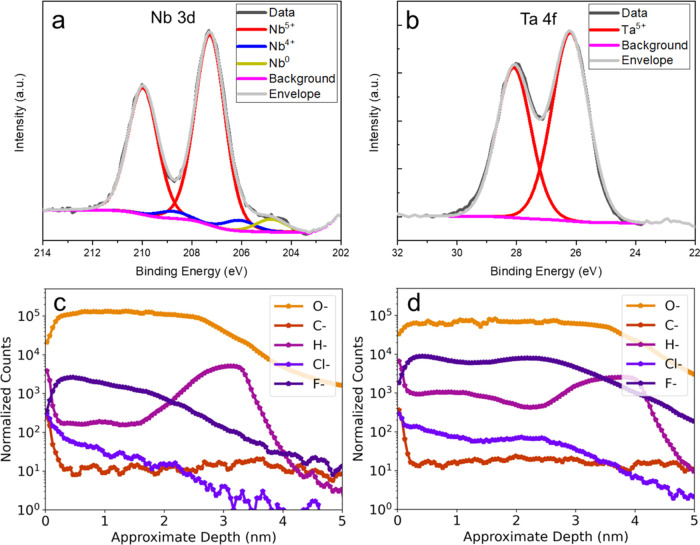
The X-ray photoelectron spectroscopy (XPS) analysis is in good agreement with the EELS results. Figure 4a shows NbO2 and metallic Nb, although most of the Nb 3d intensity is Nb2O5. We do not observe a signal attributable to the NbO peak, maybe due to the small volume fraction. On the other hand, Figure 4b shows that Ta 4f is entirely explained by Ta2O5 peak fits. The difference in oxide thickness may be the main reason why there are no peaks from metallic Ta, as well as Ta having a much higher atomic number that results in a shorter mean free path of electrons. It might imply that even if there are some suboxides, photoelectrons cannot escape to be detected due to the thicker Ta oxide layer. Nonetheless, with the same X-ray interaction conditions for the Nb and Ta surface oxides, the Ta-capped sample shows uniform surface oxide in the form of Ta2O5. In contrast, the baseline Nb sample exhibits a suboxide layer between predominant Nb2O5 and metallic Nb thin film, consistent with spatially resolved ELNES results in Figure 3.

Figure 4.

Figure 4

Open in a new tab

XPS and ToF-SIMS characterization. a, Nb 3d intensity consists of Nb2O5, NbO2, and Nb (only Nb(0) 3d 3/2 is shown). b, Ta 4f intensity only consists of Ta2O5. Black, violet, and gray lines represent the raw spectrum, background, and envelope, respectively. Normalized ToF-SIMS depth profiles showing O–, C–, H–, Cl–, and F– of c, bare Nb, and d, Ta-capped Nb thin films.

To examine the impurity content in the two surface oxides, we used time-of-flight secondary ion mass spectrometry (ToF-SIMS) to capture the signal associated with species such as C–, H–, F–, and Cl– as a function of depth for both the uncapped and Ta-capped Nb films, as shown in Figure 4c,d. Regarding H– counts, we observe a clear increase in the signal close to the oxide and metal interface for both samples. As previously reported,34,35 this may arise due to the infiltration of hydrogen atoms into the niobium metal before the formation of the surface oxide or during nanofabrication processes such as wet etching. Interestingly, the H– counts are found to be an order of magnitude higher in the uncapped film compared with that in the Ta-capped film.

On the other hand, the F– counts in the Ta oxide are almost an order of magnitude larger than those in the Nb oxide. The observed disparity in F– counts may explain why, in this case, we observe that Ta oxide is roughly 5 nm, whereas previous reports have indicated values closer to 3 nm.23,26,27,31,36−38 While it has been reported that the tunneling of H– ions has been proposed as a loss mechanism in the GHz range,39,40 it is worth noting that the F– ions are significantly larger than H– ions, and their impact on loss requires further investigation.

The experimentally observed abrupt transition in oxidation states from Ta2O5 to Ta in contrast to the gradual shift from Nb2O5 to Nb is consistent with the known thermodynamics. Thermodynamic descriptions of the Ta–O and Nb–O systems were obtained using the CALculation of PHAse Diagrams (CALPHAD) method based on existing databases, and the resulting phase diagrams are shown in Figure 5.41−44 The former has a single stable stoichiometric oxide (Ta2O5), while the latter includes three oxides (Nb2O5, NbO2, and NbO). The existence of a single valence state in the Ta–O system and three valence states in the Nb–O system is explained by the oxygen chemical potentials (μO) in both systems, which are plotted as functions of the oxygen mole fraction in Figure 5. There is a single discontinuity in μO in the Ta–O system, corresponding to an abrupt change in the oxidation state. However, in the Nb–O system, three discontinuities exist in μO, resulting in a gradual change in the oxidation state. Although the thermodynamic analysis here is based on equilibrium crystalline phases from the phase diagrams, the same trend still holds for the amorphous native oxides.

Figure 5.

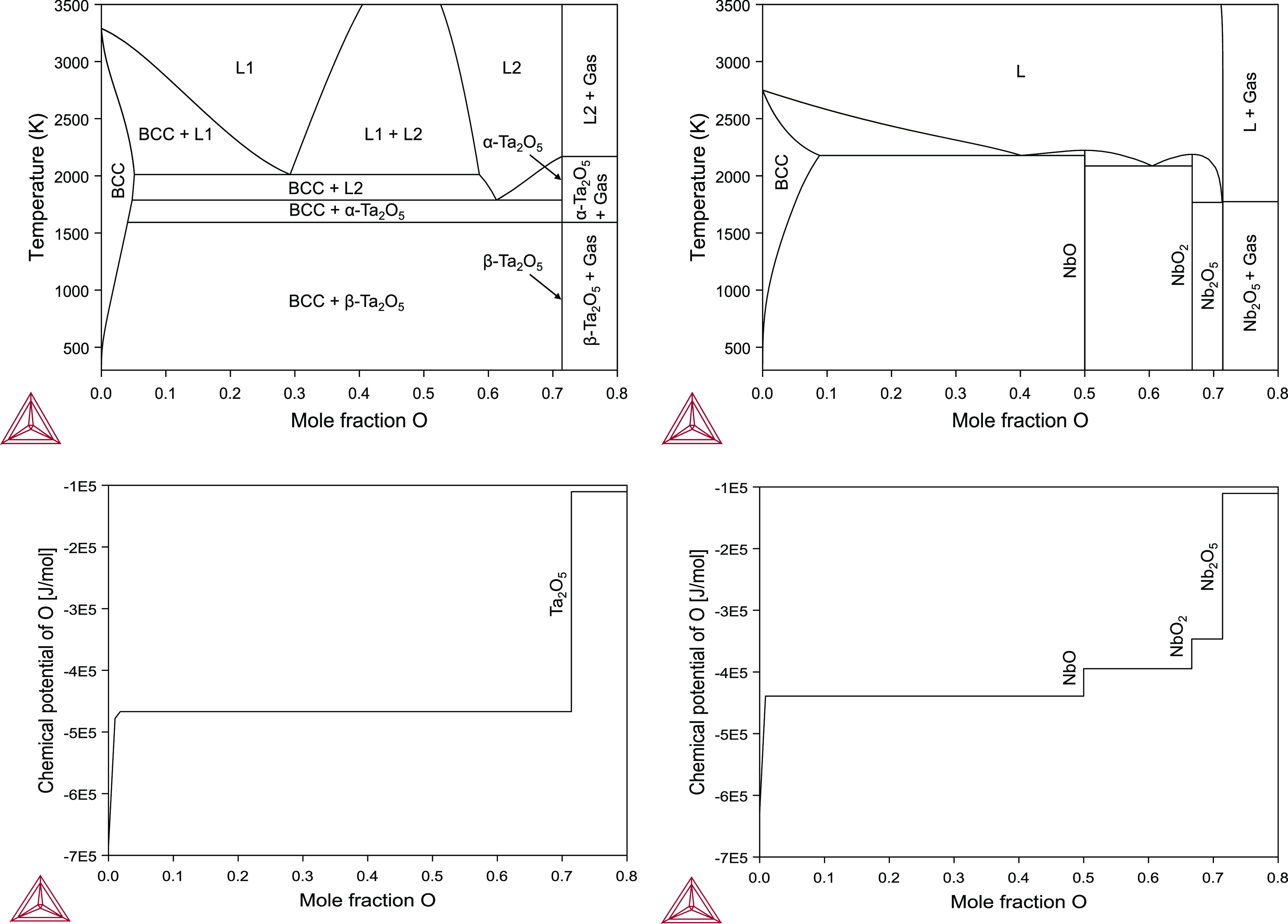
Figure 5

Open in a new tab

Calculated phase diagrams of the Ta–O and Nb–O systems and their respective oxygen chemical potentials as functions of oxygen mole fraction.

Since suboxide species may act as magnetic impurities and lead to quasiparticle loss,27,38,45,46 understanding the underlying origin of enhanced performance in Ta-based qubits is often solely attributed to suboxide species. However, given that the predominant oxide species for both Nb and Ta exist in the form of their pentoxides, and extensive research indicates that Nb2O5 is primarily accountable for two-level system (TLS) loss,17,28,29 it suggests there might be another mechanism rooted in the intrinsic material properties of amorphous Nb2O5 and Ta2O5. This mechanism could also play a crucial role in the performance improvement of Ta-based or Ta-capped qubits.

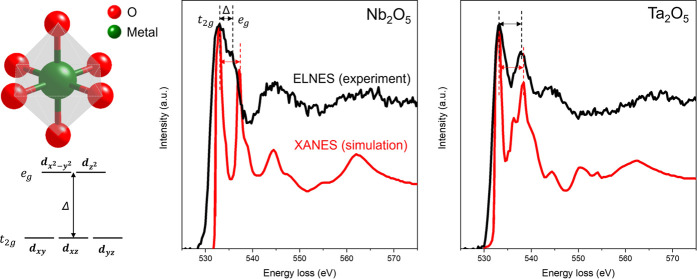
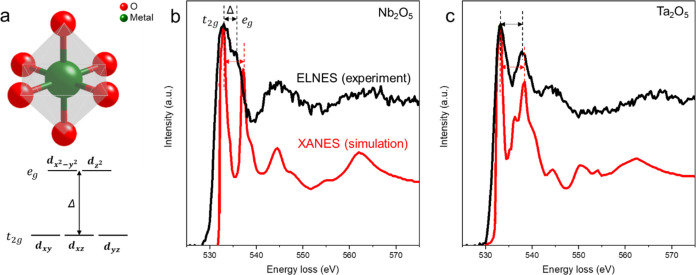
The unoccupied p-type states of the surrounding oxygen atoms are hybridized with the neighboring transition metal; the O K edge could provide information that reflects the bonding states in transition metal and O bonding and their oxidation states.47,48Figure 6 directly compares the ELNES of the O K edges for Nb2O5 and Ta2O5. Figure 6a illustrates an octahedrally coordinated transition metal atom to oxygen atoms, offering a qualitative explanation for the differences in the double-peak structure of the O K ELNES based on ligand-field theory. This structure results in the splitting of transition metal d orbitals into the upper, eg orbital, and the slightly lower in energy t2g, with a crystal-field splitting energy Δ.49,50Figure 6b,c presents the O K edges of measured EELS and calculated X-ray absorption spectroscopy (XAS) for Nb2O5 and Ta2O5. Calculated XAS for the crystalline references is employed as EELS, essentially equivalent to XAS under high primary energy and low scattering angle approximations.47Figure 6b depicts the amorphous character of Nb2O5. We observe a decrease in crystal-field splitting energy Δ compared with the crystalline counterpart and broader individual peaks. The simulated X-ray absorption near-edge structure (XANES) exhibits an Δ of 4.15 eV, whereas experimental ELNES exhibits an Δ of 2.5 eV, which is about a 40% reduction. This aligns with measured and calculated EELS and XAS in the literature for amorphous Nb2O5.48,50

Figure 6.

Figure 6

Open in a new tab

ELNES of O K edge for Nb2O5 and Ta2O5. a, Schematic of the octahedrally coordinated transition metal ion, causing a splitting Δ in the energy levels of the d-orbitals. b, O K edges of integrated experimental ELNES of amorphous Nb2O5 and simulated XANES of crystalline Nb2O5. c, O K edges of integrated experimental ELNES of amorphous Ta2O5 and simulated XANES of crystalline Ta2O5.

In comparison, Figure 6c reveals that the crystal-field splitting energy Δ of the measured ELNES and the calculated XAS of Ta2O5 are almost identical (XANES with Δ of 5.0 eV and ELNES with Δ of 4.75 eV, which is about a 5% reduction), consistent with experimental and simulated EELS data reported in ref (33). Moreover, the measured double peaks of Ta2O5 are sharper than those of Nb2O5, indicating that amorphous Ta2O5 retains a more octahedrally symmetric crystalline character.48 This implies a reduced likelihood of tunneling between the two lowest-energy states as predicted in disordered materials, resulting in fewer TLS defects being coupled with the qubit’s electric field and reduced microwave loss.9,51 On the other hand, amorphous Nb2O5, based on the measured ELNES, may have more distorted octahedrons. This distortion could lead to a higher possibility of easier tunneling between two minimum energy states, akin to the unique two-state nature of the transformation known as the umbrella flip.52 As deviations from crystalline order can lead to quantum decoherence, such a phenomenon may further limit qubits’ coherence time. More generally, TLS-type loss typically arises from local disorder; hence, an amorphous region is more likely to host such loss mechanisms than its crystalline counterparts. Finally, the less distorted Ta2O5 structure may be more effective in blocking the diffusion of H atoms toward the oxide/metal interface (Figure 4c,d), potentially further reducing TLS sources.

Conclusions

Structural and chemical investigations were conducted on the M-A interface to elucidate the reasons behind coherence time improvement when native TaOx was utilized instead of native NbOx. Our observation revealed an abrupt transition from Ta2O5 to Ta metal, marked by a significant absence of suboxide species, contrasting with the gradual valence state transition from Nb2O5 to Nb metal in native NbOx. The calculated phase diagram and oxygen chemical potential between Nb–O and Ta–O systems explain this disparity. In addition, we discovered a closer crystalline bonding nature of amorphous Ta2O5 than that of Nb2O5. We attribute this distinction to another potential origin for the enhanced T1 of Ta or Ta-capped Nb superconducting qubits. Our comprehensive approach, combining STEM-EELS and thermodynamic calculations, elucidates the formation mechanism and low-loss nature of TaOx compared to those of NbOx. This insight addresses current gaps in understanding low-loss TaOx properties, creating a foundation for subsequent in-depth theoretical investigations to validate these findings further.

Methods

Qubit Fabrication

The qubit devices were fabricated on high-resistivity Si substrates (ρ ≥ 10 kΩ·cm) with sputter-deposited Nb (∼200 nm thick) or Ta-capped (∼10 nm) Nb layers and Al/AlOx/Al Josephson junctions. Details on the thin film and device fabrication have been reported elsewhere.23

AFM Analysis

The surface morphology of the Nb- and Ta-capped Nb films was analyzed by AFM using an Asylum Cypher AFM with a Si cantilever in tapping mode at a scanning rate of 1 Hz. The image resolution was 512 × 512 pixels.

(S)TEM-EELS Analysis

Cross-sectional TEM samples were prepared by using a focused ion beam instrument with a gas injection system (Helios, Thermo Fisher Scientific Ltd.). The TEM samples were thinned to electron beam transparency by a Ga+ ion beam from 30 to 2 kV. The TEM samples were investigated using an aberration-corrected TEM (Titan Cube, Thermo Fisher Scientific Ltd.) at 200 kV. A high-angle annular dark-field (HAADF) detector was used for dark-field imaging in STEM mode with a convergent semiangle and a collection semiangle of 18 and 74–200 mrad, respectively. Energy-dispersive X-ray spectroscopy (EDS) and electron energy-loss spectroscopy (EELS) studies were carried out with probe currents of 200 and 50 pA, respectively. Dual EELS was performed to acquire all-electron energy-loss (ELL) spectra. The plural scattering effect of all of the raw ELL spectra was removed via Fourier-ratio deconvolution.

XPS Analysis

XPS analysis was conducted with a Kratos Amicus/ESCA 3400 device, utilizing 240 W Mg Kα X-rays from a twin-anode laboratory source. The emitted photoelectrons were collected at a perpendicular angle to the surface and analyzed using a DuPont-type analyzer, with the pass energy adjusted to 150 eV. To refine the spectra, a Shirley baseline correction was applied using the CasaXPS software, and charging effects were compensated by calibrating the C 1s peak binding energy to 285 eV.

ToF-SIMS Analysis

ToF-SIMS measurements were performed using a dual beam IONTOF 5 system to analyze impurities’ concentration and depth distribution in the Nb and Ta/Nb films. Secondary ion measurements were performed by using a liquid bismuth ion beam (Bi+). A cesium ion gun with an energy of 500 eV sputtered the surface for depth profile measurements. All counts were normalized to the total counts in the Nb metal layer, enabling qualitative comparison of impurities between samples.

XAS Simulation

Simulation of X-ray absorption spectra was created by Materials Project,53 for orthorhombic Nb2O554 and monoclinic Ta2O5.55

Thermodynamic Calculations

Thermodynamic models of the Ta–O and Nb–O systems using the CALPHAD method were adopted from a prior study41 and from the TCOX11 database44 in the Thermo-Calc software.43 The Ta–O models include low-temperature orthorhombic (β) and high-temperature tetragonal (α) Ta2O5 polymorphs, body-centered cubic (BCC) α-Ta, liquid, and gas phases, which were respectively described as stoichiometric compounds, a solid solution, ionic liquid,56 and ideal gas. The Nb–O models, based on unpublished work by Dupin and Ansara57 and published by Massih and Pérez,58 include monoclinic Nb2O5, tetragonal NbO2, cubic NbO, BCC Nb, liquid, and gas phases. The compounds were modeled as stoichiometric, BCC Nb as a solid solution, the liquid as an ionic liquid, and the gas as ideal.

Acknowledgments

This work was supported by the U.S. Department of Energy, Office of Science, National Quantum Information Science Research Centers, Superconducting Quantum Materials and Systems Center (SQMS) under contract No. DE-AC02-07CH11359. All electron microscopy and related work were performed using instruments in the Sensitive Instrument Facility at Ames National Lab. The Ames National Laboratory is operated for the U.S. Department of Energy by Iowa State University under Contract No. DE-AC02-07CH11358. R.Z. and B.-C.Z. acknowledge Research Computing at the University of Virginia for providing computational resources and technical support that have contributed to the results reported within this manuscript. URL: https://re.virginia.edu. The authors also thank Rigetti Computing for fabricating the devices used in this study.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsnano.4c05251.

  • Principal component analysis (PCA) of O K edge EELS spectra across the TaOx-Ta interface (PDF)

The authors declare no competing financial interest.

Notes

This work was produced by Iowa State University under Contract DE-AC02CH11358 with the U.S. Department of Energy. Publisher acknowledges the U.S. Government license and the provision to provide public access under the DOE Public Access Plan (http://energy.gov/downloads/doe-public-access-plan).

After this paper was published ASAP July 22, 2024, we corrected a spelling error in the name of author Carlos G. Torres Castanedo. The corrected version was reposted July 30, 2024.

Supplementary Material

nn4c05251_si_001.pdf (138.8KB, pdf)

References

  1. Arute F.; Arya K.; Babbush R.; Bacon D.; Bardin J. C.; Barends R.; Biswas R.; Boixo S.; Brandao F. G. S. L.; Buell D. A.; Burkett B.; Chen Y.; Chen Z.; Chiaro B.; Collins R.; Courtney W.; Dunsworth A.; Farhi E.; Foxen B.; Fowler A.; Gidney C.; Giustina M.; Graff R.; Guerin K.; Habegger S.; Harrigan M. P.; Hartmann M. J.; Ho A.; Hoffmann M.; Huang T.; Humble T. S.; Isakov S. V.; Jeffrey E.; Jiang Z.; Kafri D.; Kechedzhi K.; Kelly J.; Klimov P. V.; Knysh S.; Korotkov A.; Kostritsa F.; Landhuis D.; Lindmark M.; Lucero E.; Lyakh D.; Mandrà S.; McClean J. R.; McEwen M.; Megrant A.; Mi X.; Michielsen K.; Mohseni M.; Mutus J.; Naaman O.; Neeley M.; Neill C.; Niu M. Y.; Ostby E.; Petukhov A.; Platt J. C.; Quintana C.; Rieffel E. G.; Roushan P.; Rubin N. C.; Sank D.; Satzinger K. J.; Smelyanskiy V.; Sung K. J.; Trevithick M. D.; Vainsencher A.; Villalonga B.; White T.; Yao Z. J.; Yeh P.; Zalcman A.; Neven H.; Martinis J. M. Quantum Supremacy Using a Programmable Superconducting Processor. Nature 2019, 574, 505–510. 10.1038/s41586-019-1666-5. [DOI] [PubMed] [Google Scholar]
  2. Kim Y.; Eddins A.; Anand S.; Wei K. X.; Berg E. van den.; Rosenblatt S.; Nayfeh H.; Wu Y.; Zaletel M.; Temme K.; Kandala A. Evidence for the Utility of Quantum Computing before Fault Tolerance. Nature 2023, 618 (7965), 500–505. 10.1038/s41586-023-06096-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. McArdle S.; Endo S.; Aspuru-Guzik A.; Benjamin S. C.; Yuan X. Quantum Computational Chemistry. Rev. Mod. Phys. 2020, 92, 15003 10.1103/RevModPhys.92.015003. [DOI] [Google Scholar]
  4. Alam M. S.; Belomestnykh S.; Bornman N.; Cancelo G.; Chao Y.-C.; Checchin M.; Dinh V. S.; Grassellino A.; Gustafson E. J.; Harnik R.; McRae C. R. H.; Huang Z.; Kapoor K.; Kim T.; Kowalkowski J. B.; Kramer M. J.; Krasnikova Y.; Kumar P.; Kurkcuoglu D. M.; Lamm H.; Lyon A. L.; Milathianaki D.; Murthy A.; Mutus J.; Nekrashevich I.; Oh J.; Özgüler A. B.; Perdue G. N.; Reagor M.; Romanenko A.; Sauls J. A.; Stefanazzi L.; Venturelli D.; Wang C.; You X.; Zanten D. M. T. van.; Zhou L.; Zhu S.; Zorzetti S.. Quantum Computing Hardware for HEP Algorithms and Sensing. 2022, arXiv:2204.08605, pp 1–23. 10.48550/arXiv.2204.08605. [DOI]
  5. Nielsen M. A.; Chuang I. L.. Quantum Computation and Quantum Information, 10th Anniversary ed.; Cambridge University Press, 2010; p 708. [Google Scholar]
  6. Clarke J.; Wilhelm F. K. Superconducting Quantum Bits. Nature 2008, 453, 1031–1042. 10.1038/nature07128. [DOI] [PubMed] [Google Scholar]
  7. Kjaergaard M.; Schwartz M. E.; Braumüller J.; Krantz P.; Wang J. I. J.; Gustavsson S.; Oliver W. D. Superconducting Qubits: Current State of Play. Annu. Rev. Condens. Matter Phys. 2020, 11, 369–395. 10.1146/annurev-conmatphys-031119-050605. [DOI] [Google Scholar]
  8. Lozano D. P.; Mongillo M.; Piao X.; Couet S.; Wan D.; Canvel Y.; Vadiraj A. M.; Ivanov T.; Verjauw J.; Acharya R.; Damme J. V.; Mohiyaddin F. A.; Jussot J.; Gowda P. P.; Pacco A.; Raes B.; de Vondel J. V.; Radu I. P.; Govoreanu B.; Swerts J.; Potočnik A.; Greve K. D. Low-loss α-tantalum coplanar waveguide resonators on silicon wafers: fabrication, characterization and surface modification. Mater. Quantum Technol. 2024, 4, 025801 10.1088/2633-4356/ad4b8c. [DOI] [Google Scholar]
  9. de Leon N. P.; Itoh K. M.; Kim D.; Mehta K. K.; Northup T. E.; Paik H.; Palmer B. S.; Samarth N.; Sangtawesin S.; Steuerman D. W. Materials Challenges and Opportunities for Quantum Computing Hardware. Science 2021, 372, eabb2823 10.1126/science.abb2823. [DOI] [PubMed] [Google Scholar]
  10. Gyenis A.; Paolo A. D.; Koch J.; Blais A.; Houck A. A.; Schuster D. I. Moving beyond the Transmon: Noise-Protected Superconducting Quantum Circuits. PRX Quantum 2021, 2 (3), 030101 10.1103/prxquantum.2.030101. [DOI] [Google Scholar]
  11. Koch J.; Yu T. M.; Gambetta J.; Houck A. A.; Schuster D. I.; Majer J.; Blais A.; Devoret M. H.; Girvin S. M.; Schoelkopf R. J. Charge-Insensitive Qubit Design Derived from the Cooper Pair Box. Phys. Rev. A 2007, 76, 042319 10.1103/PhysRevA.76.042319. [DOI] [Google Scholar]
  12. Paik H.; Schuster D. I.; Bishop L. S.; Kirchmair G.; Catelani G.; Sears A. P.; Johnson B. R.; Reagor M. J.; Frunzio L.; Glazman L. I.; Girvin S. M.; Devoret M. H.; Schoelkopf R. J. Observation of High Coherence in Josephson Junction Qubits Measured in a Three-Dimensional Circuit QED Architecture. Phys. Rev. Lett. 2011, 107, 240501 10.1103/PhysRevLett.107.240501. [DOI] [PubMed] [Google Scholar]
  13. Schreier J. A.; Houck A. A.; Koch J.; Schuster D. I.; Johnson B. R.; Chow J. M.; Gambetta J. M.; Majer J.; Frunzio L.; Devoret M. H.; Girvin S. M.; Schoelkopf R. J. Suppressing Charge Noise Decoherence in Superconducting Charge Qubits. Phys. Rev. B 2008, 77, 180502(R) 10.1103/PhysRevB.77.180502. [DOI] [Google Scholar]
  14. Manucharyan V. E.; Koch J.; Glazman L. I.; Devoret M. H. Fluxonium: Single Cooper-Pair Circuit Free of Charge Offsets. Science 2009, 326 (5949), 113–116. 10.1126/science.1175552. [DOI] [PubMed] [Google Scholar]
  15. Wang C.; Axline C.; Gao Y. Y.; Brecht T.; Chu Y.; Frunzio L.; Devoret M. H.; Schoelkopf R. J. Surface Participation and Dielectric Loss in Superconducting Qubits. Appl. Phys. Lett. 2015, 107 (16), 162601 10.1063/1.4934486. [DOI] [Google Scholar]
  16. Oliver W. D.; Welander P. B. Materials in Superconducting Quantum Bits. MRS Bull. 2013, 38, 816–825. 10.1557/mrs.2013.229. [DOI] [Google Scholar]
  17. Verjauw J.; Potočnik A.; Mongillo M.; Acharya R.; Mohiyaddin F.; Simion G.; Pacco A.; Ivanov Ts.; Wan D.; Vanleenhove A.; Souriau L.; Jussot J.; Thiam A.; Swerts J.; Piao X.; Couet S.; Heyns M.; Govoreanu B.; Radu I. Investigation of Microwave Loss Induced by Oxide Regrowth in High-Q Niobium Resonators. Phys. Rev. Appl. 2021, 16 (1), 014018 10.1103/PhysRevApplied.16.014018. [DOI] [Google Scholar]
  18. Murray C. E. Material Matters in Superconducting Qubits. Mater. Sci. Eng., R 2021, 146, 100646 10.1016/j.mser.2021.100646. [DOI] [Google Scholar]
  19. Schoelkopf R. J.; Girvin S. M. Wiring up Quantum Systems. Nature 2008, 451, 664–669. 10.1038/451664a. [DOI] [PubMed] [Google Scholar]
  20. Guo X.; Degnan Z.; Steele J. A.; Solano E.; Donose B. C.; Bertling K.; Fedorov A.; Rakić A. D.; Jacobson P. Near-Field Localization of the Boson Peak on Tantalum Films for Superconducting Quantum Devices. J. Phys. Chem. Lett. 2023, 14 (20), 4892–4900. 10.1021/acs.jpclett.3c00850. [DOI] [PubMed] [Google Scholar]
  21. Premkumar A.; Weiland C.; Hwang S.; Jäck B.; Place A. P. M.; Waluyo I.; Hunt A.; Bisogni V.; Pelliciari J.; Barbour A.; Miller M. S.; Russo P.; Camino F.; Kisslinger K.; Tong X.; Hybertsen M. S.; Houck A. A.; Jarrige I. Microscopic Relaxation Channels in Materials for Superconducting Qubits. Commun. Mater. 2021, 2, 72. 10.1038/s43246-021-00174-7. [DOI] [Google Scholar]
  22. Nersisyan A.; Sete E. A.; Stanwyck S.; Bestwick A.; Reagor M.; Poletto S.; Alidoust N.; Manenti R.; Renzas R.; Bui C. V.; Vu K.; Whyland T.; Mohan Y.. Manufacturing Low Dissipation Superconducting Quantum Processors. In Technical Digest—International Electron Devices Meeting, IEDM; IEEE: San Francisco, CA, USA, 2019; pp 31.1.1–31.1.4 10.1109/iedm19573.2019.8993458. [DOI]
  23. Bal M.; Murthy A. A.; Zhu S.; Crisa F.; You X.; Huang Z.; Roy T.; Lee J.; Zanten D.; van Pilipenko R.; Nekrashevich I.; Lunin A.; Bafia D.; Krasnikova Y.; Kopas C. J.; Lachman E. O.; Miller D.; Mutus J. Y.; Reagor M. J.; Cansizoglu H.; Marshall J.; Pappas D. P.; Vu K.; Yadavalli K.; Oh J.-S.; Zhou L.; Kramer M. J.; Lecocq F. Q.; Goronzy D. P.; Torres-Castanedo C. G.; Pritchard G.; Dravid V. P.; Rondinelli J. M.; Bedzyk M. J.; Hersam M. C.; Zasadzinski J.; Koch J.; Sauls J. A.; Romanenko A.; Grassellino A. Systematic Improvements in Transmon Qubit Coherence Enabled by Niobium Surface Encapsulation. npj Quantum Inf. 2024, 10, 43 10.1038/s41534-024-00840-x. [DOI] [Google Scholar]
  24. Place A. P. M.; Rodgers L. V. H.; Mundada P.; Smitham B. M.; Fitzpatrick M.; Leng Z.; Premkumar A.; Bryon J.; Vrajitoarea A.; Sussman S.; Cheng G.; Madhavan T.; Babla H. K.; Le X. H.; Gang Y.; Jäck B.; Gyenis A.; Yao N.; Cava R. J.; Leon N. P. de.; Houck A. A. New Material Platform for Superconducting Transmon Qubits with Coherence Times Exceeding 0.3 ms. Nat. Commun. 2021, 12, 1779 10.1038/s41467-021-22030-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Wang C.; Li X.; Xu H.; Li Z.; Wang J.; Yang Z.; Mi Z.; Liang X.; Su T.; Yang C.; Wang G.; Wang W.; Li Y.; Chen M.; Li C.; Linghu K.; Han J.; Zhang Y.; Feng Y.; Song Y.; Ma T.; Zhang J.; Wang R.; Zhao P.; Liu W.; Xue G.; Jin Y.; Yu H. Towards Practical Quantum Computers: Transmon Qubit with a Lifetime Approaching 0.5 ms. npj Quantum Inf. 2022, 8, 3 10.1038/s41534-021-00510-2. [DOI] [Google Scholar]
  26. McLellan R. A.; Dutta A.; Zhou C.; Jia Y.; Weiland C.; Gui X.; Place A. P. M.; Crowley K. D.; Le X. H.; Madhavan T.; Gang Y.; Baker L.; Head A. R.; Waluyo I.; Li R.; Kisslinger K.; Hunt A.; Jarrige I.; Lyon S. A.; Barbour A. M.; Cava R. J.; Houck A. A.; Hulbert S. L.; Liu M.; Walter A. L.; Leon N. P. de. Chemical Profiles of the Oxides on Tantalum in State of the Art Superconducting Circuits. Adv. Sci. 2023, 10, e2300921 10.1002/advs.202300921. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Mun J.; Sushko P. V.; Brass E.; Zhou C.; Kisslinger K.; Qu X.; Liu M.; Zhu Y. Probing Oxidation-Driven Amorphized Surfaces in a Ta(110) Film for Superconducting Qubit. ACS Nano 2024, 18 (1), 1126–1136. 10.1021/acsnano.3c10740. [DOI] [PubMed] [Google Scholar]
  28. Romanenko A.; Pilipenko R.; Zorzetti S.; Frolov D.; Awida M.; Belomestnykh S.; Posen S.; Grassellino A. Three-Dimensional Superconducting Resonators at T < 20 MK with Photon Lifetimes up to Τ = 2 s. Phys. Rev. Appl. 2020, 13, 034032 10.1103/PhysRevApplied.13.034032. [DOI] [Google Scholar]
  29. Romanenko A.; Schuster D. I. Understanding Quality Factor Degradation in Superconducting Niobium Cavities at Low Microwave Field Amplitudes. Phys. Rev. Lett. 2017, 119, 264801 10.1103/PhysRevLett.119.264801. [DOI] [PubMed] [Google Scholar]
  30. Bach D.; Schneider R.; Gerthsen D.; Verbeeck J.; Sigle W. EELS of Niobium and Stoichiometric Niobium-Oxide Phases—Part I: Plasmon and Near-Edges Fine Structure. Microsc. Microanal. 2009, 15 (6), 505–523. 10.1017/S143192760999105X. [DOI] [PubMed] [Google Scholar]
  31. Oh J.-S.; Fang X.; Kim T.-H.; Lynn M.; Kramer M.; Zarea M.; Sauls J. A.; Romanenko A.; Posen S.; Grassellino A.; Kopas C. J.; Field M.; Marshall J.; Cansizoglu H.; Yadavalli K.; Mutus J. Y.; Reagor M.; Zhou L. In-Situ Transmission Electron Microscopy Investigation on Surface Oxides Thermal Stability of Niobium. Appl. Surf. Sci. 2023, 627, 157297 10.1016/j.apsusc.2023.157297. [DOI] [Google Scholar]
  32. Park G.-S.; Kim Y. B.; Park S. Y.; Li X. S.; Heo S.; Lee M.-J.; Chang M.; Kwon J. H.; Kim M.; Chung U.-I.; Dittmann R.; Waser R.; Kim K. In Situ Observation of Filamentary Conducting Channels in an Asymmetric Ta2O5–x/TaO2–x Bilayer Structure. Nat. Commun. 2013, 4, 2382 10.1038/ncomms3382. [DOI] [PubMed] [Google Scholar]
  33. Schaltin S.; D’Urzo L.; Zhao Q.; Vantomme A.; Plank H.; Kothleitner G.; Gspan C.; Binnemans K.; Fransaer J. Direct Electroplating of Copper on Tantalum from Ionic Liquids in High Vacuum: Origin of the Tantalum Oxide Layer. Phys. Chem. Chem. Phys. 2012, 14, 13624–13629. 10.1039/c2cp41786c. [DOI] [PubMed] [Google Scholar]
  34. Lee J.; Sung Z.; Murthy A. A.; Reagor M.; Grassellino A.; Romanenko A.. Discovery of Nb Hydride Precipitates in Superconducting Qubits. 2021, arXiv 2108.10385 10.48550/arXiv.2108.10385. [DOI]
  35. Torres-Castanedo C. G.; Goronzy D. P.; Pham T.; McFadden A.; Materise N.; Das P. M.; Cheng M.; Lebedev D.; Ribet S. M.; Walker M. J.; Garcia-Wetten D. A.; Kopas C. J.; Marshall J.; Lachman E.; Zhelev N.; Sauls J. A.; Mutus J. Y.; McRae C. R. H.; Dravid V. P.; Bedzyk M. J.; Hersam M. C.. Formation and Microwave Losses of Hydrides in Superconducting Niobium Thin Films Resulting from Fluoride Chemical Processing Adv. Funct. Mater. 20242401365 10.1002/adfm.202401365. [DOI]
  36. Murthy A. A.; Lee J.; Kopas C.; Reagor M. J.; Mcfadden A. P.; Pappas D. P.; Checchin M.; Grassellino A.; Romanenko A. TOF-SIMS Analysis of Decoherence Sources in Superconducting Qubits. Appl. Phys. Lett. 2022, 120, 044002 10.1063/5.0079321. [DOI] [Google Scholar]
  37. Murthy A. A.; Das P. M.; Ribet S. M.; Kopas C.; Lee J.; Reagor M. J.; Zhou L.; Kramer M. J.; Hersam M. C.; Checchin M.; Grassellino A.; Reis R. dos.; Dravid V. P.; Romanenko A. Developing a Chemical and Structural Understanding of the Surface Oxide in a Niobium Superconducting Qubit. ACS Nano 2022, 16, 17257–17262. 10.1021/acsnano.2c07913. [DOI] [PubMed] [Google Scholar]
  38. Altoé M. V. P.; Banerjee A.; Berk C.; Hajr A.; Schwartzberg A.; Song C.; Alghadeer M.; Aloni S.; Elowson M. J.; Kreikebaum J. M.; Wong E. K.; Griffin S. M.; Rao S.; Weber-Bargioni A.; Minor A. M.; Santiago D. I.; Cabrini S.; Siddiqi I.; Ogletree D. F. Localization and Mitigation of Loss in Niobium Superconducting Circuits. PRX Quantum 2022, 3, 020312 10.1103/PRXQuantum.3.020312. [DOI] [Google Scholar]
  39. Wang Z.; Wang H.; Yu C. C.; Wu R. Q. Hydrogen as a Source of Flux Noise in SQUIDs. Phys. Rev. B 2018, 98 (2), 020403 10.1103/PhysRevB.98.020403. [DOI] [Google Scholar]
  40. Zarea M.; Ueki H.; Sauls J. A. Effects of Anisotropy and Disorder on the Superconducting Properties of Niobium. Front. Phys. 2023, 11, 1269872 10.3389/fphy.2023.1269872. [DOI] [Google Scholar]
  41. Meisner K. J.; Zaman R.; Zhou B.-C. Thermodynamic Modeling of the Ta-O System. Calphad 2022, 76, 102391 10.1016/j.calphad.2022.102391. [DOI] [Google Scholar]
  42. Pérez R. J.; Massih A. R. Thermodynamic Evaluation of the Nb–O–Zr System. J. Nucl. Mater. 2007, 360 (3), 242–254. 10.1016/j.jnucmat.2006.10.008. [DOI] [Google Scholar]
  43. Andersson J.-O.; Helander T.; Höglund L.; Shi P.; Sundman B. Thermo-Calc & DICTRA, Computational Tools for Materials Science. Calphad 2002, 26 (2), 273–312. 10.1016/S0364-5916(02)00037-8. [DOI] [Google Scholar]
  44. Thermo-Calc . Thermo-Calc Oxide Solutions Database Version 11.1.
  45. Proslier T.; Kharitonov M.; Pellin M.; Zasadzinski J.; Ciovati G. Evidence of Surface Paramagnetism in Niobium and Consequences for the Superconducting Cavity Surface Impedance. IEEE Trans. Appl. Supercond. 2011, 21, 2619–2622. 10.1109/TASC.2011.2107491. [DOI] [Google Scholar]
  46. Sheridan E.; Harrelson T. F.; Sivonxay E.; Persson K. A.; Altoé M. V. P.; Siddiqi I.; Ogletree D. F.; Santiago D. I.; Griffin S. M.. Microscopic Theory of Magnetic Disorder-Induced Decoherence in Superconducting Nb Films. 2021, arXiv 2111.11684, pp 1–10 10.48550/arXiv.2111.11684. [DOI]
  47. Frati F.; Hunault M. O. J. Y.; de Groot F. M. F. Oxygen K-Edge X-Ray Absorption Spectra. Chem. Rev. 2020, 120, 4056–4110. 10.1021/acs.chemrev.9b00439. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Harrelson T. F.; Sheridan E.; Kennedy E.; Vinson J.; N’Diaye A. T.; Altoé M. V. P.; Schwartzberg A.; Siddiqi I.; Ogletree D. F.; Scott M. C.; Griffin S. M. Elucidating the Local Atomic and Electronic Structure of Amorphous Oxidized Superconducting Niobium Films. Appl. Phys. Lett. 2021, 119, 244004 10.1063/5.0069549. [DOI] [Google Scholar]
  49. Coulson C. A. Transition-Metal Chemistry. Nature 1961, 191 (4795), 1233–1234. 10.1038/1911233a0. [DOI] [Google Scholar]
  50. Bach D.EELS Investigations of Stoichiometric Niobium Oxides and Niobium-Based Capacitors, PhD thesis; 2009, p 210.
  51. Müller C.; Cole J. H.; Lisenfeld J. Towards Understanding Two-Level-Systems in Amorphous Solids: Insights from Quantum Circuits. Rep. Prog. Phys. 2019, 82, 124501 10.1088/1361-6633/ab3a7e. [DOI] [PubMed] [Google Scholar]
  52. Kolobov A. V.; Fons P.; Frenkel A. I.; Ankudinov A. L.; Tominaga J.; Uruga T. Understanding the Phase-Change Mechanism of Rewritable Optical Media. Nat. Mater. 2004, 3 (10), 703–708. 10.1038/nmat1215. [DOI] [PubMed] [Google Scholar]
  53. Jain A.; Ong S. P.; Hautier G.; Chen W.; Richards W. D.; Dacek S.; Cholia S.; Gunter D.; Skinner D.; Ceder G.; Persson K. A. Commentary: The Materials Project: A Materials Genome Approach to Accelerating Materials Innovation. APL Mater. 2013, 1 (1), 011002 10.1063/1.4812323. [DOI] [Google Scholar]
  54. Project T. M.Materials Data on Nb2O5 by Materials Project. 2020. 10.17188/1304538. [DOI]
  55. Project T. M.Materials Data on Ta2O5 by Materials Project. 2020. 10.17188/1307209. [DOI]
  56. Hillert M.; Jansson B.; Sundman B.; ågren J. A Two-Sublattice Model for Molten Solutions with Different Tendency for Ionization. Metall. Trans. A 1985, 16 (2), 261–266. 10.1007/BF02816052. [DOI] [Google Scholar]
  57. Dupin N.; Ansara I. Unpublished Communication with N. Dupin; 2005.
  58. Massih A. R.; Pérez R. J.. Thermodynamic Evaluation of the Nb-O System; Technical Report. 2006, PM 05–002 v2; Quantum Technologies AB: Uppsala, Sweden.

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

nn4c05251_si_001.pdf (138.8KB, pdf)

Articles from ACS Nano are provided here courtesy of American Chemical Society

RESOURCES