MPPT algorithm based on metaheuristic techniques (PSO & GA) dedicated to improve wind energy water pumping system performance

Abstract

This paper presents a comparative study between four techniques recently used to improve the wind energy conversion system (WECS) to water pumping systems. The WECS is a renewable energy source which has developed rapidly in recent years. The use of the WECS in the water pumping field is a free solution (economically) compared to the use of the electricity grid supply. The control of WECS, equipped with a permanent magnet synchronous generator, has the objective of carefully maximising power generation. A comparative study between the proposed Fuzzy Logic Control, optimised using a genetic algorithm and particle swarm optimisation algorithm, and the conventional Perturb and Observe MPPT method using Matlab/Simulink, is presented. The performance of the proposed system has been verified against the generated output voltage, current and power waveforms, intermediate circuit voltage waveform, and generator speed. The presented results demonstrate the effectiveness of the control strategy applied in this work.

Introduction

Wind energy, the most recently developed green energy source, is being transformed from a small to a major power source in the field of energy systems, due to power electronics. Solar, wind, and hydraulics are the most popular sources¹.

Wind energy is a renewable energy that requires no fuel, creates no greenhouse gases, and produces no toxic or radioactive waste. Wind energy produces electricity without degrading the quality of the air, without polluting the waters, and without polluting the soil. Wind power guarantees security of supply, in the face of fluctuating oil prices, with the possibility of reducing electricity bills. It also plays an important role in preserving biodiversity by combating climate change. The technology continues to improve, with wind turbines now being more powerful, and their efficiency has increased tenfold in the last ten years. Thus, a 12 MW wind farm, made up of four to six wind turbines, can cover the electricity consumption needs of nearly 12,000 people and avoids the emission of 8000 tons of CO₂^1,2.

As a photovoltaic system (PVS) occupies a large area for limited maximum power, wind energy also has the peculiarity of having a higher yield in winter (wind is generally stronger in the cold season). This is an important advantage because of the high costs usually ocurring during the winter period^3,4. Agricultural watering requirements are often at their highest during sunny hours when a wind energy system can pump more water^5,6.

The development of a dependable and efficient wind energy conversion system (WECS) to address the problem of water scarcity in desert locations is a very interesting project. However, WECS have nonlinear characteristics and only have one maximum power point (MPP). The operating point, as well as the MPP, will fluctuate as the meteorological conditions change. As a result, an online control approach, called maximum power point tracking (MPPT), must be utilised to track the WECS' maximum output power under various operating situations.

MPPT commands can be classified according to the type of implementation, the input parameters and the type of search they perform. However, it is more interesting to classify them according to criteria such as precision, speed and convergence towards the maximum power point. The MPPT control must have a significant level of simplicity favouring low consumption and a reasonable cost. In addition, regarding its performance, the MPPT command must have a good dynamic and static behavior to ensure rapid and precise adaptation to climate change. Several methods exist in the literature, classic method such as P&O, incremental conductance and intelligent methods such as: fuzzy logic, PSO and GA.

Because of their compact size, self-excitation, high reliability, cheap maintenance, lack of a gearbox system, and low noise, permanent magnet synchronous generators (PMSGs) were employed in this study^6,7.

The WECS was optimised using a perturb and observe (P&O) approach. The difference in output power between the current and prior states is used to define the system control in this approach. Furthermore, the P&O algorithm's mechanism has a set step size, which restricts its efficacy. As a result, a number of academics have developed a variety of variable step MPPT algorithms to address this issue^8,9. The objective of the control strategies, based on the conventional proportional-integral controllers (PICs), is to ensure the robustness and the stability of the WECS.

The best conventional proportional-integral controllers depend on the parameter calculations of nonlinear systems (electrical systems)^10,11. However, the difficulty is characterised by its high sensitivity to the variable parameters.

In order to manage the features of nonlinear dynamic systems, this study explores the performance of fuzzy logic control (FLC), which takes a different approach than proportional-integral PI methods.

Generally speaking, the FLC depends on the designer's fine-tuning membership functions (MF), while many of the classical FLCs are based on a fixed membership function (MF) and a static rule base. However, they are not sufficient to solve nonlinear systems with a high degree of uncertainty^12,13.

So, adaptive filtering techniques have been used, based on the Continuous Mixed-Normal (CMPN) algorithm. This allows the FLC scale factors to be updated online and improves the performance of a wind generator under variable speed connected to a water pump^8,14.

The benefits of a permanent magnet synchronous machine (PMSM) attached to a water pump device have piqued the attention of researchers and industry for use in a variety of applications. It generates the air gap magnetic field of permanent magnets rather than electromagnets⁴. Quick dynamics, efficient operation, and strong compatibility with various applications are all advantages of PMSM with high-level energy permanent magnet materials, but only if they are properly managed. The controller is used to solve the PMSM's nonlinearity problem and to obtain quicker response times⁵. The advancement of power electronics and electric technologies has enhanced the use of PMSM for a wide range of applications in many control systems.

Motivated by the above discussion, the work presented in this paper concerns a comparative study of MPPT algorithms based on P&O, FL controller and their optimisations, using GA and PSO methods for WECS connected to a moto-pump. These methods are compared through Matlab/Simulink software to show the performances of each MPPT technique under different weather conditions, for transient, dynamic and steady state responses.

Overview of the wind energy water pumping system

A wind pump is a complex system that consists of different interacting elements, one of which acts on the other in different ways and within limits imposed by the control strategies employed. The modelling of the different elements of the system, such as the wind turbine, the inverter, the motor, the pump and the hydraulic circuit, involves knowledge of several disciplines: meteorology, electronics and electrical engineering, and hydraulics, and requires a good understanding of the interactions between them.

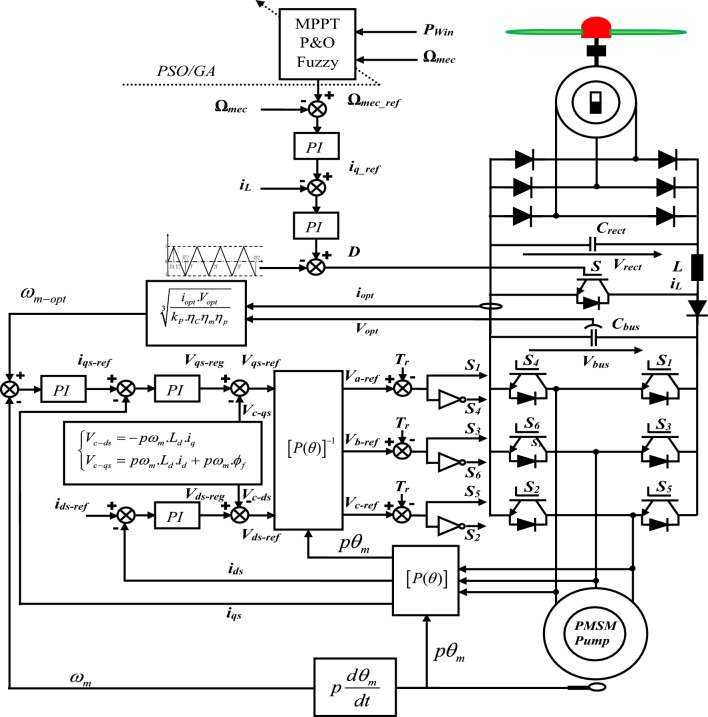
The studied wind energy conversion system consists of two parts. The power side system is a wind turbine with a three phase permanent magnet synchronous moto-pump, through a rectifier, a boost converter and a three level AC inverter. The system is controlled via the MPPT strategy based on the fuzzy logic controller and optimised by the GA and PSO. The overall structure of the system is shown in Fig. 1@@¹⁵.

Figure 1.

Overall diagram of the Wind Energy Water Pumping System.

Turbine modelling

The power value is a function of the air mass and the velocity V_w^14,16.

$$P_w=\frac{1}{2}\rho .\pi .R^2.C_p.(\lambda ,\beta ).V_w^3$$ 1

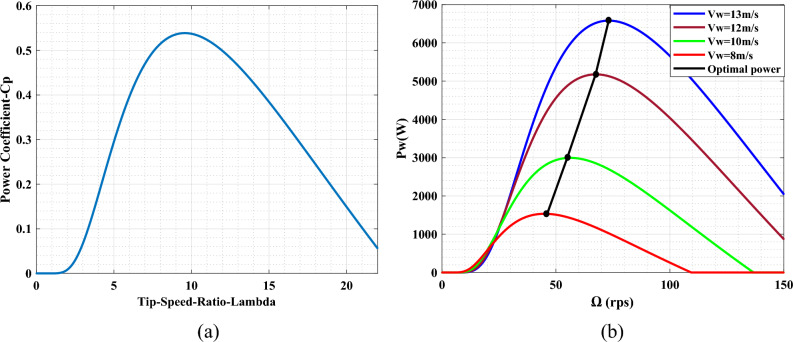
where R is the blade length, K is the gain multiplier, and C_p is the value which depends on the speed point ratio (λ) and the blade step angle (β), depending on the turbine characteristics (Fig. 2a).

$$C_p=0,5.((\frac{98}{{\lambda }^{\prime }})-0,4\beta -5)exp(\frac{-16,5}{{\lambda }^{\prime }})$$ 2

and

$${\lambda }^{\prime }=1/(\frac{1}{\lambda +0,08\beta }-\frac{0,035}{{\lambda }^3+1})$$

Figure 2.

(a) Power and (b) power coefficient characteristics at different wind level.

Figure 2 shows P_w = f(Ω) under different wind speeds. Each curve shows an optimum power point, which corresponds to a certain rotation speed.

PMSM modelling

The permanent magnet synchronous machine (PMSM) has become attractive and competes with the asynchronous machines in the field of electric drive systems because of its advantage in the elimination of slip losses. For this type of machine, the inductor is replaced by permanent magnets, creating the excitation field. This also has the advantage of eliminating brushes and rotor losses, resulting in high efficiency, and requiring no maintenance throughout its life¹⁷.

The differential model of the PMSM is given by¹⁸:

$$\left\{\begin{array}{c}\frac{d{i}_d}{\mathit{dt}}=-\frac{R_S}{L_d}{i}_d+p\omega \frac{L_q}{L_d}{i}_q-\frac{V_d}{L_d}\hfill \\ \frac{d{i}_q}{\mathit{dt}}=-p\omega \frac{L_d}{L_q}{i}_d-\frac{R_S}{L_q}{i}_d-\frac{V_q-p\omega ·{\phi }_e}{L_q}\hfill \end{array}\right)$$ 3

The electromagnetic torque will be expressed by:

$$T_e=p·\left((L_d-L_q)·i_{\mathit{sd}}+{\phi }_f\right)·i_{\mathit{qs}}$$ 4

The mechanical equation is written:

$$\frac{d{\omega }_m}{\mathit{dt}}=\frac{p}{J}·\left((L_d-L_q)i_{\mathit{ds}}+{\varphi }_f\right)·i_{\mathit{qs}}-\frac{f}{J}·{\omega }_m-\frac{p}{J}·T_L$$ 5

PMSM control

The main advantage of MCC is that it is easily controlled, as the flow and torque are decoupled and are controlled independently. For an MSAP, decoupling no longer exists, which makes the machine difficult to control. This difficulty lies in the fact that there is a coupling between the input variables (voltage, frequency) and the output variables (torque, speed). To achieve a control similar to MCC, we apply the vector control^19,20.

To control the torque (Eq. (2)), it is necessary to control the direct and quadrature components of the current. For a synchronous machine with smooth poles (L_d = L_q), the torque will be:

$$T_e=p{\phi }_f{i}_{\mathit{qs}}$$ 6

As the flux of the magnets is constant, the electromagnetic torque obtained becomes proportional to the current I_q.

$$\left\{\begin{array}{c}{V}_d=R_s·i_{\mathit{ds}}+L_d\frac{d{i}_{\mathit{ds}}}{\mathit{dt}}-p{\omega }_m·L_d·i_{\mathit{qs}}\\ V_q=R_s·i_{\mathit{qs}}+L_q\frac{d{i}_{\mathit{qs}}}{\mathit{dt}}+p{\omega }_m·L_q·i_{\mathit{ds}}+p{\omega }_m·{\varphi }_f\\ \end{array}\right)$$ 7

Adjustment of the internal loop of the current I_dqs

The expression of the reference current i_{qs_ref} is given by:

$$i_{qs-ref}=\frac{T_{e-ref}}{{\varphi }_f}$$ 8

The current regulation loop i_dqs can be represented by the block diagram in Fig. 3.

Figure 3.

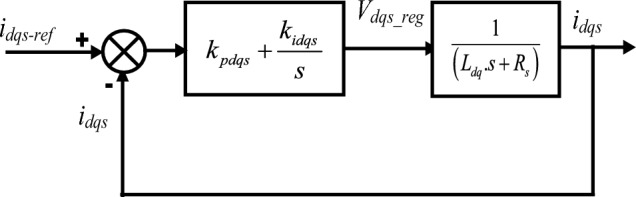
Current regulation block diagram i_dqs.

The closed loop transfer function is as follows:

$$\frac{i_{\_dqs}}{i_{\_dqs-reg}}=\frac{(k_{\_pdqs}·s+k_{\_idqs})\frac{1}{L_{\mathit{dq}}}}{\left(s^2+\frac{1}{L_{\mathit{dq}}}(R_s+k_{\_pdqs})·s+\frac{k_{\_idqs}}{L_{\mathit{dq}}}\right)}$$ 9

The characteristics polynomial is:

$$P(s)=s^2+\frac{1}{L_{\mathit{dq}}}(R_s+k_{\mathit{pdqs}})·s+\frac{k_{\mathit{idqs}}}{L_{\mathit{dq}}}$$ 10

Through a simple comparison of Eq. (9) and (10), the gains k_pdqs and k_idqs are expressed by: $k_{\mathit{pdqs}}=2L_{\mathit{dq}}\rho -R_s$ and $k_{\mathit{idqs}}=2L_{\mathit{dq}}{\rho }^2$.

Adjustment of the external speed loop

The speed regulator is used to determine the reference torque in order to maintain the corresponding speed (Fig. 4). The mechanical equation gives:

$$\frac{{\omega }_m(s)}{T_e(s)}=\frac{p}{f+J·s}$$ 11

Figure 4.

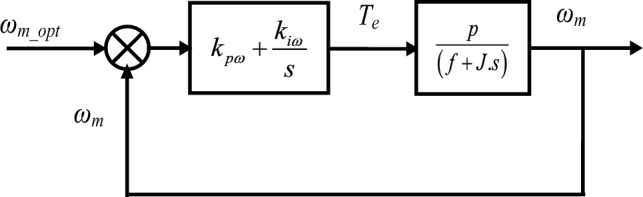
Speed control functional diagram.

By associating a PI regulator with this function, it will be:

The parameters of PMSG are given in Table 1.

Table 1.

PMSG parameters.

Rated power	Rated Voltage	Frequency	Number of poles	Inertia constant
5.5 Kw	200 V	50 Hz	12	7.856 kg m2
Stator Resistance	d-axis Reactance	q-axis Reactance	Field flux	Nominal speed
0.3676 Ω	0.00355 H	0.00355 H	0.2867 V. s	70 rps

The closed loop transfer function, calculated from the previous diagram, is given by:

The characteristics polynomial is:

$$P\left(s\right)=s^2+\frac{f+k_{p\omega }·p}{J}·s+\frac{k_{i\omega }·p}{J}=0$$ 13

Comparing Eq. (12) and (13), the gains k_pdqs and k_idqs are expressed by:$k_{\mathit{pdqs}}=2L_{\mathit{dq}}\rho -R_s\text{and}{k}_{\mathit{idqs}}=2L_{\mathit{dq}}{\rho }^2$

Static decoupling

The PMSM is supplied by the voltage inverter, according to Eq. (1), and the stator voltages are expressed by:

$$\left\{\begin{array}{c}{V}_{ds-ref}=V_{ds-reg}-V_{c-ds}\\ V_{qs-ref}=V_{qs-reg}-V_{c-qs}\\ \end{array}\right)$$ 14

Equation (14) shows that V_d and V_q depend on the stator currents on the axes (dq), which leads us to implement a decoupling. This coupling is eliminated by a compensation method. The latter consists of regulating the currents while neglecting the coupling terms, which will be added to the outputs of the current regulators in order to obtain reference voltages to supply the inverter. So:

$$\left\{\begin{array}{c}{V}_{c-ds}=-p{\omega }_m.L_d.i_q\\ V_{c-qs}=+p{\omega }_m.L_d.i_d+p{\omega }_m.{\varphi }_f\\ \end{array}\right)$$ 15

The reference speed is based on the optimum power of the wind generator. It is given by the following relation:

$${\omega }_{\mathit{opt}}=\sqrt[3]{\frac{I_{\mathit{opt}}.V_{\mathit{opt}}}{k_p.{\eta }_p.{\eta }_m.{\eta }_c.{\eta }_h}}$$ 16

Modelling of the DC/AC static converter

A DC/AC inverter is included between the wind turbine and the motor pump to convert the direct voltage from the wind turbine into three-phase alternating voltage with a variable frequency, in order to feed the PMSM.

The output voltages of the inverter are given by²¹:

$$\left[\begin{array}{c}{V}_{\mathit{fa}}\\ V_{\mathit{fb}}\\ V_{\mathit{fc}}\end{array}\right]=\frac{1}{3}{V}_{\mathit{bus}}\left[\begin{array}{ccc}2& -1& -1\\ -1& 2& -1\\ -1& -1& 2\end{array}\right]\left[\begin{array}{c}{f}_1\\ f_2\\ f_3\end{array}\right]$$ 17

f_1,3,5 are the switching functions of the inverter transistors.

Pump Modelling

The centrifugal pump is mainly characterised by a load torque proportional to the square of the motor speed, which is of the following form²²:

$$T_L=k{\omega }_m^2$$ 18

_where $k=\frac{P_L}{{\omega }_m^3}.$

MPPT control

The tracking method, known as maximum power point tracking (MPPT), is a command allowing the operation of a nonlinear electrical generator to permanently produce its maximum power^23,24.

Conventional tuning methods are based on adequate modelling of the system to be tuned and analytical processing using the transfer function or state equations. Unfortunately, these are not always available.

A wind energy water pumping system is difficult to control automatically. This difficulty comes from: their nonlinearity, the variation of their parameters, and the quality of the measurable variables. These difficulties led us to the development of new optimisation techniques.

The novelty presented in this article concerns the combination of classical optimisation methods (P&O) and metaheuristic optimisation techniques (PSO, GA). The MPPT approach relies on search algorithms (P&O, FL, FL-PSO, and FL-GA) to approximate the power limit curve without disrupting the system's normal operation.

P&O technique

The perturbation and observation (P&O) technique is widely used in industrial applications. As the algorithm is simple to implement, the objective process is to interrupt the system by increasing or decreasing the module's operating speed and observing its influence on the line's output power^5,9,25.

MPPT using FLC technique

Fuzzy logic is a very powerful problem solving technique with wide applicability in control and decision making. Fuzzy logic is very useful when the mathematical model of a problem does not exist or exists but is difficult to implement or is too complex to be evaluated quickly enough for real-time operations. Fuzzy logic is also assumed for situations where there are large uncertainties and unknown variations in system parameters and structures, such as wind power^13,26.

However, there is no general procedure for designing a fuzzy controller, since many trial errors can be encountered during its realisation and these controllers may not be suitable for other applications. The difficulties encountered in their design have guided researchers to move towards the optimisation of these controllers. This is why bio-inspired intelligence methods have been successfully applied to controller tuning in recent years²⁷.

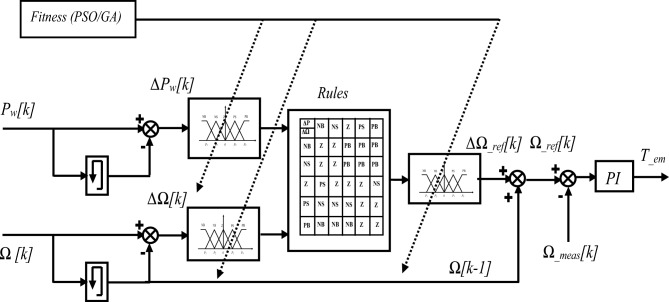
The fuzzy MPPT controller receives the error and error variation of the rotational speed and the power of the turbine generator as inputs. It is based on the measurement of the wind power (ΔP_w) variation and the wind turbine speed (ΔΩ), to determine the variation (ΔΩ_{_ref}) of the rotational speed setpoint (Ω_{_ref}), according to Eq. (19).

$$\left\{\begin{array}{c}\mathrm{\Delta }{P}_w=P_w(k)-P_w(k-1)\\ \mathrm{\Delta }\mathrm{\Omega }=\mathrm{\Omega }(k)-\mathrm{\Omega }(k-1)\\ \mathrm{\Omega }{(k)}_{\mathit{ref}}=\mathrm{\Omega }(k-1)+\mathrm{\Delta }\mathrm{\Omega }{(k)}_{\mathit{ref}}\end{array}\right)$$ 19

The wind turbine speed is controlled, in order to follow the reference speed (Ω_{_ref}), which is obtained at the output of the FLC. In addition, the output of the speed controller determines the reference of the electromagnetic torque of the studied machine (Fig. 5).

Figure 5.

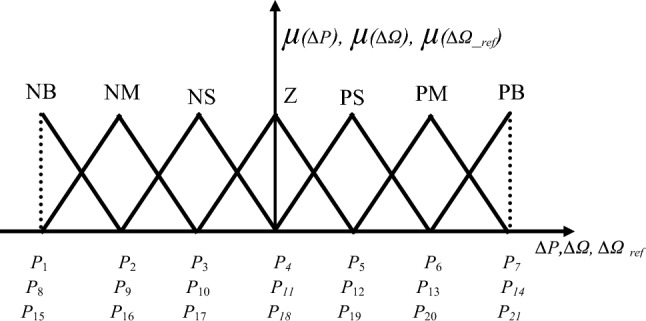
Membership functions of: ΔP_w, ΔΩ and ΔΩ__ref.

Figure 5 presents the triangular functions for the input variables of the FLC. For a high precision, the chosen FLC has seven linguistic variables, which can be defined as: Negative Big (NB), Negative Small (NS), Zero (Z), Positive Small (PS), and Positive Big (PB).

The quality of the input and output FMs can be expressed as follows^28,29:

− 1 < P₁, P₈, P₁₅ < − 0.5; − 0.5 < P₂, P₉, P₁₆ < − 0.3333; − 0.3333 < P₃, P₁₀, P₁₇ < − 0.1667; − 0.1667 < P₄, P₁₁, P₁₈ < 0; 0.166 < P₅, P₁₂, P₁₉ < 0.3333; 0.3333 < P₆, P₁₃, P₂₀ < 0.5; 0.5 < P₇, P₁₄, P₂₁ < 1.

The inference methods provide a resulting membership function µ(Ω_ref) for the output variable Ω_ref. It is, therefore, a question of fuzzy information and it must be transformed into determined information. The most widely used defuzzification method is that of determining the centre of gravity of the resulting membership function µ(Ω_ref).

The centre of gravity's abscissa is determined by³⁰:

$$\mathrm{\Delta }{\mathrm{\Omega }}_{\_ref}=\frac{\sum _{i=1}^M\mu (\mathrm{\Delta }{\mathrm{\Omega }}_i).\mathrm{\Delta }{\mathrm{\Omega }}_i}{\sum _{i=1}^M\mu (\mathrm{\Delta }{\mathrm{\Omega }}_i)}$$ 20

Metaheuristic optimisation techniques

The main inconveniences of the conventional optimisation technique P&O and fuzzy logic controllers are the gains estimation and robustness, especially for a nonlinear system such as a wind turbine or a permanent magnet synchronous generator (PMSG). Also, it becomes more difficult due to parameter uncertainties in the permanent magnet synchronous motor (PMSM).

Solving an optimisation problem involves finding the best solutions by maximising the objective function(s) of the problem, while satisfying a set of user-defined constraints. The best algorithms used to solve these optimisation problems are population metaheuristics. In order to provide a high performance and a high convergence speed in the system, two intelligent metaheuristic approaches (PSO and GA) are combined with the FLC.

The PSO algorithm

As the PSO algorithm is a metaheuristic optimisation approach, a number of particles can be dispersed in each search, which has very large spaces of candidate solutions. As each particle has a random speed, the algorithm depends on both the position and the speed of each particle.

Mathematically, the PSO algorithm uses a swarm made up of (n_p ∈ ℕ) particles, i.e. (X_i)_i=1,2,….np, to search for the suboptimal X^*solution that minimises the objective function, called J. The velocity position of the particle vectors i^th are given by X_i = (X_i,1, X_i,2…….X_i,q) and V_i = (V_i,1, V_i,2…….V_i,q). They are determined by the following iterative expressions^31–34:

$$\left\{\begin{array}{c}{V}_i^{l+1}=c_0.V_i^l+c_1.r_{1i}^l(X_i^{best,l}-X_i^l)+c_2{r}_{2,i}^l(X_{\mathit{swarm}}^{best,l}-X_i^l)\\ X_i^{l+1}=X_i^l+V_{i,j}^{l+1}\end{array}\right)$$ 21

where l = 1,2,…..l_max is the number of iterations previously provided by the user^{8, 9}. c₀, c₁ and c₂ are the inertia factor, the cognitive (individual) and social (group) learning relationships, respectively. $r_{1,i}^l$ and $r_{2,i}^l$ are random numbers which are evenly distributed over the interval [0,1], $X_i^{best,l}$ and $X_{\mathit{swarm}}^{best,l}$ are the best respective positions previously obtained by the particle and the best position obtained in the whole swarm at the current iteration l; they are given by:

$$\left\{\begin{array}{c}{X}_i^{best.l}=min\left\{J(X_i^j),0\le j\le l\right\}\\ X_{\mathit{swarm}}^{best,l}=min\left\{J(X_i^l),\forall i\right\}\end{array}\right)$$ 22

Strategy of the genetic algorithm (GA)

The GA consists of the following steps^35,36:

• Step 1 Randomly generate N chromosomes in the initial population in the search space with the chromosome = [X₁, X₂, …,X_n], where $X_{min}\le X_{1,2,\dots ,n}\le X_{max}$.

• Step 2 Calculate the objective function for each chromosome.

• Step 3 Apply the following operators:

  (a) Perform reproduction, i.e. pick the best probability chromosomes based on their objective function values.

  (b) Cross over the chromosomes selected in the above step using the crossing probabilities.

  (c) Perform a mutation on the chromosomes generated in the above step by probability of mutation.

• Step 4 The process can be stopped if the stopping condition is reached or even the optimum solution is obtained. Alternatively, repeat steps 2 to 4 until the stop condition is met.

• Step 5 The optimal solution $X_{}^{\ast }$, corresponding to the best objective function $X_{}^{\ast }={min}_{X_i^j}(J(X_i^j),\forall i,j)$ is thus obtained.

Fuzzy logic optimisation strategy using GA and PSO

According to the resolution of the optimisation problem, 21 fuzzy parameters can be determined. In addition, the objective function presents the sum of the Mean Square Error (MSE) values. Under a wind turbine value equal to 12.3 m/s, the error (which is the difference at each sampling time k) can be found between the optimum power supplied. Therefore the formula is obtained as follows:

$$J_k(k)=P_{\mathit{opt}}(k)-P_{\mathit{sim}}(k)$$ 23

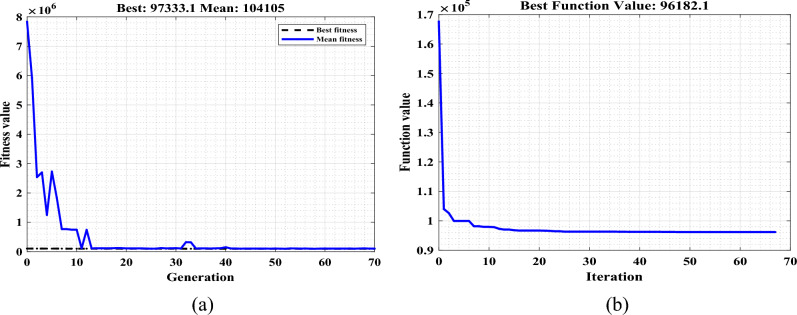
The objective function value (fitness function), during the search for the optimal solution, is presented in Fig. 6. The iteration number equals 70 when no reduction in total control error was detected.

Figure 6.

Objective function of (a): GA and (b): PSO.

The developed FL-GA controller is chosen for the final solution, trapped in a local optimal, which is considered to be a heuristic algorithm, where the best solution (Fig. 6a) is only recorded after several runs using several initialisations and settings of the GA parameters. Also, the choice of the GA to optimise the fuzzy logic control among those existing in the literature^9,24–27 is not unique. Therefore, the user is free to choose any other heuristic or metaheuristic optimisation algorithm, such as PSO; the best solution (Fig. 6b) is only recorded after several runs, using several initialisations and settings of the PSO. On the other hand, the optimisation of the parameters of fuzzy control must be performed using the same optimisation tool. This will ensure a fair comparison, in terms of control accuracy.

The tuning process of PSO/GA of the fuzzy MPPT controller, applied to the wind system, is shown in Fig. 7.

Figure 7.

Schema of tuning process by PSO/GA of Fuzzy MPPT controller applied to the wind system.

The fuzzy controller receives the error and the error variation of the wind generator power and the wind turbine speed as inputs. The turbine speed Ω is controlled so that it follows the reference speed (Ω_r_ef) obtained at the output of the fuzzy controller (FLC). In addition, the output of the speed controller determines the reference of the electromagnetic torque.

The developed controllers (LF-PSO and FL-GA) are defined to find the optimal values of the two controllers (fuzzy and PI). P₁, P₂, P₃, K₁, K₂, and K₃ are the normalisation factors of the FLC and k_p2, k_i2 k_p1, and k_i1 are the PI regulator gains, in order to minimise the given fitness function via Eq. (23).

Normalisation factors and error gains ensure the convergence response, stability and accuracy of the system. These factors affect the static error, damping and chatter, depending on the values of the gains before and after their optimisation.

Before optimisation, the membership function parameters of the inputs (∆P, ∆Ω) and the output values (∆Ω_ref) are obtained by manually varying the normalisation factors of the FLC and the gains of the PI regulator. Then, the optimisation by the developed controllers (LF-PSO, FL-GA), automatically sets the optimal values of the two controllers (FL and PI).

The membership function (MF) parameters, before and after the tuning process (PSO and GA), are presented in Tables 2, 3 and 4.

Table 2.

Membership function parameters of input (∆P) before and after the PSO/GA.

MF	P1	P2	P3	P4	P5	P6	P7
Before PSO/GA	− 1.000	− 0.670	− 0.340	0.000	0.3400	0.670	1.000
After PSO	− 0.500	− 0.373	− 0.166	− 0.125	0.0100	0.248	0.468
After GA	− 0.518	− 0.361	− 0.315	− 0.166	0.0373	0.212	0.423

Table 3.

Membership function parameters of input (∆Ω) before and after the PSO/GA.

MF	P8	P9	P10	P11	P12	P13	P14
Before PSO/GA	− 1.000	0.670	− 0.340	0.0000	0.340	0.670	1.000
After PSO	− 0.704	− 0.493	− 0.166	0.0000	0.166	0.293	0.349
After GA	− 0.948	− 0.389	− 0.166	− 0.0001	0.154	0.300	0.450

Table 4.

Membership function parameters of output (∆Ω_ref) before and after the PSO/GA.

MF	P15	P16	P17	P18	P19	P20	P21
Before PSO/GA	− 1.000	− 0.670	− 0.340	0.0000	0.340	0.670	1.000
After PSO	− 0.978	− 0.334	− 0.329	− 0.0173	0.166	0.333	0.498
After GA	− 0.889	− 0.378	− 0.270	− 0.1160	0.135	0.333	0.486

Simulation, discussion and results

A comparison of the results in recently published work (references^9,23–27) was performed to show the validity of the proposed algorithm under fast changing conditions.

The simulation was carried out using Matlab/Simulink software. To test and compare the studied MPPT algorithms (P&O, FL and FL-PSO / GA), variable wind speeds were applied to the system and distributed over three intervals, as shown in Fig. 8. The algorithms were assessed in terms of speed, accuracy, and ripple.

• From 0.0 to 0.5 s, the wind speed is equal to 12 m/s.

• From 0.5 to 1.0 s, the wind speed is equal to 8 m/s.

• From 1.0 to 1.6 s, the wind speed is equal to 10 m/s.

Figure 8.

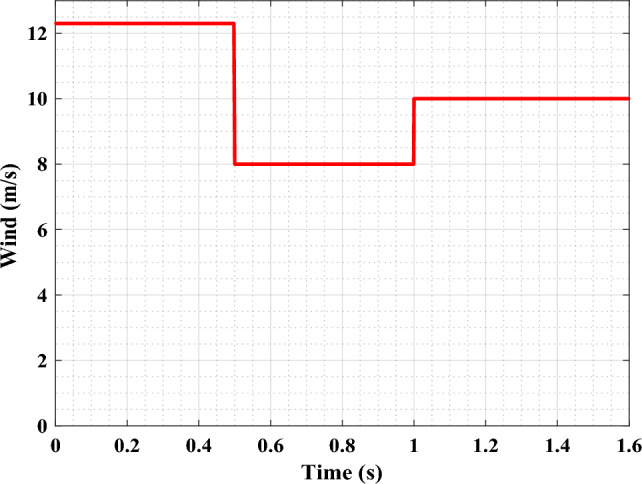
Variation in wind speed.

Figures 9, 10, and 11 depict the MPPT controllers' dynamic and transient responses to variations in the turbine's optimal mechanical power, optimal speed and optimal torque. The analysed algorithms produced almost identical output curves.

Figure 9.

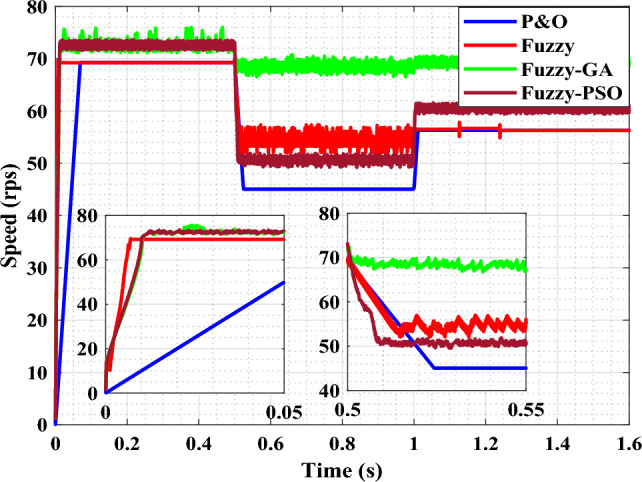
Optimal speed of the turbine.

Figure 10.

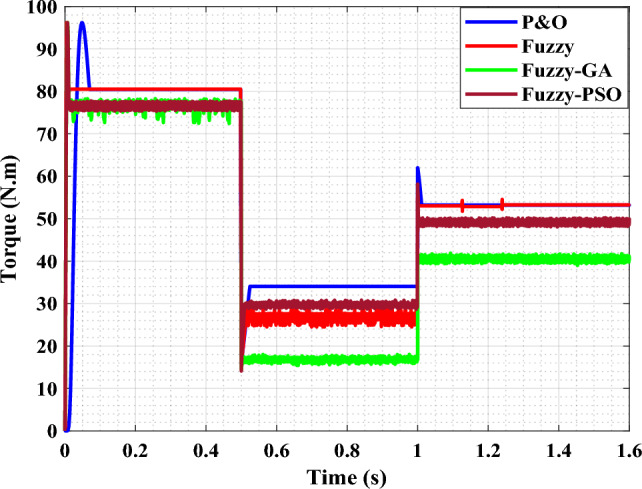
Optimal torque of the turbine.

Figure 11.

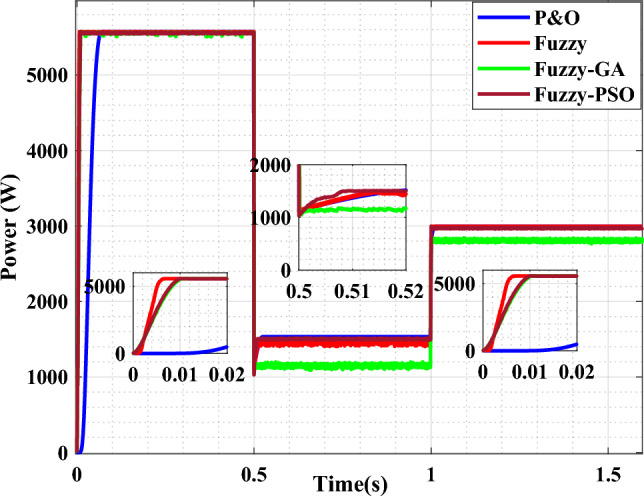
Optimal power of the turbine.

By focusing on the transient state, the P&O, FL and FL-GA controllers provide an overshoot before convergence to the target, while the fuzzy-PSO controller converges directly and rapidly compared to the others.

The results reveal that the controllers are efficient and that all of the algorithms are suitable for the system during rapid changes in wind speed levels. The FL-PSO algorithm outperforms the other algorithms, in terms of reaction time, with a response time of nearly nil. The effect of optimisation is felt at low wind speeds.

For wind speeds of 12 m/s, 8 m/s, and 10 m/s, the values obtained at equilibrium are close to the ideal values for turbine speed and power, i.e. 74 rpm, 52 rpm, and 60 rpm and 5.5 kW, 1.5 kW, and 3 kW, respectively. The MPPT controllers lead the turbine to reach its maximum power point regardless of wind speed variation.

The output magnitudes of the PMSM are close to the optimal values regardless of wind speed variation, which demonstrates the robustness of the principle of the oriented rotor flux control (Figs. 12, 13 and 14).

Figure 12.

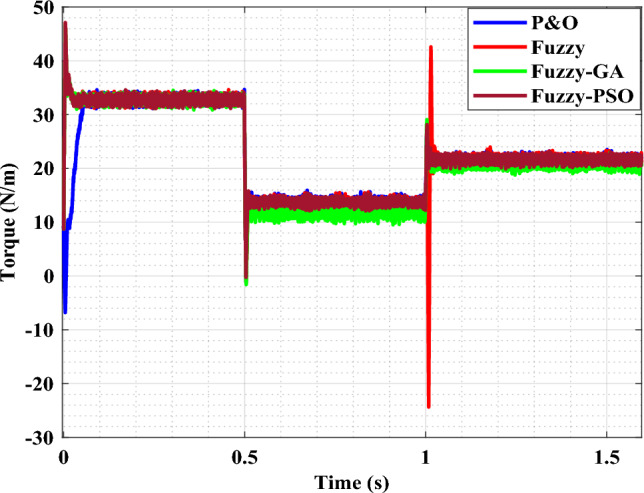
Optimal torque of the PMSM.

Figure 13.

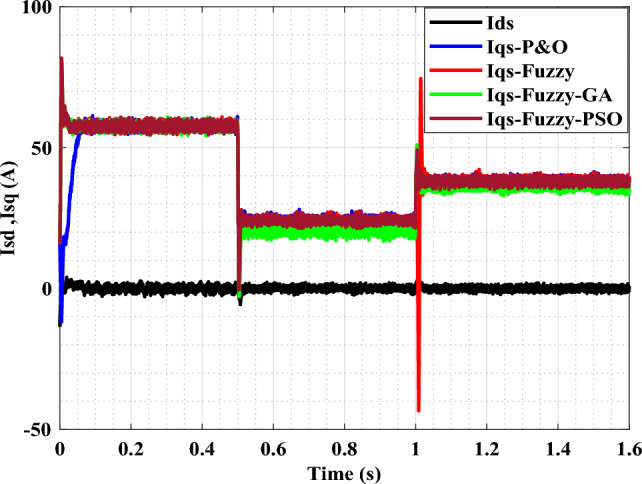
PMSM currents regulation.

Figure 14.

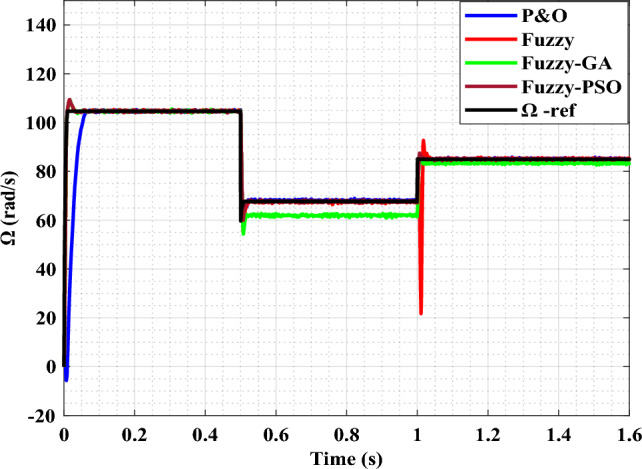
Regulation of th IM speed.

As illustrated in Fig. 12, the direct current component I_ds is adjusted to zero and the quadratic component I_qs is properly regulated in transient conditions. The perfect decoupling between rotor flux and torque is also clear, with the torque being the image of the quadratic current I_qs (vector control principle) (Fig. 13).

The speed tracking performance under wind constraints is very satisfactory (Fig. 14). The overall efficiency of the entire system (generator and motor pump) is approximately 50%. The efficiency of the motor pump for the different algorithms varies with the variation in wind speed. We notice that the efficiency of the Fuzzy-PSO algorithm is higher (53.6%) compared to the other algorithms (Fig. 15). The FL-PSO algorithm outperforms the other algorithms, in terms of reaction time (with a response time of nearly nil) and high efficiency.

Figure 15.

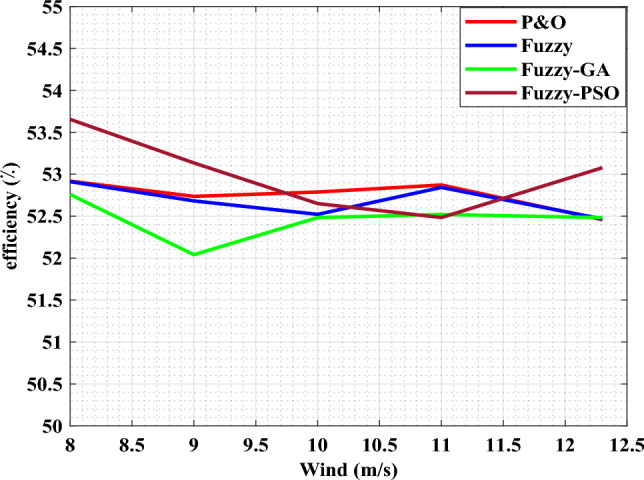
Efficiencies of the motor pump.

To assess the robustness of the proposed algorithm in seeking the global MPP, the wind energy system has been subjected to non-uniform wind speeds from the start. It can be observed that the P&O and the FL methods had low complexity but present the lowest efficiency when compared to that of the developed FLC-GA and FL-PSO, which provided the highest efficiency.

The new combination between classical optimisation methods (P&O) and metaheuristic optimisation techniques performs better control, in terms of convergence time, and does not require knowledge about the wind turbine system.

Conclusion

This research presents a comparative study of the stability and overall efficiency of four MPPT controllers, applied to a wind turbine water pumping system driven by PMSM coupled to a centrifugal pump.

The results obtained showed that, whatever the variation in wind speed, the control system ran in a stable manner and always transferred all of the energy produced by the wind energy generator to the motor-pump unit.

The fuzzy logic controller optimised by PSO or GA eliminates the drawbacks of the conventional algorithm “P&O” and the fuzzy-PSO gives a high tracking performance compared to other controllers. Furthermore, the gains of fuzzy-PSO are self-tuned and can allow stability and robustness against parameter variations of the PMSM.

A comparative experimental study will be carried out to justify the performance of the MPPT algorithms presented in the paper, in addition the application of these methods in other systems such as WECS connected to the electricity grid, as well as isolated or autonomous systems containing storage batteries.

List of symbols

P_w

Power turbine (W)

C_p

Power coefficient

V_w

Speed wind (m/s)

ρ

Air mass

R

Blades of length (m)

λ

The speed point ratio

β

The blade step angle

∆Ω_ref

Variation of the turbine reference speed (m/s)

∆P_ref

Variation of the turbine reference power (W)

V_dq

Direct & quadrature voltage (V)

i_dq

Direct & quadrature current (A)

ω_m

Mechanical speed (rad/s)

T_e

Electromagnetic torque (Nm)

T_L

Load torque (Nm)

L_dq

Direct & quadrature inductor (H)

Rs

Series resistance (Ohm)

V_bus

DC-link voltage (V)

Ф_e

PMSM flux in Web

P₁,….P₂₁

Membership function

J_k

Objective function

X^best

Best position obtained

kp2, ki2 kp1,ki1

The PI regulator gains

P₁, P₂, P₃, K₁, K₂, K₃

The normalisation factors

X*

The optimal solution

c0, c1 and c2

The inertia factor

f_1,2,3

The switching functions of the inverter

V_fa, V_fb, V_fc

The output voltages of the inverter

I_opt

Optimum current

V_opt

Optimum Voltage

Author contributions

Conception: A.B., L.Z., N.B., M.B., A.B., L.Z., A.R., A.A., M.E.-A., S.S.M.G. Data collection: A.B., L.Z., N.B., M.B., A.B., L.Z., A.R. Formal analysis: A.B., L.Z., N.B., S.S.M.G. Methodology: M.B., A.B., L.Z., A.R., A.A., M.E.-A. Software: A.B., L.Z., L.Z., A.R., A.A. Supervision: L.Z., A.R., A.A., M.E.-A., S.S.M.G. Investigation: A.B., L.Z., A.R., A.A. Project administration: L.Z., A.R., A.A., M.E.-A., S.S.M.G. Funding acquisition: A.A., M.E.-A., S.S.M.G. Writing original article: A.B., L.Z., N.B., M.B., A.B., L.Z., A.R. Review the article: L.Z., A.R., A.A., M.E.-A., S.S.M.G.

Data availability

The datasets used and/or analyzed during the current study are available from co-author Dr. Abdelaziz Rabehi (rab_ehi@hotmail.fr) on reasonable request.

Competing interests

The authors declare no competing interests.