This paper presents DFT2FEFFIT, an open-source Python-based program that regresses theoretical EXAFS spectra calculated from density functional theory structure models against experimental EXAFS spectra. DFT2FEFFIT could be of use for researchers involved in various fields of solid-state chemistry, physics and mineralogy.
Keywords: FEFF software, density functional theory, DFT, apatite, rare earth elements, cerium, EXAFS
Abstract
This article presents a Python-based program, DFT2FEFFIT, to regress theoretical extended X-ray absorption fine structure (EXAFS) spectra calculated from density functional theory structure models against experimental EXAFS spectra. To showcase its application, Ce-doped fluorapatite [Ca10(PO4)6F2] is revisited as a representative of a material difficult to analyze by conventional multi-shell least-squares fitting of EXAFS spectra. The software is open source and publicly available.
1. Introduction
Extended X-ray absorption fine structure (EXAFS) spectroscopy is an established method for characterization of the local structure of liquids, glasses and crystalline materials (Chantler et al., 2020 ▸). The chemical nature, number and distance of atoms located in successive spherical shells around the X-ray photoabsorber are obtained by fitting the experimental EXAFS signal to the theoretical χ(k) function (Stern et al., 1975 ▸; Rehr & Albers, 2000 ▸; Rehr et al., 2020 ▸):
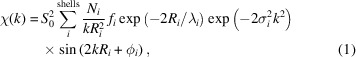 |
where k is the photoelectron wavenumber, k = 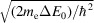 me is the mass of the electron, ΔE0 is the shift in the Fermi level between experiment and theory,
me is the mass of the electron, ΔE0 is the shift in the Fermi level between experiment and theory, 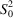 is a scale factor taking into account amplitude damping due to multielectron effects, the sum is over shells of atoms of a particular type i and at similar distance from the photoabsorber, Ni is the coordination number, Ri is the interatomic distance, fi is the photoelectron backscattered amplitude, λi is the mean free path of the photoelectron,
is a scale factor taking into account amplitude damping due to multielectron effects, the sum is over shells of atoms of a particular type i and at similar distance from the photoabsorber, Ni is the coordination number, Ri is the interatomic distance, fi is the photoelectron backscattered amplitude, λi is the mean free path of the photoelectron, 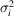 is the mean-square radial displacement of atoms in the ith shell (Debye–Waller term), and ϕi is the phase shift of the electronic wave. Although equation (1), strictly speaking, applies only to single scattering paths from neighboring shells of atoms, Rehr & Albers (1990 ▸) showed that this formula can be generalized to represent the contribution from N equivalent multiple scattering contributions of path length 2R.
is the mean-square radial displacement of atoms in the ith shell (Debye–Waller term), and ϕi is the phase shift of the electronic wave. Although equation (1), strictly speaking, applies only to single scattering paths from neighboring shells of atoms, Rehr & Albers (1990 ▸) showed that this formula can be generalized to represent the contribution from N equivalent multiple scattering contributions of path length 2R.
Characterizing the local structure requires solving the inverse problem of finding a plausible structure model that corresponds to the measured EXAFS signal (Timoshenko et al., 2019 ▸; Terry et al., 2021 ▸). As powerful a structural method as EXAFS is, the analysis of chemically complex and structurally defective materials is challenging (Boyanov et al., 1996 ▸). Because the information content of quality EXAFS data is typically bandwidth-limited to about kmax ≃ 14 Å−1, two overlapping subshells separated by less than ∼0.10–0.15 Å are unresolved in multi-elemental materials. Furthermore, EXAFS fails to distinguish neighboring atoms of similar scattering power and phase shifts (ΔZ < ∼10). Yet another difficulty arises when the interatomic distances in an atomic shell are unequal. In equation (1), the radial distribution function (RDF) of the atoms in shell i is assumed to be Gaussian,
Poorly crystalline and compositionally heterogeneous materials frequently have more complicated analytical atomic distributions than Gaussian. An asymmetric distribution of distances results in an apparent loss of coordination and usually reinforces correlations between the N and σ parameters in the fit (Marcus et al., 1986 ▸; Crozier, 1997 ▸). Still, the asymmetric shape of the distribution may be obtained by a cumulant EXAFS analysis of the disordered shell, but this model-independent method is limited to small degrees of disorder when the cumulant series rapidly converges within the EXAFS k range (Dalba & Fornasini, 1997 ▸).
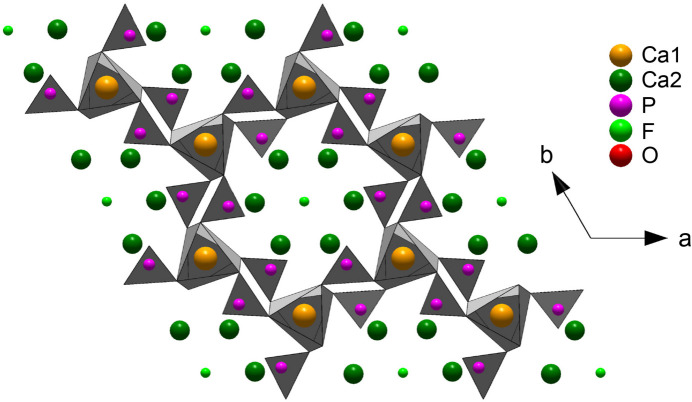
A prototypical case of a material difficult to analyze by EXAFS is fluorapatite [Ca10(PO4)6F2, FAp]. Its structure comprises two Ca sites: a larger nine-coordinated Ca1 site forming with the phosphate groups the walls of a honeycomb framework, and a smaller seven-coordinated Ca2 site along the sub-nanometre-sized tunnels containing the column F site (Hughes et al., 1989 ▸) (Fig. 1 ▸). The coordination of Ca1 is really 6 + 3 rather than 9, and that of Ca2 is 6 + 1, and the six Ca1—O and six Ca2—(O,F) distances are unequal, which is a source of uncertainty in the determination of the site occupancy of a substituent (Fig. 2 ▸). The situation is not improved beyond the first coordination shell, because the Ca—O, Ca—P and Ca—Ca distances are widely distributed and partly overlap.
Figure 1.
The structure of FAp projected in the ab plane (Hughes et al., 1989 ▸; Harlov & Rakovan, 2015 ▸). The F atom is located in the middle of the tunnel.
Figure 2.
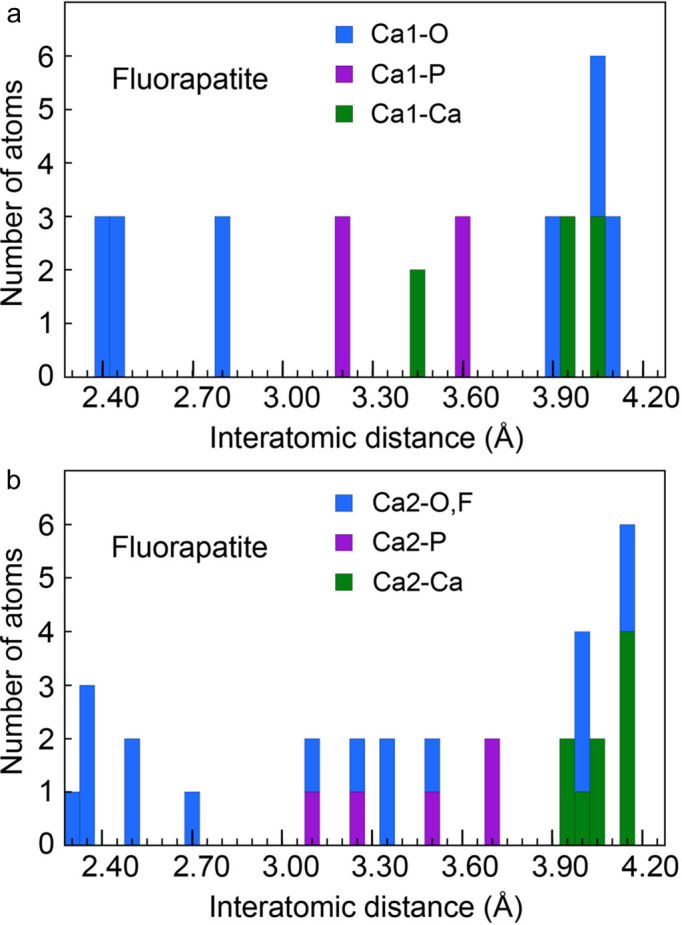
Population histograms of (a) the Ca1—(O,P,Ca) and (b) the Ca2—(O,F,P,Ca) distances in fluorapatite (Hughes et al., 1989 ▸). The number of atoms is counted in intervals of 0.05 Å.
Natural FAp is commonly enriched in trivalent rare earth elements (REE) (Harlov & Rakovan, 2015 ▸; Manceau et al., 2022 ▸). The substitution may occur on the Ca1 or Ca2 site, depending on the ionization energy of the substituent (Manceau et al., 2024 ▸). The charge excess resulting from REE3+ for Ca2+ substitution is generally considered to be balanced by parallel Na+ ↔ Ca2+ substitution on the Ca1 or Ca2 octahedral site, or Si4+ ↔ P5+ substitution on the tetrahedral site (Rønsbo, 1989 ▸; Fleet et al., 2000 ▸). Furthermore, the charge balance may occur locally, or indifferently at a short- or long-range distance. Other substitutional mechanisms can be envisaged, such as a coupled REE3+ + F− ↔ Ca2+ substitution with incorporation of an additional F− ion in the FAp tunnels, and a coupled 2REE3+ + Vac → 3Ca2+ substitution with creation of a Ca vacancy. Clearly, the conventional multi-shell EXAFS fitting approach has a high risk of failing to find the correct local structure of REE due to the inherent large number of unknowns to fit with multiple optima in parameter space. Not all of the atomic shells can be refined independently without causing correlations between parameters. Hence, a priori information is required to make educated guesses. Another inherent problem, besides the non-uniqueness of the model parameters resulting from overlapping subshells, is the lack of discrimination between Si and P backscatterers, and the low sensitivity of EXAFS spectroscopy to F, Na and vacancies.
An alternative to multi-shell EXAFS fitting is to use the geometric constraints of density functional theory (DFT) models for comparative modeling of the EXAFS spectra (Harris et al., 2006 ▸; Cotelesage et al., 2012 ▸). The EXAFS signal is a one-dimensional projection in reciprocal space of a spherically averaged three-dimensional structure. Incorporation of an impurity in a solid modifies not just its atomic pair distances but also those of its neighboring atoms and its bond angles. This information is compressed in EXAFS data and not easily and reliably accessible, motivating the use of DFT models as three-dimensional templates of the whole impurity environment. Recently, we followed this approach and showed by calculating the EXAFS spectra of DFT models that Ce3+ occupies the Ca2 site in FAp with a coupled Si4+ substituent at a short distance [d(Ce2—Si) = 3.09 Å, Ce2–Si-close model], while the coupled Na+ ↔ Ca2+ substitution on the Ca1 or Ca2 octahedral site was negated (Manceau et al., 2024 ▸).
Here, we extend our previous approach and present DFT2FEFFIT, a general regression analysis tool that best-fits an EXAFS spectrum using the χi functions generated by FEFF (Version 8.2; Ankudinov & Rehr, 1997 ▸) from a DFT model. Its capabilities are demonstrated with reconstructions of the Ce L3 edge EXAFS spectrum of the FAp reference from Cerro de Mercado near Durango, Mexico (Manceau et al., 2022 ▸). Using DFT2FEFFIT, we show that alternativeCe3+ + F− ↔ Ca2+ substitution (Ce2–F model) and 2Ce3+ + Vac → 3Ca2+ substitution (2Ce2–Vac model) are nonfitting models.
2. Software details
2.1. Input
DFT2FEFFIT is open-source code written in Python. It uses a command-line interface, which is invoked with a Python entry point. The user is then prompted to enter the input filename. The following input data are required: the experimental χ function to fit (line 1), the number of scattering paths (n, line 2), the k weighting of χ for the fit (knχ, line 3), the k range of the fit (line 4), 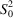 (line 5), whether ΔE is adjusted (integer 1) or fixed (integer 0) (line 6), the value of ΔE if no variation is allowed (integer 0), or its interval of variation (ΔEmin, ΔEmax) and the step size (line 7), and the list of scattering paths [lines 8 to 8 + (n − 1)]. Each path line is structured as follows: a line number (e.g. path ID); a string (e.g. chemical symbol, SS or MS for single or multiple scattering path); the path distance, only added for easy reference and not actually part of the fit; χi; the format of χi [FEFF format (chip000n) or simply two columns, k, χi]; whether σi is optimized (1) or not (0); the initial σi value; σi,min; σi,max; and the path ID with which the σi value is co-varied, −1 if the σ values are not linked. Path lines commented with a hash (#) symbol are ignored. At the end of the refinement, the code provides the optimized values, the experimental and calculated k-weighted χ functions (ASCII data and plot), the modulus and real part of the Fourier transform (i.e. RDF) of knχexp and knχcalc using a Kaiser–Bessel window (β = 2.5), and the fit residual expressed as the normalized sum of squared differences [NSS = ∑(knχexp − knχcalc)2/∑(knχexp)2].
(line 5), whether ΔE is adjusted (integer 1) or fixed (integer 0) (line 6), the value of ΔE if no variation is allowed (integer 0), or its interval of variation (ΔEmin, ΔEmax) and the step size (line 7), and the list of scattering paths [lines 8 to 8 + (n − 1)]. Each path line is structured as follows: a line number (e.g. path ID); a string (e.g. chemical symbol, SS or MS for single or multiple scattering path); the path distance, only added for easy reference and not actually part of the fit; χi; the format of χi [FEFF format (chip000n) or simply two columns, k, χi]; whether σi is optimized (1) or not (0); the initial σi value; σi,min; σi,max; and the path ID with which the σi value is co-varied, −1 if the σ values are not linked. Path lines commented with a hash (#) symbol are ignored. At the end of the refinement, the code provides the optimized values, the experimental and calculated k-weighted χ functions (ASCII data and plot), the modulus and real part of the Fourier transform (i.e. RDF) of knχexp and knχcalc using a Kaiser–Bessel window (β = 2.5), and the fit residual expressed as the normalized sum of squared differences [NSS = ∑(knχexp − knχcalc)2/∑(knχexp)2].
2.2. Calculation
The software seeks to minimize NSS by optimizing σi for each ΔE value. Because χcalc varies nonlinearly with σi [equation (1)], the minimization of NSS toward the local minimum is performed iteratively by following the negative of the first derivative of equation (1) with respect to σi (gradient-descent method) at each iteration. The scheme is iterated until NSS reaches a plateau (ΔNSS = 10−7) or for a user-defined fixed number of iterations. Convergence is speeded up by rescaling the input σi values to the [−1, 1] range according to 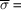 2(σi − σmean)/(σmax − σmin), with σmean = 0.5(σmax − σmin). Wolfe’s conditions (Wolfe, 1969 ▸; Nocedal & Wright, 2006 ▸) are used to determine the appropriate step size for each line search of strict descent at a point mn =
2(σi − σmean)/(σmax − σmin), with σmean = 0.5(σmax − σmin). Wolfe’s conditions (Wolfe, 1969 ▸; Nocedal & Wright, 2006 ▸) are used to determine the appropriate step size for each line search of strict descent at a point mn = 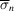 . The update to mn for the next iteration is mn+1 = mn + αnpn, where αn is the new step size computed from the line search at mn to satisfy the Wolfe conditions and pn is the search direction. The input scripts for the DFT models are deposited in the NOMAD repository (Draxl & Scheffler, 2019 ▸) at https://dx.doi.org/10.17172/NOMAD/2024.02.09-1.
. The update to mn for the next iteration is mn+1 = mn + αnpn, where αn is the new step size computed from the line search at mn to satisfy the Wolfe conditions and pn is the search direction. The input scripts for the DFT models are deposited in the NOMAD repository (Draxl & Scheffler, 2019 ▸) at https://dx.doi.org/10.17172/NOMAD/2024.02.09-1.
The gradient-descent optimization method was preferred over the Levenberg–Marquardt (LM) method for several reasons. The LM method requires an estimation of the Jacobian of the forward problem in order to build the Gauss–Newton Hessian matrix. This step is not needed with the steepest-descent algorithm. The LM method does not include a line search that would ensure proper convergence (Wolfe’s conditions) and would therefore need to be coupled with Wolfe’s conditions to ensure convergence. Lastly, the LM method requires another tuning parameter for the damping of the diagonal of the Gauss–Newton Hessian matrix.
3. Case study
EXAFS spectroscopy probes the local structure of a given element up to about 6 Å. Modeling by DFT the bonding environment of a substituent up to this distance requires optimizing the geometry of rather large clusters comprising more than one hundred atoms. DFT methods exploiting a linear combination of plane waves, as implemented in the Vienna Ab-initio Simulation Package (VASP; Kresse, 1995 ▸; Kresse & Furthmüller, 1996 ▸), are in this respect more cost effective than methods adopting a linear combination of local atomic orbitals, usually represented as Gaussian-type orbitals, as implemented in CRYSTAL (Dovesi et al., 2014 ▸). Comparison of the DFT structures obtained with VASP and CRYSTAL14 on Ce–FAp clusters of 336 atoms (2 × 2 × 2 supercell, radius ≃ 6 Å) showed that CRYSTAL14 did not provide superior models, even with the accurate PBEsol functional (Perdew et al., 2008 ▸) and basis sets of triple-zeta quality for Ca, P, O and F. Therefore, all optimizations reported in this study were performed with VASP to speed up the calculations. Details of the VASP parameters and functionals are given in the supporting information.
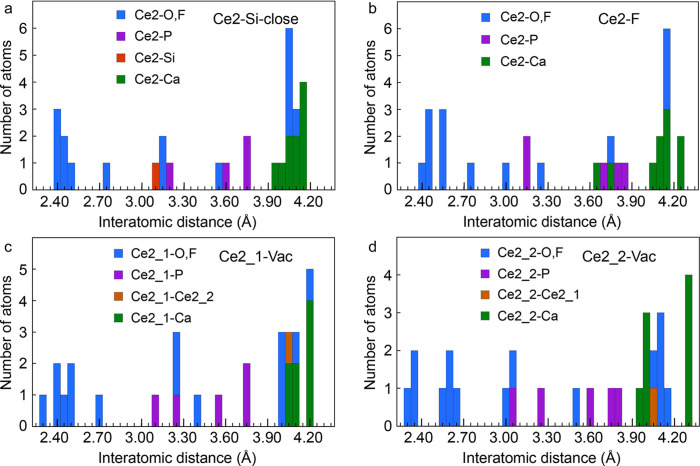
The radial distributions of Ce in the Ce2–Si-close, Ce2–F and 2Ce2–Vac models up to R = 4.3 Å are shown in Fig. 3 ▸, and the Cartesian coordinates of the models are listed in the supporting information. The Ce2–F model essentially differs from the optimal Ce2–Si-close model by (i) an increase in coordination from 6 to 7, and hence an increase in the average Ce2—(O,F) distance from 2.43 to 2.48 Å due to the incorporation of the interstitial F atom at 2.42 Å from Ce2, and (ii) the displacement to shorter distance of two Ca atoms [d(Ce2—Ca) = 3.65–3.75 Å] and to longer distance of two further Ca atoms [d(Ce2—Ca) = 4.26 Å]. Regarding the 2Ce2–Vac model, one Ce atom of the paired Ce atoms (Ce2_1) has a similar local structure to Ce in Ce2–Si-close [Fig. 3 ▸(c)], whereas the other Ce atom (Ce2_2) has a distinctive bonding environment characterized by a split of the first (O,F) shell and longer Ce2—Ca distances [Fig. 3 ▸(d)].
Figure 3.
Population histograms of the computed Ce2—(O,F,P,Ca,Ce) distances for (a) the Ce2–Si-close model, (b) the Ce2–F model and (c), (d) the two Ce atoms of the 2Ce2–Vac model. Computation details can be found in the supporting information. The number of atoms is counted in intervals of 0.05 Å.
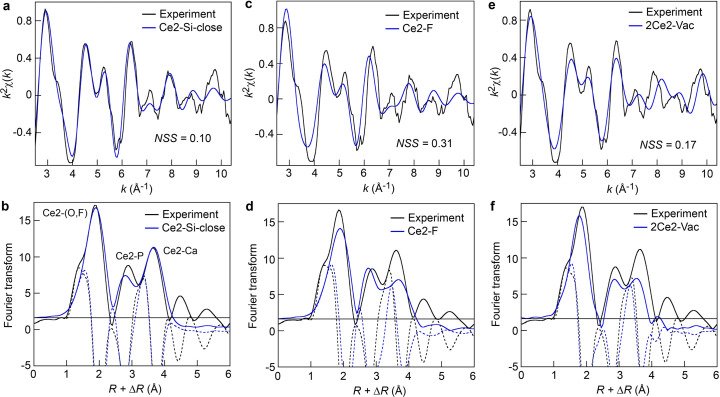
The best-fit results of the Ce L3 edge EXAFS spectrum for the Durango FAp with the calculated EXAFS spectra for the three DFT models up to R = 4.3 Å, together with the corresponding RDF, are shown in Fig. 4 ▸. The data were collected at room temperature on beamline ID24-DCM at the European Synchrotron Radiation Facility in high-energy-resolution mode (HERFD-EXAFS) using five analyzer crystals bent to a radius of 0.5 m (Rovezzi et al., 2017 ▸; Glatzel et al., 2021 ▸). Best-fit calculations were conducted by optimizing initially ΔE and one σ value for all SS paths (χNLEG=2 in FEFF). Afterwards, individual SS paths were grouped into shells (O1, P1, P2, Ca) and their σi values refined. The criterion for retaining a new SS path (i.e. σi value) was that the fit had to improve by at least 5% and be physically meaningful. A single σ value was applied to all MS paths calculated by FEFF (χNLEG=4 − χNLEG=2). The optimal ΔE value varied marginally (<1 eV) from one fit to another. 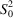 was fixed to 0.9. Best-fit EXAFS parameters of the three DFT models are reported in the supporting information.
was fixed to 0.9. Best-fit EXAFS parameters of the three DFT models are reported in the supporting information.
Figure 4.
Experimental and DFT-derived theoretical Ce L3 edge EXAFS spectra and radial distribution functions (magnitude and real part of the k2-weighted Fourier transform). (a), (b) Ce2–Si-close model, (c), (d) Ce2–F model and (e), (f) 2Ce2–Vac model.
Our results show that coupled Ce3+ + F− ↔ Ca2+ (Ce2–F model) and 2Ce3+ + Vac → 3Ca2+ (2Ce2–Vac model) are incompatible models. Adding an F atom or removing a Ca atom near a Ce atom are sources of disorder, which manifests on the calculated RDF by a misfit of the Ce2—(O,F) shell and a loss of amplitude of the Ce2—P and Ce2—Ca peaks. Thus, these results underscore the high sensitivity of DFT2FEFFIT for detailed characterization of the local structure of elements in complex environments. EXAFS alone does not allow differentiation between P and Si neighbors, because their scattering powers are similar, or the detection of a light F atom and a vacancy site. This distinction becomes possible by comparing the theoretical EXAFS spectra derived from DFT structure models with experiment. DFT2FEFFIT may, therefore, be considered as a useful tool for the validation of hypothesis-driven structure models based on EXAFS analysis.
4. Availability of DFT2FEFFIT
The Python script of DFT2FEFFIT is available online at https://gitlab.esrf.fr/scientific-software/dft2feffit and in thesupporting information.
5. Related literature
For further literature related to the supporting information, see Blöchl (1994 ▸), Gautier et al. (2015 ▸), Gonthier et al. (2012 ▸), Kresse & Joubert (1999 ▸), Perdew et al. (1996 ▸) and Steinmann & Corminboeuf (2011 ▸).
Supplementary Material
Details of DFT calculations, input scripts, EXAFS spectrum, Cartesian coordinates of the DFT models. DOI: 10.1107/S1600576724005454/vb5074sup1.pdf
Python code. DOI: 10.1107/S1600576724005454/vb5074sup2.zip
Acknowledgments
The authors are grateful to Silvia Maria Casassa for guidance on the use of CRYSTAL14. Financial support was provided by the European Research Council. Views and opinions expressed are however those of the authors only and do not necessarily reflect those of the European Union or the European Research Council. Neither the European Union nor the granting authority can be held responsible for them.
Funding Statement
This work was funded by HORIZON EUROPE European Research Council grant 101052913 to Alain Manceau.
References
- Ankudinov, A. L. & Rehr, J. J. (1997). Phys. Rev. B, 56, R1712–R1716.
- Blöchl, P. E. (1994). Phys. Rev. B, 50, 17953–17979. [DOI] [PubMed]
- Boyanov, B. I., Bunker, G. & Morrison, T. I. (1996). J. Synchrotron Rad.3, 120–128. [DOI] [PubMed]
- Chantler, C. T., Boscherini, F. & Bunker, B. (2020). Editors. International Tables for Crystallography, Vol. I, X-ray Absorption Spectroscopy and Related Techniques, 1st online ed. Chester: IUCr.
- Cotelesage, J. J. H., Pushie, M. J., Grochulski, P., Pickering, I. J. & George, G. N. (2012). J. Inorg. Biochem.115, 127–137. [DOI] [PubMed]
- Crozier, E. D. (1997). Nucl. Instrum. Methods Phys. Res. B, 133, 134–144.
- Dalba, G. & Fornasini, P. (1997). J. Synchrotron Rad.4, 243–255. [DOI] [PubMed]
- Dovesi, R., Orlando, R., Erba, A., Zicovich–Wilson, C. M., Civalleri, B., Casassa, S., Maschio, L., Ferrabone, M., De La Pierre, M., D’Arco, P., Noël, Y., Causà, M., Rérat, M. & Kirtman, B. (2014). Int. J. Quantum Chem.114, 1287–1317.
- Draxl, C. & Scheffler, M. (2019). J. Phys. Mater.2, 036001.
- Fleet, M., Liu, X. & Pan, Y. (2000). J. Solid State Chem.149, 391–398.
- Gautier, S., Steinmann, S., Michel, C., Fleurat-Lessard, P. & Sautet, P. (2015). Phys. Chem. Chem. Phys.17, 28921–28930. [DOI] [PubMed]
- Glatzel, P., Harris, A., Marion, P., Sikora, M., Weng, T.-C., Guilloud, C., Lafuerza, S., Rovezzi, M., Detlefs, B. & Ducotté, L. (2021). J. Synchrotron Rad.28, 362–371. [DOI] [PubMed]
- Gonthier, J. F., Steinmann, S. N., Wodrich, M. D. & Corminboeuf, C. (2012). Chem. Soc. Rev.41, 4671–4687. [DOI] [PubMed]
- Harlov, D. E. & Rakovan, J. F. (2015). Guest editors. Apatite: A Mineral for All Seasons.Elements, Vol. 11, No. 3. Washington, DC: Mineralogical Society of America.
- Harris, H. H., George, G. N. & Rajagopalan, K. V. (2006). Inorg. Chem.45, 493–495. [DOI] [PubMed]
- Hughes, J. M., Cameron, M. & Crowley, K. D. (1989). Am. Miner.74, 870–876.
- Kresse, G. (1995). J. Non-Cryst. Solids, 193, 2222–2229.
- Kresse, G. & Furthmüller, J. (1996). Comput. Mater. Sci.6, 15–50.
- Kresse, G. & Joubert, D. (1999). Phys. Rev. B, 59, 1758–1775.
- Manceau, A., Mathon, O., Lomachenko, K. A., Rovezzi, M., Kvashnina, K. O., Boiron, M. C., Brossier, R. & Steinmann, S. N. (2024). ACS Earth Space Chem.8, 119–128.
- Manceau, A., Paul, S., Simionovici, A., Magnin, V., Balvay, M., Findling, N., Rovezzi, M., Muller, S., Garbe-Schönberg, D. & Koschinsky, A. (2022). ACS Earth Space Chem.6, 2093–2103.
- Marcus, M. A., Chen, H. S., Espinosa, G. P. & Tsai, C. L. (1986). Solid State Commun.58, 227–230.
- Nocedal, J. & Wright, S. J. (2006). Numerical Optimization. New York: Springer.
- Perdew, J. P., Burke, K. & Ernzerhof, M. (1996). Phys. Rev. Lett.77, 3865–3868. [DOI] [PubMed]
- Perdew, J. P., Ruzsinszky, A., Csonka, G. I., Vydrov, O. A., Scuseria, G. E., Constantin, L. A., Zhou, X. L. & Burke, K. (2008). Phys. Rev. Lett.100, 136406. [DOI] [PubMed]
- Rehr, J. J. & Albers, R. C. (1990). Phys. Rev. B, 41, 8139–8149. [DOI] [PubMed]
- Rehr, J. J. & Albers, R. C. (2000). Rev. Mod. Phys.72, 621–654.
- Rehr, J. J., Kas, J. J. & Vila, F. D. (2020). EXAFS: Theory and Approaches. In International Tables for Crystallography, Vol. I, X-ray Absorption Spectroscopy and Related Techniques, 1st online ed. Chester: IUCr.
- Rønsbo, J. G. (1989). Am. Miner.74, 896–901.
- Rovezzi, M., Lapras, C., Manceau, A., Glatzel, P. & Verbeni, R. (2017). Rev. Sci. Instrum.88, 013108. [DOI] [PubMed]
- Steinmann, S. N. & Corminboeuf, C. (2011). J. Chem. Theory Comput.7, 3567–3577. [DOI] [PubMed]
- Stern, E. A., Sayers, D. E. & Lytle, F. W. (1975). Phys. Rev. B, 11, 4836–4846.
- Terry, J., Lau, M. L., Sun, J. T., Xu, C., Hendricks, B., Kise, J., Lnu, M., Bagade, S., Shah, S., Makhijani, P., Karantha, A., Boltz, T., Oellien, M., Adas, M., Argamon, S., Long, M. & Guillen, D. P. (2021). Appl. Surf. Sci.547, 149059.
- Timoshenko, J., Wrasman, C., Luneau, M., Shirman, T., Cargnello, M., Bare, S., Aizenberg, J., Friend, C. & Frenkel, A. (2019). Nano Lett.19, 520–529. [DOI] [PubMed]
- Wolfe, P. (1969). SIAM Rev.11, 226–235.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Details of DFT calculations, input scripts, EXAFS spectrum, Cartesian coordinates of the DFT models. DOI: 10.1107/S1600576724005454/vb5074sup1.pdf
Python code. DOI: 10.1107/S1600576724005454/vb5074sup2.zip