Abstract
Liquid–liquid interfaces hold the potential to serve as versatile platforms for dynamic processes, due to their inherent fluidity and capacity to accommodate surface-active materials. This study explores laser-driven actuation of liquid–liquid interfaces with and without loading of gold nanoparticles and further exploits the laser-actuated interfaces with nanoparticles for tunable photonics. Upon laser exposure, gold nanoparticles were rearranged along the interface, enabling the reconfigurable, small-aperture modulation of light transmission and the tunable lensing effect. Adapting the principles of optical and optothermal tweezers, we interpreted the underlying mechanisms of actuation and modulation as a synergy of optomechanical and optothermal effects. Our findings provide an analytical framework for understanding microscopic interfacial behaviors, contributing to potential applications in tunable photonics and interfacial material engineering.
Keywords: liquid–liquid interface, gold nanoparticles, self-assembly, optical actuation, light modulation
Graphical Abstract
Liquid–liquid interfaces, formed where two distinct liquid phases meet, exhibit phenomena that are markedly different from those observed in homogeneous bulk liquids. Serving as discontinuous and heterogeneous boundaries, these interfaces host surface-active species, ranging from common surfactants to assembled nanoparticles,1,2 bacteria,3 and rearranged liquid molecules and ions,4,5 all working to minimize interfacial energy. Under external stimuli, the inherent fluidity of liquid–liquid interfaces and the differing properties of the interfacing liquid phases give rise to dynamic phenomena, such as light-driven deformation due to refractive-index contrast,6,7 Marangoni flow,8,9 and electrical accumulation of charge.10,11 Moreover, the incorporation of stimuli-responsive particles at interfaces has allowed for dynamic manipulation of liquid droplets and channels,1,12,13 as well as reversible interfacial assembly and disassembly under external fields.14,15 A profound understanding of interfacial dynamics is pivotal for the successful development and application of liquid interface-based functional systems. The extremely thin and often indistinct boundary (e.g., gradient or step boundary) of liquid–liquid interfaces, along with the mobility of surrounding liquids, necessitate extensive analytic investigations to delineate microscopic phenomena.2,5
The fluidic nature and particle-confining capabilities of liquid–liquid interfaces position them as promising candidates for dynamic actuation elements in tunable and reconfigurable systems. Particularly intriguing are tunable photonic systems, capable of modulating optical properties (e.g., amplitude, phase, and polarization of light), which are desirable in diverse applications such as adaptive photonics, photonic integrated circuits, dynamic display, optical communication, and memory devices. Earlier examples of liquid crystals,16,17 redox reactions,18-20 photoisomerization,21,22 photothermal bubble formation,23 microfluidic diffusion,24 thermal phase change phenomena,25-28 thermo-optic effects,29,30 optomechanics,31 and optical/electrical free carrier pumping32,33 have shown their potential as active actuation mechanisms for different modulation modes, operating wavelengths, and modulation depths. It is worth noting that each system has its own benefits and limitations for targeted applications, such as in tuning range, wavelength, response time, system requirement, miniaturization, energy loss, and pixelated control.34 Tunable photonics with liquid–liquid interfaces has been conceptualized in several systems. At the interface between two immiscible electrolyte solutions, electrically driven reversible assembly of charged gold nanoparticles has shown its capability to control the reflection of light.14 Laser-induced thermocapillary flow was also employed to induce reversible rupturing of an interface and modulate light transmission.35 Additionally, tunable lensing of light across liquid–liquid interfaces has been demonstrated through electrical36 and optothermal37 modulation of interfacial curvature. Most of the research on this topic relies on macroscopic actuation scales (~ mm) and bulk dynamics (i.e., bulk-to-interface particle/charge transport and dewetting of liquids). However, when actuation is narrowed down to a microscale, the influence of interfacial phenomena on optical responses could be more dramatic, owing to the emergence of strong field gradients and entangled high degree-of-freedom phenomena. Specifically, employing a focused laser for stimulation and integrating photonic nanocrystals at a liquid–liquid interface as active materials can enable the adaptation of optical and optothermal tweezers into actuation mechanisms and associated analysis, while leveraging the two-dimensional particle confinement and the fluidity of liquid–liquid interfaces.
Building upon these foundational insights, we delve into laser-induced tunable photonics over gold nanoparticle (Au NP)-laden liquid–liquid interfaces. It was found that laser illumination on the nanoparticle-loaded liquid interface induced local clearing of the nanoparticles, leading to reversible and laser power-dependent changes in light transmittance. Furthermore, a tunable lens effect was observed from the microscopic behavior of microparticles. By correlating experimental observations and theoretical analyses, we attributed these phenomena to optomechanical and optothermal effects, which originated from the distinctive characteristics of the nanoparticle-loaded interfaces.
RESULTS AND DISCUSSION
Laser-Induced Clearance of Gold Nanoparticles at Liquid–Liquid Interface and Modulation of Transmittance.
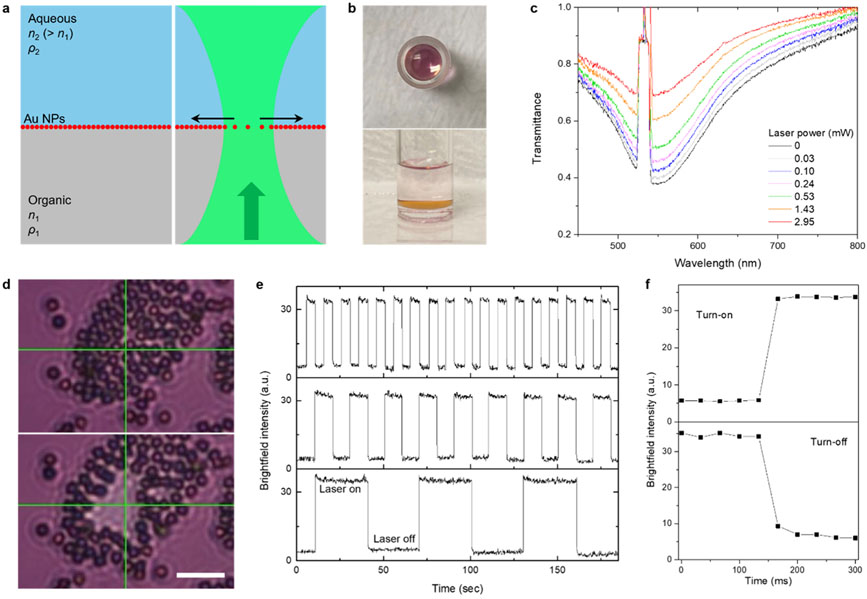
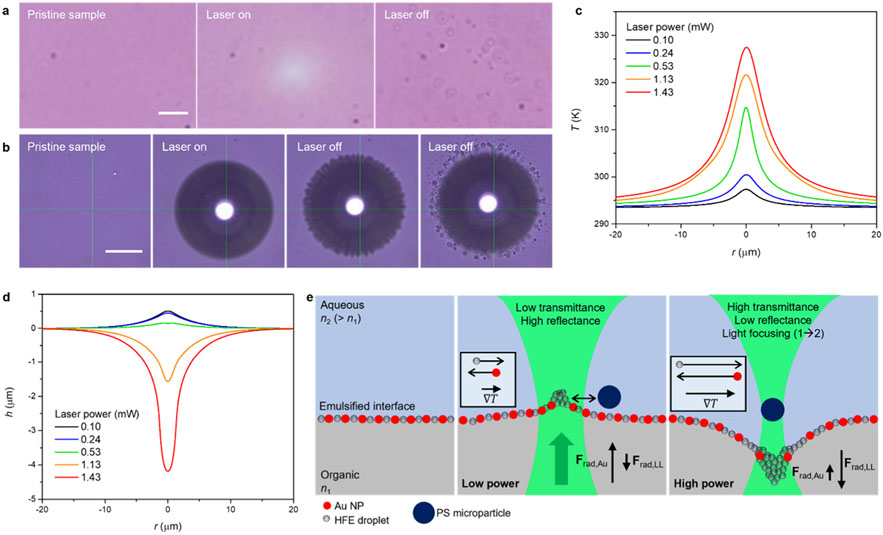
The interface model consists of a top aqueous liquid phase, a bottom organic liquid phase, and an interfacial film of 30 nm gold nanoparticles (Figure 1a,b). The sample was prepared by simply mixing a solution of semifluorinated thiol in ethanol and hydrofluoroether (HFE) with an aqueous dispersion of Au NPs. The Au NPs spontaneously assembled at the interface, forming a reflective metallic film, particularly noticeable at a high angle (side view in Figure 1b), while ethanol was mostly extracted into the top phase. The semifluorinated ligands render Au NPs superhydrophobic through their binding reactions, assisted by the extraction of ethanol into the aqueous Au NPs dispersion, thereby enabling the in situ ligand exchange and interfacial assembly.38 HFE was chosen to construct a water-on-top configuration for additional experiments involving water-dispersed microparticles. Glass containers were also hydrophobically modified with semifluorinated molecules to minimize the adhesion of Au NPs. In the modified glass container, a nearly flat interface at the glass surfaces was formed (Figure S1), suggesting minimal interaction of the fluorinated materials with the two liquid phases. An inverted optical microscope with an objective lens (numerical aperture, NA 0.5), coupled with a 532 nm continuous-wave (CW) laser (upward beam propagation) and a spectrometer, was used to observe samples under optical fields (Figure S2). As shown in Figure 1c, upon laser illumination at the interface, the transmittance around the laser beam increased with respect to the laser power, indicating a reduced packing density of Au NPs near the beam. These transmittance spectra were collected over 15 × 11 pixels (~0.5 μm/pixel) centered around the beam, thus the spectral information under laser irradiation is a combination of spatially distributed and varying transmittance entities. When a cluster of assembled polystyrene (PS) microparticles was placed atop the interface for visualizing interfacial behavior, an outward in-plane motion of the interfacial species became evident, and the particles reassembled when the laser was turned off (Figure 1d and Movie S1). In this brightfield image, a relatively large area compared to a beam waist of 0.93 μm was brightened, representing that Au NPs’ clearance and transmittance changes occurred widely around the beam. The transmittance modulation was found to be reconfigurable over repeated on/off step cycles of 5–30 s (Figure 1e). Average on and off response times were measured to be ≤33 ms, which is the minimum time frame of a recording camera, and 78 ± 12 ms, respectively (Figure 1f, mean ± standard deviation for 18 measurements).
Figure 1.
Optical clearing of gold nanoparticles at liquid–liquid interfaces and transmittance modulation. (a) Schematic of a liquid–liquid interface loaded with Au NPs and its response to a laser beam. A green arrow indicates the direction of beam propagation and black arrows indicate the radial motion of interfacial Au NPs. (b) Pictures of Au NP-loaded HFE–ethanol–water interface system. (c) Transmittance spectra of the gold interface under laser illumination at varying powers. (d) Optical clearing of interfacial species visualized by a cluster of PS microparticles (scale bar: 10 μm). Green crossbars indicate the position of the laser beam. (e) Light amplitude switching under on/off cycles for different durations: 5 s/5 s, 10 s/10 s, 30 s/30 s from the top panel. The brightfield intensity was recorded at the center position of the laser beam (0.72 μm × 0.72 μm), and two notch filters were used to block the laser beam. (f) Brightfield intensity for turn-on and turn-off switching.
Particle Trapping Behavior and Beam Focusing over Liquid–Liquid Interface.
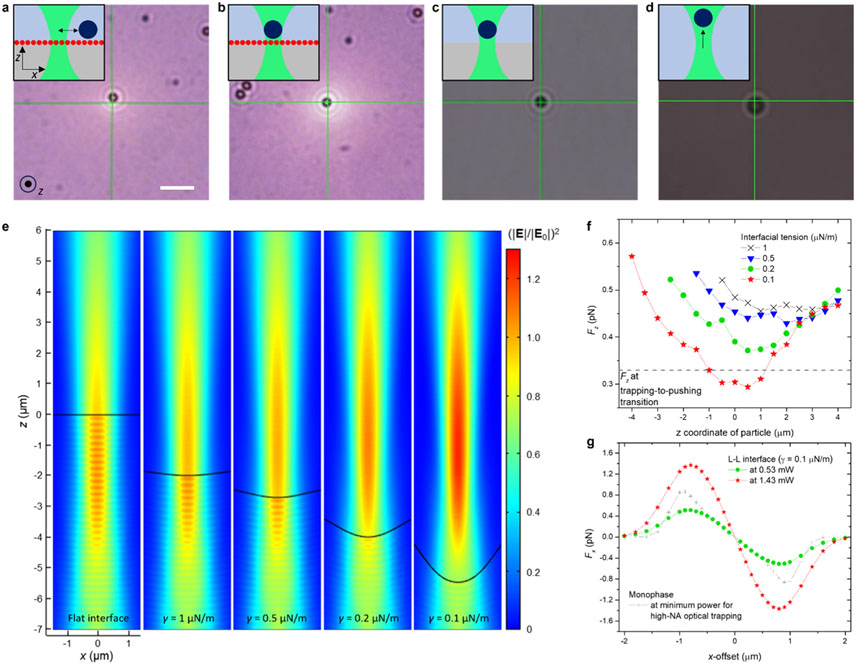
To understand the local interfacial events, we conducted comparison studies on the laser-induced trapping behavior of individual PS microparticles (2 μm in diameter) in various systems. PS particles were added to the upper aqueous phase of the prepared samples. Mobile colloidal particles, which were not adhered to the interface, were selected for the motion study (see Figure S3 for validation of the particle positions). On the gold interface, a PS particle demonstrated oscillatory motion at a distance from the laser beam center at low laser powers (0.10–0.24 mW) (Figure 2a and Movie S2). At higher laser powers (≥1.43 mW), however, the particle became trapped at the beam center (Figure 2b and Movie S2). In comparison, on a bare liquid–liquid interface, particle trapping was observed only at the higher powers (Figure 2c and Movie S2). Our initial focus was on this trapping behavior at the bare liquid–liquid interface because, in a monophasic system consisting of a continuous mixture of water and ethanol, particles were attracted to the beam but propelled along the beam axis at varying laser powers (Figure 2d and Movie S2). The absence of Au NPs in these two systems suggests that the trapping behavior can be explained by the principle of optical tweezers, as the heating effect is minimal due to the low absorption coefficients of the liquids. Notably, in the water–ethanol mixture, stable optical trapping was observed with a high NA objective lens (NA 1.3) due to a reduced optical scattering force. Thus, we inferred that the optical field of the incident laser beam is altered at the bare interface to the extent that enables optical trapping. When a beam propagates across an interface of two liquids with different refractive indices, it exerts a radiation pressure on the interface through momentum transfer, the pressure toward the medium with the lower refractive index.6,7,39 The axisymmetric steady-state deformation of the interface, , induced by the radiation pressure – defined as the force per unit interface area (unit normal vector, , with a beam propagating from medium 1 to medium 2) – is described by a force balance equation:6,7,39
| (1) |
where , , , and represent the density contrast between the two phases, the acceleration of gravity, interfacial tension, and local curvature, respectively.
Figure 2.
Motion study of individual microparticles at liquid–liquid interfaces and deformation-based laser beam tuning at bare liquid–liquid interface. (a–d) Optical microscopic images of PS particles responding to a laser over the different type of interfaces: Au NP-loaded interface at optical powers of 0.24 mW (a) and 1.43 mW (b), bare liquid–liquid interface at 1.43 mW (c), and monophasic mixture of water and ethanol at 1.43 mW (d). Insets show system configurations and characteristic particle motion. Scale bar: 5 μm. (e) Intensity profiles of a Gaussian beam propagating through flat and deformed liquid–liquid interfaces, calculated with different interfacial tensions. The beam focal plane is fixed at z = 0. (f) Longitudinal optical force (Fz) profiles of a single PS particle (2 μm) with respect to z-offset of the particle from the beam center in interfacial systems with varying interfacial tensions at 1.43 mW. (g) Transverse optical force (Fx) profiles of the particle in the interfacial systems with respect to x-offset at 0.53 and 1.43 mW.
The radiation pressure term can be further described with Gaussian beam intensity profile, , as
| (2) |
where and are the refractive indices (1: bottom phase and 2: top phase), is the speed of light in a vacuum, is a term for incident angle , is the optical power, is the beam waist, and is the Rayleigh range (). For the beam intensity, the -dependent profile was considered instead of a cylindrical beam because the deformation depth was expected to be several microns, which is comparable to . Details regarding approximation of the incident angle term, and the full equation are available in Note S1.
As the radiation pressure is counterbalanced by buoyancy () and Laplace pressure (), light-induced deformations of liquid–liquid interfaces are allowed in exceptionally soft interfaces, such as near-critical two-phase equilibrium states and Windsor III phases, which involve microemulsion phases.6,7,39 In these systems, substantial reductions in density difference and extremely low interfacial tensions on the order of 10−6–10−7 N/m are reached due to the presence of microemulsion phases (droplet size: 10 to 200 nm) that introduce a composite buffer layer. In our system, a notable density reduction was observed only in the bottom phase (~5.7% reduction compared to pure HFE) while the top phase retained the same density as the pure water–ethanol mixture. This information suggests two possibilities: (i) the formation of a water/ethanol-in-HFE microemulsion in the bottom phase or (ii) a mixture of HFE and small amount of ethanol in the bottom phase with an HFE-in-water microemulsion at the interface (Windsor III phase with a thin interface). In either case, the decrease in density difference between the two phases ( from 0.54 g/mL, measured from aliquots of the two phases) is not as significant as in the above-mentioned microemulsion systems. This observation implies that a significant reduction in interfacial tension is pivotal for interface deformation. Attempts to directly measure the interfacial tension using pendant drop tensiometry were made; however, HFE droplets fell from the needle in a few seconds, attributable to a marked decrease in interfacial tension to levels unable to sustain the droplets.13 Consequently, we opted to estimate the interfacial tension through optical trapping/pushing experiments and optical force simulations (Methods). eq 1 was numerically solved for with , eq 2, and varying interfacial tensions (Figure S4). Figures 2e and 2f show the alteration of the optical intensity field over the calculated interfaces and the resultant longitudinal optical force () exerted on a PS particle, with respect to its -offset from the beam. As the interfacial tension decreases, the incident laser beam is further focused due to deeper deformation, and the minimum falls below a threshold axial force for a trapping-pushing transition (Figure S5) at . The capillary length was calculated to be 4.7 μm. In the biphasic system with the estimated interface profile, the transverse optical gradient force was found to be sufficiently larger in magnitude than the force field at the minimum power for optical trapping in the high-NA monophasic system (Figure 2g). The trapping stiffnesses was measured as 1.11 pN/μm, similar to 1.18 pN/μm obtained in the simulation, thereby validating our optical force simulations (Figure S6). At a lower power (0.53 mW), where no trapping behavior was observed at the bare interface, the transverse optical trapping force was slightly below the minimum trapping force.
The low interfacial tension in our system was further evidenced by comparing the laser beam intensity focused on different liquid–liquid interfaces, in addition to the dripping phenomenon observed in the pendant drop measurements. At the very center, the beam intensity scattered on the interface can be considered proportional to the reflectance by the interface at normal incidence. The reflectance of the interface was increased by 66% from the theoretical value (Figure S7). The increment in reflectance implies the existence of scattering bodies at the interface, rather than pure liquid–liquid contact. Therefore, the presence of the HFE-in-water microemulsion phase at the interface is a more probable scenario. The macroscopic phase behavior of this ternary liquid system showed the immediate formation of emulsion phases (see Note S2 and Figure S8 for further description). Additional evidence of this phase configuration was observed in microscopy examinations. Some large remnant droplets were present right above the interface (i.e., HFE-in-water/ethanol), and these droplets at the gold interface exhibited trapping behavior by the laser (Movie S3). Considering the negative and small refractive index difference between pure HFE (1.28) and water/ethanol (1.36), a weak transverse optical force drives an HFE droplet away from the beam. It turns out that an optically generated temperature gradient is responsible for the trapping. Similar thermophilic behavior has been reported for perfluorocarbon droplets in aqueous media, in which microscale oil droplets were trapped by the optothermal field, and even long-range accumulation was observed at high droplet concentrations (Figure S9).40 HFE shares similarities with perfluorocarbon liquids as a fluorocarbon material, with the only difference being an ethyl ether end group. The ethyl ether moiety may facilitate interspecies interactions at aqueous interfaces, especially in the presence of cosolvents like ethanol, leading to the stable microemulsion phase that lowers the interfacial tension (Note S2 and Figure S8).
Optical and Optothermal Actuation of Au NP-Loaded Liquid–Liquid Interface.
When Au NPs are present at the interface, thermal and thermo-optical effects should be considered since a laser of the resonance wavelength is used. Depending on the absorptance of the gold layer and the laser power, a local thermal field is determined. This thermal field typically reduces the interfacial tension of liquid–liquid interfaces due to thermal perturbation, resulting in a thermocapillary pressure on the interface.41 Furthermore, the altered distribution of Au NPs and the thermophoretic accumulation of interfacial microemulsion droplets affect the interfacial tension. On the optical side, the Au NPs are subjected to an optical scattering force in the direction of beam propagation, resulting in an upward pressure (Figure S10). Since the radiation force on the bare interface acts downward due to the differing refractive indices of the two media, the net radiation force on the gold interface results from the summation of opposing contributions from areas covered and uncovered by Au NPs. Additionally, thermal variations of refractive indices influence the radiation pressure for both particle-uncovered and particle-covered interfacial regions. Given the laser-induced clearance of Au NPs, all these elements are contingent upon the spatial distribution of Au NPs at the interface. Consequently, the force balance equation needs to be modified as follows:
| (3) |
where represents the Marangoni pressure, and and are the radiation pressures contributed by Au NPs and uncovered liquid–liquid interface, respectively. The radiation and Marangoni pressures are counterbalanced by buoyancy () and Laplace pressure (), indicating that smaller density differences and smaller interfacial tensions are favorable for interfacial deformation. For particle-loaded liquid–liquid interfaces, additional factors come into play, i.e., capillary forces between the particles and the two liquids, along with interparticle interactions. The capillary force has been shown effective for larger and charged particles but is negligible for smaller and uncharged particles,42 such as the 30 nm perfluorinated nanoparticles in our study. Due to the weak van der Waals force between perfluoro moieties, the interparticle force can also be disregarded.
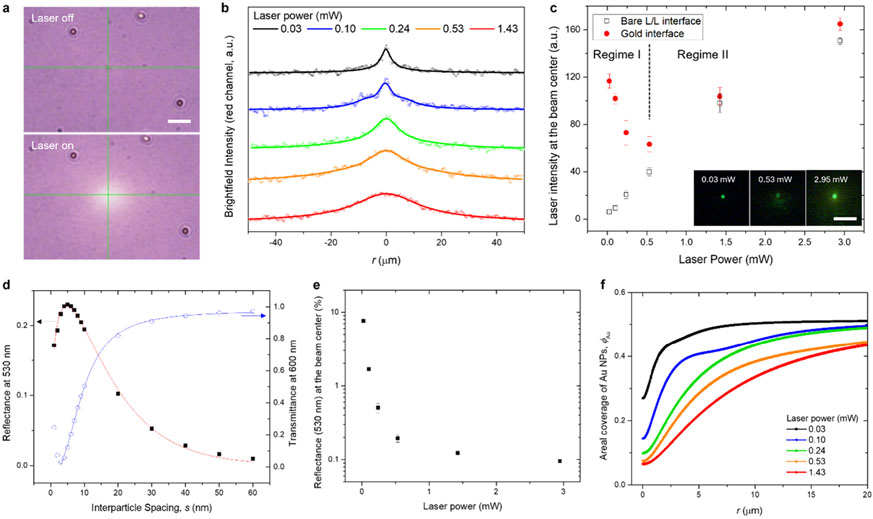
Our initial step in characterizing the interfacial distribution of Au NPs involved examining how transmittance and reflectance vary with laser power. In the transmission mode of our optical setup (Figure S2), the intensities of brightfield images indicate changes in transmittance of the interface (Figure 3a). It should be noted that the imaging conditions were set with a notch filter (533/17 nm) to render the laser beam undetectable. As laser power increases, the profile of brightfield intensity broadens (Figure 3b), suggesting a wider clearance of Au NPs from the beam center. Figure 3c illustrates the reflected laser beam intensity at the beam center for both Au NPs-loaded and bare interfaces across different laser powers. As laser power rises, beam intensity sharply decreases (regime I), followed by an increase above 0.53 mW, consistent with the linear trend observed for the bare interface (regime II). The higher beam intensity at lower power indicates that a denser Au NP coverage diminishes with increasing laser power. Once the clearance effect of Au NPs at the beam center reaches saturation, the interface at this region resembles the bare liquid–liquid interface.
Figure 3.
Derivation of interfacial coverage of Au NPs. (a) Brightfield microscopic images with laser illumination. Scale bar: 10 μm. (b) Brightfield intensity profiles under varying laser powers. Red channel intensities centered at 600 nm were used. Dots and lines represent pixel intensities and fitted curves, respectively. (c) Reflected laser intensity at the beam center for bare and Au NP-loaded interfaces across different laser powers. The focal plane was fixed, and the intensity was measured over 3 × 3 pixels (0.12 μm/px) at the beam center (mean ± standard deviation of measurement taken over 1 s). (d) Reflectance at 530 nm and transmittance at 600 nm as functions of interparticle spacing. (e) Converted reflectance of the gold interface at the beam center under varying laser powers. (f) Areal interfacial coverage of Au NPs derived at different laser powers.
The radial distribution of interfacial Au NPs was determined by integrating these results with simulated optical spectra (transmittance, reflectance, and absorptance) of a hexagonal array of Au NPs, varying by interparticle spacing (Note S3 and Figure S11). Reflectance data from the bare liquid–liquid interface (0.12%, Figure S7) and the Au NP array’s simulated reflectance (Figure 3d) were used to convert the laser intensities in Figure 3c into reflectance at the beam center (Figure 3e). This, in turn, provided the corresponding interparticle spacings at the beam center. From the spatial intensity profiles of brightfield images (Figure 3b), we derived the radial distribution of Au NPs in terms of interparticle spacing (Figure 3f), aligning with the transmittance-particle spacing relationship. We used a reference interparticle spacing of 9.9 nm, determined by matching the measured extinction peak wavelength with simulation results (Figure S12). The corresponding distributions of interparticle spacing are described in Figure S13. Figure 3f illustrates the power-dependent radial distribution of Au NPs in terms of areal coverage, showing that the clearance of Au NPs from the beam becomes more pronounced at higher optical power. Additionally, as the interfacial gold layer has a thermal conductivity different from that of a continuous gold film, an effective thermal conductivity as a function of Au NPs’ volume fraction was empirically determined by correlating the simulation with a measured temperature profile for a dried film of Au NPs (Note S4 and Figure S14). Radial functions for volume fraction (for in-plane thermal conductivity) and absorptance (for heat influx) of the gold interface were obtained from the particle distribution profiles (Figure S13). The interfacial tension term was formalized as follows:
| (4) |
where is the pristine interfacial tension, and and correspond to changes in interfacial tension due to varying Au NPs coverage and microemulsion droplets, respectively. At higher temperatures, the interfacial tension of clean liquid–liquid interfaces typically decreases (Figure S15c). However, in our system, the presence of interfacial species, i.e., Au NPs and microemulsion droplets, contributes to minimizing the interfacial tension. The reduced Au NPs coverage at elevated temperatures leads to an increased interfacial tension, while the thermal accumulation of microemulsion droplets acts to decrease it. Consequently, interface deformation is enhanced when the tension-reducing effects of droplet accumulation and thermal perturbations surpass the tension-increasing effect of the removal of Au NPs. The function of interfacial tension was estimated by scaling measured transient interfacial tensions to the estimated tension, in considerations of the screening effect by Au NPs42,43 and the thermophoretic accumulation of microemulsion droplets (Notes S5-S6 and Figure S15).
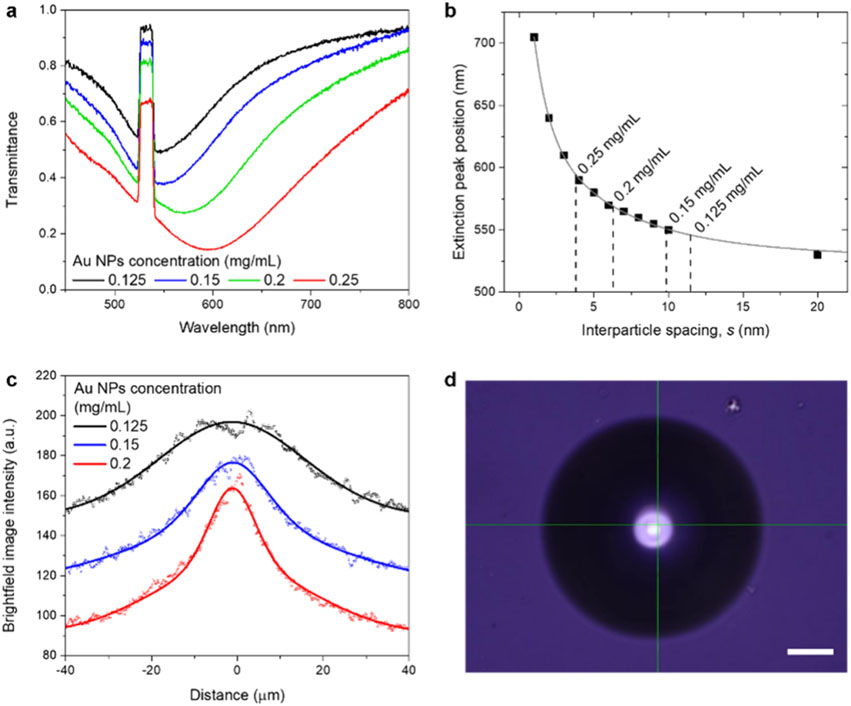
To better understand the mechanism driving the actuated motion of Au NPs and the trapping behavior of PS microparticles, we investigated interfaces with varying concentrations of Au NPs. As depicted in Figure 4a, the transmittance spectra show a red-shift and reduced transmittance with increasing NP concentrations, indicating a decrease in interparticle spacing. At concentrations of 0.05 and 0.10 mg/mL, the interfaces were not uniformly covered by gold nanoparticles (Figure S16). Figure 4b presents the interparticle spacing at different concentrations, determined from the relationship with the extinction peak wavelength, implying increasing packing densities with rising NP concentrations. The transmittance profile of the gold interfaces sharpens with increased NP concentration (Figure 4c). Notably, at a concentration of 0.25 mg/mL, a bubble was formed at the same laser power (Figure 4d), which is attributed to elevated temperatures due to the higher packing density. At NP concentrations ranging from 0.125 to 0.15 mg/mL, oscillation and trapping of PS particles were observed at relatively low and high laser powers, respectively. In contrast, at higher concentrations, PS particles were propelled upward, akin to the behavior observed with a solid gold sample (Movie S4). Thus, a higher packing density of Au NPs at the interface hampers the wider redistribution of gold nanoparticles, generates more heat, and prevents deformation-induced laser focusing.
Figure 4.
Interfaces at varying concentrations of Au NPs. (a) Transmittance spectra for interfaces prepared with different concentrations of Au NPs. (b) Interparticle spacings of interfacial Au NPs, derived from extinction peak wavelengths. (c) Brightfield intensity profiles of the interfaces. Dots and lines represent pixel intensities and fitted curves. (d) Microscopic image of a bubble formed at a concentration of 0.25 mg/mL Au NPs under a laser power of 1.43 mW. Scale bar: 20 μm.
The accumulation of interfacial microemulsion droplets was evidenced through microscopy investigations. As shown in Figure 5a and Movie S5, observable droplets appear when the laser is turned off after optical actuation of the gold interface. This phenomenon is attributed to the thermal accumulation of droplets at the beam and their subsequent release with coalescence when the laser is deactivated, further supporting the existence of a microemulsion interfacial phase and the thermophoretic accumulation of droplets, along with Figures S7-S9, and Movie S3. The droplet accumulation/release behavior was more pronounced under bubble-generating conditions (Figure 5b).
Figure 5.
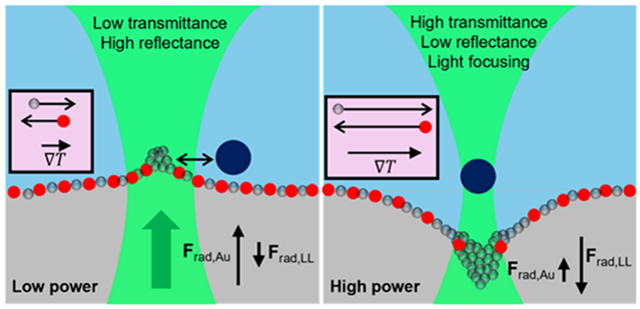
Working principle of tunable photonics over nanoparticle-loaded liquid–liquid interfaces. (a, b) Release of accumulated droplets upon deactivation of the laser after actuation (a) and bubble formation at the interface (b). Scale bars in (a) and (b) correspond to 10 and 50 μm, respectively. (c) Temperature profiles along the interface at different laser powers, using effective thermal conductivity related to volume fraction and the boundary heat source (absorptance multiplied by Gaussian beam intensity, Note S6) were used. (d) Estimated laser power-dependent interface bending profiles. (e) Schematic representation of laser-induced interfacial events at low and high laser power regimes. Boxed contents indicate the direction and magnitude of particle motion along temperature gradients.
Solutions of eq 3 for , obtained with temperature profiles (Figure 5c), are shown in Figure 5d. The radiation pressures, and , were formalized using temperature-dependent refractive index functions (Note S6), optical forces for a single Au NP (Figure S10), and the coverage function (Figure 3f). Owing to the low interfacial tension, the Marangoni pressure, , was found to be significantly smaller than the radiation pressures by 2 orders of magnitude (Figure S17). The transverse optical force acting on Au NPs was negligible (Figure S10), ruling out the possibility of their optical trapping. Taken altogether, the entire system is interpreted as follows (Figure 5e). With liquids expanding at elevated temperatures, Au NPs are displaced from the beam. Concurrently, interfacial HFE droplets accumulate at the beam, exerting a depletion force on Au NPs to move them away from high-temperature areas. At lower laser powers, the dominant on Au NPs results in a slight upward deformation of the interface (Figure 5d). The accumulation of microemulsion droplets in the high-temperature areas forms an elastic barrier, which prevents the optical trapping of a PS particle to the beam center. This explains the oscillation behavior of PS particles (Figure 2a). With an increase in laser power, the net radiation pressure turns negative due to low Au NP coverage, leading to downward deformation (Figure 5d). Enhanced thermal perturbation and droplet accumulation from larger temperature gradients push Au NPs further away. The droplets gather in the interfacial well below the focal plane, enabling the optical trapping of a PS particle. The extent of interface deformation heavily depends on the interfacial tension. Excluding the thermal accumulation of microemulsion droplets, a deformation depth less than 0.5 μm was estimated at 1.43 mW, insufficient to account for the trapping behavior of PS microparticles (Figure 2b). It is noteworthy that PS particles in a water–ethanol mixture on a deposited film of Au NPs were consistently pushed upward at various laser powers (Movie S4), negating the possibility of thermophoretic trapping. While PS particles can be trapped under an optically generated temperature gradient in water,40,44 the addition of ethanol significantly reduces the trapping force.40 Thus, we associate the high-power trapping of PS particles with interface deformation and subsequent laser focusing. Taking micro-emulsions into account, a pronounced reduction in interfacial tension at the beam center results in relatively large interface deformation. By adjusting Au NP distributions and deformation profiles with the laser, transmission/reflection and lensing of light are modulated through a small aperture. The velocity of thermally driven Marangoni flow near the beam was less than 1 μm/s (Figure S17), attributable to the small interfacial tension gradient, which is negligible given the millisecond scale of optical actuation dynamics (Figure 1e,f).
CONCLUSIONS
Our investigation into the tunable photonics of Au NP-loaded liquid–liquid interface has demonstrated the capability to optically modulate light transmission and lensing through small apertures, facilitated by the interplay of interfacial optomechanical and optothermal effects. This study advances our understanding of microscopic interfacial phenomena and suggests opportunities for their application in tunable photonics. On liquid–liquid interfaces, nano/microparticles with various optical and thermal properties, along with corresponding binding ligands, can be incorporated to enable a variety of modulation modes and wavelength ranges (e.g., chiral nanoparticles for polarity modulation45). For instance, interfaces laden with silver nanoparticles can be readily prepared using the same thiol ligands that facilely bind to soft metals (Figure S18). Furthermore, the ability to manipulate particles at the interface presents opportunities for interfacial material manufacturing46-49 and handling.50 The trapping capability applies to various sizes (2–10 μm) and other materials, including silica and iron oxide/PS (Movie S6). Additionally, bubble-concentrated interfacial reactions51,52 can be adapted by harnessing local heating (Figure S19 and Movie S7), highlighting our platform’s potential for interfacial synthesis. Given the specific liquid composition of our system, synthetic approaches that leverage heat- and light-assisted reactions with reactants separately soluble in the two liquid phases, would greatly benefit from our platform, such as interfacial synthesis of superhydrophobic metal–organic frameworks with fluorinated ligands.53-55 While liquid-based systems may encounter challenges related to long-term stability, strategic approaches in surface chemistry (e.g., using bidentate ligands) and encapsulation techniques can improve their stability. We believe that this work will stimulate extensive research in fluid interface-based photonics, fostering advancements in photonic devices and materials synthesis and structuring.
METHODS
Chemicals and Preparation of Biphasic Systems.
Aqueous dispersions of 30 nm gold nanoparticles (Au NPs, 0.05 mg/mL in 2 mM citrate solution, nanoComposix) and 2 μm polystyrene (PS) particles (10% w/w, Thermo Scientific), ethyl nonafluorobutyl ether (HFE, mixture of isomers, > 98.0%, Tokyo Chemical Industry), ethanol (200 proof, EMD Millipore Corporation), toluene (≥99.5%, Sigma-Aldrich), perfluorohexane (PFH, 98+%, Alfa Aesar), 1H,1H,2H,2H-perfluorodecanethiol (PFT, 97%, Sigma-Aldrich), trichloro(1H,1H,2H,2H-tridecafluoro-n-octyl)silane (PF-Si, > 97.0%, Tokyo Chemical Industry), sulfuric acid (H2SO4, Certified ACS Plus, Fisher Chemical), and hydrogen peroxide (H2O2, 30% in water, Fisher Chemical) were used as received. Two mM PFT solution in 1:2 (v/v) HFE and ethanol. Two equivalent volumes of PFT solution were added with 1 equiv volume of Au NPs solution (0.15 mg/mL) and aged for 30 min. For the bare liquid–liquid interface system.
Surface Modification of Glass and Microscope Chamber Fabrication.
Glassware was treated with a Piranha solution (70% H2SO4 and 30% H2O2 solution, v/v) for 30 min, washed with water, and dried at 90 °C for 30 min to introduce surface hydroxyl groups. The dried glassware was immersed in a 2.5 mM PF-Si solution in toluene for 10 min, washed by acetone in a bath sonicator (Branson 2800, 40 kHz) for 15 min three times, and dried at 90 °C for 2 h to obtain hydrophobic glassware. For glass chambers for a microscope, a microscopy cover glass (thickness: 0.17 mm) and a hollow glass cylinder (inner diameter: 6 mm) were glued using an epoxy-based glue (ClearWeld, J-B Weld).
Optical Setup and Spectroscopy.
An inverted microscope (Nikon Ti-E) with a 20x objective (Plan Fluor NA 0.5, Nikon) was coupled with a 532 nm CW laser (Laser Quantum Ventus 532) and spectroscope (Shamrock 303i-B, Andor). The laser beam was expanded by a 5x beam expander (GBE05-A, Thorlabs) and focused on a sample stage from the bottom. Images were obtained through a color charge-coupled device (CCD, DS-Fi3, 30 fps, Nikon). A notch filter (533/17 nm) was placed between the objective and CCD to block the incident laser beam. A halogen lamp (FN-LH, Nikon) was directed from the top of the stage for bright-field imaging (Figure S2 for the details of optical setup). Transmittance spectra were collected for 15 × 11 pixels (~0.5 μm/pixel) with 30 ms exposure time and 100 μm input slit. Spectra for a bare liquid interface sample and a cover glass were used as reference for gold interface and solid gold samples, respectively.
Temperature and Interfacial Tension Measurements.
Micro-scale temperature profiles were obtained through thermal imaging by quadriwave shearing interferometry (TIQSI).56 A thermal imaging camera (SID4-HR, Phasics) was coupled to the same inverted microscope setup used in imaging and spectroscopy. Water was used as a medium and images were processed through built-in software (SIDTHERMO, Phasics). Interfacial tension was measured by the pendant drop method with a drop size analyzer (DSA100, KRÜSS GmbH). HFE was loaded in a 1 mL syringe with a needle (outer diameter: 0.5 mm) and a HFE drop was formed within a water–ethanol medium. Built-in software was used to analyze the drop shape and interfacial tension.
Optical Force Simulations.
Optical forces acting on an Au NP and on a PS particle were computed using a finite-element solver (COMSOL Multiphysics, wave optics module). In a three-dimensional model, an incident Gaussian beam propagating along the z-axis was implemented with a scattering boundary condition at the bottom, and perfectly matched layers were used to terminate the simulation domain in all the other directions. A minimum particle-to-boundary separation was set at a half of light wavelength (532 nm). The maximum size of mesh was set as one-quarter wavelength in the corresponding medium, i.e., one-quarter of free-space wavelength divided by the refractive index. Once full-wave simulations were completed, the optical force exerted on a particle was obtained by calculating the surface integral of Maxwell stress tensor, , defined as 57
where and * denote time average and complex conjugate, respectively, is the vector electric (magnetic) field, is the permittivity (permeability) of the liquid where the particle is immersed, and is an identity tensor. The optical force is then given by
with the outward unit vector at the surface of the particle along the surface normal and the surface element. The integration was performed over the surface of the particle with all the field quantities taking values from adjacent outside.
Flow Dynamics Simulations.
Flow profiles were obtained by solving the Navier–Stokes differential equation coupled with the Marangoni flow equation under Boussinesq approximation of incompressible liquid (finite-element solver, COMSOL Multiphysics). A three-dimensional domain (300 μm × 200 μm, width × height) was constructed with an axis-symmetry model. An interfacial boundary of two liquids was set as a fluid–fluid interfaces with an interfacial tension formula as a function of temperature and radial position (Note S5). A boundary heat source in terms of the Gaussian beam eq (eq 2) and absorptance (Figure S13c) was implemented at this interfacial boundary (Note S6).
Supplementary Material
ACKNOWLEDGMENTS
We acknowledge the financial support from the National Science Foundation (NSF-ECCS-2001650) and the National Institute of General Medical Sciences of the National Institutes of Health (R01GM146962).
Footnotes
Supporting Information
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsnano.4c01227.
Photographs of samples, optical setup, calculation details for interfacial deformation, image analysis at varying focal planes, deformation profiles of interfaces, microscopic images for optical trapping, measured trapping stiffness, reflectance measurement and calibration, photographs for phase behavior, microscopic images for droplet accumulation, simulated optical forces, simulation details for optical spectra, estimated interfacial nanoparticle distribution, derivation details for thermal conductivity and interfacial tension, simulated flow fields, photographs and microscopic images of silver NP-loaded interfaces, microscopic images for bubble-mediated reaction, functions used in calculations for Au NP-loaded interface(PDF)
Movie S1: Motion of PS particles clustered on an Au NP-loaded liquid–liquid interface upon laser illumination (MP4)
Movie S2: Motion of PS particles upon laser illumination in different liquid systems: gold interface, bare liquid–liquid interface, and monophasic liquid (water–ethanol mixture) (MP4)
Movie S3: Optothermal trapping of remnant HFE droplets on an Au NP-loaded liquid–liquid interface (MP4)
Movie S4: Motion of a PS particle upon laser illumination on a deposited film of Au NPs and on an interface prepared at high concentration (MP4)
Movie S5: Release of accumulated droplets upon deactivation of the laser after actuation and bubble formation at the interface (MP4)
Movie S6: Trapping of PS particles with various sizes and materials (MP4)
Movie S7: Bubble-mediated sol–gel reaction of TEOS (MP4)
The authors declare no competing financial interest.
Contributor Information
Youngsun Kim, Materials Science and Engineering Program, Texas Materials Institute, The University of Texas at Austin, Austin, Texas 78712, United States.
Kan Yao, Materials Science and Engineering Program, Texas Materials Institute, The University of Texas at Austin, Austin, Texas 78712, United States; Walker Department of Mechanical Engineering, The University of Texas at Austin, Austin, Texas 78712, United States.
Carolina Ponce, Walker Department of Mechanical Engineering, The University of Texas at Austin, Austin, Texas 78712, United States.
Yuebing Zheng, Materials Science and Engineering Program, Texas Materials Institute, The University of Texas at Austin, Austin, Texas 78712, United States; Walker Department of Mechanical Engineering, The University of Texas at Austin, Austin, Texas 78712, United States.
REFERENCES
- (1).Yang Z; Wei J; Sobolev YI; Grzybowski BA Systems of Mechanized and Reactive Droplets Powered by Multi-Responsive Surfactants. Nature 2018, 553, 313–318. [DOI] [PubMed] [Google Scholar]
- (2).Chai Y; Hasnain J; Bahl K; Wong M; Li D; Geissler P; Kim PY; Jiang Y; Gu P; Li S; Lei D; Helms BA; Russell TP; Ashby PD Direct Observation of Nanoparticle-Surfactant Assembly and Jamming at the Water-Oil Interface. Sci. Adv 2020, 6, eabb8675. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (3).Deng J; Molaei M; Chisholm NG; Yao T; Read A; Stebe KJ Active Colloids on Fluid Interfaces. Curr. Opin. Colloid Interface Sci 2022, 61, 101629. [Google Scholar]
- (4).Scatena LF; Brown MG; Richmond GL Water at Hydrophobic Surfaces: Weak Hydrogen Bonding and Strong Orientation Effects. Science 2001, 292, 908–912. [DOI] [PubMed] [Google Scholar]
- (5).Agmon N; Bakker HJ; Campen RK; Henchman RH; Pohl P; Roke S; Thämer M; Hassanali A Protons and Hydroxide Ions in Aqueous Systems. Chem. Rev 2016, 116, 7642–7672. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (6).Girot A; Petit J; Saiseau R; Guérin T; Chraibi H; Delabre U; Delville JP Conical Interfaces between Two Immiscible Fluids Induced by an Optical Laser Beam. Phys. Rev. Lett 2019, 122, 174501. [DOI] [PubMed] [Google Scholar]
- (7).Casner A; Delville J-P Adaptative Lensing Driven by the Radiation Pressure of a Continuous-Wave Laser Wave upon a near-Critical Liquid-Liquid Interface. Opt. Lett 2001, 26, 1418–1420. [DOI] [PubMed] [Google Scholar]
- (8).Aibara I; Katoh T; Minamoto C; Uwada T; Hashimoto S Liquid-Liquid Interface Can Promote Micro-Scale Thermal Marangoni Convection in Liquid Binary Mixtures. J. Phys. Chem. C 2020, 124, 2427–2438. [Google Scholar]
- (9).Berg S. Marangoni-Driven Spreading along Liquid-Liquid Interfaces. Phys. Fluids 2009, 21, 032105. [Google Scholar]
- (10).Lu Y; Jiang L; Yu Y; Wang D; Sun W; Liu Y; Yu J; Zhang J; Wang K; Hu H; Wang X; Ma Q; Wang X Liquid-Liquid Triboelectric Nanogenerator Based on the Immiscible Interface of an Aqueous Two-Phase System. Nat. Commun 2022, 13, 5316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (11).Girault HH Shake, Rattle and Roll. Nat. Mater 2006, 5, 851–852. [DOI] [PubMed] [Google Scholar]
- (12).Feng W; Chai Y; Forth J; Ashby PD; Russell TP; Helms BA Harnessing Liquid-in-Liquid Printing and Micro-patterned Substrates to Fabricate 3-Dimensional All-Liquid Fluidic Devices. Nat. Commun 2019, 10, 1095. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (13).Seong HG; Fink Z; Chen Z; Emrick T; Russell TP Bottlebrush Polymers at Liquid Interfaces: Assembly Dynamics, Mechanical Properties, and All-Liquid Printed Constructs. ACS Nano 2023, 17, 14731–14741. [DOI] [PubMed] [Google Scholar]
- (14).Montelongo Y; Sikdar D; Ma Y; McIntosh AJS; Velleman L; Kucernak AR; Edel JB; Kornyshev AA Electrotunable Nanoplasmonic Liquid Mirror. Nat. Mater 2017, 16, 1127–1135. [DOI] [PubMed] [Google Scholar]
- (15).Sun H; Li M; Li L; Liu T; Luo Y; Russell TP; Shi S Redox-Responsive, Reconfigurable All-Liquid Constructs. J. Am. Chem. Soc 2021, 143, 3719–3722. [DOI] [PubMed] [Google Scholar]
- (16).Li K; Wang J; Cai W; He H; Cen M; Liu J; Luo D; Mu Q; Gérard D; Liu YJ Electrically Switchable, Polarization-Sensitive Encryption Based on Aluminum Nanoaperture Arrays Integrated with Polymer-Dispersed Liquid Crystals. Nano Lett. 2021, 21, 7183–7190. [DOI] [PubMed] [Google Scholar]
- (17).Wang J; Li K; He H; Cai W; Liu J; Yin Z; Mu Q; Hisao VKS; Gérard D; Luo D; Li G; Liu YJ Metasurface enabled High resolution Liquid crystal Alignment for Display and Modulator Applications. Laser Photon. Rev 2022, 16, 2100396. [Google Scholar]
- (18).Karst J; Floess M; Ubl M; Dingler C; Malacrida C; Steinle T; Ludwigs S; Hentschel M; Giessen H Electrically Switchable Metallic Polymer Nanoantennas. Science 2021, 374, 612–616. [DOI] [PubMed] [Google Scholar]
- (19).Peng J; Jeong HH; Smith M; Chikkaraddy R; Lin Q; Liang HL; De Volder MFL; Vignolini S; Kar-Narayan S; Baumberg JJ FullyPrinted Flexible Plasmonic Metafilms with Directional Color Dynamics. Adv. Sci 2021, 8, 2002419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (20).Zheng YB; Yang YW; Jensen L; Fang L; Juluri BK; Flood AH; Weiss PS; Stoddart JF; Huang TJ Active Molecular Plasmonics: Controlling Plasmon Resonances with Molecular Switches. Nano Lett. 2009, 9, 819–825. [DOI] [PubMed] [Google Scholar]
- (21).Hsiao VKS; Zheng YB; Juluri BK; Huang TJ Light-Driven Plasmonic Switches Based on Au Nanodisk Arrays and Photoresponsive Liquid Crystals. Adv. Mater 2008, 20, 3528–3532. [Google Scholar]
- (22).Liu YJ; Si GY; Leong ESP; Xiang N; Danner AJ; Teng JH Light-Driven Plasmonic Color Filters by Overlaying Photoresponsive Liquid Crystals on Gold Annular Aperture Arrays. Adv. Mater 2012, 24, OP131–OP135. [DOI] [PubMed] [Google Scholar]
- (23).Zhao C; Liu Y; Zhao Y; Fang N; Huang TJ A Reconfigurable Plasmofluidic Lens. Nat. Commun 2013, 4, 2305. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (24).Mao X; Lin SCS; Lapsley MI; Shi J; Juluri BK; Huang TJ Tunable Liquid Gradient Refractive Index (L-GRIN) Lens with Two Degrees of Freedom. Lab Chip 2009, 9, 2050–2058. [DOI] [PubMed] [Google Scholar]
- (25).Hosseini P; Wright CD; Bhaskaran H An Optoelectronic Framework Enabled by Low-Dimensional Phase-Change Films. Nature 2014, 511, 206–211. [DOI] [PubMed] [Google Scholar]
- (26).Rios C; Stegmaier M; Hosseini P; Wang D; Scherer T; Wright CD; Bhaskaran H; Pernice WHP Integrated All-Photonic Non-Volatile Multi-Level Memory. Nat. Photonics 2015, 9, 725–732. [Google Scholar]
- (27).Zhang Y; Fowler C; Liang J; Azhar B; Shalaginov MY; Deckoff-Jones S; An S; Chou JB; Roberts CM; Liberman V; Kang M; Ríos C; Richardson KA; Rivero-Baleine C; Gu T; Zhang H; Hu J Electrically Reconfigurable Non-Volatile Metasurface Using Low-Loss Optical Phase-Change Material. Nat. Nanotechnol 2021, 16, 661–666. [DOI] [PubMed] [Google Scholar]
- (28).Wang Y; Landreman P; Schoen D; Okabe K; Marshall A; Celano U; Wong HSP; Park J; Brongersma ML Electrical Tuning of Phase-Change Antennas and Metasurfaces. Nat. Nanotechnol 2021, 16, 667–672. [DOI] [PubMed] [Google Scholar]
- (29).Tsoulos TV; Tagliabue G Self-Induced Thermo-Optical Effects in Silicon and Germanium Dielectric Nanoresonators. Nanophotonics 2020, 9, 3849–3861. [Google Scholar]
- (30).Sheldon SJ; Knight LV; Thorne JM Laser-Induced Thermal Lens Effect: A New Theoretical Model. Appl. Opt 1982, 21, 1663. [DOI] [PubMed] [Google Scholar]
- (31).Afridi A; Gieseler J; Meyer N; Quidant R Ultrathin Tunable Optomechanical Metalens. Nano Lett. 2023, 23, 2496–2501. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (32).Shcherbakov MR; Liu S; Zubyuk VV; Vaskin A; Vabishchevich PP; Keeler G; Pertsch T; Dolgova TV; Staude I; Brener I; Fedyanin AA Ultrafast All-Optical Tuning of Direct-Gap Semiconductor Metasurfaces. Nat. Commun 2017, 8, 17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (33).Zeng B; Huang Z; Singh A; Yao Y; Azad AK; Mohite AD; Taylor AJ; Smith DR; Chen HT Hybrid Graphene Metasurfaces for High-Speed Mid-Infrared Light Modulation and Single-Pixel Imaging. Light Sci. Appl 2018, 7, 51. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (34).Ko JH; Yoo YJ; Lee Y; Jeong HH; Song YM A Review of Tunable Photonics: Optically Active Materials and Applications from Visible to Terahertz. iScience 2022, 25, 104727. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (35).Chalikkara F; Varanakkottu SN Optofluidic Modulator Based on Thermoplasmonically Controlled Liquid-Liquid Interface. Opt. Lett 2021, 46, 3993–3996. [DOI] [PubMed] [Google Scholar]
- (36).Kuiper S; Hendriks BHW Variable-Focus Liquid Lens for Miniature Cameras. Appl. Phys. Lett 2004, 85, 1128–1130. [Google Scholar]
- (37).Klyuev DS; Fliagin VM; Al-Muzaiqer M; Ivanova NA Laser-Actuated Optofluidic Diaphragm Capable of Optical Signal Tracking. Appl. Phys. Lett 2019, 114, 011602. [Google Scholar]
- (38).Song L; Xu BB; Cheng Q; Wang X; Luo X; Chen X; Chen T; Huang Y Instant Interfacial Self-Assembly for Homogeneous Nanoparticle Monolayer Enabled Conformal “Lift-on” Thin Film Technology. Sci. Adv 2021, 7, eabk2852. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (39).Wunenburger R; Casner A; Delville JP Light-Induced Deformation and Instability of a Liquid Interface. I. Statics. Phys. Rev. E - Stat. Nonlinear, Soft Matter Phys 2006, 73, 036314. [DOI] [PubMed] [Google Scholar]
- (40).Kim Y; Ding H; Zheng Y Investigating Water/Oil Interfaces with Opto-Thermophoresis. Nat. Commun 2022, 13, 3742. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (41).Bełej M; Grześkiewicz K; Miniewicz A Laser Light-Induced Deformation of Free Surface of Oil Due to Thermocapillary Marangoni Phenomenon: Experiment and Computational Fluid Dynamics Simulations. Phys. Fluids 2022, 34, 082104. [Google Scholar]
- (42).Forth J; Kim PY; Xie G; Liu X; Helms BA; Russell TP Building Reconfigurable Devices Using Complex Liquid-Fluid Interfaces. Adv. Mater 2019, 31, 1806370. [DOI] [PubMed] [Google Scholar]
- (43).Garbin V; Crocker JC; Stebe KJ Nanoparticles at Fluid Interfaces: Exploiting Capping Ligands to Control Adsorption, Stability and Dynamics. J. Colloid Interface Sci 2012, 387, 1–11. [DOI] [PubMed] [Google Scholar]
- (44).Lin L; Peng X; Mao Z; Wei X; Xie C; Zheng Y Interfacial-Entropy-Driven Thermophoretic Tweezers. Lab Chip 2017, 17, 3061–3070. [DOI] [PubMed] [Google Scholar]
- (45).Lee HE; Ahn HY; Mun J; Lee YY; Kim M; Cho NH; Chang K; Kim WS; Rho J; Nam KT Amino-Acid- and Peptide-Directed Synthesis of Chiral Plasmonic Gold Nanoparticles. Nature 2018, 556, 360–364. [DOI] [PubMed] [Google Scholar]
- (46).Wang Z; Walter LS; Wang M; Petkov PS; Liang B; Qi H; Nguyen NN; Hambsch M; Zhong H; Wang M; Park S; Renn L; Watanabe K; Taniguchi T; Mannsfeld SCB; Heine T; Kaiser U; Zhou S; Weitz RT; Feng X; Dong R Interfacial Synthesis of Layer-Oriented 2D Conjugated Metal-Organic Framework Films toward Directional Charge Transport. J. Am. Chem. Soc 2021, 143, 13624–13632. [DOI] [PubMed] [Google Scholar]
- (47).Ameloot R; Vermoortele F; Vanhove W; Roeffaers MBJ; Sels BF; De Vos DE Interfacial Synthesis of Hollow Metal-Organic Framework Capsules Demonstrating Selective Permeability. Nat. Chem 2011, 3, 382–387. [DOI] [PubMed] [Google Scholar]
- (48).Peng L; Peng H; Xu L; Wang B; Lan K; Zhao T; Che R; Li W; Zhao D Anisotropic Self-Assembly of Asymmetric Mesoporous Hemispheres with Tunable Pore Structures at Liquid-Liquid Interfaces. J. Am. Chem. Soc 2022, 144, 15754–15763. [DOI] [PubMed] [Google Scholar]
- (49).Mendez-Ortiz W; Stebe KJ; Lee D Ionic Strength-Dependent Assembly of Polyelectrolyte-Nanoparticle Membranes via Interfacial Complexation at a Water-Water Interface. ACS Nano 2022, 16, 21087–21097. [DOI] [PubMed] [Google Scholar]
- (50).Durrer J; Agrawal P; Ozgul A; Neuhauss SCF; Nama N; Ahmed D A Robot-Assisted Acoustofluidic End Effector. Nat. Commun 2022, 13, 6370. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (51).Rajeeva BB; Kunal P; Kollipara PS; Acharya PV; Joe M; Ide MS; Jarvis K; Liu Y; Bahadur V; Humphrey SM; Zheng Y Accumulation-Driven Unified Spatiotemporal Synthesis and Structuring of Immiscible Metallic Nanoalloys. Matter 2019, 1, 1606–1617. [Google Scholar]
- (52).Rajeeva BB; Wu Z; Briggs A; Acharya PV; Walker SB; Peng X; Bahadur V; Bank SR; Zheng Y Point-and-Shoot” Synthesis of Metallic Ring Arrays and Surface-Enhanced Optical Spectroscopy. Adv. Opt. Mater 2018, 6, 1701213. [Google Scholar]
- (53).Yang C; Kaipa U; Mather QZ; Wang X; Nesterov V; Venero AF; Omary MA Fluorous Metal-Organic Frameworks with Superior Adsorption and Hydrophobic Properties toward Oil Spill Cleanup and Hydrocarbon Storage. J. Am. Chem. Soc 2011, 133, 18094–18097. [DOI] [PubMed] [Google Scholar]
- (54).Jayaramulu K; Geyer F; Schneemann A; Kment Š; Otyepka M; Zboril R; Vollmer D; Fischer RA Hydrophobic Metal-Organic Frameworks. Adv. Mater 2019, 31, 1900820. [DOI] [PubMed] [Google Scholar]
- (55).Chen T-H; Popov I; Zenasni O; Daugulis O; Miljanić OŠ Superhydrophobic Perfluorinated Metal-Organic Frameworks. Chem. Commun 2013, 49, 6846. [DOI] [PubMed] [Google Scholar]
- (56).Baffou G; Bon P; Savatier J; Polleux J; Zhu M; Merlin M; Rigneault H; Monneret S Thermal Imaging of Nanostructures by Quantitative Optical Phase Analysis. ACS Nano 2012, 6, 2452–2458. [DOI] [PubMed] [Google Scholar]
- (57).Jackson JD Maxwell Equations, Macroscopic Electromagnetism, Conservation Laws. In Classical Electrodynamics; John Wiley & Sons: New York, 1999. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.