Abstract
Overloaded trucks have long posed a threat to the road safety. To assess truck payload more effectively, this study focus on tire temperature data obtained through infrared thermal imaging. It is feasible to analyse the payload by monitoring one single representative tire. Tire sidewall surface is the best area for data extraction. Truck overload caused significant increase of gas temperature in tires, as well as external temperature. The internal temperature can be calculated with real gas equation of state. By studying the relationship between internal gas temperature of tire and payload, it is demonstrated that monitoring the temperature of tire sidewall surface is an innovative, remote, and real-time method to assess the payload situation of moving trucks.
Keywords: Infrared thermal imaging, Monitoring, Overloaded truck, Payload, Tire temperature, Equation of state
1. Introduction
In China, overloaded trucks have long been recognized as one of the four major causes of road accidents, resulting in casualties, property damage, and traffic disruption [1]. Nearly one-fifth of traffic accidents and one-third of traffic accident fatalities are attributed to overloaded trucks [2]. In the United States, trucks weighing over 33,000 pounds accounted for 65 % of fatal traffic accidents in 2021 [3]. Overloading has thus emerged as a significant factor affecting transportation safety. Additionally, overloaded trucks cause substantial rutting and damage to roadbeds [4]. Roads frequented by overloaded vehicles may experience a 90 % reduction in lifespan compared to normal roads with normal vehicle traffic [5].
Therefore, it is crucial to detect vehicle overloading effectively for reducing traffic accidents and prolonging the lifespan of transportation infrastructure.
Static weighing technology for overload detection was used a long time ago. Because of its slow operation and other limitations, this technology has been gradually phased out. Dynamic weighing technology such as weighing-in-motion (WIM) was first introduced at the National Traffic Conference in the United States in 1954. Since then, it has been widely utilized in most countries [6]. This technology has been developed into three main types: bending plate WIM, piezoelectric WIM, and the latest B-WIM [[5], [6], [7], [8]]. Basic WIM uses weighing sensors and bending plates for weight measurement. Because of large equipment size and slower detection speed, it has gradually been replaced by piezoelectric WIM utilizing inductive circuits with quartz, ceramic, or polymer material. This type of WIM detects vehicle load by sensing the electric signal generated when a vehicle passes over the sensors [9,10]. B-WIM, invented later, utilizes instruments such as sensors and circuits installed on bridges to measure the response of a vehicle passing by a sensor to calculate vehicle axle load [11].
These WIM systems have the advantage of measuring the weight of the vehicles without stopping them, but also has disadvantage of error in weight detection when vehicles stop suddenly. Additionally, the WIM systems must be installed at fixed locations, they are susceptible to evasion tactics.
The force provided by pneumatic tire pressure directly support the vehicle against the gravity. The pressure and temperature of tires change with deformation under different vehicle loads. Temperature field analysis of tires was applied to the study of rubber properties [[12], [13], [14], [15], [16]]. Research methods in this area include simulation analysis and experiments. Researchers used Finite Element Analysis (FEM) to simulate the internal temperature field distribution of tires, and compare the simulation results with measurements from embedded temperature sensors [10,12,17,18]. Many studies found certain relationship between tire temperature and various factors. For example, Li Jie et al. [19] utilized infrared thermometry to investigate the cooling effect of wind on tire tread; Thanh-Cong Nguyen et al. [17] used finite element methods to illustrate the relationship between temperature and speed.
Tire failure analysis has been studied extensively [20]. Common in-service tire failures include sidewall flex break (run low), belt/tread detachment, and rapid loss of pressure through tire rupture (blow out) [21]. At fixed inflation pressure, when the vehicle load increases, the tire deflection increases. Rolling tires go through cycles of deflection and recovery, and this pumping action generate heat in tires, where temperatures of both structural materials and internal gas increase. Under heavy load, this could further cause thermal damage of tires during operation, e.g., thermal spalling, bulging, and degumming etc.
Most of previous studies address the material integrity, durability and failure prevention of tires. However, inflation air or gas play a critical role for the pneumatic tire. Weighing technologies have inherent drawbacks, and are inadequate for limited personnels to manage expanding road networks with increasing vehicles, especially in developing countries such as China. Other variables of vehicles need to be investigated for better solution.
Current project objective is to provide a new method to monitor overloaded trucks and alert the transportation law enforcement personnels to take action. This study focused on gas state inside the tire and uses proper gas equation to illustrate the relationship between temperature and pressure. Infrared thermography provides a practical tool for temperature monitoring to be used in outdoor and real-time situations, and can be a better method to prevent accidents and damages from overloaded trucks.
2. Methods
2.1. Tire temperature monitoring experiment
To obtain temperature data of tire sidewalls corresponding to different loads in real-world scenarios, experiments were conducted using passenger car (Fig. 1), bus with 52-passenger capacity (Fig. 2), and freight truck (Fig. 3). First, tire region of a SUV was filmed at a low speed of less than 20 km/h to explore suitable method of capturing infrared thermal images. Subsequently, bus tires were filmed at stops after running hourly to further refine experimental procedures such as filming distance and height above ground. Finally, freight trucks were studied, and the load was varied and infrared thermal images were recorded. The tire specifications of the car, bus, and freight truck used in this study are shown in Table 1. All tire parameters comply with the Chinese national standards GB/T 2978–2014 ″Passenger Car Tire Specifications, Dimensions, Air Pressure, and Load” and GB/T 9744–2015 ″Truck Tire Load".
Fig. 1.
Passenger car (SUV).
Fig. 2.
School bus.
Fig. 3.
Freight truck.
Table 1.
Experimental tire specifications.
| Vehicle type | Freight Truck | School Bus | Passenger Car |
|---|---|---|---|
| Specification | 11.00R20 | 11R22.5 | 265/65R17 |
| Outer Diameter(m) | 1.1 | 1.054 | 0.776 |
| Rim diameter(m) | 0.508 | 0.572 | 0.43 |
| Maximum tire load (kg) | 3550/3250 | 3150/2900 | 1120 |
| Maximum speed (km/h) | 100 | 90 | 190 |
| Recommended maximum inflation pressure | 930 KPa(26 °C) | 930 KPa(25 °C) | 290 KPa(25 °C) |
The truck is a four-axle, front-engine, rear-wheel drive flatbed truck (8 × 4) with an unladen weight of 13 tons and a payload capacity of 18 tons. The first and second axles have single tire on both sides with positive wheel offset. The third and fourth axles have dual tires on both sides with negative wheel offset.
The infrared thermal imager used in the experiment is a product of Raytron Technology Co. Ltd. (Yantai, China) model AT61F. This online infrared thermal imager has a fixed focal length and a temperature measurement range of 0 °C–550 °C, with an accuracy of ±2 % of the reading. The operating temperature range is −20 °C–60 °C, and the generated image resolution is 540 × 512 pixels. At a distance from 1 m to 10 m, the minimum detectable surface area is approximately from 1.66 mm2 to 274 mm2. The accompanying software is IR Discovery, which can perform pseudo-colour transformation on the videos or images captured by the thermal imager, and extract temperature data from specific areas, and export the data in.csv or.docx format.
The experiments were conducted with different payloads of the truck. In each experiment, the truck payload varied by percentage of capacity, and the truck travelled around the route at a fixed speed. The infrared thermal image of the passenger-side tire was captured at 10-min interval. The temperature was also checked with a handheld infrared thermometer until the tire side wall temperature stabilized. The tires were numbered from 1 to 4 sequentially from the front to the rear on the passenger side (hereinafter referred to as follows).
2.2. Selection of temperature measurement area
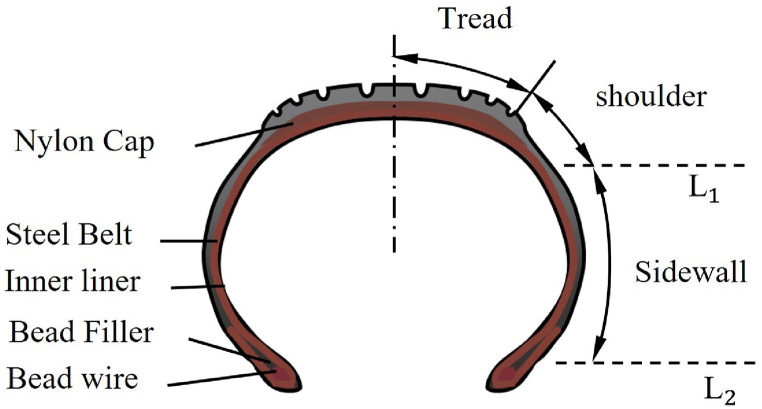
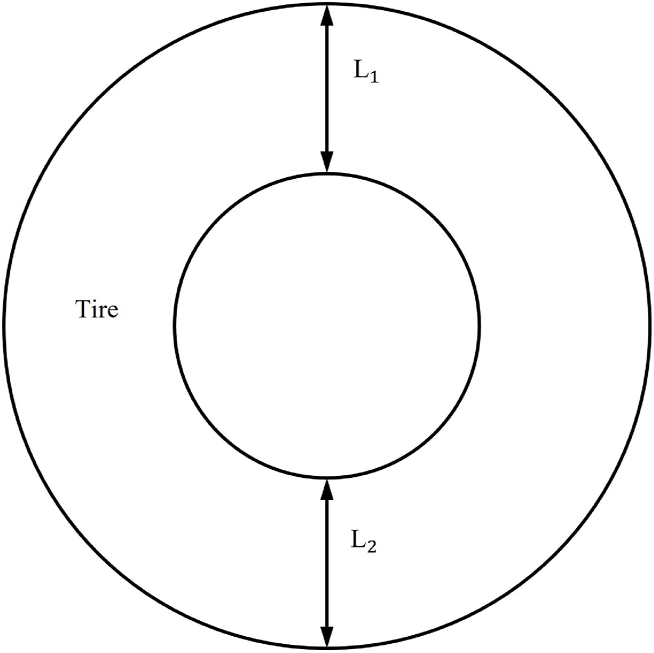
The infrared thermal imager captures continuous videos, with each picture containing the temperature distribution of objects in the field of vision. Different colours represent different temperatures, and the shapes formed by these colours maintain similarity or correlation to the actual contours of objects (Fig. 4). Selecting the temperature measurement surface, line segments, or points in each picture requires a scientific method. In each image, there are tires appearing in round shape, which can be divided with radial lines into sections, and the temperature can be further measured along the lines. Finally, these radial lines are selected as the data source for tire temperature measurement.
Fig. 4.
Sketch of Tire Cross Section. L1 is the boundary line between the tire shoulder and sidewall, L2 is the boundary line between the tire sidewall and rim.
2.3. Analysis of tire forces
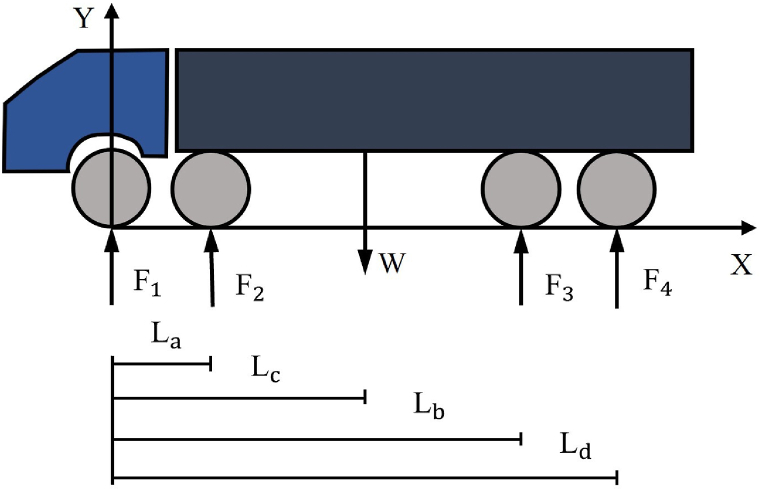
The force diagram of the four-axle truck is shown in Fig. 5. , , , and represent the support forces from the ground to the axles respectively. W represents the gravity of the truck. , , and represent the distances from the forces to the origin respectively.
Fig. 5.
Four-axle truck force diagram.
When the vehicle is stationary, based on force equilibrium in the x and y directions, we have Equation (1):
| (1) |
Based on torque equilibrium along the positive x-axis direction, we have Equation (2):
| (2) |
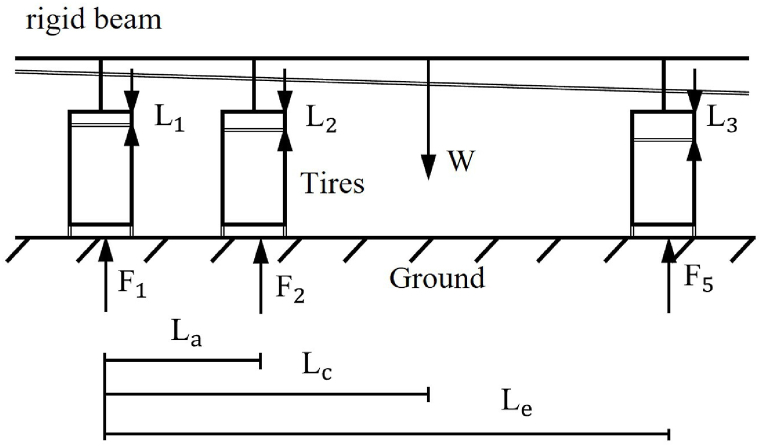
To simplify the model, the chassis is treated as an entire structure under both the cabin and the cargo, with the same stiffness. The deformation of the suspension and shock absorber devices is also assumed to be equal. The deformation of the tires will be proportional to distributed load (Fig. 6). A balance shaft connects the 3rd and 4th axles, which can evenly distribute force between the two axles, and generate the same deflection height at the 3rd and 4th wheels. Using to represent the length from the first axle to the balance shaft, Equations (1), (2)) can be simplified to Equations (3), (4), (5)):
| (3) |
| (4) |
| (5) |
Fig. 6.
Tire deflection model.
Furthermore, applying Hooke's Law, because the deformation of each tire equals the ground support force divided by the radial stiffness of the tire, it is expressed as:
| (6) |
| (7) |
Ground support forces for different tires can be calculated from Equations (3), (4), (5), (6), (7)).
Table 2 shows the axle distance data.
Table 2.
Wheelbase data.
| Wheelbase | Length(m) |
|---|---|
| La | 1.8 |
| Lb | 6.375 |
| Lc | 5.3 |
| Ld | 7.775 |
| Ld | 7.075 |
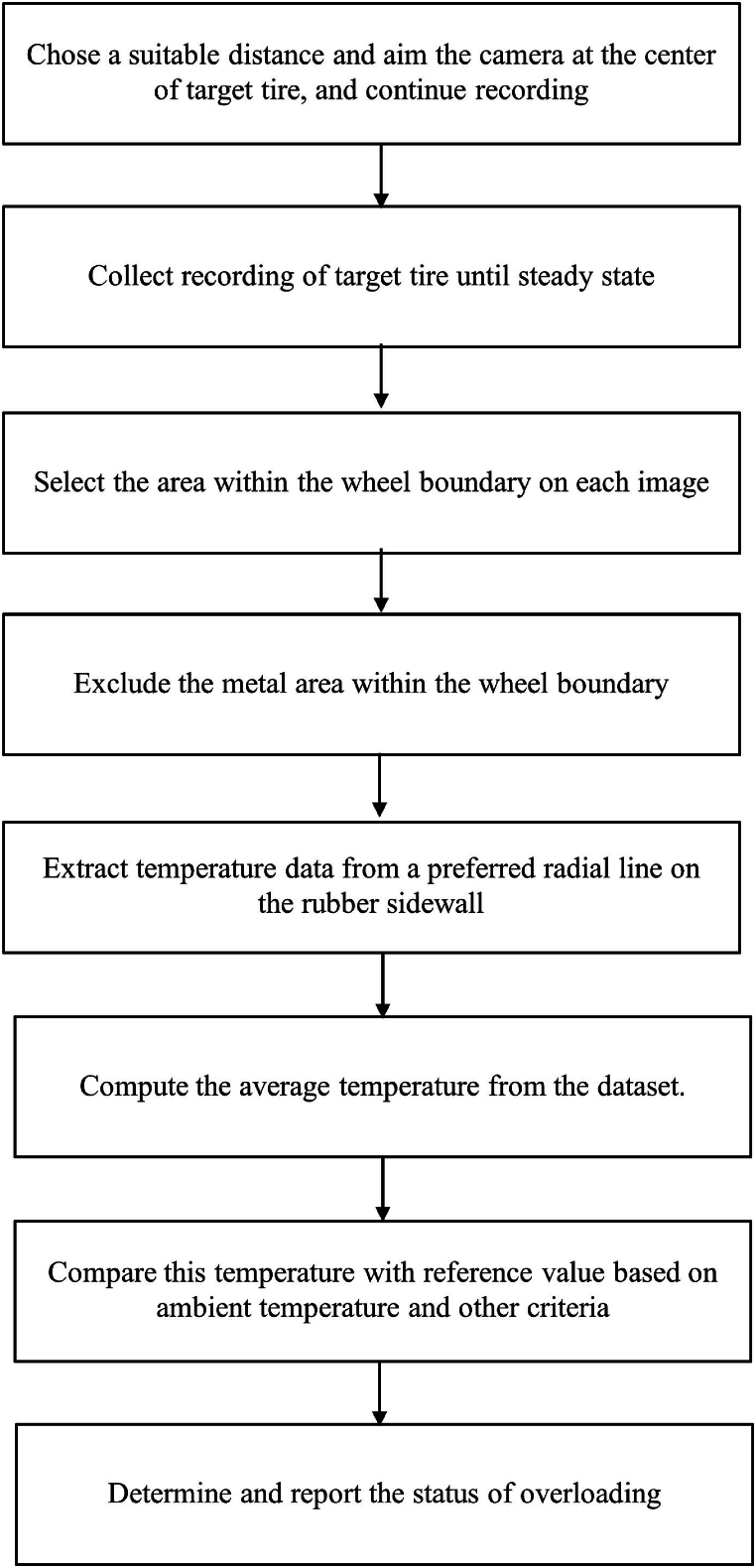
The research methodology is presented in the process flowchart of Fig. 7.
Fig. 7.
Process flowchart.
3. Results and analysis
The experiments were conducted with five different payloads of the truck (Table 3).
Table 3.
Environmental temperatures of experiment groups.
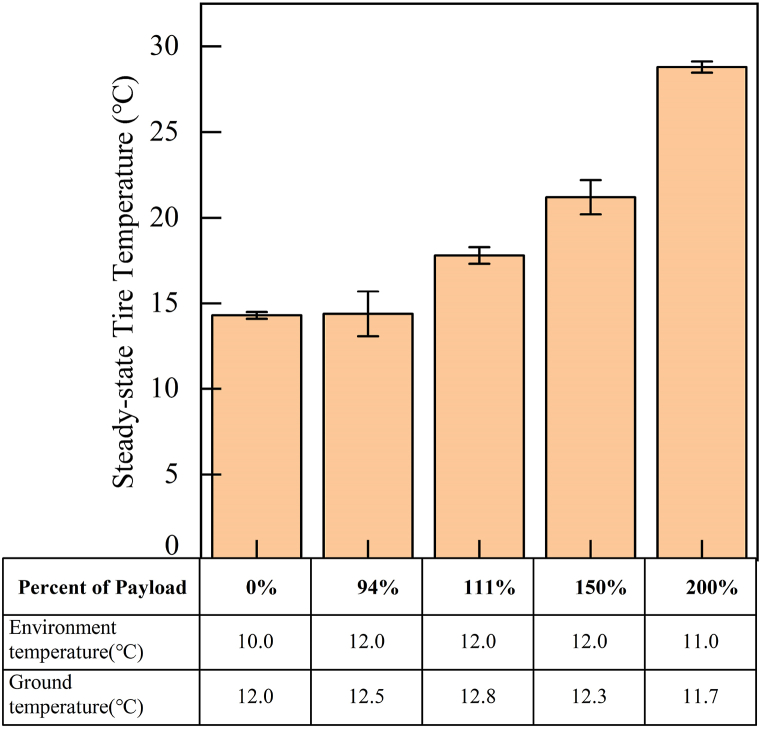
| Percentage of Payload | Air Temperature(°C) | Ground Temperature(°C) |
|---|---|---|
| 0 % | 10.0 | 12.0 |
| 94 % | 11.0 | 13.0 |
| 111 % | 12.0 | 13.0 |
| 150 % | 12.0 | 12.0 |
| 200 % | 11.0 | 12.0 |
The measured deflection heights of the 1st and 2nd tires are shown in Table 4.
Table 4.
Change of tire deflection. Relative error 2 %.
| Experimental Group | No. 1 Tire Deflection Amount(m) | No. 2 Tire Deflection Amount(m) |
|---|---|---|
| Payload 0 % | 0.0148 | 0.0185 |
| Payload 94 % | 0.0188 | 0.0197 |
| Payload 111 % | 0.0196 | 0.0234 |
| Payload 150 % | 0.0228 | 0.0228 |
| Payload 200 % | 0.0224 | 0.0224 |
Because the infrared thermal imaging cannot observe the inner tires of the dual tires, it is assumed that the truck's centre of gravity is located on the central line, and the load is equal on each tire of the same axle. Ground support forces for the tires under different payloads are calculated and shown in Table 5.
Table 5.
Ground supporting force for tires at different payloads.
| Payload Percent | F1(kN) | F2(kN) | F4(kN) |
|---|---|---|---|
| 0 % | 8.28 | 10.3 | 11.3 |
| 94 % | 20.6 | 21.6 | 26.2 |
| 111 % | 21.5 | 25.6 | 28.7 |
| 150 % | 28.2 | 28.2 | 34.9 |
| 200 % | 34.5 | 34.5 | 42.8 |
3.1. Temperature measurement area
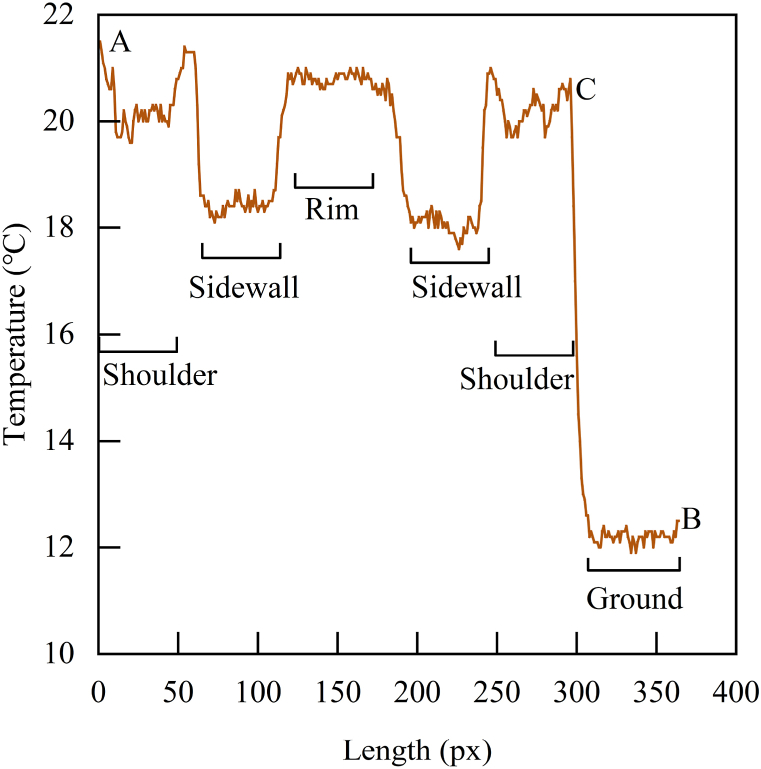
Fig. 8 shows an example of thermal images of tires after driving. Monitoring the tire temperatures of cars and school buses revealed that the tread area is uneven because of grooves and presence of steel wires under the rubber. The shoulder area has larger variation in rubber thickness and undergoes repetitive deformation, causing unstable temperature. Therefore, temperature points in the tread and shoulder areas were excluded. In this study, radial lines for temperature measurement are between the shoulder-sidewall boundary and the rim-sidewall boundary, which cover the entire sidewall. The material of tire sidewall is mainly rubber, and the rubber thickness is relatively uniform. As shown in Fig. 8, a temperature measurement line L₁ was drawn vertically from the tire shoulder through the axis of the tire, then to the ground, with the shoulder-sidewall boundary serving as the starting point (0px) for the line.
Fig. 8.
Image of the temperature measurement area and the temperature measurement line. The temperature measured in the AC section is the temperature of the wheel including the hub, and the temperature measured in the CB section is the temperature of the ground.
The temperature data extracted from this measurement line were plotted in Fig. 9. It showed the average temperature of the rim metal part was relatively high, and the overall temperature distribution was radially symmetrical. The transition zone from the tire shoulder to the sidewall had higher temperature, which was related to significant stress deformation. There was a sharp temperature drop from the tire to the ground.
Fig. 9.
Temperature profile of tire. Corresponding to L1 in Fig. 8., 1px is about 6.2 mm and the ambient temperature is 10 °C. The horizontal axis unit px is the unit pixel point of the picture, and the horizontal axis from 0px to 350px corresponds to the length of the temperature measurement line from A to B, the same as the following figures. Due to the small differences in temperature measurement distances, the actual distance represented by 1px varies from picture to picture and is labelled in the caption.
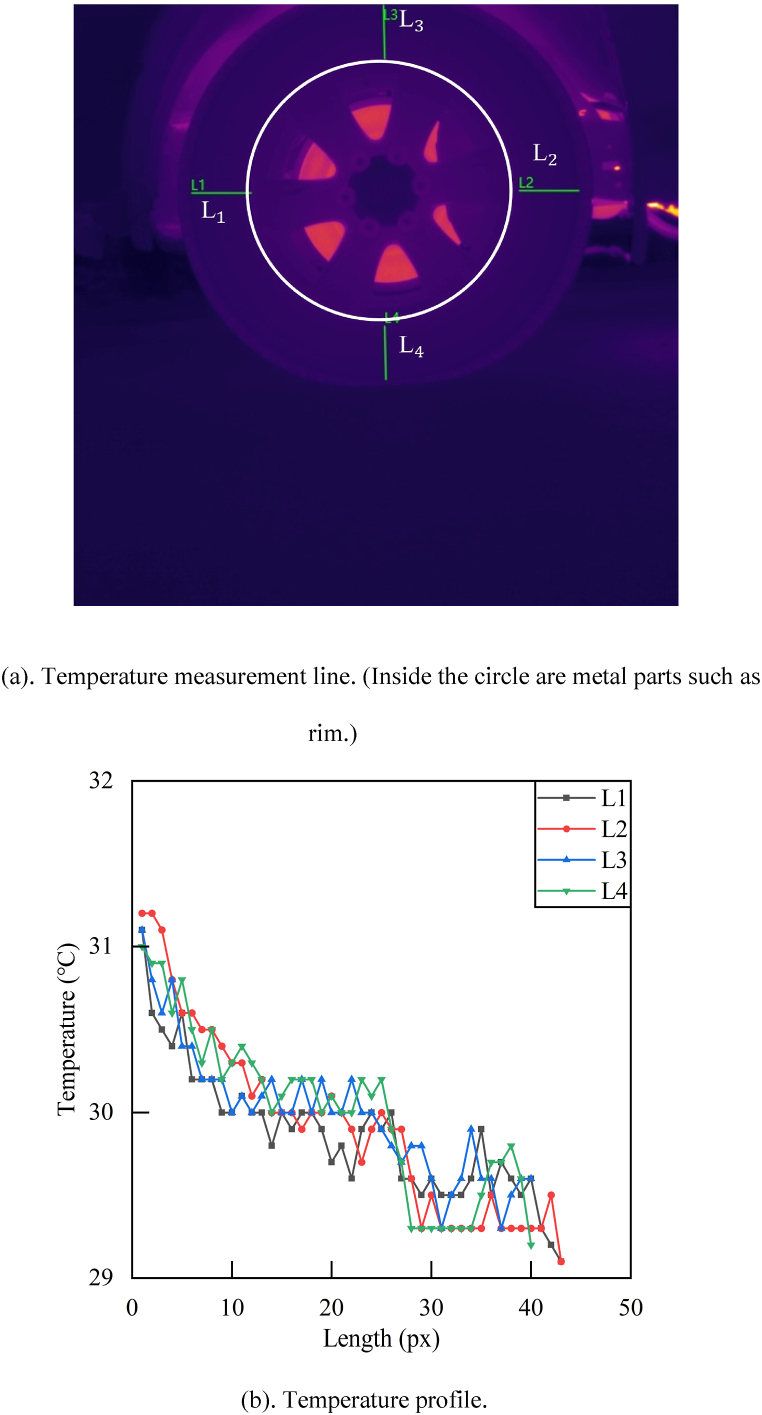
For the rubber sidewall, four temperature measurement lines were selected for data extraction, with two horizontal and two vertical lines, labelled as L₁ to L₄ (Fig. 10(a)). The direction of the measurement lines started from the sidewall towards the rim, covering only the sidewall area, with an average of 47 data points per line segment. As shown in Fig. 10(b), the temperature gradually decreased from the shoulder to the rim.
Fig. 10.
Temperature measurement line and temperature profile of off-road tire temperature.
Fig. 10(a). Temperature measurement line. (Inside the circle are metal parts such as rim.)
Fig. 10(b). Temperature profile.
To validate the symmetry of the temperature distribution, a normality test was conducted on the data from the four measurement lines. After conducting the inverse variance analysis on the four sets of data, it showed that at a confidence level of 0.05, the p-value was 0.176, which is greater than 0.05. Therefore, it can be concluded that there is no significant difference between the data sets.
In summary, the data obtained from the radial temperature measurement lines are similar after stable driving for 10 min. By identifying and excluding the rim area in the images, the measurement area of the tire in each image can be simplified to a measurement line, reducing the amount of data processing, and obtaining representative data. While processing many experimental images, the L3 measurement line on the upper part of the tire was selected as the source of temperature data sampling.
3.2. Temperature measurement tire
For vehicles with more than two axles, monitoring all tires would require a significant amount of data processing. The distribution of load in vehicles follows certain design principles. If it is possible to represent the entire vehicle's state by monitoring one or two tires, and achieving accurate temperature measurement, it would greatly improve response speed. Because of the ample space in front of the tires of the first and third axles of the truck, they bear the majority of the wind resistance while in motion, where the heat generated by tire deformation during rotation and friction with the ground were carried away by strong airflow [22]. As the vehicle's speed increases, this air-cooling effect becomes more pronounced.
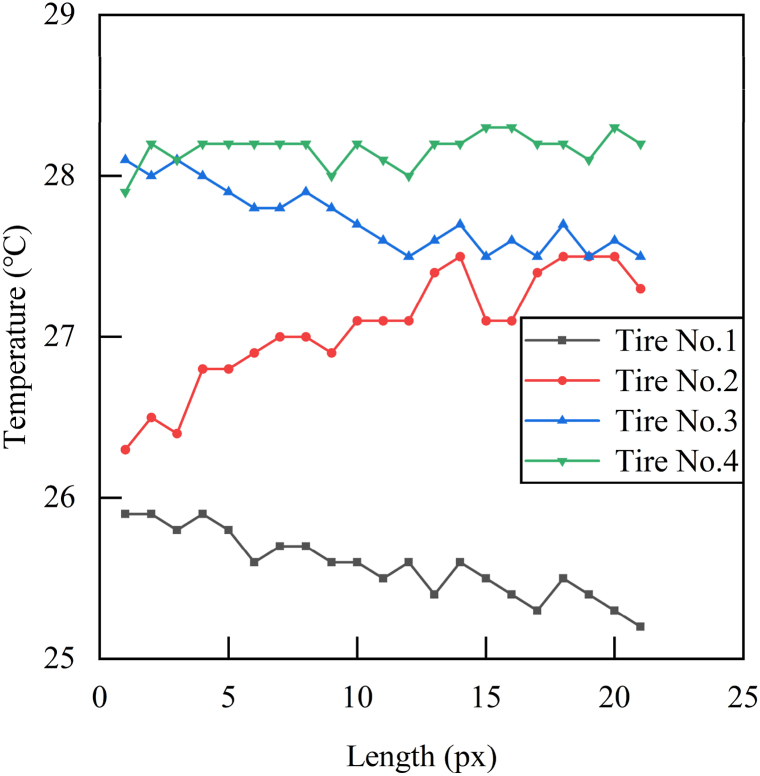
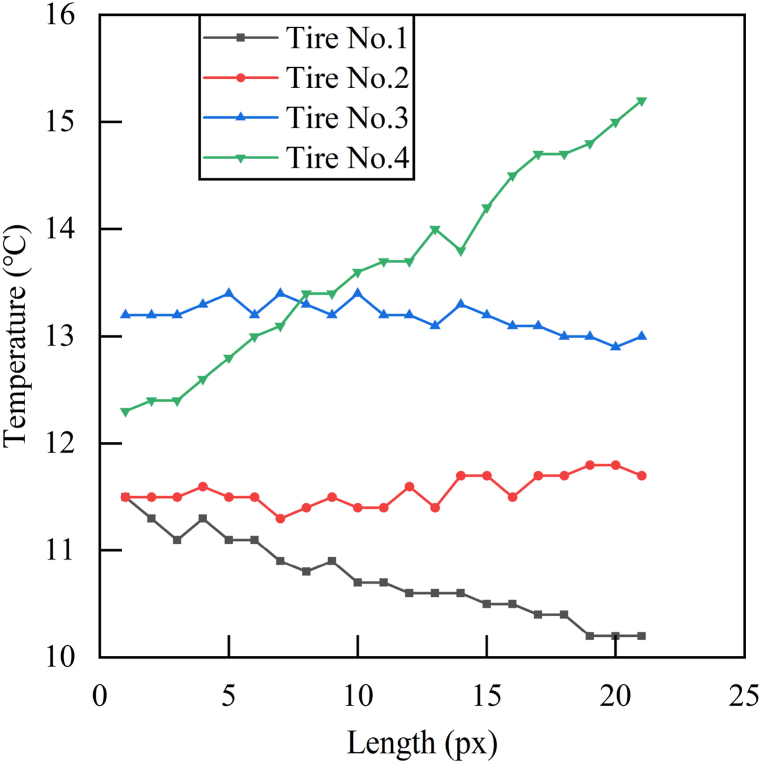
Fig. 11, Fig. 12 illustrate the tire temperatures of trucks with 200 % and 94 % payloads respectively, which were recorded immediately when the truck stopped after traveling for 75 min. It showed the temperature of tire No. 1 is lower than that of tire No. 2, and the temperature of tire No. 3 was lower than that of tire No. 4. The tire shoulder temperature of tires No. 1 and 3 was higher than the temperature near the rim, while for tires No. 2 and 4, it was the opposite. Because of the air-cooling effect, the temperature difference near the rim was very significant among different tires.
Fig. 11.
Payload 200 % tire temperature distribution (1px ~ 3.8 mm).
Fig. 12.
Payload 94 % tire temperature distribution (1px ~ 5.7 mm).
Using the Two-tailed significance tests and Spearman's rank correlation coefficient, correlation analysis of tire temperatures for tires No. 1–4 in Fig. 11, Fig. 12 were conducted in pairs, and the results are shown in Table 6.
Table 6.
Correlation analysis of experimental tires at 111 % payload, 94 % payload. 1.x indicates tire x of 111 % payload experiment; 2.x indicates tire x of 94 % payload experiment.
| Serial Number | No. 1.2 |
No. 1.4 |
No. 2.2 |
No. 2.4 |
|---|---|---|---|---|
| P Value | ||||
| No. 1.1 | <0.0001 | |||
| No. 1.3 | 0.317 | |||
| No. 2.1 | 0.00481 | |||
| No. 2.3 | 4.63e-4 | |||
The correlation coefficients between tires No. 1 and 2, as well as tires No. 3 and 4 are all less than 0.5, indicating a weak correlation. Furthermore, tire No. 1 was more affected by wind cooling, and tire No. 2 was closer to the engine and more susceptible to heat radiation. Additionally, since tire No. 3 was more affected by wind cooling compared to tire No. 4. Therefore, tires No. 4 was chosen as the experimental subject to better represent the truck load status.
In summary, it is evident that the distribution relationship of tire temperature remains consistent in each experiment for a four-axle truck, after conducting correlation analysis on the four groups of tires in the five experiments. Because tire No. 4 experienced less interference from wind cooling, it is selected as the subject of experimental analysis to minimize uncertainties and improve the reliability of experimental data.
3.3. Steady state temperature of tires
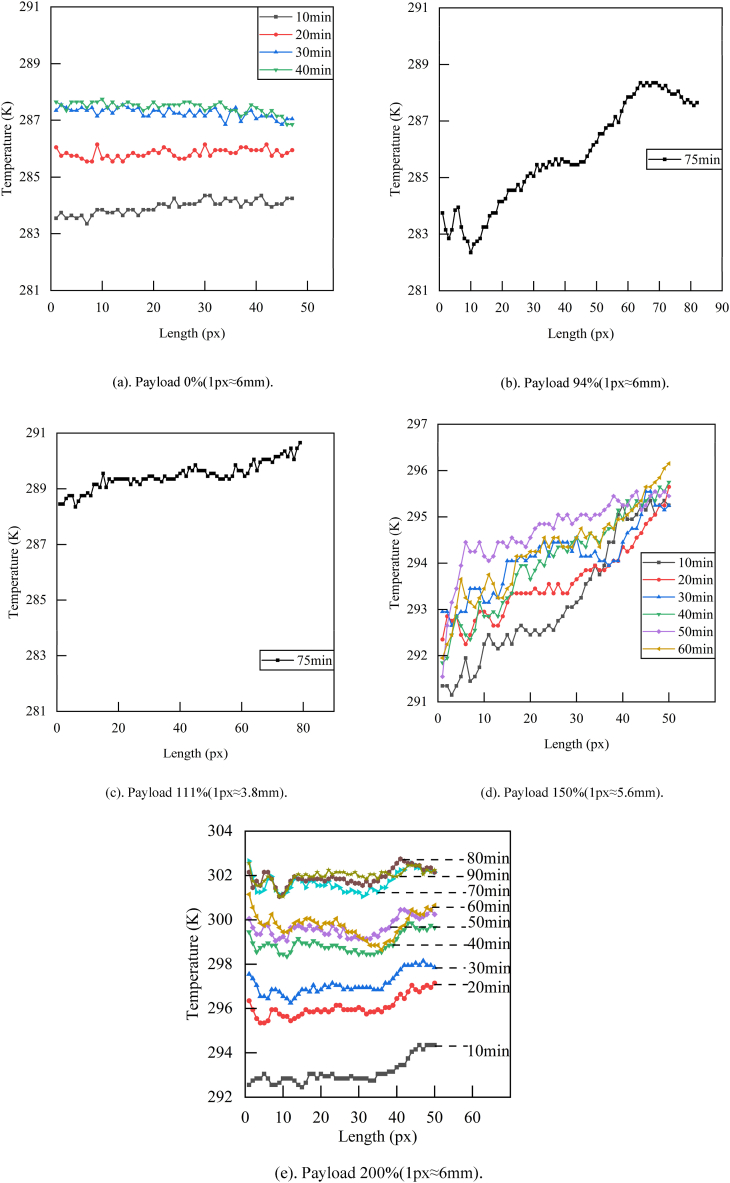
Based on previous findings, the truck was stopped after running for a certain period, and the infrared thermal image of the No. 4 tire was immediately captured. The extracted tire temperature data are shown in Fig. 13. In the experiments with 0 %, 150 %, and 200 % payload, truck images were recorded after every 10 min of continuous driving. In the experiments with 94 % and 111 % payload, truck images were recorded only after 75 min of continuous driving because of time constraints. During image recording, the truck was in an idle state.
Fig. 13.
Change of tire temperature with time for different payloads.
Fig. 13(a). Payload 0 %(1px ~ 6 mm).
Fig. 13(b). Payload 94 %(1px ~ 6 mm).
Fig. 13(c). Payload 111 %(1px ~ 3.8 mm).
Fig. 13(d). Payload 150 %(1px ~ 5.6 mm).
Fig. 13(e). Payload 200 %(1px ~ 6 mm).
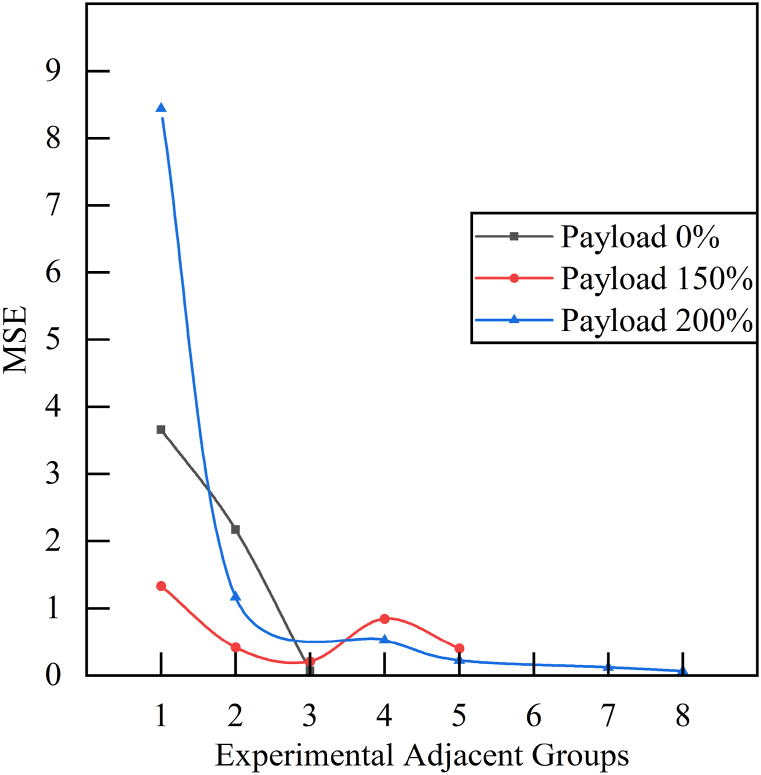
To further determine whether the tire temperature had reached a steady state, the mean square error (MSE) between adjacent tire temperature curves in Fig. 13(a), (d), and 13(e) was calculated. As shown in Fig. 14, the MSE decreased rapidly with time. The MSE of the three experimental groups decreased to below 0.5 as early as 30 min and as late as 70 min of driving. At this point, the temperature difference between the two groups was less than 0.7 °C, which was lower than 5 % of the lowest steady-state tire temperature (14.3 °C) among the five groups. Therefore, when the MSE decreased to below 0.5, temperature data could be considered as the steady-state tire temperature for the corresponding experimental group. In the experiments with 94 % and 111 % payload, the driving time of 75 min was more than the time required for the experiments with 150 % and 200 % payload to reach steady state, so that only one measurement was conducted to save vehicle occupancy time. The images obtained immediately after truck stop were used for the steady-state tire temperature of these two groups. For these two groups, three temperature measurement lines were selected, and the average temperature was taken as the steady-state tire temperature.
Fig. 14.
Mean Square Error (MSE) for each experimental group.
Table 7 shows the steady-state tire temperatures for all five groups, to be compared with internal gas temperature calculated from equation of state. Fig. 15 shows the accuracy of these temperatures and relevant ambient temperatures.
Table 7.
Average steady-state tire temperature. The number of data points is the number of temperature data points extracted from the corresponding temperature measurement line.
| Payload Weight | Data Point | Steady-State Tire Temperature(K) |
|---|---|---|
| Payload 0 % | 52 | 287 |
| Payload 94 % | 82 | 288 |
| Payload 111 % | 78 | 291 |
| Payload 150 % | 53 | 294 |
| Payload 200 % | 50 | 302 |
Fig. 15.
Steady-state tire temperature for different payloads.
As shown in Table 8, when the temperature difference was above 5.5 °C, the truck was in overload status with more than 10 % tolerance.
Table 8.
Temperature comparison. The second column is the average of the ambient air and ground temperatures, and the third column is the difference between the steady state tire temperature and the temperature in the second column.
| Payload Weight | Average of Temperature(°C) | Temperature Difference(°C) |
|---|---|---|
| Payload 0 % | 11.0 | 2.9 |
| Payload 94 % | 12.3 | 2.6 |
| Payload 111 % | 12.4 | 5.5 |
| Payload 150 % | 12.2 | 8.7 |
| Payload 200 % | 11.4 | 17.5 |
3.4. Mechanisms of temperature changes in car tires
There are already well-established standards for tire inflation pressure (GB/T2977-2016), but the internal pressure of overloaded vehicles often exceeds the inflation pressure specified in the standards. When a vehicle's payload acts on the tires, heat is generated from tire-ground friction, repeated rubber deformation, and the repeated compression of internal gas by external forces. The work done by the external forces on the tire is converted into internal energy and heat [23].
Research on the internal gas of tire was commonly based on the ideal gas law [17,18,24], but it is only applicable at standard atmospheric pressure and temperature when the interaction between gas molecules and their size can be negligible [22,25]. However, the internal pressure of heavy-duty truck tire can reach 10 times of atmospheric pressure, and both tire pressure and temperature can change significantly with external conditions [18,25,26]. Therefore, using the ideal gas law can cause significant deviations for studying tire.
Many gas state equations have been developed under specific conditions, such as the Virial equation of state, the Redlich-Kwong equation, the Peng–Robinson equation of state, and the Multiparameter equations of state. Among these equations, the van der Waals equation takes into account the attraction and repulsion of molecules, and makes concise corrections to the gas pressure and volume, making it closer to the macroscopic physical properties of real gases [27]. For better accuracy, this study uses the van der Waals equation (Equation (8)) for relevant calculations.
| (8) |
R is the gas constant, equals to 8.314 J/(mol·K). At an ambient temperature of 25 °C, the molar volume of gas corresponding to different pressures is shown in Table 9. In the experiments, nitrogen gas was used for inflating the truck tires. The parameter a represents the intermolecular attraction, and b is the sum of the volumes contained by 1 mol of molecules, shown as following [28].
| (9) |
| (10) |
Table 9.
Molar volume of nitrogen at different pressures.
| Pressure(kPa) | Vm (L/mol) |
|---|---|
| 250 | 9.908 |
| 300 | 8.256 |
| 350 | 7.076 |
| 400 | 6.191 |
There was a study on the steady-state temperature inside a small car tire using embedded sensors in the lab [29], and ideal gas equation was used to describe relationships among vehicle weight, tire pressure, and tire temperature. The experiment explored pressure only up to half of the standard inflation value and did not investigate overloaded conditions.
Adapting Meng et al.‘s formula (Equation (11)), this study incorporates the van der Waals equation to obtain Equation (12), and focuses common type of truck tire with multiple experiments.
| (11) |
| (12) |
: tire pressure (absolute pressure, kPa);
: molar amount of gas inside the tire (mol);
: tire volume under standard load pressure of the vehicle (litre);
: central angle corresponding to the tire impression on the ground (rad);
: tire radius (m);
: tire impression length under a certain load (m);
: deflection height of the tire under a certain load (m);
: width of tire cross-section, i.e., 0.317 m;
: tire internal temperature (K);
: molar gas constant, 8.314 J/(mol·K)
Guo et al. [30] conducted a simulation study on mining vehicle tires to examine the effects of increased internal temperature and pressure on tire deflection and contact area. When inflation pressure increased, the contact area decreased; whereas deflection was influenced by inflation pressure but not temperature. Specifically, increasing the tire pressure from 0.5 MPa to 0.6 MPa reduced the contact area from 0.774 m2 to 0.700 m2, and increased the deflection from approximately 153 mm–177 mm.
The actual tire impression lengths for different experimental groups are shown in Table 10.
Table 10.
The actual tire impression lengths for different experimental groups.
| Experimental Group | Actual Tire Impression Lengths(m) |
|---|---|
| Payload 0 % | 0.301 |
| Payload 94 % | 0.328 |
| Payload 111 % | 0.328 |
| Payload 150 % | 0.347 |
| Payload 200 % | 0.402 |
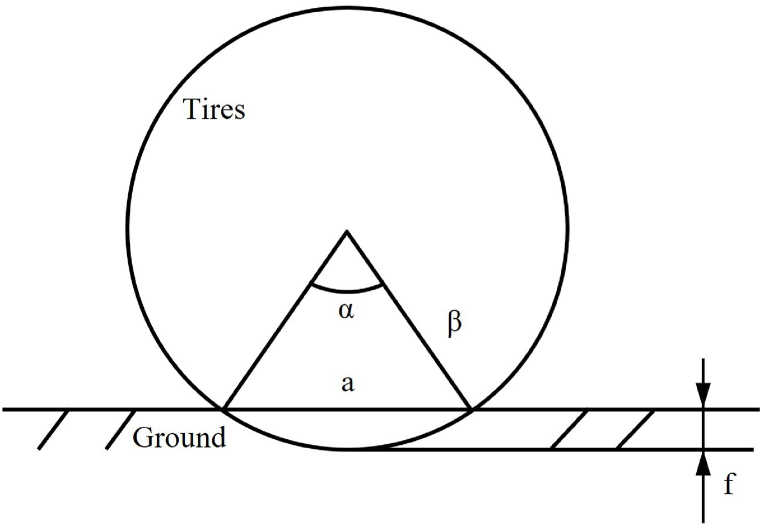
Equations (13), (14)) are obtained from Fig. 16.
| (13) |
| (14) |
Fig. 16.
Tire deflection (f) and impression (a).
The temperatures calculated using Equations (11), (12)) are shown in Table 11.
Table 11.
Tire pressure and calculated internal tire temperature for different experimental groups.
| Experimental Group | Tire Pressure(kPa) | Internal Temperature(K) |
|---|---|---|
| Payload 0 % | 250 | 295 |
| Payload 94 % | 252 | 296 |
| Payload 111 % | 276 | 315 |
| Payload 150 % | 318 | 346 |
| Payload 200 % | 336 | 382 |
For the 0 % payload condition, the tire pressure is set to the standard inflation value. For the other four groups, tire pressure is calculated based on the F4 support force in Table 5. The downward pressure of the tire at the impression area was balanced by the ground support force. This support force exceeds the truck weight distribution to the 4th wheel. Therefore, the excess deformation produced by the tire at 250 kPa provided the ‘grip force’ between the tire and the ground under 0 % payload condition. Therefore, the slip resistance and stability of the truck are better with empty cargo.
3.5. Relationship between tire deflection and support force
After being inflated properly, tire deflection and pressure increase with the vehicle payload. Tire deflection is usually determined by subtracting the vertical radius from the horizontal radius of the tire. Xiong et al. suggested the upper part of the tire had minimal deformation [31]. Therefore, a new approach is used by defining the deflection as the difference between the upper sidewall height () and the lower sidewall height () of the tire (Fig. 17). By comparing with the difference of radius between the actual tire and the rim (refer to Table 1), the actual length of 1px in the image can be determined. The deflection and support force under different loads are obtained and shown in Table 12.
Fig. 17.
Tire deflection and different sidewall heights.
Table 12.
Changes in the support force and deflection of the No. 4 tire.
| Experimental Group | Supporting Force(kN) | Tire Deflection(m) |
|---|---|---|
| Payload 0 % | 11.3 | 0.017 |
| Payload 94 % | 26.2 | 0.025 |
| Payload 111 % | 28.8 | 0.027 |
| Payload 150 % | 34.9 | 0.033 |
| Payload 200 % | 42.8 | 0.041 |
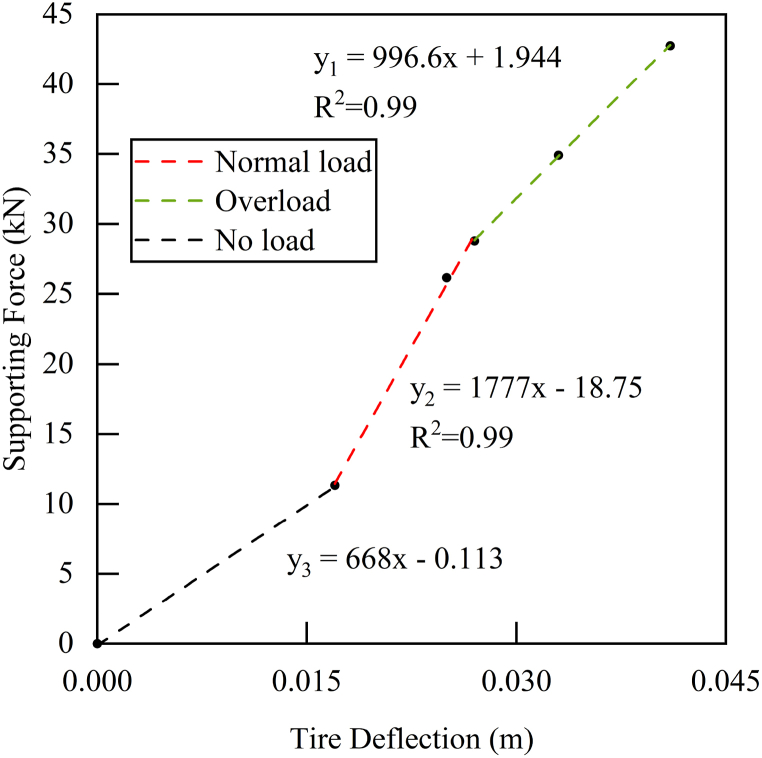
Plotting the support force versus deflection (Fig. 18) shows three regions with good fitting using linear trendlines. The y1 line represents the overloaded condition, the y2 line represents the normal load condition, and the y3 line represents the no-load condition. The y3 line passes through the origin because there is no deflection when external force is zero. At this region, the slope of trendline represents the radial stiffness of tires, i.e., the overall elasticity of parallel tires under the force. With four tires on each side of the No. 4 axle, the slope of 668 kN/m is equivalent to 167 kN/m of radial stiffness for a single tire, consistent with literature data (Table 13 and Table 14).
Fig. 18.
Change of supporting force with tire deflection. (Linear trendlines shown).
Table 13.
Review of tire stiffness data.
| Author(s) | Tire Specification | Test Platform | Splint Type and Size (mm) | Inflation Pressure (kPa) | Stiffness (N/mm) |
|---|---|---|---|---|---|
| Fan, C. j [32] | 195 60R14 | Simulate bumpy roads, flat roads | Rectangular splints with a width of 20 and a height of 10 | 250 | 190 |
| 214 | |||||
| 229 | |||||
| 244 | |||||
| 263 | |||||
| 289 | |||||
| V, Alkan [33] | 155/80R13 | Flat Tire Tester | rectangular splint with a height of 12.7 and a width of 50.8; Diameter 25.4 round splint and Triangular splint with a top angle of 90 and a height of 18 |
138 | About 70 |
Table 14.
Review of suspension stiffness data.
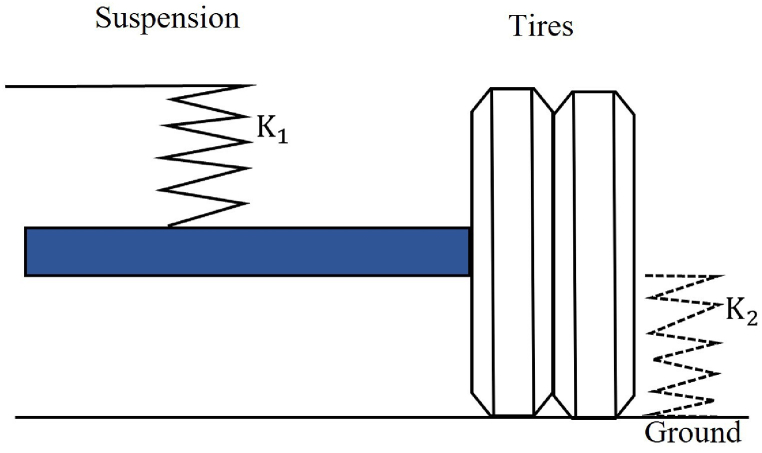
The phenomena of Fig. 18 can be explained by the structure and shock absorbing feature of the truck. The slope of 1777 kN/m in the normal load region represents the apparent stiffness of the combination from the suspensions and the tires (Fig. 19). K1 represents the apparent stiffness of parallel suspensions and multiple shock absorbers, and K2 represents the apparent stiffness of parallel tires. K1 and K2 are connected in series, and the apparent stiffness is expressed as:
| (15) |
Fig. 19.
Diagram of overall stiffness (K1 represents the apparent suspension stiffness, K2 represents the apparent tire stiffness).
At overloading region, when the payload exceeds the capacity by a certain percentage, e.g., 10 %, the tires are compressed to the state of almost losing elasticity. Therefore, the apparent stiffness approximately equals to the stiffness of the suspension system, which is represented by y1 line with a slope of 997 kN/m. Relevant data on tire and suspension stiffness from this study and literature are presented in Table 13, Table 14.
3.6. Relationship between tire temperature and pressure changes
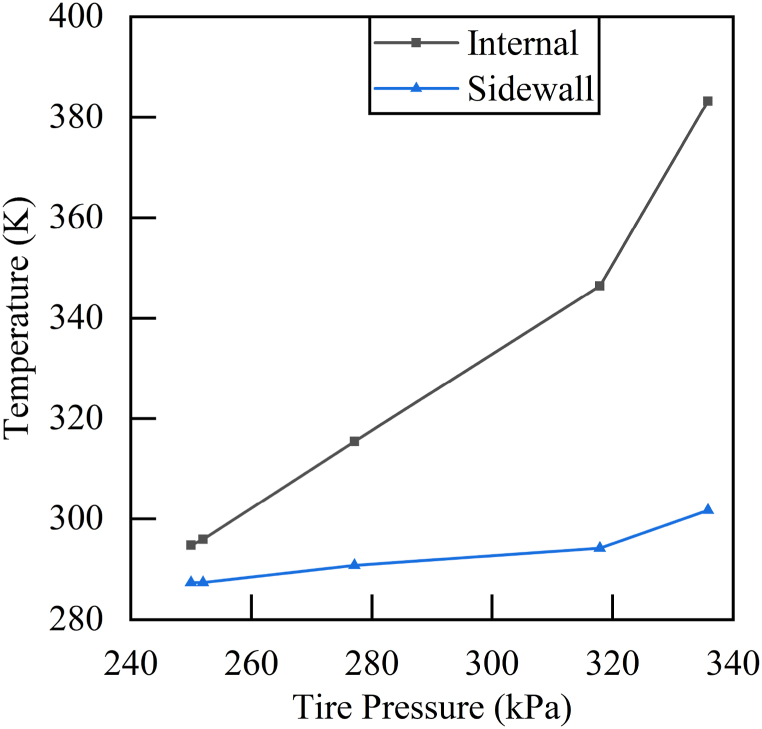
Internal temperature of tire is calculated with Equations (11), (12), (13), (14)) and shown in Table 11. Both internal temperature and sidewall temperature increase with payload (Fig. 20), and more rapidly above the 150 % payload.
Fig. 20.
The effect of increased payload on the internal temperature and the sidewall temperature of tire.
Internal experiments conducted by Izze-Racing (Fulton, Maryland, USA) [37] found in racing cars running for over 6 laps (10 min), tire pressure increased from approximately 32 psi to 39 psi (about 220 kPa–268 kPa), and the internal temperature of tire rose from around 38 °C to about 95 °C. When the tire tread was new and full, after running for 10 min, the internal temperature of tire increased from around 40 °C–116 °C, while the crown temperature of tire reached 70–90 °C because of friction and stress. When the tire tread was worn out to 33 % of its original thickness, after running for 10 min, the internal temperature of tire increased from around 40 °C–100 °C, with a slight narrowing of temperature fluctuations at the tire crown.
Ma et al. [38] monitored the 56/80R63 OTR tires after driving at 20 km/h under ambient temperature of 20 °C and found the internal temperature of tire increased from 48.9 °C to 73.1 °C, when the payload increased from 0 % to 100 %. Several studies as well as these showed a similar trend to the current study.
4. Discussions
As the results in section 3.3 show, criteria for determining truck overload can be based on the absolute temperature increase of the sidewall temperature relative to the ambient temperature. The criteria of absolute temperature increase needs to be adjusted for different range of ambient temperature, e.g., hot summer days or cold near-freezing days. The criteria could also be the percentage of increase, or specific characteristic temperatures on the outer side of multi-axle truck tires, or computed output results of multiple variables.
The main shortcoming of infrared thermal imaging is susceptible to interference by precipitation or wet tire, because accurate temperature sensing can't be obtained.
To get relatively good quality imaging, vehicle speed can't be too high, e.g., higher than 20 km/h. The current practical application of WIM technology can monitor the load of vehicles traveling at speed about 30 km/h [39]. Truck is required to travel at a speed of less than 10 km/h while passing special WIM lane at toll station in China. Monitoring accuracy decreases as vehicle speed increases.
The feasibility of this new method has been demonstrated. The mechanism has also been investigated, Future research will expand to include other truck tire models, scenarios of overloading, and alarm criteria. The selection and application of alternative gas state equations can further improve the accuracy and practicality of this new method. Through the effort and collaboration of broader community, an optimal or hopefully “universal” criteria could be established.
5. Summary
While it is known that vehicle tires heat up during driving, this study specifically delves into the mechanism behind the temperature increase of truck tires with increasing payload and travel time. Quantitative model was constructed to predict relationships among multiple variables. By utilizing the state equation of real gas within tires, it has been demonstrated the thermodynamic state change of gas under load is the primary cause of temperature increase. The sidewall temperature is closely correlated with the internal temperature, and measuring the sidewall surface temperature can indirectly assess the internal temperature of tire, thus indicating the payload status of the truck. After overload alarm criteria is programmed into infrared video camera, transportation law enforcement officers can use this remote and rapid monitoring tool for real-time temperature measurement of tires and evidence collection of moving trucks. This innovation helps in preventing and reducing the problem of truck overload, also works with other monitoring methods to enhance overall safety of public transportation.
Funding sources
This work was supported by the Fundamental Research Funds for the Central Universities of China, Chang'an Univesity Grant [300102341301].
Data availability statement
Additional data available upon request.
CRediT authorship contribution statement
Xu Li: Writing – review & editing, Supervision, Methodology, Funding acquisition, Conceptualization. Jiapeng Han: Writing – original draft, Methodology, Investigation, Formal analysis. Xuezhen Dai: Supervision, Resources. Zhuowen Zheng: Investigation. Yanhui Niu: Writing – review & editing, Conceptualization.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Contributor Information
Xu Li, Email: pir2@qq.com.
Jiapeng Han, Email: hjp16689591813@163.com.
Xuezhen Dai, Email: 165612259@qq.com.
Zhuowen Zheng, Email: 1260183995@qq.com.
Yanhui Niu, Email: niuyh@chd.edu.cn.
References
- 1.Gao Y.N., Gong J.Q. 我国道路交通事故特征及致因分析[Characteristics and mechanism of road traffic accidents] J. Saf. Environ. 2023;23(11):4013–4023. doi: 10.13637/j.issn.1009-6094.2022.1844. [DOI] [Google Scholar]
- 2.National Bureau of Statistics of China . China Statistics Press; 2021. 中国统计年鉴2021 [China Statistical Yearbook 2021] [Google Scholar]
- 3.Federal Motor Carrier Safety Administration Large truck and bus crash facts. Federal motor carrier safety administration. 2023. https://www.fmcsa.dot.gov/safety/data-and-statistics/large-truck-and-bus-crash-facts-2021#A5
- 4.Liu D.P., Yang X.H., Wang J., Du F. 超载作用下低路堤地基稳定性模型试验研究 [Model test and research on stability of low embankment foundation under overloading actions] Highways. 2021;66(9):87–93. [Google Scholar]
- 5.Hao L.J. Vehicle overload and oversize transportation controlling. National Science and Technology Library. 2006 https://www.nstl.gov.cn/paper_detail.html?id=7f39eb645ca202fdb31fcc14068b5010 [Master's thesis, Shangdong University] [Google Scholar]
- 6.Normann O.K. Weighing vehicles static and in motion by electronic scales. SAE National Transportation Meeting. 1955;63:373–378. [Google Scholar]
- 7.Burnos P., Gajda J., Piwowar P., Sroka R., Stencel M., Tadeusz Z. Measurements of road traffic parameters using inductive loops and piezoelectric sensors. Metrol. Meas. Syst. 2007;14(2):187–203. [Google Scholar]
- 8.Sujon M., Dai F. Application of weigh-in-motion technologies for pavement and bridge response monitoring: state-of-the-art review. Autom. ConStruct. 2021;130 [Google Scholar]
- 9.Gaspareto D.d.S., Gomes H.M. vol. 1. 2019. Bending plate WIM system analysis considering the dynamics of the load platform; pp. 304–313. (Proceedings of 8th International Conference on Weigh-In-Motion). [Google Scholar]
- 10.Jacob B., Cottineau L.M. Weigh-in-motion for direct enforcement of overloaded commercial vehicles. Transport. Res. Procedia. 2016;14:1413–1422. doi: 10.1016/J.TRPRO.2016.05.214. [DOI] [Google Scholar]
- 11.Feng M.Q., Leung R.Y., Eckersley C.M. Non-Contact vehicle Weigh-in-Motion using computer vision. Measurement. 2020;153 [Google Scholar]
- 12.Sarkar K., Kwon Y.D., Prevorsek D.C. A new approach for the thermomechanical analysis of tires by the finite element method. Tire Sci. Technol. 1987;15(4):261–275. doi: 10.2346/1.2148793. [DOI] [Google Scholar]
- 13.Liu Shuo, Liu Wweidong, Shen Zhou, Li Xiujuan, Zhang Qiushi. Steady-State temperature field and rolling resistance characteristics of low-speed and low-load capacity non-pneumatic tires. Lubricants. 2023;11(9):402. doi: 10.3390/lubricants11090402. [DOI] [Google Scholar]
- 14.Chen Liang, Sun Donghui, Li Changdai, Liu Ji, Ma Te, Gao Zhi. Simulation analysis of tire inflation pressure loss under synergy of temperature and oxidation. Int. J. Automot. Technol. 2023;24:693–703. doi: 10.1007/s12239-023-0058-x. [DOI] [Google Scholar]
- 15.Chen Da, Wu Jian, Su Benlong, Cui Bo, Teng Fei, An Shuang, Bai Yuzhao, Liu Xilin, Liu Yuyan, Wang Youshan. Thermo-mechanical-abrasive coupling analysis of solid rubber tire under high-speed rolling. Wear. 2023;512–513 doi: 10.1016/j.wear.2022.204546. [DOI] [Google Scholar]
- 16.Fu Hongxun, Liang Xuemeng, Wang Yan, Ku Laiyun, Zhen Xiao. Thermal mechanical coupling analysis of a flexible spoke non-pneumatic tire. J. Mech. Eng. 2022;68(3):143–154. doi: 10.5545/sv-jme.2021.7401. [DOI] [Google Scholar]
- 17.Nguyen T.C., Cong K.D.D., Dinh C.T. Rolling tires on the flat road: thermo-Investigation with changing conditions through numerical simulation. Appl. Sci. 2023;13(8) doi: 10.3390/app13084834. [DOI] [Google Scholar]
- 18.Tian T., Johnson D., Smith R.E., Felicelli S.D. Numerical evaluation of the temperature field of steady-state rolling tires. Appl. Math. Model. 2014;38(5–6):1622–1637. doi: 10.1016/J.APM.2013.08.033. [DOI] [Google Scholar]
- 19.Li Jie, Wang Qingnian, Zhao Ziliang. 中型载货汽车轮胎表面温度的稳态特性[Steady characteristic of surface temperature of tire of middle duty truck] J. Jilin Univ. (Eng. Technol. Ed.) 2003;2:1–5. doi: 10.13229/j.cnki.jdxbgxb2003.02.001. [DOI] [Google Scholar]
- 20.Kazimierz Drozd, Sławomir Tarkowski, Jacek Caban, Aleksander Nieoczym, Jan Vrábel, Zbigniew Krzysiak. Analysis of truck tractor tire damage in the context of the study of road accident causes. Appl. Sci. 2023;12(23) doi: 10.3390/app122312333. [DOI] [Google Scholar]
- 21.Alan N. Gent, Joseph D. Walter, withJ D. Gardner, B J. Queiser. Durability and Failure Analysis. U.S. Department of Transportation; 2006. The pneumatic tire: introduction to tire safety. [Google Scholar]
- 22.Li Youde, Zhao Ziliang, Wang Qingnian, Chu Liang, Li Jie. 高速滚动汽车轮胎温度场的非稳态热分析 [Non-steady state thermal analysis on temperature field of a rolling automobile tire at high speed] Automot. Eng. 2002;24(1):60–64. doi: 10.19562/j.chinasae.qcgc.2002.01.014. [DOI] [Google Scholar]
- 23.Hyun Seok Song, Sung Pil Jung, Tae Won Park. Simulation of temperature rise within a rolling tire by using FE analysis. J. Mech. Sci. Technol. 2018;32:3419–3425. doi: 10.1007/s12206-018-0645-3. [DOI] [Google Scholar]
- 24.Nallusamy S., Rajaram M.N., Rekha R.S. Design and performance analysis of vehicle tyre pattern material using finite element analysis and ANSYS R16.2. Key Eng. Mater. 2018;777:426–431. doi: 10.4028/WWW.SCIENTIFIC.NET/KEM.777.426. [DOI] [Google Scholar]
- 25.Xu Duanjun, Nie Jingjing, Liu Qing. 新编普通化学第二版 [New Edition of General Chemistry. second ed. Science Press; 2012. [Google Scholar]
- 26.Dolez P.I., Nohile C., Ha T., Anh T., Vu-Khanh R., Benoît, Bellavigna-Ladoux O. Exploring the chemical aspects of truck tire blowouts and explosions. Saf. Sci. 2008;46(9):1334–1344. doi: 10.1016/j.ssci.2007.10.004. [DOI] [Google Scholar]
- 27.Gorenstein M. Van der waals equation of state. Low Temp. Phys. 2022;48(11):914–919. doi: 10.1063/10.0014591. [DOI] [Google Scholar]
- 28.Yao Yunbin, Jie Tao, Gao Yinmin. Shanghai Scientific & Technical Publishers; 1985. 物理化学手册: 范德华常数和临界常数 [Handbook of Physical Chemistry] [Google Scholar]
- 29.Meng Qinghua, Zhao Wwenli, Guo Liping. 无线传输的轮胎状态及车辆载重检测一体化技术[Tire condition and vehicle load testing integrated technology based on wireless communication] Trans. Chin. Soc. Agric. Mach. 2008;39(6):46–49. doi: 10.3969/j.issn.1000-1298.[year].6. [sequence] [DOI] [Google Scholar]
- 30.Guo Jinquan, Ding Peng, Gao Jiahong, Huang Zhenhua, Guo Qiyan, Yang Xiaoxiang. Numerical simulation of grounding characteristics and temperature field of mine tires under multiple working conditions. Advances in Ploymer Technology. 2022 doi: 10.1155/2022/3830961. 2022. [DOI] [Google Scholar]
- 31.Xiong Y., Tuononen A. Rolling deformation of truck tires: measurement and analysis using a tire sensing approach. J. Terramechanics. 2015;61:33–42. doi: 10.1016/j.jterra.2015.07.004. [DOI] [Google Scholar]
- 32.Fan Chengjian, Duan Dihua. Tire modeling for vertical properties including enveloping properties using experimental modal parameters. Veh. Syst. Dyn. 2003;40(6):419–433. doi: 10.1076/vesd.40.6.419.17908. [DOI] [Google Scholar]
- 33.Veysel Alkan, Steven M.Karamihas, Gunay Anlas. Experimental analysis of tyre-enveloping characteristics at low speed. Veh. Syst. Dyn. 2009;47(5):575–587. doi: 10.1080/00423110802251807. [DOI] [Google Scholar]
- 34.Zhang Zhi, Lu Jianwei, Chen Yuanfeng, Wu Weiwei, Wang Xinzi. 不同摩擦系数的钢板弹簧动态特性分析[Dynamic characteristic of the leaf spring considering the different friction coefficients] Chinese Journal of Automotive Engineering. 2013;3(2):94–99. doi: 10.3969/j.issn.2095-1469.2013.02.03. [DOI] [Google Scholar]
- 35.Zhang Junhong, Long Feiqi, Lin Jiewei, Zhu Xiaolong, Dai Huwei. Modeling and simulation of the equivalent vertical stiffness of leaf spring suspensions. Adv. Mech. Eng. 2023;15(10) doi: 10.1177/16878132231200307. [DOI] [Google Scholar]
- 36.Lu Yongjie, Yang Shaopu, Li Shaohua, Chen Liqun. Numerical and experimental investigation on stochastic dynamic load of a heavy duty vehicle. Appl. Math. Model. 2010;34(10):2698–2710. doi: 10.1016/j.apm.2009.12.006. [DOI] [Google Scholar]
- 37.Izze-Racing. (n.d). White Paper: Influence of Temperature on Tire Grip https://www.izzeracing.com/ewExternalFiles/Izze_Racing_White_Paper_Tire_Temperature.pdf.
- 38.Ma Shaosen, Wu Linping, Liu W.V. Numerical investigation of temperatures in ultra-large off-the-road tires under operating conditions at mine sites. J. Therm. Sci. Eng. Appl. 2023;15(2):21010–21022. doi: 10.1115/1.4056086. [DOI] [Google Scholar]
- 39.Zhang Longwei, Yuan Luqi, Deng Lu, Chen Ning, Yuan Shuaihua. 基于最大熵正则化的桥梁动态称重算法与试验验证 [Bridge Weigh-in-Motion system based on maximum entropy regularization] China J. Highw. Transp. 2023:1–18. http://kns.cnki.net/kcms/detail/61.1313.U.20230914.1218.008.html [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Additional data available upon request.