Indium Phosphide Single Crystal Furnace Cooling Crystallization Temperature Control Model Research

Abstract

Indium phosphide (InP) single crystals, as key III–V compound semiconductor materials, play an irreplaceable role in various fields, such as optical communication and microwave millimeter-wave communication. Vertical gradient freeze (VGF) has become one of the main methods for industrial production of InP single crystals due to its advantages in temperature gradient control. However, defects such as twins and dislocations are easily generated during the production of InP single crystals by the VGF method. Through an in-depth study of the thermal field during the growth of InP single crystals, it is found that the cooling rate of the thermal field during single crystal growth is crucial and is closely related to the generation of twins, dislocations, and polycrystallization defects. Therefore, constructing a cooling model based on temperature control and the quality of InP single crystals has a positive driving effect on improving the yield of single crystal products. In this paper, by establishing a thermal field model of an InP single crystal furnace produced by the VGF method, the characteristics of temperature variation are analyzed in depth. Subsequently, numerical analysis of discrete cooling data during the cooling crystallization process is conducted, considering the quality of the InP single crystal growth. Combined with the spline regression algorithm, the optimal cooling model is fitted. Through positive and reverse experiment verification, the model shows significant effects in controlling internal stress in the crystal and reducing defect generation. Based on this model, we have successfully achieved effective suppression of defects, such as twins and dislocations, thereby significantly improving the quality of InP single crystals. This research not only provides a solid theoretical basis for the production of InP single crystals but also provides strong support for experimental applications.

1. Introduction

Indium phosphide single crystal is an important III–V compound semiconductor material, with high photoelectric conversion efficiency, good mechanical properties, and thermal conductivity.^1,2 It has wide applications in fields such as optical communication and microwave communication. The vertical gradient freeze (VGF)³ method is one of the mainstream methods for industrial production of InP single crystals. The principle is to adjust the power of heaters in different sections of the crystal furnace to form a temperature gradient from low to high and then slowly cool down the furnace. The controllable process conditions are relatively few, mainly the thermal field temperature gradient and the structure, material, and size of the thermal field. This method has a stable thermal field and a low-temperature gradient, allowing the growth of low dislocation and high-quality InP single crystals. However, during the production process of single crystals using the VGF method, defects such as twinning and dislocation are easily formed, which seriously affect the yield of crystals. Therefore, from the perspective of crystal growth, inhibiting the formation of twins remains a key focus in InP research.^4,5

China’s research on the synthesis and crystal growth of InP began in the 1970s and is one of the countries that started related research early in the world, achieving fruitful research results.^6,7 Professor Tongnian Sun from Hebei Semiconductor Research Institute is representative of this, and his development of phosphorus injection synthesis continuous crystal preparation technology has reached the international leading level.⁷

The growth of InP single crystal is closely related to the thermal environment, as InP single crystal needs to be grown in a high-temperature and high-pressure environment.^8,9 In the production of InP single crystals using the VGF method, the high-purity indium and high-purity phosphorus raw materials need to be placed in a quartz crucible inside the crystal furnace and then enter the stage of heating and melting materials. After all raw materials are melted to form a phosphorus seed crystal and become stable, they enter the crucial cooling and crystallization stage.¹⁰ In the cooling and crystallization stages, the control of the thermal field temperature is crucial to producing high-quality InP single crystals. Proper cooling gradients are conducive to crystal growth, while excessive cooling gradients can increase internal stresses in the crystal, leading to excessive internal defects.^4,11 Therefore, the selection of the cooling temperature gradient for InP single crystals and the control of its deviation range are key steps in the preparation of single crystals.

In defect analysis studies of InP single crystals in China, it was found that under unchanged thermal field and process conditions, the same type of defects easily reoccur in the same growth stage of single crystal growth.^12,13 By adjusting the cooling rate to adjust the temperature gradient, the reoccurrence of twinning and dislocations can be suppressed, thereby growing high-quality InP single crystals.¹³

Therefore, in the cooling and crystallization process of InP, the growth of InP single crystals can be influenced by rational selection and control of the cooling rate. The appropriate cooling rate can affect the growth rate of the crystal, distribution of internal stresses, and quality of the crystal. If the cooling rate is too fast, it can result in uneven temperature gradients inside the crystal, leading to increased internal stresses and affecting the structural integrity and stability of the crystal. On the other hand, if the cooling rate is too slow, it can slow down the growth rate of the crystal, leading to problems such as uneven grain growth and twinning, affecting the quality and performance of the crystal.

Therefore, determining the appropriate cooling rate can effectively suppress the generation of twinning and dislocations, improve the integrity and crystallinity of the crystal, and ensure the quality and performance of the InP single crystal.

Based on the VGF method for the InP single crystal furnace, this study established a corresponding thermal field cooling model. Through numerical analysis and spline regression fitting based on the temperature data during the cooling and crystallization process of InP single crystals, the optimal cooling model was established, and experiments were conducted in both positive and reverse directions. The results showed that the established optimal cooling model effectively suppressed the generation of InP twinning and dislocations, promoting the growth of high-quality InP single crystals. The research results provide an important theoretical foundation and experimental basis for the production of InP single crystals.

2. Materials and Methods

2.1. Establishment of the VGF Method for the InP Single Crystal Furnace Thermal Field Model

In order to conduct the thermal field analysis of crystal growth, it is necessary to understand the physical parameters of the entire crystal growth system, so as to reveal the temperature variations of the crystal growth system through corresponding mathematical models.¹⁴ Based on the VGF indium phosphide single crystal furnace independently developed by a company in Yunnan Province, this article establishes a thermal field model. Figure 1 shows a simplified model of the VGF method in the InP single crystal furnace.

Figure 1.

Schematic diagram of the internal structure of the InP single crystal furnace.

The schematic diagram in Figure 1 shows the internal structure of the InP single crystal furnace during the cooling and crystallization process of InP. The cooling heat conduction process of the single crystal is considered as non-steady-state heat conduction. It is assumed that the volume of the InP single crystal is V. The heat transfer surface area is A, the initial center temperature at the start of cooling is t₀ (t₀ is a known constant value), the temperature at the heater location is t_d(t₀ > t_d), t represents the temperature of the single crystal during heat dissipation, τ represents time, and k is the heat transfer coefficient.

The transient heat conduction equation for heat conduction is

1

The left side of eq 1 represents the non-steady-state term, and the right side represents the sum of the heat diffusion terms and internal heat source terms imported in the three coordinate directions.

Equation 1 simplifies to

2

In eq 2, α is the thermal diffusivity (unit: m²/s), c is the specific heat capacity (unit: J/kgK), and λ is the thermal conductivity (unit: W/(mK)).

Assuming that the internal thermal resistance of the single crystal is negligible and temperature is independent of spatial coordinates, the above equation can be simplified to

3

In the equation above, Φ represents a generalized heat source.

4

Based on the above content, we have

5

Let t – t_d = θ, we have

6

7

Combining the above equations, we have

8

Integrating the above expression, we obtain

9

10

Equation 10 represents the relationship between the temperature at the heater location and time, where t₀ represents the initial value of the center temperature, t_d is the temperature at the heater location, k is the heat transfer coefficient, α is the thermal diffusivity, c is the specific heat capacity, and ρ is the density of the single crystal. t represents the temperature of the single crystal during heat dissipation, and τ represents time. In eq 10, except for the parameters t_d,τ, all values can be considered as constants. Let τ = x, 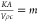, , t = c, , , 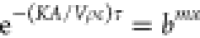eq 10 can be simplified as

11

In eq 11, where a, b, c, and m are constants and x is the variable. Taking the second derivative of eq 11, we obtain

12

In eq 12, , and when 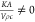, ẗ_d must be continuous.

From eqs 11 and 12, it can be seen that the functions t_d(τ) and ẗ_d(τ) are continuous within the domain. Therefore, it is known that the temperature decrease over time exhibits a continuous distribution.

2.2. Establishment of the Cooling Model for the Indium Phosphide Single Crystal Furnace Thermal Field

2.2.1. Data Source

This article is based on the temperature data extraction and analysis of the indium phosphide single crystal growth thermal field using a VGF high-pressure indium phosphide single crystal furnace developed independently by a company in Yunnan. The furnace structure of the indium phosphide single crystal furnace is shown in Figure 2.

Figure 2.

Schematic diagram of the single crystal furnace structure.

As shown in Figure 2, the heater assembly of the InP single crystal furnace consists of 4 sets of independently controlled resistance wire heaters, namely, heater 1, heater 2, heater 3, and heater 4. There are 8 temperature measurement points in the furnace, including temperature measurement points TC1–TC8. In the study, the thermal field of the furnace is divided into the upper high-temperature zone and the lower low-temperature zone based on the horizontal position of the crucible bottom. Different temperature measuring elements and heaters are used for the high- and low-temperature zones.

The temperature data in this article are derived from the temperature data of 8 measuring points in the single crystal furnace during the cooling crystallization process, as shown in Table 1, for indium phosphide temperature data. Among them, TC1–TC4 are located in the low-temperature zone of the indium phosphide single crystal furnace, while TC5–TC8 are located in the high-temperature zone of the indium phosphide single crystal furnace.

Table 1. Temperature Data of the Single Crystal Furnace.

temperature (°C)	TC1	TC2	TC3	TC4	TC5	TC6	TC7	TC8
procedures
step22	1039.6	1049.2	1048.8	1057.7	1075.6	1079.7	1088	1081.1
step23	1027.9	1039.2	1038.5	1050.6	1071.1	1076.7	1086.7	1079.2
step24	1017.6	1031.1	1029.4	1045.6	1067.4	1074.1	1085.1	1077.3
step25	987.9	1003.7	997.3	1021.8	1057.1	1069.7	1084.9	1075.9
step26	954.6	974.7	963.8	996.1	1045.8	1062.7	1081.2	1073.5
step27	921.1	948.6	932	974.7	1034.8	1055.7	1082.1	1070
step28	888.1	922.1	899.1	953.4	1022.6	1047.7	1079.2	1065
step29	855.8	896	867.4	933.3	1010.9	1039.7	1076	1030.2

As shown in Table 1, the cooling data of the indium phosphide single crystal includes the temperatures of 8 steps (total of 111 h) from step22 to step29 in the entire cooling crystallization process. This work mainly uses the temperature data of measuring point TC7 as an example. After a large amount of temperature data for measuring point, TC7 is collected, the data is cleaned, missing values are handled, outlier values are handled, and the temperature data is differentiated to obtain the cooling rate.

2.2.2. Data Analysis

When measuring the temperature of the indium phosphide single crystal furnace, factors such as improper placement or unstable installation of the temperature measuring instrument, as well as changes in the furnace conditions, can lead to data loss or abnormal data.¹⁵ Therefore, the analysis of the cooling data of the InP single crystal furnace should be based on the actual normal temperature parameter data in engineering practice. The normal distribution is one of the main distribution forms of industrial data, and the normal distribution theory has been successfully applied in fault warning, life prediction, parameter correlation analysis, and other aspects.^16,17 In this section, normal distribution theory will be used to analyze the temperature data of the indium phosphide single crystal furnace.

Assuming the normal distribution of the cooling rate parameter v as a one-dimensional normal distribution, where the cooling rate parameter v follows a probability distribution with a location parameter μ and a scale parameter σ, its probability density function is

13

The two parameters in the normal distribution, including the expected value μ and the standard deviation σ, σ² is the variance, μ is the mean of the random variable following a normal distribution, σ² is the variance of this random variable, so the normal distribution is recorded as N(μ,σ²), and μ is the position parameter of the normal distribution, describing the central trend position of the normal distribution. The probability law is the probability of taking a value adjacent to μ, while the probability of taking a value farther from μ is smaller.

We performed statistical analysis of the cooling rate values for measurement point TC7 in the thermal field of indium phosphide single crystal production from steps 22 to 29 (abbreviated as s22 to s29) and plotted a histogram. Additionally, we calculated the mathematical formula for the corresponding normal distribution curve. The results are shown in Figure 3.

Figure 3.

Histogram of the cooling rate for temperature measurement point TC7.

After a thorough analysis of Figure 3, we observed that the data distribution graph exhibits a symmetrical bell-shaped pattern, which is a significant characteristic of data conforming to a normal distribution. Subsequently, we further examined the frequency distribution histogram of the sampling data, which resembles an inverted “bell shape”, with clear symmetry on both sides, providing strong evidence for the data conforming to a normal distribution.¹⁷ Additionally, by combining the histogram with the mathematical formula of the normal distribution curve obtained through fitting, we can confidently confirm that all cooling rate samples of temperature point TC7 follow a normal distribution with their reliability validated. Following this analytical process, we systematically examined the cooling rates of all temperature points TC1–TC8, and all of the results indicated adherence to a normal distribution. The reliability of the normal distribution for all cooling rate samples of temperature point TC7 was confirmed. Following this analysis process, we individually assessed the cooling rates of all temperature points TC1–TC8, and all of the results demonstrated conformity to a normal distribution.

2.2.3. Determination of the Optimal Cooling Model Sample

From Figure 3, it can be seen that the cooling rate parameter does not strictly follow a normal distribution in a mathematical sense but the data distribution pattern is close to that of a normal distribution. For parameters that exhibit characteristics of a normal distribution, one can attempt to use normal distribution theory to calculate the probability P (confidence interval) of different data distribution ranges. Taking the data expectation μ as the center and k times the data standard deviation σ as the radius, P represents the probability of the data falling within the interval (μ – kσ, μ + kσ), where k is the constant. Through analysis and fitting of a large amount of historical data, the data range (μ – kσ, μ + kσ) corresponding to a certain probability P can be determined according to actual needs as the “reasonable” fluctuation range of the cooling rate. The boundary values μ – kσ and μ – kσ can then be defined as the lower and upper limits of the corresponding cooling rate warning values, respectively.

When calculating boundary values using normal distribution theory, for data v that follows a standard normal distribution, where v ∼ N(μ,σ²), the probability formula for the data falling within the interval (a, b) is^18,19

14

Standardizing the general normal distribution, if we let 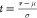, we can obtain

15

When the data interval is (μ – kσ, μ + kσ), substituting the interval boundary values into eq 15, we have the probability calculation formula for the general normal distribution

where μ is the data expectation value, σ² is the data variance, σ is the data standard deviation, and Φ(x) is the distribution function of the standard normal distribution.

Considering the hysteresis and nonlinearity characteristics of the temperature changes in the InP single crystal furnace and its actual working environment, a descending rate probability P of 60% (with a confidence interval of 60%) was selected. Taking the temperature measurement point TC7 in step22 of the production process as an example, the lower and upper limits of the cooling rate were calculated, as shown in Figure 4.

Figure 4.

Range of values for the cooling rate s22.

Based on the above theory and computational results, the cooling rate for measurement point TC7 in the indium phosphide single crystal furnace is calculated for each step over the entire time period, resulting in the range of values shown in Table 2.

Table 2. Optimal Cooling Rate Value for Temperature Measurement Point TC7.

cooling rate (°C/h)	maximum	optimal	minimum
procedures
step22	0.88	0.66	0.43
step23	0.57	0.42	0.27
step24	0.33	0.25	0.18
step25	0.21	0.15	0.09
step26	0.24	0.19	0.14
step27	0.38	0.26	0.15
step28	0.31	0.24	0.18
step29	0.37	0.29	0.20

Based on the calculation method using the TC7 cooling rate values, the cooling rate values for other temperature measurement points throughout the entire production process can be calculated.

2.2.4. Data Fitting Based on the Spline Algorithm

In engineering practice, curve fitting based on discrete sampling data is a common problem and the fitted function should be smooth and accurate. Common methods for curve fitting include Lagrange interpolation, piecewise cubic Hermite interpolation, least-squares method, and cubic spline curve method.^20,21

After thermal field analysis of the InP single crystal furnace, it was found that the temperature decrease with time follows a continuous distribution. Therefore, this study adopts the cubic spline curve to fit the temperature decrease rate curve of the single crystal furnace. Cubic splines²²⁻²⁴ are linearly smooth with continuous second derivatives, ensuring that the fitted curve passes through all sampling points. They have good adaptability to gradual and abrupt changes in the curve. By controlling the number and position of control nodes, the degrees of freedom of the cubic spline curve can be adjusted to better adapt to the characteristics of the temperature decrease rate curve of the single crystal furnace, helping to accurately describe the temperature changes with time.

Taking the time–temperature decrease rate data that need to be fitted, dividing the intervals [a, b], where the decrease rate is located into segments with nodes.

The definition of a spline function is as follows: Assuming the function S_k(x) is a k-th degree polynomial on each subinterval [t_i + t_i+1](i = 0,1,···,n) of the partition and has continuous derivatives up to the k-1 order at each node a, then the k-th degree polynomial S_k(x) is called a k-th degree spline function.

According to the Weiestrass approximation theorem, any continuous function f(x) defined on a bounded interval [a,b] can always be approximated by a k-th degree polynomial S(x), and the error between the two gradually tends to zero as the degree k increases.

16

According to eq 16, it can be seen that the higher the order of the spline function, the more accurate the fitting, but the higher the order, the more complex the function form and parameter estimation. Choosing a cubic spline function can ensure that the function and its first derivative are continuous and the function is twice differentiable. At the same time, the model will not be too complex. Therefore, cubic spline functions have been widely used in practical engineering applications. According to the definition, a cubic spline function S₃(x) can be represented as

17

The time-cooling rate data obtained from the VGF method for indium phosphide single crystal production can be fitted using the spline algorithm to establish the cooling model for the indium phosphide single crystal furnace. The data fitting results are shown in Figure 5.

Figure 5.

Cooling model for the indium phosphide single crystal furnace.

Figure 5 shows the cooling model for the indium phosphate single crystal furnace obtained through the fitting of time-cooling rate data for measurement points TC1 to TC8. The model includes the optimal cooling rate curve and its upper and lower limits within a 60% confidence interval. This cooling model will be used in practical production, with the optimal cooling rate curve as the input and the confidence interval as the inspection range, strictly controlling temperature changes within this range. The correctness and feasibility of the cooling model will be verified by the actual crystal quality produced.

3. Results and Discussion

3.1. Experimental Design

To verify the applicability of the fitted cooling model for the indium phosphide single crystal furnace, comparative tests will be conducted based on the cooling model. The experiment will be conducted using a VGF high-pressure indium phosphide single crystal furnace developed in-house. The cooling parameters, as shown in Table 3, will be input into the temperature controller UI interface of furnaces 10 and 11. Additionally, the cooling parameters, as shown in Tables 4 and 5, will be input into the temperature controller UI interface of furnaces 12 and 13.

Table 3. Input Temperature Parameters for Furnaces 10 and 11.

cooling rate (°C/h)	TC1	TC2	TC3	TC4	TC5	TC6	TC7	TC8
procedures
step22	2.59	2.37	3.10	2.16	1.25	0.92	0.66	0.61
step23	2.22	1.90	2.00	1.31	0.74	0.55	0.45	0.34
step24	1.43	1.24	1.27	0.79	0.44	0.34	0.25	0.22
step25	1.65	1.49	1.61	1.11	0.48	0.26	0.15	0.12
step26	1.65	1.49	1.62	1.15	0.63	0.41	0.19	0.13
step27	1.57	1.37	1.51	1.04	0.56	0.41	0.26	0.23
step28	1.51	1.29	1.44	0.98	0.53	0.38	0.24	0.19
step29	1.73	1.55	1.60	1.07	0.86	0.44	0.29	0.22

Table 4. Input Temperature Parameters for Furnace 12.

cooling rate (°C/h)	TC1	TC2	TC3	TC4	TC5	TC6	TC7	TC8
procedures
step22	2.63	3.17	3.17	2.43	1.53	0.97	0.80	0.57
step23	2.16	1.98	1.98	1.40	0.68	0.72	0.58	0.42
step24	1.46	1.34	1.34	0.93	0.44	0.30	0.19	0.13
step25	1.73	1.72	1.72	1.37	0.60	0.21	0.14	0.06
step26	1.71	1.68	1.68	1.34	0.78	0.39	0.18	0.09
step27	1.55	1.53	1.53	1.13	0.58	0.44	0.31	0.15
step28	1.53	1.48	1.48	1.10	0.53	0.37	0.26	0.15
step29	1.77	1.68	1.68	1.19	0.61	0.49	0.36	0.27

Table 5. Input Temperature Parameters for Furnace 13.

cooling rate (°C/h)	TC1	TC2	TC3	TC4	TC5	TC6	TC7	TC8
procedures
step22	2.16	2.93	2.93	2.23	1.37	0.83	0.63	0.30
step23	2.08	2.18	2.18	1.56	0.92	0.58	0.46	0.38
step24	1.46	1.36	1.36	0.84	0.40	0.30	0.23	0.24
step25	1.62	1.61	1.61	1.09	0.42	0.26	0.16	0.08
step26	1.57	1.64	1.64	1.19	0.68	0.42	0.21	0.09
step27	1.51	1.57	1.57	1.18	0.59	0.36	0.25	0.17
step28	1.45	1.41	1.41	1.03	0.56	0.34	0.25	0.21
step29	1.58	1.64	1.64	1.13	0.68	0.38	0.27	0.21

The cooling parameters shown in Table 3 are calculated based on the cooling model, while the cooling parameters in Tables 4 and 5 are not derived from the cooling model. Therefore, furnaces 10 and 11 are considered as positive experimental setups, while furnaces 12 and 13 are considered as reverse comparative experiments.

After inputting the above temperature parameters, the indium phosphide (InP) polycrystalline material was pretreated, including etching, cleaning, and drying, and then loaded into a hot-pressed boron nitride (p-BN) crucible, where the diameter of the equidiameter section of the crucible is approximately 100 mm. An appropriate amount of red phosphorus was loaded to generate phosphorus vapor pressure and suppress the dissociation of InP, and a proper amount of liquid sealant B₂O₃ was added. The seed crystal used had a crystal orientation of ⟨100⟩, with a doping concentration of S ranging from 1 × 10¹⁸ to 8 × 10¹⁸ cm³. The assembled polycrystalline p-BN crucible was placed in a quartz ampule, evacuated, and finally sealed by welding. The sealed ampule was then placed in a furnace for single crystal growth. After steps such as melting the polycrystalline material, joining the seed crystal, single crystal growth, and cooling, the InP single crystal was obtained by demolding from the furnace.

3.2. Experimental Results and Discussion

3.2.1. Appearance of InP Single Crystal under Different Experimental Processes

Polishing the InP single crystal is polated with sandpaper, defects such as twinning and polycrystalline features on the crystal surface can be directly observed. Figure 6a,b shows the InP single crystals obtained from the forward experimental production, where (a) shows the single crystal produced by furnace no. 10 and (b) shows the single crystal produced by furnace no. 11. Figure 7a,b shows the InP single crystals obtained from the reverse comparative experimental production, where (a) shows the single crystal produced by furnace no. 12 and (b) shows the single crystal produced by furnace no. 13.

Figure 6.

InP single crystal produced in the forward experimental production.

Figure 7.

InP single crystal produced in the reverse comparative experimental production.

Observing Figure 6a, it can be seen that apart from a small amount of fine twinning on the surface, the bottom of the single crystal is in a smooth state, and the tail part also shows good performance without other obvious defects. In Figure 6b, twinning can be seen on the shoulder of the crystal surface, but no significant defects were found in the equidiameter section, and the bottom also remained smooth. Observing Figure 7a,b, twinning and polycrystalline defects exist in both the shoulder and equidiameter sections of the single crystal. Based on the above observation results, it can be inferred that the temperature gradient and cooling rate of furnace nos. 10 and 11 are within the appropriate range.

3.2.2. Analysis of Dislocation Properties under Different Experimental Processes

Further quality checks were conducted on the InP single crystals shown in Figures 6a,b and 7a,b. Top crystal wafers were taken from the shoulder position of the InP single crystal at 3 in. (referred to as H); after cutting off 5 mm from the tail, crystal pieces from the tail were taken as tail crystal wafers (referred to as T). The dislocation density of the top and tail crystal wafers of the InP single crystal was measured at different temperature parameters. The results are shown in Figures 8a,b, 9a,b, 10a,b, and 11a,b.

Figure 8.

Dislocation detection of the head and tail of the InP single crystal produced in furnace number 10.

Figure 9.

Dislocation detection of the head and tail of the InP single crystal produced in furnace number 11.

Figure 10.

Dislocation detection of the head and tail of the InP single crystal produced in furnace number 12.

Figure 11.

Dislocation detection of the head and tail of the InP single crystal produced in furnace number 13.

Figure 8a,b shows the results of dislocation density testing of the head and tail crystals of the single crystal from furnace 10. The average dislocation density of the head crystal (H) is 2 cm^–2, with a maximum of 79 cm^–2; the average dislocation density of the tail crystal (T) is 3 cm^–2, with a maximum of 79 cm^–2. Dislocations are distributed in the central and edge regions.

Figure 9a,b shows the results of dislocation density testing of the head and tail crystals of the single crystal from furnace 11. The average dislocation density of the head crystal (H) is 4 cm^–2, with a maximum of 157 cm^–2; the average dislocation density of the tail crystal (T) is 1 cm^–2, with a maximum of 118 cm^–2. Dislocations are distributed in the edge regions.

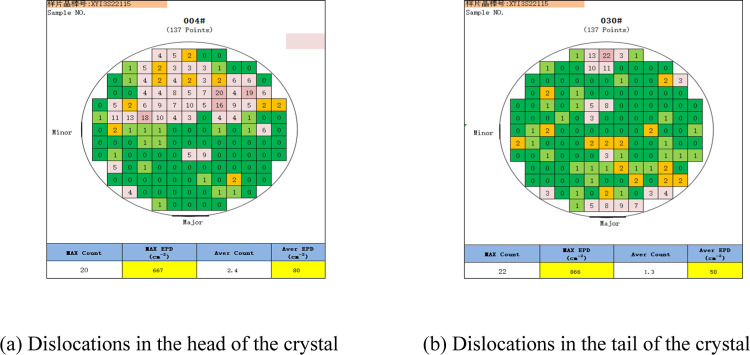
Figure 10a,b shows the results of dislocation density testing of the head and tail crystals of the single crystal from furnace 12. The average dislocation density of the head crystal (H) is 80 cm^–2, with a maximum of 667 cm^–2; the average dislocation density of the tail crystal (T) is 50 cm^–2, with a maximum of 866 cm^–2. Dislocations are distributed in the central and edge regions.

Figure 11a,b shows the results of dislocation density testing of the head and tail crystals of the single crystal from furnace 13. The average dislocation density of the head crystal (H) is 20 cm^–2, with a maximum of 800 cm^–2; the average dislocation density of the tail crystal (T) is 97 cm^–2, with a maximum of 1133 cm^–2. Dislocations are distributed in the edge regions.

Based on the dislocation testing results shown in Figures 8–11, it can be seen that the overall dislocation density testing results of the InP single crystals produced in furnaces 10 and 11 are better than those produced in furnaces 12 and 13. Therefore, using the thermal field cooling model of the InP single crystal furnace can produce InP single crystals with a lower dislocation density.

3.2.3. XRD Analysis of InP Single Crystals under Different Experimental Processes

In order to study the experiment under different temperature parameters of indium phosphorus single crystal crystal structure and crystallographic characteristics, two sets of indium phosphorus single crystals produced by multiple wire cutting, chamfering, natural dissociation, grinding, and polishing after the same process, get 3 in. InP single crystal head wafer and tail wafer. Using a Rigaku Smartlab SE instrument, the X-ray diffraction test (XRD)²⁵ was performed using Cu Kα radiation at a wavelength of 0.15406 nm. At room temperature, the sample points were selected at the same center position of the wafer for the XRD test. The XRD test results of the two groups are shown in Figures 12–15.

Figure 12.

XRD detection of the head and tail of the InP single crystal produced in furnace number 10.

Figure 15.

XRD detection of the head and tail of the InP single crystal produced in furnace number 13.

The XRD test results for the top and tail crystal wafers of the InP single crystal produced in the furnace 10 experiment are shown in Figure 12a,b. The full width at half-maximum (fwhm) of the top crystal wafer is 0.00325, and the fwhm of the tail crystal wafer is 0.00317.

The XRD test results for the top and tail crystal wafers of the InP single crystal produced in the experiment of furnace 11 are shown in Figure 13a,b. The full width at half-maximum (fwhm) of the top crystal wafer is 0.00313, and the fwhm of the tail crystal wafer is 0.00319.

Figure 13.

XRD detection of the head and tail of the InP single crystal produced in furnace number 11.

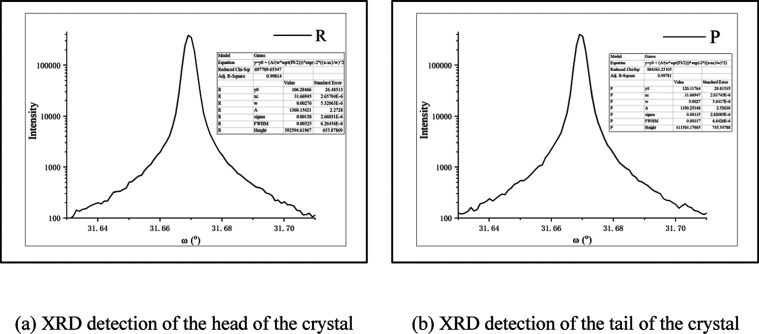
The XRD test results for the top and tail crystal wafers of the InP single crystal produced in the experiment of furnace 12 are shown in Figure 14a,b. The full width at half-maximum (fwhm) of the top crystal wafer is 0.00374, and the fwhm of the tail crystal wafer is 0.00377.

Figure 14.

XRD detection of the head and tail of the InP single crystal produced in furnace number 12.

The XRD test results for the top and tail crystal wafers of the InP single crystal produced in the experiment of furnace 13 are shown in Figure 15a,b. The full width at half-maximum (fwhm) of the top crystal wafer is 0.00377, and the fwhm of the tail crystal wafer is 0.00376.

From Figures 12–15, it can be seen that the full width at half-maximum (fwhm) values of the InP wafers vary under different temperature parameter processes. The fwhm value of the InP wafers produced in the reverse contrast experiment is greater than that of the InP wafers produced in the forward experiment. Based on this, it can be concluded that the InP cooling model adopted in the forward experiment can reduce the fwhm value, which has a positive effect on the crystalline quality of the InP single crystal.

Through the comparison of two sets of forward and reverse experiments, the experimental results demonstrate the accuracy and rationality of the best cooling rate fitted in the production process of indium phosphide single crystals. When the optimal temperature parameters were used in the forward experiment, high-quality indium phosphide single crystals with low dislocation density and high crystallinity were successfully produced. On the other hand, using poorer temperature parameters in the reverse experiment resulted in the production of low-quality indium phosphide single crystals with high dislocation density and high fwhm, further validating the rationality of the cooling rate model. Therefore, the rational setting and control of temperature parameters are crucial factors for ensuring the growth quality of indium phosphide single crystals, providing important reference significance for further improving the production efficiency and quality.

4. Conclusions

Regarding the influence of the temperature-decreasing rate in the thermal field during the cooling crystallization process of InP single crystals on single crystal growth, this article constructs a temperature control model for the cooling crystallization of InP single crystal furnaces, aiming to reduce the generation of InP twin crystals, dislocations, and other defects. The following conclusions were drawn.

A thermal field model of the VGF method for the InP single crystal furnace was constructed in this article, and it was found through research that there is a continuous distribution feature between the temperature gradient and time in the thermal field. Based on this, the paper used a cubic spline algorithm to finely fit the discrete temperature-decreasing rate data obtained during the cooling crystallization process, thereby successfully establishing a temperature control model that conforms to the characteristics of temperature changes in the furnace.

Based on the established temperature control model for the cooling crystallization of InP single crystal furnaces, positive and reverse experiments were conducted in this article for verification. The experimental results demonstrate that this model can effectively regulate internal stress in crystals, reduce the generation of defects, and have important practical significance for growing high-quality InP single crystals.

In conclusion, the research results of this paper provide important technical support and practical guidance for the growth of InP single crystals, offering new ideas and methods for the production of high-quality InP single crystals. It is believed that through continued research and exploration, the application of InP single crystals in fields, such as optical communications and microwave millimeter-wave communications, will be further promoted and developed.

The authors declare no competing financial interest.