Robust ${\mathcal{H}}_{\infty }$ filter design for discrete time switched interconnected systems with time-varying delays

Abstract

The filter design of ${\mathcal{H}}_{\infty }$ for an interconnecting system (IS) with uncertain discrete time switching is examined. Discrete-time $\mathcal{N}$-linear subsystems with coupling states that have time delays, external disturbances and uncertainty are taken into account. Utilising Lyapunov-Krasovskii functional (LKF) and the Linear-Matrix-Inequality (LMI) approach, an appropriate filter is designed for the considered interconnected system. To remove an outside disruption, ${\mathcal{H}}_{\infty }$ performances (HP) are implemented. Sufficient criteria are developed to assure the Exponentially Mean-Square Stability (EMSS). Then, using MATLAB-LMI toolbox filter parameters were established. Finally, the efficiency of the designed filter is illustrated with mathematical instances.

1. Introduction

An IS comprises a single system that provides direct communication between a number of systems of information that are utilised to distribute data along with additional information by connecting different subsystems/switched systems with coupled states, within the given time intervals. The interconnected systems frequently used to describe systems that have substantial interactions in practice, for instance, an energy-efficient system, a processing controller system, few computer networks, economical system or large-space adaptable constructions. Systems made up of coupling terms or subsystems which instantly communicate with one another by a straightforward and anticipated way to achieve a shared set of goals exist in the actual world. Also, the primary benefit of interconnected systems is the terms that have been coupling and switching are carried out at the same time [14],[19],[21] and [34]. However, when a system in the world of reality is made up of interconnected elements or subsystems which have basic interactions with other components in a simple fashion and predictable manner to maintain a shared set of goals, yet the entire system that is produced exhibits complicated characteristics.

Besides interconnecting properties, practical problems always involve time-delay. The occurrence of delays in time within dynamic systems is typically caused by exchanges of data and system functions, these are unexpectable dynamics, especially fluctuations and inadequate output. In general, the states and their derivative both exhibit time delays. The main advantage of delay independent criteria is that the result obtained are less cautious than the time-dependent approach, that are studied in [1], [2], [4] and [16]. Some researchers [13], [18], [20] have investigated many employing time-varying interruptions that are being implemented into account for practical system designs, including thermodynamic and chemical treatment. Both time-invariant and time-varying delay systems can benefit from the application of time domain techniques based on Lyapunov theories, see [25], [35], [37]. It has been further developed to the study delay systems for examination of stability by using LKT and Lyapunov-Razumikhin techniques. Such techniques are widely utilised for examining the stability for the switching interconnected system. In literatures [3], [6], [38] instability of the system occurs due to time-varying delays and unwanted external disturbance. However, [23], [29] and [33] provides an excellent stability analysis for the considered system with delay in time.

Further, the filter designing topic of uncertain systems including time lags was extensively investigated because of its wide applications in the control system and signal processing area. Many findings on filter designing problems regarding multiple types of control systems were reported in the associated research [7], [24], [27]. Usually, Kalman filter is frequently used to obtain the best possible outcomes for linear or Gaussian monitoring technique issues and it may deliver excellent tracking quality, see [36], [39]. The uniform complete observability and controllability of the underlying state-space structure serve as foundation for the Kalman filter. But, for the ${\mathcal{H}}_{\infty }$ filter, there is no requirement to establish any Gaussian assumptions about the additive noise and the simulated noise within the system's state-space visualisation. The goal of ${\mathcal{H}}_{\infty }$ filter is to reduce the incidence of domain maximum error power, while the Kalman filter reduces the mean error power. Compared to normal Kalman filter, the ${\mathcal{H}}_{\infty }$ filter is more durable since it minimises the estimated error in a worst-case scenario. Also, the significant benefit of using ${\mathcal{H}}_{\infty }$ approaches over standard control methods is its easy applicability to multivariate networks including cross-coupling among multichannel concerns. A closed-loop influence of a fluctuation can be minimised using ${\mathcal{H}}_{\infty }$ approaches; its effect is quantified by means of performance or stabilisation depending on how the problem is formulated. The main idea of the ${\mathcal{H}}_{\infty }$ filter is that it exhibits excellent robustness against uncertain systemic noises and is also used in signal analysis and control theory to accomplish stabilisation with certain performance.

Switching systems are one of the mixed dynamic system made up of different components which have its own parameters, that are among $\mathcal{N}$ modules and are regulated by certain switching rules. A variety of methods has been offered for the analysis of switching systems; the dwell-time methods were the most widely applied and have been demonstrated to provide more beneficial. Recognising that dwell-time methods are especially desirable and versatile. It has an extensive variety of necessitate in both artificial and mechanical systems, such as switched-capacitor networks, computerised motorway systems, air-traffic control systems, power electronics, and chao-generators, all of which fully enveloped in generating the switching systems. In recent days researchers have shown a significant level of desire in the investigation of switched interconnected systems, see [5], [12], [28] and references therein. Choosing a mode-dependent Lyapunov-Krasovskii functional (LKF) over a mode-independent one will yield less conservative outcomes. It should be noted that it can be challenging to delete some coupled terms that are obtained by computing the derivative of mode-dependent LKF, which could be eliminated by imposing certain tight constraints, which may introduce some conservatism.

Moreover, in real-world problems, most physical system undergoes some external disturbances. Disturbance in the system indicates that the system undergoes some unwanted input which affects the system output, it also increases the designed system errors. To handle the external noises and disturbances in the system there have been many performance used in the existing literature, among these ${\mathcal{H}}_{\infty }$ filter designing have the main advantages in-order to disable all conventional control methods, which are employed to manage disturbances and generate a controller that would provide the necessary strong performance. The primary goals of the ${\mathcal{H}}_{\infty }$ filtering technique include noise reduction and state estimation. Filter design for networked control system has been investigated in [9], [11], [32], ${\mathcal{H}}_{\infty }$ performance aids in handling control-system disturbances. In response to this outside disturbances, numerous performances have been developed. But ${\mathcal{H}}_{\infty }$ performance ensures some special advantage in filtering problems. Few researchers [8], [10], [15] have illustrated that the primary focus of ${\mathcal{H}}_{\infty }$ performance is the estimation of states in-order to minimise external disturbances affecting the system under consideration. In addition, in recent days for nonlinear as well as linear systems, ${\mathcal{H}}_{\infty }$ filter theory has many important progress and attracted considerable attention among researches. Moreover, when the parameter uncertainty appears in plant models, robust ${\mathcal{H}}_{\infty }$ analysis will guarantee the required robustness that have been clearly explained in [17] and in various literature there has been a huge number of results on continuous-time as well as discrete-time systems [22], [26], [31] and references therein.

Motivated by this aforestated discussion, we have considered discrete-time interconnected system containing time-varying delays in this study, here switching signals and the coupled terms are addressed concurrently. A suitable Lyapunov-Krasovskii functional in addition to dwell-time is employed to evaluate the results, if ‘$\mathsf{i}$’ is large the dwell-time helps to reduce the computation complexity. Further, it is noted that the whenever the uncertainties and time-varying delays occur simultaneously in an interconnected system, the robust filter designing problem is still unsolved. This motivated to focus on the switched interconnected systems. Here, we initially discussed about the consistency of an interconnected system when no external noise occurs. Furthermore, our focus is on designing ${\mathcal{H}}_{\infty }$ filters for linear switched systems. Our current work has made the following significant contributions:

• 1.To determine the effectiveness of the intended IS, the switching process together with coupled terms were carried out concurrently.
• 2.To reduce the external disturbance, an analysis involves focusing on the ${\mathcal{H}}_{\infty }$ effectiveness for discrete-time IS. A collection of necessary circumstances according to LMI is established to assure the stability for the designed IS.
• 3.An adequate filter is developed to eliminate the external interruption and to establish the system inaccuracy. Then, by building the Lyapunov-Krasovskii function together with the dwell-time, to establish the necessary stability criteria, we demonstrate that the intended filter exists.
• 4.The proposed result is implemented in the inverted pendulums and the outcomes of the simulation indicate the successful outcome for the outlined approach.

2. Problem formation

Preliminaries

Here the essential symbols that have been employed throughout this work are standard. To indicate the inverse ‘−1’ and to denote transposition of a matrix superscript ‘$\mathsf{T}$’ are used. Euclidean-space with $n\times n$ dimensions is denoted by ${\mathcal{R}}^{n\times n}$. The identity matrix is denoted by I, diagonal matrix is indicated as $diag\{.\}$, the symmetry parts are indicated by the symbol $(⁎)$.

2.1. System description

A class of switched-interconnected systems involving coupling modes and time-varying delays that are composed of N-linear discrete-time modules is considered. Its ${\mathsf{i}}^{th}$ system is outlined as:

$$x_{\mathsf{i}}(\mathsf{k}+1)={\mathcal{A}}_{\mathsf{i}}{x}_{\mathsf{i}}(\mathsf{k})+{\mathcal{A}}_{t\mathsf{i}}{x}_{\mathsf{i}}(\mathsf{k}-{\mathrm{\Upsilon }}_{\mathsf{i}}(\mathsf{k}))+\sum _{\mathsf{j}\in {{\mathrm{N}}_{\mathsf{i}}}^{in}}{\mathcal{A}}_{t\mathsf{i}\mathsf{j}}{x}_{\mathsf{j}}(\mathsf{k}-{\mathrm{\Upsilon }}_{\mathsf{i}\mathsf{j}}(\mathsf{k}))+{\mathcal{B}}_{\mathsf{i}}{d}_{\mathsf{i}}(\mathsf{k}),y_{\mathsf{i}}(\mathsf{k})={\mathcal{C}}_{\mathsf{i}}{x}_{\mathsf{i}}(\mathsf{k})+{\mathcal{D}}_{\mathsf{i}}{d}_{\mathsf{i}}(\mathsf{k}),x_{\mathsf{i}}(\mathsf{j})={\mathrm{\Phi }}_{\mathsf{i}}(\mathsf{j}),\forall \mathsf{j}\in [-\mathrm{\Upsilon },0],$$ (1)

here the state of the system is represented by $x_{\mathsf{i}}(\mathsf{k})\in {\mathcal{R}}^{n_{\mathsf{i}}}$ and measurement output is represented by $y_{\mathsf{i}}(\mathsf{k})\in {\mathcal{R}}^{m_{\mathsf{i}}}$. ${\sum }_{\mathsf{j}\in {{\mathrm{N}}_{\mathsf{i}}}^{in}}{\mathcal{A}}_{t\mathsf{i}\mathsf{j}}$ is the coupling term and ‘i’ indicates the switching between the subsystems. The coupling term and switching signal are handled simultaneously in the considered interconnected system. The symbols ${{\mathrm{N}}_{\mathsf{i}}}^{in}=\{\mathsf{j}\in \mathrm{N}-\{\mathsf{i}\}|A_{t\mathsf{i}\mathsf{j}}\ne 0\}$ as well as ${{\mathrm{N}}_{\mathsf{i}}}^{out}=\{\mathsf{j}\in \mathrm{N}-\{\mathsf{i}\}|A_{t\mathsf{j}\mathsf{i}}\ne 0\}$ denote in-neighbouring sets & out-neighbouring for ${\mathsf{i}}^{th}$ switching modes, respectively. The relationship between the ${\mathsf{i}}^{th}$ and ${\mathsf{j}}^{th}$ subsystems is specifically described by ${\mathcal{A}}_{t\mathsf{i}\mathsf{j}}>0$. There won't be any relationship among them if ${\mathcal{A}}_{t\mathsf{i}\mathsf{j}}=0$. Then, ${\mathrm{\Upsilon }}_{\mathsf{i}}(\mathsf{k})$, ${\mathrm{\Upsilon }}_{\mathsf{i}\mathsf{j}}(\mathsf{k})$ are time-delays $\mathrm{\Upsilon }=\max [-{\mathrm{\Upsilon }}_{\mathsf{i}}(M),-{\mathrm{\Upsilon }}_{\mathsf{i}\mathsf{j}}(M)]$ that satisfy $0\le {\mathrm{\Upsilon }}_{\mathsf{i}m}\le {\mathrm{\Upsilon }}_{\mathsf{i}}(\mathsf{k})\le {\mathrm{\Upsilon }}_{\mathsf{i}M}$ and $0\le {\mathrm{\Upsilon }}_{\mathsf{i}\mathsf{j}m}\le {\mathrm{\Upsilon }}_{\mathsf{i}\mathsf{j}}(\mathsf{k})\le {\mathrm{\Upsilon }}_{\mathsf{i}\mathsf{j}M}$, where the bounds ${\mathrm{\Upsilon }}_{\mathsf{i}m}$, ${\mathrm{\Upsilon }}_{\mathsf{i}M}$, ${\mathrm{\Upsilon }}_{\mathsf{i}\mathsf{j}m}$ and ${\mathrm{\Upsilon }}_{\mathsf{i}\mathsf{j}M}$ were constant values. Here external disturbances $d_{\mathsf{i}}(\mathsf{k})$ are defined on ${\mathcal{L}}_2[0,\infty )$.

2.2. Filter description

Since ${\xi }_{\mathsf{i}}(\mathsf{k})$ is an approximated output signal, it can be defined as:

$${\xi }_{\mathsf{i}}(\mathsf{k})={\mathcal{E}}_{\mathsf{i}}{x}_{\mathsf{i}}(\mathsf{k}),$$

here the known constant ${\mathcal{E}}_{\mathsf{i}}$ have the proper dimensions. The goal of the filtering analysing is to estimate ${\xi }_{\mathsf{i}}(\mathsf{k})$ using the estimated error ${\overline{\xi }}_{\mathsf{i}}(\mathsf{k})-{\xi }_{\mathsf{i}}(\mathsf{k})$. To determine the estimation for ${\xi }_{\mathsf{i}}(\mathsf{k})$, one can use the methods that follow full order filtering:

$${\overline{x}}_{\mathsf{i}}(\mathsf{k}+1)={\mathcal{A}}_{f\mathsf{i}}{\overline{x}}_{\mathsf{i}}(\mathsf{k})+{\mathcal{B}}_{f\mathsf{i}}{y}_{\mathsf{i}}(\mathsf{k}),{\overline{\xi }}_{\mathsf{i}}(\mathsf{k})={\mathcal{E}}_{f\mathsf{i}}{\overline{x}}_{\mathsf{i}}(\mathsf{k}),{\overline{x}}_{\mathsf{i}}({\mathsf{k}}_0)=0,$$ (2)

here the state vector is denoted by ${\overline{x}}_{\mathsf{i}}(\mathsf{k})\in {\mathcal{R}}^{n_{\mathsf{i}}}$, the signal that comes out of the filter is denoted by ${\overline{\xi }}_{\mathsf{i}}(\mathsf{k})\in {\mathcal{R}}^{p_{\mathsf{i}}}$, and the filtering parameters that need to be developed are ${\mathcal{A}}_{f\mathsf{i}}$, ${\mathcal{B}}_{f\mathsf{i}}$, and ${\mathcal{E}}_{f\mathsf{i}}$.

Then, ${\hat{x}}_{\mathsf{i}}(\mathsf{k})={[{x_{\mathsf{i}}}^{\mathsf{T}}(\mathsf{k}){\overline{x}}_{\mathsf{i}}^{\mathsf{T}}(\mathsf{k})]}^{\mathsf{T}}$ is the new state that should be defined and the filter error is termed as ${\hat{\xi }}_{\mathsf{i}}(\mathsf{k})={\xi }_{\mathsf{i}}(\mathsf{k})-{\overline{\xi }}_{\mathsf{i}}(\mathsf{k})$. From (1) and (2), it can be derived as:

$${\hat{x}}_{\mathsf{i}}(\mathsf{k}+1)={\overline{\mathcal{A}}}_{\mathsf{i}}{\hat{x}}_{\mathsf{i}}(\mathsf{k})+{\overline{\mathcal{A}}}_{t\mathsf{i}}\epsilon {\hat{x}}_{\mathsf{i}}(\mathsf{k}-{\mathrm{\Upsilon }}_{\mathsf{i}}(\mathsf{k}))+\sum _{\mathsf{j}\in {{\mathrm{N}}_{\mathsf{i}}}^{in}}{\overline{\mathcal{A}}}_{t\mathsf{i}\mathsf{j}}\epsilon {\hat{x}}_{\mathsf{j}}(\mathsf{k}-{\mathrm{\Upsilon }}_{\mathsf{i}\mathsf{j}}(\mathsf{k}))+{\overline{\mathcal{B}}}_{\mathsf{i}}{d}_{\mathsf{i}}(\mathsf{k}),\widehat{{\xi }_{\mathsf{i}}}(\mathsf{k})={\mathbb{E}}_{\mathsf{i}}\widehat{x_{\mathsf{i}}}(\mathsf{k}),\widehat{x_{\mathsf{i}}}({\mathsf{k}}_0)={\hat{x}}_0,$$ (3)

where

$${\overline{\mathcal{A}}}_{\mathsf{i}}=\left[\begin{array}{cc}\hfill {\mathcal{A}}_{\mathsf{i}}\hfill & \hfill 0\hfill \\ \hfill {\mathcal{B}}_{f\mathsf{i}}{\mathcal{C}}_{\mathsf{i}}\hfill & \hfill {\mathcal{A}}_{f\mathsf{i}}\hfill \end{array}\right],{\overline{\mathcal{A}}}_{t\mathsf{i}}=\left[\begin{array}{c}\hfill {\mathcal{A}}_{t\mathsf{i}}\hfill \\ \hfill 0\hfill \end{array}\right],{\overline{\mathcal{A}}}_{t\mathsf{i}\mathsf{j}}=\left[\begin{array}{c}\hfill {\mathcal{A}}_{t\mathsf{i}\mathsf{j}}\hfill \\ \hfill 0\hfill \end{array}\right],{\overline{\mathcal{B}}}_{\mathsf{i}}=\left[\begin{array}{c}\hfill {\mathcal{B}}_{\mathsf{i}}\hfill \\ \hfill {\mathcal{B}}_{f\mathsf{i}}{\mathcal{D}}_{\mathsf{i}}\hfill \end{array}\right],\epsilon =\left[\begin{array}{c}\hfill \mathcal{I}0\hfill \end{array}\right],{\mathbb{E}}_{\mathsf{i}}=\left[\begin{array}{c}\hfill {\mathcal{E}}_{\mathsf{i}}-{\mathcal{E}}_{f\mathsf{i}}\hfill \end{array}\right].$$

Next, the intended system's (1) stability is studied in both the presence and absence of disturbances.

Lemma 1

[40]For any matrix A, $\mathrm{Q}={\mathrm{Q}}^{\mathsf{T}}$, with $\mathrm{P}>0$, the condition that ${\mathrm{A}}^{\mathsf{T}}\mathrm{P}\mathrm{A}-\mathrm{Q}<0$ is true only if is present matrix S, we have

$$\left[\begin{array}{cc}\hfill -\mathrm{Q}\hfill & \hfill {\mathrm{A}}^{\mathsf{T}}{\mathrm{S}}^{\mathsf{T}}\hfill \\ \hfill ⁎\hfill & \hfill \mathrm{P}-\mathrm{S}-{\mathrm{S}}^{\mathsf{T}}\hfill \end{array}\right]<0$$

Lemma 2

[30]Presume$\mathrm{F}(\mathsf{k})$represents a matrix functional that satisfies${\mathrm{F}}^{\mathsf{T}}(\mathsf{k})\mathrm{F}(\mathsf{k})\le I$. Real matrices Ω, $\mathsf{M}$, and ${\mathrm{N}}_a$ are assumed to have the proper dimensions. Following that,

$$\mathrm{\Omega }+\mathsf{M}\mathrm{F}(\mathsf{k}){\mathrm{N}}_a+{[\mathsf{M}\mathrm{F}(\mathsf{k}){\mathrm{N}}_a]}^{\mathsf{T}}<0,$$

pertains to the case where a scalar $ϵ>0$ exists and is satisfied.

$$\mathrm{\Omega }+{ϵ}^{-1}\mathsf{M}{\mathsf{M}}^{\mathsf{T}}+ϵ{\mathrm{N}}_a^{\mathsf{T}}{\mathrm{N}}_a<0.$$

Definition 1

whenever (3) has zero initially circumstances, the systems are considered EMSS with ensured HP ${\gamma }_{\mathsf{i}}>0$, if its mean square stable which satisfies the subsequent inequality,

$$\sum _{\mathsf{i}\in \mathrm{\Omega }}\{\sum _{r={\mathsf{k}}_0}^{\infty }{\widehat{{\xi }_{\mathsf{i}}}}^{\mathsf{T}}(r)\widehat{{\xi }_{\mathsf{i}}}(r)\}\le \sum _{\mathsf{i}\in \mathrm{\Omega }}\{{\gamma }_{\mathsf{i}}^2\sum _{r={\mathsf{k}}_0}^{\infty }{d}_{\mathsf{i}}^{\mathsf{T}}(r)d_{\mathsf{i}}(r)\}.$$

Definition 2

Given a switch signal $\mathsf{i}$, for every $\mathsf{k}\ge {\mathsf{k}}_0$ & ${\mathsf{k}}_0\le \tau \le \mathsf{k}$, where ${\mathrm{N}}_{\mathsf{i}}$ indicate the number of switching of i in the range [${\mathsf{k}}_0$, $\mathsf{k}$]. In the event when ${\mathcal{T}}_b>0$ exist, then ${\mathcal{N}}_0\ge 0$ also exist, we have ${\mathcal{N}}_{\mathsf{i}}({\mathsf{k}}_0,\mathsf{k})\le {\mathcal{N}}_0+(\mathsf{k}-{\mathsf{k}}_0)/{\mathcal{T}}_b$, here dwell-time is denoted by ${\mathcal{T}}_b$, and the chatter-bound by ${\mathcal{N}}_0$. We select ${\mathcal{N}}_0=0$, as is frequently done in the literature.

Remark 1

$Q_{\mathsf{i}\mathsf{j}}$ represent an equidefinite positive matrix along with $x_{\mathsf{j}}(\mathsf{k})\in {\mathcal{R}}^{n_{\mathsf{i}}}$. In the event that the pertinent series converges, the inequality that follows is obvious

$$\sum _{\mathsf{i}=1}^{\mathrm{N}}\sum _{\mathsf{j}=1}^{\mathrm{N}}{\hat{x}}_{\mathsf{j}}^{\mathsf{T}}(\mathsf{k}){\mathcal{Q}}_{\mathsf{i}\mathsf{j}}\widehat{x_{\mathsf{j}}}(\mathsf{k})=\sum _{\mathsf{i}=1}^{\mathrm{N}}{\hat{x}}_{\mathsf{i}}^{\mathsf{T}}(\mathsf{k})\left(\sum _{\mathsf{j}=1}^{\mathrm{N}}{\mathcal{Q}}_{\mathsf{j}\mathsf{i}}\right){\hat{x}}_{\mathsf{j}}(\mathsf{k})(\text{or})\sum _{\mathsf{j}\in {{\mathrm{N}}_{\mathsf{i}}}^{in}}{\hat{x}}_{\mathsf{j}}^{\mathsf{T}}(\mathsf{k}){\mathcal{P}}_{\mathsf{i}\mathsf{j}}{\hat{x}}_{\mathsf{j}}(\mathsf{k})={\hat{x}}_{\mathsf{i}}^{\mathsf{T}}(\mathsf{k})\left(\sum _{\mathsf{j}\in {{\mathrm{N}}_{\mathsf{i}}}^{out}}{\mathcal{P}}_{\mathsf{j}\mathsf{i}}\right){\hat{x}}_{\mathsf{j}}(\mathsf{k}).$$

3. Main results

Within this segment, in the absence of disruption first we investigate EMSS for designed system. Next, we examine the necessary criteria for evaluating exponential ${\mathcal{H}}_{\infty }$ filter.

Theorem 1

Given switching signal$\mathsf{i}$and the given scalars$\mu >1$and$0<\delta <1$. In addition to the dwell-time that satisfy${\mathcal{T}}_b\ge {\mathcal{T}}_b^{⁎}=-\frac{\ln \mu }{\ln (1-\delta )}$, error(3)in the absence of disruption we state that is EMSS when$\mathsf{i}\ne \mathsf{j}$. There exists positive-definite matrix${\mathcal{P}}_{\mathsf{i}}$,${\mathcal{Q}}_{1\mathsf{i}}$,${\mathcal{Q}}_{2\mathsf{i}}$,${\mathcal{Q}}_{3\mathsf{i}}$,${\mathcal{R}}_{1\mathsf{i}\mathsf{j}}$,${\mathcal{R}}_{2\mathsf{i}\mathsf{j}}$,${\mathcal{R}}_{3\mathsf{i}\mathsf{j}}$and${\mathcal{S}}_{1\mathsf{i}}$,${\mathcal{S}}_{2\mathsf{i}}$are any suitable-dimension matrices, so that each and every$\mathsf{i}$,$\mathsf{j}\in \mathrm{N}$and, subject to LMIs

$$\left[\begin{array}{cc}\hfill {\mathrm{\Psi }}_{1\mathsf{i}}\hfill & \hfill {\mathrm{\Psi }}_{2\mathsf{i}}^{\mathsf{T}}\hfill \\ \hfill ⁎\hfill & \hfill {\mathcal{P}}_{\mathsf{i}}-{\mathcal{S}}_{\mathsf{i}}-{\mathcal{S}}_{\mathsf{i}}^{\mathsf{T}}\hfill \end{array}\right]<0,$$ (4)

where

$${\mathrm{\Psi }}_{1\mathsf{i}}=diag\{{\mathrm{\Psi }}_{(1,1)},-{(1-\delta )}^{{\mathrm{\Upsilon }}_{\mathsf{i}m}}{\mathcal{Q}}_{1\mathsf{i}},-{(1-\delta )}^{{\mathrm{\Upsilon }}_{\mathsf{i}m}}{\mathcal{Q}}_{2\mathsf{i}},-{(1-\delta )}^{{\mathrm{\Upsilon }}_{\mathsf{i}M}}{\mathcal{Q}}_{3\mathsf{i}},{\mathcal{M}}_1,{\mathcal{M}}_2,{\mathcal{M}}_3\},{\mathcal{M}}_1=\sum _{\mathsf{j}\in {{\mathrm{N}}_{\mathsf{i}}}^{in}}[-{(1-\delta )}^{{\mathrm{\Upsilon }}_{\mathsf{i}m}}{\mathcal{R}}_{1\mathsf{i}\mathsf{j}}],{\mathcal{M}}_2=\sum _{\mathsf{j}\in {{\mathrm{N}}_{\mathsf{i}}}^{in}}[-{(1-\delta )}^{{\mathrm{\Upsilon }}_{\mathsf{i}m}}{\mathcal{R}}_{2\mathsf{i}\mathsf{j}}],{\mathcal{M}}_3=\sum _{\mathsf{j}\in {{\mathrm{N}}_{\mathsf{i}}}^{in}}[-{(1-\delta )}^{{\mathrm{\Upsilon }}_{\mathsf{i}M}}{\mathcal{R}}_{3\mathsf{i}\mathsf{j}}],{\mathrm{\Psi }}_{(1,1)}=-(1-\delta ){\mathcal{P}}_{\mathsf{i}}+{\mathcal{Q}}_{1\mathsf{i}}+{\mathcal{Q}}_{3\mathsf{i}}+({\mathrm{\Upsilon }}_{\mathsf{i}M}-{\mathrm{\Upsilon }}_{\mathsf{i}m}+1){\mathcal{Q}}_{2\mathsf{i}}+\sum _{\mathsf{j}\in {{\mathrm{N}}_{\mathsf{i}}}^{out}}[({\mathcal{R}}_{1\mathsf{j}\mathsf{i}}+{\mathcal{R}}_{3\mathsf{j}\mathsf{i}})+({\mathrm{\Upsilon }}_{\mathsf{i}M}-{\mathrm{\Upsilon }}_{\mathsf{i}m}+1){\mathcal{R}}_{2\mathsf{j}\mathsf{i}}],{\mathrm{\Psi }}_{2\mathsf{i}}=\left[\begin{array}{ccccccc}\hfill {\mathcal{S}}_{1\mathsf{i}}{\overline{\mathcal{A}}}_{\mathsf{i}}\hfill & \hfill 0\hfill & \hfill {\mathcal{S}}_{1\mathsf{i}}{\overline{\mathcal{A}}}_{t\mathsf{i}}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill {\mathcal{S}}_{1\mathsf{i}}{\sum }_{\mathsf{j}\in {{\mathcal{N}}_{\mathsf{i}}}^{in}}{\overline{\mathcal{A}}}_{t\mathsf{i}\mathsf{j}}\hfill & \hfill 0\hfill \end{array}\right],$$

state decay estimation are${\sum }_{\mathsf{i}\in \mathrm{\Omega }}{\Vert {\hat{x}}_{\mathsf{i}}(\mathsf{k})\Vert }^2\le \frac{{\beta }_2}{{\beta }_1}{(1-\delta )}^{\mathsf{k}-{\mathsf{k}}_0}{\sum }_{\mathsf{i}\in \mathrm{\Omega }}{\Vert {\varphi }_{\mathsf{i}}(\mathsf{k})\Vert }_l^2$with${\beta }_1=\underset{\forall i\in \mathrm{\Omega }}{\min }{\lambda }_{\min }({\mathcal{P}}_{\mathsf{i}})$and${\beta }_2=\underset{\forall i\in \mathrm{\Omega }}{\max }{\lambda }_{\max }({\mathcal{P}}_{\mathsf{i}})+\underset{\forall i\in \mathrm{\Omega }}{\max }{\lambda }_{\max }({\mathcal{Q}}_{1\mathsf{i}})+(1+{\mathrm{\Upsilon }}_{\mathsf{i}M}-{\mathrm{\Upsilon }}_{\mathsf{i}m})\underset{\forall i\in \mathrm{\Omega }}{\max }{\lambda }_{\max }({\mathcal{Q}}_{2\mathsf{i}})+\underset{\forall i\in \mathrm{\Omega }}{\max }{\lambda }_{\max }({\mathcal{Q}}_{3\mathsf{i}})+\underset{\forall i\in \mathrm{\Omega }}{\max }{\sum }_{\mathsf{j}\in {{\mathcal{N}}_{\mathsf{i}}}^{in}}{\lambda }_{\max }({\mathcal{R}}_{1\mathsf{i}\mathsf{j}})+(1+{\mathrm{\Upsilon }}_{\mathsf{i}M}-{\mathrm{\Upsilon }}_{\mathsf{i}m})\underset{\forall i\in \mathrm{\Omega }}{\max }{\sum }_{\mathsf{j}\in {{\mathcal{N}}_{\mathsf{i}}}^{in}}{\lambda }_{\max }({\mathcal{R}}_{2\mathsf{i}\mathsf{j}})+\underset{\forall i\in \mathrm{\Omega }}{\max }{\sum }_{\mathsf{j}\in {{\mathcal{N}}_{\mathsf{i}}}^{in}}\times {\lambda }_{\max }({\mathcal{R}}_{3\mathsf{i}\mathsf{j}})$.

Proof 1

The subsequent LKF is defined to provide LMI-based sufficient-condition and to demonstrate the necessary outcome for the specified systems

$$\mathcal{V}(\mathsf{k})=\sum _{\mathsf{i}\in \mathrm{\Omega }}{\mathcal{V}}_{\mathsf{i}}(\mathsf{k})=\sum _{\mathsf{i}\in \mathrm{\Omega }}[{\mathcal{V}}_{1\mathsf{i}}+{\mathcal{V}}_{2\mathsf{i}}+{\mathcal{V}}_{3\mathsf{i}}+{\mathcal{V}}_{4\mathsf{i}}+{\mathcal{V}}_{5\mathsf{i}}],$$ (5)

we have

$${\mathcal{V}}_{1\mathsf{i}}(\mathsf{k})={\hat{x}}_{\mathsf{i}}^{\mathsf{T}}(\mathsf{k}){\mathcal{P}}_{\mathsf{i}}{\hat{x}}_{\mathsf{i}}(\mathsf{k}){\mathcal{V}}_{2\mathsf{i}}(\mathsf{k})=\sum _{\mathsf{v}=\mathsf{k}-{\mathrm{\Upsilon }}_{\mathsf{i}m}}^{\mathsf{k}-1}{(1-\delta )}^{\mathsf{k}-\mathsf{v}-1}{\hat{x}}_{\mathsf{i}}^{\mathsf{T}}(\mathsf{v}){\epsilon }^{\mathsf{T}}{\mathcal{Q}}_{1\mathsf{i}}\epsilon {\hat{x}}_{\mathsf{i}}(\mathsf{v})+\sum _{\mathsf{v}=\mathsf{k}-{\mathrm{\Upsilon }}_{\mathsf{i}(\mathsf{k})}}^{\mathsf{k}-1}{(1-\delta )}^{\mathsf{k}-\mathsf{v}-1}{\hat{x}}_{\mathsf{i}}^{\mathsf{T}}(\mathsf{v}){\epsilon }^{\mathsf{T}}{\mathcal{Q}}_{2\mathsf{i}}\epsilon {\hat{x}}_{\mathsf{i}}(\mathsf{v})+\sum _{\mathsf{v}=\mathsf{k}-{\mathrm{\Upsilon }}_{\mathsf{i}M}}^{\mathsf{k}-1}{(1-\delta )}^{\mathsf{k}-\mathsf{v}-1}{\hat{x}}_{\mathsf{i}}^{\mathsf{T}}(\mathsf{v}){\epsilon }^{\mathsf{T}}{\mathcal{Q}}_{3\mathsf{i}}\epsilon {\hat{x}}_{\mathsf{i}}(\mathsf{v}),{\mathcal{V}}_{3\mathsf{i}}(\mathsf{k})=\sum _{r=-{\mathrm{\Upsilon }}_{\mathsf{i}M+1}}^{-{\mathrm{\Upsilon }}_{\mathsf{i}m}}\sum _{\mathsf{v}=\mathsf{k}+r}^{\mathsf{k}-1}{(1-\delta )}^{\mathsf{k}-\mathsf{v}-1}{\hat{x}}_{\mathsf{i}}^{\mathsf{T}}(\mathsf{v}){\epsilon }^{\mathsf{T}}{\mathcal{Q}}_{2\mathsf{i}}\epsilon {\hat{x}}_{\mathsf{i}}(\mathsf{v}),{\mathcal{V}}_{4\mathsf{i}}(\mathsf{k})=\sum _{\mathsf{j}\in {\mathcal{N}}_{\mathsf{i}}^{in}}[\sum _{\mathsf{v}=\mathsf{k}-{\mathrm{\Upsilon }}_{\mathsf{i}\mathsf{j}m}}^{\mathsf{k}-1}{(1-\delta )}^{\mathsf{k}-\mathsf{v}-1}{\hat{x}}_{\mathsf{i}}^{\mathsf{T}}(\mathsf{v}){\epsilon }^{\mathsf{T}}{\mathcal{R}}_{1\mathsf{i}\mathsf{j}}\epsilon {\hat{x}}_{\mathsf{i}}(\mathsf{v})+\sum _{\mathsf{v}=\mathsf{k}-{\mathrm{\Upsilon }}_{\mathsf{i}\mathsf{j}(\mathsf{k})}}^{\mathsf{k}-1}{(1-\delta )}^{\mathsf{k}-\mathsf{v}-1}{\hat{x}}_{\mathsf{i}}^{\mathsf{T}}(\mathsf{v}){\epsilon }^{\mathsf{T}}{\mathcal{R}}_{2\mathsf{i}\mathsf{j}}\epsilon {\hat{x}}_{\mathsf{i}}(\mathsf{v})\sum _{\mathsf{v}=\mathsf{k}-{\mathrm{\Upsilon }}_{\mathsf{i}\mathsf{j}M}}^{\mathsf{k}-1}{(1-\delta )}^{\mathsf{k}-\mathsf{v}-1}{\hat{x}}_{\mathsf{i}}^{\mathsf{T}}(\mathsf{v}){\epsilon }^{\mathsf{T}}{\mathcal{R}}_{3\mathsf{i}\mathsf{j}}\epsilon {\hat{x}}_{\mathsf{i}}(\mathsf{v})],{\mathcal{V}}_{5\mathsf{i}}(\mathsf{k})=\sum _{\mathsf{j}\in N_{\mathsf{i}}^{in}}[\sum _{r=-{\mathrm{\Upsilon }}_{\mathsf{i}\mathsf{j}M+1}}^{-{\mathrm{\Upsilon }}_{\mathsf{i}jm}}\sum _{\mathsf{v}=\mathsf{k}+r}^{\mathsf{k}-1}{(1-\delta )}^{\mathsf{k}-\mathsf{v}-1}{\hat{x}}_{\mathsf{i}}^{\mathsf{T}}(\mathsf{v}){\epsilon }^{\mathsf{T}}{\mathcal{R}}_{2\mathsf{i}\mathsf{j}}\epsilon {\hat{x}}_{\mathsf{i}}(\mathsf{v})].$$

Now, let's signify the forward-difference $\mathrm{\Delta }{\mathcal{V}}_{\mathsf{i}}(\mathsf{k})={\mathcal{V}}_{\mathsf{i}}(\mathsf{k}+1)-{\mathcal{V}}_{\mathsf{i}}(\mathsf{k})$, we have the following

$$\mathrm{\Delta }{\mathcal{V}}_1(\mathsf{k}+1)+\delta {\mathcal{V}}_1(\mathsf{k})={\mathcal{V}}_1(\mathsf{k}+1)-(1-\delta ){\mathcal{V}}_1(\mathsf{k})={\widehat{x_{\mathsf{i}}}}^{\mathsf{T}}(\mathsf{k}+1){\mathcal{P}}_{\mathsf{i}}\widehat{x_{\mathsf{i}}}(\mathsf{k}+1)-(1-\delta ){\widehat{x_{\mathsf{i}}}}^{\mathsf{T}}(\mathsf{k}){\mathcal{P}}_{\mathsf{i}}\widehat{x_{\mathsf{i}}}(\mathsf{k})=[{\overline{\mathcal{A}}}_{\mathsf{i}}{\hat{x}}_{\mathsf{i}}(\mathsf{k})+{\overline{\mathcal{A}}}_{t\mathsf{i}}{\hat{x}}_{\mathsf{i}}(\mathsf{k}-{\mathrm{\Upsilon }}_{\mathsf{i}}(\mathsf{k}))+\sum _{\mathsf{j}\in {{\mathcal{N}}_{\mathsf{i}}}^{in}}{\overline{\mathcal{A}}}_{t\mathsf{i}\mathsf{j}}{\hat{x}}_{\mathsf{j}}(\mathsf{k}-{\mathrm{\Upsilon }}_{\mathsf{i}\mathsf{j}}(\mathsf{k})){+{\overline{\mathcal{B}}}_{\mathsf{i}}{d}_{\mathsf{i}}(\mathsf{k})]}^{\mathsf{T}}{\mathcal{P}}_{1\mathsf{i}}[{\overline{\mathcal{A}}}_{\mathsf{i}}{\hat{x}}_{\mathsf{i}}(\mathsf{k})+{\overline{\mathcal{A}}}_{t\mathsf{i}}{\hat{x}}_{\mathsf{i}}(\mathsf{k}-{\mathrm{\Upsilon }}_{\mathsf{i}}(\mathsf{k}))+\sum _{\mathsf{j}\in {{\mathcal{N}}_{\mathsf{i}}}^{in}}{\overline{\mathcal{A}}}_{t\mathsf{i}\mathsf{j}}{\hat{x}}_{\mathsf{j}}(\mathsf{k}-{\mathrm{\Upsilon }}_{\mathsf{i}\mathsf{j}}(\mathsf{k}))+{\overline{\mathcal{B}}}_{\mathsf{i}}{d}_{\mathsf{i}}(\mathsf{k})]-(1-\delta ){\hat{x}}_{\mathsf{i}}^{\mathsf{T}}(\mathsf{k}){\mathcal{P}}_{\mathsf{i}}{\hat{x}}_{\mathsf{i}}(\mathsf{k}).$$ (6)

$$\mathrm{\Delta }{\mathcal{V}}_2(\mathsf{k}+1)+\delta {\mathcal{V}}_2(\mathsf{k})={\mathcal{V}}_2(\mathsf{k}+1)-(1-\delta ){\mathcal{V}}_2(\mathsf{k})={\widehat{x_{\mathsf{i}}}}^{\mathsf{T}}(\mathsf{k}){\epsilon }^{\mathsf{T}}({\mathcal{Q}}_{1\mathsf{i}}+{\mathcal{Q}}_{2\mathsf{i}}+{\mathcal{Q}}_{3\mathsf{i}})\epsilon \widehat{x_{\mathsf{i}}}(\mathsf{k})-{(1-\delta )}^{{\mathrm{\Upsilon }}_{\mathsf{i}m}}{\widehat{x_{\mathsf{i}}}}^{\mathsf{T}}(\mathsf{k}-{\mathrm{\Upsilon }}_{\mathsf{i}m}){\epsilon }^{\mathsf{T}}{\mathcal{Q}}_{1\mathsf{i}}\epsilon \widehat{x_{\mathsf{i}}}(\mathsf{k}-{\mathrm{\Upsilon }}_{\mathsf{i}m})-{(1-\delta )}^{{\mathrm{\Upsilon }}_{\mathsf{i}m}}{\widehat{x_{\mathsf{i}}}}^{\mathsf{T}}(\mathsf{k}-{\mathrm{\Upsilon }}_{\mathsf{i}}(\mathsf{k})){\epsilon }^{\mathsf{T}}{\mathcal{Q}}_{2\mathsf{i}}\epsilon \widehat{x_{\mathsf{i}}}(\mathsf{k}-{\mathrm{\Upsilon }}_{\mathsf{i}}(\mathsf{k}))-{(1-\delta )}^{{\mathrm{\Upsilon }}_{\mathsf{i}M}}{\widehat{x_{\mathsf{i}}}}^{\mathsf{T}}(\mathsf{k}-{\mathrm{\Upsilon }}_{\mathsf{i}M}){\epsilon }^{\mathsf{T}}{\mathcal{Q}}_{3\mathsf{i}}\epsilon \widehat{x_{\mathsf{i}}}(\mathsf{k}-{\mathrm{\Upsilon }}_{\mathsf{i}M})+\sum _{\mathsf{v}=\mathsf{k}+1-{\mathrm{\Upsilon }}_{\mathsf{i}M}}^{\mathsf{k}-{\mathrm{\Upsilon }}_{\mathsf{i}m}}{(1-\delta )}^{\mathsf{k}-\mathsf{v}}{\hat{x}}_{\mathsf{i}}^{\mathsf{T}}(\mathsf{v}){\epsilon }^{\mathsf{T}}{\mathcal{Q}}_{2\mathsf{i}}\epsilon {\hat{x}}_{\mathsf{i}}(\mathsf{v}).$$ (7)

$$\mathrm{\Delta }{\mathcal{V}}_3(\mathsf{k}+1)+\delta {\mathcal{V}}_3(\mathsf{k})={\mathcal{V}}_3(\mathsf{k}+1)-(1-\delta ){\mathcal{V}}_3(\mathsf{k})=({\mathrm{\Upsilon }}_{\mathsf{i}M}-{\mathrm{\Upsilon }}_{\mathsf{i}m}){\widehat{x_{\mathsf{i}}}}^{\mathsf{T}}(\mathsf{k}){\epsilon }^{\mathsf{T}}{Q}_{2\mathsf{i}}\epsilon \widehat{x_{\mathsf{i}}}(\mathsf{k})-\sum _{r=\mathsf{k}+1-{\mathrm{\Upsilon }}_{\mathsf{i}M}}^{\mathsf{k}-{\mathrm{\Upsilon }}_{\mathsf{i}m}}{(1-\delta )}^{\mathsf{k}-r}{\hat{x}}_{\mathsf{i}}^{\mathsf{T}}(r){\epsilon }^{\mathsf{T}}{\mathcal{Q}}_{2\mathsf{i}}\epsilon {\hat{x}}_{\mathsf{i}}(r).$$ (8)

$$\mathrm{\Delta }{\mathcal{V}}_4(\mathsf{k}+1)+\delta {\mathcal{V}}_4(\mathsf{k})={\mathcal{V}}_4(\mathsf{k}+1)-(1-\delta ){\mathcal{V}}_4(\mathsf{k})=\sum _{\mathsf{j}\in {{\mathcal{N}}_{\mathsf{i}}}^{in}}[{\hat{x}}_{\mathsf{j}}^{\mathsf{T}}(\mathsf{k}){\epsilon }^{\mathsf{T}}({\mathcal{R}}_{1\mathsf{i}\mathsf{j}}+{\mathcal{R}}_{2\mathsf{i}\mathsf{j}}+{\mathcal{R}}_{3\mathsf{i}\mathsf{j}})\epsilon \widehat{x_{\mathsf{j}}}(\mathsf{k})-{(1-\delta )}^{{\mathrm{\Upsilon }}_{\mathsf{i}\mathsf{j}m}}{\hat{x}}_{\mathsf{j}}^{\mathsf{T}}(\mathsf{k}-{\mathrm{\Upsilon }}_{\mathsf{i}\mathsf{j}m}){\epsilon }^{\mathsf{T}}{\mathcal{R}}_{1\mathsf{i}\mathsf{j}}\epsilon \widehat{x_{\mathsf{j}}}(\mathsf{k}-{\mathrm{\Upsilon }}_{\mathsf{i}\mathsf{j}m})-{(1-\delta )}^{{\mathrm{\Upsilon }}_{\mathsf{i}\mathsf{j}m}}{\widehat{x_{\mathsf{j}}}}^{\mathsf{T}}(\mathsf{k}-{\mathrm{\Upsilon }}_{\mathsf{i}\mathsf{j}}(\mathsf{k})){\epsilon }^{\mathsf{T}}{\mathcal{R}}_{2\mathsf{i}\mathsf{j}}\epsilon \widehat{x_{\mathsf{j}}}(\mathsf{k}-{\mathrm{\Upsilon }}_{\mathsf{i}\mathsf{j}}(\mathsf{k}))-{(1-\delta )}^{{\mathrm{\Upsilon }}_{\mathsf{i}\mathsf{j}M}}{\widehat{x_{\mathsf{j}}}}^{\mathsf{T}}(\mathsf{k}-{\mathrm{\Upsilon }}_{\mathsf{i}\mathsf{j}M}){\epsilon }^{\mathsf{T}}{\mathcal{R}}_{3\mathsf{i}\mathsf{j}}\epsilon \widehat{x_{\mathsf{j}}}(\mathsf{k}-{\mathrm{\Upsilon }}_{\mathsf{i}\mathsf{j}M})+\sum _{\mathsf{v}=\mathsf{k}+1-{\mathrm{\Upsilon }}_{\mathsf{i}\mathsf{j}M}}^{\mathsf{k}-{\mathrm{\Upsilon }}_{\mathsf{i}\mathsf{j}m}}{(1-\delta )}^{\mathsf{k}-s}{\hat{x}}_{\mathsf{j}}^{\mathsf{T}}(\mathsf{v}){\epsilon }^{\mathsf{T}}{\mathcal{R}}_{2\mathsf{i}\mathsf{j}}\epsilon {\hat{x}}_{\mathsf{j}}(\mathsf{v})].$$ (9)

$$\mathrm{\Delta }{\mathcal{V}}_5(\mathsf{k}+1)+\delta {\mathcal{V}}_5(\mathsf{k})={\mathcal{V}}_5(\mathsf{k}+1)-(1-\delta ){\mathcal{V}}_5(\mathsf{k})=\sum _{\mathsf{j}\in {{\mathcal{N}}_{\mathsf{i}}}^{in}}[({\mathrm{\Upsilon }}_{\mathsf{i}\mathsf{j}M}-{\mathrm{\Upsilon }}_{\mathsf{i}\mathsf{j}m}){\widehat{x_{\mathsf{j}}}}^{\mathsf{T}}(\mathsf{k}){\epsilon }^{\mathsf{T}}{\mathcal{R}}_{2\mathsf{i}\mathsf{j}}\epsilon \widehat{x_{\mathsf{j}}}(\mathsf{k})-\sum _{r=\mathsf{k}+1-{\mathrm{\Upsilon }}_{\mathsf{i}\mathsf{j}M}}^{\mathsf{k}-{\mathrm{\Upsilon }}_{\mathsf{i}\mathsf{j}m}}{(1-\delta )}^{\mathsf{k}-r}{\hat{x}}_{\mathsf{j}}^{\mathsf{T}}(r){\epsilon }^{\mathsf{T}}{\mathcal{R}}_{2\mathsf{i}\mathsf{j}}\epsilon {\hat{x}}_{\mathsf{j}}(r)].$$ (10)

Utilising this Remark 1, [(9)] and [(10)] could be expressed thereby:

$$\mathrm{\Delta }{\mathcal{V}}_4(\mathsf{k}+1)+\delta {\mathcal{V}}_4(\mathsf{k})={\mathcal{V}}_4(\mathsf{k}+1)-(1-\delta ){\mathcal{V}}_4(\mathsf{k})={\hat{x}}_{\mathsf{i}}^{\mathsf{T}}(\mathsf{k}){\epsilon }^{\mathsf{T}}[\sum _{\mathsf{j}\in {{\mathrm{N}}_{\mathsf{i}}}^{out}}{\mathcal{R}}_{1\mathsf{j}\mathsf{i}}+{\mathcal{R}}_{2\mathsf{j}\mathsf{i}}+{\mathcal{R}}_{3\mathsf{j}\mathsf{i}}]\epsilon {\hat{x}}_{\mathsf{i}}(\mathsf{k})+{\hat{x}}_{\mathsf{j}}^{\mathsf{T}}(\mathsf{k}-{\mathrm{\Upsilon }}_{\mathsf{i}\mathsf{j}m}){\epsilon }^{\mathsf{T}}{\mathcal{M}}_1\epsilon \widehat{x_{\mathsf{j}}}(\mathsf{k}-{\mathrm{\Upsilon }}_{\mathsf{i}\mathsf{j}m})+{\hat{x}}_{\mathsf{j}}^{\mathsf{T}}(\mathsf{k}-{\mathrm{\Upsilon }}_{\mathsf{i}\mathsf{j}}(\mathsf{k})){\epsilon }^{\mathsf{T}}\times {\mathcal{M}}_2\epsilon {\hat{x}}_{\mathsf{j}}(\mathsf{k}-{\mathrm{\Upsilon }}_{\mathsf{i}\mathsf{j}}(\mathsf{k}))+{\widehat{x_{\mathsf{j}}}}^{\mathsf{T}}(\mathsf{k}-{\mathrm{\Upsilon }}_{\mathsf{i}\mathsf{j}M}){\epsilon }^{\mathsf{T}}{\mathcal{M}}_3\epsilon {\hat{x}}_{\mathsf{j}}(\mathsf{k}-{\mathrm{\Upsilon }}_{\mathsf{i}\mathsf{j}M})+\sum _{\mathsf{v}=\mathsf{k}+1-{\mathrm{\Upsilon }}_{\mathsf{i}\mathsf{j}M}}^{\mathsf{k}-{\mathrm{\Upsilon }}_{\mathsf{i}\mathsf{j}m}}{(1-\delta )}^{\mathsf{k}-\mathsf{v}}{\hat{x}}_{\mathsf{j}}^{\mathsf{T}}(\mathsf{v}){\epsilon }^{\mathsf{T}}{\mathcal{R}}_{2\mathsf{i}\mathsf{j}}\epsilon {\hat{x}}_{\mathsf{j}}(\mathsf{v}).$$ (11)

$$\mathrm{\Delta }{\mathcal{V}}_5(\mathsf{k}+1)+\delta {\mathcal{V}}_5(\mathsf{k})={\mathcal{V}}_5(\mathsf{k}+1)-(1-\delta ){\mathcal{V}}_5(\mathsf{k})={\hat{x}}_{\mathsf{j}}^{\mathsf{T}}(\mathsf{k}){\epsilon }^{\mathsf{T}}[\sum _{\mathsf{j}\in {{\mathcal{N}}_{\mathsf{i}}}^{out}}({\mathrm{\Upsilon }}_{\mathsf{i}\mathsf{j}M}-{\mathrm{\Upsilon }}_{\mathsf{i}\mathsf{j}m}){\mathcal{R}}_{2\mathsf{i}\mathsf{j}}]\epsilon {\hat{x}}_{\mathsf{j}}(\mathsf{k})-\sum _{r=\mathsf{k}+1-{\mathrm{\Upsilon }}_{\mathsf{i}\mathsf{j}M}}^{\mathsf{k}-{\mathrm{\Upsilon }}_{\mathsf{i}\mathsf{j}m}}{(1-\delta )}^{\mathsf{k}-r}{\hat{x}}_{\mathsf{j}}^{\mathsf{T}}(r){\epsilon }^{\mathsf{T}}{\mathcal{R}}_{2\mathsf{i}\mathsf{j}}\epsilon {\hat{x}}_{\mathsf{j}}(r).$$ (12)

In-order prove the stability results in the absence of disturbance, combining (6), (7), (8), (11) and (12), we have

$$\mathrm{\Delta }{\mathcal{V}}_{\mathsf{i}}(\mathsf{k})+\delta {\mathcal{V}}_{\mathsf{i}}(\mathsf{k})\le {\zeta }_{\mathsf{k}}^{\mathsf{T}}{\mathrm{\Psi }}_{\mathsf{i}}{\zeta }_{\mathsf{k}},$$ (13)

where ${\mathrm{\Psi }}_{\mathsf{i}}={\mathrm{\Psi }}_{1\mathsf{i}}+{\mathrm{\Psi }}_{2\mathsf{i}}^{\mathsf{T}}{\mathcal{P}}_{\mathsf{i}}{\mathrm{\Psi }}_{2\mathsf{i}}$,

$${\eta }_{\mathsf{k}}=[{\hat{x}}_{\mathsf{i}}^{\mathsf{T}}(\mathsf{k}){\epsilon }^{\mathsf{T}}{\hat{x}}_{\mathsf{i}}^{\mathsf{T}}(\mathsf{k}-{\mathrm{\Upsilon }}_{\mathsf{i}m}){\epsilon }^{\mathsf{T}}{\hat{x}}_{\mathsf{i}}^{\mathsf{T}}(\mathsf{k}-{\mathrm{\Upsilon }}_{\mathsf{i}}(\mathsf{k})){\epsilon }^{\mathsf{T}}{\hat{x}}_{\mathsf{i}}^{\mathsf{T}}(\mathsf{k}-{\mathrm{\Upsilon }}_{\mathsf{i}M}){\epsilon }^{\mathsf{T}}{\hat{x}}_{\mathsf{j}}^{\mathsf{T}}(\mathsf{k}-{\mathrm{\Upsilon }}_{\mathsf{i}\mathsf{j}m}){{\epsilon }^{\mathsf{T}}{\hat{x}}_{\mathsf{j}}^{\mathsf{T}}(\mathsf{k}-{\mathrm{\Upsilon }}_{\mathsf{i}\mathsf{j}}(\mathsf{k})){\epsilon }^{\mathsf{T}}{\hat{x}}_{\mathsf{j}}^{\mathsf{T}}(\mathsf{k}-{\mathrm{\Upsilon }}_{\mathsf{i}\mathsf{j}M})]}^{\mathsf{T}}.$$

In view of LMI [(4)] there exists ${\mathcal{S}}_{\mathsf{i}}$, utilising Lemma 1, we obtain ${\mathrm{\Psi }}_{\mathsf{i}}<0$. In-order to make it simple to confirm where $\sum _{\mathsf{i}\in \mathrm{\Omega }}[\mathrm{\Delta }{\mathcal{V}}_{\mathsf{i}}(\mathsf{k})+\delta {\mathcal{V}}_{\mathsf{i}}(\mathsf{k})]\le 0$. Thus, one can be able to obtain the subsequent:

$$\sum _{\mathsf{i}\in \mathrm{\Omega }}[\mathrm{\Delta }{\mathcal{V}}_{\mathsf{i}}(\mathsf{k}+1)-{\mathcal{V}}_{\mathsf{i}}(\mathsf{k})]\le \sum _{\mathsf{i}\in \mathrm{\Omega }}-\delta {\mathcal{V}}_{\mathsf{i}}(\mathsf{k}),$$

it indicates

$$\sum _{\mathsf{i}\in \mathrm{\Omega }}{\mathcal{V}}_{\mathsf{i}\mathsf{k}}(\mathsf{k})\le {(1-\delta )}^{\mathsf{k}-{\mathsf{k}}_t}\sum _{\mathsf{i}\in \mathrm{\Omega }}{\mathcal{V}}_{\mathsf{i}{\mathsf{k}}_t}({\mathsf{k}}_t)\le {(1-\delta )}^{\mathsf{k}-{\mathsf{k}}_t}\mu \sum _{\mathsf{i}\in \mathrm{\Omega }}{\mathcal{V}}_{\mathsf{i}{\mathsf{k}}_{t-1}}({\mathsf{k}}_t)\le \mu {(1-\delta )}^{\mathsf{k}-{\mathsf{k}}_t}{(1-\delta )}^{{\mathsf{k}}_t-{\mathsf{k}}_{t-1}}\sum _{\mathsf{i}\in \mathrm{\Omega }}{\mathcal{V}}_{\mathsf{i}{\mathsf{k}}_{t-1}}({\mathsf{k}}_{t-1})=\mu {(1-\delta )}^{\mathsf{k}-{\mathsf{k}}_{t-1}}\sum _{\mathsf{i}\in \mathrm{\Omega }}{\mathcal{V}}_{\mathsf{i}{\mathsf{k}}_{t-1}}({\mathsf{k}}_{t-1})⋮\le {\mu }^{{\mathcal{N}}_{\mathsf{i}}({\mathsf{k}}_0,\mathsf{k})}{(1-\delta )}^{\mathsf{k}-{\mathsf{k}}_0}\sum _{\mathsf{i}\in \mathrm{\Omega }}{\mathcal{V}}_{\mathsf{i}{\mathsf{k}}_0}({\mathsf{k}}_0).$$ (14)

In accordance with Definition 2, considering the chatter-bound and dwell-time, [(14)] turns into

$$\sum _{\mathsf{i}\in \mathrm{\Omega }}{\mathcal{V}}_{\mathsf{i}\mathsf{k}}(\mathsf{k})\le {((1-\delta ){\mu }^{\frac{1}{{\mathcal{T}}_b}})}^{\mathsf{k}-{\mathsf{k}}_0}\sum _{\mathsf{i}\in \mathrm{\Omega }}{\mathcal{V}}_{\mathsf{i}{\mathsf{k}}_0}({\mathsf{k}}_0).$$ (15)

From [(5)], it can be confirmed that ${\mathcal{V}}_{\mathsf{i}\mathsf{k}}(\mathsf{k})\ge {\beta }_1{\Vert {\hat{x}}_{\mathsf{i}}\Vert }^2$ and ${\mathcal{V}}_{\mathsf{i}{\mathsf{k}}_0}({\mathsf{k}}_0)\le {\beta }_2{\Vert {\hat{\varphi }}_{\mathsf{i}}\Vert }_l^2$. Then we have

$$\sum _{\mathsf{i}\in \mathrm{\Omega }}{\beta }_1{\Vert {\hat{x}}_{\mathsf{i}}\Vert }^2\le {((1-\delta ){\mu }^{\frac{1}{{\mathcal{T}}_a}})}^{\mathsf{k}-{\mathsf{k}}_0}\sum _{\mathsf{i}\in \mathrm{\Omega }}{\beta }_2{\Vert {\hat{\varphi }}_{\mathsf{i}}\Vert }_l^2\sum _{\mathsf{i}\in \mathrm{\Omega }}{\Vert {\hat{x}}_{\mathsf{i}}\Vert }^2\le \frac{{\beta }_2}{{\beta }_1}{\vartheta }^{\mathsf{k}-{\mathsf{k}}_0}\sum _{\mathsf{i}\in \mathrm{\Omega }}{\Vert {\hat{\varphi }}_{\mathsf{i}}\Vert }_l^2.$$ (16)

Here $\vartheta =((1-\delta ){\mu }^{\frac{1}{{\mathcal{T}}_a}})$, now we obtain $\vartheta <1$ by using ${\mathcal{T}}_a$. This proves the exponential stability of (3) without disturbance.

Theorem 2

For any switching signal$\mathsf{i}$and the given scalars$\mu >1$and$0<\delta <1$along with dwell-time which satisfy${\mathcal{T}}_b\ge {\mathcal{T}}_b^{⁎}=-\frac{\ln \mu }{\ln (1-\delta )}$and for every$\mathsf{i}$,$\mathsf{j}\in \mathrm{N}$, then [(3)] is termed as EMSS together with the HP${\gamma }_{\mathsf{i}}>0$, then here exists positive-definite${\mathcal{P}}_{\mathsf{i}}$,${\mathcal{Q}}_{1\mathsf{i}}$,${\mathcal{Q}}_{2\mathsf{i}}$,${\mathcal{Q}}_{3\mathsf{i}}$,${\mathcal{R}}_{1\mathsf{i}\mathsf{j}}$,${\mathcal{R}}_{2\mathsf{i}\mathsf{j}}$,${\mathcal{R}}_{3\mathsf{i}\mathsf{j}}$matrices and${\mathcal{S}}_{1\mathsf{i}}$,${\mathcal{S}}_{2\mathsf{i}}$be any matrices here$\mathsf{i}\ne \mathsf{j}$, then convex-optimization problems:

$$\underset{{\mathcal{P}}_{\mathsf{i}};{\mathcal{Q}}_{1\mathsf{i}};{\mathcal{Q}}_{2\mathsf{i}};{\mathcal{Q}}_{3\mathsf{i}};{\mathcal{R}}_{1\mathsf{i}\mathsf{j}};{\mathcal{R}}_{2\mathsf{i}\mathsf{j}};{\mathcal{R}}_{3\mathsf{i}\mathsf{j}}}{\min }{\rho }_{\mathsf{i}}\mathit{\text{with}}{\rho }_{\mathsf{i}}={\gamma }_{\mathsf{i}}^2,$$ (17)

subjected to LMI

$$\left[\begin{array}{ccccc}\hfill {\overline{\mathrm{\Psi }}}_{\mathsf{i}}\hfill & \hfill 0\hfill & \hfill {\overline{\mathrm{\Psi }}}_{1\mathsf{i}}^{\mathsf{T}}\hfill & \hfill {\overline{\mathrm{\Psi }}}_{2\mathsf{i}}^{\mathsf{T}}\hfill & \hfill {\overline{\mathrm{\Psi }}}_{3\mathsf{i}}^{\mathsf{T}}\hfill \\ \hfill ⁎\hfill & \hfill -{\gamma }_{\mathsf{i}}^{2}I\hfill & \hfill {\mathcal{B}}_{\mathsf{i}}^{\mathsf{T}}{\mathcal{S}}_{1\mathsf{i}}^{\mathsf{T}}\hfill & \hfill {\mathcal{D}}_{\mathsf{i}}^{\mathsf{T}}{\mathcal{B}}_{f\mathsf{i}}^{\mathsf{T}}{\mathcal{S}}_{2\mathsf{i}}^{\mathsf{T}}\hfill & \hfill 0\hfill \\ \hfill ⁎\hfill & \hfill ⁎\hfill & \hfill {\mathcal{P}}_{1\mathsf{i}}-{\mathcal{S}}_{1\mathsf{i}}-{\mathcal{S}}_{1\mathsf{i}}^{\mathsf{T}}\hfill & \hfill {\mathcal{P}}_{2\mathsf{i}}\hfill & \hfill 0\hfill \\ \hfill ⁎\hfill & \hfill ⁎\hfill & \hfill ⁎\hfill & \hfill {\mathcal{P}}_{3\mathsf{i}}-{\mathcal{S}}_{2\mathsf{i}}-{\mathcal{S}}_{2\mathsf{i}}^{\mathsf{T}}\hfill & \hfill 0\hfill \\ \hfill ⁎\hfill & \hfill ⁎\hfill & \hfill ⁎\hfill & \hfill ⁎\hfill & \hfill -\mathcal{I}\hfill \end{array}\right]<0,$$ (18)

here

$${\overline{\mathrm{\Psi }}}_{\mathsf{i}}=diag\{{\overline{\mathrm{\Psi }}}_{(1,1)\mathsf{i}},-(1-\delta ){\mathcal{P}}_{2\mathsf{i}},-{(1-\delta )}^{{\mathrm{\Upsilon }}_{\mathsf{i}m}}{\mathcal{Q}}_{1\mathsf{i}},-{(1-\delta )}^{{\mathrm{\Upsilon }}_{\mathsf{i}m}}{\mathcal{Q}}_{2\mathsf{i}},-{(1-\delta )}^{{\mathrm{\Upsilon }}_{\mathsf{i}M}}{\mathcal{Q}}_{3\mathsf{i}},{\mathcal{M}}_1,{\mathcal{M}}_2,{\mathcal{M}}_3\},\overline{{\mathrm{\Psi }}_{1\mathsf{i}}}=\left[\begin{array}{cccccccc}\hfill {\mathcal{S}}_{1\mathsf{i}}{\mathcal{A}}_{\mathsf{i}}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill S_{1\mathsf{i}}{\mathcal{A}}_{t\mathsf{i}}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill {\mathcal{S}}_{1\mathsf{i}}{\sum }_{\mathsf{j}\in {{\mathcal{N}}_{\mathsf{i}}}^{in}}{\mathcal{A}}_{t\mathsf{i}\mathsf{j}}\hfill & \hfill 0\hfill \end{array}\right],\overline{{\mathrm{\Psi }}_{2\mathsf{i}}}=\left[\begin{array}{cccccccc}\hfill {\mathcal{S}}_{2\mathsf{i}}{\mathcal{B}}_{f\mathsf{i}}{\mathcal{C}}_{\mathsf{i}}\hfill & \hfill {\mathcal{S}}_{1\mathsf{i}}{\mathcal{A}}_{f\mathsf{i}}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right],\overline{{\mathrm{\Psi }}_{3\mathsf{i}}}=\left[\begin{array}{cccccccc}\hfill {\mathcal{E}}_{\mathsf{i}}\hfill & \hfill -{\mathcal{E}}_{f\mathsf{i}}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right].$$

Further${\mathcal{A}}_{f\mathsf{i}}={\mathcal{S}}_{1\mathsf{i}}^{-T}{\mathcal{F}}_{1\mathsf{i}},{\mathcal{B}}_{f\mathsf{i}}={\mathcal{S}}_{2\mathsf{i}}^{-T}{\mathcal{F}}_{2\mathsf{i}}$and${\mathcal{E}}_{f\mathsf{i}}$are the filter parameters.

Proof 2

First we define ${\mathcal{P}}_{\mathsf{i}}$ as

$${\mathcal{P}}_{\mathsf{i}}=\left[\begin{array}{cc}\hfill {\mathcal{P}}_{1\mathsf{i}}\hfill & \hfill {\mathcal{P}}_{2\mathsf{i}}\hfill \\ \hfill 0\hfill & \hfill {\mathcal{P}}_{3\mathsf{i}}\hfill \end{array}\right].$$

The ${\mathcal{H}}_{\infty }$ performance of the system [(3)] will now be addressed. We take into account the performance-index described as $\mathsf{J}=\sum _{\mathsf{i}\in \mathrm{\Omega }}\{{\widehat{{\xi }_{\mathsf{i}}}}^{\mathsf{T}}(\mathsf{k})\widehat{{\xi }_{\mathsf{i}}}(\mathsf{k})-{\gamma }_{\mathsf{i}}^2{d}_{\mathsf{i}}^{\mathsf{T}}(\mathsf{k})d_{\mathsf{i}}(\mathsf{k})\}$, using LKF [(5)] along with [(4)] we obtain,

$$\mathrm{\Delta }{\mathcal{V}}_{\mathsf{i}}(\mathsf{k})+\delta {\mathcal{V}}_{\mathsf{i}}(\mathsf{k})+\sum _{\mathsf{i}\in \mathrm{\Omega }}\{{\widehat{{\xi }_{\mathsf{i}}}}^{\mathsf{T}}(\mathsf{k})\widehat{{\xi }_{\mathsf{i}}}(\mathsf{k})-{\gamma }_{\mathsf{i}}^2{d}_{\mathsf{i}}^{\mathsf{T}}(\mathsf{k})d_{\mathsf{i}}(\mathsf{k})\}\le \sum _{\mathsf{i}\in \mathrm{\Omega }}{\zeta }_{1\mathsf{k}}^{\mathsf{T}}{\hat{\mathrm{\Psi }}}_{\mathsf{i}}{\zeta }_{1\mathsf{k}},$$ (19)

where ${\zeta }_{1\mathsf{k}}^{\mathsf{T}}=[{\zeta }_{\mathsf{k}}^{\mathsf{T}}{d}_{\mathsf{i}}(\mathsf{k})]$, we consider ${\mathcal{S}}_{\mathsf{i}}=diag\{{\mathcal{S}}_{1\mathsf{i}},{\mathcal{S}}_{2\mathsf{i}}\}$

$${\hat{\mathrm{\Psi }}}_{\mathsf{i}}=\left[\begin{array}{cccc}\hfill {\overline{\mathrm{\Psi }}}_{\mathsf{i}}+{\hat{\mathrm{\Psi }}}_{3\mathsf{i}}^{\mathsf{T}}{\hat{\mathrm{\Psi }}}_{3\mathsf{i}}\hfill & \hfill 0\hfill & \hfill {\overline{{\mathrm{\Psi }}_{1\mathsf{i}}}}^{\mathsf{T}}\hfill & \hfill {\overline{{\mathrm{\Psi }}_{2\mathsf{i}}}}^{\mathsf{T}}\hfill \\ \hfill ⁎\hfill & \hfill -{\gamma }_{\mathsf{i}}^2\mathcal{I}\hfill & \hfill {\mathcal{B}}_{\mathsf{i}}^{\mathsf{T}}{\mathcal{S}}_{1\mathsf{i}}^{\mathsf{T}}\hfill & \hfill {\mathcal{D}}_{\mathsf{i}}^{\mathsf{T}}{\mathcal{B}}_{f\mathsf{i}}^{\mathsf{T}}{\mathcal{S}}_{2\mathsf{i}}^{\mathsf{T}}\hfill \\ \hfill ⁎\hfill & \hfill ⁎\hfill & \hfill {\mathcal{P}}_{1\mathsf{i}}-{\mathcal{S}}_{1\mathsf{i}}-{\mathcal{S}}_{1\mathsf{i}}^{\mathsf{T}}\hfill & \hfill {\mathcal{P}}_{2\mathsf{i}}\hfill \\ \hfill ⁎\hfill & \hfill ⁎\hfill & \hfill ⁎\hfill & \hfill {\mathcal{P}}_{3\mathsf{i}}-{\mathcal{S}}_{2\mathsf{i}}-{\mathcal{S}}_{2\mathsf{i}}^{\mathsf{T}}\hfill \end{array}\right],$$ (20)

${\hat{\mathrm{\Psi }}}_{3\mathsf{i}}^{\mathsf{T}}=\left[{\mathcal{E}}_{\mathsf{i}}{\mathcal{E}}_{f\mathsf{i}}{0}_{n,6n}\right]$. In light of Schur-complement ${\mathcal{F}}_{1\mathsf{i}}={\mathcal{S}}_{1\mathsf{i}}{\mathcal{A}}_{f\mathsf{i}},{\mathcal{PF}}_{2\mathsf{i}}={\mathcal{S}}_{2\mathsf{i}}{\mathcal{B}}_{f\mathsf{i}}$, now its simple to obtain [(20)] is alike to [(18)]. Therefore when [(18)] holds for all $0<\delta <1$, from [(19)] we have,

$$\mathrm{\Delta }{\mathcal{V}}_{\mathsf{i}}(\mathsf{k})+\delta {\mathcal{V}}_{\mathsf{i}}(\mathsf{k})+\sum _{\mathsf{i}\in \mathrm{\Omega }}\{{\hat{\xi }}_{\mathsf{i}}^{\mathsf{T}}(\mathsf{k})\widehat{{\xi }_{\mathsf{i}}}(\mathsf{k})-{\gamma }_{\mathsf{i}}^2{d}_{\mathsf{i}}^{\mathsf{T}}(\mathsf{k})d_{\mathsf{i}}(\mathsf{k})\}\le 0.$$ (21)

Using (20), to validate HP for the considered systems, one can obtain

$${\mathcal{V}}_{\mathsf{i}}(\mathsf{k})\le (1-\delta ){\mathcal{V}}_{\mathsf{i}}({\mathsf{k}}_0)-[\sum _{\mathsf{i}\in \mathrm{\Omega }}\{{\widehat{{\xi }_{\mathsf{i}}}}^{\mathsf{T}}({\mathsf{k}}_0)\widehat{{\xi }_{\mathsf{i}}}({\mathsf{k}}_0)-{\gamma }_{\mathsf{i}}^2{d}_{\mathsf{i}}^{\mathsf{T}}({\mathsf{k}}_0)d_{\mathsf{i}}({\mathsf{k}}_0)\}].$$

Repeating the above mentioned inequality, one gets as

$${\mathcal{V}}_{\mathsf{i}}(\mathsf{k})\le {(1-\delta )}^{\mathsf{k}-{\mathsf{k}}_0}{\mathcal{V}}_{\mathsf{i}}({\mathsf{k}}_0)-\left[\sum _{\mathsf{i}\in \mathrm{\Omega }}\right\{\sum _{\mathsf{v}={\mathsf{k}}_0}^{\mathsf{k}-1}{(1-\delta )}^{\mathsf{k}-\mathsf{v}-1}[{\widehat{{\xi }_{\mathsf{i}}}}^{\mathsf{T}}(\mathsf{v})\widehat{{\xi }_{\mathsf{i}}}(\mathsf{v})-{\gamma }_{\mathsf{i}}^2{d}_{\mathsf{i}}^{\mathsf{T}}(\mathsf{v})d_{\mathsf{i}}(\mathsf{v})]\left\}\right].\le {(1-\delta )}^{\mathsf{k}-{\mathsf{k}}_0}{\mathcal{V}}_{\mathsf{i}}({\mathsf{k}}_0)-\sum _{\mathsf{i}\in \mathrm{\Omega }}\sum _{\mathsf{v}={\mathsf{k}}_0}^{\mathsf{k}-1}{(1-\delta )}^{\mathsf{k}-\mathsf{v}-1}{\widehat{{\xi }_{\mathsf{i}}}}^{\mathsf{T}}(\mathsf{v})\widehat{{\xi }_{\mathsf{i}}}(\mathsf{v})+\sum _{\mathsf{i}\in \mathrm{\Omega }}\sum _{\mathsf{v}={\mathsf{k}}_0}^{\mathsf{k}-1}{(1-\delta )}^{\mathsf{k}-\mathsf{v}-1}\gamma 2_{\mathsf{i}}{d}_{\mathsf{i}}^{\mathsf{T}}(\mathsf{v})d_{\mathsf{i}}(\mathsf{v})$$

Therefore we have

$${\mathcal{V}}_{\mathsf{i}k}k\le {(1-\delta )}^{\mathsf{k}-{\mathsf{k}}_t}{\mathcal{V}}_{\mathsf{i}k}({\mathsf{k}}_t)-\sum _{\mathsf{i}\in \mathrm{\Omega }}\sum _{\mathsf{v}={\mathsf{k}}_t}^{\mathsf{k}-1}{(1-\delta )}^{\mathsf{k}-\mathsf{v}-1}{\widehat{{\xi }_{\mathsf{i}}}}^{\mathsf{T}}(\mathsf{v})\widehat{{\xi }_{\mathsf{i}}}(\mathsf{v})+\sum _{\mathsf{i}\in \mathrm{\Omega }}\sum _{\mathsf{v}={\mathsf{k}}_t}^{\mathsf{k}-1}{(1-\delta )}^{\mathsf{k}-\mathsf{v}-1}\gamma 2_{\mathsf{i}}{d}_{\mathsf{i}}^{\mathsf{T}}(\mathsf{v})d_{\mathsf{i}}(\mathsf{v})\le {(1-\delta )}^{\mathsf{k}-{\mathsf{k}}_t}\mu {\mathcal{V}}_{\mathsf{i}{\mathsf{k}}_{t-1}}({\mathsf{k}}_t)-\sum _{\mathsf{i}\in \mathrm{\Omega }}\sum _{\mathsf{v}={\mathsf{k}}_t}^{\mathsf{k}-1}{(1-\delta )}^{\mathsf{k}-\mathsf{v}-1}{\widehat{{\xi }_{\mathsf{i}}}}^{\mathsf{T}}(\mathsf{v})\widehat{{\xi }_{\mathsf{i}}}(\mathsf{v})+\sum _{\mathsf{i}\in \mathrm{\Omega }}\sum _{\mathsf{v}={\mathsf{k}}_t}^{\mathsf{k}-1}{(1-\delta )}^{\mathsf{k}-\mathsf{v}-1}\gamma 2_{\mathsf{i}}{d}_{\mathsf{i}}^{\mathsf{T}}(\mathsf{v})d_{\mathsf{i}}(\mathsf{v})={(1-\delta )}^{\mathsf{k}-{\mathsf{k}}_0}{\mu }^{\mathcal{N}({\mathsf{k}}_0,k)}{\mathcal{V}}_{\mathsf{i}{\mathsf{k}}_0}({\mathsf{k}}_0)-\sum _{\mathsf{i}\in \mathrm{\Omega }}\sum _{\mathsf{v}={\mathsf{k}}_0}^{\mathsf{k}-1}{\mu }^{\mathcal{N}(\mathsf{v},\mathsf{k})}{(1-\delta )}^{\mathsf{k}-\mathsf{v}-1}[{\widehat{{\xi }_{\mathsf{i}}}}^{\mathsf{T}}(\mathsf{v})\widehat{{\xi }_{\mathsf{i}}}(\mathsf{v})-{\gamma }_{\mathsf{i}}^2{d}_{\mathsf{i}}^{\mathsf{T}}(\mathsf{v})d_{\mathsf{i}}(\mathsf{v})],$$

using zero initial circumstance, where -${\sum }_{\mathsf{v}={\mathsf{k}}_0}^{\mathsf{k}-1}{\mu }^{\mathcal{N}(\mathsf{v},\mathsf{k})}{(1-\delta )}^{\mathsf{k}-\mathsf{v}-1}\le 0$,

$${\mu }^{-{\mathcal{N}}_{\mathsf{i}}(0,\mathsf{k})}\sum _{\mathsf{i}\in \mathrm{\Omega }}\sum _{\mathsf{v}={\mathsf{k}}_0}^{\mathsf{k}-1}{\mu }^{{\mathcal{N}}_{\mathsf{i}}(\mathsf{v},\mathsf{k})}{(1-\delta )}^{\mathsf{k}-\mathsf{v}-1}{\widehat{{\xi }_{\mathsf{i}}}}^{\mathsf{T}}(\mathsf{v})\widehat{{\xi }_{\mathsf{i}}}(\mathsf{v})\le {\mu }^{-{\mathcal{N}}_{\mathsf{i}}(0,\mathsf{k})}\sum _{\mathsf{i}\in \mathrm{\Omega }}\sum _{\mathsf{v}={\mathsf{k}}_0}^{\mathsf{k}-1}{\mu }^{{\mathcal{N}}_{\mathsf{i}}(\mathsf{v},\mathsf{k})}{(1-\delta )}^{\mathsf{k}-\mathsf{v}-1}{\gamma }_{\mathsf{i}}^2{d}_{\mathsf{i}}^{\mathsf{T}}(\mathsf{v})d_{\mathsf{i}}(\mathsf{v})\sum _{\mathsf{i}\in \mathrm{\Omega }}\sum _{\mathsf{v}={\mathsf{k}}_0}^{\mathsf{k}-1}{\mu }^{-{\mathcal{N}}_{\mathsf{i}}(0,\mathsf{v})}{(1-\delta )}^{\mathsf{k}-\mathsf{v}-1}{\widehat{{\xi }_{\mathsf{i}}}}^{\mathsf{T}}(\mathsf{v})\widehat{{\xi }_{\mathsf{i}}}(\mathsf{v})\le \sum _{\mathsf{i}\in \mathrm{\Omega }}\sum _{\mathsf{v}={\mathsf{k}}_0}^{\mathsf{k}-1}{\mu }^{-{\mathcal{N}}_{\mathsf{i}}(0,\mathsf{v})}{(1-\delta )}^{\mathsf{k}-\mathsf{v}-1}{\gamma }_{\mathsf{i}}^2{d}_{\mathsf{i}}^{\mathsf{T}}(\mathsf{v})d_{\mathsf{i}}(\mathsf{v}).$$

Now by Definition 2 and by using this ${\mathcal{N}}_{\mathsf{i}}(0,v)\le \frac{\mathsf{v}}{{\mathcal{T}}_b}\le \frac{-\mathsf{v}\ln (1-\delta )}{\ln \mu }$ its simple to get

$$\sum _{\mathsf{i}\in \mathrm{\Omega }}\sum _{\mathsf{v}={\mathsf{k}}_0}^{\mathsf{k}-1}{\mu }^{\frac{-\mathsf{v}\ln (1-\delta )}{\ln \mu }}{(1-\delta )}^{\mathsf{k}-\mathsf{v}-1}{\widehat{{\xi }_{\mathsf{i}}}}^{\mathsf{T}}(\mathsf{v})\widehat{{\xi }_{\mathsf{i}}}(\mathsf{v})\le \sum _{\mathsf{i}\in \mathrm{\Omega }}\sum _{\mathsf{v}={\mathsf{k}}_0}^{\mathsf{k}-1}{(1-\delta )}^{\mathsf{k}-\mathsf{v}-1}{\gamma }_{\mathsf{i}}^2{d}_{\mathsf{i}}^{\mathsf{T}}(\mathsf{v})d_{\mathsf{i}}(\mathsf{v})\sum _{\mathsf{i}\in \mathrm{\Omega }}\sum _{\mathsf{v}={\mathsf{k}}_0}^{\mathsf{k}-1}{(1-\delta )}^{\mathsf{v}}{(1-\delta )}^{\mathsf{k}-\mathsf{v}-1}{\widehat{{\xi }_{\mathsf{i}}}}^{\mathsf{T}}(\mathsf{v})\widehat{{\xi }_{\mathsf{i}}}(\mathsf{v})\le {\gamma }_{\mathsf{i}}^2\sum _{\mathsf{i}\in \mathrm{\Omega }}\sum _{\mathsf{v}={\mathsf{k}}_0}^{\mathsf{k}-1}{(1-\delta )}^{\mathsf{k}-\mathsf{v}-1}{d}_{\mathsf{i}}^{\mathsf{T}}(\mathsf{v})d_{\mathsf{i}}(\mathsf{v})\sum _{\mathsf{i}\in \mathrm{\Omega }}\{\sum _{\mathsf{v}={\mathsf{k}}_0}^{\infty }{(1-\delta )}^{\mathsf{v}}{\widehat{{\xi }_{\mathsf{i}}}}^{\mathsf{T}}(\mathsf{v})\widehat{{\xi }_{\mathsf{i}}}(\mathsf{v})\}\le \sum _{\mathsf{i}\in \mathrm{\Omega }}{\gamma }_{\mathsf{i}}^2\{\sum _{\mathsf{v}={\mathsf{k}}_0}^{\infty }{d}_{\mathsf{i}}^{\mathsf{T}}(\mathsf{v})d_{\mathsf{i}}(\mathsf{v})\}.$$

With reference to Definition 1, it could be established thus the interconnected system (3) remains EMSS, ensuring HP of ${\gamma }_{\mathsf{i}}>0$. Hence, this brings the proof to a conclusion.

Now, we consider the system with uncertainties is expressed by:

$$x_{\mathsf{i}}(\mathsf{k}+1)=(A_{\mathsf{i}}+\mathrm{\Delta }{A}_{\mathsf{i}})x_{\mathsf{i}}(\mathsf{k})+(A_{t\mathsf{i}}+\mathrm{\Delta }{A}_{t\mathsf{i}})x_{\mathsf{i}}(\mathsf{k}-{\mathrm{\Upsilon }}_{\mathsf{i}}(\mathsf{k}))+\sum _{\mathsf{j}\in {{\mathrm{N}}_{\mathsf{i}}}^{in}}(A_{t\mathsf{i}\mathsf{j}}x+\mathrm{\Delta }{A}_{t\mathsf{i}\mathsf{j}})(\mathsf{k}-{\mathrm{\Upsilon }}_{\mathsf{i}\mathsf{j}}(\mathsf{k}))+B_{\mathsf{i}}{d}_{\mathsf{i}}(\mathsf{k})y_{\mathsf{i}}(\mathsf{k})=(C_{\mathsf{i}}+\mathrm{\Delta }{C}_{\mathsf{i}})x_{\mathsf{i}}(\mathsf{k})+D_{\mathsf{i}}{d}_{\mathsf{i}}(\mathsf{k})x_{\mathsf{i}}(\mathsf{j})=\mathrm{\Phi }(\mathsf{j}),\forall \mathsf{j}\in [-\mathrm{\Upsilon },0].$$ (22)

The uncertainties parameter are defined as follows:

$$\left[\begin{array}{cccc}\hfill \mathrm{\Delta }{A}_{\mathsf{i}}\hfill & \hfill \mathrm{\Delta }{A}_{t\mathsf{i}}\hfill & \hfill \mathrm{\Delta }{A}_{t\mathsf{i}\mathsf{j}}\hfill & \hfill \mathrm{\Delta }{C}_{\mathsf{i}}\hfill \end{array}\right]=\left[\begin{array}{cccc}\hfill R_{a}F(\mathsf{k})N_a\hfill & \hfill R_{at\mathsf{i}}F(\mathsf{k})N_{at\mathsf{i}}\hfill & \hfill R_{at\mathsf{i}\mathsf{j}}F(\mathsf{k})N_{at\mathsf{i}\mathsf{j}}\hfill & \hfill R_{c}F(\mathsf{k})N_c\hfill \end{array}\right],$$

where $R_a$, $N_a$, $R_{at\mathsf{i}}$, $N_{at\mathsf{i}}$, $R_{at\mathsf{i}\mathsf{j}}$, $N_{at\mathsf{i}\mathsf{j}}$ recognised as real matrices where time-varying matrix is represented as $F(\mathsf{k})$ satisfy $F^{\mathsf{T}}(\mathsf{k})F(\mathsf{k})\le$ $\mathcal{I}$ and $\mathrm{\Upsilon }=\max [-{\mathrm{\Upsilon }}_{\mathsf{i}}(M),-{\mathrm{\Upsilon }}_{\mathsf{i}\mathsf{j}}(M)]$. Considering filter system (2), the augmented system is defined as

$${\hat{x}}_{\mathsf{i}}(\mathsf{k}+1)={\overline{A}}_{\mathsf{i}}{\hat{x}}_{\mathsf{i}}(\mathsf{k})+{\overline{A}}_{t\mathsf{i}}\epsilon {\hat{x}}_{\mathsf{i}}(\mathsf{k}-{\mathrm{\Upsilon }}_{\mathsf{i}}(\mathsf{k}))+\sum _{\mathsf{j}\in {{\mathrm{N}}_{\mathsf{i}}}^{in}}{\overline{A}}_{t\mathsf{i}\mathsf{j}}\epsilon {\hat{x}}_{\mathsf{j}}(\mathsf{k}-{\mathrm{\Upsilon }}_{\mathsf{i}\mathsf{j}}(\mathsf{k}))+{\overline{B}}_{\mathsf{i}}{d}_{\mathsf{i}}(\mathsf{k}),{\hat{\xi }}_{\mathsf{i}}(\mathsf{k})={\mathbb{E}}_{\mathsf{i}}{\hat{x}}_{\mathsf{i}}(\mathsf{k}),{\hat{x}}_{\mathsf{i}}({\mathsf{k}}_0)={\hat{x}}_0.$$ (23)

Now denote

$${\overline{A}}_{\mathsf{i}}=\left[\begin{array}{cc}\hfill A_{\mathsf{i}}+\mathrm{\Delta }{A}_{\mathsf{i}}\hfill & \hfill 0\hfill \\ \hfill B_{f\mathsf{i}}(C_{\mathsf{i}}+\mathrm{\Delta }{C}_{\mathsf{i}})\hfill & \hfill A_{f\mathsf{i}}\hfill \end{array}\right],{\overline{A}}_{t\mathsf{i}}=\left[\begin{array}{c}\hfill A_{t\mathsf{i}}+\mathrm{\Delta }{A}_{t\mathsf{i}}\hfill \\ \hfill 0\hfill \end{array}\right],{\overline{A}}_{t\mathsf{i}j}=\left[\begin{array}{c}\hfill A_{t\mathsf{i}j}+\mathrm{\Delta }{A}_{t\mathsf{i}j}\hfill \\ \hfill 0\hfill \end{array}\right],$$

$${\overline{B}}_{\mathsf{i}}=\left[\begin{array}{c}\hfill B_{\mathsf{i}}\hfill \\ \hfill B_{f\mathsf{i}}{D}_{\mathsf{i}}\hfill \end{array}\right],\epsilon =\left[\begin{array}{c}\hfill I0\hfill \end{array}\right],{\mathbb{E}}_{\mathsf{i}}=\left[\begin{array}{c}\hfill {\mathcal{E}}_{\mathsf{i}}-{\mathcal{E}}_{f\mathsf{i}}\hfill \end{array}\right].$$

Below theorem illustrates that the designed system is stable with uncertainties.

Theorem 3

Consider the uncertainty for the designed systems (3) . The $H_{\infty }$ performance is achieved for every non zero $w_{\mathsf{i}}(\mathsf{k})$ . For any switching signal $\mathsf{i}$ and the given scalars $\mu >1$ and $0<\delta <1$ along with dwell-time that satisfy ${\mathcal{T}}_b\ge {\mathcal{T}}_b^{⁎}=-\frac{\ln \mu }{\ln (1-\delta )}$ , it has been implied that the systems (3) are EMSS along with HP ${\gamma }_{\mathsf{i}}>0$ , then here exists positive-definite matrices ${\mathcal{P}}_{\mathsf{i}}$ , ${\mathcal{Q}}_{1\mathsf{i}}$ , ${\mathcal{Q}}_{2\mathsf{i}}$ , ${\mathcal{Q}}_{3\mathsf{i}}$ , ${\mathcal{R}}_{1\mathsf{i}\mathsf{j}}$ , ${\mathcal{R}}_{2\mathsf{i}\mathsf{j}}$ , ${\mathcal{R}}_{3\mathsf{i}\mathsf{j}}$ , ${\mathcal{S}}_{1\mathsf{i}}$ , ${\mathcal{S}}_{2\mathsf{i}}$ are any suitable-dimension matrices and non negative real scalars be ${ϵ}_1>0$ , ${ϵ}_2>0$ , ${ϵ}_3>0$ and ${ϵ}_4>0$ satisfying the following matrix inequality,

$$\left[\begin{array}{ccccccccc}\hfill {\hat{\psi }}_{\mathsf{i}}\hfill & \hfill R_a\hfill & \hfill {\hat{\psi }}_1\hfill & \hfill R_c\hfill & \hfill {\hat{\psi }}_2\hfill & \hfill {\hat{\psi }}_3\hfill & \hfill {\hat{\psi }}_4\hfill & \hfill {\hat{\psi }}_5\hfill & \hfill {\hat{\psi }}_6\hfill \\ \hfill ⁎\hfill & \hfill -{ϵ}_{1}I\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill ⁎\hfill & \hfill ⁎\hfill & \hfill -{ϵ}_{1}I\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill ⁎\hfill & \hfill ⁎\hfill & \hfill ⁎\hfill & \hfill -{ϵ}_{2}I\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill ⁎\hfill & \hfill ⁎\hfill & \hfill ⁎\hfill & \hfill ⁎\hfill & \hfill -{ϵ}_{2}I\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill ⁎\hfill & \hfill ⁎\hfill & \hfill ⁎\hfill & \hfill ⁎\hfill & \hfill ⁎\hfill & \hfill -{ϵ}_{3}I\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill ⁎\hfill & \hfill ⁎\hfill & \hfill ⁎\hfill & \hfill ⁎\hfill & \hfill ⁎\hfill & \hfill ⁎\hfill & \hfill -{ϵ}_{3}I\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill ⁎\hfill & \hfill ⁎\hfill & \hfill ⁎\hfill & \hfill ⁎\hfill & \hfill ⁎\hfill & \hfill ⁎\hfill & \hfill ⁎\hfill & \hfill -{ϵ}_{4}I\hfill & \hfill 0\hfill \\ \hfill ⁎\hfill & \hfill ⁎\hfill & \hfill ⁎\hfill & \hfill ⁎\hfill & \hfill ⁎\hfill & \hfill ⁎\hfill & \hfill ⁎\hfill & \hfill ⁎\hfill & \hfill -{ϵ}_{4}I\hfill \end{array}\right]<0,$$ (24)

where

$$R_a=\left[\begin{array}{cc}\hfill {ϵ}_1{R}_{ai}\hfill & \hfill 0_{n,11n}\hfill \end{array}\right],{\hat{\psi }}_1=\left[\begin{array}{cccc}\hfill 0_{n,9n}\hfill & \hfill N_{ai}^{\mathsf{T}}\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right],R_c=\left[\begin{array}{cc}\hfill {ϵ}_2{R}_{ci}\hfill & \hfill 0_{n,11n}\hfill \end{array}\right],{\hat{\psi }}_2=\left[\begin{array}{ccc}\hfill 0_{n,10n}\hfill & \hfill N_{ci}^{\mathsf{T}}\hfill & \hfill 0\hfill \end{array}\right],{\hat{\psi }}_3=\left[\begin{array}{ccccc}\hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill {ϵ}_3{R}_{adi}\hfill & \hfill 0_{n,8n}\hfill \end{array}\right],{\hat{\psi }}_4=\left[\begin{array}{cccc}\hfill 0_{n,9n}\hfill & \hfill N_{adi}^{\mathsf{T}}\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right],{\hat{\psi }}_5=\left[\begin{array}{ccccccc}\hfill 0_{n,6n}\hfill & \hfill {ϵ}_4{R}_{adij}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right],{\hat{\psi }}_6=\left[\begin{array}{cccc}\hfill 0_{n,9n}\hfill & \hfill N_{adij}^{\mathsf{T}}\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right].$$

$A_{f\mathsf{i}}=S_{1\mathsf{i}}^{-T}{F}_{1\mathsf{i}},B_{f\mathsf{i}}=S_{2\mathsf{i}}^{-T}{F}_{2\mathsf{i}}$ and ${\mathcal{E}}_{f\mathsf{i}}$ are the designed filter parameters.

Proof 3

As of right now, we are going to speculate about the ${\mathcal{H}}_{\infty }$ performance for (23). In light of HP described below: $\mathsf{J}=\sum _{\mathsf{i}\in \mathrm{\Omega }}\{{\widehat{{\xi }_{\mathsf{i}}}}^{\mathsf{T}}(\mathsf{k})\widehat{{\xi }_{\mathsf{i}}}(\mathsf{k})-{\gamma }_{\mathsf{i}}^2{d}_{\mathsf{i}}^{\mathsf{T}}(\mathsf{k})d_{\mathsf{i}}(\mathsf{k})\}$, by combining (4) with LKF (5), we can determine

$$\mathrm{\Delta }{\mathcal{V}}_{\mathsf{i}}(\mathsf{k})+\delta {\mathcal{V}}_{\mathsf{i}}(\mathsf{k})+\sum _{\mathsf{i}\in \mathrm{\Omega }}\{{\widehat{{\xi }_{\mathsf{i}}}}^{\mathsf{T}}(\mathsf{k})\widehat{{\xi }_{\mathsf{i}}}(\mathsf{k})-{\gamma }_{\mathsf{i}}^2{d}_{\mathsf{i}}^{\mathsf{T}}(\mathsf{k})d_{\mathsf{i}}(\mathsf{k})\}\le \sum _{\mathsf{i}\in \mathrm{\Omega }}{\zeta }_{1\mathsf{k}}^{\mathsf{T}}{\hat{\psi }}_{\mathsf{i}}{\zeta }_{1\mathsf{k}},$$ (25)

where ${\zeta }_{1\mathsf{k}}^{\mathsf{T}}=[{\zeta }_{\mathsf{k}}^{\mathsf{T}}{d}_{\mathsf{i}}(\mathsf{k})]$.

$${\hat{\psi }}_{\mathsf{i}}=\left[\begin{array}{ccc}\hfill {\overline{\mathrm{\Psi }}}_{\mathsf{i}}+{\overline{\mathrm{\Psi }}}_{3\mathsf{i}}^{\mathsf{T}}{\overline{\mathrm{\Psi }}}_{3\mathsf{i}}\hfill & \hfill {\overline{\mathrm{\Psi }}}_{1\mathsf{i}}^{\mathsf{T}}\hfill & \hfill {\overline{\mathrm{\Psi }}}_{2\mathsf{i}}^{\mathsf{T}}\hfill \\ \hfill ⁎\hfill & \hfill P_{1\mathsf{i}}-S_{1\mathsf{i}}-S_{1\mathsf{i}}^{\mathsf{T}}\hfill & \hfill P_{2\mathsf{i}}\hfill \\ \hfill ⁎\hfill & \hfill ⁎\hfill & \hfill P_{3\mathsf{i}}-S_{2\mathsf{i}}-S_{2\mathsf{i}}^{\mathsf{T}}\hfill \\ \hfill ⁎\hfill & \hfill ⁎\hfill & \hfill ⁎\hfill \end{array}\right]$$

${\overline{\mathrm{\Psi }}}_{3\mathsf{i}}^{\mathsf{T}}=\left[{\mathcal{E}}_{\mathsf{i}}{\mathcal{E}}_{f\mathsf{i}}{0}_{n,6n}\right]$. In view of Schur-complement, here we take ${\mathcal{S}}_{\mathsf{i}}=\text{diag}\{{\mathcal{S}}_{1\mathsf{i}},{\mathcal{S}}_{2\mathsf{i}}\}$ and ${\mathcal{F}}_{1\mathsf{i}}={\mathcal{S}}_{1\mathsf{i}}{\mathcal{A}}_{f\mathsf{i}},{\mathcal{PF}}_{2\mathsf{i}}={\mathcal{S}}_{2\mathsf{i}}{\mathcal{B}}_{f\mathsf{i}}$, we obtain

$$\left[\begin{array}{cccc}\hfill \overline{{\mathrm{\Psi }}_{\mathsf{i}}}\hfill & \hfill {\overline{\mathrm{\Psi }}}_{1\mathsf{i}}^{\mathsf{T}}\hfill & \hfill {\overline{\mathrm{\Psi }}}_{2\mathsf{i}}^{\mathsf{T}}\hfill & \hfill {\overline{\mathrm{\Psi }}}_{3\mathsf{i}}^{\mathsf{T}}\hfill \\ \hfill ⁎\hfill & \hfill P_{1\mathsf{i}}-S_{1\mathsf{i}}-S_{1\mathsf{i}}^{\mathsf{T}}\hfill & \hfill P_{2\mathsf{i}}\hfill & \hfill 0\hfill \\ \hfill ⁎\hfill & \hfill ⁎\hfill & \hfill P_{3\mathsf{i}}-S_{2\mathsf{i}}-S_{2\mathsf{i}}^{\mathsf{T}}\hfill & \hfill 0\hfill \\ \hfill ⁎\hfill & \hfill ⁎\hfill & \hfill ⁎\hfill & \hfill -I\hfill \end{array}\right]<0,$$ (26)

here

$${\overline{\mathrm{\Psi }}}_{\mathsf{i}}=diag\{{\overline{\mathrm{\Psi }}}_{(1,1)\mathsf{i}},-(1-\delta )P_{2\mathsf{i}},-{(1-\delta )}^{{\mathrm{\Upsilon }}_{\mathsf{i}m}}{Q}_{1\mathsf{i}},-{(1-\delta )}^{{\mathrm{\Upsilon }}_{\mathsf{i}m}}{Q}_{2\mathsf{i}},-{(1-\delta )}^{{\mathrm{\Upsilon }}_{\mathsf{i}M}}{Q}_{3\mathsf{i}},{\mathcal{M}}_1,{\mathcal{M}}_2,{\mathcal{M}}_3,-{\gamma }_{\mathsf{i}}^{2}I\},{\overline{\mathrm{\Psi }}}_{1\mathsf{i}}=\left[\begin{array}{ccccccccc}\hfill S_{1\mathsf{i}}(A_{\mathsf{i}}+\mathrm{\Delta }{A}_{\mathsf{i}})\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill S_{1\mathsf{i}}(A_{t\mathsf{i}}+\mathrm{\Delta }{A}_{t\mathsf{i}})\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill S_{1\mathsf{i}}{\sum }_{\mathsf{j}\in {{\mathrm{N}}_{\mathsf{i}}}^{in}}(A_{t\mathsf{i}\mathsf{j}}+\mathrm{\Delta }{A}_{t\mathsf{i}\mathsf{j}})\hfill & \hfill 0\hfill & \hfill S_{1\mathsf{i}}{B}_{\mathsf{i}}\hfill \end{array}\right],{\overline{\mathrm{\Psi }}}_{2\mathsf{i}}=\left[\begin{array}{ccccccccc}\hfill S_{2\mathsf{i}}B{f}_{\mathsf{i}}(C_{\mathsf{i}}+\mathrm{\Delta }{C}_{\mathsf{i}})\hfill & \hfill S_{2\mathsf{i}}A{f}_{\mathsf{i}}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill S_{2\mathsf{i}}B{f}_{\mathsf{i}}{D}_{\mathsf{i}}\hfill \end{array}\right],{\overline{\mathrm{\Psi }}}_{3\mathsf{i}}=\left[\begin{array}{ccc}\hfill {\mathcal{E}}_{\mathsf{i}}\hfill & \hfill -{\mathcal{E}}_{f\mathsf{i}}\hfill & \hfill 0_{n,7n}\hfill \end{array}\right].$$

Here by using Lemma 2, $\mathrm{\Delta }{A}_{\mathsf{i}}$ is replaced by $R_{ai}{\mathcal{F}}_{\mathsf{i}}{N}_{a\mathsf{i}}$, $\mathrm{\Delta }{A}_{t\mathsf{i}}$ is replaced by $R_{at\mathsf{i}}{\mathcal{F}}_{\mathsf{i}}{N}_{at\mathsf{i}}$, $\mathrm{\Delta }{A}_{t\mathsf{i}j}$ is replaced by $R_{adij}{\mathcal{F}}_{\mathsf{i}}{N}_{at\mathsf{i}\mathsf{j}}$ and $\mathrm{\Delta }{C}_{\mathsf{i}}$ is replaced by $R_{c\mathsf{i}}{\mathcal{F}}_{\mathsf{i}}{N}_{c\mathsf{i}}$ Therefore it implies that if for $0<\delta <1$ LMI (26) holds, then it follows (25) we obtain,

$$\mathrm{\Delta }{\mathcal{V}}_{\mathsf{i}}(\mathsf{k})+\delta {\mathcal{V}}_{\mathsf{i}}(\mathsf{k})+\sum _{\mathsf{i}\in \mathrm{\Omega }}\{{\widehat{{\xi }_{\mathsf{i}}}}^{\mathsf{T}}(\mathsf{k})\widehat{{\xi }_{\mathsf{i}}}(\mathsf{k})-{\gamma }_{\mathsf{i}}^2{d}_{\mathsf{i}}^{\mathsf{T}}(\mathsf{k})d_{\mathsf{i}}(\mathsf{k})\}\le 0.$$ (27)

The proof of the ${\mathcal{H}}_{\infty }$ performance and the remaining portion of this theorem's proof is identical to that of Theorem 2, so it has been excluded here.

Remark 2

It ought to be mentioned, the results obtained using mode and delay-dependent LKF will be much useful in practice. The state vector with delay information is utilised to establish a new LKF for the considered system. Choice of mode and delay-dependent LKF over a mode-delay-independent one will yield less conservative outcomes. But it could be challenging to deal the time difference of mode-dependent LKF and may result in some high computational time.

4. Numerical examples

The utility and efficacy of the filter design created in this research are demonstrated numerically in this section.

Example 1

Case 1

First, we take into account the system [3] without uncertainty, with each subsystem parameter being:

Subsystem 1

$${\mathcal{A}}_1=\left[\begin{array}{ccc}\hfill 0.02\hfill & \hfill -0.2\hfill & \hfill 0.2\hfill \\ \hfill 0.01\hfill & \hfill 0.01\hfill & \hfill -0.02\hfill \\ \hfill -0.01\hfill & \hfill -0.03\hfill & \hfill 0.02\hfill \end{array}\right],{\mathcal{A}}_{t1}=\left[\begin{array}{ccc}\hfill 0.3\hfill & \hfill 0.01\hfill & \hfill 0.1\hfill \\ \hfill 0.3\hfill & \hfill -0.05\hfill & \hfill -0.1\hfill \\ \hfill 0.1\hfill & \hfill 0\hfill & \hfill -0.09\hfill \end{array}\right],{\mathcal{B}}_1=\left[\begin{array}{c}\hfill 0.1\hfill \\ \hfill -0.1\hfill \\ \hfill 0.4\hfill \end{array}\right],{\mathcal{A}}_{t12}=\left[\begin{array}{ccc}\hfill -0.2\hfill & \hfill 0.1\hfill & \hfill -0.2\hfill \\ \hfill 0.2\hfill & \hfill 0.2\hfill & \hfill -0.1\hfill \\ \hfill 0.2\hfill & \hfill 0.1\hfill & \hfill 0.2\hfill \end{array}\right],{\mathcal{C}}_1={\left[\begin{array}{c}\hfill 0.3\hfill \\ \hfill 0.2\hfill \\ \hfill 0.1\hfill \end{array}\right]}^{\mathsf{T}},{\mathcal{A}}_{t13}=\left[\begin{array}{ccc}\hfill 0.1\hfill & \hfill 0.1\hfill & \hfill -0.1\hfill \\ \hfill 0.2\hfill & \hfill 0.2\hfill & \hfill -0.1\hfill \\ \hfill 0.1\hfill & \hfill 0.1\hfill & \hfill 0.2\hfill \end{array}\right],{\mathcal{D}}_1=0.2$$

Subsystem 2

$${\mathcal{A}}_2=\left[\begin{array}{ccc}\hfill 0.03\hfill & \hfill 0.01\hfill & \hfill 0.02\hfill \\ \hfill -0.1\hfill & \hfill -0.03\hfill & \hfill -0.01\hfill \\ \hfill 0.01\hfill & \hfill 0.01\hfill & \hfill 0.03\hfill \end{array}\right],{\mathcal{A}}_{t2}=\left[\begin{array}{ccc}\hfill -0.03\hfill & \hfill 0.01\hfill & \hfill 0.02\hfill \\ \hfill 0.03\hfill & \hfill -0.02\hfill & \hfill 0.02\hfill \\ \hfill 0\hfill & \hfill 0.01\hfill & \hfill -0.1\hfill \end{array}\right],{\mathcal{B}}_2=\left[\begin{array}{c}\hfill 0.3\hfill \\ \hfill 0.3\hfill \\ \hfill -0.2\hfill \end{array}\right],{\mathcal{A}}_{t21}=\left[\begin{array}{ccc}\hfill 0.01\hfill & \hfill 0.1\hfill & \hfill 0.1\hfill \\ \hfill -0.02\hfill & \hfill 0.1\hfill & \hfill 0.1\hfill \\ \hfill 0.2\hfill & \hfill 0.09\hfill & \hfill 0.2\hfill \end{array}\right],{\mathcal{C}}_2={\left[\begin{array}{c}\hfill 0.1\hfill \\ \hfill 0.1\hfill \\ \hfill 0.2\hfill \end{array}\right]}^{\mathsf{T}},{\mathcal{A}}_{t23}=\left[\begin{array}{ccc}\hfill -0.2\hfill & \hfill 0.2\hfill & \hfill 0.1\hfill \\ \hfill -0.01\hfill & \hfill 0.1\hfill & \hfill 0.2\hfill \\ \hfill 0.2\hfill & \hfill 0.09\hfill & \hfill 0.1\hfill \end{array}\right],{\mathcal{D}}_2=-0.3$$

Subsystem 3

$${\mathcal{A}}_3=\left[\begin{array}{ccc}\hfill 0.03\hfill & \hfill -0.01\hfill & \hfill -0.01\hfill \\ \hfill -0.01\hfill & \hfill 0\hfill & \hfill -0.01\hfill \\ \hfill 0.001\hfill & \hfill -0.02\hfill & \hfill -0.01\hfill \end{array}\right],{\mathcal{A}}_{t3}=\left[\begin{array}{ccc}\hfill 0.1\hfill & \hfill 0.2\hfill & \hfill -0.2\hfill \\ \hfill 0.1\hfill & \hfill 0.2\hfill & \hfill -0.1\hfill \\ \hfill 0.01\hfill & \hfill -0.1\hfill & \hfill 0.2\hfill \end{array}\right],{\mathcal{B}}_3=\left[\begin{array}{c}\hfill -0.3\hfill \\ \hfill -0.2\hfill \\ \hfill 0.1\hfill \end{array}\right],{\mathcal{A}}_{t31}=\left[\begin{array}{ccc}\hfill 0.1\hfill & \hfill -0.2\hfill & \hfill -0.2\hfill \\ \hfill 0.1\hfill & \hfill 0.2\hfill & \hfill -0.1\hfill \\ \hfill 0.1\hfill & \hfill -0.2\hfill & \hfill 0.2\hfill \end{array}\right],{\mathcal{C}}_3={\left[\begin{array}{c}\hfill 0.2\hfill \\ \hfill -0.1\hfill \\ \hfill 0.1\hfill \end{array}\right]}^{\mathsf{T}},{\mathcal{A}}_{t32}=\left[\begin{array}{ccc}\hfill -0.2\hfill & \hfill 0.1\hfill & \hfill -0.2\hfill \\ \hfill 0.1\hfill & \hfill 0.2\hfill & \hfill -0.1\hfill \\ \hfill 0.1\hfill & \hfill -0.1\hfill & \hfill -0.2\hfill \end{array}\right],{\mathcal{D}}_3=-0.1.$$

$\delta =0.02$ is the chosen switching signal and weight of the output signal is provided by

$${\mathcal{E}}_1=\left[\begin{array}{ccc}\hfill 0.1\hfill & \hfill -0.3\hfill & \hfill 0.7\hfill \end{array}\right],{\mathcal{E}}_2=\left[\begin{array}{ccc}\hfill -0.4\hfill & \hfill -0.2\hfill & \hfill -0.4\hfill \end{array}\right],{\mathcal{E}}_3=\left[\begin{array}{ccc}\hfill 0.3\hfill & \hfill -0.2\hfill & \hfill 0.3\hfill \end{array}\right],$$

the time-varying delays satisfying $1\le {\mathrm{\Upsilon }}_{\mathsf{i}}(\mathsf{k})\le 4$, $2\le {\mathrm{\Upsilon }}_{\mathsf{i}\mathsf{j}}(\mathsf{k})\le 4$. Then the LMI in 1 are figured out by the help of minimum ${\mathcal{H}}_{\infty }$ level, here we obtain the parameters for the developed filters

$${\mathcal{A}}_{f1}=\left[\begin{array}{ccc}\hfill 0.0076\hfill & \hfill 0.0004\hfill & \hfill 0.0239\hfill \\ \hfill -0.0201\hfill & \hfill 0.0276\hfill & \hfill -0.0238\hfill \\ \hfill 0.0387\hfill & \hfill -0.0213\hfill & \hfill -0.0324\hfill \end{array}\right],{\mathcal{B}}_{f1}=\left[\begin{array}{c}\hfill 0.0946\hfill \\ \hfill -0.0240\hfill \\ \hfill -0.0320\hfill \end{array}\right],{\mathcal{E}}_{f1}={\left[\begin{array}{c}\hfill 1.3294\hfill \\ \hfill 2.2003\hfill \\ \hfill -6.5068\hfill \end{array}\right]}^{\mathsf{T}},{\mathcal{A}}_{f2}=\left[\begin{array}{ccc}\hfill -0.0237\hfill & \hfill -0.0128\hfill & \hfill 0.0266\hfill \\ \hfill -0.0350\hfill & \hfill -0.0141\hfill & \hfill 0.0478\hfill \\ \hfill 0.0110\hfill & \hfill 0.0077\hfill & \hfill -0.0345\hfill \end{array}\right],{\mathcal{B}}_{f2}=\left[\begin{array}{c}\hfill 0.0054\hfill \\ \hfill 0.2843\hfill \\ \hfill -0.1447\hfill \end{array}\right],{\mathcal{E}}_{f2}={\left[\begin{array}{c}\hfill 4.9233\hfill \\ \hfill 3.9463\hfill \\ \hfill 5.9750\hfill \end{array}\right]}^{\mathsf{T}},{\mathcal{A}}_{f3}=\left[\begin{array}{ccc}\hfill 0.0260\hfill & \hfill 0.0551\hfill & \hfill -0.0135\hfill \\ \hfill -0.0116\hfill & \hfill -0.0433\hfill & \hfill -0.0171\hfill \\ \hfill -0.0417\hfill & \hfill -0.1037\hfill & \hfill 0.0120\hfill \end{array}\right],{\mathcal{B}}_{f3}=\left[\begin{array}{c}\hfill -0.0877\hfill \\ \hfill -0.0347\hfill \\ \hfill 0.0163\hfill \end{array}\right],{\mathcal{E}}_{f3}={\left[\begin{array}{c}\hfill -1.3709\hfill \\ \hfill 2.7770\hfill \\ \hfill -2.1914\hfill \end{array}\right]}^{\mathsf{T}}.$$

Moreover, the error system has a ${\mathcal{H}}_{\infty }$ performance level of $\gamma =0.6979$, indicating exponential stability. Furthermore, we demonstrate the versatility of the filter established after figuring out an effective solution. The disturbances for each modes are: $d_{1\mathsf{i}}(\mathsf{k})=1.1\sin (0.02\mathsf{k})$, $d_{2\mathsf{i}}(\mathsf{k})=0.5\sin (0.03\mathsf{k})$ and $d_{3\mathsf{i}}(\mathsf{k})=0.2\sin (0.01\mathsf{k})$.

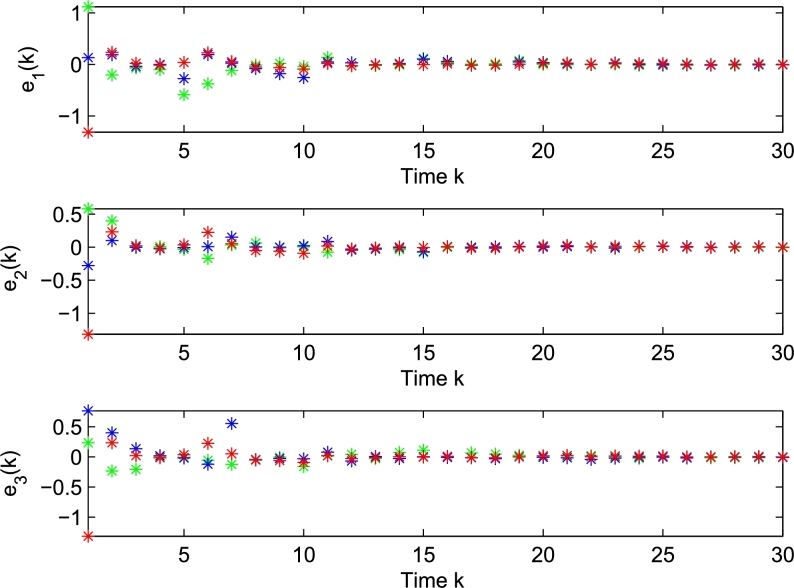
The signal that switches between every subsystem within the specified time frames is denoted in Fig. 1. The outcome for the state vectors $x_{\mathsf{i}}(\mathsf{k})$ and filtering state $x_{f\mathsf{i}}(\mathsf{k})$ were shown in Figure 2, Figure 3, Figure 4, here $\mathsf{i}=1,2,3$. This illustration explains the switching and coupled terms were managed concurrently, and the convergence indicates the system is stable. The error state performance is shown in Fig. 5. It is simple to demonstrated the filter developed here minimises the disturbances within the designed systems together with time-varying delay.

Case 2

We consider linear uncertain system [23] made up of three subsystems:

Subsystem 1

$$A_1=\left[\begin{array}{ccc}\hfill -0.01\hfill & \hfill -0.02\hfill & \hfill 0.02\hfill \\ \hfill 0.03\hfill & \hfill 0.03\hfill & \hfill -0.03\hfill \\ \hfill -0.02\hfill & \hfill -0.01\hfill & \hfill 0.02\hfill \end{array}\right],A_{t1}=\left[\begin{array}{ccc}\hfill 0.02\hfill & \hfill 0.1\hfill & \hfill 0\hfill \\ \hfill 0.4\hfill & \hfill -0.02\hfill & \hfill -0.1\hfill \\ \hfill 0.1\hfill & \hfill 0\hfill & \hfill -0.03\hfill \end{array}\right],A_{t12}=\left[\begin{array}{ccc}\hfill -0.2\hfill & \hfill 0.1\hfill & \hfill -0.2\hfill \\ \hfill 0.2\hfill & \hfill 0.2\hfill & \hfill -0.1\hfill \\ \hfill 0.1\hfill & \hfill 0.1\hfill & \hfill 0.1\hfill \end{array}\right],A_{t13}=\left[\begin{array}{ccc}\hfill 0.2\hfill & \hfill 0.1\hfill & \hfill -0.2\hfill \\ \hfill 0.2\hfill & \hfill 0.1\hfill & \hfill -0.1\hfill \\ \hfill 0.1\hfill & \hfill 0.1\hfill & \hfill 0.2\hfill \end{array}\right],B_1={\left[\begin{array}{ccc}\hfill 0.1\hfill & \hfill -0.1\hfill & \hfill 0.5\hfill \end{array}\right]}^{\mathsf{T}},C_1=\left[\begin{array}{ccc}\hfill 0.6\hfill & \hfill 0.3\hfill & \hfill 0.1\hfill \end{array}\right],D_1=0.5,R_{a1}=\left[\begin{array}{c}\hfill 0.2\hfill \\ \hfill 0.1\hfill \\ \hfill -0.1\hfill \end{array}\right],R_{ad1}=\left[\begin{array}{c}\hfill -0.1\hfill \\ \hfill 0.2\hfill \\ \hfill -0.2\hfill \end{array}\right],R_{ad12}=\left[\begin{array}{c}\hfill -0.1\hfill \\ \hfill -0.2\hfill \\ \hfill -0.5\hfill \end{array}\right],R_{ad13}=\left[\begin{array}{c}\hfill -0.2\hfill \\ \hfill -0.3\hfill \\ \hfill 0.2\hfill \end{array}\right],R_{c1}=\left[\begin{array}{c}\hfill -0.1\hfill \\ \hfill 0.2\hfill \\ \hfill -0.5\hfill \end{array}\right],N_{a1}={\left[\begin{array}{c}\hfill 0.3\hfill \\ \hfill -0.2\hfill \\ \hfill 0.1\hfill \end{array}\right]}^{\mathsf{T}},N_{ad1}={\left[\begin{array}{c}\hfill 0.4\hfill \\ \hfill -0.1\hfill \\ \hfill 0.1\hfill \end{array}\right]}^{\mathsf{T}},N_{ad12}={\left[\begin{array}{c}\hfill 0.2\hfill \\ \hfill -0.1\hfill \\ \hfill 0.1\hfill \end{array}\right]}^{\mathsf{T}},N_{ad13}={\left[\begin{array}{c}\hfill 0.3\hfill \\ \hfill -0.2\hfill \\ \hfill 0.1\hfill \end{array}\right]}^{\mathsf{T}},N_{c1}={\left[\begin{array}{c}\hfill 0.1\hfill \\ \hfill 0.2\hfill \\ \hfill 0.1\hfill \end{array}\right]}^{\mathsf{T}}.$$

Subsystem 2

$$A_2=\left[\begin{array}{ccc}\hfill 0.02\hfill & \hfill 0.01\hfill & \hfill 0.03\hfill \\ \hfill -0.1\hfill & \hfill -0.01\hfill & \hfill -0.02\hfill \\ \hfill 0.01\hfill & \hfill 0.01\hfill & \hfill 0.02\hfill \end{array}\right],A_{t2}=\left[\begin{array}{ccc}\hfill -0.01\hfill & \hfill 0.02\hfill & \hfill 0.02\hfill \\ \hfill 0.01\hfill & \hfill -0.02\hfill & \hfill 0.01\hfill \\ \hfill 0\hfill & \hfill 0.01\hfill & \hfill 0.1\hfill \end{array}\right],B_2={\left[\begin{array}{ccc}\hfill 0.4\hfill & \hfill 0.3\hfill & \hfill -0.6\hfill \end{array}\right]}^{\mathsf{T}},A_{t21}=\left[\begin{array}{ccc}\hfill 0.2\hfill & \hfill 0.1\hfill & \hfill 0.1\hfill \\ \hfill -0.03\hfill & \hfill 0.1\hfill & \hfill 0.2\hfill \\ \hfill 0.2\hfill & \hfill 0.09\hfill & \hfill 0.1\hfill \end{array}\right],C_2={\left[\begin{array}{c}\hfill 0.5\hfill \\ \hfill 0.2\hfill \\ \hfill 0.1\hfill \end{array}\right]}^{\mathsf{T}},A_{t23}=\left[\begin{array}{ccc}\hfill -0.2\hfill & \hfill 0.1\hfill & \hfill 0.1\hfill \\ \hfill -0.02\hfill & \hfill 0.1\hfill & \hfill 0.2\hfill \\ \hfill 0.2\hfill & \hfill 0.09\hfill & \hfill 0.2\hfill \end{array}\right],D_2=-0.6,R_{a2}=\left[\begin{array}{c}\hfill -0.3\hfill \\ \hfill 0.2\hfill \\ \hfill -0.1\hfill \end{array}\right],R_{ad2}=\left[\begin{array}{c}\hfill 0.1\hfill \\ \hfill 0.4\hfill \\ \hfill 0.1\hfill \end{array}\right],R_{ad21}=\left[\begin{array}{c}\hfill -0.3\hfill \\ \hfill -0.4\hfill \\ \hfill 0.5\hfill \end{array}\right],R_{ad23}=\left[\begin{array}{c}\hfill -0.1\hfill \\ \hfill 0.1\hfill \\ \hfill -1.2\hfill \end{array}\right],R_{c2}=\left[\begin{array}{c}\hfill -0.2\hfill \\ \hfill -0.1\hfill \\ \hfill -0.1\hfill \end{array}\right],N_{a2}={\left[\begin{array}{c}\hfill 0.1\hfill \\ \hfill -0.2\hfill \\ \hfill 0.1\hfill \end{array}\right]}^{\mathsf{T}},N_{ad2}={\left[\begin{array}{c}\hfill -0.2\hfill \\ \hfill -0.2\hfill \\ \hfill 0.1\hfill \end{array}\right]}^{\mathsf{T}},N_{ad21}={\left[\begin{array}{c}\hfill -0.1\hfill \\ \hfill -0.1\hfill \\ \hfill 0.1\hfill \end{array}\right]}^{\mathsf{T}},N_{ad23}={\left[\begin{array}{c}\hfill -0.3\hfill \\ \hfill -0.2\hfill \\ \hfill 0.2\hfill \end{array}\right]}^{\mathsf{T}},N_{c2}={\left[\begin{array}{c}\hfill -0.1\hfill \\ \hfill 0.2\hfill \\ \hfill 0.1\hfill \end{array}\right]}^{\mathsf{T}}.$$

Subsystem 3

$$A_3=\left[\begin{array}{ccc}\hfill 0.02\hfill & \hfill -0.02\hfill & \hfill -0.01\hfill \\ \hfill -0.01\hfill & \hfill 0.02\hfill & \hfill -0.02\hfill \\ \hfill 0.01\hfill & \hfill -0.02\hfill & \hfill -0.01\hfill \end{array}\right],A_{t3}=\left[\begin{array}{ccc}\hfill 0.1\hfill & \hfill 0.1\hfill & \hfill -0.2\hfill \\ \hfill 0.1\hfill & \hfill 0.2\hfill & \hfill -0.1\hfill \\ \hfill 0.01\hfill & \hfill -0.1\hfill & \hfill 0.2\hfill \end{array}\right],B_3={\left[\begin{array}{ccc}\hfill -0.4\hfill & \hfill -0.5\hfill & \hfill 0.2\hfill \end{array}\right]}^{\mathsf{T}},A_{t31}=\left[\begin{array}{ccc}\hfill 0.2\hfill & \hfill -0.3\hfill & \hfill -0.1\hfill \\ \hfill 0.1\hfill & \hfill 0.2\hfill & \hfill -0.1\hfill \\ \hfill 0.1\hfill & \hfill -0.1\hfill & \hfill 0.2\hfill \end{array}\right],C_3={\left[\begin{array}{c}\hfill 0.1\hfill \\ \hfill -0.2\hfill \\ \hfill 0.1\hfill \end{array}\right]}^{\mathsf{T}},A_{t32}=\left[\begin{array}{ccc}\hfill -0.2\hfill & \hfill 0.1\hfill & \hfill -0.1\hfill \\ \hfill -0.01\hfill & \hfill 0.1\hfill & \hfill 0.2\hfill \\ \hfill -0.2\hfill & \hfill 0.1\hfill & \hfill -0.2\hfill \end{array}\right],D_3=-0.1,R_{a3}=\left[\begin{array}{c}\hfill 0.2\hfill \\ \hfill 0.4\hfill \\ \hfill 0.3\hfill \end{array}\right],R_{ad3}=\left[\begin{array}{c}\hfill -0.1\hfill \\ \hfill 0.2\hfill \\ \hfill -0.3\hfill \end{array}\right],R_{ad31}=\left[\begin{array}{c}\hfill -0.3\hfill \\ \hfill 0.1\hfill \\ \hfill 1.2\hfill \end{array}\right],R_{ad32}=\left[\begin{array}{c}\hfill -0.2\hfill \\ \hfill 0.1\hfill \\ \hfill -0.2\hfill \end{array}\right],R_{c3}=\left[\begin{array}{c}\hfill -0.3\hfill \\ \hfill 0.3\hfill \\ \hfill 0.1\hfill \end{array}\right],N_{a3}={\left[\begin{array}{c}\hfill 0.1\hfill \\ \hfill -0.2\hfill \\ \hfill 0.1\hfill \end{array}\right]}^{\mathsf{T}},N_{ad3}={\left[\begin{array}{c}\hfill -0.2\hfill \\ \hfill -0.1\hfill \\ \hfill 0.3\hfill \end{array}\right]}^{\mathsf{T}},N_{ad31}={\left[\begin{array}{c}\hfill -0.1\hfill \\ \hfill -0.1\hfill \\ \hfill 0.1\hfill \end{array}\right]}^{\mathsf{T}},N_{ad32}={\left[\begin{array}{c}\hfill -0.2\hfill \\ \hfill -0.2\hfill \\ \hfill 0.3\hfill \end{array}\right]}^{\mathsf{T}},N_{c3}={\left[\begin{array}{c}\hfill -0.1\hfill \\ \hfill 0.2\hfill \\ \hfill 0.1\hfill \end{array}\right]}^{\mathsf{T}}.$$

$\delta =0.01$ is the chosen switching signal and weight of the outcome-signal is:

$${\mathcal{E}}_1=\left[\begin{array}{ccc}\hfill 0.2\hfill & \hfill 0.5\hfill & \hfill -0.7\hfill \end{array}\right],{\mathcal{E}}_2=\left[\begin{array}{ccc}\hfill 0.6\hfill & \hfill 0.3\hfill & \hfill -0.7\hfill \end{array}\right],{\mathcal{E}}_3=\left[\begin{array}{ccc}\hfill 0.3\hfill & \hfill 0.2\hfill & \hfill 0.5\hfill \end{array}\right],$$

The time-varying delays satisfying $2\le {\mathrm{\Upsilon }}_{\mathsf{i}}(\mathsf{k})\le 4$, $2\le {\mathrm{\Upsilon }}_{\mathsf{i}\mathsf{j}}(\mathsf{k})\le 6$, we obtain

$$A_{f1}=\left[\begin{array}{ccc}\hfill 0.0163\hfill & \hfill -0.0315\hfill & \hfill 0.0353\hfill \\ \hfill -0.0080\hfill & \hfill 0.0298\hfill & \hfill -0.0457\hfill \\ \hfill -0.0137\hfill & \hfill -0.0061\hfill & \hfill 0.0265\hfill \end{array}\right],B_{f1}=\left[\begin{array}{c}\hfill 0.0177\hfill \\ \hfill -0.0559\hfill \\ \hfill 0.0231\hfill \end{array}\right],{\mathcal{E}}_{f1}={\left[\begin{array}{c}\hfill -3.3984\hfill \\ \hfill 5.5292\hfill \\ \hfill 4.5890\hfill \end{array}\right]}^{\mathsf{T}},A_{f2}=\left[\begin{array}{ccc}\hfill -0.0105\hfill & \hfill 0.0162\hfill & \hfill 0.0664\hfill \\ \hfill -0.0199\hfill & \hfill 0.0237\hfill & \hfill -0.0091\hfill \\ \hfill -0.0523\hfill & \hfill -0.0191\hfill & \hfill 0.0470\hfill \end{array}\right],B_{f2}=\left[\begin{array}{c}\hfill 0.1146\hfill \\ \hfill 0.1900\hfill \\ \hfill -0.1028\hfill \end{array}\right],{\mathcal{E}}_{f2}={\left[\begin{array}{c}\hfill 4.4193\hfill \\ \hfill 4.6185\hfill \\ \hfill 6.4272\hfill \end{array}\right]}^{\mathsf{T}},A_{f3}=\left[\begin{array}{ccc}\hfill 0.0487\hfill & \hfill 0.0168\hfill & \hfill -0.0382\hfill \\ \hfill 0.0247\hfill & \hfill 0.0125\hfill & \hfill -0.0469\hfill \\ \hfill 0.0126\hfill & \hfill -0.0216\hfill & \hfill -0.0381\hfill \end{array}\right],B_{f3}=\left[\begin{array}{c}\hfill -0.2382\hfill \\ \hfill 0.2616\hfill \\ \hfill -0.2087\hfill \end{array}\right],{\mathcal{E}}_{f3}={\left[\begin{array}{c}\hfill -2.2164\hfill \\ \hfill 4.0686\hfill \\ \hfill -2.2682\hfill \end{array}\right]}^{\mathsf{T}}.$$

Further, system is exponentially-stable where the obtained ${\mathcal{H}}_{\infty }$ level is ${\gamma }_{\mathsf{i}}=0.8386$, the switching and error responses are shown in Figure 6, Figure 7, respectively. This demonstrates the applicability of the proposed outcomes.

Figure 1.

Switching signal.

Figure 2.

Response of states $x_1(\mathsf{k})$ & $x_{f1}(\mathsf{k})$.

Figure 3.

Response of states $x_2(\mathsf{k})$ & $x_{f2}(\mathsf{k})$.

Figure 4.

Response of states $x_3(\mathsf{k})$ & $x_{f3}(\mathsf{k})$.

Figure 5.

Error state $e(\mathsf{k})$.

Figure 6.

Switching signal.

Figure 7.

Error state $e(\mathsf{k})$.

5. Conclusion

For the discrete-time interconnected systems, we have examined the EMSS with time-varying delays and the ${\mathcal{H}}_{\infty }$ filter method is also examined in this study. Designing a suitable filter for the described interconnected systems is the primary contribution. To demonstrate the exponential stability for the designed system, a set of LMI are provided with the disturbance rejection level ${\gamma }_{\mathsf{i}}>0$. Standard packages are used to solve this set of LMI constraints. Finally, examples with two cases are demonstrated for the prescribed system with and without uncertainty in-order to deliver the positive impact for the intended outcomes. It is important to remember that when the switching signal ‘$\mathsf{i}$’ is large the results still hold, but the computation complexity will be high, that is, the duration for convergence is also increased. This could lead to wide research analysis and will be our future topic of research.

Funding

The work of Yong-Ki Ma was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (No. 2021R1F1A1048937). The work of G. Arthi was supported by PSGR Krishnammal College for Women research grant.

CRediT authorship contribution statement

G. Arthi: Writing – review & editing, Writing – original draft, Validation, Supervision, Methodology, Investigation, Formal analysis, Conceptualization. M. Antonyronika: Writing – original draft, Methodology, Investigation, Conceptualization. Yong-Ki Ma: Writing – review & editing, Supervision, Methodology, Investigation, Funding acquisition, Conceptualization.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Data availability

Data sharing is not applicable to this article as no new data were created or analyzed in this study.