Abstract
Mixed convective nanofluid flow has substantial importance in improvement of thermal performance, and thermal engineering to meet the global energy crisis. In this study, mixed convective nanofluid flow in a porous-wavy channel with an inner heated triangular obstacle under magnetic field effect is numerically examined. Nanofluid within the channel is heated and cooled from its bottom and top wavy-surfaces. A heated triangular cylinder is located at the centerline of the wavy-channel. Finite element method is utilized to solve the non-dimensional governing equations. The code is validated comparing present results with published numerical and experimental results. The response surface method is also implemented to analyze the obtained results and its sensitivity. The numerical results indicate that strength of flow velocity is accelerated with rising Reynolds number, Darcy numbers and inlet-outlet ports length but declined for Hartmann number and volume fraction. Heat transferring rate and heat transfer irreversibility are substantially increased for higher values of Reynolds number, inlet-outlet ports length, Darcy number and nanoparticle volume fraction but a reverse trend is occurred for magnetic field effect. The thermal performance is found significantly improved with simultaneous increment in Re, ϕ, Da and decrement in Ha. Positive sensitivity is achieved for input factors Re, ϕ, Da in computing while negative sensitivity to Ha. Heat transfer rate is found more sensitive to the impact of Re and ϕ compared to Da and Ha. 45.59 % more heat transmission potentiality is developed for using Al2O3–H2O nanofluid (vol.5 %) instead of using base fluid water. Heat transfer enhancement rate is decreased by 36.22 % due to impact of magnetic field strength. In addition, 84.12 % more heat transferring rate is recorded in presence of triangular obstacle. Moreover, irreversibility components are influenced significantly for the presence of heated triangular obstacle. Bejan number is also found declined for increasing physical parameters. The findings of this investigation may offer a guideline for finding experimental results to design high-performance convective heat exchangers.
Keywords: Mixed convection, Nanofluids, Magnetic field, Porous medium, Finite element method, Response surface method
1. Introduction
Mixed convection frequently occurs during operation of heat exchangers, cooling of electronic devices, cooling or heating of buildings, nuclear reactors, solidification, float glass production, lubrication technologies and geophysics, etc. The performance of these equipment can be improved utilizing improved design and proper modelling, etc. Another innovated method is the suspension of nano-metered sized particles in conventional liquids, named as nanofluids which improves the thermal conductivity of conventional fluids. The complex interaction of fluid inertia with buoyancy flow has sustainable impact on enhancing flow mixing and heat transfer rate. The thermal performance is also found correlated to the controlling of entropy generation. Accordingly, entropy generation analysis is an important issue to optimize the performance of thermal-equipment.
Fereidoon et al. [1] studied mixed convection in a lid driven square inclined cavity and demonstrated that heat transfer rate increases for increasing solid volume fraction of nanoparticles at constant Re. After that, Selimefendigil and Öztop [2] analyzed mixed convection in a triangular cavity and revealed that heat transfer rate increases with the increase in elastic modulus of flexible-wall and volume fraction. Nithyadevi et al. [3] used control volume method to examine mixed convection in a rectangular porous cavity. They observed that heat transfer rate enhances due to presence of cupper nanoparticles in fluid-saturated porous media. Motlagh and Soltanipour [4] utilized two-phase Buongiorno's model to explore natural convection in an inclined square cavity and found that heat transfer enhancement for higher inclination angles and volume fraction depends on Rayleigh number. Lam and Prakash [5] implemented SUPG-finite element method to perform numerical study of natural convection in porous enclosure with heat sources and observed maximum entropy generation near the heat sources resulting of high thermal gradient there. Later on, Hemmat Esfe et al. [6] presented comprehensive review on mixed convection in nanofluid inside different cavities and highlighted that suitable designs are important in energy conversion system. Aljabair et al. [7] studied mixed convection of Cu-water nanofluid in an arc cavity using FORTRAN code and showed that increased volume fraction or Reynolds and Richardson numbers causes increment in local and average Nusselt number. Zaydan et al. [8] performed comparative study of nanoparticles shaped effects on mixed convection by implementing finite difference methods and concluded that spherical shaped is more effective for higher heat transferring rate compared to cylindrical shaped nanoparticles. Later on, Alsabery et al. [9] applied two phase nanofluid model to conduct non-homogeneous study of mixed convection in a wavy enclosure and reported that heat transfer is augmented for increasing volume fraction, amplitude and wave number, and heat source aspect ratio. Khan et al. [10] utilized finite difference method to analyze double-diffusive natural convection in a porous trapezoidal cavity and observed that dimensionless temperature reduces for the impact of buoyancy parameter while dimensionless concentration is increased. Saleh et al. [11] examined sinusoidal temperature impact on mixed convection in a cavity with moving walls and noticed that flow field and thermal performance are influenced by the concentration of nanoparticles at constant Reynolds number whereas high Reynolds number reduces the impact of concentration of nanoparticles.
Recently, magnetic field impact on mixed convection has received extensive interest in engineering and industrial fields because of its substantial applications in liquid crystal growth, nuclear reactor cooling, electronic devices and geophysics, etc. Azizian et al. [12] accomplished experimental investigation of magnetic field effect on pressure drop and heat transfer in magnetite nanofluid. They confirmed that heat transmission rate is more pronounced at high Reynolds number, and pressure increases up to 7.5 % while magnetic field intensity of 430 mT. Mejri et al. [13] examined magnetic field effect on natural convection inside a square cavity and showed that entropy generation is increased for volume fraction at Ra = 5×104 and Ha = 20. Elshehabey and Ahmed [14] studied mixed convection in a lid driven cavity and demonstrated that inclined magnetic field reduces the fluid movement. Later on, Cho [15] investigated magnetic field effect on natural convection in a complex wavy cavity and suggested that a minimum Nusselt number for high Rayleigh number, and maximum total entropy generation for high values of Ha. Afrand et al. [16] analyzed the influence of magnetic field on natural convection in an inclined cylindrical annulus and recorded that average Nusselt number gets a constant value for increasing Harmann number. Sarlak et al. [17] numerically investigated magnetic field effect on heat transfer and laminar flow in a lid driven T-shaped enclosure filled by nanofluid. They reported the heat transfer enhancement for higher volume fraction and lower Richardson and Hartmann numbers. Talebizadehsardari et al. [18] conducted experimental study of magnetic field effect on water CNT-Fe3O4 nanofluid flow and found that external magnetic effect causes increment in the viscosity of water CNT-Fe3O4 nanofluid. Later on, Malik and Nayak [19] presented numerical investigation of magneto-hydrodynamic nanofluid flow in square cavity saturated by porous medium. After that, Akhter et al. [20] accomplished a similar study and pointed out that optimum heat transferring rate for higher Ra, Da and volume fraction. Ibrahim et al. [21] investigated magnetic field effect on forced convection in a microtube with twisted porous blocks. Their results highlighted that pressure drop and heat transfer coefficient are increased by increasing Reynolds number but friction factor is decreased. Al-Kouz et al. [22] presented theoretical and computational study of magnetic field effect on heat transfer and entropy generation of hybrid nanofluid flow in a wavy-walled trapezoidal enclosure with a permeable medium layer. They concluded that average Bejan number is decreased significantly with increased Hartmann and Rayleigh numbers whereas average Nusselt number is depleted with high Rayleigh and Hartmann numbers. Geridonmez and Oztop [23] investigated mixed convection in a lid driven cavity and recommended that the flow and thermal fields are affected with the partial magnetic field, and convective heat transfer is reduced for increase in length of partial magnetic field. After that, Shehata et al. [24] examined nanoparticles effect on hydro-magnetic mixed convection flow in a square cavity and concluded that effect of orientation of lid wall on heat and fluid flow more effective for increased magnetic field effect and heat transfer rate increases with increased solid volume fraction.
Moreover, the presence of appropriate obstruction within different configurations influences flow and heat transferring where fluid flow is bifurcated. Gangawane and Manikandan [25] studied convective flow in a square chamber with hexagonal obstacle at different thermal conditions. They found a remarkable change in flow and temperature distribution due to thermal conditions. Ali et al. [26] investigated magnetohydrodynamic flow in a hexagonal cavity with tilted blockage and showed that over all heat transfer rate is increased for high Ra and ϕ at low Ha. Mehmood et al. [27] analyzed mixed convection of nanofluid in a lid driven cavity with square block subjected to magnetic field effect. Their results highlighted that average Nusselt number and heat transfer irreversibility reduce with increasing magnetic field strength. Hussain et al. [28] performed mixed convection in a horizontal channel with an adiabatic square obstacle and concluded that fluid motion, average heat transfer rate and heat transfer entropy decrease for increased Ha while fluid friction entropy generation is increased. Al-Rashed et al. [29] examined mixed convection of nanofluid flow and recommended that heat transferring rate rises for higher volume fraction and temperature difference between hot elliptic cylinder and cold wall of the cavity. Al-Farhany et al. [30] used COMSOL Multiphysics software to analyze MHD effects on laminar flow in a horizontal channel and showed that heat transfer increases for increased Richardson number and decreased Hartmann number. Ali et al. [31] investigated mixed convection in lid driven cavity with a solid circular obstacle and observed that heat transfer enhancement due to Reynolds number respectively increase and decrease for higher Casson fluid parameter and Hartmann number. After that, Ali et al. [32] conducted a similar study incorporating rotating cylinder and horizontal baffles inside the cavity and found that flow velocity and heat transfer rate increase with cylinder rotational speed and Reynolds number. Singh and Khandelwal [33] analyzed stability of mixed convection for different nanofluids in a vertical channel using single -phase nanofluid model and Chebyshev spectral collocation method and suggested that basic flow stability is improved by suspending nanoparticles in base fluid whereas instability is occurred with increasing Reynolds number. Islam et al. [34] studied mixed convection in a hexagonal heat exchanger implementing finite element method and noted 17.69 % heat transfer increment in nanofluid of 10 % volume fraction. Khan et al. [35] used Galerkin finite element method to investigate mixed convection in a split lid-driven trapezoidal cavity with triangular-shaped cold obstacle filled by hybrid nanofluid. They suggested that nanoparticle volume fraction, Richardson, and Reynold numbers affect the Nusselt number significantly. Later on, Khan et al. [36] studied magnetohydrodynamic natural convection in a trapezoidal cavity with solid obstacles using finite element method and found noticeable improvement in heat transfer rate for rising Rayleigh number with diminishing magnetic field strength. After that, Khan et al. [37] used similar method to analyze magnetic and Joule effects on mixed convection in a channel with a dimpled surface and cylindrical obstacle. They noticed that average Nusselt number reduces with increasing Hartmann number and Joule heating parameter while it increases for increasing Prandtl, Rayleigh, and Reynolds numbers. Thereafter, Song et al. [38] conducted numerical analysis for ferromagnetic nanofluid flow in a channel with dimpled cavity and rectangular obstacle by implementing Galerkin weighted residual finite element method and showed a significant improvement in heat transfer rate near dimpled surface for high Reynolds number. Bentoto et al. [39] used perturbation method to analyze MHD nanofluid flow in a vertical channel. Their results indicated that fluid temperature and velocity are influenced with the use of nanofluid, and heat transfer rate improves for thermal radiation effect. Hussien and Hussein [40] studied mixed convection in a horizontal rectangular channel with a lid driven cavity and found that aspect ratio affects the flow and thermal fields and maximum heat transmission is occurred at Ri = 100 for all cases considered.
In literature review, it is noticed that mixed convection under magnetic field effect becomes an interesting topic in the field of industry and engineering. It is also found that the geometrical configuration plays an important role on the fluid flow and heat transfer behaviours. In addition, the presence of obstruction in different shapes is either attached or detached, improves its potential applications. Moreover, corner edges of such obstructions can influence the features of fluid flow and heat transferring rate. Furthermore, nanoparticles of higher thermal conductivity are used for the purpose of heat transfer enhancement in base fluid. In addition, the thermal performance is also closely related to minimization of entropy generation. Although numerous investigations have been accomplished on mixed convection in various geometries to date, to the authors' knowledge no significant research works were found considering these issues yet to analyze the transport phenomena in nanofluid flow for a porous wavy channel. Consequently, the objective of the present study is to numerically examine magnetic field effect on mixed convection in Al2O3-water nanofluid filled wavy porous channel having a heated triangular cylinder acting as the centred obstruction. Additionally, Al2O3 nanoparticles Brownian motion is considered to modify the Maxwell's thermal conductivity model. Moreover, response surface analysis and sensitivity study are performed using response surface method (RSM) for advanced visualization of heat transferring. Simulations are carried out implementing finite element method. The findings of this study are presented graphically and discussed in details from physical point of view. To the authors' opinion, it is an innovative research which may be significant in practical applications in thermal engineering as a means high-performance convective heat exchangers. The study has been accomplished numerically due to lack of experimental laboratory facilities. Although, the authors have considered a fixed geometry, the findings of this investigation can be extended to the other geometrical configurations for convective channel flow and it would be a useful guide to the experimentalists to analyze convective heat transfer in nanofluid filled channels of different shapes.
Nomenclature
| Amplitude of the wavy channel (m) | Greek symbols | ||
| Magnitude of the applied magnetic field | Thermal diffusivity | ||
| Bejan number | Thermal expansion coefficient | ||
| Specific heat at constant pressure | Dimensionless wave length (m) | ||
| Da | Darcy number | Volume fraction of nanoparticles | |
| Nanoparticle diameter | Dimensionless temperature | ||
| Gravitational acceleration | Dynamic viscosity | ||
| Grashof number | Kinematic viscosity | ||
| Height of the channel | Density | ||
| Hartmann number | Electrical conductivity | ||
| Permeability of the porous medium | Irreversibility distribution ratio | ||
| Thermal conductivity | Channel porosity | ||
| Boltzmann constant | Subscripts | ||
| Length of the channel | Alumina (Al2O3) | ||
| Normal unit vector | Average or mean | ||
| Local Nusselt Number | Cold | ||
| Average Nusselt number | Base fluid | ||
| Prandtl number | Hot | ||
| Dimensional pressure | Nanofluid | ||
| Dimensionless pressure | Abbreviations | ||
| Heat flux | CWHTC | Channel with heated triangular cylinder | |
| Reynolds number | CWOHTC | Channel without heated triangular cylinder | |
| Surface length of channel | Liop | Length of inlet and outlet ports | |
| Entropy generation | Fluid friction irreversibility | ||
| Total entropy generation | Heat transfer irreversibility | ||
| Dimensional temperature | Magnetic force irreversibility | ||
| Mean temperature | FEM | Finite element method | |
| Reference temperature | RSM | Response surface model | |
| Dimensional velocity components | CCD | Central composite design | |
| Dimensionless velocity components | |||
| Dimensional coordinates | |||
| Dimensionless coordinates | |||
| volume of the enclosure | |||
2. Model specification
Fig. 1 represents geometrical model of this investigation which is filled with nanofluid [27] where the size of nanoparticles is considered as 10 nm, and saturated by porous medium with uniform porosity (ε = 0.5). The length and height of the channel is denoted by L and H (=0.40L) and its wave length is λ and amplitude . The channel is also heated and cooled respectively from its bottom and top wavy-surfaces maintaining temperature Th and Tc (Th > Tc), and includes a triangular heated obstacle at its centerline. The surfaces of the channel except the inlet-out ports and hot-cold sections are kept adiabatic. In addition, cold nanofluid enters through inlet-port at uniform velocity, ui and temperature, Tc. The following assumption are considered for the present study:
Fig. 1.
-
⁃The nanofluid utilized in this study is considered to be laminar, incompressible, and Newtonian.
-
⁃The channel is permeated a uniform magnetic field (B0).
-
⁃The Brinkman-Darcy model is considered for the mass and momentum equations.
-
⁃The properties of porous medium are assumed to be homogeneous.
-
⁃The base fluid and nanoparticles are in thermally equilibrium.
-
⁃Fluid properties are assumed to be constant, except for density variation with temperature based on the Boussinesq approximation.
-
⁃The effects of radiation, viscous dissipation, and Joule heating are neglected.
-
⁃The thermophysical properties of the base fluid and nanoparticles are given in Table 1.
3. Mathematical analysis
The governing equations of this study relating to the model specification and Boussinesq approximation are [5,9,15,19,20,28,[41], [42], [43]]:
| (1) |
| (2) |
| (3) |
and the entropy generation in dimensional form is also defined as:
| (4) |
Where .
The properties of Al2O3-water nanofluid are [27,28,[44], [45], [46], [47]].
| Density | : | |
|---|---|---|
| Dynamic viscosity | : | |
| Thermal expansion coefficient | : | |
| Buoyancy co-efficient | : | |
| Heat capacity | : | |
| Thermal conductivity | : | |
| Thermal diffusivity | : | |
| Electrical conductivity | : |
The corresponding boundary conditions are [4, 28, 41]:
| (5a) |
| (5b) |
| (5c) |
| (5d) |
| (5e) |
| (5f) |
Where is a unit vector normal to the surface [4].
The governing equations are converted into dimensionless form with the help of variables as specified in Eq. (6) [4,41]:
| (6) |
Therefore, converted dimensionless governing equations are:
| (7) |
| (8) |
| (9) |
and entropy generation in dimensionless form also obtained as follows:
| (10) |
In Eq. (10), irreversibility components are presented respectively as , and . The Bejan number is defined as where and is the irreversibility factor which is defined by .
and the no-dimensional boundary conditions are:
| (11a) |
| (11b) |
| (11c) |
| (11d) |
| (11e) |
| (11f) |
3.1. Heat transfer and temperature
The local and average Nusselt number are estimated using the following expression [48]:
| (12) |
and the average temperature is also estimated using the flowing expression [48]:
| (13) |
3.2. Computational procedure
The governing partial differential equations in dimensionless from (7), (8), (9) subjected to the well-defined dimensionless boundary conditions (11a-f) are solved numerically using finite element method. In this computational process, the solution domain is discretized into finite element mesh, and the governing equations are transformed into finite element integral equations using Galerkin weighted residual method [49]. These integral equations are then converted into linear algebraic equations using the Newton-Rahson method [50]. Subsequently, the linear algebraic equations are solved using the reduced integration method and Triangular Factorization technique [51,52]. The detailed simulation procedure was discussed by Taylor and Hood [53], and Dechaumphai [54] and can also be found in the earlier study [55].
The advantages of the finite element method are that it allows easier way to deal complex geometrical or irregular shapes in two dimensional or three-dimensional domain with higher accuracy and rapid convergence. In this method, complex domain is sub-divided into smaller components or elements refers to finite elements at which the values of unknowns of each equation are calculated and complex domain can be analyzed easily using FEM. Thus, the finite elements make the method a versatile tool for solving boundary value problems found in various fields of engineering. Moreover, the equations for each element are accumulated into a system of equations for whole domain results addition of new elements in mesh refinement is a simple task. In addition, appropriate boundary conditions can easily incorporate to respond a model. There are different numerical methods, among them FEM offers better flexibility to deal complex geometrical or irregular shapes and boundary conditions. It allows for higher-order approximations of the solution that provides greater accuracy. Furthermore, it has a more systematic and structured approach for discretization of solution domain that leads to better rapid convergence. That is why, finite element method has been selected to solve the governing equations of the present work.
3.3. Mesh generation and grid sensitivity test
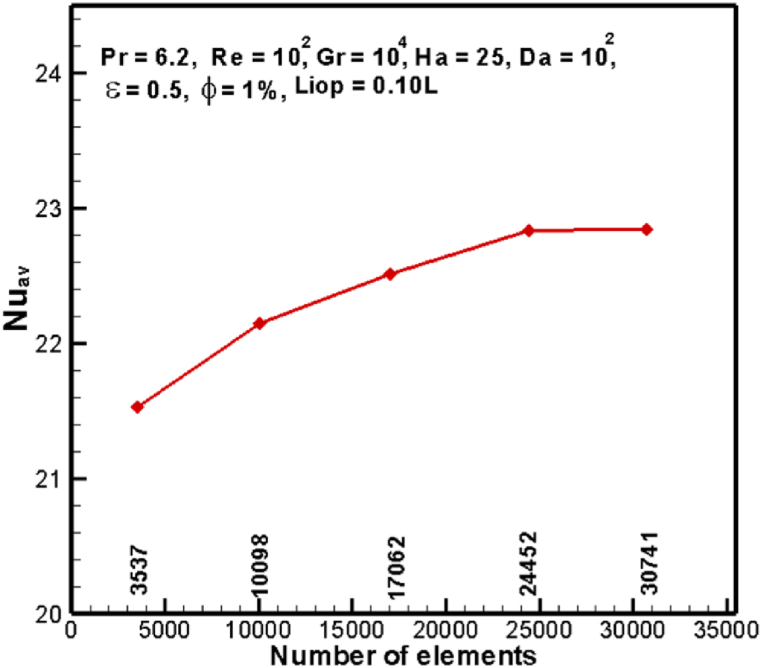
Mesh generation procedure is performed using small elements which are triangular or quadrilateral shaped with specific nodes for implementing finite element method. Thus, appropriate meshing in an important part of practical applications of finite element method. In order to select appropriate meshing, grid sensitivity test is accomplished estimating (Table 2). From Tables 2 and it is revealed that further meshing does not reflect significant impact on calculating average Nusselt number. Accordingly, mesh size of 12561 nodes and 24452 elements ensures appropriate solution for the present study and corresponding grid test and meshing are shown in Fig. 2 and Fig. 3, respectively.
Table 1.
Thermo-physical properties of water and alumina [27].
| Physical properties | water | Alumina (Al2O3) |
|---|---|---|
| 4179 | 765 | |
| 997.1 | 3970 | |
| 0.613 | 40 | |
| 21 10−5 | 0.85 10−5 | |
| 0.05 | 1 10−1 |
Table 2.
at different mesh systems.
| Nodes (Elements) | 1919 (3537) | 5227 (10098) | 8773 (17062) | 12561 (24452) | 15799 (30741) |
|---|---|---|---|---|---|
| 21.527 | 22.147 | 22.510 | 22.837 | 22.846 |
Fig. 2.
Grid sensitivity test.
Fig. 3.
Mesh configuration of the present model.
3.4. Code validation
The present code is validated performing numerical and graphical comparisons.
3.4.1. Validation case no. 1
Hussain et al. [28] studied MHD mixed convection channel flow and validated their results performing comparisons with numerical results available in Refs. [[56], [57], [58]]. The authors have simulated their problems for special cases, and set a numerical comparison in Table 3 considering the results of earlier studies [28,[56], [57], [58]] and present study where maximum deviation is found less than 2 % contrasting with results of Hussain et al. [28].
Table 3.
Comparative results of .
3.4.2. Validation case no. 2
Al-Farhany et al. [30] studied mixed convection fluid flow in a two-dimensional channel with an open cavity in presence of magmatic filed implementing COMSOL Multiphysics software and compared their results with the results reported by Laouira et al. [59]. We have simulated their problems (Refs. [30,59]) using the present simulation procedure and compared as exhibited in Fig. 4a.
Fig. 4(a).
Comparisons of streamlines (left) and isotherms (right).
3.4.3. Validation case no. 3
Al- Kouz et al. [22] presented theoretical and computational study of electrically conducting hybrid nanofluid flow in a wavy-walled trapezoidal cavity. In their study, COMSOL computations was verified comparing results against experimental results of Krane and Jessee [60] for a special case. We have considered the present finite element-based numerical procedure to simulate the identical problem [22] for the special case and compared by plotting the present results and the results of Al- Kouz et al. [22] and Krane and Jessee [60] (data has been collected using Data Digitizer) in Fig. 4b where excellent agreements are reflected.
Fig. 4(b).
Comparison of temperature distribution of the results of present study and results available in Refs. [22,60].
These comparisons ensure desire accuracy of the present study using numerical technique developed. Consequently, authors have performed numerical simulation of the present problem and discussed from technological point of view in the following section 4.
4. Results and discussion
The numerical outcomes of mixed convective nanofluid flow in a wavy porous channel under a magnetic field effect are plotted using streamlines, isotherms, average Nusselt number and fluid temperature, irreversibility components, Bejan number and sensitivity in this section and discussed in details to predict the behaviors of fluid flow, heat transferring rate, irreversibility, and sensitivity inside the channel. The following parametric ranges are considered to accomplish the numerical simulations (Table 4).
Table 4.
Ranges of physical parameters.
| Parameter | Parametric ranges |
|---|---|
| Re | 10 to 200 |
| Ha | 0 to 100 |
| Da | 10−4 to 10−1 |
| ϕ | 0 %–5 % |
| Liop | 0.10L–0.25L |
| Pr | 6.2 |
| Gr | 104 |
| ε | 0.5 |
4.1. Effect of Re on streamlines and isotherms
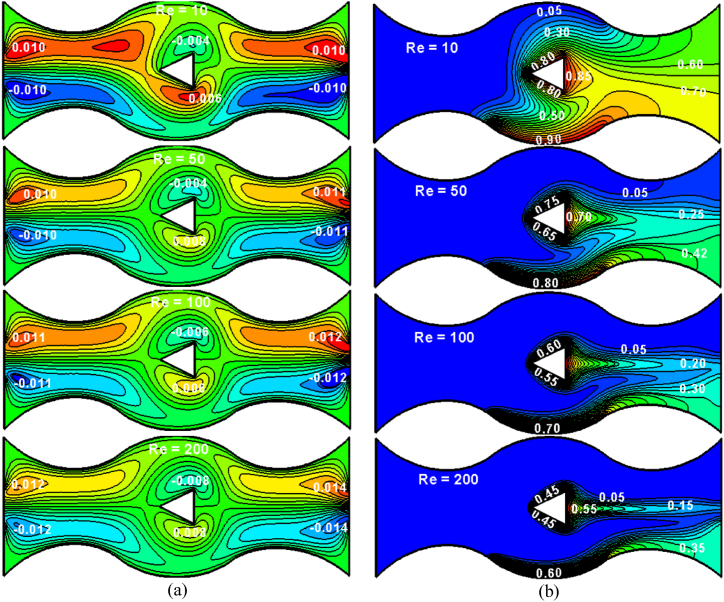
Fig. 5 illustrates streamlines and temperature contours inside the porous channel for varying of Re while values of other controlling parameters are kept fixed (Pr = 6.2, Ha = 25, ϕ = 1 %, Da = 10−2, Liop = 0.10L). In Fig. 5a, flow circulation is developed for simultaneous effect of fluid inertia through inlet port and buoyancy flow due to applied thermal condition. Two pairs of long incomplete streamlines circulations are also developed near the inlet-outlet ports of the channel where flow strength is found higher near the outlet port compared to the inlet port. It is worth to note that streamlines circulations near bottom part of the inlet-outlet ports are rotated in clockwise direction whereas the circulations near top part of the inlet-outlet ports rotated in counter clockwise direction. In addition, a pair of strong vortices is visualized beside the heated triangular obstacle because fluid flow bifurcated there due to presence of obstacle's corner edges. Moreover, streamlines circulation near the top corner edge of the triangular obstacle is rotated in clockwise direction while circulation near the bottom corner edge is in counter clockwise direction. The numerical values of the flow velocity within the channel indicates that flow velocity is gradually accelerated with rising of Reynolds number and streamlines are intensified. Because, higher Re leads to more fluid inertia inside the wavy channel. Streamlines patterns are found slightly changes with higher Re compared to lower Re which are also reflected with the change in color zone and circulations of streamlines inside the channel. In addition, streamlines patterns are also found depends on wavy shaped of the channel. Consequently, it can be concluded that higher Re accelerates flow rate through the channel and affects the streamlines circulations. On the other hand, Fig. 5b represents the distribution of temperature contours inside the channel. In Fig. 5b at Re = 10, it is clearly appeared that temperature contours are emanated from the bottom heated wavy-surface and also heated triangular hollow cylinder and then blows over the obstacle in the direction of flow. The dense isotherm contours pack is also noticed around the heated triangular cylinder and near the bottom wavy surface due to high temperature there. When Re increases to 50, fluid inertia increases results isotherms suppressed toward the obstacle and bottom surface and also gets additional blowing force toward the outlet port. As a results, isotherms pack concentrated around the triangular obstacle and also near the bottom hot surface. After that, at higher Re (>50), isotherms are found more intensified around the triangular obstacle as well as near the bottom hot surface. The isotherms in the direction of flow are also found squeezing towards the rear port of the channel. From the temperature plotting in Fig. 5b, it is clear that high temperature around the obstacle and near the bottom surface decreases with each increment in Re and isotherms pack is extruded near bottom wavy surface and rounding the obstacle. This is an indicative of the of convective mode of heat transfer over other modes with increasing Re. Moreover, reduced thermal boundary layer with increasing Re signifies more convective effects and heat transferring rate as well.
Fig. 5.
(a) Streamlines and (b) isotherms plotting for different Re.
4.2. Effect of Ha on streamlines and isotherms
Fig. 6 delineates the effect of Ha on streamlines and isotherms distributions inside the wavy porous channel at certain values of other parameters (Pr = 6.2, Re = 50, ϕ = 1 %, Da = 10−2, Liop = 0.10L). As the development of flow circulation and thermal field has been discussed in details in section 4.1, only the variation of magnetic field effect, which is characterized by Ha, on streamlines and isotherms plotting are illustrated in this section. In Fig. 6a, at Ha = 0, it is evident that strong flow circulation is generated with highest magnitude. After that, while magnetic field effect is imposed at strength Ha = 25, very small change is found in streamlines distribution with lower flow strength compared to the earlier case (Ha = 0). Thereafter, when Ha increases to 50, streamlines distribution and color regime are minutely changed but the flow velocity is found decreased. Then at Ha = 100, significant change is visualized in streamlines distribution especially near the triangular edges and also inlet-outlet ports of the channel. In addition, lowest flow velocity is recorded at highest Ha. The reason behind its that the complex interaction of magnetic force with fluid inertia and buoyancy force produces Lorentz force and hence increased Lorentz force due to increase in magnetic field effect suppresses the fluid motion within the channel. Thus, it is reflected that higher magnetic field strength has a significant impact on the formation of flow circulation and its strength as well. Besides, Fig. 6b represents the distribution of temperature contours for different values of Ha. In Fig. 6b, in absence of magnetic field, isotherms are densely distributed around the triangular obstacle and also close to the bottom surface. In addition, lower temperature is noticed there compared to the effect of higher Ha. The pattern of isotherms remains all most same for increasing Ha which is an indication of lower heat transferring from the heat sources of the channel. These are expected as the interaction of magnetic field force with fluid inertia and buoyancy flow produces more heat and reduces temperature difference from the flowing fluid to heat sources.
Fig. 6.
(a) Streamlines and (b) isotherms plotting for different Ha.
4.3. Effect of ϕ on streamlines and isotherms
The effect of nanoparticle concentrations (ϕ) on streamlines and isotherms plotting is depicted in Fig. 7. In Fig. 7a, the pattern of streamlines is found relatively similar for amalgamating nanoparticles of 1 % volume fraction in base fluid which signifies that concentration level of nanoparticles (vol.1 %) has no significant effect on the formation of streamlines circulations. It is also observed that flow velocity in base fluid is greater than that of nanofluid containing 1 % volume fraction. Further increasing in concentration of nanoparticles in base fluid up to 5 %, the patterns of streamlines remain same for all cases but flow velocity considerably diminishes. The reason of this phenomena is that effective density and viscosity of nanofluid is increased with higher concentration of nanoparticles results generates clogging force within the channel and retards fluid motion inside the channel. In Fig. 7b, isotherms are found emanating from the hot surfaces in base fluid due to combined effects of fluid inertia and thermal condition. Observing the figures, it is evident that temperature contours maintained similar pattern with different temperatures when 1 % nanoparticles are amalgamated in base fluid water. Further increasing in concentration of nanoparticles in base fluid up to 5 %, no considerable changes are visualized in isotherms distributions. Moreover, high temperature near the bottom surface and obstacle is found reduced which signifies that higher concentration of nanoparticles increases the heat transferring rate significantly.
Fig. 7.
(a) Streamlines and (b) isotherms plotting for different ϕ.
4.4. Effect of Da on streamlines and isotherms
Fig. 8 illustrates the influence of Darcy number on the fluid flow and temperature field by plotting streamlines and isotherms inside the porous wavy channel. As detail formation of streamlines circulation has been presented in section 4.1, the changes in streamlines distribution due to varying of Darcy value are discussed in this section. As Darcy number is directly correlated to the magnitude of permeability of the porous medium results lower Darcy number implies a lower permeability that causes a lower fluid flow through the porous channel and vice versa. In Fig. 8a, at low Darcy number (Da = 10−4) convective flow circulation is developed within the channel resulting of fluid inertia, buoyancy flow and also effect of certain values of parameters. After that, Da increases to 10−3, a noticeable change is observed in streamlines distribution and the flow magnitude is accelerated rapidly. The numerical results of the flow magnitude shows that the maximum flow velocity is 0.005 at Da = 10−4 and it increases to 0.010 at Da = 10−3. It is necessary to note that circulation cells in each vortex near the inlet-out ports are remarkably affected while Da increase to 10−3. The fact behind its that with increasing Da causes a higher channel permeability and also reduces the pore resistance of the wavy porous channel. Thus, lowest fluid flow velocity is recorded at lowest value of Darcy number whereas relative highest flow velocity is found at highest value of Darcy number. Further increase in Darcy values up to 10−1, strong convective flow circulation is occurred and significant change is visualized in streamlines distribution and its intensity. These are consistent to the physics of Darcy number. Besides this, the corresponding temperature contours distributions are delineated in Fig. 8b where the pattern of isotherms are found almost similar and maintained different temperature for increasing values of Darcy number. The high temperature near the triangular obstacle and bottom surface is found decreasing with each increment in Darcy value which signifies a higher convective heat transferring rate for increasing Darcy number. These are expected as the higher Da causes a higher convective flow rate through the wavy channel.
Fig. 8.
(a) Streamlines and (b) isotherms plotting for different Da.
4.5. Effect of length of inlet-outlet (Liop)on streamlines and isotherms
Fig. 9 demonstrates the flow circulation and thermal field due to change in length of inlet-outlet ports. As the formation of flow circulation via streamlines plotting has been discussed in the earlier section in details, the influence of inlet-outlet ports length on streamlines plotting are presented in this section. The streamlines plotting in Fig. 9a confirm that flow circulation and its pattern are significantly affected with increase in length of inlet-outlet ports. The incomplete circulations near inlet-outlet ports are restructured with strong complete circulations at higher length of inlet-outlet ports. The vortices beside the triangular obstacle also changed in size and strengths. The numerical results of flow velocity indicates that flow strength remarkably increases with each increment in inlet-outlet ports length. In order to understand the effect of inlet-outlet ports length on flow field more precisely, the flow velocity is calculated at different length of inlet-outlet ports and the maximum flow velocity are found as 0.012, 0.017, 0.022 and 0.030 respectively at Liop = 0.10L, 0.15L, 0.20L and 0.25L. These are expected as the higher length of inlet-outlet ports allows more fluid flow with more fluid inertia through the inlet port results causes more fluid flows inside the channel. In addition, it is noticed that all eddies and streamlines circulations are increase in size for higher length of inlet-outlet ports. On the other hand, in Fig. 9b, the isotherms distributions are found remarkably influenced with each increment in length of inlet-outlet ports. It is apparent that emanated isotherms are compressed toward the bottom surface and outlet port and also around the triangular obstacle with increasing length of inlet-outlet ports which is prominent at maximum length of inlet-outlet ports. The fact behind its that higher length of inlet-outlet ports causes higher flow rate through the channel. Moreover, thermal boundary layer is found reducing with the higher length of inlet-outlet ports and high temperature close to the obstacle and bottom surface becomes lower.
Fig. 9.
(a) Streamlines and (b) isotherms plotting for different length of inlet-outlet ports (Liop).
4.6. Effect of Re and Ha on local entropy generation
Fig. 10 shows the local entropy generation for various values of Re and Ha, while keeping other controlling parameters fixed. The local entropy generation is occurred resulting of heat transfer, fluid friction and magnetic irreversibilities while magnetic field effect is imposed. In all diagrams of Fig. 10a, isentropic contours are found near the heated bottom wavy surface and triangular obstacle resulting of temperature gradient there. At Re = 10, generated entropy contours are distributed in upward direction, around the cylinder and also rear part of the wavy channel. After that, isentropic contours are found compressing toward the bottom arc surface and rear directions of the channel while Re increases to 50 resulting of higher fluid inertia and heat transferring rate with increased Reynolds number. Further increase in Reynolds number, more inertia force is induced that leads to more fluid flow with higher strength through the channel results local entropy contours are found more squeezed in its blow-path. Besides this, Fig. 10b shows magnetic field effect on local entropy generation which is visualized by the distributions of isentropic contours and change in color regions. In absence of magnetic field effect, generated local entropy contours blows toward the outlet port of the channel. While magnetic field effect is imposed, local entropy production increases. With the increasing magnetic field effect from Ha = 25 to Ha = 100, more entropy is generated and considerable changes are found in both isentropic contours distribution and its color zones inside the wavy channel. It is happened due to the increased magnetic irreversibility with the effect of higher magnetic field strength.
Fig. 10.
Local entropy generation for different (a) Re and (b)Ha.
4.7. Effect of ϕ and Da on local entropy generation
Local entropy generation due to variation of volume fraction, Darcy number and inlet-outlet port's lengths is depicted in Fig. 11a–c. In Fig. 11, isentropic contours are developed around the triangular obstacle and near bottom arc surface due to imposed thermal conditions there and blows toward the rear port of the wavy porous channel resulting of inertia force due to Re (=100). From Fig. 11a, it is obvious that no significant change is occurred in local entropy generation with the addition of Al2O3-nanoparticles (vol.1 %) in base fluid water. Moreover, the pattern of local entropy generation distribution remains similar even volume fraction of nanoparticles increases up to 5 % in base fluid water. It is also found that magnitude of entropy generation reduces with the amalgamation of nanoparticles which is prominent at higher volume fraction of nanoparticles. Besides in Fig. 11b, variation of local entropy generation is depicted for Darcy number. From these figures, it is evident that isentropic lines distribution minutely influenced at higher values of Darcy number. The most significant changes in local entropy generation are illustrated in Fig. 11c due to change in length of inlet-outlet ports while other physical parameters are kept fixed. It is observed that isentropic lines are effectively squeezed with increasing length of inlet-outlet ports and the color zones of entropy production are changed remarkably and hence the strength of entropy generation promptly increased as well. The fact behind it is that more fluid enters with higher velocity with an increment in length of inlet-outlet ports results causes a strong local entropy generation.
Fig. 11.
Local entropy generation for different (a) ϕ and (b) Da. Fig. 11. Local entropy generation for different (c) Liop.
4.8. Effect of Re, Ha, ϕ, Da and Liop on heat transferring and average temperature
Fig. 12 demonstrates average Nusselt number () and temperature () profiles to evaluate heat transferring rate for different values of physical parameters. The solid and dash lines in Fig. 12 correspond to the values of and profiles in presence of heated triangular obstacle and in absence of triangular obstacle, respectively. In Fig. 12 (a, c, e, g), heat transferring rate increases monotonically with increasing Reynolds number. Accordingly, Reynolds number causes a substantial enhancement in heat transfer rate. The physics behind its that greater Re causes greater fluid inertia, and higher flow circulation within the wavy channel that leads to increase heat transfer rate. In addition, from Fig. 12a it is noticed that the profiles of considerably decreases with increasing magnetic field strength. Thus, Hartmann number causes decrement in heat transfer rate. The numerical results in Fig. 12a confirm 158.06 % increment in heat transfer rate for varying Reynolds number from 10 to 200 at Ha = 0 in absence of triangular obstacle and it reduces to 121.84 % at Ha = 100. When a heated triangular cylinder is placed at the center of the wavy channel, the increasing rate of heat transfer expedites to 242.18 % and 202.62 % respectively at Ha = 0 and Ha = 100. Thus, 84.12 % and 80.78 % more heat transfer rate are recorded for varying Re (at Ha = 0 and Ha = 100) in presence of triangular obstacle within the channel. In Fig. 12c, heat transfer rate significantly increases as the concentration of nanoparticles in base fluid rises. This phenomenon is happened as the suspended nanoparticles increases the thermal conductivity of nanofluid results causes heat transfer enhancement with the addition of nanoparticles. Moreover, heat transfer rate increases by 163.57 % for the same variation of Re (at Ha = 25) in base fluid water while triangular obstacle is absent and it becomes 171.90 % and 201.13 % respectively with the addition of 1 % and 5 % nanoparticles in base fluid. These increasing rates of heat transfer are rapidly augmented with the presence of triangular obstacles inside the channel which are found 254.34 %, 263.98 % and 299.93 % respectively (all percentage has been calculated comparing results for ϕ = 0 %, base fluid up to ϕ = 5 %, nanofluids). In Fig. 12e, heat transfer rate increases monotonically for rising Darcy number as higher Darcy value causes higher fluid flow rate within the channel which accelerates heat transmission from heated surface to the flowing fluid inside the channel. From Fig. 12e, it is also estimated that heat transfer rate increases by 212.01 % at Da = 10−4, 264.12 % at Da = 10−2 and 286.61 % at Da = 10−1 for the variation of Re (10–200) in presence of triangular obstacle (all percentage has been calculated comparing results for Da = 10−4 up to Da = 10−1). Fig. 12g delineates the sustainable improvement in heat transferring rate due to increasing length of inlet-outlet ports. Moreover, heat transferring rate is found increases by 157.57 %, 195.29 %, 225.52 % and 251.02 % respectively at Liop = 0.10L, 0.15L, 0.20L and 0.25L in absence of triangular heated obstacle while Re varies from 10 to 200 which are reached to 244.80 %, 297.53 %, 339.38 % and 374.77 % for the same variation of Reynolds number and length of inlet-outlet ports in presence of triangular obstacle (all percentage has been calculated comparing results for Liop = 0.10L, up to Liop = 0.25L at Ha = 25, ϕ = 1 %, Da = 10−2). The physics behind it that more fluid flow occurs inside the channel with higher length of inlet-outlet ports results more heat transfer occurred inside the channel. Besides the average temperature profiles are presented in Fig. 12b, d, f, h. In all diagrams, it is noticed that temperature profiles swiftly turn down for increasing Re from 10 to 50 and then consistently decline for each increment of Re from 50 to 200. In Fig. 12(b–d), it is also perceived that average temperature increases due to effect of magnetic field and presence of nanoparticles at different concentrations in base fluid. These are expected as the imposed magnetic field effect generates more heat within the fluid domain due to interaction of magnetic force, fluid inertia and buoyancy force, and suspended nanoparticles in base fluid increases heat storage capability results fluid temperature becomes higher with higher concentration of nanoparticles. In Fig. 12 (f, h), it is also found that the fluid temperature considerably decreases with greater values of Da and Liop as higher Da and Liop both causes higher flow rate within the channel. In all diagrams of Fig. 12, the solid and dashed profiles of average Nusselt number ensures that the presence of triangular obstacles substantially improves the heat transfer rate,
Fig. 12.
(a–f). Average Nusselt number (left) and temperature (right) for different Re, Ha, ϕ, Da and Liop.
4.9. Effect of Re, Ha, ϕ, Da and (Liop) on entropy generation components
The irreversibility components relating to the fluid friction, heat transfer and magnetic field effects for varying of physical parameters are plotted in Fig. 13, Fig. 14, Fig. 15. In these figures, it is apparent that fluid friction irreversibly and magnetic irreversibility both are decreased with the increasing values of Re (10–200) while heat transfer irreversibility increases expeditiously with the same variation of Re. The decreasing rate of fluid friction and magnetic irreversibilities and increasing rate of heat transfer irreversibility are found notable for a range of 10–50 compare to the range of 50–200. In addition, heat transfer irreversibility is found diminishing with the effect of Ha whereas the fluid friction irreversibly and magnetic irreversibility both are boosting up remarkably with higher Hartmann number (as seen in Fig. 13, Fig. 14, Fig. 15a). The fact of these phenomena is that higher Ha causes a reduction in heat flow rate from source to flowing fluid and the magnetic irreversibility component is correlated to the squared function of Ha and magnetic force also increases fluid frictional irreversibly (detailed discussion has been provided in the earlier sections). Besides in Fig. 13b–15b, it is noticed that the irreversibility components are found getting higher values with higher concentration of nanoparticles as the presence of nanoparticles in base fluid increases the effective thermal conductivity and density of base fluid. On the contrary, the effects of Darcy number and length of inlet-outlet ports on different irreversibility components are respectively visualized in Fig.13c-d-15c-d. Here, the corresponding fluid friction, heat transfer and magnetic irreversibility are found increased with increase in Da and Liop. These are consistent to the impact of the variations of Da and Liop. In all diagrams of Figs. 13–15, the comparative results presented by solid and dashed lines ensure that the presence of triangular obstacle improves the average entropy generation components for varying of all physical parameters.
Fig. 13.
Plotting of fluid friction irreversibility for different Re, Ha, ϕ, Da and Liop.
Fig. 14.
Plotting of heat transfer irreversibility for different Re, Ha, ϕ, Da and Liop.
Fig. 15.
Plotting of magnetic field irreversibility for different Re, Ha, ϕ, Da and Liop.
4.10. Effect of Re, Ha, ϕ, Da and length of inlet-outlet ports (Liop) on Bejan number
Fig. 16 represents Bejan number profiles for varying of Re, Ha, ϕ, Da and Liop, respectively. From Fig. 16a-d, it is perceived that Bejan number profiles declines significantly for increasing of Reynolds number in both cases while triangular obstacle is placed or not. It is also found that values of Bejan number are relatively higher at lower range of Re than higher range. In addition, Bejan number gets lower values for each increment in Ha, ϕ, Da and Liop which are reflected in Fig. 16a–d. Moreover, the comparirative results of Bejan number are presented by solid and dashed lines which signifies that the presence of triangular obstacle has a significant effect to improve Bejan number. From Fig. 16, it can also be remarked that Bejan number becomes highest at lower values of Re along with lowest Ha (Ha = 0), volume fraction (base fluid), permeability and length of inlet-outlet ports whereas opposite behaviours are noticed for higher range of Re along with highest values of Ha, ϕ, permeability and length of inlet-outlet ports. Accordingly, entropy generation domination due to fluid friction irreversibility is prominent at higher range of Reynolds number (Re ≥ 50) for all Ha, ϕ, permeability and length of inlet-outlet ports in absence of triangular obstacle which remains same for all Ha, ϕ and length of inlet-outlet ports in presences of triangular obstacle whereas heat transfer irreversibility becomes predominant for lower values of mentioned parameters for Re ≤ 50.
Fig. 16.
Plotting of Bejan number (Be) for different Re, Ha, ϕ, Da and Liop.
4.11. Response surface methodology
In this section, statistical response surface methodology (RSM) is implemented to optimize the model performance by describing response function () involving parameters Re, Ha, Da and ϕ (Liop = 0.10L). RSM is a useful method to analyze multivariable problems when the interest-generating responses are influenced simultaneously with the variation in input factors [61]. Among the different RSM models, second-order RSM model is an effective procedure for approximating the response function involving all linear, square and interactional factors.
The quadratic polynomial model is written as follows:
| (14) |
Here represents output of the model analysis, is the intercept, is the -th regression coefficient of linear terms, is the -th regression coefficient of quadratic terms and is the -th and -th regression coefficient of interaction terms. In this study, relevant input factors are considered as Re, Ha, Da and ϕ to evaluate as the response function (y). In 1992, Box and Wilson [62] first proposed the central composite design (CCD) to develop second order RSM model. In this study, the input factors Re, Ha, Da and ϕ are ranged as 10 ≤ Re ≤ 100, 0 ≤ Ha ≤100, 0.0001 ≤ Da ≤0.10 and 0 % ≤ ϕ ≤ 5 % at Pr = 6.2 and Liop = 0.10L. The statistical RSM based on CCD has 30 runs consisting 6 center, 8 axial and 16 factorials. Table 5 represents the codded levels with real values of the input factors for CCD process and Table 6 shows the run setups consisting real values of input factor and response function.
Table 5.
Design variables for CCD.
| Input Factor | Level |
||
|---|---|---|---|
| −1 (Low) | 0 (average) | +1 (high) | |
| Re | 10 | 105 | 200 |
| Ha | 0 | 50 | 100 |
| Da | 0.0001 | 0.05005 | 0.1 |
| ϕ | 0.0 | 0.025 | 0.05 |
Table 6.
Values of input factor and response function.
| Std | Runs | Space type | Real values of input factors |
Response |
|||
|---|---|---|---|---|---|---|---|
| Re | Ha | Da | ϕ | Nuav | |||
| 11 | 1 | Factorial | 10 | 100 | 0.0001 | 0.05 | 5.9407 |
| 24 | 2 | Axial | 105 | 50 | 0.05005 | 0.05 | 24.2661 |
| 13 | 3 | Factorial | 10 | 0 | 0.1 | 0.05 | 8.0879 |
| 10 | 4 | Factorial | 200 | 0 | 0.0001 | 0.05 | 33.1374 |
| 29 | 5 | Center | 105 | 50 | 0.05005 | 0.025 | 22.7962 |
| 22 | 6 | Axial | 105 | 50 | 0.1 | 0.025 | 25.2086 |
| 26 | 7 | Center | 105 | 50 | 0.05005 | 0.025 | 22.7962 |
| 6 | 8 | Factorial | 200 | 0 | 0.1 | 0 | 30.4645 |
| 8 | 9 | Factorial | 200 | 100 | 0.1 | 0 | 25.5415 |
| 9 | 10 | Factorial | 10 | 0 | 0.0001 | 0.05 | 5.9647 |
| 27 | 11 | Center | 105 | 50 | 0.05005 | 0.025 | 22.7962 |
| 14 | 12 | Factorial | 200 | 0 | 0.1 | 0.05 | 33.0937 |
| 7 | 13 | Factorial | 10 | 100 | 0.1 | 0 | 8.8396 |
| 4 | 14 | Factorial | 200 | 100 | 0.0001 | 0 | 26.9011 |
| 25 | 15 | Center | 105 | 50 | 0.05005 | 0.025 | 22.7962 |
| 16 | 16 | Factorial | 200 | 100 | 0.1 | 0.05 | 32.536 |
| 19 | 17 | Axial | 105 | 0 | 0.05005 | 0.025 | 23.2654 |
| 3 | 18 | Factorial | 10 | 100 | 0.0001 | 0 | 5.8842 |
| 20 | 19 | Axial | 105 | 100 | 0.05005 | 0.025 | 21.57 |
| 30 | 20 | Center | 105 | 50 | 0.05005 | 0.025 | 22.7962 |
| 18 | 21 | Axial | 200 | 50 | 0.05005 | 0.025 | 28.0734 |
| 21 | 22 | Axial | 105 | 50 | 0.0001 | 0.025 | 22.6508 |
| 28 | 23 | Center | 105 | 50 | 0.05005 | 0.025 | 22.7962 |
| 5 | 24 | Factorial | 10 | 0 | 0.1 | 0 | 11.1528 |
| 2 | 25 | Factorial | 200 | 0 | 0.0001 | 0 | 29.0743 |
| 23 | 26 | Axial | 105 | 50 | 0.05005 | 0 | 21.0334 |
| 1 | 27 | Factorial | 10 | 0 | 0.0001 | 0 | 6.0445 |
| 12 | 28 | Factorial | 200 | 100 | 0.0001 | 0.05 | 30.813 |
| 17 | 29 | Axial | 10 | 50 | 0.05005 | 0.025 | 8.4309 |
| 15 | 30 | Factorial | 10 | 100 | 0.1 | 0.05 | 9.56024 |
The numerical findings of statistical analysis of the present model are displayed in Table 7. The maximum number of independent terms are presented by the degree of freedom (DOF). Here, SS (sum of the squares) signifies over all variation due to several cases, the values of MSS (mean sum of squares) is 173.32 which is significant, model F-value of 263.40 implies the model is significant. A very low value of p (topically <0.05) indicates the model terms are significant. Consequently, based on the values of SS, MSS, F-values and p-values, considered model is statistically significant. Moreover, Adeq precision ratio (signal to noise) of 48.705 (>4) indicates a significant signal, suggesting that present model can effectively navigate the design space. In addition, the testing procedure of the statistical analysis suggests that high the value of R2 (99.59 %), demonstrates the model is appropriate for computing response function . Furthermore, the predicted R2 (97.34 %) is in reasonable agreement with the adjusted R2 (99.22 %) (difference is less than 2 %) for computing response function , indicates that the model sufficiently matches the experimental data. A very low value of Lack-of-Fit is required for an appropriate model which is also found in Table 7. The following general models can be developed by using RSM to build effective relationship between response function () and input factors (Re, Ha, Da and ϕ).
| (14) |
Where , , , , , , , , , , , , , , are the coefficient of best fitted regression model for this RSM model. Table 8 displayed the estimated coefficients of Eq. (14) which are estimated as coded units. It is worth to note that the significant model terms which have low p-values are considered to set an appropriate regression equation where non-significant terms are disregarded. Thus, based on low p-values (<0.0500) and regression coefficients in Table 8, the effective mathematical relationship between response-function () and input factors (Re, Ha, Da and ϕ) can be summarized as:
| (15) |
Table 7.
Analysis of variance (ANOVA) for Nuav while Liop = 0.10L.
| Source | DOF | SS | MSS | F-values | p-Values | Comment |
|---|---|---|---|---|---|---|
| Model | 14 | 2426.46 | 173.32 | 263.40 | <0.0001 | Significant |
| Re | 1 | 2216.21 | 2216.21 | 3368.13 | <0.0001 | |
| Ha | 1 | 8.96 | 8.96 | 13.62 | 0.0022 | |
| Da | 1 | 18.15 | 18.15 | 27.58 | <0.0001 | |
| f | 1 | 18.94 | 18.94 | 28.78 | <0.0001 | |
| Re*Ha | 1 | 5.01 | 5.01 | 7.61 | 0.0146 | |
| Re*Da | 1 | 9.15 | 9.15 | 13.90 | 0.0020 | |
| Re*ϕ | 1 | 24.92 | 24.92 | 37.87 | <0.0001 | |
| Ha*Da | 1 | 0.1680 | 0.1680 | 0.2554 | 0.6207 | |
| Ha* ϕ | 1 | 4.14 | 4.14 | 6.29 | 0.0241 | |
| Da* ϕ | 1 | 0.0282 | 0.0282 | 0.0429 | 0.8386 | |
| Re2 | 1 | 52.98 | 52.98 | 80.51 | <0.0001 | |
| Ha2 | 1 | 0.3289 | 0.3289 | 0.4999 | 0.4904 | |
| Da2 | 1 | 3.46 | 3.46 | 5.26 | 0.0367 | |
| ϕ2 | 1 | 0.0400 | 0.0400 | 0.0608 | 0.8086 | |
| Residual | 15 | 9.87 | 0.6580 | |||
| Lack of Fit | 10 | 9.87 | 0.9870 | Insignificant | ||
| Pure Error | 5 | 0.0000 | 0.0000 | |||
| Cor Total | 29 | 2436.33 |
Here R2 = 99.59 %, Adjusted R2 = 99.22 %, Predicted R2 = 97.34 % and Adeq precision = 48.705.
Table 8.
Projected regression coefficient for Nuav while Liop = 0.10L.
| coefficient | ||||||||
|---|---|---|---|---|---|---|---|---|
| values | 22.7851 | 11.096 | −0.705 | 1.004 | 1.025 | −0.559 | −0.756 | 1.247 |
| p-values | <0.0001 | 0.0022 | <0.0001 | <0.0001 | 0.0146 | 0.0020 | <0.0001 | |
| coefficient | ||||||||
| values | −0.1024 | −0.508 | −0.042 | −4.521 | −0.356 | 1.155 | 0.124 | |
| p-values | 0.6207 | 0.0241 | 0.8386 | <0.0001 | 0.4904 | 0.0367 | 0.8086 |
4.11.1. Response surface analysis
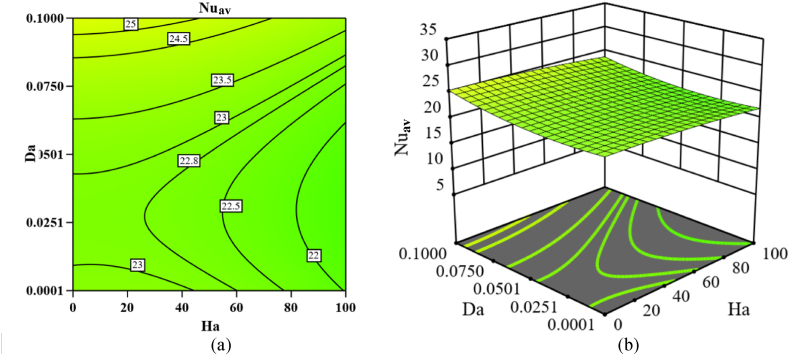
Fig. 17, Fig. 18, Fig. 19, Fig. 20, Fig. 21, Fig. 22 represent 2D and 3D contour plotting of response function estimated using RSM to examine the impacts of effective parameters on the response function . In Fig. 17a, the interaction of Re and Ha indicates considerable augmentation in due to simultaneous increasing Re and decreasing Ha while other factors are remained constant. The color topology and numeric values guarantee that become highest at Re = 200 and Ha = 0 whereas it becomes lowest at Re = 10 and Ha = 100. For better understanding of performance, the effect of input parameter on response is shown in a 3D surface plot (Fig. 17b). This 3D surface plot shows similar phenomenon of response function due to input parameters Re and Ha. The variation of due to combined effect of Re and ϕ is shown in Fig. 18. In 2D and 3D graphical presentations, it is evident that the heat transfer rate progressively increases while Re and ϕ are increased simultaneously. It is also noticed in 2D and 3D surface plots that highest is occurred at highest values of Re and ϕ whereas lowest for lowest values of Re and ϕ which are expected correlation among the response and input factors Re and ϕ. A similar 2D and 3D surface plots are shown in Fig. 19 to visualize the impact of increasing Re and Da on the enchantment of response . The response function is found reaches to its maximum values at Re 200 and Da = 0.10 and its minimum value at Re 10 and Da = 0.0001. The 2D and 3D surface plots in Fig. 20, Fig. 21 respectively suggest that the response function is an increasing function of input factors ϕ and Da and decreasing function of Ha results increases with increasing ϕ and Da, and decreasing Ha simultaneously and hence highest is found at higher ϕ and Da with lower Ha = 0. In addition, the interaction of Da and ϕ in 2D surface plot (Fig. 22a) shows that increases gradually with increasing ϕ and Da. Similar trend is also reflected in 3D surface plot as shown in Fig. 22b.
Fig. 17.
(a). Fig. 17 (b).
Fig. 18.
(a)Fig. 18 (b).
Fig. 19.
(a). Fig. 19 (b).
Fig. 20.
(a). Fig. 20 (b).
Fig. 21.
(a). Fig. 21 (b).
Fig. 22.
(a). Fig. 22 (b).
4.11.2. Sensitivity study
Sensitivity study plays an important role in perfection of numerical simulations, is a technique to determine how much impact of input factors on its output as a response function. The most influence parameters can be selected using sensitivity study results to rank their influence on the output function [63]. The output variables for sensitivity study relating to the specific effective parameters are determined by the partial differentiation of the response function in Eq. (15) and which are:
| (16) |
| (17) |
| (18) |
| (19) |
The results of sensitivity analysis for response function () due to coded values of dimensionless parameters (Re, Ha, Da and ϕ) are calculated using equations (16), (17), (18), (19)) and presented in Table 9 and in Fig. 23. These values are computed considering Re at a level of 1 (200), Da at a level of 1 (0.10) and ϕ at a level of 1 (0.05 or 5 %) while Ha at a level of −1, 0 and 1 (0, 50 and 100). In addition, the length of bar diagram in Fig. 23 shows the rating of sensitivity. It is worth to note that positive sensitivity signifies that rising input factor causes increment in response function whereas negative sensitivity reflects that response function declines with rising input factors. This proves that the input factors Re, Da and ϕ have a positive impact on the response function and hence must be increased with simultaneous rising Re, Da and ϕ. Moreover, the sensitivity study ensures that is more sensitive to Re and ϕ. On the other hand, it is noticed that Ha has a negative impact on the response function as negative sensitivity occurred for Ha results average Nusselt number declines with increasing Ha.
Table 9.
Sensitivity study of .
| 1 | −1 | 1 | 1 | 3.104 | −1.771 | 2.558 | 2.780 |
| 0 | 2.545 | −1.771 | 2.558 | 2.272 | |||
| 1 | 1.986 | −1.771 | 2.558 | 1.764 |
Fig. 23.
Sensitivity of at Re = 1, Da = 1, ϕ = 1.
5. Conclusions
In this study, the behaviors of fluid flow, heat transferring rate and irreversibility of mixed convection nanofluid flow in a porous wavy channel with heated triangular obstacle is numerically investigated by implementing FEM. The channel is permeated an external magnetic field. Sensitivity study and response surface analysis are also performed using RSM to examine the effectiveness of the model and input parameters on the thermal performance. 2D and 3D surface plots are added to visualize the crucial impacts of Re, Ha, Da and ϕ on heat transferring rate, . Detailed parametric discussions are presented using obtain numerical results. The important findings based on the results and discussion are compiled as follows:
-
•
Increased Reynolds number accelerates flow velocity and heat transfer rate. Heat transfer irreversibility is remarkably increased with rising Reynolds number but Bejan number is declined.
-
•
Flow velocity and enhancement of heat transfer gradually are decreased for magnetic field effect. Heat transfer enhancement rate decreases by 36.22 % while Ha changes from 0 to 100. Fluid friction and magnetic irreversibilities are increased with higher Ha while reverse phenomena are occurred in heat transfer irreversibility and Bejan number.
-
•
Thermal performance substantially improves with increasing nanoparticle volume fraction in base fluid. 45.59 % more heat transfer increment is recorded in nanofluid (vol.5 %) in presence of triangular obstacle. Moreover, entropy generation tools are considerably increased while Bejan number is declined for increasing nanoparticle volume fraction.
-
•
Fluid flow velocity is found accelerated with the increasing length of inlet-outlet ports and optimum thermal performance is recorded at higher length of inlet-outlet ports. Numerically, 15.01 %, 26.63 % and 36.52 % more heat transfer enhancement are recorded respectively at Liop = 0.15L, 0.20L and 0.25L. In addition, heat transfer irreversibility is appreciably increased while Bejan number gets lower values for increasing length of inlet-outlet ports.
-
•
The increase in Darcy number significantly accelerates flow and heat transferring rate. Increasing rate of heat transfer is found 74.60 % more at Da = 10−1 compared to heat transfer at Da = 10−4 (Re = 10–200). Besides, irreversibility components are augmented with increased Darcy number whereas Bejan number is decreased.
-
•
RSM based 2D and 3D surface plots present improved visualization of heat transfer process.
-
•
Highest heat transfer rate is recorded at Re = 200 and ϕ = 5 % vol, Re = 200 and Da = 0.1 and Re = 200 and Ha = 0 which are confirmed in 2D and 3D surface plots.
-
•
The sensitivity study confirms that heat transfer rate is more sensitive to the impact of Re and ϕ compared to Da and Ha. Positive sensitivity is reported for Re, ϕ and Da while negative sensitivity for Ha.
-
•
Heat transferring and irreversibility components as well as Bejan number influenced with the presence of triangular obstacle for all physical parameters.
-
•
At high Reynolds numbers, heat transfer irreversibility becomes more significant in entropy generation compared to fluid fiction irreversibility, regardless for all Ha, Da, ϕ and length of inlet-outlet ports.
-
•
Sensitivity study and response surface analysis based on RSM ensure improved performance of the model studied.
6. Future research directions
The present study has been conducted numerically to introduce sophisticated applications of improved design and significant parametric ranges in nanofluid to improve the thermal performance of thermal equipment. Since authors have accomplished the study numerically, experimental work is required for better perfection of the simulated findings.
Funding
This research work did not receive any financial support from any organization.
CRediT authorship contribution statement
Rowsanara Akhter: Writing – review & editing, Writing – original draft, Visualization, Validation, Methodology, Formal analysis, Conceptualization. Mohammad Mokaddes Ali: Writing – review & editing, Writing – original draft, Visualization, Validation, Supervision, Resources, Methodology, Conceptualization. M.A. Alim: Writing – review & editing, Writing – original draft, Formal analysis, Conceptualization.
Declaration of competing interest
The authors declare that they have no competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- 1.Fereidoon A., Saedodin S., Hemmat Esfe M., Noroozi M.J. Evaluation of mixed convection in inclined square lid-driven cavity filled with Al2O3/water nano-fluid. Engineering Applications of Computational Fluid Mechanics. 2013;7(1):55–65. [Google Scholar]
- 2.Selimefendigil F., Öztop H.F. Mixed convection in a partially heated triangular cavity filled with nanofluid having a partially flexible wall and internal heat generation. J. Taiwan Inst. Chem. Eng. 2017;70:168–178. [Google Scholar]
- 3.Nithyadevi N., Begum A.S., Oztop H.F., Al-Salem K. Effects of inclination angle and non-uniform heating on mixed convection of a nanofluid filled porous enclosure with active mid-horizontal moving. Int. J. Heat Mass Tran. 2017;104:1217–1228. [Google Scholar]
- 4.Motlagh S.Y., Soltanipour H. Natural convection of Al2O3-water nanofluid in an inclined cavity using Buongiorno's two-phase model. Int. J. Therm. Sci. 2017;111:310–320. [Google Scholar]
- 5.Lam P.A.K., Prakash K.A. A numerical study on natural convection and entropy generation in a porous enclosure with heat sources. Int. J. Heat Mass Tran. 2014;69:390–407. [Google Scholar]
- 6.Hemmat Esfe M., Saedodin S., Hasani Malekshah E., Babaie A., Rostamian H. Mixed convection inside lid-driven cavities filled with nanofluids: a comprehensive review. J. Therm. Anal. Calorim. 2019;135:813–859. [Google Scholar]
- 7.Aljabair S., Ekaid A.L., Ibrahim S.H., Alesbe I. Mixed convection in sinusoidal lid driven cavity with non-uniform temperature distribution on the wall utilizing nanofluid. Heliyon. 2021;7(5) doi: 10.1016/j.heliyon.2021.e06907. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Zaydan M., Riahi M., Mebarek-Oudina F., Sehaqui R. Mixed convection in a two-sided lid-driven square cavity filled with different types of nanoparticles: a comparative study assuming nanoparticles with different shapes. Fluid Dynam. Mater. Process. 2021;17:789–818. [Google Scholar]
- 9.Alsabery A.I., Vaezi M., Tayebi T., Hashim I., Ghalambaz M., Chamkha A.J. Nanofluid mixed convection inside wavy cavity with heat source: a non-homogeneous study. Case Stud. Therm. Eng. 2022;34 [Google Scholar]
- 10.Khan Z.H., Khan W.A., Qasim M., Du M. Double‐diffusive flow in a porous right‐angle trapezoidal enclosure with constant heat flux. Math. Methods Appl. Sci. 2022;45(6):3305–3317. [Google Scholar]
- 11.Saleh M.S., Mekroussi S., Kherris S., Zebbar D., Belghar N. A numerical investigation of the effect of sinusoidal temperature on mixed convection flow in a cavity filled with a nanofluid with moving vertical walls. Heat Transfer. 2023;52(1):7–27. [Google Scholar]
- 12.Azizian R., Doroodchi E., McKrell T., Buongiorno J., Hu L.W., Moghtaderi B. Effect of magnetic field on laminar convective heat transfer of magnetite nanofluids. Int. J. Heat Mass Tran. 2014;68:94–109. [Google Scholar]
- 13.Mejri I., Mahmoudi A., Abbassi M.A., Omri A. Magnetic field effect on entropy generation in a nanofluid-filled enclosure with sinusoidal heating on both side walls. Powder Technol. 2014;266:340–353. [Google Scholar]
- 14.Elshehabey H.M., Ahmed S.E. MHD mixed convection in a lid-driven cavity filled by a nanofluid with sinusoidal temperature distribution on the both vertical walls using Buongiorno's nanofluid model. Int. J. Heat Mass Tran. 2015;88:181–202. [Google Scholar]
- 15.Cho C.C. Influence of magnetic field on natural convection and entropy generation in Cu–water nanofluid-filled cavity with wavy surfaces. Int. J. Heat Mass Tran. 2016;101:637–647. [Google Scholar]
- 16.Afrand M., Sina N., Teimouri H., Mazaheri A., Safaei M.R., Esfe M.H.…Toghraie D. Effect of magnetic field on free convection in inclined cylindrical annulus containing molten potassium. International Journal of Applied Mechanics. 2015;7(4) [Google Scholar]
- 17.Sarlak R., Yousefzadeh S., Akbari O.A., Toghraie D., Sarlak S. The investigation of simultaneous heat transfer of water/Al2O3 nanofluid in a close enclosure by applying homogeneous magnetic field. Int. J. Mech. Sci. 2017;133:674–688. [Google Scholar]
- 18.Talebizadehsardari P., Shahsavar A., Toghraie D., Barnoon P. An experimental investigation for study the rheological behavior of water–carbon nanotube/magnetite nanofluid subjected to a magnetic field. Phys. Stat. Mech. Appl. 2019;534 [Google Scholar]
- 19.Malik S., Nayak A.K. MHD convection and entropy generation of nanofluid in a porous enclosure with sinusoidal heating. Int. J. Heat Mass Tran. 2017;111:329–345. [Google Scholar]
- 20.Akhter R., Ali M.M., Alim M.A. Hydromagnetic natural convection heat transfer in a partially heated enclosure filled with porous medium saturated by nanofluid. Int. J. Algorithm. Comput. Math. 2019;5:1–27. [Google Scholar]
- 21.Ibrahim M., Saeed T., Bani F.R., Sedeh S.N., Chu Y.M., Toghraie D. Two-phase analysis of heat transfer and entropy generation of water-based magnetite nanofluid flow in a circular microtube with twisted porous blocks under a uniform magnetic field. Powder Technol. 2021;384:522–541. [Google Scholar]
- 22.Al-Kouz W., Abderrahmane A., Shamshuddin M.D., Younis O., Mohammed S., Bég O.A., Toghraie D. Heat transfer and entropy generation analysis of water-Fe3O4/CNT hybrid magnetic nanofluid flow in a trapezoidal wavy enclosure containing porous media with the Galerkin finite element method. The European Physical Journal Plus. 2021;136(11):1–23. [Google Scholar]
- 23.Geridonmez B.P., Oztop H.F. Mixed convection heat transfer in a lid-driven cavity under the effect of a partial magnetic field. Heat Tran. Eng. 2021;42(10):875–887. [Google Scholar]
- 24.Shehata A.I., Dawood M.M.K., Amer M., William M.A. Enhancement of mixed convection in a lid driven enclosure based on magnetic field presence with nanofluid. Adv. Mech. Eng. 2023;15(2) [Google Scholar]
- 25.Gangawane K.M., Manikandan B. Laminar natural convection characteristics in an enclosure with heated hexagonal block for non-Newtonian power law fluids. Chin. J. Chem. Eng. 2017;25(5):555–571. [Google Scholar]
- 26.Ali M.M., Alim M.A., Akhter R., Ahmed S.S. MHD natural convection flow of CuO/water nanofluid in a differentially heated hexagonal enclosure with a tilted square block. Int. J. Algorithm. Comput. Math. 2017;3:1047–1069. [Google Scholar]
- 27.Mehmood K., Hussain S., Sagheer M. Mixed convection in alumina-water nanofluid filled lid-driven square cavity with an isothermally heated square blockage inside with magnetic field effect: Introduction. Int. J. Heat Mass Tran. 2017;109:397–409. [Google Scholar]
- 28.Hussain S., Ahmed S.E., Akbar T. Entropy generation analysis in MHD mixed convection of hybrid nanofluid in an open cavity with a horizontal channel containing an adiabatic obstacle. Int. J. Heat Mass Tran. 2017;114:1054–1066. [Google Scholar]
- 29.Al-Rashed A.A., Shahsavar A., Akbari M., Toghraie D., Akbari M., Afrand M. Finite volume simulation of mixed convection in an inclined lid-driven cavity filled with nanofluids: effects of a hot elliptical centric cylinder, cavity angle and volume fraction of nanoparticles. Phys. Stat. Mech. Appl. 2019;527 [Google Scholar]
- 30.Al-Farhany K., Alomari M.A., Faisal A.E. Magnetohydrodynamics mixed convection effects on the open enclosure in a horizontal channel heated partially from the bottom. IOP Conf. Ser. Mater. Sci. Eng. 2020, June;870(1) IOP Publishing. [Google Scholar]
- 31.Ali M.M., Akhter R., Alim M.A. Performance of flow and heat transfer analysis of mixed convection in Casson fluid filled lid driven cavity including solid obstacle with magnetic impact. SN Appl. Sci. 2021;3:1–15. [Google Scholar]
- 32.Ali M.M., Akhter R., Alim M.A., Miah M.M. Magnetic-mixed convection in nanofluid-filled cavity containing baffles and rotating hollow-cylinders with roughness components. Math. Probl Eng. 2022;2022 [Google Scholar]
- 33.Singh N., Khandelwal M.K. Linear stability perspective on mixed convection flow of nanofluids in a differentially heated vertical channel. Int. Commun. Heat Mass Tran. 2022;134 [Google Scholar]
- 34.Islam S., Islam M.M., Rana B.M.J., Islam M.S., Reza-E-Rabbi S., Hossain M.S., Rahman M.M. Numerical investigation with sensitivity study of MHD mixed convective hexagonal heat exchanger using TiO2–H2O nanofluid. Results in Engineering. 2023;18 [Google Scholar]
- 35.Khan Z.H., Khan W.A., Qasim M., Alharbi S.O., Hamid M., Du M. Hybrid nanofluid flow around a triangular-shaped obstacle inside a split lid-driven trapezoidal cavity. Eur. Phys. J. Spec. Top. 2022;231(13):2749–2759. [Google Scholar]
- 36.Khan Z.H., Yang Z., Khan W.A., Sheremet M.A., Wu W. Computational investigation of magnetohydrodynamic convective flow in a trapezoidal cavity with multiple obstacles via finite element analysis. Therm. Sci. Eng. Prog. 2024;50 [Google Scholar]
- 37.Khan Z.H., Khan W.A., Yang Z., Hamid M., Qasim M. Mixed convection flow in a channel with a dimpled section and adiabatic cylindrical obstacle under the influence of magnetic and Joule effects. Results Phys. 2023;49 [Google Scholar]
- 38.Song Z.J., Khan Z.H., Ahmad R., Khan W.A., Wei Y. Thermal analysis of ferromagnetic nanofluid flow in a channel over a dimpled cavity. J. Magn. Magn Mater. 2023;573 [Google Scholar]
- 39.Bentoto W., Zaydan M., Alaoui H.A., Essaghir E., Sehaqui R. Mixed convection of a MHD oscillatory laminar flow of a nanofluid (Gold-Kerosene oil) in a vertical channel. Statistics, Optimization & Information Computing. 2023;11(1):55–69. [Google Scholar]
- 40.Hussien A.A.A., Hussein A.K. Mixed convection in an open lid-driven cavity attached with a rectangular channel. AIP Conf. Proc. 2023, March;2651 [Google Scholar]
- 41.Abbaszadeh M., Ababaei A., Abbasian Arani A.A., Abbasi Sharifabadi A. MHD forced convection and entropy generation of CuO-water nanofluid in a microchannel considering slip velocity and temperature jump. J. Braz. Soc. Mech. Sci. Eng. 2017;39:775–790. [Google Scholar]
- 42.Anandalakshmi R., Basak T. Analysis of energy management via entropy generation approach during natural convection in porous rhombic enclosures. Chem. Eng. Sci. 2012;79:75–93. [Google Scholar]
- 43.Cho C.C. Effects of porous medium and wavy surface on heat transfer and entropy generation of Cu-water nanofluid natural convection in square cavity containing partially-heated surface. Int. Commun. Heat Mass Tran. 2020;119 [Google Scholar]
- 44.Das S., Jana R.N., Makinde O.D. Mixed convective magnetohydrodynamic flow in a vertical channel filled with nanofluids. Engineering Science and Technology, an International Journal. 2015;18(2):244–255. [Google Scholar]
- 45.Maiga S.E.B., Palm S.J., Nguyen C.T., Roy G., Galanis N. Heat transfer enhancement by using nanofluids in forced convection flows. Int. J. Heat Fluid Flow. 2005;26(4):530–546. [Google Scholar]
- 46.Maxwell J.C. vol. 1. Clarendon Press; Oxford: 1873. (A Treatise on Electricity and Magnetism). [Google Scholar]
- 47.Cui W., Shen Z., Yang J., Wu S. Modified prediction model for thermal conductivity of spherical nanoparticle suspensions (nanofluids) by introducing static and dynamic mechanisms. Ind. Eng. Chem. Res. 2014;53(46):18071–18080. [Google Scholar]
- 48.Nasrin R., Alim M.A., Chamkha A.J. Buoyancy-driven heat transfer of water–Al2O3 nanofluid in a closed chamber: effects of solid volume fraction, Prandtl number and aspect ratio. Int. J. Heat Mass Tran. 2012;55(25–26):7355–7365. [Google Scholar]
- 49.Zienkiewicz O.C., Taylor R.L. fourth ed. McGraw-Hill; 1991. The Finite Element Method. [Google Scholar]
- 50.Reddy J.N. McGraw-Hill; New-York: 1993. An Introduction to Finite Element Analysis. [Google Scholar]
- 51.Bunch J.R., Hopcroft J.E. Triangular factorization and inversion by fast matrix multiplication. Math. Comput. 1974;28(125):231–236. [Google Scholar]
- 52.Zeinkiewicz O.C., Taylor R.L., Too J.M. Reduced integration technique in general analysis of plates and shells. Int. J. Numer. Methods Eng. 1971;3:275–290. [Google Scholar]
- 53.Taylor C., Hood P. A numerical solution of the Navier-Stokes equations using the finite element technique. Comput. Fluids. 1973;1:73–89. [Google Scholar]
- 54.Dechaumphai P. second ed. Chulalongkorn University Press; Bangkok: 1999. Finite Element Method in Engineering. [Google Scholar]
- 55.Akhter R., Ali M.M., Billah M.M., Uddin M.N. Hybrid-nanofluid mixed convection in square cavity subjected to oriented magnetic field and multiple rotating rough cylinders. Results in Engineering. 2023;18 [Google Scholar]
- 56.Iwatsu R., Hyun J.M., Kuwahara K. Mixed convection in a driven cavity with a stable vertical temperature gradient. Int. J. Heat Mass Tran. 1993;36(6):1601–1608. [Google Scholar]
- 57.Sheremet M.A., Pop I. Mixed convection in a lid-driven square cavity filled by a nanofluid: Buongiorno's mathematical model. Appl. Math. Comput. 2015;266:792–808. [Google Scholar]
- 58.Malleswaran A., Sivasankaran S. A numerical simulation on MHD mixed convection in a lid-driven cavity with corner heaters. J. Appl. Fluid Mech. 2015;9(1):311–319. [Google Scholar]
- 59.Laouira H., Mebarek‐Oudina F., Hussein A.K., Kolsi L., Merah A., Younis O. Heat transfer inside a horizontal channel with an open trapezoidal enclosure subjected to a heat source of different lengths. Heat Tran. Asian Res. 2020;49(1):406–423. [Google Scholar]
- 60.Krane R., Jessee J. Some detailed field measurements for a natural convection flow in a vertical square enclosure. Proceedings of the First ASME-JSME Thermal Engineering Joint Conference, 1983. 1983;1:323–329. [Google Scholar]
- 61.Montgomery D.C. John wiley & sons; 2017. Design and Analysis of Experiments. [Google Scholar]
- 62.Box G.E., Wilson K.B. Breakthroughs in Statistics: Methodology and Distribution. Springer New York; New York, NY: 1992. On the experimental attainment of optimum conditions; pp. 270–310. [Google Scholar]
- 63.Campolongo F., Braddock R. The use of graph theory in the sensitivity analysis of the model output: a second order screening method. Reliab. Eng. Syst. Saf. 1999;64(1):1–12. [Google Scholar]