On the origin of Lake Malawi cichlid species: A population genetic analysis of divergence

Abstract

The cichlid fishes of Lake Malawi are famously diverse. However, phylogenetic and population genetic studies of their history have been difficult because of the great amount of genetic variation that is shared between species. We apply a recently developed method for fitting the “isolation with migration” divergence model to a data set of specially designed compound loci to develop portraits of cichlid species divergence. Outgroup sequences from a cichlid from Lake Tanganyika permit model parameter estimates in units of years and effective population sizes. Estimated speciation times range from 1,000 to 17,000 years for species in the genus Tropheops. These exceptionally recent dates suggest that Malawi cichlids as a group experience a very active and dynamic diversification process. Current effective population size estimates range form 2,000 to near 40,000, and to >120,000 for estimates of ancestral population sizes. It appears that very recent speciation and gene flow are among the reasons why it has been difficult to discern the phylogenetic history of Malawi cichlids.

The extraordinary number of species of cichlid fishes (Teleostei: Cichlidae) of the African great lakes Malawi, Tanganyika and Victoria are a classic evolutionary mystery, and biologists have long wondered how so many species could have evolved over short time periods. In the case of Lake Malawi, the estimated geological age of the lake is 4-5 million years, but the lake probably dried out at times, perhaps as recently as 570,000 years ago (1).

A complicating factor for phylogenetic and population genetic investigations of the Lake Malawi cichlids is that species tend to share much of their genetic variation, which has been seen with allozymes (2-4), mitochondrial haplotype data (5, 6), microsatellite or short-tandem repeat (STR) loci (7), and nuclear DNA sequences (8). The fact of shared variation means that neither allelic nor haplotypic data from individual loci (or from a small number of loci) can provide phylogenetic resolution (5-7), and in recent years investigators have had to turn to using very large numbers of amplified fragment-length polymorphism markers to estimate phylogenies (9, 10).

Shared genetic variation also raises important, albeit difficult, population genetic questions. The extensive sharing of genetic variation by closely related cichlid species has traditionally been attributed to the simple persistence of variation that was present in ancestral species (5, 6, 9). However, shared variation and low levels of divergence between cichlid species have also been interpreted as evidence of ongoing low levels of gene flow (11). Direct evidence of interspecies gene flow comes from hybrids and hybrid populations (12-14). If cichlid species are diverging in the presence of gene flow, then it is also necessary to consider the role that natural selection plays, either in driving divergence and/or limiting gene flow.

Hey et al. (8) developed the use of compound loci that have a low-mutation rate component and a high-mutation rate component and then analyzed the data by using a recently developed parameter-rich model of population divergence (Fig. 1). Here we extend this approach to a larger set of loci and species. In addition, we include dated outgroup sequences that allow us to estimate the actual times and effective population sizes associated with speciation events.

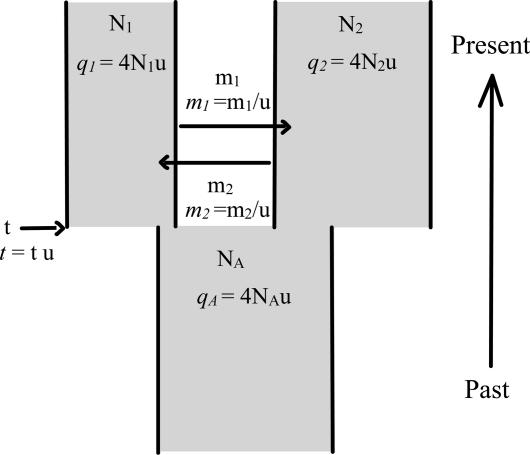
Fig. 1.

The IM model is depicted with two parameter sets. The basic demographic parameters are constant effective population sizes (N₁, N₂ and N_A), gene flow rates per gene copy per generation (m₁ and m₂), and the time of population splitting at t generations in the past. The parameters in the second set (in italics) are all scaled by the neutral mutation rate u, and these parameters are actually used in the model fitting.

Methods

Species and Sample Collection. Species of the genus Tropheops are members of the large group of rock-dwelling (mbuna) cichlids (15). Ten individuals from each of three species of Tropheops were sampled from two locations: Otter point, on the northwestern part of the Nankumba peninsula in the southern end of the lake, and Harbor Island, a small island in the mouth of Monkey Bay on the eastern side of the Nankumba peninsula. The two sites are separated by ≈18 km along the shore. The protocols for sample collection are given in ref. 8.

HapSTR Loci. We developed a set of compound loci, each including a STR or microsatellite and the flanking unique sequence that may include multiple polymorphic sites. Inspired by a similar approach in which loci that have a SNP and an adjacent STR are referred to as SNPSTRs (16), we call the these loci HapSTRs (8). A given HapSTR haplotype contains a sequence and the number of repeats in the linked STR allele. Six HapSTR loci were developed, and haplotypes were determined from both chromosomes of each of the sampled individuals by following the methods of Hey et al. (8). Oligonucleotide primer information is given in Tables 3 and 4, which are published as supporting information on the PNAS web site.

Outgroup Sequencing. To estimate the times of species formation, an outgroup with a known common ancestry time is required. Phylogenetic studies suggest that the Malawi and Victorian cichlids derive from the tribe Haplochromini, which arose in Lake Tanganyika (17). Unlike the relatively shallow radiations of Lakes Malawi and Victoria, the much older Lake Tanganyika has cichlids of 12 tribes (including eight endemic tribes) (18, 19). Given that Lake Tanganyika has a long history of cichlid diversification and that it is the likely source for the radiations in Lakes Malawi and Tanganyika, we elected to use as an outgroup a representative of tribe Eretmodini, the oldest monophyletic, endemic clade of Tanganyikan cichlids (20, 21). The oldest parts of Lake Tanganyika have been estimated to be 9-12 million years old (22), and we used a date of 7 million years for the common ancestor of the outgroup and Tropheops (23). A representative of Eretmodus cyanostictus was obtained from a Lake Tanganyika fish importer, and DNA sequences were obtained from those regions corresponding to the sequence portions of the HapSTR loci. A nested PCR method was used to increase accuracy in PCR amplification. The product of the initial round of PCR, which includes the flanking sequence and the STR segment, was used as template for a secondary PCR that amplified only the flanking DNA sequences. The primer pairs for these nested PCR are given in Tables 3 and 4. Final PCR products were used directly as templates for bidirectional sequencing on a Li-Cor (Lincoln, NE) 4200 sequencer using dye-labeled M13 forward and reverse primers. PCR amplification and DNA sequencing for one locus, PZMSAT2, were not successful for the outgroup.

Divergence Model and Parameter Estimation. The data for six loci, for pairs of species and populations, were analyzed by using a computer program that estimates the posterior probability density for parameters in the “isolation with migration” (IM) model. This version of the IM model has six demographic parameters (24), each scaled by the overall neutral mutation rate (Fig. 1). For the current multilocus study, we implemented migration in a new way, with each locus having its own pair of migration rate parameters. The new migration method is a straightforward extension of the original procedure.

For each of the six HapSTR loci, there are two mutation-rate scalar parameters (one for the sequence portion and one for the STR portion) included in the model (25). The procedure, as implemented in a computer program, is to run a Markov chain simulation with appropriate Metropolis-Hastings update criteria as specified under the model (24, 25). Each simulation is based on a user-specified uniform prior distribution of parameter ranges. The settings for the prior distributions were empirically obtained after preliminary runs using higher upper bounds on parameter distributions (26). Ideally, the posterior distribution that is obtained should fall completely within the prior distribution. However, for some parameters, it was often found that posterior distributions included a peak at a low or intermediate location in the distribution with a flat, or nearly flat, tail over an extended range of higher parameter values. In these cases, it was necessary to choose a prior upper bound that did not include the flat tail of the distribution.

Over the course of the run, for each of the model parameters, a marginal density was recorded as a histogram with 1,000 equally sized bins. The distributions were smoothed by averaging over adjacent points, and the peaks of the resulting distributions were taken as estimates of the parameters (24). Depending on the data, the duration of the simulation needed to ensure that the marginal density estimates are based on a good sample of effectively independent values can be very long. In the case of the six-locus HapSTR data sets, the autocorrelation of parameter values over the course of individual runs of the computer program proved to be quite high, indicating that it would be difficult to achieve large samples of effectively independent observations. To improve mixing of the Markov chain and shorten the time needed for simulation, runs were done by using multiple Markov chains under the Metropolis coupling protocol (25-27). As many as 110 coupled Markov chains were used for some species pairs, with each multichain simulation lasting several days or weeks. Runs were monitored by using estimates of the effective sample size based on the measured autocorrelation of parameter values over the course of the run. Each analysis was repeated three or more times to ensure that similar density estimates were obtained.

Parameter Scale Conversion. Estimates of the mutation rates for those loci for which outgroup sequence is available can be used to convert model parameter estimates, which are scaled by mutation rate, to more interpretable scales. Each HapSTR locus requires two mutation rate scalar parameters, one for the STR and one for the flanking sequence, for which the probability density is estimated along with the demographic parameters under the IM model (8, 25). The procedure for converting parameter estimates, for the case when outgroup data are available for only a subset of the loci that are in the IM analysis, requires two values: a quantity, X, which is the geometric mean of the mutation rate scalar estimates that are generated by the IM analysis, for just those loci for which mutation rate estimates are available based on the outgroup; and a quantity, U, which is the geometric mean of the mutation rate per year, for those same loci based on the outgroup divergence and known time of common ancestry. With these values, the scale of the estimate of the divergence time parameter, which is in units of mutations (i.e., t = tu), can be converted to one of years by t̂ = tX/U. If G is an estimate of the number of generations per year, then an estimate of the number of generations since speciation is t̂/G. Similarly, if 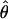is an estimate of 4Nu for one of the populations, then an estimate of the effective population size, N, can be obtained as 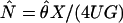. In captivity, mbuna cichlids can reach reproductive age in less than a year; however, the generation time of mbuna cichlids in the wild is not known. Different authors have used times of 1, 2, or 3 years (6, 14, 28), and here we have used 2 years.

For most population genetic purposes, the relevant scale for migration is the population migration rate, 2Nm, or the effective number of migrants per generation. To show the probability density of the migration parameters on this scale, the migration rate parameters were rescaled by multiplying by the corresponding estimate of 2Nu from the same analysis (e.g., for the m₁ (= m₁/u) parameter, multiply the estimated values by values by ).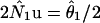

Results

Outgroup Divergence. A summary of polymorphism among the Tropheops species and between these and the outgroup E. cyanostictus is given in Table 1. Each locus revealed a large number of STR alleles and at least one polymorphic site in the flanking sequence. At each HapSTR locus (including sequences together with the linked STR alleles) we observed a large amount of haplotype sharing among species, as expected (8). Assuming that the time of common ancestry with the outgroup was 7 million years ago, the mean substitution rate among these loci (not weighted by sequence length) is 1.1 × 10^-9 substitutions per site per year, roughly one-third of the estimated rates for noncoding nuclear DNA in mammals and birds (29, 30).

Table 1. Polymorphism summaries.

Locus	Flanking sequence	No. of STR alleles	No. of SNPs	No. of haplotypes	Divergence	Source
UNH001	278	29	1	2	3.4	40
U66815	192	31	2	3	1.5	41
U66814	634	19	2	3	9	41
U14396	453	26	4	6	14.5	42
DXTUCA3	417	23	1	2	4.5	U94850*
PZMSAT2	648	29	4	4	—	43

Shown is the length of the flanking sequence in base pairs, the number of distinct STR alleles observed across three species of Tropheops, the number of SNPs observed in the flanking sequence in the entire sample, the number of distinct sequence (not including STRs) haplotypes across the entire sample, and the average number of sequence differences (divergence) between the outgroup, E. cyanostictus, and Tropheops over the full length of the flanking sequence. —, not determined.

^*GenBank accession number.

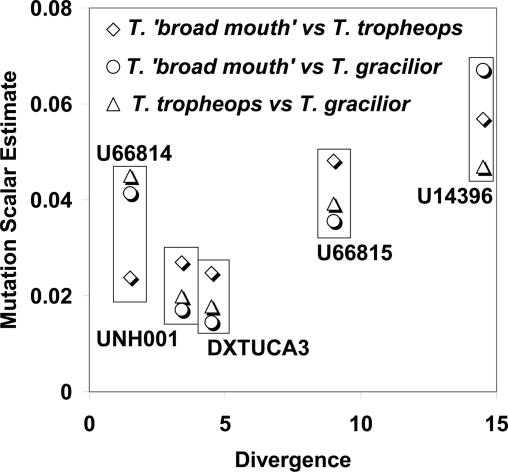
To check whether levels of polymorphism are consistent with a neutral model, we compared the estimated mutation rate scalars for the sequence portions of the six loci with the amount of divergence observed between Tropheops and Eretmodus, the outgroup. Although only five loci could be included, there is a general positive relationship between the two independent assessments of the mutation rate (Fig. 2) as expected under the neutral model. It is important to note that these scalars have no units and that their magnitude is constrained under the implementation of the model such that the product of all 12 mutation rate scalars (including those for six loci, each with sequenced portions and STR portions) in a given run of the program have a product of one (25). The scalar values are all <1 because they were estimated in runs in which the scalars for the STR regions were also estimated, and these scalar values all have values >1 (i.e., the STR regions are estimated to have high mutation rates, as expected, relative to the flanking sequence).

Fig. 2.

Mutation rate scalars, estimated in separate analyses for each species pair, are plotted against the average amount of sequence divergence between Tropheops and Eretmodus. The scalars are the estimated mutation rates relative to other loci (including STRs that are not shown) obtained by fitting the data to the IM model. Points are grouped for each of the five loci for which divergence could be measured.

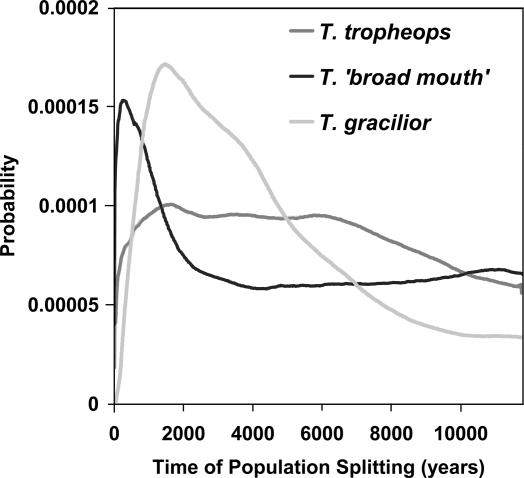
IM Model Analysis. We have sampled six populations (two each of three species); however, our method of analysis can only accommodate pairs of populations. Therefore, the first step is to consider the pairs of populations of each species and to ask how recently they have diverged. Fig. 3 shows the posterior probability density estimates of the time of divergence between the two populations for each species pair. For Tropheops“broad mouth,” the estimated time of splitting is at or near zero, suggesting that the two populations are recently derived from a single population. For Tropheops tropheops, the shape of the distribution is fairly flat, with considerable density near zero. In contrast, Tropheops gracilior shows a clear peak at ≈2,200 years and an estimated density at zero years that is itself zero. On the basis of these results, we have pooled the two populations of T. tropheops and the two populations of T. broad mouth and kept the two populations of T. gracilior separate for the remainder of the analyses.

Fig. 3.

Probability estimates for the time of population splitting for two populations of each species. The time scale as been converted to years, based on mutation rate scalar estimates and outgroup divergence, as described in Methods.

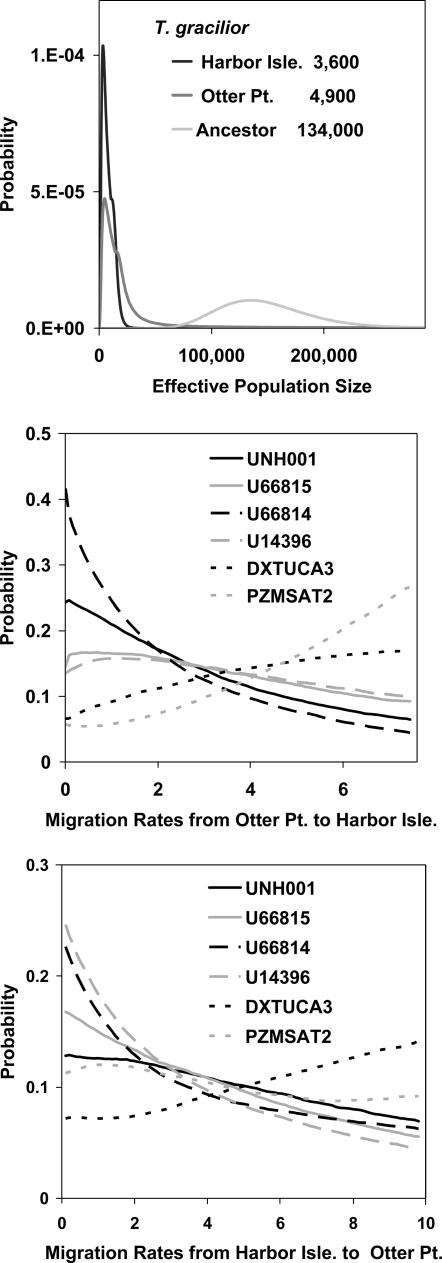
Fig. 4 shows the marginal probability densities for the population size and migration rate parameters in the contrast between the two populations of T. gracilior. The population size parameter scales are numbers of individuals. The scale for migration is different from the other parameters because it is set by an estimate obtained from the analysis of one of those other parameters (see Methods). For migration, that scale is in units of 2Nm, the population migration rate, where N is the effective size of the receiving population and m is the probability of migration per gene copy per generation. The population size parameters are the most clearly resolved, with posterior distributions that have a clear single peak and bounds that fall within the prior distribution. It is noteworthy that the ancestral population is estimated to have been much larger than either of the present day populations. The densities for the migration rates vary among loci; however, only one locus has a curve that might be interpreted as clear evidence of nonzero gene flow (Fig. 4 Middle, PZMSAT2). The densities for the migration rate parameters are fairly flat, indicating that the data contain little information on migration within the framework of the IM model. Because the model assumes a constant rate of gene flow after the population separation, it is expected that migration rates between populations that have recently split, as appears to be the case, will be hard to estimate.

Fig. 4.

Results for two populations of T. gracilior. Probability density estimates are shown for effective population sizes (Top) and migration rates from Otter Point to Harbor Isle (Middle) and from Harbor Isle to Otter Point (Bottom). The estimates for effective population size are given in the key in Top. The scales for migration rates are set by using these estimates of the effective population size (see Methods).

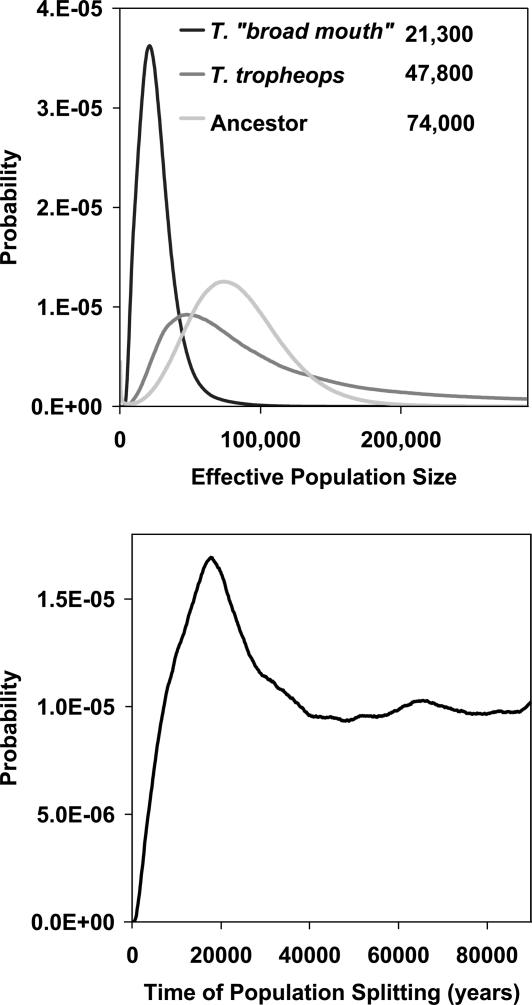
Findings similar to those for the two populations of T. gracilior are also found in the other analyses between these populations and the pooled samples of T. tropheops and T. broad mouth. The parameter estimates for these pairs of populations are given in Table 2, and, because each population occurs in multiple contrasts, several recurrent patterns emerge (1). The effective population sizes for the two T. gracilior populations are smaller, with values ranging from 1,500 to 4,900, than those for T. tropheops and T. broad mouth, which have values ranging form 15,400 to 19,000 (2). The size of the estimated ancestral populations are considerably larger than the current populations, with estimates in the range of 120,900-128,200 (3). The estimates of population splitting time are all very recent and range from 1,000 to 2,300 years.

Table 2. Model parameter estimates in pairs of populations.

Population 1	Population 2	N1	N2	NA	t	2 N1m1>0	2 N2m2>0
T. gracilior (HI)	T. gracilior (OP)	3,600	4,900	134,000	2,300	PZMSAT2	—
T. tropheops	T. gracilior (HI)	18,800	2,000	120,900	1,600	—	U14396, PZMSAT2, DXTUCA3
T. tropheops	T. gracilior (OP)	19,100	2,500	121,800	1,100	—	U66815, U14396, PZMSAT2
T. broad mouth	T. gracilior (HI)	15,400	1,500	128,200	1,000	—	U14396, DXTUCA3, PZMSAT2,
T. broad mouth	T. gracilior (OP)	21,500	3,200	122,100	1,800	—	—
T. broad mouth	T. tropheops	21,300	47,800	74,000	17,700	—	—

Shown are the species population pairs, with the location of the T. gracilior population shown in parentheses: HI, Harbor Isle; OP, Otter Point. The loci that showed a migration parameter curve indicating a low probability of zero migration and a high probability of non-zero migration are listed under 2 N₁m₁ > 0 and 2 N₂m₂ > 0. —, No loci suggested a high probability of non-zero migration.

For the migration parameters, all of the analyses that include T. gracilior generated curves that are like those in Fig. 4, in which most curves lack a clear peak and loci vary in whether or not they suggest a history of gene flow. Table 2 lists those loci that showed a lower probability of zero gene flow relative to the probability at the high end of the distribution. Depending on the contrast, evidence of gene flow was found primarily in the direction of gene flow into the T. gracilior population, as opposed to the reverse.

The analyses of T. broad mouth and T. tropheops yielded a different picture (Fig. 5), with an estimated divergence time of 17,700 years and estimated effective population sizes several fold larger (21,300 for T. broad mouth and 47,800 for T. tropheops) than estimated in the contrasts with T. gracilior. The size of the ancestral population in this case (74,000), although larger than for the descendant species, was not as large as the estimates from the contrasts with T. gracilior. The migration rate density estimates were nearly all very flat in this analysis (data not shown), so we do not have a clear picture of how much gene flow may have been occuring in this case.

Fig. 5.

Results for T. broad mouth and T. tropheops. Probability density estimates are shown for effective population sizes (Upper) and estimated time of divergence (Lower). The estimates for effective population size are given in the key.

Discussion

Because of low levels of divergence and widespread shared variation among Malawi cichlids, questions about their phylogenetic history have been difficult. The difficulty has generally been described as a consequence of very recent divergence (6, 31, 32). However, in the absence of phylogenetic assessments, it is difficult to know to what degree recent speciation is the cause of shared variation and the lack of phylogenetic resolution. Another possible cause for the lack of phylogenetic resolution in genetic data, in addition to recent speciation, is that genetic variation is shared because of gene exchange. Disentangling the relative contributions of variation shared since ancestry and shared via gene flow is necessary for estimating the time since speciation and for assessing speciation models. Recently, with the use of very large numbers of amplified fragment-length polymorphisms (9, 10), it has become possible to estimate phylogenetic trees. However, it is difficult to model the substitution process for these markers and therefore it is difficult to use amplified fragment-length polymorphisms to estimate the time since speciation events.

The protocol used here, in which compound loci with high- and low-mutation-rate components are analyzed under a parameter-rich model of population divergence, was designed to address questions about cichlid speciation (8). In brief, it appears that very recent speciation and gene flow contribute to the shared variation and, therefore, to the difficulty of assessing phylogenetic history.

To answer the first question (How long ago did Malawi cichlid species undergo speciation?), our estimate for Tropheops species varies from a low range of 1,000-2,300 years in the case of T. gracilior and an estimate of 17,200 years for the divergence of T. broad mouth and T. tropheops. If such recent dates apply to Malawi cichlids in general, then they suggest that the Malawi cichlid flock is extraordinarily evolutionarily dynamic. To get a feel for the implications, consider that if we take 10,000 years as the typical time between speciation events and apply it to all of the ≈230 formally described species of mbuna, then a new mbuna species arises every 43 years (i.e., 10,000 years/230 species). If the radiation of mbuna began 1,000,000 years ago with such high rates of speciation, then there may have been >23,000 different species over the years, assuming a steady state process of speciation and extinction. This estimate does not count the >270 other described, non-mbuna, species of Malawi cichlids. These calculations are simplistic and do not take into account the very high level of species uncertainty that is associated with various aspects of research on Malawi cichlids; however, they do suggest an exceptional rate of diversification.

Could these estimated dates be quite wrong, such that the true values actually lie outside the range of the peaks of the estimated probability densities? Because of the many parameters and the complexity of the method, this question is difficult address. There are at least two general sets of assumptions of which to be aware. First, we have imposed a model of population splitting that assumes that an ancestral population that persisted long before the moment of splitting. Complex population dynamics within the ancestral population are not accounted for and neither is gene exchange with other populations not included within a particular analysis. It is likely that the very large estimated sizes of the ancestral populations (Table 2) are the result of gene exchange between ancestral populations. This kind of gene exchange cannot be estimated by the method, although it will elevate the amount of variation in ancestral populations and lead to inflated effective population size estimates. However, it is not clear that such processes would lead to biased estimates of the divergence time of populations.

When considering the appropriateness of the model, the analyses of T. broad mouth and T. tropheops raised some interesting problems. All of the individual population pair analyses that involved T. gracilior required long runs of the computer program and large numbers of coupled Markov chains; however, in the case of T. broad mouth and T. tropheops it was necessary to run 110 chains, each distinguished by very slight differences in heating level (27). This high number of chains were required to break up the very strong autocorrelation of parameter values (primarily t) that arose in the course of the simulation and to obtain enough effectively independent measurements so as to have some confidence in the final distribution. Furthermore, the final distribution for t, although showing a peak at 17,700 years, is very broad and appears to plateau to the right of the peak. It is possible that part of the reason for this broad distribution is that each species actually included samples from two separate populations, although the separation of these individual pairs of populations appeared to have been quite recent, as suggested by Fig. 3.

A second possible source of bias that needs to be considered are the STR loci. The IM analysis assumes a stepwise mutation model for these loci, and it is possible that a failure of this assumption may bias the results. Care was taken to use loci with STR regions that have simple repeats. In the IM analyses the estimated mutation rate scalars for the STR portions of the compound loci were typically ≈300,000 times higher than the mutation rate per site in the flanking sequence. If the mutation rate in the flanking sequence is 2 × 10^-9 per site per generation (i.e., the per site per year estimate based on the outgroup divergence × 2 years per generation), then our estimate of the STR mutation rate would be 300,000 times higher than this, or ≈6 × 10^-4 per generation, which is a fairly typical rate (33).

The IM analyses suggest that populations and species have been exchanging genes, particularly from T. tropheops and T. broad mouth into populations of T. gracilior. However the estimated densities of migration parameters are mostly flat, and there is little resolution of migration rates in most cases. In recent years several authors have argued that some gene flow between species is probably occurring (13, 34-36), and in particular Kocher and colleagues (11, 37) have argued in support of the “divergence with gene flow” model of speciation (38, 39) for Malawi cichlids. In such models, two populations may diverge in parapatry or sympatry because of selective forces, even in the presence of gene flow. These models differ fundamentally from strictly allopatric models of speciation in that they directly entail a role for divergent natural selection as a cause of species diversity (38).

Although the use of dated outgroup sequences and a parameter-rich model of divergence allows us to address difficult questions about the divergence of Malawi cichlids, there are clear limitations to these interpretations. Necessarily, the divergence process has been viewed through the lens of the IM model, and it is not yet clear how the picture would change if we were able to consider more than two populations simultaneously or could better assess the impact of assuming the stepwise mutation model for the STR portions of loci. The consistently very large estimates for ancestral population sizes do suggest that our samples contain variation that arose not just in single ancestral populations but in a wider array of partly intermingled populations. This interpretation is consistent with the evidence for recent gene exchange among populations and species.