Calculation of hydrodynamic properties of small nucleic acids from their atomic structure

Abstract

Hydrodynamic properties (translational diffusion, sedimentation coefficients and correlation times) of short B-DNA oligonucleotides are calculated from the atomic-level structure using a bead modeling procedure in which each non-hydrogen atom is represented by a bead. Using available experimental data of hydrodynamic properties for several oligonucleotides, the best fit for the hydrodynamic radius of the atoms is found to be ∼2.8 Å. Using this value, the predictions for the properties corresponding to translational motion and end-over-end rotation are accurate to within a few percent error. Analysis of NMR correlation times requires accounting for the internal flexibility of the double helix, and allows an estimation of ∼0.85 for the Lipari–Szabo generalized order parameter. Also, the degree of hydration can be determined from hydrodynamics, with a result of ∼0.3 g (water)/g (DNA). These numerical results are quite similar to those found for globular proteins. If the hydrodynamic model for the short DNA is simply a cylindrical rod, the predictions for overall translation and rotation are slightly worse, but the NMR correlation times and the degree of hydration, which depend more on the cross-sectional structure, are more severely affected.

INTRODUCTION

Hydrodynamic quantities and other solution properties are classical sources of information on the structure of nucleic acids (1). Duplex DNA is customarily represented as a worm-like filament whose dimensions (contour length and diameter) reflect the geometrical features of the double helix. For many years, analysis of the hydrodynamic properties of DNA in terms of the worm-like model yielded a diameter of 25–30 Å (2), considerably larger than the diameter of the B-DNA double helix. Such work was done on high molecular weight DNA, and analysis of the solution properties required the simultaneous determination of the flexibility parameter, i.e. the persistence length.

For very short oligonucleotides, the contour length is much smaller than the persistence length and therefore they behave as rigid particles. The availability of experimental data for hydrodynamic properties of short B-DNA duplex molecules (3,4), which are not influenced by the bending flexibility, along with theoretical improvements in the description of the hydrodynamics of cylindrical particles (5–7), made it possible to determine a diameter for B-DNA of ∼20 Å. This seems quite reasonable if one considers that the outer radius of the helix, measured as the distance from the helical axis to the phosphorous atoms, is ∼10 Å.

Although the good performance of the cylindrical rod model for short oligonucleotide duplexes is well established from those studies (3,4), it is evident that the circular, uniform cross-section is an idealization of the double-helical structure. This idealization is similar to the classical approach to protein hydrodynamics, in which globular proteins in solution are hydrodynamically modeled as ellipsoids (8–10). However, since the pioneering work of Bloomfield and co-workers (11–13), bead modeling has been proposed as the proper methodology to compute hydrodynamic properties of rigid macromolecules with arbitrary shape. Nowadays, the theoretical foundations and computational implementations of bead modeling are well developed (14,15). Although bead modeling was initially conceived for modeling at a large spatial scale (with the model elements, the beads, representing large portions of the macromolecular structure), it has been shown that it also works at a molecular level, with beads representing small chemical entities. In the particular case of nucleic acids, it has been shown that a double-helical bead model, in which each bead represents a nucleotide, gives a good description of the hydrodynamics of short duplex DNA (16,17). While in such a model the level of resolution was that of the repeating nucleotide units, it has been described very recently that the resolution of the hydrodynamic model can be pushed at the ultimate, atomic level. This has been demonstrated thoroughly for globular proteins (18–20), hydrodynamically represented as bead models in which each non-hydrogen atom is represented by a bead. Such a detailed description has opened promising perspectives in the structural determination of proteins from NMR relaxation measurements (19). In the present work we describe how this approach can also be employed for the analysis of hydrodynamic properties of nucleic acids employing atomic-level bead models.

MATERIALS AND METHODS

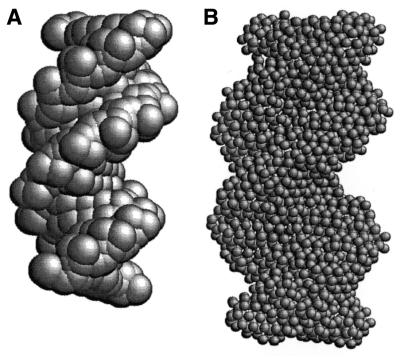
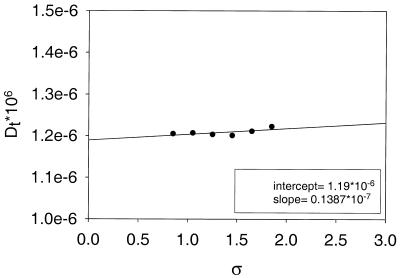
The procedure employed to build a hydrodynamic model of oligonucleotides and compute their solution properties closely follows that described for globular proteins, and therefore we present only a brief summary here. In the first stage, all the non-hydrogen atoms are represented by spheres that, for the sake of simplicity, are all of the same size, with radius a. In principle, the value of a should be of the order of the van der Waals radius of typical nucleic acid atoms (1.5–2.0 Å) (21–23). However, higher values are expected—and indeed found for globular proteins (18)—when one accounts for hydration effects (20). The diameter 2a of the spheres clearly exceeds typical bond distances and therefore this primary hydrodynamic model consists of spheres that overlap with their neighbors to a remarkable extent. An example of a primary hydrodynamic model for a B-DNA oligonucleotide with 14 bp (see Table 1 for a list of the fragments considered in this work) is shown in Figure 1A. For reasons that have been described in detail elsewhere, a model of extensively overlapping spheres is not adequate for hydrodynamic calculations (15,18). Therefore, in the next step of the modeling procedure, such a cluster of overlapping spheres is replaced by a shell of smaller, tangent beads of radius σ. Thus, the frictional resistance is represented at the surface of the particle, where it actually takes place. Calculations are repeated for various values of σ and the results are extrapolated to the shell-model limit of σ = 0. The rationale for this shell-model methodology was first described in the pioneering studies of Bloomfield et al. (11,24,25). Figure 2 shows an example of shell-model limit extrapolations.

Table 1. List of the nucleotides for which experimental hydrodynamic data are available from the indicated reference, along with the codes used here to name them subsequently.

Sequence	Code
Eimer et al. (3,4)
CGCGCGCG	8e
ATATCGATAT	10e
CGCGCGCGCGCG	12e
CGCGCGTATACGCGCG	16e
CGTACTAGTTAACTAGTACG	20e
Bonifacio et al. (29)
GAAGAGAAGC (CUUCUCUUCG)	10b
CGCGAATTCGCG	12b1
CGCAAATTTGCG	12b2
CGCGTATATACGCG	14b
CATGTGACGTCACATG	16b
Lapham et al. (27)
CGCGAATTCGCG	12l
GCTATAAAAAGGGA(TCCCTTTTTATAGC)	14l
CGCGAATTCGCGCGCGAATTCGCG	24l
Birchall and Lane (26)
CGTACG	6bi
CGCGAATTCGCG	12bi
GCTGTTGACAATTA (CGACAACTGTTAAT)	14bi
CGTACTAGTTAACTAGTACG	20bi1
CGTACTGATTAATCAGTACG	20bi2
Stellwagen et al. (28)
CGAAATTTCGCGAAATTTCG	20s1
CGTTTAAACGCGTTTAAACG	20s2
CGCAAAAACGCGAAAAACG (GCGTTTTTGCGCTTTTTTGC)	20s3

The first digits in the code correspond to the number of base pairs.

Figure 1.

(A) Primary hydrodynamic model of oligonucleotide 14b. Each non-hydrogen atom is represented by a sphere with radius a = 3.0 Å. (B) Shell model corresponding to this primary model, with minibeads of radius σ = 0.85 Å.

Figure 2.

Shell-model extrapolations for oligonucleotide 14b.

The hydrodynamic properties to be considered in this work are the translational diffusion, sedimentation coefficients and correlation times that describe the rotational dynamics of the oligonucleotide molecules. The calculation of the translational diffusion coefficient, D_t, is straightforward, and the sedimentation coefficient is obtained from it as:

s = D_tM(1 – v ρ)RT 1

where M is the molecular weight, v is the partial specific volume, ρ is the density of the solvent, R is the constant of ideal gases and T is the absolute temperature.

The rotational dynamics are fully characterized by the rotational diffusion tensor D_r. Because of the symmetry of the double-helical structure, this tensor takes a nearly diagonal form with three terms in the diagonal, one component corresponding to the helical axis, denoted as , and two others corresponding to perpendicular axes, that are nearly identical and are indicated as . The technique of depolarized dynamic light scattering, from which experimental data are available, monitors the end-over-end tumbling of the molecule. The observed correlation time, τ_ddls, is related to as:

2

NMR relaxation experiments provide cross-relaxation rate measurements from the time dependence of the NOE from H6 to H5 of the cytosine bases (3,4). These rates can be expressed in terms of a correlation time, τ_nmr. As the H6–H5 vector is in the plane of the bases, it is approximately perpendicular to the helical axis and, therefore, due to the above-mentioned symmetry, it can be shown that for a rigid body it is determined by the rotational coefficients as:

3

where the rb superscript means that this is valid strictly for a rigid structure. However, this is not the case for the duplex oligonucleotides; on the contrary, the re-orientational dynamics of the H6–H5 vector are not purely rotational but have an important contribution from the internal torsional dynamics, that we shall consider later on.

RESULTS AND DISCUSSION

We have calculated the hydrodynamic properties for various short oligonucleotides (Table 1) for which experimental data are available, and for transfer RNA.

Oligonucleotides: overall translational and rotational dynamics

Table 2 contains a compilation of experimental data for short, duplex B-DNA oligonucleotides for which experimental data of the hydrodynamic properties are available. In the study of Eimer and Pecora (4), values of D_t and τ_ddls were determined by polarized and depolarized dynamic light scattering, respectively. The correlation time τ_nmr has been determined by, among others, Eimer et al. (3 and references cited therein) and by Birchall and Lane (26). D_t has also been measured by pulsed-field gradient NMR by Lapham et al. (27) and from capillary electrophoresis by Stellwagen et al. (28). Analytical ultracentrifugation has been employed by Bonifacio et al. (29) to obtain both s and D_t. All the data (experimental and computed) to be presented hereafter will be referred to the standard condition of T = 293 K and aqueous solvent.

Table 2. Experimental values of the hydrodynamic properties (D_t, s, τ_ddls and τ_nmr) of the oligonucleotides considered in this work.

Code	Dt × 106 (cm2/s)	s (s)	τddls (ns)	τnmr (ns)	% Error (Dt)	% Error (s)	% Error (τddls)
8e	1.53		3.2	1.55	0.6		2.5
10e				2.5
12e	1.34		6.35	2.95	–3.0		–2.7
16e				4.2
20e	1.09		16.2	5.75	2.0		1.8
10b	1.40	1.5			0.4	5.9
12b1	1.45	1.77			–11.0	–1.1
12b2	1.22	1.65			4.9	3.6
14b	1.17	1.85			2.6	3.2
16b	1.11	2.1			1.8	–2.9
12l	1.23				4.9
14l	1.19				–6.7
24l	0.95				–2.1
6bi				1.8
12bi				3.3
14bi				4.5
20bi1				4.8
20bi2				6.7
20s1	1.07				2.8
20s2	1.02				1.0
20s3	1.00				3.0
Absolute mean error					3.4	3.1	2.3

The percentage errors found in the results calculated, for a = 2.84 Å, with respect to the experimental value are also indicated. The mean of the absolute value of the percentage errors is given for each property.

The calculations were carried out using our computer program HYDROPRO (18). The atomic structure of the oligonucleotides can be generated using molecular modeling programs. We employed the software package HyperChem (Hypercube, ON, Canada) to produce atomic coordinates of oligonucleotides of a given sequence in the canonical, duplex B-DNA form. In some cases where real atomic structures were available the calculations were repeated with such structures and the results were found to be nearly identical to those from the canonical structure.

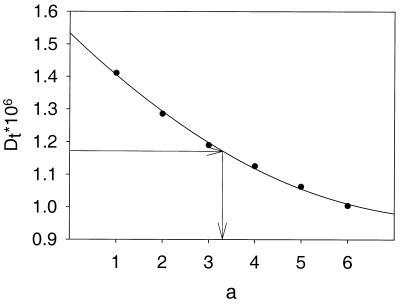
We analyzed the experimental data trying to find the proper value of the hydrodynamic radius, a, for the atoms represented by the spherical elements in the primary hydrodynamic model. Calculations of the properties were carried out for several values of a, and the value of this parameter corresponding to the experimental value was found by interpolation. An example of the dependence of properties on a is presented in Figure 3.

Figure 3.

Dependence of the translational diffusion coefficient on the hydrodynamic radius of the atoms a, and interpolation of the value of this parameter that fits the experimental value of the property for oligonucleotide 14b.

In Table 3 we collect the values of a fitted for each property of each nucleotide. We observe that most of them fall in the range 2–4 Å, with a mean value a = 2.8 Å. This is the value that we take hereafter as the standard value of the hydrodynamic radius of the atoms in nucleic acids. It is remarkable that it is very close to the value a ≈ 3.2 Å, obtained in our previous similar study of a large set of globular proteins (18–20) (a difference of some tenths of an angstrom can be attributed to typical experimental errors; see below). As the average van der Waals radius of the nucleic acid atoms is a_vdW ≈ 1.7 Å, then the difference a – avdW ≈ 1.1 Å may be attributed to hydration. This aspect is discussed in more detail below.

Table 3. Values of a for each oligonucleotide that fit the experimental values of the considered properties and results for the degree of hydration (using the average of a).

Code	a (Å) from:			d (g/g) (a = 2.84 Å)
	Dt	s	τddls
8e	2.9		2.7	0.39
10e				0.26
12e	2.5		3.0	0.26
16e				0.41
20e	1.8		3.0	0.35
10b	2.9	3.6		0.31
12b1	1.6	2.7		0.38
12b2	3.7	3.8		0.43
14b	3.3	3.3		0.31
16b	3.1	2.5		0.35
12l	3.6			0.38
14l	2.1			0.29
24l	2.2			0.31
20s1	2.1			0.30
20s2	2.9			0.30
20s3	3.3			0.30
Mean a	2.84 ± 0.62			0.33 ± 0.05

The variability that we observe in the values of a in Table 2 could be due to diverse reasons. Either some marginal bending flexibility or (more likely) some slight permanent bending curvature could influence the hydrodynamic behavior in a way that could produce deviation in the resulting fitted value of a, as it is not represented as such in our model. However, there is a more important (and somehow obvious) source of uncertainty in the results for this parameter: the error of the experimental data themselves. This circumstance has already been discussed for the case of globular proteins (20), and the situation is analogous for nucleic acids. Let us consider, for instance, the determination of a from translational diffusion data. The D_t value of oligonucleotides may be affected by an experimental error of ±5% or even larger [Eimer and Pecora (4) have reported that, just from the uncertainty of the extrapolation to zero concentration, there are expected errors in D_t of £4%]. If the experimental D_t of a fragment of, say, 14 bp is ±5% [e.g. for sample 14b (29) we would have 1.17 ± 0.06 × 10^–6 cm²/s), then the fitted value of a is in the range a = 3.3 ± 0.8. Thus, we expect that the variability found in the results for a is, to a great extent, due to the errors in experimental data.

Accepting the best fitting value, a = 2.8 Å, as the standard value for the radius of the atomic elements in the primary hydrodynamic model, we have evaluated the various hydrodynamic properties of all the oligonucleotides: the calculated results are compared with the experimental values, thus obtaining for each molecule and each property the error in the prediction. Such errors, which are listed in Table 2, are on average ∼2–3% (quite small) and not greater than typical errors of the experimental data. Therefore, we can conclude that our model predicts well the translational properties, i.e. D_t, s and the relaxation time for end-over-end rotation, τ_ddls.

Hydration

From the hydrodynamic volume of the model, V_hyd, it is possible to determine the degree of hydration of the B-DNA helix. V_hyd is the volume of the array of overlapping spheres that constitute the primary hydrodynamic model with atomic radius a = 2.84 Å as obtained from hydrodynamic properties, and it is calculated by our program HYDROPRO. The anhydrous volume can be calculated from the partial specific volume as V_anh = v N_A/M, where N_A is Avogadro’s number. The difference V_hyd – V_anh is the volume of the hydrodynamically bound water. It is customary to express the degree of hydration as the ratio, δ, of grams of water per gram of dry molecule. This is related to the hydrated and anhydrous volumes as:

4

For each oligonucleotide, V_hyd was calculated for a = 2.84 Å, and δ (g/g) was determined from equation 4. The results are collated in Table 3. The values of δ are rather similar for all the fragments; as expected, they are clearly independent of the oligonucleotide length. The small fluctuations are unimportant, and the mean value δ = 0.33 g/g can be taken as representative of the hydration of duplex B-DNA. This value is very similar to the classically accepted (30) [and recently confirmed (20)] degree of hydration of globular proteins.

Classic infrared spectroscopy measurements (31) indicated that there are about 20 molecules of water per nucleotide, which gives a value of 1 g/g for δ. However, the hydration determined from the hydrodynamic measurement does not include all the water molecules that interact somehow with the nucleic acid; instead, only those with a residence time sufficiently longer than the hydrodynamic relaxation times (say, longer than 10 ns) should be considered to constitute the hydrodynamic hydration layer. As pointed out by Bloomfield et al. (1), only six water molecules are tightly bound to the nucleotide, which corresponds to δ = 0.3 g/g. This last value is similar to the value for hydration of nucleic acids determined by hydrodynamic techniques which is δ = 0.35 (1). The value for δ obtained in our calculations correlates best with the value of δ obtained by hydrodynamic techniques and can be regarded as the value for the ‘hydrodynamic hydration’ of nucleic acids.

Oligonucleotides: NMR correlation times and internal dynamics

As mentioned above, the NMR correlation time, extracted from cross-relaxation rates between cytosine H5 and H6, cannot be analyzed just in terms of a rigid model because it contains an important contribution from internal motions. A simple, useful way to treat τ_nmr data, which starts from rigid-body results and includes the contribution of internal dynamics, is the Lipari–Szabo model-free approach (32,33). The internal motion is characterized by a relaxation time, τ_int. If the rigid-body rotations are much slower than the internal motion (i.e. if τ_int is appreciably smaller than ), and τ_int is in the extreme narrowing limit, then the experimental can be approximated by:

τ_nmr = S² + (1 – S²)τ_int 5

where S is the so-called general order Lipari–Szabo parameter, which would be unity if the pertinent vector (the H5–H6 internuclear vector) were rigidly fixed. For internal motions of small amplitude, the values expected for S will be appreciably close to unity.

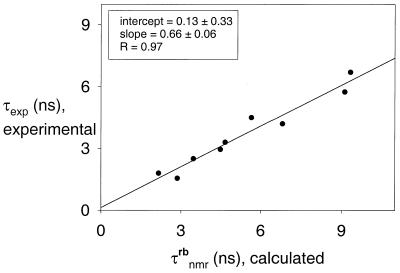
Using for τ_nmr, in the left-hand side of equation 5, the experimental values (Table 2), and for the results of the rigid-body calculation, then a plot of τ_nmr versus should show a linear dependence with slope S² and intercept (1 – S²)τ_int, so that S² and τ_int can be extracted from a plot such as shown in Figure 4. As discussed by Eimer et al. (3), values of τ_int are expected to be <0.1 ps, and the term (1 – S²)τ_int will be even smaller since S is close to 1. On the other hand, the rigid-body correlation times are up to 6 ps (Table 2). As a consequence, the intercept will be quite small and very influenced by experimental error. This is, indeed, the outcome of our analysis (Fig. 4). However, the slope in the plot is reliable, and gives S² = 0.66 ± 0.04, so that the generalized order parameter is found to be S = 0.81 ± 0.04. This result confirms the estimation of Eimer et al. (3) (S = 0.82), made with a more reduced data set, and is similar to the order parameter for quasi-rigid globular proteins (S ≈ 0.85).

Figure 4.

Plot of τ_nmr (experimental) versus 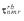(calculated). The intercept and the slope of the least-squares fit are indicated.

Comparison with the cylindrical rod model

In order to show how the atomic-resolution hydrodynamic model improves the results from the cylindrical rod model, we have carried out a parallel analysis, in which the hydrodynamic properties D_t, D^ and are calculated, using the equations of Tirado et al. (5–7) for a cylinder with length L = 3.4 ¥ nbp, where nbp is the number of base pairs and diameter d. Like a in the case of the atomic model, d is now the parameter for which we first seek a best fitting value. Repeating the same procedure (i.e. finding d for each property of every DNA fragment) we find values (not shown) that are similar for all the molecules and properties, with an average of d = 22.8 Å, close to previous estimates that found values of ∼20 Å (3,4,29). With this d, the predicted results are recalculated and the deviation from each experimental data is evaluated. The typical (average) differences are of ∼4–6% for the translational properties D_t and s, and ∼8% for τ_ddls. The deviations are appreciably larger than those found with the atomic-resolution model, perhaps slightly higher (but not much larger) than typical experimental errors. This finding confirms the conclusions reached by other authors (with more limited sets of data) that the Tirado et al. equations for the rod-like model give an acceptable prediction for the overall translational and end-over-end rotational diffusivity of short duplex oligonucleotides.

However, other properties are more sensitive to the structural details and dimensions of the cross-sectional structure; such is the case for , which plays an important role in the calculation of , and the hydrodynamic volume V_hyd which determines the degree of hydration δ. We repeated for the cylindrical rod an analysis of τ_nmr (experimental) versus (calculated). A plot similar to that in Figure 4 gives a non-negligible intercept (0.6 ± 0.5), a worse regression (R = 0.89) and a generalized order parameter (S = 0.70 ± 0.05), which seems too low. Regarding hydration, the hydrated volume is now simply calculated as V_hyd = Lπ(d/2)². Thus, δ is estimated for each oligonucleotide, with results (not shown) that are all close to 0.8 g/g, similar to those of other authors who used the cylindrical model to estimate the hydration of DNA (29).

In summary, although the cylindrical rod-like model may be useful to characterize the global translational and rotational dynamics, it can yield erroneous results for properties that are rather sensitive to the details of the cross-sectional, double-helical structure of DNA. In such cases, the advantage of the hydrodynamic calculations with atomic resolution is evident.

Transfer RNA

tRNA is a good example of a small nucleic acid molecule with a peculiar (not a simple regular helix) structure that is susceptible of hydrodynamic modeling. The ‘L-shaped’ structure observed in the X-ray determination is not essentially rigid; instead, it has been proposed that the molecule has some bending flexibility located at the hinge between the two arms (34,35). However, the amplitude of the internal motion is moderate, and the structural fluctuations take place both increasing and decreasing the angle between the arms, whose equilibrium or most probable value is ∼90°, as in the crystallographic structure, which can be therefore employed for the hydrodynamic calculation. Thus, we have taken from the Protein Data Bank the atomic structure for yeast tRNA^Phe with 1.93 Å resolution (36) (PDB entry 1EHZ).

The molecular weight and partial specific volume of tRNA^Phe are M = 23 560 and v = 0.550 (cm³/g), respectively. For the HYDROPRO calculation we employed a = 2.84 Å deduced in the analysis of oligonucleotides. The primary hydrodynamic model is shown in Figure 5. Experimental results taken from the literature (37–40) are listed and compared with the calculations in Table 4. The experimental relaxation time is in this case obtained from electric dichroism decay experiments. As tRNA is not straight and symmetric, the rotational time to be compared with the experimental is an average of the five rotational times (13,15,41) characteristic of an arbitrarily shaped structure, and a proper choice for this average is the harmonic mean of them, τ_h (42). We also include in the comparison a non-hydrodynamic property, the radius of gyration, R_g. It is clear from Table 3 that our hydrodynamic predictions, with the optimum value of a found in this work, are in excellent agreement with those of tRNA.

Figure 5.

Primary hydrodynamic model of tRNA^Phe with spherical elements having a = 3.0 Å.

Table 4. Experimental and calculated (a = 2.84 Å) values of solution properties of yeast tRNA^Phe.

Property	Experimental	Calculated
Dt × 107 (cm2/s)	7.3 (36); 7.9 (37)	7.89
τh (ns)	23.4 (38)	24.2
Rg (Å)	23.1 (38)	24.1

CONCLUSIONS

We calculated hydrodynamic properties of short B-DNA oligonucleotides from the atomic-level structure using bead modeling. Using available experimental data of hydrodynamic properties for several oligonucleotides, we found that 2.8 Å is the best fit for the hydrodynamic radius of the atoms. Using this value, the predictions for the properties corresponding to translational motion and end-over-end rotation are very accurate. We also calculated the degree of hydration for the oligonucleotides and found a result of ∼0.3 g (water)/g (DNA), close to that found in proteins. These numerical results ensure the validity of the proposed modeling procedure for the prediction of hydrodynamic properties of short fragments of nucleic acids.

Computer programs

HYDROPRO and other related computer programs are freely available from our web site at http://leonardo.fcu.um.es/macromol.