Building a learnable universal coordinate system for single-cell atlas with a joint-VAE model

Abstract

A universal coordinate system that can ensemble the huge number of cells and capture their heterogeneities is of vital importance for constructing large-scale cell atlases as references for molecular and cellular studies. Studies have shown that cells exhibit multifaceted heterogeneities in their transcriptomic features at multiple resolutions. This nature of complexity makes it hard to design a fixed coordinate system through a combination of known features. It is desirable to build a learnable universal coordinate model that can capture major heterogeneities and serve as a controlled generative model for data augmentation. We developed UniCoord, a specially-tuned joint-VAE model to represent single-cell transcriptomic data in a lower-dimensional latent space with high interpretability. Each latent dimension can represent either discrete or continuous feature, and either supervised by prior knowledge or unsupervised. The latent dimensions can be easily reconfigured to generate pseudo transcriptomic profiles with desired properties. UniCoord can also be used as a pre-trained model to analyze new data with unseen cell types and thus can serve as a feasible framework for cell annotation and comparison. UniCoord provides a prototype for a learnable universal coordinate framework to enable better analysis and generation of cells with highly orchestrated functions and heterogeneities.

UniCoord is a joint-VAE model designed to create a universal coordinate system for singlecell transcriptomic data, capturing major heterogeneities in a lower-dimensional latent space to enhance cell annotation and data augmentation.

Introduction

Cells in complex organs exhibit multifaceted heterogeneities, determining the various physiological and pathological phenomena of life. Since the discovery of cells, researchers have always been trying to classify cells into different cell types with their morphological features, molecular markers or cellular functions¹. With the rapid development of single-cell omics technology, there arises the ambition to build cell atlases that can serve as a reference to describe the multifaceted heterogeneities of cells^2–4. When given a cell, a desired cell atlas should be able to locate the cell to a specific body position and differentiation stage by assigning spatial and temporal coordinates. Moreover, the atlas should describe cell types/states as well as the activities of various biological processes of the cell, all of which can be summarized as functional coordinates. A universal coordinate system is essential to achieve this goal. A well-designed universal coordinate system can organize the huge number of cells within a cell atlas in a quantitative way, and thus benefit future molecular and cellular studies.

Many studies have been proposed to quantify the spatial, temporal, and functional features of cells. For example, a variation of tools has been developed to construct temporal trajectories or assign a pseudo-time score to each cell in single-cell RNA-seq (scRNA-seq) data^5–10. Similarly, with the rapid development of spatial profiling technologies, tools keep emerging to infer cell positions for scRNA-seq data^11–15. Diverse features or systems were proposed to illustrate the multifaceted functional characteristics of cells, such as hierarchically organized cell types^4,16,17, the continuum of cell states related to tumor progression^18,19 and cell cycle²⁰, and the index of macrophage activation states²¹. Beyond these approaches focusing on specialized cellular features, some works attempted to build information systems that organize these features within a unified framework, such as a spatial coordinate system that labels the original sampling site of cells²², and methods that embed transcriptomic profiles of cells into a latent space without explicit interpretations^23,24.

All these attempts tried to describe cells with specific features, which can hardly serve as a universal coordinate system as they do not match the complex nature of cells. For example, anatomic structures of human bodies are conserved in the population, but there are great variations and flexibilities in morphology and sizes among individuals, except the cellular conformation²⁵. Studies have shown that cells exhibit multifaceted heterogeneities in their transcriptomic features, including spatial, temporal and functional gradients at multiple resolutions^26–30. This makes it hard to design a fixed coordinate system with known cell types, locations and sampling time points to capture and index all the gradients, especially when considering the fact that the currently measured features are still far from providing the whole information of cells. It is desirable to build a learnable universal coordinate system that can capture all major heterogeneities in currently available data and can be compatible for future extensions when data with richer information are available. Such a system should be able to integrate both discrete and continuous coordinates within a single model, and these coordinates are preferable with interpretability. The system should also provide possibilities of generating pseudo cells by reconfiguring coordinates to help explore cell states that are not included in existing data or can hardly be observed by experimental approaches.

In this work, we developed a Universal Coordinate model (UniCoord) that learns to represent cells with a series of discrete and continuous features according to transcriptomic profiles. It used a specially tuned joint variational autoencoder (VAE) model to learn key features that best represent cellular heterogeneities. Each feature can be either discrete or continuous, and either supervised by prior knowledge or unsupervised. We applied UniCoord on several datasets, and the results showed that UniCoord is able to capture multiple key cellular features such as spatial, temporal and functional gradients from massive data. These features are powerful for accurate data reconstruction and label identification. Furthermore, UniCoord can serve as a controlled generative model for data augmentation, such as generating pseudo cells with desired features and interpolating extra cells in spatial or temporal gradients to fill the gaps between sampled cell states. UniCoord can be used as a pretrained model feasible to analyze new data with unseen cell types, such as using a UniCoord model trained by healthy data to analyze disease data. UniCoord provides a prototype for a learnable universal coordinate framework for analyzing the highly orchestrated functions and multifaceted heterogeneities of diverse cells, and paves the way towards a seamless cell atlas by unified organization and data augmentation.

Results

Overview of UniCoord

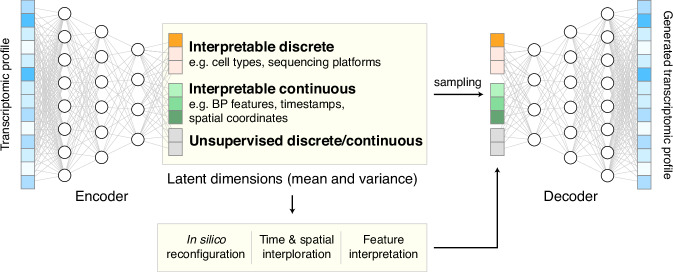
We developed UniCoord to learn key features that represent cellular heterogeneities from scRNA-seq data. We devised a specially tuned joint-VAE model to represent the transcriptomic profile of a single cell in a low-dimensional latent space. A conventional VAE model³¹ includes an encoder and a decoder (Fig. 1, see “Methods” for details). The encoder transforms the transcriptomic profile of a single cell into a set of means to represent the features about cellular heterogeneities, and a set of variances to deal with uncertainty. The decoder samples from the latent space according to the distribution defined by the means and variances learned by the encoder, and then transformed the sample into a generated transcriptomic profile.

Fig. 1. The schematic diagram of UniCoord.

The encoder transforms the transcriptomic profile of a single cell into a low-dimensional latent space. The decoder samples from the latent space and transformed the sample into a generated transcriptomic profile. The latent dimensions can either be interpretable (supervised) or unsupervised, and can either be discrete or continuous. The latent dimensions can be reconfigured to generate pseudo transcriptomic profiles with desired properties.

The goal of UniCoord is to represent the transcriptomic profiles of cells in the latent space with interpretability. We thus designed each dimension in the latent space to be either supervised by prior knowledge or unsupervised. We trained the supervised dimensions to capture information corresponding to well-defined features of the cell, such as the activity of a biological pathway, the differentiation stage, or the clinical diagnosis of the cell’s donor. We trained the unsupervised dimensions to capture complementary, yet unknown information of the cell, such as an unsupervised classification or score of cells. Through this approach, the latent dimensions can be regarded as the universal coordinates of cells.

Both discrete and continuous features can be used to represent cellular heterogeneities. For instance, the cell type and sequencing platform are commonly considered discrete features in RNA-seq studies. The spatial, temporal, and functional gradients are continuous features of vital importance to the analysis of biological processes. We proposed a model based on joint-VAE³², a disentangled representation framework that can deal with both discrete and continuous features in a single model, to handle these multifaceted heterogeneities. We considered two main aspects of loss in model training. We considered the reconstruction loss between the original and constructed data, which guaranteed the accuracy of the VAE model. Besides, we designed different loss functions for different forms of supervised features to make these features consistent with prior knowledge (see “Methods” for details).

Generating pseudo-single-cell data by in silico reconfiguration

Abundant transcriptomic profiles of cells are essential in the analysis of physiological and pathological processes. However, the cell numbers in existing data are often not sufficient, and it is challenging to experimentally observe certain cell types or states, especially for intermediate states. We thus introduced a feature of UniCoord named in silico reconfiguration to generate cell pseudo-single-cell transcriptomic profile data with desired features. After training, we can modify the value of any latent dimension of any cell to the value we expect (such as altering a sequencing platform to another), and then use UniCoord to generate a new transcriptomic profile. By this way, we can “reconfigure” the cell into a new one with desired properties.

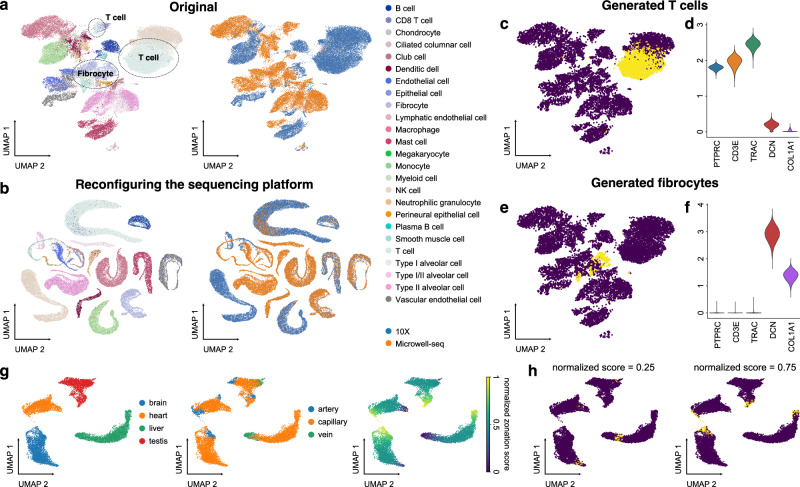
We first evaluated in silico reconfiguration of discrete features, such as the sequencing platforms and cell types. We trained a UniCoord model with the lung data in the human Ensemble Cell Atlas (hECA)⁴, and used cell types, sequencing platforms, and unsupervised continuous latent dimensions as the latent dimensions. The original scRNA-seq data derived from different sequencing platforms were separated in the Uniform Manifold Approximation and Projection (UMAP) plot (Fig. 2a), which is mainly due to the distinct distribution of data such as the median number of expressed genes in each cell (Supplementary Fig. 1a). We used the latent representation of original cells as the seed and reconfigured the mean value of the latent dimension corresponding to the sequencing platform into “10X”. We then sampled random variables from the modified distribution and used the decoder to generate pseudotranscriptomic profiles according to these sampled random variables. We found that the generated cells were joined together and clustered well by cell types (Fig. 2b). These generated cells showed similar distributions of the number of expressed genes, regardless the platform that their corresponding original cells were derived from (Supplementary Fig. 1b). We then reconfigured the cell types of all cells into a specified one. When we reconfigured the cell type as T cells and the sequencing platform as “10X”, the generated data highly expressed markers of T cells, including PTPRC, CD3E, and TRAC (Fig. 2c, d). When we reconfigured the cell type as fibrocytes and the sequencing platform as “10X”, these immune-related markers were turned off, and extracellular matrix markers such as DCN and COL1A1 were highly expressed (Fig. 2e, f). We also reconfigured the cell type as T cells/CD8 T cells and the sequencing platform as “Microwell-seq” of all cells. The generated cells also showed to be similar to the corresponding original cells (Supplementary Fig. 1c, d).

Fig. 2. In silico reconfiguration with UniCoord generates cells with designated features.

a UMAP plots showing the original hECA lung cells colored by cell types (left) or sequencing platforms (right). b UMAP plots showing the generated hECA lung cells with the sequencing platform reconfigured into “10X”, colored by cell types (left) and original sequencing platforms (right). c The UMAP plot of original cells (blue) and cells with the cell type reconfigured into T cells (yellow). d Expression levels of T-cell and fibrocyte markers in cells with the cell type reconfigured into T cells. e The UMAP plot of original cells (blue) and cells with the cell type reconfigured into fibrocytes (yellow). f Expression levels of T-cell and fibrocyte markers in cells with the cell type reconfigured into fibrocytes. g Vascular endothelial cells from four mouse organs, colored by tissues (left), vessel types (middle), or normalized artery-capillary-vein zonation scores (right). The zonation scores were normalized to be between 0 and 1. h UMAP plots of original cells (blue) and cells with zonation scores reconfigured into different values (yellow). For both models, all genes in the dataset were adopted to perform the experiments, and the number of unsupervised latent dimensions was set as 50. a, b All genes were used for visualization. c, e, g, h Highly variable genes (HVGs) were used for visualization. c, e, h For each generated cell, we calculated its nearest neighbor in the original dataset for visualization.

In silico reconfiguration can also be applied to continuous features. To demonstrate this, we trained a UniCoord model with the data of vascular endothelial cells from four tissues (brain, heart, liver, and testis) in a mouse endothelial atlas³³, with tissue origin, zonation scores, and unsupervised continuous latent dimensions as the latent dimensions. The original study discovered an artery-capillary-vein trajectory in vascular endothelial cells and raised a zonation score to describe the location of a cell on the trajectory. Thus, we used the information of tissues, zonation scores (normalized to be between 0 and 1), and unsupervised continuous latent dimensions as the latent dimensions. The result showed that UniCoord successfully reconstructed the information of tissues as well as the zonation trajectory (Fig. 2g). We then reconfigured the zonation scores of all cells and generated pseudo vascular endothelial cells. The generated cells were accurately placed at the designated locations on the trajectory (Fig. 2h and Supplementary Movie 1). These results demonstrated the advantage of in silico reconfiguration with UniCoord in generating pseudo cells with desired properties, which could help analyze and integrate datasets from different sources.

Interpolating timestamps or spatial coordinates to fill data gaps

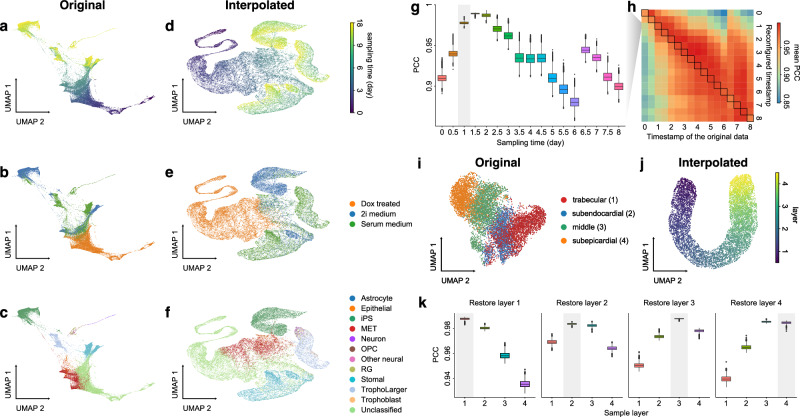
Cell state transitions are always continuous, but it is impossible to obtain continuous observation of cellular transcriptomic profiles through high-throughput sequencing technologies. One common approach to obtain time-series single-cell transcriptomic data is to measure samples at different time points. However, there still exist inevitable gaps between time points. We thus used the in silico reconfiguration approach to obtain a more continuous and comprehensive view of cell state transitions by timestamp interpolation. We trained a UniCoord model with a mouse iPSC reprogramming dataset³⁴. In this dataset, cells were treated with doxycycline to induce mouse embryonic fibroblasts (MEFs) de-differentiating into iPSCs, and were then transferred to either serum-free 2i medium or serum medium on day 8 (Fig. 3a). Cells in the serum medium are more likely to re-differentiate into stromal cells and neurons (Fig. 3b, c). The dataset covered a total of 18 days at half-day intervals, forming a discrete trajectory (Fig. 3a). We used timestamps and unsupervised continuous latent dimensions as the latent dimensions. After training, we sampled cells from each time point and used their latent representations as seeds. We reconfigured the latent dimension denoting the timestamp of each sampled cell by adding the original value with a uniformly random variable between –0.5 to 0.5 day. Through this approach, we interpolated the missing time points and created a continuous trajectory (Fig. 3d). We found that the trend in the evolution of cell types became more evident (Fig. 3f). Furthermore, though we did not encode any information about the experimental design, the interpolated results showed clear subgroups of cells with different treatments (Fig. 3e).

Fig. 3. UniCoord interpolated discrete timestamps or spatial coordinates into continuous trajectories.

a–c Mouse iPSC reprogramming data visualized by the low-dimensional visualization provided by the original study, cells colored by sampling days (a), treatments (b), and cell types (c). d–f UniCoord-interpolated mouse iPSC reprogramming data, cells colored by continuous sampling time (d), treatments (e), or cell types (f). Dox doxycycline, iPS induced pluripotent stem cells, MET cells undergoing a mesenchymal-to-epithelial transition, OPC oligodendrocyte precursor cells, RG radial glial cells. g PCCs between the restored data of day 1 and the mean gene expression of the original data. h Mean PCCs between restored data of each timestamp and the mean gene expression of the original data. g, h Data of a timestamp were excluded, and then the unclassified cells of this timestamp were restored by reconfiguring the timestamp of all other unclassified cells as this timestamp. Cells in days 0–8 were restored and compared in this experiment. i, j UMAP plots showing real (i) and interpolated (j) CMs from the left ventricle. The corresponding layer number was shown in the legend of (i). For both models, all genes in the dataset were adopted to perform the experiments, and the number of unsupervised latent dimensions was set as 50. HVGs were used for visualization all UMAP plots. k PCCs between restored data and the mean gene expression of the original data. Data of each sample layer are excluded, respectively, and then restored by reconfiguring cells of all other sample layers. The reconfigured target timestamp/sample layer is shaded in gray in (g, k).

We then investigated whether UniCoord can restore the transcriptomic profiles of cells unseen in training. We excluded the data with a certain timestamp during UniCoord training and tried to restore the excluded data by timestamp reconfiguration (see “Methods” for details). We first excluded the data of day 1 and restored the cells with the “unclassified” label by reconfiguring the timestamp of all other unclassified cells as day 1. We calculated the mean gene expression of the unclassified cells of each day and compared the restored data with them by the Pearson’s correlation coefficient (PCC). As shown in Fig. 3g, the restored unclassified cells showed to be most similar to the original unclassified cells of day 1.5. We performed similar experiments to restore unclassified cells from day 0 to day 8. We found that though the restored data showed a high PCC with the original data with the corresponding timestamp, they showed to be most similar to the original data with adjacent timestamps (Fig. 3h). This may be due to the absence of the corresponding timestamp data in the training dataset preventing the model from precisely capture the trend of the data and preferring to infer it from data with adjacent timestamps.

UniCoord can also be applied to reconstruct spatial trajectories by interpolating spatial coordinates. In our recent work on human heart cell atlas²⁸, we sampled cardiomyocytes (CMs) from four layers of the left ventricle with different depths, and found these CMs from different layers exhibited distinct characteristics (Fig. 3i). We used UniCoord to interpolate the continuous change between these layers. We trained a UniCoord model with the data using the information of sample layers and unsupervised continuous latent dimensions as the latent dimensions, where the four sample layers are treated as numeric layer 1–4, respectively. After training, we sampled cells from each layer, and reconfigured the latent dimension denoting the layer information by adding the original value with a uniformly random variable between –1 to 1. We generated pseudo cells with this approach and found that the generated data formed a continuous spatial trajectory (Fig. 3j). We then excluded data from layers 1, 2, 3, and 4, respectively, and used UniCoord to restore these unseen data by reconfiguring cells of all other sample layers (“Methods”). As shown in Fig. 3k, the restored data of layers 1, 2, and 3 showed most similar to the original data for the corresponding layer. The restored data of layer 4 showed comparable similarity to the original data of layers 3 and 4, which may be due to the fact that the extrapolation task is more difficult than the interpolation task. All the results demonstrated the versatility and potential of UniCoord in reconstructing spatial and temporal trajectories by interpolating timestamps or spatial coordinates, allowing for more comprehensive and accurate analyses of complex biological processes.

Pre-training UniCoord model with cell atlas data for analyzing disease-related cells

We applied UniCoord on the hECA data⁴ which has a total of 1.09 million cells to represent the cellular heterogeneity in the atlas. We randomly sampled 50,000 cells from the dataset and used these cells to train a UniCoord model. We used three aspects as the latent dimensions: cell types, sequencing platforms, and biological process (BP) features that represent the information of specific biological processes. To calculate BP features, we first applied AUCell³⁵ on the transcriptomic profiles of the training cells to convert gene expression levels into the activity strengths of Gene Ontology Biological Process (GOBP) terms^36,37. We then trained a random forest model that used these strengths to classify cell types, and identified the top 100 GOBP terms with the highest important scores. After, we clustered these terms into 30 groups and selected the term that showed the activity strength in each group. These selected GOBP terms were regarded as the key GOBPs (Supplementary Fig. 2 and Supplementary Table S1), and the AUCell scores of these key GOBPs were regarded as values of BP features (see “Methods” for details).

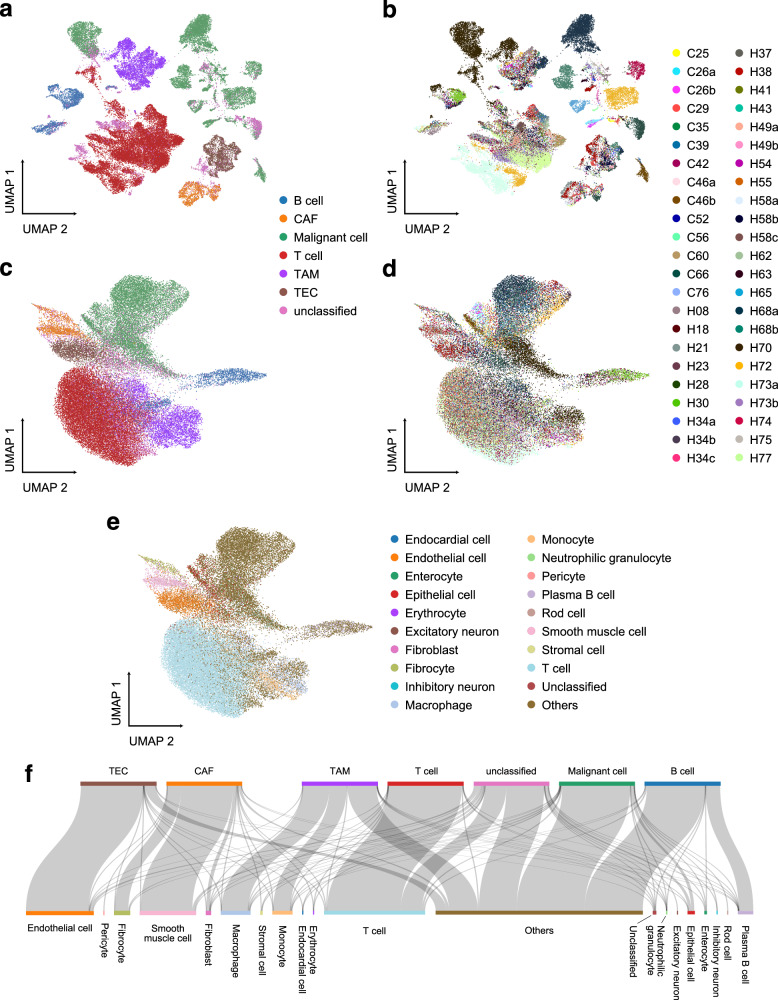
We took the UniCoord model trained by hECA data as a pretrained model to analyze data that were not included in the training dataset. We used the model to represent cells in a hepatocellular carcinoma (HCC) dataset³⁸. The dataset contains 56,721 cells from 46 distinct liver tumor samples (Fig. 4a, b). As shown in Fig. 4c, d, cells represented by the UniCoord model were less sensitive to the batch of samples. UMAP visualizations of the GOBP latent dimensions of these cells showed similar results (Supplementary Fig. 3b), suggesting that the batch effects were eliminated during the calculation of GOBP activity strength. However, when visualizing the representation results of malignant cells, we can still find some differences among different patients (Supplementary Fig. 3c, d), suggesting that the heterogeneities of malignant cells were not totally overlooked by the UniCoord model.

Fig. 4. Analyze HCC data using the UniCoord model pretrained by hECA data.

a, b The UMAP plot showing the landscape of the HCC dataset, represented by PCA. Cells are colored by cell types (a) or sample IDs (b). c–e The UMAP plot showing the landscape of the HCC dataset, represented by the pretrained UniCoord model. Cells are colored by cell types (c), sample IDs (d), and UniCoord-predicted cell types (e). f The relations between original labels (top) and cell types predicted by UniCoord (bottom). Protein coding genes in the dataset were adopted to perform the experiments. All genes were used for visualization all UMAP plots.

We then used UniCoord to annotate cell types of the HCC data (Fig. 4e). We found that the cell types unseen in hECA data were predicted as the related cell types (Fig. 4f). For example, cancer-associated fibroblasts (CAFs) were mainly annotated as smooth muscle cells as they share several important markers such as α-smooth muscle actin³⁹. Besides, tumor-associated macrophages (TAMs) and tumor endothelial cells (TECs) were mainly annotated as their corresponding progenitor cell type, respectively. Interestingly, malignant cells were predicted as “others” which is a mixture of all cell types with small quantities in hECA. This suggested that the pretrained UniCoord model successfully discovered that malignant cells were different from any cell type encoded in the model. Besides, B cells in the HCC data were also mainly predicted as “others”, suggesting that the state of these B cells was deviated from healthy B cells.

We investigated the BP features in the representation of the HCC data (Supplementary Fig. 3a, see “Methods” for details). We found that BP features such as B cell receptor signaling pathway, phagocytosis & recognition, and peptide cross-linking were highly activated in B cells. Connective tissue development, muscle cell development, and extracellular matrix organization were highly activated in CAFs. These BP features are highly related to the functions of the corresponding cell type. Malignant cells exhibited the lowest score of positive regulation of cell killing, which is consistent with their uncontrolled proliferation. The results showed the feasibility of UniCoord as an interpretable pretrained model for representing and decoding complex cell heterogeneities.

We then investigated whether UniCoord can capture patient-specific information. We trained a UniCoord model with patient IDs and cell types as latent dimensions. We analyzed the five patients with the highest number of malignant cells. We generated new cells by reconfiguring the patient ID of malignant cells from patient H72 as H70. We calculated the correlation between each generated cell and the mean gene expression (Supplementary Fig. 3e). It can be seen that although the generated cells were reconfigured from H72, they showed much higher correlation with H70. This result indicated that UniCoord can be used to identify patient-specific features.

Discussion

In this work, we presented UniCoord, a universal coordinate model that can represent cells with discrete and continuous features computationally derived from gene expression and/or metadata. We showed that UniCoord can efficiently capture the information in single-cell transcriptomic profiles. The resulting features can be used to well reconstruct the original transcriptional profiles and generate pseudo cells. The features can be either unsupervised or supervised by prior knowledge. The supervised features can be further interpreted for understanding cellular heterogeneities, and the unsupervised features can help extract information remaining to be characterized in current studies. Moreover, we demonstrated that UniCoord can serve as a pretrained model that can be generalized to unseen data or cell types. These capabilities make UniCoord a powerful tool for analyzing the highly orchestrated functions and multifaceted heterogeneities of scRNA-seq data.

One major advantage of UniCoord is its capability to generate pseudo-single-cell data by in silico reconfiguration, which can serve as a controlled generative model for data augmentation. This may be helpful to obtain transcriptomic profiles of desired cells or cell states that can hardly be observed experimentally. We demonstrated in silico reconfiguration by configuring sequencing platforms and cell types. We also showed that by in silico reconfiguration, UniCoord can reconstruct continuous trajectories from discrete data by interpolating the missing time points or unsampled spatial locations. This approach can help integrate datasets from different sources and generate pseudo cells to fill spatial, temporal or functional gaps in current data, both of which will contribute to the construction of cell atlases by unified organization and data augmentation. With the rapid development of generative deep learning models, there have been several other studies to conditionally generate pseudo-single-cell data which also have the potential for augmenting data^40–42. Benchmarking these methods is an important issue for future improvement and utilization of UniCoord. Furthermore, as an interpretable model, UniCoord is complemented with the fashionable large-scale pretrained models^42–45. The results produced by these large models can be interpreted by UniCoord, and UniCoord can generate pseudo cells with high confidence to fit the huge demand of data for large model training.

It should be noted that the performance of UniCoord may be influenced by the quality and quantity of training data, particularly in smaller or less diverse datasets. Although UniCoord can interpolate data to fill gaps, the accuracy of the interpolated values could be limited in situations with high data sparsity or large gaps. UniCoord could benefit from the development of a more comprehensive and refined cell atlas that covers a wider range of cell types and aspects of cellular heterogeneities. Besides, the design of BP features can be further improved to enhance the clarity. In the future, UniCoord can be extended to more types of omics data to form a multiscale framework for representing cellular complexity, and more applications, such as measures of cellular functional distance and in silico perturbation of cell states can be further explored based on the framework.

Methods

The model of UniCoord

UniCoord was derived from the joint-VAE model³² with some refinements. The latent space of UniCoord differs from conventional VAE in two aspects: (a) the latent space of UniCoord is a combination of discrete and continuous dimensions, while conventional VAE only contain continuous dimensions; (b) each dimension in UniCoord could be physically interpretable if supervised by prior knowledge.

The gene expression level x_i of cell i could be modeled by a conditional distribution $p\left(x_i\mid I{D}_i,U{D}_i,I{C}_i,U{C}_i\right)$, where ID_i, UD_i, IC_i, and UC_i stand for interpretable discrete, unsupervised discrete, interpretable continuous and unsupervised continuous latent dimensions for cell n, respectively. ID_i and IC_i capture information corresponding to well-defined features of the cell, such as the activity of a certain biological process, the differentiation stage of the cell, or clinical diagnoses of the cell’s donor. UD_i and UC_i capture complementary, yet unknown information in the data. UD_i and UC_i also play auxiliary roles that help the model reconstruct the original data. The mapping function p from these latent dimensions to expression levels is learned by training a neural network called decoder, and the posterior distribution of latent variables $q\left(I{D}_i,U{D}_i,I{C}_i,U{C}_i\mid x_i\right)$ is learned by training another neural network called encoder.

Model structure

The UniCoord model consists of an encoding module, a reparameterization module, and a decoding module. The encoding module processes the input data through three linear layers, with dimensions of 512, 256, and 128, respectively. The first and second linear layers have a dropout probability of 0.1. All three linear layers use the ReLU activation function. The output of the third linear layer was then transformed into two groups of parameters serving as the latent space. For continuous latent dimensions, two linear layers are used to map the output of third linear layer to mean and logarithm of variance, respectively. For each discrete latent dimension, a linear layer is used to map the output to its one-hot encoded value.

The reparameterization module samples from the latent space constructed by the encoder. The reparameterization trick can disentangle random variables with parameters and make back propagation algorithm possible. For continuous latent dimensions, we kept the conventional reparameterization trick used in VAE³¹. For discrete latent dimensions, we applied the Gumbel-softmax reparameterization⁴⁶ for sampling.

The decoding module maps the samples provided by the reparameterization module back to the representation of the original data. The decoding model uses four linear layers to map the data from the dimensions of the latent samples to 128, 256, 512, and the dimensions of the original data, respectively. The second and third linear layers have a dropout probability of 0.1. All four linear layers use ReLU activation functions. The output of the decoding module is regarded as the generated data.

In all experiments of this study, the interpretable discrete dimensions, such as cell types and sequencing platforms, were encoded by one-hot encoding. The method for constructing BP features were explained below. All other interpretable continuous dimensions, such as timestamps and spatial coordinates, were encoded as their original values. For all models with unsupervised latent dimensions, the number of unsupervised continuous dimensions was set as 50, the number of unsupervised discrete dimensions was set as 0.

Loss functions

The loss function of UniCoord is composed of several parts, and each part gives the model a specific feature. In general,

$$\mathrm{Loss}={\lambda }_{\mathrm{recons}\mathrm{ruction}}*L_{\mathrm{recons}\mathrm{ruction}}+\beta *\left(L_{\mathrm{GaussianKL}}+L_{C\mathrm{ategoryKL}}\right){+\lambda }_{\mathrm{diffusion}}*L_{\mathrm{diffusion}}+{\lambda }_{\mathrm{regression}}*L_{\mathrm{regression}}+{\lambda }_{\mathrm{classification}}*L_{\mathrm{classification}}+{\lambda }_{\mathrm{hi}\mathrm{erarchical}}*L_{\mathrm{hi}\mathrm{erarchical}}$$

All λs are hyperparameters that control the weight of each part, and details of each loss are introduced below.

Reconstruction loss

The reconstruction loss is the basic part of losses that make the model an autoencoder. It is defined as the MSE between the reconstructed data x’ and original data x:

$$L_{\mathrm{recons}\mathrm{ruction}}=\frac{1}{n}{\sum }_{i=1}^n{\sum }_{j=1}^m{\left(x_{ij}^{\prime }-x_{ij}\right)}^2$$

Where n is the number of cells, m is the number of genes, $x_{ij}$ represents the expression level of gene j in cell i, and $x_{ij}^{\prime }$ represents the reconstructed expression level of gene j in cell i.

KL divergence

KL divergence works as the regularization component that prevents over-fitting. For continuous dimensions, KL divergence constrains the posterior distribution to be close to a standard normal distribution. For discrete dimensions, KL divergence constrains the posterior distribution to be close to a uniform categorical distribution.

Diffusion loss

Some of the continuous dimensions can be defined as diffusion dimensions, playing the same roles as reductions in the diffusion map. We desired cells with similar scores in diffusion dimensions should also be similar in expression levels. So, we first constructed k-nearest neighbors for all cells and then calculated the average of the latent distribution of one cell’s neighbors. The average was inputted into the decoder to generate a reconstruction expression vector x”. The diffusion loss is defined as the MSE between x” and the original data x.

Regression loss

The regression loss is the MSE loss between the original label and the mean parameter of the corresponding latent continuous dimension.

Classification loss

The classification loss is the cross entropy between the original label and the corresponding latent discrete dimension.

Hierarchical loss

The hierarchical loss is the cross entropy between two latent discrete dimensions that are designed to have hierarchical relationships. The descendant layer labels are first aggregated to ancestor labels following the designed relationship. Then the cross entropy between the aggregated labels and the model-generated ancestor labels is defined as the hierarchical loss.

Model training

The “chunk_size” parameter is used to divide the training dataset into multiple parts for training in chunks. This is particularly useful for large datasets as it can reduce the memory and computation resources required for each iteration to improve training efficiency. By default, the “chunk_size” is set to 20,000. The model is optimized using the Adam optimizer by default, and the default learning rate is 5e-4.

Computational performance

We evaluated the computational performance of UniCoord during training on the hECA dataset. We employed an NVIDIA GTX 1080 Ti GPU to train on the dataset, which consists of 56,721 cells. The training process took ~4 min to complete. During this process, the GPU memory consumption was observed to be around 9GB. It is noteworthy that the usage of CPU resources and system memory was not substantial. This provides practical insight into the feasibility of implementing UniCoord on similar-scale datasets using commonly available high-performance computing resources.

Generation of BP features

The BP features are selected from GOBPs. To avoid outliers of enrichment analysis, we kept GOBP gene sets with gene numbers between 50 and 500, which resulted in 2535 gene sets. Each of these gene sets was used to calculate an enrichment score for all cells in hECA data. Enrichment scores were calculated for each gene set across all cells in hECA data using the AUCell function in the SCENIC package³⁵ with default parameters. Information entropy was then calculated for the AUCell scores of each gene set, and 10,000-fold permutation tests were performed to obtain P values of the information entropy. We kept gene sets with P values <0.001 to train a random forest classifier to classify cell types in the hECA dataset annotated by the unified Hierarchal Annotation Framework (uHAF)⁴. The feature importance was evaluated using the feature_importance score of the classifier, and gene sets with the top 100 most important scores were selected to calculate the Pearson’s correlation coefficients between each other’s scores. Hierarchical clustering was performed to identify gene set groups with high correlations. We cut the hierarchical clustering to 30 groups and selected the one with the highest information entropy from each group. These 30 gene sets and their corresponding AUCell scores make up the BP features.

Cell generation and evaluation

For the cell restoration experiment of the mouse iPSC reprogramming dataset, we excluded the data with the timestamp to be inferred from the dataset. For the cell restoration experiment of the left ventricle CM dataset, we excluded the data with the sample layer to be inferred. For all cell restoration experiments, we divided the dataset as a training set (80%) and a test set (20%). We trained the UniCoord model with the training set, and then restored the excluded data with the testing set (20%) by reconfiguring the corresponding timestamp/layer. After, we calculated the mean gene expression of each timestamp/layer in the original data and calculated the PCC between the mean gene expression and the restored data.

scRNA-seq data analysis

Details of all scRNA-seq datasets used in this study can be found in Data Availability. The scRNA-seq data analysis was based on the Python package Scanpy⁴⁷. As UniCoord needed the normalized data, we applied sc.pp.normalize_total (target_sum = 1e4, exclude_highly_expressed = True), and sc.pp.log1p (default parameters) before feeding data into our model. For visualizing the landscape of single cells, we follow the standard analysis tutorial of Scanpy, and the data generated from UniCoord were also handled with the same procedure.

Analysis related to UniCoord was conducted with our Python package, unicoord. Differentially expressed genes and differential BP feature activities (Supplementary Fig. 2) were detected using the tl.rank_genes_groups function in Scanpy.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.

Author contributions

X.Z., L.W., H.G., and K.H. conceived the study. X.Z. and L.W. supervised the study. H.G. and K.H. designed the model. H.G., K.H., and X.W. performed model training and data analysis. S.C., Q.Y., and R.J. contributed to the improvement of the model and the interpretation of results. X.Z., L.W., H.G., K.H., and X.W. wrote the manuscript. All authors read and approved the final manuscript.

Peer review

Peer review information

Communications Biology thanks Chenxu Zhu and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Primary Handling Editors: Chien-Yu Chen and Christina Karlsson Rosenthal.

Data availability

We only used public datasets in this study. The hECA data can be downloaded through the Python package ECAUGT⁴⁸. The mouse endothelial atlas dataset is available on the ArrayExpress database, with the Entrez accession number E-MTAB-8077. The mouse iPSC reprogramming trajectory data is available on the Gene Expression Omnibus (GEO) database with the accession number GSE122662. The human heart cell atlas data can be downloaded from its interactive website (http://xglab.tech/hahca). The HCC dataset is available on the GEO database with the accession number GSE151530.

Code availability

The Python package UniCoord is available at https://github.com/pluto-the-lost/unicoord or Zenodo⁴⁹.

Competing interests

The authors declare no competing interests.

Supplementary information

The online version contains supplementary material available at 10.1038/s42003-024-06564-0.