Abstract

Indoor air quality is critical to human health, as individuals spend an average of 90% of their time indoors. However, indoor particulate matter (PM) sensor networks are not deployed as often as outdoor sensor networks. In this study, indoor PM2.5 exposure is investigated via 2 low-cost sensor networks in Pittsburgh. The concentrations reported by the networks were fed into a Monte Carlo simulation to predict daily PM2.5 exposure for 4 demographics (indoor workers, outdoor workers, schoolchildren, and retirees). Additionally, this study compares the effects of 4 different correction factors on reported concentrations from the PurpleAir sensors, including both empirical and physics-based corrections. The results of the Monte Carlo simulation show that mean PM2.5 exposure varied by 1.5 μg/m3 or less when indoor and outdoor concentrations were similar. When indoor PM concentrations were lower than outdoor, increasing the time spent outdoors on the simulation increased exposure by up to 3 μg/m3. These differences in exposure highlight the importance of carefully selecting sites for sensor deployment and show the value of having a robust low-cost sensor network with both indoor and outdoor sensor placement.
Keywords: Low-cost sensor, indoor air quality, Monte Carlo, community air monitoring, exposure, PurpleAir
Short abstract
A shortage of indoor air quality data has historically necessitated the use of outdoor particulate matter concentrations to estimate exposure levels. In this work, we estimate exposure using an indoor-outdoor sensor network.
1. Introduction
Particulate matter (PM) refers to small solid and liquid particles suspended in the air. PM2.5 refers to PM particles with diameters 2.5 μm and smaller. PM2.5 can be inhaled into the lungs, which elevates the health risk posed by these fine particles, in comparison to larger particles.1,2 Exposure to PM2.5 correlates to an increased likelihood of lung cancer3 and cardiovascular disease.4 In addition, PM2.5 is significantly associated with increased daily mortality.2 Due to its health impacts, government organizations in many countries regulate and monitor PM levels. In the United States, the federal reference method (FRM) for measuring PM is the gravimetric method, in which the difference in the mass of a filter before and after sampling is used to find the PM mass concentration. In addition to the gravimetric method, several federal equivalent methods (FEM) can also provide high-quality PM measurements. Among these are Beta Attenuation Monitors and tapered element oscillating microbalances.5−8 While FRM and FEM are the gold standards for PM measurement, their large size, high cost, intensive siting requirements, and frequent maintenance needs pose significant challenges that limit the number of sites where they can be deployed9 and make them unsuitable for estimating personal PM exposures.
Another drawback of existing regulatory PM measurements is that the EPA regulates and monitors outdoor PM concentrations and not indoor levels. Seeing as people spend only 7.6% of their time outdoors,10 this measurement scheme may not fully reflect individuals’ PM exposure. Despite the high percentage of time people spend inside, the lack of easily accessible indoor air quality data has necessitated the use of outdoor concentrations in epidemiological and public health settings. Most epidemiological research on the health effects of PM exposure relies on outdoor data exclusively.1,11−14 Yet, since most people spend disproportionately more time indoors, relying on outdoor concentrations can create an exposure misclassification. To fully understand how PM impacts human health, indoor air quality must also be considered.
Outdoor-located sensors are not poised to detect PM from pollutants unique to the indoors. For example, inside-only activities such as cooking, heating, and the use of consumer products are known to produce PM pollution.15,16 Due to their location, outdoor sensors cannot detect these pollutants, and as a result, there is uncertainty about whether outdoor measurements reflect the reality of indoor PM exposure levels. For example, Ebelt et al.17 indicate that, for pooled correlations, there is only a moderate correlation between personal PM exposure and ambient exposure due to variability in personal lifestyle and home infrastructure.
There is already sufficient evidence of the detrimental health impacts of PM, as well as evidence that indoor air contains PM with a different make-up than outdoor PM.18 However, due to the difficulties of monitoring indoor PM, there is a shortage of research on exposure levels to indoor PM. One possible solution to this issue is to use low-cost sensors (LCS) to measure indoor air pollution.19 LCS are gaining increasing attention due to their capability to be deployed for personalized monitoring. Their cost is orders of magnitude less than FEM and FRM, they are generally small and have lenient siting requirements, with infrequent maintenance needs. LCS can provide minute-scale or even second-scale resolution data, enabling the detection of transient and dynamic PM emission events. Dense LCS networks have shown promise for use in pollution mapping on both large and small extents globally, ranging from the scale of a room to a national scale.20−24 Dense LCS networks provide an increased spatial resolution, leading to more accurate and individualized exposure estimates. In addition, laboratory evaluations of LCS have shown moderate to high correlations with FRM/FEM,25−27 showing they can function in a wide range of concentrations and conditions, making them suitable for use indoors. This study uses PurpleAir LCS (PurpleAir, Inc, Draper, Utah, USA), which rely on light scattering as their operating principle. One advantage of using PurpleAir sensors is that PurpleAir has created a publicly accessible map of the data from their sensors. These sensors may be placed either indoors or outdoors.
While PurpleAir sensors come with 2 pre-set calibration factors, it is recommended to further calibrate them to account for climate, temperature, regional effects, particle composition, and other variables.28 For example, since PurpleAir units do not include dryers, the sensors’ results are often affected by high relative humidity (RH).25,27,28 Generally, temperature has a negligible impact on LCS functionality,28−30 likely since light scattering/absorption is temperature independent. There is a diversity of existing correction models, including theoretical, empirically derived, and linear methods.28 Some models consider only RH, and some also consider temperature. When choosing between these models, it is important to consider their merits and drawbacks. For instance, in comparison to theoretical equations, empirical methods are likely to result in a lower mean absolute error and higher correlation values with reference instruments.25 However, empirical models should be used only in the RH/temperature range for which they were trained, unlike theoretical models, which apply to all RH/temperature values.28 Calibration models of all 3 types (empirical, linear, and theoretical) are evaluated in this paper as they pertain to the indoor-outdoor PurpleAir network.
This study examines the role LCS could have in determining exposure to particulates, with a focus on the role played by indoor PM concentrations. The aim is to demonstrate whether using outdoor PM as an exposure metric is sufficient, or whether indoor PM must also be considered. First, 2 datasets were selected. The first dataset comes from PurpleAir sensors deployed in Pittsburgh from the Real-time, Affordable, Multi-Pollutant (RAMP) sensor network.25,28,31 The second dataset consists of all publicly accessible PurpleAir data from Pittsburgh during the same timeframe as the RAMPs monitoring. Both datasets differentiate between sensors located in homes, workplaces, and the outdoors. Finally, to improve sample representativeness, a Monte Carlo simulation was run by coupling the datasets with personal schedules. The simulation’s results were used to examine the potential of indoor and outdoor PurpleAir sensors for estimating personal PM exposure. The results of the Monte Carlo simulation were compared for a range of calibration algorithms to examine the sensitivity of the dataset to different correction factors. In addition, the Monte Carlo results are provided for different demographics (based on age and employment) to determine how residential environment and personal lifestyle influence exposure.
2. Materials and Methods
2.1. Data Acquisition
The RAMPs dataset is maintained by the Center for Atmospheric Particle Studies (CAPS) at Carnegie Mellon University. They monitor a suite of pollutants and use dual-channel PA-II PurpleAir sensors for PM2.5 concentration measurements. A total of 21 RAMPs were deployed in Pittsburgh between January 1st, 2019, and April 21st, 2020. Two sensors were rotated to be deployed in 11 homes and 5 workplaces. Additionally, 4 outdoor sensors close to these homes were selected. As cooking contributes significantly to indoor PM concentrations, participants were instructed to install the PurpleAir sensor near the kitchen, in the dining room, or in the living room, based on the accessibility of power outlets. All homes had at least 1 sensor, generally placed near the kitchen, and one home had a second sensor located in the bedroom, per the participant’s request. For clarity, this paper will refer to this dataset as the ‘RAMPs dataset.’
The RAMPs team found participating homes through word of mouth, which may limit the socioeconomic diversity of the homes represented in that dataset. To obtain a more representative sample of homes, data from PurpleAir’s online map (https://map.purpleair.com/) was downloaded for all sensors active in Pittsburgh between July 24th, 2019, and April 21st, 2020, including 12 indoor PurpleAir sensors and 65 outdoor PurpleAir sensors. When downloading data, PurpleAir allows users to select either indoor or outdoor sensors, users to choose one or the other. Due to the large initial number of outdoor sensors, the 4 outdoor PurpleAir sensors located closest to each of the 4 outdoor RAMPs sensors were included in the dataset used in this study and the rest were disregarded. Proximity to RAMPs sensors was considered so that comparisons may be made between the concentrations reported in both datasets, as outdoor PM varies temporospatially. Of the indoor sensors, 8 were in homes and 4 were in workplaces, categorized by location using Google Maps street view (https://www.google.com/maps). Google Maps was also used to verify that no indoor sensors had been misclassified as outdoor and vice versa. For further assurance, the diurnal profiles of all sensors were reviewed for discrepancies that may indicate a sensor was wrongfully labeled as “outdoor” or ‘indoor.’ See the supplemental information for more details. Five of the homes in the PurpleAir dataset had names indicating participation in the Low-Cost Monitoring Project run by ROCIS (https://rocis.org/low-cost-monitoring-project/), an organization devoted to improving indoor air quality in the Pittsburgh area. As a part of the low-cost monitoring project, participants test out best management practices like filters, fans, and induction stoves. The sensors in this dataset were a mixture of single-channel PA-I models and dual-channel PA-II models.
Both the RAMPs dataset and the PurpleAir dataset had entries for 15 min PM2.5 concentrations, RH, and temperature.
2.2. PurpleAir Sensors
PurpleAir manufactures 3 models of sensors: PA-I-Indoor, PA-II, and PA-II-SD. The PA-I-Indoor model contains only a single PMS-1003 laser particle counter, manufactured by Plantower (Plantower Technology, Nanchang City, China). In contrast, the PA-II and PA-II-SD sensors contain 2 laser particle counters in each, of the models PMS-5003 and PMS-6003, respectively. Since it only has 1 laser particle counter, PA-I-Indoor will be referred to as a single-channel sensor. PA-II and PA-II-SD will be referred to as dual-channel sensors. The dual-channel sensors store the concentrations reported by each of their 2 laser particle counters. As the particles pass through the sensor, they affect the light intensity from a laser that is measured by a nearby detector. Knowledge of light scattering and how it relates to particle size at different regimes (Rayleigh, Mie, geometric) enables the calculation of a particle’s diameter based on its effect on the measured light intensity. The concentrations are stored in 2 channels, which PurpleAir calls channel A and channel B. In each channel, the Plantower laser particle counter reports particle concentrations in units of count per deciliter. The advantage of having 2 laser particle counters is the ability to check for agreement between the 2 channels as a form of data quality assurance. To obtain a mass concentration, Plantower employs 2 proprietary algorithms: cf_1 (calibrated for indoor monitoring) and cf_atm (calibrated for ambient monitoring). Additionally, every PurpleAir sensor is equipped with Bosch (Robert Bosch GmbH, Gerlingen, Germany) temperature-pressure-humidity sensors.32,33
2.3. Data Quality Assurance
Data quality and reliability are always concerns in LCS applications.25 To ensure data quality, clean-up was conducted using procedures combining elements from those described in Barkjohn et al. (2021) and Krebs et al. (2021). All quality control procedures were enacted on the 15 min averaged data downloaded from the PurpleAir sensors. The first step in data clean-up was removing points in which dual-channel sensors differed, as when these channels do not agree, there is a possibility that one or both channels are malfunctioning. To account for this, following the procedure in Krebs et al. (2021), if channel A and channel B both reported concentrations below 100 μg/m3, the points where they differed by at least 10 μg/m3 were removed. If either channel reported a value above 100 μg/m3, the data points where the percent difference was at least 10% were removed. Next, the remaining values in channels A and B were averaged. Regardless of channel agreement, all data points with values above 500 μg/m3 were removed, as this value approaches the accuracy threshold of PurpleAir sensors.35 All data points where the temperature was above 50 °C were removed, as it is unlikely that temperatures in Pittsburgh would exceed this value either indoors and outdoors. Additionally, all points where RH is not between 0% and 100% were removed, as sensors have been known to report RH above 200% when malfunctioning.34
After applying the method described above, 2,286 data points (out of 1,553,658) were removed due to a discrepancy between channel A and channel B. A single data point was removed due to a temperature above 540 °C (besides that point, the maximum temperature recorded by a sensor was 34.5 °C) and 45 data points were removed because the reported concentration was above 500 μg/m3.
2.4. Sensor Correction Factor
Plantower sensors require further calibration and correction as they are sensitive to their environments and PM properties.36,37 To optimize sensor performance, a correction factor is introduced. Correction factors are a key component of understanding PM2.5 concentration readings from LCS. In the interest of further exploring the effect of correction factors on LCS network function, in this paper, the effects of 4 calibration models are compared. All correction factors were applied to cf_1 data since that is the input they were calibrated for. In addition, cf_atm shows a nonlinearity that is not seen in cf_1.38 First is a physics-based model calibrated in Pittsburgh by Malings et al. (2020). This model accounts for hygroscopicity, as at high RH, Plantower sensors are known to overestimate PM concentrations.37,39 Correction using only a hygroscopic growth factor was insufficient, so this model also incorporates a linear correction. The second model, also by Malings et al. (2020), is a two-piece, linear function of the sensor reading, temperature, RH, and dewpoint. Both models by Malings et al. (2020) were calibrated in Pittsburgh using PM concentration measurements from all seasons of the year. The third model, also empirical, was developed by Barkjohn et al. (2021) for the United States Environmental Protection Agency (EPA). It is a United-States-wide correction created with concentration measurements from 16 states across all seasons. The fourth, and last, correction is a parsimonious linear calibration established by Liang et al. (2021) to assess the effects of wildfire smoke on indoor PM concentrations in California.
The physics-based model (from here on out, referred to as the “hygroscopic model”) depends on fRH(T,RH), which is the hygroscopic growth factor, as well as 2 linear correction terms, θ0 and θ1:
| 1 |
Details for calculating fRH(T,RH), θ1, and θ0 are included in the supplementary material. The parameter fRH(T,RH) represents the ratio of PM concentration at a given temperature and RH to the PM concentration at 22 °C and 35% RH, and it depends on temperature, humidity, and water activity. The terms θ1, and θ0 are linear correction coefficients.
The second model by Malings et al. (2020) which will, from now on, be referred to as the “two-piece model”, is given by
 |
2 |
Details regarding the coefficients β and γ and the calculation of DP can be found in the SI.
The third correction factor, the United-States-Wide correction,34 is a multilinear model with an additive RH term:
| 3 |
As this model was developed by the EPA, this paper shall refer to it as the “EPA correction.” This correction factor has the advantage of being applicable to multiple locations in the country, as it was calibrated using 24-hour average PM concentration measurements from 39 sites across 16 states, with a total of 12,635 points. Pittsburgh was not one of the calibration sites, so the use of the EPA model in this study may show how a site-specific correction compares to a general correction.
Lastly, one model is included that is site-specific and pollutant specific. Liang et al. (2021) developed the following parsimonious correction based on their observations of PM concentrations during wildfires in California:
| 4 |
As it was created for LCS measuring PM concentrations from wildfire smoke, this correction factor will be referred to as the “wildfire correction.” Its formula is simpler than the others used in this study, and its performance compared to the other corrections can assist in quantifying the value of complexity versus accuracy in a correction.
The 4 selected corrections were chosen to encompass a range of geographies and PM make-ups. In selecting certain corrections, the authors excluded others. In particular, the CF3 and CF3.440−42 corrections may be useful, as the latter has been calibrated with both PA-I and PA-II sensors, making it an apt choice for an indoor-outdoor network; the correction factors chosen for this study show a breadth of the available selection, but there are other good candidates which were not included due to the study’s scope.
2.5. Monte Carlo Simulation
The datasets were run through a Monte Carlo simulation to predict the levels of daily PM exposure a person would experience from inhabiting the sampled spaces. The Monte Carlo simulation takes a stochastic process and repeats it to show the possible outcomes of the process.43 The advantage of the Monte Carlo simulation is that it combines data from all sensor locations and all times of day into a single probability distribution for PM exposure. To improve representativeness, two major inputs to the Monte Carlo Simulation are the diurnal profiles of PM concentration at the sampling sites, and a set of randomly varied schedules for Pittsburgh residents. The schedules were collected and devised based on statistics shared by the U.S. Census Bureau for Allegheny County,44 including the portion of remote workers (roughly 1 in 5) and of schoolchildren–approximated here from the portion of the population between 10 and 19 as roughly 11% of the county. Certain assumptions are made about work and personal schedules based on social conventions, e.g., that a 40-hour work week between 9:00 A.M. to 5:00 P.M. is representative of a typical schedule of a working adult.
The diurnal pattern is obtained by applying a correction factor and calculating the 15 min average concentrations during the entire deployment period (i.e., the average concentration at 0:00, 0:15, 0:30, and so on). These averages were fed into a Monte Carlo simulation designed to approximate a random individual’s daily PM exposure. The simulation was run for N = 1,000 repetitions for 4 demographics of individuals: employed indoors, employed outdoors, schoolchildren, and work from home (WFH).
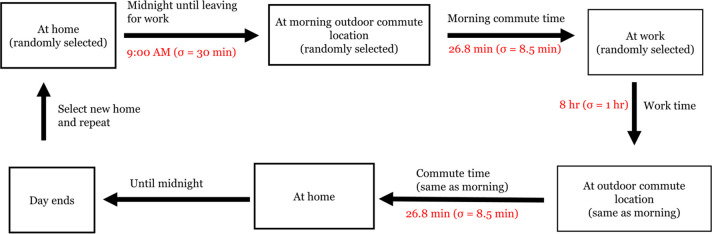
During each iteration, the Monte Carlo simulation randomly selected a home, workplace, and outdoor area. Then, the simulation places the individual at those locations during the appropriate times of day. This process is illustrated in Figure 1. For instance, on an average day, an individual in the “employed indoors” demographic is in their house until they leave home to commute at 9:00 AM. They commute for 26.8 min, which is the average commute time in Allegheny County.44 Next, they work for 8 h and commute for 26.8 min to return home. Lastly, they stay in their home until the day ends at midnight. To mirror variations in day-to-day schedule, the simulation randomizes the length of each activity with the normal distribution parameters in Table 1. After the simulation reaches midnight and a “full day” has elapsed, it uses the diurnal profiles to locate the PM concentration measurement corresponding to each 15 min time step in the day at the appropriate location. Lastly, the average PM2.5 exposure concentrations are calculated with equation (5):
| 5 |
where Δt is always 15 min, 96 is the number of 15 min increments in a day, and Ci is the concentration at the chosen locations at each time step.
Figure 1.
Daily schedules that were programmed into the Monte Carlo simulation. Red text shows an example of what the simulation looks like for the “indoors employee” demographic.
Table 1. Time Parameters Utilized in the Monte Carlo Simulationa.
| Leave for work/school/walk | Commute timeb | Work time | |
|---|---|---|---|
| Employed indoors | 9:00 AM (σ = 30 min) | 26.8 min (σ = 8.5 min) | 8 h (σ = 1 h) |
| Employed outdoorsc | 9:00 AM (σ = 30 min) | 26.8 min (σ = 8.5 min) | 8 h (σ = 1 h) |
| Schoolchildrend | - | 26.8 min (σ = 8.5 min) | 8:00 (σ = 20 min) to 3:00 (σ = 0 min) |
| Work from homee | 9:00 AM (σ = 30 min) | 30 min (σ = 10 min) | - |
Value listed is the mean (σ = standard deviation).
Commute time is repeated twice a day (to and from work). It is calculated once per day: the same value is used for both the morning and evening commute.
The “workplace” chosen in this scenario is an outdoor sensing site.
Schools operate on a set schedule, so the time at which the student leaves home is calculated backwards from the arrival time and commute time.
In the WFH scenario, the “commute” is a walk outside.
3. Results and Discussion
3.1. Correction Factor Effects on Concentration Measurements
The raw concentrations recorded by the sensors ranged from 0 to 497 μg/m3 (RAMPs) and 0 to 492 μg/m3 (PurpleAir). The raw mean concentrations were 8.3 μg/m3 (RAMPs) and 5.5 μg/m3 (PurpleAir). When inspecting for differences between indoor and outdoor measurements, in the RAMPs dataset, the raw mean outdoor concentration was 63.0% greater than the raw mean indoor concentration. However, the maximum raw concentration recorded indoors was 90.9% greater than the maximum raw concentration recorded outdoors. In the PurpleAir dataset, the raw mean outdoor concentration was 314.1% greater than the raw mean indoor concentration. The raw maximum concentration in this dataset was also highest indoors and was 47.2% greater than the raw maximum recorded outdoors. Applying the correction factors resulted in certain clear trends. The EPA and fire corrections yielded lower average concentrations in both datasets, when compared to the other corrections.
Figure 2 shows box plots illustrating the effect of the correction factors on the raw data, including the median and quartiles of each dataset with various corrections applied. The median concentration is an average measure of a dataset that is not skewed by outliers. If a dataset’s outdoor-located sensors have median concentrations close to those of the indoor sensors (meaning sensors in homes and workplaces), that serves as an indicator that the baseline PM concentrations are at a similar level both indoors and outdoors. Across the 4 corrections applied, the median concentrations vary, as do the differences between indoor and outdoor differences. For example, as illustrated in Figure 2, the raw indoor-outdoor median gap was 4.1 μg/m3 in the RAMPs dataset and 12.5 μg/m3 in the PurpleAir dataset. In comparison, the hygroscopic correction factor resulted in gaps of 1.5 μg/m3 and 7.9 μg/m3 in the RAMPs and PurpleAir datasets, respectively. The EPA correction factor resulted in the minimum difference in medians between indoor and outdoor sensor readings, 2.9 μg/m3 in the PurpleAir data and 0.03 μg/m3 in the RAMPs data, respectively. When the two-piece correction was applied to the PurpleAir dataset, the outdoor median was 4.26 μg/m3 greater than the indoor median (0.9 μg/m3 for RAMPs). The wildfire correction reduced each concentration by a factor of 0.53, but it did not mitigate the gap between indoor and outdoor medians, as it simply proportionally shrunk the gap without involving environmental factors.
Figure 2.
Box plots of the RAMPs (A) and PurpleAir (B) datasets with the hygroscopic, EPA, two-piece, and wildfire correction factors, and the raw data. Indoor (home and workplace) data is shown in blue, outdoor in orange. Outliers not shown. Data is from the entire duration of the study. Box boundaries represent the 1st and 3rd quartiles, with the median indicated by a bar in the center. The whiskers show the rest of the distribution, excluding outliers.
The interquartile range (IQR) of the dataset represents a robust measure of the results while excluding outliers. Comparing interquartile ranges is a way to check if a correction shifted concentrations upwards or downwards, or whether it shrunk or expanded the range of exposures. The two-piece correction and the EPA correction resulted in similar interquartile ranges that were smaller than that of the raw data. For example, for the outdoor PurpleAir measurements, the interquartile range was 6.1 μg/m3 with the two-piece correction and 6.3 μg/m3 with the EPA correction, compared to 13.1 μg/m3 without any correction applied. The hygroscopic correction factor consistently resulted in a larger interquartile range (as high as 9.7 μg/m3 for the PurpleAir dataset outdoor data and 3.8 μg/m3 for the RAMPs outdoor data). However, for the outdoor concentrations, the raw data had a larger interquartile range than any correction factor. These correction factor effects indicate that the hygroscopic-based correction will preserve a larger set of concentration values, while the EPA and empirical corrections will emphasize values closer to the median, though effects may vary if sensors are placed in a different climate or if PM composition is different. If directly determining the accuracy of a sensor correction is not feasible, it is beneficial to understand the strengths, weaknesses, and effects that the applied correction factor has on the data. The trends outlined in this section can guide interpretation of data in such cases.
Every correction except the wildfire correction (indoor and outdoor) and the EPA correction (outdoor only) caused an increase in the median concentration when compared to the raw data. The indoor PurpleAir data, which included predominantly low concentrations (raw median = 1.2 μg/m3), saw an increase in the reported median with every correction factor save the wildfire model. By nature of being a parsimonious linear correction with a slope less than 1.0, the wildfire correction cannot increase the reported value regardless of other factors. PurpleAir sensors are known to overestimate PM concentrations, by roughly 40%, and as RH increases, PurpleAir sensors’ error increases.25,26,45 As such, one might expect correction factors for PurpleAir sensors to decrease the reported concentrations. That the correction factors increased them may indicate that for datasets with predominantly low PM concentrations, these correction factors are overly conservative. Another explanation is that these correction factors account for the sensitivity of the sensors’ limit of detection.28,36 Plantower sensors’ limits of detection are known to depend on numerous factors, and as a result, their literature values vary widely.28,36 Sensors located in indoor/lab settings will report different (usually lower) limits of detection than sensors placed outdoors. Further, correction factors can lower the limit of detection of Plantower sensors.46 Thus, differences in correction factor performance may be occurring because some of these correction factors result in a lower limit of detection, while others may only be reliable at higher concentrations.
The different correction factors led to different post-correction distributions in the same data. Notably, the two-piece and hygroscopic correction factors, which were calibrated using concentrations from the same sites, had different effects of slightly shrinking (hygroscopic) and more noticeably shrinking (two-piece) the range of the dataset. While they were established based on outdoor measurements, the effects of the two-piece and hygroscopic corrections on indoor and outdoor concentrations are similar. The EPA correction minimized the gap between indoor and outdoor concentrations. The wildfire correction factor performs differently, possibly due to the fact it was calibrated at a different location under heavily polluted environments. The correction factors showed consistency in their effects across the two datasets.
3.2. Assessment of PM Concentrations
This section uses concentrations that have been corrected with the hygroscopic model, as this model was developed to be applicable for sites across Pittsburgh and is the default for RAMPs sensors. Inspection of the RAMPs dataset shows that the mean PM concentration is highest in homes (10.7 μg/m3) and lowest in workplaces (5.2 μg/m3), with outdoor locations falling in the middle (8.8 μg/m3). These findings vary from the PurpleAir dataset, where workplaces still maintained the lowest average, but homes reported the second-lowest mean (4.6 μg/m3) and, notably, the average outdoor concentration was 12.4 μg/m3, which is above the federal standard for primary emissions of 9.0 μg/m3. The homes in the PurpleAir dataset had characteristically lower concentrations than the homes in the RAMPs datasets, but 5 of these homes participated in the ROCIS Low-Cost Monitoring Project. As a part of the project, participants test out best management practices like filters, fans, and conduction stoves. This may explain in part why the PurpleAir dataset’s homes have low concentrations, and these homes had a mean concentration that was 2.1 μg/m3 lower than non-ROCIS ones. In contrast, indoor RAMPs sensors were located close to the kitchen, which can cause higher concentrations, and RAMPs outdoor sensors were deployed based on EPA guidelines to capture the city background. However, no significant details were documented for outdoor sensors from the PurpleAir dataset. Since indoor locations in the PurpleAir dataset had much lower averages than in the RAMPs dataset, simulation results from the PurpleAir dataset are taken to represent scenarios where indoor air quality is often much better than outdoor air quality. Such scenarios may occur either if a building has very clean air, with good filtration and a lack of polluting events, or conversely if the outdoor air has high PM concentrations, as is usually the case during fire events, smoggy days, or in industrial areas. The RAMPs dataset represents a scenario where indoor air quality is slightly worse than outdoor air quality, like homes where the windows are often open or where there is minimal AC and ventilation.
3.3. Characteristic Diurnal Patterns
Figure 3 presents diurnal patterns representing 4 examples of daily PM fluctuations at locations sampled in this study. The outdoor locations both saw a spike in PM concentrations around 9:00 AM, most likely due to commuter traffic and domestic activity. The RAMPs outdoor location experienced a more prolonged spike beginning at roughly 4:00 AM, which could be because this location is more central, causing it to be impacted by emissions from early-morning traffic. After this spike, both outdoor locations see a dip in PM concentrations until about 5:00 PM, possibly due to losses of semi-volatile ambient PM due to higher temperatures during midday hours, or due to shifts in the boundary layer. In the afternoon, concentrations steadily increase until the end of the day, but remain below the early morning’s peak.
Figure 3.
Sample diurnal patterns from sensors located at a: RAMPs workplace (A), outdoor RAMPs location (B), RAMPs home (C), PurpleAir workplace (D), outdoor PurpleAir location (E), and PurpleAir home (F). Diurnal patterns represent averages of selected sites throughout the whole sampling period.
The RAMPs workplace sensor experienced spikes in PM concentration from around 6:00 AM until 9:00 PM, with the largest peak around 11:00 AM. This location represents a gym, so the spikes are likely due to increased human traffic during human hours and the ensuing emission events. The PurpleAir home location shows 2 sets of spikes. The first occurs in the morning and early afternoon, between 6:00 and 2:00, with peaks between 9:00 and 1:00. Presumably, these peaks are due to domestic activities in the morning. In the evening, there is a large spike around dinnertime, roughly 6:00 PM, most likely due to emissions from a gas stove.
3.4. The Effect of Correction Factors on the Monte Carlo Simulation
Once the Monte Carlo model is applied to the data, some patterns emerge. A violin plot depicting the probability distribution of a range of exposures is shown in Figure 4 for each correction and demographics. The RAMPs dataset does not exhibit a large variation among the different groups: the average PM exposure of each demographic was always within 0.75 μg/m3 of the average exposures of the other demographics. This did not change when different corrections were applied, and some corrections even further decreased this value. The pattern in the PurpleAir dataset, however, is that the outdoor worker demographic experiences a greater exposure than the other demographics. Even in the correction with the least gap between the outdoor workers and the other groups (EPA correction), this demographic experienced an average exposure over 1.1 μg/m3 greater than the average exposure of the other 3 groups, and this gap increases up to nearly 2.9 μg/m3 when other corrections are applied. Also, in the RAMPs dataset, the choice of indoor environment seems to have a minor effect on the predicted PM exposure. That is, the WFH demographic, which spends the day at home, has similar predicted exposure to the indoor employee, who spends about 8 h at work. This is despite the average concentrations from RAMPs in homes being higher than the average concentrations from RAMPs in workplaces. This may be due to the time-variation of home PM concentrations, as several of the RAMPs homes had near-zero PM concentrations during workday hours, but a high average concentration resulting from a spike in PM concentrations during the early mornings and in the evening, in the hours where inhabitants may have been cooking or cleaning.
Figure 4.
Top: violin plot of Monte Carlo simulation results for the RAMPs dataset (A-D) Bottom: PurpleAir dataset (E-H). The plots show the probability density of exposure concentration of four demographics, with a box plot in the center. Circles indicate the medians, and each box encompasses the interquartile range. (If there was a notable probability of an exposure of 0 μg/m3, there is an appearance of a flat bottom). The black lines represent the average outdoor concentrations.
The effects of the correction factors on the Monte Carlo simulation are reminiscent of their effects on the raw data. Correction factors that shrunk the interquartile range (2-piece, EPA, and wildfire) resulted in compact probability densities in comparison to corrections with a larger IQR. The Monte Carlo simulation outputs results for 4 demographics, 3 of which spend most of their day indoors. The differences between the indoors-heavy demographics and the outdoors-intensive demographics depend on which inputs the correction factors use, as variables like temperature and humidity can look different indoors versus outdoors. For example, the EPA correction minimized the differences between indoor and outdoor medians as seen in Figure 2, while the hygroscopic correction resulted in the maximum differences between these medians. With the EPA correction applied, the difference in medians between the indoor and outdoor worker demographics decreases by 41% (RAMPs) and 63% (PurpleAir) when compared to the hygroscopic correction.
The violin plot in Figure 4 shows the “peaks” and “valleys” of the probability density of PM exposure depending on the correction factor. Each violin is a mirrored and flipped density plot, such that the width is proportional to the number of points that occupied the corresponding value. The “peaks” represent PM exposures that occurred most frequently in the Monte Carlo model (the modes). The “valleys” represent the exposures that occurred least frequently.
The indoor employee demographic has 2-3 modes, depending on the correction factor used. The median daily exposure experienced by this demographic ranges from 3.6 μg/m3 to 8.3 μg/m3 (RAMPs) or 2.1 μg/m3 to 4.7 μg/m3 (PurpleAir). This demographic’s modes are consistently prominent and well-defined. This may be due to the large number of hours the employee spends in their office. Offices are more likely to have stable PM concentrations due to HVAC and a lack of indoors cooking and cleaning during working hours. Thus, spending time at different offices with different PM levels may lead to a noticeable effect on exposure. The schoolchildren demographics’ violin plots are visually similar to those of the indoor employees. The WFH demographic experiences a wider range of PM exposures, from 0.2 μg/m3 to 22.0 μg/m3 (RAMPs dataset) and 0.01 μg/m3 to 9.6 μg/m3 (PurpleAir dataset), though its medians are in line with the indoor employees and schoolchildren.
In the RAMPs dataset, the outdoors employees show similar trends as the schoolchildren and indoors employees (median exposures ranging from 4.5 to 8.8 μg/m3 with 2-3 modes). In contrast, in the PurpleAir dataset, the outdoors employees experience higher median exposures ranging from 3.8 μg/m3 to 7.7 μg/m3 depending on the correction factor used. Indoor and outdoor concentrations in the RAMPs dataset were similar, while indoor concentrations were lower than outdoor concentrations in the PurpleAir dataset. This may be due to the comparatively low indoor concentrations reported in the PurpleAir dataset, which are likely attributable to the ROCIS Low-Cost Monitoring Project. Additionally, in the RAMPs dataset, outdoor sensors were placed in known locations with the goal of monitoring the ambient air. But in the PurpleAir dataset, it is possible that the sensors were purchased specifically to monitor an outdoor source, as the sensors were all purchased by consumers with significant enough concern about air quality to invest in a PM sensor. Thus, the higher outdoor employee medians in the PurpleAir dataset reflect that those outdoor concentrations are greater than the corresponding indoor concentrations, but the reasons for these differences may be social or environmental.
In addition to differences among demographics, there are also differences in the expected exposures depending on the correction factor chosen. While there are similarities amongst demographics regardless of the correction factor, each correction affects the shape of the PM exposure distribution. The hygroscopic correction resulted in the greatest number of distinct “peaks” from frequently occurring values. Other correction factors had smoother distributions, implying that predictions made based on the hygroscopic correction factor will result in a larger set of likely concentrations, while the other correction factors will emphasize only the most prominent recurring concentrations. The two-piece correction resulted in median values closest to those of the hygroscopic correction, but its “peaks” and “valleys” from frequently occurring exposures were less noticeable.
The EPA’s correction factor stabilized the range of exposure values. In the PurpleAir dataset, the EPA correction minimized the difference between the outdoor worker’s median exposure and the other demographics. For instance, with the EPA correction, the outdoor worker’s median exposure was within 0.79 μg/m3 of all 3 other demographics, compared to the maximum of 3.24 μg/m3 with the two-piece correction. The EPA correction is the only formula considered in this paper that considers RH without considering temperature. Perhaps due to the differences in indoor and outdoor temperature-RH dependencies, this had the effecting of raising indoor exposures and reducing outdoor exposures. Another possibility is that the EPA’s correction factor stabilizes the data because it has been calibrated to work with sensors across a range of climates using data from 16 states.34 In comparison, the other correction factors were each devised for LCS in one region only.
The wildfire correction’s effect is to shrink each data point to 0.53 times its original value, leading to the lowest predicted exposures of all corrections considered in this analysis. This correction factor was developed for a study on PM from smoke infiltration, so the low concentrations it predicts may be indicative of the difference between PurpleAir sensor’s ability to detect PM from wildfires compared to urban PM in Pittsburgh.
3.5. Monte Carlo Simulation Outputs
For the analysis in this section, the Monte Carlo predicted exposures for the hygroscopic correction are examined in more detail. The hygroscopic correction was selected as it had a greater number of distinct modes than other correction factors and was calibrated in Pittsburgh, where the data in this analysis was collected. Figure 5 presents a detailed histogram of the Monte Carlo simulation showing the frequency of predicted exposures. A greater “counts” value indicates that exposures in a bin occurred more frequently in the Monte Carlo.
Figure 5.
A-D: histogram of the Monte Carlo simulation results for the RAMPs dataset using the hygroscopic correction factor. E-H: PurpleAir dataset. The blue lines show the simulations’ average exposure and the black lines show the average concentrations of the outdoor sensors. The count depicted on the y axis represents the number of times exposure in a given bin was obtained in the simulation.
The Monte Carlo results for the RAMPs dataset showed a consistent average daily exposure, with the largest to smallest average exposures varying by less than 0.7 μg/m3. The average daily exposure was within 1.3 μg/m3 of the outdoor average concentration for all 4 demographics. With RAMPs as the input, regardless of time spent outside, individual daily exposure is predicted to mirror the ambient average concentration, although discrepancies among individuals exist. Some discrepancies between demographics do exist, and in particular the “employed outdoors” demographic is likelier to experience exposures that are above the average outdoor concentration when compared to the WFH demographic. However, when the WFH demographic experiences high exposures, they are higher than those of other demographics. It is the only demographic of the 4 that experienced exposures above 20 μg/m3.
When using the PurpleAir data as the input, the Monte Carlo simulation showed greater sensitivity to the amount of time spent outdoors. With the exception of the “employed outdoors” demographic, the other 3 demographics’ averages were within 0.21 μg/m3 of each other, signifying that exposure would be similar for individuals in the 3 demographics. For the outdoors employee— the only demographic where the simulation accounts for large amounts of time outdoors— the simulation mean was nearly 3 μg/m3 greater than the other demographics. In other words, the predicted exposure is sensitive to time spent outdoors when the PurpleAir dataset is used as the input.
In the case of the RAMPs dataset, where the indoor and outdoor concentrations had similar averages, outdoor concentration data is a useful metric for estimating personal exposure, as seen from the similarity between exposure levels estimated for the outdoor employee versus the other demographics. In the PurpleAir dataset, where indoor averages were lower than outdoor averages, exposure cannot be inferred with a purely indoor or purely outdoor network.
Furthermore, the simulation’s sensitivity to several parameters was examined. To determine sensitivity to the number of iterations, N, the value of N was varied from 500 to 2,000 while running the simulation. Across this range, the average concentrations varied on the order of 0.1 μg/m3 or less. As there is a discrete and limited number of locations used as inputs, even at low N values the simulation converges to a steady mean.
The simulation’s sensitivity to the time spent at work was examined by varying the mean and variance of the workday’s length. The workday variance had a minor impact on the mean exposure. When the variance was varied from 1 to 4 h, the mean exposure remained within 0.2 μg/m3, but the maximum exposure experienced by the worker (for both indoor and outdoor employees) increased by an average of 48% with a variance of 4 h compared to 1 h.
The exposures found in this work are comparable to findings in other exposure studies across various methodologies. Steinle et al.47 utilized the wearable Dylos 1700 on 35 participants in Edinburgh, Scotland for a 1-day duration, and observed mean exposures ranging from less than 2 μg/m3 to nearly 30 μg/m3. Median exposures were below 10 μg/m3 for nearly all participants. The results shown here fall on the lower end of that spectrum, though still quite higher than the minimum of 1.9 μg/m3. Steinle et al. also utilized GPS, enabling a correlation between microenvironments and exposure, and, similarly to this work, found low concentrations at workplaces. Exposure was higher during the transport microenvironment and was low at home, which is similar to the results of the PurpleAir dataset. He et al.48 predicted exposures during a wildfire event in the Pacific Northwest via Plantower a LCS network combined with wearable monitors. In a case study of one study participant, there was a nearly 70% reduction in PM2.5 from the wearable sensor compared to the ambient setting, which is lower than the estimated reduction from considering only the indoor sensors. In contrast to the results in this paper, spending more time in the home environment in He et al. resulted in lower exposures than the workplace environment. This highlights that different pollutant sources and lifestyles will alter where the majority of exposure takes place. VoPham et al.49 used a spatial model based on EPA monitoring station datasets and obtained a range of exposures across the country from 5.5 μg/m3 to 19.8 μg/m3, which this study is on the lower end of. That the exposures resulting from this study fall on the lower end of that value points that considering a full schedule, instead of purely considering ambient concentrations, could decrease predicted exposures on a population level.
These conclusions are applicable to the communities which were included in the study. However, there are numerous limitations that should be considered in their interpretation. To begin, the study’s participants’ socioeconomic status was not considered when selecting sensor sites. In the PurpleAir dataset, many of the sensors were ostensibly purchased by their owners, which could indicate having a certain amount of disposable income. As such, these findings may or may not be representative across socioeconomic spectra. Next, the corrections selected were developed for outdoor PurpleAir sensors, and no collocation was done in this study to test how the corrections functioned indoors compared to a reference. This may have implications if most of the indoor pollution during a particular event was indoor-generated (not from infiltration). There is a wealth of correction factors available–the ones included in this study represent only a fraction. Each was chosen such that a range of geographies and particle make-ups was considered, yet in choosing to include these corrections, others were excluded. Additionally, the results and discussion are meant to be applied at a demographic level only. The impacts of especially polluted microenvironments, such as restaurants or areas in near proximity to highways, are not given special consideration, though it is possible that exposure will increase if demographics spent relatively little time in these environments. Notably, outdoor concentrations are used as a proxy for the commuting microenvironment, though the outdoor sensors in this study were not placed in areas representative of a typical commute (on a busy highway, a bus, or similar setting). Indoor air quality was explored purely through the lens of indoor PM concentrations, and indoor infiltration of outdoor PM is not explored in depth, though depending on time of year, lifestyle, and building age, it may have a notable effect on exposure.
4. Conclusions
While people spend the majority of their time indoors, public health guidance and research is often based on outdoor PM measurements due to their accessibility. In this project, an indoor-outdoor sensor network was used to predict personal exposure to PM. To increase the representativeness of the samples, this study employs Monte Carlo simulations to investigate the efficacy of LCS when placed both indoors and outdoors for predicting personal PM exposure on a demographic level. Two datasets were constructed for analysis: the first is comprised of RAMPs with a PurpleAir monitor attached, which was placed in homes and public spaces around Pittsburgh. The second dataset is built from public PM measurements in Pittsburgh downloaded from PurpleAir. These datasets are also used to examine how the correction factor used on the PurpleAir measurements affects the outcome of the Monte Carlo analysis.
In the RAMPs dataset, using outdoor PM was sufficient to estimate personal exposure, as the differences between estimates based on spending several hours outside (“outdoor employee”) versus remaining almost exclusively indoors (“work from home”) were within 1.0 μg/m3 of each other no matter which correction factor was used. In addition, in this dataset, the estimated exposures from the Monte Carlo model were always very close to the outdoor average concentration. In the PurpleAir dataset, estimated exposures did depend on the time spent outdoors. In the Monte Carlo model, the difference between exposure estimates of the indoor-intensive demographics were small, but the differences between the indoor-intensive demographics and outdoor employee were nearly 15 times larger. If only the average outdoor concentration were considered, exposure would be overestimated to about 3 times its value. A different dataset in a different location may yield different results, but the analysis here shows that outdoor PM concentrations are not necessarily sufficient to estimate personal exposure.
In the PurpleAir dataset, the Monte Carlo estimated exposure showed sensitivity to the number of hours spent outside, while the RAMPs dataset did not show this sensitivity. It is possible that this is due to the low indoor concentrations in the public PurpleAir dataset, which are in part due to the large number of ROCIS (Reducing Outdoor Contaminants in Indoor Spaces) participating homes in that dataset. Additionally, sensor locations within the house could be exaggerating these differences; further work on monitoring indoor air with low-cost sensors may illuminate how sensor placement affects results. Overall, the findings indicate that, for cases where the indoor and outdoor concentrations share similar averages, outdoor concentration data is a useful metric for estimating personal exposure. When indoor and outdoor averages vary (for example, if the outdoors is heavily polluted, or if there is an indoor exposure event such as cooking or a fire), more careful consideration is warranted.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsestair.3c00105.
More detailed methods for applying the sensor correction factors, correction factor descriptive statistics, a timeline of sensor deployment, sensor deployment maps, diurnal profiles for each site, and comparisons of ROCIS and non-ROCIS homes (PDF)
This publication was partially funded with support from the Heinz Endowments and with a grant from the US Environmental Protection Agency P3 program (grant #SU840167). It has not been formally reviewed by EPA and South Coast Air Quality Management District. The views expressed in this document are solely those of the authors and do not necessarily reflect those of the Agencies. EPA and South Coast Air Quality Management District do not endorse any products or commercial services mentioned in this publication.
The authors declare no competing financial interest.
Supplementary Material
References
- Kim K.-H.; Kabir E.; Kabir S. A Review on the Human Health Impact of Airborne Particulate Matter. Environ. Int. 2015, 74, 136–143. 10.1016/j.envint.2014.10.005. [DOI] [PubMed] [Google Scholar]
- Tian F.; Qi J.; Wang L.; Yin P.; Qian Z.; Ruan Z.; Liu J.; Liu Y.; McMillin S. E.; Wang C.; Lin H.; Zhou M. Differentiating the Effects of Ambient Fine and Coarse Particles on Mortality from Cardiopulmonary Diseases: A Nationwide Multicity Study. Environ. Int. 2020, 145, 106096 10.1016/j.envint.2020.106096. [DOI] [PubMed] [Google Scholar]
- Pope C. A.; Burnett R. T.; Thun M. J.; Calle E. E.; Krewski D.; Ito K.; Thurston G. D. Lung Cancer, Cardiopulmonary Mortality, and Long-Term Exposure to Fine Particulate Air Pollution. JAMA 2002, 287 (9), 1132–1141. 10.1001/jama.287.9.1132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brook R. D.; Rajagopalan S.; Pope C. A.; Brook J. R.; Bhatnagar A.; Diez-Roux A. V.; Holguin F.; Hong Y.; Luepker R. V.; Mittleman M. A.; Peters A.; Siscovick D.; Smith S. C.; Whitsel L.; Kaufman J. D. Particulate Matter Air Pollution and Cardiovascular Disease: An Update to the Scientific Statement from the American Heart Association. Circulation 2010, 121 (21), 2331–2378. 10.1161/CIR.0b013e3181dbece1. [DOI] [PubMed] [Google Scholar]
- Allen G.; Sioutas C.; Koutrakis P.; Reiss R.; Lurmann F. W.; Roberts P. T. Evaluation of the TEOM ® Method for Measurement of Ambient Particulate Mass in Urban Areas. J. Air Waste Manage Assoc 1997, 47 (6), 682–689. 10.1080/10473289.1997.10463923. [DOI] [PubMed] [Google Scholar]
- Chung A.; Chang D. P. Y.; Kleeman M. J.; Perry K. D.; Cahill T. A.; Dutcher D.; McDougall E. M.; Stroud K. Comparison of Real-Time Instruments Used To Monitor Airborne Particulate Matter. J. Air Waste Manage Assoc 2001, 51 (1), 109–120. 10.1080/10473289.2001.10464254. [DOI] [PubMed] [Google Scholar]
- Hauck H.; Berner A.; Gomiscek B.; Stopper S.; Puxbaum H.; Kundi M.; Preining O. On the Equivalence of Gravimetric PM Data with TEOM and Beta-Attenuation Measurements. J. Aerosol Sci. 2004, 35 (9), 1135–1149. 10.1016/j.jaerosci.2004.04.004. [DOI] [Google Scholar]
- Takahashi K.; Minoura H.; Sakamoto K. Examination of Discrepancies between Beta-Attenuation and Gravimetric Methods for the Monitoring of Particulate Matter. Atmos Environ 2008, 42 (21), 5232–5240. 10.1016/j.atmosenv.2008.02.057. [DOI] [Google Scholar]
- Snyder E. G.; Watkins T. H.; Solomon P. A.; Thoma E. D.; Williams R. W.; Hagler G. S. W.; Shelow D.; Hindin D. A.; Kilaru V. J.; Preuss P. W. The Changing Paradigm of Air Pollution Monitoring. Environ. Sci. Technol. 2013, 47 (20), 11369–11377. 10.1021/es4022602. [DOI] [PubMed] [Google Scholar]
- Klepeis N. E.; Nelson W. C.; Ott W. R.; Robinson J. P.; Tsang A. M.; Switzer P.; Behar J. V.; Hern S. C.; Engelmann W. H. The National Human Activity Pattern Survey (NHAPS): A Resource for Assessing Exposure to Environmental Pollutants. J. Expo Sci. Environ. Epidemiol 2001, 11 (3), 231–252. 10.1038/sj.jea.7500165. [DOI] [PubMed] [Google Scholar]
- Cadelis G.; Tourres R.; Molinie J. Short-Term Effects of the Particulate Pollutants Contained in Saharan Dust on the Visits of Children to the Emergency Department Due to Asthmatic Conditions in Guadeloupe (French Archipelago of the Caribbean). PLoS One 2014, 9 (3), e91136 10.1371/journal.pone.0091136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sofer T.; Baccarelli A.; Cantone L.; Coull B.; Maity A.; Lin X.; Schwartz J. Exposure to Airborne Particulate Matter Is Associated with Methylation Pattern in the Asthma Pathway. Epigenomics 2013, 5 (2), 147–154. 10.2217/epi.13.16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brauer M.; Amann M.; Burnett R. T.; Cohen A.; Dentener F.; Ezzati M.; Henderson S. B.; Krzyzanowski M.; Martin R. V.; Van Dingenen R.; van Donkelaar A.; Thurston G. D. Exposure Assessment for Estimation of the Global Burden of Disease Attributable to Outdoor Air Pollution. Environ. Sci. Technol. 2012, 46 (2), 652–660. 10.1021/es2025752. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perez L.; Tobías A.; Querol X.; Pey J.; Alastuey A.; Díaz J.; Sunyer J. Saharan Dust, Particulate Matter and Cause-Specific Mortality: A Case–Crossover Study in Barcelona (Spain). Environ. Int. 2012, 48, 150–155. 10.1016/j.envint.2012.07.001. [DOI] [PubMed] [Google Scholar]
- Connolly R. E.; Yu Q.; Wang Z.; Chen Y.-H.; Liu J. Z.; Collier-Oxandale A.; Papapostolou V.; Polidori A.; Zhu Y. Long-Term Evaluation of a Low-Cost Air Sensor Network for Monitoring Indoor and Outdoor Air Quality at the Community Scale. Sci. Total Environ 2022, 807 (Pt 2), 150797 10.1016/j.scitotenv.2021.150797. [DOI] [PubMed] [Google Scholar]
- Patel S.; Sankhyan S.; Boedicker E. K.; DeCarlo P. F.; Farmer D. K.; Goldstein A. H.; Katz E. F.; Nazaroff W. W.; Tian Y.; Vanhanen J.; Vance M. E. Indoor Particulate Matter during HOMEChem: Concentrations, Size Distributions, and Exposures. Environ. Sci. Technol. 2020, 54 (12), 7107–7116. 10.1021/acs.est.0c00740. [DOI] [PubMed] [Google Scholar]
- Ebelt S. T.; Petkau A. J.; Vedal S.; Fisher T. V.; Brauer M. Exposure of Chronic Obstructive Pulmonary Disease Patients to Particulate Matter: Relationships between Personal and Ambient Air Concentrations. J. Air Waste Manage Assoc 2000, 50 (7), 1081–1094. 10.1080/10473289.2000.10464166. [DOI] [PubMed] [Google Scholar]
- Abbatt J. P. D.; Wang C. The Atmospheric Chemistry of Indoor Environments. Environ. Sci. Process Impacts 2020, 22 (1), 25–48. 10.1039/C9EM00386J. [DOI] [PubMed] [Google Scholar]
- Liang Y.; Sengupta D.; Campmier M. J.; Lunderberg D. M.; Apte J. S.; Goldstein A. H. Wildfire Smoke Impacts on Indoor Air Quality Assessed Using Crowdsourced Data in California. Proc. Natl. Acad. Sci. U. S. A. 2021, 118 (36), e2106478118 10.1073/pnas.2106478118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li J.; Zhang H.; Chao C.-Y.; Chien C.-H.; Wu C.-Y.; Luo C. H.; Chen L.-J.; Biswas P. Integrating Low-Cost Air Quality Sensor Networks with Fixed and Satellite Monitoring Systems to Study Ground-Level PM2.5. Atmos Environ 2020, 223, 117293 10.1016/j.atmosenv.2020.117293. [DOI] [Google Scholar]
- Li J.; Li H.; Ma Y.; Wang Y.; Abokifa A. A.; Lu C.; Biswas P. Spatiotemporal Distribution of Indoor Particulate Matter Concentration with a Low-Cost Sensor Network. Build Environ 2018, 127, 138–147. 10.1016/j.buildenv.2017.11.001. [DOI] [Google Scholar]
- Snik F.; Rietjens J. H. H.; Apituley A.; Volten H.; Mijling B.; Di Noia A.; Heikamp S.; Heinsbroek R. C.; Hasekamp O. P.; Smit J. M.; Vonk J.; Stam D. M.; van Harten G.; de Boer J.; Keller C. U. Mapping Atmospheric Aerosols with a Citizen Science Network of Smartphone Spectropolarimeters. Geophys Res. Lett. 2014, 41 (20), 7351–7358. 10.1002/2014GL061462. [DOI] [Google Scholar]
- Gao M.; Cao J.; Seto E. A Distributed Network of Low-Cost Continuous Reading Sensors to Measure Spatiotemporal Variations of PM2.5 in Xi’an, China. Environmental Pollution 2015, 199, 56–65. 10.1016/j.envpol.2015.01.013. [DOI] [PubMed] [Google Scholar]
- Holstius D. M.; Pillarisetti A.; Smith K. R.; Seto E. Field Calibrations of a Low-Cost Aerosol Sensor at a Regulatory Monitoring Site in California. Atmos Meas Tech 2014, 7 (4), 1121–1131. 10.5194/amt-7-1121-2014. [DOI] [Google Scholar]
- Malings C.; Tanzer R.; Hauryliuk A.; Saha P. K.; Robinson A. L.; Presto A. A.; Subramanian R. Fine Particle Mass Monitoring with Low-Cost Sensors: Corrections and Long-Term Performance Evaluation. Aerosol Science and Technology 2020, 54 (2), 160–174. 10.1080/02786826.2019.1623863. [DOI] [Google Scholar]
- Tryner J.; L’Orange C.; Mehaffy J.; Miller-Lionberg D.; Hofstetter J. C.; Wilson A.; Volckens J. Laboratory Evaluation of Low-Cost PurpleAir PM Monitors and in-Field Correction Using Co-Located Portable Filter Samplers. Atmos Environ 2020, 220, 117067 10.1016/j.atmosenv.2019.117067. [DOI] [Google Scholar]
- Magi B. I.; Cupini C.; Francis J.; Green M.; Hauser C. Evaluation of PM2.5 Measured in an Urban Setting Using a Low-Cost Optical Particle Counter and a Federal Equivalent Method Beta Attenuation Monitor. Aerosol Science and Technology 2020, 54 (2), 147–159. 10.1080/02786826.2019.1619915. [DOI] [Google Scholar]
- Giordano M. R.; Malings C.; Pandis S. N.; Presto A. A.; McNeill V. F.; Westervelt D. M.; Beekmann M.; Subramanian R. From Low-Cost Sensors to High-Quality Data: A Summary of Challenges and Best Practices for Effectively Calibrating Low-Cost Particulate Matter Mass Sensors. J. Aerosol Sci. 2021, 158, 105833 10.1016/j.jaerosci.2021.105833. [DOI] [Google Scholar]
- Wang Y.; Li J.; Jing H.; Zhang Q.; Jiang J.; Biswas P. Laboratory Evaluation and Calibration of Three Low-Cost Particle Sensors for Particulate Matter Measurement. Aerosol Science and Technology 2015, 49 (11), 1063–1077. 10.1080/02786826.2015.1100710. [DOI] [Google Scholar]
- Liu H.-Y.; Schneider P.; Haugen R.; Vogt M. Performance Assessment of a Low-Cost PM2.5 Sensor for a near Four-Month Period in Oslo, Norway. Atmosphere (Basel) 2019, 10 (2), 41. 10.3390/atmos10020041. [DOI] [Google Scholar]
- Jain S.; Presto A. A.; Zimmerman N. Spatial Modeling of Daily PM2.5, NO2, and CO Concentrations Measured by a Low-Cost Sensor Network: Comparison of Linear, Machine Learning, and Hybrid Land Use Models. Environ. Sci. Technol. 2021, 55 (13), 8631–8641. 10.1021/acs.est.1c02653. [DOI] [PubMed] [Google Scholar]
- PurpleAir Inc. PurpleAir. https://www2.purpleair.com/ (accessed 2022-12-31).
- South Coast AQMD. Sensor List. http://www.aqmd.gov/sensors/-in-department/departments/filter-for/manufacturer/purpleair (accessed 2023-01-15).
- Barkjohn K. K.; Gantt B.; Clements A. L. Development and Application of a United States-Wide Correction for PM2.5 Data Collected with the PurpleAir Sensor. Atmos Meas Tech 2021, 14 (6), 4617–4637. 10.5194/amt-14-4617-2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krebs B.; Burney J.; Zivin J. G.; Neidell M. Using Crowd-Sourced Data to Assess the Temporal and Spatial Relationship between Indoor and Outdoor Particulate Matter. Environ. Sci. Technol. 2021, 55 (9), 6107–6115. 10.1021/acs.est.0c08469. [DOI] [PubMed] [Google Scholar]
- Kelly K. E.; Whitaker J.; Petty A.; Widmer C.; Dybwad A.; Sleeth D.; Martin R.; Butterfield A. Ambient and Laboratory Evaluation of a Low-Cost Particulate Matter Sensor. Environ. Pollut 2017, 221, 491–500. 10.1016/j.envpol.2016.12.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levy Zamora M.; Xiong F.; Gentner D.; Kerkez B.; Kohrman-Glaser J.; Koehler K. Field and Laboratory Evaluations of the Low-Cost Plantower Particulate Matter Sensor. Environ. Sci. Technol. 2019, 53 (2), 838–849. 10.1021/acs.est.8b05174. [DOI] [PubMed] [Google Scholar]
- Wallace L. A.; Zhao T.; Klepeis N. E. Indoor Contribution to PM2.5 Exposure Using All PurpleAir Sites in Washington, Oregon, and California. Indoor Air 2022, 32 (9), e13105 10.1111/ina.13105. [DOI] [PubMed] [Google Scholar]
- Jayaratne R.; Liu X.; Thai P.; Dunbabin M.; Morawska L. The Influence of Humidity on the Performance of a Low-Cost Air Particle Mass Sensor and the Effect of Atmospheric Fog. Atmos Meas Tech 2018, 11 (8), 4883–4890. 10.5194/amt-11-4883-2018. [DOI] [Google Scholar]
- Wallace L.; Zhao T.; Klepeis N. E. Calibration of PurpleAir PA-I and PA-II Monitors Using Daily Mean PM2.5 Concentrations Measured in California, Washington, and Oregon from 2017 to 2021. Sensors 2022, 22 (13), 4741. 10.3390/s22134741. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wallace L.; Bi J.; Ott W. R.; Sarnat J.; Liu Y. Calibration of Low-Cost PurpleAir Outdoor Monitors Using an Improved Method of Calculating PM. Atmos Environ 2021, 256, 118432 10.1016/j.atmosenv.2021.118432. [DOI] [Google Scholar]
- Bi J.; Wallace L. A.; Sarnat J. A.; Liu Y. Characterizing Outdoor Infiltration and Indoor Contribution of PM2.5 with Citizen-Based Low-Cost Monitoring Data. Environ. Pollut 2021, 276, 116763 10.1016/j.envpol.2021.116763. [DOI] [PubMed] [Google Scholar]
- Kroese D. P.; Brereton T.; Taimre T.; Botev Z. I. Why the Monte Carlo Method Is so Important Today. WIREs Computational Statistics 2014, 6 (6), 386–392. 10.1002/wics.1314. [DOI] [Google Scholar]
- U.S. Census Bureau . American Community Survey 5-year estimates. http://censusreporter.org/profiles/05000US42003-allegheny-county-pa/ (accessed 2023-09-09).
- Kim S.; Park S.; Lee J. Evaluation of Performance of Inexpensive Laser Based PM2.5 Sensor Monitors for Typical Indoor and Outdoor Hotspots of South Korea. Applied Sciences 2019, 9 (9), 1947. 10.3390/app9091947. [DOI] [Google Scholar]
- Wallace L. Intercomparison of PurpleAir Sensor Performance over Three Years Indoors and Outdoors at a Home: Bias, Precision, and Limit of Detection Using an Improved Algorithm for Calculating PM2.5. Sensors 2022, 22 (7), 2755. 10.3390/s22072755. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Steinle S.; Reis S.; Sabel C. E.; Semple S.; Twigg M. M.; Braban C. F.; Leeson S. R.; Heal M. R.; Harrison D.; Lin C.; Wu H. Personal Exposure Monitoring of PM 2.5 in Indoor and Outdoor Microenvironments. Science of The Total Environment 2015, 508, 383–394. 10.1016/j.scitotenv.2014.12.003. [DOI] [PubMed] [Google Scholar]
- He J.; Huang C.-H.; Yuan N.; Austin E.; Seto E.; Novosselov I. Network of Low-Cost Air Quality Sensors for Monitoring Indoor, Outdoor, and Personal PM2.5 Exposure in Seattle during the 2020 Wildfire Season. Atmos Environ 2022, 285, 119244 10.1016/j.atmosenv.2022.119244. [DOI] [Google Scholar]
- VoPham T.; Bertrand K. A.; Tamimi R. M.; Laden F.; Hart J. E. Ambient PM2.5 Air Pollution Exposure and Hepatocellular Carcinoma Incidence in the United States. Cancer Causes & Control 2018, 29 (6), 563–572. 10.1007/s10552-018-1036-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.