Skip to main content
NCBI home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2024 Aug 13.
Published in final edited form as: J Am Chem Soc. 2021 Apr 22;143(17):6601–6608. doi: 10.1021/jacs.1c01856

Computational Exploration of the Mechanism of Critical Steps in the Biomimetic Synthesis of Preuisolactone A, and Discovery of New Ambimodal (5 + 2)/(4 + 2) Cycloadditions

Hong Zhang 1, Alexander J E Novak 2, Cooper S Jamieson 3, Xiao-Song Xue 4, Shuming Chen 5, Dirk Trauner 6, K N Houk 7
PMCID: PMC11321821  NIHMSID: NIHMS2011123  PMID: 33887906

Abstract

Computational studies with ωB97X-D density functional theory of the mechanisms of the steps in Trauner’s biomimetic synthesis of preuisolactone A have elaborated and refined mechanisms of several unique processes. An ambimodal transition state has been identified for the cycloaddition between an o-quinone and a hydroxy-o-quinone; this leads to both (5 + 2) (with H shift) and (4 + 2) cycloaddition products, which can in principle interconvert via α-ketol rearrangements. The origins of periselectivity of this ambimodal cycloaddition have been investigated computationally with molecular dynamics simulations and tested further by an experimental study. In the presence of bicarbonate ions, the deprotonated hydroxy-o-quinone leads to only the (5 + 2) cycloaddition adduct. A new mechanism for a benzilic acid rearrangement resulting in ring contraction is proposed.

Graphical Abstract

graphic file with name nihms-2011123-f0001.jpg

INTRODUCTION

Cycloaddition reactions of readily available feedstock alkenes or alkynes are powerful transformations to convert simple starting materials into ring systems and have been used extensively in the synthesis of complex biologically active molecules.1–3 The understanding of the cycloaddition reactions performed under a variety of reaction conditions has attracted the sustaining interest of both experimentalists and theoreticians.4–7 A number of recently discovered cycloaddition reactions show ambimodal transition states (TSs) that connect one set of reactants and two or more different products.8–12 These reactions feature post-transition state bifurcations (PTSB), which lead to the formation of two or more products through a lower energy transition state connected to the single (ambimodal) transition state, with no intermediate intervening. Since the first ambimodal bispericyclic cycloaddition discovered by Caramella et al. in the dimerization of cyclopentadiene (Figure 1a),13 numerous pericyclic reactions with a bifurcating PES have been reported in the past few decades.14–21 Although the outcomes of such reactions cannot be predicted with conventional transition state theory, they can be investigated by molecular dynamics (MD) trajectory simulations.22,23

Figure 1.

Figure 1.

Open in a new tab

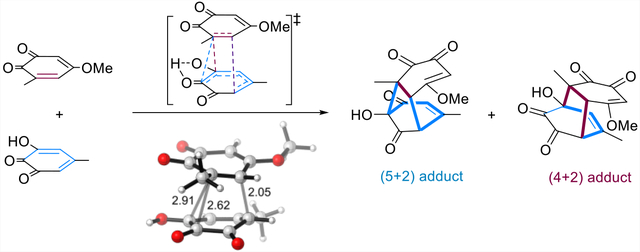
(a) Representative example of ambimodal TSs with two competing Diels–Alder reaction pathways. (b) Our recent prediction of ambimodal TS in bifurcating dipolar/Diels–Alder cycloaddition. (c) Ambimodal transition state leading to both (5 + 2) and (4 + 2) cycloaddition products, which could interconvert via α-ketol rearrangements.

We have had a long interest in understanding how periselectivity, selectivity in formation of the pericyclic reaction products, is controlled. In 2018, we predicted a (4 + 2)/(5 + 2) ambimodal TS in the cycloaddition between two molecules of an ortho-quinone produced via the oxidation of pyrogallol (Figure 1b).19 However, such ambimodal (4 + 2)/(5 + 2) cycloadditions have never been observed experimentally. Recently, a short, biomimetic synthesis of the fungal metabolite preuisolactone A24 was described by Trauner et al.25 They developed a synthetic pathway starting from catechol 1 and pyrogallol 2 (Figure 2). The initial key step involves o-quinone 3 and hydroxy-o-quinone 4, obtained by oxidation of 1 and 2, which could undergo a (5 + 2) cycloaddition to furnish tricyclic intermediate 5.

Figure 2.

Figure 2.

Open in a new tab

(a) Mechanism for the formation of preuisolactone A using catechol 1 and pyrogallol 2 as starting materials. (b) Computed structures and free energies of TSs, intermediates and products in the formation of preuisolactone A. All energies are denoted in kcal/mol, and interatomic distances are shown in angstroms. Energy profile in blue corresponds to the revised mechanism (path c).

We have now carried out computational studies of the cycloaddition reactions in the reaction course, concentrating mainly on the factors that govern the reaction pathways for the (5 + 2) cycloaddition reaction. We report computational and additional experimental investigations of (1) revision of the steps in Trauner’s biomimetic synthesis of preuisolactone A with the aid of density functional theory (DFT) calculation, (2) the periselectivity of the plausible cycloadditions between o-quinone 3 and hydroxy-o-quinone 4, and (3) quasi-classical direct molecular dynamics (MD) simulations to elucidate the control of reaction outcomes in ambimodal transition states leading to both (5 + 2) and (4 + 2) cycloaddition products.

COMPUTATIONAL METHODS

All quantum mechanical calculations were performed using the Gaussian 16 Rev. A.03 (sse4).26 Given the benchmark study done by Brinck and co-workers,27 geometry optimizations and frequency calculations were performed at the ωB97X-D28 /6–31+G(d, p) level of theory. The effect of solvation on molecular geometries was accounted for during optimizations using the SMD29 solvation model. Frequency calculations were carried out at the same level of theory to confirm the presence of local minima (no imaginary frequencies) and transition states (one imaginary frequency) on the PES. Transition structures have also been verified by intrinsic reaction coordinate (IRC) calculations.30,31 IRC calculations were performed to ensure that the saddle points found were true TSs connecting the reactants and the products. 3D renderings of stationary points were generated using CYLview 1.032 and PyMol 2.7. GaussView 5.0.9 was used to construct initial structures used in our calculations. Geometry optimizations were also performed with the M06–2X and B3LYPD3 functionals and the 6–31G(d) basis set for selected compounds and TSs to support the generality of our conclusions (see Table S1 in the SI).

MD simulations were performed at the same level of theory as those used for the geometry optimizations. Trajectories were propagated using the Progdyn/Gaussian interface developed by Singleton.21 Quasiclassical trajectories were initialized in the PES region near the TS. This involves normal mode sampling by adding the zero-point energy for each real normal mode and performing a Boltzmann sampling of geometries to afford the thermal energy available at 298 K with a random phase. The TS ensemble were then propagated for 400 fs in both the forward and backward directions until either one of the products is formed (second forming C–C bond shorter than 1.5 Å) or the reactants are generated. The classical equations of motion were integrated with a velocity-Verlet algorithm using Singleton’s program Progdyn with the energies and derivatives computed on the fly at ωB97XD/6–31+G(d, p) using Gaussian 16. The time step for integration is 1 fs.

RESULTS AND DISCUSSION

The reaction of catechol 1 and pyrogallol 2 in the presence of potassium ferricyanide produces a mixture of interconverting isomers comprising the diosphenol 7 and its acetal form 8 (Figure 2a).25 The fundamental step responsible for the tricyclic framework in 7/8 is C–C bond formation through a (5 + 2) cycloaddition. Details about the (5 + 2) cycloaddition can be obtained via the MD simulations (vide infra). In the second phase of the synthesis, Koser’s reagent was used to oxidize the mixture of 7 and 8 to afford diketo lactone 9 as intermediate. In the original proposed mechanism,25 intermediate 9 undergoes a benzilic acid type rearrangement with ring-contraction via oxetane 10 to simultaneously form one of the butyrolactones and the adjacent tertiary alcohol of preuisolactone A.

We began our investigation by comparing the computed relative stabilities of the proposed intermediates. The formation of diosphenol 7 from o-quinone 3 and hydroxy-o-quinone 4 is exoergic by 25 kcal/mol (Figure 2b). Isomer 7 is less stable than the isomer 8 by 4.7 kcal/mol, consistent with the experimental observation. Surprisingly, our computations reveal that the originally proposed intermediate 10 (path a, Figure 2a), in the conversion of 9 to final product, is dramatically higher in energy than 9 by 40.7 kcal/mol. The ring strain in the four-membered oxo-heterocycle might account for the high relative energy of 10. Specifically, the C–O–C angle is 87.4°, which is far from the ideal angle of 110° in ethers. We proposed another intermediate 11 with five-membered oxo-heterocycle, which could undergo a dyotropic shift33 to form the final product preuisolactone A (path b, Figure 2a). In water, 11 is more stable than 10 by 28.2 kcal/mol in terms of free energy. An angle of 97.3° shows that the ether bond in 11 has not been greatly distorted in the same manner as the intermediate 10. However, we could not find the TS for the conversion of 11 to preuisolactone A. Notably the experiment was carried out with aqueous phosphate buffer (pH = 8) during workup.25 Hence it is possible that PO43− or HPO42− could undergo intermolecular nucleophilic attack on the carbonyl. We thus explored path c, shown in Figure 2a, as an alternative that would facilitate a benzilic rearrangement, followed by spontaneous γ-lactonization involving a mixed carboxylic/phosphoric acid anhydride. As shown in Figure 2b, the PO43− attack (energy profile in blue) was calculated to be favored by 12.9 kcal/mol than the HPO42− attack (energy profile in red). The favorability of path c might be attributed to extra stabilization conferred by an OH···O hydrogen bond between the hydroxyl group and the carbonyl group. In other paths, this stabilizing interaction is diminished or difficult to achieve because of either geometric constraint or steric hindrance.

We next explored the detailed mechanism of the (5 + 2) cycloaddition reaction between o-quinone 3 and hydroxy-o-quinone 4. For ortho-quinone, we previously determined that two products are formed from an ambimodal TS because such units can not only serve as dienes for Diels–Alder cycloadditions but also undergo an intramolecular proton transfer to furnish the noncharge-separated (5 + 2) adduct (Figure 1b).19 Since 4 contains a α-hydroxy keto unit, it should also engage in ambimodal dipolar/Diels–Alder cycloadditions. The FMOs of the nucleophilic hydroxy-o-quinone 4 and the relatively electrophilic o-quinone 3 and are shown in Figure 3a.

Figure 3.

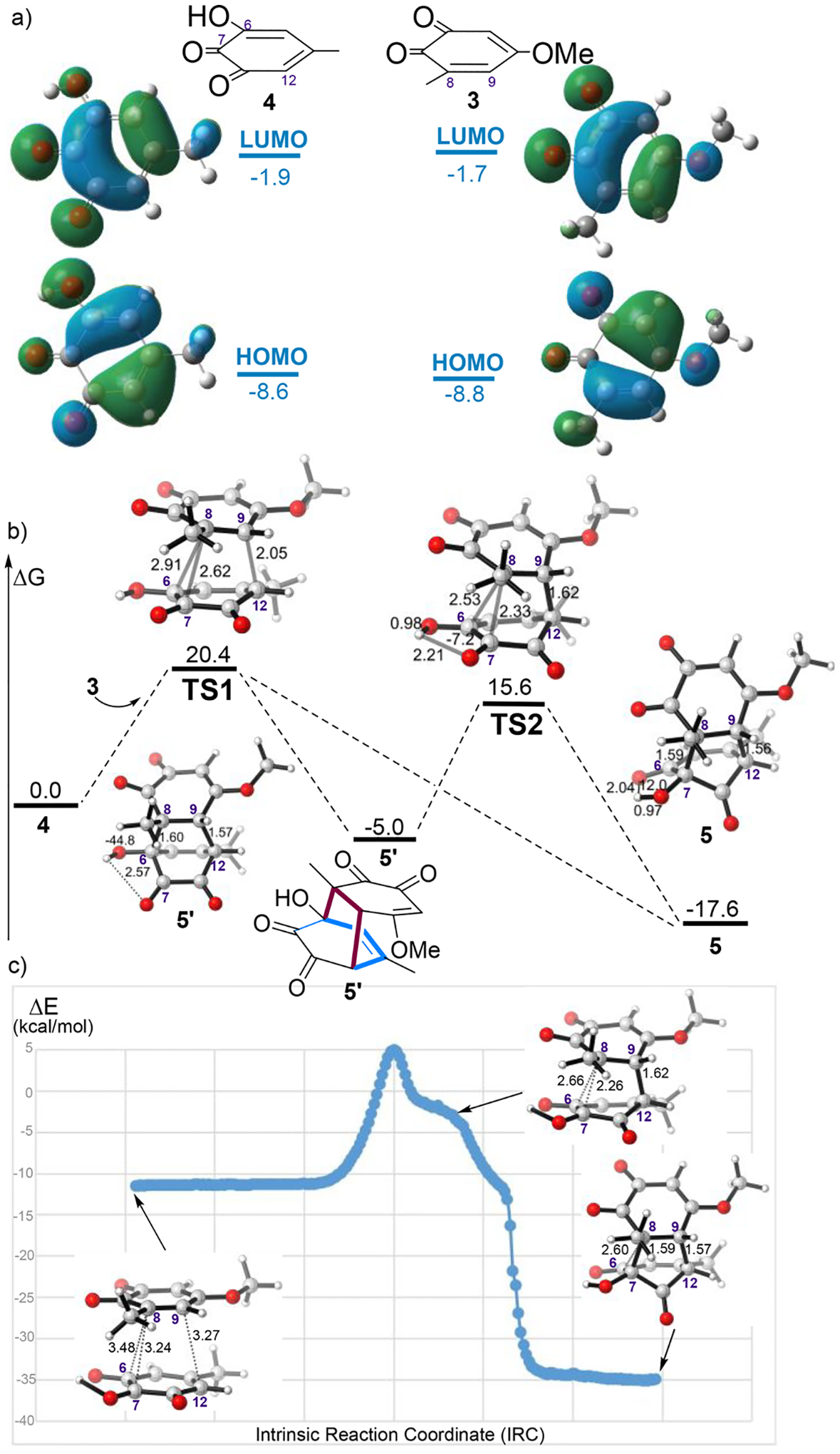
Figure 3.

Open in a new tab

(a) Computed FMOs of o-quinone 3 and hydroxy-o-quinone 4. (b) Computed structures and free energies of TSs and products in the reaction of 3 with 4. All energies are denoted in kcal/mol, and interatomic distances are shown in angstroms. (c) Plot of energies (ωB97XD/6–31+G(d, p)) versus points along the computed IRC starts from TS1. Molecular geometries are shown for select points on the IRC.

Figure 3b shows the free energy landscape of this reaction based on the transition structure TS1. TS1 has activation free energies of 20.4 kcal/mol in water with respect to the isolated reactants. As shown in Figure 3b, TS1 is highly asynchronous and features three partially formed σ-bonds, C8–C6, C8–C7, and C9–C12 with forming bond distances of 2.91, 2.62, and 2.05 Å, respectively, which are comparable to our previously discovered ambimodal TS of ortho-quinone system (2.52, 2.80, and 1.94 Å).19 The (4 + 2) cycloadduct 5′ is calculated to be 12.6 kcal/mol higher in energy than (5 + 2) cycloadduct 5. The two cycloadducts can interconvert through an α-ketol rearrangement,34 including a 1,2-sigmatropic alkyl shift and a proton transfer, with TS2 of relative free energies of 15.6 kcal/mol, corresponding to a barrier of 20.6 kcal/mol. At TS1, the forming bond for formation of the (5 + 2) cycloaddition is shorter in length and appears to be favored geometrically, in good agreement with the steepest-descent path from TS1 along the PES in mass-weighted coordinates (the minimum energy path (MEP), or IRC). The IRC displays that the two C–C bond formations in the (5 + 2) reaction are concerted but asynchronous, with no intervening minimum on the PES (Figure 3c). We thus hypothesized that TS1 is an ambimodal transition structure that could lead to (5 + 2)- and (4 + 2)-cycloadducts.

Quasi-classical direct dynamics simulations were used to evaluate the competition between the (5 + 2) and (4 + 2) pathways (Figure 4). Trajectories passing through TS1 lead to one of three possible outcomes. Out of 132 trajectories propagated, 20 (15%) afford the (4 + 2) adduct, 109 (83%) afford the (5 + 2) adduct, while 3 (2%) recross to reform the starting materials either with or without fully forming the C9–C12 bond. Figure 4b shows one example of each of these three reaction trajectories. These simulations demonstrate that the (5 + 2) pathway is much more favorable. We have defined reactions to be dynamically concerted when the time-gap between bond formation (defined as ≤1.7 Å) is <60 fs and dynamically stepwise when ≥60 fs.35 Trajectories leading to the (5 + 2) product have shorter time gaps between the two C–C forming events where the average time gaps are 115 fs for the (5 + 2) reaction and 171 fs for the (4 + 2) reaction. These results indicate that both pathways shown in Figure 4b are dynamically stepwise, which we have defined as reactions with time gaps of more than 60 fs, but the shape of the free energy surface may be more steeply descending on the (5 + 2) side of the bifurcation. We previously established the empirical linear equations that correlate MD product ratios to TS forming bond lengths.36 According to the equation, (5 + 2)/(4 + 2) ratio is calculated to be 15.3:1 in this case, in a good agreement to the major product predicted by trajectory simulation (5.1:1).

Figure 4.

Figure 4.

Open in a new tab

Three-dimensional plots of trajectory geometries. TS ensemble geometries for TS1 (red), TS2 (gold) are overlaid in contrasting colors for clarity. (a) Plot of all 136 trajectories propagated from TS1. (b) Randomly selected trajectories propagated from TS1 leading to each product.

Although MD calculation shows the dominance of the (5 + 2) pathway for this reaction, no (4 + 2) adduct was observed in the previous experiment.7 Since the experiment was performed in the presence of excess NaHCO3, we further investigated the role of bicarbonate ions on the periselectivity of the (5 + 2) cycloaddition. The relative acidity of the hydroxyl group in 4 was derived from the computed thermodynamics of model acid–base reactions involving intermolecular deprotonation of 4 by acetate.37,38 Using this method, the pKa value of 4 is calculated as 2.16, which is comparable to the pKa value of carbonic acid in water (3.58). The HOMO and the LUMO of 3 and 4a (anion of 4) are shown in Figure 5a. The HOMO energies of 4 and 4a are −8.6 and −7.3 eV, respectively. With a higher lying HOMO, the strength of the primary FMO interactions with 4a are more favorable than with 4. Both of the transition states TS1 and TS3 should be favored by the electrophilic nature of 3 and nucleophilic tendency of the 4/4a. Distortion/interaction analysis39–42 was used to compare the reactions of 3 with 4 or 4a (see Figure S6 in the Supporting Information). There is a stronger interaction between 3 and 4a in TS3 because of more favorable orbital interactions. Thus, a lower activation energy is found in the reaction of 3 with 4a due to the small distortion energy (of both 3 and 4a) and the relatively better overlap in the transition state.

Figure 5.

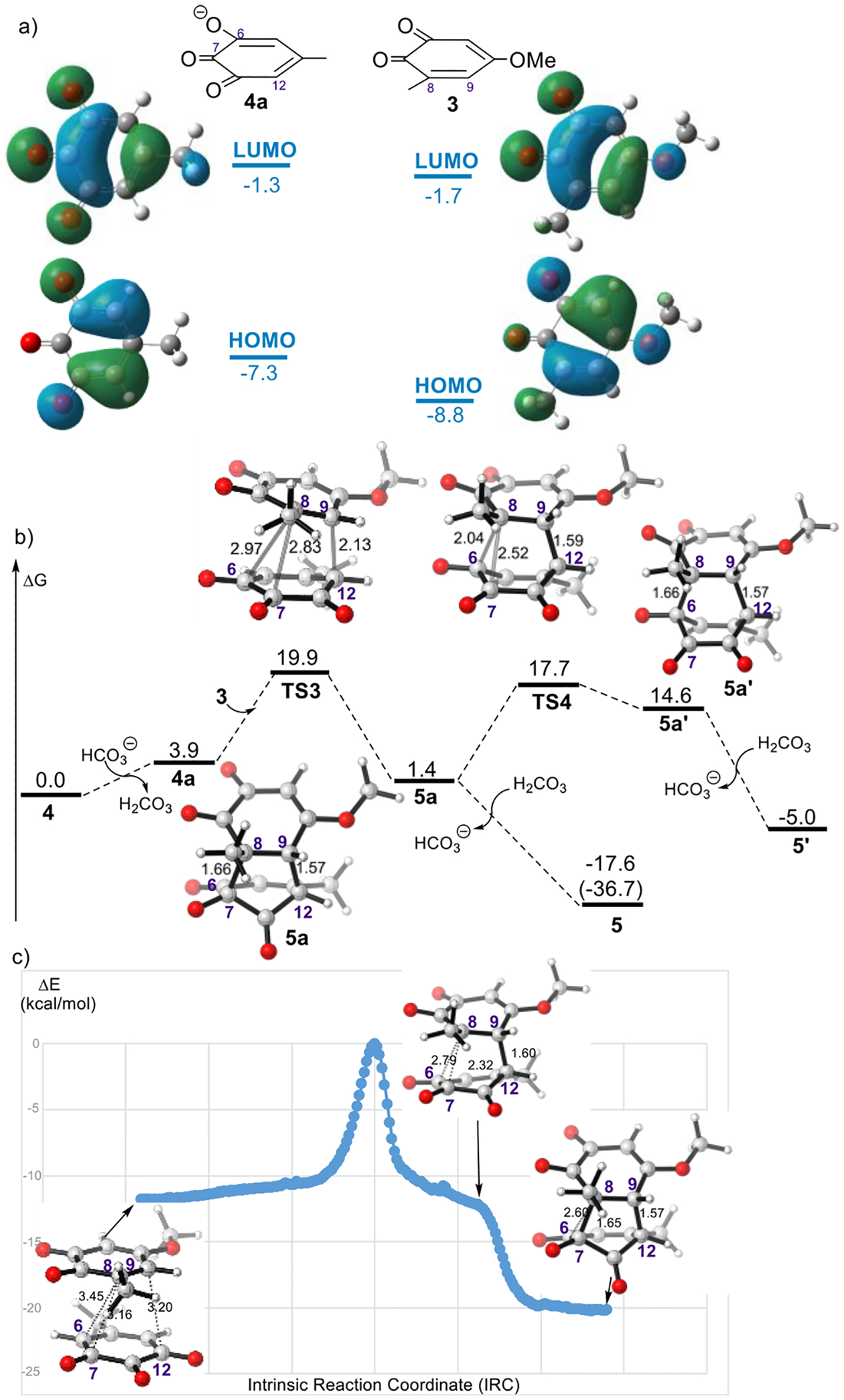
Figure 5.

Open in a new tab

(a) Computed FMOs of o-quinone 3 and hydroxy-o-quinone 4a. (b) Computed structures and free energies of TSs and products in the reaction of 3 with 4 in the presence of NaHCO3. All energies are denoted in kcal/mol, and interatomic distances are shown in angstroms. (c) Plot of energies (ωB97XD/6–31+G(d, p)) versus points along the computed IRC starts from TS3. Molecular geometries are shown for select points on the IRC.

We mapped out the free energy landscape of this reaction in the presence of excess bicarbonate ions (Figure 5b). The calculated free energies show that, compared to the neutral mode, the barrier is slightly lower for the ambimodal TS3. The (5 + 2) cycloadduct is significantly more stable than the (4 + 2) cycloadduct. Geometrically, TS3 is less biased toward (5 + 2) cycloaddition than TS1, with the C–C distance for the (5 + 2) cycloadduct being 0.14 Å shorter than the C–C distance for (4 + 2) cycloadduct. The TS structure, TS4, arising from the less stable intermediate 5a is 2.1 kcal/mol less stable than the TS2. The generation of ionic 5a is slightly endergonic by 1.4 kcal/mol. The exchange of a proton with the in situ generated H2CO3 furnishes 5, completing the (5 + 2) reaction. In contrast, the (4 + 2) cycloadduct in anion form, 5a′ is now significantly less stable than the (5 + 2) cycloadduct 5a. The IRC of TS3 indicates that the MEP of the reaction leads to the (5 + 2) product (Figure 5c). The IRC in water involves intramolecular proton transfer after the second C–C bond is virtually fully formed. We also analyzed the influence of a hydrogen-bonded tight-ion pair with water close to the carbonyl in the reaction of o-quinone 3 and hydroxy-o-quinone 4a. The calculated free energies show that (see Figure S7 in the Supporting Information), compared to the reaction in absence of water shown in Figure 5b, the barriers are lower for both the ambimodal TS and the product interconversion TS. But the solvent does not influence the nature of the ambimodal TS and we do not expect it to alter the product ratio.

To further rationalize the experimental outcomes in the presence of excess NaHCO3, we carried out the MD trajectory simulation of TS3 (Figure 6). Although the C8–C7 forming bond is only 0.14 Å shorter than C8–C6 in TS3, trajectory simulations show the (5 + 2) pathway to be overwhelmingly more favorable. Out of 210 trajectories, 12 (6%) recross, 198 (94%) yield the (5 + 2) adduct, but none yield the (4 + 2) adduct. In our previous investigation,36 when the difference between two bond lengths is 0.40 Å or greater, the percentage of the major product is >98%, nearly exclusive formation of one single product. This model fails to predict the dominance of the (5 + 2) pathway for this reaction. These results might be attributed to the instability of the (4 + 2) adduct anion, which apparently result in both kinetically and thermodynamically unfavorable to form the (4 + 2) adduct. The high periselectivity calculated in system with bicarbonate ions is consistent with the net (5 + 2) adduct observed experimentally. We thus proposed the mechanism in the presence of bicarbonate ions shown in Figure 7a, which proceeds through anionic intermediates.

Figure 6.

Figure 6.

Open in a new tab

Three-dimensional plots of trajectory geometries. TS ensemble geometries for TS1 (red), TS2 (gold) are overlaid in contrasting colors for clarity. (a) Plot of all 136 trajectories propagated from TS3. (b) Randomly selected trajectories propagated from TS3.

Figure 7.

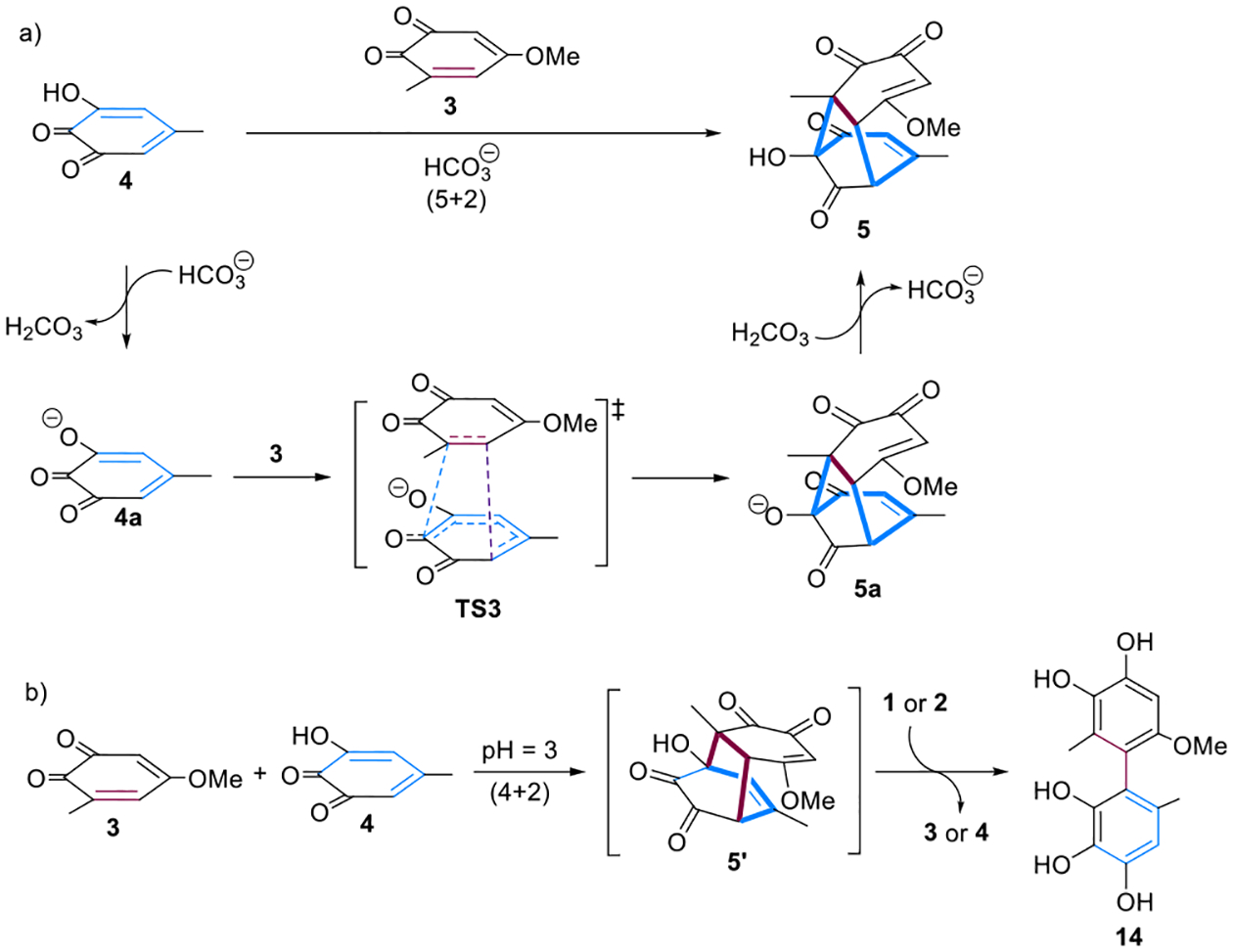
Figure 7.

Open in a new tab

Rationalization of the experimentally observations. (a) Proposed mechanism for the net (5 + 2) cycloaddition reaction in the presence of bicarbonate ions. (b) Experimental investigations and the isolation of the biphenyl derived from 5′.

The role of the bicarbonate ion was studied experimentally by performing the reaction in their absence, i.e., under more acidic conditions (see SI). Although the proposed (4 + 2) adduct 5′ could not be isolated from the reaction performed at low pH, we were able to identify biphenyl 14 as a product formed under these conditions. We hypothesize that it is formed from 5′ via retro-aldol reaction, tautomerizations, and redox-disproportionation (Figure 7b; see also SI). Compound 14 was calculated to be more stable than the (4 + 2) adduct 5′ by 19.0 kcal/mol (Figure S5). Under alkaline conditions, the (5 + 2) adduct 5 is notably also not isolated due to its instability and subsequent retro–Dieckmann reaction.

We also tested other cycloaddition possibilities of 3 and 4 (Figure 8). For the other conformation of TS1, i.e., TS1a, the steric repulsion might hinder the approach of 3 and 4. Using another double bond in 3 is also expected to be a less favorable pathway, as a methoxy group is more electron-donating than a methyl group. The calculated free energies show that TS1 is lowest in energy than other TS isomers. We then explored the homodimerization of 4. For the four TS isomers, TS44d is the lowest in energy, which involves the cycloaddition of the hydroxyl substituted double bond fragment. TS44d and TS1 are almost the same in energy. According to the reaction conditions, TS44d was also experimented by deprotonation one of the hydroxyl substituent (TS44d1) and two of the hydroxyl substituents (TS44d2). Both of the monoanionic TS44d1 and dianionic TS44d2 were found to be less favorable than anionic TS3 of the experimentally observed pathway. Note that the three partially formed σ-bonds are all elongated in anionic systems and the difference of the two dynamically competing bond lengths are more than 0.4 Å in the monoanionic TS44d1 and dianionic TS44d2.

Figure 8.

Figure 8.

Open in a new tab

Computed free energies of possible TSs in the reaction of o-quinone 3 and hydroxy-o-quinone 4 and the homodimerization of hydroxy-o-quinone 4. All energies are denoted in kcal/mol, and interatomic distances are shown in angstroms.

CONCLUSIONS

DFT calculations demonstrated the mechanism and origins of the cycloaddition reactions in the biomimetic synthesis of preuisolactone A. The aqueous phosphate buffer promotes benzilic rearrangement and spontaneous γ-lactonization to furnish preuisolactone A due to the intermediate structure featuring a strong hydrogen-bonding interaction between the hydroxyl and the carbonyl. For the reaction between o-quinone and hydroxy-o-quinone, the first ambimodal (4 + 2)/(5 + 2) cycloadditions have been detected experimentally with the aid of DFT calculations. We demonstrate experimentally and computationally that bicarbonate ions can direct the selectivity of these ambimodal reactions to the net dipolar cycloadducts via decreasing the stabilization of the Diels–Alder cycloaddition product by deprotonation.

Supplementary Material

Supporting Information

ACKNOWLEDGMENTS

We are grateful to the National Science Foundation (NSF CHE-1764328 to K.N.H.), the Fundamental Research Funds for the Central Universities the Natural Science Foundation of China (Grant 20720190042 to H.Z.) and National Institutes of Health for financial support (Grant R01GM126228 to D.T.). H.Z. is grateful for additional funding from the China Scholarship Council (CSC). A.J.E.N. is grateful for additional funding from New York University for a MacCracken and a Ted Keusseff fellowship. All calculations were performed on computational resources provided by the UCLA Institute of Digital Research and Education. We thank Dr. Tony Hu at the X-ray Diffraction Facility for his help with the crystal structure determination. The X-ray facility was supported partially by the National Science Foundation (NSF) Chemistry Research Instrumentation and Facilities Program (CHE-0840277) and Materials Research Science and Engineering Center (MRSEC) Program (DMR-1420073).

Footnotes

Supporting Information

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/jacs.1c01856.

Computational results; experimental details; coordinates and energies of stationary points (PDF)

Accession Codes

CCDC 2058287 contains the supplementary crystallographic data for this paper. These data can be obtained free of charge via www.ccdc.cam.ac.uk/data_request/cif, or by emailing data_request@ccdc.cam.ac.uk, or by contacting The Cambridge Crystallographic Data Centre, 12 Union Road, Cambridge CB2 1EZ, UK; fax: +44 1223 336033.

Complete contact information is available at: https://pubs.acs.org/10.1021/jacs.1c01856

The authors declare no competing financial interest.

Contributor Information

Hong Zhang, Department of Chemistry and Biochemistry, University of California, Los Angeles, California 90095, United States; College of Chemistry and Chemical Engineering, Xiamen University, Xiamen 361005, China.

Alexander J. E. Novak, Department of Chemistry, New York University, New York 10002, United States

Cooper S. Jamieson, Department of Chemistry and Biochemistry, University of California, Los Angeles, California 90095, United States

Xiao-Song Xue, Department of Chemistry and Biochemistry, University of California, Los Angeles, California 90095, United States.

Shuming Chen, Department of Chemistry and Biochemistry, University of California, Los Angeles, California 90095, United States.

Dirk Trauner, Department of Chemistry, New York University, New York 10002, United States.

K. N. Houk, Department of Chemistry and Biochemistry, University of California, Los Angeles, California 90095, United States

REFERENCES

  • (1).Carruthers W Cycloaddition Reactions in Organic Synthesis; Pergamon Press: Oxford, UK, 1990. [Google Scholar]
  • (2).Kobayashi S, Jørgensen KA Cycloaddition Reactions in Organic Synthesis; WileyVCH: Weinheim, Germany, 2002. [Google Scholar]
  • (3).Ishihara K; Sakakura A In Comprehensive Organic Synthesis II, 2nd ed.; Knochel P, Ed.; Elsevier, 2014. [Google Scholar]
  • (4).Woodward RB; Katz TJ The Mechanism of the Diels-Alder Rreaction. Tetrahedron 1959, 5, 70. [Google Scholar]
  • (5).Dewar MJS; Olivella S; Stewart JJP Mechanism of the Diels-Alder Reaction: Reactions of Butadiene with Ethylene and Cyanoethylenes. J. Am. Chem. Soc 1986, 108, 5771. [DOI] [PubMed] [Google Scholar]
  • (6).Goldstein E; Beno B; Houk KN Density Functional Theory Prediction of the Relative Energies and Isotope Effects for the Concerted and Stepwise Mechanisms of the Diels–Alder Reaction of Butadiene and Ethylene. J. Am. Chem. Soc 1996, 118, 6036. [Google Scholar]
  • (7).McLeod D; Nicolaj IJ; Thøgersen MK; Jessen NI; Jørgensen KA; Jamieson CS; Xue X-S; Houk KN; Liu F; Hoffmann R Expanding the Frontiers of Higher-Order Cycloadditions. Acc. Chem. Res 2019, 52, 3488. [DOI] [PubMed] [Google Scholar]
  • (8).Pham HV; Houk KN Diels–Alder Reactions of Allene with Benzene and Butadiene: Concerted, Stepwise, and Ambimodal Transition States. J. Org. Chem 2014, 79, 8968. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • (9).Ess DH; Wheeler SE; Iafe RG; Xu L;Çelebi-Ölçöm N; Houk KN Bifurcations on Potential Energy Surfaces of Organic Reactions. Angew. Chem., Int. Ed 2008, 47, 7592. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • (10).Rehbein J; Carpenter BK Do We Fully Understand What Controls Chemical Selectivity? Phys. Chem. Chem. Phys 2011, 13, 20906. [DOI] [PubMed] [Google Scholar]
  • (11).Hare SR; Tantillo DJ Post-Transition State Bifurcations Gain Momentum - Current State of The Field. Pure Appl. Chem 2017, 89, 679. [Google Scholar]
  • (12).Xue X-S; Jamieson CS; Garcia-Borras M; Dong X; Yang Z; Houk KN Ambimodal Trispericyclic Transition State and Dynamic Control of Periselectivity. J. Am. Chem. Soc 2019, 141, 1217. [DOI] [PubMed] [Google Scholar]
  • (13).Caramella P; Quadrelli P; Toma L An Unexpected Bispericyclic Transition Structure Leading to 4 + 2 and 2 + 4 Cycloadducts in the Endo Dimerization of Cyclopentadiene. J. Am. Chem. Soc 2002, 124, 1130. [DOI] [PubMed] [Google Scholar]
  • (14).See for example:; Celei-Olcm N; Ess DH; Aviyente V; Houk KN Lewis Acid Catalysis Alters the Shapes and Products of Bis-Pericyclic Diels - Alder Transition States. J. Am. Chem. Soc 2007, 1, 4528. [DOI] [PubMed] [Google Scholar]
  • (15).Yu P; Chen TQ; Yang Z; He CQ; Patel A; Lam YH; Liu CY; Houk KN Mechanisms and Origins of Periselectivity of the Ambimodal [6 + 4] Cycloadditions of Tropone to Dimethylfulvene. J. Am. Chem. Soc 2017, 139, 8251. [DOI] [PubMed] [Google Scholar]
  • (16).Thomas JB; Waas JR; Harmata M; Singleton DA Control Elements in Dynamically Determined Selectivity on a Bifurcating Surface. J. Am. Chem. Soc 2008, 130, 14544. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • (17).Wang Z; Hirschi JS; Singleton DA Recrossing and Dynamic Matching Effects on Selectivity in a Diels-Alder Reaction. Angew. Chem., Int. Ed 2009, 48, 9156. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • (18).Limanto J; Khuong KS; Houk KN; Snapper ML Intramolecular Cycloadditions of Cyclobutadiene with Dienes: Experimental and Computational Studies of the Competing (2 + 2) and (4 + 2) Modes of Reaction. J. Am. Chem. Soc 2003, 125, 16310. [DOI] [PubMed] [Google Scholar]
  • (19).Chen S; Yu P; Houk KN Ambimodal Dipolar/Diels-Alder Cycloaddition Transition States Involving Proton Transfers. J. Am. Chem. Soc 2018, 140, 18124. [DOI] [PubMed] [Google Scholar]
  • (20).Yu P; Patel A; Houk KN Transannular [6 + 4] and Ambimodal Cycloaddition in the Biosynthesis of Heronamide A. J. Am. Chem. Soc 2015, 137, 13518. [DOI] [PubMed] [Google Scholar]
  • (21).Ussing BR; Hang C; Singleton DA Dynamic Effects on the Periselectivity, Rate, Isotope Effects, and Mechanism of Cycloadditions of Ketenes with Cyclopentadiene. J. Am. Chem. Soc 2006, 128, 7594. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • (22).Pratihar S; Ma X; Homayoon Z; Barnes GL; Hase WL Direct Chemical Dynamics Simulations. J. Am. Chem. Soc 2017, 139, 3570. [DOI] [PubMed] [Google Scholar]
  • (23).Carpenter BK Nonstatistical Dynamics in Thermal Reactions of Polyatomic Molecules. Annu. Rev. Phys. Chem 2005, 56, 57. [DOI] [PubMed] [Google Scholar]
  • (24).Xu L-L; Chen H-L; Hai P; Gao Y; Xie C-D; Yang X-L; Abe I (+)- and (−)-Preuisolactone A: A Pair of Caged Norse-squiterpenoidal Enantiomers with a Tricyclo[4.4.01,6.02,8]decane Carbon Skeleton from the Endophytic Fungus Preussia isomera. Org. Lett 2019, 21, 1078. [DOI] [PubMed] [Google Scholar]
  • (25).Novak AJE; Grigglestone CE; Trauner D A Biomimetic Synthesis Elucidates the Origin of Preuisolactone A. J. Am. Chem. Soc 2019, 141, 15515. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • (26).Frisch MJ, et al. Gaussian 16 Revision A.03 2016.
  • (27).Brinck T; Linder M On the Method-dependence of Transition State Asynchronicity in Diels–Alder Reactions. Phys. Chem. Chem. Phys 2013, 15, 5108. [DOI] [PubMed] [Google Scholar]
  • (28).Chai JD; Head-Gordon M Long-Range Corrected Hybrid Density Functionals with Damped Atom-Atom Dispersion Corrections. Phys. Chem. Chem. Phys 2008, 10, 6615. [DOI] [PubMed] [Google Scholar]
  • (29).Marenich AV; Cramer CJ; Truhlar DG Universal Solvation Model Based on Solute Electron Density and on a Continuum Model of the Solvent Defined by the Bulk Dielectric Constant and Atomic Surface Tensions. J. Phys. Chem. B 2009, 113, 6378. [DOI] [PubMed] [Google Scholar]
  • (30).Fukui K Formulation of the Reaction Coordinate. J. Phys. Chem 1970, 74, 4161. [Google Scholar]
  • (31).Fukui K The Path of Chemical Reactions-the IRC Approach. Acc. Chem. Res 1981, 14, 363. [Google Scholar]
  • (32).Legault CY CYLview, 1.0 b; Universitéde Sherbrooke, 2009. [Google Scholar]
  • (33).For a review, see:; Fernandez I; Cossío FP; Sierra MA Dyotropic Reactions: Mechanisms and Synthetic Applications. Chem. Rev 2009, 109, 6687. [DOI] [PubMed] [Google Scholar]
  • (34).For a review, see:; Paquette LA; Hofferberth JE The α-hydroxy Ketone (α-Ketol) and Related Rearrangements. Org. React 2003, 62, 477. [Google Scholar]
  • (35).Black K; Liu P; Xu L; Doubleday C; Houk KN Dynamics, Transition States, and Timing of Bond Formations in Diels-Alder Reactions. Proc. Natl. Acad. Sci. U. S. A 2012, 109, 12860. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • (36).Yang Z; Dong X; Yu Y; Yu P; Li Y; Jamieson C; Houk KN Relationships between Product Ratios in Ambimodal Pericyclic Reactions and Bond Lengths in Transition Structures. J. Am. Chem. Soc 2018, 140, 3061. [DOI] [PubMed] [Google Scholar]
  • (37).Neufeldt SR; Jiménez-Osés G; Huckins JR; Thiel OR; Houk KN Pyridine N-Oxide vs Pyridine Substrates for Rh (III)-Catalyzed Oxidative C–H Bond Functionalization. J. Am. Chem. Soc 2015, 137, 9843. [DOI] [PubMed] [Google Scholar]
  • (38).Shen K; Fu Y; Li J; Liu L; Guo Q What Are the pKa Values of C–H Bonds in Aromatic Heterocyclic Compounds in DMSO? Tetrahedron 2007, 63, 1568. [Google Scholar]
  • (39).Ess DH; Houk KN Distortion/Interaction Energy Control of 1,3-Dipolar Cycloaddition Reactivity. J. Am. Chem. Soc 2007, 129, 10646. [DOI] [PubMed] [Google Scholar]
  • (40).Bickelhaupt FM The Activation Strain Model and Molecular Orbital Theory: Understanding and Designing Chemical Reactions. J. Comput. Chem 1999, 20, 114. [DOI] [PubMed] [Google Scholar]
  • (41).Fernández I; Bickelhaupt FM The Activation Strain Model and Molecular Orbital Theory: Understanding and Designing Chemical Reactions. Chem. Soc. Rev 2014, 43, 4953. [DOI] [PubMed] [Google Scholar]
  • (42).Bickelhaupt FM; Houk KN Analyzing Reaction Rates with the Distortion/Interaction-Activation Strain Model. Angew. Chem., Int. Ed 2017, 56, 10070. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supporting Information
NIHMS2011123-supplement-Supporting_Information.pdf (678.2KB, pdf)

RESOURCES