The global distribution and climate resilience of marine heterotrophic prokaryotes

Abstract

Heterotrophic Bacteria and Archaea (prokaryotes) are a major component of marine food webs and global biogeochemical cycles. Yet, there is limited understanding about how prokaryotes vary across global environmental gradients, and how their global abundance and metabolic activity (production and respiration) may be affected by climate change. Using global datasets of prokaryotic abundance, cell carbon and metabolic activity we reveal that mean prokaryotic biomass varies by just under 3-fold across the global surface ocean, while total prokaryotic metabolic activity increases by more than one order of magnitude from polar to tropical coastal and upwelling regions. Under climate change, global prokaryotic biomass in surface waters is projected to decline ~1.5% per °C of warming, while prokaryotic respiration will increase ~3.5% ( ~ 0.85 Pg C yr⁻¹). The rate of prokaryotic biomass decline is one-third that of zooplankton and fish, while the rate of increase in prokaryotic respiration is double. This suggests that future, warmer oceans could be increasingly dominated by prokaryotes, diverting a growing proportion of primary production into microbial food webs and away from higher trophic levels as well as reducing the capacity of the deep ocean to sequester carbon, all else being equal.

This study uses global datasets of marine prokaryotes to reveal that prokaryotic biomass varies by just under 3-fold across the global surface ocean, while metabolic activity increases by more than one order of magnitude from polar to tropical coastal and upwelling regions. The findings also suggest that shifts under climate change could lead to an increasingly microbial-dominated ocean.

Introduction

Marine heterotrophic prokaryotes (heterotrophic Bacteria and Archaea; hereafter prokaryotes) serve a key role in marine food webs and biogeochemical cycles^1,2. Across the global ocean, prokaryotes have been estimated to comprise ~30% of the biomass in the water column³ and respire over 50% of net primary production in surface waters^4,5. As a result, they represent an important pathway by which dissolved organic matter can be passed to higher trophic levels or sequestered in the deep ocean⁶. As oceans warm with climate change, impacts on prokaryotes could alter the transfer of energy between phytoplankton and larger heterotrophs (zooplankton and fish), as well as the global ocean’s capacity to sequester carbon^7,8.

From decades of observational studies, it is known that prokaryotes are abundant and metabolically active across the world’s oceans, from the tropics to the poles and from surface waters to under the seabed^9,10. These observations have been used to estimate total global marine prokaryotic abundance and biomass^3,9,11–13 and for assessments of prokaryotic community structure over smaller scales^12,14–16. However, unlike other groups such as phytoplankton^17–20 and zooplankton^21–23, there exists no synthesis of prokaryote observations to determine how their abundance and metabolic activity (production and respiration) change across global environmental gradients. This lack of large-scale, quantitative understanding limits our ability to develop and validate global models that explicitly incorporate prokaryotes, and to assess how they may be impacted by climate change. This limitation is illustrated by the fact that, although there are no less than 17 earth-system models from the Coupled Model Intercomparison Project Phase 6²⁴ that explicitly include phytoplankton and zooplankton, only two resolve prokaryotic biomass. Even for larger organisms, there are at least nine global marine ecosystem models that resolve climate impacts on fish biomass within the Fisheries and Marine Ecosystem Model Intercomparison Project²⁵ (FishMIP).

In this work, we use a global dataset to explore key environmental drivers of prokaryotic abundance, cell-specific biomass, and metabolic activity across the global ocean now and into the future under climate change. We use an ensemble approach with random forest regression and generalized additive models to inform variable selection and explore non-linear relationships before developing parametric statistical models of prokaryotic abundance, cell-specific carbon biomass, and metabolic activity. We use these parametric models to show that, in contrast with larger heterotrophs such as zooplankton and fish, variability in prokaryotic biomass is low across the world’s oceans, while prokaryotic respiration varies by over one order of magnitude. We show that prokaryotic biomass is likely to be remarkably resilient to climate change, while climate-driven increases in their total respiration in surface waters could outpace changes in carbon demand from larger heterotrophs. These combined shifts suggest an increasing microbialisation of marine ecosystems under climate change.

Results

Environmental drivers of prokaryotic abundance, size, and metabolic activity

To predict prokaryotic abundance, cell-specific carbon, and biomass across the global ocean, we compiled 41,881 measurements of heterotrophic bacterial and archaeal abundance from three published studies^9,26,27 (Fig. 1a). For cell-specific carbon, we used a global dataset of 1087 cell biovolume observations from the Malaspina-2010 expedition²⁸ (Fig. S1). Cell biovolume (μm³) was converted to cell-specific carbon (fg C cell⁻¹) using a published equation for open-ocean prokaryotes²⁹. We appended measurements of nine candidate environmental variables (chlorophyll a, nitrate, oxygen, phosphate, silicate, N*, Si*, apparent oxygen utilization (AOU) and temperature) to each observation of abundance, using each sample’s time and location data (Fig. S2). N* and Si* measure excess dissolved inorganic nitrogen relative to the Redfield ratio and the ratio of silicate to nitrate respectively³⁰. Surface chlorophyll a measurements from 2002 to 2016 were obtained from the Moderate Resolution Imaging Spectroradiometer aboard the Aqua satellite. Nitrate, AOU, phosphate, silicate, and temperature measurements at depth were provided by the 2018 World Ocean Atlas.

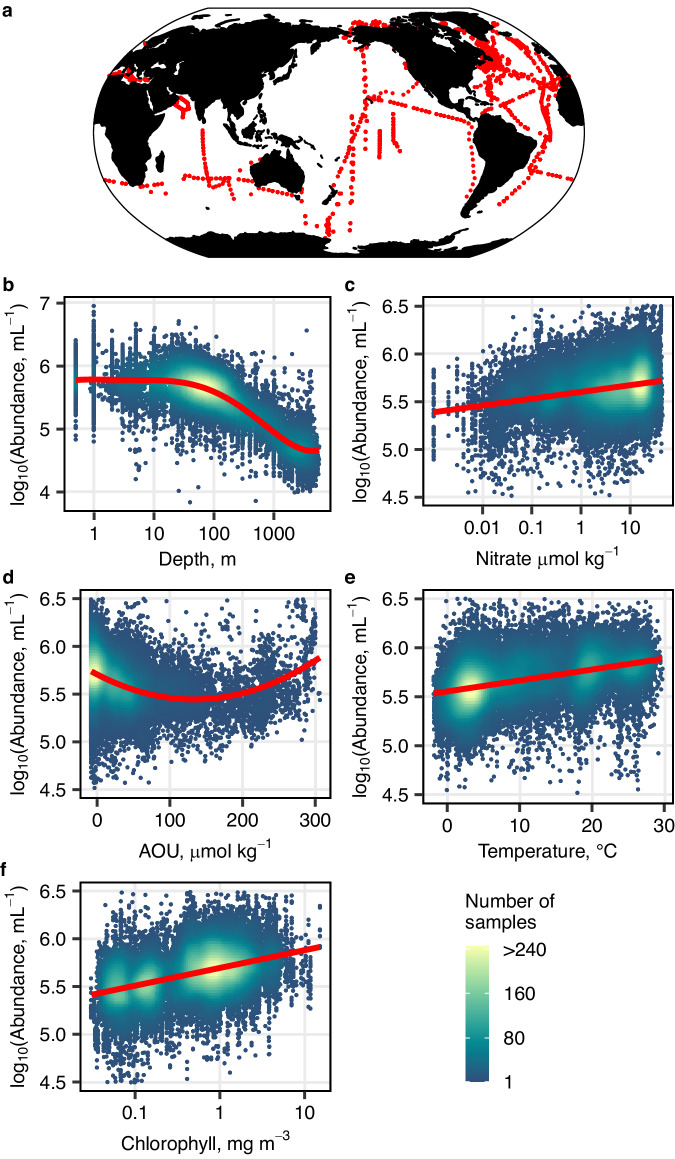
Fig. 1. Prokaryotic abundance statistical model.

a Distribution of 41,718 in situ unique samples of heterotrophic bacterial and archaeal abundance that were used in this study. The main effects of different environmental variables in our final parametric model of prokaryotic abundance (holding all other covariates constant), are shown as log₁₀ prokaryotic abundance (mL⁻¹) versus  b log₁₀ depth (m), c log₁₀ nitrate (μmol kg⁻¹), d apparent oxygen utilization (AOU; μmol kg⁻¹), e temperature (°C) and f log₁₀ chlorophyll (mg m⁻³). The red line is the fitted response for each environmental variable, with partial residuals shown as dots colored by the number of samples. Source data are provided as a Source Data file.

We fit our parametric model of prokaryotic abundance in three steps (see the “Methods” section). First, we used random forest variable selection to rank our 10 candidate variables (nine environmental variables plus depth) in order of importance for predicting prokaryotic abundance (Fig. S3). Second, we used generalized additive models³¹ (GAMs) to identify the shape of the relationship between prokaryotic abundance and the environmental variables. Highly correlated predictor variables were then removed from the GAM, beginning with those identified as least important by the initial random forest ranking, until five variables remained (sample depth, temperature, AOU, nitrate, and chlorophyll a). Finally, we used the shape of the relationships between prokaryotic abundance and the five variables from the GAM (Fig. S4) to fit a parametric model of prokaryotic abundance (Fig. 1). The R² of the parametric model was 76.6%, indicating little predictive power was lost between the GAM (R² = 77.9%) and the parametric model.

Prokaryotic abundance varied most strongly with sample depth (Fig. 1b), with mean abundance decreasing by over one order of magnitude from epipelagic (0–200 m) to bathypelagic (>1000 m) waters. Mean prokaryotic abundance increased by about ~50% for each order of magnitude increase in chlorophyll a, ~17% per order of magnitude for nitrate, and ~2.6% for a degree of temperature, °C⁻¹ (Fig. 1c, e, f). In contrast to these three environmental variables, mean prokaryotic abundance did not change linearly with AOU; declining as AOU increased from −5 to 150 μmol kg⁻¹, before increasing again for AOU > 150 μmol kg⁻¹ (Fig. 1d). AOU values > 150 μmol kg⁻¹ occur mostly in deeper (>200 m) waters that have accumulated respiration products while isolated from the atmosphere (Fig. S5f, i).

Cell-specific prokaryotic carbon biomass declined with temperature (Fig. S1b). This decrease was greatest from 0 to 10 °C, where mean cell-specific carbon biomass shrank from ~10 to 7 fg C cell⁻¹. From 10 to 25 °C, there was little change in cell biomass, but from 25 to 30 °C it declined again from 7 to 5.5 fg C cell⁻¹. However, although temperature was a significant predictor of cell-specific carbon biomass, it only explained about 10% of the variability in the cell-specific carbon data. In contrast, the variance explained by the sample location, which was incorporated into our cell biomass model as a random effect, was 68% (see the “Methods” section). Although (to our knowledge) our dataset of prokaryotic cell carbon is the largest and most spatially extensive ever published, it does not include observations from polar waters (Fig. S1a). Since temperature and depth are highly correlated (R = −0.88), this means that all low-temperature observations in our dataset are from deep waters. Therefore, when calculating total prokaryotic biomass, we are assuming that the relationship between cell-specific carbon and temperature is similar across both depth and latitude in colder waters. Cell biovolumes in polar waters might not differ substantially from our Malaspina dataset³², and latitudinal increases in cell-specific carbon biomass have previously been reported³³, which would support our assumption here.

Finally, to predict prokaryotic metabolic activity, we compiled a global dataset of 2092 observations of cell-specific production rates (SPR) from five different studies covering the global ocean (see the “Methods” section; Fig. S6a). Total cell-specific metabolic activity is the sum of P and the specific respiration rate (SRR). To calculate SRR we used a global dataset of 305 observations of prokaryotic growth efficiency³⁴ (PGE, the fraction of total carbon demand that supports SPR; Fig. S6b). Therefore, SRR can be estimated using PGE and SPR: SRR = SPR/PGE−SPR. Prokaryotic growth efficiency data were collected exclusively from epipelagic waters (<200 m), so we excluded deeper waters from our assessment of present and future global prokaryotic metabolic activity. Similar to cell-specific carbon biomass, our final model of prokaryotic metabolic activity was a linear mixed effects model with a random effect for each of the five different studies from which we gathered cell-specific production rates. Temperature and chlorophyll a were linear fixed effects that explained about 25% of the variability in cell-specific production rates (see the “Methods” section). From our model, cell-specific prokaryotic metabolic rates increased by ~7.4% °C⁻¹ and ~36% per order of magnitude increase in chlorophyll a (Fig. S7).

Contemporary global distribution of prokaryotes

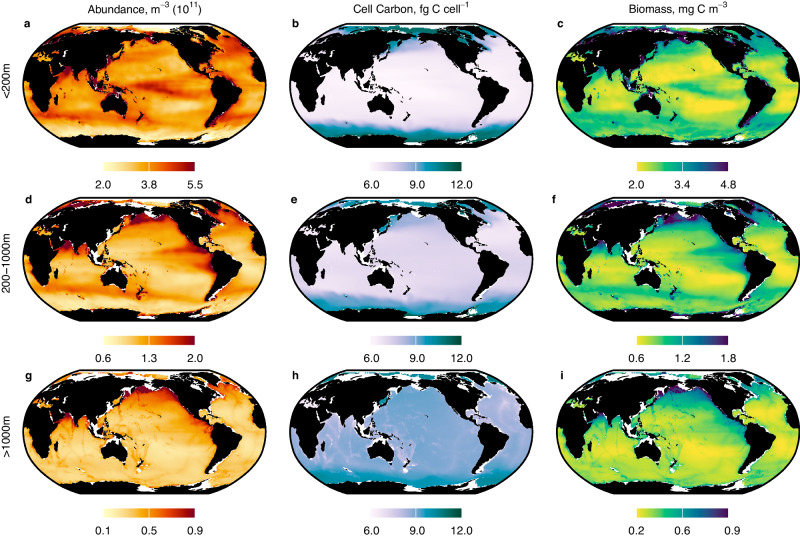
Changes in prokaryotic abundance and biomass in epipelagic waters were relatively small compared to the magnitude of variability in environmental conditions. Across the world’s oceans, chlorophyll a concentration varies by more than 2 orders of magnitude (Fig. S8), yet mean (across depth) prokaryotic abundance in the top 200m only varies by just under3-fold in epipelagic waters, from ≤2.0 × 10¹¹ m⁻³ in oligotrophic waters, to ≥5.5 × 10¹¹ m⁻³ in eutrophic coastal and upwelling regions (Fig. 2a). The spatial distribution of prokaryotic biomass was similar to abundance outside polar regions in epipelagic waters (Fig. 2a, c), and across the global mesopelagic (Fig. 2g, i), since individual cell-specific carbon varied little in these areas (Fig. 2e, h). Prokaryotic biomass in epipelagic polar waters did not decline with abundance, because decreases in abundance in those areas were balanced out by greater cell-specific carbon (Fig. 2b).

Fig. 2. Contemporary global distribution of prokaryotes.

Mean (across depth) prokaryotic a, d, g abundance (m⁻³); b, e, h cell-specific carbon (fg C cell⁻¹), and c, f, i biomass (mg C m⁻³) in the a–c top 200 m (epipelagic); d–f 200–1000 m (mesopelagic); and g–i >1000 m (bathypelagic). Note that color scales for abundance and biomass changes with the layer. Source data are provided as a Source Data file.

In contrast with cell-carbon (Fig. 2b, e, h), relative spatial variability in prokaryotic abundance and, ultimately, biomass increased with depth. In the bathypelagic, prokaryotic biomass varied by just under a factor of five (Fig. 2i), from ≤0.2 mg C m⁻³ under the oligotrophic ocean gyres and polar waters, to ≥0.9 mg C m⁻³ in waters where AOU and nitrate concentrations were highest (Fig. S5). The relative invariance of prokaryotic biomass in epipelagic waters contrasts with that of larger heterotrophs; zooplankton and fish biomass vary by more than one order of magnitude from low to high chlorophyll regions³. As a result, prokaryotes are a larger fraction of total epipelagic heterotrophic biomass in the oligotrophic ocean gyres but become less dominant in productive coastal and upwelling regions, where larger heterotrophs are relatively more prevalent (Fig. S9).

Prokaryotic metabolic activity in the top 200m varies far more than abundance or biomass across the global ocean (Fig. 3)³⁵. Total prokaryotic metabolic activity (the sum of production and respiration) in the epipelagic increases by >1 order of magnitude from polar (≤10 g C m⁻² yr⁻¹) to tropical coastal and upwelling regions (≥200 g C m⁻² yr⁻¹). Thus, despite relatively small changes in prokaryotic abundance and biomass, prokaryotic carbon demand varies substantially across global environmental gradients³⁵.

Fig. 3. Contemporary global prokaryotic metabolic activity.

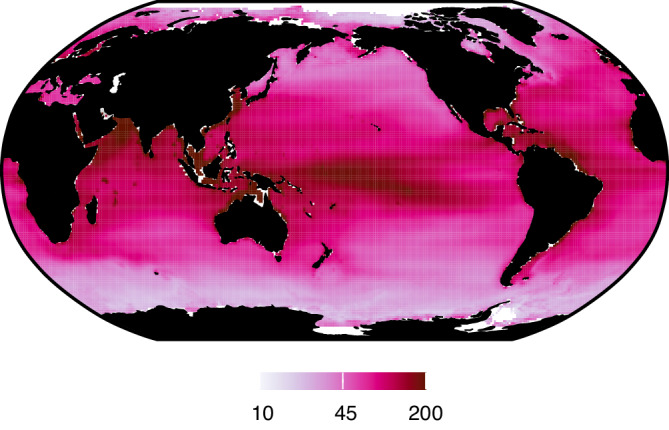
Mean (across depth) prokaryotic metabolic activity (production and respiration) in epipelagic (<200 m) waters (g C m⁻² yr⁻¹). Source data are provided as a Source Data file.

The relative invariance of global prokaryotic biomass—in contrast with total metabolic activity—likely reflects their wide variety of metabolic maintenance and survival strategies. Prokaryotes are capable of lowering or even arresting their metabolic activity, allowing long-term survival under nutrient-poor conditions by maintaining relatively high yet inactive biomass³⁶. The average percentage of active prokaryotic cells varies from 10% to 45% (depending on the measurement method), with the proportion of cells that are active generally increases with overall prokaryotic abundance³⁶. Chemolithoautotrophic prokaryotes—which can fix dissolved inorganic carbon—provide a significant source of organic carbon to heterotrophic prokaryotes in deep waters, independent of surface primary production in the short-term³⁷. Finally, protistan grazing is one of the main sources of prokaryotic mortality across the water column³⁸. However, prokaryotes have phenotypic features to escape protistan grazing, including high-speed motility, reduced body size (to avoid size-selective predation), and toxin production³⁸. These metabolic maintenance and survival characteristics, largely unique to prokaryotes, may explain the relative decoupling between the distribution of prokaryotic biomass and global environmental gradients found here.

Projected climate change impacts on marine biomass and heterotrophic respiration

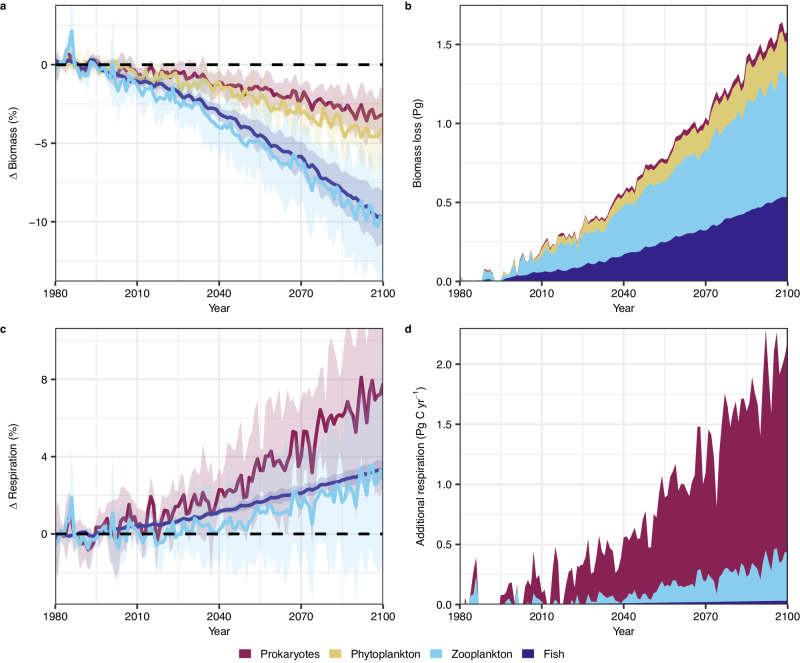
Prokaryotes will likely increase as a proportion of total marine biomass in the future. Our results suggest that, from 1980 to 2100 under a ~2 °C ocean warming scenario (Shared Socioeconomic Pathway 3-7.0; SSP3-7.0), global prokaryotic biomass in epipelagic waters (<200 m) will decline by ~3% (±2%) with climate change, while phytoplankton biomass will decrease by ~4% (±2%). Both zooplankton (covering micro-, meso- and macro-zooplankton) and fish biomass will decline by 10% (±5% for zooplankton and ±2% for fish, Fig. 4a). Thus, global prokaryotic biomass in the epipelagic is projected to decrease by ~1.5% and phytoplankton by ~2% for per 1 °C of warming, while zooplankton and fish decrease by ~5%. These disparate rates of decline with warming across different groups mean that prokaryotes, despite contributing ~8% to the 20.5 Pg of contemporary marine biomass in epipelagic waters³, would only be ~3% (0.05 Pg) of the total 1.6 Pg of marine animal biomass lost from climate change this century under SSP3-7.0 (Fig. 4b).

Fig. 4. Impacts of projected climate change on global marine biomass and heterotrophic respiration in epipelagic (<200 m) waters.

Relative (%) change in global a biomass, and c respiration; and global b biomass lost (Pg wet biomass); and d additional respiration (Pg C yr⁻¹) from prokaryotes, zooplankton (covering micro-, meso- and macro-zooplankton) and fish in the top 200 m, under Shared Socioeconomic Pathway 3-7.0, compared to 1980–2000 levels. Contemporary (1980–2000) global biomass of prokaryotes (1.7 Pg) was calculated using statistical models derived here (assuming a carbon-to-biomass ratio of 0.1; see the “Methods” section). Global contemporary biomass of phytoplankton (5.4 Pg), zooplankton (7.9 Pg), and fish (5.5 Pg) were obtained from Hatton et al. (2021)³, while respiration of zooplankton (12.4 Pg C yr⁻¹) and fish (1.0 Pg C yr⁻¹) were taken from Nowicki et al.⁵ and Bianchi et al.⁴⁵, respectively. Contemporary global prokaryotic respiration (22.6 Pg C yr⁻¹) was calculated using statistical models derived here (see the “Methods” section). In a and c, solid lines represent the ensemble mean change, and shaded areas are the standard deviation from four separate simulations, each forced by one of four earth-system models (see the “Methods” section). Source data are provided as a Source Data file.

Temperature-driven changes in prokaryotic biomass could be driven directly by warming effects on metabolic processes³⁹, or indirectly by changes in community composition^40,41. Given that our data do not explicitly resolve community composition, we are unable to identify these potential drivers here. However, temperature-driven increases in prokaryotic biomass, arising from declining cell size being outpaced by increasing abundance, are consistent with observations over local⁴² and global temperature gradients³⁹. All else being equal, prokaryotic biomass from our models increases with warming in ~8–27 °C waters but declines in areas outside this range (Figs. 1e, 2b; S10). Temperature-driven declines in total biomass in <8 and >27 °C waters are caused here by decreases in cell carbon (Fig. S1b) outpacing temperature-driven increases in prokaryotic abundance (Fig. 1e). Morán et al.³⁹ found a similar pattern (increases in prokaryotic biomass, but only in waters <26 °C) and argued this non-linear relationship between temperature and prokaryotic biomass was driven by a shift between bottom-up (resource availability) and top-down control (predation and viral lysis) across the global temperature gradient.

Climate impacts on biomass combine with impacts on specific-respiration rates to determine increases in global heterotrophic respiration. From 1980 to 2100, prokaryotic respiration in epipelagic waters is projected to increase by ~7.5% (±6%) under SSP3-7.0, double that of zooplankton and fish (~3.5%, ±4.5% for zooplankton and ±0.5% for fish; Fig. 4c). This translates to an additional 2.1 Pg C yr⁻¹ (Fig. 4d) of total heterotrophic respiration in epipelagic waters, or just over 1 billion tonnes of additional carbon respired per year per 1 °C of surface warming. All else being equal, this additional respiration in surface waters would cause a shallowing of the remineralization depth—the depth at which sinking organic carbon is converted to carbon dioxide—consistent with a postulated weakening of the biological pump, driving a climate-amplifying feedback loop between declining oceanic carbon sequestration with increasing global temperatures^43,44.

In contrast with climate-driven marine biomass loss, which is projected to come primarily from zooplankton and fish (Fig. 4b), ~80% (~1.7 Pg C yr⁻¹) of additional heterotrophic respiration under 2 °C warming is caused by prokaryotes (Fig. 4d), even though they produce ~63% (22.6 Pg C yr⁻¹) of total contemporary heterotrophic respiration (36 Pg C yr⁻¹)^5,45. Thus, prokaryotes in surface waters are projected to divert a larger proportion of primary production into microbial food webs with warming, which would decrease the energy available for higher trophic levels. Therefore, current projections of warming-driven zooplankton and fish biomass decline^25,46–48 (including those shown here) may be underestimating climate impacts, since they do not consider warming impacts on microbial food webs.

Discussion

Our models integrate decades of observations^{9,26–29,34,49–51} to map the present global distribution and metabolic activity of prokaryotes, as well as how their global biomass and respiration in epipelagic waters may be affected by climate change. These integrated observational datasets, as well as global 1° resolution, depth-resolved predictions of prokaryotic abundance, cell carbon, biomass, and epipelagic metabolic activity from our statistical models, are freely available with this study (Data Availability Statement). Parametric statistical models of prokaryotic abundance, cell carbon and metabolic activity  developed in this study are also freely available (Code Availability Statement).

To our knowledge, our model of cell-specific carbon is the first to show that the temperature-size rule⁵²—organisms are generally smaller with increasing temperature—appears to hold also for unicellular heterotrophic prokaryotes across the global ocean temperature gradient; we estimate that at the global scale, mean prokaryotic cell-specific carbon will decrease by ~2% per °C of warming (Fig. S11). This is similar to the 1.8% per °C decline estimated for larger unicellular plankton but lower than the 3.8% per °C decline calculated for larger marine metazoa⁵³. However, more rapid declines in prokaryotic cell size with warming have already been observed within smaller regions such as the Bay of Biscay⁴².

The projected global loss of marine biomass from 2 °C warming (1.6 Pg; Fig. 4b) is of a similar magnitude to the 2 Pg already lost to fishing and hunting since the Industrial Revolution³. Historical losses to fishing and hunting are concentrated within larger size classes (>10 g; primarily fish and marine mammals) and have thus already profoundly altered the size-distribution of global marine life³. In contrast, losses projected here from climate change are more evenly spread across the entire global ocean size-spectrum; ~65% of projected losses come from prokaryotes, phytoplankton, and zooplankton (Fig. 4b). The marked impact of fishing and hunting on the size distribution of ocean life means humans have already profoundly altered energy flow through marine ecosystems^3,45, removing ~1.4 Pg C yr⁻¹ of fish and marine mammal respiration from epipelagic waters³. At the global scale, the fate of this lost respiration is largely unknown, although evidence exists linking overfishing in coastal and reef systems with microbialisation of food webs^54,55. This suggests that the combined impacts of fishing and climate change will cause significantly greater microbialisation of ocean ecosystems than estimated here from warming alone.

Besides depth, prokaryotic abundance is primarily driven by temperature, apparent oxygen utilization (AOU), and chlorophyll a and nitrate concentrations (Fig. 1). Prokaryotic abundance is positively related to each of these environmental variables except for AOU. However, we note that the global, multi-decadal scale of our synthesis means these relationships would have less explanatory power at smaller scales, where environmental and ecological factors not identified here would likely affect the structure of prokaryotic communities. The presence of seemingly anomalous observations in our dataset of prokaryotic cell-specific carbon (see the “Methods” section) highlights this reality, demonstrating there may be many other unobserved phenomena affecting regional prokaryotic communities at smaller time scales that are not represented in our global-scale models.

By using statistical models built on historical observation, our projections of future prokaryotic biomass and respiration implicitly assume that the relationships between environmental drivers and prokaryotes will not be altered by climate change. However, their enormous global population size, typical generation times of hours to days⁵⁶ and high genetic diversity^57,58 mean rapid evolutionary adaptation to climate change is likely for prokaryotes as environmental conditions move beyond historical conditions⁷. At the same time, climate change will drive shifts in the structure and function of marine food webs and biogeochemical fluxes^7,59, which may affect prokaryotic communities in ways that are currently unobserved and thus not captured by our analysis.

We estimate that contemporary global prokaryotic respiration in epipelagic waters is ~22.6 Pg C yr⁻¹. This estimate was obtained using global datasets of prokaryotic specific-production rates (SPRs) and prokaryotic growth efficiency (PGE), which together give prokaryotic specific-respiration rates (SRRs): SRR = SPR/PGE−SPR. There are large uncertainties associated with both SPR and PGE, which are compounded in our estimate of SRR (Fig. S12). For example, we used the median PGE from our dataset of 14% to calculate SRRs (see the “Methods” section), but if we recalculate SRR across the interquartile range of PGE from our dataset (6–27%), the resulting interquartile range of global prokaryotic respiration is ~14–30 Pg C yr⁻¹ (with a full range of ~10–60 Pg C yr⁻¹; Fig S12a). Similarly, across the 95% confidence interval for our statistical model of SPRs (Fig. S7), the interquartile range of global prokaryotic respiration is ~20–28 Pg C yr⁻¹ (with a full range of ~14–40 Pg C yr⁻¹; Fig. S12b). When these two sources of uncertainty are combined, the interquartile range of global prokaryotic respiration is ~14–31 Pg C yr⁻¹ (with a full range of ~6-101 Pg C yr⁻¹; Fig. S12c). As shown by these comparisons, PGE uncertainty—likely resulting from the sparseness of available data—was the largest driver of total uncertainty in our estimate. Nevertheless, despite the large uncertainty suggested by the variability of measured PGE, our estimate of ~22.6 Pg C yr⁻¹ contemporary global prokaryotic respiration is remarkably similar to two independent assessments: 20.5 Pg C yr⁻¹ from a recently published global biogeochemical model⁵; and 20.4 Pg C yr⁻¹ using empirical relationships from Lopez-Urrutia et al.⁶⁰ and assuming 10% of prokaryotes are metabolically active³⁶.

Prokaryotic specific-production and -respiration rates in surface waters have a Q₁₀ of 2.05 (see the “Methods” section). This is within the range of previous studies that estimate a Q₁₀ value close to two for metabolic rates of microorganisms in surface waters^44,61,62. However, Smith et al.⁶³ found that the Q₁₀ of prokaryotic respiration could be as high as four (equivalent to an Arrhenius activation energy of ~0.97 eV). All else being equal, a Q₁₀ of four would cause global prokaryotic respiration in surface waters to increase by 4.3 Pg C yr⁻¹ under 2 °C of warming, over 10 times the projected increase of 0.4 Pg C yr⁻¹ for zooplankton and fish (Fig. 4d). At the same time, prokaryotic metabolism in the deep ocean may have a Q₁₀ value of around 28 (equivalent to an Arrhenius activation energy of 2.36 eV⁶⁴). Yet, the paucity of available data precluded applying our methods to assess the present and future carbon demand of prokaryotes in the deep ocean⁶⁵. The wide uncertainties in the temperature sensitivity of prokaryotic respiration—as well as uncertainties in PGE as highlighted above—present significant risks for a growing global population, whose demand on marine ecosystems for food (from fisheries) and carbon storage in the deep ocean will almost certainly increase this century^66–68.

Using a synthesis of global data, we have developed interpretable, parametric statistical models that uncover key environmental drivers of prokaryotes across the global ocean. Our results address a critical gap for skill assessment and calibration for models that explicitly resolve prokaryotes; despite their importance, heterotrophic prokaryotes have been neglected in earth-system model development⁶⁹ and remain a major source of uncertainty in projections of future climate impacts on the ocean biological carbon pump⁷⁰. More broadly, our results give motivation for further exploration of energy and carbon fluxes through the world’s ocean food webs, from microbes to large heterotrophs, and how they may be affected not only by climate change but by other sources of human disturbance, such as fishing.

Methods

Global prokaryotic abundance

Dataset

Our prokaryotic abundance dataset covered all major ocean basins to a maximum depth of 5931 m, with over 90% of the samples from the Northern Hemisphere (Fig. 1a). The distributions of prokaryotic abundance, sample depth, nitrate, phosphate, silicate, and chlorophyll a concentrations were right-skewed, so we log₁₀-transformed these variables before conducting any analysis. N* and Si*—tracer variables, respectively measuring excess dissolved inorganic nitrogen relative to the Redfield ratio and the ratio of silicate to nitrate—were also included in our candidate variable set (Fig. S2). All analyses were conducted with R version 4.4.0⁷¹.

Variable Selection

We used the random forest algorithm^72,73 to perform variable selection and identify which variables were significant predictors of prokaryotic abundance across the global ocean. Using some form of statistical variable selection is preferable to relying solely on expert knowledge because a model does not have preconceived ideas about relationships between variables. This is useful for many domains, such as ecology^74,75, as it can either provide evidence in support of existing ideas about relationships between variables in nature or alternatively suggest unexpected relationships that can be further explored.

Random forest is a non-parametric ensemble of trees method that uses a bagging algorithm to take bootstrap samples of training data, randomly selecting variables and constructing many individual decision trees in order to ultimately reach predictions⁷³. Random forest has been used for variable selection in ecological settings^74,75. A key benefit of using random forest for variable selection relative to univariate selection methods is that the random forest model estimates the influence of an individual predictor variable on the dependent variable, as well as its influence on multivariate interactions with other predictor variables^76,77.

We fit five random forest models with different initial seed values and found this was a sufficient number because the variable importance results were consistent, and the models had low errors. To train and test each random forest, we split observations into two sets: 80% for training and 20% for testing (with model error on the testing set measured by root mean square error, RMSE, and mean absolute error, MAE). The training process involves ‘learning’ which variables are important for predicting values of the dependent variable based on the training set. After the training process, each random forest model was used to make predictions of prokaryotic abundance on the test set, which is unknown to the trained models. On average, the five fitted random forests were able to account for 85.1% of the variance in sampled log₁₀ prokaryotic abundance, and there was an average low model error using all candidate environmental variables, as measured by RMSE (0.003) and MAE (0.132).

From the random forest, log₁₀ sample depth was identified as the most important variable for predicting log₁₀ prokaryotic abundance, followed by log₁₀ nitrate, log₁₀ phosphate, AOU, log₁₀ silicate, temperature, log₁₀ chlorophyll, N*, oxygen, and Si* (Fig. S3). We proceeded to fit our parametric model using the random forest variable importance assessment and co-author knowledge, as a guide for variable selection.

Fitting GAMs and parametric models

Random forest models are a powerful way to identify the most important predictor variables for fitting a statistical model. However, since these models are non-parametric, they are not suitable for identifying parametric relationships between variables. To identify the shape of the relationship between prokaryotic abundance and environmental variables, we built generalized additive models³¹ (GAMs) that used penalized regression splines. Similar to the random forest step, we split observations into two sets to fit and test the GAM: 80% for training and 20% for testing (with GAM error measured by RMSE and MAE).

Individual variables accounted for between 4.7% (log₁₀ chlorophyll) and 72.2% (log₁₀ depth) of the deviance in prokaryotic abundance, while the GAM fitted with all possible variables was able to account for 78.9% of the deviance and had an RMSE of 0.001 and MAE of 0.160 (Table S1). From our full model, we assessed the concurvity of the independent variables and removed predictors with concurvity indices >0.90, beginning with variables identified as least important by the random forest. Concurvity is the degree to which predictor variables can be explained by one or more of the other independent variables in the GAM^53,78. After removing variables with concurvity indices >0.90 one at a time in order of least importance, log₁₀ depth, log₁₀ nitrate, AOU, temperature and log₁₀ chlorophyll remained, with 77.9% of the deviance explained by these variables and an RMSE and MAE of 0.001 and 0.165, respectively.

We then used the shape of the relationships between log₁₀ prokaryotic abundance and predictor variables in the GAMs (Fig. S4) to fit our final parametric model for log₁₀ prokaryotic abundance. In the parametric model, log₁₀ prokaryotic abundance is predicted with a fifth-order polynomial for log₁₀ depth, a second-order polynomial for AOU, and linear relationships for log₁₀ nitrate, temperature, and log₁₀ chlorophyll (Fig. S13). The R² of the final parametric model was 76.6% and the RMSE and MAE were 0.001 and 0.171, respectively, indicating that little predictive power was lost between the GAM and the final parametric model. We also assessed the effect of including all interactions between predictor variables in the GLM. When all ~130 interactions were included, the R² increased by 2.5% and RMSE and MAE remained almost unchanged at 0.032 and 0.159. Thus, for parsimony and ease of interpretation, our final parametric model excluded interactions between predictor variables.

Sensitivity analysis

Before using our final parametric model, we assessed its sensitivity to observational data in two ways. First, we explored the sensitivity of the parametric model’s parameters and R² to the number of observations used to fit the model using a bootstrap resampling method with 1000 iterations for 1000, 5000, 10,000, 20,000, and 30,000 samples. We found that variance in the model’s parameter values and R² decreased with the number of samples, but their mean values were stable (Fig. S14). Second, we assessed the model’s ability to predict observed prokaryotic abundance across polar (>60°), temperate (30°–60°), and tropical (<30°) marine regions, over the entire water column. The variance explained by the model varied across the regions, from 63.3% in tropical to 78.1% in temperate regions (Fig. S15). Variability in R² across regions primarily reflects the fact that over 75% of the observations used to fit the models come from temperate regions, but <5% come from tropical and the remaining ~20% from polar regions.

Cell-specific prokaryotic carbon content

Dataset

At present, there are no global models of prokaryotic cell biovolume or cell-specific prokaryotic biomass. This is partly because combining measurements from different studies is difficult since different methodologies deployed across studies can yield divergent size estimations. For example, the two most commonly used allometric models^29,79 for transforming cell biovolume into carbon biomass yield a 2-fold difference in cell carbon for a 0.035 μm³ bacterium (corresponding to a diameter of 0.41 μm assuming spherical shape). To address the challenge of combining data from different studies, we obtained 1087 in situ unique samples of heterotrophic prokaryotic cell biovolume estimates from the Malaspina-2010 Expedition²⁸. Malaspina-2010 was a global circumnavigation expedition that collected data from 126 stations in the tropical and subtropical Atlantic, Indian, and Pacific Oceans, from surface waters to 4000 m. Prokaryotic cell-specific biovolumes (μm³) were determined across the entire expedition using flow cytometric measurements of the population mean side light scatter, which was converted to cell size using an empirically derived allometric equation⁷⁸, assuming all cells to be spheres. We then calculated cell-specific carbon biomass (fg C cell⁻¹) from cell biovolume using a published equation for open-ocean prokaryotes²⁹. Similar to all studies, the accuracy of our estimates of prokaryotic biovolume and carbon is dependent on the methods we chose. However, by using a uniform approach across all observations our dataset makes it possible to develop a consistent, global-scale model of prokaryotic cell size.

All 1087 cell-specific carbon samples recorded temperature, sample depth, and station position (Fig. S16). Other ocean attributes such as nitrate, phosphate, and silicate were also recorded, but only for a subset of samples, so they were not included in the statistical model for cell-specific carbon. Sample depth was right-skewed, so it was log₁₀-transformed before conducting any analysis. Since we only had two variables (temperature and sample depth) to construct our model for cell carbon, the random forest step was not necessary, and we proceeded to construct the GAM analysis.

Statistical model

To identify the shape of the relationship between individual prokaryotic cell-specific carbon biomass and environmental variables, we first built a GAM of cell carbon with penalized regression splines for sample depth and temperature and a fixed effect for the sample station. The GAM allowed us to explore the shape of the relationships between cell carbon and these predictor variables. However, sample depth and temperature were highly correlated (R = −0.88), so we removed sample depth from the model since it explained less of the variance in prokaryotic cell carbon than temperature (Table S2). Based on the GAM (Fig. S17), we then fit parametric statistical models for prokaryotic cell carbon with a third-order polynomial for temperature and a random effect on the intercept for the station (Fig. S18). We used a random effect for the station to control for station-specific heterogeneity in the samples, which was not captured by temperature. To obtain an estimate of R² from the whole model and from fixed effects alone, we used the r.squaredGLMM function in R⁸⁰. Temperature alone explained only 9.8% of the variance in prokaryotic cell carbon out of the total 78% for the whole model (including the random effect for the station).

The high proportion of total variance explained by the station random effect is due to the large difference in sample cell carbon from stations on Leg 5 of the circumnavigation (between New Zealand and Hawaii; average prokaryotic cell carbon of 15 fg C), compared to all other stations (average prokaryotic cell carbon of 7 fg C; Fig. S16c). When Leg 5 stations were removed, the variance explained by temperature alone increased to 27%, out of a total of 47% for this secondary model. However, from other data obtained at the same stations, it appears that the particle export from surface waters in this region was elevated compared to other regions, due to high active zooplankton flux⁸¹. The input from migrating zooplankton may explain why prokaryotes in these regions—especially in the bathypelagic zone—were so much larger than at other stations. Both viral and protist abundances in the bathypelagic across Leg 5 were unusual, as were eukaryotic and prokaryotic microbial communities, suggesting our prokaryotic biovolume data from Leg 5 are not in error but are likely describing real phenomena unique to this region at the time of sampling. Therefore, we retained these stations in our dataset and proceeded to predict the global distribution of prokaryotic cell carbon using the parametric model with a third-order polynomial for the temperature and a random effect for the station (Fig. S18).

Leg 5’s apparently anomalous data (compared to all other Legs) highlight the challenge of potential undersampling, even in a comprehensive dataset of prokaryotic cell carbon such as ours; it is possible that other important, regional phenomena may exist that affect prokaryotic cell carbon that was not captured during the Malaspina-2010 circumnavigation.

Specific-production and -respiration rates for prokaryotes

Datasets

To calculate specific-respiration rates (SRRs) for prokaryotes we used global datasets of specific-production rates (SPRs) and prokaryotic growth efficiency (PGE), which are more abundant than SRR data. Total metabolic activity is just the sum of SPR and SRR. Therefore, SRR can be calculated from SPR and PGE: SRR = SPR/PGE−SPR. Our SPR dataset contains 2092 samples of specific-production rates, chlorophyll a concentration and temperature from across the global ocean (Fig. S6a; Fig. S19), including data from the Malaspina-2010²⁸ (n = 1019), Hotmix (n = 344; previously unpublished) and Latitud⁵¹ (n = 432) expeditions, the Blanes Bay Microbial Observatory (n = 209; http://bbmo.icm.csic.es/) and the Western Arctic and Ross Sea⁵⁰ (n = 88). The PGE dataset contains 305 observations of PGE from surface waters (<140 m), with most also including in situ measurements of temperature, chlorophyll a, nitrate, phosphate, and dissolved organic carbon (DOC). This dataset was compiled by Carol Robinson³⁴, primarily from the North Sea, but also covers the Southern, Atlantic, and Pacific Oceans as well (Fig. S6b).

Statistical models

As for prokaryotic abundance and cell carbon, to identify the shape of the relationships between SPR and environmental variables, we first built a GAM of SPR with penalized regression splines for temperature and chlorophyll a, and a fixed effect for dataset ID (Fig. S20). Based on the GAM, we then fit a mixed effects model, with linear covariates for temperature and chlorophyll a, and a random effect for dataset ID (Fig. S7). The mixed effects model explains about 25% of the variance in the data. We calculated the statistical relationship between SPR and temperature across all observations, irrespective of sample depth. We did this because the relationship between SPR and temperature was not significantly different for epipelagic (<200 m) data that included a chlorophyll a measurement, and deeper waters that did not have a chlorophyll measurement.

Finally, PGE did increase linearly with log₁₀ chlorophyll, which agrees with Lopez-Urrutia et al.⁶⁰, but this relationship was not significant (p-value = 0.17). Therefore, we used a single value of 14% for BGE, which is the median of the dataset.

Calculating present and future marine biomass and heterotrophic respiration

To assess climate impacts on global marine biomass (prokaryotes, phytoplankton, zooplankton and fish) and heterotrophic respiration (prokaryotes, zooplankton and fish) in epipelagic (<200 m) waters, we sourced environmental drivers from four Coupled Model Intercomparison Project Phase 6 earth system models (GFDL-ESM4, IPSL-CM6A-LR, CMCC-ESM2, MPI-ESM1-2-LR) under a high emissions scenario (Shared Socioeconomic Pathway 3-7.0; SSP3-7.0), from 1980 to 2100. Changes in prokaryotic biomass and respiration were calculated using the statistical models for abundance, cell-specific carbon and specific-production rates derived here. Changes in phytoplankton biomass were sourced directly from the four earth-system models. For zooplankton, changes in total biomass were calculated using statistical models of global micro-, meso- and macrozooplankton biomass from Hatton et al.³, which use chlorophyll a, sea-surface temperature and depth to estimate zooplankton biomass. Finally, climate impacts on global fish biomass were calculated assuming a 5% decrease in global biomass for every 1 °C of warming, which was calculated from the projections of six FishMIP models⁴⁷. For both zooplankton and fish, changes in specific-respiration rates with warming were calculated using the widely published Q₁₀ temperature-scaling of two^82–85. This temperature-scaling is close to our derived estimate of 2.05 for the Q₁₀ of prokaryotic specific-production and respiration rates.

To address any systemic bias in the earth-system models⁸⁶, we re-scaled environmental drivers using globally constant scalars, so that the mean surface values for each variable in tropical and temperate (<60°) waters from 2002 to 2016 in each of the earth-system models were equal to values obtained from the MODIS-Aqua (for chlorophyll a) and World Ocean Atlas (for temperature, nitrate and AOU) climatologies, which were used to fit the statistical model. For example, if an earth-system model’s mean surface temperature in <60° waters from 2002 to 2016 was 2 °C higher than the temperature from the World Ocean Atlas, that model’s temperature was reduced by 2 °C.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.

Author contributions

R.F.H. and E.D.G. defined the research question for this study, with feedback from J.M.G., G.J.H., and X.A.G.M. J.M.G., X.A.G.M., and G.J.H. provided unpublished data. R.F.H. and J.H.-B. developed the statistical models. R.F.H. drafted the manuscript, with assistance and feedback from all co-authors.

Peer review

Peer review information

Nature Communications thanks the anonymous reviewer(s) for their contribution to the peer review of this work. A peer review file is available.

Data availability

Raw prokaryotic abundance, cell carbon, specific-production rates and growth efficiency data used in this study are available here: 10.5281/zenodo.12741063. Heterotrophic bacterial and archaeal abundance were obtained from three published studies^9,26,27, while cell-specific carbon data (previously unpublished) were obtained from the Malaspina-2010 expedition²⁸. Specific-production rate data were compiled from the Malaspina-2010²⁸ (previously unpublished in the form used here, but can be derived from data published in ref. ³⁹), Hotmix⁸⁷ (previously unpublished) and Latitud⁵¹ expeditions, the Blanes Bay Microbial Observatory (previously unpublished; http://bbmo.icm.csic.es/) and the Western Arctic and Ross Sea⁵⁰. Finally, prokaryotic growth efficiency data were compiled and published previously by Carol Robinson³⁴. Global, depth-resolved predictions of prokaryotic abundance, cell carbon, biomass and metabolic activity generated in this study are available here: 10.5281/zenodo.12541052. Environmental data used to generate these predictions were obtained from World Ocean Atlas 2018 and MODIS-Aqua (for chlorophyll a only), and is also available here: 10.5281/zenodo.12741063. For the climate change projections, environmental inputs were sourced from four climate models from CMIP6 (Methods). Climate model data are available from the Earth System Grid Federation here: https://esgf-data.dkrz.de/projects/esgf-dkrz/). Source data are provided with this paper.

Code availability

The code used to conduct all analyses in this study is available at 10.5281/zenodo.12741078 (ref. ⁸⁸).

Competing interests

The authors declare no competing interests.

Supplementary information

The online version contains supplementary material available at 10.1038/s41467-024-50635-z.