Exploratory Structural Equation Modeling Analysis of the Anxiety Sensitivity Index 3

Abstract

Objective:

Anxiety sensitivity is associated with the onset and progression of various emotional disorders. The Anxiety Sensitivity Index 3 (ASI-3) is a self-report scale for anxiety sensitivity. This study aims to resolve the ongoing controversy about the factorial structure of the ASI-3 using exploratory structural equation modeling (ESEM), a newly advanced technique.

Methods:

Confirmatory factor analysis (CFA), ESEM, bifactor-CFA, and bifactor-ESEM were used to investigate the factorial structure of the ASI-3. Three hundred Korean college students (female = 195, age: 21.74 ± 2.34) filled out the ASI-3 and the Distress Intolerance Index.

Results:

The bifactor-ESEM model exhibited a model fit superior to the 4 alternative models. The general factor showed higher loadings and reliability and explained common variance than the 3 specific factors in the bifactor-ESEM model. Most items reflected the global factor, but 6 items (Items 2, 3, 5, 7, 10, and 17) from the specific factors had insufficient loadings. Moreover, the global factor of the ASI-3 was associated with distress intolerance scores, indicating adequate criterion-related validity.

Conclusion:

The factorial structure of the ASI-3 is best described as a bifactor-ESEM model for Korean college students. Additionally, the bifactor-ESEM model of the ASI-3 includes a strong global factor that explains a large amount of the observed variance in the ASI-3 items.

Main Points

• The bifactor-exploratory structural equation modeling (ESEM) model of Anxiety Sensitivity Index 3 (ASI-3) provided a better fit than the other models.

• In the bifactor-ESEM model of the ASI-3, the global factor showed higher loadings, reliability coefficients, and explained common variance values than the 3 specific factors.

• The global factor of ASI-3 was significantly associated with distress intolerance, which showed adequate criterion-related validity.

Introduction

Anxiety sensitivity is defined as the fear of anxiety-related sensations arising from the belief that these sensations have harmful somatic, social, or cognitive consequences. Anxiety sensitivity amplifies anxiety symptoms by avoiding or escaping anxiety-related sensations.¹ According to previous research, anxiety sensitivity functions as a causal and maintaining variable in depression and anxiety disorders. Although anxiety sensitivity is a fairly stable variable, it can be reduced through interventions. Therefore, reducing anxiety sensitivity has become a target for intervention.² Various tools have been developed to measure anxiety sensitivity. The Anxiety Sensitivity Index,³ Anxiety Sensitivity Index-Revised,⁴ and Anxiety Sensitivity Profile⁵ were developed to measure anxiety sensitivity. These instruments have reported different findings regarding factor structures. The Anxiety Sensitivity Index 3 (ASI-3) was developed to resolve the differences in factor structure by dividing anxiety sensitivity into physical, cognitive, and social concerns,⁶ Physical concerns include fear of anxiety-related sensations due to fear of physical harm that anxiety-related sensations may bring; cognitive concerns encompass fear of anxiety-related sensations due to concerns about mental illness caused by anxiety-related sensations. Further, social concerns include fear of anxiety-related sensations due to concerns about the social embarrassment that anxiety-related sensations may bring.⁶ Moreover, the ASI-3 has demonstrated good psychometric properties and has been validated in diverse samples and several languages.⁷

This study examined the factorial structure of anxiety sensitivity using ASI-3. ASI-3 includes 6 items each for measuring physical, cognitive, and social concerns, respectively. An initial validation study of the factorial structure of the ASI-3 using traditional confirmatory factor analysis (CFA) showed that ASI-3 measures 3 related but distinct factors of anxiety sensitivity.⁶

However, relatively strong associations were observed between physical, social, and cognitive concerns in studies using the CFA model. For example, correlation coefficients among the factors of the ASI-3 ranged between 0.61 and 0.67 in a mixed sample of undergraduate students and individuals with anxiety disorder,⁸ between 0.67 and 0.76 in an Iranian sample of medical college students,⁹ and between 0.70 and 0.80 in a Chinese sample of military personnel.¹⁰ High correlations between factors cause multicollinearity problems and call into question the discriminant validity of the ASI-3.

Although the 3 factors of the ASI-3 are perceived as distinct concepts, recent research suggests that they may reflect a single construct. Some studies introduced a bifactor-CFA model with 1 global factor and 3 specific factors.^11-13 In the model, all ASI-3 items loaded on a general factor and, simultaneously, on 1 of the 3 specific factors. In a sample of Turkish non-clinical residents, the bifactor-CFA model showed a superior fit to the CFA 3-factor first-order model.¹¹ In their study, most items loaded more strongly on the general factor than on specific factors. Support for the bifactor-CFA model was also observed in a U.S. sample of undergraduate students¹² and a South Korean sample of college students.¹³

Nevertheless, to confirm that the factorial structure of ASI-3 is well described by the bifactor-CFA model, the issue of cross-loadings must be considered. To claim that a global factor exists in ASI-3, it is necessary to clarify that the existence of a global factor is not due to the assumption of zero cross-loading in the CFA model¹⁴—global factor strength could be exaggerated by the unspecified cross-loadings of specific factors in the bifactor-CFA model. For example, in the CFA model, it was assumed that 1 item (e.g., When I begin to sweat in a social situation, I fear people will think negatively about me.) of ASI-3 loads on 1 factor (e.g., social concerns). Nonetheless, this item may have cross-loading on secondary dimensions (e.g., physical concerns) simultaneously. If so, this cross-loading is not reflected in the CFA model; therefore, the association between the 2 dimensions (e.g., social and physical concerns) is inevitably reported to be more inflated than it actually is.

An exploratory structural equation modeling (ESEM) technique was proposed to overcome the weaknesses of CFA. ESEM is a newly developed technique that combines exploratory factor analysis (EFA) and CFA to complement the weaknesses of each other. This method is known to be effective in revealing the factor structure of a scale containing multiple factors by allowing cross-loading and prespecified factors on which each item loads.¹⁵ Global factor strength could be exaggerated by the unspecified cross-loadings of specific factors in the bifactor-CFA model.

The argument that the general factor strength of the ASI-3 is exaggerated in the bifactor-CFA model has not yet been tested. This can be tested using bifactor-ESEM, which integrates a bifactor model and an ESEM model.¹⁵ Even when bifactor-ESEM is used, as with bifactor-CFA, if the general factor has higher explained common variance (ECV) values than the 3 specific factors and a strong general factor exists, it can be concluded that a global factor exists in ASI-3.

Current Study

To the best of our knowledge, there has never been an attempt to examine the factorial structure of ASI-3. Accordingly, this study examines whether the bifactor-ESEM model is a better representation of ASI-3’s factorial structure than the existing models of ASI-3. This study has the following objectives: (1) verify whether the bifactor-ESEM model has a better fit than the one-factor CFA, three-factor CFA, three-factor ESEM, and bifactor-CFA models; (2) examine whether the global factor in the bifactor-ESEM model shows high loadings, reliability coefficients, and ECV values; (3) examine the criterion-related validity of the general factor in the bifactor-ESEM model. Criterion-related validity refers to the extent to which the ASI-3 correlates with a specific criterion.

Material and Methods

Participants

A total of 300 college students from South Korea was recruited using convenience sampling. The participants responded to the scale using a pencil or pen. Information regarding participants’ psychiatric history, history of psychiatric interventions, and history of psychological interventions was not collected by the researchers. Those aged greater than or equal to 18 years were included. However, college students not fluent in Korean were excluded. This study was approved by the Institutional Review Board of Gachon University (approval number: 1044396-202308-HR-156-01). Written consent for participation was obtained from all participants before they answered the questionnaire.

Measures

Anxiety Sensitivity Index 3:

The ASI-3⁶ is an 18-item anxiety sensitivity scale. Respondents rated it on a 5-point Likert-type response scale (0 = very little to 4 = very much). The Korean version of the ASI-3 was used.¹⁶ This scale includes 3 dimensions: physical, cognitive, and social. The total score on the ASI-3 ranged from 0 to 72, and the 3 dimensions ranged from 0 to 24. The means of the total score of the ASI-3 for males and females were 13.53 (Standard Deviation [SD] = 9.13) and 14.35 (SD = 9.82), respectively, in Korean non-clinical samples.¹⁶ The internal consistency of this scale was 0.87 for the general scale, with Cronbach’s α values of 0.73, 0.83, and 0.86, respectively, for physical, social, and cognitive concerns.¹⁶

Distress Intolerance Index:

The Distress Intolerance Index (DII) contains 10 items that measure the tendency to avoid negative emotions.¹⁷ Respondents were asked to rate the items on a 5-point Likert scale (0 = very little to 4 = very much). Cronbach’s α of the DII was 0.87.¹⁸ The DII was used to assess the criterion-related validity of the ASI-3.

Statistical Analyses

The quantitative data collected in this study was analyzed using Statistical Package for the Social Sciences (SPSS) version 27.0 (IBM SPSS Corp.; Armonk, NY, USA) and Mplus ver. 8.8. Statistical significance was set at P < 0.05. The factor structure of the ASI-3 was examined using CFA or ESEM. Exploratory structural equation modeling was performed using an oblique target rotation procedure. Table 1 presents the standards of the fit indices introduced in this study.¹⁹

Table 1.

Model Fit Indices and Cutoff Criteria

Model Fit Indices	Good Model Fit	Acceptable Model Fit
χ 2 /df	0 ≤ χ2/df ≤ 3	3 < χ2/df ≤ 5
CFI	0.970 ≤ CFI < 1.000	0.950 ≤ CFI < 0.970
TLI	0.970 ≤ TLI < 1.000	0.950 ≤ TLI < 0.970
SRMR	0 ≤ SRMR ≤ 0.050	0.050 < SRMR ≤ 0.100
RMSEA	0 ≤ RMSEA ≤ 0.050	0.050 < RMSEA ≤ 0.080

χ², chi-square goodness of fit test; CFI, = comparative fit index; df, degrees of freedom; SRMR, standardized root mean square residual; TLI, Tucker–Lewis coefficient index; RMSEA, root-mean-square error of approximation.

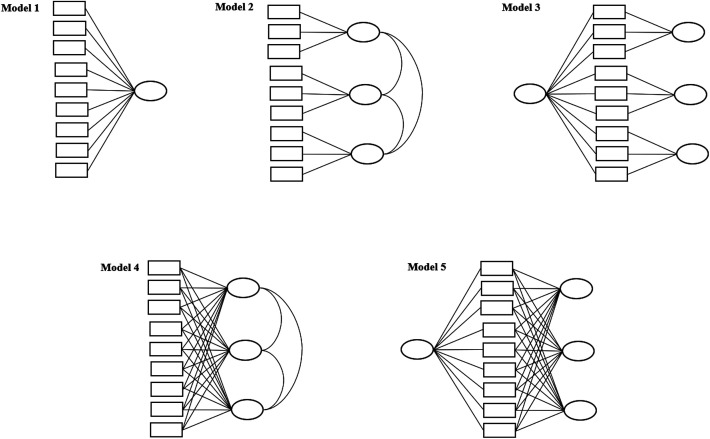
The fit indices of the ASI-3 models were compared as follows: (model 1) 1-factor CFA model; (model 2) 3e-factor CFA model; (model 3) bifactor-CFA model; (model 4) 3-factor ESEM; (model 5) bifactor-ESEM. These 5 models are illustrated in Figure 1. Additionally, the Akaike Information Criterion (AIC) was computed to examine the relative model fit. A model with a smaller AIC score indicated a better fit. If the difference in AIC value (ΔAIC) between 2 models is 6 or more, it is considered that there is a difference in goodness of fit between the 2 models.²⁰ Finally, an additional bifactor-ESEM analysis was conducted to investigate whether the specific factors of the ASI-3 significantly explained distress intolerance after accounting for variance in the general anxiety sensitivity factor.

Figure 1.

Proposed study models.

The lowest loadings and mean loadings on the target factor were obtained in the bifactor-ESEM model. For the factor to be well-defined, the lowest loadings on the target factor should be higher than 0.30, and the mean loadings on the target factor should be higher than 0.50.²¹ Coefficient omega hierarchical (ωh) and coefficient omega hierarchical subscale (ωhs) were used to calculate the internal consistency of the alternative model with the best fit. The appropriate cutoff score for ωh was 0.50.²² Additionally, the ECV was calculated using global and specific factors.

Mardia’s multivariate normality test²³ showed that the data deviated from multivariate normality (skewness b = 104.81, z = 5240.45, P < 0.001; kurtosis b = 551.91, z = 61.94, P < 0.001). Therefore, the robust maximum likelihood estimator, which is less affected by violations of multivariate normal distribution, was used for all analyses.

Results

The age of the participants ranged from 18 to 32 years (mean 21.74 (2.34) years). Of the participants, 65.0% were female, and 35.0% were male. The inter-item correlation matrix is presented in Table 2.

Table 2.

Inter-Item Correlation Matrix

Item	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18
1	–
2	0.331	–
3	0.324	0.535	–
4	0.195	0.447	0.554	–
5	0.281	0.468	0.475	0.431	–
6	0.500	0.267	0.424	0.285	0.423	–
7	0.266	0.360	0.594	0.474	0.405	0.469	–
8	0.212	0.333	0.541	0.579	0.358	0.283	0.492	–
9	0.529	0.272	0.450	0.262	0.361	0.685	0.400	0.313	–
10	0.146	0.329	0.368	0.263	0.350	0.192	0.285	0.304	0.305	–
11	0.368	0.249	0.428	0.242	0.335	0.543	0.265	0.219	0.604	0.256	–
12	0.250	0.353	0.527	0.605	0.380	0.345	0.469	0.711	0.354	0.319	0.299	–
13	0.403	0.329	0.388	0.316	0.428	0.535	0.391	0.290	0.570	0.285	0.549	0.313	–
14	0.217	0.415	0.415	0.387	0.414	0.285	0.324	0.401	0.330	0.481	0.241	0.426	0.322	–
15	0.123	0.349	0.494	0.412	0.268	0.285	0.552	0.577	0.286	0.345	0.235	0.468	0.293	0.393	–
16	0.266	0.363	0.366	0.432	0.458	0.357	0.333	0.377	0.395	0.435	0.323	0.460	0.452	0.581	0.337	–
17	0.330	0.291	0.203	0.246	0.353	0.348	0.362	0.172	0.397	0.239	0.327	0.252	0.450	0.246	0.304	0.410	–
18	0.312	0.467	0.411	0.420	0.466	0.376	0.408	0.332	0.359	0.360	0.280	0.441	0.369	0.514	0.326	0.659	0.364	–

All coefficients are significant at the level of 0.05.

Factor Analysis

The model fit indices for the 5 alternative models are listed in Table 3. The comparative fit index (CFI), Tucker–Lewis coefficient index (TLI), and root-mean-square error of approximation (RMSEA) values for the CFA 1-factor first-order model showed a poor model fit, and the SRMR and χ²/df showed an acceptable model fit to the data (χ² = 568.871, df = 135, CFI = 0.737, TLI = 0.702, RMSEA = 0.104, RMSEA CI = [0.095, 0.112], SRMR = 0.085). Comparative fit index and TLI values for the CFA 3-factor first-order model showed a poor model fit, the RMSEA and SRMR values showed an acceptable fit, and the χ²/df index showed a good model fit (χ² = 271.012, df = 132, CFI = 0.916, TLI = 0.903, RMSEA = 0.059, RMSEA CI = [0.049, 0.069], SRMR = 0.056). For the bifactor-CFA model, CFI and TLI showed a poor model fit, the RMSEA value showed an acceptable model fit, and χ²/df and SRMR indicated a good fit (χ² = 209.826, df = 114, CFI = 0.942, TLI = 0.922, RMSEA = 0.053, RMSEA CI = [0.042, 0.064], SRMR = 0.042). For the ESEM 3-factor first-order model, CFI and TLI showed a poor model fit, the RMSEA showed acceptable model fit, and the SRMR and χ²/df indexes indicated a good model fit (χ² = 224.574, df = 102, CFI = 0.926, TLI = 0.889, RMSEA = 0.063, RMSEA CI = [0.052, 0.075], SRMR = 0.036). For the bifactor-ESEM model, the CFI index indicated a poor model fit, TLI and RMSEA showed an acceptable model fit, and the SRMR and χ²/df indices indicated a good model fit (χ² = 163.098, df = 87, CFI = 0.954, TLI = 0.919, RMSEA = 0.054, RMSEA CI = [0.041, 0.067], SRMR = 0.030).

Table 3.

Goodness-of-Fit Indices

Model	χ2	df	χ2/df	CFI	TLI	SRMR	RMSEA	90% CI	AIC
1-CFA	568.871	135	4.214	0.737	0.702	0.085	0.104	0.095-0.112	12631.180
3-CFA	271.012	132	2.053	0.916	0.903	0.056	0.059	0.049-0.069	12189.216
B-CFA	209.826	114	1.840	0.942	0.922	0.042	0.053	0.042-0.064	12104.864
3-ESEM	224.574	102	2.201	0.926	0.889	0.036	0.063	0.052-0.075	12148.536
B-ESEM	163.098	87	1.875	0.954	0.919	0.030	0.054	0.041-0.067	12090.685

AIC, Akaike information criteria; B-CFA, bifactor confirmatory factor analysis; B-ESEM, bifactor exploratory structural equation modeling; CFI, comparative fit index; df, degrees of freedom; SRMR, standardized root mean square residual; TLI, Tucker–Lewis coefficient index; RMSEA, root-mean-square error of approximation;1-CFA, one-factor confirmatory factor analysis; 3-CFA, three-factor confirmatory factor analysis; 3-ESEM, three-factor exploratory structural equation modeling; CI, Confidence Interval.

The relative model fit—the determination of which of 2 or more models best reflects specific data—was evaluated using the AIC. Model 2 (three-factor CFA model) showed a better model fit than model 1 (one-factor CFA model) (ΔAIC = −441.964). Model 4 (three-factor ESEM model) was a better model fit than model 2 (three-factor CFA model) (ΔAIC = −40.680). Model 3 (bifactor-CFA model) had a superior model fit to model 4 (three-factor ESEM model) (ΔAIC = −43.672). Furthermore, the fit of model 5 (bifactor-ESEM model) was better than that of model 3 (bifactor-CFA model) (ΔAIC = −14.179). Model 5 (the bifactor-ESEM model) exhibited the best model fit among the alternative models.

The item parameter estimates from the bifactor-ESEM solution of ASI-3 are shown in Table 4. In the bifactor-ESEM model, the mean loadings on the global factor were more than 0.50 (λ = 0.420-0.768, M = 0.558). However, the mean loadings were below 0.50, and the lowest loadings were below 0.30 on physical concerns (λ = 0.256-0.741, M = 0.438), social concerns (λ = 0.263-0.685, M = 0.495), and cognitive concerns (λ = 0.017-0.692, M = 0.320) factors—each item explained little of each specific factor after controlling for the global factor. In the physical concerns factor, 4 items (items 4, 8, 12, and 15) showed a substantial loading on the physical concerns factor (λ ≥ 0.30), whereas 2 items (items 3 and 7) failed to load on this dimension (λ < 0.30). Five items (items 1, 6, 9, 11, and 13) showed a substantial loading on the social concerns dimension (λ ≥ 0.30), whereas 1 item (item 17) failed to load on the target factor (λ < 0.30). In the cognitive concerns dimension, 3 items (items 14, 16, and 18) had a substantial loading on the cognitive concerns dimension (λ ≥ 0.30), while 3 items (items 2, 5, and 10) failed to load on the target dimension (λ < 0.30).

Table 4.

Standardized Factor Loadings for the Bifactor Exploratory Structural Equation Modeling Solution of Anxiety Sensitivity Index 3

Item	Global Factor	Factor I	Factor II	Factor III
1	0.429	−0.045	0.429	−0.038
2	0.723	−0.048	−0.139	0.017
3	0.768	0.256	0.052	−0.163
4	0.612	0.373	−0.109	0.071
5	0.647	0.000	0.067	0.137
6	0.523	0.031	0.608	−0.053
7	0.631	0.279	0.114	−0.100
8	0.497	0.741	−0.021	0.002
9	0.511	0.050	0.685	−0.011
10	0.486	0.053	−0.005	0.250
11	0.458	−0.010	0.535	−0.031
12	0.538	0.569	0.028	0.116
13	0.529	−0.016	0.452	0.112
14	0.560	0.092	−0.043	0.381
15	0.517	0.411	−0.015	−0.003
16	0.549	0.014	0.071	0.692
17	0.420	−0.078	0.263	0.208
18	0.629	−0.041	0.005	0.442
ωh	0.874
ωhs		0.259	0.314	0.146
ECV	0.713	0.100	0.119	0.068

The target loadings are shown in bold.

ECV, explained common variance; factor I, physical concerns; factor II, social concerns; factor III, cognitive concerns; ωh, coefficient omega hierarchical; ωhs, coefficient omega hierarchical subscale.

Internal Consistency

As shown in Table 4, ωh was 0.874 for the global factor (18 items), while ωhs was 0.259 for the physical concerns dimension, 0.341 for the social concerns dimension, and 0.146 for the cognitive concerns dimension. Only ωh for the global factor met the threshold of 0.500. The ECV for the general factor was 0.713, whereas those for the physical, social, and cognitive concerns dimensions were 0.100, 0.119, and 0.068, respectively. Thus, the global factor of ASI-3 explained more common variance than the 3 specific dimensions of ASI-3.

Criterion-Related Validity

For evaluating the criterion-related validity of the ASI-3, the latent CFA factor representing distress intolerance was added to the bifactor-ESEM model (χ² = 541.655, df = 298, CFI = 0.926, TLI = 0.906, RMSEA = 0.052, RMSEA CI = [0.045, 0.059], SRMR = 0.043). The results from this analysis revealed that the global factor of the ASI-3 correlated positively with the DII (r = 0.696, P < 0.001). Nevertheless, the correlation coefficient between the DII and the physical concerns factor was −0.076 (P = 0.397), that between the DII and the social concerns factor was 0.303 (P < 0.001), and that between the DII and the cognitive concerns factor was 0.104 (P = 0.522). These results show that the main factor explaining distress intolerance was the global factor of anxiety sensitivity, whereas the specific dimensions of physical and cognitive concerns did not significantly explain distress intolerance.

Discussion

This study aimed to investigate alternative models of the factorial structure of the ASI-3. The ASI-3 was developed to reflect these 3 factors; however, the factor structure of this scale has not yet been established. Therefore, to establish the factor validity of the ASI-3, the 3-factor ESEM and bifactor-ESEM models were evaluated in addition to the existing models previously adopted to examine the factor validity of the ASI-3. This is the first study to use ESEM to examine the internal structure of anxiety sensitivity, as measured by the ASI-3.

The findings showed that the bifactor-ESEM model had a better fit than the 1-factor CFA model, the 3-factor CFA model, the 3-factor ESEM model, and the bifactor-CFA model. In the bifactor-ESEM model, the global factor showed higher loadings, reliability, and ECV values than the 3 specific factors. When controlling for the global factor of the ASI-3, 3 specific factors displayed low reliability in the bifactor-ESEM model. In the bifactor-ESEM model, 6 items (items 2, 3, 5, 7, 10, and 17) from the specific factors had insufficient loadings. Moreover, the specific factor had inadequate ωh, while the general factor’s ωh was sufficient in the bifactor-ESEM model.

The findings showed that one general factor existed in ASI-3 but did not show that 3 specific factors existed after controlling for variance explained by general factors. Therefore, it is questionable whether it is appropriate to calculate 3 specific scores, and caution should be exercised when interpreting the three-factor scores of the ASI-3. Additionally, the finding that a general factor exists in ASI-3 provides a rationale for calculating the overall score of the ASI-3.

The results of this study provide important suggestions for researchers and practitioners. Researchers who want to include specific factors of physical, social, and cognitive concerns in their research model are encouraged to use appropriate statistical procedures to describe the internal structure of anxiety sensitivity and include general and specific factors of anxiety sensitivity. For practitioners who want to develop interventions to alleviate anxiety sensitivity, understanding the accurate factor structure of the ASI-3 can help them diagnose and treat individuals accurately based on their unique factor profiles. For example, when a client has high cognitive and low physical concerns, anxiety sensitivity interventions may focus on reducing cognitive concerns.

These results are consistent with those of previous studies that showed that the bifactor-CFA model had a superior fit to the 3-factor CFA model and that the global factor in the bifactor-CFA model exhibited relatively high loadings, reliability, and ECV values.^11-13 Including cross-loadings in the bifactor-ESEM model did not significantly affect the bifactor structure of ASI-3, and the global factor remained the strongest. These results show that the existence of the global factor in the bifactor-CFA model of the ASI-3 was not a result of the exclusion of cross-loadings.

These findings support the expectation that the general factor of ASI-3 would be associated with distress intolerance. This association suggests that the global anxiety sensitivity factor explained a large amount of the variance in distress intolerance. This result is in line with an existing study that showed that the global factor in the bifactor-CFA model of the ASI-3 had the strongest association with an external anxiety criterion.¹²

There are 2 reasons why the 1-factor CFA model of the ASI-3 showed a poor fit to the data, although a strong general factor existed in the factorial structure of the ASI-3. First, the number of ASI-3 items was excessively large. It has been argued that the larger the number of items within a scale, the more difficult it is for the scale to represent a single factor.²⁴ Second, anxiety sensitivity measured by the ASI-3 is a broad construct. According to previous research, it is difficult for scales measuring broad constructs such as intelligence or well-being to have a single-factor structure.²⁵

The finding that the factor structure of anxiety sensitivity included general factors is not new. A general factor was observed in the factor structure of the ASI-3 in studies targeting Western and Eastern populations.^11-13 However, the patterns of relationships between items and specific factors found in this study might not be found in studies with samples from other cultures. Therefore, it is necessary to examine whether the results of this study are applicable to other cultures.

This study had some limitations. First, as only college students participated in this study, there are limitations in terms of generalization owing to the lack of sample diversity. Second, only a self-reported questionnaire was used to measure the research variables. As only self-report measures were used, the relationships between the variables may have been overestimated. Therefore, it is necessary to replicate the results of this study using methods other than self-reporting. Third, the internal structure of anxiety sensitivity derived from this study may have had a different appearance in clinical samples. Thus, it is necessary to examine how the model used in this study differs in various groups with mental disorders. Fourth, none of the models included in this study showed perfect model fit. The reason for these results may be an insufficient sample size. In bifactor-ESEM, the number of parameters to be estimated is large, and a larger number of samples is necessary. Hence, a robust maximum likelihood estimation method was used because it is robust for small sample sizes. In follow-up studies, it will be necessary to replicate the results of this study using other estimation methods or larger sample sizes. Finally, as the data were obtained at a single point in time, longitudinal research is required to confirm the stability of the general anxiety sensitivity factor. For example, additional analyses could show consistent patterns of the bifactor-ESEM model across a 12-month period.

Overall, this study showed that there are limitations to using the ASI-3 subscales, and it seems preferable to use the total score. Additionally, it is necessary to confirm whether our results can be replicated in clinical groups or using a longitudinal study design.

Funding Statement

This work was supported by the Gachon University research fund of 2023.(GCU- 202304900001).