Abstract
Ambulation is defined by duration, distance traversed, number and size of directional changes and the interval separating successive movement episodes; more complex measures of ambulation can be created by aggregating these features. This review article of published findings defines random changes in direction during movement as “movement path tortuosity”, and relates tortuosity to the understanding of cognitive impairments of persons of all ages. Path tortuosity is quantified by subjecting tracking data to fractal analysis, specifically Fractal Dimension (Fractal D), which ranges from a value of 1 when the movement path is perfectly straight to a value of 2 when the movement path is random, resembling the “drunkard’s walk”. The review elucidates the mathematical assumptions underlying Fractal D, its use in the analysis of movements of free ranging animals, and its application to the study of cognitive impairment and the prediction of falls in older adults. We conclude Fractal D offers a reliable, valid, sensitive and easily interpreted real-time longitudinal measure of unrestricted movement path tortuosity unaffected by mobility aid use.
Keywords: Fractals, Numerical analysis, Ultra wideband technology, Cognition, Mental disorders, Pervasive computing, Animal behavior
I. INTRODUCTION
Age-related slowing of upper and lower extremity movements is partly due to cognitive factors required for their execution. Age-related slowing of movements includes both quantitative and qualitative features of movement. Quantitative features are based on time to complete a task—speed of movement required to initiate or execute a movement. Historically, other observable features—hesitancies and directional changes during a single movement or variability among repetitive movements—are less studied, partly because they often considered as errors in studies of movement speed and partly because quantitative analytic tools were unavailable.
Age differences in cognition related to behavioral slowing present both as relatively longer total movement times in response to increasing task difficulty as well as the static perceptual-motor and variable decision making components of the reaction time (1) (2). Qualitative movement features related to cognition are demonstrated by studies showing that changes in movement speed during pointing movement trajectories are greater in older persons (3). Movement times as well as pointer placements in a repetitive tapping task are more variable in older age (4). The coefficient of variation of an individual’s distribution of simple and forced choice reaction times increases with age in a variety of tasks (5). Dykiert et al.’s review identified several studies showing that the age effect is relatively greater in patients with Parkinson’s disease, and Alzheimer’s disease.
Slowing of lower extremity movements appears in reaction times and walking speed on predefined paths (3); walking is slowed significantly when performing effortful cognitive tasks such as counting down by threes or monitoring an auditory channel for a predefined target (6). Using short walking samples on a prescribed course, differences in gait sequencing have been observed (7) using very precise movement tracking tools. Older persons take a wider but shorter stride (8, 9) and show more stride to stride variability (10). As with upper extremity movements the age differences in normal aging are exaggerated in older persons with dementia.
The age differences in movement summarized above employed methods restricting the degree to which movement could vary qualitatively, e.g., 6–8m gait mats for walking, or visually defined targets for upper extremity movements. Except for reports using the coefficient of variation in speed of repeated responses (5, 11), methods to study direction changes or hesitancies in a path have lacked novel approaches. Readily observable changes in path direction that occur in dementia-related wandering, the staggering of the inebriate, or the “punch drunk” boxer, requires new methods of observation and quantification. Police employ field sobriety tests to determine how well inebriated drivers “can walk a straight line” and in the case of wandering behavior in dementia, Algase and colleagues (12, 13) have devised rating systems for trained observers that distinguish purposeful vs. wandering movements, with the latter subdivided into random, pacing and lapping. Among the subdivisions, the determination of “random” has proved the most difficult for human observers to recognize reliably, probably because humans are well suited to detecting periodic events (lapping & pacing) but not estimating how random one pattern of walking is compared to another.
Recent developments in both indoor and outdoor movement tracking technologies have increased the opportunity to measure qualitative and quantitative features of unrestricted movements. The remainder of this article describes: 1) the derivation and applications of a measure of movement path tortuosity called Fractal Dimension (Fractal D); 2) studies of age-associated differences in human movement using modified procedures developed by animal ecologists to study exploratory and food seeking behaviors; 3) summarizes results of several studies describing age-related changes in path variability to cognitive functioning and the prediction of future falls; and 4) discusses directions for future research.
II. MEASURING MOVEMENT PATH TORTUOSITY
There is a long history of ecologists measuring the tortuosity of movement paths, mostly to measure foraging intensity. Typically animals travel with continuous movement paths that we discretize by sampling at fixed time intervals (Fig. 1). Thus we are representing a continuous function as a discrete one. The discretization is both easy to visualize and is mathematically tractable. If we start sampling at location , then the animal visits location after steps.
Fig. 1.
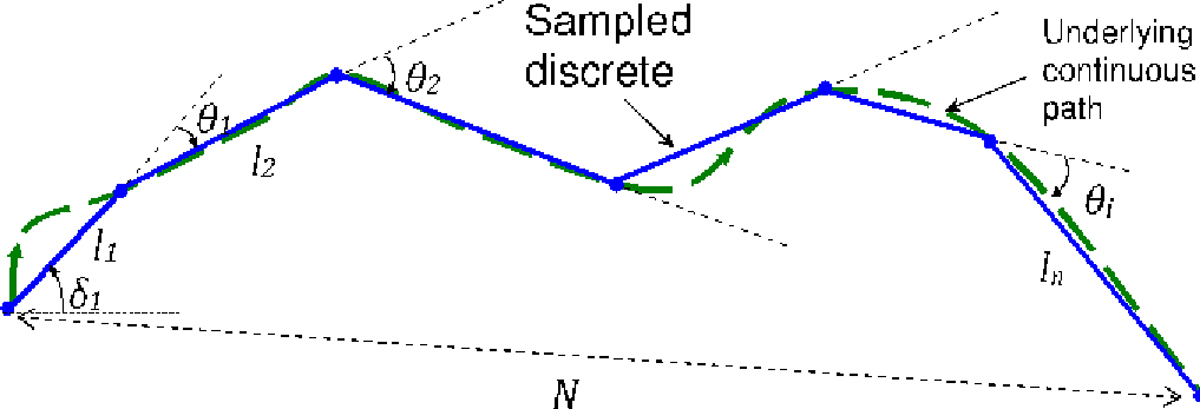
Illustration of discretized sampling (solid blue) of an underlying continuous movement path (dashed green), showing the various parameters of the sampled path. There are n steps in the path, the length and angle of step are and , and the angle between steps , and steps , is . Path net displacement is .
The length of step , , is the distance from location to , and the angle of step , , is the angle between step and horizontal. The turn angle is the angle between steps and :
| (1) |
The simplest earliest measure of tortuosity involves tracking the animal for a fixed distance and then measuring a “straightness index” (14). Straightness compares the overall net displacement of a path with n steps and total path length , and is given by:
| (2) |
| (3) |
Straightness is 0 when the animal returns to its starting point and is 1 when the path is completely straight. This measure is intuitively appealing because it has a range from 0 to 1 and is easy to calculate. There have been various other tortuosity indices proposed that are variations on Straightness (15). The main problem with all of them is that they are affected by spatial scale in ways that are not always obvious (16). Thus a measure is needed that incorporates scale explicitly.
One tortuosity measure that incorporates scale explicitly was first proposed by Mandelbrot (17), who posed the question — what is the length of coastline of Britain? The answer is that it depends on the scale of measure. But more importantly, at each scale the coastline looks similar. For example, Fig. 2 shows a section of the coastline of Britain at three spatial scales.
Fig. 2.

A section of the coastline of Britain, viewed at 3 different spatial scales. Note that tortuosity is similar at all scales - i.e. the coastline is a fractal.
If you donť know the actual scales, it is difficult to tell which is the zoomed-in vs. zoomed-out version simply by looking at the patterns. Thus while the 3 maps do look different, all three have a similar geometrical pattern — the coastline shape is self-similar. Mandelbrot (17) introduced the term “fractal”; a geometrical shape is fractal if it has a similar pattern over a wide range of spatial scales. The map of the coastline of Britain is scale-free. We see examples of fractals in many other places in nature — for example, many species of fern leaves, and the branching in our lungs, show similar patterns at different spatial scales (18).
We can measure this pattern using the statistic “fractal dimension”. Strictly, fractal refers to a mathematical series in which the Hausdorff-Besicovitch dimension, or fractal, exceeds the Euclidean dimension (19), but “Fractal D” has a nice intuitive explanation — it is the continuous analogue to geometrical dimensions. For example, a straight line has a dimension of 1, and a plane has a dimension of 2. Lines have fractal dimensions ranging from 1 to 2, where at 1 they are completely straight and at 2 they are so tortuous as to completely cover the surface. The coastlines in Fig. 2 have a fractal dimension of 1.04, 1.05, and 1.05.
We can extend this idea to measuring the tortuosity of animal movement paths (19). We estimate Fractal D, by measuring the gross path length at different scales, . At each scale, length is measured by walking a pair of dividers along the map. Then, solving for D in the following equation:
| (4) |
where is some constant of proportionality (Fig 3, blue symbols). Taking s to the power of 1-D instead of D allows D to be interpreted as the continuous analogue to geometrical dimensions.
Fig 3.

The blue symbols show Fractal D estimation. The green symbols show Fractal D estimation over a range of scales centered at , with a width of .
A. Ecological Basis for Fractal D
Animal ecologists have developed conceptual models about how animals travel, that help us to understand how humans' cognition might affect their movement paths. We will first consider the simplest form of movement, and then add in two layers of realism. At each stage we will also discuss how this applies to the movement of people. These sections highlight how behavior varies with spatial scale and thus describing movements without considering spatial scale is dangerous.
B. Aimless Wandering
There are three parts to the simplest form of movement. First, animals have a natural gait that determines how fast they travel, how much they turn and how long each step is. Second, animals have a directional inertia, in that they tend to continue travelling in the direction they have been going in the past. Finally, when animals do turn, the direction and amount that they turn is not affected by any previous movement — there is a random component to it (20). Intuitively, this is what one imagines as being “aimless wandering”.
We represent such movement paths mathematically, as follows. Move lengths and turning angles are distributed with probability distributions and . If movements are a series of independent, random draws, from the and then the animal is travelling with a correlated random walk (CRW). The term “correlated” denotes that the are correlated to each other, while the are not. This means that the animal tends to walk in the same direction as it did in the past, but that at each step the turning angle is independent of the previous step length and angle. It is important to consider how CRW's are fractal. We do this by considering how straightness varies with total number of steps. It can be shown that
| (5) |
for some constant (21) (22). Thus, since
| (6) |
| (7) |
Thus path Straightness depends on the number of steps. Furthermore, since
| (8) |
therefore path Straightness is 0 at very large scales. This means that as spatial scale increases, path tortuosity increases for CRW. Thus CRW's are not self-similar.
One can understand this increase in path tortuosity intuitively as follows (Fig 3.). At smaller spatial scales the shape of a movement path is primarily determined by the animal's gait, and thus is usually quite straight. It is more tortuous if the steps are shorter, if the animal is travelling slower, and if it is heavier. But at larger scales the random turning effect increases and adds to the gait effect, causing path tortuosity to increase. Thus as we zoom out the path becomes more and more tortuous, until at large scales it is a completely random walk (23, 24).
Overlaid on top of this is that animals need to avoid obstacles, which occur at various spatial scales. Thus, there is an added component to tortuosity that depends on the habitat. Imagine an inebriated person staggering down the street. At a small scale the person turns a bit at each step. But at larger scales the person goes here and there with no seeming pattern.
This increase of tortuosity with scale at first glance seems contrary to the idea of Fractal , since was originally defined only for self-similar geometrical structures. However, we can adapt the idea of Fractal to non self-similar structures by estimating as a function of scale, as follows. Choose m discrete values of scale, , for , such that are equally spaced. is the estimate of Fractal for . For each , apply equation (4), solving for , to give
| (9) |
but only over the range of scales from to , for fixed values of . Effectively this uses a sliding window of fixed width on the Log(scale) axis to estimate as a function of (see Fig 3, green symbols).
There are some potential sampling issues caused by being a function of scale. First, estimates may be affected by the placement of the first step of the dividers. However simulations show that the estimates for are slightly improved by walking the dividers both forward and backward along the path, and using the mean of those two estimates, but that there is no benefit to starting the sampling at other places in the path (25) Second, experiments must be designed to ensure that spatial scale is held constant across all treatments.
C. Directed Movement
However, animals rarely travel aimlessly. Typically they are travelling with some intent; they are going towards some place. For example, wolves regularly patrol their territory boundaries, marking them with urine (26) and zebras travel from one waterhole to another during the dry season (27). People also usually travel with directed movement — you are going somewhere when you are walking. Thus we will define directed walks as moving towards a known goal.
What does the movement path of directed travel look like? You might expect to see a completely straight path, but in the wild this rarely happens. Consider this example. Suppose some wild animal wants to go to its home den. On the way there, it may have to go around a pond. But on the way to the pond it may have to go around a thick clump of trees. And on the way to the clump of trees it may have to go around a large deadfall. And on the way to the deadfall it may have to go around individual trees or bushes. Thus at each spatial scale there are obstacles that it needs to go around, even though it is travelling in a directed manner. This can be modeled as follows. Suppose the start and end-point of a path is () and , and the distance and angle between the points are and . Then the middle coordinate would formed by
| (10) |
with randomly drawn from some probability distribution , with and - i.e. determines how far along the line segment you move between the two points and determines how far you vary orthogonally to this line segment. Then the coordinates between and , and and would be chosen similarly, using the same probability distribution for . This would be repeated for each pair of location coordinates. The structure of the habitat would determine the tortuosity of the movement path. Since natural landscapes are often self-similar over a wide ranges of scales (28, 29) directed paths such as this are fractal (30).
Consider an example with people. If you were walking across an open field then your path would be quite straight. But if you are going from your home to your office, then, although you might be taking the straightest path possible, at a large scale your path is constrained by the patterns of streets, and on a small scale your path is constrained by the arrangements of rooms inside buildings. Directed paths look more like the coast of Britain than like aimless wandering.
D. Perceptual Range
One last level of added realism is that animals can only see a limited distance around them — they have a certain perceptual range (31). Animals' perceptual range can be visual (31, 32), olfactory (33) or auditory (34). Furthermore, perceptual range is not limited to what animals can immediately perceive — animals form memory maps (35) and thus, more generally, perceptual range is the distance that animals can perceive their world, whether immediately or in memory.
How does perceptual range affect movement paths? It creates a threshold effect: at scales smaller than the perceptual range paths quite straight, but at scales larger than the perceptual range paths are more tortuous (36). Thus decreasing the perceptual range makes paths more tortuous (37). This effect can be used to test whether a movement path is directed - directed movement paths should travel further than a CRW at larger spatial scales [27].
At first glance the idea of perceptual range might not seem relevant to people — although we can only see a limited distance around us, typically we know the surrounding areas in our day-to-day travel. If we travel to our office, we know the route and the obstacles on the way. Thus most of our movements seem to be inside the bounds of our perceptual range.
However perceptual range is also temporal, not just spatial. In your mind you plan your movements a certain time ahead. For example, although you may have a general idea of what you will be doing after supper, you may wait till you finish supper to decide exactly where to move to — whether to travel to the bathroom, or the TV room, or out somewhere. Or, even if you have decided what you will do after supper, your movement path still has an extreme change in direction at the supper-table. Thus, practically, we travel both within and outside of our bounds of perceptual range.
E. Combining it all
We can combine the ideas of directed movement, perceptual range and aimless wandering for a more realistic view of how animals (and people) travel — and for an understanding of how dementia can affect the movement of people. An animal decides where to travel based on its perceptual range. It goes there in directed travel. Then, at that node, it decides anew where to go. This creates directed travel on a small scale between nodes, but aimless wandering at a large scale from node to node (Fig. 5). For example, wood mice travel in quite straight patterns on a small scale from one shrub to another, but travel with aimless wandering on a large scale between shrubs (38).
Fig. 5.

A movement path of an animal travelling in a directed manner between nodes, but revealing aimless wandering (correlated random walk) on a large scale
Consider the travel of a resident of a nursing home or assisted-living facility, throughout a day. Their nodes might be their bedroom, the bathroom, the dining room, and a commons area. On a small scale their path between those is inherently straight, but constrained by furniture and the arrangements of the rooms. But at a large scale their path from one node to the other is quite tortuous, as at each node they decide where to travel again.
But then suppose someone is walking from one room to another and becomes confused, not sure where they were going. Conceptually, their temporal perceptual range has suddenly decreased. They might turn and go in a different direction than they had been going, adding a node in their path — i.e. the distances between nodes would decrease, causing path tortuosity to increase. Thus we would expect that Fractal D of movement paths would increase with the onset of dementia. Thus, although Fractal D does vary with spatial scale, we expect that Fractal D will increase overall.
III. FRACTAL D IN RELATION TO AGING AND BRAIN DISEASE
Our motive for relating movement path tortuosity to age associated cognitive deficits was driven by a need to develop an operational definition of the random elements of wandering. Algase, Moore et al. (13) identified 23 different definitions of dementia related wandering; the common feature among all definitions was apparently aimless ambulation that proved difficult for observers to quantify. In the landmark study of Algase and colleagues (12) trained observers were able to identify purposeful walking, lapping and pacing and, somewhat by a process of elimination, what they termed random ambulation.
Since humans clearly were unable to definitively observe and quantify “random” movement, we sought a mechanical observer that could gather data continuously on many elders for months at a time and not suffer observer fatigue while measuring small directional changes in unrestricted ambulation of as many as 100 persons at once. We selected the Ubisense (Ubisense, LLC, Cambridge, UK) Ultra-wideband Real Time Location System (UWB-RTLS) system. Elders wore a small wrist transponder whose position was triangulated by four sensors, which yielded 3D positioning relative to an arbitrary origin in the corner of a 9 × 15m lobby of an assisted living facility (ALF). The spatial resolution of the transponder was 20cm in all three axes, and the sampling rate was 0.43s. X, Y, and Z coordinate data were written to a database in near real-time for all tags. The accuracy of the system was determined in a published pilot investigation (39) and the accuracy of the UWB-RTLS tracking data was compared against a Vicon, Inc. system employed in kinematic studies.
To compute tortuosity from the raw tracking data we initially adopted the published procedures of Nams (24), but in later work Fractal D was calculated automatically using a Real-Time Fractal Path Analysis algorithm developed by Craighead (40). A path was defined as a period of movement bounded by 60s of immobility of the transponder. In addition to each path’s tortuosity index, the duration and distance of the movement and walking speed during the path were calculated. The estimates are aggregated as needed for the project in question, usually over 24 hours.
Since Fractal D does vary with scale, yet we are estimating one overall Fractal D value, it is important that studies be designed so results do not depend on spatial scales used. We ensured this in three ways: First, we estimated one D-value over a wide range of scales (e.g. using equation (4)). Second, the ranges of scales were wide enough to cover all of the potentially interesting behaviors - from below step size to the limits set by the size of the buildings. Finally, in each experiment we used the same range for all treatments.
The particular algorithm we used to estimate D varied among studies because of differences in our intent. Initially we were testing whether path tortuosity can be used to measure cognitive impairment. We set specific scales and then estimated D-values from the whole dataset after the end of sampling. But in later studies we were testing the applicability of this approach to real-world situations. For this technique to be useful we need continuously updated predictions of cognitive impairment. We cannot wait till the end of all the sampling to estimate path tortuosity. Thus we used an algorithm that automatically sets the range of scales from ½ of step size to 10x the step size, and gives continuously updated estimates of Fractal D (40).
All published human subjects research conducted by Kearns et al., and presented hereafter was approved by Institutional Review Board of the University of South Florida. Kearns, Nams, and Fozard (41) evaluated movement path tortuosity in 14 elderly ALF residents for 30 days as residents passed through an instrumented lobby separating bedroom, functional, and dining areas. Consenting participants were administered the Mini Mental State Exam (MMSE) (42) by a trained examiner. The Mini Mental State Exam is a widely used 30 item test for cognitive impairment, used by clinicians and researchers studying older adults to evaluate deficits in short term memory, temporal and spatial orientation, ability to follow commands, attention, language, and calculation and registration. The test results are frequently used to help determine a diagnosis of dementia. The main finding was a statistically significant −.47 correlation between Fractal D and MMSE; greater path tortuosity predicted lower MMSE scores (poorer cognitive performance). The study was replicated on a larger sample of 28 residents across two ALFs (43), which included residents with a clinical diagnoses of dementia. An unexpected finding was that Fractal D was considerably better at classifying persons with a dementia diagnosis; 2 misclassifications, compared to 6 for the MMSE (Fig. 6).
Fig. 6.

Classification of persons with clinical diagnosis of dementia using Fractal Dimension vs. the Mini Mental State Exam
The relationship between path tortuosity and cognitive impairment is shown in another way in Figs. 7 & 8 which shows a representation of the paths generated by two residents of one ALF over the same two hour period as they walked through the monitored lobby, passing from the dormitory to the dining area, which also housed a medication dispensing station and staff offices.
Fig. 7.
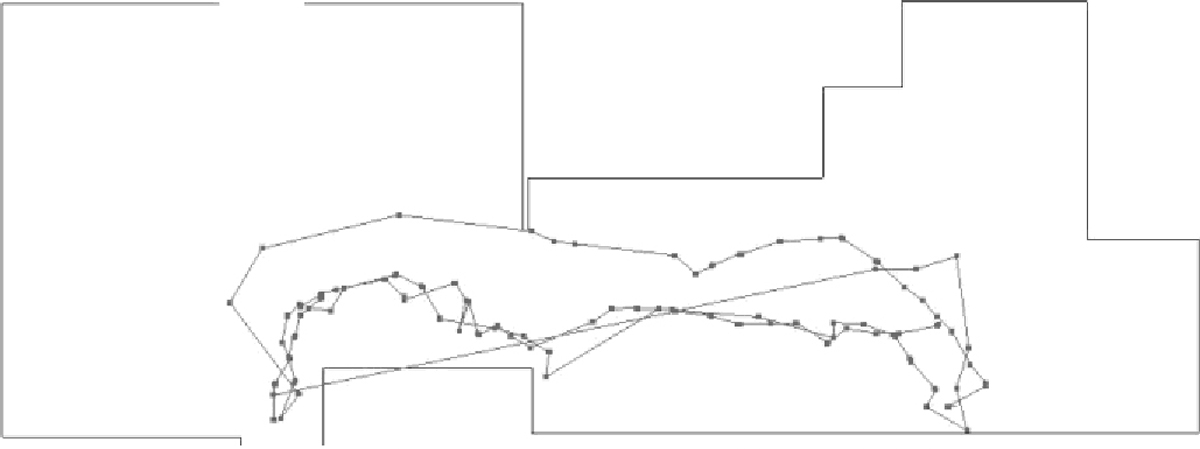
shows the paths of Subject 1, a woman with an MMSE of 25 (normal cognition) and a Fractal D of 1.2. Note the linearity of the paths across the lobby space.
Fig. 8.

shows the paths of Subject 2, a woman with a MMSE score of 21 indicating cognitive impairment and a Fractal D of 1.40.
It is possible that the movements of the participant with high Fractal D made many stops for social interactions. One indirect approach to evaluating this hypothesis would be to measure the number of tag-wearing residents who were in close proximity to or in tandem movement with the participant. This was not possible because only a subset of residents occupying the space wore transponders.
A subsequent published study of 53 ALF residents by Kearns et al. (44) examined tortuosity in the week before the resident fell. Using logistic regression we found high tortuosity (higher Fractal D) and the presence of a fall in the prior year yielded an 80% correct classification of faller status. An attempt at a three-factor model incorporating walking speed, Fractal D, and past fall history failed, with walking speed’s influence eclipsed by Fractal D. The results clearly indicated that walking tortuous paths (having a “drunkard’s walk”) was a risk factor for future falls, and confirmed that the best long-term predictor of future falls was having a prior fall. Moreover, the results also showed that Fractal D was a dynamic measure, subject to change over periods of days if not hours. The relationship between Fractal D and future falls decayed as a function of time with “stale” readings (those older than a week) having little prognostic value. The underlying neurological mechanisms determining Fractal D deserve attention, and these likely include executive function, spatial orientation, vision and balance.
Traumatic brain injuries provide additional evidence for the significance of temporal variability in Fractal D. Kearns et al. (45) gathered mean daily Fractal D on 22 veterans over their months-long rehabilitation in a residential polytrauma facility. Ten patients had discernable declines in Fractal D during their residency while 12 did not. Independent clinicians judged those with declining trends to have significantly better clinical outcomes on the Mayo Portland Adaptability Index, the facility’s primary assessment tool. Thus long-term changes in Fractal D may serve as a useful adjunct to clinical care for persons with head trauma, potentially alerting clinicians to unanticipated reversals in progress and facilitating the staging of treatments.
A later study with veterans in the same residential polytrauma facility (46) found Fractal D at admission predicted their ability to successfully perform prompted behaviors during months of subsequent therapy for TBI. Prompts to attend scheduled appointments, and take medications while observed at the nurses’ station were delivered to the nearest of 30 wall mounted displays. A behavior occurring within a half hour of a prompt was deemed successful. Success was verified by the location tracking data that indicated the veteran appeared at the locations specified. More than 60% of responses occurred within 15 min. of delivery of the first prompt.
In the study just described, the Fractal D at admission was derived from data from a GPS logger worn in a shirt pocket by the veteran during a single self-determined half hour walk outdoors. The veteran was allowed to determine the course, while an attending research assistant prevented the veteran from coming to harm. The latitude and longitude were read each second to a spatial resolution of approximately 2.5m, and the successful compliance with prompts was accomplished using data from the indoor movement tracking system previously described (47). The validity of the Fractal D assessments using the GPS logger was determined in an earlier study comparing the outdoor ambulation of two groups of community veterans; one with a history of TBI and a comparable group of veterans without TBI. Veterans in the TBI group had incurred injuries while in military service up to 10 years earlier. Successfully measuring Fractal D with two somewhat different systems provided an increased degree of confidence that the assessment method was robust and not simply an artifact of the chosen method of measurement.
IV. DISCUSSION
A. Movement tracking of unrestricted movements and in conditioning
In ecological studies Fractal D quantifies spatial variability of animal movements along a continuum from extremely random, with values approaching 2 for movements characterizing exploratory activities such as locating food and mates, to highly goal-directed movements, involving nearly straight line travel with values approaching 1 that an animal might take to gain the safety of a burrow when foraging is complete. During goal directed movements, high Fractal D values may occur when changes in path direction are necessary to circumnavigate environmental barriers. Cognition is not usually studied as an independent factor in ecological studies; poor cognitive abilities in an animal typically result in an animal falling prey, and being removed from the gene pool. While studies of maturation to adulthood in wild animals do exist, movement path tortuosity has, to our knowledge, not been employed in the study of aging in wild animals.
In contrast, studies of animal and human conditioning and learning have focused on the conditions that influence how well or how fast the target behavior is isolated from the repertoire of behaviors of the learner. In operant conditioning studies, the process of “magazine training” involves pairing the sound of the electromechanical feeder with the delivery of a food pellet so that the pellet’s delivery may be used to reinforce some novel behavior (48). A very hungry subject is introduced to the new environment and begins an aggressive search for food (Fractal D is high), which continues until the first food pellet is delivered. After delivery of the first reinforcer, competing non-productive responses are progressively eliminated as the subject takes a progressively straighter line to the magazine (yielding lower fractal D – more goal directed behavior). Once magazine training is complete, the “method of successive approximations to a goal” (aka Shaping) is used to train the subject to manipulate the response lever on its own, thereby allowing it to deliver food reinforcers autonomously. During shaping the subject may generate more search behavior and competing responses (resulting in a higher Fractal D) as it attempts, through trial and error, to make its behavior conform to the new contingencies established by the experimenter. In this example, active search behaviors facilitate learning the new contingencies of reinforcement, but as they are learned, search behaviors (and higher Fractal D movement components) cease and are replaced by progressively more efficient responding (i.e. response lever pressing), which meets the new contingency with a minimum of wasted effort (and a return to lower Fractal D levels).
In alleyways or similar restricted test environments, an animal’s maximum running speed is often taken as an index of the effectiveness of the conditioning, and is principally attributed to the elimination of competing responses such as hesitancies while exploring the alleyway. While movement path tortuosity could, in principle, serve as a direct measure of the reduction of competing responses during alleyway conditioning, the choice of measures, details of scaling, and type of apparatus used would require specification. The strongest link between learning and environmental factors has been provided by studies concerning the role of distal and proximal visual cues in maze learning (49). As in ecological studies, the independent assessment of cognitive abilities in animal learning is rarely conducted. In studies of aging’s impact on human learning and performance, independent assessments of cognitive factors required to successfully perform a task are common, particularly for tasks requiring sustained attention and attentional control (49). We conclude from these observations that path tortuosity offers a direct method for exploring mechanisms underlying learning and skill acquisition.
The studies of humans summarized above have focused on the relationship between cognitive deficits and elevated movement path tortuosity in older persons with and without a clinical diagnosis of dementia, and young and middle-aged persons suffering TBI. In these studies increased path tortuosity is attributed to a change in a highly overlearned performance as a result of both normal and pathological aging and brain disease. The longitudinal study showing decreasing Fractal D in veterans indicates recovery of cognitive functioning over the course of treatment is accompanied by a decline in Fractal D (45).
B. Path tortuosity and other descriptive schemes for movement
The movement ecology paradigm (50) provides a broad conceptual framework for analyzing movements of both living and inanimate objects. The paradigm is built around three questions: why move; where to move; how to move. In both the study of animals’ movements in natural habitats and our human studies, the primary link between cognition and movement is where to move. In animal studies the why and how questions are answered in terms of the distinction between random and directed movement. In human studies greater path tortuosity is attributed to difficulty in choosing or maintaining a desired movement path resulting from spatial disorientation and certain failures of memory—sometimes referred to as executive function. A consistent finding in all of the human studies described was that differences in how the movement is accomplished does not alter Fractal D—the relation between cognitive deficit and Fractal D persists across persons using wheelchairs, walkers or other mobility aids—elevated Fractal D results from difficulty in navigating a movement path rather than how it is traversed. In animal and human studies, the question of “why move” has been assumed to be a given—the issue is where to move in order to meet the goal of the movement. In very advanced cases of dementia seen in institutional settings the person with dementia may require assistance in determining “why move” as well; (s)he eventually requires personal escorting to specific locations—bedroom, dining area, etc. (51).
C. New opportunities for research and intervention
While our research has shown that short-term increases in Fractal D are predictive of falls within the next 7 days, the underpinnings of the elevation are not understood and limit the options for intervening. Of all the predictors evaluated in Kearns et al. [41] only a history of one or more falls in the prior year, a common finding in such research, contributed to future falls. Another hypothesized fall predictor was antipsychotic and antidepressant medication use, but that hypothesis was not supported; almost all participants were receiving one or more of those medications for the entire study period, so their adaptation or tolerance to the drug had long since been complete. We also examined the influence of other medications, particularly antibiotics, to treat short-term infections. Given that short-term cognitive impairment is linked to increased path tortuosity, we expected that painkiller and antibiotic use might be a mediating factor. We found suggestive but inconclusive evidence of a relationship between the timing of falls and the treatment of those infections.
An improvement in future studies of path-tortuosity related falls would be to employ automated fall detectors to indicate precisely where and when they occurred. Only 51 of 71 staff-reported falls in our study met our definition of a movement-related fall. Our automatic measures of movement path tortuosity were gathered as participants traveled within a monitored lobby; yet almost all falls occurred in their private bed and bathroom areas and were inferred from staff-generated “incident reports” which often contained only information about the fall provided by the faller.
In addition to measuring short-term path tortuosity changes predictive of future falls, Fractal D may be useful for evaluating the long-term consequences of a fall or the all too common concussion in contact sports. Our research to date has identified long-term effects of TBI on Fractal D as well as documented changes in the measure over the course of TBI rehabilitation.
V. CONCLUSION
The main goal of the research summarized by this review was to create an additional tool for describing the relationships between cognitive changes in aging and/or brain disease and human ambulation. The added value of the tool, called Fractal D, to existing procedures for studying speed of human ambulation is that it provides a direct measure of the spatial variability of ambulation. Fractal D deals with the geometry of lines and as employed here is used to study changes in path direction. The present application of Fractal D measures spatial variability of multiple free-ranging individuals simultaneously over extended periods indoors to address primary research questions relating movement path tortuosity changes to cognitive declines in middle aged and elderly persons, some with dementia and some with traumatic brain injury. In each of these areas Fractal D has augmented earlier research findings by elucidating the severity and trajectory of cognitive deficit as recovery occurs over successive episodes of rehabilitation. Elevated Fractal D is also a potent predictor of movement related falls in the elderly.
Fractal D has been employed by animal ecologists to describe exploratory and directed movements of animals in their natural environments. The present essay reviews and summarizes some of that seminal work and describes its adaptation to the study of voluntary human ambulation. Several areas of research and clinical intervention were described.
Fig. 4.
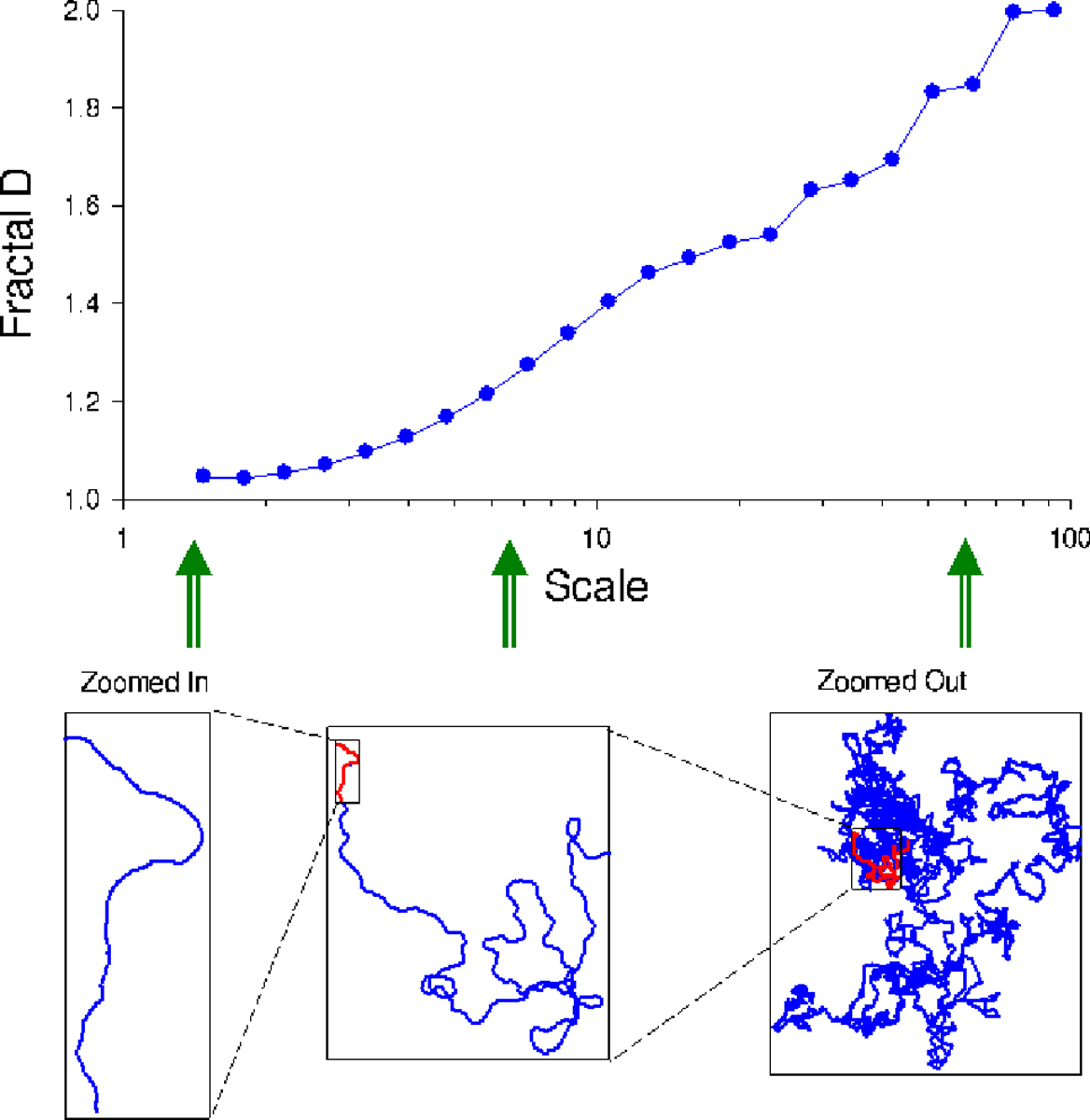
An idealized animal travelling with a correlated random walk. The top plot shows Fractal D as a function of spatial scale. Note that path tortuosity increases at larger scales. The bottom plots show the movement paths viewed at 3 specific different spatial scales.
Fig. 9.

Left panel, GPS track of a traumatic brain injury victim with Fractal D of 1.37. Right panel, a normal subject with a Fractal D of 1.11.
Acknowledgments
This work was supported in part by the U.S. Department of Defense under Grant W81XWH-11-1-0634, the U.S. Agency for Healthcare Research and Quality Grant R21HS18205-01, and the Natural Sciences and Engineering Research Council of Canada under Discovery Grant RGPIN-2015-05201.
Biographies

William D. Kearns Received his Ph.D. in experimental psychology from the University of South Florida in Tampa, Florida, USA in 1989.
He joined the University of South Florida’s Florida Mental Health Institute faculty in 1989, was the Director of the Institute’s Office of Information Technology from 1992–2003, and from 1997–2003 served as USF’s Representative to the national Internet2 Project. He is currently an Associate Professor in Rehabilitation and Mental Health Counseling in the Department of Child and Family Studies, which resides in USF’s College of Behavioral and Community Sciences. His current publications include: W. D. Kearns, S. Scott, J. Fozard, C. Dillahunt-Aspillaga, and J. Jasiewicz, “Decreased movement path tortuosity is associated with improved functional status in TBI patients.,” Journal of Head Trauma Rehabilitation, 2015 (in press). W. D. Kearns, J. Fozard, R. Ray, S. Scott, J. Jasiewicz, J. Craighead, and C. Pagano, “Movement path tortuosity predicts compliance with therapeutic behavioral prompts in TBI patients.,” Journal of Head Trauma Rehabilitation, 2015 (in press). His research interests include cognition, directed travel, navigational problems and fall risk in elderly and veterans with head injuries.
Professor Kearns is the President of the North American Chapter of the International Society for Gerontechnology and an Associate Editor for its journal Gerontechnology. He regularly reviews for the National Institutes of Health, the National Science Foundation and the Agency for Health Care Research and Quality, has over 65 publications and holds one patent.

James L. Fozard earned his doctorate in experimental psychology from Lehigh University and completed a post-doctoral fellowship in human memory at the Massachusetts Institute of Technology. He has devoted 48 years to gerontology, the study of aging. Fozard is best known for his work on longitudinal studies of human aging with the U.S. Department of Veterans Affairs Normative Aging Study, and the National Institute on Aging’s Baltimore Longitudinal Study of Aging, which he directed for 13 years. For seven years he directed the U.S. Department of Veterans Affairs Extended Care Programs. He is cofounder of the multidisciplinary field, gerontechnology, devoted to developing and adapting technology services and products for the benefit of aged and aging adults. Prior to his current appointment Fozard was on the psychiatry faculty of Harvard Medical School, the Johns Hopkins School of Hygiene and Public Health and a visiting professor of gerontechnology at the Eindhoven (NL) University of Technology, and the Nan Kai University of Technology in Taiwan. He is the author or coauthor of 195 scientific book chapters and articles. In 2010 the International Society for Gerontechnology named him the first Grandmaster of gerontechnology in recognition to his contributions to the field.

Vilis O. Nams received his B.Sc. degree in zoology from the University of Toronto, Canada, in 1977, his MSc in zoology from the University of Alberta, Canada, and his PhD in biology from Victoria University, Canada, in 1989.
From 1990 to 2012 he was an Assistant Professor at the Nova Scotia Agricultural College, and is currently a Professor in the Department of Environmental Sciences at Dalhousie University. He is the author of 42 articles and 4 book chapters. His research interest includes spatial aspects of wild animal movement and mathematical models in behavioral ecology.
Dr. Nams' awards and honors include the SETWG 2011 award of the Wildlife Society of America, the Hugh Kelley Fellowship award at Rhodes University, and the Senior Landcare Hayward Fellow award at Landcare, New Zealand.
Contributor Information
William D Kearns, Rehabilitation and Mental Health Counseling Program in Department of Child and Family Studies at the University of South Florida, Tampa, FL 33612 USA.
James L. Fozard, School of Aging Studies at the University of South Florida, Tampa, FL 33612 USA.
Vilis O. Nams, Department of Environmental Sciences, the Faculty of Agriculture, at Dalhousie University, Truro, NS, B2N 5E3 Canada.
References
- 1.Anders RT, Fozard JL. Effects of age upon retrieval from primary and secondary memory. Developmental Psychology. 1973;9:411–5. [Google Scholar]
- 2.Madden DJ. Speed and timing of behavioural processes. In: Birren JD, Schaie KW, editors. The Handbook of the Psychology of Aging. Burlington, MA: Elsevier Academic Press; 2001. p. 288–312. [Google Scholar]
- 3.Ketcham CJ, Stelmach GE, Birren JD, Schaie KW. Age-related declines in motor control. In: Birren JD, Schaie KW, editors. The Handbook of the Psychology of Aging. Burlington, MA: Elsevier Academic Press; 2001. p. 313–48. [Google Scholar]
- 4.Welford AT, Norris AH, Shock NW. Speed and accuracy of movement and their changes with age. Acta Psychologica. 1969;30:3–15. [DOI] [PubMed] [Google Scholar]
- 5.Dykiert D, Der G, Starr JM, Deary IJ. Age differences in intra-individual variability in simple and choice reaction time: Systematic review and meta-analysis. PLoS One. 2012;7(10):e45759. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Ble A, Volpato S, Zuliani G, Guralnik JM, Bandinelli S, Lauretani F, et al. Executive function correlates with walking speed in older persons: The InCHIANTI study. J Am Geriatr Soc. 2005;53(3):410–5. [DOI] [PubMed] [Google Scholar]
- 7.Najafi B, Aminian K, Paraschiv-Ionescu A, Loew F, Bula CJ, Robert P. Ambulatory system for human motion analysis using a kinematic sensor: monitoring of daily physical activity in the elderly. IEEE Transactions on Bio-medical Engineering. 2003;50(6):711–23. [DOI] [PubMed] [Google Scholar]
- 8.Hausdorff JM, Yogev G, Springer S, Simon ES, Giladi N. Walking is more like catching than tapping: Gait in the elderly as a complex cognitive Task. Experimental Brain Research. 2005;164(4):541–8. [DOI] [PubMed] [Google Scholar]
- 9.Yogev G, Giladi N, Peretz C, Springer S, Simon ES, Hausdorff JM. Dual tasking, gait rhythmicity, and Parkinson's disease: which aspects of gait are attention demanding? The European Journal of Neuroscience. 2005;22(5):1248–56. [DOI] [PubMed] [Google Scholar]
- 10.Herman T, Giladi N, Gurevich T, Hausdorff JM. Gait instability and fractal dynamics of older adults with a “cautious” gait: why do certain older adults walk fearfully? Gait & Posture. 2005;21(2):178–85. [DOI] [PubMed] [Google Scholar]
- 11.Hausdorff JM. Gait dynamics, fractals and falls: Finding meaning in the stride-to-stride fluctuations of human walking. Human Movement Science. 2007;26(4):555–89. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Algase DL, Beattie ERA, Song JA, Milke D, Duffield C, Cowan B. Validation of the Algase wandering scale (version 2) in a cross cultural sample. Aging & Mental Health. 2004;8(2):133–42. [DOI] [PubMed] [Google Scholar]
- 13.Algase D, Moore D, Vandeweerd C, Gavin-Dreschnack DJ. Mapping the maze of terms and definitions in dementia-related wandering. Aging & Mental Health. 2007;11(6):686–98. [DOI] [PubMed] [Google Scholar]
- 14.Batschelet E Circular statistics in biology. London, UK: Academic Press; 1981. [Google Scholar]
- 15.Benhamou S How to reliably estimate the tortuosity of an animal’s path: Straightness, sinuosity, or fractal dimension? Journal of Theoretical Biology. 2004;229(2):209–20. [DOI] [PubMed] [Google Scholar]
- 16.Codling EA, Plank MJ, Benhamou S. Random walk models in biology. J R Soc Interface. 2008;5(25):813–34. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Mandelbrot B How long is the coast of Britain? Statistical self-similarity and fractional dimension. Science. 1967;156:636–8. [DOI] [PubMed] [Google Scholar]
- 18.Mandelbrot BB. The fractal geometry of nature. Macmillan; 1983. 1983. [Google Scholar]
- 19.Dicke M, Burrough PA. Using fractal dimensions for characterizing the tortuosity of animal trails. Physiological Entomology. 1988;13(4):393–8. [Google Scholar]
- 20.McCulloch CE, Cain ML. Analyzing discrete movement data as a correlated random walk. Ecology. 1989;70(2):383–8. [Google Scholar]
- 21.Bovet P, Benhamou S. Spatial analysis of animals' movements using a correlated random walk model. Journal of Theoretical Biology. 1988;131(4):419–33. [Google Scholar]
- 22.Byers JA. Correlated random walk equations of animal dispersal resolved by simulation. Ecology. 2001;82(6):1680–90. [Google Scholar]
- 23.Turchin P Fractal analyses of animal movement - a critique. Ecology. 1996;77(7):2086–90. [Google Scholar]
- 24.Nams VO. Using animal movement paths to measure response to spatial scale. Oecologia. 2005;143:179–88. [DOI] [PubMed] [Google Scholar]
- 25.Nams VO. Improving accuracy and precision in estimating fractal dimension of animal movement paths. Acta Biotheoretica. 2006;54:1–11. [DOI] [PubMed] [Google Scholar]
- 26.Peters RP, Mech LD. Scent-marking in wolves: Radio-tracking of wolf packs has provided definite evidence that olfactory sign is used for territory maintenance and may serve for other forms of communication within the pack as well. American Scientist. 1975;63(6):628–37. [PubMed] [Google Scholar]
- 27.Brooks CJ, Harris S. Directed movement and orientation across a large natural landscape by zebras, Equus burchelli antiquorum. Animal Behaviour. 2008;76(2):277–85. [Google Scholar]
- 28.Krummel JR, Gardner G, Sugihara G, Oneill RV, Coleman PR. Landscape patterns in a disturbed environment. Oikos. 1987;48:321–4. [Google Scholar]
- 29.Sole RV, Manrubia SV. Are rainforests self-organized in a critical state? Journal of Theoretical Biology. 1995;173(1):31–40. [Google Scholar]
- 30.Nams VO. Detecting oriented movement of animals. Animal Behaviour. 2006;72(5):1197–203. [Google Scholar]
- 31.Zollner PA, Lima SL. Landscape-level perceptual abilities in white-footed mice: perceptual range and the detection of forested habitat. Oikos. 1997;80(1):51–60. [Google Scholar]
- 32.Gillis EA, Nams VO. How red-backed voles find habitat patches. Canadian Journal of Zoology. 1998;76(5):791–4. [Google Scholar]
- 33.Schooley RL, Branch LC. Limited perceptual range and anemotaxis in marsh rice rats Oryzomys palustris. Acta Theriologica. 2005;50(1):59–66. [Google Scholar]
- 34.Wells MC, Bekoff M. Predation by wild coyotes: Behavioral and ecological analyses. Journal of Mammalogy. 1982;63(1):118–27. [Google Scholar]
- 35.Gautestad AO, Mysterud I. Complex animal distribution and abundance from memory-dependent kinetics. Ecological Complexity. 2006;3(1):44–55. [Google Scholar]
- 36.Prevedello JA, Forero-Medina G, Vieira MV. Movement behaviour within and beyond perceptual ranges in three small mammals: Effects of matrix type and body mass. Journal of Animal Ecology. 2010;79(6):1315–23. [DOI] [PubMed] [Google Scholar]
- 37.Pe’er G, Kramer-Schadt S. Incorporating the perceptual range of animals into connectivity models. Ecological Modelling. 2008;213(1):73–85. [Google Scholar]
- 38.Benhamou S An analysis of movements of the wood mouse Apodemus sylvaticus in its home range. Behavioural Processes. 1990;22(3):235–50. [DOI] [PubMed] [Google Scholar]
- 39.Kearns W, Algase D, Moore D, Ahmed S. Ultra wideband radio: A novel method for measuring wandering in persons with dementia. Gerontechnology. 2008;7(1):48–57. [Google Scholar]
- 40.Craighead J Using fractal dimension to assess robot operator search skill. Safety, Security & Rescue Robotics (SSRR), 2009 IEEE International Workshop on; 2009 3–6 Nov. 2009; Denver, CO2009. [Google Scholar]
- 41.Kearns WD, Nams VO, Fozard JL. Tortuosity in movement paths is related to cognitive impairment. Wireless fractal estimation in assisted living facility residents. Methods Inf Med. 2010;49(6):592–8. [DOI] [PubMed] [Google Scholar]
- 42.Crum RM, Anthony JC, Bassett SS, Folstein MF. Population-based norms for the Mini-Mental State Examination by age and educational level. JAMA. 1993;269(18):2386–91. [PubMed] [Google Scholar]
- 43.Kearns W, Fozard JL, Nams VO & Craighead JD. Wireless telesurveillance system for detecting dementia. Gerontechnology. 2011;10:90–102. [Google Scholar]
- 44.Kearns WD, Fozard JL, Becker M, Jasiewicz JM, Craighead JD, Holtsclaw L, et al. Path tortuosity in everyday movements of elderly persons increases fall prediction beyond knowledge of fall history, medication use, and standardized gait and balance assessments. Journal of the American Medical Directors Association. 2012;13(7):665.e7–.e13. [DOI] [PubMed] [Google Scholar]
- 45.Kearns WD, Scott S, Fozard J, Dillahunt-Aspillaga C, Jasiewicz J. Decreased movement path tortuosity is associated with improved functional status in TBI patients. Journal of Head Trauma Rehabilitation. 2015. (in press). [DOI] [PubMed] [Google Scholar]
- 46.Kearns WD, Fozard J, Ray R, Scott S, Jasiewicz J, Craighead J, et al. Movement path tortuosity predicts compliance with therapeutic behavioral prompts in patients with traumatic brain injury. Journal of Head Trauma Rehabilitation. 2015;30(2):1–8. [DOI] [PubMed] [Google Scholar]
- 47.Jasiewicz J, Kearns W, Craighead J, Fozard JL, Scott S, McCarthy J Jr. Smart rehabilitation for the 21st century: the Tampa Smart Home for veterans with traumatic brain injury. Journal of rehabilitation research and development. 2011;48(8):vii–xviii. [DOI] [PubMed] [Google Scholar]
- 48.Ferster C, Skinner B. Schedules of reinforcement. Cambridge, MA: B. F. Skinner Foundation; 1957. [Google Scholar]
- 49.Rogers WA, Fisk AD. Understanding the role of attention in cognitive aging research. In: Birren JD, Schaie KW, editors. The Handbook of the Psychology of Aging. Burlington, MA: Elsevier Academic Press; 2001. p. 267–87. [Google Scholar]
- 50.Nathan R, Getz WM, Revilla E, Holyoak M, Kadmon R, Saltz D, et al. A movement ecology paradigm for unifying organismal movement research. Proceedings of the National Academy of Sciences of the United States of America. 2008;105(49):19052–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Mace NL, Rabins PV. The 36-hour day : A family guide to caring for people who have Alzheimer's disease, related dementias, and memory loss. 5th ed. Baltimore: Johns Hopkins University Press; 2011. xxiv, 353 p. p. [Google Scholar]


