Unsupervised detection and analysis of changes in everyday physical activity data

Abstract

Sensor-based time series data can be utilized to monitor changes in human behavior as a person makes a significant lifestyle change, such as progress toward a fitness goal. Recently, wearable sensors have increased in popularity as people aspire to be more conscientious of their physical health. Automatically detecting and tracking behavior changes from wearable sensor-collected physical activity data can provide a valuable monitoring and motivating tool. In this paper, we formalize the problem of unsupervised physical activity change detection and address the problem with our Physical Activity Change Detection (PACD) approach. PACD is a framework that detects changes between time periods, determines significance of the detected changes, and analyzes the nature of the changes. We compare the abilities of three change detection algorithms from the literature and one proposed algorithm to capture different types of changes as part of PACD. We illustrate and evaluate PACD on synthetic data and using Fitbit data collected from older adults who participated in a health intervention study. Results indicate PACD detects several changes in both datasets. The proposed change algorithms and analysis methods are useful data mining techniques for unsupervised, window-based change detection with potential to track users’ physical activity and motivate progress toward their health goals.

1. Introduction

In recent years, sensors have become ubiquitous in our everyday lives. Sensors are ambient in the environment, embedded in smartphones, and worn on the body. Data collected from sensors form a time series, where each sample of data is paired with an associated timestamp. This sensor-based time series data is valuable when monitoring human behavior to detect and analyze changes. Such analysis can be used to detect seasonal variations, new family or job situations, or health events. Analyzing sensor-based time series data can also be used to monitor changes in human behavior as a person makes progress toward a fitness goal. Making a significant lifestyle change often takes weeks or months of establishing new behavior patterns [1], which can be challenging to sustain. Automatically detecting and tracking behavior changes from sensor data can provide a valuable motivating and monitoring tool.

Recently, wearable sensors have increased in popularity as people aspire to be more conscientious of their physical health. Many consumers purchase a pedometer or wearable fitness device in order to track their physical activity (PA), often in pursuit of a goal such as increasing cardiovascular strength, losing weight, or improving overall health. Physical activity is estimated by pedometers and fitness trackers in terms of the steps taken by the wearer [2]. To track different types of changes in physical activity data, two or more time periods, or windows, of PA data can be quantitatively and objectively compared. If the two time windows contain significantly different sensor data then this may indicate a significant behavior change. Existing off-the-shelf change point detection methods are available to detect change in time series data, but the methods do not provide context or explanation regarding the detected change. For PA data, algorithmic approaches to change detection require additional information about what type of change is detected and its magnitude to potentially report progress to users for motivation and encouragement purposes. Furthermore, existing approaches often do not provide a method for determining if a detected change is significant, meaning the magnitude of change is high enough to suspect it likely resulted from a lifestyle alteration. A personalized, data-driven approach to significance testing for fitness tracker users is a necessary feature of physical activity change detection.

Currently, there is no clear consensus regarding which change detection approaches are best for detecting and analyzing changes in PA data. Consequently, we formalize the problem of unsupervised physical activity change detection and address the problem with our Physical Activity Change Detection (PACD) approach. PACD is a framework that (1) segments time series data into time periods, (2) detects changes between time periods, (3) determines significance of the detected changes, and (4) analyzes the nature of the significant changes. We review recently proposed change detection methods and we evaluate the ability of four different change detection approaches to capture pattern changes in synthetic PA data. Next, we illustrate how the change approaches are used to monitor, quantify, and explain behavior differences in Fitbit data collected from older adults who participated in a health behavior intervention. Finally, we conclude with discussions about the limitations of current approaches and suggestions for continued research on unsupervised sensor-based change detection.

2. Related work

In the literature, a few studies have aimed to detect change specifically in human behavior patterns. These approaches have quantified change statistically [3,4], graphically [4-6], and algorithmically [5,7-9]. Recently, Merilahti et al. [3] extracted features derived from actigraphy data collected for at least one year. Each feature was individually correlated with a component of the Resident Assessment Instrument for insights into how longitudinal changes in actigraphy and functioning are associated. While this approach provides insight into the relationship between wearable sensor data and clinical assessment scores, this study does not directly quantify sensor-based change.

Wang et al. [5] introduced another activity-based change detection approach in which passive infrared motion sensors were installed in apartments and utilized to estimate physical activity in the home and time away from home. The data were converted into co-occurrence matrices for computation of image-based texture features. Their case studies suggest the proposed texture method can detect lifestyle changes, such as knee replacement surgery and recovery. Though the approach does not provide explanation of the detected changes over time, visual inspection of the data is suggested with activity density maps. More recently, Tan et al. [6] applied the texture method to data from Fitbit Flex sensors for tracking changes in daily activity patterns for elderly participants. Another approach for activity monitoring is the Permutation-based Change Detection in Activity Routine (PCAR) algorithm [7]. PCAR researchers modeled activity distributions for time windows of size three months. Changes between windows were quantified with probabilities of change acquired via hypothesis testing.

The change detection algorithms described previously are intended for monitoring human activity behavior. There are several additional approaches that are not specific to activity data, but instead represent generic statistical approaches to detecting changes in time series data. Change point detection, the problem of identifying abrupt changes in time series data [10], constitutes an extensive body of research as there are many applications requiring efficient, effective algorithms for reliably detecting variation. There are many families of change detection algorithms that are suitable for different applications [11]. Algorithms appropriately handling two sample, unlabeled data are most relevant to the current study due to their data-driven change score computation and no need for ground truth information. Unsupervised change detection approaches include subspace models and likelihood ratio methods [8]. One particular subgroup of likelihood ratio methods, direct density ratio estimator methods, is used in various applications [12,13]. Relative Unconstrained Least-Squares Importance Fitting (RuLSIF) [8] is one such approach used to measure the difference between two samples of data surrounding a candidate change point. Other recent change point detection research includes work on multidimensional [14,15] and streaming time series data [11].

The above approaches are effective methods for detecting change between two samples of data; however, they are not explanatory methods as they only identify if two samples are different and do not provide information on how the samples are different. Once a change is detected and determined significant, additional analyses are required to explain the change that occurred. Hido et al. [9] formalized this problem as change analysis, a method of examination beyond change detection to explain the nature of discrepancy. Hido’s solution to change analysis utilizes supervised machine learning algorithms, specifically virtual binary classifiers (VCs), to identify and describe changes in unsupervised data. Research by Ng and Dash [16] and Yamada et al. [10] have also explored methods for detecting and explaining change in time series data.

The aforementioned methods provide several options for change detection and analysis, each with their own suitability for various applications. In this paper, we evaluate the following methods for use in our PACD method: (1) RuLSIF [8], (2) texture-based dissimilarity [5,6], (3) our proposed adaptation of PCAR [7] to handle small window sizes (sw-PCAR), and (4) VC-based change analysis [9].

3. Methods

Physical activity is often defined as any bodily movement by skeletal muscles that results in caloric energy expenditure [17]. Physical activity consists of bouts of movement that are separated by periods of rest. Physical activity bouts are composed of four dimensions [17]:

1. Frequency: the number of bouts of physical activity within a time period, such as a day.

2. Duration: the length of time an individual participates in a single bout.

3. Intensity: the physiological effort associated with a particular type of physical activity bout.

4. Activity type: the kind of exercise performed during the bout.

To add exercise throughout the day, individuals can increase their number of bouts (frequency), increase the length of bouts (duration), increase the intensity of bouts, and vary the type of physical activity performed during the bouts. These four components of PA represent four distinct types of changes that can reflect progress toward many different health goals, such as increasing physical activity or consistency in one’s daily routine.

We study the problem of detecting and analyzing change in physical activity patterns. More specifically, we introduce methods to determine if a significant change exists between two windows of time series step data sampled from a physical activity sensor. Algorithm 1, PACD, outlines this process. Let $X$ denote a sample of time series step data segmented into days, $D=\{x_1,x_2,\dots ,x_t,\dots ,x_m\}$, where $x_t$ is a scalar number of steps taken at time interval $t=1,2,\dots ,m$ and $m$ is the number of equal-sized time intervals in a day. Let $t_{mins}$ denote the number of minutes per time interval, $t$. For example, if the sampling rate of the wearable sensor device is one reading per minute, $t_{mins}=1$ min and $m=1440$ $\text{min}∕t_{mins}=1400$ intervals. Now, let $W$ be a window of $n$ days such that $W\subseteq X$. Furthermore, an aggregate window, $\widehat{W}$, represents the average of all days within the window $W$:

$$\widehat{W}=\frac{1}{n}\sum _{i=1}^n{D}_i,D_i\in W$$ (1)

We can compare windows of data within time series data $X$. These windows may represent consecutive times (e.g., days, weeks, months), a baseline window (e.g., the first week) with each subsequent time window, or overlapping windows. Let $W_i$ denote a window starting at day number $i$ of $X(i⩾1)$ such that $W_i=X[i:i+n-1]=\{D_i,D_{i+1},\dots ,D_{i+n-1}\}$. Suppose we have two windows of data, $W_i$ and $W_j(i⩽j)$. Windows $W_i$ and $W_j$ can be formed as subsets of $X$ based on the initial value of $i$ and a parameter $offset$ that determines the initial value of $j(j=i+offset)$. For change detection and analysis, a function $F$ computes a change score, $CS=F(W_i,W_j)$ between $W_i$ and $W_j$. Iteration advancements $ad{v}_i$ and $ad{v}_j$ move windows $W_i$ and $W_j$ respectively for the next comparison. Two windows can be compared in either baseline or sliding window mode. For a baseline window comparison, the first window is a reference window that occurs at the beginning of the time series ($i$ is initialized to 1) and is used in each comparison, so $ad{j}_i=0$. All subsequent windows are compared to the baseline window. Thus $j$ is initialized to $1+offset$ and is subsequently advanced by $ad{v}_j$. In the case of a sliding window comparison, both windows used for comparison are advanced through the time series data. Typically $ad{v}_i=ad{v}_j$ for consistently spaced comparisons. In Algorithm 1, PACD, $i$ is initialized to 1 and $j$ is initialized to $1+offset$. In steps 17 and 18, $i$ is advanced to $i+ad{v}_i$ and $j$ is advanced to $j+ad{v}_j$.

Algorithm 1. PACD($X$, $n$, $offset$, $ad{v}_i$, $ad{v}_j$)

$$\begin{array}{cc}\hfill & 1:\text{Input:}X=\text{time series data}\hfill \\ \hfill & 2:\text{Input:}n=\text{window length in days}\hfill \\ \hfill & 3:\text{Input:}offset=\text{number of days separating windows}\hfill \\ \hfill & 4:\text{Input:}ad{v}_i=\text{number of days to advance the first window}\hfill \\ \hfill & 5:\text{Input:}ad{v}_j=\text{number of days to advance the second}\hfill \\ \hfill & \text{window}\hfill \\ \hfill & 6:\text{Output:}V=\text{vector of change scores}\hfill \\ \hfill & 7:\text{Initialize:}i=1\text{and}j=1+offset\hfill \\ \hfill & 8:\mathbf{for}\mathbf{each}\text{pair of windows to compare},W_i\text{and}{W}_j\text{of time}\hfill \\ \hfill & \text{sries}X:\hfill \\ \hfill & 9:W_i=X[i:i+n-1]\hfill \\ \hfill & 10:W_j=X[j:j+n-1]\hfill \\ \hfill & 11:\text{Compute}CS=F(W_i,W_j)\hfill \\ \hfill & 12:\text{Determine if}CS\text{is significant}\hfill \\ \hfill & 13:\text{Identify the type of change that is exhibited}\hfill \\ \hfill & 14:\text{Manual inspection of change}\hfill \\ \hfill & 15:\text{Unsupervised inspection (change analysis)}\hfill \\ \hfill & 16:\text{Append}CS\text{to change score vector}V\hfill \\ \hfill & 17:i=i+ad{v}_i\hfill \\ \hfill & 18:j=j+ad{v}_j\hfill \\ \hfill & \mathbf{end}\mathbf{for}\hfill \\ \hfill & 19:\mathbf{return}\text{Change score vector}V\hfill \end{array}$$

The choice of window size, $n$, limits the algorithms that can be applied to the data. For example, the PCAR algorithm [7] is designed for longitudinal data comprising several months; consequently sensitivity decreases with small window sizes. For PACD, we categorize choices for window size $n$ into the following descriptors:

1. Small window ($n=1$ day). Suitable for performing day-to-day comparisons (e.g. $D_{i(Monday)}$ compared to $D_{j(Monday)}$, $D_{i(Tuesday)}$ compared to $D_{j(Tuesday)},\dots$) or aggregate day comparisons (e.g. ${\widehat{W}}_i$ compared to ${\widehat{W}}_j$, ${\widehat{W}}_{i+ad{v}_i}$ compared to ${\widehat{W}}_{j+ad{v}_j},\dots$).

2. Medium window (2 days $⩽n⩽5$ days). Suitable for performing weekday-to-weekday comparisons (e.g. $W_i$ compared to $W_j$ where $W_i=\{D_{i(Monday)},D_{i(Tuesday)},D_{i(Wednesday)},D_{i(Thursday)},D_{i(Friday)}\}$ and $W_j=\{D_{j(Monday)},D_{j(Tuesday)},D_{j(Wednesday)},D_{j(Thursda)},D_{j(Friday)}\}$) or weekend-to-weekend comparisons.

3. Large window ($n>5$ days). Suitable for performing week-to-week or month-to-month comparisons.

3.1. Change detection algorithms

In the following sections, we describe algorithmic options for the window-based change score function, $F$. A summary and comparison of the algorithms is listed in Table 1.

Table 1.

Window-based change detection algorithms.

Approach	Window size	Window preprocessing	Change score	Change significance test
RuLSIF [8]	Any	Hankel matrix	Probability density ratio estimation with Pearson divergence	Threshold learning in supervised applications. N/A for unsupervised applications
Texture-based [5,6]	Any	Grey-level co-occurrence matrix, texture features	Weighted normalized Euclidean distance	N/A
PCAR [7]	Large	$m\times N$ KL distance permutation matrix	Count of time intervals with significant changes (proportion of permuted KL distances greater than observed window)	N/A
sw-PCAR	Any	$N$ KL distance permutation vector	KL distance	Non-parametric outlier detection based on Boxplot analysis
Virtual classifier [9]	Large	Physical activity features (intra-day and inter-day if window size > 1)	Cross validation prediction accuracy of binary classifier	Hypothesis testing based on prediction accuracy exceeding a threshold

KL = Kullback-Leibler, $m$ = number of time intervals, $N$ = number of permutations.

3.1.1. RuLSIF

Non-parametric approaches to change point detection include a family of methods comparing the probability distributions of two time series samples to determine the corresponding dissimilarity. A greater difference between the two distributions implies a higher likelihood that a change occurred between the two samples. Instead of estimating the probability distributions, their ratio can be estimated and used to detect changes in the underlying probability distributions. Direct density ratio estimation between two windows of time series data is substantially simpler to solve than computing the windows’ probability densities independently and then using these to compute the ratio. Unconstrained Least-Squares Importance Fitting (uLSIF) [8] is one such ratio estimation approach that measures the difference between two samples of data surrounding a candidate change point. For this approach, the density ratio between two probability distributions is estimated directly with the Pearson divergence dissimilarity measure. Depending upon the data, the Pearson divergence can be unbounded. Consequently, a modification to uLSIF, relative uLSIF (RuLSIF), utilizes an alpha-relative Pearson divergence to bound the change score above by 1/α for α > 0 [8].

3.1.2. Texture-based dissimilarity

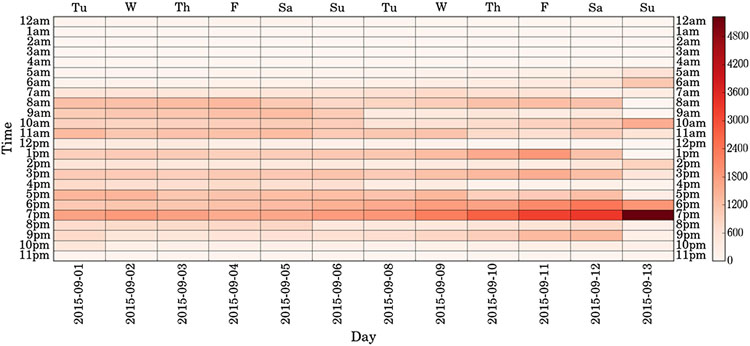
For the texture-based approach, two windows of PA data, $W_i$ and $W_j$, are considered 2-dimensional matrices with rows corresponding to time intervals, columns corresponding to days, and cells containing step values measured from a PA device (see Section 4.1 for visualizations of PA matrices in Figs. 2-5). In order to extract texture features from the data, each matrix is converted into a grey-level co-occurrence matrix, a histogram of co-occurring grey scale values of an image [18]. Next, texture features are computed from each co-occurrence matrix, including contrast, homogeneity, angular second moment, energy, density, and correlation features [5,6,18]. The features from each window produce feature vectors $T_i$ and $T_j$. Finally, to compare two windows $W_i$ and $W_j$ for changes, a weighted normalized Euclidean distance measure is used as a change score to quantify the differences between the corresponding feature vectors $T_i$ and $T_j$. The smaller the Euclidean distance between these two vectors, the more similar the two windows of data are. The texture-based approach can operate on small or large window sizes; however, the method lends itself more appropriately to large window sizes (Wang et al. [5] used window size of one month).

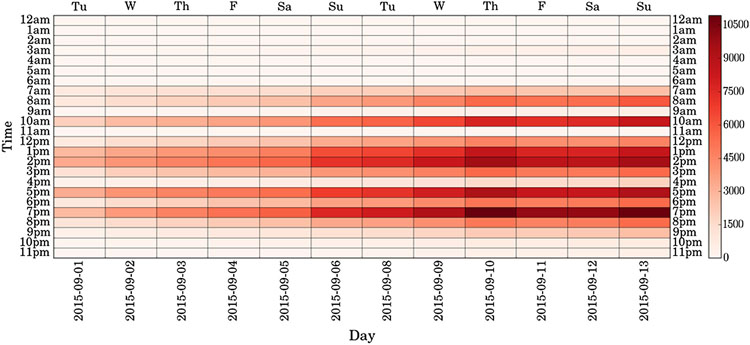
Fig. 2.

Hybrid-synthetic (HS) step density map for HS1.

Fig. 5.

Hybrid-synthetic (HS) step density map for HS4.

3.1.3. sw-PCAR

We propose an enhancement of PCAR to allow permutation-based change detection for any window size. Before introducing sw-PCAR, we will provide an overview of the PCAR approach. PCAR utilizes smart home sensor data to detect changes in behavioral routines with an activity curve model [7]. The PCAR approach assumes that an activity recognition algorithm [19] is available to label the sensor data with corresponding activity names. Using PCAR, each day within a window is broken into $m$ time intervals. The activities occurring within each time interval are modeled by a probability distribution, which form an activity curve for the corresponding window. To compute a change score CS between two windows $W_i$, and $W_j$, the two corresponding activity curves are first maximally aligned with dynamic time warping (DTW). Next, the symmetric Kullback-Leibler (KL) divergence is used to compute the distance between each pair of DTW-aligned activity distributions [7]. To test significance of the distance values, $W_i$ and $W_j$ are concatenated to form a window $W$ of length $2n$ days. Next, all days within $W$ are shuffled. The first half of the shuffled days form a new first window, $W_i^{\ast }$, while the second half form a new second window, $W_j^{\ast }$. KL distances for each time interval pair in $W_i^{\ast }$ and $W_j^{\ast }$ form a vector that is inserted into a matrix. This shuffling procedure is repeated $N$ times, producing a $N\times m$ permutation matrix, $M$. If $N$ is large enough, $M$ forms an empirical distribution of the possible permutations of activity data within the two windows of time. Next, for each time interval, the number of permuted KL distances that exceed the original DTW-aligned distance is divided by $N$ to form a p-value. After computing a p-value for each time interval, the Benjamini-Hochberg correction [20] is applied for a given α (α < 0.05). Finally, the remaining significant p-values are counted to produce the change score, $CS$.

While the PCAR algorithm is intended for activity distribution data available from activity recognition algorithms, in this paper we adapt PCAR to analyze physical activity data as part of our PACD method. Instead of activity distribution vectors, we use scalar step counts. Additionally, PCAR is suitable for only large window sizes due to the requirement of permuting daily time series data. We propose a version of PCAR that is more suitable for small to medium-sized windows (sw-PCAR) as required by PACD. Finally, PCAR was originally proposed for correlating change scores with standardized clinical assessments to determine if ambient smart home sensor-based algorithms can detect cognitive decline [7]. Consequently, there is not a test for significance of PCAR change scores. In Section 3.2 we propose an accompanying significance test for sw-PCAR.

Algorithm 2 outlines the sw-PCAR approach. For sw-PCAR, two windows $W_i$ and $W_j$ are averaged to yield aggregate windows ${\widehat{W}}_i$, and ${\widehat{W}}_j$ (see Eq. (1)). A change score $CS$ is derived by computing the KL distance between the average number of steps taken in ${\widehat{W}}_i$ and the average number of steps taken in ${\widehat{W}}_j$. Next, ${\widehat{W}}_i$ and ${\widehat{W}}_j$ are concatenated to form a window $W$ of length two days. All time intervals within $W$ are shuffled. The first half of the shuffled intervals form a new first window, $W_i^{\ast }$, while the second half form a new second window, $W_j^{\ast }$. $W_i^{\ast }$ and $W_j^{\ast }$ are each averaged to produce two step values. The KL distance between the two values is computed and inserted into a vector. This is repeated $N$ times to produce a $N$-length vector $V$ of KL distances. Vector $V$ is later used for change score significance testing (see Section 3.2).

Algorithm 2. sw-PCAR($W_i$, $W_j$, $N$)

$$\begin{array}{cc}\hfill & 1:\text{Input:}{W}_i,W_j=\text{two windows of time series data}\hfill \\ \hfill & 2:\text{Input:}N=\text{number of permutaions}\hfill \\ \hfill & 3:\text{Output:}CS=\text{change score}\hfill \\ \hfill & 4:\text{Output:}sig=(\text{Boolean})\text{significance of}CS\hfill \\ \hfill & 5:\text{Initialize:}k=0\hfill \\ \hfill & 6:\text{Initialize:}V\text{as a vector of length}N\hfill \\ \hfill & 7:\text{Compute}{\widehat{W}}_i,{\widehat{W}}_j\text{aggregate window}\hfill \\ \hfill & 8:\text{Compute}CS,\text{the KL distance between}{\widehat{W}}_i\text{and}{\widehat{W}}_j\hfill \\ \hfill & 9:\mathbf{while}k<N:\hfill \\ \hfill & 10:\text{Shuffle the time intervals of}{\widehat{W}}_i\text{and}{\widehat{W}}_j\hfill \\ \hfill & 11:\text{Generate new aggregate windows}{W}_i^{\ast }\text{and}{W}_j^{\ast }\hfill \\ \hfill & 12:\text{Compute the KL distance between}{W}_i^{\ast }\text{and}{W}_j^{\ast }\hfill \\ \hfill & 13:\text{Store resulting distance in}V\hfill \\ \hfill & 14:k=k+1\hfill \\ \hfill & \mathbf{end}\mathbf{while}\hfill \\ \hfill & 15:sig=\text{BoxplotOutlierDetection}(CS,V)(\text{see}\mathsf{Algorithm}3)\hfill \\ \hfill & 16:\mathbf{return}CS,sig\hfill \end{array}$$

3.1.4. Virtual classifier

Change analysis, as proposed by Hido et al. [9], utilizes a virtual binary classifier to detect and investigate change. We apply the VC approach as part of PACD for large window sizes. First, a feature extraction step reduces two windows $W_i$ and $W_j$ into two $n\times z$ feature matrices, $M_i$ and $M_j$, where $n$ is the window size (in days) and $z$ is the number of features that are extracted (see Section 3.3 for feature descriptions). Next, each daily feature vector of $M_i$ is labeled with a positive class and each daily feature vector of $M_j$ is labeled with a negative class. VC trains a decision tree to learn the decision boundary between the virtual positive and negative classes. The resulting average prediction accuracy based on k-fold cross validation is represented as $p_{VC}$. If a significant change exists between $W_i$ and $W_j$, the average classification accuracy $p_{VC}$ of the learner should be significantly higher than the accuracy expected from random noise, $p_{rand}=0.5$, the binomial maximum likelihood of two equal length windows [9].

3.2. Change significance testing

Significance testing of change score $CS$ is necessary to interpret change score values. For the VC approach, Hido et al. [9] proposed a test of significance to determine if $p_{VC}$ is significantly greater than $p_{rand}$. For this test, the inverse survival function of a binomial distribution is used to determine a critical value, $p_{critical}$, at which $n$ Bernoulli trials are expected to exceed $p_{rand}$ at α significance. If $p_{VC}⩾p_{critical}$, a significant change exists between the two windows, $W_i$ and $W_j$.

The PCAR approach does not have an accompanying test of significance. We address this with our proposed sw-PCAR technique. sw-PCAR computes change significance by comparing $CS$ to the permutation vector $V$ with boxplot-based outlier detection (see Algorithm 3). An outlier can be defined as an observation which appears to be inconsistent with other observations in the dataset [21]. For this method, the interquartile range (75th percentile–25th percentile) of $V$ is computed. Values outside of the 75th percentile + 1.5 · interquartile range are considered outliers [22]. If $CS$ is determined to be an outlier of $V$, then the change score is considered significant. There are alternative approaches to test membership of an observation (i.e. $CS$) to a sample distribution (i.e. $V$) other than boxplot outlier detection. If the sample is normal, statistical tests such as Grubb’s test for outliers [23] can be applied. However, the assumption of normality does not hold for all samples of human behavior data. More advanced alternatives include data mining techniques relevant to outlier detection [21,24]. Exploration and testing of such data mining techniques are outside the scope of this paper.

Algorithm 3. BoxplotOutlierDetection($CS$, $V$)

$$\begin{array}{cc}\hfill & 1:\text{Input:}CS=\text{change score between two windows}\hfill \\ \hfill & 2:\text{Input:}V=\text{sample distribution vector}\hfill \\ \hfill & 3:\text{Output:}sig=(\text{Boolean})\text{significance of}CS\hfill \\ \hfill & 4:\text{Arrange}V\text{in ascending order}\hfill \\ \hfill & 5:\text{Compute}{Q}_1,\text{the}25\text{th percentile of}V\hfill \\ \hfill & 6:\text{Compute}{Q}_3,\text{the}75\text{th percentile of}V\hfill \\ \hfill & 7:\text{Compute the interquartile range of}V,IQR=Q_3-Q_1\hfill \\ \hfill & 8:\mathbf{if}CS>Q_3+1.5\cdot IQR:\hfill \\ \hfill & 9:sig=True\hfill \\ \hfill & 10:\mathrm{else}:\hfill \\ \hfill & 11:sig=False\hfill \\ \hfill & 12:\mathbf{return}sig\hfill \end{array}$$

RuLSIF does not explicitly provide a method to determine a cut-off threshold for values of the Pearson divergence function that are considered significant change scores. In supervised applications where ground truth change labels are available, a threshold parameter is typically learned by repeated training and testing with different parameter values. For unsupervised applications, domain knowledge and/or alternative data-driven approaches are necessary. Like RuLSIF, the texture-based method also does not provide a test of change significance. For the RulSIF and texture-based approaches, we propose a large window change significance test based on intra-window variability and outlier detection.

Our proposed change significance test utilizes the existence of day-to-day variability in human behavior patterns [25]. In order to consider a change between two windows as significant, the magnitude of change should exceed the day-to-day variability within each window. To illustrate, consider two adjacent, non-overlapping windows $W_1$ and $W_7$, each of length $n=6$ days. Now run a pairwise sliding window change algorithm over $W_1$ concatenated with $W_7$. If there is a significant change between the windows, the magnitude of change should be higher for the inter-window comparison (between days 6 and 7) than any other intra-window comparison. Fig. 1 shows an example plot of sw-PCAR change scores for real Fitbit data illustrating this phenomenon. There are small, noisy day-to-day changes for all comparisons except the largest maximum occurring for the inter-window comparison (6th change score).

Fig. 1.

Pairwise sliding window sw-PCAR change scores.

Based on the assumption that a significant inter-window change should exceed intra-window change, we propose an intra-window change significance test (see Algorithm 4). Given a change score $CS$ between two windows, the task is to determine if $CS$ is significant. To do this, first compute a list of all possible daily change scores, DCS, within each window. DCS contains 2 · Combination ($n$, 2) change scores (see Algorithm 5). For example, a week-to-week comparison ($n=7$) would generate an intra-window daily change score sample of 42 day-to-day variations. Next, apply the outlier detection method (see Algorithm 3) from sw-PCAR to test if $CS$ is an outlier score when compared to the distribution of intra-window daily change scores DCS. Advantages of the proposed test include it is non-parametric and can be coupled with any small window change detection function, F. Furthermore, the candidate change score, $CS$, can be computed based on any window size (e.g. Monday-to-Monday, aggregate-to-aggregate, week-to-week, etc.).

Algorithm 4. IntraWindowSignificance($W_i$, $W_j$, $n$, $CS$, $F$)

$$\begin{array}{cc}\hfill & 1:\text{Input:}{W}_i,W_j=\text{two windows of time series data}\hfill \\ \hfill & 2:\text{Input:}n=\text{window size}\hfill \\ \hfill & 3:\text{Input:}CS=\text{change score between}{W}_i\text{and}{W}_j\hfill \\ \hfill & 4:\text{Input:}F=\text{change score function}\hfill \\ \hfill & 5:\text{Output:}sig=(\text{Boolean})\text{significance of}CS\hfill \\ \hfill & 6:\text{Initialize:}DCS=\text{vector of daily change scores}\hfill \\ \hfill & 7:\text{Append IntraWindowChange}(W_i,n,F)\text{to}DCS(\text{see}\hfill \\ \hfill & \mathsf{Algorithm}5)\hfill \\ \hfill & 8:\text{Append IntraWindwoChange}(W_j,n,F)\text{to}DCS(\text{see}\hfill \\ \hfill & \mathsf{Algorithm}5)\hfill \\ \hfill & 9:\text{Compute}sig=\text{BoxplotOutlierDetection}(CS,DCS)(\text{see}\hfill \\ \hfill & \mathsf{Algorithm}3)\hfill \\ \hfill & 10:\mathbf{return}sig\hfill \end{array}$$

Algorithm 5. IntraWindowChange($W$, $n$, $F$)

$$\begin{array}{cc}\hfill & 1:\text{Input:}W=\text{window of time series data}\hfill \\ \hfill & 2:\text{Input:}n=\text{window size}\hfill \\ \hfill & 3:\text{Input:}F=\text{change score function}\hfill \\ \hfill & 4:\text{Output:}DCS=\text{vector of daily change scores}\hfill \\ \hfill & 5:\text{Initialize:}i=1,j=1\hfill \\ \hfill & 6:\mathbf{while}i⩽n-1:\hfill \\ \hfill & 7:j=i+1\hfill \\ \hfill & 8:\mathbf{while}j⩽n:\hfill \\ \hfill & 9:CS=F[W[i],W[j])\hfill \\ \hfill & 10:\text{Append}CS\text{to}DCS\hfill \\ \hfill & 11:j=j+1\hfill \\ \hfill & 12:\mathbf{end}\mathbf{while}\hfill \\ \hfill & 13:i=i+1\hfill \\ \hfill & \mathbf{end}\mathbf{while}\hfill \\ \hfill & 14:\mathrm{return}DCS\hfill \end{array}$$

3.3. Change analysis

If a change significance test concludes a change score is significant, the next step is to determine the source of change (see Algorithm 1 for an overview of the PACD process). Often this step requires the computation of features that summarize the data and provide a meaningful context for change. For example, the number of daily steps taken is an example of a simple PA feature. The change between daily steps from one window of time to the next can be quantified and used for an explanation of change. Several approaches exist to capture change across time in individual metrics. A straightforward method is to compute the percent change for a feature $f$ from a previous window $W_i$ to a current window $W_j:\Delta \%=(f_{W_j}-f_{W_i})∕f_{W_i}$. Statistical approaches such as two sample tests or effect size analyses can also be applied to quantify change; however, in applying repeated statistical tests, the multiple testing problem should be accounted for with a method such as the Bonferroni or Benjamini-Hochberg correction [20].

One of the advantages of the VC approach over other change point detection algorithms is it includes an explanation of the source of change without reliance on statistical tests. Upon significant change detection, retraining a decision tree on the entire dataset and inspecting the tree reveals which features are most discriminatory in learning the differences between two windows. Naturally, this approach requires a pre-processing step to extract relevant features from the windowed PA time series data.

Features extracted from the PA data (see Table 2) serve two purposes: (1) as features for the VC approach (RulSIF, texture-based dissimilarity, and sw-PCAR do not make use of features for change detection) and (2) for explanation of changes discovered by change detection algorithms (see Section 3.1). Features are grouped together based on the number of days required for computation: (1) one day, (2) at least one day, or (3) two or more days. Daily features include PA summaries based on intensity, frequency, duration, and variability of PA bouts. Sequences of time series data with steps greater than a threshold, $S$, are considered a bout of PA. If ground truth activity labels, such as walking, biking, and chores, are available from the device user and/or an activity recognition algorithm [19], PA type can be inferred and $S$ can be updated dynamically for different activities. For this study, we assume such labeled information is not available and set $S=t_{mins}$, assuming physical activity is characterized by at least one step per minute. Features requiring at least two days of data summarize activity across or between days or quantify the user’s circadian rhythm (the periodicity from day-to-day [25]). Poincare-plot analysis [4] provides an additional set of useful PA features.

Table 2.

Physical activity features used for training virtual classifiers and for explanation of changes discovered by change detection algorithms. Features are categorized by time period (window size).

Period	Metric	Description
1 Day	Bout steps	Mean and SD of number of steps per bout
	Period steps [4]	Total, mean, and SD per period: (1) 24 h period (full days), (2) Day (9am–9 pm), and (3) Night (12am–6am).
		Normalized by 24 h mean
	Night/day ratio	See period steps definition
	Number of bouts	Count of detected PA bouts
	Bout minutes	Mean and SD of duration of bouts
	Physical activity intensity percentage	Mean percentage of (1) sedentary (<5 steps/min), (2) low (5 ⩽ 6 steps/min < 40), (3) moderate (40 6 steps/min < 100), and (4) high (⩾100 steps/min) activity levels
	Rest minutes	Mean and SD of duration of rest periods.
⩾1 Day	Relative amplitude	Normalized ratio between the most active 8 h and the least active 4 h
	Texture features [18]	See Section 3.1.2
⩾2 Days	Inter-daily stability (IS) [3]	Quantifies stability between days
	Intra-daily variability [3]	Quantifies the fragmentation of rhythm and activity. Ratio of variance of consecutive time intervals and overall variance
	Circadian rhythm strength [3]	Ratio of average night-time activity (11 pm–5am) by the average activity of the previous day (8am–8 pm)
	Cosinor mesor [3,4]	Time series mean from fitting a cosinor functional model with a 24 h period to time series data via least squares method
	Cosinor amplitude	Difference between the mesor and peak (or trough)
	Cosinor acrophase	Time of day at which the peak of a rhythm occurs
	Poincare SD1 [4]	Standard deviation of Poincare data against the axis x = y
	Poincare SD2 [4]	Standard deviation of Poincare data against the axis orthogonal to x = y and crosses this axis at the center of mass
	Poincare circadian rhythm	Day-to-day circadian rhythm preservation based on dispersion values from SD1 and SD2 with delays of 24 h and 12 h
	preservation (CRP) [4]	$CRP=SD{2}_{24h}+SD{1}_{12h}-SD{1}_{24h}-SD{2}_{12h}$

SD = standard deviation.

4. Results

To demonstrate the PACD approach, two datasets are presented, Hybrid-synthetic (HS) and B-Fit (BF). The HS dataset comprises synthetic data and the BF dataset comprises real-world Fitbit data collected from a health intervention study. HS and BF data are subject to pre-processing prior to serving as input to PACD. Pre-processing includes down sampling the data for a given time interval length, $t_{mins}$, by summing the steps every $t_{mins}$ minutes. For the case of sw-PCAR, add one smoothing is applied to avoid division by zero during KL divergence computations. Furthermore, missing data are identified and handled for BF data. Days with zero steps taken during the day (9am–9pm) are considered missing data. First, to fill a missing day, $D_{missing}$, the day in the opposite window, $D_{other}$, with the same day of the week as $D_{missing}$ is identified. Euclidean distance-based clustering is applied to find the k nearest neighbor days, $N{N}_{other}$, of $D_{other}$ (k = 3). The days of the week for each day in $N{N}_{other}$ are then identified. These are used to select days, $N{N}_{missing}$ in the original window containing $D_{missing}$. The k days of $N{N}_{missing}$ are aggregated (see Eq. (1)) and used to fill $D_{missing}$.

For PACD computations, the following algorithm parameter values are used: window size $n$: 6 days; window $offset$: 6 days; RuLSIF α: 0.1; RuLSIF cross validation folds: 5; number of sw-PCAR permutations $N$: 1000; VC cross validation folds: 4; VC prediction threshold $p_{critical}$: 0.75; minimum steps in a bout $S:t_{mins}$. The time interval aggregation size $t_{mins}$ is tested with values of $t_{mins}=\{1,5,10,15,\dots ,60\text{min}\}$. We hypothesize that PACD will find PA changes (bout frequency, intensity, duration, and variability), using each of the change detection methods. However, we anticipate that the significance of the change will vary depending on the algorithm used, the parameter value choices, and the level of change that is inherent in each dataset.

4.1. Hybrid-synthetic dataset

To generate the HS dataset, step data collected from a volunteer wearing a Fitbit Charge Heart Rate fitness tracker was re-sampled and modified the data to produce five different synthetic physical activity profiles, each exhibiting a different type of change. The length of HS profiles was set to 12 days, resulting in two equal size windows of 6 days for comparison (days 1–6 compared to days 7–12). Twelve days was chosen for similarity to the BF dataset. The HS profiles with their profile identification (HS0-4) and a description are as follows:

1. HS0: No significant day-to-day or window-to-window change. Data is subject to small daily variation. HS0 represents a baseline for “no change”.

2. HS1: Medium day-to-day change and consequently significant window-to-window change. Increased bout duration and intensity from day-to-day.

3. HS2: No significant day-to-day change but significant window-to-window change. Increased activity for days 7–12.

4. HS3: Medium day-to-day change and consequently significant window-to-window change. Increased activity variability from day-to-day.

5. HS4: No significant day-to-day change for days 1–6. Significant day-to-day activity variability for days 7–12. Consequently significant window-to-window change.

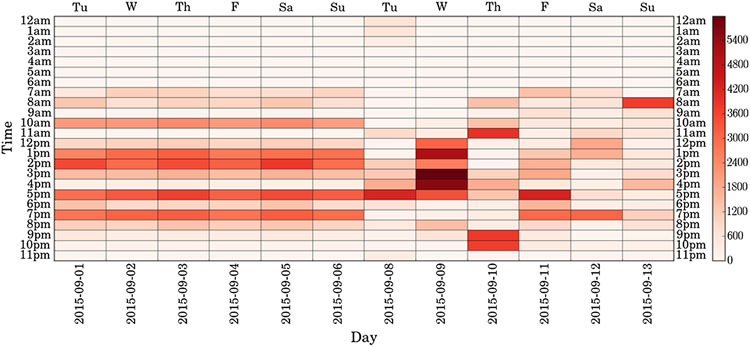
Figs. 2-5 show the associated activity density maps for HS profiles HS1-4. An activity density map is a heat map proposed by Wang et al. [5] to visualize daily activity (steps for this study) as a function of 24 h time (Y-axis) and window time (X-axis). Table 3 shows RuLSIF, Texture-based, sw-PCAR, and VC significant change results for each HS profile for each time interval length $t_{mins}$. Window one (days 1–6) and window two (days 7–12) values (mean ± standard deviation) for the contextual features of number of bouts, bout minutes, daily steps, and sedentary minutes percent are listed in Table 4. Results in Table 4 have time interval length $t_{mins}=1$ min in order to report the most detailed feature values. For further change analysis, decision trees are shown in Fig. 6 for HS profiles HS1-4.

Table 3.

Hybrid-synthetic (HS) significant change detection as a function of time interval size $t_{mins}$ for each HS profile. Results are in the form count: Boolean (significant change 0: false, 1: true) {HS0, HS1, HS2, HS3, HS4}.

$t_{mins}$	RulSIF	Texture-based	sw-PCAR	Virtual classifier	Total
1	2:0,0,1,0,1	1:0,0,1,0,0	3:0,1,1,0,1	4:0,1,1,1,1	10
5	3:0,1,1,0,1	2:0,0,1,0,1	3:0,1,1,0,1	4:0,1,1,1,1	12
10	2:0,0,1,0,1	2:0,0,1,1,0	2:0,1,1,0,0	3:0,0,1,1,1	9
15	3:0,1,1,0,1	2:0,0,1,1,0	1:0,1,0,0,0	3:0,0,1,1,1	9
20	3:0,1,1,0,1	3:0,0,1,1,1	1:0,1,0,0,0	3:0,0,1,1,1	10
25	1:0,0,1,0,0	1:0,0,1,0,0	1:0,1,0,0,0	3:0,0,1,1,1	6
30	3:0,1,1,0,1	1:0,0,0,1,0	1:0,1,0,0,0	4:0,1,1,1,1	9
35	2:0,1,1,0,0	1:0,0,0,1,0	1:0,1,0,0,0	3:0,1,1,0,1	7
40	3:0,1,1,1,0	0:0,0,0,0,0	1:0,1,0,0,0	3:0,0,1,1,1	7
45	2:0,0,1,0,1	1:0,0,1,0,0	1:0,1,0,0,0	2:0,0,1,0,1	6
50	2:0,0,1,0,1	0:0,0,0,0,0	1:0,1,0,0,0	4:0,1,1,1,1	7
55	3:0,1,1,1,0	1:0,1,0,0,0	0:0,0,0,0,0	3:0,1,1,0,1	7
60	4:0,1,1,1,1	0:0,0,0,0,0	1:0,1,0,0,0	4:0,1,1,1,1	9
Total	33:0,8,13,3,9	15:0,1,7,5,2	17:0,12,3,0,2	43:0,7,13,10,13	108

Table 4.

Hybrid-synthetic (HS) feature results (mean ± standard deviation) with $t_{mins}=1$ min. First and second window values are separated by a comma.

ID	Number of bouts	Bout minutes	Daily steps	Sedentary %
HS0	70.33, 70.00	5.10 ± 9.91, 5.13 ± 9.92	20601.65, 21274.32	75.65, 75.56
HS1	34.50, 14.17	19.39 ± 23.93, 46.82 ± 56.78	36409.49, 72769.11	64.57, 54.59
HS2	71.50, 62.50	5.07 ± 9.83, 7.63 ± 11.13	20755.53, 30037.48	75.62, 67.44
HS3	54.83, 102.83	18.71 ± 51.74, 6.49 ± 14.49	14395.85, 14746.43	45.22, 63.72
HS4	53.50, 81.33	8.14 ± 12.61, 4.56 ± 8.48	22048.02, 17327.00	70.66, 77.86

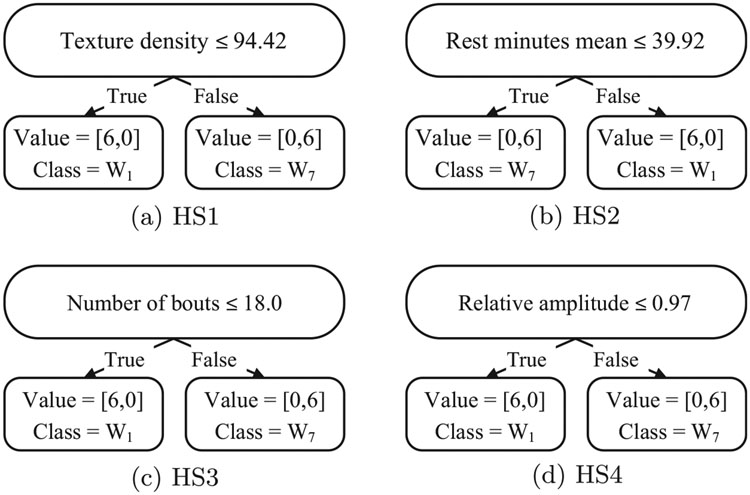
Fig. 6.

Decision trees for Hybrid-synthetic (HS) profiles with significant virtual classifier change scores for $t_{mins}=5\text{min}$.

4.2. B-Fit dataset

The BF dataset consists of data collected from 11 older adults (Male = 3, Female = 8; age 57.09 ± 8.79 years) participating in a 10-week health intervention. Study inclusion criteria consisted of older adults over the age of 55 who had risk factors for developing dementia. At risk individuals were defined as those who had at least one first degree relative with Alzheimers disease or dementia, or who had cardiovascular disease risk factors (e.g., diabetes, mid-life obesity, smoking, hypertension). Participants had to be able to provide their own informed consent. As part of this study, participants’ PA profiles were assessed with wrist-worn Fitbit Flex fitness trackers for one week (six full 24 h days) before and after the intervention. During weeks two through nine, the participants were educated in eight different subjects related to health (e.g., exercise, nutrition, sleep) and set personal goals for each subject. To track goal achievement each week, individuals rated themselves on each personalized goal that they set using a 0–3 rating scale (0: did not meet goal, 1: partly met goal, 2: completely met goal, and 3: exceeded goal). For the BF dataset, each participant’s change significance testing results are presented in Table 5. Four contextual features (number of bouts, bout minutes, daily steps, and sedentary percent) pre and post-intervention values are listed in Table 6. Finally, decision trees are shown in Fig. 7 for select BF participants with a significant VC change score (P2, P7, and P10).

Table 5.

Health intervention study significant change detection as a function of time interval size $t_{mins}$. Results are in the sparse form count: {IDs}: Boolean (significant change: 0 false, 1 true).

$t_{mins}$	RulSIF	Texture- based	sw-PCAR	Virtual classifier	Total
1	1:P2:1	0	10:P10:0	5:P2,7,10,11:1	16
5	2:P2,7:1	0	5:P1,2,3,4,8:1	6:P2,6,7,8,10,11:1	13
10	1:P2:1	0	4:P1,2,4,8:1	6:P2,3,6,7,8,10:1	11
15	1:P2:1	0	4:P1,2,4,8:1	4:P2,7,10,11:1	9
20	2:P2,7:1	0	3:P2,4,8:1	4:P2,7,10,11:1	9
25	1:P2:1	0	3:P2,4,8:1	2:P7,10:1	6
30	2:P2,8:1	0	3:P2,4,8:1	2:P6,10:1	7
35	3:P2,4,8:1	0	3:P2,4,8:1	5:P2,6,7,10,11:1	11
40	1:P2:1	0	3:P2,4,8:1	3:P2,7,10:1	7
45	4:P2,3,4,6	0	1:P2:1	2:P2,10:1	7
50	1:P2:1	0	1:P2:1	5:P2,6,7,9,10:1	7
55	1:P10:1	0	1:P2:1	3:P2,4,10:1	5
60	2:P4,9:1	0	1:P2:1	4:P2,6,10,11	7
Total	22	0	42	51	115

Table 6.

B-Fit (BF) feature results (mean ± standard deviation) with $t_{mins}=1$ min. Pre and post-intervention values are separated by a comma.

ID	Number of bouts	Bout minutes	Daily steps	Sedentary %
P1	73.50, 89.67	2.35 ± 1.93, 2.63 ± 2.61	3479.00, 4658.33	88.37%, 84.43%
P2	81.00, 15.83	2.57 ± 2.54, 2.75 ± 1.85	4279.50, 1161.44	86.30%, 97.44%
P3	88.50, 27.50	2.72 ± 2.86, 2.36 ± 2.08	5886.67, 4558.50	84.06%, 86.32%
P4	81.17, 60.33	3.90 ± 5.27, 3.71 ± 4.85	11177.00, 7399.67	79.11%, 85.71%
P5	73.67, 76.50	2.96 ± 4.06, 2.60 ± 3.22	6994.17, 5470.50	85.71%, 86.22%
P6	105.33, 88.00	2.63 ± 2.46, 2.66 ± 2.39	7127.00, 6207.67	81.82%, 84.85%
P7	64.33, 63.50	3.30 ± 4.20, 3.45 ± 3.61	7354.67, 6181.17	85.78%, 85.90%
P8	104.17, 102.50	5.52 ± 7.51, 3.35 ± 3.79	17680.78, 11440.00	66.66%, 77.18%
P9	99.50, 116.67	2.40 ± 2.49, 2.40 ± 2.57	5844.50, 6731.83	84.11%, 81.46%
P10	85.00, 80.50	2.99 ± 3.24, 3.58 ± 4.29	1136.51, 1210.85	82.94%, 81.62%
P11	83.00, 89.50	2.51 ± 2.73, 2.31 ± 2.23	5753.50, 4868.83	86.16%, 86.44%

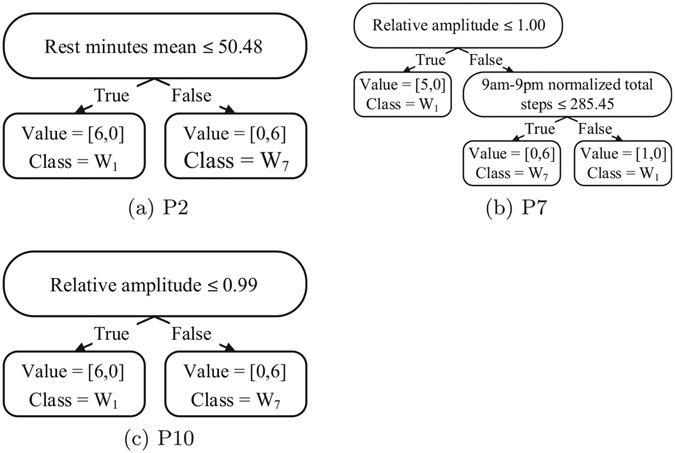
Fig. 7.

Decision trees for B-Fit (BF) participants with significant virtual classifier change scores for $t_{mins}=5\text{min}$.

5. Discussion

In this paper, we investigate the PACD approach for unsupervised change detection and analysis of PA time series. The abilities of four presented methods to detect change are evaluated on two original datasets: (1) the HS dataset, comprised of 5 synthetic profiles and (2) the BF dataset, comprised of 11 participants’ Fitbit data from an intervention study.

5.1. Hybrid-synthetic dataset

The HS dataset reveals several insights into the change detection algorithms. First, the time interval length yielding the highest number of significant changes is $t_{mins}=5$ min with 12 changes, closely followed by $t_{mins}=1$ and $t_{mins}=20$ min with 10 changes (see Table 3). Since HS profiles are sampled from a volunteer’s real Fitbit data, these intervals suggest movement patterns occur in 1, 5, and 20 min chunks for this individual. For all time interval lengths, the algorithms correctly do not detect a significant change between first and second window data for the HS0 profile. HS0 is generated to exhibit small day-to-day variation in step intensity and is not characterized by large changes between windows.

For HS1-4 profiles, significant changes between windows are detected. For all time interval lengths, the VC approach picks up the most changes (43 changes), followed by RuLSIF (33), sw-PCAR (17), and texture-based (15). As a group, the algorithms’ are able to sense changes in value (HS1, HS2) and changes in variability (HS3, HS4), with 64 and 44 changes respectively. Changes for HS2 (36) are the most frequently detected, followed by HS1 (28), HS4 (26), and HS3 (18). The lower number of changes detected for HS3 is possibly due to high intra-window daily change scores for days 7–12 (see Fig. 4) used for Boxplot significance testing (see Algorithm 3). Window-based change (HS2, HS4) is perfectly detected for all time intervals by VC (HS2, HS4: 13) and RuLSIF (HS2: 13). Investigating the $t_{mins}=5$ min results reveal all four algorithms determine significant changes for HS2 and HS4 (see Table 3). For HS1, near perfect detections are made by sw-PCAR (12).

Fig. 4.

Hybrid-synthetic (HS) step density map for HS3.

Upon inspection of the associated decision trees for HS1-4 (see Fig. 6), the features of texture density, average daily rest minutes, number of bouts, and relative amplitude are discriminatory features. The explanatory power of the features is potentially useful for reporting to the wearable sensor user the dimensions of change in their physical activity. Features useful for such purposes are simple, common features that do not require explanation to the user. For example, texture density or relative amplitude are useful features for detecting changes in PA patterns, but are relatively unimportant to a user. More meaningful features to a user include number of bouts, minutes per bout, daily steps taken, and sedentary percent. Table 4 shows these features for the HS profiles. HS0 exhibits quite similar window one and window two values for all features. HS2 and HS4 both have small standard deviations due to window-based change in lieu of day-to-day change (HS1 and HS3).

5.2. B-Fit dataset

Analyzing the BF participants’ data poses additional challenges that are not present with the HS profiles. Real-world human subject data is inherently noisy, characterized by seemingly random bouts of PA and rest periods. Furthermore, self-report and direct measurement of physical activity are often not congruent, with previous studies reporting correlations in as wide a range of −0.71 to 0.96 [26]. For the BF group, the participants demonstrated a wide spread of self-reported goal achievement ratings for the exercise category, 1.59 ± 1.05. For example, P6, P9, and P10 rated their exercise goal achievements as low (exercise rating: 1, 0, 0.5 respectively). Due to heart problems, P9’s doctor instructed him not participate in exercise-related activities. On the other hand, P2 rated her exercise goal achievement the highest (exercise rating: 3). Upon inspection of P2’s data, it is evident there is a discrepancy between the participant’s perception of her PA and the steps recorded by the Fitbit. It is not uncommon for self-reported measures of physical activity to be inconsistent with direct measures [26]; therefore, the participants’ self-ratings are used for insights into individual goal achievements, not as ground truth information for changes exhibited. The issues with self-reported PA measures exacerbate the need for unsupervised change detection and analysis methods.

Depending on the algorithm, significant changes are commonly detected for 5 out of the 11 BF participants: P2: 35; P10: 14; P4: 13; P8: 13; P7: 12 (see Table 3). Virtual classifier and sw-PCAR detect the highest number of changes (51 and 42 changes each). The distribution of detected changes by sw-PCAR is highly influenced by time interval length (sw-PCAR: 3.23 ± 2.42 number of changes detected compared to VC: 3.92 ± 1.44). sw-PCAR is not sensitive for small time intervals ($t_{mins}=1\text{min}$) or large time intervals ($t_{mins}=\{45,50,55,60\text{min}\}$), and the number of changes detected decreases as time interval length increases. Virtual classifier does not appear to be as heavily influenced by the time interval length. The texture-based approach is the least sensitive algorithm and did not detect any changes in the BF data.

Performing change analysis and investigating the detected changes yields insights for several of the participants. P2 rated herself as completely meeting her exercise goal of walking more; however, the Fitbit data tells a different story. Several features in Table 4 show decreased PA for P2: average number of bouts (pre: 81.00, post: 15.83), daily steps (pre: 4279.50, post: 1161.44 steps), and percentage of time sedentary (pre: 86.30%, post: 97.44%). Additionally, P2’s decision tree (see Fig. 7a) provides evidence that she rested more during post-intervention testing. In summary, the features suggest the changes detected by the algorithms are actually changes in the opposite direction of her goal. Contrary to P2, P10 exhibited a significant change (as detected consistently by VC) in the direction toward her goal of walking more. Inspection of P10’s features shows an increase in bout minutes and average steps per day. Average daily steps increased from 1136.51 steps pre-intervention to 1210.85 steps post-intervention testing, a 6.54% increase. The remaining participants with significant changes (P4, P7, and P8) demonstrated a decrease in average daily steps taken from pre to post intervention. It should be noted that during the week of post-test data collection the weather conditions were adverse and this may have partially contributed to the decrease observed in average daily steps. Research has shown PA levels can be influenced by adverse weather conditions [27]. It is also worth noting the participants exhibited improvements in other PA features. For example, relative amplitude has been reported to decrease with worsening health [28], thus P7 and P10’s increased relative amplitude post-intervention is healthy (see Fig. 7b and c). Also, P9 was not planning on increasing exercise; however, P9 increased his daily steps post-intervention by 15.18%.

One of the limitations of this study includes having only one week of pre-intervention Fitbit data for BF participants. With at least two weeks of pre-intervention data, change scores can be computed between week one and two of pre-intervention data to provide an estimate of inter-week variability. With a quantification of inter-week variability, we can determine if the measured change between pre and post-intervention weeks is due to the intervention or natural variability. An additional limitation includes not having a full 7 days of BF data during pre and post-intervention weeks. Finally, more sophisticated methods to fill missing data could be utilized with fitness trackers that include heart rate monitors, due to more reliable detection of sensor donned/doffed. Consequently, future work includes performing change analysis on real-world datasets from different fitness trackers, multidimensional data (e.g. heart rate, elevation, etc.), labeled activity data, and longer windows of time. With time series data longer than two years, several additional analyses could be performed including: daily/weekly/monthly/yearly period analysis and slicing along different dimensions (e.g. Mondays, weekends, holidays, or activities if labeled information is available).

6. Conclusions

We address the problem of unsupervised physical activity change detection and analysis with our proposed Physical Activity Change Detection approach. PACD is a framework we designed to detect and analyze changes in physical activity data. We compare the abilities of three change detection algorithms from the literature and one proposed algorithm, sw-PCAR, to capture different types of changes in synthetic and real-world datasets. Results indicate the approaches detect several changes in both datasets; particularly for physical activity profiles exhibiting large changes between windows instead of incremental day-to-day changes. Contextual features such as average number of daily steps, minutes per bout, and sedentary percent provide an explanation of the changes that are detected. The algorithms and analysis methods are useful data mining techniques for unsupervised, window-based change detection. Future work involves quantifying the change in accuracy (ability to find true positives and not false positives in synthetic data) as parameters such as time window length is incremented or decremented. Additional future work includes implementing our PACD method in an online, smartphone application to track users’ physical activity and motivate progress toward their health goals.

Fig. 3.

Hybrid-synthetic (HS) step density map for HS2.