Abstract
Source analysis of magnetoencephalography (MEG) data requires the computation of the magnetic fields induced by current sources in the brain. This so‐called MEG forward problem includes an accurate estimation of the volume conduction effects in the human head. Here, we introduce the Cut finite element method (CutFEM) for the MEG forward problem. CutFEM's meshing process imposes fewer restrictions on tissue anatomy than tetrahedral meshes while being able to mesh curved geometries contrary to hexahedral meshing. To evaluate the new approach, we compare CutFEM with a boundary element method (BEM) that distinguishes three tissue compartments and a 6‐compartment hexahedral FEM in an n = 19 group study of somatosensory evoked fields (SEF). The neural generators of the 20 ms post‐stimulus SEF components (M20) are reconstructed using both an unregularized and a regularized inversion approach. Changing the forward model resulted in reconstruction differences of about 1 centimeter in location and considerable differences in orientation. The tested 6‐compartment FEM approaches significantly increase the goodness of fit to the measured data compared with the 3‐compartment BEM. They also demonstrate higher quasi‐radial contributions for sources below the gyral crowns. Furthermore, CutFEM improves source separability compared with both other approaches. We conclude that head models with 6 compartments rather than 3 and the new CutFEM approach are valuable additions to MEG source reconstruction, in particular for sources that are predominantly radial.
Keywords: finite element method (FEM), MEG forward problem, quasi‐radial sources, realistic head modeling, somatosensory evoked fields, unfitted FEM, volume conductor modeling
CutFEM is a new magnetoencephalography (MEG) forward modeling technique, facilitating the mesh generation process. CutFEM enhances sensitivity to quasi‐radial source contributions and improves the ability to distinguish proximate neural sources compared to two competing boundary and finite element approaches.
1. INTRODUCTION
A central step in the localization of neural sources using magnetoencephalography (MEG) is solving the forward problem, where the magnetic field for a given source in the brain is simulated using the Biot‐Savart law. In doing so, one has to set up a model that captures the volume conduction properties of the human head. That model's setup can differ in several ways.
First, the magnetic field is influenced by the electric conductivity of the different tissues of the head. This implies the decision about the complexity of the model: while more compartments yield more realistic models, the accurate modeling of an increasing number of tissues is limited by the data resolution and requires methodological comprehension of the user. Less detailed models distinguish only between a small set of tissues, often the three compartments skin, skull, and brain, and some even assume them to be spherical (Eaton, 1992). More complex ones segment individual anatomical data from magnetic resonance imaging (MRI) into three or more compartments (van den Broek et al., 1998). Modern toolboxes distinguish up to 15 or more tissues (Puonti et al., 2020) given sufficient MRI quality.
Second, the distribution of the magnetic field outside the head induced by an electric current source in the brain can be computed using Biot‐Savart's law which splits the magnetic field into a directly computable component and one related to the electric potential induced by the source. The electric potential can then be computed as the solution of a partial differential equation (PDE) that is solved using a numerical method. For spherical models, analytic formulas (Sarvas, 1987) exist. In 3‐layer models that consist of skin, skull and brain, the boundary element method (BEM) (Gramfort et al., 2010; Makarov et al., 2020; Mosher et al., 1999; Stenroos et al., 2014) is widely used to solve the PDE, whereas for models with a larger number of tissues, the BEM fast multipole method (Makarov et al., 2020), the finite difference method (FDM) (Cuartas Morales et al., 2019), and finite element method (FEM) (Medani et al., 2015; Vallaghé & Papadopoulo, 2010) are typical choices. The latter two approaches have the advantage that tissue anisotropy such as white matter fiber bundles could be modeled (Beltrachini, 2018; Hallez et al., 2005; He et al., 2020; Nüßing et al., 2016; Schimpf et al., 2002; van Uitert et al., 2004; Vermaas et al., 2020; Wolters et al., 2007).
This article describes the implementation of a new FEM‐based MEG forward modeling approach, the Cut finite element method (CutFEM) (Burman, 2010; Burman et al., 2015; Burman & Hansbo, 2012). CutFEM was previously introduced to electroencephalography (EEG) source analysis (Erdbrügger et al., 2023) where it was validated in multi‐layer sphere scenarios and evaluated in a somatosensory evoked potential (SEP) study. Here, for the first time, we will describe CutFEM as a method to solve the MEG forward problem. CutFEM is intended to simplify the way anatomical information from MR imaging can be included in the numerical models, without modifying the anatomical input. CutFEM can represent arbitrary geometric shapes and thin or vanishing tissues such as the cerebrospinal fluid (CSF) in occipital areas. The focus lies in creating a computational domain as close to the segmentation result as possible, whichever shape that segmentation input takes.
After the presentation of the CutFEM methodology for MEG, we evaluate the new methodology in a group study on somatosensory evoked fields (SEF). The SEF data stems from electric wrist stimulation, yielding a clear and focal response in Brodmann area 3B in the postcentral cortex, the so‐called M20 component (Nakamura et al., 1998). Somatosensory evoked responses are analyzed for example for intraoperative neurophysiological monitoring (Sarnthein et al., 2022), diagnostic purposes (Cruccu et al., 2008), as well as skull conductivity calibration (Baysal & Haueisen, 2004). The well‐described neurophysiological features of the M20 component, its high signal‐to‐noise ratio (SNR), and the insensitivity of MEG to additional contributions of deep thalamic sources allows the use of a simple MEG dipole scan inverse approach (Fuchs et al., 1998) that identifies a single dipole source, that is, a location, orientation, and strength, in the brain as the best‐fitting source. The location and orientation are also relevant for applications such as transcranial electric or magnetic stimulation. Personalized stimulation montages can be created that optimize both the intensity in the target region as well as the orientation of the applied electric field (Antonakakis et al., 2024; Dmochowski et al., 2011; Khan et al., 2022).
The MEG has a strong sensitivity bias towards tangential sources, and is less sensitive to sources that point radially outward. Note that the word “radial” is only well‐defined in spherical head models. When used in realistic scenarios, we refer to “quasi‐radial” as the vector pointing from the source location in the gray matter towards the inner skull surface. If the underlying volume conductor is spherical, such radial sources do not produce any magnetic field outside of the scalp. Spherically symmetric head models are thus completely blind to radial sources (Sarvas, 1987). However, in non‐spherical volume conductors, the signal strength depending on the source orientation can be calculated to estimate the EEG/MEG sensitivity to different cortical regions (Ahlfors et al., 2010; Piastra et al., 2021; Vorwerk et al., 2014).
In the methods section, we introduce CutFEM for the MEG forward problem. We then compute lead field matrices based on 6‐compartment CutFEM (6C‐CutFEM) as well as a 3‐layer BEM (3C‐BEM) (Gramfort et al., 2010) and a 6‐compartment hexahedral FEM method (6C‐HexFEM) (Wolters et al., 2007) for comparison. We quantify the impact of the forward modeling method on the location, orientation, and strength of reconstructed SEF sources. Furthermore, we investigate how well the reconstructions match the measured data by assessing how the amount of unexplained data, measured as residual variance, changes when using the different forward models. We also measure the source separability by quantifying the rise in residual variance with increasing distance from the optimal dipole fit. In other words, we investigate if two spatially proximate source candidates for our localization can be better distinguished with CutFEM. We hypothesize that more complex anatomical models lead to a better separability.
Finally, following Goldenholz et al. (2009) and Piastra et al. (2021), we compute SNR‐maps to investigate whether a change in the forward model leads to a different sensitivity profile for quasi‐radial sources. We assume that since the 6‐compartment models deviate more strongly from sphere models they also feature higher quasi‐radial contributions.
We conclude with the main contributions of 6C‐CutFEM modeling for the MEG forward problem.
2. METHODS
2.1. CutFEM for the MEG forward problem
Magnetometers measure the magnetic flux
| (1) |
the integral of the magnetic Field through a sensor surface . When performing numerical integration to approximate this integral we need the magnetic field at one or several quadrature points . Following Biot‐Savart, the electric current density in the head volume conductor creates a magnetic field
| (2) |
at an MEG sensor position outside (Sarvas, 1987). is the magnetic permeability of the vacuum. Separating the current into a primary current from neural activity and the secondary volume currents throughout the volume conductor, , allows us to split the Equation (2) into the calculation of a primary and a secondary magnetic field. Here, is the electric potential induced by , and is the electric conductivity of the different head tissues. The primary field can be calculated analytically while the secondary, stated as
| (3) |
is calculated numerically from the solution to the EEG forward problem which yields (Sarvas, 1987). As CutFEM has already been introduced for EEG, where it was validated in multi‐layer sphere scenarios and evaluated in a somatosensory evoked potential (SEP) study (Erdbrügger et al., 2023), we make use of this implementation.
In FEM, is approximated using so‐called trial functions. These functions are defined on a computational domain, the mesh. It consists of a set of polygons, usually tetrahedra or hexahedra, that must resemble the segmentation from the MRI as closely as possible. Both options have certain advantages and limitations. While hexahedral meshes are easy to create from voxel‐based MRIs, they cannot properly represent curved geometries (Wolters et al., 2007). Tetrahedra are well suited to model smooth complex geometries but they require surface triangulations that may impose restrictions such as nested compartments, meaning that for example the gray matter must be surrounded by CSF and may not be in contact with the skull (Nielsen et al., 2018; Windhoff et al., 2013). The goal of CutFEM is to integrate the strengths of tetrahedral and hexahedral mesh generation to accurately resemble the anatomical data. For CutFEM, the segmentation result is transformed to level set functions, one function per tissue type. For each point in space, these functions define whether it lies in‐ or outside the respective tissue with 0‐values defining the boundary. Contrary to a hexahedral or tetrahedral meshing process, CutFEM operates on a background mesh that does not conform to the tissue boundaries. On this background mesh, we define sets of trial functions, also one set per tissue. The functions in each set are then restricted to the inside of their respective level set function, meaning that they are cut off at the boundary. To integrate the trial functions inside the tissue we use a topology‐preserving marching cubes algorithm (TPMC) (Engwer & Nüßing, 2017). The discontinuities that arise from the cut‐offs are alleviated by introducing penalty terms based on Nitsche coupling (Nitsche, 1971). The Nitsche penalty is defined on the boundary that separates the compartments. Cuts over small volumes can lead to a deterioration of the condition number, leading to high computation times. This is resolved through the use of a ghost‐penalty term (Burman, 2010) which acts on the internal skeleton of the fundamental mesh. See Figure 1 for a schematic overview.
FIGURE 1.
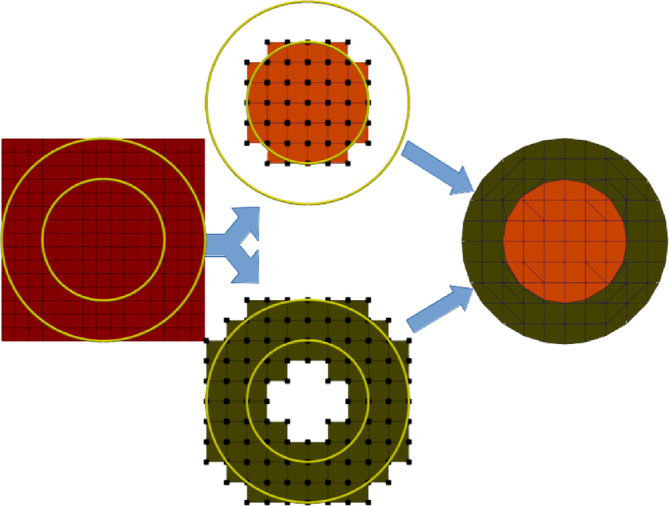
Schematic overview of the Cut finite element method. Left: Fundamental mesh and level sets for two spherical compartments. Center: Submeshes and trial functions for each compartment. Black dots represent trial functions of the respective submeshes. Right: Cut mesh representation created by TPMC. The green and orange colors represent the areas that the trial functions from the previous step are restricted to.
In summary, the weak form of the MEG forward problem using CutFEM is stated as finding the electric potential such that
| (4) |
with
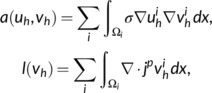 |
and
| (5) |
The primary current is typically modeled as a point dipole (Sarvas, 1987). is the direct sum of the vector spaces of each compartment, measures the jump at an interface, and are scaling parameters depending on the polynomial degree of the finite element functions, the conductivity ratio at an interface and the size of the TPMC snippets respectively (Di Pietro & Ern, 2012; Erdbrügger et al., 2023; Nüßing et al., 2016). The free penalty parameters , have to be chosen large enough to ensure coercivity and a fast computation time but small enough not to distort the numerical accuracy. Their size was determined based on a sphere model analysis. From the that has been computed in Equation (4), we then proceed to evaluate the secondary magnetic field from (3). For more information on CutFEM in general, see Burman et al. (2015) and Burman and Hansbo (2012). For a more thorough explanation in the context of bioelectromagnetism, see Erdbruegger et al. (2023). In practice, the potential has to be calculated for several thousand of sources, making the process computationally expensive. Instead we make use of a transfer matrix approach (Wolters et al., 2004) that reduces the number of required solutions to the forward problem from one per source point to one per sensor.
2.2. Data acquisition
2.2.1. MEG data
Nineteen participants (aged 19–49, mean age 26.15 7.76 SD, 8 male, 11 female) were included in this study. They gave written informed consent according to the declaration of Helsinki prior to the experiment and the study was approved by the ethics committees of the Universities of Münster and Lübeck (#2015‐263‐f‐S and #20‐459). Magnetoencephalography (MEG; 275 axial gradiometers; VSM MedTech Ltd., Vancouver, Canada; 600 Hz sampling rate) data was recorded during median nerve stimulation (1932 monophasic electrical square‐wave pulses of length 0.5 ms; the inter‐stimulus interval was uniformly jittered between 350 and 450 ms). Preprocessing the MEG data included a band‐pass filter between 20 to 250 Hz and a 50 Hz notch filter (considering harmonics) to account for the power line artifact (Buchner et al., 1994). Data was epoched between −50 and 150 ms relative to the onset of electrical pulses and bad trials were removed semi‐automatically. After averaging the data across trials, the individual component 20 ms post‐stimulus, that is, the so‐called M20 component (Nakamura et al., 1998), was determined (Figure 2). The M20 response is generated in the primary somatosensory cortex (Allison et al., 1991).
FIGURE 2.
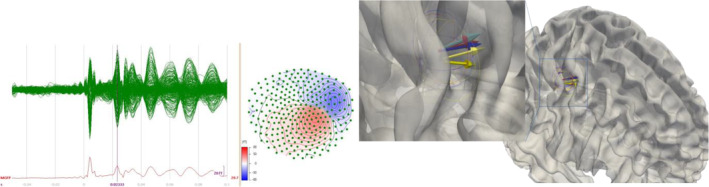
Left: Butterfly Plot and topography of one subject's preprocessed and averaged somatosensory evoked field (SEF) data. Right: Averaged M20 reconstructions of 6C‐CutFEM (red), 6C‐HexFEM (blue) and 3C‐BEM (yellow) mapped on MNI white matter surface. Lighter shades indicate TSVD‐regularized reconstructions. Ellipsoid radii correspond to one standard deviation in each spatial direction and are based on the unregularized reconstructions.
2.2.2. MRI data
Using a 3 T Siemens Magnetom Skyra scanner (Siemens, Erlangen, Germany; 64‐channel head coil), structural T1 and T2 images were acquired (1 × 1 × 1 mm resolution; 192 × 256 × 256 mm FoV; T1: 3D MP‐RAGE sequence, TR = 2300 ms, TE = 3.6 ms, TI = 1100 ms, FA = 8°; T2: spin echo (SE) pulse sequence, TR = 3200 ms; TE = 408 ms, FA = 120°).
2.3. Segmentation and head modeling
2.3.1. 6‐Compartment HexFEM
We used T1‐ and T2‐weighted MRI data for the generation of individual 6‐compartment head models that include scalp, skull compacta, skull spongiosa, cerebrospinal fluid (CSF), gray matter, and white matter tissues. After registering the T2 onto the T1 using FSL FLIRT (Jenkinson et al., 2002), tissue probability maps (TPM) were segmented and thresholded using CAT12 (Gaser et al., 2022). The T1 image was used for the segmentation of gray matter, white matter, and scalp, whereas the CSF and skull compacta were segmented from the T2. The spongiosa compartment was created by Otsu thresholding (Otsu, 1979) of the 2 mm eroded skull mask. We used custom MATLAB scripts including Boolean and morphological operations (Antonakakis et al., 2020) to remove possible overlap of brain tissues and skull/CSF and to fill unrealistic holes within the masks. The model was cut using an axial plane 4 cm below the skull, following the recommendations of Lanfer et al. (2012). Geometry‐adapted hexahedral meshes with a node shift of 0.33 were created (Wolters et al., 2007) from the segmentation masks. Lead field matrices and results generated by this process will be referred to as 6C‐HexFEM from now on.
2.3.2. 6‐Compartment CutFEM
For 6C‐CutFEM, we need to transform the segmentation results into level‐set functions. This transformation depends on the segmentation input. Tissue probability maps range between 0 and 1, we can thus simply subtract a threshold between 0 and 1 and multiply the result by −1, yielding a level set between −1 and 1 with negative values on the inside and the subtracted threshold marking the boundary. Binary segmentations are transformed into signed distance functions using Matlab's bwdist function, each point then states the distance to the boundary of the segmentation. Surface triangulations can also directly be transformed into signed distance functions, however, we did not create any surface triangulations for this study. For the models in this study, gray and white matter level sets are created based on the tissue probability maps from the T1 image as the contrast for these tissues is best in the T1. TPMs are not used for skull or skin level sets. Skull TPMs often have holes near thin areas such as temples while the ones for the skin suffer strongly from noise. Rather, the binary maps created for the hexahedral models are transformed into level sets. Finally, the CSF level set is defined to fill any remaining holes within the union of skull compacta, spongiosa, gray, and white matter.
All level sets are then smoothed using diffusion anisotropy filtering based on Perona & Malik (1990) as implemented into the Matlab function imdiffusefilt.
2.3.3. 3‐Compartment BEM
The three 3C‐BEM surfaces are based on the binary segmentations used for the hexahedral models as well. The brain is defined as the union of gray and white matter plus CSF. The compacta and spongiosa are defined as skull and the skin represents the outermost layer. Any holes in the skull were closed to ensure nested compartments and smooth surfaces are extracted using the fieldtrip (Oostenveld et al., 2011) function ft_prepare_mesh.
2.4. Source spaces
The different models impose different restrictions on the feasibility of source positions. For the 3C‐BEM model, any point within CSF, gray or white matter can be considered. However, too close proximity to the skull surface may lead to numerical inaccuracies (Gramfort et al., 2010). In a six compartment model, the sources are in the gray matter compartment. To maintain comparability, we used a regular grid with 2 mm spacing. Each grid node outside the gray matter was removed and the remaining nodes moved such that they conform to the Venant condition (see section 2.5). The source space is created individually for each subject and then used for all 3 methods. They have an average of 33,940 14,088 SD nodes.
2.5. Lead field matrix generation
The finite element lead field matrices are created using the DUNEuro toolbox (https://www.medizin.uni-muenster.de/duneuro [Schrader et al., 2021]) where we now also implemented the MEG CutFEM approach. Based on the principle of St. Venant, the divergence of the source term is approximated by a set of monopoles (Buchner et al., 1997; Medani et al., 2015; Nüßing, 2018; Vorwerk et al., 2019). For fitted meshes, these monopoles are placed on mesh vertices. The closest vertex thus has to be enclosed by gray matter to ensure numerical stability. For CutFEM, the monopole locations are based on a second order Gauss‐Legendre quadrature rule (Johansson & Mezzarobba, 2018) within cut cells that contain gray matter. We use the mixed moments venant (Nüßing, 2018). The 3C‐BEM lead field matrices are created using the fieldtrip integration of OpenMEEG (Gramfort et al., 2010).
Computation times depend strongly on the chosen method, ranging from less than 30 min for 3C‐BEM, about 90 min for 6C‐HexFEM to currently still 9–12 h for CutFEM. CutFEMs computation times are expected to drop with the integration of better preconditioning and smoothing. For EEG, it is already on par with the 6C‐HexFEM (Erdbrügger et al., 2023). DUNEuro is integrated into brainstorm (Medani et al., 2023) and fieldtrip (Schrader et al., 2021) and CutFEM will be part of future updates into those pipelines.
2.6. Source reconstruction
In its simplest form, the MEG dipole scan is the least squares solution of
| (6) |
where is the measured data of the M20 component at different sensors, is the lead field matrix at position and characterizes the direction and magnitude of the dipolar source. The MEG has a strong sensitivity bias towards quasi‐tangential sources (Ahlfors et al., 2010). This is problematic as noise in the data could be amplified by the ill‐conditioned MEG lead field matrix into high quasi‐radial source orientation components in our reconstructions.
To alleviate this issue, a common approach is to truncate the lead field matrix. Quasi‐radial and quasi‐tangential source orientations can be identified by singular value decomposition (SVD). Let be a SVD of the lead field matrix at an arbitrary source location. is then a diagonal matrix with 3 non‐zero entries containing the singular values of , two large ones for the quasi‐tangential directions, and a small one for the quasi‐radial. Setting the small one to zero cuts out any quasi‐radial contribution. The truncation is performed for each point in the source space. This prevents a noise‐related blow‐up of but also cuts out any possible quasi‐radial contribution that originates from the actual neural source. In software toolboxes such as fieldtrip (Oostenveld et al., 2011), the default is to eliminate the smallest singular value. Alternatively, the truncation can be based on both the size of the smallest singular value and the noise level of the data (Wolters et al., 1999). If the measurement noise exceeds the signal strength of a quasi‐radial source at point , the lead field matrix truncation is performed. Following Goldenholz et al. (2009) and Piastra et al., 2021 we define the signal‐to‐noise‐ratio (SNR) at a point in the source space as
| (7) |
is the number of MEG sensors, the amplitude of the quasi‐radial source, the lead field matrix at position , the singular vector corresponding to the smallest singular value and the noise level at sensor . can be based on either 3C‐BEM, 6C‐CutFEM or 6C‐HexFEM, leading to three different SNR‐values for each position in the source space. The noise amplitude is calculated for each of the channels separately based on the standard deviation of the pre‐stimulus interval, i.e. the period from −50 to 0 ms in the left panel Figure 2. In Antonakakis et al. (2020), we find 21 nAm source strength for the M20 source. If we expect M20 sources to be about 10° out of the quasi‐tangential plane, then we could expect a quasi‐radial source strength of about 4 nAm (), which we will use here. This is considerably lower than the 10 nAm used in Goldenholz et al. (2009) and Piastra et al., 2021. The 10 nAm were for realistic source orientations normal to the cortical surface. Our intent here is to model only the quasi‐radial contributions of a source that consists of both quasi‐radial and quasi‐tangential parts. Due to the logarithmic scaling of the SNR, a value larger than 3 implies that the average signal power across all channels is at least twice the power of the noise. We therefore choose to truncate the smallest singular value at all positions where the SNR is smaller than 3.
Note that the truncation we perform here is heavily adapted to the SEF‐data we analyze. It may require strong modifications in the definition of noise level and signal strength for other applications.
2.7. Location and orientation differences
We perform two kinds of dipole scans. The first will be referred to as unregularized and is based on the full lead field matrices, without considering the SNR and thus without any truncation. The second, where is truncated if the SNR is smaller than 3 will be referred to as regularized by truncated singular value decomposition (TSVD‐regularized). We examine differences in location, orientation, and amplitude of the reconstructed dipole. Boxplots are shown depicting the pairwise Euclidean distances and orientation differences between forward models. This is done for each dipole scan approach separately.
Furthermore, the fieldtrip function ft_warp_apply is used to normalize each subject's MRI to MNI (Montreal Neurological institute) (Collins et al., 1994) coordinates to visualize the reconstructed dipoles using Paraview (https://www.paraview.org/). As the transformation is non‐linear, it is not immediately clear how to transform the orientations sensibly. For each orientation at position we opted to warp both the points and with a small . The orientation in MNI space is then the difference vector between the two transformed points. For each forward model and dipole scan approach an averaged position and orientation are calculated. Ellipsoids mark for each spatial direction the standard deviation of the reconstructed dipoles across the n = 19 subjects from the study.
2.8. Residual variance and source separability
The central measure for the dipole scan is the residual variance that characterizes the proportion of data that remains unexplained by a dipolar source at location with optimal orientation and strength . First, we examine whether one of the forward methods is better able to explain the measured data than the others. To do so, we perform a repeated measures ANOVA in R (R Core Team, 2013) using the rstatix toolbox. Therein, the main effect of the factor forward method (6C‐HexFEM, 6C‐CutFEM, 3C‐BEM) on the residual variance is evaluated. In case of a significant main effect, paired t‐tests are calculated and corrected for multiple comparisons. Test values, Holm‐corrected p‐values (Holm, 1979) and effect size estimates (Cohen's d) are reported.
Secondly, the source separability of the different lead field matrices is examined. We think of the residual variance as a function over the source space. That function may have an arbitrary shape but will have one global minimum. The source separability now states how clear this minimum is, meaning how quickly the residual variance increases as we move away from the minimum. A steeper increase means that the reconstructed sources can be better distinguished from the sources surrounding them. For each subject, we first look at the 6C‐CutFEM MEG dipole scan results. We extract all possible source locations that are within 20 mm distance. At each of these points , the ratio of the residual variance is calculated from the 6C‐CutFEM lead field matrix. refers to the 6C‐CutFEM solution to (6). This ratio indicates the source separability. The same process is performed for the 6C‐HexFEM and 3C‐BEM lead field matrices as well, yielding three sets of ratios and spatial distances (30,702 total) to the optimal source. We perform an ANCOVA to analyze the main effect of forward method (6C‐HexFEM, 6C‐CutFEM, 3C‐BEM), distance to the minimum, and their interaction on ‐ratio. The ‐ratio is expected to increase with increasing distance. The R function estimate_contrasts from the modelbased toolbox is used to estimate pairwise contrasts (6C‐CutFEM – 3C‐BEM, 6C‐CutFEM – 6C‐HexFEM, 6C‐HexFEM – 3C‐BEM) at 4 bins of source distance levels (5, 10, 15, 20 mm) and Holm adjusted p‐values are calculated at each level while ggplot is used for visualization.
Note that source separability states, given one active source, how confident we are in choosing one location over another in close vicinity. It does not tell us how well we can distinguish two proximate active sources.
2.9. Sensitivity to quasi‐radial sources
Finally, we investigate how the sensitivity to quasi‐radial sources depends on the forward model. We calculate the SNR defined in section 2.6 for the entire source space of each subject for each of the 3 forward modeling approaches. Similar to the source reconstructions before, each subject's source space is then normalized to MNI space and interpolated on the same MNI cortical surface where the average SNR across all 19 subjects is calculated and visualized. The cortical sheet and its inflated representation are taken from the Freesurfer surfrend toolbox (Fischl, 2012).
3. RESULTS
First, we look at the dipole source averages in MNI space depicted in Figure 2. On average, all three methods reconstructed the M20 source well within Brodmann area 3B. The descriptive differences in location and orientation estimates are small across the three methods. On average, 6C‐CutFEM and 6C‐HexFEM localize to nearly the same position and orientation, whereas 3C‐BEM localizes the M20 source about 3 mm more lateral. All methods except the unregularized 3C‐BEM feature a similar average orientation, pointing anterior from the somatosensory to the motor cortex.
Single‐subject differences between the forward models in orientation and location are found in Figure 3. The differences between the 6‐compartment FEM methods are smaller than the differences between any FEM method and 3C‐BEM. Truncation has a limited effect on localization differences but strongly affects the angle differences in 3C‐BEM, corresponding to the averaged reconstructions in MNI space. 6C‐CutFEM and 6C‐HexFEM have a median distance of 0 mm but differ in outlier cases by up to 10 mm. Median differences between 3C‐BEM and 6C‐CutFEM are at 3.5 mm and can reach up to 13 mm. 3‐compartment versus 6‐compartment angles without TSVD‐regularization exceed 45° on average for both 6C‐CutFEM – 3C‐BEM and 6C‐HexFEM – 3C‐BEM, whereas the angles between 6C‐CutFEM and 6C‐HexFEM only average 16°. TSVD‐regularization reduces these angles to an average of 8.1, 13.9, and 13.5° for 6C‐CutFEM – 6C‐HexFEM, 6C‐CutFEM – 3C‐BEM, and 6C‐HexFEM – 3C‐BEM respectively. In outlier cases, the angle between 6C‐CutFEM and 6C‐HexFEM can exceed 23° even when TSVD‐regularization is performed. The average SNR of the quasi‐radial contribution from formula (7) at the reconstructed location was 4.53 for 6C‐HexFEM, 5.12 for 6C‐CutFEM, and 1.32 for 3C‐BEM. Hence, the lead field matrix at the reconstructed location was truncated in only 4 cases for 6C‐HexFEM, 3 for 6C‐CutFEM, whereas the 3C‐BEM lead field matrix was truncated in 12 of the 19 cases.
FIGURE 3.
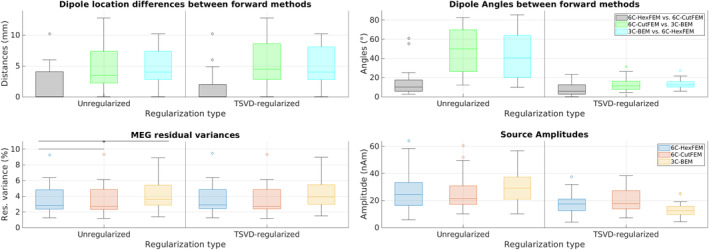
Top row: Pairwise comparison of M20 dipole scan reconstruction location (mm) and orientation (°). In black is the difference between 6C‐HexFEM and 6C‐CutFEM reconstructions, green is 6C‐CutFEM versus 3C‐BEM, and blue is 3C‐BEM versus 6C‐HexFEM. Bottom row: Residual variance (%) and source amplitudes (nAm) of the M20 reconstruction using lead field matrices from different forward models. Asterisk marks significant differences (statistical comparisons were calculated for residual variance in unregularized dipole scans only). 6C‐HexFEM in blue, 6C‐CutFEM in red, and 3C‐BEM in yellow. Outliers are depicted as circles, the horizontal bar inside the boxes state median values. The x‐axis is divided by the regularization schemes. Unregularized on the left and TSVD‐regularization on the right.
We further investigated the differences in residual variance of the dipole scans in Figure 3. For the unregularized dipole scans, the average s for 6C‐HexFEM and 6C‐CutFEM are identical at 3.48% (SD: 2.00% and 3.48% 2.03%), whereas the average for 3C‐BEM is 4.17% 2.05%, a relative increase of over 19%. The repeated measures ANOVA revealed a significant main effect of forward method (F(1.05, 18.84) = 15.102, p = .027, = 0.027). Post‐hoc comparisons show no significant differences between 6C‐CutFEM and 6C‐HexFEM. Comparing 6C‐CutFEM to 3C‐BEM leads to significant differences with a p‐value of .003 and a large effect size of 0.885 measured by Cohen's d. Comparing 6C‐HexFEM and 3C‐BEM also yielded a p‐value of .003 and an effect size of .913.
Regarding source amplitudes, we found that unregularized dipole scans lead to an average source amplitude of 26.1, 24.8 and 25.9 nAm for 6C‐HexFEM, 6C‐CutFEM and 3C‐BEM respectively. TSVD‐regularization leads to the strongest amplitude reductions for 3C‐BEM, on average 50%, followed by 6C‐HexFEM with 32% and 6C‐CutFEM with 20%.
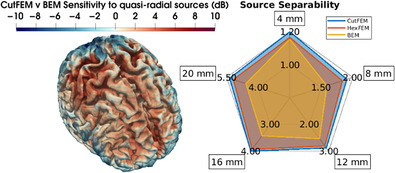
We measure source separability as the increase in residual variance of the unregularized dipole scan with increasing distance to the reconstruction. The ANCOVA analysis showed two significant main and an interaction effect (Forward Model: F(2, 30696) = 132.591, p < .0001, = 0.009; Distance to Minimum: F(2, 30696) = 6141.538, p < .0001, = 0.167; Interaction: F(2, 30696) = 7.742, p = 4.35e‐4, = 0.0005). Figure 4 shows that 6C‐CutFEM has a steeper rising curve than 6C‐HexFEM which increases more steeply than 3C‐BEM. Table 1 shows the differences and their statistical significance at 5, 10, 15, and 20 mm distance to the optimum. At 15 mm, a reconstruction using 6C‐CutFEM has on average a 1.8 times higher increase in residual variance than when using 3C‐BEM and a 1.21 times higher increase compared with 6C‐HexFEM. Notably, using 6C‐CutFEM yields significant differences compared with 3C‐BEM already at a 5 mm distance, where the difference between 6C‐HexFEM and 3C‐BEM is not yet significant.
FIGURE 4.
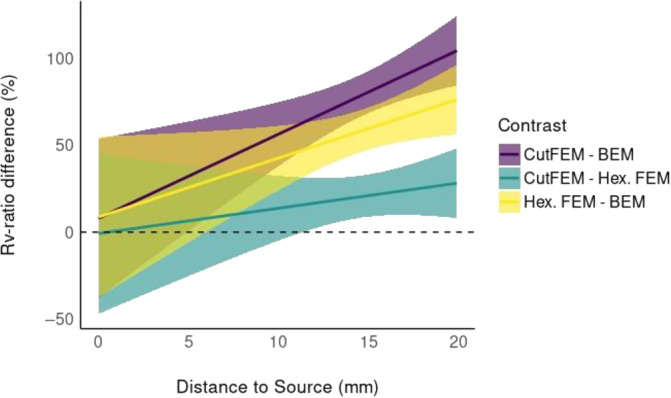
Source Separability: Relative increase in residual variance ratio () with increasing distance (mm) to the minimal . Pairwise contrasts of the three different forward models. Purple: 6C‐CutFEM ‐ratio minus 3C‐BEM ratio. green: 6C‐CutFEM – 6C‐HexFEM. yellow: 6C‐HexFEM – 3C‐BEM. Differences are stated in percent.
TABLE 1.
Source separability: Relative increase in residual variance () ratio with increasing distance (mm) to the minimal source location .
| Contrast | Distance to source (mm) | Difference | p | CI_low | CI_high |
|---|---|---|---|---|---|
| 6C‐CutFEM – 3C‐BEM | 5 | 32.0 | 0.044 | 0.006 | 0.640 |
| 6C‐CutFEM – 3C‐BEM | 10 | 56.1 | <0.001 | 0.376 | 0.746 |
| 6C‐CutFEM – 3C‐BEM | 15 | 80.2 | <0.001 | 0.682 | 0.922 |
| 6C‐CutFEM – 3C‐BEM | 20 | 104.3 | <0.001 | 0.843 | 1.242 |
| 6C‐CutFEM – 6C‐HexFEM | 5 | 6.4 | 0.627 | −0.253 | 0.382 |
| 6C‐CutFEM – 6C‐HexFEM | 10 | 13.7 | 0.079 | −0.050 | 0.323 |
| 6C‐CutFEM – 6C‐HexFEM | 15 | 20.9 | <0.001 | 0.088 | 0.330 |
| 6C‐CutFEM – 6C‐HexFEM | 20 | 28.1 | <0.001 | 0.081 | 0.481 |
| 6C‐HexFEM – 3C‐BEM | 5 | 25.6 | 0.106 | −0.061 | 0.573 |
| 6C‐HexFEM – 3C‐BEM | 10 | 42.4 | <0.001 | 0.238 | 0.610 |
| 6C‐HexFEM – 3C‐BEM | 15 | 59.3 | <0.001 | 0.472 | 0.714 |
| 6C‐HexFEM – 3C‐BEM | 20 | 76.1 | <0.001 | 0.560 | 0.962 |
Note: Pairwise contrasts of the three different forward models. Columns from left to right: Contrast formula (reads Model1 ‘minus’ Model2), distance to the source that minimizes the , Difference between the methods in %, p‐value, and the 95% Confidence Interval for the difference in ‐ratio. Bold p‐values indicate significant (p < .05) differences.
A minimization of the MEG dipole scan using 6C‐CutFEM thus has the clearest minimum and therefore best source separability followed by 6C‐HexFEM and 3C‐BEM.
Finally, we investigated the sensitivity to quasi‐radially oriented sources. In Figure 5, we see that for 6C‐CutFEM the SNR increases as we move further from the gyral crown and deeper into the sulcus. This behavior is consistent over the cortex. For 3C‐BEM, the differences between the gyral crown and sulci are also present but appear more smeared. Additionally, the differences appear to be much more dependent on where in the cortex the source lies, with high SNRs in the frontal and occipital regions and low SNRs in centro‐parietal areas. This behavior is also shown by the difference map (Figure 5, lower row), where we again see that 6C‐CutFEM has lower SNRs on gyral crowns and higher SNR in the cortical folds. The overall average SNR for 6C‐CutFEM is 3.51 dB, and the one for 3C‐BEM is 2.29 dB. 6C‐HexFEM has an average SNR of 3.32 dB. The differences between 6C‐CutFEM and 6C‐HexFEM are small, but 6C‐CutFEM features slightly sharper transitions between gyral crown and sulci. For reference, the SNR of the M20 components is 19.54 3.2SD. In Figure S1, we present maps of lead field matrix condition numbers, that is, the ratios of largest to smallest singular value. Note that in areas where Figure 5 shows increasing SNR with source depth, the condition number decreases.
FIGURE 5.
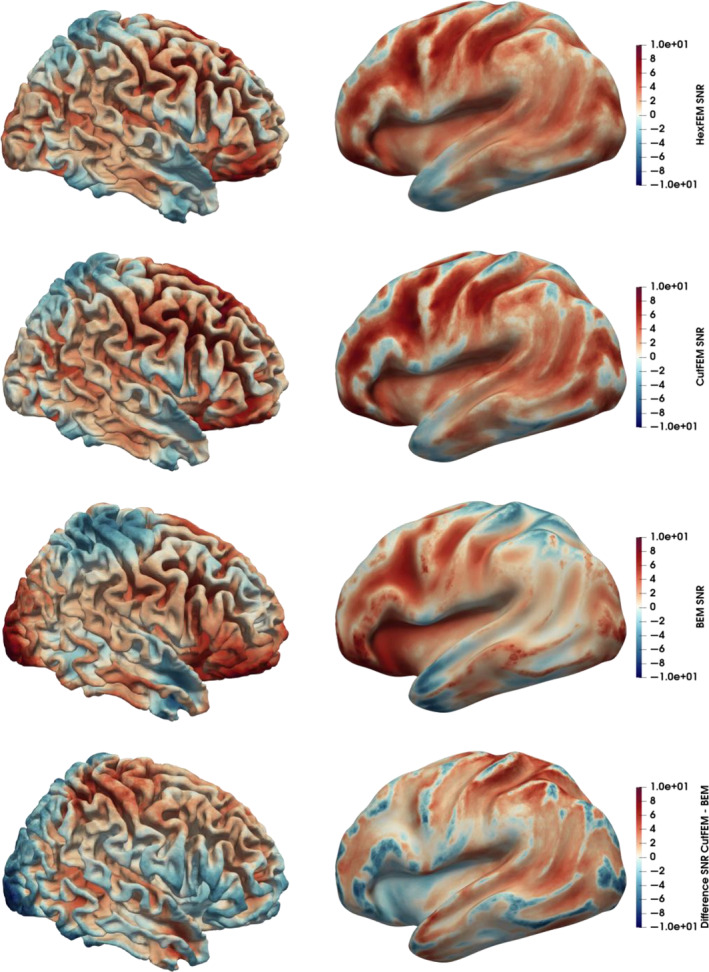
Signal‐to‐noise ratio (SNR) induced by quasi‐radial sources with 4 nAm amplitude. Upper 3 rows: SNR maps for 6C‐HexFEM, 6C‐CutFEM, and 3C‐BEM on MNI normalized cortex and inflated cortex. Bottom row: Difference between 6C‐CutFEM and 3C‐BEM SNR. Scaled from −10 to 10 dB.
4. DISCUSSION
In this work, we introduced CutFEM to MEG forward modeling and compared it with two established forward modeling approaches, a 6‐compartment geometry‐adapted hexahedral FEM (6C‐HexFEM) and a 3‐compartment boundary element method (3C‐BEM). The data for evaluating the new methodology and comparison with standard methods was an n = 19 group study of somatosensory evoked fields induced by electric wrist stimulation. We found that on average all methods localize close to Brodmann area 3b, where the neural generators of the M20 component are located (Nakamura et al., 1998). This desirable outcome states that all three methods lead to roughly similar results. We found that the differences between the two 6C‐FEM methods, in particular the orientations of the reconstructed dipoles, are smaller than compared with 3‐C‐BEM, indicating that the difference between them is a 3‐compartment versus 6‐compartment difference rather than a BEM versus FEM difference, corresponding to the EEG results in Vorwerk et al. (2012), where 3C‐BEM and 3C‐FEM models were examined. However, in individual cases, the difference between the two 6‐compartment‐based reconstructions can reach up to 1 cm in location and 23° in orientation in both regularized and unregularized scenarios, highlighting that the choice of the numerical method and the differences in volume conductors between 6C‐HexFEM and 6C‐CutFEM may also play an important role in source reconstruction. The angle and orientation differences between the 3‐ and 6‐compartment head models we found are in line with previous investigations in Antonakakis et al. (2019), who additionally investigated the use of three different kinds of somatosensory stimulation (pneumato‐tactile, Braille‐tactile and electric‐wrist).
Furthermore, we have gained three main insights from our study. First, using a lead field matrix from the 6‐compartment methods significantly reduced the amount of unexplained data by more than 19%, as measured by the residual variance (Figure 3, lower left panel). Adding more anatomical information to the forward model can thus improve the fit to the measured data. Adding TSVD‐regularization had a limited effect on the observed residual variances, giving a first indication that the better fit may not be due to an overfitting to the noise in the data. However, the residual variance depends on multiple factors, ranging from remaining inaccuracies in our forward model, a discrete source space, electrode positioning, to biological and ambient noise. These uncertainties limit the reliability of exact statements about the expected value of the residual variance.
Second, we investigated the source separability, that is, how steeply the residual variance increases when moving away from the optimal dipole estimate. Here, 6C‐CutFEM outperformed the hexahedral FEM which in turn yielded a steeper curve than 3C‐BEM as shown in Figure 4 and Table 1. Sources localized by 6C‐CutFEM are thus more clearly distinguishable from neighboring sources than for the other two methods, especially 3C‐BEM, increasing source separability. The source separability estimates for our given source how quickly the lead field matrix and consequently the measured MEG data would change if the source were to move by a small distance. If this estimate is too low, then the lead field matrices of all sources in a certain region look more similar than they should in reality. The parts of the measurement corresponding to this lack of distinction may not be explainable by the lead field matrix. This would then lead to a higher residual variance in a dipole scan, giving us a second indication that the better fit to the measured data may not be due to overfitting but rather stems from a more accurate representation of the underlying neural source.
Finally, we compared each method's sensitivity with quasi‐radial sources by calculating a cortical signal‐to‐noise‐ratio (SNR) map based on the SNR definition from Goldenholz et al. (2009) and Piastra et al., 2021. We found that 6C‐CutFEM and 6C‐HexFEM are insensitive to quasi‐radial sources on the gyral crowns but particularly sensitive to sources deeper in the cortical folds. The primary neural generators of EEG and MEG are pyramidal cells in the cortical layer 5, which are aligned normally to the cortical surface (Murakami & Okada, 2006). High SNR values on the crowns would pose the question of why signals from gyral crowns are not seen in actual MEG measurements. Our results are thus in line with the commonly held view that purely quasi‐radial sources cannot be seen in the MEG. However, our findings indicate that sources slightly below the gyral crowns, where the cortical normal is neither purely quasi‐radial nor purely quasi‐tangential, can contribute significantly to the MEG signal. This adds to the result in Piastra et al. (2021), where SNR‐maps were calculated using the cortical normal rather than the smallest singular vector as source orientation. The authors found that using 6‐compartment FEM models rather than 3‐compartment models reduces the areas of the cortex that the MEG is insensitive to, when compared with the complementary EEG modality. In particular, areas near to, but not on gyral crowns are affected. We now state that this is not purely due to quasi‐tangential contributions but also due to higher quasi‐radial influences. Compared with 6C‐HexFEM, 6C‐CutFEM showed slightly smoother transitions in sensitivity when moving from gyral crowns down to the sulci.
The noise levels described here stem from a very controlled scenario with almost 2000 averaged trials per subject. While we have a strong indication that we can analyze the small quasi‐radial contributions to the MEG signal in this test scenario, further investigations will have to show whether this generalizes to lower SNR scenarios. The gradiometers used in this study were set up in a radial manner. Tangential gradiometer positioning can be used to increase the sensitivity of the MEG to quasi‐radial sources (Haueisen et al., 2012).
The motivation behind CutFEM is to create a computational domain as close to the segmentation result as possible. Creating the level set functions in the manner described in the head modeling section highlights the versatility regarding input segmentations. Tissue probability maps, binary segmentations, surface triangulations, or any combination thereof can be transformed into level sets. In particular, it is possible to accurately model the thickness of CSF in areas where it vanishes between the skull and brain. Rice et al. (2013) found that the difference in CSF thickness between prone and supine subject positioning in the MRI was up to 30%. EEG amplitudes differed by up to 80%. However, the impact on MEG measurements is at this point unclear.
In Beumer et al. (2022), a workflow to create personalized transcranial direct current stimulation montages for epilepsy patients is outlined. The stimulation target is based on epileptic spike data measured by EEG and a dipole‐fit was used to determine the location and orientation in the brain. The orientation of the reconstructed dipole is important here as it determines the desired orientation of the electric field applied by the stimulation electrodes (Antonakakis et al., 2024; Dmochowski et al., 2011; Khan et al., 2022). The EEG has in theory no sensitivity bias towards any source direction. In practice however, superficial quasi‐radial sources from the gyral crowns may produce stronger signals. The forward simulated signals are also more strongly affected by skull and scalp modeling (Antonakakis et al., 2020). The decision which modality to chose for the definition of a stimulation target can therefore not be generalized. Furthermore, Iwasaki et al. (2005) and Knake et al. (2006) found that 18% and 13% of epileptic patients showed interictal epileptiform activity in MEG but not in EEG. For such patients an MEG‐based target definition may have to be performed, highlighting the importance of reliable orientation estimation and the differences found in our investigations.
In Ahlfors et al. (2010), the average ratio of smallest to largest singular value, the inverse of the condition we describe in Figure S1, was determined to be 0.06 for a 3C‐BEM model, corresponding to the across subject average of 0.0591 for 3C‐BEM we found in this study. The average 6C‐CutFEM ratio is 21 percent higher at 0.072 and 6C‐HexFEM is on average at 0.071. This implies that relative to the dominant quasi‐tangential orientation, the FEM approaches model quasi‐radial sources as slightly stronger.
Overall, our results agree with the commonly held view that the MEG is primarily sensitive to quasi‐tangential source orientations. As only small areas of the cortex generate purely quasi‐radial sources, source depth remains the most relevant factor determining measurability. However, realistic models and their higher sensitivity to sources with quasi‐radial contributions may allow us to better estimate MEG activity in deeper regions towards the fundus of the sulci and also to better define stimulation targets for non‐invasive brain stimulation (Antonakakis et al., 2024; Khan et al., 2022), especially in the absence of EEG measurements. Also for the large number of potential applications of personalized transcranial electric stimulation (Radecke et al., 2023), an accurate orientation estimate using MEG with 6C‐CutFEM might add to the available methodological options (Buschermöhle et al., 2024). In any case, location differences of ~1 cm, orientation differences of over 20° and a significantly lower residual variance are sufficient to justify the additional computational load of finite element approaches.
Future examinations will show whether the quasi‐radial contributions can be properly reconstructed when using less restrictive regularization methods such as Tikhonov‐regularization (Tikhonov & Arsenin, 1977). A benchmark could be the orientation reconstructed from simultaneous EEG measurements. Additionally, our results focus on evoked fields in the somatosensory cortex. Further evaluations of the contribution of 6C‐CutFEM to for example auditory (AEF) or visually evoked fields (VEF) or clinical applications such as presurgical epilepsy diagnosis could be the topic of future research. A CutFEM‐based EEG lead field matrix can already be calculated rapidly, but additional work on the numerical solver is needed to achieve faster computation times in the MEG case.
5. CONCLUSION
In this article, we introduced CutFEM, an unfitted finite element method, to MEG source analysis. After a short overview of the method that has previously been proposed, validated and evaluated for EEG (Erdbrügger et al., 2023), we compared it for MEG with two established forward modeling approaches, a 6‐compartment geometry adapted hexahedral FEM and a 3‐compartment boundary element method. We compared the lead field matrices of n = 19 subjects and analyzed their M20 somatosensory evoked response to an electric wrist stimulation of the median nerve. We found that using CutFEM yields source reconstructions that can differ from reconstructions calculated with a 3‐compartment BEM or a 6‐compartment hexahedral FEM by up to 1 cm in location and more than 20° in orientation. CutFEM also improves source separability, goodness of fit to the measured data, and sensitivity to cortical sources that are (predominantly) radial.
Our results highlight the importance of creating individualized high‐quality head models for MEG source analysis, both in integrating realistic tissue compartments and using sophisticated numerical schemes. All investigations were carried out over a group of 19 subjects, increasing the stability of the findings.
AUTHOR CONTRIBUTIONS
Conceptualization: C. Engwer, T. Erdbruegger, C.H. Wolters. Methodology: C. Engwer, T. Erdbruegger, C.H. Wolters. Software: C. Engwer, T. Erdbruegger. Investigation: T. Erdbruegger. Writing – original draft: T. Erdbruegger. Writing – review and editing: Y. Buschermoehle, C. Engwer, T. Erdbruegger, J. Gross, M. Hoeltershinken, R. Lencer, S. Pursiainen, J.O. Radecke, C.H. Wolters. Supervision: C. Engwer, C.H. Wolters. Funding acquisition: J. Gross, R. Lencer, S. Pursiainen, F. Wallois, C.H. Wolters.
CONFLICT OF INTEREST STATEMENT
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Supporting information
Data S1. Supporting information.
ACKNOWLEDGMENTS
This study was supported by the Deutsche Forschungsgemeinschaft (DFG), projects WO1425/10‐1, GR2024/8‐1, LE1122/7‐1. CE was supported by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany's Excellence Strategy EXC 2044‐390685587, Mathematics Münster: Dynamics‐Geometry‐Structure and by ERA PerMed as project ERAPERMED2020‐227 PerEpi (Bundesministerium für Gesundheit, project ZMI1‐2521FSB006; Academy of Finland, project 344712; Bundesministerium für Bildung und Forschung, project FKZ 01KU2101; French National Research Agency, project RPV21010EEA).TE, MH, CW, and SP were additionally supported by the DAAD/AoF researcher mobility project (DAAD project 57663920, AoF decision 354976) and SP by the AoF Centre of Excellence (CoE) in Inverse Modelling and Imaging 2018–2025 (AoF decision 353089). We acknowledge support from the Open Access Publication Fund of the University of Muenster. Open Access funding enabled and organized by Projekt DEAL.
Erdbrügger, T. , Höltershinken, M. , Radecke, J.‐O. , Buschermöhle, Y. , Wallois, F. , Pursiainen, S. , Gross, J. , Lencer, R. , Engwer, C. , & Wolters, C. (2024). CutFEM‐based MEG forward modeling improves source separability and sensitivity to quasi‐radial sources: A somatosensory group study. Human Brain Mapping, 45(11), e26810. 10.1002/hbm.26810
DATA AVAILABILITY STATEMENT
The software in which the new methodology was implemented can be found under https://www.medizin.uni-muenster.de/duneuro, an example data set can be found under https://zenodo.org/record/3888381#.Yf0tT_so9H4. The data that support the findings of this study are available from the corresponding author upon reasonable request.
REFERENCES
- Ahlfors, S. P. , Han, J. , Belliveau, J. W. , & Hämäläinen, M. S. (2010). Sensitivity of meg and eeg to source orientation. Brain Topography, 23, 227–232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Allison, T. , Wood, C. C. , McCARTHY, G. , & Spencer, D. D. (1991). Cortical somatosensory evoked potentials. II. Effects of excision of somatosensory or motor cortex in humans and monkeys. Journal of Neurophysiology, 66(1), 64–82. [DOI] [PubMed] [Google Scholar]
- Antonakakis, M. , Kaiser, F. , Rampp, S. , Kovac, S. , Wiendl, H. , Stummer, W. , Gross, J. , Kellinghaus, C. , Khaleghi‐Ghadiri, M. , Möddel, G. , & Wolters, C. H. (2024). Targeted and optimized multi‐channel transcranial direct current stimulation for focal epilepsy: An n‐of‐1 trial. Brain Stimulation, 17(2), 221–223. 10.1016/j.brs.2024.02.010 [DOI] [PubMed] [Google Scholar]
- Antonakakis, M. , Schrader, S. , Aydin, Ü. , Khan, A. , Gross, J. , Zervakis, M. , Rampp, S. , & Wolters, C. H. (2020). Inter‐subject variability of skull conductivity and thickness in calibrated realistic head models. NeuroImage, 223, 117353. [DOI] [PubMed] [Google Scholar]
- Antonakakis, M. , Schrader, S. , Wollbrink, A. , Oostenveld, R. , Rampp, S. , Haueisen, J. , & Wolters, C. H. (2019). The effect of stimulation type, head modeling, and combined eeg and meg on the source reconstruction of the somatosensory p20/n20 component. Human Brain Mapping, 40(17), 5011–5028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baysal, U. , & Haueisen, J. (2004). Use of a priori information in estimating tissue resistivities—Application to human data in vivo. Physiological Measurement, 25(3), 737–748. [DOI] [PubMed] [Google Scholar]
- Beltrachini, L. (2018). Sensitivity of the projected subtraction approach to mesh degeneracies and its impact on the forward problem in eeg. IEEE Transactions on Biomedical Engineering, 66(1), 273–282. [DOI] [PubMed] [Google Scholar]
- Beumer, S. , Boon, P. , Klooster, D. C. W. , van Ee, R. , Carrette, E. , Paulides, M. M. , & Mestrom, R. M. C. (2022). Personalized tdcs for focal epilepsy—a narrative review: A data‐driven workflow based on imaging and eeg data. Brain Sciences, 12, 610. 10.3390/brainsci12050610 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buchner, H. , Fuchs, M. , Wischmann, H. A. , Dössel, O. , Ludwig, I. , Knepper, A. , & Berg, P. (1994). Source analysis of median nerve and finger stimulated somatosensory evoked potentials: Multichannel simultaneous recording of electric and magnetic fields combined with 3d‐mr tomography. Brain Topography, 6(4), 299–310. 10.1007/BF01211175 [DOI] [PubMed] [Google Scholar]
- Buchner, H. , Knoll, G. , Fuchs, M. , Rienäcker, A. , Beckmann, R. , Wagner, M. , Silny, J. , & Pesch, J. (1997). Inverse localization of electric dipole current sources in finite element models of the human head. Electroencephalography and Clinical Neurophysiology, 102(4), 267–278. [DOI] [PubMed] [Google Scholar]
- Burman, E. (2010). Ghost penalty. Comptes Rendus Mathematique, 348(21–22), 1217–1220. [Google Scholar]
- Burman, E. , & Hansbo, P. (2012). Fictitious domain finite element methods using cut elements: II. A stabilized nitsche method. Applied Numerical Mathematics, 62(4), 328–341. 10.1016/j.apnum.2011.01.008 [DOI] [Google Scholar]
- Burman, E. , Claus, S. , Hansbo, P. , Larson, M. G. , & Massing, A. (2015). Cutfem: Discretizing geometry and partial differential equations. International Journal for Numerical Methods in Engineering, 104(7), 472–501. [Google Scholar]
- Buschermöhle, Y. , Höltershinken, M. B. , Erdbrügger, T. , Radecke, J.‐O. , Sprenger, A. , Schneider, T. R. , Lencer, R. , Gross, J. , & Wolters, C. H. (2024). Comparing the performance of beamformer algorithms in estimating or ientations of neural sources. iScience, 27(3), 109150. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Collins, D. L. , Neelin, P. , Peters, T. M. , & Evans, A. C. (1994). Automatic 3D intersubject registration of MR volumetric data in standardized Talairach space. Journal of Computer Assisted Tomography, 18(2), 192–205. [PubMed] [Google Scholar]
- Cruccu, G. , Aminoff, M. J. , Curio, G. , Guerit, J. M. , Kakigi, R. , Mauguiere, F. , Rossini, P. M. , Treede, R.‐D. , & Garcia‐Larrea, L. (2008). Recommendations for the clinical use of somatosensory‐evoked potentials. Clinical Neurophysiology, 119(8), 1705–1719. 10.1016/j.clinph.2008.03.016 [DOI] [PubMed] [Google Scholar]
- Cuartas Morales, E. , Acosta‐Medina, C. D. , Castellanos‐Dominguez, G. , & Mantini, D. (2019). A finite‐difference solution for the eeg forward problem in inhomogeneous anisotropic media. Brain Topography, 32(2), 229–239. 10.1007/s10548-018-0683-2 [DOI] [PubMed] [Google Scholar]
- Di Pietro, D. , & Ern, A. (2012). Mathematical aspects of discontinuous Galerkin methods (Vol. 69). Springer. [Google Scholar]
- Dmochowski, J. P. , Datta, A. , Bikson, M. , Su, Y. , & Parra, L. C. (2011). Optimized multi‐electrode stimulation increases focality and intensity at target. Journal of Neural Engineering, 8(4), 046011. [DOI] [PubMed] [Google Scholar]
- Eaton, H. (1992). Electric field induced in a spherical volume conductor from arbitrary coils: Application to magnetic stimulation and meg. Medical and Biological Engineering and Computing, 30, 433–440. [DOI] [PubMed] [Google Scholar]
- Engwer, C. , & Nüßing, A. (2017). Geometric reconstruction of implicitly defined surfaces and domains with topological guarantees. ACM Transactions on Mathematical Software (TOMS), 44(2), 1–20. [Google Scholar]
- Erdbrügger, T. , Westhoff, A. , Höltershinken, M. , Radecke, J.‐O. , Buschermöhle, Y. , Buyx, A. , Wallois, F. , Pursiainen, S. , Gross, J. , & Lencer, R. (2023). Cutfem forward modeling for eeg source analysis. Frontiers in Human Neuroscience, 17, 1216758. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fischl, B. (2012). FreeSurfer. NeuroImage, 62(2), 774–781. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fuchs, M. , Wagner, M. , Wischmann, H.‐A. , Köhler, T. , Theißen, A. , Drenckhahn, R. , & Buchner, H. (1998). Improving source reconstructions by combining bioelectric and biomagnetic data. Electroencephalography and Clinical Neurophysiology, 107(2), 93–111. [DOI] [PubMed] [Google Scholar]
- Gaser, C. , Dahnke, R. , Thompson, P. M. , Kurth, F. , Luders, E. , & Alzheimer's Disease Neuroimaging Initiative . (2022). Cat–a computational anatomy toolbox for the analysis of structural MRI data. biorxiv, 2022–06. [DOI] [PMC free article] [PubMed]
- Goldenholz, D. M. , Ahlfors, S. P. , Hämäläinen, M. S. , Sharon, D. , Ishitobi, M. , Vaina, L. M. , & Stufflebeam, S. M. (2009). Mapping the signal‐to‐noise‐ratios of cortical sources in magnetoencephalography and electroencephalography. Human brain mapping, 30(4), 1077–1086. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gramfort, A. , Papadopoulo, T. , Olivi, E. , & Clerc, M. (2010). Openmeeg: Opensource software for quasistatic bioelectromagnetics. Biomedical Engineering Online, 9, 1–20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hallez, H. , Vanrumste, B. , van Hese, P. , D'Asseler, Y. , Lemahieu, I. , & van de Walle, R. (2005). A finite difference method with reciprocity used to incorporate anisotropy in electroencephalogram dipole source localization. Physics in Medicine & Biology, 50(16), 3787–3806. [DOI] [PubMed] [Google Scholar]
- Haueisen, J. , Fleissig, K. , Strohmeier, D. , Elsarnagawy, T. , Huonker, R. , Liehr, M. , & Witte, O. W. (2012). Reconstruction of quasi‐radial dipolar activity using three‐component magnetic field measurements. Clinical Neurophysiology: Official Journal of the International Federation of Clinical Neurophysiology, 123(8), 1581–1585. 10.1016/j.clinph.2011.12.020 [DOI] [PubMed] [Google Scholar]
- He, Q. , Rezaei, A. , & Pursiainen, S. (2020). Zeffiro user interface for electromagnetic brain imaging: A gpu accelerated fem tool for forward and inverse computations in matlab. Neuroinformatics, 18(2), 237–250. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holm, S. (1979). A simple sequentially rejective multiple test procedure. Scandinavian Journal of Statistics, 6(2), 65–70. [Google Scholar]
- Iwasaki, M. , Pestana, E. , Burgess, R. C. , Lüders, H. O. , Shamoto, H. , & Nakasato, N. (2005). Detection of epileptiform activity by human interpreters: Blinded comparison between electroencephalography and magnetoencephalography. Epilepsia, 46(1), 59–68. [DOI] [PubMed] [Google Scholar]
- Jenkinson, M. , Bannister, P. , Brady, M. , & Smith, S. (2002). Improved optimization for the robust and accurate linear registration and motion correction of brain images. NeuroImage, 17(2), 825–841. [DOI] [PubMed] [Google Scholar]
- Johansson, F. , & Mezzarobba, M. (2018). Fast and rigorous arbitrary‐precision computation of gauss–legendre quadrature nodes and weights. SIAM Journal on Scientific Computing, 40(6), C726–C747. 10.1137/18M1170133 [DOI] [Google Scholar]
- Khan, A. , Antonakakis, M. , Vogenauer, N. , Haueisen, J. , & Wolters, C. H. (2022). Individually optimized multi‐channel tdcs for targeting somatosensory cortex. Clinical Neurophysiology, 134, 9–26. [DOI] [PubMed] [Google Scholar]
- Knake, S. , Halgren, E. , Shiraishi, H. , Hara, K. , Hamer, H. M. , Grant, P. E. , Carr, V. A. , Foxe, D. , Camposano, S. , & Busa, E. (2006). The value of multichannel meg and eeg in the presurgical evaluation of 70 epilepsy patients. Epilepsy Research, 69(1), 80–86. [DOI] [PubMed] [Google Scholar]
- Lanfer, B. , Scherg, M. , Dannhauer, M. , Knösche, T. R. , Burger, M. , & Wolters, C. H. (2012). Influences of skull segmentation inaccuracies on eeg source analysis. NeuroImage, 62(1), 418–431. [DOI] [PubMed] [Google Scholar]
- Makarov, S. N. , Hämäläinen, M. , Okada, Y. , Noetscher, G. M. , Ahveninen, J. , & Nummenmaa, A. (2020). Boundary element fast multipole method for enhanced modeling of neurophysiological recordings. IEEE Transactions on Biomedical Engineering, 68(1), 308–318. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Medani, T. , Garcia‐Prieto, J. , Tadel, F. , Antonakakis, M. , Erdbrügger, T. , Höltershinken, M. , Mead, W. , Schrader, S. , Joshi, A. , Engwer, C. , Wolters, C. H. , Mosher, J. C. , & Leahy, R. M. (2023). Brainstorm‐duneuro: An integrated and user‐friendly finite element method for modeling electromagnetic brain activity. NeuroImage, 267, 119851. 10.1016/j.neuroimage.2022.119851 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Medani, T. , Lautru, D. , Schwartz, D. , Ren, Z. , & Sou, G. (2015). Fem method for the eeg forward problem and improvement based on modification of the saint venant's method. Progress in Electromagnetics Research, 153, 11–22. [Google Scholar]
- Mosher, J. C. , Leahy, R. M. , & Lewis, P. S. (1999). Eeg and meg: Forward solutions for inverse methods. IEEE Transactions on Biomedical Engineering, 46(3), 245–259. [DOI] [PubMed] [Google Scholar]
- Murakami, S. , & Okada, Y. (2006). Contributions of principal neocortical neurons to magnetoencephalography and electroencephalography signals. The Journal of Physiology, 575(3), 925–936. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nakamura, A. , Yamada, T. , Goto, A. , Kato, T. , Ito, K. , Abe, Y. , Kachi, T. , & Kakigi, R. (1998). Somatosensory homunculus as drawn by meg. NeuroImage, 7(4), 377–386. [DOI] [PubMed] [Google Scholar]
- Nielsen, J. D. , Madsen, K. H. , Puonti, O. , Siebner, H. R. , Bauer, C. , Madsen, C. G. , Saturnino, G. B. , & Thielscher, A. (2018). Automatic skull segmentation from mr images for realistic volume conductor models of the head: Assessment of the state‐of‐the‐art. NeuroImage, 174, 587–598. [DOI] [PubMed] [Google Scholar]
- Nitsche, J. (1971). Über ein variationsprinzip zur lösung von dirichlet‐problemen bei verwendung von teilräumen, die keinen randbedingungen unterworfen sind.
- Nüßing, A. (2018). Fitted and unfitted finite element methods for solving the EEG forward problem. Universitäts‐und Landesbibliothek Münster. [Google Scholar]
- Nüßing, A. , Wolters, C. H. , Brinck, H. , & Engwer, C. (2016). The unfitted discontinuous galerkin method for solving the eeg forward problem. IEEE Transactions on Biomedical Engineering, 63(12), 2564–2575. [DOI] [PubMed] [Google Scholar]
- Oostenveld, R. , Fries, P. , Maris, E. , & Schoffelen, J.‐M. (2011). Fieldtrip: Open source software for advanced analysis of meg, eeg, and invasive electrophysiological data. Computational Intelligence and Neuroscience, 2011, 1–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Otsu, N. (1979). A threshold selection method from gray‐level histograms. IEEE Transactions on Systems, Man, and Cybernetics, 9(1), 62–66. [Google Scholar]
- Perona, P. , & Malik, J. (1990). Scale‐space and edge detection using anisotropic diffusion. IEEE Transactions on Pattern Analysis and Machine Intelligence, 12(7), 629–639. [Google Scholar]
- Piastra, M. C. , Nüßing, A. , Vorwerk, J. , Clerc, M. , Engwer, C. , & Wolters, C. H. (2021). A comprehensive study on electroencephalography and magnetoencephalography sensitivity to cortical and subcortical sources. Human Brain Mapping, 42(4), 978–992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Puonti, O. , van Leemput, K. , Saturnino, G. B. , Siebner, H. R. , Madsen, K. H. , & Thielscher, A. (2020). Accurate and robust whole‐head segmentation from magnetic resonance images for individualized head modeling. NeuroImage, 219, 117044. 10.1016/j.neuroimage.2020.117044 [DOI] [PMC free article] [PubMed] [Google Scholar]
- R Core Team 2013: R: A language and environment for statistical computing. http://www.R-project.org/ [Google Scholar]
- Radecke, J.‐O. , Fiene, M. , Misselhorn, J. , Herrmann, C. S. , Engel, A. K. , Wolters, C. H. , & Schneider, T. R. (2023). Personalized alpha‐tacs targeting left posterior parietal cortex modulates visuo‐spatial attention and posterior evoked eeg activity. Brain Stimulation, 16, 1047–1061. [DOI] [PubMed] [Google Scholar]
- Rice, J. K. , Rorden, C. , Little, J. S. , & Parra, L. C. (2013). Subject position affects eeg magnitudes. NeuroImage, 64, 476–484. 10.1016/j.neuroimage.2012.09.041 [DOI] [PubMed] [Google Scholar]
- Sarnthein, J. , Seidel, K. , Neidert, M. C. , Raabe, A. , Sala, F. , Tonn, J. C. , Thon, N. , & Szelenyi, A. (2022). Evaluation of a new cortical strip electrode for intraoperative somatosensory monitoring during perirolandic brain surgery. Clinical Neurophysiology, 142, 44–51. 10.1016/j.clinph.2022.07.497 [DOI] [PubMed] [Google Scholar]
- Sarvas, J. (1987). Basic mathematical and electromagnetic concepts of the biomagnetic inverse problem. Physics in Medicine & Biology, 32(1), 11–22. [DOI] [PubMed] [Google Scholar]
- Schimpf, P. H. , Ramon, C. , & Haueisen, J. (2002). Dipole models for the eeg and meg. IEEE Transactions on Biomedical Engineering, 49(5), 409–418. [DOI] [PubMed] [Google Scholar]
- Schrader, S. , Westhoff, A. , Piastra, M. C. , Miinalainen, T. , Pursiainen, S. , Vorwerk, J. , Brinck, H. , Wolters, C. H. , & Engwer, C. (2021). Duneuro—A software toolbox for forward modeling in bioelectromagnetism. PLoS One, 16(6), e0252431. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stenroos, M. , Hunold, A. , & Haueisen, J. (2014). Comparison of three‐shell and simplified volume conductor models in magnetoencephalography. NeuroImage, 94, 337–348. 10.1016/j.neuroimage.2014.01.006 [DOI] [PubMed] [Google Scholar]
- Tikhonov, A. N. , & Arsenin, V. (1977). Solutions of ill‐posed problems. (No Title).
- Vallaghé, S. , & Papadopoulo, T. (2010). A trilinear immersed finite element method for solving the eeg forward problem. SIAM J. Sci. Comp., accepted for publication .
- van den Broek, S. P. , Reinders, F. , Donderwinkel, M. , & Peters, M. J. (1998). Volume conduction effects in eeg and meg. Electroencephalography and Clinical Neurophysiology, 106(6), 522–534. [DOI] [PubMed] [Google Scholar]
- van Uitert, R. , Johnson, C. , & Zhukov, L. (2004). Influence of head tissue conductivity in forward and inverse magnetoencephalographic simulations using realistic head models. IEEE Transactions on Biomedical Engineering, 51(12), 2129–2137. [DOI] [PubMed] [Google Scholar]
- Vermaas, M. , Piastra, M. C. , Oostendorp, T. F. , Ramsey, N. F. , & Tiesinga, P. H. E. (2020). Femfuns: A volume conduction modeling pipeline that includes resistive, capacitive or dispersive tissue and electrodes. Neuroinformatics, 18(4), 569–580. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vorwerk, J. , Cho, J.‐H. , Rampp, S. , Hamer, H. , Knösche, T. R. , & Wolters, C. H. (2014). A guideline for head volume conductor modeling in eeg and meg. NeuroImage, 100, 590–607. [DOI] [PubMed] [Google Scholar]
- Vorwerk, J. , Clerc, M. , Burger, M. , & Wolters, C. H. (2012). Comparison of boundary element and finite element approaches to the EEG forward problem. Biomedizinische Technik. Biomedical engineering, 57, 795–798. [DOI] [PubMed] [Google Scholar]
- Vorwerk, J. , Hanrath, A. , Wolters, C. H. , & Grasedyck, L. (2019). The multipole approach for eeg forward modeling using the finite element method. NeuroImage, 201, 116039. [DOI] [PubMed] [Google Scholar]
- Windhoff, M. , Opitz, A. , & Thielscher, A. (2013). Electric field calculations in brain stimulation based on finite elements: An optimized processing pipeline for the generation and usage of accurate individual head models. Human Brain Mapping, 34(4), 923–935. 10.1002/hbm.21479 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wolters, C. H. , Anwander, A. , Berti, G. , & Hartmann, U. (2007). Geometry‐adapted hexahedral meshes improve accuracy of finite‐element‐method‐based eeg source analysis. IEEE Transactions on Biomedical Engineering, 54(8), 1446–1453. [DOI] [PubMed] [Google Scholar]
- Wolters, C. H. , Beckmann, R. F. , Rienäcker, A. , & Buchner, H. (1999). Comparing regularized and non‐regularized nonlinear dipole fit methods: A study in a simulated sulcus structure. Brain Topography, 12, 3–18. [DOI] [PubMed] [Google Scholar]
- Wolters, C. , Grasedyck, L. , & Hackbusch, W. (2004). Efficient computation of lead field bases and influence matrix for the fem‐based eeg and meg inverse problem. Inverse Problems, 20, 1099–1116. 10.1088/0266-5611/20/4/007 [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data S1. Supporting information.
Data Availability Statement
The software in which the new methodology was implemented can be found under https://www.medizin.uni-muenster.de/duneuro, an example data set can be found under https://zenodo.org/record/3888381#.Yf0tT_so9H4. The data that support the findings of this study are available from the corresponding author upon reasonable request.


