Influence of rapid heat treatment on the photocatalytic activity and stability of calcium titanates against a broad range of pollutants

Abstract

Calcium titanate (CTO) photocatalysts were synthesized using a sol–gel method by adopting a cost-efficient, rapid calcination technique. The CTOs were characterized by X-ray diffractometry, X-ray photoelectron spectroscopy, infrared spectroscopy, nitrogen adsorption, porosimetry measurements, scanning/transmission electron microscopy, and diffuse reflectance spectroscopy. Their photocatalytic activity was assessed through the photocatalytic degradation of phenol, oxalic acid, and chlorophenol under UV light exposure, using a commercial CTO as a reference. The stability of the samples was evaluated using compounds with –OH, –COOH, and –Cl functional groups. Characterization results showed that CTO composites containing anatase, rutile, and brookite titania were obtained. Increasing the calcination temperature led to various crystalline compositions, higher crystallinity, larger primary crystallite sizes, and smaller specific surface areas. The photocatalytic activity of all CTO/TiO₂ composites was superior compared to the commercial CTO we used as a reference. The high photocatalytic activity of the best-performing composites was attributed to their higher specific surface areas and the synergistic effect between the crystal phases. A cost comparison was also made between our unique calcination technique and conventional calcination, and it was found that our method is approximately 35% more cost-effective, while retaining the photocatalytic activity.

Graphical abstract

Highlights

• •Rapid calcined samples had better photoactivity and were more cost-efficient.
• •CaTiO₃/TiO₂ composites were obtained containing mixed-phase TiO₂ constituents.
• •Enhanced photoactivity was attributed to better charge separation and surface area.
• •Stability was evaluated against compounds with –OH, –COOH, –X, and –CHO groups.

1. Introduction

Photocatalysis is recognized as an eco-friendly and sustainable approach to tackle the dual challenges of energy scarcity and environmental pollution [1,2]. In particular, calcium titanate (CTO), a multi-metal oxide, has garnered significant interest in recent times. This is primarily due to its distinctive structural characteristics and flexibility in its structural transformations [3,4], exceptional chemical stability, high dielectric constant, affordability, minimal toxicity, and straightforward synthesis [[5], [6], [7], [8]]. A key factor influencing the effectiveness of CTOs is their crystal structure [9,10] which is intricately associated with the chemical composition [11] and the synthesis method employed [6,12] especially the heat treatment process [13].

The chosen synthesis route for CTOs often plays a critical role in shaping their structure, composition, and performance as a photocatalyst [6]. Sol–gel processes provide control over stoichiometry and homogeneity, resulting in well-defined crystalline structures [14]. This method is a widely adopted technique in the preparation of perovskites [[15], [16], [17]]. However, sol–gel techniques require an expensive, high-temperature calcination process to obtain crystalline materials [18]. The temperature of calcination significantly impacts the characteristics of photocatalysts, influencing the photocatalytic activity due to specific surface area changes [19], optical changes [20], morphology changes [21], crystalline composition changes [22], and surface changes [23,24]. Heating rate and calcination time are also important parameters that are only rarely investigated. For example, Joung et al. reported that N-doped TiO₂ samples prepared at shorter calcination times were more efficient for the degradation of trichloroethylene under visible light irradiation [25]. In another work, Beydoun et al. used Fe₃O₄–TiO₂ catalysts and found that increasing the calcination time past 20 min did not increase the photocatalytic activity for sucrose decomposition under UV light [26]. Moreover, applying shorter calcination times is also important in terms of the preparation costs of photocatalysts. Ryu et al. found that Degussa P25 TiO₂ prepared by flame hydrolysis (which involves a near-instantaneous crystallization step [27]) was the most cost-effective for the degradation of various organic pollutants [28]. Last, there are some publications that investigate the effect of calcination on the characteristics of CTO; however, these papers focus only on the dependence of calcination temperature on material characteristics such as crystal phase composition, particle size, specific surface area, and pore volume [[29], [30], [31], [32]]. To our knowledge, the effect of calcination time on the photocatalytic properties of CTO has not been investigated so far. Understanding these aspects is of paramount importance when developing CTOs to address various environmental remediation needs and enhancing their efficiency in photocatalytic applications.

In most cases, researchers focus on achieving the highest possible photocatalytic activity. However, high photocatalytic activity must be combined with reasonable stability for a catalyst to be applicable in practice [33]. To our knowledge, the stability of CTOs against compounds with various functional groups has not been investigated so far.

This study investigates the effect of rapid calcination on the properties of CTOs. Another novelty of this work is that it uses compounds with various functional groups (phenolic –OH, –COOH, –Cl) to evaluate photoactivity; in most cases, dyes are used for this purpose. These compounds are used to evaluate their stability as well. Last, the economic benefits of the rapid calcination method are also considered.

2. Experimental

2.1. Materials

Calcium nitrate (Sigma-Aldrich, 99 %), and titanium(IV) butoxide (Sigma-Aldrich, reagent grade, ≥97 %) were used as CTO precursors. Absolute ethanol (VWR Chemicals, Reag. Ph. Eur) was used as a solvent. As a chelating agent, oxalic acid (Sigma-Aldrich, ≥99 %) was applied. Oxalic acid (VWR Chemicals, Reag. Ph. Eur.), phenol (Spektrum 3D, analytical grade), and chlorophenol (Sigma-Aldrich, ≥97 %) were used for evaluating photoactivity and stability.

2.2. Synthesis

The sol–gel method of Hosseini et al. [12] was used to synthesize our samples. First, 4.43 g (0.02 mol) of calcium nitrate was added to 24 mL of ethanol, which was followed by the addition of 5.67 g of oxalic acid at 50 °C during continuous stirring. At the same time, 6.8 mL (0.02 mol) of titanium(IV) butoxide was added to 20 mL of ethanol in a separate beaker. Second, the contents of the latter beaker were added dropwise to the former one. The mixture was placed on a magnetic stirrer, which was then gradually heated from 50 °C to 70 °C for 4 h, then kept at 70 °C for 18 h. Last, we collected the amorphous powder and ground the xerogel in an agate mortar.

The amorphous powder resulting from the sol–gel procedure was exposed to a heat treatment process in a ceramic vessel in a tube furnace (Thermolyne 21100; l_furnace = 38 cm, l_{quartz tube} = 64 cm, d_{quartz tube, exterior} = 5.5 cm, d_{quartz tube, interior} = 4 cm). Throughout the calcination, a continuous supply of air (0.5 L∙min⁻¹) was maintained. A unique calcination technique named “rapid heating–short exposure” (RHSE) was used in accordance with the publication of Pap et al. [23]. For this purpose, a high initial heating rate of 60 °C min⁻¹ was used, which was then lowered to 20 and 10 °C min⁻¹ as we reached T_target–200 °C and T_target–100 °C, respectively. The photocatalysts then were kept at the target temperature for 5 min. After the calcination, the samples were ground in an agate mortar.

The samples were named „CTO_RHSE_X”, where „X” corresponds to the temperature used during calcination.

2.3. Characterization methods and instrumentation

X-ray diffraction (XRD) measurements were conducted using a Rigaku Miniflex II diffractometer with the following parameters: λ_{Cu Kα} = 0.15406 nm, 30 mA, 40 kV, 20–80 (2θ°) region. The crystalline compositions were calculated using the peak areas of the most intense diffraction peaks. For morphology assessment, scanning electron microscopy (SEM) and transmission electron microscopy (TEM) images were taken using a Hitachi S-4700 Type II microscope at an acceleration voltage of 10 kV and a FEI Tecnai G2 20 high-resolution microscope at an acceleration voltage of 200 kV, respectively. Specific surface area and porosity measurements were carried out via conducting nitrogen adsorption–desorption measurements with a NOVA 3000e device, employing the Brunauer–Emmett–Teller (BET) method [34]. The specific surface areas were evaluated by the single-point BET method. Diffuse reflectance (DR) spectroscopy measurements were carried out with a Jasco-V650 spectrophotometer. An ILV-724-type integration sphere was used to collect the photons originating from the light source following diffuse reflection. The first-order derivative of the spectra were used to determine the band gaps of the samples. The temperature required for calcination was evaluated by thermal gravimetry (TG), by using a TA Instruments TGA Q500 device and applying a heating rate of 10 °C min⁻¹ within the 20–900 °C range in air atmosphere. Fourier transform infrared (FTIR) spectra were collected with a Bruker Vertex 70 FTIR instrument using the following parameters: wavenumber range = 400–4000 cm⁻¹ and resolution = 4 cm⁻¹. XPS spectra were obtained using a SPECS PHOIBOS 150 MCD system, consisting of a monochromatic Al-Kα source (1486.6 eV), a hemispherical analyzer, and a charge neutralization device. The samples were affixed to a double-sided carbon tape. The X-ray source was operated at 200 W, while the pressure of the analysis chamber ranged from 10⁻⁹ to 10⁻¹⁰ mbar. The binding energy scale was calibrated to the C 1s peak at 284.6 eV. Elemental composition was ascertained via the survey spectra recorded with a pass energy of 60 eV. High-resolution spectra were captured using a pass energy of 20 eV. Data analysis was performed in CasaXPS, employing a Shirley background and a Gaussian/Lorentzian product form (70 % Gaussian and 30 % Lorentzian) for curve fitting.

2.4. Determination of photocatalytic activity and stability

The photocatalytic activity of the samples was assessed by the photocatalytic degradation of phenol (c_{0, phenol} = 0.1 mM), chlorophenol (c_{0, chlorophenol} = 0.1 mM), and oxalic acid (c_{0, oxalic acid} = 10 mM). These photocatalytic experiments were conducted in a controlled environment, using six UV fluorescent tubes (Vilber-Lourmat T-6L, UV-A, 6 W) for the irradiation (λ_max = 365 nm). The photocatalyst suspensions were placed in a double-walled glass vessel. The temperature was maintained at 25 °C, and air was constantly introduced into the reactor to keep the dissolved oxygen level constant during the 4-h-long experiments. The changes in pollutant concentrations were monitored by high-performance liquid chromatography (HPLC). The chromatograph consisted of a Merck Hitachi L-7100 low-pressure gradient pump and a Merck-Hitachi L-4250 UV–vis detector. For phenol and chlorophenol, a 50:50 (V/V) methanol/water mixture was applied as the eluent, while the detection wavelengths were λ_phenol = 210 nm and λ_chlorophenol = 223 nm. For oxalic acid, a 19.3 mM sulfuric acid solution was used as the eluent, and the detection wavelength was λ_{oxalic acid} = 206 nm.

Additionally, sample stabilities against compounds with various functional (phenolic/alcoholic hydroxyl, carboxylic, and halide) groups were also investigated by rerecording the XRD patterns after the photoactivity evaluation (the stability measurements were carried out under the same conditions used for the photoactivity tests).

3. Results and discussion

3.1. Characterization of the photocatalysts

First, we carried out the synthesis of CTO photocatalysts until the sol–gel transformation took place. At this point, we carried out a TG measurement to identify the temperature where weight loss does not occur anymore (Fig. S1). We found that after some major weight losses (corresponding to the elimination of surface water, crystal water, and carbonaceous compounds originating from titanium(IV) butoxide), the weight did not change above 610 °C. We attributed the remaining ∼40 % mass to incombustible CTO. Based on these results, we chose 650, 700, 800, 900, and 1000 °C temperatures to carry out the unique calcination of the samples (named “rapid heating – short exposure” (RHSE)).

3.1.1. Structural characterization

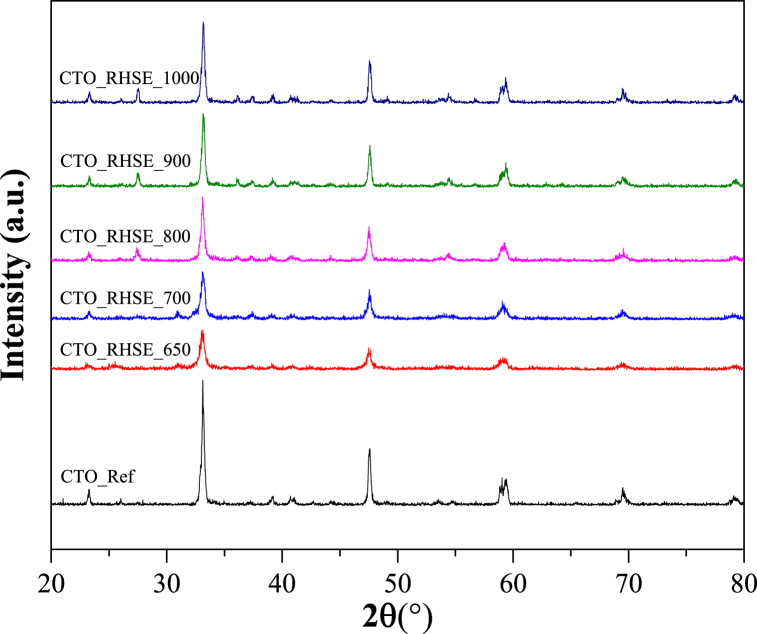
After obtaining the TG results and carrying out the RHSE calcination of the samples, we recorded their XRD patterns (Fig. 1). Since CTO has many diffraction peaks, we started evaluating the results by identifying the XRD pattern of 100 % crystalline, commercial CTO (CTO_Ref). The main diffraction peaks at 23.32, 33.16, 47.56, 58.98, 59.36, 69.5, and 79.26 2θ° can be attributed to the (101), (121), (202), (321), (123), (242), and (161) crystallographic planes of orthorhombic CTO (JCPDS No. 42–0423), respectively [[35], [36], [37]]. For the sake of completeness, it is worth mentioning that we detected many more, less intense diffraction peaks (at 26.14, 36.1, 37.4, 39.14, 40.76, 41.02, 42.72, 44.46, 49.06, 52.36, 53.48, 54.68, 56.7, 65.42, and 73.2 2θ°) that also belong to CTO. Then, we proceeded with the investigation of the CTO_RHSE_800, CTO_RHSE_900, and CTO_RHSE_1000 samples. We observed one new, very distinct diffraction peak at 27.5 2θ° that we attributed to the (110) crystallographic plane of rutile TiO₂. This statement is supported by the fact that we also detected the (002) and (310) crystallographic planes of rutile with very low intensities at 62.86 and 64.26 2θ°, respectively [38]. It is plausible that the TiO₂ originates from some unreacted titanium precursors we used for the synthesis, which transformed into the thermodynamically most stable rutile phase at high temperatures [39]. Interestingly, in these three samples, the amount of rutile increases slightly with decreasing calcination temperature, while the amount of CTO consistently increases with increasing calcination temperature (Table 1). We presume that with increasing temperature, an increasing amount of initially amorphous calcium-containing compounds crystallize, decreasing the amount of rutile and increasing the amount of CTO. After this, we continued our investigation with the CTO_RHSE_700 sample and found that the amount of rutile was significantly decreased, as expected. However, a new diffraction peak appeared at 30.88 2θ°, and for its identification, we considered two approaches: i) the appearance of anatase would have been plausible; however, its diffraction at 25.54 2θ° was largely absent; ii) we studied the XRD patterns of various calcium-based compounds (i.e., CaO, Ca(OH)₂, CaCO₃, and CaTi₂O₅), but none of them have a diffraction peak at 30.88 2θ°. Excluding all other possibilities, we concluded that the new peak must correspond to the (121) crystallographic plane of oriented brookite TiO₂ [40]. Last, we identified the XRD pattern of the CTO_RHSE_650 sample and found that: i) the diffraction of rutile was absent; ii) the diffraction of brookite did not change significantly; iii) and a new diffraction peak appeared at 25.54 2θ° that can be attributed to the (101) crystallographic plane of anatase [38]. For some further investigation, we compared our results with the literature. Sreekantan et al. prepared anatase–rutile TiO₂ nanotubes by anodization and found that between 400 and 600 °C anatase was formed, but starting from 700 °C rutile was obtained, similar to our results [41]. More importantly, the transformation of titanate nanotubes (sodium titanate) to anatase–rutile phase TiO₂ at high temperatures was also observed by Brunatova et al. [42]. A similar observation was reported by Church et al. following the calcination of titanate nanotubes at 700 °C; however, they did not only detect anatase and rutile at this temperature but brookite too [43], which is in good accordance with our findings. To further prove the presence of these various forms of TiO₂, we carried out DRS measurements that we discuss in detail in the next section.

Fig. 1.

XRD patterns for CTO reference and CTO samples calcined at different temperatures with a rapid heat treatment technique.

Table 1.

Phase composition, average primer crystallite sizes, band gaps, and specific surface areas of the investigated samples.

Sample Name	Crystalline composition (%)				CTO Crystallite Size (nm)	Specific Surface Area (m2 g−1)	Band Gap (eV)
	CTO	Anatase	Rutile	Brookite
CTO_RHSE_650	>79.6	11.3	<1	8.1	25.0	51.7	3.71
CTO_RHSE_700	>85.1	<1	5.9	8.0	33.4	38.4	3.70
CTO_RHSE_800	86.3	–	13.7	–	38.7	23.5	3.70
CTO_RHSE_900	88.6	–	11.4	–	47.7	13.5	3.69
CTO_RHSE_1000	90.3	–	9.7	–	50.7	∼2.2	3.68
CTO_Ref	>99	–	–	–	58.1	3.3	3.63

The primary crystallite sizes were calculated via the Scherrer equation (Eq. (1)), while the specific surface areas were determined based on Eqs. (2), (3)):

$$D=\frac{K{\lambda }_x}{{\beta }_{hkl}\mathit{cos}\theta }$$ (1)

D is the primary crystallite size, K is the shape factor (0.9), λ_x is the wavelength of the X-rays (0.15406 nm), β_hkl is the full width at half maximum, and θ is the Bragg angle.

$$\frac{1}{V_a\times \left(\frac{P_0}{P}-1\right)}=\frac{\left(C-1\right)}{V_m\times C}\times \frac{P}{P_0}+\frac{1}{V_m\times C}$$ (2)

$$S=\frac{V_m\times N_{Av}\times a}{m\times 22400}$$ (3)

N_Av is the Avogadro number (6.022 × 10²³ mol⁻¹), a is the effective cross-sectional area of one nitrogen molecule (0.162 nm²), m is the mass of the powder used in grams, and 22400 is the volume occupied by 1 mol of nitrogen gas. The primary crystallite sizes of CTO increased with increasing temperature from 25.0 nm (CTO_RHSE_650) to 50.7 nm (CTO_RHSE_1000) while the specific surface areas decreased from 51.7 m² g⁻¹ to ∼2.2 m² g⁻¹, respectively (Table 1).

3.1.2. Optical properties

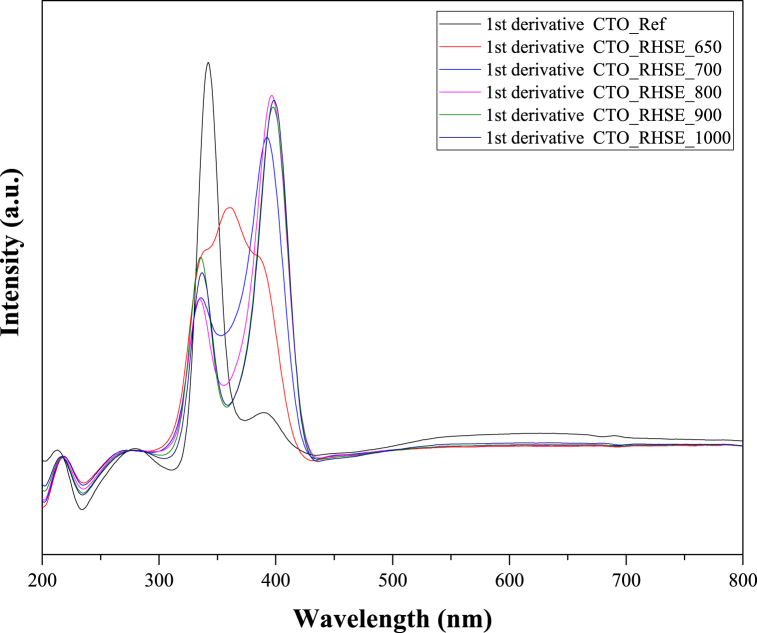
We characterized the optical properties of the samples by DRS measurements (Fig. S2). For the evaluation, we considered the first-order derivative of the reflectance spectra (Fig. 2). Same as in the previous section, we first evaluated the spectrum of CTO_Ref. We observed the main peak corresponding to the absorption edge at 342 nm, which equals a band gap of 3.62 eV (Table 1). This value is in good agreement with the values reported in the literature [35]. Comparing the spectra of CTO_RHSE_700–CTO_RHSE_1000, we found the following. First, interestingly, the CTO-related peaks are not the most intense ones but the ones between 392 nm (CTO_RHSE_700) and 399 nm (CTO_RHSE_1000). We attributed the former peak to a mixture of anatase and rutile TiO₂, and the latter one to rutile TiO₂ (the literature data is ∼3.2 eV that equals ∼387.5 nm for anatase and 3.02 eV that equals 410.5 nm for rutile [44]. We believe that the reason that the TiO₂-related peaks have higher intensities than the CTO-related ones is that the unreacted titanium precursors crystallized on the surface at high temperatures. Second, the CTO peak undergoes a slight redshift from 335 nm to 337 nm with the increase in calcination temperature, as expected [45]. The DR spectrum of CTO_RHSE_650 has an overlapping triplet. After deconvolution, we identified the position of the three peaks at 334, 360, and 390 nm. The first one corresponds to CTO, while the last one corresponds to anatase TiO₂; both of them fit into the trend (originating from the redshift) very well (Table 1). The middle one at 360 nm equals a band gap of 3.44 eV, which can be attributed to the band gap of brookite TiO₂ [46,47], confirming its presence in this sample. This brookite peak is also present in CTO_RHSE_700, causing the descending part of the curve after the CTO peak to be at a significantly higher intensity compared to those in the other samples.

Fig. 2.

First-order diffuse reflectance derivative spectra of the CTO_RHSE and CTO_Ref samples.

3.1.3. Morphology

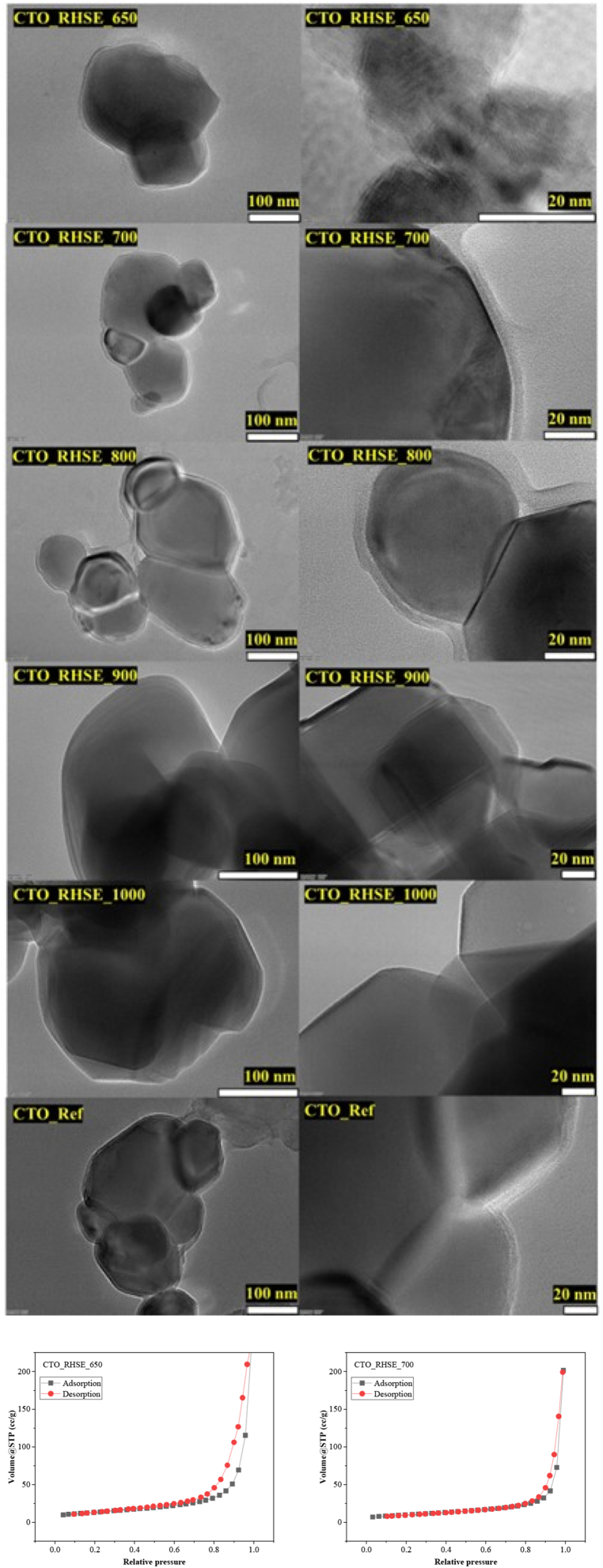
We took SEM micrographs to investigate the morphology of the samples and the results are shown in Fig. S3. The samples are polycrystalline, containing predominantly shapeless, round particles that cannot be characterized with a well-defined morphology. The morphology of CTO_RHSE_650 and CTO_RHSE_700 is largely the same; however, starting with the CTO_RHSE_800 sample, oval, rounded shapes also appear on the surface, which increasingly coalesce with the increase of calcination temperature. Taking the XRD and DRS results into consideration, we know that rutile TiO₂ mainly appears after applying a calcination temperature of 800 °C (XRD result), and we also know that the titania should be on the surface (DRS result). Based on this reasoning, it is plausible to assume that the oval, rounded shapes that appear in CTO_RHSE_800, CTO_RHSE_900, and CTO_RHSE_1000 (which are absent in CTO_RHSE_650 and CTO_RHSE_700) are rutile titania on the surface.

We also carried out TEM measurements to study morphology further. The TEM micrographs (Fig. 3) reinforce our previous SEM results: polycrystalline, round particles were obtained. The high-resolution micrographs also show that the surface of our samples is smooth and does not contain pores, which is in good agreement with the small specific surface areas. To reinforce this statement, we investigated the possible porosity of CTO_RHSE_650 and CTO_RHSE_700 further. The isotherms obtained resemble type V isotherms normally obtained for mesoporous materials. However, mesopores cannot be observed based on the micrographs, so it can be concluded that the apparent porosity (i.e., hysteresis loops) originates from the surrounding network of interparticle voids [48].

Fig. 3.

High-resolution TEM micrographs of the samples and isotherms obtained for CTO_RHSE_650 and CTO_RHSE_700.

3.1.4. Surface properties

The presence of titania in the CTO samples was further investigated. For this purpose, two issues were considered: i) Having a dynamic crystalline system that includes different titania crystal phases and CTO is a clear sign of continuous recrystallization, which should be detectable (i.e., evaluating the changes in Ti oxidation states can be used to follow the crystallization process); ii) As the presence of titania is more apparent in the DR spectra than in the XRD patterns, it can be assumed that the changes occurred mostly on the surface. Accordingly, the surface of the samples was characterized by IR and XPS measurements, and the results are discussed taking into account the previous results.

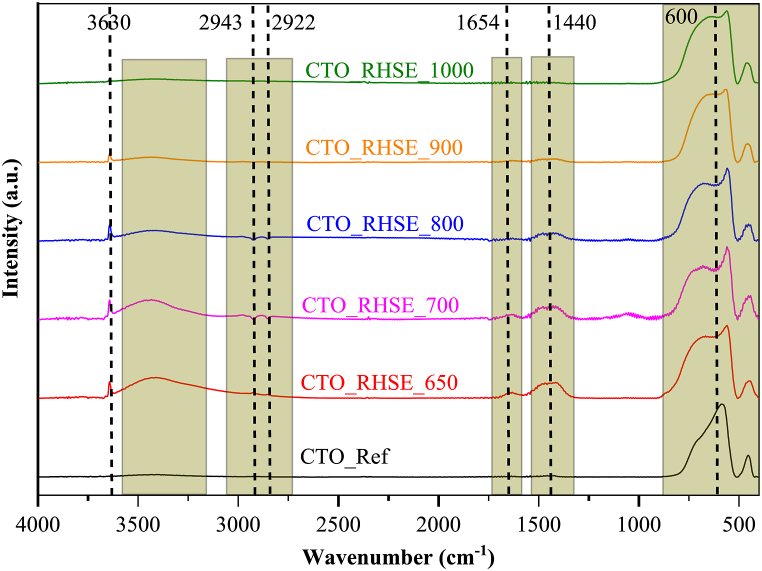
First, the oxide region of the samples was examined in the IR spectra (Fig. 4). The shape of the band relating to the different metal–oxygen vibrations at 410–880 cm⁻¹ [49,50] varied with the calcination temperature. This difference is the most apparent when comparing the metal–oxygen band in CTO_RHSE_650 and CTO_Ref (the band at ∼700 cm⁻¹ is more intense), emphasizing the presence of titania. For CTO_RHSE_700, the intensity of the region at ∼605 cm⁻¹ decreases. This coincides with the transformation of anatase to brookite (Table 1, Fig. 1, Fig. 2). The intensity of this region increases again in CTO_RHSE_800–1000 as a function of calcination temperature, which is consistent with the appearance of rutile. The significant contribution of the rutile phase to the intensity of this band is not surprising as rutile possesses excellent infrared absorption [51]. Regarding the other regions, a wide band centered at 1440 cm⁻¹ (O–H bending) and a less intense band centered at 1650 cm⁻¹ (C O stretching) [52] appeared, both corresponding to oxalate species. At 2950 cm⁻¹, multiple C–H stretching [53] signals appeared, suggesting the decomposition of organic matter. The presence of these bands is plausible, as oxalic acid was used during the synthesis of the samples. Moreover, the RHSE calcination method we applied probably resulted in the incomplete decomposition of organic compounds on the surface. The intensity of these three bands decreased as a function of calcination temperature, as expected, because of the more efficient elimination of organic compounds at higher temperatures. Increasing the calcination temperature also decreased the hydrophobicity of the surface, as evidenced by the large O–H stretching band at 3150–3600 cm⁻¹ originating from surface O–H groups, carboxylic acids, and associated hydrogen bonding. The intensity of this band was high in CTO_RHSE_650 and very low in CTO_RHSE_1000. The same trend was observed for the sharp band located at 3630 cm⁻¹, which can be attributed to –OH groups associated with alcohols [54] originating from the decomposition of the organic precursor.

Fig. 4.

IR spectra of the CTO_RHSE and CTO_Ref samples.

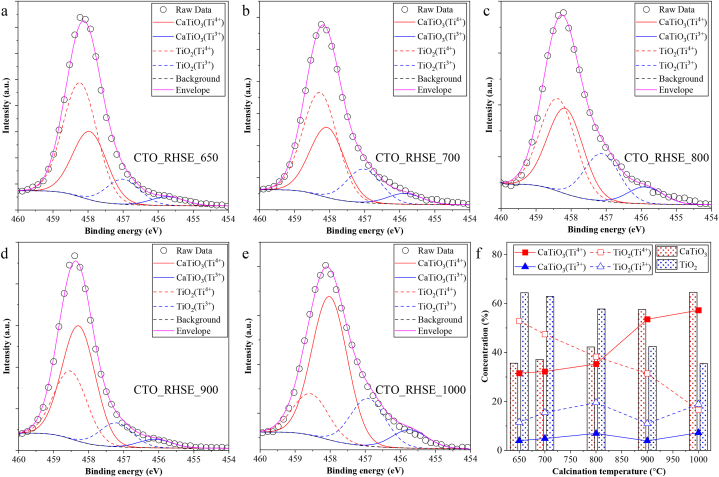
Second, the XPS spectra of the samples were investigated to further elucidate the composition of the surface of the samples. Before the in-depth analysis, their survey spectra were also recorded (one representative one is shown in Fig. S4a). No foreign elements were detected besides the ones we expected to appear, that is, Ca, Ti, O, and C (C is an omnipresent element in all XPS spectra). The Ca 2p XPS spectra of the samples are nearly identical (Fig. S4b). The only observable species is Ca²⁺ originating from CTO at 346.2 and 349.7 eV, corresponding to the Ca 2p_3/2 and Ca 2p_1/2 signals, respectively [55]. No signs of other Ca-based compounds were found, which is consistent with the XRD and DRS results. The O 1s spectra of the catalysts varied with increasing calcination temperature; however, these changes were not consistent (Fig. S4c). The following species were detected: adsorbed H₂O and surface OH groups (531.4 eV), lattice O (529.7 eV), and low binding energy oxygen (527.0 eV) that is often associated with the presence of Ti³⁺ [56]. It should be noted that these O signals originate from both TiO₂ and CTO and are not distinguishable under these circumstances, due to the small difference in binding energies. Hence, no quantification and further peak separation were carried out. As the next step, the Ti 2p_3/2 XPS spectra (Fig. 5a–e) were analyzed since Ti species can be separated following the deconvolution of this signal [57] (the Ti 2p_1/2 signal was also investigated but not included). Four components were identified: Ti⁴⁺ (457.9 eV) and Ti³⁺ (455.8 eV) in CTO, and Ti⁴⁺ (458.2 eV) and Ti³⁺ (457.0 eV) in TiO₂. Based on the XRD patterns, the samples contain anatase, brookite, and rutile as well (depending on the calcination temperature); however, they could not be distinguished in the XPS spectra. Somewhat surprisingly, titania was present in all the investigated samples, including CTO_Ref. The XRD and DRS results imply that titania is present mostly on the surface due to the low diffraction peak intensity and high optical contribution, respectively. The results also show that the quantity of titania decreases with the increase of calcination temperature (Table 1), which was confirmed based on the XPS spectra too. In CTO_RHSE_650, the surface contained 68 % TiO₂ and 32 % CTO (Fig. 5f). These values were practically reversed in CTO_RHSE_1000: the surface contained 37 % TiO₂ and 63 % CTO. This shows that as the calcination temperature increases, the titania on the surface converts into CTO. The other evidence which supports the gradual recrystallization is the presence of Ti³⁺ in CTO and TiO₂. The concentration of Ti³⁺ was nearly constant in all samples (17 % in TiO₂ and 4 % in CTO on average), suggesting a significant mass transfer and crystallization. Moreover, based on the XRD and DRS results, we know that the titania changes its crystalline phase composition as a function of calcination temperature, starting from anatase and brookite to pure rutile. This internal transformation contributes considerably to the relatively high amount of Ti³⁺. Last, the photocatalytic activity is known to depend on the presence of Ti³⁺ centers [58]; however, in the present case, Ti³⁺ concentration was nearly constant, hence no such correlation was made.

Fig. 5.

Ti 2p XPs spectra of the CTO_RHSE and CTO_Ref samples (a–e) and dependence of the content of Ti³⁺/Ti⁴⁺ species in CTO and TiO₂ as a function of calcination temperature (f).

3.2. Photocatalytic activity

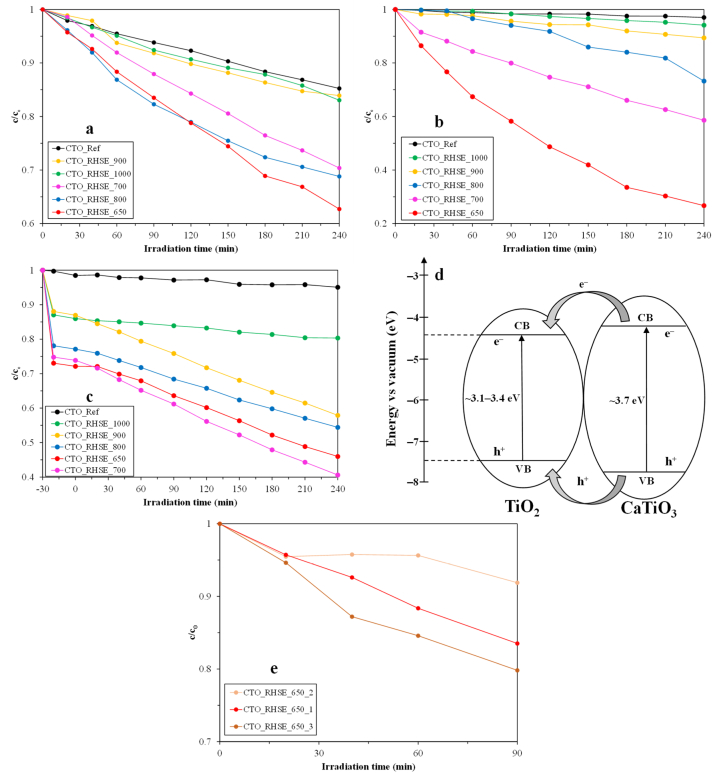
The photocatalytic activity of the samples was assessed via the degradation of various model pollutants, including phenol, chlorophenol, and oxalic acid. Before switching on the lamps, the photocatalysts were stirred in the dark (5 min for phenol and chlorophenol, 30 min for oxalic acid) to establish an adsorption–desorption equilibrium. No significant adsorption (<2 %) occurred for phenol (Fig. 6a) and chlorophenol (Fig. 6b) as expected since they are poorly adsorbing compounds. However, for oxalic acid (Fig. 6c), the adsorption values varied between 13 % (CTO_RHSE_1000) and 27 % (CTO_RHSE_650) which correspond well with the measured specific surface areas. Remarkably, in each case, our CTO_RHSE samples exhibited superior efficacy in degrading these pollutants when compared to CTO_Ref. This enhanced photocatalytic activity aligns well with the XRD results. Specifically, lower calcination temperatures led to smaller primary crystallite sizes and larger specific surface areas, resulting in improved conversions in most cases. It is well-known that in general, larger specific surface areas are desirable for photocatalytic processes, by providing more active sites for such reactions to occur [59]. Consequently, the CTO_RHSE_900 and CTO_RHSE_1000 samples exhibited the lowest efficiency in all cases (apart from CTO_Ref). However, it is worth mentioning that for oxalic acid, if we disregard adsorption and only consider photocatalytic degradation, 26.2, 33.3, 22.7, 29.0, 5.6, 3.4 % conversions were measured for CTO_RHSE_650, 700, 800, 900, 1000, and CTO_Ref, respectively. The best-performing samples degraded ∼40 % phenol, ∼75 % chlorophenol, and (disregarding adsorption) ∼30 % oxalic acid. The initial reaction rates were also calculated, and the results are shown in Table 2. The reason that the photocatalysts performed the worst for oxalic acid despite it adsorbing the best might be because oxalic acid is a hole scavenger [60]; this indirectly implies that holes took part in the photocatalytic degradation. As for phenol versus chlorophenol degradation, it is plausible that the reason that the photocatalytic activity for the latter was nearly twice as high as for the former is because of the attached substituent. Chlorine is an electron-withdrawing substituent, distorting the electron cloud and destabilizing the resonance-stabilized aromatic ring by generating an active site where the reactive oxygen species can attack [61]. Last, it is worth highlighting that even though the photocatalytic activity difference between the individual samples (calcined at similar temperatures) was not significant in most cases, a conversion difference as high as 32 % was observed between CTO_RHSE_650 and CTO_RHSE_700 for chlorophenol degradation. The reason that CTO_RHSE_650 performed better than CTO_RHSE_700 might lie in its crystalline phase composition. Both samples contain the same amount of brookite (Table 1); however, CTO_RHSE_650 contains anatase, while CTO_RHSE_700 contains rutile. First, it is well-known that anatase is usually considered better-performing than rutile in photocatalytic applications owing to differences in surface hydroxyl group amounts, oxygen adsorption properties, and light absorption properties [62,63]. Second, Snejana et al. obtained similar results: samples with higher anatase content performed better for 4-chlorophenol degradation than samples with higher rutile content [64]. They also speculated that using mixtures of photocatalysts can result in improved photocatalytic activity. Indeed, there are many papers in the literature reporting on a synergistic effect between brookite and anatase [65] and brookite and rutile [66], originating from the heterojunctions formed that lead to better charge separation. Third, Szołdra et al. found that anatase/brookite-containing photocatalysts had higher photocatalytic activity than single-phase anatase and anatase/rutile-containing photocatalysts [67], which is in good agreement with our results. Considering these synergies between the titania phases and that they form a heterojunction with CTO, the following mechanism can be proposed. Based on the publication of Ehsan et al., the conduction band potential of CTO is more negative, while the valence band potential of CTO is more positive than those of TiO₂ [68]. In our binary heterojunctions (CTO/rutile TiO₂, CTO/anatase TiO₂, and CTO/brookite TiO₂), the UV light we used for excitation can activate both the CTO and TiO₂ simultaneously (Fig. S5). As a result, photogenerated electrons move to their corresponding conduction bands, leaving behind holes. Due to the band positions, the photogenerated electrons and holes of CTO move to the respective conduction band and valence band of TiO₂ (Fig. 6d). Electrons accumulate in the conduction band of TiO₂, increasing the Fermi-level (negative shift) and thus lowering their work function. Consequently, adsorbed molecules can receive electrons more easily; this facilitated charge transfer can increase photoactivity. Even though we propose similar charge-transfer mechanisms, it is worth noting that the brookite- and anatase-containing samples performed better than the rutile-containing ones. However, as discussed in Section 3.1.1, the rutile-containing samples were prepared at higher calcination temperatures, resulting in decreased specific surface areas. The result of these multiple factors led to the photocatalytic activities we measured. It is thus plausible that the photocatalytic activities were different despite the similar charge-transfer mechanisms.

Fig. 6.

Degradation curves for phenol (a), chlorophenol (b), and oxalic acid (c). Proposed photocatalytic mechanism (d). Reusability of CTO_RHSE_650 investigated by three consecutive phenol degradation experiments (e).

Table 2.

Initial reaction rates determined for phenol, chlorophenol, and oxalic acid degradation under UV light irradiation.

Sample Name	r0,phenol (10−9 M s−1)	r0,chlorophenol (10−9 M s−1)	r0,oxalic acid (10−9 M s−1)
CTO_RHSE_650	2.6	6.9	2.0
CTO_RHSE_700	2.1	2.7	2.4
CTO_RHSE_800	2.2	1.8	1.6
CTO_RHSE_900	1.2	0.7	2.0
CTO_RHSE_1000	1.1	0.4	0.4
CTO_Ref	1.0	0.2	0.2

The best overall sample (i.e., CTO_RHSE_650) was selected to investigate reusability in three cycles for phenol degradation (Fig. 6e), and we found that the difference in conversion values between the first and last cycle was only ∼3 %. Even photocatalysts with good reusability tend to show a slight decrease in photoactivity due to unavoidable losses during their collection or loss of adsorption sites originating from the adsorption of the pollutant and its intermediates. However, in our case, the latter can be largely disregarded due to the poor adsorption properties of phenol. That can be why a similar, even slightly (∼3 %) higher conversion value was obtained, which difference originates from the sum of instrumental and methodical errors. Last, the possible photocatalytic degradation steps were considered based on the literature. For oxalic acid, the possible steps can be summarized based on the publication of AlSalka et al. [69] as follows:

H₂C₂O₄ ←→ H₂C₂O₄⁻ + H⁺ (4)

OH⁻_(ads) + cat.(h⁺) ←→ •OH + cat (5)

HC₂O₄⁻ + •OH → HC₂O₄• + OH⁻ (6)

HC₂O₄⁻ + cat.(h⁺) → HC₂O₄• + cat (7)

HC₂O₄• → HCO₂• + CO₂ (8)

HCO₂• ←→CO₂•^– + H⁺ (9)

CO₂•^– + cat. → CO₂ + cat.(e^–) (10)

H⁺ + cat.(e^–) → H• + cat (11)

CO₂•^– + H• → HCOO⁻ (12)

HCOO• + cat.(e^–) → HCOO⁻ + cat (13)

CO₂•^– + CO₂•^– → CO₂ + CO₂²⁻ (14)

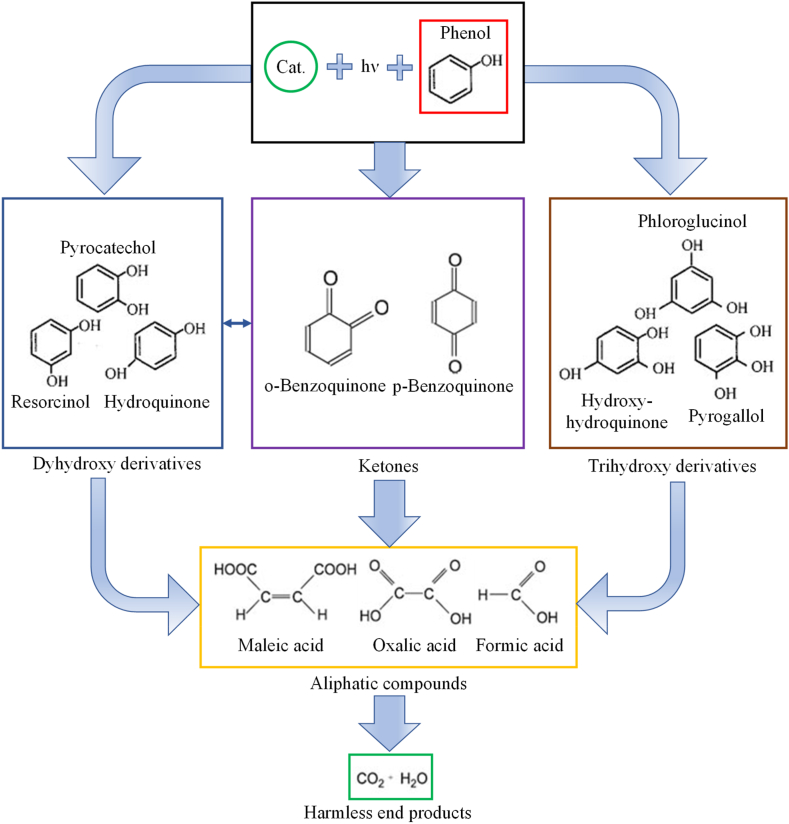
For phenolic compounds, the possible degradation pathways [70] can be summarized based on Fig. 7. First, multisubstituted (di-/trihydroxy) phenol derivatives or ketones form, followed by ring opening and the formation of aliphatic compounds, which then can break down into water and CO₂ if enough time is given.

Fig. 7.

Possible degradation pathways of phenolic compounds.

3.3. Stability

Some additional measurements were also carried out to investigate the stability of our photocatalysts against compounds with various functional groups (i.e., phenolic –OH in phenol, –COOH in oxalic acid, –X in chlorophenol) by recording their XRD patterns before and after exposure to them. For phenol (Fig. S6a) and chlorophenol (Fig. S6b), the XRD patterns of our samples were largely identical before and after the measurements. However, a new diffraction peak at 29.4 2θ° appeared that corresponds to the (104) crystallographic plane of CaCO₃ [71]. This might be because from the degradation of phenol and chlorophenol, carboxylic acids form after ring opening [72], which can lead to the formation of yellow peroxo-titanium complexes [73], explaining the color change of the samples from white to pale yellow. Then, the dissolved calcium ions can form Ca(OH)₂ due to the hydroxyl radicals generated during the photocatalytic processes, which can finally be converted to CaCO₃ due to the CO₂ originating from the air or photocatalytic degradation. For oxalic acid (Fig. S6c), these CaCO₃ diffraction peaks were absent, which is plausible due to its acidic nature, releasing CO₂ from the system. However, three new diffraction peaks were observed at 24.4, 30.2, and 36.94 2θ°, corresponding to Ca-oxalate [74,75]. The CTO_Ref sample was also investigated in this regard, in which the formation of Ca-oxalate was observed too; however, the formation of CaCO₃ was not (in the case of exposure to phenol and chlorophenol). This can be explained by the fact that the photocatalytic activity of CTO_Ref was so low that reactive oxygen species could not form which would have resulted in the processes detailed above. For some additional stability measurements, aldehyde groups (glucose; Fig. S6d) and alcoholic –OH groups (2-propanol; Fig. S6e) were also investigated and the results and discussion are shown in the supplementary material.

3.4. Cost efficiency comparison of conventional calcination and the RHSE method

In our recent publication, we calculated the energy required to prepare strontium titanate using our RHSE method and conventional calcination [24]. The calculations and considerations are shown in detail in this publication. In short, the CTO_RHSE_700 sample was selected, and its synthesis method was used to prepare a “CTO_700” sample by conventional calcination (700 °C temperature, 5 °C·min⁻¹ heating rate, and 2 h exposure). The considerations we used were as follows: i) 1 cm² sample surface and 1 mm depth, ii) heat transfer only occurs by convection, iii) natural convection is neglectable, iv) local heat transfer only occurs on the surface, v) thermodynamic-related parameters can be neglected as the samples were prepared the same way (apart from the calcination step). The equations used were as follows:

$$P=\nabla \left(T,v,j\right)$$ (15)

$$\nabla T=\frac{\partial T}{\partial x}+\frac{\partial T}{\partial y}+\frac{\partial T}{\partial z}$$ (16)

where P is the energy required for the synthesis, T is the temperature, υ is the vectorial sum of the hydrodynamic parameters (0 in our case), and j is the sum of the intrinsic properties of the material (0 in our case). Accordingly, the energy required to prepare CTO_700 is 1920 kW, while the energy required to prepare CTO_RHSE_700 is 1260 kW. Considering that we carried out phenol degradation measurements for these samples and obtained comparable conversions (Fig. S7), it can be ascertained that conventional calcination can be replaced by our RHSE method without a loss in photocatalytic activity. Similar conclusions were drawn by Pap et al. for TiO₂ samples [23].

4. Conclusions

An investigation was conducted into the impact of rapid heat treatment on the characteristics of CTO photocatalysts. The composite samples contained ∼10–20 % of titania: rutile was formed at higher calcination temperatures, while a mixture of anatase and brookite was predominant when lower temperatures were applied during the synthesis. Increasing the temperature from 650 to 1000 °C resulted in the primary crystallite sizes increasing from 25 to 50.7 nm, the specific surface areas decreasing from 51.7 to ∼2.2 m² g⁻¹, and the band gap values undergoing a redshift from 3.71 to 3.68 eV. The TiO₂/CTO composites were not porous, which was proved by high-magnification TEM measurements. The hysteresis obtained during porosity measurements was attributed to interparticle voids. The nonporosity of the samples is in good accordance with their relatively small specific surface areas.

Our CTO_RHSE samples exhibited superior efficacy in degrading various pollutants compared to a reference commercial CTO with conversion values as high as ∼40, ∼75, and ∼35 % (disregarding adsorption) for phenol, chlorophenol, and oxalic acid, respectively. The composites prepared at lower calcination temperatures had higher photocatalytic activity, which was attributed to the resultant effect of their higher specific surface area and better charge separation originating from the heterojunction formed. The results of consecutive phenol degradation showed only a ∼3 % difference in conversion between the first and last degradation cycles, proving the reusability of the composites.

Exposure to various compounds with different functional groups (i.e., phenolic –OH, –COOH, and –Cl) revealed that the photocatalysts underwent minor alterations in their crystalline composition. Exposure to phenol and chlorophenol resulted in the formation of CaCO₃, while exposure to oxalic resulted in the formation of calcium oxalate in low amounts.

The economic aspect was also investigated, and it was found that the energy required for conventional calcination (at 700 °C) was 1920 kW, whereas applying the rapid calcination method reduced this number by approximately 35 % to1260 kW.

Data availability statement

Data are included in the manuscript and supplementary material.

CRediT authorship contribution statement

Mahsa Abedi: Writing – original draft, Visualization, Investigation, Conceptualization, Software. Zsejke-Réka Tóth: Investigation, Methodology, Writing – original draft, Software. Milica Todea: Investigation, Methodology, Writing – original draft, Software. Áron Ágoston: Investigation, Methodology, Writing – original draft, Software. Ákos Kukovecz: Resources, Formal analysis, Funding acquisition, Writing – review & editing. Zoltán Kónya: Resources, Funding acquisition, Writing – review & editing, Formal analysis. Zsolt Pap: Writing – review & editing, Visualization, Validation, Supervision, Funding acquisition, Conceptualization. Tamás Gyulavári: Writing – review & editing, Visualization, Validation, Supervision, Investigation, Funding acquisition, Conceptualization, Writing – original draft.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary data

The following is the supplementary data to this article: