Predicting lncRNA–Disease Associations Based on a Dual-Path Feature Extraction Network with Multiple Sources of Information Integration

Abstract

Identifying the associations between long noncoding RNAs (lncRNAs) and disease is critical for disease prevention, diagnosis and treatment. However, conducting wet experiments to discover these associations is time-consuming and costly. Therefore, computational modeling for predicting lncRNA-disease associations (LDAs) has become an important alternative. To enhance the accuracy of LDAs prediction and alleviate the issue of node feature oversmoothing when exploring the potential features of nodes using graph neural networks, we introduce DPFELDA, a dual-path feature extraction network that leverages the integration of information from multiple sources to predict LDA. Initially, we establish a dual-view structure of lncRNAs and disease and a heterogeneous network of lncRNA-disease-microRNA (miRNA) interactions. Subsequently, features are extracted using a dual-path feature extraction network. In particular, we employ a combination of a graph convolutional network, a convolutional block attention module, and a node aggregation layer to perform multilayer topology feature extraction for the dual-view structure of lncRNAs and diseases. Additionally, we utilize a Transformer model to construct the node topology feature residual network for obtaining node-specific features in heterogeneous networks. Finally, XGBoost is employed for LDA prediction. The experimental results demonstrate that DPFELDA outperforms the benchmark model on various benchmark data sets. In the course of model exploration, it becomes evident that DPFELDA successfully alleviates the issue of node feature oversmoothing induced by graph-based learning. Ablation experiments confirm the effectiveness of the innovative module, and a case study substantiates the accuracy of DPFELDA model in predicting novel LDAs for characteristic diseases.

1. Introduction

Long noncoding RNAs (lncRNAs) are a class of RNAs that are more than 200 nucleotides in length and that cannot encode proteins.¹ lncRNAs are usually expressed at lower levels than microRNAs. However, they play very important roles in life-regulating activities, including transcriptional regulation, translational regulation, RNA processing regulation and cell life cycle regulation.^2,3 Recently, it has been found that lncRNAs are closely related to disease pathogenesis,⁴ so the detection of more disease-associated lncRNAs may be a good way to understand the occurrence, development, prevention, and treatment of diseases at the molecular level.

In previous studies, researchers used living organisms to validate disease associations with lncRNAs. This method is not only time-consuming but also difficult to use for determining the association pairs of lncRNAs with diseases. To increase the validation accuracy in wet experiments and to reduce the cost of conducting experiments, researchers have used the experimental data summarized by previous researchers combined with state-of-the-art computer models for the preferential selection of disease–lncRNA association pairs.⁵⁻⁷

Previous studies have employed the LDA matrix along with its computed similarity matrix to explore the features of individual nodes. LRLSLDA⁸ used the lncRNA similarity matrices as the input features of the nodes and reconstructs the association matrices for prediction using the least-squares method with Laplacian regularization. MFLDA⁹ explored the matrix three-factor decomposition technique to derive the disease, lncRNA and implicit feature matrices, and the reconstructed predictive association matrix can be derived by multiplying these matrices. SIMCLDA¹⁰ used principal component analysis (PCA) to extract key features and a neural-induced complementation matrix to explore potential lncRNA–disease associations. Regarding IPCARF,¹¹ association prediction was performed with the Random Forest technique after feature extraction via PCA. GCHIRFLDA¹² is a method for extracting potential features using an autoencoder and combining it with a Random Forest classifier for prediction. SCCPMD¹³ first performed similarity enhancement using logistic functions and then performs prediction of potential association pairs using the probabilistic matrix decomposition method with corrected similarity constraints. These traditional machine learning and matrix factorization methods have achieved acceptable performance, but they neglect the information regarding neighboring nodes that is available in both the LDA association network and the lncRNA–disease similarity network.

To fully leverage the information from neighboring nodes, LDA-LNSUBRW¹⁴ used linear neighborhood similarity in the lncRNA network and disease network for unbalanced birandom walk and finally fused these components to produce the final predicted LDA. LRWRHLDA,¹⁵ Laplace normalization of similarities and interactions between diseases, genes and noncoding RNAs, can be used to make a final prediction after several rounds of iterative training, and a similar method is MHRWR.¹⁶ Birandom walks are also available in MSF-UBRW,¹⁷ where the interaction between lncRNAs and diseases was reconstructed using WKNKN¹⁸ based on unbalanced birandom walks and used as a transfer matrix for the respective networks. Similar birandom walk methods are used in NCP-BiRW¹⁹ and lung cancer prediction.²⁰ Although existing network propagation random walk algorithms can utilize the neighbor information on nodes, the experimental process is cumbersome, and the resulting association scores are relatively low.

In recent years, deep learning models, due to their powerful representation learning ability, have greatly promoted the development of bioinformatics and are increasingly being used in various bioinformatics analysis tasks. For example, SpatialGlue²¹ applied graph learning and attention mechanisms to the process of spatial transcriptomics data integration, unleashing the full potential of multimodal data. DrlGCL²² used graph learning and contrastive learning methods to infer potential associations between drugs and diseases, not only improving the accuracy of association prediction, but also saving time and costs. PractiCPP²³ and IGT²⁴ both utilized Transformer technology to further understand drug delivery systems, which is beneficial for enhancing drug efficacy. This shows that the graph learning model and Transformer model in deep learning have good feature capturing ability. Graph convolutional neural networks (GCNs)²⁵ in deep learning excel at efficiently aggregating information from neighboring nodes, enriching the features of each node and enhancing the prediction accuracy of association pairs. MAGCNSE,²⁶ MMGCN,²⁷ and MAGCN²⁸ used multiview graph convolutional neural networks with feature-level attention mechanisms for feature extraction and ensemble learning classifiers for node classification. HGATLDA²⁹ and MCHNLDA³⁰ fully explored the topological features in the lncRNA and disease similarity network by using a graph attention network (GAT) and enhanced the learning of topological features by using techniques such as multihopping metapath information, a neural-induced complementation matrix and contrast learning. MGLDA,³¹ NCPred,³² and GTAN³³ used metapaths, convolutional neural networks and multiple attention mechanisms to extract features from multimodal lncRNA, disease and miRNA data and then classify the final association pairs using MLP classifiers. While these models can efficiently extract neighbor node features, GCN and GAT may suffer from a lack of node specificity, leading to information loss and hindering the accurate prediction of newly associated nodes.

In summary, first, we found that most of the current LDA association prediction models are using graph learning to explore the topological features of the nodes for diseases and lncRNAs in homogeneous or heterogeneous networks, then the obtained topological features of the disease and lncRNA are processed using feature fusion techniques in deep learning. However, they ignore the fact that a node’s associative relationships with other types of nodes in a heterogeneous network may contain information specific to the node itself when constructing a topological network using interaction relationships such as disease-LncRNA and so on. Adding node-specific features on top of node topological features will effectively alleviate the problem of vanishing node specificity caused by graph learning. Therefore, we propose a new model (DPFELDA) which combines a node topology feature extraction network with a node topology feature residual network. The key contributions of DPFELDA include the following aspects:

First, we construct a dual-path node feature extraction network to extract the full node features of lncRNAs and diseases, and this network comprises a node topology feature extraction network and a node topology residual network. The former extracts comprehensive information from neighboring nodes with diverse topologies in the dual perspective of lncRNA and disease, while the latter learns distinctive node features from the overall information on lncRNA and disease.

Second, the node topology feature extraction network leverages the two-view structure of diseases and lncRNAs as input. It extracts neighborhood node information from lncRNAs and diseases using GCNs on various network structures. The enhancement and interaction of multilayered node topological information are facilitated through channel attention and spatial attention in the convolutional block attention module (CBAM) framework. Subsequently, a node aggregation layer (NAL) aggregates these topological features.

Finally, we design a node topology residual network within the dual-path feature extraction network to address the issue of vanishing node specificity. It employs the global attention mechanism of the Transformer to extract specific features for each node, facilitating enhanced information complementarity for the node topology feature extraction network.

2. Materials and Methods

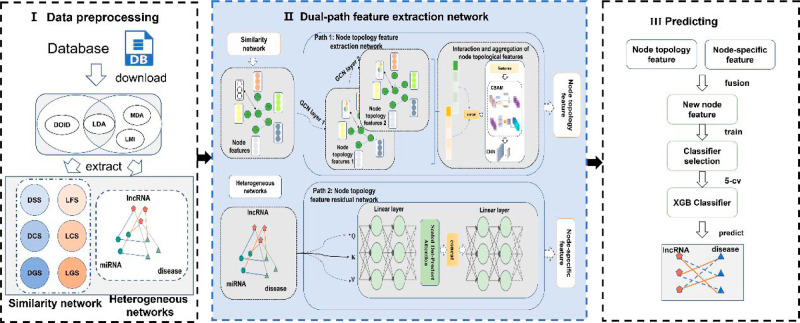
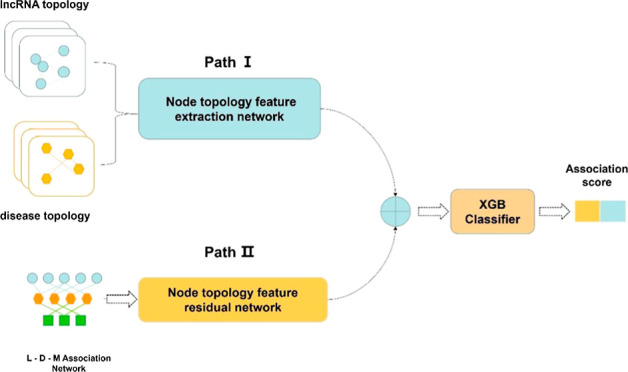
As shown in Figure 1, we developed a novel disease–lncRNA association prediction model, DPFELDA, comprising three phases: data preprocessing, dual-path feature extraction, and a prediction model. During the data preprocessing stage, the similarity matrix between lncRNAs and diseases was calculated based on the association matrix and the Disease-Ontology ID (DOID),³⁴ utilizing three association matrices [the LncRNA–Disease Association Matrix (LDM), MiRNA–Disease Association Matrix (MDM), and LncRNA–MiRNA Interaction Matrix (LMM)] to construct the disease-lncRNA–miRNA heterogeneous network. In the dual-path feature extraction stage, the network is bifurcated into a node topological feature extraction network and a node topological feature residual extraction network. The former operates with a dual-view structure employing lncRNA and disease similarity network as input, utilizing techniques such as CBAM and NAL for processing node topological features. Moreover, the node topology feature residual extraction network takes the mutual relationships in the lncRNA-disease-miRNA heterogeneous network as input. It utilizes the Transformer to extract specific features of nodes, which serve as compensatory features for the nodes. In the prediction model, the features extracted from both networks are combined and input into the final classifier XGBoost for LDA prediction.

Figure 1.

Flowchart of DPFELDA.

2.1. Data Sets

We utilized four data sets to assess the model’s performance. First, Data set 1, from MFLDA,⁹ comprises 240 lncRNAs and 412 diseases involving 495 miRNAs. This data set encompasses 2697 lncRNA–disease associations, 13,562 miRNA–disease associations, and 1002 miRNA–lncRNA interactions. Data set 1 was used to investigate the feasibility and generalizability of the model.

Data set 2 from LDAformer.³⁵ It incorporated experimentally validated associations of lncRNAs with diseases sourced from the Lnc2Cancer v3.0³⁶ and LncRNADisease v2.0³⁷ databases. Additionally, for a more comprehensive analysis of the nodal features and specific features of lncRNAs and diseases, they utilized HMDD v3.2³⁸ to incorporate 8540 association relationships between 316 diseases and 295 miRNAs, leading to the identification of 2108 lncRNA–miRNA interactions from the starBase v2.0³⁹ database. Subsequently, Data set 2 was optimized based on the model parameters, and its performance was compared against that of other baseline models. Furthermore, we conducted model exploration using this data.

Data set 3 differs slightly from Data set 1. Several existing prediction models for LDA utilize this data set3 as a benchmark database. To reaffirm the superiority of DPFELDA, we performed additional model comparisons using this data set. Additional data set details are presented in Table 1.

Table 1. Information on the Dataset.

	lncRNA	disease	miRNA	LDA	MDA	MLI
Data set1	240	412	495	2697	13 562	1002
Data set2	665	316	295	3833	8540	2108
Data set3	240	405	495	2687	13 359	1002
Data set4	636	204	262	4748	7696	2091

Additionally, we constructed the data set4 by updating the data sources from lncRNAdisease v2.0 to lncRNAdisease v3.0 and HMDD v3.2 to HMDD v4.0 based on the data set2. It is mainly used for model robustness studies.

In Table 1, LDA represents the association between lncRNAs and disease, MDA represents the relationship between miRNAs and disease, and MLI represents the interaction relationship between miRNAs and lncRNAs.

2.2. Methods

2.2.1. Similarity Matrix Calculation

2.2.1.1. Disease Semantic Similarity

Disease–lncRNA association prediction is based on the hypothesis proposed by Chen and Yan⁸ that similar diseases tend to be associated with functionally similar lncRNAs. Therefore, we obtained disease semantic information from Disease Ontology³⁴ and used the disease ontology to represent the parent–child relationships between diseases in the data structure of the directed acyclic graph. We calculated the semantic similarity matrix of diseases according to Wang’s method⁴⁰ and the semantic contribution score of diseases to diseases according to the directed acyclic graph. Assuming that D is the ancestor node of the DAG and D′ is the child node of D, the semantic contribution score S_D1 of D₁ node in the DAG is

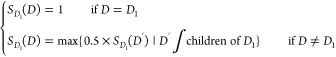1

After the contribution scores is obtained, the semantic score S_v1 is calculated for D₁

2

T(D) represents the DAG topology of disease D₁, where D is a child node of D₁.

Finally, the semantic similarity of the two diseases is calculated with the following formula

3

where t represents the union of the two diseases in terms of topological structure.

2.2.1.2. LncRNA Functional Similarity

We calculated the functional similarity matrix of lncRNAs based on the known LDA matrix and the computed semantic similarity matrix of diseases by Wang’s method⁵ with the following formula

4

For lncRNAs l₁ and l₂, if there are n₁ diseases associated with l₁ and n₂ diseases associated with l₂, DSS denotes the semantic similarity score between the two diseases, and d_1i and so on represent the disease types.

2.2.1.3. Gaussian Interaction Profile Kernel Similarity for lncRNAs and Diseases

Due to the sparsity of the LFS and DSS similarity matrices, it may be challenging to explore potential internal associations fully through disease semantic and lncRNA functional similarities. This inherent difficulty could introduce bias into the prediction results. To counteract this limitation, we incorporated the Gaussian interaction profile kernel similarity.⁴¹ The formula is calculated as follows

5

6

where RGS stands for the Gaussian kernel similarity of disease or lncRNA, r₁ and r₂ stand for the two lncRNAs or diseases, IP(r_i) is a binary vector representing the ith row in the LDA matrix, and b_i is a parameter in the Gaussian kernel computation. After previous experimental investigations and validations, we chose to set the parameter to 1. The definition of notations is detailed in Table 8.

Table 8. Table of Abbreviations and Symbols.

lncRNA	long noncoding RNA
GCN	graph convolutional network
CBAM	convolutional block attention module
NAL	node aggregation layer
l	LncRNA number
d	disease number
m	MiRNA number
∥·∥	Modulo operation
∥	concatenate
⊗	dot product

2.2.1.4. Disease and lncRNA Cosine Similarity

To enhance the richness of node features, this study employs cosine similarity based on Euclidean distance to augment the diversity of bioinformatic networks. This approach is beneficial for the feature extraction process using graph convolutional neural networks, enabling the acquisition of more comprehensive node topology information. The calculation formula is as follows

7

8

∥·∥represents the modulus length, A_ld (i,:) represents the ith column of the association matrix, and T represents the transpose symbol.

2.2.2. Representation of Association Information between lncRNAs and Diseases in Heterogeneous Networks

In this method, there are l lncRNAs, d diseases, and m miRNAs, so the association matrix and interaction matrix can be defined as

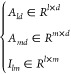9

The heterogeneous association information on lncRNAs with diseases in heterogeneous networks can be expressed as follows

10

11

A_ld represents the LDM, A_md represents the MDM, I_lm is the LMM, l_r represents the multivariate data feature of lncRNAs, d_r represents the disease multivariate data feature, and R represents real numbers.

2.2.3. Dual-path Feature Extraction

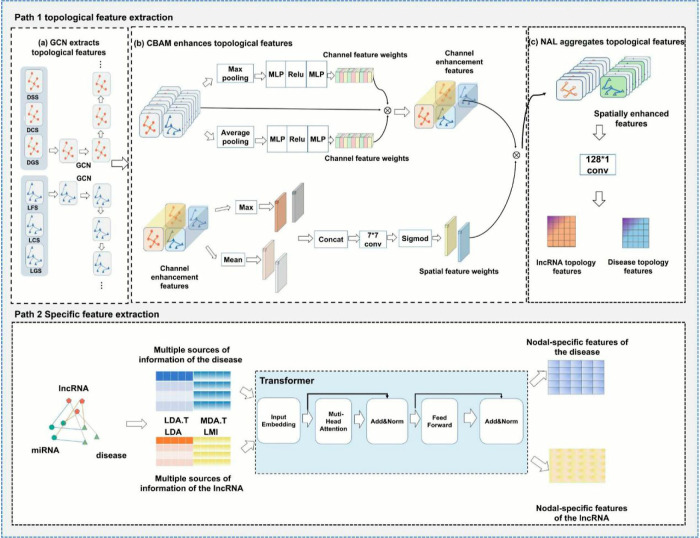
Based on the association information between lncRNAs and diseases in the dual-view structure and the lncRNA-disease-miRNA heterogeneous network, we propose a dual-path feature extraction model which combines the node topology feature extraction network with the node topology feature residual network, as shown in Figure 2.

Figure 2.

Presents the framework of the model, which consists of two parts. The first part is the node topology feature extraction network, which is responsible for extracting the node topology features. The node features from various convolutional layers of the GCN are enhanced using CBAM for channelwise and spatialwise feature enhancement. Then, the aggregated features are passed through the NAL for multichannel convolutional dimension reduction. The second part is the node topology feature residual network, which utilizes the heterogeneous association information between lncRNAs and diseases, along with the Transformer, to extract node-specific features. This network focuses on capturing the specific features of the nodes related to lncRNAs and diseases.

2.2.3.1. Node Topology Feature Extraction Network

Graph Convolutional Neural Network: We utilized the GCN²⁵ as a theoretical motivation for extracting the topological features of lncRNAs associated with diseases, so we considered using a multilayer GCN with hierarchical propagation rules to explore the topological features of the network of diseases associated with lncRNAs, and the formula for the GCN is shown below

12

13

where A is the similarity matrix, and the sizes of the similarity matrices for lncRNAs and diseases are l × l and d × d, respectively. Â is the self-connection of A, D̂ is the degree matrix of Â, H^(l) is the node feature, W^(l) is the linear transformation matrix and σ is the ReLU activation function. In this method, a three-layer GCN is chosen to explore the topological features present in the lncRNA–disease similarity network, where the input and output features of each node are 128-dimensional.

CBAM: Taking as input the intermediate features, H_l, H_d ∈ R^C×H×F, of each similar network in which the GCN has explored the given 1ncRNA and disease, CBAM⁴² sequentially infers a 1D channel attention matrix, M_C ∈ R^C×1×1, and a 2D spatial attention matrix, M_S ∈ R^1×H×W.

The following formula is used for the channel attention module

14

where H is the feature matrix of multiple channels, σ₁ is the ReLU activation function, σ₂ is the sigmoid activation function for the purpose of exploring more potential nonlinear features, MLP is the multilayer perceptron for extracting linear features between channels, AvgPool is the average pooling layer for obtaining the information on the global perceptron field of the channels, and MaxPool is used to extract the key features between channels. H is the intermediate features that have GCN explored and spliced together, F is the node feature dimension, H_l and H_d are the input features of lncRNA or disease for CBAM, the input feature of disease is 1 × 9 × d × 128, the output is 1 × 9 × 1 × 1, the input feature of lncRNA is 1 × 9 × l × 128, and the output is 1 × 9 × 1 × 1.

For the spatial attention module, the formula is shown below

15

where f^7×7 represents the convolution kernel of size 7 × 7, which is derived from the experimental validation of the model,⁴² where H₁ is the input feature of the lncRNA or disease for CBAM, the input feature of the disease is 1 × 9 × d × 128, the output is 1 × 1 × d × 128, the input feature of the lncRNA is 1 × 9 × l × 128, and the output is 1 × 1 × l × 128.

Finally, we can obtain the feature matrix enhanced by CBAM features with the following formula

16

17

where ⊗ represents the element-by-element multiplication, during which the attention values are broadcasted accordingly, and the channel attention is broadcasted along the channel dimension; otherwise, H₂ is the final feature-enhanced feature.

In addition, CBAM attention can be adaptively adjusted according to the characteristics of different views, thus improving the generalizability and adaptability of the model.

NAL: After the graph convolutional layer and convolutional attention, we obtain the feature matrix with node neighborhood topology information and interchannel interactions, which tend to introduce noise due to the high dimensionality of the obtained features. Therefore, in this method, a rectangular convolution kernel is chosen to aggregate only the individual node features, thus reducing the dimensionality of the data and maintaining the integrity and interpretability of the data to be explored. The formula is as follows

18

19

where H_l and H_d are the topological features of lncRNAs and diseases derived from the final training, the convolution kernel is 128 × 1 with a step size of 1, the number of input channels is 9, and the number of output channels is 128. h^l1₂ represents the node features explored by different GCN layers and enhanced by CBAM for different lncRNA views.

2.2.3.2. Node Topology Feature Residual Network

In neighborhood feature aggregation, the effectiveness of the GCN network heavily relies on the degrees of both the central node and its neighboring nodes. Following the graph convolution formula 12, if nodes A and B are connected and the degree of node B is lower than that of node A, the features of node A’s aggregation can be diluted by those of node B. Consequently, node A may lose its unique characteristics, potentially leading to oversmoothing of node features. To address this issue, we employ the Transformer architecture, which utilizes the self-attention mechanism to learn global features while preserving the specificity of the node features.

In this method, we construct a node topology feature residual extraction network using the encoder layer of the Transformer⁴³ model. The encoder layer of the Transformer model comprises N identical stacked layers, with each layer consisting of two sublayers. The first sublayer employs a multihead self-attention mechanism, while the second sublayer is a feedforward neural network based on a fully connected layer. To harness the advantages of residual neural networks, we incorporate residual connections in each sublayer. Additionally, a layer of normalization is introduced. To ensure consistency in the residual connections, all sublayers in the model, including their embeddings, yield 128-dimensional outputs.

Regarding the Multi-Head Attention layer, in this method, the resulting compensated feature matrix is coded for dimensionality reduction using fully connected layers to explore potential linear features. The formula is as follows

20

21

where b̂_l and b̂_d are linear transformations of l_r and d_r. l_r and d_r are multivariate data features of lncRNA and disease, respectively. Matrices such as W are linearly transformed with respect to the features.

As the methodology for investigating compensatory features of lncRNAs and diseases remains consistent, the subsequent section will delineate the approach to exploring the node-specific attributes of an lncRNA node.

After obtaining the features after the completion of the transformation, the similarity between the nodes is determined, and the similarity is used to calculate the weight parameters of each feature with the following formula

22

where ⊗ represents the function matmul in Python. b̂_i, b̂_n represent the node features of the ith and nth lncRNAs, and d_k is the scale factor, which is 128.

After determining the similarity between each node and each node, using the softmax function, the feature weights α are derived with the following formula

23

After calculating the weights, i.e., it is possible to obtain the node features containing new and richer information after the attention mechanism. The formula is as follows

24

here, 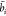represents the node feature of the ith lncRNA derived through exploration, encompassing its unique node-specific details and integrating information from other nodes within the lncRNA perspective.

The idea of multihead attention is the same as the idea of self-attention; only the feature matrix is segmented. First, the self-attention mechanism is performed on each part of the segmentation, and then splicing is performed after the process of the attention mechanism. The feature splicing of lncRNAs is taken as an example, and the splicing formula is as follows

25

|| denotes splicing. B_i represents the features trained in the initial sublayer of the Transformer architecture, where H is designated as the eight-headed attention mechanism in this study.

In addition to the attention sublayer, each layer of the coding layer contains a fully connected feed-forward neural network that consists of two linear transformations with an activation function, as shown in the following equation

26

where W₁ and W₂ are the weight matrices of the fully connected layer and b₁ and b₂ are the biases.

2.2.3.3. Loss Function

To mitigate the reliance on known association nodes in the dual-path feature extraction network, we optimize the loss function by employing matrix multiplication. This approach reduces the two sets of lncRNAs acquired with the updated disease features into an association matrix. By utilizing the association matrix, we aim to obtain more precise potential features. The optimized formula for the loss function is presented below

27

28

2.2.4. Prediction Model

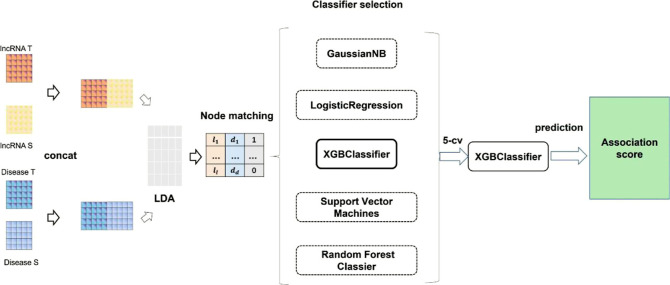
As shown in Figure 3, the prediction of lncRNA–disease association classification is accomplished based on the node features of lncRNAs and diseases obtained from the dual-path feature extraction network. These features are paired through association and labeled. We conducted comparisons with various classifiers, including the Naïve Bayes classifier,⁴⁴ logistic regression,⁴⁵ XGBoost,⁴⁶ support vector machine,⁴⁷ and random forest classifiers.⁴⁸ We ultimately selected the XGBoost classifier to carry out the classification task.

Figure 3.

Feature splicing, node matching and final classification, where lncRNA T and disease T represent topology node features explored by the node topology feature extraction network, and lncRNA S and disease S represent node-specific features explored by the node topology feature residual network.

2.2.5. Experimental Environment

Our method was implemented using the torch_geometric package based on the PyTorch framework. The experiments were conducted on a Windows 10 operating system with an Intel(R) Core(TM) i7–8550U processor and 16 GB of RAM. The maximum number of epochs in our model was set to 500, and all the trainable parameters were optimized using the Adam optimizer with a learning rate of 0.001 and a weight decay rate of 0.05.

Since the data set is imbalanced, with a much larger number of negative samples than positive samples, it is crucial to evaluate the model’s ability to retrieve true positive samples from the predicted positive samples. Here, positive samples are node pairs where 1 is located in the LDM, and negative samples are node pairs where 0 is located in the LDM. In our experiments, we evaluated the model using the following two approaches:

5-fold cross-validation (CV1): The positive and negative samples are divided into five equal parts, with one part randomly selected as the test set and the remaining four parts used as the training set. This evaluation method is mainly employed on Data set 2 in ablation experiments, parametric analysis, and other model building experiments.

5-fold cross-validation (CV2): Repeatedly perform 5-fold cross-validation experiments and select the group of experimental results with the smallest variance as the final result. This evaluation method is utilized for comparisons with baseline models, and model exploration in comparison with the substitution of the dual-path feature extraction network.

2.2.6. Evaluation Metrics

To better evaluate the model performance, based on the evaluation methods of existing studies,³⁵ we used the area under the receiver operating characteristic curve (AUC) and the area under the precision–recall curve (AUPR) as the comprehensive performance evaluation metrics of DPFELDA. Additionally, we used six other evaluation metrics, including accuracy, sensitivity, specificity, precision, F1-score, and Matthews correlation coefficient (MCC). These indicators were calculated as follows

29

30

31

32

33

3. Results

3.1. Performance Comparisons

To verify the validity of the model, we choose the state-of-the-art model in the literature that can work properly through debugging as the baseline model, and to ensure fairness, the model comparison experiments use the same data set with the same experimental environment. The baseline models include LDAformer,³⁵ which mainly utilizes multihop metapaths as original features and uses a Transformer for feature extraction. GAEMCLDA⁴⁹ uses matrix factorization and a graph autoencoder for association prediction of LDA. SDLDA,⁵⁰ exploring lncRNA-disease associations using matrix decomposition with fully connected layers. IPCARF¹¹ is an association prediction method based on a machine learning prediction of association methods using PCA and random forest for prediction. HOPEXGB,⁵¹ exploring heterogeneous graphs using high-order proximity preserved embedding and using XGB to predict the association of lncRNAs with disease. GCLMTP⁵² explores lncRNA and disease node features using graph Contrastive Learning and uses machine learning classifiers for association classification. NAGTLDA⁵³ utilized GCN to explore potential global and local features, and utilized Transformer’s attention mechanism for feature fusion.

The baseline models in this study were constructed using traditional machine learning algorithms and deep learning algorithms. The parameters suggested in the literature were used to run each of these methods. Specifically, GAEMCLDA, LDAformer, NAGTLDA and GCLMTP incorporate the concept of learning graph structures. The evaluation metrics based on 5-CV2 averaging are shown Table 2. To establish the statistical distinction in the predictive performance of DPFELDA relative to the compared methods, we performed Wilcoxon test analyses on the AUC and AUPR evaluation criteria of the baseline methods, as detailed in Supporting Information Table S4. The results revealed that all p-values were below 0.05, signifying a significant superiority of DPFELDA’s performance over the other methods.

Table 2. Performance of the Compared Methods on dataset1 and dataset2 by 5cv2^a.

metric	data set	HOPEXGB	SDLDA	GAEMCLDA	IPCARF	LDAformer	GCLMTP	NAGTLDA	DPFELDA
ACC	data set1	0.8988	0.9870	0.4897	0.9824	0.8794	0.7510	0.9431	0.9956
	data set2	0.8069	0.9852	0.4895	0.9857	0.9054	0.8403	0.9387	0.9943
precision	data set1	0.9531	0.8594	0.0101	0.8579	0.0427	0.0169	0.7086	0.9796
	data set2	0.8882	0.7970	0.0060	0.7825	0.0763	0.0197	0.6560	0.9427
recall	data set1	0.7987	0.3772	0.9444	0.4263	0.8863	0.7498	0.6422	0.8565
	data set2	0.6152	0.3776	0.8699	0.3210	0.7596	0.8618	0.6945	0.7349
MCC	data set1	0.8693	0.7314	0.4831	0.5975	0.1774	0.0866	0.6432	0.9139
	data set2	0.7354	0.5430	0.4931	0.4957	0.1516	0.1156	0.6289	0.8297
F1-score	data set1	0.8691	0.5242	0.0201	0.5691	0.0811	0.0329	0.6727	0.9139
	data set2	0.7269	0.5122	0.0118	0.4551	0.0661	0.0347	0.6738	0.8259
AUC	data set1	0.8988	0.9812	0.9324	0.9261	0.9561	0.8231	0.9381	0.9967
	data set2	0.8069	0.9560	0.8676	0.9132	0.9271	0.9175	0.9348	0.9888
AUPR	data set1	0.7667	0.7990	0.0372	0.6836	0.3568	0.0658	0.7629	0.9671
	data set2	0.5534	0.6040	0.0244	0.5762	0.2273	0.0996	0.7381	0.9222

^aBolding indicates that the evaluation indicator has reached its optimal value under the baseline model.

For two different data sets, Data set1 and Data set2, the same method shows certain differences between the databases. Considering that this may be due to the different ratio of positive to negative samples in the two data sets, with data set1 having a ratio of (1:37) and data set2 having a ratio of (1:54), it can be inferred that a sparse network structure is not conducive to association prediction by LDA. In the comparison of both data sets, DPFELDA demonstrated a significant superiority over the baseline model in both evaluations. In data set 1, DPFELDA outperforms the second-ranked SDLDA by 1.55% in AUC and 16.81% in AUPR. Regarding the evaluation metrics MCC and F1-score for the unbalanced data set, DPFELDA surpasses the second-ranked HOPEXGB by 4.46 and 4.48%, respectively. In data set 2, DPFELDA surpasses the second-ranked SDLDA by 3.28% in AUC and 31.82% in AUPR. Similarly, concerning the evaluation metrics MCC and F-score for the unbalanced data set, DPFELDA exceeds the second-ranked HOPEXGB by 9.43 and 9.9% respectively. The comparison of the baseline models demonstrates the superior performance of DPFELDA. In addition, the comparison with the dual data set in the baseline model highlights the improved suitability of DPFELDA for predicting correlations in unbalanced data sets compared to other LDA prediction models.

Data set 3 serves as a widely adopted benchmark data set, enabling the comparison of DPFELDA with a broader range of graph-structured learning LDA association prediction models. We also explore advanced methods, specifically GTAN,³³ NCPred,³² MGLDA,³¹ GAIRD,⁵⁴ and AGLDA,⁵⁵ which integrate additional deep learning techniques like graph learning and dual paths, showcasing strong performance. In Table 3, DPFELDA achieves the highest AUC, surpassing the second-best AGLDA by 0.8%. Additionally, DPFELDA demonstrates strong performance in AUPR, with most other prediction models having AUPR values between 0.4 and 0.6, while DPFELDA achieves a better 0.967, a notable 28.3% higher than the second-best AGLDA. These results highlight the superior predictive capabilities of DPFELDA.

Table 3. Further Comparisons on Dataset 3.

method	average AUC	average AUPR
GTAN (2022)	0.983	0.454
NCPred (2023)	0.984	0.640
MGLDA (2023)	0.987	0.512
GAIRD (2023)	0.988	0.649
AGLDA (2024)	0.988	0.684
DPFELDA	0.997	0.968

3.2. Ablation Experiment

3.2.1. Feature Extraction Network

To validate the effectiveness of our innovative components, including the dual-path feature extraction network, CBAM, and NAL, we conducted ablation experiments in data set2. As shown in Table 4, the DPFELDA model, which combines the dual-path feature extraction network, CBAM, and NAL, achieved the best performance. Compared to the single-path feature extraction network, the dual-path network with residual connections for node topology features demonstrated an average improvement of 0.3725% in AUC and 3.195% in AUPR. Within the dual-path feature extraction network, removing the CBAM layer resulted in decreases of 1.11% in the AUC and 5.58% in the AUPR, while removing the NAL layer led to reductions of 0.67% in the AUC and 5.96% in the AUPR. Moreover, similar trends were observed in the single-path feature extraction network (after removing CBAM, the AUC and AUPR decreased by 1.03 and 6.25%, respectively; after removing NAL, the AUC and AUPR decreased by 0.56 and 10.97%, respectively).

Table 4. Performance of DPFELDA and Its Variants of 5cv1 in Dataset 2.

single-path network	AUC (%)	AUPR (%)	dual-path network	AUC (%)	AUPR (%)
GCN	96.91	79.65	GCN + Transformer	97.36	84.09
GCN + CBAM	98.07	81.16	GCN + CBAM + Transformer	98.29	86.47
GCN + NAL	97.66	85.00	GCN + NAL + Transformer	97.85	86.85
GCN + CBAM + NAL	98.63	91.25	GCN + CBAM + NAL + Transformer	98.96	92.43

3.2.2. Multiview Fusion

We explored the impact of similarity networks and their combinations on disease-lncRNA prediction in data set2 via a dual-pathway feature extraction network and the XGBoost classifier. As shown in Table 5, the effects of different similarity networks and their combinations on LDA prediction are not simply linear relationships. Compared with the DSS + LFS combination, the DCS + LCS combination achieved a greater AUC and AUPR (0.13 and 0.05%, respectively). Among the two-view combinations, DCS + LCS outperformed DSS + LFS, with higher AUC and AUPR values (0.99 and 3.17%, respectively), and DCS + LCS also outperformed DGS + LGS, with higher AUC and AUPR values (0.58 and 0.43%, respectively). Among the combinations of the two similarity networks, DGS + LGS and DCS + LCS achieved greater AUC and AUPR values than did DSS + LFS and DGS + LGS (1.15 and 6.35% and 0.99 and 6.78%, respectively). The combination of DGS + LGS, DCS + LCS and DSS + LFS yielded the best prediction performance.

Table 5. Performance of DPFELDA with Different Views of 5cv1 in Dataset 2.

metric	AUC (%)	AUPR (%)
DCS + LCS	97.77	84.70
DSS + LFS	96.78	81.53
DGS + LGS	97.19	84.27
(DSS + LFS) & (DGS + LGS)	97.48	85.08
(DSS + LFS) & (DCS + LCS)	97.64	84.65
(DGS + LGS) & (DCS + LCS)	98.63	91.43
(DGS + LGS) & (DCS + LCS) & (DSS + LFS)	98.96	92.43

3.3. Parameter Analysis

In this study, all the hyperparameters used in DPFELDA are referenced in the Materials and Methods Section. As shown in Table 6, we adjusted the important hyperparameters: the number of heads of the multihead attention and encoder layers in the Transformer and the number of graph convolution layers. In Supporting Information Figure S2, we chose 8 heads among (2, 4, 6, 8) for attention and 1 layer among (1, 2, 3, 4) for the encoder under the path of node topological features to extract the residual network. As shown in Supporting Information Figure S1, we selected 3 layers for graph convolution among (1, 2, 3, 4, 5) under the path of the node topological feature extraction network. In Supporting Information Figure S3, we selected two output dimensions for the topology extraction networks among (32, 64, 128, 256), and the final feature output dimensions for both networks were set to 128 under the dual-path feature extraction network.

Table 6. Hyperparameter Settings for DPFELDA.

hyperparameter	setting
transformer self-attention heads	(2, 4, 6, 8)
transformer encoder layers	(1, 2, 3, 4)
GCN layers	(1, 2, 3, 4, 5)
node feature output dimensions	(32, 64, 128, 256)

3.4. Model Exploration

In addition, to validate the role of the dual path extraction network in DPFELDA, we explore the option of replacing the DPFELDA dual path feature extraction network with the graph attention (GAT) topological feature extraction network in data set2. The model details are shown in the Supporting Information Figure S5. Also, in order to validate the role of the topological feature residual network, we considered the option of using the GAT topological feature extraction network to replace the topological feature extraction network in the DPFELDA scheme. The model details are shown in the Supporting Information (Figure S6).

To validate whether the DPFELDA dual-path feature extraction network alleviates the issue of node-specific disappearance, we considered replacing the dual-path feature extraction network with the GAT topology feature extraction network, as shown in Supporting Information Table S3. The dual-path feature extraction network outperformed GAT with a 5.69% higher AUC and a 42.71% higher AUPR, and DPFELDA demonstrated better performance than GAT in other evaluation metrics. To verify the effectiveness of the topology residual network, we replaced DPFELDA topology feature extraction network with the GAT topology feature extraction network. The addition of the topology residual network on top of the GAT topology feature network resulted in a 3.21% increase in the AUC and a 29.51% increase in the AUPR. Other evaluation metrics also showed varying degrees of improvement, indicating the effectiveness of the topology residual feature extraction network. Inspired by the IPCRF model,¹¹ we considered four different dimensionality reduction techniques, as shown in Supporting Information Table S2: PCA⁵⁶ for principal component analysis, ICA⁵⁷ for independent component analysis, RP⁵⁸ for random projection, and NAL as a dimensionality reduction technique based on CNNs and fully connected layers. The results indicated that NAL was more helpful for node classification tasks.

3.5. Case Study

To investigate the model’s feasibility, this paper conducts case study experiment. The experiment involves removing the feature columns related to a specific disease and excluding the disease from participating in the training of the classifier model during the training phase. Finally, the particular disease is used to make predictions with lncRNA associations to validate the accuracy of the association prediction results. Hepatocellular carcinoma, breast cancer, gastric cancer, and colorectal cancer were chosen for analysis and prediction in data set 1 and data set 2, respectively. For each disease within different data sets, the top 30 candidate lncRNAs were selected based on their prediction scores. To further validate the predictive ability of DPFELDA, we selected LncRNADisease 3.0,⁵⁹ lnc2Cancer v3.0, EVlncRNA s3,⁶⁰ and literature-based candidate association pairs for validation. Table 7 displays the candidate lncRNAs identified for hepatocellular carcinoma in data set 1, where 28 lncRNAs are associated with hepatocellular carcinoma. After validation, 26 candidate lncRNAs were confirmed to be associated with breast cancer (see Supporting Information Table S5), 28 with gastric cancer (see Supporting Information Table S6) and 28 with colorectal cancer (see Supporting Information Table S7). In the case study of data set2 with (Supporting Information Tables S8–S11), 30 candidate lncRNAs for breast, gastric, and hepatocellular carcinomas were experimentally validated, while 28 candidate lncRNAs for colorectal cancer were validated.

Table 7. Top 30 Predicted lncRNAs Associated with Hepatocellular Cancer in dataset1.

rank	lncRNA	evidence	PMID	rank	lncRNA	evidence	PMID
1	MEG3	LncRNADisease	21625215	16	MIR194-2HG	LncRNADisease	33116574
2	H19	LncRNADisease	21489289	17	HNF1A-AS1	LncRNADisease	27084450
3	GAS5	LncRNADisease	26163879	18	ZEB1-AS1	LncRNADisease	25025236
4	MALAT1	LncRNADisease	26614531	19	PVT1	LncRNADisease	27495068
5	CDKN2B-AS1	LncRNADisease	25966845	20	SNHG1	LncRNADisease	27133041
6	TUG1	LncRNADisease	27339553	21	AFAP1-AS1	lnc2Cancer	26803513
7	UCA1	LncRNADisease	26551349	22	DANCR	LncRNADisease	27919960
8	LINC00687	UNKNOWN		23	HOTTIP	LncRNADisease	24114970
9	PANDAR	lnc2Cancer	26054684	24	HULC	LncRNADisease	27285757
10	DBH-AS1	LncRNADisease	26393879	25	CCAT2	LncRNADisease	28280353
11	LINC00602	UNKNOWN		26	NEAT1	LncRNADisease	28526689
12	LINC00974	lnc2Cancer	25476897	27	MIR7–3HG	LncRNADisease	24296588
13	HCCAT5	Literature	23314567	28	XIST	LncRNADisease	27776968
14	CYTOR	LncRNADisease	26356260	29	SPRY4-IT1	LncRNADisease	27899259
15	HOTAIR	lnc2Cancer	32062551	30	TRERNA1	lnc2Cancer	31012192

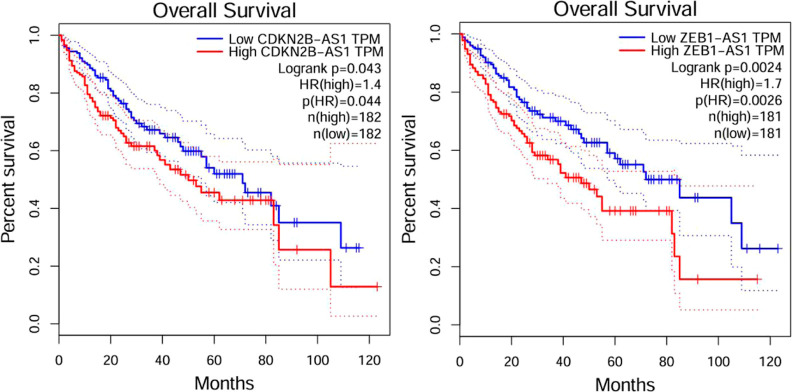
In data set1, in order to verify the accuracy of the experiment, we made use of TCGA data to do survival analysis of hepatocellular carcinoma with CDKN2B-AS1, ZEB1-AS1. As shown in Figure 4, the lower the expression of LncRNAs leading to hepatocellular carcinoma over time, the higher the survival probability of the patients. This also indicates that our prediction has a positive prognostic effect on the disease. In addition, as shown in Supporting Information Figure S9, we also did a survival analysis of breast cancer with STXBP5-AS1 in data set2. It was found that the lower the expression of LncRNAs leading to breast cancer over time, the higher the probability of patient survival.

Figure 4.

Survival analysis of hepatocellular cancer cells.

4. Discussion

To alleviate the issues of node specificity loss in lncRNA disease association prediction, this study proposes an innovative DPFELDA prediction model. The model utilizes a dual-pathway model feature extraction network to enhance the representation of node features and combines it with an XGBoost classifier for disease association prediction. Through 5-fold cross-validation, the performance of the model was found to be superior to that of other existing LDA prediction models.

Several researchers have adopted the dual-pathway approach (MGLDA,³¹ NCPred,³² and GTAN³³) for LDA prediction models. Similarly, our DPFELDA model also adopts the dual-pathway feature extraction approach. However, our model uses heterogeneous networks as input and enhances feature acquisition through a similar residual connection, improving the model’s predictive performance.

To construct an accurate LDA prediction model, as shown in Supporting Information Table S1 and Figure S4, we compared several classifiers, including naive Bayes, random forest, support vector machines, logistic regression, and XGBoost. Among these classifiers, XGBoost exhibited the best performance, so we chose XGBoost as the classifier for our model.

The LDAformer model utilizes a heterogeneous graph of a similarity network and an association matrix to extract multihop metapath information for nodes via matrix multiplication. As shown in Table 2. The AUC of LDAformer in data set2 reaches 0.9271, but due to the influence of sample imbalance, the AUPR is only 0.2273. In DPFELDA, the node topology feature residual pathway also uses the association information on the heterogeneous graph as input. Under sample imbalance, the AUC and AUPR of the DPFELDA model constructed using the dual-pathway feature extraction approach are 0.0617 and 0.6949 greater than those of the LDAformer, respectively. This indicates that DPFELDA not only improves the predictive performance of LDA but also alleviates the low AUPR caused by sample imbalance.

GAEMCLDA is an LDA prediction model based on graph autoencoders (in data set2 AUC: 0.8676, AUPR: 0.0244). Consistent with the node topology feature extraction network of DPFELDA, both models use graph structure learning methods. As shown in Table 4, under the single pathway of the node topology feature extraction network, utilizing a GCN model combined with various similarity networks to extract node topology features (in data set2 AUC: 96.91, AUPR: 79.65) performed better than the GAEMCLDA model. After adding the CBAM model, its performance improved. However, in the process of graph structure learning, the average feature smoothing of nodes may lead to a decrease in the model’s predictive performance. As shown in Table 4, adding the node topology residual network in the dual-pathway network improves the performance of the model, indicating that the DPFELDA node topology residual network alleviates this problem to a certain extent and provides a new way to address the feature smoothing problem. It should be noted that GAEMCLDA compresses the disease feature matrix and the lncRNA feature matrix into a new LDA correlation matrix. It then evaluates the model using this new LDA matrix in comparison with the original LDA matrix. This behavior results in GAEMCLDA classifying a significant number of unknown samples as positive, consequently contributing to its high Recall value.

IPCARF utilizes the PCA technique for dimensionality reduction, which enhances the overall performance of the model. Inspired by the existing research on IPCARF, we NAL to the node topology feature extraction network. However, due to the limitations of the PCA technique, it cannot fully explore and aggregate the extracted node features. Therefore, we innovatively combined the CNN and fully connected layers for feature aggregation, as shown in Table 4 and Figure 2. Under the single-pathway network, the combination of GCN and NAL achieved an AUC and AUPR that were 7.32 and 33.63% greater than those of IPCARF (91.32 and 57.62%, respectively) in data set2. Furthermore, as shown in Table 4, under the dual-pathway network structure, the use of NAL or CBAM as innovative elements does not overshadow their role in improving model performance despite the increase in model complexity.

In order to verify the robustness of the model, we evaluated the generalization of the model using data set1, data set2, data set3, data set4, the results show that the model has a low dependency on the data and achieves a good performance on the four different data sets. See (Supporting Information Table S12).

However, the DPFELDA model still has some limitations. (1) To enhance the complexity of lncRNA-disease topology in constructing the lncRNA-disease view, we computed the similarity matrix between lncRNA and disease based on the existing association matrix. However, this approach results in the training features being reliant on the association matrix, potentially hindering the accurate prediction of new association pairs. (2) As the DPFELDA model is founded on a deep learning model, its learning process requires manual adjustments by individuals, and the hyperparameters within the model structure must also be fine-tuned for varying data volumes and features, thereby intensifying the training workload. In the future, we will continue to explore deep learning models suitable for generalization of lncRNA-disease association prediction and improve the adaptability of the models themselves to data input. Additionally, as bioinformatics progresses, we aim to incorporate multimodal biological data on disease and lncRNA as primary feature inputs, reducing reliance on association matrices. This approach will facilitate the exploration of novel lncRNA-disease associations and potentially aid wet experiments, further enhancing our understanding of the role of lncRNA in disease pathogenesis.

5. Conclusion

This paper presents a dual-pathway-based prediction model for lncRNA–disease associations, and through comparative experiments, it demonstrates the superiority of DPFELDA. We also conducted case studies and performed survival analysis experiments on the associations between lncRNAs and diseases, validating the accuracy of lncRNA–disease association prediction. These findings will facilitate the selection of diseases and lncRNAs for use in biological experiments. Further exploration of the role of lncRNAs in disease development will contribute to a better understanding of disease pathogenesis and provide improved treatment strategies.

Data Availability Statement

All code and data are available at https://github.com/ydkvictory/DPFELDA

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.4c05365.

• Parametric analyses, classifier comparisons, model exploration, Wilcoxon test analysis, case studies with survivability analysis, Robustness experiments (PDF)

Author Contributions

D.Y. directed the research and revised the paper. B.Z. conceived and implemented the model, performed the experiments, and wrote the paper. X.Z. and B.Z. analyzed the experimental results and revised the paper. X.K.L. performed the experiments and revised the paper. All the authors have read and approved the final manuscript.

This work is supported by the National Natural Science Foundation of China (grant no. 62172128). The funding body did not play any role in the design of the study; the collection, analysis, or interpretation of the data; or the writing of the manuscript.

The authors declare no competing financial interest.