Abstract
Complex coacervation plays an important role in various fields. Here, the influences of the backbone chemistry and ionic functional groups of five pairs of oppositely charged polyelectrolytes on complex coacervation were investigated. These pairs include synthetic polymers with aliphatic hydrocarbon backbones, peptides with amide bonds, and carbohydrates with glycosidic linkages. Despite sharing identical charged groups, specific pairs displayed distinct liquid/liquid and liquid/solid phase separations depending on the polyelectrolyte mixing ratio, buffer, and ionic strength. The coacervate phase boundary broadened in the orders: glycosidic linkages > amide backbone > aliphatic hydrocarbon backbone, and Tris-phosphate > Tris-acetate > Tris-chloride buffers. Coacervates prepared from polyelectrolytes with lower solubilities in water resisted disassembly at high salt concentrations, and their merge rate was slow. These observations suggest that the hydrophobic segments in polyelectrolytes interfere with the formation of complex coacervates; however, following coacervate formation, the hydrophobic segments render the coacervates stable and elastic.
Subject terms: Soft materials, Physical chemistry, Chemical synthesis, Organic molecules in materials science
Complex coacervation is propelled by the electrostatic association between oppositely charged polyelectrolytes, but the factors that drive complex coacervation have yet to be fully understood. Here, the authors investigate the influence of the backbone chemistry and ionic functional groups of five pairs of oppositely charged polyelectrolytes on complex coacervation.
Introduction
Coacervation, which is also known as liquid–liquid phase separation (LLPS), refers to the spontaneous separation of dissolved macromolecules in an aqueous solution to generate two distinct phases, namely a polymer-rich dense coacervate phase and a polymer-depleted dilute phase1,2. This process is driven by a multitude of attractive forces including electrostatic interactions, cation–π interactions, hydrogen bonds, hydrophobic interactions, and van der Waals forces3,4.
Complex coacervation, which is propelled by the electrostatic association between oppositely charged polyelectrolytes, has been extensively investigated using a wide range of synthetic polymers and biopolymers, such as proteins and carbohydrates5,6. Its importance transcends various fields, including materials science, food technology, pharmaceuticals, and biological systems7–9.
Thermodynamically, complex coacervation can be viewed as a two-stage process involving the formation of polyion pairs through the complexation of polycations and polyanions, followed by condensation of the polyion pairs to generate the coacervate phase10,11. Notably, the first stage corresponding to ion pairing is characterized by substantial entropic contributions in their free energy changes, which are commonly believed to be due to counterion release upon complexation between the oppositely charged polyelectrolyte chains12–14. However, recent findings from coarse-grained simulations have revealed the significance of solvent reorganization as a major entropic component15. Furthermore, experimental evidence suggests that partial dehydration plays a role in driving complex coacervation16, thereby highlighting the growing importance of polyelectrolyte hydration properties in complex coacervation.
Complex coacervation is also intricately influenced by several other factors, including the molecular weight, charge density, polymer architecture, charged structures, and hydrophilicity of the involved species. As a result, the resulting coacervate phases exhibit a diverse spectrum of material and physical properties, ranging from liquid-like to gel- or solid-like states. For instance, in complex coacervations involving polypeptides or synthetic polymers bearing polyethylene-, polymethacrylate-, and polyether-based backbones, increases in the molecular weight and charge density tend to broaden the phase boundary and can even induce precipitation in certain cases17–20. In addition, the guanidinium ionic groups of arginine have been reported to contribute to a larger two-phase region and a more viscous coacervate phase than the ammonium ionic groups of lysine17,21. Although significant progress has been made in elucidating the molecular characteristics that govern coacervation with synthetic polymers, the direct translation of this knowledge to proteins or carbohydrates remains an ongoing area of research. To date, a range of synthetic polymers with diverse backbone chemistries and structures have been studied. In terms of natural polymers, proteins are composed of peptide backbones, while the majority of carbohydrates are composed of furanose and/or pyranose rings. Given the critical role of the polymer backbone with respect to its hydration during folding and nucleation22,23, this disparity in the backbone composition is likely to result in different complex coacervation properties.
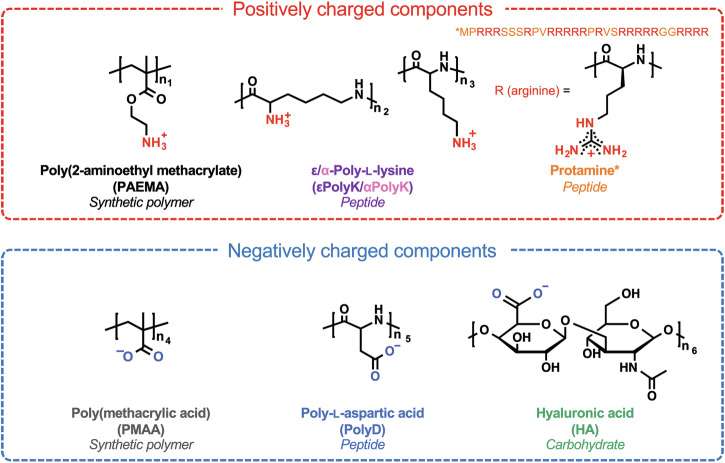
Thus, the current study aims to systematically compare complex coacervation using a range of synthetic polymers, peptides, and carbohydrates with similar molecular weights (3–7 kDa) and ionization degrees. Relatively low-molecular-weight polyelectrolytes are used to rule out the contribution of chain entanglement. The selected cationic polyelectrolytes include poly(2-aminoethyl methacrylate) (PAEMA) with an aliphatic carbon backbone, ε-poly-L-lysine (εPolyK) and α-poly-L-lysine (αPolyK) with ammonium groups, and protamine, an arginine-rich peptide (~65 mol% arginine; MPRRRSSSRPVRRRRRPRVSRRRRRGGRRRR) possessing numerous guanidinium groups. Notably, protamine lacks lysine and other anionic or aromatic amino acids. For the anionic polyelectrolytes bearing carboxyl groups, poly(methacrylic acid) (PMAA) with an aliphatic carbon backbone, α-poly-L-aspartic acid (PolyD) with a peptide backbone, and hyaluronic acid (HA) composed of D-glucuronic acid and N-acetyl-D-glucosamine are employed. Given that charged peptides typically feature positively charged amine and guanidinium groups, as well as negatively charged carboxyl groups, this study aims to establish a better understanding of the physical chemistry of coacervate systems. Moreover, to understand the effects of different backbones and ionic functional groups on complex coacervation, five pairs of cationic:anionic polyelectrolytes are examined for complex coacervation, namely PAEMA:PMAA, εPolyK:PMAA, αPolyK:PMAA, Protamine:PMAA, PAEMA:PolyD, and PAEMA:HA. This is achieved through variation in the weight ratios of the two oppositely charged polyelectrolytes. Subsequently, the influences of the polyelectrolyte backbone chemistry on the coacervation tendencies in response to different buffers and salt concentrations are evaluated, as well as the viscoelastic properties of the resulting coacervates. This comparative approach aims to highlight the underlying principles of complex coacervation across diverse molecular species.
Results
Polyelectrolyte solubility in different buffer systems
Initially, εPolyK, αPolyK, Protamine, PolyD, and HA with similar ionization degrees and molecular weights (3–7 kDa) were prepared, as outlined in Fig. 1. More specifically, to prepare synthetic polymers with the same number of charged moieties, PMAA and PAEMA with a degree of polymerization (DP) of 40 were employed. A well-controlled DP was successfully obtained for each polymer with a desired monomer conversion, DP, and polydispersity index (PDI) being confirmed by 1H nuclear magnetic resonance (NMR) spectroscopy and gel permeation chromatography (GPC) (Supplementary Figs. 1–2). To assess the impact of the polyelectrolyte hydration properties on complex coacervation, the solubility of each polyelectrolyte was measured in an aqueous buffer (Table 1). Since the polymer solubility can be influenced by a wide range of factors, such as the temperature, pH, salt content, and buffer composition, a 19 mM Tris-chloride (Tris-Cl) buffer at pH 7.5 was employed due to its ability to dissolve all polyelectrolytes at room temperature. Saturated solutions were prepared by collecting the supernatants of the supersaturated polyelectrolyte solutions after centrifugation. The solubility of each polyelectrolyte was quantified by measuring the weights of the dried saturated solutions of specific volumes. It was found that the solubilities of εPolyK (326.67 mg/mL) and αPolyK (>1000 mg/mL) were approximately one order of magnitude higher than that of PAEMA (63.33 mg/mL), despite both sharing the same ionic functional group. This suggests that εPolyK and αPolyK, which each possess a peptide backbone, are more hydrophilic than PAEMA, which possesses an aliphatic hydrocarbon backbone. Additionally, the higher solubility limit of αPolyK compared to that of εPolyK clearly demonstrates the influence of the backbone hydrophilicity, since these two structures exist as two different isoforms of the same species. In the case of protamine, at concentrations >40 mg/mL, simple coacervation occurred, characterized by a spherical shape, indicating that phase separation driven by hydrophobic arginine–arginine stacking had taken place21. The occurrence of simple coacervation in protamine, rather than precipitation, suggests that protamine exhibits a greater degree of hydration24. Nonetheless, it should be noted that coacervation is more favored in its salt form (i.e., protamine sulfate), as shown in Supplementary Fig. 3. In the case of dialyzed protamine (protamine sulfate thoroughly dialyzed against deionized water), its coacervation assembly in the 19 mM Tris-HCl buffer pH 7.4 was also observed using a microscope. At 40 mg/mL, the dialyzed protamine still underwent coacervation, although the yield of coacervates was smaller than that observed in the case of protamine sulfate. We also confirmed that coacervation is more dominant at a higher concentration of 100 mg/mL. This demonstrates that although protamine on its own undergoes simple coacervation above 40 mg/mL, the impact of counter ions (i.e., sulfate) should also be considered. Among the anionic polyelectrolytes, PMAA, PolyD, and HA exhibited significantly higher solubilities than the cationic polyelectrolytes, exceeding 1000 mg/mL. However, measuring the solubility beyond 1000 mg/mL was not feasible because of the large volume of polymer powder required, and the high viscosity of the resulting solution.
Fig. 1. Chemical structures of the selected polyelectrolytes.
The asterisk (*) indicates the primary sequence of protamine. The values n1 = 40, n2 = 25–35, n3 = 30, n4 = 40, n5 = 30, and n6 = 1.2–25 correspond to the respective polymer repeating units.
Table 1.
Average degrees of polymerization, molecular weights, solubilities, and SASA values of the polyelectrolytes
| Polyelectrolyte | Degree of polymerizationa | Molecular weightb (g/mol) | Solubility (mg/mL) | SASA(Å2)c |
|---|---|---|---|---|
| PAEMA | 40 | 7098 | 63.33 ± 9.43 | 954 |
| εPolyK | 30 | 4000 | 326.67 ± 81.34 | 1309 |
| ɑPolyK | 30 | 4900 | >1000 | 1219 |
| Protamined | 31 | 4068 | <40 | 1383 |
| PMAA | 40 | 3750 | >1000 | 757 |
| PolyD | 30 | 4100 | >1000 | 816 |
| HA | 12 | 5000 | >1000 | 2196 |
All experiments were conducted in triplicate, and the data are presented as mean values ± SD.
aFor PAEMA and PMAA, the values are determined using Eq. (2) in the “Methods” section. For protamine, the value indicates the number of amino acids in the primary sequence.
bFor PAEMA and PMAA, the average molecular weights were determined using Eq. (1) in the “Methods” section. The average molecular weight was determined as per the manufacturer’s specifications.
cSASA calculations were performed on a pentamer, with polyarginine serving as the basis for protamine analysis, as detailed in the “Methods” section.
dThe solubility of protamine was determined through turbidity measurements, which marked the transition from a two-phase to a one-phase solution.
Subsequently, density functional theory (DFT) calculations were employed to further explore the solubility differences between polyelectrolytes. This involved calculating the optimized structures and atomic charges of the polyelectrolytes. Their solvent accessible surface areas (SASAs) were also determined, along with their atomic charge distributions. Additional details are provided in the “Methods” section.
Based on the calculation results, the main difference between the cationic polyelectrolytes was determined to be the optimized structure. More specifically, PAEMA exhibits a short backbone with long, radiating side chains, while εPolyK features a long backbone and no side chains, resulting in a linear elongated shape (Supplementary Fig. 4a and b). This leads to different levels of accessibility in a solvated environment, wherein εPolyK exposes nearly all atoms, while PAEMA, which contains many overlapping areas, exposes relatively fewer atoms, as verified by the computed SASA values (Table 1 and Supplementary Fig. 5). More specifically, the larger SASA value of εPolyK (1309 Å2) compared to that of PAEMA (953 Å2) indicates that εPolyK is more hydrated. Thus, despite their identical charged groups, the different backbone shapes render εPolyK more soluble than PAEMA. Similar to PAEMA, poly-arginine, a simplified model that was used herein to represent protamine, possesses a short backbone bearing long side chains (Supplementary Fig. 4c). However, due to its β-sheet-like structure, the overlapping areas are expected to be much smaller, as evidenced by its SASA value, which is comparable to that of εPolyK (Table 1). Poly-arginine is therefore expected to maintain its hydrated state without undergoing precipitation. Moreover, the amphiphilic and quasi-aromatic properties of the arginine guanidine group likely promote π stacking and lead to the formation and stabilization of simple coacervation21,25,26. In the cases of εPolyK (1309 Å2) and αPolyK (1219 Å2), only a minor difference was observed between their SASA values. This was likely due to the limitations of the pentamer system since discernable differences were observed in the experimental results (as detailed in the subsequent sections).
For the anionic PMAA and PolyD species, no significant variations were found for their optimized structures or SASA values (Table 1 and Supplementary Fig. 6a and b). However, their atomic charges differed, demonstrating that the peptide backbone of PolyD possesses a distinct and wider range of charges than the hydrocarbon backbone of PMAA (Supplementary Fig. 7). Such a discrepancy in the charge distribution, which originated from the backbone type, will therefore be expected to influence the interaction strengths between these species and the cationic polyelectrolytes, ultimately leading to different coacervation behaviors. It was also found that the optimized structure of hyaluronic acid (HA) was linear and that the SASA value of this species was exceptionally large (Table 1 and Supplementary Fig. 6c). Thus, the large accessible area of HA, along with its abundant hydroxyl groups, should promote interactions with water molecules and ions to render HA highly soluble.
Effect of the polycation:polyanion ratio on the phase behavior
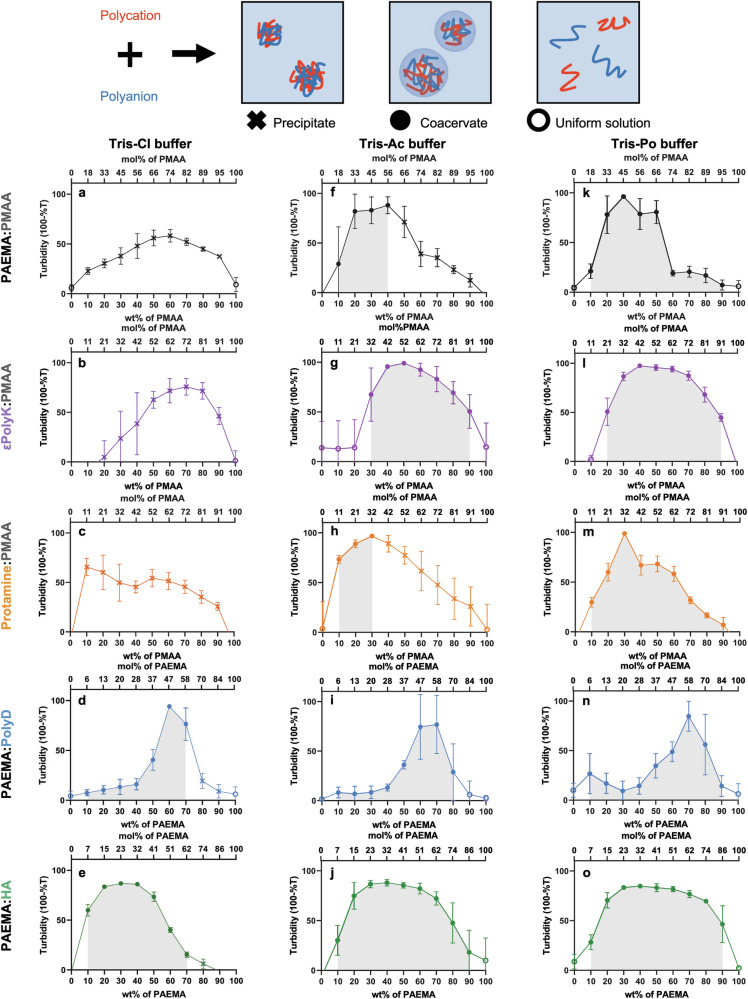
Subsequently, the coacervation phase behavior was observed as a function of the cationic:anionic polyelectrolyte mixing ratio using 10 mM Tris-Cl buffer (pH 7.5, Fig. 2a–e). This assessment was conducted by measuring the relative turbidity and by observing the liquid–liquid phase separation using an optical microscope.
Fig. 2. Complex coacervation behaviors in different buffers.
Schematic representation (top) and plots of turbidity vs. the polymer mixing ratio (bottom) for phase separation. a–e In Tris-Chloride (Tris-Cl) buffer; (f–j) In Tris-Acetate (Tris-Ac) buffer; (k–o) In Tris-Phosphate (Tris-Po) buffer. Black plots = PAEMA:PMAA pairs; purple plots = εPolyK:PMAA pairs; orange plots = Protamine:PMAA pairs; blue plots = PAEMA:PolyD pairs; green plots = PAEMA:HA pairs. In the phase diagrams, closed markers indicate the mixing ratios wherein phase separation was observed using an optical microscope. The open markers indicate the mixing ratios wherein phase separation did not occur. The X marks indicate the mixing ratios wherein aggregation was observed. The gray region in each phase diagram represents the coacervation region where phase separation of the polyelectrolytes occurs. Each data point is based on at least three replicate experiments carried out for each respective polyelectrolyte.
In the PAEMA:PMAA, εPolyK:PMAA, and Protamine:PMAA systems, precipitates were observed by optical microscopy at all mixing ratios evaluated herein (marked with an “X” in Fig. 2a–c, see also Supplementary Figs. 8–10). However, for the PAEMA:PolyD and PAEMA:HA systems, broader coacervate ranges were observed (marked as filled circles in Fig. 2d and e, see also Supplementary Figs. 11 and 12).
In the cases of the PAEMA:PMAA, εPolyK:PMAA, and Protamine:PMAA systems in 10 mM Tris-Cl buffer, precipitation occurred at all mixing ratios, rendering it difficult to observe any coacervation tendencies. To address this, a higher-ionic-strength buffer was employed (19 mM Tris-Cl buffer, pH 7.5) to investigate the formation of coacervates through charge screening (Supplementary Fig. 13). Under these conditions, coacervates were formed at narrow regions where, in most cases, the turbidity reached a maximum value (marked as filled circles in Supplementary Fig. 13a–c). This aligns with a previous study showing that coacervates are dominant at their maximum and net charge points27,28. For the majority of other mixing ratios, precipitates were noticeable under optical microscopy observations (marked with an “X” in Supplementary Fig. 13a–c). Interestingly, the αPolyK:PMAA pair formed coacervates at all phase-separated mixing ratios, highlighting the substantial influence of the backbone hydrophobicity on the phase behaviors of such polyelectrolyte complexes (Supplementary Fig. 14e and h). In the case of the PAEMA:PolyD and PAEMA:HA pairs, coacervates were observed at almost all phase-separated mixing ratios; however, their phase separation propensities decreased compared to those observed in the 10 mM buffer, and this was attributed to the increased ionic strength.
Given that the tight binding of molecules and the corresponding expulsion of water and counterions leads to precipitation, the coacervate phase region can provide insights into the hydrophobicity of a polyelectrolyte. While a direct comparison of the solubilities of PMAA, PolyD, and HA poses challenges due to their high solubilities (i.e., >1000 mg/mL), the observed coacervate phase regions suggest that both PolyD (with an amide backbone) and HA (with a carbohydrate backbone) are more hydrophilic than PMAA (with an aliphatic chain). Notably, this observation correlates with the DFT calculation results. Moreover, when comparing the coacervate phase regions of εPolyK:PMAA and εPolyK:HA, in addition to those of Protamine:PMAA and Protamine:HA, in 19 mM Tris-HCl buffer pH 7.4 (Fig. 2b and c, see also Supplementary Fig. 15), it was clear that coacervate formation was more favored in the HA combinations. This preference is likely due to the higher hydrophilicity of HA (Supplementary Fig. 15). This can be further supported by the refractive index and average droplet size (Supplementary Fig. 16), which showed a tendency toward a negative correlation. This implies that coacervates with larger sizes, such as the PAEMA:HA and PAEMA:PolyD pairs, are more hydrated, resulting in a lower refractive index29. These results therefore demonstrate that the mixing ratio of oppositely charged polyelectrolytes affects the phase behavior, and that the solubility of the polyelectrolyte plays a crucial role in determining the coacervate region.
Effect of the buffer anions on complex coacervation
To further investigate the impact of buffer ions on complex coacervation, different salts were introduced into the Tris buffer, namely chloride, acetate, and phosphate, denoted as Tris-Cl, Tris-Ac, and Tris-Po, respectively (10 mM, pH 7.5). By analyzing the turbidity and microscopic images, shifts in the coacervate and precipitate phase regions of certain polymer pairs were observed (Fig. 2 and Supplementary Figs. 8–12). In all cases, the liquid coacervate regions expanded in the order: Tris-Cl < Tris-Ac < Tris-Po buffers. More specifically, in the case of the PAEMA:PMAA, εPolyK:PMAA, and Protamine:PMAA pairs, the precipitate phase dominated when dissolved in the Tris-Cl buffer. However, when dissolved in the Tris-Ac buffer, the coacervate regions were broadened. Intriguingly, in the Tris-Po buffer, all precipitate regions vanished, and coacervates formed at all phase-separated ratios. Moreover, the PAEMA:PolyD and PAEMA:HA pairs predominantly formed coacervates in the Tris-Cl buffer, although precipitates were observed at certain mixing ratios. Similar to the behavior of the PAEMA:PMAA, εPolyK:PMAA, and Protamine:PMAA pairs, in both the Tris-Ac and Tris-Po buffers, the PAEMA:PolyD and PAEMA:HA pairs exclusively formed a coacervate phase (Fig. 2d, i, n, e, j, o, and Supplementary Figs. 11 and 12). Considering that a broader coacervate phase region is indicative of hydrated and loosely formed complexes, these results are consistent with the solubility outcomes. Specifically, the significantly broader coacervate region observed for the εPolyK:PMAA pair compared to the PAEMA:PMAA and Protamine:PMAA pairs correlates with the higher solubility of εPolyK. Notably, the observed increase in the coacervate phase region according to the order chloride < acetate < phosphate, represents an inversion of the Hofmeister series30.
Effect of the salt on complex coacervation
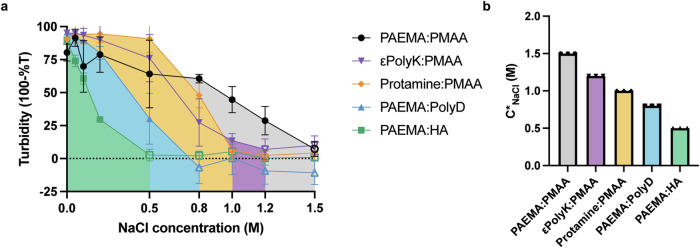
As mentioned previously, electrostatic interactions play a critical role in driving complex coacervation. Owing to the screening effect of salts on the polyelectrolyte charges, the addition of a salt induces disassembly of the complex coacervation system. The amount of NaCl required to dissolve the coacervates (referred to as the salt resistance, C*) depends on the interaction strength between the polymers. Thus, the salt resistance of each polymer coacervate pair formed at the optimal stoichiometry was determined by adjusting the NaCl concentration until the turbid coacervate suspension (indicated by filled marks) transformed into a uniform liquid phase (indicated by open marks) (Fig. 3). From this point onward, the experiments were conducted using 19 mM Tris-Cl buffer at a mixing ratio favoring coacervate formation rather than precipitation. The complex coacervation of the PAEMA:PMAA pair exhibited the highest salt resistance, remaining stable up to a NaCl concentration of 1.5 M. The salt resistance of the other pairs followed the order: εPolyK:PMAA at 1.2 M NaCl > Protamine:PMAA at 1.0 M NaCl > αPolyK:PMAA and PAEMA:PolyD at 0.8 M NaCl > PAEMA:HA at 0.5 M NaCl.
Fig. 3. Salt resistance of the complex coacervates.
a Turbidity results obtained across various sodium chloride salt concentrations. The areas filled with colors indicate the corresponding coacervate regions. b NaCl salt resistance characteristics for the various coacervate pairs. In each case, the polymer concentration (Cp) was 1 mg/mL, and the samples were analyzed immediately after complexation. The error bars indicate the standard deviations determined from three separate measurements.
Overall, the obtained results demonstrated a negative correlation between the solubility and simulation outcomes. The maintenance of coacervates at higher salt concentrations indicates that complexation and coacervation contributed not only to the electrostatic attractions but also to other non-ionic interactions. To investigate the impact of hydrophobic interactions, 10% 1,6-hexanediol was introduced into each coacervate pair dissolved in 19 mM Tris-Cl buffer (pH 7.4) containing 100 mM NaCl (Supplementary Fig. 17). The reduction in ionic strength caused by the presence of NaCl was expected to facilitate the observation of hydrophobic-driven coacervates. In addition, the presence of 1,6-hexanediol, a weak hydrophobic interaction disruptor31,32, was anticipated to provide insights into the role of hydrophobic interactions in coacervate formation. In the case of the PAEMA:PMAA pair, coacervate deformation was observed after the addition of 1,6-hexanediol. This indicates that hydrophobic interactions stemming from their hydrophobic aliphatic backbones played a significant role in driving coacervate formation. Conversely, in the case of the highly hydrated PAEMA:HA pair, the contribution of the hydrophobic interactions to maintaining LLPS seemed to be weaker. Taking the above results into account, the PAEMA:HA pair was considered to be mainly dependent on electrostatic interactions. Additionally, it was observed that αPolyK:PMAA coacervates bearing a shorter backbone chain disappeared at a lower NaCl concentration than the ɛPolyK:PMAA coacervates (Supplementary Fig. 14), indicating that a more hydrophobic backbone contributes to an improved salt resistance. This agrees with previous findings, in which the phase separation of complex coacervates is also dependent on the hydrophobic interactions present in a high-salt regime33.
Coalescence behaviors of the complex coacervates
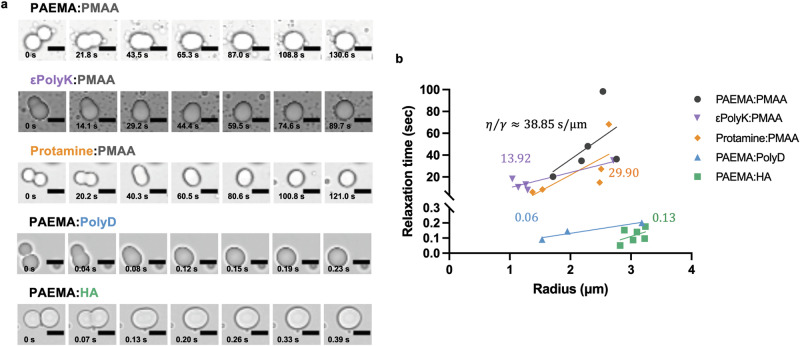
Having demonstrated that both the polymer backbone and the ionic functional groups can influence the phase separation properties of complex coacervates, the ability of these polyelectrolyte characteristics to be manifested in the viscoelastic properties of the resulting coacervates was evaluated. Thus, to characterize the viscoelastic properties of the coacervates, the coalescence behaviors of five pairs of complex coacervates were observed, focusing on the mixing ratios at which the coacervates exhibited the maximum turbidity. As shown in Fig. 4a, when the two liquid droplets come into contact, they merge into a single ellipsoidal liquid body, which subsequently relaxes from this deformed state to yield a spherical shape. The linear slopes obtained for the relaxation time curves of the coalescing coacervates were then used to determine the ratio (η/γ) of the viscosity (η) to the surface tension (γ), which is otherwise known as the inverse capillary velocity (Fig. 4b).
Fig. 4. Coalescence behaviors of the complex coacervates.
a Representative images of the complex coacervate droplets formed in the 19 mM Tris-Cl buffer. For imaging purposes, all liquid/condensate pairs were prepared at the maximum fixed total polymer concentration (i.e., Cp = 1 mg/mL). The time scale units are seconds (s), and the scale bars are 5 μM in all images. b Relaxation time vs. length scale for each polymer pair. The inverse capillary velocity values (s/μm) are indicated for each pair. All samples were prepared using the optimal stoichiometry. Each data image is representative of the observed behavior from at least three test replicates of each respective polyelectrolyte pair.
It was found that the coacervates formed by the aliphatic synthetic polymer pair (i.e., PAEMA:PMAA, ~38.85 s/μm) exhibited an approximately three-fold slower fusion than the εPolyK:PMAA coacervates (~13.92 s/μm), wherein εPolyK shares the same ionic functional groups as PAEMA but possesses a peptide backbone. Additionally, the coacervates of the Protamine:PMAA pair exhibited an approximately two-fold slower fusion (~29.90 s/μm) than that of the εPolyK:PMAA coacervates. This finding agrees with previous literature21, suggesting that arginine is more hydrophobic than lysine and that it contributes to the enhanced physical properties of arginine-rich coacervates. Similarly, despite the fact that PolyD shares the same ionic functional groups as PMAA and possesses a peptide backbone, the PAEMA:PolyD coacervates (~0.06 s/μm) exhibited a significantly faster rate of fusion than the PAEMA:PMAA coacervates (~38.85 s/μm). This result indicates that more hydrated peptides undergo faster fusion than aliphatic synthetic polymers. Furthermore, it was found that the coacervates of the PAEMA:HA pair fused quickly with an inverse capillary velocity of ~0.12 s/μm. Since the hindered relaxation process represents the solid-like properties of a coacervate with viscoelastic properties, this finding highlights the influence of the hydration properties of the polyelectrolyte backbone on the material properties of the resulting coacervate.
Discussion
The pioneering observation of coacervates dates back to the mixing of gelatin as a polycation and gum Arabic as a polyanion in an aqueous medium34. Subsequently, an array of coacervate systems exhibiting diverse properties were elucidated through the use of various peptides, carbohydrates, or polymer-based polyelectrolytes. Notably, coacervates have recently gained public attention as bimolecular condensates in the context of LLPS within cellular environments, and in vitro models have also been developed that replicate the behavior of membrane-less organelles (MLOs). Nevertheless, the intrinsic complexities arising from the diverse primary sequences exhibited by proteins and the challenges posed by controlling the molecular weights of polysaccharides have led to systematic investigations of the physicochemical properties of biomacromolecule-based coacervates. In contrast, the utility of polymer-based polyelectrolytes, whose molecular weights can be controlled by varying the degree of polymerization and the incorporation of specific functional groups, affords a simplified system. This enabled a more systematic exploration and interpretation of the properties inherent to biological coacervates and condensates. In the current study, the properties of five different complex coacervation pairs were systematically characterized based on five factors, namely the solubility, the mixing ratio, the buffer specificity, the salt resistance, and the coalescence rate. The polyelectrolytes in this system differed in their backbone composition (aliphatic hydrocarbons, amide bonds, and glycosidic bonds) and polymer residues (amine, guanidinium, and carboxyl groups), although each contained charged segments of ~3–7 kDa (Fig. 1).
The overall solubility propensity of the polyelectrolytes decreased in the order: polyanions (PolyD, HA, and PMAA) > εPolyK > Protamine ≈ PAEMA. Previously, it has been reported that arginine is more hydrophobic than lysine due to its electron-delocalized quasi-aromatic structure21. This characteristic of arginine-rich protamine therefore appears to explain its lower solubility compared to that of εPolyK. However, it should be noted that Protamine undergoes simple coacervation instead of precipitation at high polymer concentrations >40 mg/mL. Due to this phenomenon, it is illogical to directly compare lysine and arginine based on solubility. Interestingly, despite possessing the same charged functional groups, εPolyK and PAEMA displayed significantly different solubilities, suggesting that the backbone hydration properties have a substantial impact on the polymer solubility. However, this distinction was not observed between the highly soluble PolyD and PMAA. This can be accounted for by considering that the aliphatic hydrocarbon backbone of a polymer is generally more hydrophobic than an amide backbone of a peptide, and HA is a highly soluble polysaccharide that tends to form hydrogels. Therefore, it was expected that the hydration properties of the polyanions would follow this order: HA ≈ PolyD > PMAA.
Similar to the hydration propensities of the polyelectrolytes, the coacervate phase regions, which vary depending on the mixing ratio and choice of buffer ion, exhibit the following order: PAEMA:HA ≈ PAEMA:PolyD ≈ αPolyK:PMAA > εPolyK:PMAA > Protamine:PMAA ≈ PAEMA:PMAA (Fig. 2 and Supplementary Figs. 13 and 14). In line with previous studies demonstrating that coacervation occurs within a range centered around stoichiometric charge compositions, which can be adjusted through salt addition and is influenced by surface charge patches (i.e., particularly in proteins due to their zwitterionic nature and structural complexity), it was observed that coacervation predominantly occurred around the stoichiometric molar ratios. However, an exception was noted in the case of Protamine:PMAA. This deviation was attributed to the unique conformational properties of protamine, as well as the differences in molecular weight and charge density as discussed in the literature27,28. Moreover, for the εPolyK:PMAA and αPolyK:PMAA pairs, the mixing ratios at their highest turbidity values (i.e., the optimal mixing ratios) exhibited minimal variations. Instead, their tendencies to form coacervates or precipitations were significantly different (Supplementary Fig. 14), showing more favorable coacervation for αPolyK:PMAA than for εPolyK:PMAA. This observation suggests that hydrophobicity may have a more significant impact on this system than the charge density. This inference is drawn from the fact that significant variations in the optimal mixing ratios would be anticipated if the charge density played a substantial role.
Interestingly, reversed Hofmeister effects were clearly observed in the PAEMA:PMAA, PolyD:PMAA, and Protamine:PMAA pairs across the Tris-Po, Tris-Ac, and Tris-Cl buffers. Since anions display stronger ion-specific effects than cations due to their greater polarizability ranges35, chloride, acetate, and phosphate were selected as the ionic species of the Tris-buffer to investigate the effects of the Hofmeister series on coacervation formation. Typically, the Hofmeister series for anions follows the order: phosphate > acetate > chloride30. More specifically, the salts earlier in the series induce “salting out” effects and are strongly hydrated, whereas the latter ions induce “salting in” effects and are weakly hydrated. Reversed Hofmeister effects are often observed in colloids, polymers, and proteins with hydrophilic surfaces because of the lower partial dehydration cost associated with the surface binding of well-hydrated ions36–38.
In line with the solubility and coacervation propensities, the salt resistance was found to decrease in the following order: PAEMA:PMAA > εPolyK:PMAA > Protamine:PMAA > αPolyK:PMAA ≈ PAEMA:PolyD > PAEMA:HA (Fig. 3 and Supplementary Fig. 14). The higher salt resistance observed in the PAEMA:PMAA coacervates and the difference found between the εPolyK:PMAA and αPolyK:PMAA pairs indicate that their coacervation is primarily driven by electrostatic interactions, and that additional contributions from non-ionic interactions are also involved. These non-ionic interactions likely stem from the hydrophobic aliphatic hydrocarbon backbones of the synthetic polymers, as supported by the deformation of coacervation observed when adding 1,6-hexanediol as a hydrophobic interaction disruptor (Supplementary Fig. 17). Furthermore, previous studies have suggested that electrostatic interactions can be enhanced close to hydrophobic molecules because of the decreased dielectric constant of water39. More specifically, molecular dynamics simulations have shown that the dielectric constant of water near a hydrophobic surface decreases owing to the reduced water density and the decreased water dipole correlation34. This implies that the responses of the coacervates toward changes in the ionic strength could be attributed to the hydrophilic and hydrophobic properties of their polymer backbones. Furthermore, during the merging event (Fig. 4), it was found that the coacervates formed by the synthetic polymer pairs containing hydrophobic aliphatic backbones exhibited slower merging, indicating a higher viscosity. In contrast, the coacervates formed from peptides bearing amide backbones exhibited faster merging, implying a lower viscosity, and those containing the highly soluble PolyD or glycosidic-linked carbohydrates displayed even faster coalescence, indicative of liquid droplets.
Overall, this study demonstrates that although the complex coacervation of synthetic polymers, peptides, and carbohydrates, is primarily driven by electrostatic interactions and is influenced by the mixing ratios and buffer types, the generated pairs display distinct physical properties, including variations in the coacervate phase region, the salt resistance, and the interface instability. In addition, the hydrophobic segment of the polyelectrolyte also appears to play a role in determining the solubility of the polyelectrolyte and significantly influences whether the polyelectrolyte forms a coacervate or undergoes precipitation. This implies that the conditions for coacervate formation must be meticulously controlled to avoid precipitation. However, once a coacervate is formed, its stability is enhanced even at high salt concentrations, possibly due to enhanced hydrophobic interactions in a charge-screened environment.
These observations suggest that the presence of hydrophobic segments within the coacervate affects its stability and viscoelastic characteristics. Furthermore, the obtained results suggest that hydrophobic residues or segments within biological condensates inside cells or in biological tissues may similarly influence the stabilities and viscoelastic behaviors of biological LLPS systems. Additionally, while hydrophobic segments can contribute to differences in the phase behavior, it is essential to note that the disparity in the charge density among different polymers may also play a role, particularly when electrostatic interactions are favored. Although the charge density was not considered as a variable in this study due to control difficulties, it remains an important factor. A follow-up study is therefore required to explore this aspect further. Moreover, the relatively low stability of the coacervates necessitates careful control during their application in industrial encapsulants. Hence, the insights gleaned from this study can be utilized to regulate the stability of coacervates in different salt and buffer solutions.
Methods
Materials
Poly(2-aminoethyl methacrylate) (PAEMA, molecular weight = 7098 g/mol, DP = 40) and poly(methacrylic acid) (PMAA, molecular weight = 3750 g/mol, DP = 40) were synthesized according to the literature40,41. Methacrylic acid, 2-aminoethyl methacrylate hydrochloride, 2,2′-azobis(2-methylpropionamidine) dihydrochloride (V-50), 4-((((2-carboxyethyl)thio)carbonothioyl)thio)-4-cyanopentanoic acid (CETCPA), sodium nitrate (NaNO3), sodium phosphate monobasic (NaH2PO4), sodium phosphate dibasic (Na2HPO4), and deuterium oxide (D2O) were purchased from Sigma-Aldrich (St. Louis, MO, USA). ɛ-Poly-L-Lysine (ɛPolyK, molecular weight = 4000 g/mol, DP = 25–35) was purchased from Shinseung Hichem (Seoul, Korea). Protamine sulfate salt from salmon (protamine, molecular weight = 4100 g/mol, DP = 31) was purchased from Sigma-Aldrich (St. Louis, MO, USA). Hyaluronic acid (HA, molecular weight 5000 g/mol) was purchased from Bioland (Seoul, Korea). Poly L-aspartic acid sodium salt (PolyD, molecular weight = 4100 g/mol, DP 27–33) & α-poly-L-Lysine (αPolyK, molecular weight = 4900 g/mol, DP = 27–33) were purchased from Alamanda Polymers (Alabama, CA, USA). Sodium chloride was purchased from Sigma-Aldrich (St. Louis, MO, USA). Tris(hydroxyethyl)aminomethane (Tris), 99.8% glacial acetic acid, and 85% phosphoric acid were purchased from Samchun (Seoul, South Korea).
Synthesis of the polyelectrolytes by RAFT polymerization
Synthesis of poly(methacrylic acid)
Phosphate buffer solution (6 mL, 10 mM, pH 7), 4-((((2-carboxyethyl)thio)carbonothioyl)thio)-4-cyanopentanoic acid (CETCPA) (95%, 17.9 mg, 9.2 mM), methacrylic acid (99%, 0.187 mL, 0.367 M), and 2,2′-azobis(2-methylpropionamidine) dihydrochloride (V-50, 97%, 3.0 mg, 1.79 mM) were introduced into a 100 mL flask equipped with a magnetic stirrer bar and sealed with a rubber septum. The mixture was then deoxygenated by freeze–pump–thaw cycling for a minimum of 3 cycles, after which polymerization was performed at 70 °C using a temperature-controlled heating mantle, followed by stirring at 60 rpm for 2 h to reach nearly full conversion. A sample was extracted from the polymerization medium using a degassed syringe for analysis by 1H nuclear magnetic resonance (NMR) spectroscopy and gel permeation chromatography (GPC) to determine the monomer conversion, the experimental molar mass (Mn,GPC), and the dispersity (Ð) values.
Synthesis of poly(2-aminoethyl methacrylate hydrochloride)
Phosphate buffer solution (36 mL, 10 mM, pH 7), CETCPA (95%, 17.9 mg, 1.5 mM), 2-aminoethyl methacrylate hydrochloride (90%, 0.642 g, 0.09 M), and V-50 (97%, 3.0 mg, 0.3 mM) were introduced into a 100 mL flask equipped with a magnetic stirrer bar and sealed with a rubber septum. The mixture was then deoxygenated by freeze–pump–thaw cycling for a minimum of 3 cycles, after which polymerization was performed at 70 °C using a temperature-controlled heating mantle, followed by stirring at 60 rpm for 2 h to reach nearly 67% conversion. A sample was extracted from the polymerization medium using a degassed syringe for analysis by 1H NMR spectroscopy and GPC to determine the monomer conversion, the experimental molar mass, and the dispersity values.
NMR spectroscopy
The 1H NMR spectra were recorded on a Bruker Avance III 500 spectrometer at 25 °C and with a frequency of 500 MHz. The delay time was set to 2.5 s. All polymer samples were prepared in D2O. Chemical shift values (δ) were reported in ppm and were determined with respect to the non-deuterated solvent residue as an internal reference.
Determination of the monomer conversion
The monomer conversion of PMAA was determined by comparing the decrease in the integrated intensity of the 1H NMR vinyl proton signals (δ = 6.00–5.50 ppm) of the monomer with those of the R group protons (δ = 1.30–0.85 ppm) of the polymer after polymerization. In the case of PAEMA, the monomer conversion was determined by comparing the decrease in the integrated intensity of the 1H NMR vinyl proton signals (δ = 6.15–5.60 ppm) of the monomer with those of the R group protons (δ = 3.40–3.20 ppm) of the polymer after polymerization.
Determination of the Mn,th and DP values
The theoretical number-average molar mass (Mn,th) was calculated as follows:
| 1 |
| 2 |
where and are the initial concentrations of the monomer and the chain-transfer agent, respectively, and is the monomer conversion determined by 1H NMR spectroscopy. and represent the molar masses (g/mol) of the monomer and the chain transfer agent, respectively.
GPC studies
The molar mass distributions were measured using a Shimadzu LC-20AD liquid chromatography system with dedicated columns for the anionic and cationic polymers. More specifically, for the anionic polymers, an Agilent PL-Aquagel-OH 8 µm MIXED-M column (300 × 7.5 mm) and an Agilent PL-Aquagel-OH 8 µm guard column (50 × 7.5 mm) were employed. The mobile phase consisted of 90% aqueous 0.15 M NaNO3 and 10% methanol. The flow rate was 1.0 mL/min and the column temperature was 40 °C. The instrument was calibrated using low-dispersity poly(ethyleneoxide) standards (Scientific Polymer) whose molar masses varied between 0.2 and 800 kg/mol. For the cationic polymers, a TOSOH TSKgel 10 µm G5000PWXL-CP column (300 × 7.8 mm) and a TOSOH TSKgel 13 µm PWXL-CP guard column (40 × 6 mm) were used. The mobile phase consisted of a 0.3 M aqueous NaNO3 solution at pH 3 (adjusted using 95% sulfuric acid). The flow rate was 1.0 mL/min and the column temperature was 40 °C. The instrument was calibrated using low-dispersity poly(ethyleneoxide) standards (Scientific Polymer) whose molar masses varied between 0.2 and 800 kg/mol. Prior to analysis, the samples were filtered through a polyvinylidene fluoride membrane with a 0.2 µm pore diameter. The experimental molar mass (Mn,GPC) and the dispersity (Ð) values of the synthesized polymers were determined by conventional calibration using LC Solution software with a known refractive index detector calibration constant.
Buffer preparation
The Tris-chloride buffer (Tris-Cl, 10 × 10−3 M, pH 7.57) was prepared by combining 5.34 mM Tris base with 4.66 mM HCl in distilled water. To achieve a Tris-Cl buffer with higher ionic strength (Tris-Cl, 19 × 10−3 M, pH 7.5), 10 mM Tris base was mixed with 8.89 mM HCl in distilled water. The Tris-Ac buffer (Tris Ac, 10 × 10−3 M, pH 7.55) was prepared by mixing 6.6 mM Tris base with 3.3 mM glacial acetic acid in distilled water. For the Tris-Po buffer (Tris-Po, 10 × 10−3 M, pH 7.59), 7.67 mM Tris base was mixed with 2.33 mM phosphoric acid in distilled water. All buffers were subjected to filtration through a 0.22 μm PVDF syringe filter (Whatman) prior to use.
Complex coacervate formation
Sample solutions (1 mg/mL) were prepared and dissolved in the desired Tris-Cl, Tris-Ac, or Tris-Po buffer in a tube. Complex coacervation was performed at weight ratios ranging from 1:9 to 9:1 for each polyelectrolyte pair, and the solutions were mixed by gentle pipetting. The formation of coacervates was confirmed using optical microscopy (BX63, Olympus, Tokyo, Japan). The corresponding images are provided in the Supplementary Information. To confirm complete polymer ionization, the pH values of the polymers and polymer pairs at their optimal stoichiometric ratios (as determined by turbidity measurements) were measured at a final concentration of 1 mg/mL in 10 mM Tris-HCl buffer at pH 7.5 (Supplementary Fig. 18).
Turbidity measurements
The turbidity measurements were carried out at a wavelength of 600 nm using a microplate reader (BioTek Synergy HTX). The absorbance of the coacervate solution as a function of the mixing ratio, buffer, and NaCl concentration was monitored at room temperature in 384-well plates. The turbidity was defined as (100-%T). Three replicates were analyzed for each sample condition. The coacervates were observed under an optical microscope (BX63, Olympus, Tokyo, Japan).
Salt resistance measurements
Sample solutions were prepared using the 19 mM Tris-Cl buffer. Complex coacervation was performed at the optimal stoichiometric ratios, as determined above. To achieve various NaCl concentrations, precise volumes of NaCl stock solutions (0.1, 0.2, 0.4, 1, 1.6, 2, 2.4, and 3 M) were added accordingly. All coacervate solutions attained a standardized final concentration of 1 mg/mL. The turbidities of the mixed solutions were measured using a microplate reader at a wavelength of 600 nm at room temperature as indicated above. Three replicates were analyzed for each sample condition. The coacervates were observed under an optical microscope (BX63, Olympus, Tokyo, Japan).
Coalescence measurements
The coalescence of each pair of coacervate droplets was observed over time using an Olympus FLUOVIEW FV3000 confocal laser scanning microscope. The coacervate solution was injected into a coverslip-sandwiched fluid chamber with a flat oil–water interface to minimize friction from the chamber surface. The coalescence events were recorded at specific intervals. The relaxation time () was obtained by fitting the aspect ratio vs. time plot to an exponential decay. The aspect ratio was calculated as follows:
| 3 |
where and are the length and the width of between two condensates, respectively. The droplet radius (R) was measured after coalescence.
DFT calculations
Density functional theory (DFT) calculations were used to obtain the optimal structures and atomic partial charges of the polyelectrolytes. Due to the high computational cost and time limitations, it was not feasible to model polyelectrolytes with dozens of degrees of polymerization. Instead, pentamers composed of five monomers were used (e.g., Lys-Lys-Lys-Lys-Lys instead of εPolyK with 30 degrees of polymerization). For Protamine, poly-arginine with a β-sheet structure was employed as a simplified model, referencing the work by Morga et al. 42 and based on a previous study that used molecular dynamics simulations to demonstrate similar hydrophobic and conformational properties between poly-arginine and protamine21. For HA, the structure in the Protein Data Bank with PDB ID 3HYA43,44 was used as an initial condition. An aqueous environment was implemented using the Polarizable Continuum Model45. B3LYP46–48 and 6-311++G(d,p)49,50 were employed as the functional and the basis set, respectively. After structural optimization, vibrational frequency analysis was performed to obtain the optimal structures at a stable point. All calculations were conducted using the Gaussian16 program package51.
Supplementary information
Acknowledgements
This research was supported by the Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (RS-2023-00250609). This work was also financially supported by a National Research Foundation of Korea (NRF) grant funded by the Korean government (MSIT) (No. RS-2024-00408989 & RS-2024-00408795).
Author contributions
Y.H. and S.Y. performed the coacervation experiments and data analyses; J.H. synthesized and characterized the polymers; J.K. and Y.L. performed the DFT calculations; Y.S.J., Y.S.K., and D.S.H. supervised the work. All authors contributed to writing and editing the manuscript.
Peer review
Peer review information
Communications Chemistry thanks the anonymous reviewers for their contribution to the peer review of this work. A peer review file is available.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
These authors contributed equally: Yuri Hong, Surim Yoo, Jihoon Han.
Contributor Information
Youn Soo Kim, Email: ysookim@postech.ac.kr.
Dong Soo Hwang, Email: dshwang@postech.ac.kr.
Supplementary information
The online version contains supplementary material available at 10.1038/s42004-024-01271-7.
References
- 1.de Jong, H. & Kruyt, H. Koazervation. Kolloid-Z.50, 39–48 (1930). 10.1007/BF01422833 [DOI] [Google Scholar]
- 2.Overbeek’, J. T. G. & Voorn, M. J. Phase separation in polyelectrolyte solutions. Theory of complex coacervation. J. Cell. Comp. Physiol. 49, 7–26 (1957). [PubMed]
- 3.Kim, S. et al. Complexation and coacervation of like-charged polyelectrolytes inspired by mussels. Proc. Natl Acad. Sci. USA113, E847–E853 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Dignon, G. L., Best, R. B. & Mittal, J. Annual review of physical chemistry biomolecular phase separation: from molecular driving forces to macroscopic properties. 10.1146/annurev-physchem-071819 (2020). [DOI] [PMC free article] [PubMed]
- 5.De Kruif, C. G., Weinbreck, F. & De Vries, R. Complex coacervation of proteins and anionic polysaccharides. Curr. Opin. Colloid Interface Sci.9, 340–349 (2004).
- 6.Timilsena, Y. P., Akanbi, T. O., Khalid, N., Adhikari, B. & Barrow, C. J. Complex coacervation: principles, mechanisms and applications in microencapsulation. Int. J. Biol. Macromol. 121, 1276–1286 (2019). [DOI] [PubMed]
- 7.Banani, S. F., Lee, H. O., Hyman, A. A. & Rosen, M. K. Biomolecular condensates: Organizers of cellular biochemistry. Nat. Rev. Mol. Cell Biol. 18, 285–298 (2017). [DOI] [PMC free article] [PubMed]
- 8.Jho, Y. S., Yoo, H. Y., Lin, Y., Han, S. & Hwang, D. S. Molecular and structural basis of low interfacial energy of complex coacervates in water. Adv. Colloid Interface Sci. 239, 61–73 (2017). [DOI] [PubMed]
- 9.Blocher McTigue, W. C. & Perry, S. L. Protein encapsulation using complex coacervates: what nature has to teach us. Small.16, 10.1002/smll.201907671 (2020). [DOI] [PubMed]
- 10.Perry, S. L., Li, Y., Priftis, D., Leon, L. & Tirrell, M. The effect of salt on the complex coacervation of vinyl polyelectrolytes. Polymers6, 1756–1772 (2014). 10.3390/polym6061756 [DOI] [Google Scholar]
- 11.Aberkane, L., Jasniewski, J., Gaiani, C., Scher, J. & Sanchez, C. Thermodynamic characterization of acacia gum-β-lactoglobulin complex coacervation. Langmuir26, 12523–12533 (2010). 10.1021/la100705d [DOI] [PubMed] [Google Scholar]
- 12.Priftis, D., Laugel, N. & Tirrell, M. Thermodynamic characterization of polypeptide complex coacervation. Langmuir28, 15947–15957 (2012). 10.1021/la302729r [DOI] [PubMed] [Google Scholar]
- 13.Priftis, D., Megley, K., Laugel, N. & Tirrell, M. Complex coacervation of poly(ethylene-imine)/polypeptide aqueous solutions: Thermodynamic and rheological characterization. J. Colloid Interface Sci.398, 39–50 (2013). 10.1016/j.jcis.2013.01.055 [DOI] [PubMed] [Google Scholar]
- 14.Chang, L. W. et al. Sequence and entropy-based control of complex coacervates. Nat. Commun.8, 1273 (2017). [DOI] [PMC free article] [PubMed]
- 15.Chen, S. & Wang, Z.-G. Driving force and pathway in polyelectrolyte complex coacervation. 10.1073/pnas (2022). [DOI] [PMC free article] [PubMed]
- 16.Park, S. et al. Dehydration entropy drives liquid-liquid phase separation by molecular crowding. Commun. Chem.3, 83 (2020). [DOI] [PMC free article] [PubMed]
- 17.Kim, S., Lee, M., Lee, W. B. & Choi, S. H. Ionic-group dependence of polyelectrolyte coacervate phase behavior. Macromolecules54, 7572–7581 (2021). 10.1021/acs.macromol.1c00216 [DOI] [Google Scholar]
- 18.Cakmak, F. P., Choi, S., Meyer, M. C. O., Bevilacqua, P. C. & Keating, C. D. Prebiotically-relevant low polyion multivalency can improve functionality of membraneless compartments. Nat. Commun.11, 5949 (2020). [DOI] [PMC free article] [PubMed]
- 19.Spruijt, E., Westphal, A. H., Borst, J. W., Cohen Stuart, M. A. & Van Der Gucht, J. Binodal compositions of polyelectrolyte complexes. Macromolecules43, 6476–6484 (2010). 10.1021/ma101031t [DOI] [Google Scholar]
- 20.Neitzel, A. E. et al. Polyelectrolyte complex coacervation across a broad range of charge densities. Macromolecules54, 6878–6890 (2021). 10.1021/acs.macromol.1c00703 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Hong, Y. et al. Hydrophobicity of arginine leads to reentrant liquid-liquid phase separation behaviors of arginine-rich proteins. Nat. Commun.13, 7326 (2022). 10.1038/s41467-022-35001-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Camino, J. D., Gracia, P. & Cremades, N. The role of water in the primary nucleation of protein amyloid aggregation. Biophys. Chem.269, 106520 (2021). [DOI] [PubMed]
- 23.Bignucolo, O., Leung, H. T. A., Grzesiek, S. & Berneìche, S. Backbone hydration determines the folding signature of amino acid residues. J. Am. Chem. Soc.137, 4300–4303 (2015). 10.1021/jacs.5b00660 [DOI] [PubMed] [Google Scholar]
- 24.Liu, X. et al. The correlation between thermally induced precipitate-to-coacervate transition and glass transition in a polyelectrolyte-bolaamphiphile complex. Aggregate4, e363 (2023).
- 25.Vazdar, M. et al. Arginine ‘magic’: guanidinium like-charge ion pairing from aqueous salts to cell penetrating peptides. Acc. Chem. Res.51, 1455–1464 (2018). 10.1021/acs.accounts.8b00098 [DOI] [PubMed] [Google Scholar]
- 26.Gund, P. Guanidine, trimethylenemethane, and ‘Y-delocalization.’ Can acyclic compounds have ‘aromatic’ stability? J. Chem. Educ.49, 100–103 (1972). 10.1021/ed049p100 [DOI] [Google Scholar]
- 27.Blocher, W. C. & Perry, S. L. Complex coacervate-based materials for biomedicine. Wiley Interdiscip. Rev.9, 10.1002/wnan.1442 (2017). [DOI] [PubMed]
- 28.Gucht, J., van der, Spruijt, E., Lemmers, M. & Cohen Stuart, M. A. Polyelectrolyte complexes: bulk phases and colloidal systems. J. Colloid Interface Sci.361, 407–422 (2011). 10.1016/j.jcis.2011.05.080 [DOI] [PubMed] [Google Scholar]
- 29.Hong, Y. et al. Label-free quantitative analysis of coacervates via 3D phase imaging. Adv. Opt. Mater.9, 2100697 (2021). 10.1002/adom.202100697 [DOI] [Google Scholar]
- 30.Okur, H. I. et al. Beyond the Hofmeister series: ion-specific effects on proteins and their biological functions. J. Phys. Chem. B.121, 1997–2014 (2017). [DOI] [PubMed]
- 31.Lin, Y. X. et al. Liquid-liquid phase separation of tau driven by hydrophobic interaction facilitates fibrillization of tau. J. Mol. Biol.433, 166731 (2021). 10.1016/j.jmb.2020.166731 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Ribbeck, K. & Görlich, D. The permeability barrier of nuclear pore complexes appears to operate via hydrophobic exclusion. EMBO J.21, 2664–2671 (2002). 10.1093/emboj/21.11.2664 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Li, L. et al. Effect of solvent quality on the phase behavior of polyelectrolyte complexes. Macromolecules54, 105–114 (2021). 10.1021/acs.macromol.0c01000 [DOI] [Google Scholar]
- 34.Bungenberg de Jong, H. G. in Colloid Science 2, Reversible Systems. (ed Kruyt, H. R.) 335 (Elsevier Publ. Co., New York, 1949).
- 35.Lo Nostro, P. & Ninham, B. W. Hofmeister phenomena: an update on ion specificity in biology. Chem. Rev. 112, 2286–2322 (2012). [DOI] [PubMed]
- 36.Peula-García, J. M., Ortega-Vinuesa, J. L. & Bastos-González, D. Inversion of Hofmeister series by changing the surface of colloidal particles from hydrophobic to hydrophilic. J. Phys. Chem. C.114, 11133–11139 (2010). 10.1021/jp912035v [DOI] [Google Scholar]
- 37.Oncsik, T., Trefalt, G., Borkovec, M. & Szilagyi, I. Specific ion effects on particle aggregation induced by monovalent salts within the Hofmeister series. Langmuir31, 3799–3807 (2015). 10.1021/acs.langmuir.5b00225 [DOI] [PubMed] [Google Scholar]
- 38.Schwierz, N., Horinek, D., Sivan, U. & Netz, R. R. Reversed Hofmeister series—the rule rather than the exception. Curr. Opin. Colloid Interface Sci.23, 10–18 (2016).
- 39.Sato, T., Sasaki, T., Ohnuki, J., Umezawa, K. & Takano, M. Hydrophobic surface enhances electrostatic interaction in water. Phys. Rev. Lett.121, 206002 (2018). [DOI] [PubMed]
- 40.Chaduc, I., Lansalot, M., D’Agosto, F. & Charleux, B. RAFT polymerization of methacrylic acid in water. Macromolecules45, 1241–1247 (2012). 10.1021/ma2023815 [DOI] [Google Scholar]
- 41.Alidedeoglu, A. H., York, A. W., McCormick, C. L. & Morgan, S. E. Aqueous RAFT polymerization of 2-aminoethyl methacrylate to produce well-defined, primary amine functional homo- and copolymers. J. Polym. Sci. A Polym. Chem.47, 5405–5415 (2009). 10.1002/pola.23590 [DOI] [Google Scholar]
- 42.Morga, M., Batys, P., Kosior, D., Bonarek, P. & Adamczyk, Z. Poly-L-arginine molecule properties in simple electrolytes: molecular dynamic modeling and experiments. Int. J. Environ. Res. Public Health19, 3588 (2022). [DOI] [PMC free article] [PubMed]
- 43.Arnott, S. Hyaluronic acid, molecular conformations and interactions in two sodium salts. Protein Data Bank. initial deposition: 20 November (1977). Initial release: 28 March (1980). Latest revision: 13 July (2011).
- 44.Goss, J. M. et al. Hyaluronic acid: molecular conformations and interactions in two sodium salts. J. Mol. Biol.95, 359–364 (1975). [DOI] [PubMed]
- 45.Tomasi, J., Mennucci, B. & Cammi, R. Quantum mechanical continuum solvation models. Chem. Rev.105, 2999–3093 (2005). [DOI] [PubMed]
- 46.Becke, A. D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys.98, 5648–5652 (1993). 10.1063/1.464913 [DOI] [Google Scholar]
- 47.Lee, C., Yang, Eitao & Parr, R. G. Development of the Colic-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B Condens. Matter. 37, 785–789 (1988). [DOI] [PubMed]
- 48.Stephens, P. J., Devlin, F. J., Chabalowski, C. F. & Frisch, M. J. Ab initio calculation of vibrational absorption and circular dichroism spectra using density functional force fields. J. Phys. Chem.98https://pubs.acs.org/sharingguidelines (1994).
- 49.Krishnan, R., Binkley, J. S., Seeger, R. & Pople, J. A. Self-consistent molecular orbital methods. XX. A basis set for correlated wave functions. J. Chem. Phys.72, 650–654 (1980). 10.1063/1.438955 [DOI] [Google Scholar]
- 50.Clark, T., Chandrasekhar, J., Spitznagel, G. W., Von, P. & Schleyer, R. Efficient diffuse function-augmented basis sets for anion calculations. III.† The 3-21+G basis set for first-row elements, Li-F. J. Comput. Chem.4, 294–301 (1980).
- 51.Frisch, M. J. et al. Gaussian 16, Revision C.01; (Gaussian, Inc.: Wallingford, CT, 2016).
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.