Abstract
Scale-free statistics of coordinated neuronal activity, suggesting a universal operating mechanism across spatio-temporal scales, have been proposed as a necessary condition of healthy resting-state brain activity. Recent studies have focused on anesthetic agents to induce distinct neural states in which consciousness is altered to understand the importance of critical dynamics. However, variation in experimental techniques, species, and anesthetics, have made comparisons across studies difficult. Here we conduct a survey of several common anesthetics (isoflurane, pentobarbital, ketamine) at multiple dosages, using calcium wide-field optical imaging of the mouse cortex. We show that while low-dose anesthesia largely preserves scale-free statistics, surgical plane anesthesia induces multiple dynamical modes, most of which do not maintain critical avalanche dynamics. Our findings indicate multiple pathways away from default critical dynamics associated with quiet wakefulness, not only reflecting differences between these common anesthetics but also showing significant variations in individual responses. This is suggestive of a non-trivial relationship between criticality and the underlying state of the subject.
Subject terms: Dynamical systems, Neural circuits, Power law, Phase transitions and critical phenomena
The significance of deviations from scale-free (SF) neural activity for consciousness is unclear. Using anesthetics, the authors show multiple paths from SF activity, indicating a complex relationship between non-SF activity and the participant’s state.
Introduction
The critical brain hypothesis has been proposed as a theoretical framework with which to study multi-scale neuronal dynamics1–4. Proponents suggest that a self-organized critical state, situated between high and low entropy operating regimes, imbues the brain with computational advantages that are necessary for normal brain function5–7. Renormalization group theory suggests that the existence of such a critical state—or potentially critical region8—would imply collective neuronal dynamics are independent of superficial complexities and differences across scales and species9, and could instead be understood by a handful of relevant parameters such as excitation-inhibition balance10,11. This would be in line with recent efforts to re-frame neural dynamics as occurring on low-dimensional manifolds12,13, but would additionally suggest that such a dimensionality reduction could be made across spatial and temporal scales. The critical hypothesis has been, at least initially, motivated by the observation that clusters of neuronal firings organize in a scale-free manner, which would be a prerequisite for criticality14,15. However, it is also understood that signatures of criticality are not unique to resting-state brain function, as evidenced by the fact that in vitro neuronal cultures and tissues also exhibit scale-free neuronal firings1,16.
To better understand the role critical dynamics play in brain function, researchers have utilized anesthesia as a method of pharmacological manipulation of the critical state17–19. Generally speaking, the goal of any such experiment is to relate deviations from homeostatic equilibrium to changes in the critical state. Despite divergent pharmacological properties between various anesthetics, the outcome is often qualitatively similar—various levels of artificially reduced responsiveness20. While these studies offer key insights into brain criticality, such as either loss of criticality17,18, or a reduced domain over which criticality can be established21, comparisons between experiments are difficult to make as many of these studies use different anesthetics. For example, isoflurane and ketamine, both common choices for anesthetic, have been observed to induce radically different brain dynamics - the former enhances beta frequencies, while the latter enhances delta frequencies22.
Despite mechanistic and physiological differences, anesthetics achieve a loss of sensation and awareness. Whether these involve a common path away from a critical state is not known. This leaves a fundamental question unanswered—what are the possible paths away from the critical state? Sub or super-criticality, or potential changes in the universality class? Because individual studies often focus on one drug (or other method)16–18,23 to alter the critical state, it is not clear that all of these different paths are available, or that the observed deviations do not simply reflect details of the experiment (species, in vivo versus in vitro, recording technique, etc.) in some way. Here, we use avalanche analysis to identify deviations from critical states induced by several anesthetic agents at both low-dose and surgical planes of anesthesia. We use mesoscale cortical calcium imaging in mouse, in which a large expanse of dorsal neocortex is simultaneously sampled with high spatiotemporal fidelity. Specifically, we examine the barbiturate pentobarbital, that is selective to GABA-A receptors24, the dissociative anesthetic ketamine that acts preferentially on NMDA receptors25, and the volatile anesthetic isoflurane, that acts on both GABA-A receptors and NMDA receptors26,27. We found surgical-plane doses of isoflurane and ketamine can induce changes from scale-free statistics in quiet wakefulness, while low doses did not. Conversely, pentobarbital-induced changes appear dose-independent. We also observed multiple distinct calcium dynamics for a surgical plane level of anesthesia. In particular, surgical plane levels of isoflurane and ketamine typically induced large system-sized bursts and wave-like dynamics, respectively, while a small number of recordings displaying critical avalanche statistics could still be observed, despite the same loss-of-responsiveness state, suggestive of non-universal responses across individuals.
Results
Scale-free avalanches in quiet wakefulness
A necessary feature of critical dynamics is scale-free statistics15 in the form of
| 1 |
where S is the spatiotemporal size of clustered activity (in this case, calcium transients), also known as an avalanche, and τ is the critical exponent. To define calcium-transience avalanches across the field of view, we first binarized the processed Thy1-jRGECO1a calcium fluorescence signal (here on out referred to as “the calcium signal”) using a per-pixel threshold of ϕ standard deviations above the mean (see also methods for further details). We utilize jRGECO as this sensor has a favorable combination of brightness (high SNR) and decay time28, and (as with other red-shifted calcium biosensors) reduced hemodynamics contamination. An example of the mean binarized signal (ϕ = 1) across the duration of a single recording is shown in Fig. 1a. Above threshold, or “active”, pixels are clustered into avalanches.
Fig. 1. Avalanche analysis of quiet wakefulness controls (QW).
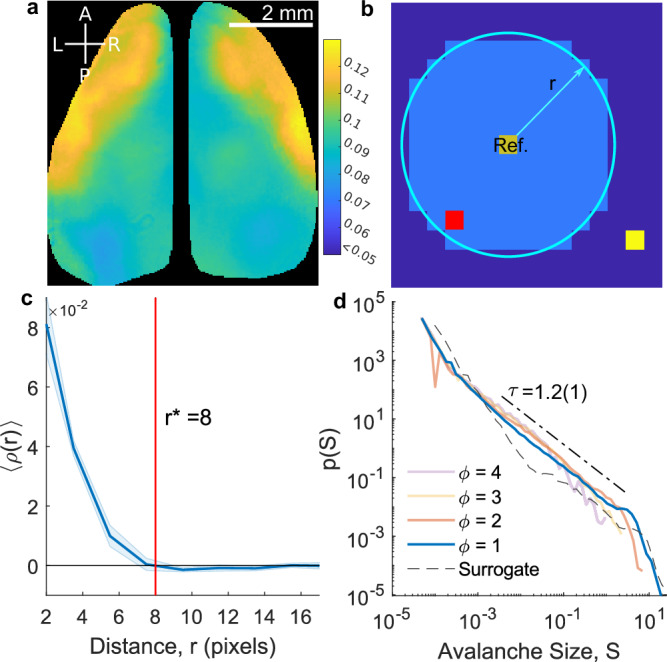
a The average number of activations for a single QW recording is illustrated (ϕ = 1). The midline overlying the sagittal sinus is removed to prevent cross-hemisphere merging. b An example of activity clustering is illustrated. Any active site within both one frame and a neighborhood of radius r of the active reference pixel (Ref.), such as the red pixel but not the yellow one, is clustered to the same avalanche as Ref. c The mean partial correlation function averaged over all awake recordings (N = 12) is shown, with shaded area denoting standard deviation. The zero crossing (r*) defines the neighborhood used to classify avalanches. d Avalanche size distributions for various thresholds ϕ are shown (in units of standard deviations), with the space shuffled surrogate distribution and the dot-dashed line representing τ. Source data are provided as a Source data file.
Cortical dynamics have long-range functional connectivity extending beyond a single pixel. As such, clustering schemes based only on the nearest neighboring pixels may break up causally related avalanches. To account for this we define a radius of direct influence, r. Two active pixels within a distance r, and one time frame of one another, are clustered within the same avalanche (Fig. 1b)29. Pre-existing avalanches crossing this boundary are “merged”, and both are (retroactively) relabeled to be the same avalanche. The radius r is estimated from the first zero crossing of the partial correlation function (PCF, see also methods), occurring at r* = 8 ± 2 (Fig. 1c). Once clustered, the normalized avalanche size (S) is a unit-less value defined as the total number of active pixels participating in the avalanche (repeat activation included), divided by the number of cortical pixels per hemisphere ().
Probability densities were estimated via logarithmic binning of avalanche sizes for all quiet wakefulness (QW) recordings (N = 12). For ϕ = 1, the avalanche rate across recordings was 13 ± 6 avalanches/second, and a total of 7(2) × 102 avalanches/recording. QW avalanche size distributions followed scale-free statistics with an estimated mean exponent, averaged across recordings, τ = 1.2(1), and a typical dynamic range of . Figure 1d presents the avalanche size distribution across multiple thresholds obtained by concatenating across all recordings, which is representative of individual recordings (see S1).
We also analyzed surrogate distributions generated by random shuffling of pixels in space, and random cyclic permutations of pixel signals in time17,30. The former, shown as the dashed curve in Fig. 1d, preserves the tail (due to finite size effects) but changes the head of the distribution. The latter consistently generated never-ending, system-sized avalanches, with smaller events being almost entirely non-existent (not shown for figure clarity). This analysis suggests both spatial-temporal correlations are important aspects of the avalanche distribution p(S).
In addition to avalanche sizes, we analyzed avalanche durations, T, defined as the number of seconds (or frames) that an avalanche took to occur. Their range of values is much smaller than that of avalanche sizes, covering only about two orders of magnitude. Nevertheless, their distributions, p(T), also followed power-law statistics typically over one order of magnitude with an exponent α = 1.7(2) (more on durations in S2). If criticality holds, α and τ uniquely determine the relation between the average avalanche duration for a given size, 〈T 〉(S), and S16. Specifically, 〈T 〉(S) ∝ Sγ with
| 2 |
γ can be directly estimated via robust linear fit to 〈T 〉(S) (see S2), and compared to γ(α, τ), which is calculated from the above equation. The independent equivalency of γ and γ(α, τ) can be considered a test for criticality31. We found that in ten out of twelve recordings, the equivalence between γ and γ(α, τ) held within statistical uncertainties of one σ. Of the two recordings where the scaling relation only held within three σ, we found that it was because the size exponent τ was very close to 1, where the scaling relation given by Eq. (2) becomes problematic and systematic uncertainties are large. Averaged over the twelve recordings we found γ = 0.31(4), and γ(α, τ) = 0.34(9). The exponents mentioned above, as well as those obtained in the following sections, are all summarized in Table 1.
Table 1.
Estimated critical exponents averaged across recordings belonging to the different conditions, with the number of recordings in brackets
| Condition (n) | τ | α | γ | γ(α, τ) | SR | Δ AICLogN | ||
|---|---|---|---|---|---|---|---|---|
| QW (12) | 1.2(1) | 1.7(2) | 0.31(4) | 0.34(9) | 10/12 | −28.99 | 2.14 | 3.41 |
| Iso. 1 % (6) | 1.24(4) | 1.5(2) | 0.41(4) | 0.51(2) | 6/6 | 0.34 | 1.79 | 2.02 |
| Iso. 2 % (7) | — | — | — | — | — | — | — | — |
| A.L. Iso. 2 % (3) | 1.17(4) | 1.5(1) | 0.37(3) | 0.33(6) | 3/3 | −1.15 | 1.54 | 2.30 |
| Ket. 10 mg/kg (8) | 1.08(7) | 1.9(3) | 0.28(5) | 0.10(8) | 5/7 | −24.44 | −2.08 | 2.10 |
| Ket. 100 mg/kg (6) | — | — | — | — | — | — | — | — |
| A.L. Ket. 100 mg/kg (1) | 1.05(2) | 1.8(3) | 0.27(3) | 0.06(2) | 0/1 | N/A | 1.35 | N/A |
| Pen. 12.5 mg/kg (6) | 1.0(1) | 1.7(2) | 0.28(5) | 0.31(6) | 3/3 | −2.04 | 0.49 | 2.26 |
| Pen. 80 mg/kg (4) | 1.04(8) | 1.8(5) | 0.25(5) | 0.1(1) | 2/3 | 1.29 | 1.96 | 2.08 |
Cases in which no scale-free statistics were observed have been left blank. Uncertainties for the exponents represent one standard deviation except in the case of awake-like (A.L.) ketamine, where the 95th percentile of MLE was used as there was only one recording. γ(α, τ) is presented as the average over all recordings for which the scaling relation in Eq. (2) was testable (i.e., τ > 1). SR is the fraction of recordings for which the scaling relation in Eq. (2) was satisfied within two σ, likewise relative to the number of recordings for which the scaling relation was testable. ΔAIC is presented as the tenth, median, and 90th percentiles (from left to right). Uncertainties for AL ketamine 100 mg/kg could not be established as there was only one such documented case.
Avalanche statistics in the presence of anesthetics
Low-dose anesthesia
Next, we analyzed low-dose anesthesia recordings corresponding to isoflurane 1% (N=6), ketamine 10 mg/kg (N=8), and pentobarbital 12.5 mg/kg (N=6). Examples of the cortex-wide average calcium trace in a window of 20 s is shown in Fig. 2a for each anesthetic and QW. Figure 2b shows no significant changes to the PCF in any case. At ϕ = 1, avalanche size distributions follow a power-law distribution (Fig. 2c). The average exponents for isoflurane and ketamine were estimated to be τ = 1.24(4) and τ = 1.08(7), respectively. Pentobarbital recordings had a lower average exponent (τ = 1.0(1)), and in three recordings τ < 1. For all three anesthetics, the fitting domain was reduced to .
Fig. 2. Avalanche analysis of low-dose anesthetic recordings.
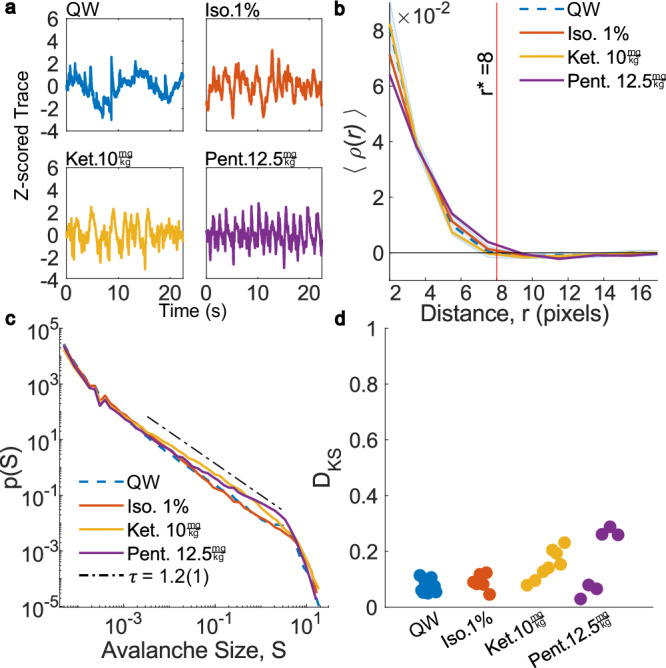
a Examples of (z-scored) traces of the total calcium activity. b The mean estimated PCF for isoflurane 1% (N = 6), ketamine 10 mg/kg (N = 8), and pentobarbital 12.5 mg/kg (N = 6) with quiet wakefulness (QW) for reference. The vertical line shows the first zero crossing for QW. The shaded area for QW denotes uncertainty standard deviation (omitted from others for clarity). c Avalanche size statistics along with QW for reference. The dot-dashed reference line is the QW reference. d KS distance between individual recordings, against the concatenated QW distribution. Axis limits expanded to allow for direct comparison with surgical plane anesthesia in Fig. 3. Source data are provided as a Source data file.
Per recording, avalanche durations had an average exponent of α = 1.5(2) for isoflurane, α = 1.9(3) for ketamine, and α = 1.7(2) for pentobarbital. The scaling relation given by Eq. (2) held for all testable (i.e., τ > 1) isoflurane and pentobarbital recordings within two σ, while it held in five out of seven ketamine recordings. For the other two recordings, τ was very close to 1 where systematic uncertainties can become very large as mentioned above. The aforementioned exponents are shown in Table 1.
We also calculated the Kolmogorov–Smirnov distance (DKS) of avalanches on a per-recording basis against the concatenated QW statistics as a binning-independent measure of (dis)similarity (Fig. 2d) (see methods). Per-recording QW recordings were tested for consistency and had a mean value of 0.07(4). Isoflurane exhibited similar behavior (〈DKS〉 = 0.09(3)), whereas ketamine recordings showed larger deviations (〈DKS〉 = 0.15(5)), which is consistent with what is observed in Fig. 2c. Pentobarbital recordings had a KS distance of 〈DKS〉 = 0.2(1), but also showed higher variability.
To test statistical significance, we performed a two-sample Wilcoxon rank-sum test (rank-sum, MATLAB) with Bonferroni–Holm correction between both avalanche size exponents and DKS values of QW and all low-dose cases. Specifically, for the critical exponents τ, we found that all low-dose cases were not statistically different from QW at the 95% significance level. The rank-sum test between the distributions of DKS values suggested that only the low-dose pentobarbital is statistically different (p = 0.002).
Surgical plane anesthesia: predominant dynamics
Examples of the total calcium activity under surgical plane anesthesia levels are shown in Fig. 3a. Isoflurane and ketamine each produced two distinct dynamical modes. Isoflurane 2% predominantly produced smallscale fluctuations interrupted by aperiodic cortex-wide bursts (7 recordings out of N = 10 total), whereas ketamine 100 mg/kg was typically (6 out of N = 7) associated with wave-like activity. In these cases, which we call the “predominant” case, the changes in calcium dynamics can be clearly differentiated from QW by way of phase-space representations obtained by Hilbert transform (S3). The other recordings, which could not be differentiated from QW, are discussed in the next section.
Fig. 3. Avalanche analysis of predominant dynamics for surgical plane anesthesia.
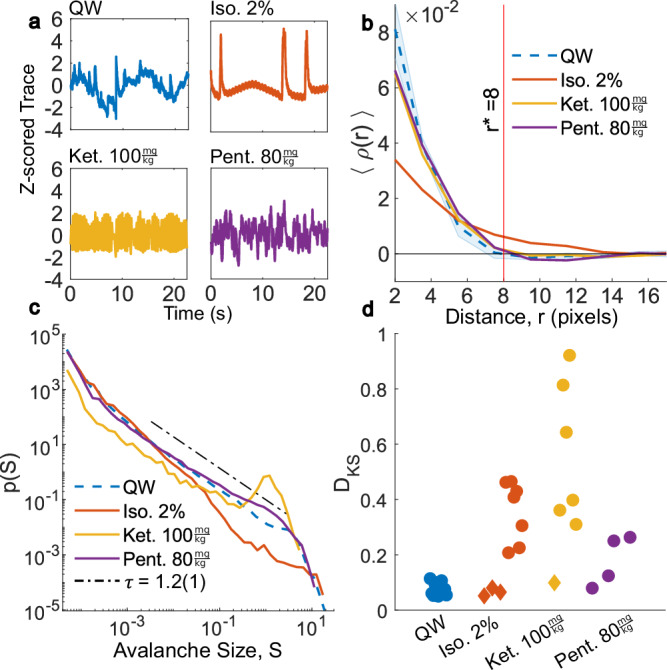
a Examples of (z-scored) traces of the total calcium activity. b The mean estimated PCF for the isoflurane 2% (N = 7), ketamine 100 mg/kg (N = 6) and pentobarbital 80 mg/kg (N = 4) with quiet wakefulness (QW) for reference. The vertical line shows the first zero crossing for QW. The shaded area for QW denotes uncertainty standard deviation (omitted from others for clarity). c Avalanche statistics along with QW for reference. The dot-dashed reference line is the QW reference. d KS distance between individual recordings, against the concatenated QW distribution. Awake-like recordings (indicated by diamonds) are included for comparison. Source data are provided as a Source data file.
As Fig. 3a shows, Pentobarbital 80 mg/kg (N = 4) produced more qualitatively regular dynamics, though not to the same extent as ketamine. Figure 3b shows the mean PCF, averaged across recordings. We found that isoflurane heavily reduced the PCF while ketamine and pentobarbital appeared to produce a minor suppression of the PCF, but more statistics would be needed to make a definitive claim. Figure 3c shows the avalanche size distributions. The wave-like dynamics under ketamine produce a characteristic size which manifest as a large peak near S ≈1, indicating excessive cortex-wide avalanches consistent with wave-like dynamics. Conversely, isoflurane produced a reduction in large avalanche sizes. We also tested increasing the neighborhood radius to r = 14 for the isoflurane analysis due to the elongated PCF in 3b, but found no significant differences. Interestingly, the higher dose of pentobarbital (80 mg/kg) produced a similar result to the lower dose (12.5 mg/kg)—a shift in the exponent to τ = 1.0(1), and a duration exponent of α = 1.8(5). A two-sample Wilcoxon rank-sum test with Bonferroni–Holm correction between QW and pentobarbital for τ indicated that the estimated critical exponents were statistically different (p = 0.004). The scaling relation (Eq. (2)) held within two σ in two of the three testable recordings. Finally, Fig. 3d shows the per-recording KS distance relative to QW. Relative to the low-dose anesthetics, surgical plane levels of ketamine and isoflurane both showed substantially increased deviations away from QW (〈DKS〉 = 0.4(1) for isoflurane and 〈DKS〉 = 0.6(2) for ketamine). Conversely, pentobarbital was consistent with sub-anesthetic results in Fig. 2d (〈DKS〉 = 0.2(1)).
Surgical plane anesthesia: awake-like dynamics
Interestingly, we also observed dynamics under ketamine (1 out of 7) and isoflurane (3 out of 10) resembling QW (see S3 and Fig. S6a), despite the surgical plane of anesthesia (S4). We will refer to these as awake-like (AL). AL recordings exhibited statistics different from other in-group recordings. For example, the avalanche rate of the AL ketamine recording was 15 Hz (consistent with QW), as opposed to 4 ± 1 Hz for the other ketamine recordings. In both AL ketamine and isoflurane, both the PCF and avalanche statistics resembled QW (Fig. S6b, c). The estimated exponents were also consistent with QW; τ = 1.17(4) for isoflurane, and τ = 1.05(5) for ketamine (uncertainty here is from MLE as there is only one recording), and had comparable dynamical ranges (). AL recordings also had the lowest KS distance of surgical plane anesthesia recordings (Fig. 3d), emphasizing the similarity with QW further. Moreover, in all awake-like isoflurane recordings, the scaling relation (Eq. (2)) held within two σ, while it was not in the single ketamine recording because τ was very close to unity. Note that no meaningful statistical comparison between QW and AL could be performed due to the low sample size of AL.
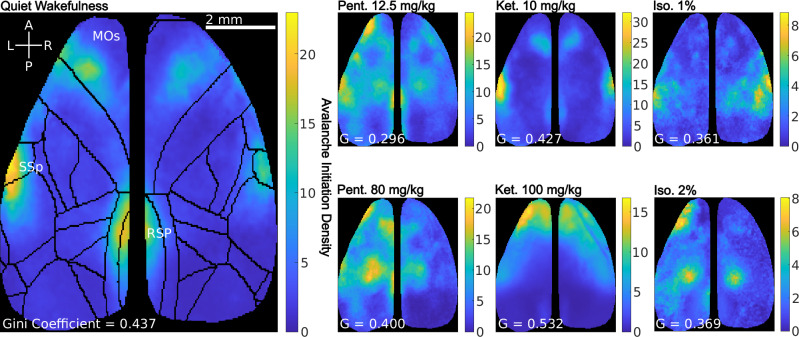
Spatial analysis
Here we study avalanche initiation/nucleation sites across the cortical surface (see spatial analysis in methods). In all cases, avalanches are preferentially initiated in key locations, as seen in Fig. 4, but are sensitive to pharmacological manipulation. Three regions generated the most avalanches in QW—the primary Somatosensory (SSp) area, particularly areas associated with both the mouth and nose, the retrosplenial (RSP) area, and the secondary somatomotor (MOs) area. The Gini coefficient, G, is also calculated as a measure of focalization32:
| 3 |
where xi is the value of the ith pixel, and is the average across all pixels. G = 0 indicates a perfectly uniform distribution of activity, while G = 1 indicates entirely localized. For QW, we found G = 0.437. We organize our observations on a per-drug basis.
Fig. 4. The average avalanche initiation maps for each case.
Color bars indicate the number of times a pixel was classified as an initiation site, averaged over all in-group maps, weighted by the number of observed avalanches with the Gini coefficient G indicated. Awake-like recordings were kept separate as per the previous analysis. The somatomotor (MOs), somatosensory (SSp), and retrosplenial (RSP) areas are also labeled as regions of interest for reference in the first panel. The panel for quiet wakefulness has the Allen Institute atlas outlined for reference.
Pentobarbital
Spatial maps of for both 12.5 mg/kg and 80 mg/kg pentobarbital resembled QW. However, the heavier doses also showed recruitment of additional sub-regions, which is reflected in G initially decreasing (relative to QW) under low doses, but then increasing in high doses. Along with the mouth and nose sub-regions, we also observe increased activation in upper, lower, and truck areas of the SSp, as well as greater coverage of the MOs.
Isoflurane
Isoflurane 1% was associated with SSp avalanche initiation similar to QW, but reduced initiation in RSP and MOs. At a surgical plane of anesthesia (2% isoflurane), we observed initiations confined to the hind-limb region of SSp, and a reduction of initiations in facial SSp regions. Spatial maps of AL recordings resembled those of isoflurane 1% (see S3A). Interestingly, despite low-dose baring the most resemblance to QW in terms of avalanches, all isoflurane-associated maps are overall more homogeneous, which is reflected by the Gini coefficient.
Ketamine
Ketamine 10 mg/kg recordings displayed activations in the SSp. A suppression of activation in the RSC and MOs was also observed, though not as drastic as in the isoflurane case. Ketamine 100 mg/kg recordings exhibited wave-like dynamics, predominately initiating in the MOs, the result of which leads to the highest observed G among all cases. The single AL recording did not show significant activation in the MOs and instead resembled the 10 mg/kg ketamine map (see S3A).
Discussion
Here we used multiple anesthetics at different doses to pharmacologically manipulate the critical state and examine whether or not multiple pathways from the critical state exist. We first established that avalanches during QW were indeed best described by power-law statistics. While the avalanche size statistics we observed followed a slope different from the often-cited τ = 1.5 mean-field directed percolation exponent (e.g., refs. 1,17,18, among others), non-mean-field critical exponents are not uncommon in the literature (e.g., ref. 33 details them extensively). The value of τ ≈ 1.2 for QW indicates that, in our case, the underlying network structure of the cortex is quite distinct from an all-to-all coupling, consistent with our analysis of the partial correlation function. In fact, these smaller values of τ are closer to what is expected for a branching process on a two-dimensional lattice, namely τ ≈ 1.26. Note that a more local coupling at the mesoscale resolution at which we observe the dynamics of the cortex does not necessarily contradict the observations with different imaging modalities at smaller scales with very limited fields of view (see, for example, ref. 33), for which an all-to-all coupling e.g., a mean-field branching process could be more appropriate. Moreover, recent efforts have been devoted to understanding how critical exponents may be changed by experimental artifacts such as sub-sampling29,34, and demonstrations that sub-sampling can change the observed exponents, despite the underlying universality class31. While our analysis could be sensitive to temporal sub-sampling due to the relatively slow response of calcium (when compared against voltage-sensitive dyes used in ref. 17), this would affect each recording equally and so a comparison between the cases would remain meaningful.
Previous work regarding the effect of sub-anesthetic ketamine has shown the drug acts on interneurons35,36 with a global effect on cortical glutamate signaling37. The dis-inhibition of inhibitory interneurons38 may result in greater neuronal activity and, therefore, calcium transients. Avalanche size and duration statistics were similar to QW, and the scaling relation typically held indicative of criticality. This implies that first-order avalanche statistics are not particularly sensitive to sub-anesthetic ketamine. Surgical-plane doses of ketamine are markedly different, however. Large, regular, calcium waves originating at the somatomotor area establish a characteristic scale and destroy scale-free statistics.
Sub-anesthetic isoflurane produced no significant changes in the avalanche statistics relative to control (same exponent, similar fitting ranges, scaling relation satisfied). Isoflurane 1% is commonly used for functional mapping experiments involving evoked responses to stimuli, such as retinotopic mapping39, the barrel cortex40, or simultaneous areas across the cortex41. We speculate the resemblance of isoflurane 1% to QW is related to this - the maintained critical dynamics allow for an evoked activity that corresponds to functional areas of the cortex to be preserved.
Surgical plane levels of isoflurane produced widespread small fluctuations, in line with those reported in ref. 42. These manifested as a reduced amount of large avalanches. Interestingly, the authors of ref. 42 studied functional connectivity in the mouse cortex, and reported that surgical depth isoflurane disrupted typical functional connectivity patterns, while ketamine-xylazine (100, 5 mg/kg) did not. This is consistent with what is observed in the corresponding PCF, which under ketamine is largely the same as in QW, but is significantly broader under isoflurane.
While surgical-plane isoflurane and ketamine produced apparently sub- or super-critical deviations from homeostatic criticality, certain features inconsistent with this categorization deserve highlighting. In the case of ketamine, large regular wave patterns are not well described by the first-order statistics of traditional avalanche analysis15. Likewise, isoflurane featured widespread fluctuations that might be indicative of a sub-critical state, were it not for frequent (though irregular) system-sized bursts that are incompatible with a sub-critical state. This requires that additional higher-order statistics are included to fully categorize dynamics away from the homeostatic critical state and suggests a breakdown of universality.
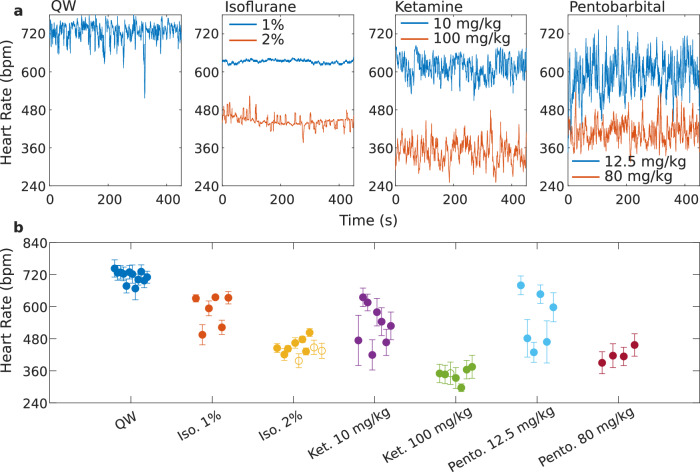
We also observed recordings with calcium transients resembling QW recordings under surgical-plane levels of isoflurane (3 in 10) and ketamine (1 in 7). Distributions of avalanches from these “awake-like” (AL) recordings very closely resembled QW and were stationary over our observation period. While the critical state is not a sufficient condition for consciousness3, the observation of both critical and non-critical statistics producing a common loss-of-responsiveness state with similar and robust physiological parameters (see Fig. 5 and S4) is surprising and, to our knowledge, previously unobserved. This could be indicative of significant natural variability between animals.
Fig. 5. Heartbeat analysis for each case.
a Continuous physiological monitoring: Examples of extracted heart rate from the raw calcium recordings as a function of time for quiet wakefulness (QW) and the various drugs considered for different dosages. b The average heart rate for each recording, across each drug case, and the QW control. Error bars correspond to one standard deviation of the heart rate across the individual recording, which quantifies the variability of the heart rate and indicates stationary behavior over the duration of the recordings. Hollow circles in isoflurane 2% and ketamine 100 mg/kg denote the awake-like cases. Source data are provided as a Source data file.
Unlike surgical plane levels of isoflurane and ketamine, which produced non-critical dynamics (aside from AL recordings), pentobarbital produced potentially scale-free distributions with smaller exponents τ, indicating an increased propensity for larger avalanches. This increase is consistent with the work conducted in ref. 17, but differs in that the avalanche distributions shown in the aforementioned work are clearly super-critical. Given the reduced fitting range in our analysis, and the observation of size exponents less than 1 (though τ > 1 can not be ruled out at the two σ levels) in three of six recordings, a super-critical state should not be ruled out, but it is also not as pronounced as in ref. 17, despite the same dosage (80 mg/kg). One key experimental difference between the two analyses is our use of calcium indicators instead of genetically encoded voltage indicators. The differences in the time scales involved (e.g., calcium response and decay is typically slower than voltage43) could be a contributing factor to the differences we observe, though a direct study comparing avalanche statistics with both modalities has not been performed to our knowledge.
Interestingly, both pentobarbital 12.5 and 80 mg/kg produced similar PCFs, avalanche distributions, and spatial initiation maps, where the latter are similar to QW. The fact that both high and low doses resulted in similar avalanche statistics is very different from what is observed in ketamine and isoflurane. This suggests a saturation effect as opposed to a monotonic dose-dependant effect, and may reveal an abrupt, discrete transition between QW dynamics and another state made accessible by even low doses of pentobarbital, which potentially maintains critical dynamics but belongs to a separate universality class.
Regarding measures of criticality, QW, all low-dose anesthetics, high-dose pentobarbital, and awake-like isoflurane, consistently satisfied the scaling relation (Eq. (2)) for all testable cases (i.e., τ > 1), suggesting criticality. It is surprising that critical statistics can be observed despite anesthetics altering excitation/inhibition (E/I) balance18. One possibility is that anesthetics induce spatially heterogeneous changes in E/I balance, where compensatory effects maintain global criticality, but local analysis may reveal deviations. Preliminary findings using an E/I balance estimation method44 support this idea in general (see S5), but further validation is needed. Although surgical plane anesthesia generally disrupts criticality, the occasional presence of criticality in individual recordings suggests that animal variability might play a role. Therefore, the impact of anesthetics on criticality is more nuanced than a binary classification of “critical” or “non-critical” states.
In summary, we observe, in the same experimental setups, multiple transitions away from the homeostatic critical state observed during QW. This addresses a fundamental knowledge gap—whether different previous studies showing changes in avalanche statistics due to anesthetics truly reflect underlying state changes, or simply reflect trivial differences between experimental setups. The existence of multiple pathways and behaviors suggests a non-trivial relationship between neuronal avalanches and loss-of-awareness states.
Methods
Animals
Adult male and female C57BL/6J-Tg (Thy14jRGECO1a)GP8.58Dkim/J mice (8–12 weeks old) were studied. The jRGECO1a sensor is a genetically encoded red-shifted calcium sensor. Animals were group-housed on a 12:12 light cycle with ad libitum access to food and water. All procedures were approved by the University of Calgary Animal Care Committee (ACC) in accordance with the ethical standards set forth by the Canadian Council on Animal Care (CCAC).
Drugs
Ketamine hydrochloride (Ketalean, Bimeda-MTC, Canada) was administered at a dose of 10 or 100 mg/kg via intraperitoneal (IP) injection in 0.9% saline and an injection volume of 200 μl. The 100 mg/kg dose was paired with 20 mg/kg Xylazine (Bayer, Canada). Sodium pentobarbital (Rafter 8 Products, Canada) was similarly administered at a dose of 12.5 or 80 mg/kg. Isoflurane (Fresenius Kabi, Canada) was regulated with a tabletop single-animal anesthesia system with passive scavenging (Harvard Apparatus).
Surgeries
Chronic window surgeries were performed in 7–8-week-old mice as previously described45. Briefly, under isoflurane anesthesia, the skull was exposed with a skin excision from 3 mm anterior to bregma to 2 mm posterior to lambda, exposing the temporalis muscles. A metal screw was fixed to the skull with cyanoacrylate prior to embedding it in transparent dental cement (C&B-Metabond, Parkell). A flat 8 × 8 mm2 glass coverslip (tapered by 2 mm anteriorly) was affixed to the skull with the same transparent dental cement. Mice recovered for 7 days prior to any manipulations, including habituation to head-fixation or pharmacological interventions.
Imaging protocol
Cortical calcium activity was sampled using a LabeoTech system (Montreal, QC) employing a macroscope (Nikon 55 mm lens, f/2.8 aperture) and a Quantalux 2.1 MP Monochrome sCMOS Camera (Thorlabs). The 9.5 × 9.5 mm2 field of view permits simultaneous sampling of fluorescence signal across a large expanse of dorsal neocortex. We acquired 16-bit images with 19.7 ms temporal resolution (50 Hz) and 256 × 256-pixel resolution (26.2 px/mm). The genetically encoded calcium sensor, jrGECO1a, was excited with a 567 nm LED (540/80 filter, Semrock) attached to an articulating arm (10–15 mW/cm2), and fluorescence emission was filtered with a 629/56 bandpass filter (Semrock). Illumination and frame capture was controlled using commercial software (Labeo Technologies, Inc).
Mice were habituated to handling and head-fixation with the embedded screw over 5 days prior to quiet wakefulness and anesthetic acquisitions. Epochs of 22,500 frames (7.5 min, 50 Hz) were sampled. For all experiments, the animal temperature was maintained at 37 ∘C with a feedback thermistor and a rectal thermometer, which the animals tolerated under both low-dose and high-dose anesthesia conditions, and eyes were lubricated (Opticare, CLC Medica). For high-dose anesthetic experiments, the surgical plane was verified with both tail and foot pinch prior to mesoscale calcium dynamic acquisitions. Continuous measurements of heart rate during imaging showed minimal variability in this physiological indicator of anesthetic depth in animals with high-dose anesthesia and greater variability in low-dose anesthesia (see Fig. 5 and S4 for details), consistent with existing literature46–53. For each drug, a one-sided ANOVA comparison of the distribution of average heart rates obtained in QW, low, and high dose recordings indicated each case to be statistically different from the other at very high significance levels (p < 0.001, see S4 for details). An additional three isoflurane and ketamine recordings taken for twice the duration were used to further test the consistency of anesthetic depth over the duration of the recordings (see S6 for details). With the exception of isoflurane, animals were naïve to the anesthetic agents used in all experiments and were used in a single experimental condition.
Image analysis
Image stacks were analyzed using custom-written MATLAB 2022b code (Mathworks, MA). jRGECO1a signals were expressed as fluctuations in fluorescence (ΔF/F0) relative to each individual pixel’s mean fluorescence over the entire recording (alternatively, using the first 1000 frames to calculate F0 did not change the results). Individual time-varying pixel signals were filtered to 0.1–15 Hz. Movement episodes during imaging were identified as frames with outlier deviations in image mean square error from a spatial highpass filtered median image and removed to restrict our analyses to periods of quiet wakefulness. An affine transformation (imwarp, MATLAB) to the Allen Institute for Brain Science mouse brain atlas54 was implemented using five anatomical landmarks (the boundaries and midpoint where olfactory bulb meets cortex, bregma, and the base of retrosplenial cortex), and one functional landmark (primary sensory hind-limb region).
Avalanche analysis
Definition of avalanches
The pre-processed time-series of each pixel was binarized using a per-pixel threshold, ϕ, of one standard deviation above the mean. The pixel is considered active for all above-threshold frames, as opposed to a point-processing or calcium-transience extraction approaches17,55. Neither point-processing nor calcium-transience extraction methods change our main results (S7).
As calcium signals may be spatially correlated well beyond neighboring pixels, avalanches generated from the clustering of contiguously adjacent active pixels can break up avalanches due to long-range activation. To account for this, we allow two active pixels to belong to the same avalanche if they satisfy both of the following conditions: they occur both within one frame and within a given radius of one another. This radius is estimated from the spatial partial correlation function (PCF) 〈ρ(r)〉. The partial correlation ρi, j between pixels i and j measures direct linear interaction (unlike Pearson correlation which can be indirect) by conditioning i and j on the activity of all other pixels. The partial correlation function is the mean correlation averaged over all pixels i, j with pairwise distance di, j equal to r:
| 4 |
where nr is the number of pairs of pixels at a distance r. The first zero crossing of the QW PCF (r* = 8) pixels was chosen as the radius of the extended region. Clustering using only nearest-neighbor pixels (e.g., as in ref. 55), did not change our main results (S7).
Due to the highly symmetrical activity, we also stipulate that avalanches cannot merge across hemispheres which is accomplished by removing the middle portion of the FOV (see Fig. 1a). Without this, merging between avalanches would have a spatial dependency; clusters occurring near the middle of the FOV (e.g., in the RSP) would be likely to merge across hemispheres, whereas clusters occurring at the periphery (e.g., SSp) would not. In principle, this could be rectified by incorporating the underlying network56, but this introduces additional network reconstruction complications. Given this, the avalanche size is calculated as S = n/Λ18. Here n is the total number of active pixels that participated in the avalanche, Λ is the total number of pixels per hemisphere.
Analysis of avalanche statistics
The critical exponent τ is estimated following57. First, maximum likelihood on avalanche sizes estimates τ using the following estimator:
| 5 |
This estimation is done between sizes and , chosen such it is the largest possible domain satisfying p > 0.1, when tested (one-sample Kolmogorov–Smirnov KS test) against a theoretical power-law with p(S) ∝ S−τ. The exponents across all cases that followed power-law statistics is shown in Table 1. A potential drawback is that differences in the fitting domain may change τ. Alternatively, the fitting domain can be fixed to that of QW, with the drawback that p > 0.1 is not guaranteed. This produced similar exponents and conclusions and is presented separately (S1). Per-recording estimates were also found to be consistent with the concatenated results.
To test the plausibility of the power-law, we perform alternate hypothesis testing against the commonly used exponential, stretched-exponential, and log-normal distributions57. To establish uncertainty, we utilized boot-strapping. A single trial consists of randomly choosing half of the recordings corresponding to that condition (with replacement), and then using MLE to estimate the appropriate parameters within . For each bootstrapped sample, the Akaike information criterion (AICX) is calculated;
| 6 |
Here k is the number of parameters in the model and is the maximum of the log-likelihood function of the candidate model X. We then calculate ΔAIC = AICX − AICpl, where pl denotes the power-law hypothesis33. If ΔAIC > 0 implies the power-law hypothesis is favored, and the alternate hypothesis is favored if ΔAIC < 0. This test is similar to the log-ratio test57 but penalizes the number of parameters to avoid over-fitting. Table 1 shows the 10th, median, and 90th percentiles values of ΔAIC values. In all cases, exponential and stretched-exponentials performed significantly worse than power-law, thus only log-normal is reported in Table 1 (for others, S8).
The two-sample KS test (two-sided, kstest2 in MATLAB) was used as an alternative bin-independent measure of similarly, and is defined by
| 7 |
where F and G are empirical CDFs of the two samples. For non-QW recordings, G is the CDF of the concatenated avalanches across all QW recordings. For QW recordings, G is the concatenated avalanches across all QW recordings except for the specific QW recording being tested. All DKS values were calculated over a common domain.
Spatial analysis
To generate the spatial nucleation maps (Fig. 4) we identify the initiating sites for each avalanche with size greater than , to avoid potential spurious signals, (no qualitative change if these avalanches were included). Pixels active in the first frame of avalanches constitute trivial initiating sites. To account for the merging of avalanches, an active cluster at frame t is classified as an initiating cluster if, at frame t − 1, there are no active pixels within a neighborhood determined by r* (from the PCF). Per recording, maps are generated by counting the number of times a pixel has participated in initiating clusters. Finally, a single map is obtained by taking the average across all recordings, weighted by the number of initiating points in each recording.
Functional regions of interest were identified by first taking regions with the 10 percent highest number of activation as candidates. Next, clusters comprising less than 100 pixels were discarded to limit spurious identifications. The locations of the remaining clusters were then compared against the Allen brain atlas parcellation54. Any region in the atlas with less than 100 pixels were also removed (for example, the Ventral auditory area corresponded to 10 pixels across the two hemispheres). Initiation clusters aligned well with the atlas, but not perfectly so. Regions with less than 10% overlap with the candidate cluster were thus discarded, with one exception—we consistently observed strong activation in a sub-section of the secondary (and occasionally primary) somatomotor areas. This region is the largest one in the Allen brain atlas, which results in the overlap criterion failing. We observed this area reliably enough we felt it appropriate to drop the overlap criterion for this one region.
Reporting summary
Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.
Supplementary information
Source data
Acknowledgements
We would like to thank Dr. Lyle Muller and Dr. Javier Orlandi for their insightful discussions. D.C. would like to acknowledge support from the Izaak Walton Killam Memorial Trusts. J.D. was supported by the Natural Sciences and Engineering Research Council of Canada (RGPIN/05221-2020). A.M. received support from the Natural Sciences and Engineering Research Council of Canada (RGPIN-2020-05273). D.M.A. received a post-doctoral fellowship from the Canadian Open Neuroscience Platform.
Author contributions
D.C. and J.D. conceived the study. Animal handling, recording, and data preprocessing was handled by D.M.A. and A.M. D.C. performed all analysis, with assistance from D.M.A., and wrote the manuscript. All authors contributed to the editing and revisions of the manuscript.
Peer review
Peer review information
Nature Communications thanks Dante Chialvo, Dietmar Plenz and Jordi Soriano for their contribution to the peer review of this work. A peer review file is available.
Data availability
The processed avalanche data for all recordings are available at 10.5281/zenodo.12690412 (DOI)58, as well as an example calcium recording used to obtain the avalanches59. Source data are provided with this paper.
Code availability
The code generating the results in the current study are available in the following repository: https://github.com/davorcuricGit/anestheticsAnalysis.git(10.5281/zenodo.12690413)59.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
The online version contains supplementary material available at 10.1038/s41467-024-51399-2.
References
- 1.Beggs, J. M. & Plenz, D. Neuronal avalanches in neocortical circuits. J. Neurosci.23, 11167–11177 (2003). 10.1523/JNEUROSCI.23-35-11167.2003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Cocchi, L., Gollo, L. L., Zalesky, A. & Breakspear, M. Criticality in the brain: a synthesis of neurobiology, models and cognition. Progr. Neurobiol.158, 132–152 (2017). 10.1016/j.pneurobio.2017.07.002 [DOI] [PubMed] [Google Scholar]
- 3.Beggs, J. M. The Cortex and the Critical Point: Understanding the Power of Emergence (MIT Press, 2022).
- 4.Curic, D. et al. Deconstructing scale-free neuronal avalanches: behavioral transitions and neuronal response. J. Phys.2, 045010 (2021). [Google Scholar]
- 5.Levina, A., Herrmann, J. M. & Geisel, T. Dynamical synapses causing self-organized criticality in neural networks. Nat. Phys.3, 857–860 (2007). 10.1038/nphys758 [DOI] [Google Scholar]
- 6.Yang, H., Shew, W. L., Roy, R. & Plenz, D. Maximal variability of phase synchrony in cortical networks with neuronal avalanches. J. Neurosci.32, 1061–1072 (2012). 10.1523/JNEUROSCI.2771-11.2012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Chialvo, D. R. Emergent complex neural dynamics. Nat. Phys.6, 744–750 (2010). 10.1038/nphys1803 [DOI] [Google Scholar]
- 8.Moretti, P. & Muñoz, M. A. Griffiths phases and the stretching of criticality in brain networks. Nat. Commun.4, 1–10 (2013). 10.1038/ncomms3521 [DOI] [PubMed] [Google Scholar]
- 9.Meshulam, L., Gauthier, J. L., Brody, C. D., Tank, D. W. & Bialek, W. Coarse graining, fixed points, and scaling in a large population of neurons. Phys. Rev. Lett.123, 178103 (2019). 10.1103/PhysRevLett.123.178103 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Poil, S.-S., Hardstone, R., Mansvelder, H. D. & Linkenkaer-Hansen, K. Critical-state dynamics of avalanches and oscillations jointly emerge from balanced excitation/inhibition in neuronal networks. J. Neurosci.32, 9817–9823 (2012). 10.1523/JNEUROSCI.5990-11.2012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Corral López, R., Buendía, V. & Muñoz, M. A. Excitatory-inhibitory branching process: a parsimonious view of cortical asynchronous states, excitability, and criticality. Phys. Rev. Res.4, L042027 (2022). 10.1103/PhysRevResearch.4.L042027 [DOI] [Google Scholar]
- 12.MacDowell, C. J. & Buschman, T. J. Low-dimensional spatiotemporal dynamics underlie cortex-wide neural activity. Curr. Biol.30, 2665–2680 (2020). 10.1016/j.cub.2020.04.090 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Williams, A. H. et al. Unsupervised discovery of demixed, low-dimensional neural dynamics across multiple timescales through tensor component analysis. Neuron98, 1099–1115 (2018). 10.1016/j.neuron.2018.05.015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Sethna, J. P., Dahmen, K. A. & Myers, C. R. Crackling noise. Nature410, 242–250 (2001). 10.1038/35065675 [DOI] [PubMed] [Google Scholar]
- 15.Christensen, K. & Moloney, N. R. Complexity and Criticality Vol. 1 (World Scientific Publishing Company, 2005).
- 16.Yaghoubi, M. et al. Neuronal avalanche dynamics indicates different universality classes in neuronal cultures. Sci. Rep.8, 1–11 (2018). 10.1038/s41598-018-21730-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Scott, G. et al. Voltage imaging of waking mouse cortex reveals emergence of critical neuronal dynamics. J. Neurosci.34, 16611–16620 (2014). 10.1523/JNEUROSCI.3474-14.2014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Bellay, T., Klaus, A., Seshadri, S. & Plenz, D. Irregular spiking of pyramidal neurons organizes as scale-invariant neuronal avalanches in the awake state. Elife4, e07224 (2015). 10.7554/eLife.07224 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Fekete, T. et al. Critical dynamics, anesthesia and information integration: lessons from multi-scale criticality analysis of voltage imaging data. Neuroimage183, 919–933 (2018). 10.1016/j.neuroimage.2018.08.026 [DOI] [PubMed] [Google Scholar]
- 20.Alkire, M. T., Hudetz, A. G. & Tononi, G. Consciousness and anesthesia. Science322, 876–880 (2008). 10.1126/science.1149213 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Varley, T. F., Sporns, O., Puce, A. & Beggs, J. Differential effects of propofol and ketamine on critical brain dynamics. PLoS Comput. Biol.16, e1008418 (2020). 10.1371/journal.pcbi.1008418 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Michelson, N. J. & Kozai, T. D. Isoflurane and ketamine differentially influence spontaneous and evoked laminar electrophysiology in mouse v1. J. Neurophysiol.120, 2232–2245 (2018). 10.1152/jn.00299.2018 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Priesemann, V., Valderrama, M., Wibral, M. & Le Van Quyen, M. Neuronal avalanches differ from wakefulness to deep sleep–evidence from intracranial depth recordings in humans. PLoS Comput. Biol.9, e1002985 (2013). 10.1371/journal.pcbi.1002985 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Amin, J. & Weiss, D. S. Gabaa receptor needs two homologous domains of the & beta;-subunit for activation by gaba but not by pentobarbital. Nature366, 565–569 (1993). 10.1038/366565a0 [DOI] [PubMed] [Google Scholar]
- 25.Sleigh, J., Harvey, M., Voss, L. & Denny, B. Ketamine–more mechanisms of action than just nmda blockade. Trends Anaesth. Crit. Care4, 76–81 (2014). 10.1016/j.tacc.2014.03.002 [DOI] [Google Scholar]
- 26.Nishikawa, K.-i & MacIver, M. B. Excitatory synaptic transmission mediated by NMDA receptors is more sensitive to isoflurane than are non-nmda receptor-mediated responses. Anesthesiology92, 228–228 (2000). 10.1097/00000542-200001000-00035 [DOI] [PubMed] [Google Scholar]
- 27.Jones, M. V., Brooks, P. A. & Harrison, N. L. Enhancement of gamma-aminobutyric acid-activated cl-currents in cultured rat hippocampal neurones by three volatile anaesthetics. J. Physiol.449, 279–293 (1992). 10.1113/jphysiol.1992.sp019086 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Dana, H. et al. Sensitive red protein calcium indicators for imaging neural activity. eLife5, e12727 (2016). 10.7554/eLife.12727 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Levina, A., Priesemann, V. & Zierenberg, J. Tackling the subsampling problem to infer collective properties from limited data. Nat. Rev. Phys.4, 770–784 (2022). 10.1038/s42254-022-00532-5 [DOI] [Google Scholar]
- 30.Ponce-Alvarez, A., Jouary, A., Privat, M., Deco, G. & Sumbre, G. Whole-brain neuronal activity displays crackling noise dynamics. Neuron100, 1446–1459 (2018). 10.1016/j.neuron.2018.10.045 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Carvalho, T. T. et al. Subsampled directed-percolation models explain scaling relations experimentally observed in the brain. Front. Neural Circuits14, 576727 (2021). 10.3389/fncir.2020.576727 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Montalà-Flaquer, M. et al. Rich dynamics and functional organization on topographically designed neuronal networks in vitro. iScience25, 105680 (2022). 10.1016/j.isci.2022.105680 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Fontenele, A. J. et al. Criticality between cortical states. Phys. Rev. Lett.122, 208101 (2019). 10.1103/PhysRevLett.122.208101 [DOI] [PubMed] [Google Scholar]
- 34.Levina, A. & Priesemann, V. Subsampling scaling. Nat. Commun.8, 1–9 (2017). 10.1038/ncomms15140 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Behrens, M. M. et al. Ketamine-induced loss of phenotype of fast-spiking interneurons is mediated by nadph-oxidase. Science318, 1645–1647 (2007). 10.1126/science.1148045 [DOI] [PubMed] [Google Scholar]
- 36.Gerhard, D. M. et al. Gaba interneurons are the cellular trigger for ketamine’s rapid antidepressant actions. J. Clin. Invest.130, 1336–1349 (2020). 10.1172/JCI130808 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.McGirr, A. et al. Adjunctive ketamine in electroconvulsive therapy: updated systematic review and meta-analysis. Br. J. Psychiatry210, 403–407 (2017). 10.1192/bjp.bp.116.195826 [DOI] [PubMed] [Google Scholar]
- 38.Ali, F. et al. Ketamine disinhibits dendrites and enhances calcium signals in prefrontal dendritic spines. Nat. Commun.11, 1–15 (2020). 10.1038/s41467-019-13809-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Zhuang, J. et al. An extended retinotopic map of mouse cortex. elife6, e18372 (2017). 10.7554/eLife.18372 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Sato, T. R., Gray, N. W., Mainen, Z. F. & Svoboda, K. The functional microarchitecture of the mouse barrel cortex. PLoS Biol.5, e189 (2007). 10.1371/journal.pbio.0050189 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Scott, B. B. et al. Imaging cortical dynamics in gcamp transgenic rats with a head-mounted widefield macroscope. Neuron100, 1045–1058 (2018). 10.1016/j.neuron.2018.09.050 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Xie, H. et al. Differential effects of anesthetics on resting state functional connectivity in the mouse. J. Cereb. Blood Flow Metab.40, 875–884 (2020). 10.1177/0271678X19847123 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Zhu, M. H., Jang, J., Milosevic, M. M. & Antic, S. D. Population imaging discrepancies between a genetically-encoded calcium indicator (geci) versus a genetically-encoded voltage indicator (gevi). Sci. Rep.11, 1–15 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Bruining, H. et al. Measurement of excitation-inhibition ratio in autism spectrum disorder using critical brain dynamics. Sci. Rep.10, 9195 (2020). 10.1038/s41598-020-65500-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.McGirr, A., LeDue, J., Chan, A. W., Xie, Y. & Murphy, T. H. Cortical functional hyperconnectivity in a mouse model of depression and selective network effects of ketamine. Brain140, 2210–2225 (2017). [DOI] [PubMed]
- 46.Janssen, B. J. et al. Effects of anesthetics on systemic hemodynamics in mice. Am. J. Physiol. Heart Circ. Physiol.287, H1618–H1624 (2004). 10.1152/ajpheart.01192.2003 [DOI] [PubMed] [Google Scholar]
- 47.Chu, D. K., Jordan, M. C., Kim, J. K., Couto, M. A. & Roos, K. P. Comparing isoflurane with tribromoethanol anesthesia for echocardiographic phenotyping of transgenic mice. J. Am. Assoc. Lab Animal Sci.45, 8–13 (2006). [PubMed] [Google Scholar]
- 48.Ewald, A. J., Werb, Z. & Egeblad, M. Monitoring of vital signs for long-term survival of mice under anesthesia. Cold Spring Harb. Protoc.2011, pdb–prot5563 (2011). 10.1101/pdb.prot5563 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Constantinides, C., Mean, R. & Janssen, B. J. Effects of isoflurane anesthesia on the cardiovascular function of the c57bl/6 mouse. ILAR J.52, e21 (2011). [PMC free article] [PubMed] [Google Scholar]
- 50.Tsukamoto, A., Serizawa, K., Sato, R., Yamazaki, J. & Inomata, T. Vital signs monitoring during injectable and inhalant anesthesia in mice. Exp. Anim.64, 57–64 (2015). 10.1538/expanim.14-0050 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Low, L. A., Bauer, L. C. & Klaunberg, B. A. Comparing the effects of isoflurane and alpha chloralose upon mouse physiology. PLoS ONE11, e0154936 (2016). 10.1371/journal.pone.0154936 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Lee, C. & Jones, T. A. Effects of ketamine compared with urethane anesthesia on vestibular sensory evoked potentials and systemic physiology in mice. J. Am. Assoc. Lab. Anim. Sci.57, 268–277 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Kazdağli, H., Özel, H. F., Özbek, M., Alpay, Ş. & Alenbey, M. Classical heart rate variability and non-linear heart rate analysis in mice under na-pentobarbital and ketamine/xylazine anesthesia. Turk. J. Med. Sci.52, 858–869 (2022). 10.55730/1300-0144.5383 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Wang, Q. et al. The allen mouse brain common coordinate framework: a 3d reference atlas. Cell181, 936–953 (2020). 10.1016/j.cell.2020.04.007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Tagliazucchi, E., Balenzuela, P., Fraiman, D. & Chialvo, D. R. Criticality in large-scale brain fmri dynamics unveiled by a novel point process analysis. Front. Physiol.3, 15 (2012). 10.3389/fphys.2012.00015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Korchinski, D. J., Orlandi, J. G., Son, S.-W. & Davidsen, J. Criticality in spreading processes without timescale separation and the critical brain hypothesis. Phys. Rev. X11, 021059 (2021). [Google Scholar]
- 57.Clauset, A., Shalizi, C. R. & Newman, M. E. Power-law distributions in empirical data. SIAM Rev.51, 661–703 (2009). 10.1137/070710111 [DOI] [Google Scholar]
- 58.Curic, D. Avalanches and sample recording for “existence of multiple transitions of the critical state due to anesthetics”. 10.5281/zenodo.12725850 (2024). [DOI] [PMC free article] [PubMed]
- 59.davorcuricGit. davorcuricGit/anestheticsAnalysis: anesthetics_curic_etal. 10.5281/zenodo.12690413 (2024).
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The processed avalanche data for all recordings are available at 10.5281/zenodo.12690412 (DOI)58, as well as an example calcium recording used to obtain the avalanches59. Source data are provided with this paper.
The code generating the results in the current study are available in the following repository: https://github.com/davorcuricGit/anestheticsAnalysis.git(10.5281/zenodo.12690413)59.