Abstract
Researchers are now focusing on inorganic halide-based cubic metal perovskites that are not toxic as they strive to commercialize optoelectronic products and solar cells derived from perovskites. This study explores the properties of new lead-free compounds, specifically GaGeX3 (where X = Cl, Br, and I), by executing first-principles Density Functional Theory (DFT) to analyze their optical, electronic, mechanical, and structural characteristics under pressure. Assessing the reliability of all compounds is done meticulously by applying the criteria of Born stability and calculating the formation energy. As discovered through elastic investigations, these materials showed anisotropic behavior, flexibility, and excellent elastic stability. The electronic band structures, calculated using both HSE06 and GGA-PBE functionals at 0 GPa, reveal fascinating behavior. However, computed band structures with non-zero pressures using GGA-PBE. Here, the conduction band moved to the lower energy when the halide Cl was changed with Br or I. In addition, the application of hydrostatic pressure can lead to tunable band gap properties in all compounds such as from 0.779 eV to 0 eV for GaGeCl3, from 0.462 eV to 0 eV for GaGeBr3 and from 0.330 eV to 0 eV for GaGeI3, resulting transformation from semiconductor to metallic. Understanding the origins of bandgap changes can be illuminated by examining the partial and total density of states (PDOS & TDOS). When subjected to pressure, all the studied compounds showed an impactful increase in absorption coefficients and displayed exceptional optical conductivity in both the visible and UV zones. Yet, GaGeCl3 is a more effective UV absorber because it absorbs light more strongly in the UV area. Moreover, GaGeI3 stands out among the compounds examined due to its impressive visible absorption and optical conductivity, which remain consistent under varying pressure conditions. Besides, GaGeI3 exhibits higher reflectivity when subjected to pressure making them suitable for UV shielding applications. At last, these metal cubic halide perovskites without lead present promising opportunities for advancing optoelectronic technologies. With their tunable properties and favorable optical characteristics, these materials are highly sought after for their potential in solar cells, multi-junctional solar cells, and different optoelectronic functions.
Keywords: DFT, Renewable energy, Solar cell, Band gap, Density of states, Optoelectronics, Elastic stability
1. Introduction
The world's population is continuing to expand, which is driving up energy consumption. Having access to affordable, reliable, and abundant energy sources is crucial for our modern industrial society. Regrettably, finite resources such as fossil fuels are limited in supply and eventually deplete, serving as the primary source for our energy requirements. In addition, the combustion of fossil fuels results in the emission of greenhouse gases, contributing significantly to the overall global energy production. This further worsens the effects of climate change. Investigating alternate renewable energy sources, like solar power, is essential for reducing greenhouse gas emissions and addressing the effects of climate change [[1], [2], [3], [4], [5], [6]]. In the fields of science and industry, solar cells have achieved a lot of interest and attention [[7], [8], [9], [10], [11]]. A solar cell comprises an upper electron transportation layer, a lower hole transportation layer, and a center absorber layer. The absorber layer normally absorbs light and generates electron-hole pairs. That's why, this layer is crucial in the solar cells structure. So, the physical characteristics of this layer such as optical, electronic, structural, and mechanical play a significant role in solar cell's performance.
Inorganic metal halide cubic perovskites have a higher solar cell efficiency than Si-based technology. These perovskites are used in a wide range of applications such as light-emitting diodes (LEDs), solar cells, energy conversion, and different optoelectronic systems because of their unique properties including long diffusion lengths, high mobility of charge carriers, low carrier recombination rates, and adjustable band gaps [[12], [13], [14]]. Also, these perovskites are economical and feasible when compared with Si-based technology [[15], [16], [17], [18]]. The formula ABX3 defines these perovskite structures where A and B are different types of cations and X is an anion. So, studying the physical characteristics of perovskite-based materials both theoretically and practically increases the scope of solar cells and various optoelectronics uses. As of right now, solar cells based on perovskites (PSCs) have a 22.1 % power conversion efficiency (PCE) [19], which represents a considerable advancement in their growth path. Despite having the greatest PCE of 25.2 % at the moment, lead-based perovskite solar cells are less durable because of their vulnerability to UV radiation, moisture, temperature, and humidity. The PCE of lead-free tin halide perovskites containing ethyl ammonium iodide, on the other hand, is 13 % [20]. Early organic PSCs using metallic Pb2+ were created, such as CH3NH3PbI3 (or MAPbX3) [21,22], but they ran into toxicity issues, especially because lead (Pb) is known to be dangerous. As such, efforts have been focused on replacing Pb2+ with non-toxic cations like Ge2+ and Sn2+ or using substitute A+ cations instead of their organic equivalents [23]. The continuous quest to produce lead-free halide-based perovskites is one of the main impediments to the commercial viability of perovskite-based solar cells.
To improve the performance of optoelectronic devices, pressure is an important factor. For regulating the physical and chemical characteristics of any kind of material, pressure plays a critical role [24,25]. Because pressure application may alter optical and electrical characteristics as well as induce structural changes, it is thought to be one of the practical ways to boost the solar energy conversion efficiency of these materials. Pressure-induced modifications can modify the band gap of the material, increase light absorption, decrease charge carrier recombination, and maximize charge separation [[26], [27], [28]]. For example, M. Aktary reported hydrostatic pressure effects of CsPbX3 (X = Cl, Br, and I). Here, the electronic, optical responses were enhanced by applied pressure. Also, tuning the band gap of the compounds from semiconductor to metallic nature. In a recent study, we investigated the properties of cubic metal halide perovskites of GaGeX3 (X = Cl, Br, and I) and examined their physical characteristics without the influence of pressure [29]. However, there is no comparative study on pressure-induced lead-free cubic halide GaGeX3 (X = Cl, Br, and I) perovskites. This research investigates the potential of perovskite materials in solar energy conversion by examining how they respond to pressure-induced modification. Here, we incorporate Ge on the perovskite materials instead of Pb, and also, Ge-based perovskites exhibit enhanced optical absorption and conductivity [30,31]. We use Ga instead of CH3NH3 that's why remove the instability of organic compounds. Also, Ga has a low melting point, malleable nature, easily formable, non-toxic, corrosion-resistant, and semiconductor characteristics. That's why, in this research, we concentrate on Ga-based perovskites.
In this article, our objective is to obtain an understanding of the features of GaGeX3 (X = Cl, Br, and I) under pressure and their potential as efficient lead-free photovoltaic materials by variation of pressure, systematically. This work examines the structural, electrical, mechanical, and optical properties of Ge-based halide GaGeX3 (X = Cl, Br, and I) perovskites using first-principles simulations with applied pressure up to 15 GPa. Moreover, the study of the material's optical characteristics and structural stability is made easier by pressure, and these two aspects are essential for creating solar cells with increased efficiency. Therefore, our goal is to evaluate how perovskite structures' optoelectronic properties might be adjusted under various pressure levels to improve their applicability for multijunction solar cell applications.
2. Computational methodology
Using the CASTEP software [32], DFT-based calculations were conducted [33,34]. In order to determine the bandgap and electronic exchange-correlation energy, the GGA-PBE and HSE06 functionals were used [35]. It was thought that the presence of the ultrasoft pseudopotential of the Vanderbilt-type OTFG [36] would help control the electron interactions. The BFGS method was exercised to get the best possible crystal structure [37]. By adjusting the k-points to 7 × 7 × 7 and the plane wave cutoff energy to 600 eV, the optimal structure and properties were computed. The Monkhorst-Pack method was applied to sample the k-points in the high-symmetry Brillouin zone, [38]. With larger k-points, optical properties were evaluated. The elastic constants of our models were estimated using the stress-strain method under normal conditions [39]. Using the CASTEP software, the elastic stiffness constants (Cij) were determined, in accordance with the finite strain theory. Using the ELATE software, three-dimensional anisotropic contour plots for Young's modulus, Poisson's ratio, and Shear modulus parameters were represented. The optimal convergence factors were determined by ensuring that the total energy variation remained in the midst of 5 × 10−6 eV/atom, that the maximum Hellmann-Feynman force was restricted to 0.01 eV/Å, that the maximum displacement was maintained at 5 × 10−4 Å, and that the maximum tension was maintained at 0.02 GPa. The optimal value for the strain magnitude was found that 0.003. The same convergence criteria were utilized that were mentioned before.
3. Results and discussions
3.1. Structural properties
Fig. 1 depicts the cubic crystal structure of GaGeX3 (X = Cl, Br, and I) in a 3D schematic representation. Within this structure, Ga and Ge occupy specific Wyckoff coordinates: Ga is positioned at (0,0,0), while Ge is located at (0.5,0.5,0.5). Additionally, three X atoms are situated at (0.5,0,0.5), (0.5,0.5,0), and (0,0.5,0.5). This study focused on investigating three perovskites, which possess crystal structures of cubic and belong to space group 221: pm3m. Employing the GGA technique, various structural properties such as formation energy (ΔHf), volume (V), and lattice constant (a) were determined through a volume optimization procedure to ascertain the stable ground state unit cell. Moreover, energy values relative to volume were matched to the Birch-Murnaghan equation of state [40]. Utilizing this fit, lattice parameters were computed under varying hydrostatic pressure conditions. The stability of GaGeCl3, GaGeBr3, and GaGeI3 is contingent upon both the type and magnitude of applied stress. In this investigation, pressure was incrementally applied until these compounds transitioned into a metallic state. As positive pressure increases, the lattice parameter diminishes. Fig. 2 illustrates the variation in lattice parameters under applied compressive pressure. Supplementary Tables S1(a–c) presents a comprehensive record of lattice parameter values corresponding to different pressures. Analysis of Tables S1(a–c) indicates that as the halogen size escalates (from Cl to I), both the optimal lattice constant and volume expand.
Fig. 1.
This diagram illustrates the ABX3 structure, accompanied by the supercell of GaGeX3 (X = Cl, Br, and I) metal cubic halide perovskites.
Fig. 2.
Investigating the lattice constant of GaGeX3 (X = Cl, Br, and I) compounds with the impact of pressures.
Additionally, the thermodynamic and mechanical stability of GaGeX3 are explored under varying pressures. The Born stability criteria are utilized to assess the stability of the mechanical of a compound derived from elastic constants.
| C11 + 2C12 > 0, C44 > 0, C11 – C12 > 0 |
The estimated elastic constants of three materials fully meet this criterion, showing mechanical stability which will be further discussed in the mechanical section. The graph depicted in Fig. 3 illustrates the impact of pressure on the formation energy of GaGeX3. The energies of GaGeX3 are calculated using equation (1).
| (1) |
Fig. 3.
Investigating the impact of pressure on GaGeX3 (X = Cl, Br, and I) compounds' formation energy.
Here, the total energy of the ground state of GaGeX3 is represented by the symbol (GaGeX3), while the energies of Ga, Ge, and X (where X can be Cl, Br, or I) per unit cell are represented by the symbols Es (Ga), Es (Ge), and Es (X). The symbol N denotes the total atoms in a unit cell.
Based on the computed energy, it is evident that the energy (ΔHf) exhibits negative values up to 4 GPa, 3 GPa, and 2 GPa for GaGeCl3, GaGeBr3, and GaGeI3, respectively, under compressive stress, as indicated in Tables S1(a–c). Application of external compressive pressure results in further negativity in the formation energy of all compounds. The observed results with applied external pressure suggest that the GaGeX3 structure being studied exhibits notable structural stability and tunability. Given perovskites' customizable structural and electrical characteristics, materials possessing desirable traits can be tailored for diverse applications. Supplementary Table S2 indicates that bond lengths decrease towards lower values in response to applied pressure, resulting from the unit cell's interatomic spaces contracting. When pressure is applied, the propensity of bond lengths to shorten indicates that the bonds between atoms are strengthened.
Moreover, it has been discovered that these compounds display direct band gaps and demonstrate semiconducting behavior. Consequently, they emerge as extremely favorable applicants for optoelectronic applications, notably in solar cells. The electrical and optical properties will be thoroughly discussed in the upcoming sections in order to provide additional validation for the results presented above.
3.2. Electronic properties
The electronic band structure (BS) and Density of States (DOS) are two methods used to gather information about the electronic properties of a material. We calculated the energy band structures (EBSs) of GaGeX3 (X = Cl, Br, I) by analyzing the high symmetry route in k-space based on the energy regarding the Fermi energy (E-EF). For the hydrostatic pressure (0–4 GPa), Figs. S1–3 illustrates the outcomes of band structure calculations, and the band gap changing by applied pressure is shown in Fig. 4. The shown EBSs have an energy spectrum that spans from −5 to 5 eV, encompassing the conduction band (CB) and the valence band (VB) located at the upper and lower ends of the structure, respectively. The Fermi position energy is denoted via the horizontal dashed red line, positioned at 0 eV. The predicted band gaps for the compounds of interest are shown in Tables S1(a–c) through tabular data. Fig. 5 displays the band gaps obtained through calculations using the HSE06 and PBE functional. Based on PBE, it can be observed that GaGeCl3 has an energy gap of 0.779 eV at normal pressure. Its band nature is direct, specifically (R–R). However, when the Cl in GaGeCl3 is substituted with larger halogens like Br and I, the band gap decreases to 0.462 eV for GaGeBr3 and 0.330 eV for GaGeI3. The HSE06 functional is employed to ascertain the precise band gap of the compounds. In the absence of pressure, the band gaps calculated using the HSE06 functional for GaGeCl3, GaGeBr3, and GaGeI3 are in order, 1.632 eV, 1.284 eV, and 1.140 eV.
Fig. 4.
Band gap value of GaGeX3 (where X = Cl, Br, and I) changes based on the pressure.
Fig. 5.
Using the GGA-PBE and HSE06 functional, calculations of the electronic band structures of (a) GaGeCl3, (b) GaGeBr3, and (c) GaGeI3.
Based on PBE, the energy gap for GaGeCl3 at zero pressure has been determined to be 0.770 eV, as illustrated in Fig. S1. As pressure increases, the R point conduction band minimum shifts closer to the Fermi energy level, suggesting the narrowing of the energy gap. At a pressure of 4 GPa, the VB maxima and the CB minima for GaGeCl3 coincide. As a result, Eg disappears, which is evidence that GaGeCl3 transforms from being semiconducting to being conducting [41]. The computed total and partial density of states (TDOS & PDOS) of all compounds are displayed in Figs. S4–6. Here the dashed line that is black located at 0 eV denotes the level of Fermi. Distinguishing the contribution to both the VBs and CBs is a frequent use of the DOS. GaGeCl3 exhibits no TDOS value at EF until 3 GPa, which further demonstrates its semiconducting nature. As the pressure for GaGeCl3 rises to 4 GPa, the value of TDOS that is not zero indicates the shift from a semiconductor to a metal. Since all of the high points in the conduction band move steadily in the direction of the EF as applied pressure increases, there is a significant pressure influence on TDOS. This leads to a shrinkage in the band gap energy, which is in alignment with the band structure shown in the Supplementary Fig. S1. The PDOS graph was employed to illustrate the elemental electronic contribution. The highest contribution was noted from the Cl-3p states, although the VBs of both under and without pressure of GaGeCl3 systems also contained Ga-4s, Ga-4p, Ge-4s, and Ge-4p states. In contrast to the CBs, where Ga-4p states obviously predominate and all other states contribute just a little.
The electronic energy band structure of GaGeBr3 was computed under pressure ranging from 0 to 3 GPa along the high symmetry regions, as seen in Fig. S2. Just like GaGeCl3, at zero pressure, it has a band gap of 0.462 eV, making it a direct band semiconductor. It transitions to a metallic state (Eg = 0 eV) when the VB surpasses the Fermi level EF and intersects with the CB at 3 GPa. To comprehend the electrical characteristics of GaGeBr3 more clearly, the TDOS and the PDOS have been calculated and illustrated in Fig. S5. The zero TDOS value validates the semiconductors' band gap value found in Fig. S2. Increasing pressure leads to a drop in the TDOS value. In PDOS analysis, Br-4p makes up the majority of the atomic contribution seen in the VB, with a slight contribution of Ge-4p. Regarding the CB, the main contribution originates from Ga-4p, while Ge-4p and Cl-3p states make a minor contribution. As pressure increases, a peak shift towards the fermi level can be observed, suggesting a reduction in the band gap as shown in Fig. 4 [42].
An analogous electronic property is observed in GaGeI3, with a band gap of 0.330 eV in its non-pressurized state. As Increasing in pressure that's why the semiconductor band shrinks, transitioning the material into a metallic state where the band gap is equal to zero at a pressure of 2 GPa. GaGeI3 is also a direct narrow band gap semiconductor, just like GaGeCl3 and GaGeBr3, even if the transition into a metallic state occurs. The PDOS in Fig. S6 was used to demonstrate the electrical contribution of each constituent for GaGeI3. The I-5p states made the most significant contribution, but the VBs of both under and without-pressure of GaGeI3 systems also included Ga-4p, Ge-4s, and Ge-4p, I-5s states. Conversely, the CBs exhibit a preponderance of Ga-4p states and minimal contributions from the remaining states.
3.3. Optical properties
Scientific interest in metal halide perovskites has increased due to their remarkable optical characteristics, particularly within the fields of optoelectronics and photovoltaics. Additionally, it is essential to assess the optical properties in relation to applied pressure to advance material research toward the creation of optoelectronic devices and solar cell applications [43]. The characteristics of optical of GaGeX3 (X = Cl, Br, I) under applied pressure which include the refractive index, dielectric's real and imaginary portion, conductivity, absorption, and reflectivity are discussed in this section using solar energy up to 30 eV. The most crucial optical property of a particular material is its dielectric function. Moreover, there is a significant correlation between the dielectric function and the electronic band structure because optical transitions that contribute to the dielectric function include electron migrations over various bands of energy. Examining additional optical properties requires first determining the dielectric function and it is , where , and represent the real and imaginary components of the dielectric function, respectively. The Kramer-Kronig connection [44] reveals the formula of the real part.
The static dielectric function is clarified as the value of at 0 eV. It's a crucial indicator of how well optoelectronic devices work. A material's elevated static dielectric indicates reduced Eb (exciton binding energy) and lower charge carrier recombination rate [44]. For the momentum representation of matrix components in between electrical states that are occupied and vacant, the imaginary component , of the complex dielectric function can be calculated utilizing the CASTEP-supported formula given as follows:
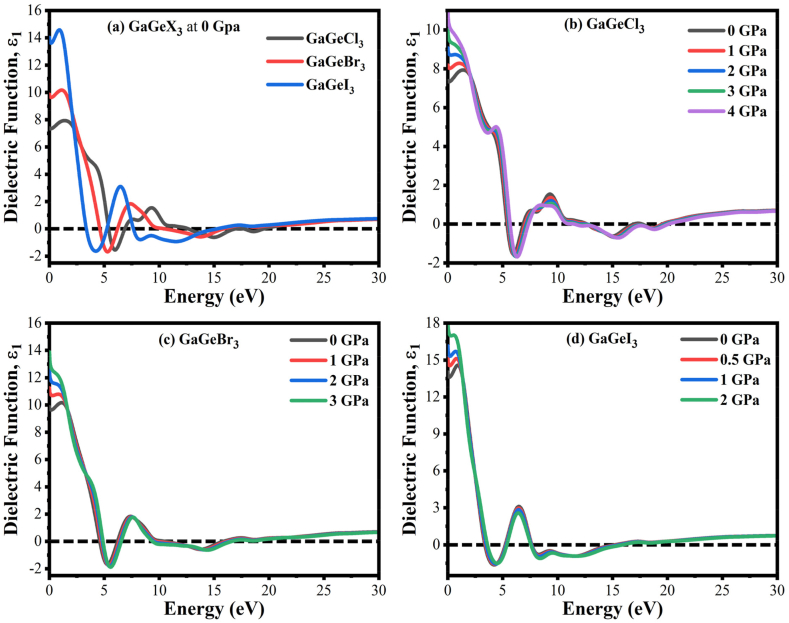
In this work, we looked at how the dielectric function fluctuated at various pressures in all perovskite materials, including the real and imaginary components. The findings are shown in Figs. 6(a–d) and 7(a–d) with up to 30 eV. The dielectric function's imaginary part (ε2) is directly associated with electron excitation, whereas the real part (ε1) offers details about the electronic polarization of the material. The way a material responds to incoming light radiation determines the dielectric constant values [45]. The long-term execution of optoelectronic devices is significantly enhanced via lower charge carrier recombination rates, which are linked to higher dielectric ε1 values. At 0 GPa, the compound is better suitable for application in optoelectronic devices when halogen Br and I are substituted for Cl, as shown by an increase in the value of ε1 in the IR zone and a decreasing nature in the visible energy area. In the same way, the imaginary dielectric constant (ε2) intensifies its shifting towards the low-energy region. Furthermore, there is greater absorption and bigger values of (ε2) in the visible and early UV areas. In the visible and infrared zones, both dielectric values are higher for all perovskite materials, whereas they dropped in the ultraviolet.
Fig. 6.
Pressure-driven real component of GaGeX3's dielectric constant (where X = Cl, Br, and I).
Fig. 7.
Calculating how pressure affects the dielectric's imaginary component of GaGeX3 (X = Cl, Br, and I) compounds.
Next, we looked at GaGeX3's pressure-induced dielectric function which is illustrated in Figs. 6(b–d) and 7(b–d). Pressure increases from 0 to 4 GPa, leading to an increase in the real component of the dielectric value in the region of low-energy of GaGeCl3. The value of ε1 is 10.3 for GaGeCl3 at 0 eV when the pressure reaches 4 GPa and at energy levels above 0 eV, ε1 declines. Next, it displays a negative value in the area with greater energy, suggesting that it is metallic. The ε1 component in the region of low energy of the GaGeBr3 and GaGeI3 materials is seen in Fig. 6(c and d) to rise when the pressure is increased from 0 to 3 GPa for GaGeBr3 and 0–2 GPa for GaGeI3, respectively. The true dielectric value for the higher energy area does not significantly change as pressure rises for both but declines to negative.
Also, the value imaginary dielectric constant increases in the whole spectrum as pressure rises for all compounds. There are three notable (ε2) peaks are seen in the low-energy area for GaGeCl3 and GaGeBr3 compounds. The first maximum peaks are at 2.46 eV and 2.05 eV; the second highest peaks are at 5.47 eV and 4.52 eV; the third maximum peaks are at 10.02 eV and 8.37 eV, respectively for GaGeCl3 and GaGeBr3 are depicted in Fig. 7(b and c). On the other hand, GaGeI3 also has two significant imaginary peaks at 1.82 eV and 7.33 eV which is shown in Fig. 7(d). Also, the value of ε2 is higher for GaGeI3 compared to other compounds. Then in the higher energy region, the value of ε2 drops under pressures for all compounds.
Looking at both dielectric constants, it is clear that GaGeI3 has a much bigger dielectric constant amplitude under pressure and without pressure contrasted with the other compounds in the visible area. As a result, both the Eb and the charge carrier recombination rate decrease. Thus, GaGeI3 functions excellent for use in solar cell systems within the sector of photovoltaic.
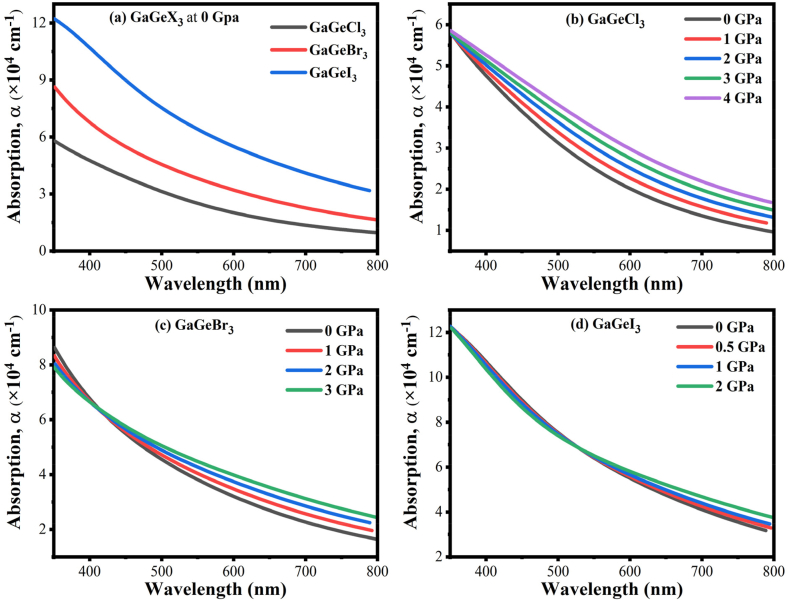
The optical absorption coefficient, denoted as (α), quantifies the fraction of energy that a material absorbs per unit distance. It also affects the different optoelectronic devices' efficiency along with solar cells. It is only one of the many optical properties that have a big impact on performance [46]. The variation of at 0 GPa with the energy of the photon is seen in Fig. 8, Fig. 9. For each compound, there are four distinct peaks seen within the energy spectrum of 0–30 eV. GaGeCl3 is shown to attain its greatest peak at 14.7 eV in Fig. 8(a). Conversely, the replacement of Cl for Br and I resulting a redshift; the highest peaks of GaGeBr3 and GaGeI3 are found at 13.5 eV and 11.4 eV, separately.
Fig. 8.
Illustrated the absorption spectra of GaGeX3 (where X = Cl, Br, and I) with energy under pressure.
Fig. 9.
Pressure-induced optical absorption of GaGeX3 concerning wavelength, where X is equal to Cl, Br, and I.
The difference in optical absorption of GaGeX3 (X = Cl, Br, and I) perovskites when pressured, is illustrated in Fig. 8(b–d). In the visible range, GaGeX3 exhibits pressure-induced band gap shifting, and its absorption edge moves to the area of low energy (redshift). Pressure significantly boosts the absorption edge of GaGeX3, as displayed in Fig. 9(b–d) inside the visible region. However, the absorption of all compounds increased with blueshift at higher energy levels. In comparison to GaGeBr3 and GaGeI3 perovskites, GaGeCl3 material exhibits the highest value of absorption in the ultraviolet region (ranging from 14.7 eV to 15.2 eV). The band gap for the energy of GaGeX3, which is uniform with the absorption in the visible region, is as follows: Eg (GaGeCl3) > Eg (GaGeBr3) > Eg (GaGeI3). Furthermore, as per Fig. 9(a–d), GaGeI3 is the material with the highest absorption efficiency out of the three in the visible area. It implies that GaGeI3 is a superior option to the other two when it comes to solar cell material. Because of their high absorption coefficients, all compounds are generally suitable for using multijunction solar cells.
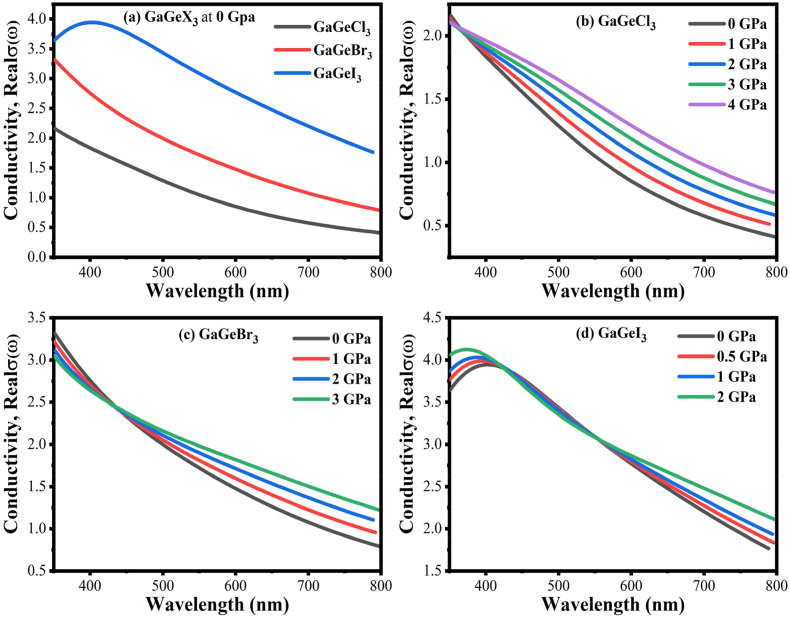
The photoconductivity (σ) of a substance is a measure of how many photons it can transmit. The spectrum of conductance of GaGeX3 (X = Cl, Br, and I) at 0 GPa are presented in Fig. 10, Fig. 11. The absorption patterns of GaGeX3 and these spectra resemble one other since these are derived from above. In the visible spectrum, GaGeI3 exhibits higher photoconductivity, at about 3.95 fs−1, compared to 3.44 fs−1 and 2.21 fs−1 for GaGeBr3 and GaGeCl3, respectively, as shown in Fig. 11(a). When Cl is replaced by the heavy halogens (Br and I), a redshift occurs. Each compound has two prominent peaks within the energy band at 0–30 eV.
Fig. 10.
Exploring the conductivity spectra of GaGeX3 compounds (X = Cl, Br, and I) with energy.
Fig. 11.
Exploring the variations in conductivity at different wavelengths while studying the effects of different pressures on GaGeX3 compounds (with X being Cl, Br, and I).
GaGeX3 (X = Cl, Br, and I) perovskites' pressure-dependent conductivity is shown in Figs. 10(b–d) and 11(b–d). Increased pressure leads to improved conductivity. A change in the conductivity edge toward the low-energy zone is brought about by the applied pressure. High energy levels and increased pressure cause a blueshift of conductivity peaks. To make things simpler to implement, Fig. 11(b–d) shows the conductivity in the visible area under applied pressure. With applied pressure, the perovskite containing I exhibits superior conductivity in the visible region when compared to Cl and Br. Conductivity peaks in the higher energy area are blue-shifted as seen in Fig. 10(b–d). The conductivity value range is σ (GaGeI3) > σ (GaGeBr3) > σ (GaGeCl3). Throughout the whole spectrum, materials made of GaGeX3 have certain conductivity peaks. These peaks, with the largest peak at 5.26 eV, are seen in GaGeCl3 at 5–5.5 eV and 9.5–10.5 eV ranges at different pressures. Consequently, GaGeBr3 exhibits notable peaks at 4.5–5 eV and 8.5–9.5 eV, separately, with 4.47 eV being the largest peak. On the other hand, GaGeI3 holds two primary peaks, located at 2.5–3.5 eV and 7–8 eV, respectively. Also, GaGeI3 has the highest intensity peak occurring at 7.44 eV.
Fig. 12(a) illustrates the reflectivity spectra of the substances under investigation, which helps to know about the topology of compounds. Solar efficiency is reduced when there is more reflection in the spectrum of visible light. Fig. 12(a) shows the reflectance (R) of GaGeX3 (X = Cl, Br, and I) at 0Gpa. At 0 eV, GaGeCl3 has a very low reflectance of around 0.22, as seen in Fig. 12(a). Nevertheless, when Cl is replaced with Br and I, respectively, the reflectance for GaGeBr3 and GaGeI3 increases to 0.27 and 0.34. Fig. 12(a) further demonstrates that in the visible range, GaGeX3 (X = Cl, Br, and I) exhibits increased reflectivity, whereas GaGeI3 has the highest level. The solar material's utility is diminished by GaGeI3's elevated optical reflection. Hence, more research is required to enhance the photovoltaic efficiency of GaGeI3 and decrease its reflectance.
Fig. 12.
The optical reflectivity of GaGeX3 (where X = Cl, Br, and I) induces by pressure.
The reflectivity that varies with pressure is seen in Fig. 12 (b–d). Based on these figures, the reflectivity spectra undergo a redshift at low energy, and then a blueshift at high energy as a result of applied pressure, respectively. But for any compound, the rise in reflectivity value is negligible. Throughout the whole spectrum, GaGeX3 materials display some peaks when subjected to pressure. Approximately at 2.12 eV, the first absorption peak for GaGeCl3 was observed. In addition, additional peaks were noted for the following compounds: GaGeCl3 at about 6.2 eV, 10.6 eV, 16.1 eV, and 19.5 eV; GaGeBr3 at 1.46 eV, 5.43 eV, 9.57 eV, 15 eV, and 18.7 eV; and GaGeI3 at 1.38 eV, 3.77 eV, 8.34 eV, 13.2 eV, and 18.5 eV. The low reflectivity of all materials throughout the spectrum, especially in the visible area, may be advantageous for the applications of solar cells due to their considerable absorptivity. According to Fig. 12(a–d), GaGeX3 compounds have excellent reflectivity within the UV region, suggesting that they might be used as coating materials to mitigate solar heating in this electromagnetic spectrum. In addition, GaGeI3's larger UV reflectance spectrum makes it an attractive candidate for UV shielding applications.
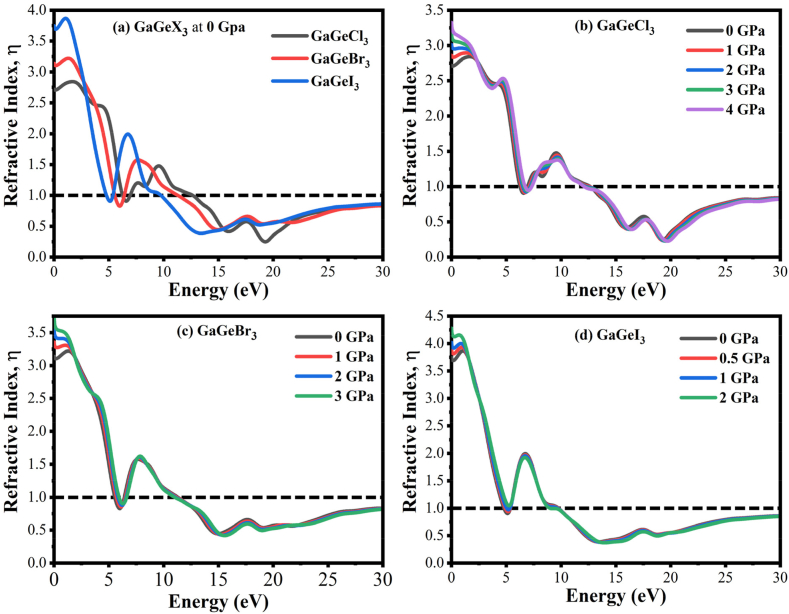
The refractive index spectrum at 0 GPa is depicted in Fig. 13(a). It clearly shows a decreasing trend with increasing light energy, with the highest peak taking place at 0 eV. Fig. 13(a) further shows that GaGeCl3 has a static refractive index of 2.72. The trend indicates an upward movement from Cl to I, with GaGeBr3 reaching 3.11 and GaGeI3 reaching 3.7, respectively. The infrared area of the compounds has the greatest refractive index, but the lowest in the UV portion. Among the compounds, GaGeI3 is most suited for waveguide applications due to its high refractive index at 0 eV [47].
Fig. 13.
Exploring the refractive index of GaGeX3 (X = Cl, Br, and I) with applied pressure.
The refractive index of GaGeX3 (X = Cl, Br, and I) perovskites with applied pressure is presented in Fig. 13 (b–d). Under applied pressure, the refractive values of all substances are increased in the low-energy area. All studied materials have the maximum refractive value at 0 eV. In regions of higher energy, the refractive index of GaGeCl3 may reduce and even blueshift sometimes. However, in the higher energy range, there are no notable changes in the refractive index for GaGeBr3 and GaGeI3 materials. In the visible area, the refractive index of any substance is minimal. Solar cells and other optoelectronic applications benefit from these materials for that reason.
With no crystallographic distortion of the materials, we now know that semiconductors emerged as conductors when pressure was applied, and that this overlapping of CB and VB is the reason why GaGeX3 (X = Cl, Br, and I) perovskites improved their optical and electronic properties. Because hydrostatic pressure may be used to tune the characteristics of any compound. In this study, the materials we studied have great potential as solar cells, UV absorbers, waveguide applications, and other optoelectronic devices.
3.4. Mechanical properties
In order to estimate elastic constants, it is necessary to calculate the stress tensor for a diversity of deformed structures. With the help of the CASTEP Elastic Constants task, we can get the full 6 × 6 tensor of elastic constants for any symmetric three-dimensional periodic structure. For assessing the mechanical stability of compounds, a table of elastic constants (Cij) is provided in Tables S3–S5 [48]. Conditions for Born stability are met by all three elastic constants for GaGeX3 (X = Cl, Br, and I) under investigation when pressure is applied [49], where three main components are C11, C12, C44 denoting longitudinal stiffness, off-diagonal stiffness, and shear stiffness respectively.
| C11 > 0; C44 > 0; C11 > C12 |
| C11 + 2C12 > 0; C12 < B < C11 |
According to the Voigt, Reuss, and Hill schemes, the output comprises the averages of Young's, the bulk, and the shear modulus, along with Poisson's ratio. In relation to the corresponding single-crystal properties, the VRH approximation provides practical values for the elastic moduli with polycrystalline crystal. The Voigt and Reuss bulk modulus (B), shear modulus (G), and Pugh's ratio are expressed as [50],
| (2) |
| (3) |
| (4) |
The final shear modulus and bulk modulus are calculated by [51],
| (5) |
| (6) |
By utilizing B and G, we derived the average the Poisson's ratio v and Young's modulus E, thereby facilitating comprehension of mechanical properties in the context of DFT calculations [48],
| (7) |
| (8) |
| (9) |
| (10) |
The subsequent hardness of GaGeX3 (X = Cl, Br, I) is computed utilizing Tian's model [52],
| (11) |
Here, K = B/G.
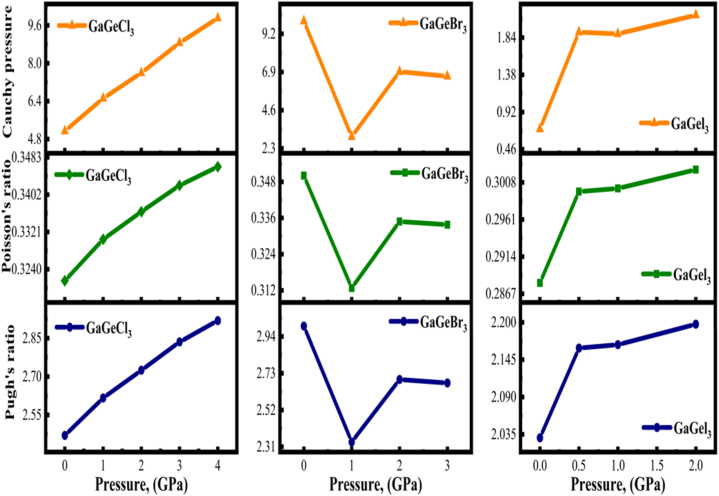
The data from Tables S3(a), S4(a), and S5(a) indicate that the elastic constant Cij rises as pressure increases, but C44 is less affected by hydrostatic pressure. The fluctuation of elastic constants is depicted in Fig. 14 with different pressures. The Cauchy pressure (C12–C44) is a crucial measure of a material's ductility or brittleness. When this characteristic has a negative value, it signifies that the material is brittle. Conversely, a positive value suggests the ductility of a material. The ductile behavior of GaGeX3 is reflected according to the positive Cauchy pressure in Tables S3(a), S4(a), and S5(a). Furthermore, as pressure increases, the ductility of these compounds increases except GaGeBr3 as shown in Fig. 16. However, an examination of the GaGeBr3 reveals that the Cauchy pressure decreases when pressure increases, which reveals a reduction in the number of void spaces between particles. The subsequent increase in Cauchy pressure is due to the material reaching a critical density, at which point its resistance to compression diminishes.
Fig. 14.
Elastic constants of C11, C12, and C44 for GaGeX3 (X = Cl, Br, and I) vary with pressure.
Fig. 16.
Examining the changes in Cauchy pressure, Pugh's, and Poisson's ratio of cubic GaGeX3 (X = Cl, Br, and I) at different pressures.
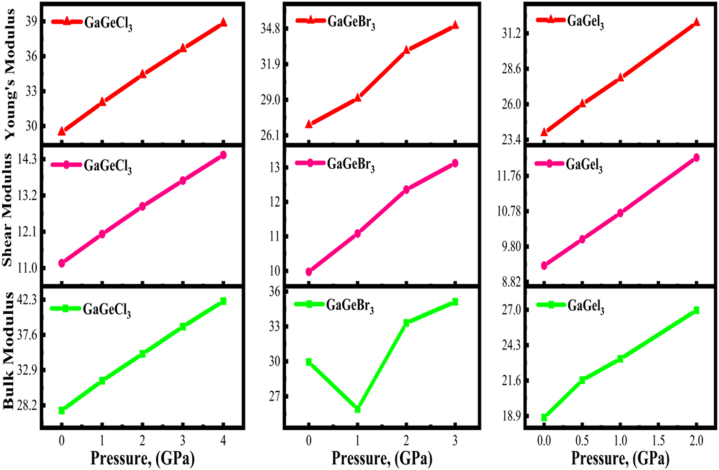
The changes in shear, bulk, and Young's modulus of GaGeX3 (where X is equal to Cl, Br, and I) under pressure are illustrated in Fig. 15. From Fig. 15, it is clear that the bulk modulus value for GaGeCl3 increases when pressure increases, denoting more resistance to external deformation and is stiffer compared to non-pressurized states. The same result was also found for GaGeI3 leading to close-packed atoms. However, the fact that the GaGeBr3's bulk modulus decreases initially with increasing pressure (up to 1 GPa) suggests that atomic bond interactions may change slightly; however, as pressure increases above 1 GPa, B increases again, also increasing plastic deformation resistance. The material's shear modulus (G) also denotes its fracture resistance. The G values of GaGeX3 (X = Cl, Br, and I) are increasing linearly with increasing pressure which is aligned with Fig. 15 and Tables S3(a), S4(a) and S5(a). But if we compare B and G among the three compounds at 2 GPa, GaGeCl3 shows better values of B and G. Consequently, materials with higher E values are associated with greater stiffness. E increases linearly as the pressure increases for GaGeX3 (X = Cl, Br, I) perovskites. Since pressure is increased, GaGeCl3 exhibits the greatest rigidity among the three perovskites.
Fig. 15.
Investigating the Young's, Shear, and Bulk Modulus of GaGeX3 (X = Cl, Br, and I) with variation of pressure.
If the ratio of B to G is more than 1.75, the material exhibits ductile behavior; otherwise, it exhibits brittle behavior [53]. All three compounds show ductile nature at both pressurized and non-pressurized states according to Tables S3(a), S4(b), and S5(c). The variety in Cauchy pressure, Pugh's, and Poisson's ratio of cubic GaGeX3 (X = Cl, Br, and I) at varying pressures are displayed in Fig. 16. Here, the Pugh's ratio increases when pressure increases for GaGeI3 and GaGeCl3 but for GaGeBr3 initially decreases at 1 GPa, followed by a slight increase. The Poisson's ratio for ductility is above 0.26 [54]. From this point of view, all the compounds have Poisson's ratio above this value. This situation is evident in the ductile behavior of all compounds.
The GaGeCl3's hardness decreases under applied pressure, consequently machinability index increases as in Table S3(a). The machinability index reflects a material's ability to be shaped and its lubricating characteristics. As a result of applying pressure, the machinability of GaGeCl3 is significantly increased which is attributed to the reduction in hardness, which results in improved lubricity properties. The hardness of GaGeBr3 and GaGeI3 at ambient pressure show non-linear nature as shown in Fig. 17. But both GaGeBr3 and GaGeI3 exhibit improved machinability at increasing pressure, identical to GaGeCl3. The machinability of GaGeCl3 was found to be superior among the three perovskites.
Fig. 17.
Investigating the impact of pressure on the hardness and machinability index of GaGeX3 (X = Cl, Br, and I).
One approach to assess the directional variability of a system's attributes is to use the anisotropic index. When assessing the atomic bond strength's degree of anisotropy across several crystallographic planes, including {100}, {010}, and {001}, the shear anisotropy factor in cubic systems is useful. Three shear anisotropy factors (A1, A2, and A3) for these planes are computed using a particular equation [55].
| (12) |
A similar expression for the Zener anisotropy factor (A) follows [56].
| (13) |
Anisotropy indicates a departure from unity in isotropic materials, where A = 1 [56]. Tables S3(b), S4(b), and S5(b) show that the GaGeX3's (X = Cl, Br, and I) elastic anisotropy has increased at increasing pressures. For different crystal planes, it is preferable to use a single anisotropy index rather than several components to more easily capture this anisotropy. Chung and Buessem also determined the anisotropy percentage using an empirical method in both shear and bulk [57]. Elastic isotropy is shown when AB and AG equals zero. However, both the pressurized and non-pressurized conditions show that the computed values of AB and AG are non-zero. This indicates that all GaGeX3 (where X = Cl, Br, and I) are anisotropic. The fact that the universal anisotropy factor (AU), which Ranganathan and Ostoja-Starzewski initially proposed, may be used for any crystal symmetry makes it very attractive. AU is 0 for isotropic materials [58]. Tables S3(b), S4(b), and S5(b) emphasize that the substances under study have elastic anisotropy, with anisotropy increasing significantly with pressure. To demonstrate the directional dependence of elastic characteristics in GaGeX3 perovskites, 3D anisotropic contour plots for E, G, and ʋ were created and shown in Figs. S7–9. The deviation found in these contour plots from the spherical shape indicates the anisotropic nature of the perovskites under investigation [41]. Pressure exerts a significant impact on the directional elasticity of GaGeX3 perovskites, as evidenced by the sharp rise in anisotropy when pressure increases from 0 GPa up to 4 GPa.
4. Conclusion
In conclusion, exploring the effects of hydrostatic pressures on material properties is an intriguing area of study. Applying pressure to compounds like GaGeX3 (X = Cl, Br, and I) can modify their electronic structure, bandgap, and other important properties. This flexibility allows for a variety of useful applications such as solar cells and different optoelectronic devices. Based on the born stability criterion, all perovskites are stable mechanically under applied pressure. Positive Cauchy pressure and Pugh's ratio exhibit ductile behavior of all investigated compounds. These perovskite materials have low bulk modulus that's why these are ideal for thin-layer fabrication. They also experience increasing shear and Young's modulus as increasing pressure. GaGeCl3, the stiffest of the three perovskites, exhibits the most marked rigidity under pressure. The substantial enhancement in machinability of GaGeX3 resulting a decrease in hardness under pressure, which in turn leads to enhanced lubricity characteristics. In addition, these substances possess important mechanical properties: anisotropy, ductility, and mechanical stability, which are further enhanced when subjected to pressure. When subjected to positive hydrostatic pressure, the lattice parameter experiences a decrease, resulting in a more negative formation energy that reveals their thermodynamic stability. Also, the decreasing nature of bond length under pressure makes stronger bonding between atoms. These attributes are crucial for the development of multi-junctional solar cells and high-performance optoelectronic devices. The band gap values are calculated with PBE along with HSE06 potentials that exhibit the direct band gap and semiconducting character of each compound. The metallic transition takes place after a certain pressure is applied. The participation of atoms in the VB and CBs can be determined from TDOS and PDOS, respectively. In the VBs, various orbitals such as Ga-4s, Cl-3p, Br-4p, and I-5p are involved. On the other hand, the conduction bands involve Ga-4p and Ge-4p orbitals. After investigation of optical properties, these materials became more viable for optoelectronic applications, both pressure and non-pressure conditions. In addition, our research reveals that all compounds exhibit higher values of () and greater absorption in the visible and early UV regions. When comparing the three compounds, however, it becomes evident that GaGeI3 has a significantly larger dielectric constant amplitude under pressure and without pressure in the visible range (1.8 eV and 7.33 eV) than the other two samples. This characteristic renders GaGeI3 particularly well-suited for solar cell applications. However, GaGeCl3 exhibits stronger absorption in the UV region (ranging from 14.7 eV to 15.2 eV). So, it is evident that GaGeCl3 is a superior absorber of UV radiation. In addition, GaGeI3 exhibited higher reflectivity when subjected to pressure making them suitable for UV shielding application. Regarding the refractive index, all three compounds exhibit a minimum value in the lower energy range, which is advantageous for optoelectronic applications.
CRediT authorship contribution statement
Md. Mehedi Hasan: Data curation, Formal analysis, Software, Writing – original draft. Md. Amran Sarker: Conceptualization, Data curation, Formal analysis, Investigation, Software, Writing – original draft. Mohshina Binte Mansur: Data curation, Formal analysis, Methodology, Writing – original draft. Md. Rasidul Islam: Conceptualization, Investigation, Resources, Supervision, Validation, Writing – review & editing. Sohail Ahmad: Funding acquisition, Project administration, Resources, Validation, Writing – review & editing.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
The authors extend their appreciation to the Deanship of Research and Graduate Studies at King Khalid University for funding this work through Large Research Project under grant number RGP2/415/45.
Footnotes
Supplementary data to this article can be found online at https://doi.org/10.1016/j.heliyon.2024.e34824.
Appendix A. Supplementary data
The following is the Supplementary data to this article:
References
- 1.Jung H.S., Park N. Perovskite solar cells: from materials to devices. Small. 2015;11:10–25. doi: 10.1002/smll.201402767. [DOI] [PubMed] [Google Scholar]
- 2.Boix P.P., Nonomura K., Mathews N., Mhaisalkar S.G. Current progress and future perspectives for organic/inorganic perovskite solar cells. Mater. Today. 2014;17:16–23. doi: 10.1016/j.mattod.2013.12.002. [DOI] [Google Scholar]
- 3.Correa-Baena J.-P., Saliba M., Buonassisi T., Grätzel M., Abate A., Tress W., Hagfeldt A. Promises and challenges of perovskite solar cells. Science. 2017;358:739–744. doi: 10.1126/science.aam6323. [DOI] [PubMed] [Google Scholar]
- 4.Hussain I., Tran H.P., Jaksik J., Moore J., Islam N., Uddin M.J. Functional materials, device architecture, and flexibility of perovskite solar cell. Emergent Mater. 2018;1:133–154. doi: 10.1007/s42247-018-0013-1. [DOI] [Google Scholar]
- 5.Green M.A., Ho-Baillie A., Snaith H.J. The emergence of perovskite solar cells. Nat. Photonics. 2014;8:506–514. doi: 10.1038/nphoton.2014.134. [DOI] [Google Scholar]
- 6.Solayman M., Islam M.R., Sarker M.A., Sharme R.K., Al Momin M., Islam M.R., Khan A.A. A deep dive into structural, electronic, optical, and mechanical properties of ATiO 3 (A = Ba, Th): DFT insights. Phys. Scr. 2023;98 doi: 10.1088/1402-4896/ad0a27. [DOI] [Google Scholar]
- 7.Humada A.M., Hojabri M., Mekhilef S., Hamada H.M. Solar cell parameters extraction based on single and double-diode models: a review. Renew. Sustain. Energy Rev. 2016;56:494–509. doi: 10.1016/j.rser.2015.11.051. [DOI] [Google Scholar]
- 8.Lee T.D., Ebong A.U. A review of thin film solar cell technologies and challenges. Renew. Sustain. Energy Rev. 2017;70:1286–1297. doi: 10.1016/J.RSER.2016.12.028. [DOI] [Google Scholar]
- 9.Hossain M.K., Bhattarai S., Arnab A.A., Mohammed M.K.A., Pandey R., Ali M.H., Rahman MdF., Islam MdR., Samajdar D.P., Madan J., Bencherif H., Dwivedi D.K., Amami M. Harnessing the potential of CsPbBr 3 -based perovskite solar cells using efficient charge transport materials and global optimization. RSC Adv. 2023;13:21044–21062. doi: 10.1039/D3RA02485G. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Sun Y., Zhang W., Chi H., Liu Y., Hou C.L., Fang D. Recent development of graphene materials applied in polymer solar cell. Renew. Sustain. Energy Rev. 2015;43:973–980. doi: 10.1016/j.rser.2014.11.040. [DOI] [Google Scholar]
- 11.Islam MdR., Wu Y., Liu K., Wang Z., Qu S., Wang Z. Recent progress and future prospects for light management of all‐perovskite tandem solar cells. Adv. Mater. Interfaces. 2022;9 doi: 10.1002/admi.202101144. [DOI] [Google Scholar]
- 12.Padmavathy R., Amudhavalli A., Manikandan M., Rajeswarapalanichamy R., Iyakutti K., Kushwaha A.K. Electronic and optical properties of CsSnI3−yCly (y = 0, 1, 2, 3) perovskites: a DFT study. J. Electron. Mater. 2019;48:1243–1251. doi: 10.1007/s11664-018-06850-8. [DOI] [Google Scholar]
- 13.Eperon G.E., Paternò G.M., Sutton R.J., Zampetti A., Haghighirad A.A., Cacialli F., Snaith H.J. Inorganic caesium lead iodide perovskite solar cells. J. Mater. Chem. A Mater. 2015;3:19688–19695. doi: 10.1039/C5TA06398A. [DOI] [Google Scholar]
- 14.Li J., Han Z., Gu Y., Yu D., Liu J., Hu D., Xu X., Zeng H. Perovskite single crystals: synthesis, optoelectronic properties, and application. Adv. Funct. Mater. 2021;31 doi: 10.1002/adfm.202008684. [DOI] [Google Scholar]
- 15.Chouhan L., Ghimire S., Subrahmanyam C., Miyasaka T., Biju V. Synthesis, optoelectronic properties and applications of halide perovskites. Chem. Soc. Rev. 2020;49:2869–2885. doi: 10.1039/C9CS00848A. [DOI] [PubMed] [Google Scholar]
- 16.Zhang W., Eperon G.E., Snaith H.J. Metal halide perovskites for energy applications. Nat. Energy. 2016;1 doi: 10.1038/nenergy.2016.48. [DOI] [Google Scholar]
- 17.Yin W., Shi T., Yan Y. Unique properties of halide perovskites as possible origins of the superior solar cell performance. Adv. Mater. 2014;26:4653–4658. doi: 10.1002/adma.201306281. [DOI] [PubMed] [Google Scholar]
- 18.Padmavathy R., Amudhavalli A., Rajeswarapalanichamy R., Iyakutti K. Electronic and optical properties of cubic perovskites CsPbCl3− yIy (y = 0, 1, 2, 3) Z. Naturforsch. 2019;74:905–913. doi: 10.1515/zna-2018-0516. [DOI] [Google Scholar]
- 19.Yang W.S., Park B.-W., Jung E.H., Jeon N.J., Kim Y.C., Lee D.U., Shin S.S., Seo J., Kim E.K., Noh J.H., Il Seok S. Iodide management in formamidinium-lead-halide–based perovskite layers for efficient solar cells. Science. 2017;356:1376–1379. doi: 10.1126/science.aan2301. [DOI] [PubMed] [Google Scholar]
- 20.Nishimura K., Kamarudin M.A., Hirotani D., Hamada K., Shen Q., Iikubo S., Minemoto T., Yoshino K., Hayase S. Lead-free tin-halide perovskite solar cells with 13% efficiency. Nano Energy. 2020;74 doi: 10.1016/j.nanoen.2020.104858. [DOI] [Google Scholar]
- 21.Yuan Y., Xu R., Xu H.-T., Hong F., Xu F., Wang L.-J. Nature of the band gap of halide perovskites ABX3 (A = CH3 NH3, Cs; B = Sn, Pb; X = Cl, Br, I): first-principles calculations. Chin. Phys. B. 2015;24 doi: 10.1088/1674-1056/24/11/116302. [DOI] [Google Scholar]
- 22.Roknuzzaman M., Ken Ostrikov K., Chandula Wasalathilake K., Yan C., Wang H., Tesfamichael T. Insight into lead-free organic-inorganic hybrid perovskites for photovoltaics and optoelectronics: a first-principles study. Org. Electron. 2018;59:99–106. doi: 10.1016/j.orgel.2018.04.051. [DOI] [Google Scholar]
- 23.Berhe T.A., Su W.-N., Chen C.-H., Pan C.-J., Cheng J.-H., Chen H.-M., Tsai M.-C., Chen L.-Y., Dubale A.A., Hwang B.-J. Organometal halide perovskite solar cells: degradation and stability. Energy Environ. Sci. 2016;9:323–356. doi: 10.1039/C5EE02733K. [DOI] [Google Scholar]
- 24.Coduri M., Shiell T.B., Strobel T.A., Mahata A., Cova F., Mosconi E., De Angelis F., Malavasi L. Origin of pressure-induced band gap tuning in tin halide perovskites. Mater. Adv. 2020;1:2840–2845. doi: 10.1039/D0MA00731E. [DOI] [Google Scholar]
- 25.Kholil M.I., Bhuiyan M.T.H. Effects of pressure on narrowing the band gap, visible light absorption, and semi-metallic transition of lead-free perovskite CsSnBr3 for optoelectronic applications. J. Phys. Chem. Solid. 2021;154 doi: 10.1016/J.JPCS.2021.110083. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Guo S., Zhao Y., Bu K., Fu Y., Luo H., Chen M., Hautzinger M.P., Wang Y., Jin S., Yang W., Lü X. Pressure‐suppressed carrier trapping leads to enhanced emission in two‐dimensional perovskite (HA) 2 (GA)Pb 2 I 7. Angew. Chem. 2020;132:17686–17692. doi: 10.1002/ange.202001635. [DOI] [PubMed] [Google Scholar]
- 27.Solayman Md, Sarker MdA., Muntasir M., Sharme R.K., Islam MdR. Pressure-induced investigation of structural, electronic, optical, and mechanical properties of BaCeO3. Opt. Mater. 2024;148 doi: 10.1016/j.optmat.2023.114699. [DOI] [Google Scholar]
- 28.Rahman MdF., Islam MdA.I., Islam MdR., Ali MdH., Barman P., Rahman MdA., Harun‐Or‐Rashid Md, Hasan M., Hossain M.K. Investigation of a novel inorganic cubic perovskite Ca 3 PI 3 with unique strain‐driven optical, electronic, and mechanical properties. Nano Select. 2023;4:632–645. doi: 10.1002/nano.202300066. [DOI] [Google Scholar]
- 29.Sarker MdA., Hasan M.M., Al Momin Md, Irfan A., Islam MdR., Sharif A. Band gap engineering in lead free halide cubic perovskites GaGeX 3 (X = Cl, Br, and I) based on first-principles calculations. RSC Adv. 2024;14:9805–9818. doi: 10.1039/d4ra00224e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Hoefler S.F., Trimmel G., Rath T. Progress on lead-free metal halide perovskites for photovoltaic applications: a review. Monatsh. Chem. - Chem. Mon. 2017;148:795–826. doi: 10.1007/s00706-017-1933-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Roknuzzaman M., Ostrikov K., Wang H., Du A., Tesfamichael T. Towards lead-free perovskite photovoltaics and optoelectronics by ab-initio simulations. Sci. Rep. 2017;7 doi: 10.1038/s41598-017-13172-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Clark S.J., Segall M.D., Pickard C.J., Hasnip P.J., Probert M.I.J., Refson K., Payne M.C. First principles methods using CASTEP. Z. für Kristallogr. - Cryst. Mater. 2005;220:567–570. doi: 10.1524/zkri.220.5.567.65075. [DOI] [Google Scholar]
- 33.Daw M.S., Baskes M.I. Semiempirical, quantum mechanical calculation of hydrogen embrittlement in metals. Phys. Rev. Lett. 1983;50:1285–1288. doi: 10.1103/PhysRevLett.50.1285. [DOI] [Google Scholar]
- 34.Kohn W. Density functional and density matrix method scaling linearly with the number of atoms. Phys. Rev. Lett. 1996;76:3168–3171. doi: 10.1103/PhysRevLett.76.3168. [DOI] [PubMed] [Google Scholar]
- 35.Perdew J.P., Burke K., Ernzerhof M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996;77:3865–3868. doi: 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
- 36.Vanderbilt D. Soft self-consistent pseudopotentials in a generalized eigenvalue formalism. Phys. Rev. B. 1990;41:7892–7895. doi: 10.1103/PhysRevB.41.7892. [DOI] [PubMed] [Google Scholar]
- 37.Fischer T.H., Almlof J. General methods for geometry and wave function optimization. J. Phys. Chem. 1992;96:9768–9774. doi: 10.1021/j100203a036. [DOI] [Google Scholar]
- 38.Monkhorst H.J., Pack J.D. Special points for Brillouin-zone integrations. Phys. Rev. B. 1976;13:5188–5192. doi: 10.1103/PhysRevB.13.5188. [DOI] [Google Scholar]
- 39.Kang J., Lee E.-C., Chang K.J. First-principles study of the structural phase transformation of hafnia under pressure. Phys. Rev. B. 2003;68 doi: 10.1103/PhysRevB.68.054106. [DOI] [Google Scholar]
- 40.Murnaghan F.D. The compressibility of media under extreme pressures. Proc. Natl. Acad. Sci. USA. 1944;30:244–247. doi: 10.1073/pnas.30.9.244. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Alam MdS., Saiduzzaman M., Biswas A., Ahmed T., Sultana A., Hossain K.M. Tuning band gap and enhancing optical functions of AGeF3 (A = K, Rb) under pressure for improved optoelectronic applications. Sci. Rep. 2022;12:8663. doi: 10.1038/s41598-022-12713-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Aktary M., Kamruzzaman M., Afrose R. Pressure-dependent comparative study of the mechanical, electronic, and optical properties of CsPbX 3 (X = Cl, Br, I): a DFT study for optoelectronic applications. Mater. Adv. 2023;4:4494–4508. doi: 10.1039/D3MA00311F. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Rahman MdF., Rahman MdH., Islam MdR., Hossain M.K., Ghosh A., Islam MdS., Islam MdM., Harun-Or-Rashid Md, Albalawi H., Mahmood Q. The optical and electronic properties of inorganic halide perovskite Sr3NCl3 under applied biaxial strain. J. Mater. Sci. 2023;58:13100–13117. doi: 10.1007/s10853-023-08825-5. [DOI] [Google Scholar]
- 44.Humada A.M., Hojabri M., Mekhilef S., Hamada H.M. Solar cell parameters extraction based on single and double-diode models: a review. Renew. Sustain. Energy Rev. 2016;56:494–509. doi: 10.1016/j.rser.2015.11.051. [DOI] [Google Scholar]
- 45.Islam MdR., Islam A.S.M.J., Liu K., Wang Z., Qu S., Zhao C., Wang X., Wang Z. Strain-induced tunability of the optoelectronic properties of inorganic lead iodide perovskites APbI3 (A= Rb and Cs) Phys. B Condens. Matter. 2022;638 doi: 10.1016/j.physb.2022.413960. [DOI] [Google Scholar]
- 46.Shanto MdA.B., Rahman MdF., Islam MdR., Ghosh A., Azzouz-Rached A., Albalawi H., Mahmood Q. Investigating how the electronic and optical properties of a novel cubic inorganic halide perovskite, Sr3NI3 are affected by strain. F1000Res. 2023;12:1005. doi: 10.12688/f1000research.137044.1. [DOI] [Google Scholar]
- 47.Rasheduzzaman Md, Hossain K.M., Mitro S.K., Hadi M.A., Modak J.K., Hasan MdZ. Structural, mechanical, thermal, and optical properties of inverse-Heusler alloys Cr2CoZ (Z = Al, In): a first-principles investigation. Phys. Lett. 2021;A 385 doi: 10.1016/j.physleta.2020.126967. [DOI] [Google Scholar]
- 48.Mehl M.J. Pressure dependence of the elastic moduli in aluminum-rich Al-Li compounds. Phys. Rev. B. 1993;47:2493–2500. doi: 10.1103/PhysRevB.47.2493. [DOI] [PubMed] [Google Scholar]
- 49.Mouhat F., Coudert F.-X. Necessary and sufficient elastic stability conditions in various crystal systems. Phys. Rev. B. 2014;90 doi: 10.1103/PhysRevB.90.224104. [DOI] [Google Scholar]
- 50.Chung D.H., Buessem W.R. The voigt-Reuss-Hill (VRH) approximation and the elastic moduli of polycrystalline ZnO, TiO2 (Rutile), and α-Al2O3. J. Appl. Phys. 1968;39:2777–2782. doi: 10.1063/1.1656672. [DOI] [Google Scholar]
- 51.Hill R. The elastic behaviour of a crystalline aggregate. Proc. Phys. Soc. 1952;65:349–354. doi: 10.1088/0370-1298/65/5/307. [DOI] [Google Scholar]
- 52.Al-Fahdi M., Rodriguez A., Ouyang T., Hu M. High-throughput computation of new carbon allotropes with diverse hybridization and ultrahigh hardness. Crystals. 2021;11:783. doi: 10.3390/cryst11070783. [DOI] [Google Scholar]
- 53.Pugh S.F. XCII. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals. London, Edinburgh Dublin Phil. Mag. J. Sci. 1954;45:823–843. doi: 10.1080/14786440808520496. [DOI] [Google Scholar]
- 54.Fleischer R.L., Gilmore R.S., Zabala R.J. Elastic moduli of polycrystalline, high-temperature binary intermetallic compounds. Acta Metall. 1989;37:2801–2803. doi: 10.1016/0001-6160(89)90314-3. [DOI] [Google Scholar]
- 55.Gao X., Jiang Y., Zhou R., Feng J. Stability and elastic properties of Y–C binary compounds investigated by first principles calculations. J. Alloys Compd. 2014;587:819–826. doi: 10.1016/j.jallcom.2013.11.005. [DOI] [Google Scholar]
- 56.Zener C.M., Siegel S. Elasticity and anelasticity of metals. J. Phys. Colloid Chem. 1949;53:1468. doi: 10.1021/j150474a017. [DOI] [Google Scholar]
- 57.Sharme R.K., Islam MdR., Sarker MdA., Solayman Md, Al Momin Md, Islam MdR. First-principles study on electronic, mechanical, and optical properties of pressure-induced vanadium-based perovskite KVO3. Phys. B Condens. Matter. 2024;681 doi: 10.1016/j.physb.2024.415785. [DOI] [Google Scholar]
- 58.Ranganathan S.I., Ostoja-Starzewski M. Universal elastic anisotropy index. Phys. Rev. Lett. 2008;101 doi: 10.1103/PhysRevLett.101.055504. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.