The spike-and-slab lasso and scalable algorithm to accommodate multinomial outcomes in variable selection problems

Abstract

Spike-and-slab prior distributions are used to impose variable selection in Bayesian regression-style problems with many possible predictors. These priors are a mixture of two zero-centered distributions with differing variances, resulting in different shrinkage levels on parameter estimates based on whether they are relevant to the outcome. The spike-and-slab lasso assigns mixtures of double exponential distributions as priors for the parameters. This framework was initially developed for linear models, later developed for generalized linear models, and shown to perform well in scenarios requiring sparse solutions. Standard formulations of generalized linear models cannot immediately accommodate categorical outcomes with > 2 categories, i.e. multinomial outcomes, and require modifications to model specification and parameter estimation. Such modifications are relatively straightforward in a Classical setting but require additional theoretical and computational considerations in Bayesian settings, which can depend on the choice of prior distributions for the parameters of interest. While previous developments of the spike-and-slab lasso focused on continuous, count, and/or binary outcomes, we generalize the spike-and-slab lasso to accommodate multinomial outcomes, developing both the theoretical basis for the model and an expectation-maximization algorithm to fit the model. To our knowledge, this is the first generalization of the spike-and-slab lasso to allow for multinomial outcomes.

1. Introduction

Spike-and-slab priors have a long history in Bayesian variable selection [16,24]. The spike-and-slab prior is a mixture of two distributions, both with mean zero, but with differing scale parameters that serve to vary the degree of shrinkage imposed on parameter estimates. The narrower ‘spike’ distribution models predictors that are irrelevant to the outcome of interest and imposes strong shrinkage towards the prior mean of zero, whereas the wider ‘slab’ distribution models predictors that are relevant to the outcome of interest and thus imposes weak shrinkage towards the prior mean of zero. The practical effect of the spike-and-slab framework is to increase the probability that relevant predictors remain in the model while irrelevant predictors are shrunk to zero, effectively excluding them from the model.

While traditionally spike-and-slab priors were mixtures of Normal distributions, other distributions may be more optimal in some circumstances. For example, when a relatively small percentage of a large number of possible predictors are expected to be relevant to the outcome of interest, a mixture of double exponential distributions, i.e. the spike-and-slab lasso (SSL), may be more appropriate, especially in cases where the number of predictors is larger than the number of subjects and/or some subsets of the predictors are highly correlated [29]. In classical settings, penalized regression models can handle correlated predictors and cases where predictors outnumber subjects, and many of these penalized regression models have Bayesian interpretations.

For example, ridge regression was developed to address multicollinearity and constrains the sum of squared parameter estimates to be less than some constant [20]. The ridge penalty is equivalent to placing Normal priors on parameters, but cannot perform variable selection [17]. In contrast, the least absolute shrinkage and selection operator (lasso) constrains the sum of the absolute value of parameter estimates to be less than some constant and is equivalent to placing double exponential priors on parameters; this results in a sparse solution, i.e. performs variable selection [26,35]. However, the lasso is not without limitations. For example, if there are J predictors and N subjects, then when J>N, at most N predictors can remain in the model, and when predictors are highly correlated, the lasso tends to select one and discard the others [38]. Together, these limitations highlight the severity of the lasso penalty.

The elastic net is a compromise between ridge and lasso penalties, allowing for variable selection (lasso) with a less severe penalty and better handling of correlated predictors (ridge), and contains ridge and lasso as special cases [38]. The downside of the elastic net framework is that it uses a single penalty parameter, which results in applying uniform shrinkage to parameter estimates, and in a Bayesian context is equivalent to assuming that all parameter values are drawn from a single distribution. Thus, how likely a parameter is to be relevant to the outcome of interest plays no role in the level of shrinkage applied to its estimates. In contrast, the spike-and-slab lasso uses two penalty parameters, which in a Bayesian context implies different distributions for parameter values of irrelevant and relevant predictors, respectively. Such a framework allows for adaptive shrinkage, i.e. the degree of shrinkage applied to a parameter estimate depends on how likely the predictor is to be relevant to the outcome [29,35].

The spike-and-slab lasso was initially developed in the context of linear models and later developed for generalized linear models (GLM), and has been especially useful in genetic/genomics studies, where often a small number of genes are relevant to an outcome of interest and the number of possible predictors, e.g. genes or single nucleotide polymorphisms (SNPs), is vastly larger than the number of subjects (J>N) [2,29,33,34]. In previous work, we generalized the spike-and-slab lasso for GLMs to the spike-and-slab elastic net (SSEN), which includes the spike-and-slab ridge/lasso as special cases, and otherwise compromises between ridge and lasso penalties; further modifications allowed incorporating spatial information into the variable selection process, e.g. when using medical images to model some clinical outcome [21]. We also demonstrated the utility of the spike-and-slab elastic net framework for prediction and/or classification in Alzheimer's disease [22]. Thus, the spike-and-slab elastic net framework may be useful for explicit variable selection where some interpretation of the selected parameters is desired and/or prediction modeling where the primary goal is to build a predictive model that performs well on novel data.

Many applications have categorical outcomes, a significant subset of which are binary, i.e. outcomes with two options. Disease outcomes are often binary by nature, e.g. whether or not a subject has had a stroke, has developed a particular type of cancer, or is cognitively normal versus having dementia. Binary outcomes are usually assumed to follow a binomial distribution, and logistic regression, a special case of GLMs, can be used to model binary outcomes as a function of some set of predictors. However, many categorical outcomes have more than two mutually exclusive categories, even in applications where a binary outcome is often used. For example, progression from cognitive normal to dementia has intermediate (prodromal) stages, e.g. mild cognitive impairment (MCI), resulting in 3 categories of interest: cognitive normal, MCI, or dementia [7]. Similarly, cancers are divided into 5 categories, cancer-free and stages I-IV.

A simple approach to modeling outcomes with more than 2 categories is to choose a reference category and fit several logistic regression models, e.g. by choosing cognitive normal as the reference, we would fit a logistic regression for MCI vs. cognitive normal and another for dementia vs. cognitive normal. However, such an approach is flawed because there is no assurance that the estimated probabilities of each outcome category will sum to 1. Moreover, categorical outcomes with $>2$ mutually exclusive categories are modeled by a multinomial distribution, which is the generalization of the binomial distribution, and the corresponding generalization of logistic regression is multinomial regression, which does assure the estimated probabilities of each outcome category sum to 1.

Multinomial regression requires modifications to the standard GLM framework, namely that while standard GLMs estimate a single parameter for each predictor, multinomial regression requires multiple parameter estimates for each predictor. Multinomial regression has long existed in the classical framework and has been adapted for several Bayesian or penalized regression contexts, e.g. the elastic net, which includes the lasso as a special case [1,15]. In the same way that classical and elastic net frameworks required theoretical and computational modifications to accommodate categorical outcomes with $>2$ categories, so too does the spike-and-slab lasso/elastic net framework, which has not been adapted to accommodate multinomial outcomes. This work aims to fill that gap by developing a theoretical and computational framework for incorporating the spike-and-slab elastic net prior into regression-style problems that have categorical outcomes with greater than two mutually exclusive categories.

In the first place, it is necessary to specify the log joint posterior distribution for the most general case of a spike-and-slab lasso model for multinomial regression. In contrast to logistic regression, where each predictor has a single parameter, multinomial regression results in each predictor having one parameter per outcome, e.g. if the outcomes are cognitive normal, MCI, or dementia, then each MRI-derived predictor of disease class has 3 parameters. This complicated setting requires choices regarding how shrinkage penalties are applied to parameters. We develop the most general case and argue for several simplifications that are defensible for many practical problems. These simplifications reduce the complexity of the optimization problem for fitting the proposed model. Finally, since the existing algorithm for fitting spike-and-slab lasso/elastic net GLMs cannot accommodate categorical outcomes with $>2$ categories, it must be modified in order to fit the class of models developed in this work. To our knowledge, this is the first generalization of the spike-and-slab lasso to allow for multinomial outcomes.

The outline of this work is as follows. In Section 2, we define and review multinomial regression and the spike-and-slab lasso, after which we develop a generalization of the spike-and-slab lasso for multinomial outcomes as well as an EM algorithm to fit the model. We then generalize the model and EM algorithm to incorporate the spike-and-slab elastic net prior, so that the spike-and-slab lasso is a special case of the final framework. We also describe an approach for incorporating structured prior information into the variable selection process. In Section 3, we present a simulation study to demonstrate the methodology and examine some of its statistical properties related to variable selection and apply the methodology to a classification task using data from the Alzheimer's Disease Neuroimaging Initiative (ADNI) in Section 4. Section 5 concludes.

2. Methodology

2.1. Multinomial regression

GLMs are models of the expectation of an outcome whose distribution is assumed to be in the exponential family, and for subjects $i=1,\dots ,N$ is given by [1,23]:

$$g(\mathrm{E}(Y_i|{\mathit{X}}_i))={\mathit{X}}_i^{\mathrm{\top }}\mathit{\beta },$$ (1)

where $g(\cdot )$ is an appropriate link function, $Y_i$ is the outcome of interest, ${\mathit{X}}_i^{\mathrm{\top }}$ is a vector of covariates/predictors, and $\mathit{\beta }$ is an unknown vector of parameters determining the effect of the covariates on the (linked) expectation of the outcome given the covariates. Herein we assume that there are J covariates and an intercept, so that ${\mathit{X}}_i^{\mathrm{\top }}$ and $\mathit{\beta }$ have length J + 1. We denote individual parameters by ${\beta }_j$, $j=1,\dots ,J$.

Logistic regression is a special case of GLMs that obtains when the outcome of interest is binary with logit link function, i.e. if ${\mu }_i=\mathrm{E}(Y_i|{\mathit{X}}_i)=Pr(Y_i=1|{\mathit{X}}_i)$, then $g({\mu }_i)=\mathrm{logit}({\mu }_i)=\log ({\mu }_i/(1-{\mu }_i))$. The generalization of logistic regression obtains when the outcome of interest consists of V >2 categories, in which case the outcome is assumed to have a multinomial distribution, and multinomial regression is required to model the effects of the covariates, ${\mathit{X}}_i^{\mathrm{\top }}$, on the outcome, $Y_i$. This scenario requires a model of the probability of each possible outcome for each subject, i.e. the following model [15]:

$$Pr(Y_i=k|{\mathit{X}}_i)=\frac{\exp ({\mathit{X}}_i^{\mathrm{\top }}{\mathit{\beta }}^k)}{\sum _{v=1}^V\exp ({\mathit{X}}_i^{\mathrm{\top }}{\mathit{\beta }}^v)},$$ (2)

where ${\mathit{\beta }}^k$ denotes the vector of length J + 1 containing the parameters corresponding to the $k^{\mathrm{th}}$ outcome; that is, ${\mathit{\beta }}^k=[{\beta }_0^k,{\beta }_1^k,\dots ,{\beta }_J^k]$, where ${\beta }_j^k$ indicates the $j^{\mathrm{th}}$ parameter for the $k^{\mathrm{th}}$ outcome. Thus, there is a set of J + 1 parameters, including an intercept, associated with each of the $k=1,\dots ,V$ possible outcomes, i.e. each outcome category has its own function to describe how the predictors affect the probability of that outcome category. In classical settings the model given in Equation (2) is not identifiable, which is addressed by choosing one of the possible outcomes to be a reference group, i.e. the parameter vector for that outcome is assumed to be a vector of zeroes. In this case, the parameters are interpretable as comparisons between each category and the reference group, which is analogous to logistic regression, except that instead of one reference and one ‘event,’ we have one reference and multiple ‘events.’ However, it is not necessary to choose a reference category when applying penalized models such as the elastic net or lasso, whose built-in constraints allow for unique parameter estimates under Equation (2) [15].

2.2. Spike-and-slab lasso

Many applications have a large set of predictors that may be associated with an outcome of interest, of which we wish to select a (possibly small) subset to remain in a model of the outcome. The spike-and-slab prior framework is a commonly applied Bayesian solution to this problem [16,24]. This formulation for variable selection assumes that predictors arise from a mixture distribution where the indicator variable, ${\gamma }_j$, indicates whether the $j^{\mathrm{th}}$ predictor should be included in the model, i.e. for the GLM formulation in Equation (1), the prior distribution for each parameter, ${\beta }_j$, is given by the following mixture distribution:

$$p({\beta }_j|{\gamma }_j)={\gamma }_j{p}_1({\beta }_j|{\gamma }_j=1)+(1-{\gamma }_j)p_0({\beta }_j|{\gamma }_j=0),$$ (3)

where the slab prior, $p_1$, has a wider distribution than the spike prior, $p_0$, i.e. the variance of $p_1$ is larger than that of $p_0$. Thus, a wide distribution obtains for parameters relevant to the outcome $({\gamma }_j=1)$, which results in weak penalization/shrinkage on ${\beta }_j$, and a narrow distribution obtains for parameters irrelevant to the outcome $({\gamma }_j=0)$, which results in strong penalization/shrinkage on ${\beta }_j$. Traditionally, Gaussian priors were given for both distributions, but the spike-and-slab lasso assigns double exponential (DE) distributions, and ultimately provides adaptive variable selection by using parameter-specific shrinkage penalties [29]:

$${\beta }_j|{\gamma }_j,s_0,s_1\sim \mathrm{DE}({\beta }_j|0,S_j)=\frac{1}{2S_j}\exp (-\frac{|{\beta }_j|}{S_j}),$$ (4)

where $S_j=(1-{\gamma }_j)s_0+{\gamma }_j{s}_1$, the indicator variable ${\gamma }_j$ determines the inclusion status of the $j^{\mathrm{th}}$ variable, and $s_1>s_0>0$ are slab and spike scale parameters, respectively. The value of ${\gamma }_j$ is unknown a priori and uncertainty about its value is incorporated via a Binomial prior:

$$p(\mathit{\gamma }|\theta )=\prod _{j=1}^J{\theta }^{{\gamma }_j}(1-\theta {)}^{1-{\gamma }_j},$$ (5)

where $\theta =p({\gamma }_j=1|\theta )$ is a global probability of inclusion for the ${\beta }_j$. The relevant theory and implementation for the spike-and-slab lasso initially focused on standard linear models, but an Expectation Maximization (EM) algorithm to fit the spike-and-slab lasso for GLMs was later developed [29,34].

Here we briefly review the model formulation and EM-algorithm, as it is the foundation of the algorithm developed to fit the models proposed in this work. The log posterior for the spike-and-slab lasso GLM is derived as follows [34]:

$$\begin{array}{rl}\log p(\mathit{\beta },\varphi ,\mathit{\gamma },\theta |\mathit{y})& =\log p(\mathit{y}|\mathit{\beta },\varphi )+\sum _{j=1}^J\log p({\beta }_j|S_j)+\sum _{j=1}^J\log p({\gamma }_j|\theta )+\log p(\theta )\\ & \propto \ell (\mathit{\beta },\varphi )-\sum _{j=1}^J\frac{1}{S_j}|{\beta }_j|+\sum _{j=1}^J({\gamma }_j\log \theta +(1-{\gamma }_j)\log (1-\theta ))+p(\theta ),\end{array}$$ (6)

where $\ell (\mathit{\beta },\varphi )=\log p(\mathit{y}|\mathit{\beta },\varphi )$, $\mathit{y}=[y_1,\dots ,y_N]$ is the N-length outcome vector, $\mathit{\beta }=[{\beta }_0,{\beta }_1,\dots ,{\beta }_J]$ is a $(J+1)$-length parameter vector, $\mathit{\gamma }=[{\gamma }_1,\dots ,{\gamma }_J]$ is a J-length vector of inclusion indicators, ϕ is a dispersion parameter, and $p(\theta )$ is the prior distribution for θ. The prior $p(\theta )$ is often assumed to follow a beta $(a,b)$ distribution, which is a natural choice as a prior distribution for probability parameters as it is bounded between 0 and 1, can take a wide range of possible shapes (symmetric, skewed, U-shaped, etc.), and includes the uniform distribution on (0, 1) as a special case when a = b = 1. Henceforth, we assume that $p(\theta )\sim U(0,1)$, in which case $p(\theta )$ drops out of Equation (6).

The general EM algorithm was developed to address missing ‘data’ or information of some form, and has two general steps, the expectation (E-step) and maximization (M-step) steps [10]. Given the likelihood, or in our case posterior distribution, one wishes to maximize, we take the conditional expectation with respect to the missing information (E-step), replace the missing information in the objective function with the conditional expectations, and then maximize in terms of the parameters of interest (M-step); the process continues until some convergence criteria is reached.

In the case of the spike-and-slab lasso, we treat the indicator variables, ${\gamma }_j$, as missing. Therefore, we find the conditional expectation of the ${\gamma }_j$, i.e. $p_j=p({\gamma }_j=1|{\beta }_j,{\theta }_j)$, replace ${\gamma }_j$ with $p_j$ in Equation (6), then maximize to estimate $(\mathit{\beta },\varphi )$. Specifically, Equation (6) can be split into two terms:

$$\begin{array}{rl}{Q}_1(\mathit{\beta },\varphi )& =\ell (\mathit{\beta },\varphi )-\sum _{j=1}^J\frac{1}{S_j}|{\beta }_j|,\end{array}$$ (7)

$$\begin{array}{rl}{Q}_2(\theta )& =\sum _{j=1}^J({\gamma }_j\log \theta +(1-{\gamma }_j)\log (1-\theta )).\end{array}$$ (8)

$Q_1(\mathit{\beta },\varphi )$ is the log likelihood for the (Bayesian) lasso and can be fit with appropriate software, specifically glmnet in R, after replacing ${\gamma }_j$ and $S_j^{-1}$ with their conditional expectations, $p_j=p({\gamma }_j=1|{\beta }_j,{\theta }_j)$ and $\mathrm{E}(S_j^{-1}|{\beta }_j)$, respectively [15]. Assuming a uniform prior for θ, the global inclusion probability is updated with $\theta =(1/J)\sum _{j=1}^J{p}_j$. We follow previous work in setting the following convergence criteria [34]:

$$\frac{|d^{(t)}-d^{(t-1)}|}{(0.1+|d^{(t)}|)}<ϵ,$$ (9)

where $d^{(t)}=-2\sum _{i=1}^N\log p(y_i|{\mathit{X}}_i{\mathit{\beta }}^{(t)},{\varphi }^{(t)})$ is the estimated deviance at iteration t.

To our knowledge, no one has yet published a generalization of the spike-and-slab lasso to allow for multinomial outcomes. Having described the spike-and-slab lasso for GLMs and the EM algorithm for fitting the model, we now develop a generalization of the spike-and-slab lasso that accommodates categorical outcomes with $>2$ categories, after which we further generalize the model and algorithm to incorporate the spike-and-slab elastic net, which contains the spike-and-slab lasso as a special case.

2.3. Generalization of the spike-and-slab lasso for multinomial outcomes

As mentioned above, when the outcome consists of V >2 categories, there will be V sets of parameters, one for each outcome. Hereafter, we denote the parameters associated with the $j^{\mathrm{th}}$ predictor and $v^{\mathrm{th}}$ outcome with the subscript j and superscript v, i.e. ${\beta }_j^v$. Additionally, bolded parameters with subscripts indicate the vector of all parameters associated with the $j^{\mathrm{th}}$ predictor, e.g. ${\mathit{\beta }}_j$. The log joint posterior therefore differs from both the spike-and-slab lasso and traditional elastic net model for multinomial regression and can be derived as two independent terms as follows:

$$\begin{array}{rl}{Q}_1(\mathit{\beta },\varphi )& =\ell (\{{\beta }_0^v,{\mathit{\beta }}^v{\}}_1^V)-\sum _{j=1}^J\frac{1}{S_j}||{\mathit{\beta }}_j|{|}_q,\end{array}$$ (10)

$$\begin{array}{rl}{Q}_2(\mathit{\theta })& =\sum _{v=1}^V\sum _{j=1}^J{\gamma }_j^v\log {\theta }_j^v+(1-{\gamma }_j^v)\log (1-{\theta }_j^v),\end{array}$$ (11)

where by reference [18],

$$\ell (\{{\beta }_0^v,{\mathit{\beta }}^v{\}}_1^V)=-\left[\frac{1}{N}\sum _{i=1}^N(\sum _{v=1}^V{y}_{\mathrm{ik}}({\beta }_0^v+{\mathit{X}}_i^{\mathrm{\top }}{\mathit{\beta }}^v)-\log \sum _{\ell =1}^K\exp \{{\beta }_0^{\ell }+{\mathit{X}}_i^{\mathrm{\top }}{\mathit{\beta }}^{\ell }\})\right]$$ (12)

Here we assume that the V parameters associated with the $j^{\mathrm{th}}$ predictor are drawn from the same distribution, i.e. ${\beta }_j^v\sim \mathrm{DE}(0,S_j)$, and that $p({\theta }_j^v)\sim U(0,1)$. If we make the additional assumption that the parameters associated with the $j^{\mathrm{th}}$ predictor have the same inclusion probability, i.e. ${\theta }_j^1=\cdots ={\theta }_j^V={\theta }_j$, and that they should be included or excluded from the model together, i.e. ${\gamma }_j^1=\cdots ={\gamma }_j^V={\gamma }_j$, then $Q_2(\mathit{\theta })$ is further simplified as:

$$Q_2(\mathit{\theta })=\sum _{j=1}^J{\gamma }_j\log {\theta }_j+(1-{\gamma }_j)\log (1-{\theta }_j).$$ (13)

Note finally that the term $||{\mathit{\beta }}_j|{|}_q$ determines whether parameters associated with the $j^{\mathrm{th}}$ predictor are included or excluded together; when q = 1 the lasso penalty is applied to each predictor separately, but when q = 2 all parameters associated with the $j^{\mathrm{th}}$ predictor are either zero or non-zero together [15,18]. In what follows, we assume q = 2 since we desire grouped variable selection but note that Equations (10) and (11) permit a more general scenario.

2.4. The EM algorithm

The EM algorithm for fitting the joint log posterior defined by Equations (10) and (13) is analogous to the EM-algorithm for fitting the spike-and-slab lasso for GLMs but is distinct from that algorithm in its inclusion of V parameters for each of the J predictors.

In the E-step we take the conditional expectation of ${\gamma }_j$ and $S_j$ with respect to the ${\mathit{\beta }}_j$ (and if necessary, ϕ), i.e. $p_j=p({\gamma }_j=1|{\beta }_j^1,\dots ,{\beta }_j^V,{\theta }_j)$ and $\mathrm{E}(S_j^{-1}|{\beta }_j^1,\dots ,{\beta }_j^V)$. These calculations differ from previous work since both conditional expectations now depend on a vector of parameters, ${\mathit{\beta }}_j$, rather than a single parameter, ${\beta }_j$. The spike-and-slab lasso for GLMs can be modified to accommodate group-specific penalties, and we employ a similar approach in this case in order impose a single penalty to the set of parameters, ${\mathit{\beta }}_j$, i.e. we treat the parameters associated with the $j^{\mathrm{th}}$ predictor as being a group [33,37].

Since we require a single penalty for the parameters associated with each of the j predictors, we must estimate the conditional expectations of the corresponding indicator variables, $p({\gamma }_j=1|{\mathit{\beta }}_j,{\theta }_j)=p_j=p({\gamma }_j=1|{\beta }_j^1,\dots ,{\beta }_j^V,{\theta }_j)$, which is dependent on the vector of predictors ${\mathit{\beta }}_j=\{{\beta }_j^1,\dots ,{\beta }_j^V\}$, rather than a single scalar value, ${\beta }_j^v$, which by Bayes' rule is derived as:

$$\begin{array}{rl}{p}_j& =p({\gamma }_j=1|{\beta }_j^1,\dots ,{\beta }_j^V,{\theta }_j)\\ & =\frac{p({\gamma }_j=1|{\theta }_j)\prod _{v=1}^{V}p({\beta }_j^v|{\gamma }_j=1,s_1)}{p({\gamma }_j=1|{\theta }_j)\prod _{v=1}^{V}p({\beta }_j^v|{\gamma }_j=1,s_1)+p({\gamma }_j=0|{\theta }_j)\prod _{v=1}^{V}p({\beta }_j^v|{\gamma }_j=0,s_0)},\end{array}$$ (14)

where $p({\gamma }_j=1|{\theta }_j)={\theta }_j$, $p({\gamma }_j=0|{\theta }_j)=1-{\theta }_j$, $p({\beta }_j^v|{\gamma }_j=1,s_1)=\mathrm{DE}({\beta }_j^v|0,s_1)$, and $p({\beta }_j^v|{\gamma }_j=0,s_0)=\mathrm{DE}({\beta }_j^v|0,s_0)$.

Here it is the case that the conditional probability of inclusion for the $j^{\mathrm{th}}$ predictor, $p_j$, is also the update for ${\theta }_j$. Similar in spirit to the initial development of the spike-and-slab lasso for GLMs, it follows that the conditional expectation of $S_j^{-1}$ is found by [33,34]:

$$\mathrm{E}(S_j^{-1}|{\beta }_j^1,\dots ,{\beta }_j^V)=\frac{1-p_j}{s_0}+\frac{p_j}{s_1}.$$ (15)

This concludes the E-step, i.e. we have obtained the conditional estimates for the ${\gamma }_j$ and $S_j$ using Equations (14) and (15), respectively.

In the M-step the conditional expectation estimates replace the ${\gamma }_j$ and $S_j$ in the log joint posterior distribution, i.e. defined by the sum of Equations (10) and (13), each of which can be updated separately. Equation (10) is the (Bayesian) lasso for multinomial outcomes, and is maximized using cyclic coordinate descent to obtain estimates for the ${\beta }_j^v$ given conditional expectations $\mathrm{E}(S_j^{-1}|{\beta }_j)$ and $p_j$, which allows for some of the ${\mathit{\beta }}_j$ to be estimated as exactly 0 for all parameters contained in ${\mathit{\beta }}_j$ and in practice results in variable selection [14,15,18]. As stated above, ${\theta }_j$ in Equation (13) is updated with the current estimate $p_j$. This process is iterated until convergence using Equation (9).

2.5. Elastic net generalization

The elastic net is a compromise between the ridge and lasso penalty, and its Bayesian interpretation is a mixture of Gaussian and double exponential distributions. In previous work we generalize the spike-and-slab lasso GLM to the spike-and-slab elastic net GLM, i.e. the spike-and-slab prior consists of a mixture of elastic net distributions rather than a mixture of double exponential distributions [21]:

$$\begin{array}{rl}\mathrm{SSEN}({\beta }_j|0,S_j)& =(1-\alpha )\exp (-\log (\sqrt{2\pi S_j})-\frac{{\beta }_j^2}{S_j})\\ & +\mathrm{\alpha exp}(-\log (2S_j)-\frac{|{\beta }_j|}{S_j}),\end{array}$$ (16)

where $S_j=(1-{\gamma }_j)s_0+{\gamma }_j{s}_1$, $s_1$ is the slab scale, $s_0$ is the spike scale, $s_1>s_0>0$, and $\alpha \in [0,1]$. Note that $\alpha =0$ corresponds to a ridge penalty and $\alpha =1$ to a lasso penalty, whereas $\alpha \in (0,1)$ results in a compromise between the two penalties. In what follows we modify the log joint posterior and EM algorithm for fitting the spike-and-slab lasso for multinomial outcomes, described in the previous sections, to accommodate the spike-and-slab elastic net prior in Equation (16), which contains the spike-and-slab lasso as a special case ( $\alpha =1$).

The log joint posterior can still be divided into two terms that can be updated independently. First, we modify the term $Q_1$, i.e. Equation (10), which in the M-step can still be maximized using cyclic coordinate descent, e.g. by the R package glmnet [15]:

$$Q_{1,\mathrm{SSEN}}(\mathit{\beta })=\ell (\{{\beta }_0^v,{\mathit{\beta }}^v{\}}_1^V)-\sum _{j=1}^J\frac{1}{S_j}[(1-\alpha )||\mathit{\beta }|{|}_F^2+\alpha ||{\mathit{\beta }}_j|{|}_q],$$ (17)

where $||\cdot |{|}_F$ is the Frobenius norm and $\mathit{\beta }$ is a $J\times V$ coefficient matrix.

The second term to maximize in the M-step, $Q_2(\mathit{\theta })$, is still described by Equation (13), but the E-step must be modified. While the conditional expectation of ${\gamma }_j$ in Equation (14) maintains the same form, the definitions for the conditional expectations of the parameters of interest are modified to take an elastic net distribution rather than a double exponential distribution, i.e. now $p({\beta }_j^v|{\gamma }_j=1,s_1)=\mathrm{SSEN}({\beta }_j^v|0,s_1)$ and $p({\beta }_j|{\gamma }_j^v=0,s_0)=\mathrm{SSEN}({\beta }_j^v|0,s_0)$.

2.6. Structured prior information

In some applications there may be prior information regarding combinations of predictors that are likely to be included or excluded together, e.g. networks of genes, or when predictors are spatial in nature, we often expect relevant predictors to cluster spatially. One approach to imposing prior structure in Bayesian variable selection is to assign structured priors to the indicators, ${\gamma }_j$, e.g. with an Ising prior or Markov random field [8,28]. In our setting it is more natural to incorporate structure into the prior probabilities of inclusion, ${\theta }_j$, because the amount of skrinkage applied to a parameter estimate is a function of the update to ${\theta }_j$ at each iteration of the EM algorithm [21]. For example, an approach especially appropriate for spatial settings is a variant of Conditional Autoregressive (CAR) models, Intrinsic Autoregressions (IAR) [3,5,6,30]:

$$\log p({\psi }_j|{\psi }_i,\tau )\propto \frac{-{\tau }^2}{2}(\sum _{j\sim i}({\psi }_j-{\psi }_i{)}^2),$$ (18)

where ${\psi }_j=\mathrm{logit}({\theta }_j)$ and $j\sim i$ indicates the location/predictor i is a neighbor of location/predictor j, i.e. the summation is over all the neighbors of location/predictor j. For example, in spatial settings we often desire to impose spatially correlated probabilities of inclusion with decaying correlation over space; that is, a random variable at a given location is more strongly correlated with random variables at nearby locations than far away locations. However, with large dimensions it can be computationally prohibitive to take the inverse of a large covariance matrix, which makes it undesirable to specify such decaying correlation structures explicitly. Since CAR/IAR models define such structure implicitly through conditional relationships and use the inverse variance (precision: ${\tau }^2$), there is no need to specify or take the inverse of a large covariance matrix.

Including the IAR prior on the ${\theta }_j$ only requires updating the $Q_2(\mathit{\theta })$ term of the log joint posterior distribution, and only affects the M-step in the EM algorithm, i.e. Equation (13) is easily modified to accommodate the IAR prior and the solution for the estimates of ${\theta }_j$ can be found with standard numerical algorithms, especially if as is common practice, we set $\tau =1$ [21,25]:

$$\begin{array}{rl}{Q}_{2,\mathrm{IAR}}(\mathit{\theta })& =\sum _{j=1}^J{\gamma }_j\log {\theta }_j+(1-{\gamma }_j)\log (1-{\theta }_j)-\frac{1}{2}(\sum _{j:j\sim i}({\psi }_j-{\psi }_i{)}^2)\end{array}$$ (19)

2.7. R package

In previous work we developed an R package, ssnet, to fit spike-and-slab elastic net GLMs [21]. We have updated ssnet to include the EM algorithm described in this work, i.e. it now possesses the capabilities necessary to fit spike-and-slab elastic net multinomial regression. This package is freely available on GitHub (https://github.com/jmleach-bst/ssnet).

3. Simulation study

3.1. Simulation description

The spike-and-slab lasso and its generalizations have been shown to be useful for variable selection when the solution is sparse, i.e. a relatively small percentage of the set of predictors is relevant to the outcome of interest, as well as when subsets of predictors are highly correlated, as can occur in practice, e.g. in genetic expression or imaging data [21,29,34]. Our simulation study focuses specifically on this situation and is inspired by the original spike-and-slab lasso paper but adapted for multinomial outcomes [29].

Specifically, the design vector for each subject, ${\mathit{X}}_i$, contains 1000 predictors which are generated from a multivariate normal distribution with mean zero, unit variance, and a block correlation structure consisting of 20 blocks of 50 predictors each, where within each block the predictors have 0.90 correlation with each other and 0 correlation with predictors outside the block. That is, ${\mathit{X}}_i\sim \mathrm{MVN}(\mathit{\mu },\mathbf{\Sigma })$ where $\mathit{\mu }=[0,\dots ,0]$ is a vector of length 1000 and $\mathbf{\Sigma }$ is a 1000 ×1000 block covariance matrix with $50\times 50$, ${\mathbf{\Sigma }}_{\ell ,\ell }$, matrices along its diagonal defined as follows:

$$\mathbf{\Sigma }=\left[\begin{array}{cccc}{\mathbf{\Sigma }}_{1,1}& \mathbf{0}& \cdots & \mathbf{0}\\ \mathbf{0}& {\mathbf{\Sigma }}_{2,2}& \cdots & \mathbf{0}\\ ⋮& ⋮& \ddots & ⋮\\ \mathbf{0}& \mathbf{0}& \mathbf{0}& {\mathbf{\Sigma }}_{50,50}\end{array}\right],$$

where

$${\mathbf{\Sigma }}_{\ell ,\ell }=\left[\begin{array}{ccccc}1& 0.9& 0.9& \cdots & 0.9\\ 0.9& 1& 0.9& \cdots & 0.9\\ 0.9& 0.9& 1& \cdots & 0.9\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ 0.9& 0.9& 0.9& \cdots & 1\end{array}\right],$$

for $\ell =1,\dots ,50$.

A total of 6 predictors are given non-zero values, specifically those predictors with indices 1, 51, 101, 151, 201, 251, which results in 0.6% of the parameters being relevant to the outcome. We examine 3 effect size scenarios, each of which treats one group as a reference, i.e. all parameter values are 0. The second and third groups are given non-zero values at the appropriate indices. The settings are as follows, and are generally interpreted as representing gradually larger effect sizes:

1. Class 2: ${\beta }_0^2=-0.15$, ${\beta }_{j\ast }^2=0.0075$; Class 3: ${\beta }_0^3=-0.5$, ${\beta }_{j\ast }^3=0.015$.

2. Class 2: ${\beta }_0^2=-0.15$, ${\beta }_{j\ast }^2=0.0125$; Class 3: ${\beta }_0^3=-0.5$, ${\beta }_{j\ast }^3=0.025$.

3. Class 2: ${\beta }_0^2=-0.15$, ${\beta }_{j\ast }^2=0.0250$; Class 3: ${\beta }_0^3=-0.5$, ${\beta }_{j\ast }^3=0.05$.

where $j^{\ast }\in \{1,51,101,151,201,251\}$ defines the indices for parameters that are non-zero and ${\beta }_j^v$ is the parameter associated with the $j^{\mathrm{th}}$ predictor and $v^{\mathrm{th}}$ outcome category with v = 1, 2, 3.

We generate 5000 simulations under each scenario by drawing outcomes from the multinomial distribution with probabilities of each event, $Pr(Y_i=k|{\mathit{X}}_i)$, given by Equation (2). Each simulated consists of a ‘training’ data set of size N = 300 and a ‘test’ data set of size N = 100, which as described below allows for variable selection to be conducted in on the training data and model performance estimated in the test data. These scenarios generate imbalanced data, where group 1 (reference) is most common, group 2 second most common, and group 3 least common. The imbalance is similar in all scenarios as seen in Table 1.

Table 1.

Mean frequency and percentage of each class by simulation scenario (training data).

	Class 1	Class 2	Class 3
Scenario 1	121.94 (40.51%)	103.44 (34.62%)	74.62 (24.87%)
Scenario 2	122.23 (40.62%)	101.75 (34.04%)	76.02 (25.34%)
Scenario 3	123.67 (41.08%)	94.82 (31.72%)	81.51 (27.20%)

3.2. Simulation analysis approach

For each simulation the training data set is used to perform 5-fold cross validation to select optimal penalty parameters for the elastic net ( $\alpha =0.5$), lasso ( $\alpha =1$), and spike-and-slab elastic net, and spike-and-slab lasso. That is, $\lambda =s_0=s_1$ for the traditional models and a spike scale, $s_0$, and slab scale, $s_1$, for the spike-and-slab models. For the traditional models, the range of λ is chosen internally by the R package glmnet [15,18]. A grid of values is preselected for the spike-and-slab models, $s_0=\{0.01,0.02,0.03,\dots ,0.1\}$ and $s1=\{1,2,3,4\}$, which are then fit using the EM algorithm developed above with the R package ssnet. We then use the selected penalty parameters to fit the model on the entire training data. This model is then applied to predict the observations in the test data and calculate measures of model fitness.

We present cross-validated deviance as a general measure of model fitness and then focus on the variable selection properties of the spike-and-slab framework compared to the traditional framework. Deviance is defined as [32,34]:

$$d=-2\ell (\{{\hat{\beta }}_0^v,{\hat{\mathit{\beta }}}^v{\}}_1^V).$$ (20)

where $\{{\hat{\beta }}_0^v,{\hat{\mathit{\beta }}}^v{\}}_1^V$ are the final mode estimates.

We assess the ability of the models to avoid selecting irrelevant predictors by estimating the false discovery rate (FDR) [4]. That is, we calculate the proportion of irrelevant predictors included out of all non-zero estimates in each simulation, i.e. the false discovery proportion (FDP). We can obtain an estimate of the FDR by averaging the FDP values over the simulations; better performing models will have relatively lower FDR. We assess the methods' ability to correctly select the 6 non-zero, or relevant, predictors by calculating the proportion of these 6 predictors that were estimated to be non-zero in each simulation; the average of these proportions over the simulations we call ‘Power;’ better performing models will have relatively higher ‘Power.’ Finally, we estimate the probabilities of inclusion for each predictor by the proportion of simulations in which the predictors were estimated to be non-zero.

3.3. Simulation results

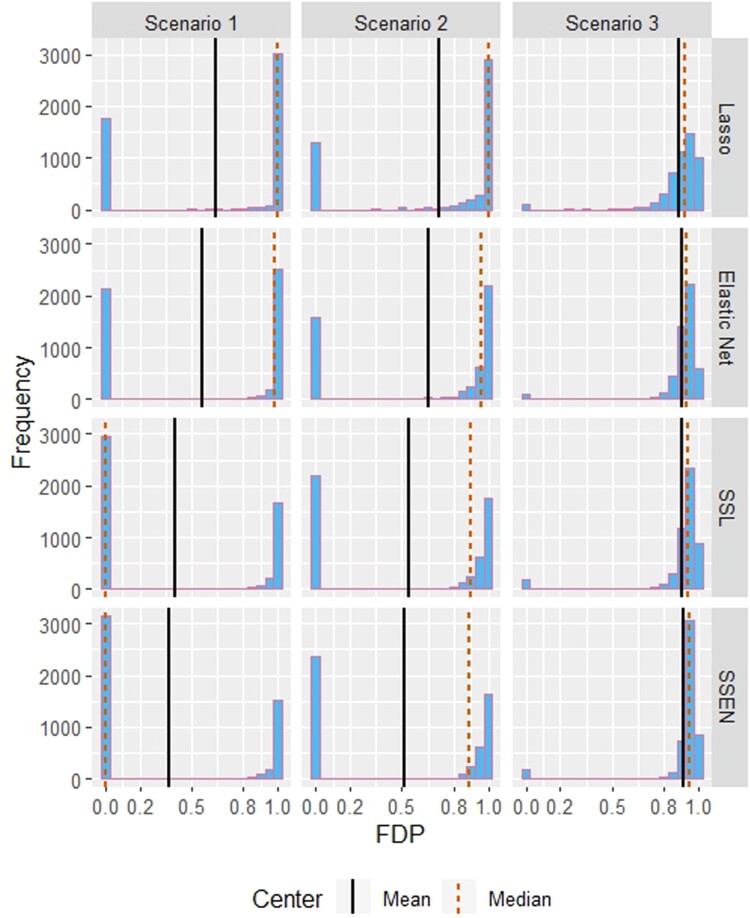
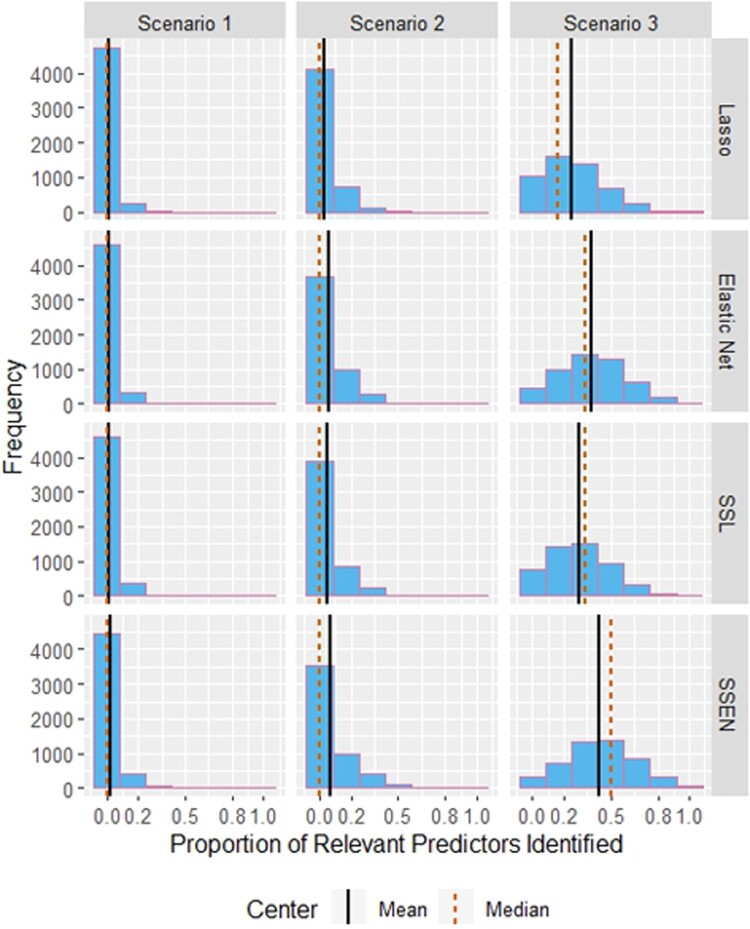
Table 2 shows the average penalty parameter estimates, deviance, false discovery proportion (FDR), and Power across the 5000 simulations for each scenario. While the traditional elastic net ( $\alpha =0.5$) had the lowest deviance for all scenarios, the variability of deviance across models was slight; noticeable differences across models were with respect to FDR and Power. In scenarios 1 and 2, the spike-and-slab elastic net had the lowest FDR, while in scenario 3 all models had FDR near 0.90 with lasso having the lowest (0.8917), but the Power was highest for the spike-and-slab elastic net in all 3 scenarios. Notably, while lasso has the lowest FDR in Scenario 3, if barely, its Power is nearly half that of the spike-and-slab elastic net. Figures 1 and 2 display the distribution of FDR and Power across the 5000 simulations, which we can see are generally not symmetric. FDR is bimodal in all cases, although Scenario 3 is less striking in this respect. FDR differences between the traditional and spike-and-slab frameworks are most striking in Scenario 1, where the median FDR is zero for the spike-and-slab models, but near one for the traditional models. The distributions for ‘Power’ are generally right skewed, most severely for Scenario 1 and approaching symmetry as the effect sizes increase.

Table 2.

Model fitness and variable selection metrics by simulation scenario.

	Model	$s_0$	$s_1$	Deviance	FDP	Power*
Scenario 1	Lasso	0.1031	0.1031	216.80	0.6437	0.0090
	EN	0.2020	0.2020	216.80	0.5637	0.0143
	SSL	0.0243	1.7258	217.27	0.4052	0.0150
	SSEN	0.0152	1.6154	217.23	0.3661	0.0211
Scenario 2	Lasso	0.1001	0.1001	216.71	0.7166	0.0338
	EN	0.1937	0.1937	216.66	0.6555	0.0557
	SSL	0.0308	2.0642	217.24	0.5435	0.0479
	SSEN	0.0180	1.9542	217.18	0.5100	0.0697
Scenario 3	Lasso	0.0770	0.0770	210.90	0.8917	0.2519
	EN	0.1445	0.1445	210.69	0.9067	0.3799
	SSL	0.0553	3.0590	210.95	0.9016	0.2955
	SSEN	0.0301	2.9224	210.83	0.9139	0.4264

*Proportion of Non-zero Parameters Estimated as Non-zero. Notes: EN = elastic net ; SSL = spike-and-slab lasso; SSEN = spike-and-slab elastic net.

Figure 1.

Histograms for the distribution of FDP over the 5000 simulations by model and scenario. Abbreviations are SSL = spike-and-slab lasso and SSEN = spike-and-slab elastic net.

Figure 2.

Histograms for the distribution of ‘Power’ over the 5000 simulations by model and scenario. Abbreviations are SSL = spike-and-slab lasso and SSEN = spike-and-slab elastic net.

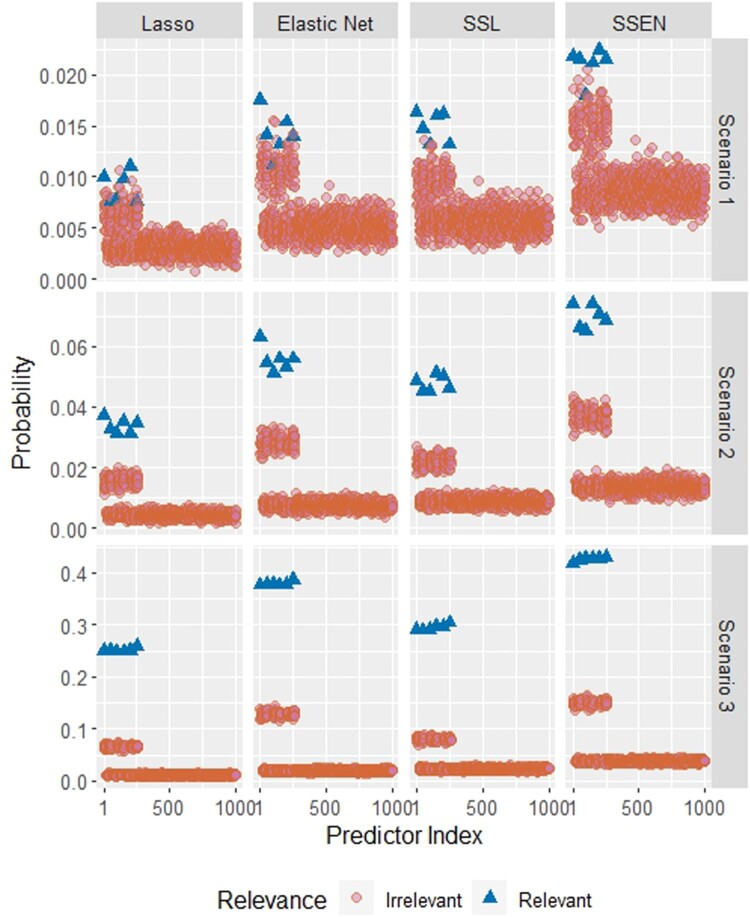
Similarly, Table 3 and Figure 3 display the inclusion probabilities for each of the 6 non-zero parameters in each scenario. In each scenario and for each predictor, the spike-and-slab elastic net had the highest probability of inclusion. The spike-and-slab elastic net also tends to have slightly higher estimates for irrelevant parameters, but the difference is less extreme across models as the effect sizes increase.

Table 3.

Probabilities of inclusion for predictors with non-zero parameters.

	Model	$X_1$	$X_{51}$	$X_{101}$	$X_{151}$	$X_{201}$	$X_{251}$
Scenario 1	Lasso	0.0100	0.0076	0.0078	0.0098	0.0110	0.0076
	EN	0.0176	0.0142	0.0112	0.0132	0.0154	0.0140
	SSL	0.0164	0.0148	0.0132	0.0160	0.0162	0.0132
	SSEN	0.0218	0.0216	0.0180	0.0212	0.0224	0.0216
Scenario 2	Lasso	0.0372	0.0328	0.0314	0.0354	0.0314	0.0348
	EN	0.0630	0.0548	0.0512	0.0560	0.0532	0.0560
	SSL	0.0488	0.0454	0.0454	0.0514	0.0502	0.0464
	SSEN	0.0740	0.0662	0.0650	0.0740	0.0706	0.0686
Scenario 3	Lasso	0.2514	0.2522	0.2492	0.2492	0.2504	0.2588
	EN	0.3772	0.3792	0.3800	0.3770	0.3778	0.3880
	SSL	0.2922	0.2900	0.2916	0.2964	0.2982	0.3046
	SSEN	0.4196	0.4238	0.4292	0.4270	0.4286	0.4302

Notes: EN = elastic net; SSL = spike-and-slab lasso; SSEN = spike-and-slab elastic net.

Figure 3.

Estimated inclusion probabilities for each predictor, where blue triangles indicate predictors relevant to the outcome and pink circles indicate predictors irrelevant to the outcome. Abbreviations are SSL = spike-and-slab lasso and SSEN = spike-and-slab elastic net.

4. Application to ADNI data

4.1. Analysis setting and data description

In the simulation study we examined explicit variable selection properties of the proposed methodology, but we shift gears in the data application to demonstrate how to apply the methodology for classification problems. Consider the example from Alzheimer's disease research in Section 1 where subjects may be cognitively normal (CN), have mild cognitive impairment (MCI), or have dementia, i.e. 3 relevant categories for the outcome of interest. Suppose that we wish to use medical images to classify subjects, or perhaps to predict their future disease status. Multinomial regression of the sort proposed in this work may be appropriate for such a circumstance, since medical images are often high-dimensional and highly correlated, and the methods are straightforward to apply to classification problems because the models can produce subject-specific predicted/expected probabilities of belonging to each category. The subject is then classified as whichever class has the highest predicted probability.

Our demonstration uses data obtained from the Alzheimer's Disease Neuroimaging Initiative (ADNI) database (adni.loni.usc.edu). The ADNI was launched in 2003 as a public-private partnership, led by Principal Investigator Michael W. Weiner, MD. The primary goal of ADNI has been to test whether serial magnetic resonance imaging (MRI), positron emission tomography (PET), other biological markers, and clinical and neuropsychological assessment can be combined to measure the progression of mild cognitive impairment (MCI) and early Alzheimer's disease (AD) [27,36].

We examine two scenarios, both of which model disease class (cognitive normal, MCI, or dementia). The first scenario models disease class using cortical thickness measures, which are estimated from structural MRI using FreeSurfer [9,12,13]. The second scenario models disease class using Tau PET images. Both scenarios have imaging measures on the Desikan-Killiany atlas, which consists of 34 regions per hemisphere for a total of 68 brain regions [11]. The data for both scenarios are imbalanced with respect to the distributions of disease classes, as seen in Table 4, with cognitive normal the most common, followed by MCI then dementia.

Table 4.

Class frequencies/percentages for cortical thickness and tau PET data.

	Cognitive normal	MCI	Dementia
Cortical Thickness	261 (60.84%)	127 (29.60%)	41 (9.56%)
Tau PET	234 (60.15%)	116 (29.82%)	39 (10.03%)

4.2. Model evaluation

Model evaluation is tricky for multi-class classification compared to binary classification because standard measures such as sensitivity, specificity, positive and negative predictive value, $F_1$, and Matthews Correlation Coefficient cannot be applied without modification [31]. We present and examine several appropriate metrics for cases where the number of classes exceeds two. The average accuracy (AA) and error rate (ER) are the average per-class effectiveness and classification error, respectively:

$$\begin{array}{rl}\mathrm{AverageAccuracy}(\mathrm{AA})& =\frac{1}{V}\sum _{v=1}^V\frac{t{p}_v+t{n}_v}{t{p}_v+t{n}_v+f{p}_v+f{n}_v},\end{array}$$ (21)

$$\begin{array}{rl}\mathrm{ErrorRate}(\mathrm{PCE})& =\frac{1}{V}\sum _{v=1}^V\frac{f{p}_v+f{n}_v}{t{p}_v+t{n}_v+f{p}_v+f{n}_v},\end{array}$$ (22)

where $t{p}_v$, $t{n}_v$, $f{p}_v$, and $f{n}_v$ are true positive, true negative, false positive, and false negative for class v.

Positive predictive value (PPV; alternatively, precision in the machine learning literature), sensitivity (SN; alternatively recall in the machine learning literature), and $F_1$ score can be averaged in one of two ways: micro- or macro-averaged. Micro-averaged values are given subscript μ and are calculated using cumulative counts of true positives, false positives, true negatives, and false negatives.

$$\begin{array}{rl}{\mathrm{PPV}}_{\mu }& =\frac{\sum _{v=1}^{V}t{p}_v}{\sum _{v=1}^V(t{p}_v+f{p}_v)},\end{array}$$ (23)

$$\begin{array}{rl}{\mathrm{SN}}_{\mu }& =\frac{\sum _{v=1}^{V}t{p}_v}{\sum _{v=1}^V(t{p}_v+f{n}_v)},\end{array}$$ (24)

$$\begin{array}{rl}{\mathrm{F}}_{1,\mu }& =\frac{2\times \mathrm{PP}{V}_{\mu }\times S{N}_{\mu }}{\mathrm{PP}{V}_{\mu }+S{N}_{\mu }}.\end{array}$$ (25)

Macro averaged values are given subscript M and are obtained as the averages of the aforementioned values over each class.

$$\begin{array}{rl}{\mathrm{PPV}}_M& =\frac{1}{V}\sum _{v=1}^V\frac{t{p}_v}{t{p}_v+f{p}_v},\end{array}$$ (26)

$$\begin{array}{rl}{\mathrm{SN}}_M& =\frac{1}{V}\sum _{v=1}^V\frac{t{p}_v}{t{p}_v+f{n}_v},\end{array}$$ (27)

$$\begin{array}{rl}{\mathrm{F}}_{1,M}& =\frac{2\times \mathrm{PP}{V}_M\times S{N}_M}{\mathrm{PP}{V}_M+S{N}_M}.\end{array}$$ (28)

Micro-averaging favors classes/categories with relatively larger proportions of subjects, while macro-averaging treats classes/categories equally. All the metrics presented produce values between 0 and 1, and better performing models will have values near 1 in all cases except for PCE, where lower values (near 0) indicate better performance.

4.3. Analysis approach

For each model, optimal penalty parameters were chosen by 5-fold cross validation with deviance as the measure of model performance. The R package glmnet was used to fit the traditional lasso and elastic net and the range of penalty parameters was chosen internally by the glmnet function [15,18]. The R package ssnet was used to fit the spike-and-slab models. The grid of possible spike and slab scales were $s_0=\{0.01,0.02,\dots ,0.2\}$ and $s_1=\{1,2,\dots ,5\}$, respectively. We considered two values for α: $\alpha =1$, which corresponds to the spike-and-slab lasso, and $\alpha =0.5$, which corresponds to a halfway compromise between ridge and lasso penalties. Given the spatial nature of the predictors, structured priors of the sort described in Section 2.6 may be appropriate. In addition to examining the traditional and spike-and-slab frameworks, we also examine the spike-and-slab framework with IAR priors on logit inclusion probabilities where the Desikan-Killiany atlas was used to specify the neighborhood matrix. Specifically, two regions of the atlas were considered neighbors if they were in the same hemisphere and shared a border.

Tables 5 and 6 show the results for the cortical thickness data, while Tables 7 and 8 show results for the tau PET data. In both cases, metrics are similar across models, which may be the result of the relatively coarse Desikan-Killiany atlas, but which nevertheless demonstrate the methodology. In both cases the elastic net has the lowest deviance. For the cortical thickness data, the elastic net is the best performing model for all metrics except ${\mathrm{PPV}}_M$, where spike-and-slab elastic net is highest. For the tau PET data, spike-and-slab elastic net with IAR priors on logit inclusion probabilities has the best metrics across the board, except for deviance. Thus, while the differences across models are slight, even for coarse spatial predictors used here we can see the utility of both the spike-and-slab framework and the structured priors on inclusion probabilities.

Table 5.

Model fitness metrics for cortical thickness data.

Model	$s_0$	$s_1$	Dev.	AA	PCE
Lasso	0.02	0.02	115.38	0.7758	0.2242
EN	0.04	0.04	114.57	0.7808	0.2192
SSL	0.09	2.00	119.65	0.7770	0.2230
SSEN	0.19	1.00	117.71	0.7774	0.2226
SSL-IAR	0.20	1.00	118.99	0.7804	0.2196
SSEN-IAR	0.20	2.00	116.54	0.7806	0.2194

Notes: EN = elastic net ; SSL = spike-and-slab lasso; SSEN = spike-and-slab elastic net; SSL = spike-and-slab lasso w/ IAR prior; SSEN = spike-and-slab elastic net w/ IAR prior.

Table 6.

Macro- and micro-averaged metrics for cortical thickness data.

Model	$s_0$	$s_1$	${\mathrm{PPV}}_M$	${\mathrm{SN}}_M$	$F_{1,M}$	${\mathrm{PPV}}_{\mu }$	${\mathrm{SN}}_{\mu }$	$F_{1,\mu }$
Lasso	0.02	0.02	0.6195	0.5361	0.5738	0.6637	0.6637	0.6637
EN	0.04	0.04	0.6323	0.5391	0.5811	0.6712	0.6712	0.6712
SSL	0.09	2.00	0.6397	0.4894	0.5506	0.6655	0.6655	0.6655
SSEN	0.19	1.00	0.6666	0.4935	0.5644	0.6661	0.6661	0.6661
SSL-IAR	0.20	1.00	0.6366	0.5103	0.5613	0.6706	0.6706	0.6706
SSEN-IAR	0.20	2.00	0.6119	0.5127	0.5562	0.6709	0.6709	0.6709

Notes: EN = elastic net ; SSL = spike-and-slab lasso; SSEN = spike-and-slab elastic net; SSL = spike-and-slab lasso w/ IAR prior; SSEN = spike-and-slab elastic net w/ IAR prior.

Table 7.

Model fitness metrics for tau PET data.

Model	$s_0$	$s_1$	Dev.	AA	PCE
Lasso	0.019	0.019	131.38	0.7670	0.2330
EN	0.028	0.028	131.00	0.7701	0.2299
SSL	0.20	9.00	135.12	0.7672	0.2328
SSEN	0.18	1.00	133.01	0.7764	0.2236
SSL-IAR	0.07	1.00	136.00	0.7671	0.2329
SSEN-IAR	0.20	5.00	132.55	0.7796	0.2204

Notes: EN = elastic net ; SSL = spike-and-slab lasso; SSEN = spike-and-slab elastic net; SSL = spike-and-slab lasso w/ IAR prior; SSEN = spike-and-slab elastic net w/ IAR prior.

Table 8.

Macro- and micro-averaged metrics for tau PET data.

Model	$s_0$	$s_1$	${\mathrm{PPV}}_M$	${\mathrm{SN}}_M$	$F_{1,M}$	${\mathrm{PPV}}_{\mu }$	${\mathrm{SN}}_{\mu }$	$F_{1,\mu }$
Lasso	0.019	0.019	0.5326	0.4477	0.4856	0.6504	0.6504	0.6504
EN	0.028	0.028	0.5355	0.4572	0.4926	0.6551	0.6551	0.6551
SSL	0.20	9.00	0.5963	0.4192	0.5116	0.6508	0.6508	0.6508
SSEN	0.18	1.00	0.6088	0.4519	0.5159	0.6646	0.6646	0.6646
SSL-IAR	0.07	1.00	0.5890	0.4185	0.4971	0.6507	0.6507	0.6507
SSEN-IAR	0.20	5.00	0.6104	0.4582	0.5210	0.6694	0.6694	0.6694

Notes: EN = elastic net , SSL = spike-and-slab lasso, SSEN = spike-and-slab elastic net, SSL = spike-and-slab lasso w/ IAR prior, SSEN = spike-and-slab elastic net w/ IAR prior.

5. Conclusion and discussion

In this work we generalized the spike-and-slab lasso to accommodate categorical outcomes with $\ge 2$ categories and to incorporate the spike-and-slab elastic net prior, which contains the spike-and-slab lasso prior as a special case. To our knowledge this is the first generalization of the spike-and-slab lasso and/or spike-and-slab elastic net to accommodate categorical outcomes with $>2$ categories.

We have also demonstrated applications of the methodology and shown circumstances where the proposed framework outperforms the traditional lasso and elastic net. The methodology developed in this work may prove useful to researchers in genetics/genomics or medical imaging research and can be generally useful in circumstances where the outcome consists of $>2$ categories and the predictors are high-dimensional, whether in scientific, medical, or economic applications. The benefits of the spike-and-slab lasso, or its generalization, the spike-and-slab elastic net, for this setting are the same or similar to previous work, i.e. that the framework allows for adaptive shrinkage of estimates, thereby increasing the probability that predictors relevant to the outcome of interest remain in the model and retain the relatively large size, while predictors irrelevant to the outcome of interest are shrunk towards or to exactly zero [21,29,34]. We demonstrated these advantages empirically through a simulation study, where the spike-and-slab elastic net had the smallest FDR and largest Power in all simulation scenarios except that with the largest effect sizes for true non-zero parameters, in which case the FDR estimates were essentially the same for all models, but the spike-and-slab elastic net had the highest Power. Thus, the spike-and-slab elastic net was the preferable model in all simulation scenarios.

We also demonstrated the utility of the spike-and-slab elastic net for purpose of predictive modeling with an application using MRI- and PET-derived brain images from the ADNI study. While the results are very similar across models for the MRI-derived cortical thickness data, the spike-and-slab elastic net with structured priors was the best performing model with respect to every metric except for deviance when using the Tau PET data as predictors of dementia status. Thus, while the Desikan-Killiany atlas is perhaps coarser than we would prefer (68 predictors), it is instructive that the spike-and-slab elastic net with structured priors is still the best performing model for the Tau PET predictors, and it is possible that a finer-resolution atlas would show greater improvements, since the methodology is designed to accommodate high-dimensional data.

The primary complication of generalizing this methodology for multinomial outcomes is that rather than a single set of parameters to estimate, there is a set of parameters associated with each category, which necessitates decisions regarding how and where shrinkage penalties are applied to the parameter estimates. The approach developed in this work depends on the assumption that the parameters associated with each predictor should be included or excluded from the model together, which allows us to use the grouped lasso penalty as part of the estimation strategy and significantly simplifies the complexity of the EM-algorithm developed to fit the model [15,33,37]. However, it is possible to conceive of circumstances where this assumption fails, and such circumstances would require modification of the approach developed and demonstrated in the present work.

We have also generalized the approach to the spike-and-slab elastic net, of which the spike-and-slab lasso is a special case, and provided an example for how structured priors could be incorporated for inclusion probabilities, thereby providing additional structure to variable selection. However, while the IAR prior presented here is versatile and can be applied beyond spatial settings to accommodate a wide variety of neighborhood structures, other structured priors may be appropriate depending on the circumstances. The main takeaway is that incorporating structured information into the inclusion probabilities rather than the inclusion indicators has considerable computational benefits in the context of the EM-algorithm presented here, and future work could focus on exploring a wider variety of structures in various applications.

Our estimation approach employs an EM-based mode-search algorithm. This approach departs from many standard approaches in Bayesian statistics, which usually involve estimating the joint posterior distribution and often employs simulation-based Markov Chain Monte Carlo (MCMC) methods to do so. For computational reasons MCMC may be impractical in high-dimensional variable selection problems, which has led to the development of mode-search algorithms as an alternative, since such algorithms can converge much faster than MCMC methods [21,28,29,33,34]. However, the computational benefits do come with a cost, namely that the results consist of modes rather than entire posterior distributions, which limits the ability to quantify uncertainty around the resulting parameter (mode) estimates.

A last consideration is that it is not necessarily straightforward to select penalty parameters a priori; thus, methods such as k-fold cross-validation should be employed to select the spike and slab scales, $s_0$ and $s_1$, respectively, to avoid overfitting the model to the data [19]. For demonstration purposes, in this work we selected a prior values for α parameter of the spike-and-slab elastic net, but in practice it may also be wise to select α during the cross validation process.

Finally, an R package, ssnet, for fitting the methodology presented here is available on GitHub (https://github.com/jmleach-bst/ssnet).

Funding Statement

Data collection and sharing for this project was funded by the Alzheimer's Disease Neuroimaging Initiative (ADNI) (National Institutes of Health [grant number U01 AG024904] and DOD ADNI (Department of Defense award number W81XWH-12-2-0012). ADNI is funded by the National Institute on Aging, the National Institute of Biomedical Imaging and Bioengineering, and through generous contributions from the following: AbbVie, Alzheimer's Association; Alzheimer's Drug Discovery Foundation; Araclon Biotech; BioClinica, Inc.; Biogen; Bristol-Myers Squibb Company; CereSpir, Inc.; Cogstate; Eisai Inc.; Elan Pharmaceuticals, Inc.; Eli Lilly and Company; EuroImmun; F. Hoffmann-La Roche Ltd and its affiliated company Genentech, Inc.; Fujirebio; GE Healthcare; IXICO Ltd.;Janssen Alzheimer Immunotherapy Research & Development, LLC.; Johnson & Johnson Pharmaceutical Research & Development LLC.; Lumosity; Lundbeck; Merck & Co., Inc.;Meso Scale Diagnostics, LLC.; NeuroRx Research; Neurotrack Technologies; Novartis Pharmaceuticals Corporation; Pfizer Inc.; Piramal Imaging; Servier; Takeda Pharmaceutical Company; and Transition Therapeutics. The Canadian Institutes of Health Research is providing funds to support ADNI clinical sites in Canada. Private sector contributions are facilitated by the Foundation for the National Institutes of Health (www.fnih.org). The grantee organization is the Northern California Institute for Research and Education, and the study is coordinated by the Alzheimer's Therapeutic Research Institute at the University of Southern California. ADNI data are disseminated by the Laboratory for Neuro Imaging at the University of Southern California.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Data availability statement

Code to reproduce the results of the simulation study and data analysis is available on GitHub (https://github.com/jmleach-bst/multinomial_ssnet_analyses). Note that while code for performing analysis on ADNI data is included, the ADNI data sets themselves are not, because we are not authorized to share data from ADNI. Details for access to these data can be found at http://adni.loni.usc.edu/data-samples/access-data/.