An ensemble machine learning model to uncover potential sites of hazardous waste illegal dumping based on limited supervision experience

Abstract

With the soaring generation of hazardous waste (HW) during industrialization and urbanization, HW illegal dumping continues to be an intractable global issue. Particularly in developing regions with lax regulations, it has become a major source of soil and groundwater contamination. One dominant challenge for HW illegal dumping supervision is the invisibility of dumping sites, which makes HW illegal dumping difficult to be found, thereby causing a long-term adverse impact on the environment. How to utilize the limited historic supervision records to screen the potential dumping sites in the whole region is a key challenge to be addressed. In this study, a novel machine learning model based on the positive-unlabeled (PU) learning algorithm was proposed to resolve this problem through the ensemble method which could iteratively mine the features of limited historic cases. Validation of the random forest-based PU model showed that the predicted top 30% of high-risk areas could cover 68.1% of newly reported cases in the studied region, indicating the reliability of the model prediction. This novel framework will also be promising in other environmental management scenarios to deal with numerous unknown samples based on limited prior experience.

Graphical abstract

1. Introduction

Waste illegal dumping, referring to the open-dumping of waste without proper treatment, remains an intractable global issue, widely reported in both developing and developed countries, such as Australia, Italy, and Pakistan, in recent years [1], [2], [3], [4], [5], [6], [7]. It has attracted worldwide attention because waste illegal dumping is a major source of soil and underground water pollution and will cause severe effects on human health [5]. The consequence of hazardous waste (HW) illegal dumping is of particular severity due to the toxicity, corrosiveness, and flammability of HW. For example, HW dumping in Campania, Italy has caused high incidences of cancer, respiratory illnesses, and genetic malformations in the dumping region [2]. With the soaring generation of HW globally, the environmental burden from HW illegal dumping remained greater today than in any previous period and is set to intensify.

As one of the largest economies in the world, China has generated a large amount of HW and the quantity increased dramatically by 128% during the last decade. Correspondingly, the environmental burden of HW illegal dumping is also unprecedented in China. A total of 1539 HW illegal dumping cases were found nationwide by the special campaign to combat environmental violations and crimes jointly launched by the Ministry of Environmental Protection and the Ministry of Public Security in 2016 [8]. In addition, most of these cases had a massive scale, leading to serious consequences. For example, 60,000 tons of strong alkali waste were illegally dumped on the Yangtze Riverside in Tongling and Chizhou City, which caused great concern at the national level [9].

To curb the HW illegal dumping, strict supervision and regulation are urgent. However, one primary challenge for HW illegal dumping supervision is that HW illegal dumping sites are difficult to be found [9,10], thereby causing a long-term adverse impact on the environment. To improve the accuracy and efficiency of supervision, some studies have combined Geographic Information System (GIS) [3,11,12], multi-factor spatial analysis [11], factor analysis [6], and discriminant analysis [13] to predict the distribution of illegal dumping sites, supporting accurate identification of these sites for following remediation. The major principle of these studies was to find other potential sites sharing the same characteristics as the reported illegal dumping cases. Commonly, at first, the key factors influencing the spatial distribution of illegal dumping sites were identified based on historic cases. Then, the possibility of illegal dumping occurring in each candidate site was determined by integrating spatial data of the key factors. It has been revealed that various factors, including personal awareness [14], the quantity and cost of waste treatment [6,15,16], location of road network [15], [16], [17], road accessibility [6], degree of monitoring coverage [3,15], and social-economic development [16,18,19], could influence the occurrence of waste illegal dumping.

Nevertheless, due to the limitation in enforcement resources, the historic cases of waste illegal dumping sites are always finite, which thereby causes uncertainty in the identification of dominant factors of illegal dumping occurrence. Also, the experience learned from the finite-size set of historic cases might not be well applicable in a large region, thereby decreasing the accuracy of the prediction results of potential illegal dumping sites. In such cases, compared with traditional statistical methods, the positive-unlabeled (PU) learning algorithm [20], [21], [22], [23], a type of semi-supervised machine learning (ML) algorithm [24], emerges as a more promising tool to tackle this challenge. PU learning algorithm is developed for the situation that one is given a finite set of data of interest sharing a particular property and wishes to find other targets sharing the same property from a large set of unlabeled samples [21]. It could incorporate not only the given finite labeled dataset but also large unlabeled data into the learning process to build a generalized model to discriminate the interesting targets from the large dataset [25,26]. The PU learning scheme has presented superior performances in many applications to deal with numerous unknown samples based on limited experiences [23,27], such as medical diagnosis and knowledge base completion.

Overall, the objective of this paper was to develop a general and ensemble scheme based on a PU learning algorithm to predict the whole spatial pattern of HW illegal dumping risk according to limited supervision experience. This ensemble model contained 5,000 base classifiers developed from newly constructed sub-datasets, each containing the historic cases and unlabeled data sampled from the region we need to scan. These 5000 base classifiers could iteratively mine the characteristics of limited historic cases and then be aggregated using bagging techniques to predict the possibility of the unlabeled target being the illegal dumping site. Results were verified by checking the consistency between the high-risk regions predicted by the model and the distributions of newly reported HW illegal dumping sites which were not included in the training data. This study also shed light on how to predict the behavior of unknown targets based on limited supervision experience in the field of environmental management.

2. Materials and methods

2.1. Site description and data collection

The study was carried out with data from Jiangsu, China. Jiangsu is one of the most industrialized provinces in China and had an HW quantity mass of ∼5,220,500 tons in 2020, ranking 3rd in China. The collected data used for model development included the illegal HW dumping sites and 7 predictor variables, including population density, gross domestic product (GDP), distance to the nearest roads, distance to the nearest waterways, industrial enterprise density, secondary land use type, and HW generation quantity. These 7 predictor variables, representing the socioeconomic characteristics, geographic features, and HW generation intensity, have been demonstrated to be strongly related to the probability of HW illegal dumping [6], [7], [8], [9], [10], [11],28]. HW illegal dumping sites were screened from records of administrative supervision in Jiangsu, China from 2013 to 2018. The data from 2013 to 2017 was used for model development and the data in 2018 was used for model validation. The data of predictor variables, except for distance to the nearest roads (2016), was in 2015. Considering that these 7 predictor variables used in this study were stable over a short period of several years, while some variables such as population density were updated every 5 years or more, we made the hypothesis that the predicted data collected during 2015−2016 can be used to predict the HW illegal dumping risk during 2013−2018, which is a five-year period with 2015 as the midline. Detailed information about the data preparation could be found in Supplementary Materials.

We constructed a 1 km × 1 km modeling grid across the study region, with a total of 101,988 grid cells, for data integration. A total of 214 HW illegal dumping sites reported in 2013−2017 were spatially joined with the modeling grid. Cells with HW illegal dumping sites reported were defined as positive targets, while others were defined as unlabeled targets. Except for the HW generation quantity, the other 6 predictor variables were prepared at a resolution of 1 km × 1 km (Supplementary Materials). The data of HW generation quantity was at the city level and the HW generation in the grid was defined as the total HW generation quantity of the city to which the grid cell belongs. Finally, all the data were matched by their grid cell ID for model development.

2.2. Model development and evaluation

An ensemble ML model, PU bagging, was adopted in this study to develop the prediction model of HW illegal dumping risk, referring to the relative possibility of HW illegal dumping occurring in a 1 km × 1 km grid. The framework of the PU bagging model, including sample preparation, base classifier training, and results aggregation, was shown in Fig. 1.

Fig. 1.

The framework of the ensemble PU learning model. (a) Sampling of all the positive cells with HW illegal dumping sites and bootstrap resampling of unlabeled cells to obtain 5000 mixed datasets. (b) 5 ML algorithms (kK nearest neighbors (KNN), random forest (RF), multi-layer perceptron (MLP), logistic regression (LOG), and decision tree (DT)) were used to train the binary classifier for each dataset. (c) results of 5000 classifiers were aggregated using a weighted average method based on the accuracy of each classifier.

S represents the set of all grid cells, and the S set is split up into a P set and a U set; the P set consists of all positive cells (214) with HW illegal dumping sites; the U set consists of other unlabeled cells (101,774). First, with regard to sample preparation, a set of data U_i was randomly selected from the dataset U and temporarily labeled as negative class. Then the dataset U_i was combined with dataset P to form the mixed dataset M_i for base binary classification modeling development [29]. To ensure data balance, the size of dataset U_i was the same as dataset P. Then, the sampling of dataset U_i was iterated 5000 times to ensure that unlabeled grid cells could be well sampled and learned, which means that there were 5,000 M_i in total for model development.

Secondary, for each dataset M_i, 5 ML algorithms, k nearest neighbors (KNN), random forest (RF) [30,31], multi-layer percetron (MLP) [32], logistic regression (LOG) [33], and decision tree (DT) [34], were used to train the binary classifier, respectively. To improve the training process of ML models for rapid convergence, the input features were normalized to obtain a similar scale and distribution. Following normalization, the dataset M_i was split up into training and testing sets at the ratio of 8:2. The hyper-parameters (Table S2) for each algorithm were adjusted to improve accuracy based on 10-fold cross-validation for the training data. Different hyper-parameters were included in various ML algorithms during the tuning process [35]. The performance of each classifier was evaluated by 6 metrics [36], [37], [38], [39] for binary classification, including accuracy, precision, recall, F1 score, the area under curve (AUC) [32,36], and L&L metric [21,40] (Supplementary Materials).

Third, for each ML algorithm, there were 5000 individual classifiers trained from 5,000 datasets M_i. Each classifier was used to predict the possibility of an unlabeled dataset U being a positive class. Then the results of 5,000 classifiers were aggregated using a weighted average method based on the accuracy of each classifier (PC, Eq. (1)). Since the accuracy gives a good indication of the reliability of classifier, the accuracy of each base classifier was transformed into a weighting coefficient using the min-max normalization method, so that the results predicted by the base classifier with higher accuracy could contribute more to the final aggregated results. The final results indicated the possibility of HW illegal dumping occurring in the unlabeled cells:

$$PC=\frac{{\sum }_{i=1}^{5000}\left[A{N}_i\times P{C}_i\times I(L\&L_i\ne 0)\right]}{{\sum }_{i=1}^{5000}\left[A{N}_i\times I(L\&L_i\ne 0)\right]}$$ (1)

where PC is the possibility of the cell belonging to the positive class, implying that HW illegal dumping occurred in this cell; PC_i is the prediction score of the cell being positive class assigned by classifier i; AN_i is the normalized accuracy of classifier i. Normalized values were obtained using the min-max normalization for the 5000 classifiers. L&L_i is the L&L metric value of classifier i (Eq. S3). L&L metric is a comprehensive performance metric specifically designed for the PU learning model to evaluate whether the model can accurately retrieve more true positive samples and fewer false positive samples from the unlabeled dataset. I(L&L_i ≠ 0) is an indicator function whose value is 1 when L&L ≠ 0 for classifier i; otherwise, its value is 0. Based on this indicator function I(L&L ≠ 0), the poor-performing classifiers whose L&L metric is 0 will be discarded.

2.3. Model explanation

The Shapley additive explanation (SHAP) method was adopted to compute the relative importance of all features. Extensively used in coalitional game theory, the Shapley value currently provides a unique solution to satisfy properties (local accuracy, consistency, and missingness) desired for explanatory ML analysis [41,42]. This approach considers the learning process of the ML model as a game, where each feature can generate a contribution to the prediction, and the contribution is indicated by SHAP value. However, it is noteworthy that SHAP analysis quantified the importance of input feature based on its marginal effect on the prediction results, and the importance might change with different machine learning algorithms. Therefore, the SHAP analysis could provide only a preliminary interpretation of input features’ roles in the prediction, but not the rigorous causal inference between input features and the response variable.

In this study, the SHAP values of all features were calculated using 100 samples for each base classifier, which were selected through the K-means clustering algorithm [43] to reduce the information loss and improve computational efficiency. Specifically, the K-means clustering algorithm divided the total 428 samples into 100 groups based on data characteristics for each base classifier. Then, one sample was randomly drawn from each group to make up a dataset consisting of 100 samples for SHAP calculation. These 100 samples with divergence were capable of covering the characteristics of all the 428 samples in the training dataset, explaining the whole model, and thereby avoiding information loss. In addition, using these 100 samples to calculate the SHAP values could decrease the computational cost by more than 75% compared with using all 418 samples in each base classifier to calculate SHAP value. The importance of each parameter for the base classifier was calculated by the mean absolute SHAP (MAS, Eq. (2)) value of these 100 samples. Then for the PU bagging model with 5000 base classifiers, the importance of each feature was obtained using the weighted average MAS values (WMAS, Eq. (3)) of 5000 classifiers based on the accuracy of each classifier:

$${\mathit{MAS}}_{i,j}=\frac{{\sum }_{n=1}^{100}abs\left({\mathit{SHAP}}_{n,i,j}\right)}{100}$$ (2)

$${\mathit{WMAS}}_j=\frac{{\sum }_{i=1}^{5000}[{\mathit{AN}}_i\times {\mathit{MAS}}_{i,j}\times I(L\&L_i\ne 0)]}{{\sum }_{i=1}^{5000}[{\mathit{AN}}_i\times I(L\&L_i\ne 0)]}$$ (3)

where SHAP_{n, i, j} is the SHAP value of sample n in classifier i for feature j; MAS_i,j is the mean absolute SHAP value of 100 samples in classifier i for feature j; WMAS_i,j is the weighted average MAS value of 5000 classifiers for feature j; AN_i is the normalized accuracy of classifier i; I(L&L_i≠0) is an indicator function (its value is 1 when L&L ≠ 0 in classifier i; otherwise its value is 0).

2.4. Model validation

185 HW illegal dumping sites which were not included in the training data and reported in 2018 were used to validate the reliability of the model results. Since the absolute values of HW illegal dumping risk predicted by different models might not be identical, a relative risk level was used to quantify the risk of occurring HW illegal dumping at each cell, which will benefit the comparison among different models. There were 10 relative risk levels based on the decile of PC values across the whole region. The risk decreases from level 10, referring to the first decile, to level 1, referring to the tenth decile. A high relative risk level was assigned when there was a high possibility of HW illegal dumping occurring in the target. Then, the relative risk level of cells where the 185 HW illegal dumping sites belong were obtained and the cumulative percentage curves of the 185 cells as a function of risk level were plotted to check the consistency between the prediction results and the on-site survey. Among the 185 cells, more cells belonging to high relative risk levels indicated higher reliability of model prediction results.

In addition, the reliability of the PU bagging-based model was compared with the traditional statistical method, discriminant analysis (DA), to demonstrate the superiority of the ML method developed in this study. DA is a multivariate statistical analysis method that discriminates the attribution of samples based on their features, which has been widely used in risk evaluation and prediction [13]. In this study, the DA model based on Fisher discriminant criteria was established to predict the probability of cells being illegal HW dumping sites, referring to the risk of HW illegal dumping. Briefly, a set of negative samples were selected randomly from the unlabeled dataset and then combined with the positive targets with HW illegal dumping sites (214) to form the training dataset. Then the canonical discriminant function was built as a linear combination of the 7 input features based on the training dataset. Finally, for other unlabeled samples, the discriminant score can be calculated according to the canonical discriminant function, and the sample was projected to the negative or positive class based on the distance of the discriminant score to the centroids. Detailed descriptions of the DA method and results could be found in the Supplementary Materials.

3. Results and discussion

3.1. Model performance

According to binary classification algorithms used in the PU model training, there are five types of PU bagging models, namely PU-DT, PU-KNN, PU-LOG, PU-MLP, and PU-RF, developed in this study. Each PU bagging model had 5,000 base classifiers and the average values of evaluation metrics for these 5,000 classifiers were shown in Table 1. Based on the 6 evaluation metrics, the PU-KNN and PU-RF outperformed than other three models and thus were selected for future discussion. The average accuracy of PU-KNN and PU-RF were 0.73 and 0.72, respectively. The probability distribution curves of the evaluation metrics for 5000 classifiers were shown in Fig. 2. It was obvious that for PU-KNN and PU-RF, all 6 evaluation metrics varied within a certain narrow range. For example, 99.64% and 99.08% of the 5,000 base classifiers had an accuracy > 0.6, illustrating the stability and robustness of the models. Even though the model of PU-MLP also had good performance in the average value of evaluation metrics, the recall of 5,000 base classifiers did not perform consistently well, showing a wide range between 0.3 and 1.0.

Table 1.

Average values of evaluation metrics for all PU models with different base classifiers.

Metric	PU-KNN	PU-RF	PU-MLP	PU-LOG	PU-DT
Accuracy	0.73	0.72	0.70	0.70	0.65
Precision	0.74	0.75	0.76	0.78	0.68
Recall	0.74	0.71	0.65	0.60	0.62
F1 score	0.74	0.72	0.67	0.67	0.64
AUC	0.73	0.72	0.70	0.70	0.65
L&L	1.05	1.01	0.94	0.88	0.81

Fig. 2.

Probability distribution curves of 6 evaluation metrics, (a) Accuracy, (b) AUC, (c) Precision, (d) Recall, (e) F1 score, and (f) L&L score, for all 5000 base classifiers in different PU bagging models.

3.2. Model interpretation

Influences of input parameters on the risk of HW illegal dumping were investigated using the SHAP method as shown in Figs. 3, 4. Fig. 3 displayed the probability distributions of MAS values of all 5000 base classifiers for PU-KNN and PU-RF. An information-dense summary of how each feature impacted the prediction results in a single sample was displayed in Fig. 4.

Fig. 3.

The distribution of the mean absolute SHAP values for 5,000 base classifiers in (a) PU-KNN and (b) PU-RF and the importance ranking of 7 predictor variables for (c) PU-KNN and (d) PU-RF. The mean absolute SHAP value (MAS) reflects the contribution of each feature to the prediction results in each base classifier. The feature importance was obtained using the WMAS of all 5,000 base classifiers. IED denotes industrial enterprise density; LUT denotes land use type; HWG denotes HW generation; DNW denotes the distance to the nearest waterways; DNR denotes the distance to the nearest roads; GDP denotes the total GDP per unit area; PD denotes population density.

Fig. 4.

SHAP values for all input descriptors with 5000 data points included in the model of (a) PU-KNN and (b) PU-RF. There were 5000 data points obtained from 50 different base classifiers, which were randomly selected from 5000 base classifiers. IED denotes industrial enterprise density; HWG denotes HW generation quantity; DNW denotes distance to the nearest waterways; DNR denotes distance to the nearest roads; GDP denotes the total GDP per unit area; PD denotes population density.

As shown in Fig. 3c, for PU-KNN, the importance of 7 features was found to follow the order of industrial enterprise density > land use type > HW generation quantity > distance to the nearest roads > distance to the nearest waterways > GDP > population density. The first three most important features of industrial enterprise density, land use type, and HW generation quantity accounted for 68.05% of the total WMAS values.

For industrial enterprise density, the samples with low feature values were mainly on the left side, while the points with high feature values were mainly on the right side (Fig. 4a), suggesting the positive correlation between industrial enterprise density and the predicted risk of HW illegal dumping [44]. This interaction indicated that in areas with more developed industries, the probability of discovering illegal dumping sites might be higher, which was consistent with most previous studies [3,6,11]. For example, Biotto et al. [11] revealed that the presence of open areas in industrial zones was significantly associated with illegal waste dumping. Jordá-Borrell et al. [6] reported that there were 44.31% of the dumping sites located near industrial zones. This is because many enterprises tend to dump HW illegally in nearby areas to diminish transportation costs. In contrast, there were still some studies that reported that uncontrolled landfills were always located in remote areas far from the origination [19]. The difference among these studies may result from a trade-off between the transportation cost and the risk of being punished. Land use type ranked second to the industrial enterprise density in terms of feature importance for PU-KNN. To identify the land use type which was more likely to occur HW illegal dumping, the density distribution curves of HW illegal dumping risk for different land use types were depicted as shown in Fig. S8. The prediction results revealed that the probability of HW illegal dumping occurring in construction land was higher than the other five major land use types. In addition, the urban land was most likely to occur HW illegal dumping among the 21 secondary land use types. Also, the tight affinity between land use type and the illegal dumping site has been well reported in previous studies. Similar to this study, Quesada-Ruiz et al. [13] reported that urban cadastral surfaces, areas close to sports facilities, and the areas with the highest building densities tended to be predicted with greater illegal landfill potential occurrence. Conversely, some studies revealed waste illegal dumping is likely to occur in rural areas. For example, Jordá-Borrell et al. [6] showed that up to 60.23% of the sites were located in rural areas, which were described as ‘agrarian’, ‘uncultivated’, and ‘rustic’. These areas far from the urban center, temporarily unoccupied, and not very isolated, may be attractive to HW illegal dumping. Although the most relevant land use type to illegal dumping varied in different studies due to study regional differences, it is identical that land use factor has a significant influence on the occurrence of HW illegal dumping [3,9,13]. As for HW generation quantity, there was a positive correlation between its feature value and the predicted risk of HW illegal dumping, which means that HW illegal dumping tended to occur in cities with higher HW generation. If the waste generation of an area is higher than its capacity to dispose of the waste, there may be a high possibility of local enterprises illegally storing or dumping waste [14,15].

For PU-RF, the importance of 7 features followed the order of industrial enterprise density > distance to the nearest roads > population density > GDP > land use type > distance to the nearest waterways > HW generation quantity (Fig. 3d). The feature importance of PU-RF model was slightly different from PU-KNN. The influence of distance on the nearest roads was more significant on PU-RF than PU-KNN. The first two most important features of industrial enterprise density and distance to the nearest roads accounted for 66.89% of the total WMAS values.

Concerning the feature of distance to the nearest roads, samples with high values for the variable distributed on the left side (Fig. 4b), showing negative correlations with the predicted risk of HW illegal dumping. This implies that zones with lower distances to roads had a higher risk of occurring HW illegal dumping, which was consistent with previous studies [7,13,14]. For instance, a study conducted in Israel reported that 57% of all the detected illegal waste sites were found at a distance of less than 1 km from main roads [3]. Tasaki et al. [28] revealed that most uncontrolled dumping sites occurred in areas within a distance of 100 m from roads. Proximity to main roads is positively correlated with the occurrence of illegal dumping since it affects the accessibility to a potential dumping site [10,13].

3.3. Model prediction and validation

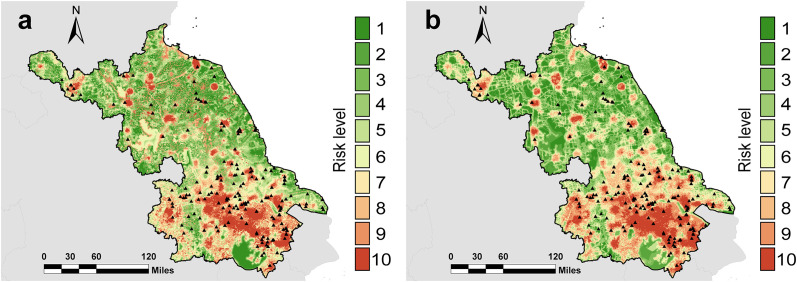
The spatial patterns of HW illegal dumping risk across the whole study region predicted by PU-KNN and PU-RF models were shown in Fig. 5. It was evident that the spatial patterns of HW illegal dumping risk predicted by PU-KNN and PU-RF were similar to each other. There were large and continuous high-risk areas in the southern part and scattered high-risk centers in the northern part of the study region. It was consistent with the spatial distribution of historic reported HW illegal dumping sites and the majority (74.9%) of these cases from 2013 to 2018 occurred in the southern region. The high-risk areas in the southern part could be associated with the distribution of industrial enterprise (Fig. S7) as implied by the feature importance analysis [3]. The scattered high-risk centers in the northern part were almost located in the urban, rural residential, and construction land, which was congruent with the finding that the illegal dumping sites were likely to occur in the urban-rural transition areas [9]. It was interesting that some high-risk zones identified by PU-RF overlapped with the main roads and transport hubs due to the significant influence of proximity to roads on the illegal dumping risk for PU-RF.

Fig. 5.

Risk levels of HW illegal dumping across the studied region predicted by (a) PU-KNN and (b) PU-RF. Black dots denote the location of newly reported illegal dumping sites (185 sites in total) used for model validation. All maps in this study are generated based on the standard map GS(2019)1822.

The model validation revealed that most of the newly reported sites were located in the high-risk region predicted by PU-KNN and PU-RF. Quantitative analysis (Fig. 6) showed that the percentage of newly reported dumping sites located in the region with the highest risk level was 31.9% for PU-RF and 27% for PU-KNN. Moreover, the percentage declined with the decrease in the risk level. The cumulative percentage curves indicated that for PU-RF, the regions with risk levels 8–10 covered 68.1% of the newly reported sites, and the corresponding value for PU-KNN was 62.2%. This implied that most of the illegal dumping occurred in the predicted high-risk regions which accounted for only 30% of the total area, verifying the accuracy of the model to predict the whole spatial patterns of HW illegal dumping risk.

Fig. 6.

The distribution of newly reported HW illegal dumping sites at each risk level and cumulative percentage curves for the model of DA, PU-KNN, and PU-RF.

In addition, the results predicted by PU-KNN and PU-RF were more accurate than the traditional multivariate statistical method, the DA model. As shown in Fig. 6, compared with two PU models, fewer newly reported dumping sites (53%) were located in the high-risk regions (with a risk level of 8–10) predicted by the DA method, indicating the inferiority of the DA model than the PU learning methods. Therefore, the PU model provides a reliable method to screen the high-risk and focal areas for supervision, which will greatly improve the cost-effectiveness and efficiency of HW illegal dumping supervision [1].

4. Conclusion

With the rapid economic development all over the world, there is an unprecedented increase in HW generation during industrialization and urbanization [9,14]. At the same time, the environmental burden from illegal dumping of HW driven by enterprises’ motivation to avoid treatment costs is set to intensify, particularly in developing regions with lax regulations. In this context, curbing illegal dumping and mitigating the serious impact of open-dumping waste on the environment are essential tasks for HW management [15]. One dominant task in dealing with HW illegal dumping is to find out and remediate the sites in time, thereby avoiding the long-term adverse impacts of the dumped waste, while the invisibility of waste illegal dumping sites makes it challenging to accurately detect these sites [3]. Utilizing the limited supervision knowledge about the distribution of HW illegal dumping sites to predict the potential dumping sites is a key solution to address the challenge.

In this study, an ensemble ML framework based on PU learning was proposed to calculate the possibility of the location being the HW illegal dumping sites, thereby supporting screening the regions with a high likelihood of HW illegal dumping occurrences. Compared with traditional multivariate statistical analysis, the PU learning model could improve the model accuracy by iteratively mining the features of the HW illegal dumping sites. The validation of the PU-RF model showed that 68.1% of the newly reported sites were in the regions with the top 30% highest predicted risk. That is to say, the enforcement department can focus on only 30% of the regulation region, but find out about 70% of illegal dumping sites. It implied that enforcement based on the risk maps predicted by this novel model could increase the efficiency by more than one-fold than the random supervision from the spatial perspective. Meanwhile, the PU bagging model interpretation revealed that HW illegal dumping is likely to occur in zones with high industrial enterprise density and proximity to roads.

Some limitations remain and deserve further study. The first limitation is that there existed some bias in prediction results. For example, some reported HW illegal dumping sites occurred in the predicted low-risk areas. The limitation in prediction accuracy might be mainly attributable to lacking consistent records of HW illegal dumping for modeling development. The limited quantity of illegal dumping cases caused the data imbalance with a large size (101,774) of unlabeled data but a small size (214) of positive data, which may affect the performance of the model [29]. Also, due to the cases’ quantity limitation, illegal landfill, open-air stacking, and illegal transfer are taken into consideration as HW illegal dumping cases in a wide sense. With the improvement in data size and normativity of HW illegal dumping records, the model performance could be further improved. Also, considering the data accessibility and reliability, only 7 predictor variables, representing the socioeconomic characteristics, geographic features, and HW generation intensity, were taken into consideration for model development. When data is available, introducing more relevant input features, such as proximity to a video surveillance network, might bring more information for model development. Another limitation is some simplified assumptions we have made, such as the socioeconomic characteristics and geographic features remaining stable over a short period of time, so that the predictor data collected during 2015−2016 was used to predict the HW illegal dumping risk during 2013−2018, a five-year period with 2015 as the median. However, despite these limitations, this PU learning model has superior performance and higher accuracy than traditional statistical methods. This scheme proved practical in resolving the challenge of leveraging limited authentic observations to predict the behaviors of most objects during environmental enforcement.

Declaration of competing interest

The authors declare that they have no conflicts of interest in this work.

Biographies

Jinghua Geng is a Ph.D. student in the state key laboratory of Pollution Control and Resource Reuse at Nanjing University. Her research focuses on solid waste environmental risk assessment using data-driven approaches.

Wen Fang(BRID: 06371.00.65608) is an assistant professor in the state key laboratory of Pollution Control and Resource Reuse at Nanjing University. Her research focuses on environmental risk assessment and resource management of solid waste.