Ultra-efficient and parameter-free computation of submicron thermal transport with phonon Boltzmann transport equation

Abstract

Understanding thermal transport at the submicron scale is crucial for engineering applications, especially in the thermal management of electronics and tailoring the thermal conductivity of thermoelectric materials. At the submicron scale, the macroscopic heat diffusion equation is no longer valid and the phonon Boltzmann transport equation (BTE) becomes the governing equation for thermal transport. However, previous thermal simulations based on the phonon BTE have two main limitations: relying on empirical parameters and prohibitive computational costs. Therefore, the phonon BTE is commonly used for qualitatively studying the non-Fourier thermal transport phenomena of toy problems. In this work, we demonstrate an ultra-efficient and parameter-free computational method of the phonon BTE to achieve quantitatively accurate thermal simulation for realistic materials and devices. By properly integrating the phonon properties from first-principles calculations, our method does not rely on empirical material properties input. It can be generally applicable for different materials and the predicted results can match well with experimental results. Moreover, by developing a suitable ensemble of advanced numerical algorithms, our method exhibits superior numerical efficiency. The full-scale (from ballistic to diffusive) thermal simulation of a 3-dimensional fin field-effect transistor with 13 million degrees of freedom, which is prohibitive for existing phonon BTE solvers even on supercomputers, can now be completed within two hours on a single personal computer. Our method makes it possible to achieve the predictive design of realistic nanostructures for the desired thermal conductivity. It also enables accurately resolving the temperature profiles at the transistor level, which helps in better understanding the self-heating effect of electronics.

Graphical abstract

1. Introduction

Understanding the micro and nanoscale thermal transport is crucial for many applications, such as thermal management of electronics, high-efficiency thermoelectric energy conversion, and improved thermal barriers [1]. For example, the shrinking size of semiconductor devices (transistors) to submicrons imposes grand challenges on the heat dissipation of electronics [1]. Accurate transistor-level thermal simulation can help to achieve more efficient heat extraction from transistors [2] and better understand the self-heating effects of electronics [3], [4]. In the applications of thermal barriers and thermoelectric energy conversion, where thermal conductivity is a key metric, designing nanostructures to manipulate thermal transport in these applications is an important strategy [5], [6]. Efficient and accurate thermal simulations can better guide the design of these nanomaterials.

At the submicron scale, it has long been recognized that macroscopic heat diffusion equation is not valid [7]. Therefore, to study the micro and nanoscale effects of thermal transport, atomistic simulation methods are widely adopted [8], [9], especially the nonequilibrium Green’s function [10], [11], anharmonic lattice dynamics [12], [13], and molecular dynamics [14], [15]. While these atomistic simulation methods can be utilized to investigate the phenomena like the size effect of thermal conductivity and interfacial thermal resistance [8], [9], they are typically limited in very small system size (several nanometers) and not capable of performing thermal simulations of realistic systems in applications, such as nanocomposite materials and electronic devices. The phonon Boltzmann transport equation (BTE) that governs the thermal transport at a scale comparable to the mean free path (typically several nanometers to several microns) [16], provides the only promising solution that can possibly meet the requirements of thermal simulation in real applications. Unlike the electrical simulation with the electron BTE, which has been a relatively mature tool for a long time [17], the development of thermal simulation with the phonon BTE is very challenging due to the uniquely large spread in phonon properties [18]. Many previous studies have tried to develop numerical solvers for the phonon BTE using various methods including deterministic methods [19], [20], statistical methods [21], [22] and machine learning methods [23]. However, to date, the computational cost of phonon BTE is still believed to be prohibitive for sizes and geometries of realistic materials and devices [19], [22], [24], and thermal simulations of 3-dimensional problems are rare [17], [19], [22]. Two studies have demonstrated the computational costs associated with simulating 3-dimensional devices [19], [22]. In one study [19], the simulation of a 3-dimensional toy device is far from steady-state but requires several hours using hundreds of CPU cores. Another simulation shows even larger computational costs [22]. Besides, many of these simulations rely on empirical models for the input material properties [17], [19], [25], [26] and therefore cannot be used as a predictive tool for accurately simulating thermal transport.

In this study, we demonstrate a numerical method for nanoscale thermal simulations with the phonon BTE. The present method has the following advantages: (1) by properly integrating the phonon properties from first-principles calculations into our method, it is accurate, parameter-free and general for different material systems; (2) by developing a suitable ensemble of advanced numerical algorithms, our method exhibits superiority in efficiency compared to existing solvers.

2. Methods

In this section, we introduce the phonon BTE and the present method for solving the phonon BTE. The present method solves the non-gray phonon BTE (details are provided in Sections 2.1 and 2.2) based on the framework of the discrete ordinates method (DOM) [19], [27]. To ensure the ability to address arbitrary geometries, unstructured spatial meshes are adopted. In this method, we solve the two main challenges of previous solvers: dependence on empirical models for phonon properties and prohibitive computational costs. To solve the former challenge, we integrate the phonon properties from first-principles calculations into the method. First-principles prediction of phonon properties has been proven to be comparable to experimental results [28]. However, first-principles calculations provide properties for millions of phonon modes [28], which are prohibitive to be directly sampled in the phonon BTE. To resolve this issue, we develop a band discretization scheme combined with directional discretization to sample a small number of phonon modes from the first-principle phonon modes and also ensure good accuracy. The details of the band discretization scheme and the directional discretization scheme are provided in Section 2.3. To solve the challenges of computational costs, we develop an ensemble of advanced numerical algorithms to improve the efficiency of the solver in all aspects including reducing the number of degrees of freedom, improving the convergence rate of iterations, and optimizing the parallelization. The details are provided in Section 2.4.

2.1. Non-gray phonon BTE

When the characteristic length is comparable to the phonon mean free path, the thermal transport can be described by the non-gray phonon BTE. Under the relaxation time approximation, the phonon BTE can be expressed as

$$\begin{array}{c}\hfill {\mathbf{v}}_{\omega ,p}·\nabla e_{\omega ,p,\mathbf{s}}=-\frac{e_{\omega ,p,\mathbf{s}}-e_{\omega ,p}^{\text{eq}}}{{\tau }_{\omega ,p}}+{\dot{q}}_{\omega ,p}\end{array}$$ (1)

where $e=e\left(\mathbf{r},\mathbf{s},\omega ,p\right)$ is the distribution function of the phonon energy density. $e^{\text{eq}}$ is the energy density distribution function of the equilibrium state, which follows the Bose–Einstein distribution. $\mathbf{r}$ is the spatial coordinates. $\omega ,p$ are the frequency and branch index. $\mathbf{s}$ is the unit vector in the direction of group velocity $\mathbf{v}$, which is assumed to be isotropic [29]. $\tau$ is the relaxation time. $\dot{q}$ is the volumetric heat generation term. The volumetric heat generation can originate from moving electrons through the electron-phonon interaction [30], [31].

According to the energy conservation [19], $e_{\omega ,p}^{\text{eq}}$ is related to $e_{\omega ,p,\mathbf{s}}$ through:

$$\begin{array}{ccc}\hfill e_{\omega ,p}^{\text{eq}}& =& C_{\omega ,p}{T}_L\hfill \\ \hfill T_L& =& \frac{\frac{1}{4\pi }\int {\sum }_p{\int }_{{\omega }_{\min }}^{{\omega }_{\max }}\frac{e_{\omega ,p,\mathbf{s}}}{{\tau }_{\omega ,p}}d\omega d\Omega }{{\sum }_p{\int }_{{\omega }_{\min }}^{{\omega }_{\max }}\frac{C_{{\omega }^{\prime },p}}{{\tau }_{{\omega }^{\prime },p}}d\omega }\hfill \end{array}$$ (2)

where $C$ is the volumetric heat capacity. $T_L$ is the lattice temperature [32]. $\Omega$ is the control angle. The phonon information of $C$, $v$ and $\tau$ was previously taken from empirical values [17], [19], [25], [26], but can now be obtained by the more accurate first-principles calculations [33].

Eqs. 1 and 2 are the closed form of the phonon BTE. If proper boundary conditions are specified, they can be numerically solved to obtain the local energy density $e$. The local temperature and heat flux can then be calculated by

$$\begin{array}{ccc}\hfill T& =& \frac{\frac{1}{4\pi }\int {\sum }_p{\int }_{{\omega }_{\min }}^{{\omega }_{\max }}{e}_{\omega ,p,\mathbf{s}}d\omega d\Omega }{{\sum }_p{\int }_{{\omega }_{\min }}^{{\omega }_{\max }}{C}_{\omega ,p,\mathbf{s}}d\omega }\hfill \\ \hfill \mathbf{q}& =& \int \sum _p{\int }_{{\omega }_{\min }}^{{\omega }_{\max }}{\mathbf{v}}_{\omega ,p}{e}_{\omega ,p,\mathbf{s}}d\omega d\Omega \hfill \end{array}$$ (3)

2.2. Boundary conditions

• (i)
  At thermalizing boundaries, all phonons are emitted from the boundary with a temperature of $T_1$, i.e.

  $$\begin{array}{c}\hfill e_{\omega ,p,\mathbf{s}}=-\frac{C_{\omega ,p}}{4\pi }{T}_1(\mathbf{s}·\mathbf{n}<0)\end{array}$$ (4)

  where n is the exterior normal unit vector of the boundary. This kind of boundary usually exists at the interface between metals and semiconductors and the boundary away from the ballistic regime.

• (ii)
  The specularly reflecting boundary condition is an adiabatic boundary condition, in which the reflected angle of phonon equals the incident angle of phonon, i.e.

  $$\begin{array}{c}\hfill e_{\omega ,p,\mathbf{s}}=e_{\omega ,p,{\mathbf{s}}_r}(\mathbf{s}·\mathbf{n}<0)\end{array}$$ (5)

  where ${\mathbf{s}}_r$ is the incident direction before specularly reflecting to direction $\mathbf{s}$, which is calculated by ${\mathbf{s}}_r=\mathbf{s}-\mathbf{n}(\mathbf{n}·\mathbf{s})$. The specularly reflecting boundary is the symmetric boundary, which can cut the symmetry domain into one half [29], [34].
• (iii)
  The diffusely reflecting boundary condition is another type of adiabatic boundary condition, in which the energy of the phonon reflected from the boundary is the same along each direction, i.e.

  $$\begin{array}{c}\hfill e_{\omega ,p,\mathbf{s}}=\frac{1}{\pi }{\int }_{{\mathbf{s}}^{\text{'}}·\mathbf{n}>0}{e}_{\omega ,p,{\mathbf{s}}^{\text{'}}}{\mathbf{s}}^{\text{'}}·\mathbf{n}d\Omega \end{array}$$ (6)

  The diffusely reflecting boundary condition exists at the surface of the semiconductor or the dioxide layer [35], [36].
• (iv)
  The periodic boundary condition represents that two boundaries are connected with each other, i.e.

  $$\begin{array}{c}\hfill e_{\omega ,p,\mathbf{s}}\left({\mathbf{r}}_{\mathrm{B}1}\right)=e_{\omega ,p,\mathbf{s}}\left({\mathbf{r}}_{\mathrm{B}2}\right)\end{array}$$ (7)

  where B1 and B2 are indexes of the two periodic boundaries. Sometimes, a temperature difference is applied between two periodic boundaries to mimic a uniform temperature gradient, then Eq. 7 is expressed as

  $$e_{\omega ,p,\mathbf{s}}\left({\mathbf{r}}_{\mathrm{B}1}\right)=e_{\omega ,p,\mathbf{s}}\left({\mathbf{r}}_{\mathrm{B}2}\right)+\frac{1}{4\pi }{C}_{\omega ,p}\Delta T$$

2.3. Integrating phonon properties from first-principles calculations

We integrate the phonon properties from first-principles calculations into numerically solving the phonon Boltzmann transport equation. First-principles calculations provide properties for millions of phonon modes [28], [33]. For example, in our first-principles calculations of silicon in this study, we have phonon properties for 70 $\times$ 70 $\times$ 70 $\times$ 6 phonon modes. To integrate with phonon BTE, we use band discretization and directional discretization. Note that the previous schemes for phonon properties from the first-principles calculations are all designed for the phonon BTE without the heat generation term, which does not apply to simulation of many devices and materials [18], [37]. For the band discretization, we first collect all phonon properties (including heat capacity $C$, group velocity $\mathbf{v}$, and relaxation time $\tau$ from lattice dynamics calculations) and find the maximum mean free path ${\Lambda }_{\max }$ and minimum mean free path ${\Lambda }_{\min }$. Then we divide the mean free path domain $[{\Lambda }_{\min },{\Lambda }_{\max }]$ into several bins $[{\Lambda }_0,\dots ,{\Lambda }_n]$. For each bin, we obtain the representative phonon properties as

$$\begin{array}{ccc}\hfill C_n& =& \sum _{\Lambda ={\Lambda }_{\mathrm{n}-1}}^{{\Lambda }_{\mathrm{n}}}{C}_{\Lambda }\hfill \\ \hfill v_n& =& \frac{{\displaystyle \sum _{\Lambda ={\Lambda }_{\mathrm{n}-1}}^{{\Lambda }_{\mathrm{n}}}{C}_{\Lambda }{v}_{\Lambda }}}{{\displaystyle \sum _{\Lambda ={\Lambda }_{\mathrm{n}-1}}^{{\Lambda }_{\mathrm{n}}}{C}_{\Lambda }}}\hfill \\ \hfill {\tau }_n& =& \frac{{\displaystyle \sum _{\Lambda ={\Lambda }_{\mathrm{n}-1}}^{{\Lambda }_{\mathrm{n}}}{C}_{\Lambda }{v}_{\Lambda }^2{\tau }_{\Lambda }}}{{\displaystyle v_n\sum _{\Lambda ={\Lambda }_{\mathrm{n}-1}}^{{\Lambda }_{\mathrm{n}}}{C}_{\Lambda }{v}_{\Lambda }}}\hfill \end{array}$$ (8)

The mode-level heat generation term depends on the type of heat generation. For example, the equilibrium mode-level heat generation term is proportional to the heat capacity of the phonon [29]. The mode-level heat generation originating from moving electrons through the electron-phonon interaction can be obtained from electron-phonon coupling calculations [38], [39]. For each bin, we obtain the heat generation term for representative phonon the mode-level heat generation as

$$\begin{array}{c}\hfill {\dot{q}}_n=\sum _{\Lambda ={\Lambda }_{n-1}}^{{\Lambda }_n}{\dot{q}}_{\Lambda }\end{array}$$ (9)

These formulas obey the additivity of energy, heat flux, and thermal conductivity. There are several integrations related to the phonon frequency and branch. The band discretization transforms the integration into summation:

$$\begin{array}{ccc}\hfill \sum _p{\int }_{{\omega }_{\min }}^{{\omega }_{\max }}\frac{e_{\omega ,p,\mathbf{s}}}{{\tau }_{\omega ,p}}d\omega & =& \sum _p\sum _{\omega }\frac{e_{\omega ,p,\mathbf{s}}}{{\tau }_{\omega ,p}}\hfill \\ \hfill \sum _p{\int }_{{\omega }_{\min }}^{{\omega }_{\max }}\frac{C_{\omega ,p}}{{\tau }_{\omega ,p}}d\omega & =& \sum _p\sum _{\omega }\frac{C_{\omega ,p}}{{\tau }_{\omega ,p}}\hfill \\ \hfill \sum _p{\int }_{{\omega }_{\min }}^{{\omega }_{\max }}{\mathbf{v}}_{\omega ,p}{e}_{\omega ,p,\mathbf{s}}d\omega & =& \sum _p\sum _{\omega }{\mathbf{v}}_{\omega ,p}{e}_{\omega ,p,\mathbf{s}}\hfill \end{array}$$ (10)

There are also several integrations over the velocity directions. Directional discretization transforms those integrations into summations:

$$\begin{array}{ccc}\hfill \underset{\Omega }{\int }{e}_{\omega ,p,\mathbf{s}}d\Omega & =& \underset{{\theta }_{\min }}{\stackrel{{\theta }_{\max }}{\int }}\underset{{\phi }_{\min }}{\stackrel{\phi }{\int }}{e}_{\omega ,p,\mathbf{s}}\sin \theta d\theta d\phi \hfill \\ & =& \sum _i\sum _j{w}_i{w}_j{e}_{\omega ,p,{\mathbf{s}}_{i,j}}\sin {\theta }_i\hfill \\ \hfill \underset{\Omega }{\int }{e}_{\omega ,p,\mathbf{s}}\mathbf{s}d\Omega & =& \underset{{\theta }_{\min }}{\stackrel{{\theta }_{\max }}{\int }}\underset{{\phi }_{\min }}{\stackrel{\phi }{\int }}{e}_{\omega ,p,\mathbf{s}}\mathbf{s}\sin \theta d\theta d\phi \hfill \\ & =& \sum _i\sum _j{w}_i{w}_j{e}_{\omega ,p,{\mathbf{s}}_{i,j}}{\mathbf{s}}_{i,j}\sin {\theta }_i\hfill \\ \hfill \underset{\Omega }{\int }{e}_{\omega ,p,\mathbf{s}}\mathbf{s}·\mathbf{n}d\Omega & =& \underset{{\theta }_{\min }}{\stackrel{{\theta }_{\max }}{\int }}\underset{{\phi }_{\min }}{\stackrel{\phi }{\int }}{e}_{\omega ,p,\mathbf{s}}\mathbf{s}·\mathbf{n}\sin \theta d\theta d\phi \hfill \\ & =& \sum _i\sum _j{w}_i{w}_j{e}_{\omega ,p,{\mathbf{s}}_{i,j}}{\mathbf{s}}_{i,j}\sin {\theta }_i\hfill \end{array}$$ (11)

where $w_i$ and $w_j$ are the weights of corresponding moving direction ${\mathbf{s}}_{i,j}$ $=\{\text{sin}{\theta }_i\cos {\phi }_j$ $,\sin {\theta }_i\sin {\phi }_j,\cos {\theta }_i\}$ and are obtained by the Gauss-Legendre quadrature over the intervals $[{\theta }_{\min },{\theta }_{\max }]$ and $[{\phi }_{\min },{\phi }_{\max }]$. Sometimes we have multiple intervals of $[{\theta }_{\text{min},n},{\theta }_{\text{max},n}]$ and $[{\phi }_{\text{min},m},{\phi }_{\text{max},m}]$ for different boundaries, which are decided by ${\mathbf{s}}^{\prime }·\mathbf{n}>0$ (Eq. 6). We need to collect all ${\theta }_{\min }$, ${\theta }_{\max }$, ${\phi }_{\text{min},m}$, and ${\phi }_{\text{max},m}$ and then sort them as $[{\theta }_1,\dots ,{\theta }_n,{\theta }_{n+1},\dots ,{\theta }_N]$ and $[{\phi }_1,\dots ,{\phi }_m,{\phi }_{m+1},\dots ,{\phi }_M]$. For each interval $[{\theta }_n,{\theta }_{n+1}]$ and $[{\phi }_m,{\phi }_{m+1}]$, we can obtain the direction and direction weight according to the Gauss–Legendre quadrature. The total number of sampled phonon modes is the number of bands multiply the number of directions, which would be much smaller than the number from first-principles calculations.

2.4. Numerical method

The numerical method contains several important components, including a spatial discretization method, an iterative method, and parallelization strategies. The spatial discretization transforms the spatial partial derivative into algebraic expressions. The discretized form of the BTE is

$$\begin{array}{ccc}& & \frac{\Delta e_{i,\omega ,p,\mathbf{s}}^{n+1}}{{\tau }_{i,\omega ,p}}+\frac{1}{V_i}\sum _{j\in N\left(i\right)}\Delta e_{ij,\omega ,p,\mathbf{s}}^{n+1}{\mathbf{v}}_{i,\omega ,p}·{\mathbf{n}}_{ij}{S}_{ij}\hfill \\ & & =-\frac{1}{V_i}\sum _{j\in N\left(i\right)}{e}_{ij,\omega ,p,\mathbf{s}}^n{\mathbf{v}}_{i,\omega ,p}·{\mathbf{n}}_{ij}{S}_{ij}-\frac{e_{i,\omega ,p,\mathbf{s}}^n-e_{i,\omega ,p}^{n,\text{eq}}}{{\tau }_{i,\omega ,p}}+{\dot{q}}_{\omega ,p},\hfill \end{array}$$ (12)

where $\Delta e_{i,\omega ,p,\mathbf{s}}^{n+1}=e_{i,\omega ,p,\mathbf{s}}^{n+1}-e_{i,\omega ,p,\mathbf{s}}^n$ and $n$ is the iteration index. $V_i$ is the volume of the spatial cell $i$, $N\left(i\right)$ is the sets of face neighbor cells of cell $i$, $ij$ is the face between cell $i$ and cell $j$, $S_{ij}$ is the area of the face $ij$, and ${\mathbf{n}}_{ij}$ is the exterior normal unit vector of the face $ij$ directing from cell $i$ to cell $j$. When the system is in the steady state, the left-hand side is zero and only the right-hand side remains. In previous studies involving unstructured meshes, only the first-order scheme of spatial discretization was applied [19], [27]. However, the first-order scheme will have a limitation on the mesh size, which should be smaller than the mean free path of phonons to ensure the accuracy [19], [27]. Considering the small mean free path of some phonons (the phonon mean free path of silicon is provided in Supplementary Material S3), this limitation can induce extremely large computational costs for large sizes. In this study, we adopt the first-order up-wind scheme for the $\Delta e_{ij}$ to ensure the sparsity and the second-order scheme for the $e_{ij}$ to ensure the piece-wise linear results, which is crucial for eliminating the limitation of mesh size [40], [41]. For the first-order up-wind scheme, the energy on the face is the energy density of the cell in up-wind direction, i.e., $\mathbf{s}·\mathbf{n}>0$ for this cell. To achieve the second-order scheme, the energy density $e_{ij,s}$ on the face is calculated by $e_i+\nabla e_i·{\mathbf{l}}_{i,ij}$, where cell $i$ is also the cell in up-wind direction and ${\mathbf{l}}_{i,ij}$ is the vector between cell’s center of the cell and the center of the face. The gradient $\nabla e_i$ is calculated by the least squares method, which performs well for unstructured meshes.

Previous studies mainly adopted the sequential method to iteratively solve the phonon BTE with unstructured meshes [19]. However, the sequential method encountered slow convergence rates for non-gray solvers. A hybrid BTE-diffusion method was proposed to accelerate convergence [42]. This method solves the phonon BTE for some bands and solves the heat diffusion equation for other bands. However, the performance of this method relies on the choice of a cutoff Knudsen number (the ratio of the mean free path over the characteristic length), which is difficult to be decided for real 3-dimensional problems with multiple characteristic lengths. To iteratively solve the algebraic equations, we adopt the synthetic iterative method [41]. This method was developed for a structured solver of the phonon BTE without the heat generation term and largely improved the convergence rate of the phonon BTE. In our method, we extend this method to unstructured meshes and incorporate the heat generation term. Following the derivation of Zhang et al., a diffusion-type equation can be obtained from non-gray phonon BTE with the heat generation term [41]

$$\begin{array}{c}{e}_{\omega ,p}^{\text{eq}}=C_{\omega ,p}{T}_L\hfill \\ k_{\mathrm{bulk}}{\nabla }^2{T}_L=\nabla ·\left({\mathbf{q}}_{\text{non}-\text{Fourier}}\right)-4\pi \sum _{\omega ,p}{\dot{q}}_{\omega ,p}\hfill \\ {\mathbf{q}}_{\text{non}-\text{Fourier}}=-\sum _{\omega ,p}{w}_{\omega ,p}\sum _s{w}_s\hfill \\ ({\tau }_{\omega ,p}{v}_{\omega ,p}^2\mathbf{ss}-k_{\mathrm{bulk}}({\tau }_{\omega ,p}\sum _{\omega ,p}{w}_{\omega ,p}{C}_{\omega ,p}/{\tau }_{\omega ,p})\mathbf{I})·\nabla e_{\omega ,p,\mathbf{s}}\hfill \end{array}$$ (13)

where $k_{\mathrm{bulk}}$ is the bulk thermal conductivity expressed as $k_{\mathrm{bulk}}=\frac{1}{3}{\sum }_{\omega ,p}{w}_{\omega ,p}{C}_{\omega ,p}{v}_{\omega ,p}^2{\tau }_{\omega ,p}$. This diffusion-type equation strengthens the coupling of phonon bands and therefore facilitates fast convergence from the diffusive regime to the ballistic regime [41]. This equation is solved by the finite volume method:

$$\begin{array}{ccc}& & e_{i,\omega ,p}^{n+1,\text{eq}}=C_{\omega ,p}{T}_{L,i}^{n+1}\hfill \\ & & k_{\mathrm{bulk}}\sum _{j\in N\left(i\right)}{S}_{ij}{\mathbf{n}}_{ij}·\nabla T_{L,ij}^{n+1}\hfill \\ & & =\sum _{j\in N\left(i\right)}{S}_{ij}{\mathbf{n}}_{ij}·{\left({\mathbf{q}}_{\text{non}-\text{Fourier}}\right)}_{ij}^{n+\frac{1}{2}}-4\pi \sum _{\omega ,p}{\dot{q}}_{\omega ,p}\hfill \end{array}$$ (14)

$$\begin{array}{c}{\left({\mathbf{q}}_{\text{non}-\text{Fourier}}\right)}_{\mathit{ij}}^{n+\frac{1}{2}}=-\sum _{\omega ,p}{w}_{\omega ,p}\sum _s{w}_s\hfill \\ ({\tau }_{\omega ,p}{v}_{\omega ,p}^2\mathbf{ss}-k_{\mathrm{bulk}}({\tau }_{\omega ,p}\sum _{\omega ,p}{w}_{\omega ,p}{C}_{\omega ,p}/{\tau }_{\omega ,p})\mathbf{I})·\nabla e_{\mathit{ij},\omega ,p,\mathbf{s}}^{n+1}\hfill \end{array}$$ (15)

To solve this equation, we require the gradient on the faces of the cells. We adopt the non-orthogonal correction to obtain the gradient for unstructured meshes.

The complete procedure of the present method is as follows, which is also depicted in Supplementary Materials S1:

Step 1 Set initial guess for equilibrium energy density $e_{\omega ,p}^{\text{eq}}$. Step 2 Solve the discretized form of the BTE (Eq. 12) subject the boundary conditions to obtain the energy density $e_{\omega ,p}$. For the matrix in each band and direction, we solve it by using Generalized Minimal Residual method (GMRES) with Incomplete LU factorization (ILU) preconditioner. Step 3 Calculate ${\mathbf{q}}_{\text{non}-\text{Fourier}}$ based on Eq. 15. Step 4 Solve the Eq. 14 to update the $e_{\omega ,p}^{\text{eq}}$. The matrix is solved by using the biconjugate gradient stabilized method (BICGSTAB) with ILU preconditioner. Step 5 Repeat Step 2 to Step 5 until convergence. The iteration is converged when $\epsilon =\frac{\sqrt{{\sum }_i^{N_{\mathrm{cell}}}{(T_i^n-T_i^{n+1})}^2/N_{\mathrm{cell}}}}{T_{\max }}<{10}^{-5}$ and $\epsilon =\frac{\sqrt{{\sum }_i^{N_{\mathrm{cell}}}{({\left|\mathbf{q}\right|}_i^n-{\left|\mathbf{q}\right|}_i^{n+1})}^2/N_{\mathrm{cell}}}}{{\left|\mathbf{q}\right|}_{\max }}<{10}^{-3}$ is satisfied, where $N_{\mathrm{cell}}$ is the number of spatial cells. The temperature $T$ and heat flux $\mathbf{q}$ can be obtained according to Eq. 3.

Two frameworks of parallelization are widely used: the CPU parallelization based on the message passing interface (MPI) and the GPU parallelization. For the MPI parallelization, we adopt the direction-based strategy for the CPU parallelization of our numerical method. Since the number of directions may be limited, we also apply the band-based parallelization when the number of CPU cores exceeds the number of directions. In this strategy, the loops over the directions and bands are expanded and different CPU cores solve the equations in different directions simultaneously. The matrix in Step 2 is solved by Petsc serial package [43]. For Step 4, the matrix is solved by different CPU cores in parallel using the Hypre package [44]. The overall procedure of CPU paralleled version and the discussion on the parallelization strategy are shown in Supplementary Materials S1. We also adopt the GPU parallelization. For the GPU version, in Steps 2 and 4, the matrix is solved by the Viennacl package with GPU parallelization [45]. In all other steps, different spatial cells are solved simultaneously by different CUDA threads in a GPU. The overall procedure of GPU paralleled version is also shown in Supplementary Materials S1. The performance of parallelization is provided in Supplementary Materials S6.

We also verify the numerical implementation with analytical solutions and reference results, which is provided in Supplementary Material S7.

As will be shown later, this method has significant efficiency improvements compared with the previous implementation of the unstructured DOM [19]. The significant efficiency improvement comes from two major improvements of the present method compared with the implicit DOM: (i) the piece-wise linear spatial distribution of solutions of the present method largely reduces the convergent number of meshes compared with the piece-wise constant spatial distribution in implicit DOM (see Supplementary material S4 and S5); (ii) the synthetic iterative method [41] adopted in the present method largely reduces the number of iterations although slightly increases the computational time of the single iteration compared with the sequential iterative method (see Supplementary material S5). Apart from these two major improvements compared with the implicit DOM, the optimized parallelization (see Supplementary material S6) and band discretization (see Supplementary material S4 and S5) combined with the directional discretization in this method further ensure excellent efficiency.

3. Results

In this section, we evaluate the performance of the present method. We use the silicon system as an example. The phonon properties of silicon are obtained from our own first-principles calculations based on the anharmonic lattice dynamics method [28], [33]. In our first-principles calculations, 70 $\times$ 70 $\times$ 70 q-points are used to sample the Brillouin zone. As such, we have phonon properties for 70 $\times$ 70 $\times$ 70 $\times$ 6 phonon modes. The bulk thermal conductivity of silicon is 156.5 W/m-K, which is close to the value of the literature [28], [33]. By adopting our discretization scheme combined with directional discretization, we only need to sample 960 phonon modes in our subsequent calculations. In this section, we first validate the present method on the silicon thin film (in-plane), which has widely recognized experimental results. To demonstrate the success of the present method on nanoscale simulations, we then investigate the thermal transport of a typical 3-dimensional device: silicon fin field-effect transistor (FinFET). The present method can also be applied to other materials and devices. The excellent computational performance is emphasized by comparing it with the state-of-the-art implementation of unstructured DOM [19].

3.1. Validation against experimental results on silicon thin film

Due to the difficulty of the nanoscale thermal measurement, quantitative validation by experiments is rare [48]. The measurements on size-dependent in-plane thermal conductivity of silicon thin films are widely recognized experimental measurements [19], [46], [47]. We first validate our method using these experimental results [46], [47]. The schematic of in-plane thermal transport in the silicon thin film is shown in Fig. 1a. A uniform temperature gradient is imposed in a thin film with a thickness $L$ along the $x$ direction. Since the length in the $z$ direction is much larger than that in the $y$ direction and the $z$ direction is perpendicular to the transport direction, this problem can be simplified as a 2-dimensional problem (Fig. 1b). To simulate this problem, we extract a section of the thin film. Since the length in the $x$ direction is large, the periodic boundary condition (see Methods section) is applied at the left and right boundaries (Fig. 1b). Since the surfaces of experimental samples often have large roughness or are coated by an amorphous layer [49], the diffusely reflecting boundary condition, which is equivalent to the rough surface and the amorphous layer [35], [36], is applied at the top and bottom boundaries. After a convergence test, we adopt 15 phonon bands, 64 directions (i.e., sample 960 phonon modes), and 2900 triangular meshes to solve the phonon BTE for this problem.

Fig. 1.

Validation against experimental results on in-plane thermal transport in the silicon thin film. (a) The schematic of in-plane thermal transport in the silicon thin film with a thickness of $L$. (b) The simulation cell of in-plane thermal transport in the silicon thin film. A uniform temperature gradient $dT/dx$ is imposed in a thin film along the $x$ direction. (c) Comparison of in-plane thermal conductivity predicted by the present method and experimental results [46], [47].

It shows the in-plane thermal conductivity of the silicon thin film (Fig. 1c). The thermal conductivity is calculated as $q/\left|\nabla T\right|$, where $q$ is the heat flux and $\left|\nabla T\right|$ is the temperature gradient (see the Methods section). It can be seen that the in-plane thermal conductivity of the silicon thin film decreases with the thickness, as a result of the effects of boundary scattering [7]. When the thickness decreases, the boundary scattering, which impedes thermal transport, becomes more prominent. The predicted results using the present method are compared with the previous experimental results in Fig. 1c [46], [47]. Our prediction matches the experimental results very well. These results demonstrate that our simulation based on the present method not only captures the nanoscale effect, but also matches the experimental data without any fitting parameters, which shows good accuracy of the present method.

3.2. Temperature prediction of silicon FinFET

We then take the 3-dimensional transistor: silicon FinFET as an example to further demonstrate the performance of the present method. The structure and the boundary condition setup of the FinFET are shown in Fig. 2a, which is extracted from Ref. [50]. The thermalizing boundary is the boundary that is in contact with the metal electrode (source and drain) or away from the hot spot (substrate) [17], [51]. The thermalizing boundary is set as 300 K to mimic a test environment at room temperature [52]. The diffusely reflecting boundary describes the boundary contact with an amorphous layer [35], [36]. As such, we set the boundary that is in contact with the dielectric layer (amorphous silicon oxide) [50] as the diffusely reflecting boundary (as shown in Fig. 2a). The other boundaries are all set as specularly reflecting boundaries, which mimic the symmetric boundary between two devices [29], [34]. The hot spot is set as a semi-ellipse with two axles of $L_7$ and $L_8$ near the drain, which is typically discovered in an enhancement transistor [17]. The dimensionless geometrical parameters are presented in Table 1. We test the absolute values for these parameters at different scales, by multiplying the ratio scales of 1 nm, 10 nm, 100 nm, and 1 $\mathrm{\mu }$m (i.e., these cases have fin-width of 12 nm, 120 nm, 1.2 $\mathrm{\mu }$m and 12 $\mathrm{\mu }$m) for checking the performance of our method from the ballistic regime to the diffusive regime. The total volumetric heat generation rates $4\pi \sum _{\omega ,p}{\dot{q}}_{\omega ,p}$ inside the hot spot (See Methods section) are ${10}^{19},{10}^{17},{10}^{15},{10}^{13}\mathrm{W}/{\mathrm{m}}^3$ for fin-width of 12 nm, 120 nm, 1.2 $\mathrm{\mu }$m and 12 $\mathrm{\mu }$m respectively. These volumetric heat generation rates are chosen so that temperature profiles for different cases are the same if they are solved by the heat diffusion equation, in which we adopt the bulk thermal conductivity of silicon: 156.5 W/m-K (the result is shown in Fig. 2c). The mode-level heat generation rates are assumed to be uniformly distributed in different directions and proportional to the heat capacity for different bands, mimicking an equilibrium heat source [29]. The properties of the heat generation in this study are set for demonstration purposes. To capture the rigorous heat generation due to phonons emitted by hot electrons, the electron BTE considering electron-phonon coupling is required to solve simultaneously [2], [4], [39], [53]. After a convergence test, we adopt 15 phonon bands, 64 directions (i.e., sample 960 phonon modes) and 14,442 hexahedron meshes (The convergence test is provided in Supplementary material S4). The unstructured hexahedron meshes to discrete FinFET are shown in Fig. 2b as an example.

Fig. 2.

Temperature prediction of the silicon FinFET. (a) The structure, boundary conditions and the hot spot of the silicon FinFET. (b) An example of unstructured meshes. (c) Temperature distribution predicted by the macroscopic simulation. (d–h) Temperature distribution predicted by the present method for the phonon BTE with the fin-width of (d) 12 $\mathrm{\mu }$m, (e) 1.2 $\mathrm{\mu }$m, (f) 120 nm, and (h) 12 nm. Note that the color scale differs for each figure.

Table 1.

The dimensionless geometrical parameters of the FinFET.

$L_1$	$L_2$	$L_3$	$L_4$	$L_5$	$L_6$	$L_7$	$L_8$
60	30	12	50	12.5	50	15	10

The temperature profiles for different scales predicted by the present method are shown in Fig. 2d–h. When the size decreases, the difference between the results of the BTE simulation and the results of the heat diffusion simulation is greater. In the case of the 12 nm fin-width, the maximum temperature rise predicted by the BTE is 74 K and about 26 times greater than that predicted by the heat diffusion equation (Fig. 2h), which indicates significant non-Fourier effects. These non-Fourier effects arise when ballistic transport and boundary scattering, which impede thermal transport, become prominent at small sizes [7]. Higher temperature rise would limit electrical performance of nanoscale devices more seriously [3], which is crucial for understanding the self-heating effect. Although this result cannot be quantitatively validated with experimental data, such a trend has also been discovered in experiments qualitatively: when the size of the transistor is small, the temperature of the transistor is larger than that predicted by the heat diffusion equation [25]. The difference between the BTE simulation and the heat diffusion equation reduces with increasing size. When the fin-width is 12 $\mathrm{\mu }$m, the difference between the BTE simulation and the heat diffusion simulation is negligible, which indicates that the thermal transport is nearly diffusive. The small difference between the BTE simulation and the heat diffusion simulation in this large case indicates that the contribution of the extremely large mean free path phonons in silicon (See Supplementary Material S3) is also resolved by the present method. From the results above, one can see that full 3-dimensional nanoscale simulations from the ballistic regime to the diffusive regime are now possible with our method.

3.3. Computational performance of FinFET simulation

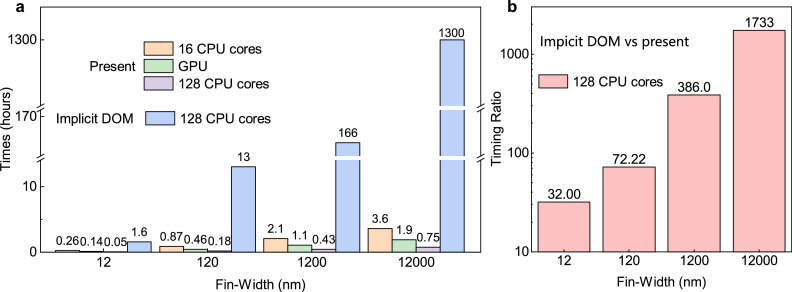
To make it possible for predictive thermal design of realistic materials and devices, simulation efficiency is vital. To demonstrate the excellent efficiency of the present method, the computational times of the above cases are summarized in Fig. 3. We test the performance on a cluster of Intel Xeon Scalable Cascade Lake 6248 CPU and a single NVIDIA GeForce RTX 3060. The computational times using 16 CPU cores, a single GPU, and 128 CPU cores are presented. In all cases, the simulation can be completed within several hours. It should be noted that larger computational cost is needed for more diffusive cases, due to the larger number of iterations needed to reach convergence [41]. In our GPU implementation, a full-scale thermal simulation of a 12 $\mathrm{\mu }$m FinFET, which is nearly diffusive, can be completed within 1.9 h. Since the NVIDIA GeForce RTX 3060 is a commonly used GPU in personal computers, we actually demonstrate that with the present method, it is feasible to perform an accurate nanoscale thermal simulation of the 3-dimensional problem using a single personal computer.

Fig. 3.

Computational time of the FinFET simulation. (a) The computational time of simulating the silicon FinFET by the present method and the implicit DOM [19], [27]. (b) The ratio of the computational time of the implicit DOM [19], [27] over the computational time of the present method.

To further demonstrate the excellent performance of the present method, we compare the computational time of the present method with a state-of-the-art implementation of the unstructured phonon BTE solver (implicit DOM) [19], [27]. The details of the previous implicit DOM solver are provided in Supplementary Material S2. In the previous study [19], the CPU parallelization of implicit DOM is discussed. We adopt the fastest strategy to do the parallelization for implicit DOM. The acceleration rate is comparable to that in the previous study (See Supplementary material S6). After convergence tests, we adopt 128 directions and 880,000 hexahedron meshes to do the simulation using implicit DOM. These numbers are on the same order as those used in the previous study for a 3-dimensional structure [19]. We still use 15 phonon bands (the same as in the present method) since previous studies adopt empirical models and the band discretization scheme for first-principles properties is lacking in implicit DOM. We provide the computational time of the implicit DOM when using 128 CPU cores. It can be seen that the computational time of the implicit DOM is much larger than that of the present method. The computational time for the largest size (12 $\mathrm{\mu }$m fin-width) is unaffordable due to the extremely slow convergence rate in the diffusive limit [19], [27]. For this case, we estimate this time by multiplying the time of one iteration for 880,000 spatial meshes by the number of iterations for the 14,000 meshes because the convergence rate is similar for different numbers of meshes for the same case. We also show the ratio of the computational time of the implicit DOM over the computational time of the present method. The implicit DOM takes 32 times to 1,733 times more computational time than our method. The 1,733 times faster computation for the nearly diffusive case is especially important since it makes the simulation of large sizes affordable and only requires less than one hour with 128 CPU cores. As such, the full 3-dimensional solution of phonon BTE from the ballistic to diffusive regime are very efficient with our method. Even larger cases fall in to diffusive regime and can be calculated with a heat diffusion equation solver.

Next we compare results of first-principles based phonon properties and empirical models to show the unique accuracy of first-principles based phonon properties. We choose two empirical models [54], [55], which are widely adopted in other literature [20], [27], [41]. The details of these two models are provided in Supplementary Material S3. The temperature field predicted by these models is shown in Fig. 4 bench-marked by the first-principles properties used in the present method. Comparing the temperature distribution profiles, it can be seen that Empirical Model 1 from Ref. [54] largely overestimates the temperature rise of the silicon FinFET. The maximum temperature rise predicted by Empirical Model 2 from Ref. [55] is more accurate, but still has a nearly 10% error compared with the first-principles phonon properties. The reason for the difference can be understood by the difference in the mean free path accumulated thermal conductivity and the mean free path accumulated heat capacity (Fig. S2). The model in Ref. [55] has very similar properties compared with the first-principles properties and could be a good approximation for silicon properties. The model in Ref. [54] shows a large difference in properties that may be due to the uncertainties in fitting or ignoring the contribution of optical phonons. Apart from the possible large error, the empirical model is limited to specific materials. The present method can both have good accuracy and be easily extended to other materials because of the generality of first-principles properties [33].

Fig. 4.

Comparison of temperature distribution predicted by BTE simulations with first-principles properties and empirical models. (a) Temperature distribution predicted by BTE simulation with first-principles properties. (b) Temperature distribution predicted by BTE simulation with empirical properties model in Ref. [54]. (c) Temperature distribution predicted by BTE simulation with empirical properties model in Ref. [55]. Note that the color scale differs for each figure.

4. Discussion

The present method adopts the framework of DOM, which is the representative framework of the deterministic method. Apart from the deterministic method, there are two other frameworks: the statistical Monte Carlo method (MC) [22] and a machine learning method (physics-informed neural networks) [23]. When discussing the deterministic method with the MC method and machine learning method, the efficiency of the deterministic method is sometimes thought to be shortcoming [22], [23]. The recently developed machine learning method also shows better efficiency compared with the implicit DOM [23]. However, the present method has demonstrated the excellent efficiency of the deterministic method. Simulating the complicated transistor structure using the present method is even much faster than training time in predicting toy problems using machine learning methods [23]. Also compared with the machine learning methods which have the risk of misconvergence [56], the present method can always converge to correct results. The deterministic method also has no statistical error in the MC method [22] and our method is also much faster than the previous MC method [22]. Additionally, for the device simulations, since many commercial electrical simulation packages adopt deterministic methods [52], the present method can be more easily integrated with these packages. Although some electron BTE solvers are based on MC methods, adopting deterministic methods for the phonon BTE also has the advantage of overcoming the convergence problem because of the absence of statistical error [57]. As such, the present method has many advantages over other frameworks and can potentially replace the current heat diffusion solver to act as a predictive thermal design tool for nanostructured materials and nanoscale devices.

Finally, we note that solving the matrix parallelly is the bottleneck to the overall efficiency of our method (See Supplementary Material S6). Since the present method is designed for unstructured meshes, the most stable method to solve the matrix in this method is the Generalized Minimal Residual method (GMRES) or biconjugate gradient stabilized method (BICGSTAB) with the incomplete LU factorization (ILU) preconditioner. A major limitation is the parallelization of the ILU preconditioner [58]. If an efficient parallel ILU preconditioner can be developed, the efficiency of the present method can be further improved.

5. Conclusion

In this study, we demonstrate an efficient and parameter-free computational method for nanoscale thermal simulation with the phonon BTE. In this method, we integrate the phonon properties from first-principles calculations into the phonon BTE solver and develop a suitable ensemble of advanced numerical methods for solving the phonon BTE. The accuracy of the method is demonstrated with the widely recognized experimental results: the in-plane thermal conductivity of silicon thin film. The results match the experimental data without any fitting parameters. The efficiency of the method is demonstrated in the full-scale thermal simulation of the 3-dimensional silicon FinFET with difference characteristic sizes, which can be completed within two hours on a personal computer. The computational time can be reduced by thousands of times compared with a state-of-the-art unstructured method. Our method makes it possible to achieve the predictive design of realistic nanostructures for the desired thermal conductivity. It also enables accurate resolution of the temperature profiles at the transistor level, which helps in better understanding the self-heating effect of electronics.

During the peer review process, we noticed a thorough review of the computation of submicron thermal transport with the phonon BTE by Mazumder [59]. As pointed out in this review, providing better phonon properties for the phonon BTE, solving the phonon BTE for realistic 3D device structures, and making better use of advanced parallel processing paradigms are major challenges that require further research [59]. We believe this work provides a solution to address these challenges.

Data availability

The data that support the findings of this study are available upon reasonable request from the authors.

Declaration of competing interest

The authors declare that they have no conflicts of interest in this work.

Biographies

Yue Hu is currently a Ph.D. candidate under the supervision of Prof. Hua Bao, at Shanghai Jiao Tong University. He received his B.S. from Xi’an Jiaotong University, China, in 2018. His research interests focus on non-equilibrium thermal transport and the Boltzmann transport equation.

Hua Bao(BRID: 08558.00.92907) is an associate professor at University of Michigan-Shanghai Jiao Tong University Joint Institute. He received his B.S. in physics from Tsinghua University, China, in 2006, and his Ph.D. in mechanical engineering from Purdue University in 2012. His research interests are in micro/nanoscale thermal energy transport, thermophysical properties, and applications on thermal management and energy conversion.

Appendix A. Supplementary materials

Supplementary Data S1

Supplementary Raw Research Data. This is open data under the CC BY license http://creativecommons.org/licenses/by/4.0/