Significance
Numerous diseases are associated with changes in the blood plasma viscosity (PV). Measuring these is time consuming and typically requires significant volumes of plasma not always available. Here, we show that Brillouin light scattering (BLS) spectroscopy—a technique that probes the propagation and attenuation of high-frequency longitudinal acoustic modes—can identify changes in the viscosity from microliter-sized volumes in a fraction of a second. This is demonstrated for plasma from COVID-19 (CoV) patients that exhibited an elevated PV. It is also shown that the viscosity measured using BLS contains additional unique information that can discern the abundance of suspensions which may be of diagnostic value, that appear to be more present in CoV patients with severe disease progressions.
Keywords: Brillouin light scattering, longitudinal viscosity, blood plasma viscosity, COVID-19
Abstract
Blood plasma viscosity (PV) is an established biomarker for numerous diseases. Measurement of the shear PV using conventional rheological techniques is, however, time consuming and requires significant plasma volumes. Here, we show that Brillouin light scattering (BLS) and angle-resolved spectroscopy measurements of the longitudinal PV from microliter-sized plasma volumes can serve as a proxy for the shear PV measured using conventional viscometers. This is not trivial given the distinct frequency regime probed and the longitudinal viscosity, a combination of the shear and bulk viscosity, representing a unique material property on account of the latter. We demonstrate this for plasma from healthy persons and patients suffering from different severities of COVID-19 (CoV), which has been associated with an increased shear PV. We further show that the additional information contained in the BLS-measured effective longitudinal PV and its temperature scaling can provide unique insight into the chemical constituents and physical properties of plasma that can be of diagnostic value. In particular, we find that changes in the effective longitudinal viscosity are consistent with an increased suspension concentration in CoV patient samples at elevated temperatures that is correlated with disease severity and progression. This is supported by results from rapid BLS spatial-mapping, angle-resolved BLS measurements, changes in the elastic scattering, and anomalies in the temperature scaling of the shear viscosity. Finally, we introduce a compact BLS probe to rapidly perform measurements in plastic transport tubes. Our results open a broad avenue for PV diagnostics based on the high-frequency effective longitudinal PV and show that BLS can provide a means for its implementation.
A major component of blood (~55% by volume) is blood plasma, a semitransparent dense electrolyte and protein solution. Changes in the viscosity of plasma are known indicators of numerous pathologies; however, they are less frequently used in diagnostics owing in part to large patient variability (1). Plasma is often assumed to be a Newtonian fluid (have a shear-rate independent viscosity); however, studies have revealed elastic properties with relaxation times on the order of milliseconds, attributed to constituent proteins (2). While these relaxation times might be too fast to affect macroscopic fluid dynamics under most physiological conditions, the viscoelastic properties at short time scales may serve as a measure for the abundance of soluble and insoluble constituents to which they can be acutely sensitive. It is challenging to probe viscoelastic properties at such short time scales using conventional viscometers and shear-plate rheometers (3, 4). One technique that probes at very short time scales, and has been receiving renewed interest for biomedical applications, is Brillouin light scattering (BLS) spectroscopy which measures the hypersonic longitudinal sound velocity and attenuation (5–7).
BLS Spectroscopy.
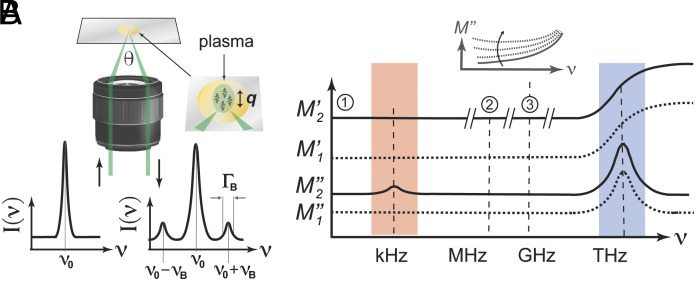
BLS spectroscopy measures the hypersonic velocity and attenuation in a label-free all-optical fashion via the inelastic scattering of a single-frequency probing laser from collective molecular vibrations (5–7). The measured spectrum in a BLS experiment consists of an elastic scattering peak straddled by two Brillouin scattering peaks (centered at frequencies and relative to the elastic peak) that result from the creation and annihilation of longitudinal acoustic phonons (5) (Fig. 1A). From the fitted peak positions and linewidths of these peaks, parameters such as the longitudinal elastic modulus, longitudinal acoustic attenuation, and effective longitudinal viscosity can be calculated (Materials and Methods). Two important aspects differentiate BLS-derived viscoelastic properties from those obtained using conventional viscometers and rheometers.
Fig. 1.
Brillouin light scattering (BLS) in pure liquids and blood plasma. (A) BLS spectroscopy measurement geometry and spectrum from an incident laser with frequency . The BLS peaks are at , with linewidth (). Probed phonon wavevector = q. (B) Sketch of the elastic and viscous longitudinal moduli frequency dispersion in a pure liquid () and what might be expected for blood plasma (). ①, ② and ② indicate the frequencies probed using quasistatic techniques, acoustic spectroscopy, and BLS. No discernable increase in is shown at kHz frequencies (shaded red) given that this is likely small compared to the absolute value of ; however, depending on the nature of the relaxation process, this may be significant. Inset: Expected change of the frequency dependence of at ~MHz–GHz frequencies for increasing strength of the low-frequency relaxation process.
First, in fluids, BLS typically probes the longitudinal viscosity (5), which depends not only on the shear but also the compressive properties, and is given by:
| [1] |
Here, is the shear viscosity, and the bulk (also referred to as volume, dilatational, or second) viscosity (8). Despite usually being about the same magnitude for fluids as , is a distinct material property dependent also on the constituent chemistry, such as the abundance and hydrostatic properties of solutes and suspensions (7). While usually not being directly relevant for describing macroscopic fluid dynamics, it can become relevant in turbulent flow and provide unique insight into fluid composition. can also be measured using acoustic spectroscopy (AS) at lower (~MHz) frequencies (9), that, unlike BLS, requires significantly larger sample volumes (9) (>15 mL compared to <100 µL for BLS), making it challenging for routine analysis of scarcely available biofluids. (SI Appendix, Table S1 for a list of differences between BLS and AS).
Second, BLS measures the viscoelastic properties at picosecond-nanosecond time scales—i.e., at the GHz frequencies of the probed phonons. To appreciate how this can differ from measurements at lower frequencies in liquids, Fig. 1B shows a schematic of the frequency dependence of the complex longitudinal modulus () in a pure fluid () and what might be expected in blood plasma (). Here, and are the elastic (storage) and viscous (loss) contributions, respectively, which can be decomposed into contributions from the bulk () and shear () properties: for the elastic and Eq. 1 for the viscous components (10). The scenario for plasma can be expected to be more complex than that of a pure liquid, on account of its different solid-like suspensions (proteins and aggregates thereof) and their interactions with each other and water. These could, e.g., give rise to concentration fluctuations that can couple with density fluctuations and potentially also directly with dielectric fluctuations that significantly modify the viscoelastic (dispersion) landscape. While different scenarios are possible with distinct origins of the relaxation processes, some features can be depicted on the basis that each dispersion is associated with absorption (Kramers–Kronig) and the high rigidity of water. In both a pure fluid and plasma, BLS can be presumed to probe the lower asymptotic limit of fast (>THz) relaxation processes. In a pure fluid, which does not support shear modes, the BLS-measured would be comparable to that at lower frequencies (9), and is expected to scale linearly with frequency (asymptotic limit of fast α-relaxation processes). Adding a solute can result in viscoelastic shear relaxation induced by the solute network (11) at lower frequencies. Since any such shear deformations would be included in longitudinal acoustic modes (10), these would be manifested in both elastic and viscous longitudinal properties. This contribution to the longitudinal elastic modulus () would, however, be subtle, to the point that it may in practice be undiscernible (12), on account of the dominant bulk elastic modulus. As such no increase in at kHz frequencies is shown in Fig. 1B. Should there, however, exist a structural relaxation (13) at lower frequencies that also affects , one could have a more pronounced change in the BLS-measured , and a significant contribution to the longitudinal attenuation that counters the increasing contribution from the faster (higher frequency) relaxation process (inset Fig. 1B). The dispersion for blood plasma is still poorly understood (it is, e.g., unclear what frequency structural relaxations occur), but it has been shown to undergo significant viscoelastic relaxation in the kHz-regime (2). Ultrasonic measurements at MHz frequencies of the longitudinal properties have also shown the attenuation scales with frequency as (14): (slower than of pure liquids). This notable departure from hydrodynamic behavior could hint at a structural relaxation at < MHz frequencies. Based on the above, a slow (~kHz) relaxation process is included in the schematic for the plasma dispersion () in Fig. 1B, noting that its strength and characteristics are as yet uncertain. It is almost certainly the case that the dispersion for plasma is significantly more complex than depicted, with a spectrum of relaxation times dependent on its many constituents and their interactions, as well as how the sample is prepared, but this paints a simple picture of what one might expect.
From the above, it should also be clear that any quantitative relation between a viscometer-measured and a BLS-measured would be phenomenological, given the probed times scales are many decades apart (and we have little idea of what is going on in between them). We note also that while both quasistatic shear viscosities and BLS-measured longitudinal viscosities may be expected [and have been shown (11, 15)] to depend on the volume fraction of inclusions, they in general will do so in a functionally independent manner, on account of the above.
COVID and PV.
Already early on in the COVID-19 (CoV) pandemic, it was reported that acute CoV infection is often associated with an increase in shear PV (15). This was largely attributed to elevated fibrinogen levels in response to infection (16, 17). It has since become apparent that while CoV infection manifests itself as a respiratory disease, its lethality usually stems from the disruption of coagulation processes (18). Indeed, almost all CoV critically ill ICU patients suffer from some form of clotting/lysis anomaly as diagnosed by Fibrin Degradation Product (FDP) blood values (19). This insight—addressing it as a vascular/endothelial disease and coagulopathy (20, 21)—shifted treatment strategies in ICUs around the world saving many lives.
Despite the clear markers of a coagulopathy, the puzzling thing that remained was that pathological analysis in many cases did not reveal the gross clots expected from blood chemistry (D-dimer) analysis (22). It has been suggested that this is a result of the macrophage attack (23), and gradual infusion of thrombin during infection into the pulmonary circulation (24), resulting in soluble fibrin monomer complexes (SF) in the bloodstream (and thereby elevated FDP values). High levels of circulating SF may then lead to the formation of insoluble fibrin protofibrils and subsequently microclots (24), which have been observed in CoV, as well as Long-CoV, patients (25). The mobility of such microclots and their ability to cause blockage in narrow vasculature, together with delayed fibrinolytic shutdown (26), may explain the multiple organ failure observed in CoV patients (27). A means for rapidly assessing changes in the physical properties of blood due to soluble or insoluble protein constituents would thus be highly desirable for deciding and developing optimal treatment strategies and monitoring their effectiveness.
Considering the above, we here investigate whether the effective longitudinal PV measured using BLS can detect differences in the plasma between patients with different disease outcomes, how these scale with respect to the shear properties, what these might tell us about changes in the viscoelastic relaxation spectrum, and whether these can provide additional information indicative of disease progression.
Results
Blood plasma from 39 hospitalized patients with PCR-confirmed SARS-CoV-2 infection and 20 PCR-confirmed SARS-CoV-2-negative and otherwise healthy persons was obtained and prepared as described in Materials and Methods. The CoV-positive samples were classed based on the World Health Organization (WHO) clinical progression scale, which is a measure of the implemented medical resources and disease trajectory (28) (Materials and Methods). Given that PV is sensitive to a multitude of pathologies (1) and lifestyle choices (29), we focus on a subset of samples from nonsmokers with none of the reported underlying conditions (Materials and Methods and SI Appendix, Table S2), as it is unclear how these would perturb results. For these, temperature sweep BLS and shear viscosity measurements were performed on a custom-built BLS microscope and a commercial rolling-ball viscometer, respectively, installed directly in a hospital blood bank (Materials and Methods). For BLS measurements, the fitted frequency shift and linewidth after deconvolution, together with the separately measured refractive index and estimated mass density, were used to calculate the shear and longitudinal viscoelastic parameters (Materials and Methods). We found no correlation between viscoelastic parameters and patient age or gender (SI Appendix, Fig. S1), consistent with previous shear viscosity studies on healthy plasma (29).
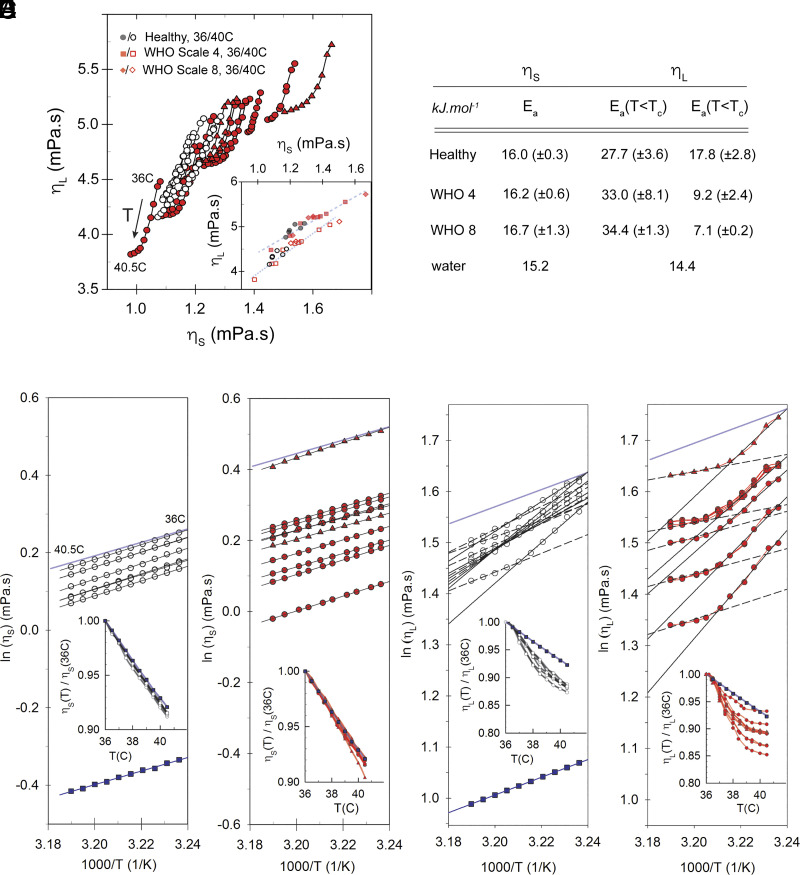
While plasma from CoV patients revealed an elevated mean shear and effective longitudinal viscosity compared to that of healthy persons (SI Appendix, Table S3 and SI Appendix, Fig. S2), patient–patient variability would limit its stand-alone diagnostic value on an individual basis. We thus in each case focus on the temperature-scaling behavior between 36 and 40.5 °C. Plotting the shear viscosity measured using a rolling-ball viscometer, as a function of the BLS-measured effective longitudinal viscosity for healthy and CoV patient plasma at different temperatures, it is apparent that the two viscosities both decrease with increasing temperature but in a functionally distinct manner (inset Fig. 2C and SI Appendix, Fig. S2B). We note that the BLS measurements were performed with low-NA and are spatial averages over many positions, and the propagated uncertainties in the presented values are smaller than the symbol size (Materials and Methods and SI Appendix, Fig. S3). We may estimate an effective activation energy for viscous flow assuming an Arrhenius-like relation (where J.mol−1.K−1 is the gas constant) by plotting with respect to inverse temperature (Fig. 2 B–D). While we cannot rule out a slightly distinct activation at lower and higher temperatures, within the measured temperature range, our data are reasonably well described by a single activation energy. One may make a similar Arrhenius plot for the effective longitudinal viscosity (Fig. 2 E and F). This resembles a much more fragile liquid and can be described by two distinct activation energies below and above ~38 °C (Fig. 2B). While obtained from has a conceivable biophysical relevance, that of obtained from is less obvious. Nevertheless, given the notable deviations between CoV and healthy plasma, it may serve as a potential characteristic prognostic/diagnostic parameter.
Fig. 2.
Temperature dependence of shear and effective longitudinal viscosities. (A) BLS-measured effective longitudinal viscosity plotted as a function of viscometer-measured shear viscosity . ○ =healthy, ● = CoV WHO scale 4, ▲ = CoV WHO scale 8. Inset: Same data shown for T = 40.5 °C (solid symbols) and T = 36 °C (open symbols) (B) Mean activation energy of measured shear and effective longitudinal viscosity derived from their respective temperature scaling (SD in parenthesis). (C–F) Arrhenius plots of (C–D) and (E–F), for healthy (open circles) and CoV patient (red circles and triangles) plasma. Also shown are values for distilled water (blue squares). The light blue shaded line in (C–F) shows slope for distilled water in each case. Insets: Respective viscosities normalized to values at T = 36 °C. All BLS measurements are in backscattering geometry with low NA (Materials and Methods).
We can probe the frequency scaling of the effective longitudinal viscosity over a narrow frequency range, via angle-resolved BLS measurements, by tuning the measured scattering wavevector (and thereby the frequency). This is possible using a high Numerical Aperture (NA) objective and spatially masking different segments of the detection path (30) (Materials and Methods). Doing so, we perform measurements on 3 healthy and 3 WHO scale 8 CoV patient plasma samples. If at the probed frequency () we are exclusively sensitive to an α-relaxation process at a much higher frequency () , the longitudinal acoustic attenuation coefficient would scale as (and the longitudinal loss modulus as ) with . Since , the linewidth would scale with frequency as , where is the refractive index, and the scattering angle (180° = backscattering). Plots of vs. would thus have a slope and reveal deviations from (expected for single relaxation time in asymptotic limit). Deviations from this could be indicative of a significant (structural) relaxation process at lower frequencies and/or a more complex relaxation spectrum at higher frequencies. In Fig. 3A, we show measurements for six samples at 36 °C. Both healthy and WHO scale 8 CoV patient plasma exhibit a negative slope (), with two of the 3 WHO scale 8 CoV patient samples having a steeper slope, indicative of a larger deviation from quadratic frequency scaling of the longitudinal attenuation coefficient. In the inset, we show a plot of as a function of , suggesting no discernable changes in the elastic properties over the probed frequency range and linear acoustic behavior. Performing the same measurements at 39 °C (Fig. 3B) shows the slope of to be notably more pronounced, corresponding to a decrease in . This may suggest the additional presence or increased strength of slower relaxation process(es) in WHO scale 8 CoV samples at elevated temperatures (viz. Fig. 1B, inset). These could result from enhanced viscous shear relaxation of the solute network due to increased presence of solid-like suspensions at higher temperatures (e.g., through reduced solubility/miscibility or aggregation). However, such an effect alone would, as mentioned above, expected to be small (given the magnitude of longitudinal moduli), and the notable change in the longitudinal attenuation could suggest structural changes associated with lower characteristic frequencies.
Fig. 3.
Anomalous dispersion, elastic scattering, and shear PV temperature scaling of CoV patient plasma. (A) Plot of as a function of measured at different scattering wavevectors () for healthy and CoV WHO scale 8 patient plasma (open symbols = healthy; solid symbols = CoV) at T = 36 °C. The slopes are given by , where is the frequency exponent of the attenuation coefficient (Main Text). Fitted slopes of the healthy plasma samples are −0.143, −0.150, and −0.123, whereas those of CoV patient samples are −0.321, −0.305, and −0.157, consistent with a larger deviation from a pure fluid behavior. Inset: as a function of for the same samples suggesting linear acoustic behavior. (B) Same measurements performed at T = 39 °C (slope = −0.162, −0.136, and −0.124 for healthy patient samples and −0.496, −0.440, and −0.202 for CoV WHO scale 8 patient samples). (C) Elastic scattering peak intensity (normalized to value at T = 36 °C) as a function of temperature for the same samples. (D) Temperature-dependent shear PV () of three CoV WHO scale 8 patient samples suggesting a discontinuity in the slope at 38C. The final (rightmost) panel is from a patient who also suffered from coronary artery disease and diabetes and was thus excluded from previous analyses (Figs. 2 and 3), but is included here to illustrate the increased effect for higher . Also shown are suspension-fraction concentrations () that could result in the observed temperature dependence (Main text).
We note that the anomalous deviation from quadratic scaling of the attenuation observed in all plasma samples would also result in a slight sample-specific correction to the calculated which assumes hydrodynamic behavior (). As such the calculated should more correctly be referred to as an effective longitudinal viscosity.
The presence of a suspension may also manifest itself by an increase in the elastic scattering. Elastic scattering is associated with thermally diffusive modes (Rayleigh scattering) and other collective relaxation processes; however, it is usually dominated by specular reflections in the optical setup and Tyndall scattering in the sample (31). While specular reflection in the optical setup is sample independent, Tyndall scattering can be expected to increase with the presence of a solid-like suspension or aggregate. Plotting the normalized elastic scattering intensity as a function of temperature (Fig. 3C) reveals that at elevated temperatures (above 38 °C), there is a notable increase in the elastic backscattering for the WHO scale 8 CoV patient samples, consistent with an increase in solid-like constituents at elevated temperatures. There is a possible discontinuity in the slope (at around 38 °C) for the CoV patient samples; however, based on the sparsity of the data, this cannot be statistically concluded. This increase, which can be interpreted as an indirect measure of an increase in the optical opacity of the sample, may result in BLS line broadening by virtue of multiple scattering; however, this effect is expected to not be too significant given that we are performing confocal measurements not very deep inside the sample (close to the sample glass-interface).
Interestingly, a closer inspection of the temperature dependence of the shear viscosity of CoV WHO scale 8 plasma samples also suggests that there may be a kink in the temperature-scaling at around 38 to 39 °C, above which the slope is smaller (Fig. 3D), consistent with a change in the physical properties occurring at these temperatures. This appears to also be more significant for samples with a higher (Fig. 3D). We note that the last panel in Fig. 3D represents a sample excluded from previous analyses on account of having a copathology (coronary artery disease and diabetes) but is shown here to illustrate the more pronounced presence of this feature in samples with a higher .
To investigate whether any sizable suspensions might be present in the CoV patient plasma, we perform fast spatial BLS scans of healthy and CoV patient samples (Materials and Methods). We observe a spatial heterogeneity in several of the latter, marked by a punctuated presence of distinct viscoelastic features, that become more pronounced at elevated temperatures. This is shown in Fig. 4 A and B, where we plot the loss tangent defined as . In contrast to and , should be independent of mass density, and (given our observations in Fig. 3 A and B) have a weaker (sublinear) dependence on and hence refractive index (compared to a linear and superlinear dependence of and ). We note that due to diffusion and finite voxel dwell times in our scans, these spatial maps are not representative of the absolute size of such heterogeneities (but still indicative of their relative size at the same temperature), and by extension the values will not be a true quantitative measure of their viscoelastic properties (Materials and Methods).
Fig. 4.
(A) Confocal BLS spatial maps of the loss tangent () in 3 samples from healthy (open circles) and CoV patients with WHO Scale 4 (solid red circles) and 8 (solid red triangles), showing an increased heterogeneous viscoelastic landscape in CoV patients that is more pronounced at elevated temperatures. Scan in each case is 200 × 200 µm. (B) Quantification of scans showing the presence of viscoelastically distinct regions in CoV patient samples (T = 36 °C). (C) Collated values of the product , which would increase with increasing suspension-fraction concentration (Main Text), calculated as the mean value of spatial scans on respective samples. Boxes indicate interquartile ranges with median line, and whiskers are 5%/95% range. Statistics were performed using the unpaired t test with Welch’s correction (*P < 0.05, **P < 0.01, and ***P < 0.001).
The data presented in Fig. 4B are averages of many individual measurements over ~µm-mm sized volumes (Materials and Methods). As such, the effective measured complex longitudinal moduli of plasma containing solid-like constituents with a distinct effective modulus , may be written as a weighted average: , where is the solid-constituent volume fraction and the effective modulus of the plasma (water, electrolytes, nonaggregated proteins, etc.) in their absence. This is simply a statistical average [independent of the mixing law (6, 7, 32)] given the apparent size of the inclusions, and values of and should also be seen as effective rather than true values for the constituents. It follows that at a given temperature the spatial average will scale linearly with respect to as where superscripts “a” and “0” denote the respective (effective) values for the solid-constituents and for the plasma in their absence. Collated values of for CoV (WHO scale 8) and healthy patient plasma are shown in Fig. 4C, revealing that is notably larger for plasma from CoV WHO scale 8 patients than both that of WHO scale 4 patients and healthy patients. Interestingly, the difference seems to be more pronounced at higher temperatures, consistent with an increased solid-like constituent volume fraction at higher temperatures, as is suggested also by our observations for the frequency scaling (Fig. 3 A and B) and elastic scattering (Fig. 3C) data.
To check whether an increased solid fraction at higher temperatures could explain the observed shear and bulk viscosity–temperature scaling, we theoretically consider the effect of solid-like suspensions on the scaling of the two viscosities. The shear viscosity can to a first approximation be assumed to depend on suspension concentration as (33):
| [2] |
where is the shear viscosity in the absence of the suspension. The precise functional dependence will in general be more complicated, and depend on the suspension size, properties of the solvent, maximum volume fraction, etc. (33); however, this (Einstein approximation) is a reasonable functional approximation at the relevant time scales of the measured shear viscosity. Assuming the contribution from suspensions only becomes significant in CoV patient samples, we take sample averaged values of the shear viscosity from healthy plasma samples for and calculate for different . Based on the monotonic increase in the elastic scattering for CoV patient samples above 38 to 39 °C (Fig. 3C), we can as a first approximation take:
| [3] |
Here, the parameter will determine the rate of suspension change with respect to temperature. The scaling with respect to is motivated by the observation that the change in is more pronounced in samples with a stronger shear viscosity–temperature dependence (Fig. 3D).
The effect of a suspension on the bulk viscosity, while the subject of several theoretical investigations, is less trivial and will depend on their bulk properties relative to the solvent (34, 35). For solid-like inclusions, we may as a first approximation write (34):
| [4] |
where is the bulk viscosity in the absence of solid-like inclusions. Eq. 4 is derived for low frequencies and its extension to the high-frequency regime is not trivial, however, for low inclusion concentrations a linear dependence on inclusion concentration has been reported for the longitudinal viscosity at GHz frequencies (15), and it may thus serve as a first approximation. Taking sample averaged values of the effective bulk viscosity (estimated via Eq. 1) from healthy plasma samples for and using the same temperature-dependent suspension volume fraction as for the shear viscosity (Eq. 3), we estimate for different values of . The temperature scaling of the shear and bulk viscosity calculated from Eqs. 1–4 for different values of is shown in Fig. 5 A and B. The former reveals a discontinuity in the temperature scaling of akin to that observed in Fig. 3D. A plot of the predicted scaling of with respect to for different values of (Fig. 5C), is seen to predict a saturation of with respect to as is observed in CoV plasma samples (Fig. 2A), which becomes more pronounced with increasing . We note that these qualitative features are also observed if one assumes a functionally different scaling behavior with respect to suspension concentration (Eqs. 2 and 4). While this simple semi-empirical picture does not explicitly describe any structural changes, it does show that the observed temperature scaling can arise from a solid-like fraction that increases linearly with temperature at a rate that is more pronounced in CoV patient plasma.
Fig. 5.
Scaling of shear, bulk, and effective longitudinal viscosity for increasing suspension concentrations. (A) and (B): Shear and bulk viscosity calculated using Eqs. 2 and 4 with the suspension concentration given by Eq. 3, for increasing values of the parameter (Main text). Inset: Heat map of respective plots showing the trajectory of . (C): Calculated as a function of for increasing values of . Also shown are corresponding experimental results for healthy (open circles), and CoV patients with WHO Scale 4 (solid red circles) and 8 (solid red triangles).
To facilitate easy measurements on plasma, we have developed a custom fiber-coupled probe (depicted in Fig. 6 A and described in Materials and Methods). Using this, it is possible to perform measurements in standard plastic transport tubes by immersing a stainless-steel probe-tip in the plasma (Materials and Methods) and thus remove the need for a bulky microscope-frame and time-consuming sample preparation steps (pipetting on glass slides and focusing). The obtained BLS frequency shift using this probe is in good agreement with that obtained using our conventional low-NA confocal setup (Fig. 6B), although we observe a slight offset in the linewidth (Fig. 6C). This offset which persists even after spectral deconvolution is attributed to the effectively larger excitation/detection NA of the probe, which will result in spectral broadening (36), and may be corrected for by applying a constant offset (Materials and Methods).
Fig. 6.
Hand-held plasma measurement probe. (A): Schematic of fiber-coupled Brillouin light scattering (BLS) probe for rapid measurement of blood plasma directly in plastic transport tubes (not to scale). Measurement between the sample and a calibration (reference) sample can be controlled via mechanical shutters and adjustment of half-wave plate (). PBS = polarizing beam splitter, VIPA = virtual imaged phased array, SM = single mode, = quarter-wave plate. (B) and (C): Plot of fitted BLS frequency shift () and linewidth () obtained on 20 plasma samples using the probe (vertical axis) compared to what is obtained using a conventional low-NA confocal BLS microscope (deconvolved). While the former are in good agreement, there is a constant offset in the latter that needs to be corrected for (Main Text).
Discussion
We present a study of the BLS-measured effective longitudinal viscosity of CoV-19 patient blood plasma with different disease outcomes and compared these to the viscometer-measured shear viscosity . We find can serve as a proxy for the viscometer-measured but observe no clear sample independent proportionality between the two, consistent with representing an independent material property. Our results suggest that BLS may be used to assess increased PV; however, quantitative comparisons to conventional PV measurements should be approached with caution. Our results also show that although increased and may be indicative of CoV infection severity, patient–patient variability may limit their stand-alone diagnostic usefulness.
Interestingly, we find that at temperatures above ~38 °C, exhibits a saturation behavior which is more pronounced in severe CoV patient samples, that is also accompanied by a possible kink in the temperature scaling of . A simple theoretical description of the scaling of and with respect to suspension concentration shows that this can result if there is an increase in suspension concentration above ~38 °C in severe CoV patient samples. This is supported by BLS confocal maps which reveal >micron-sized spatial heterogeneities in CoV patient plasma absent in healthy patient samples, that increase at elevated temperatures, and are accompanied by an increase in the elastic scattering cross-section. Measurements of the frequency scaling of by angle-resolved BLS also may suggest the existence of more pronounced longer relaxation processes in CoV patient samples at elevated temperatures, related to an increased suspension concentration. We note that we cannot rule out if rather than an increasing abundance of inclusions, there is a change in mass density, structure or size of the inclusions with increasing temperature. This is, however, less likely, given that their sizes do not appear to change significantly between CoV WHO scale 4 and scale 8 samples or as a function of temperature (Fig. 4A). To this end, q-dependent quasielastic dynamic light scattering studies (37) may shed more light.
Our results here suggest that the dynamic physical/structural and chemical properties of plasma are significantly more complicated than those of a simple liquid and that these may be intricately tied to pathologies such as CoV. From a physical perspective, the observed deviation from hydrodynamic behavior can have different origins (38, 39). is notably larger than water (SI Appendix, Fig. S4), consistent with inclusions being larger than the probed wavelength (15), as they are indeed seen to be (Fig. 4A). Given that we do not see any significant dispersion in , we can assume that we are not in the immediate vicinity of any relaxation processes. The decrease of with frequency (wavevector) can suggest that the probed BLS frequency is above a structural relaxation frequency, which is consistent with the notably larger values of M’ relative to water. The increase in with increasing probing length (1/q) would also be suggestive of nonlocality, given at large q the values for healthy and CoV patient samples are more comparable. Our results appear to suggest the existence of something akin to a Lower Critical Solution Temperature (LCST) in CoV plasma samples, above which the miscibility is altered. While our observations might be qualitatively described by a simple model based on the increasing abundance of inclusions, this does not account for any changes in chemistry (e.g., changes in pH which can affect screening and ultimately hydrodynamic modes), nor structural relaxation processes at sub-GHz frequencies which some of our observations are suggestive of. Furthermore, it should also be noted that scattering from heterogeneities larger than the phonon wavelength can also lead to additional broadening of the BLS peak that is not associated with multiple-scattering, and compromise the measurement of the true longitudinal viscosity (6) which may need to be considered.
From a chemical perspective, while a significant increase of FDPs can conceivably result in viscoelastic changes, these would be too small in size to explain the observed spatial heterogeneities, and would not explain the lack of any significant hysteresis in up–down temperature sweeps observed (which also rule out the denaturing of proteins). Our observations are also somewhat surprising given that our samples were collected and stored in anticoagulation tubes (Materials and Methods), although reports have hinted at the reduced effectiveness of anticoagulants in CoV patients (40, 41). While ultrastructural and biochemical studies on suspensions is still needed, one can speculate whether the observed heterogeneities might be related to cross-linked microfibrin/fibrin microclots reported to exist in CoV patient samples (42). Should this be the case this would suggest that the balance between increased fibrin cross-linking (clot formation) and the increased dissociation rate with increasing temperature (43) is perturbed in CoV patient plasma. To this end, BLS temperature-scaling measurements, in addition to potentially providing a means of assessing CoV severity, could also serve as a useful tool for exploring the viability of different drugs in mitigating clot formation. Given the persistence of cross-linked fibrin aggregates and microclots also in Long-CoV patient plasma (42), a means of quantitatively assessing their abundance would be of prognostic and diagnostic value.
While the last decade has seen significant technological strides in BLS spectrometers for life-science applications (44), the field has largely focused on the more easily obtainable longitudinal storage modulus. There is, however, growing awareness that changes in the longitudinal viscosity might offer a clearer indicator of structural-physical changes in soft matter (32, 45). While the linewidth is more challenging to obtain using finite NA optics, it can be estimated using low NA measurements or accounting for the induced broadening due to the finite NA (46). Unlike the longitudinal storage modulus, which will in pure liquids be given by the bulk modulus (and often dominated by this in soft matter (47)), the contribution of shear and bulk components to are on roughly equal footing: with values of for different fluids of the same order of magnitude as .
BLS has numerous desirable features including its nondestructive all-optical label-free nature, fast acquisition times (<second), high sensitivity/repeatability, and small required sample volumes (~microliter). The practical limitations associated with accurately calculating viscoelastic parameters are for the most part surmountable. To serve as a rapid diagnostic/prognostic tool, one is thus primarily limited by the need for separating plasma from erythrocytes. For this, the combination with existing techniques based on, e.g., commercial plasmapheresis-devices, or separation using standing acoustic waves (48), may be envisioned for real-time monitoring. Together with progress in BLS spectrometer miniaturization (49) and compact probes (50) optimized for fluid measurements (introduced here), this may allow for the realization of instruments suitable for routine point-of-care/ICU applications to asses disease criticality. While our current approach employed spontaneous BLS, we note that stimulated BLS (51–54) can offer faster acquisition times and better spectral resolution, albeit at the expense of currently still more elaborate and costly instrumentation.
Finally, performing correlative studies with changes in erythrocyte deformability (which have been associated with CoV infection and extended CoV symptoms (55)) may also give fundamental mechanistic insight into the role that the longitudinal PV plays in disease progression.
Materials and Methods
Blood Plasma.
Patient age ranged from 32 to 78 y (mean 61 y, median 62 y), with a male to female ratio of approximately 2:1 (SI Appendix, Table S2). Of the 39 CoV patients, 18 were WHO scale 4 (no oxygen therapy), 2 were WHO scale 5 (oxygen by mask), and 19 were WHO scale 8 (intubated/mechanical ventilation) (28). In addition to age and gender, body mass index (BMI) on admittance to the hospital, the 28- and 90-d mortality, blood pressure/hypertension, and underlying conditions including diabetes, coronary heart disease, chronic heart failure, chronic renal failure, immunosuppression, thyroid disorders, chronic lung diseases, active hematological diseases, active cancers, as well as whether they were active smokers, were recorded. A significantly larger fraction of WHO scale 8 patients than WHO scale 4 to 5 patients had one or more of these underlying conditions (84% vs. 35%), and a notably larger fraction also exhibited hypertension (74% vs.15%) (SI Appendix, Table S2). Blood samples from patients were collected in EDTA tubes and immediately centrifuged at 3,000 rpm for 15 min. The plasma was subsequently transferred to Eppendorf transport tubes for BLS and viscometer measurements (see below).
BLS Microspectroscopy.
The BLS spectrometer used was a dual (cross-dispersion) Virtual Imaged Phased Array (VIPA) based imaging spectrometer (56) similar in design to that previously described (57). Notable differences where that it was designed to operate at 660 nm (laser source: “Flamenco” SLM 660 nm 200 mW by Cobolt/Huber Photonics, Germany). The choice of using 660 nm rather than the more common 532 nm for this setup was based on the lower absorption of blood plasma at these wavelengths (58) that would result in reduced unwanted laser heating and potential protein photodamage. The two VIPAs (Light Machinery, Canada) each had a free spectral range of 15 GHz at 660 nm, with reflective and antireflection coatings on the entrance window optimized for this wavelength. The spectra were imaged using an sCMOS (Edge 4.0, PCO, Germany) prior to which a Lyott stop was included (59) to serve as a low pass filter for removing interference scattering effects from the sample and optical setup. Owing to the reasonable transparency of the plasma no extra elastic suppression was required, beyond the spatial masking of the elastic scattering by two slits at intermediate image planes. In the final spectral projection, the magnification was such that the Brillouin peaks occupied around 5 to 10 camera pixels (example spectra of BLS peaks are shown in SI Appendix, Fig. S3A).
The microscope setup itself consisted of a custom-built inverted microscope with a 2.5 cm × 2.5 cm motor translations stage (ASI, Canada) and temperature-controlled sample box (Ibidi, Germany). Measurements were performed in backscattering geometry with a low NA objective (0.13 NA 4X, RMS4X-PF, Olympus, Japan) to minimize line broadening (36). The polarization of the laser light was adjusted with a half waveplate, expanded to ~18 mm with a relay lens system (to overfill the back aperture of the objective lens), and coupled into the optical setup via a Polarizing Beam Splitter (PBS), with a quarter waveplate prior to the objective lens. As such, the sample was probed with circularly polarized light, but given that in the backscattering geometry and in liquids, we would only measure longitudinal modes this is not an issue. The scattered light was focused using a similar 0.13 NA objective into a single mode fiber (which served as a pinhole of effective size 1 to 2 Airy Units) that ran to the BLS spectrometer. By adjusting the half-waveplate in front of the laser, the light could alternatively be preferentially coupled to a calibration sample in a cuvette (water and PMMA) behind the PBS, that was used for spectral registration prior to each imaging session as previously described (50). All components and acquisition were controlled by a LabView-based script developed by THATec Innovations (Germany), while spectral registration, deconvolution, and data analysis were performed in Matlab (MathWorks, Germany) as previously described (57). Deconvolution to extract the true linewidth was performed by noting that in Fourier space the measured signal is simply the product of the spectral response function and the true signal. For the former, we used a measurement of the elastic scattered signal made before each imaging session obtained by placing a mirror flat in place of the sample, attenuating the laser with neutral density filters, and opening the masking slits in the spectrometer. We note that deconvolution appeared to reduce the linewidth by a small almost constant amount and had no effect on any of the trends or qualitative conclusions presented.
For each measurement, ~750µL of plasma from the EDTA storage tubes was pipetted onto a high-precision glass-bottom dish (Matek, Slovenia), after shaking the former for ~20 s with a vortex mixer. We note that given the probed confocal volume, this volume of plasma is much more than is needed (and one could theoretically work with microliter-sized volumes). The glass bottom dish was subsequently placed in the temperature enclosure (set at 36 °C) on the microscope stage (Ibidi, Germany). We waited for 15 min for the sample temperature to equilibrate (during which spectral registration measurements were performed), before performing the first measurements. The temperature of the sample was monitored by means of a needle temperature probe in contact with the sample with an accuracy of <0.1 °C prior to each measurement, and the temperature and humidity of the sample enclosure via an additional temperature probe. The upper temperature limit of 40.5 °C for the temperature sweeps was set based on the observed nonreversibility of properties above these temperatures for some samples (presumably due to protein degradations).
For measurements, we focused the laser approximately 100 µm above the coverslip surface (such that the probed confocal volume is fully within the plasma). Measurements consisted of a 4 × 4 lateral square grid scan with step-spacing 250 µm in approximately the center of the sample and was controlled by the stepper motor. The summed spectra of these 16 points were used for further analysis. In each case, the laser power at the sample was approximately 40 mW and the exposure time 250 ms.
The Brillouin frequency shift () and line width () were obtained by fitting the measured spectrum , after spectral registration and deconvolution, with a Damped Harmonic Oscillator (DHO):
The longitudinal viscosity () was calculated from the Brillouin linewidth via:
Here, is the density, is the thermal compressibility, and , where and are the specific heat at constant pressure and volume, respectively. Since to a good approximation in plasma, the second term in the parenthesis disappears and the line width becomes directly proportional to the longitudinal viscosity. Here, , where is the free-space probing wavelength, is the refractive index, and here is the scattering angle (180° in backscattering). In the backscattering geometry with low numerical aperture probe/detection, we can assume . The refractive index of aliquots of the same samples was measured using an Abbe refractometer and ranged from 1.338 to 1.348. Measurements of the same samples at 40.5 °C resulted in a change of <1% for a given sample, and as such, the temperature dependence could be ignored for our calculations.
The loss tangent was calculated via
The precision with which the BLS shift and linewidth is measured by performing a 10x10 grid scan of 100 points (5 µm step size) of distilled water, and calculating the SD of the obtained values for the frequency shift and linewidth. This is shown for different exposure times in SI Appendix, Fig. S3, where we see for the employed laser power (40mW) and exposure time (250 ms) the precision in and are 3.1 MHz and 6.1 MHz. Propagating this uncertainty for the derived parameters in Figs. 2–4 would result in error bars smaller than the size of the respective symbols. Decreasing the laser power by 25% and 50% decreased the SNR correspondingly (and thereby reduced the precision), as is shown in SI Appendix, Fig. S3. Here, the SNR was calculated as the average maximum intensity of the BLS peak of the 100-point scan, divided by the SD of these maxima. Importantly, decreasing the laser intensity negligibly affected the mean peak position and width (SI Appendix, Fig. S3B), which remained in agreement within experimental uncertainties, suggesting that the employed laser intensity does not affect our results. This also suggests that there are no significant perturbations due to local heating/damage of the sample which would potentially increase the BLS shift and decrease the linewidth. We note that the high precision (exceeding the resolution of the spectrometer) is due to (1) the determination of peak position ultimately being a localization problem (akin to localization microscopy with the accuracy increasing with photon count), (2) the spread of values obtained from grid scans being dependent on the stability of the setup (and not the spectrometer resolution).
Confocal BLS spatial maps (Fig. 4) were performed using a different dual-VIPA Brillouin microscope of a conceptually similar optical design but optimized for 532 nm with an FSR of 30 GHz, equipped with a Piezo and Motor scanning stage and sample heater, as previously described (50, 57). This was additionally equipped with an Apodization filter (44), Lyot Stop (59), and Iodine absorption cell (60). The pixel dwell time was 25 ms, and the excitation power at the sample was 30 to 35 mW. Measurements were performed by continuously sweeping the scanning stage (linear ramp) during acquisition and as such the value for each pixel corresponds to the average of the distance between adjacent pixels which was 2 µm. For this reason, the maps in Fig. 4 can also not be quantitatively interpreted to represent the heterogeneity on spatial scales below this. The variable power was the result of the laser current being modulated to lock the laser frequency to an absorption line of the gas cell via a feedback loop (50) which differed slightly between consecutive measurements. The precision of these measurements for both the fitted peak position and linewidth was <5 MHz (based on a 100-pixel scan of distilled water as described above). As such the spatial variations observed could be considered significant.
The housing of the probe shown in Fig. 6A was constructed from standard opto-mechanics components available from Thorlabs and Edmund Optics. The collimators used had an effective NA = 0.15 with an output beam waste of 2.46 mm (PAF2P-A15A, Thorlabs, Germany). For the probe, we used a 304 Stainless steel capillary tube (outer diameter = 8 mm, inner diameter = 6 mm, length = 250 mm) which could be immersed in standard plastic transport tubes for the measurements. At the tip of the steel capillary a 4.7 mm f = 2.76 mm, (NA = 0.26, WD = 1.86) aspheric lens (C440TMD-A, Thorlabs) was adhered to a rubber washer was glued (using Norland 62 optical adhesive). Given the smaller beam diameter from the collimators, this corresponded to probing the sample with an NA = 0.15 to 0.2. Aside from this, the optics were the same as those in the confocal BLS microscope (albeit on a slightly smaller scale). The measured precision, calculated as the SD of 20 consecutive measurements of a distilled water sample at 40 mW laser power (at sample) and 250 ms exposure time, was found to be 9 MHz for the BLS peak position and 13 MHz for the linewidth at the employed laser powers.
Angle-Resolved BLS Measurements.
Angle-resolved BLS measurements (Fig. 3 A and B) were performed using the same setup as for the BLS mapping at 532 nm with the following modifications. The objective was replaced with a high numerical (NA) objective (1.4 NA immersion 60× Olympus). The relay lens system used to expand the laser beam to fill the back aperture of the objective was modified such that the collimated beam incident on the back aperture had a diameter of about 1 mm. On the detection side, we placed an annular mask (406 aluminum coated quartz, custom made by Photo-Sciences Inc.) which consisted of angular rings with different diameters (61). The mask itself contained >20 different angular ring diameters, and by selectively placing different ring diameter masks in the light path, we can probe the BLS at different scattering wavevectors (with a detection NA of <0.1). In our experiments, we used four different ring diameters. The scattering angles in the sample (and probed wavevector) could readily be calculated from the ring diameter and refractive index of the plasma sample. The acquisition time for these measurements was 5 to 10 s, which was required to obtain a satisfactory SNR of the BLS peaks. Analyzed spectra were taken as the sum of a 10 × 10 grid scan and spectrally deconvolved with the instrument spectral response in the same manner as with the conventional BLS measurements.
Elastic Scattering Measurements.
The elastic scattering measurements (Fig. 3C) were performed in the same manner as the BLS point-measurements using the 660 nm excitation but with the intermediate imaging plane masking slits in the spectrometer open, and the signal attenuated by a neutral density filter placed immediately prior to coupling into the spectrometer (such that the elastic peaks were only ~50% saturated on the spectrometer camera). The intensity (in arbitrary units) was taken as the average of the peak maximum of two elastic scattering peaks from the same adjacent orders in each case. The elastic scattering from specular reflections in the spectrometer and Tyndall scattering were assumed to dominate, given that the contribution from other collective modes are much weaker (62). Also the Rayleigh scattering can be assumed to be comparatively small as it will to a first approximation scale as , where and are the specific heats at constant volume and pressure, which are comparable. Since the contribution from specular reflection inside the spectrometer is sample independent, changes in the elastic scattering intensity can be attributed to changes in the Tyndall scattering. Extra care was taken to assure that there was no additional contamination on the sample mounting side, with new sterile individually packaged high-precision glass bottom dishes (Matek) used for each measurement, and maintaining the same axial focus position for each measurement. As such changes in the scattering can be attributed to changes in sample optical inhomogeneities.
Shear Viscosity Measurements.
Temperature-dependent measurements of the shear viscosity were performed on aliquots of the same plasma samples in parallel to or immediately following BLS measurements. For these, a commercial rolling-ball shear viscometer (Lovis 2000, Anton Paar, Austria) calibrated to ASTM D2162/ UKAS ISO 17025 /ISO 17034 certified water viscosity standard, was used. Routine annual calibration of the instrument by the manufacturer assured that the measurements can be considered reliable. Following established manufacturer-provided protocols, automated programmed temperature ramps 36 °C 40.5 °C 36 °C were performed, with for each temperature step the averages of two iterations taken. The respective uncertainties were smaller than the symbol sizes in Figs. 2 and 3.
Modeling of the suspension dependence of the shear and effective longitudinal viscosity was performed using Matlab (MathWorks, Germany), and all statistical analysis was performed using Sigmaplot 13.0 (Sysworks, Germany).
The study was performed in accordance with the recommendations of the Declaration of Helsinki. Experimental protocols were approved by the Ethics Committee of the Austrian Federal Agency for Safety in Health Care – BASG (ECS 1372/2021, Ethics votum: EK-21-068-VK, BASG Operation number:14043408), and written informed consent was obtained from the patients.
Supplementary Material
Appendix 01 (PDF)
Acknowledgments
This work was supported by funding from the Austrian Science Fund—FWF (Grant No. P34783). No funding sources had any role in the writing of the manuscript or the decision to submit.
Author contributions
J.I., T.C.-S., and K.E. performed research; J.I., T.C.-S., and K.E. analyzed data; A.Z., J.H.A., M.F., and K.E. designed research; A.Z., J.H.A., W.J.W., M.F., and K.E. contributed new reagents/analytic tools; and K.E. wrote the paper.
Competing interests
The authors declare no competing interest.
Footnotes
This article is a PNAS Direct Submission. G.S. is a Guest Editor invited by the Editorial Board.
Data, Materials, and Software Availability
All data in manuscript have been deposited in Zenodo (63). Code used for analysis of data that has not already been published elsewhere is available upon reasonable request.
Supporting Information
References
- 1.Késmárky G., Kenyeres P., Rábai M., Tóth K., Plasma viscosity: A forgotten variable. Clin. Hemorheol. Microcirc. 39, 243–246 (2008). [PubMed] [Google Scholar]
- 2.Brust M., et al. , Rheology of human blood plasma: Viscoelastic versus newtonian behavior. Phys. Rev. Lett. 110, 078305 (2013). [DOI] [PubMed] [Google Scholar]
- 3.Mezger T., The Rheology Handbook (Vincentz Network, Hannover. Germany, 2020), 10.1515/9783748603702. [DOI] [Google Scholar]
- 4.Ewoldt R. H., Johnston M. T., Caretta L. M., “Experimental challenges of shear rheology: How to avoid bad data” in Complex Fluids in Biological Systems: Experiment, Theory, and Computation, Spagnolie S. E., Ed. (Springer New York, New York, NY, 2015), pp. 207–241. 10.1007/978-1-4939-2065-5_6. [DOI] [Google Scholar]
- 5.Berne B. J., Pecora R., Dynamic Light Scattering: With Applications to Chemistry, Biology, and Physics (Dover Publications, 2000). [Google Scholar]
- 6.Palombo F., Fioretto D., Brillouin light scattering: Applications in biomedical sciences. Chem. Rev. 119, 7833–7847 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Adichtchev S. V., et al. , Brillouin spectroscopy of biorelevant fluids in relation to viscosity and solute concentration. Phys. Rev. E 99, 062410 (2019). [DOI] [PubMed] [Google Scholar]
- 8.Landau L. D., Lifschitz E. M.. Fluid Mechanics (Pergamon Press, ed. 2, 1987), vol. 6. [Google Scholar]
- 9.Dukhin A. S., Goetz P. J., Bulk viscosity and compressibility measurement using acoustic spectroscopy. J. Chem. Phys. 130, 124519 (2009). [DOI] [PubMed] [Google Scholar]
- 10.Boon J. P., Yip S., Molecular Hydrodynamics (Dover Publications, 1991). [Google Scholar]
- 11.Rodríguez-López R., et al. , Network viscoelasticity from brillouin spectroscopy. Biomacromolecules 25, 955–963 (2024). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Hecksher T., et al. , Toward broadband mechanical spectroscopy. Proc. Natl. Acad. Sci. U.S.A. 114, 8710–8715 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Pochylski M., Structural relaxation in the wave-vector dependence of the longitudinal rigidity modulus. Biomed. Opt. Express 10, 1957–1964 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Treeby B. E., Zhang E. Z., Thomas A. S., Cox B. T., Measurement of the ultrasound attenuation and dispersion in whole human blood and its components from 0–70 MHz. Ultrasound Med. Biol. 37, 289–300 (2011). [DOI] [PubMed] [Google Scholar]
- 15.Riese D. O., Wegdam G. H., Sound propagation in suspensions of colloidal spheres with viscous coupling. Phys. Rev. Lett. 82, 1676–1679 (1999). [Google Scholar]
- 16.Maier C. L., et al. , COVID-19-associated hyperviscosity: A link between inflammation and thrombophilia?. Lancet 395, 1758–1759 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Gleghorn D. M., et al. , Diagnostic value of plasma viscosity testing for patients with COVID-19. Int. J. Laboratory Hematol. 43, O227–O229 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Levi M., Thachil J., Iba T., Levy J. H., Coagulation abnormalities and thrombosis in patients with COVID-19. The Lancet Haematol. 7, e438–e440 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Gorog D. A., et al. , Current and novel biomarkers of thrombotic risk in COVID-19: A consensus statement from the international COVID-19 thrombosis biomarkers colloquium. Nat. Rev. Cardiol. 19, 475–495 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Laubscher G. J., Lourens P. J., Venter C., Kell D. B., Pretorius E., TEG(®), microclot and platelet mapping for guiding early management of severe COVID-19 coagulopathy. J. Clin. Med. 10, 5381 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Quintana-Díaz M., et al. , Coagulation parameters: An efficient measure for predicting the prognosis and clinical management of patients with COVID-19. J. Clin. Med. 9, 3482 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Wichmann D., et al. , Autopsy findings and venous thromboembolism in patients with COVID-19: A prospective cohort study. Ann. Intern Med. 173, 268–277 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Bull B. S., Hay K. L., A macrophage attack culminating in microthromboses characterizes COVID 19 pneumonia. Immun Inflamm Dis. 9, 1336–1342 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Bull B. S., Hay K. L., Herrmann P. C., Fibrin strands will grow from soluble fibrin and hang up in an in vitro microcirculatory viscoelastic model: Is this a major cause of COVID-19 associated coagulopathy? J. Clin. Med. 11, 2084 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Pretorius E., et al. , Persistent clotting protein pathology in Long COVID/post-acute sequelae of COVID-19 (PASC) is accompanied by increased levels of antiplasmin. Cardiovascular Diabetol. 20, 172 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Bachler M., et al. , Impaired fibrinolysis in critically ill COVID-19 patients. Br. J. Anaesth. 126, 590–598 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Wu T., et al. , Multi-organ dysfunction in patients with COVID-19: A systematic review and meta-analysis. Aging Dis. 11, 874–894 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Marshall J. C., et al. , A minimal common outcome measure set for COVID-19 clinical research. The Lancet Infectious Dis. 20, e192–e197 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Jung F., et al. , Effect of sex, age, body weight, and smoking on plasma viscosity. Klin Wochenschr 64, 1076–1081 (1986). [PubMed] [Google Scholar]
- 30.Elsayad K., et al. , Mechanical properties of cellulose fibers measured by Brillouin spectroscopy. Cellulose 27, 4209–4220 (2020), 10.1007/s10570-020-03075-z. [DOI] [Google Scholar]
- 31.Figgins R., Inelastic light scattering in liquids: Brillouin scattering. Contemp. Phys. 12, 283–297 (1971). [Google Scholar]
- 32.Bailey M., et al. , Viscoelastic properties of biopolymer hydrogels determined by Brillouin spectroscopy: A probe of tissue micromechanics. Sci. Adv. 6, eabc1937 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Konijn B. J., Sanderink O. B. J., Kruyt N. P., Experimental study of the viscosity of suspensions: Effect of solid fraction, particle size and suspending liquid. Powder Technol. 266, 61–69 (2014). [Google Scholar]
- 34.Brady J. F., Khair A. S., Swaroop M., On the bulk viscosity of suspensions. J. Fluid Mechanics 554, 109–123 (2006). [Google Scholar]
- 35.Swaroop M., Brady J. F., The bulk viscosity of suspensions. J. Rheol. 51, 409–428 (2007). [Google Scholar]
- 36.Antonacci G., Foreman M. R., Paterson C., Török P., Spectral broadening in Brillouin imaging. Appl. Phys. Lett. 103, 221105 (2013). [Google Scholar]
- 37.Chen C., et al. , Polymer cyclization for the emergence of hierarchical nanostructures. Nat. Commun. 12, 3959 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.O’Steen B. L., Wang C. H., Fytas G., Rayleigh-Brillouin scattering studies of the rotation-translation coupling and bulk viscosity relaxation of liquids composed of anisotropic molecules: P-Anisaldehyde and aniline. J. Chem. Phys. 80, 3774–3780 (1984). [Google Scholar]
- 39.Voudouris P., et al. , Does Brillouin light scattering probe the primary glass transition process at temperatures well above glass transition?. J. Chem. Phys. 132, 074906 (2010). [DOI] [PubMed] [Google Scholar]
- 40.Janes F., et al. , Failure of therapeutic anticoagulation in COVID-19 patients with acute ischemic stroke. A retrospective multicenter study. Front. Neurol. 13, 834469 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.The REMAP-CAP, ACTIV-4a, and ATTACC Investigators, Therapeutic anticoagulation with heparin in critically Ill patients with Covid-19. New Engl. J. Med. 385, 777–789 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Pretorius E., et al. , Prevalence of symptoms, comorbidities, fibrin amyloid microclots and platelet pathology in individuals with Long COVID/post-acute sequelae of COVID-19 (PASC). Cardiovasc. Diabetol. 21, 148 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Kaibara M., Fukada E., Effect of temperature on dynamic viscoelasticity during the clotting reaction of fibrin. Biochim. Biophys. Acta 499, 352–361 (1977). [DOI] [PubMed] [Google Scholar]
- 44.Scarcelli G., et al. , Noncontact three-dimensional mapping of intracellular hydromechanical properties by Brillouin microscopy. Nat. Methods 12, 1132–1134 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Margueritat J., et al. , High-frequency mechanical properties of tumors measured by brillouin light scattering. Phys. Rev. Lett. 122, 018101 (2019). [DOI] [PubMed] [Google Scholar]
- 46.Mattana S., et al. , Non-contact mechanical and chemical analysis of single living cells by microspectroscopic techniques. Light: Sci. Appl. 7, 17139–17139 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Wu P. J., et al. , Water content, not stiffness, dominates Brillouin spectroscopy measurements in hydrated materials. Nat. Methods 15, 561–562 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Lenshof A., et al. , Acoustic whole blood plasmapheresis chip for prostate specific antigen microarray diagnostics. Anal. Chem. 81, 6030–6037 (2009). [DOI] [PubMed] [Google Scholar]
- 49.Antonacci G., Elsayad K., Polli D., On-chip notch filter on a silicon nitride ring resonator for brillouin spectroscopy. ACS Photonics 9, 772–777 (2022). [Google Scholar]
- 50.Pruidze P., Chayleva E., Weninger W. J., Elsayad K., Brillouin scattering spectroscopy for studying human anatomy: Towards in situ mechanical characterization of soft tissue. J. Eur. Opt. Soc.-Rapid Publ. 19, 31 (2023). [Google Scholar]
- 51.Remer I., Shaashoua R., Shemesh N., Ben-Zvi A., Bilenca A., High-sensitivity and high-specificity biomechanical imaging by stimulated Brillouin scattering microscopy. Nat. Methods 17, 913–916 (2020). [DOI] [PubMed] [Google Scholar]
- 52.Ballmann C. W., Meng Z., Traverso A. J., Scully M. O., Yakovlev V. V., Impulsive Brillouin microscopy. Optica 4, 124–128 (2017). [Google Scholar]
- 53.Krug B., Koukourakis N., Guck J., Czarske J., Nonlinear microscopy using impulsive stimulated Brillouin scattering for high-speed elastography. Opt Express 30, 4748–4758 (2022). [DOI] [PubMed] [Google Scholar]
- 54.Shi C., Zhang H., Zhang J., Non-contact and label-free biomechanical imaging: Stimulated Brillouin microscopy and beyond. Front. Phys. 11, 1175653 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Kubánková M., et al. , Physical phenotype of blood cells is altered in COVID-19. Biophys. J. 120, 2838–2847 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Scarcelli G., Yun S. H., Multistage VIPA etalons for high-extinction parallel Brillouin spectroscopy. Opt Express 19, 10913–10922 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Elsayad K., et al. , Mapping the subcellular mechanical properties of live cells in tissues with fluorescence emission-Brillouin imaging. Sci. Signal 9, rs5 (2016). [DOI] [PubMed] [Google Scholar]
- 58.Meinke M., Müller G., Helfmann J., Friebel M., Optical properties of platelets and blood plasma and their influence on the optical behavior of whole blood in the visible to near infrared wavelength range. J. Biomed. Opt. 12, 014024 (2007). [DOI] [PubMed] [Google Scholar]
- 59.Edrei E., Gather M. C., Scarcelli G., Integration of spectral coronagraphy within VIPA-based spectrometers for high extinction Brillouin imaging. Opt. Express 25, 6895–6903 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Meng Z., Traverso A. J., Yakovlev V. V., Background clean-up in Brillouin microspectroscopy of scattering medium. Opt. Express 22, 5410–5415 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Chen B. C., et al. , Lattice light-sheet microscopy: Imaging molecules to embryos at high spatiotemporal resolution. Science 346, 1257998 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Carroll P. J., Patterson G. D., Rayleigh-Brillouin spectroscopy of simple viscoelastic liquids. J. Chem. Phys. 81, 1666–1675 (1984). [Google Scholar]
- 63.Illibauer J., et al. , Data for: Diagnostic potential of blood plasma longitudinal viscosity measured using Brillouin light scattering. Zenodo. https://zenodo.org/records/12750548. Deposited 16 July 2024. [DOI] [PMC free article] [PubMed]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Appendix 01 (PDF)
Data Availability Statement
All data in manuscript have been deposited in Zenodo (63). Code used for analysis of data that has not already been published elsewhere is available upon reasonable request.