Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2024 Aug 2;15(32):8187–8195. doi: 10.1021/acs.jpclett.4c01636

How Solvation Alters the Thermodynamics of Asymmetric Bond-Breaking: Quantum Simulation of NaK+ in Liquid Tetrahydrofuran

Kenneth J Mei †, Benjamin J Schwartz †,*
PMCID: PMC11331520  PMID: 39093598

Abstract

graphic file with name jz4c01636_0004.jpg

Gas-phase potential energy surfaces (PESs) are often used to provide an intuitive understanding of molecular chemical reactivity. Most chemical reactions, however, take place in solution, and it is unclear whether gas-phase PESs accurately represent chemical processes in solvent environments. In this work we use quantum simulations to investigate the dissociation energetics of NaK+ in liquid tetrahydrofuran (THF) to understand the degree to which solvent interactions alter the gas-phase picture. Using umbrella sampling and thermodynamic integration techniques, we construct condensed-phase free energy surfaces of NaK+ on THF in both the ground and electronic excited states. We find that solvation by THF completely alters the nature of the NaK+ bond by reordering the thermodynamic dissociation products. Reaching the thermodynamic dissociation limit in THF also requires a long-range charge transfer process that has no counterpart in the gas phase. Gas-phase PESs, even with perturbations, cannot adequately describe the reactivity of simple asymmetric molecules in solution.

Our basic understanding of the reactivity of a molecule or reaction in the gas phase is usually based on potential energy surfaces (PESs).1−3 Potential energy surfaces make the assumption that the electrons respond instantaneously to the motions of nuclei so that the electronic energies are then a function of nuclear coordinates such as bond distances, angles, or torsions. With a PES in hand, various molecular properties such as the reactant and product equilibrium geometries, relative energetics, electronic and vibrational spectra, and even the rates of reaction can be directly determined.4 Commonly, PESs are calculated for isolated molecules in vacuum; however, the majority of chemical reactions occur in solution. This leads to the question of whether a gas-phase PES can adequately describe a molecular species or reaction in the presence of a complex solvent environment. Features of PESs such as conical intersections can be induced by coupling with the solvent, or pre-existing intersections can be displaced or even disappear completely due to environmental interactions.5−7 Reaction barriers can also be enhanced8,9 or diminshed10 by solvation, and processes such as collisions11,12 with the surrounding solvent cage can alter bond-breaking and bond-formation dynamics.13−15 Even the relative stabilities of reactants and products may differ once temperature, kinetics, and thermodynamics are considered in solution-phase chemical systems.

In previous work, we investigated the effect of solvation on the PESs and reactivity of simple diatomic solutes like Na2 and Na2+.15−20 In weakly interacting, nonpolar solvents like liquid argon, the solvent compresses the density of the bonding electron(s), altering the PES by decreasing the equilibrium bond distance and increasing the bond vibrational frequency.16,17,20 Even though both Ar and Na2 are nonpolar, collisions between the solvent and solute can induce instantaneous solute dipoles due to Pauli repulsive interactions that displace the bonding electron density, changing vibrational selection rules.16,17,20 We also saw that during photodissociation of Na2+, asynchronous collisions between Ar solvent atoms and the Na+ photofragments induce decoherence of the bonding electron, localizing it onto a single Na+ and thus breaking the symmetry and determining the dissociation products.19

In moderately polar solvents like tetrahydrofuran (THF), on the other hand, the solvent molecules can make weak (∼1 kcal/mol) dative bonds with Na+, forming discrete solvation structures. For example, the Na2 molecule in liquid THF forms three distinct solvent coordination states, which we referred to as (2,4), (3,3), and (3,4), where the numbers denote how many THF molecules are datively bound to each Na+ core.16 We saw barriers of ∼7–8 kBT for these structures to interconvert, which make them chemically distinct. These coordination structures have distinct equilibrium bond lengths, vibrational frequencies, and electronic spectroscopic signatures, indicating that solvent interactions actually change the chemical identity of solutes.16 The Na2+ molecule undergoes similar effects when solvated in THF, exhibiting (4,5) and (5,5) coordination states.17 Moreover, although Na2+ readily photodissociates in the gas phase, in THF the solvent complexes must undergo a solvent-related photoisomerization reaction prior to dissociation, requiring a 2-D effective energy surface to describe the basic reactivity of the solution-phase system.18

To date, the most detailed investigations of solvent effects on small molecules have explored symmetric diatomics, where there is only a single set of possible reaction products.15−19,21−29 This leads to the question of what happens when solvents interact with small molecules that are asymmetric: can the local asymmetry of a solvent environment enhance or even reverse the inherent asymmetry of a solute? To address this question, we extend our previous simulation studies to examine the behavior of NaK+ in THF solution. NaK+ is well studied in the gas phase, and the PESs of the ground and higher-lying electronic states have been calculated at various levels of theory;30−32 the lowest two surfaces can be seen in Figure 1a. The PESs predict that the NaK+ dissociation products in the gas phase are Na0 + K+ on the ground state and Na+ + K0 on the lowest excited state.30−32 The different products result from the fact that Na and K have different ionization energies, with K being ∼860 meV easier to ionize than Na.33,34

Figure 1.

Figure 1

Open in a new tab

Potential energy and free energy surfaces of NaK+ along the bond distance coordinate in the gas phase (panel a) and liquid THF (panels b and c) environments. Green curves are energy surfaces for the electronic ground state while purple curves are for the first excited electronic state. Panel a shows that in the gas phase, the dissociation products on the ground-state surface are Na0 + K+ while those on the excited state are Na+ + K0; the energy difference of ∼860 meV (or ∼33.7 kBT) between the long-distance asymptotes of these surfaces is the difference between the ionization energies of isolated Na and K atoms. Panel b shows PMFs of the NaK+ molecule in liquid THF calculated via umbrella sampling (data points), with the zero of energy set to that of the gas-phase ground-state product, Na0 + K+, at an assumed separation of 40 Å. The pink arrow at long separations represents the solution-phase free energy difference between Na0 + K+ (the gas-phase, ground-state product) and Na+ + K0 (the gas-phase, excited-state product) calculated via thermodynamic integration (cf. Figure 2); solvation inverts the stability of the possible products relative to the gas phase. The solid curves in panels b and c are fits of the ground- and excited-state PMFs and the long-distance free energy asymptotes to Morse and exponential potential functions, respectively, with parameters given in the SI. Panel c shows an expansion of the free energy surfaces depicted in panel b; the dotted curves are quasi-adiabatic free energy surfaces created from the PMFs via the decoupling procedure outlined in the text and SI.

Here, we perform a series of quantum simulations of the behavior of the NaK+ molecule in liquid THF. We find that in solution the thermodynamically stable ground and excited-state dissociation reaction products are inverted relative to the gas phase. This is because the Na+ and K+ dissociation products are differently solvated, changing not only the shape of the PES in the Franck–Condon region but also the nature of the asymptotes at infinite fragment separation. Because of the change in reaction products, our calculations show that there must be an avoided crossing in the solution-phase potentials of mean force that does not exist in the gas-phase PES’s. The fact that there is a crossing of the energy surfaces indicates that a long-range electron transfer process must occur for the reaction to reach the thermodynamic products, all because of the presence of only modest locally specific solute–solvent interactions.

The theoretical approach we use to simulate NaK+ in solution is summarized in Methods and described in more detail in the Supporting Information (SI). Briefly, we use mixed quantum/classical (MQC) molecular dynamics (MD) simulations, where the nuclear components of the solute and the solvent are treated classically, the solute bonding electron is treated quantum mechanically, and the interactions between the quantum and classical subsystems are described using pseudopotentials that are rigorously determined from quantum chemistry calculations using the Phillips–Kleinman formalism.35,36 All of the methods are the same as those used in our previously published work studying the properties of Na2 and Na2+ in solution.15−17 The cubic simulation box, treated with periodic boundary conditions, spans a length of 32.5 Å and contains 254 THF solvent molecules and one NaK+ solute in the N, V, E ensemble at an average temperature of 298 K. The quantum mechanical bonding electron’s wave function is described on a 64 × 64 × 64 grid that spans the simulation box. Condensed-phase free-energy surfaces (potentials of mean force (PMFs)) were determined via umbrella sampling,37 making use of the multistate Bennet acceptance ratio (MBAR) method.38

Unfortunately, computational expense prevents us from significantly increasing the number of grid points that describe the NaK+ bonding electron, and the need for a fine grid resolution prevents us from expanding the size of the simulation box and thus the grid spacing. This is because expanding the grid to the sizes needed for direct simulation would require trajectories with wall times of years, well beyond the bounds of computational feasibility given the months of wall time already spent for the results presented here. Thus, we unfortunately cannot explore separations of the molecule larger than half the simulation box size, which given the presence of cation-THF dative bonds limits our ability to directly simulate Na–K separation distances of ≳8 Å, a value well below the dissociation limit. Thus, to explore the dissociation limit, we took advantage of thermodynamic integration (TI)39,40 to calculate the free energy difference between the Na0 + K+ and Na+ + K0 possible dissociation products. The free energy difference was determined via a pair of alchemical transformations, described in Figure 2, with more details provided in the SI. To connect the directly sampled PMFs at bond distances ≤8 Å to the dissociation limit, we fit the umbrella-sampled free energy points to functional forms (with details found in the SI) that resemble the gas-phase PESs in order to interpolate the PMFs in the transition region where direct simulation is not feasible.

Figure 2.

Figure 2

Open in a new tab

Free energy differences between the possible products of the NaK+ dissociation in liquid THF, calculated using thermodynamic integration. In the snapshots, the red and turquoise sticks are THF solvents, the blue spheres are Na+, the pink spheres are K+, and the wire mesh shows the wave function of the electron in the cation:electron tight-contact pairs. ΔFCl and ΔFQM are the free energy differences involved with the alchemical transformations Na+ → K+ and Na0 → K0, respectively. ΔΔF = ΔFCL + ΔFQM gives the free energy difference between the two possible sets of infinitely separated solvated product species. The calculations give ΔΔF ≈ −200 meV, indicating that due to solvation, the Na+ + K0 gas-phase excited-state product is actually the stable ground-state product in liquid THF.

We begin our investigation of the thermodynamics of NaK+ dissociation by examining the nature of NaK+ in liquid THF and how it differs from that in the gas phase. In Figure 1a, we calculate NaK+ gas-phase PESs, which reproduce previous calculations in the literature.30−32 As mentioned above, our past work has shown that THF molecules can form weak dative bonds to alkali metal cation cores, forming discrete coordination structures and changing chemical identity.16,17 The enthalpic strength of the Na+–THF interaction is ∼1 kcal/mol (which we mis-stated as ∼4 kcal/mol in our previous work),16,17 so that the ∼7 kBT barrier between the different coordination structures is due primarily to reorganization of solvent molecules that are not involved in making dative bonds to the metal cations. We note that the enthalpic strength of the K+–THF interaction is roughly 5 times smaller than that of the Na+–THF dative bond, or less than kBT at room temperature. The decreased strength of the K+–THF interaction thus changes the speciation of NaK+ relative to that seen previously with Na2+. We observe 3 separate coordination states for NaK+ in liquid THF—(4,5), (5,5), and (4,6) chemical species—where the first number represents THF coordination to Na+ and the second to K+. All three coordinated NaK+ species lie within a kBT of each other in terms of their respective free energies, with interconversion barriers of ∼3–6 kBT (see Figure S4 in the SI). Similar to what we saw previously for Na2+ in THF,17 each of the three solvent-induced chemical identities for NaK+ has a different equilibrium bond distance and vibrational frequency, as discussed in more detail in Figure S5 of the SI. For the analysis discussed below, the condensed-phase free energy surfaces along the Na–K distance are ensemble averaged over all three coordination states.

To see how the behavior of NaK+ changes once it is solvated in liquid THF, we need to calculate the PMFs along the Na–K distance coordinate (R) on both the ground and first excited electronic states. This requires umbrella sampling in order to find the free energies at each value of R averaged over both the solvent coordination number and other solvent fluctuations. The green (ground electronic) and purple (first excited electronic) data points in Figures 1b,c show the calculated PMFs, which have shapes that are generally similar to those of the gas-phase PESs but with some important differences. One such difference is that the equilibrium bond length in the ground state now extends to 5.4 Å, nearly an entire angstrom longer than in the gas phase (4.5 Å). Another difference is that the gas-phase NaK+ PESs level off in energy by a bond distance of 8 Å, but the solution PMFs show rising ground-state and steeply descending excited-state surfaces even past 8 Å, the farthest bond distance that we can simulate directly, given computational limitations on the quantum grid representing the bonding electron. This means that based on these direct simulations, we do not know the relative free energies of the possible dissociation products in the limit of large bond distances.

To overcome this limitation, we take advantage of thermodynamic integration (TI) to determine the free energy difference between the two possible sets of products, Na0 + K+ (ground-state product in gas phase) and Na+ + K0 (excited-state product in gas phase). When the two possible sets of NaK+ fragments are infinitely separated and noninteracting, we can consider their solvated free energy differences in pairs. This means that we need to consider only two separate TI paths that can then be summed to give the total free energy difference between the possible products. Figure 2 illustrates how we performed this calculation. Our starting point is the gas-phase ground-state dissociation products, Na0 + K+, shown at the bottom of Figure 2. We then consider the alchemical transformation of Na0 into K0, indicated by the turquoise arrow. Along this TI path, the Na+ Lennard-Jones potential and Na+-e– pseudopotential are both gradually transformed into those associated with K+: in other words, the Hamiltonian of the Na0 system is linearly switched to that of K0 using a single parameter, λ, which interconverts the two systems over ∼10 substeps. The integral of the derivative of the potential energy versus λ then gives a free energy difference, ΔFQM = 1.428 ± 0.058 eV. The calculated 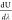Inline graphic curves, the convergence of the free energy difference, the details of the different λ trajectories run, and the integration are all shown in Figures S1 and S2 in the SI.

The fact that the free energy difference between Na0 and K0 is positive results both from the fact that the electron is more strongly attracted to Na+ than K+ and the fact that K0 is less well solvated than Na0 in liquid THF. Both experimental results41−52 and theoretical work53−55 show that neutral alkali atoms in ether solvents form cation:electron tight-contact pairs (TCPs). In a TCP, weak dative bonds between the ether solvent molecules and the metal cation core displace the metal’s valence electron density, so that the electron is partially supported by the surrounding solvent.41,51−53,55 Although partly displacing the electron off the metal cation costs electronic energy, the resulting induced dipole has a larger free energy of solvation than this cost, explaining why TCPs form.55 The net result is that TCPs have equilibrium properties between those of a solvated neutral metal atom and a separate solvated electron:cation pair.52,53,55 For both solvated alkali atoms in this work, our simulations correctly predict the formation of TCPs that match experimental observations.48

Our simulations show that the quantum binding energy of the electron in the Na0 TCP is ∼0.4 eV larger than that in the K0 TCP, due primarily to the larger electron affinity of the Na+ core. We also see that Na0 has on average 4.2 datively bound THF molecules while K0 has an average THF coordination number of 5.0, as shown in more detail in Figure S3 in the SI. The SI also shows that K0 has a greater degree of fluctuations in the number of coordinated THFs, but our calculations also show that the entropy change along the Na0 → K0 TI path (calculated by subtracting the change in potential energy from the free energy difference and dividing by the negative temperature) is less than 1% of the total free energy difference. Figure S5 in the SI displays the calculated electron density distribution as a function of distance from the cation for each of these TCPs, showing that the valence electron of K0 sits at a farther distance than that of Na0, reflecting both the larger size and lower electron affinity of the K+ core, a result consistent with the free energy difference between the two species being primarily enthalpic.

The yellow arrow in Figure 2 shows what happens for the alchemical conversion of K+ to Na+ in THF (i.e., the reverse process as above without the bonding electron); TI over this path gives a free energy difference ΔFCL = −1.612 ± 0.065 eV. This shows that Na+ is much more favorably solvated by liquid THF than K+. Figure S3 in the SI compares the coordination numbers of the two cations, showing that Na+ has an average coordination number of 6.0 while K+ has an average of 6.4 with a broader distribution. Once again, we find the entropic contribution to the free energy difference is fairly negligible, suggesting that the more favorable solvation of Na+ in liquid THF is due both to the five-times-greater Na+-THF dative bond strength and to the solvation of the datively bonded cations by other THF molecules.

The sum of the free energy changes along the two TI paths gives the free energy difference, ΔΔF, between Na0 + K+ and Na+ + K0 (pink arrow in Figure 2), which is −0.18 eV. This means that in THF solution, the Na+ + K0 products are actually more stable than the Na0 + K+ products: the relative stability of the products is inverted from the gas phase, which is one of the principal results of this work. This inversion results primarily from the fact that the solvation free energy of Na+ in liquid THF is much more favorable than that of K+, stabilizing the Na+ + K0 products even though Na0 is more stable than K0.

What does this inversion of the ground- and excited-state products imply about NaK+ PMFs in THF? To answer this question, we start by setting Na0 + K+ (the gas-phase most stable products) at the infinite separation limit (40 Å) as zero free energy. The TI calculation tells us that the Na+ + K0 products sit ∼200 meV below our chosen zero of free energy, as illustrated by the pink arrow in Figure 1b. We also can set the offset between the ground and first-excited state free energy surfaces in the Franck–Condon (FC) region as the sum of the vertical excitation energy and the reorganization energy of the solvent in response to the change in electron density from the electronic excitation. By combining this free energy difference between the ground- and excited-state PMF curves in the FC region with the asymptotic offset from the TI calculations, we were able to use umbrella sampling to produce the free energy data points in Figure 1b,c. We then fit these data points and the large-distance offset to a Morse potential for the ground state (green solid curve) and an exponential decay for the excited state (purple solid curve), with details on the construction and fitting of these free energy surfaces given in SI. The purpose of these fits is to allow us to interpolate the PMFs at bond separations larger than what is feasible to directly simulate; that is, in the regime between 8 and 40 Å.

One important issue with these calculated PMFs is that given the directly sampled data points in the Franck–Condon region and the asymptotic energy offset, the two curves must cross somewhere in the region R ≈ 10 Å. This means that these surfaces must be quasi-diabatic states, since true adiabatic surfaces with the same symmetry should never cross.56,57 This suggests that the PMFs we have calculated are coupled and that we can estimate the true adiabatic free energy surfaces by removing the coupling.58 Treating our ground- and excited-state surfaces as a two-level system, our estimated adiabatic surfaces are calculated via diagonalizing the modified Hamiltonian (i.e., the diabatic energies and coupling matrix elements) of the system. Unfortunately, there is no easy way to calculate the coupling matrix elements in the condensed phase,59 so we estimated a degree of coupling using a blip function that produces a reasonable curvature for the estimated adiabatic surfaces; the results are shown as the dotted curves in Figure 1c. The equations for our diagonalization as well as the parameters and functional form of the blip function we used are detailed in the SI.

Clearly, the gas-phase NaK+ PESs and condensed-phase PMFs show significant qualitative differences: the dissociation products are inverted, they have different ground state equilibrium bond distances (4.5 Å in the gas phase vs 5.4 Å in THF solution), different vibrational frequencies (74.1 cm–1 in the gas phase versus 57.7 cm–1 in solution), and different bond energies (22.4 kBT in the gas phase versus 6.7 kBT in the condensed phase), etc., emphasizing the importance of solvent effects on even relatively simple molecules. This difference is due to the change in chemical identity when the NaK+ molecule is placed in THF solution, as discussed above and in our previous work.16,17 All of this indicates that solvation changes not only the reactivity of this species but also the dynamics and actual outcomes of its reaction on different electronic surfaces.

To better understand how solvent interactions affect the properties of NaK+ in liquid THF, we performed a detailed investigation of the behavior of the bonding electron on both the electronic ground and excited states. We do this by integrating the electron density within the van der Waals radii of Na+ and K+ to determine the overlap of the bonding electron with each atomic core. We note that with this definition not all of the bonding electron is included in the integration regions, so the total overlap does not necessarily sum to unity. We performed this integration as a function of the bond length R both in the gas phase (dashed curves) and in solution (data points) using the same umbrella sampling simulations used to construct the PMFs in Figure 1; the results for the ground and excited electronic states are plotted in Figure 3c,d, respectively.

Figure 3.

Figure 3

Open in a new tab

Electron–cation overlap and THF dative bond coordination number along the ground- (left column) and excited-state (right column) dissociation paths of NaK+ in liquid THF. Simulation snapshots of NaK+ in THF at the 8 Å simulation limit in the ground (panel a) and excited (panel b) electronic states. Panels c and e show the electron overlap (integration of electron density around each cation) and THF coordination states on the ground state, while panels d and f show the same measures for the excited state. Dashed curves show the gas-phase overlap in panels c and d, while the blue and red data points and solid lines represent the overlap (and in panels e and f the coordination number) on Na+ and K+, respectively, in THF solution. The results show that in THF, the electron overlap is anticorrelated with the coordination number on each fragment on the ground state. At 8 Å, prior to the predicted crossing point of the free energy surfaces in Figure 1b, the ground-state electron is clearly becoming associated with Na+, so a long-range electron transfer must occur at larger bond distances to reach the lower-energy Na+ + K0 ground-state products. On the excited state, there is little overlap of the bonding electron with either fragment at 8 Å bond separation, again indicating that the final products do not form until further distances are accessed.

The dashed curves in Figure 3c represent the electron flow during gas-phase ground-state thermal dissociation, showing a smooth progression of electron overlap as Na+ and K+ separate. The electron roughly equally overlaps with the two cations in the FC region, and as the bond is stretched, the overlap of the electron with both cations decreases as the bonding electron density becomes more diffuse. However, as R approaches ∼6 Å, the bonding electron overlap with the Na+ core increases with increasing R while that with the K+ core goes to zero, indicating that the charge transfer in the ground state from K+ to Na+ fully takes place once the bond approaches the dissociation limit.

In THF solution, however, the data points in Figure 3c show that the electron overlap stays roughly equally split between the two metal cations as the bond separation increases until a critical separation distance of ∼7.4 Å is reached, at which point the electron is essentially fully transferred from K+ to Na+. We can understand the suddenness of this transfer by examining the THF coordination of each cation. Figure 3e shows that the electron overlap on each cation is anticorrelated with the degree of solvent coordination, which makes sense since the addition of datively bonded THF solvent molecules helps to push electron density off of each cation. At the critical ∼7.4 Å bond separation where the electron overlap jumps, there is a corresponding jump in coordination number, with K+ becoming fully solvated with ∼7 datively bonded THFs, while Na+ reduces its coordination to only 4 datively bonded THFs, the number that is known to characterize an equilibrium Na+:electron TCP in THF.20,55 In other words, 7.4 Å is the distance where there is room to squeeze in an extra THF molecule around K+, forcing the electron onto the Na+ cation. Figure 3a shows a snapshot at R = 8 Å where it is clear that the electron resides in a Na+:electron tight contact pair and that the K+ ion is essentially fully solvated.

Figure 3d shows an even more striking difference in the equilibrium dissociation behavior of the NaK+ bonding electron between the gas and condensed phases in the excited state. In the gas phase, the dashed curves show a smooth transition from roughly equal overlap in the FC region to the electron residing nearly fully on the K+ core as the bond lengthens, indicating that photoexcitation effectively drives electron transfer from Na+ to K+. In liquid THF, however, the electron tends to remain near the bond midpoint, losing overlap with both cations as the bond dissociates. Part of this is driven by increases in THF coordination number on both cations. The electron overlap remains near zero on both cations at the longest bond distances we can directly simulate, showing clearly that dissociation has not reached completion by R = 8 Å. Figure 3b shows a snapshot of the excited-state NaK+ bonding electron density in THF at R = 8 Å, verifying that the bonding electron density has relatively little overlap with either cation.

The localization of the bonding electron in solution to form the final products of dissociation is not observed on the excited state for the longest distances that we can simulate. This fits with the PMFs shown in Figure 1b,c, which also suggest that solvation in THF greatly extends the length scales required for the dissociation reaction to go to completion. Clearly, the molecular nature of NaK(THF)n+ is quite different from that of NaK+, likely due to the fact that the datively bound THF molecules displace electron density off of both cation cores, increasing the effective size of each dissociation fragment and necessitating a larger separation to screen the interactions between fragments.

Of course, all of the analysis in Figure 3 is done for configurations with R ≤ 8 Å, which is prior to the ∼10 Å crossing point of the diabatic PMFs seen in Figure 1b,c. This implies that the adiabatic PMFs, the dotted curves in Figure 1c, undergo a qualitative change in character as the reaction traverses the avoided crossing. In other words, the bonding electron behavior should be more similar to that in the gas phase at bond distances smaller than the crossing point (as we indeed see in Figure 3), but it should become more similar to the thermodynamically favored products at bond distances beyond the crossing point. This means that as NaK+ in THF traverses this crossing regime, a long-range electron transfer process must take place for the molecule to reach the thermodynamic product:60,61 this long-range transfer must take the electron from the Na+ core to the K+ core on the ground state and vice versa on the excited state. Although there is clearly a thermodynamic driving force for this long-range electron transfer, it is difficult to deduce the actual mechanism by which this transfer might take place. It is possible that direct long-range electron transfer might occur via tunneling, although work by Gray and Winkler suggests that this type of process across a 10 Å separation occurs on a nanosecond time scale, at least in 2-methyltetrahydrofuran glass.60 Alternatively, an indirect superexchange-like mechanism might be possible, where a short-range electron transfer from the Na0 tight-contact pair takes place to one of the naturally occurring cavities in liquid THF,42,62−64 forming a transient solvated electron-like intermediate, followed by electron transfer from the cavity to K+ to form the K0 tight contact pair. Such a mechanism would provide a clear spectroscopic signature that could be monitored in ultrafast transient absorption experiments.

In conclusion, we find markedly different solute properties and dissociation behavior for NaK+ solvated in liquid THF compared to those of the bare molecule in the gas phase. As the Na–K+ bond is broken in liquid THF, the distance at which the electron chooses to reside on one of the two fragment atoms is greatly increased compared with that in the gas phase. Strikingly, the thermodynamic products of dissociation are reversed between the gas and solution phases. This is because solvation of the Na+ cation causes the Na+ + K0 products to be more stable in solution, even though these products correlate with the excited state in the gas phase. As the bond is stretched on the ground state in THF, the bonding electron appears to have somewhat gas-phase-like character, tending to associate with the Na+ ion at distances up to ∼8 Å, indicating that at even longer bond distances some type of long-range electron transfer must take place to produce the thermodynamically stable solution ground state. Clearly, the presence of explicit solvent molecules completely alters the properties of solutes, including the energetics of dissociation, the flow of charge between atomic centers, and even the choice of dissociation products.

We note in closing that all of the work shown here, including the PMFs, electron overlaps, and solvent coordination numbers, was computed for the system at equilibrium. This means that at each bond distance and on each potential surface the solvent has had essentially infinite time to relax. Upon nonequilibrium photoexcitation of NaK+ in solution, however, changes in the local THF dative bonding environment may not be able to keep up with the changing internuclear separation, especially if the datively bonded THF molecules need to isomerize prior to bond separation.18 Thus, in addition to the thermodynamics that we explore here, there may be kinetic limitations that cause the dissociating NaK+ molecule to follow the diabatic PMFs more than the adiabatic surfaces. We note that the condensed-phase PMFs that we presented, with their ∼10 Å crossing point, are averaged over all three solvent-induced chemical identities of NaK+. We expect that the dissociation of the different NaK+/THF complexes will have slightly different barriers to dissociation and show slightly different crossing points between the ground- and excited-state PMFs. We note, however, that the free energy difference associated with the reversal of the thermodynamic products is an order of magnitude larger than the free energy differences between the different NaK+ coordination states, so that our conclusions about the Na+ + K0 products being more stable in THF should be robust with respect to the coordination state. In future work, we will address the interplay between chemical identity, kinetics, and thermodynamics through nonequilibrium simulations exploring the photodissociation of NaK+ in liquid THF. Nonequilibrium dynamics can be complicated by the fact that coordination states can change on-the-fly during photodissociation, although the particular chemical identity at which the reaction starts can present different behaviors for each solute coordination state.18 Clearly, there is a richness to how solvents affect the energy surfaces and chemistry of even very simple molecules that requires a great deal of further exploration.

Methods

Overview of Mixed Quantum/Classical Molecular Dynamics Simulations. In our MQC MD simulations, the Na+ and K+ cores and the THF solvent molecules are treated classically while the single bonding electron of NaK+ is treated quantum mechanically, defining classical and quantum subsystems. The interactions with the classical subsystem are determined through pairwise Coulomb and Lennard-Jones potentials using the standard Lorentz–Berthelot mixing rules.65,66 The quantum subsystem consisting of the single bonding electron is treated using a 643 grid basis set, which spans our entire simulation box. The time-independent Schrödinger equation is solved for our quantum subsystem at every time step. Interactions between the classical and quantum subsystems are accounted for using Phillips–Kleinman67 (PK) pseudopotentials that have been previously developed and benchmarked.35,36 Contributions by the quantum subsystem to the classical nuclear dynamics are calculated through the Hellman–Feynman force.68

Potentials of Mean Force. To construct the free energy surfaces shown in Figure 1b,c, we use umbrella sampling37 to study regions along a chosen (collective) variable. Because regions along a collective coordinate may be high in free energy (e.g., at free energy barriers), a harmonic restraining potential is applied at the desired coordinate value to sample these regions:

graphic file with name jz4c01636_m002.jpg 1

where U(r) is the external umbrella potential, k is the force constant, r is the collective variable of interest, and ξ is the target value of the collective variable of interest. Since the form of the biasing potential is known, the statistics of the unbiased system can be recovered from the biased statistics.37 We then use a series of separate simulations where ξ is set to different target values along the collective variable to sample the free energy surface. The free energy differences between adjacent collective variable states are calculated using the multistate Bennet acceptance ratio (MBAR) method.38 At each harmonically restricted value, umbrella-sampled simulations were run for ∼20–40 ps as needed to sufficiently sample the solute–solvent dative bond fluctuations on both the electronic ground and excited states.

Thermodynamic Integration. The thermodynamic integration (TI)39,40 calculations to determine the free energy difference between our two dissociation product (ΔΔF) use two separate TI paths since the products of dissociation are two infinitely separated, noninteracting fragments. Along the TI paths, an alchemical transformation is used to gradually switch Na0 to K0 or Na+ to K+ using the switching parameter, λ. In the ΔΔF calculation, the sign of the Na+ to K+ transformation is flipped to reflect the appropriate direction of the transformation. The free energy difference of each path, ΔF, is calculated via

graphic file with name jz4c01636_m003.jpg 2

where K is the number of states along the transformation path, Wi is the weight of each state, which depends on the integration method, and 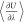Inline graphic is the ensemble-averaged derivative of the potential energy with respect to the switching parameter λ, which ranges from 0 to 1. The alchemical transformation of Na+ to K+, the classical path, has λ converting the solute–solvent Lennard-Jones potential of Na+ to that of K+. In the quantum Na0-to-K0 transformation, λ converts both the solute–solvent Lennard-Jones potential and the solute–electron pseudopotential from that of Na+ to that of K+. Along the quantum path, potential energy U includes both the classical potential and the electronic energy of the quantum electron. The free energy difference (ΔF) along each of these two paths is determined from the derivative of the potential energy with respect to the alchemical transformation parameter λ, and the results are summed to give the ΔΔF between the two sets of dissociation products. A simulation is run at each value of λ consisting of a single solute (either Na0, K0, Na+, or K+) with 254 THF molecules, a 323 grid point basis when the quantum electron is included (to yield the same grid density as our full quantum box simulations of NaK+), and a total equilibrated simulation time of 100 ps at ∼298 K. We ran ∼10 distinct lambda points for each of the two paths. 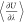We performed the integration of Inline graphic using a natural cubic spline with uncorrelated configurations. The reported error bars in our TI calculations represent the standard errors of the mean. The raw Inline graphic curves and convergence plots of the free energy are shown in the SI.

Acknowledgments

This work was supported by the U.S. Department of Energy Condensed Phase and Interfacial Molecular Science program under Grant DE-SC0017800. We gratefully acknowledge the Institute for Digital Research and Education (IDRE) at UCLA for use of the Hoffman2 computing cluster.

Data Availability Statement

Any data generated and analyzed for this study that are not included in this Letter and its Supporting Information are available from the authors upon reasonable request. The computer code used in this study is available from the authors upon reasonable request.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpclett.4c01636.

  • Additional simulation details, methodology for free energy calculations, parameters for PMF fits, and supporting figures (PDF)

The authors declare no competing financial interest.

Supplementary Material

jz4c01636_si_001.pdf (700.4KB, pdf)

References

  1. Born M.; Heisenberg W. Zur quantentheorie der molekeln. Original Scientific Papers Wissenschaftliche Originalarbeiten 1985, 216–246. 10.1007/978-3-642-61659-4_16. [DOI] [Google Scholar]
  2. Heitler W.; London F. Wechselwirkung neutraler Atome und homöopolare Bindung nach der Quantenmechanik. Zeitschrift für Physik 1927, 44, 455–472. 10.1007/BF01397394. [DOI] [Google Scholar]
  3. Mustroph H. Potential-Energy Surfaces, the Born–Oppenheimer Approximations, and the Franck-Condon Principle: Back to the Roots. ChemPhysChem 2016, 17, 2616–2629. 10.1002/cphc.201600243. [DOI] [PubMed] [Google Scholar]
  4. Schlegel H. B. Exploring potential energy surfaces for chemical reactions: an overview of some practical methods. Journal of computational chemistry 2003, 24, 1514–1527. 10.1002/jcc.10231. [DOI] [PubMed] [Google Scholar]
  5. Peslherbe G. H.; Bianco R.; Hynes J. T.; Ladanyi B. M. On the photodissociation of alkali-metal halides in solution. Journal of The Chemical Society, Faraday Transactions 1997, 93, 977–988. 10.1039/a606120f. [DOI] [Google Scholar]
  6. Koch D. M.; Peslherbe G. H. Importance of polarization in quantum mechanics/molecular mechanics descriptions of electronic excited states: NaI (H2O) n photodissociation dynamics as a case study. J. Phys. Chem. B 2008, 112, 636–649. 10.1021/jp709656z. [DOI] [PubMed] [Google Scholar]
  7. Burghardt I.; Cederbaum L. S.; Hynes J. T. Environmental effects on a conical intersection: A model study. Faraday Discuss. 2004, 127, 395–411. 10.1039/b315071b. [DOI] [PubMed] [Google Scholar]
  8. Ensing B.; Meijer E. J.; Blöchl P.; Baerends E. J. Solvation effects on the SN 2 reaction between CH3Cl and Cl-in water. J. Phys. Chem. A 2001, 105, 3300–3310. 10.1021/jp003468x. [DOI] [Google Scholar]
  9. Regan C. K.; Craig S. L.; Brauman J. I. Steric effects and solvent effects in ionic reactions. Science 2002, 295, 2245–2247. 10.1126/science.1068849. [DOI] [PubMed] [Google Scholar]
  10. Li Y.; Hartke B. Assessing solvation effects on chemical reactions with globally optimized solvent clusters. ChemPhysChem 2013, 14, 2678–2686. 10.1002/cphc.201300323. [DOI] [PubMed] [Google Scholar]
  11. Hynes J. T. Chemical reaction dynamics in solution. Annu. Rev. Phys. Chem. 1985, 36, 573–597. 10.1146/annurev.pc.36.100185.003041. [DOI] [Google Scholar]
  12. Truhlar D. G.; Hase W. L.; Hynes J. T. Current status of transition-state theory. J. Phys. Chem. 1983, 87, 2664–2682. 10.1021/j100238a003. [DOI] [Google Scholar]
  13. Franck J.; Rabinowitsch E. Some remarks about free radicals and the photochemistry of solutions. Trans. Faraday Soc. 1934, 30, 120–130. 10.1039/tf9343000120. [DOI] [Google Scholar]
  14. Slavícek P.; Žďánská P.; Jungwirth P.; Baumfalk R.; Buck U. Size effects on photodissociation and caging of hydrogen bromide inside or on the surface of large inert clusters: From one to three icosahedral argon layers. J. Phys. Chem. A 2000, 104, 7793–7802. 10.1021/jp001262q. [DOI] [Google Scholar]
  15. Vong A.; Widmer D. R.; Schwartz B. J. Nonequilibrium solvent effects during photodissociation in liquids: Dynamical energy surfaces, caging, and chemical identity. J. Phys. Chem. Lett. 2020, 11, 9230–9238. 10.1021/acs.jpclett.0c02515. [DOI] [PubMed] [Google Scholar]
  16. Widmer D. R.; Schwartz B. J. Solvents can control solute molecular identity. Nat. Chem. 2018, 10, 910–916. 10.1038/s41557-018-0066-z. [DOI] [PubMed] [Google Scholar]
  17. Widmer D. R.; Schwartz B. J. The role of the solvent in the condensed-phase dynamics and identity of chemical bonds: The case of the sodium dimer cation in THF. J. Phys. Chem. B 2020, 124, 6603–6616. 10.1021/acs.jpcb.0c03298. [DOI] [PubMed] [Google Scholar]
  18. Vong A.; Mei K. J.; Widmer D. R.; Schwartz B. J. Solvent Control of Chemical Identity Can Change Photodissociation into Photoisomerization. J. Phys. Chem. Lett. 2022, 13, 7931–7938. 10.1021/acs.jpclett.2c01955. [DOI] [PubMed] [Google Scholar]
  19. Mei K. J.; Borrelli W. R.; Vong A.; Schwartz B. J. Using Machine Learning to Understand the Causes of Quantum Decoherence in Solution-Phase Bond-Breaking Reactions. J. Phys. Chem. Lett. 2024, 15, 903–911. 10.1021/acs.jpclett.3c03474. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Glover W. J.; Larsen R. E.; Schwartz B. J. How does a solvent affect chemical bonds? Mixed quantum/classical simulations with a full CI treatment of the bonding electrons. J. Phys. Chem. Lett. 2010, 1, 165–169. 10.1021/jz9000938. [DOI] [Google Scholar]
  21. Vong A.; Schwartz B. J. Bond-Breaking Reactions Encounter Distinct Solvent Environments Causing Breakdown of Linear Response. J. Phys. Chem. Lett. 2022, 13, 6783–6791. 10.1021/acs.jpclett.2c01656. [DOI] [PubMed] [Google Scholar]
  22. Douady J.; Jacquet E.; Giglio E.; Zanuttini D.; Gervais B. Non-adiabatic molecular dynamics of excited Na2+ solvated in Ar17 clusters. Chem. Phys. Lett. 2009, 476, 163–167. 10.1016/j.cplett.2009.06.032. [DOI] [Google Scholar]
  23. Bado P.; Dupuy C.; Magde D.; Wilson K. R.; Malley M. M. Molecular dynamics of chemical reactions in solution: Experimental picosecond transient spectra for I2 photodissociation. J. Chem. Phys. 1984, 80, 5531–5538. 10.1063/1.446664. [DOI] [Google Scholar]
  24. Batista V.; Coker D. Nonadiabatic molecular dynamics simulation of photodissociation and geminate recombination of I2 liquid xenon. J. Chem. Phys. 1996, 105, 4033–4054. 10.1063/1.472277. [DOI] [Google Scholar]
  25. Delaney N.; Faeder J.; Maslen P.; Parson R. Photodissociation, Recombination, and Electron Transfer in Cluster Ions: A Nonadiabatic Molecular Dynamics Study of I2-(CO2) n. J. Phys. Chem. A 1997, 101, 8147–8151. 10.1021/jp972435n. [DOI] [Google Scholar]
  26. Vila A.; Gonzalez M.; Mayol R. Photodissociation dynamics of homonuclear diatomic molecules in helium nanodroplets. The case of Cl2@(4He) N. J. Chem. Theory Comput. 2015, 11, 899–906. 10.1021/ct5011642. [DOI] [PubMed] [Google Scholar]
  27. Nandi S.; Sanov A.; Delaney N.; Faeder J.; Parson R.; Lineberger W. Photodissociation of I2-(OCS) n cluster ions: structural implications. J. Phys. Chem. A 1998, 102, 8827–8835. 10.1021/jp982794y. [DOI] [Google Scholar]
  28. Zadoyan R.; Li Z.; Martens C.; Apkarian V. The breaking and remaking of a bond: Caging of I2 in solid Kr. J. Chem. Phys. 1994, 101, 6648–6657. 10.1063/1.468359. [DOI] [Google Scholar]
  29. Bardeen C. J.; Che J.; Wilson K. R.; Yakovlev V. V.; Apkarian V.; Martens C.; Zadoyan R.; Kohler B.; Messina M. Quantum control of I 2 in the gas phase and in condensed phase solid Kr matrix. J. Chem. Phys. 1997, 106, 8486–8503. 10.1063/1.473906. [DOI] [Google Scholar]
  30. Valance A. Adiabatic potential energies for NaK+, NaRb+, NaCs+, KRb+, KCs+, RbCs+, Na+ 2, K2+, Rb+ 2, and Cs+ 2 molecular ions. J. Chem. Phys. 1978, 69, 355–366. 10.1063/1.436361. [DOI] [Google Scholar]
  31. Valance A.; Bernier A.; El Maddarsi M. Σ and Π molecular states for NaK+, KRb+ and NaRb+ molecular ions. Chemical physics 1986, 103, 151–162. 10.1016/0301-0104(86)85110-2. [DOI] [Google Scholar]
  32. Musiał M.; Bewicz A.; Skupin P.; Kucharski S. A.. Adv. Quantum Chem.; Elsevier, 2018; Vol. 76; pp 333–349. [Google Scholar]
  33. Ciocca M.; Burkhardt C. E.; Leventhal J. J.; Bergeman T. Precision Stark spectroscopy of sodium: Improved values for the ionization limit and bound states. Phys. Rev. A 1992, 45, 4720–4730. 10.1103/PhysRevA.45.4720. [DOI] [PubMed] [Google Scholar]
  34. Lorenzen C.-J.; Niemax K.; Pendrill L. Precise measurements of 39K nS and nD energy levels with an evaluated wavemeter. Opt. Commun. 1981, 39, 370–374. 10.1016/0030-4018(81)90225-X. [DOI] [Google Scholar]
  35. Smallwood C. J.; Larsen R. E.; Glover W. G.; Schwartz B. J. A Computationally Efficient Exact Pseudopotential Method. I. Analytic Reformulation of the Philips-Kleinman Theory. J. Chem. Phys. 2006, 125, 074102. 10.1063/1.2218834. [DOI] [PubMed] [Google Scholar]
  36. Smallwood C. J.; Mejia C. N.; Glover W. G.; Larsen R. E.; Schwartz B. J. A Computationally Efficient Exact Pseudopotential Method. II. Application to the Molecular Pseudopotential of an Excess Electron Interacting with Tetrahydrofuran (THF). J. Chem. Phys. 2006, 125, 074103. 10.1063/1.2218835. [DOI] [PubMed] [Google Scholar]
  37. Torrie G. M.; Valleau J. P. Nonphysical sampling distributions in Monte Carlo free-energy estimation: Umbrella sampling. J. Comput. Phys. 1977, 23, 187–199. 10.1016/0021-9991(77)90121-8. [DOI] [Google Scholar]
  38. Shirts M. R.; Chodera J. D. Statistically optimal analysis of samples from multiple equilibrium states. J. Chem. Phys. 2008, 129, 124105. 10.1063/1.2978177. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Kirkwood J. G. Statistical mechanics of fluid mixtures. J. Chem. Phys. 1935, 3, 300–313. 10.1063/1.1749657. [DOI] [Google Scholar]
  40. Klimovich P. V.; Shirts M. R.; Mobley D. L. Guidelines for the analysis of free energy calculations. Journal of computer-aided molecular design 2015, 29, 397–411. 10.1007/s10822-015-9840-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Cavanagh M. C.; Larsen R. E.; Schwartz B. J. Watching Na Atoms Solvate into (Na+, e-) Contact Pairs: Untangling the Ultrafast Charge-Transfer-to-Solvent Dynamics of Na-in Tetrahydrofuran (THF). J. Phys. Chem. A 2007, 111, 5144–5157. 10.1021/jp071132i. [DOI] [PubMed] [Google Scholar]
  42. Bragg A. E.; Schwartz B. J. Ultrafast charge-transfer-to-solvent dynamics of iodide in tetrahydrofuran. 2. Photoinduced electron transfer to counterions in solution. J. Phys. Chem. A 2008, 112, 3530–3543. 10.1021/jp712039u. [DOI] [PubMed] [Google Scholar]
  43. Bockrath B.; Dorfman L. M. Pulse radiolysis studies. XXII. Spectrum and kinetics of the sodium cation-electron pair in tetrahydrofuran solutions. J. Phys. Chem. 1973, 77, 1002–1006. 10.1021/j100627a007. [DOI] [Google Scholar]
  44. Fletcher J.; Seddon W. Alkali metal species in liquid amines, ammonia, and ethers. Formation by pulse radiolysis. J. Phys. Chem. 1975, 79, 3055–3064. 10.1021/j100593a054. [DOI] [Google Scholar]
  45. Seddon W.; Fletcher J.; Sopchyshyn F.; Selkirk E. Flash photolysis of alkali metal anions in tetrahydrofuran and dimethoxyethane. Can. J. Chem. 1979, 57, 1792–1800. 10.1139/v79-286. [DOI] [Google Scholar]
  46. Piotrowiak P.; Miller J. R. Spectra of the solvated electron in the presence of sodium cation in tetrahydrofuran and in its. alpha.,. alpha.’-methylated derivatives. J. Am. Chem. Soc. 1991, 113, 5086–5087. 10.1021/ja00013a069. [DOI] [Google Scholar]
  47. Shoshana O.; Lustres J. P.; Ernsting N.; Ruhman S. Mapping CTTS dynamics of Na- in tetrahydrofurane with ultrafast multichannel pump-probe spectroscopy. Phys. Chem. Chem. Phys. 2006, 8, 2599–2609. 10.1039/B602933G. [DOI] [PubMed] [Google Scholar]
  48. Cavanagh M. C.; Young R. M.; Schwartz B. J. The roles of the solute and solvent cavities in charge-transfer-to-solvent dynamics: Ultrafast studies of potasside and sodide in diethyl ether. J. Chem. Phys. 2008, 129, 134503. 10.1063/1.2977995. [DOI] [PubMed] [Google Scholar]
  49. Catterall R.; Slater J.; Symons M. Electron spin resonance studies of preferential solvation in solutions of potassium in amines and ethers. Can. J. Chem. 1977, 55, 1979–1984. 10.1139/v77-276. [DOI] [Google Scholar]
  50. Seddon W. A.; Fletcher J. W.; Sopchyshyn F. C.; Catterall R. Solvated electrons and the effect of coordination on the optical spectra of alkali metal cation–electron pairs in ethers. Can. J. Chem. 1977, 55, 3356–3363. 10.1139/v77-470. [DOI] [Google Scholar]
  51. Seddon W.; Fletcher J. The contribution of pulse radiolysis to the chemistry of alkali metal solutions. Radiation Physics and Chemistry (1977) 1980, 15, 247–254. 10.1016/0146-5724(80)90138-7. [DOI] [Google Scholar]
  52. Bragg A. E.; Cavanagh M. C.; Schwartz B. J. Linear response breakdown in solvation dynamics induced by atomic electron-transfer reactions. Science 2008, 321, 1817–1822. 10.1126/science.1161511. [DOI] [PubMed] [Google Scholar]
  53. Glover W. J.; Larsen R. E.; Schwartz B. J. Simulating the formation of sodium: electron tight-contact pairs: Watching the solvation of atoms in liquids one molecule at a time. J. Phys. Chem. A 2011, 115, 5887–5894. 10.1021/jp1101434. [DOI] [PubMed] [Google Scholar]
  54. Bragg A. E.; Glover W. J.; Schwartz B. J. Watching the solvation of atoms in liquids one solvent molecule at a time. Physical review letters 2010, 104, 233005. 10.1103/PhysRevLett.104.233005. [DOI] [PubMed] [Google Scholar]
  55. Glover W. J.; Larsen R. E.; Schwartz B. J. Nature of sodium atoms/(Na+, e-) contact pairs in liquid tetrahydrofuran. J. Phys. Chem. B 2010, 114, 11535–11543. 10.1021/jp103961j. [DOI] [PubMed] [Google Scholar]
  56. Hund F. Zur deutung der molekelspektren. i. Zeitschrift für Physik 1927, 40, 742–764. 10.1007/BF01400234. [DOI] [Google Scholar]
  57. Teller E. The Crossing of Potential Surfaces. J. Phys. Chem. 1937, 41, 109–116. 10.1021/j150379a010. [DOI] [Google Scholar]
  58. Tchang-Brillet W.-Ü. L.; Julienne P.; Robbe J.-M.; Letzelter C.; Rostas F. A model of the B 1Σ+-D 1Σ+ Rydberg-valence predissociating interaction in the CO molecule. J. Chem. Phys. 1992, 96, 6735–6745. 10.1063/1.462561. [DOI] [Google Scholar]
  59. Yu N.; Margulis C.; Coker D. Influence of solvation environment on excited state avoided crossings and photodissociation dynamics. J. Phys. Chem. B 2001, 105, 6728–6737. 10.1021/jp0108925. [DOI] [Google Scholar]
  60. Gray H. B.; Winkler J. R. Long-range electron transfer. Proc. Natl. Acad. Sci. U. S. A. 2005, 102, 3534–3539. 10.1073/pnas.0408029102. [DOI] [PMC free article] [PubMed] [Google Scholar]
  61. Winkler J. R.; Gray H. B. Long-range electron tunneling. J. Am. Chem. Soc. 2014, 136, 2930–2939. 10.1021/ja500215j. [DOI] [PMC free article] [PubMed] [Google Scholar]
  62. Bragg A. E.; Schwartz B. J. The ultrafast charge-transfer-to-solvent dynamics of iodide in tetrahydrofuran. 1. Exploring the roles of solvent and solute electronic structure in condensed-phase charge-transfer reactions. J. Phys. Chem. B 2008, 112, 483–494. 10.1021/jp076934s. [DOI] [PubMed] [Google Scholar]
  63. Bedard-Hearn M. J.; Larsen R. E.; Schwartz B. J. The role of solvent structure in the absorption spectrum of solvated electrons: Mixed quantum/classical simulations in tetrahydrofuran. J. Chem. Phys. 2005, 122, 134506. 10.1063/1.1867378. [DOI] [PubMed] [Google Scholar]
  64. Bedard-Hearn M. J.; Larsen R. E.; Schwartz B. J. Moving solvated electrons with light: Nonadiabatic mixed quantum/classical molecular dynamics simulations of the relocalization of photoexcited solvated electrons in tetrahydrofuran (THF). J. Chem. Phys. 2006, 125, 194509. 10.1063/1.2358131. [DOI] [PubMed] [Google Scholar]
  65. Lorentz H. A. Ueber die Anwendung des Satzes vom Virial in der kinetischen Theorie der Gase. Annalen der physik 1881, 248, 127–136. 10.1002/andp.18812480110. [DOI] [Google Scholar]
  66. Berthelot D. Sur le mélange des gaz. Compt. Rendus 1898, 126, 15. [Google Scholar]
  67. Phillips J. C.; Kleinman L. New Method for Calculating Wave Functions in Crystals and Molecules. Phys. Rev. 1959, 116, 287–294. 10.1103/PhysRev.116.287. [DOI] [Google Scholar]
  68. Feynman R. P. Forces in molecules. Physical review 1939, 56, 340. 10.1103/PhysRev.56.340. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jz4c01636_si_001.pdf (700.4KB, pdf)

Data Availability Statement

Any data generated and analyzed for this study that are not included in this Letter and its Supporting Information are available from the authors upon reasonable request. The computer code used in this study is available from the authors upon reasonable request.

Articles from The Journal of Physical Chemistry Letters are provided here courtesy of American Chemical Society

RESOURCES