Benchmarking Quantum Mechanical Levels of Theory for Valence Parametrization in Force Fields

Abstract

A wide range of density functional methods and basis sets are available to derive the electronic structure and properties of molecules. Quantum mechanical calculations are too computationally intensive for routine simulation of molecules in the condensed phase, prompting the development of computationally efficient force fields based on quantum mechanical data. Parametrizing general force fields, which cover a vast chemical space, necessitates the generation of sizable quantum mechanical data sets with optimized geometries and torsion scans. To achieve this efficiently, choosing a quantum mechanical method that balances computational cost and accuracy is crucial. In this study, we seek to assess the accuracy of quantum mechanical theory for specific properties such as conformer energies and torsion energetics. To comprehensively evaluate various methods, we focus on a representative set of 59 diverse small molecules, comparing approximately 25 combinations of functional and basis sets against the reference level coupled cluster calculations at the complete basis set limit.

1. Introduction

General force fields offer a computationally efficient alternative to quantum mechanical (QM) calculations,¹⁻¹³ in particular for pharmaceutical and biomolecular applications. Parametrizing general force fields or training machine learning (ML) potentials, for molecular mechanics (MM), requires extensive quantum chemistry data sets, with molecules covering a large chemical space, that inform the bonded parameters, typically bonds, angles, and torsions as well as nonbonded terms.¹⁴⁻²¹ The data sets include optimized chemical structures of different conformers of molecules and associated properties such as charges, bond orders, dipole moments, Hessian matrices, and torsion energy profiles for rotatable bonds, dimer interaction energies, among other data. A quantum mechanical method is needed that is globally accurate for different chemistries and properties, is computationally cost-effective, and can converge with a predefined set of hyperparameters (or a template with minimal changes) without too much human intervention, thus enabling automated generation of larger data sets essential for this effort. There are hundreds of density functionals, post Hartree–Fock methods, and basis sets to choose from, and it is cumbersome to pick one without a proper benchmark study.

Recent benchmark studies address the issue of how accurate a quantum mechanical method is with respect to a highly accurate gold standard such as coupled cluster with singles, doubles and perturbative triples in the complete basis set limit (CCSD(T)/CBS). Some studies are from the viewpoint of quantum chemistry method developers, where one would be concerned by a difference of even 0.1 kcal/mol in mean accuracy of absolute energies, with respect to the reference level of theory. However, from the perspective of practitioners engaged in force field development and general biochemical simulations, where relative energies such as conformer energetics and torsional profiles are of primary concern (as emphasized in Sellers et al.²²), it is crucial that the quantum mechanical (QM) methods used to generate reference data for force field parametrization can reproduce torsion energy profiles with deviations of approximately 0.5 to 1.0 kcal/mol or smaller. This level of accuracy, as demonstrated in high-level QM calculations, is vital for ensuring the accuracy of trained force fields, and boosts the reliability of property predictions like protein–ligand binding affinities.^22,23 By achieving accuracy within this specified range for the QM reference data employed in force field parametrization, and assuming the trained force field mimics the QM training data quite well, we can effectively capture the essential conformational behavior and energetic trends exhibited by the molecules under investigation. Our focus here is precisely in this area, conformational energetics, and not on modeling long-range electrostatic interactions, which may involve different considerations.²⁴⁻²⁷

Our primary focus is on accurately modeling small molecule organic compounds within pharmaceutically relevant regions of chemical space using force fields. As a result, we do not concern ourselves with evaluating the performance of quantum mechanical (QM) methods for compounds involving transition elements, lanthanides, noble gases, and other elements not directly implicated in the fundamental molecular interactions governing the binding and recognition of small molecule drugs. At the Open Force Field (OpenFF) Initiative,^3,28 our attention lies on achieving performance benchmarks for organic molecules within the chemical space that is pertinent to small molecule drugs and that our force fields are currently capable of modeling. This chemical space encompasses C, H, O, N, P, S, F, Cl, Br, and I, as well as the monatomic ions Li⁺, Na⁺, K⁺, Rb⁺, F^–, Cl^–, Br^–, and I^–.

A variety of different method and basis set combinations in gas-phase calculations have been used in building various general force fields as well as ML potentials, depending on the force field and application. Some other common models were derived as follows:

• GAFF: MP2/6-31G* was used as one of the sources of training bond and angle parameters. For the torsional parameters MP4/6-311G**//MP2/6-31G* was used.⁴

• CHARMm: valence parameters were trained on QM data calculated at the MP2/6-31G* and MP2/6-31+G* levels.²⁹

• ANI-1: Training data generated at ωB97X/6-31G* level of theory. ANI-1ccx used CCSD(T)/CBS extrapolated structures.³⁰

• OPLS3e: M06-2X/cc-pVTZ(-f)//B3LYP/6-31G* level of theory was used for their training set.¹⁰

• TorsionNet: a mix of data generated at B3LYP/6-31G**//HF/3-21G and B3LYP/6-31+G**//HF/3-21G.³¹

• OrbNet Denali: ωB97X-D3/def2-TZVP level of theory.³²

• Open Force Field (OpenFF): B3LYP-D3(BJ)/DZVP was the default level of theory.²

• Espaloma: A mix of SPICE¹⁶ data set and OpenFF data sets, all of the data generated at B3LYP-D3(BJ)/DZVP level of theory.¹⁸

• MACE-OFF23: SPICE¹⁶ data set at ωB97M-D3(BJ)/def2-TZVPPD level of theory.²¹

Traditionally there are five rungs on “Jacob’s ladder” of chemical accuracy corresponding to the density functional theory (DFT) method used.³³ Starting with the Local Density Approximation (LDA), we progress one level up the accuracy ladder each with Generalized Gradient Approximation (GGA), meta-GGA, hybrid functionals, and then double hybrid functionals. Although, all hybrid functionals do not necessarily include the ingredient added in “meta-GGA” which uses the second derivative of the density in the energy functional. For example, B3LYP does not have the meta-GGA term, but M06 does. Hybrid and double-hybrid functionals are distinguished by including a percentage of HF exchange, and a percentage of MP2 correlation, respectively. Therefore, double hybrid functionals are at least the cost of a MP2 calculation. Range separated functionals (RSF) are another very important development in DFT methods. In RSFs, such as ωB97 family, the percentage of HF exchange depends on the distance between the electrons. This accounts for the electron self-interaction error, and has become incorporated into several of the most modern functionals (i.e., the ones starting with LC or ω). DFT methods with dispersion corrections, which can be either ab initio,³⁴⁻³⁶ or empirical in nature,³⁷ are notably more accurate than their standard forms as they improve the description of the noncovalent interactions. Grimme’s DFT-D3,^38,39 along with Becke-Johnson (BJ) damping,⁴⁰ is one of the most prominent dispersion corrections widely used in the field. On the other hand, wave function based methods (WFT) include Hartree–Fock, post-Hartree–Fock methods viz., Møller–Plesset perturbation theory of different orders (MP2, MP3, MP4), configuration interaction (CI), coupled cluster (CC), and multireference methods such as complete active space self-consistent field (CASSCF), in increasing order of complexity in describing electron correlation, and approaching higher accuracy.

Recent studies have utilized several benchmark data sets to assess the general quality of QM methods for specific molecular properties. Notable among these data sets are Database2015B,⁴¹ GMTKN30⁴² and its expanded version GMTKN55,⁴³ MGCDB84,⁴⁴ CHAL336,⁴⁵ MPCONF196,⁴⁶ YMPJ,⁴⁷ S22,⁴⁸ S66,⁴⁹ HB375,⁵⁰ TorsionNet500,³¹ Dakota Folmsbee’s set,⁵¹ XB18,⁵² CTB-279.⁵³ The subsets of these data sets emphasize performance on predicting:

• noncovalent interactions, both inter- and intramolecular

• isomerization energies

• chemical reaction barrier heights

• relative conformer energies for various chemical moieties

• torsional strain, and barriers

In our present study we want to address

• the extent to which benchmark results of quantum mechanical methods obtained from larger basis sets, as documented in existing literature, are informative when deployed with smaller basis sets

• how good OpenFF’s current choice of DZVP basis set is in describing conformational energetics for charged entities, and whether the error in relative energies of torsion profiles is within the desired range (0.5–1 kcal/mol) without addition of more diffuse functions to the basis set

• how well different QM methods predict torsional energy profiles and whether the accuracy gain is significant enough that it warrants a change in QM reference for force field training

2. Motivation and Approach

2.1. Prior Studies and Selection of Molecules

Based on earlier benchmark studies,^2,54 the OpenFF initiative initially chose B3LYP-D3(BJ)/DZVP as the method for generating QM training data to train OpenFF force fields, with the expectation that this choice might need to be revisited at a later date. Such a “revisit” is our focus here. The prior benchmarks² included assessing accuracy of conformer energetics on the MPCONF196 set,⁴⁶ which is a data set of conformers of smaller peptides and medium-sized macrocycles, that were all neutral, and of relative energies of torsional profiles on a curated set of 15 one-dimensional torsion scans. A good compromise between accuracy and cost on MPCONF196 and the smaller set of torsion scans led to the choice of the B3LYP-D3(BJ) functional along with Salahub’s double-ζ split-valence + polarization (DZVP) basis set⁵⁵ for building OpenFF force fields.

Although very insightful, this prior benchmark study did not include charged molecules, and was limited to [C, H, N, O] chemical space. Because of these limitations, here we focused on running a new benchmark which would more adequately represent the pharmaceutically relevant chemical space that our force field needs to describe accurately. Thus, to expand the scope of the prior benchmark we selected 59 torsions from molecules in OpenFF’s Roche (general, and tautomer+protomer data set) and Coverage molecule sets.

Molecule selection followed these criteria:

• ensuring a comprehensive representation of chemical diversity

• prioritizing size similarity among molecules to mitigate the influence of intrinsic size-related effects on electronic properties

• incorporating variations in central bonds, formal charges, element compositions, and intramolecular interactions

• and, inclusion of molecules that added additional complexity beyond those in the prior set, such as those with

  • nonzero formal charges

  • strong internal interactions

  • conjugated central rotatable bonds (>10 kcal/mol rotational barrier)

  • halogens

The extracted charged molecules were further subdivided into groups based on the type of charged functional group. Here are the SMARTS patterns of the subgroups which include,

• functional groups with a charge of −1

  • phenolate: c[O-]

  • carboxamide: C(=O)[N-]

  • aromatic carbons connected to a nitrogen with a negative charge: c[N-]c

  • sulfonamide: S(=O)(=O)[N-]

  • sulfinamide: S(=[N-])(=O)

• functional groups with a charge of +1:

  • protonated amine with carbon bond: [NH+,nH+](=,:[C,c])[C,c]

  • protonated amine: [NH+]([*])[*]

  • protonated primary amine: [NH2+]([*])[*]

  • protonated ammonium: [NH3+][*]

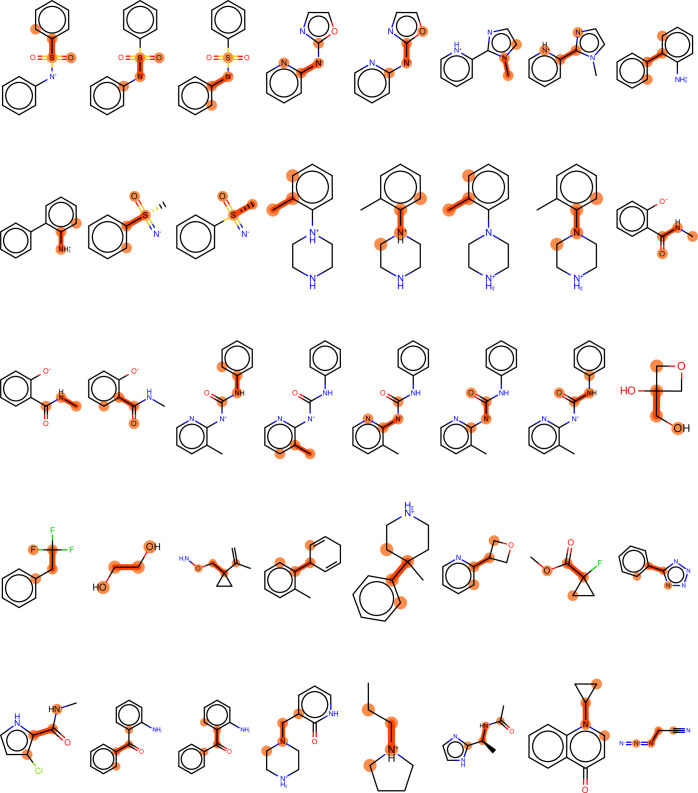
We then performed one-dimensional torsion scans on one selected molecule per cluster. We selected one molecule per cluster by picking the centroid using the MACCS keys fingerprint method.⁵⁶ Following selection, we performed one-dimensional torsion scans by rotating around the central bond in the chosen dihedral. In total, 59 torsions were scanned in 36 unique molecules, shown in Figure 1 with the dihedral atoms highlighted, in this benchmark study.

Figure 1.

Molecules used in this benchmark study. The atoms and central bonds engaged in the driven torsions are highlighted.

2.2. Computational Details

Torsion scans were performed with a 15-degree grid spacing, using Torsiondrive,⁵⁷ resulting in a total of 24 points on the grid within the range of [-180°, 180°]. More details on the compute infrastructure were provided in SI section 1.2.

2.2.1. Choice of Reference Theory

The benchmark geometries were the final geometries from the torsion scan at MP2/heavy-aug-cc-pVTZ level of theory. Whereas, the benchmark relative energies were obtained using coupled cluster with single, double, and perturbative triple excitations at the complete basis set limit, CCSD(T)/CBS. It is to be noted that MP2 is a wave function-based method that treats electron correlation explicitly, and does not rely on the same approximations as DFT functionals. Hence, MP2 geometries offer a more neutral and consistent basis for benchmarking devoid of the specific biases inherent to individual DFT functionals. For the complete basis set calculation, Helgaker’s 2-point extrapolation scheme was used as implemented in Psi4.⁵⁸⁻⁶⁰ Helgaker extrapolation scheme here includes a reference total energy from Hartree–Fock, correlation correction which includes correlation effects beyond HF with the MP2 method, and a delta correction, which gives a highly accurate correlation calculation with CCSD(T), accounting for the error in MP2. The difference between CCSD(T) and MP2 converges quickly with increase in basis functions and hence a smaller basis set can be used for this part of calculation. Psi4 performs these calculations in stages and the treatment follows this equation:⁶⁰

1

where 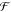is an energy or energy extrapolation scheme. And, in our case this translates to

2

Although heavy-aug-cc-pVDZ (or haDZ) is computationally affordable it may fall short of the gold standard reference level of theory often used in the community.^61,62 It is expected that the delta correction error with haDZ would fall somewhere in between 0.1 and 0.25 kcal/mol, the errors observed with aug-cc-pVDZ and cc-pVDZ on either end of the range.^63,64 To assess how good our choice of reference theory level is we have performed energy calculations with the gold standard reference theory level for a subset of 7 molecules from the benchmark set⁶¹ at CCSD(T)/CBS, where for the extrapolation to CBS the correlation basis is aug-cc-pV[TQ]Z, and delta basis is aug-cc-pVTZ. The gold standard energy is calculated as,⁶⁰

3

Our reference theory level employed a computationally efficient smaller basis set (haDZ) for delta correction when compared to a larger basis (aTZ) used in the gold standard reference. And, the RMSE in relative energies for the 7 molecule subset (7 × 24 grid points) of our reference theory with respect to the gold standard was 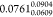kcal/mol (the subscript and superscript are the 95% confidence intervals). So, the difference with respect to the gold standard was one tenths of a kcal/mol for our choice of reference theory level, which was accurate enough and quite affordable for our study.

2.2.2. Choice of Density Functionals to Benchmark

We have chosen a smaller pool of density functional approximations (DFA) that are cost-effective from the get go and we are not looking into a comprehensive evaluation of all available DFAs. The choice of DFAs include those commonly used in developing force fields and charge models, and better performing ones from other benchmark studies. From our prior studies DZVP has been proven cost friendly and all of the DFAs were tested with this basis set. And, within our current choice of DFA used in developing OpenFF force fields, B3LYP-D3BJ, we tested Ahlrichs def2 basis sets incrementing them systematically in size, and the Pople basis sets in increasing size as they are commonly used in practice in industry. Also, one of the purposes of the study was to determine which DFAs are useful at medium sized basis sets. The rankings and differences might vary from the benchmarks at larger basis sets. This selection represents different rungs on the Jacob’s ladder of chemical accuracy.

• B97 (GGA), with D3(BJ) dispersion correction and with def2-TZVP basis set

• B3LYP hybrid family (hybrid-GGA), with⁶⁵

  • D3(BJ) dispersion correction, and following basis sets^55,66−75

    • DZVP

    • def2-SV(P)

    • def2-SVP

    • def2-TZVP

    • def2-QZVP

    • def2-TZVPP

    • def2-TZVPD

    • def2-TZVPPD

    • 6-31G*

    • 6-31+G**

    • 6-311+G**

  • D3MBJ⁷⁶ dispersion correction and DZVP basis

  • NL dispersion correction and DZVP basis

• Berkeley range separated functionals (meta-GGA),⁷⁷ with DZVP basis and dispersion corrections,

  • ωB97M-V, ωB97M-D3(BJ)

  • ωB97X-D3(BJ)

• Minnesota functionals (meta-GGA),⁷⁸⁻⁸¹ with DZVP basis and dispersion corrections

  • M05-2X-D3

  • M06-2X-D3

  • M08-HX-D3

• PW6B95 (meta-GGA),⁸² with DZVP and dispersion corrections

  • D3(BJ)

  • D3

• Double hybrid DSD-BLYP-D3(BJ)⁸³ with haTZ basis

3. Results and Discussion

3.1. Comparison of Different Levels of Theory

In the context of force field fitting, apart from conformer energies and optimized geometries, torsion energy profiles are another important source of molecular geometries/energetics data. The energy barriers observed in torsion energy profiles are a measure of the strength of steric hindrance or strong intramolecular interactions that prevent certain conformations. Thus, accurately capturing torsion profiles is relevant for understanding molecular recognition, binding, and other interactions that occur in complex systems. Our aim here is to pick an accurate and computationally efficient QM level of theory to train the valence parameters in a general small molecule force field. For this purpose, single point energies were evaluated at different levels of theory for comparison at the benchmark geometries, and the RMSE in relative energies was tabulated. Single point energies were evaluated at the same geometry to ensure parity between the methods since performing a geometry optimization with each of the methods will result in minor differences in final geometries, and sometimes TorsionDrive may push them to a completely different minima. SI Table S1 lists the RMSE in torsion profile energies for each of the molecules considered in this benchmark set with respect to the reference level of theory, CCSD(T)/[haTQZ; δ:haDZ].

The relative energies were calculated by subtracting the minimum energy for each of the methods. And, the RMSE was calculated with respect to the reference theory level.

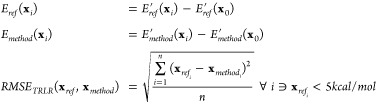4

where E’ represents the absolute energies, x₀ represents the minimum energy point. And, the RMSE and MUE were evaluated with the relative energies. For calculating the RMSE of thermally relevant low-energy region (TRLR), only the relative energies below 5 kcal/mol on the reference energy surface were chosen. The cutoff of 5 kcal/mol was chosen to favor low-energy regions in state space.^3,28,84

From Table 1 we can see that RMSE values of relative energies for most of the functional and basis set combinations studied here fall in the range of 0.4–0.7 kcal/mol with respect to CCSD(T)/[haTQZ; δ:haDZ], the reference level of theory. ωB97M-D3(BJ)/DZVP is the most accurate among those tested here with an RMSE in torsion profile energies of 0.41 kcal/mol. This range-separated hybrid functional has been one of the top performers in several other recent studies that were done with larger basis sets.^43,44 Our current choice of theory, B3LYP-D3(BJ)/DZVP, has an RMSE of 0.52 kcal/mol and it closely trails by a difference of 0.1 kcal/mol when compared to the best functional in this study. Almost half of the of the other tested levels of theory were within 0.1 kcal/mol of the best functional. No method is consistently the most accurate across all of the subsets, highlighting the importance of considering a large and diverse benchmark set.

Table 1. Overall RMSE and MUE (in kcal/mol) in Torsion Profile Energies of the Molecule Set with Respect to the Reference Level CCSD(T)/[haTQZ; δ:haDZ]//MP2/heavy-aug-cc-pVTZ Level of Theory^a.

	metric (kcal/mol)
specification	RMSE	MUE	RMSE-TRLR
B97-D3(BJ)/def2-TZVP
M05-2X-D3/DZVP
M06-2X-D3/DZVP
M08-HX-D3/DZVP
ωB97X-D3BJ/DZVP
ωB97M-D3BJ/DZVP
ωB97M-V/DZVP
PW6B95-D3(BJ)/DZVP
PW6B95-D3/DZVP
MP2/aug-cc-pVTZ
MP2/heavy-aug-cc-pVTZ
DSD-BLYP-D3(BJ)/heavy-aug-cc-pVTZ
B3LYP-D3(BJ)/DZVP
B3LYP-D3MBJ/DZVP
B3LYP-NL/DZVP
B3LYP-D3(BJ)/def2-SV(P)
B3LYP-D3(BJ)/def2-SVP
B3LYP-D3(BJ)/def2-TZVP
B3LYP-D3(BJ)/def2-TZVPD
B3LYP-D3(BJ)/def2-TZVPP
B3LYP-D3(BJ)/def2-TZVPPD
B3LYP-D3(BJ)/def2-QZVP
B3LYP-D3(BJ)/6-31G*
B3LYP-D3(BJ)/6-31+G**
B3LYP-D3(BJ)/6-311+G**

^aThe 95% confidence intervals, calculated with cinnabar, are presented as subscripts and superscripts. Furthermore, the last column includes the RMSE within the thermally relevant low-energy region (TRLR) with energies of <5 kcal/mol, averaged over all of the molecules, which serves as a metric for assessing accuracy in low-energy regions. The best performer on this set of molecules is ωB97M-D3(BJ)/DZVP, and our current choice of theory level, B3LYP-D3(BJ)/DZVP, lags behind it by only 0.1 kcal/mol in RMSE.

The RMSEs on the whole set and the subsets of neutral and charged molecule sets were depicted in Figure 3 and tabulated in Table 2. We can see from Figure 3(f), and from Table 2, that the accuracy of B3LYP-D3(BJ) functional increases for charged molecules with addition of polarization and diffuse functions from DZVP to def2-TZVP and higher. Within B3LYP-D3(BJ) it is to be noted that the high quality DZVP basis set yields comparable results to the larger triple-ζ level basis set, def2-TZVP. PW6B95-D3(BJ)/DZVP is the best among the tested methods for neutral molecules with an RMSE of 0.43 kcal/mol. ωB97M-D3(BJ)/DZVP is also on the same level with statistically insignificant difference. And, B3LYP-D3(BJ)/DZVP, has an RMSE of 0.45 kcal/mol and it closely trails these two functionals by a negligible difference of 0.02 kcal/mol for neutral molecules.

Figure 3.

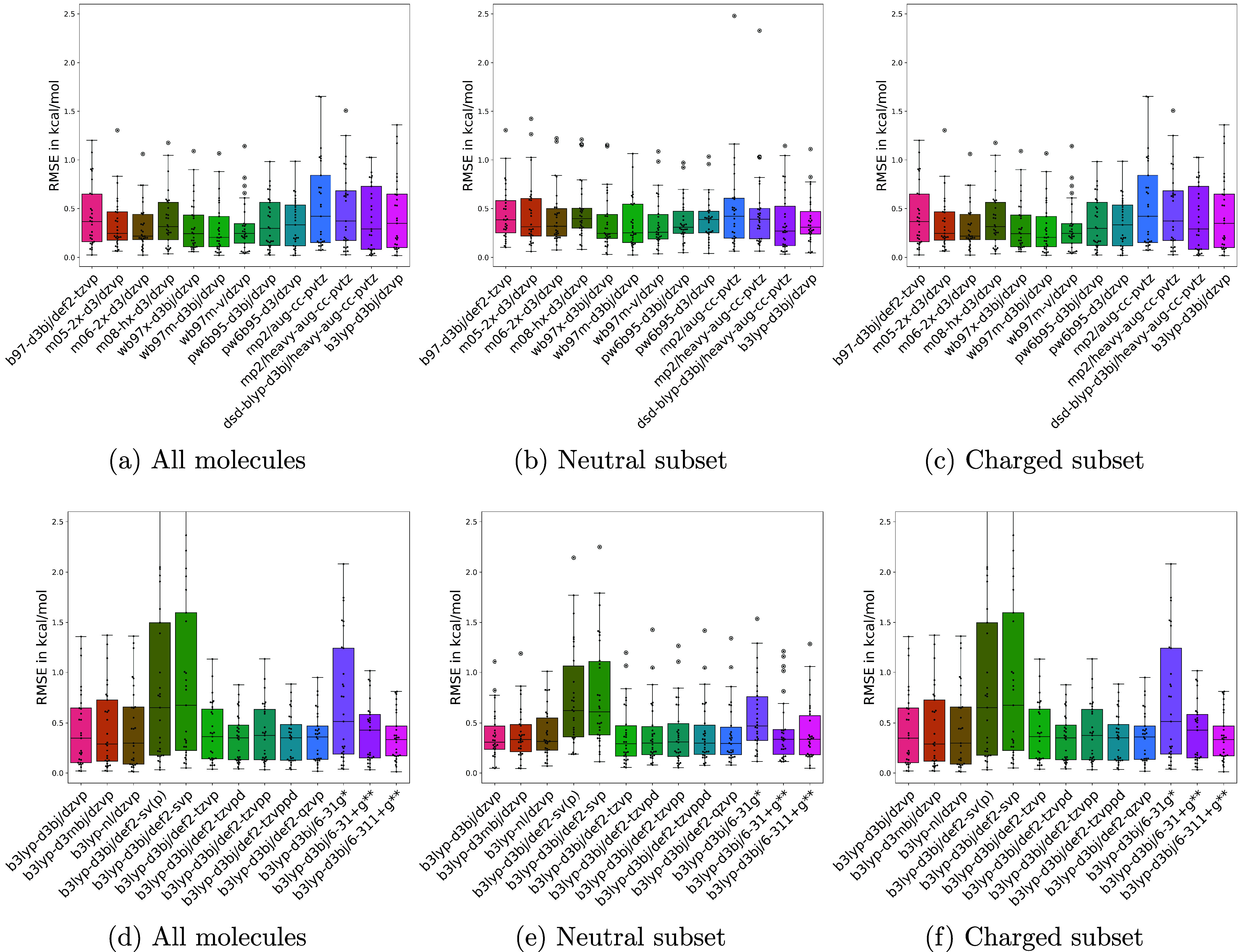
RMSE on the entire benchmark data set and on subsets of neutral and charged molecules. The top row shows the RMSE in torsion profile energies with different functional and basis set combinations. The bottom row shows the RMSE within the B3LYP functional.

Table 2. Comparison between Neutral and Charged Molecule Subsets^a.

	RMSE (kcal/mol)
specification	whole set	neutral subset	charged subset
B97-D3(BJ)/def2-TZVP
M05-2X-D3/DZVP
M06-2X-D3/DZVP
M08-HX-D3/DZVP
ωB97X-D3(BJ)/DZVP
ωB97M-D3BJ/DZVP
ωB97M-V/DZVP
PW6B95-D3(BJ)/DZVP
PW6B95-D3/DZVP
MP2/aug-cc-pVTZ
MP2/heavy-aug-cc-pVTZ
DSD-BLYP-D3(BJ)/heavy-aug-cc-pVTZ
B3LYP-D3(BJ)/DZVP
B3LYP-D3MBJ/DZVP
B3LYP-NL/DZVP
B3LYP-D3(BJ)/def2-SV(P)
B3LYP-D3(BJ)/def2-SVP
B3LYP-D3(BJ)/def2-TZVP
B3LYP-D3(BJ)/def2-TZVPD
B3LYP-D3(BJ)/def2-TZVPP
B3LYP-D3(BJ)/def2-TZVPPD
B3LYP-D3(BJ)/def2-QZVP
B3LYP-D3(BJ)/6-31G*
B3LYP-D3(BJ)/6-31+G**
B3LYP-D3(BJ)/6-311+G**

^aThe overall RMSE in torsion profile energies of the molecule set with respect to the reference level CCSD(T)/[haTQZ; δ:haDZ]//MP2/heavy-aug-cc-pVTZ level of theory for the whole benchmark set and subsets of neutral and charged molecules. The 95% confidence intervals, calculated with cinnabar, are presented as subscripts and superscripts. The RMSE of neutral molecules for OpenFF’s default theory level, B3LYP-D3(BJ)/DZVP, is comparable to the best functional.

Some of the larger errors were seen in the subset of charged molecules, when compared to the neutral molecules, among the whole set of molecules used in this benchmark. ωB97M-D3(BJ)/DZVP is the best among the tested methods for the charged subset of molecules. And, OpenFF’s default level of theory, B3LYP-D3(BJ)/DZVP, has an RMSE error 0.18 kcal/mol worse than the best method, with an overall RMSE of 0.58 kcal/mol. The difference in RMSE between charged molecules and the neutral molecules is slightly higher for B3LYP-D3(BJ)/DZVP level of theory, and addition of basis functions helped drive this error down. The addition of basis functions from DZVP to def2-TZVPD basis set shows a significant improvement, with B3LYP-D3(BJ) functional, and can be a choice for fine-tuning the force field with more accurate data.

Despite observing higher errors in certain molecules, the methodology used to construct the torsion profile target data, which prioritizes the match to low energy regions, has the potential to mitigate some of these discrepancies. During the training of OpenFF force fields we construct a torsion profile target and optimize the force field using ForceBalance,^85,86 and the objective function in terms of relative energies is defined as follows:³

5

where the primes indicate the absolute energies at each grid point and the weighted differences in relative energy profiles serve as the loss function to minimize:

6

where x_i represents the coordinates of i^th conformer, the 0^th conformer is the minimum energy conformer in respective potential energy landscapes, θ is the force field parameter set at that iteration, and OptMM(x_i, θ) corresponds to the MM energy obtained via constrained minimization and d_E = 1 kcal/mol is a conversion factor to make the sum over deviations dimensionless. The applied weights w(E_QM) in eq 6 prioritize matching the torsion profile at energy minima since Boltzmann sampling favors low-energy regions in state space.⁸⁴

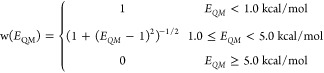7

In the context of fitting OpenFF force fields, the torsion profile energy loss function defined above in eq 6 may further mitigate the differences between the methods since we applied a hard cutoff of 5 kcal/mol to exclude the higher energy regions from torsion fits for the OpenFF Parsley and Sage line of force fields.^3,28

The RMSE on thermally relevant low-energy region (TRLR), only considering the energies less than 5 kcal/mol with respect to the minima on the torsion profile, were tabulated in the last column of Table 1. We can see that ωB97M-D3(BJ)/DZVP still holds its place as the most accurate functional with torsion target score as well, and the differences between various methods drop drastically in the low energy regions. In a sense, the modeling of low-energy, thermally relevant regions was quite accurate, while it was in the high-energy regions where the influence of stereoelectronic and steric effects became prominent, leading to discernible differences between various methods.

The error in the subset of neutral molecules (30 data points) is small for OpenFF’s default of B3LYP-D3(BJ) and close to the best functional, ωB97M-D3(BJ). However, the error is larger for the charged subset of molecules (29 data points) with OpenFF’s default, compared to the best functional, and yet remains accurate in low-energy regions. Most of the large deviations come from high energy regions which were (and usually are) excluded in fitting to torsion profile energies as they are thermally irrelevant. In this sense, our default method may remain appealing given its low computational cost and relatively low error in key regions of torsion profiles. For charged molecules, addition of more basis functions would help as seen in Figure 3, subplot (f).

Referring to SI Table S1, when we examine the molecule with the largest error using OpenFF’s default, B3LYP-D3(BJ)/DZVP, which exhibits an RMSE in relative energies of 1.36 kcal/mol, we observe that the majority of discrepancies arise from the high-energy region exceeding 5 kcal/mol. The torsion profile for this molecule with respect to different basis sets was shown in Figure 2. It is worth reiterating that we exclude this high-energy region during the training process.

Figure 2.

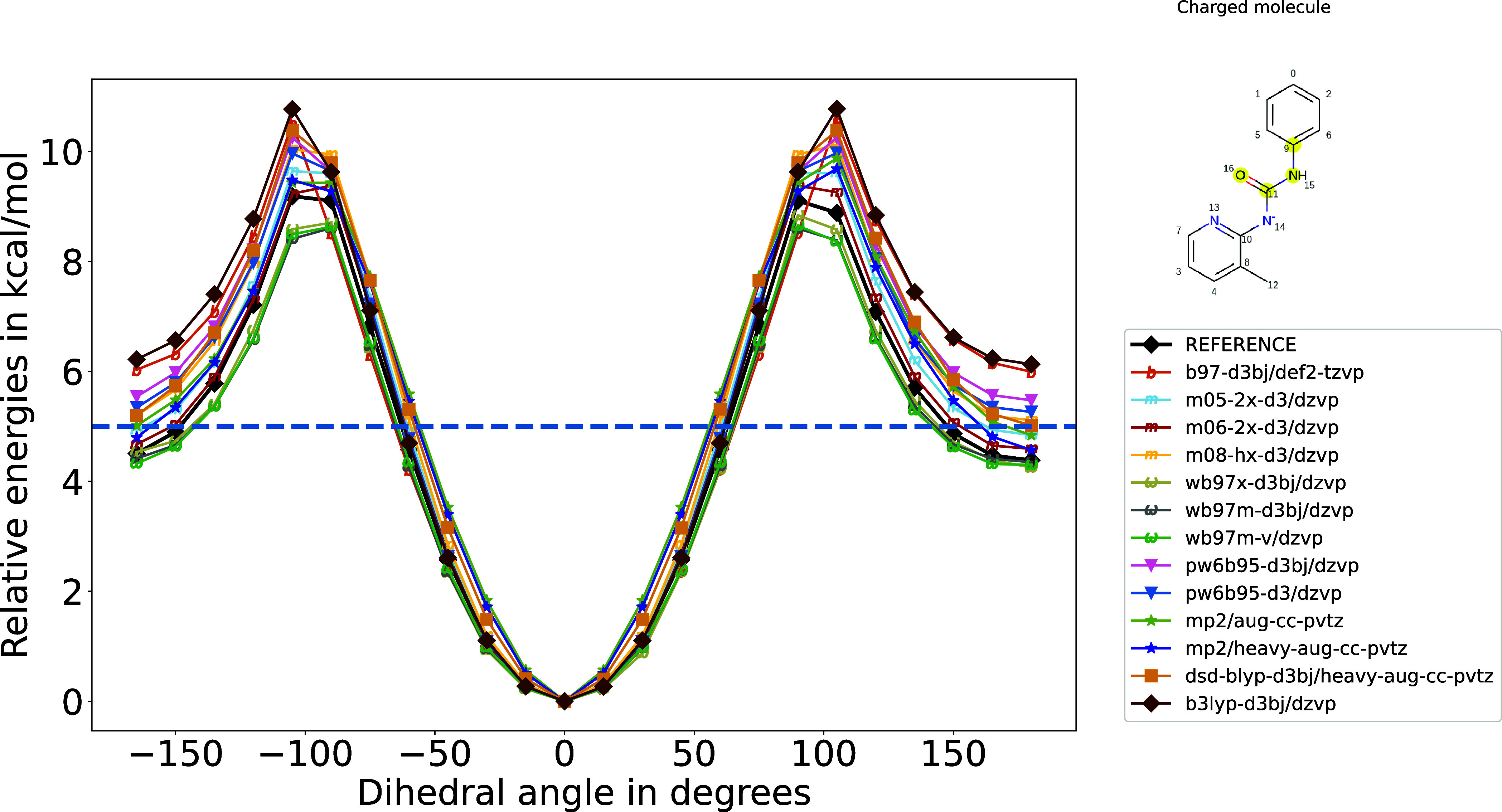
Torsion profile that corresponds to a molecule with a high RMSE at relative energies of >1.0 kcal/mol for most of the methods (row 23 from Table S1). The horizontal dashed line represents 5 kcal/mol, and if we truncate the energies above it, we can see that the low-energy regions were captured better than were the high-energy regions.

3.2. Comparison of Timings and Accuracy

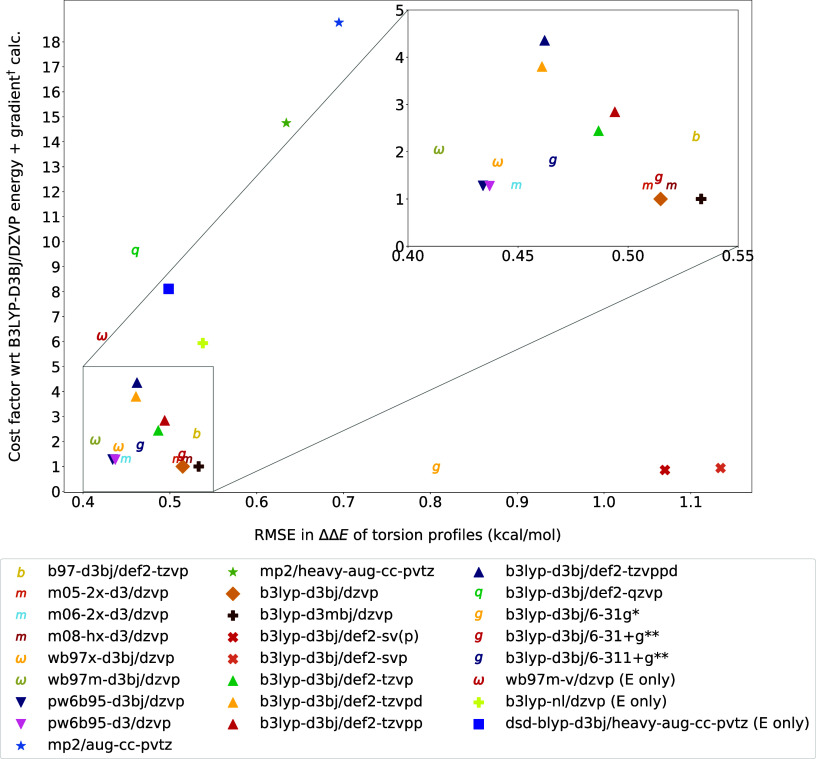
The computation time of a single point (energy + gradient) calculation provides a rough approximation of the method’s cost for a torsion scan or geometry optimization. When examining the OpenFF QM data sets of small molecules, it is observed that a geometry optimization typically requires a median of 42 gradient calculations (based on data from approximately 8000 geometry optimizations). Additionally, a 1D torsion scan with 24 grid points generally costs around 788 gradient calculations (from data on roughly 4000 torsion scans). As a rule of thumb, a geometry optimization calculation is 40x costlier than a single point energy and gradient calculation, and a 1D torsion scan is 800x costlier if executed serially, or nearly 72-fold for parallelized torsion scans (considering the median of maximum number of optimization steps taken among all grid points). So, the differences scale up pretty quickly with the type of calculation. To provide a reference point, we present timing data for a molecule containing 16 heavy atoms. The timings were normalized with the time for a B3LYP-D3(BJ)/DZVP calculation. The cost factor versus RMSE plot is shown in Figure 4, and the most accurate functional is almost twice the cost of a B3LYP-D3(BJ)/DZVP calculation, despite only a modest accuracy benefit. It is to be noted that Psi4, as of v1.4.1, does not yet have analytic gradients for NL and VV10 dispersion terms, and also for DSD-BLYP method, so for these methods only the costs of an energy calculation were reported and scaled with respect to the cost of a B3LYP-D3(BJ) energy calculation (Table 3).

Figure 4.

Cost factor of a single point energy and gradient calculations within each method, averaged over 10 runs of different conformations of the same molecule (with 16 heavy atoms) for all of the methods. All of the run times of each method were normalized with the time taken for a B3LYP-D3(BJ)/DZVP calculation. All of the calculations were run on an Intel(R) Xeon(R) Gold 6148 CPU @ 2.40 GHz CPU using 16 threads and 48 GB of memory. The best functional, ωB97M-D3(BJ)/DZVP, is indicated with an ω, while OpenFF’s default, B3LYP-D3(BJ)/DZVP, is indicated with a ◆.

Table 3. Cost Factors of a Single Energy + Gradient Calculation of Various Methods with Respect to a B3LYP-D3(BJ) Calculation^a.

specification	mean wall time ± standard deviation (s)	cost factor
B97-D3(BJ)/def2-TZVP	49.41 ± 1.10	2.33
M05-2X-D3/DZVP	27.05 ± 0.42	1.28
M06-2X-D3/DZVP	27.26 ± 0.35	1.29
M08-HX-D3/DZVP	27.06 ± 0.49	1.28
ωB97X-D3(BJ)/DZVP	37.49 ± 0.84	1.77
ωB97M-D3(BJ)/DZVP	43.17 ± 0.82	2.04
PW6B95-D3(BJ)/DZVP	27.11 ± 0.39	1.28
PW6B95-D3/DZVP	26.98 ± 0.33	1.27
MP2/aug-cc-pVTZ	397.87 ± 15.91	18.78
MP2/heavy-aug-cc-pVTZ	312.62 ± 12.16	14.75
B3LYP-D3(BJ)/DZVP	21.19 ± 0.24	1.00
B3LYP-D3MBJ/DZVP	21.21 ± 0.21	1.00
B3LYP-D3(BJ)/def2-SV(P)	18.21 ± 0.36	0.86
B3LYP-D3(BJ)/def2-SVP	19.89 ± 0.17	0.94
B3LYP-D3(BJ)/def2-TZVP	51.80 ± 0.63	2.44
B3LYP-D3(BJ)/def2-TZVPD	80.60 ± 0.63	3.80
B3LYP-D3(BJ)/def2-TZVPP	60.27 ± 0.95	2.84
B3LYP-D3(BJ)/def2-TZVPPD	92.33 ± 1.18	4.36
B3LYP-D3(BJ)/def2-QZVP	203.17 ± 3.71	9.59
B3LYP-D3(BJ)/6-31G*	19.41 ± 0.32	0.92
B3LYP-D3(BJ)/6-31+G**	30.22 ± 0.49	1.43
B3LYP-D3(BJ)/6-311+G**	37.98 ± 0.46	1.79
Energy Calculation Only
ωB97M-V/DZVP	66.97 ± 0.61	6.21
B3LYP-NL/DZVP	64.02 ± 0.47	5.94
DSD-BLYP-D3(BJ)/heavy-aug-cc-pVTZ	87.43 ± 1.13	8.11
B3LYP-D3(BJ)/DZVP	10.78 ± 0.17	1.00

^aAll of the wall times were averaged over 10 different runs of 10 different conformers of the same molecule, molecule 1 in Table 1, which contains 16 heavy atoms. For a few methods for which timings for an energy calculation were reported, they were scaled with respect to the cost of a B3LYP-D3(BJ) energy calculation.

B3LYP-D3(BJ) with def2-SVP and def2-SV(P) were lower in accuracy but cheaper, and by adding more basis functions to improve accuracy the cost increases, and it can be seen from Figure 4 that Salahub’s DZVP offers a perfect balance in cost and accuracy for this functional. In the basis set study using B3LYP, 6-311+G** is already very close to the basis set limit (def2-QZVP) in terms of accuracy, in fact it is closer than def2-TZVP and def2-TZVPP, yet it is much cheaper than all of those. When comparing the Pople basis sets, perhaps the largest improvement in accuracy for B3LYP came from adding the first set of diffuse functions (from 6-31g* to 6-31+g*). In the Minnesota functionals, M06-2X-D3 performs better than M05-2X-D3 and M08-HX-D3. In both the B3LYP and ωB97 M tests, the ab initio nonlocal dispersion correction actually gives larger RMSEs than the empirical dispersion.

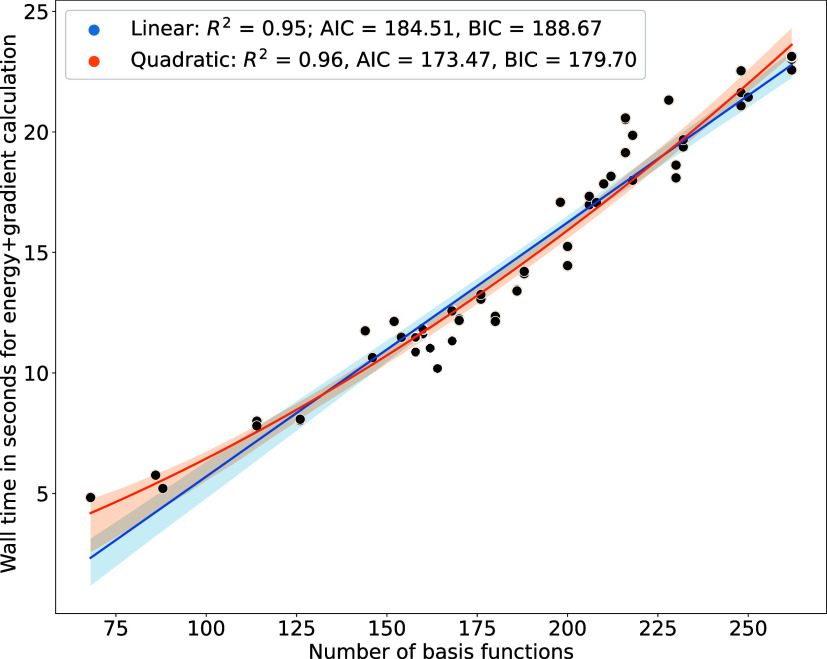
Psi4’s efficient implementation results in quadratic scaling of DFT calculation time with an increase in molecule size.⁸⁷ Both the quadratic and linear fits of the data yielded a similar R², which prompted considering the Akaike information criterion (AIC) and the Bayesian information criterion (BIC) to differentiate the models better. Higher R², lower AIC, and lower BIC values indicate a better fit to the quadratic model. From Figure 5 we can see that with an increase in number of atoms represented by an increase in number of basis functions and the scaling of computation cost for a B3LYP-D3(BJ)/DZVP single point energy plus gradient calculation.

Figure 5.

Scaling of B3LYP-D3(BJ)/DZVP single point energy plus gradient calculation with an increase in the number of basis functions, which in turn represents an increase in the number of atoms. The time of calculation for the dispersion correction term is not included as it is negligible, on the order of a fraction of a second. The quadratic (orange) and linear (blue) fits to the data are shown along with the metrics R², Akaike information criterion (AIC), and the Bayesian information criterion (BIC). The quadratic scaling model seems appropriate from these metrics.

3.3. Faster Parametrization with SQM/ML Potentials

Creating bespoke force fields on-the-fly adds a lot of new torsion parameters, which in turn requires generation of new QM reference data for training them.⁸⁸ Generation of new QM data is time-consuming, and a possible alternative for faster parametrization, without too much loss in accuracy, can be a semiempirical method, or a couterpoise corrected method with minimal basis, or machine learning potentials.^21,89−96 Here we checked the performance of the semiempirical method GFN2-XTB,⁹⁵ Grimme’s 3-corrected Hartree–Fock method (HF-3c),⁹³ and two recent machine learning potentials, AIMNET2⁹⁶ and MACE-OFF23,²¹ the ML potentials which have demonstrated accuracy very close to the level of DFT that they were trained on. Only single point energies were evaluated here, as in the comparisons above.

Table 4 summarizes the performance of the four methods across the whole benchmark set, and also broken down into neutral and charged subsets (see also Table 2). GFN2-XTB shows reasonable accuracy, but is not competitive with the DFT methods. AIMNet2 shows very good accuracy, close to DFT, consistently across both neutral and charged species. MACE-OFF23 shows remarkable accuracy for the neutral subset, in fact more accurate than any of the DFT methods studied here. Note that MACE-OFF23 was not trained on charged species, and hence the error is much higher for this subset, but this will be addressed in future models. HF-3c does not perform well here. Thus, machine learning potentials such as these are a reasonable alternative to DFT, particularly for high-throughput, bespoke parametrization work.⁸⁸

Table 4. Comparison of SQM, DFT-3c, and ML Methods on This Benchmark Set^a.

	RMSE (kcal/mol)
specification	whole set	neutral subset	charged subset
GFN2-XTB
AIMNET2
MACE-OFF23
HF-3c

^aThe overall RMSE in torsion profile energies of the molecule set with respect to the reference level CCSD(T)/[haTQZ; δ:haDZ]//MP2/heavy-aug-cc-pVTZ level of theory for the whole benchmark set and subsets of neutral and charged molecules. The 95% confidence intervals, calculated with cinnabar, are presented as subscripts and superscripts.

4. Conclusion

We conducted a benchmark of QM levels of theory that strike a balance between accuracy and computational efficiency for generating large QM data sets with diverse chemistries to train the valence parameters in a general small molecule force field. The benchmark set of molecules included charged molecules, biaryls, complex hypervalent sulfur chemistry, and complex nitrogen chemistry. This benchmark study is an extension to an earlier work² on benchmarking conformer energies, which suggested B3LYP-D3(BJ)/DZVP as the level of theory to generate OpenFF force field training and validation data. In the context of force field development, aside from conformer energies and optimized geometries, torsion energy profiles represent another indispensable source of molecular interaction data. Achieving accuracy in torsion profile energies relative to a highly accurate QM level of theory reflects in the trained force field. For this purpose, relative energies were compared against CCSD(T)/[haTQZ; δ:haDZ]//MP2/haTZ level of theory for different functional and basis set combinations. And, among the tested methods, ωB97M-D3(BJ) outperforms the others even within a smaller basis set of DZVP, boasting an RMSE in torsion profile energies of just 0.41 kcal/mol. This range-separated hybrid functional has consistently ranked among the top performers in various recent studies^43,44 which were done with a larger basis set. OpenFF’s choice of B3LYP-D3(BJ)/DZVP closely follows it with an RMSE in relative energies of 0.52 kcal/mol. And, the computational cost of B3LYP-D3(BJ)/DZVP for a single gradient is only half of the best functional, but depending on the type of data set, geometry optimization or torsion scans, the cost would scale up with the number of steps taken during the calculation. Within a subset of neutral molecules the RMSE in relative energies with B3LYP-D3(BJ)/DZVP is comparable to the most accurate method. And, the larger errors appear to originate from molecules with charges. However, in practice, the distinctions between levels of theory become evident in the high-energy regions, which are typically excluded during force field training with torsion profiles as they are thermally irrelevant.

Data Availability Statement

The scripts to download the structure data from QCArchive and the downloaded energy and dipole data are available at https://github.com/MobleyLab/qm-theory-benchmark/tree/master.

Supporting Information Available

Supporting Information includes tables on individual errors in each molecule, details on compute infrastructure used, dipole moments comparison, correlation between energy and delta energy difference wrt reference, error estimates in barriers. The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpcb.4c03167.

• (PDF)

The authors declare the following competing financial interest(s): D.L.M. serves on the scientific advisory boards of Anagenex and OpenEye Scientific Software, Cadence Molecular Sciences, and is an Open Science Fellow with Psivant.