Commentary: Pharmacokinetic Theory Must Consider Published Experimental Data

Abstract

Recently, we have proposed simple methodology to derive clearance and rate constant equations, independent of differential equations, based on Kirchhoff’s Laws, a common methodology from physics used to describe rate-defining processes either in series or parallel. Our approach has been challenged in three recent publications, two published in this journal, but notably what is lacking is that none evaluate experimental pharmacokinetic data. As reviewed here, manuscripts from our laboratory have evaluated published experimental data, demonstrating that the Kirchhoff’s Laws approach explains (1) why all of the experimental perfused liver clearance data appear to fit the equation that was previously believed to be the well-stirred model, (2) why linear pharmacokinetic systemic bioavailability determinations can be greater than 1, (3) why renal clearance can be a function of drug input processes, and (4) why statistically different bioavailability measures may be found for urinary excretion versus systemic concentration measurements. Our most recent paper demonstrates (5) how the universally accepted steady-state clearance approach used by the field for the past 50 years leads to unrealistic outcomes concerning the relationship between liver-to-blood Kp_uu and hepatic availability F_H, highlighting the potential for errors in pharmacokinetic evaluations based on differential equations. The Kirchhoff’s Laws approach is applicable to all pharmacokinetic analyses of quality experimental data, those that were previously adequately explained with present pharmacokinetic theory, and those that were not. The publications that have attempted to rebut our position do not address unexplained experimental data, and we show here why their analyses are not valid.

SIGNIFICANCE STATEMENT

The Kirchhoff’s Laws approach to deriving clearance equations for linear systems in parallel or in series, independent of differential equations, successfully describes published pharmacokinetic data that has previously been unexplained. Three recent publications claim to refute our proposed methodology; these publications only make theoretical arguments, do not evaluate experimental data, and never demonstrate that the Kirchhoff methodology provides incorrect interpretations of experimental pharmacokinetic data, including statistically significant data not explained by present pharmacokinetic theory. We demonstrate why these analyses are invalid.

Introduction

Recently, in this journal, Rowland et al. (2023) maintained that the approach of using Kirchhoff’s Laws from physics to derive pharmacokinetic relationships independent of differential equations for clearance and the overall rate constant for elimination “was groundless and fraught with errors”, concluding that “there is no place for the application of Kirchhoff’s laws to organ clearance concepts.” The other two published critiques are Korzekwa and Nagar (2023) and Siegel (2024). Rowland et al. (2023) ended their Commentary with a quote from Popper (1962) concerning theory, who asked “Does it solve the problem? Does it solve it better than other theories? Has it perhaps merely shifted the problem? Is the solution simple? Is it fruitful?” Rowland et al. (2023) answered each of these questions with “no”, which we will revisit in the Conclusion portion of this manuscript. However, we prefer a different philosophy, as we have addressed previously in this journal (Sodhi et al., 2020), from Nobel prize physicist Richard Feynman (1965): “It doesn’t matter how beautiful your theory is, it doesn’t matter how smart you are. If it doesn’t agree with experiment, it’s wrong.”

The Rowland et al. critique was written after publication of our first two papers on this topic (Patcher et al., 2022; Benet and Sodhi, 2023), where we demonstrated in “adapting Kirchhoff’s Laws from physics, that overall rate constants for a linear kinetic process or overall clearance for that process can be directly derived without the need to use differential equations. …the application … to clearance can be summarized in eq. 1 for parallel processes and eq. 2 for processes in series.”

We further demonstrated that Kirchhoff’s Laws may also be applied to rate constants, but since the Rowland et al. (2023) commentary only addresses clearance relationships, we will limit our current discussion to that topic.

In applying Kirchhoff’s Laws to in vivo relationships, it is critical to understand the definition of a rate-defining process. This is a limitation that Kirchhoff did not encounter when he derived his laws related to electric circuits involving resistors, conductors, and wires, since all of these were rate-defining processes. However, in vivo for drugs, many other aspects of drug disposition may not be rate-defining processes. As we recently wrote (Wakuda et al., 2024): “A rate-defining process is defined by a parameter that describes an elimination or movement process for which it is possible under certain conditions that the total clearance or total rate constant may be equal to this parameter. For example, a rate-defining clearance process for hepatic elimination could be hepatic blood flow, i.e., the rate at which the drug arrives to the liver is the maximum value that hepatic elimination can be. Thus, for a very high hepatic clearance (CL_H) drug, the total CL_H could equal hepatic blood flow (Q_H). To exemplify a rate-defining rate constant process, for a series of chemical reactions in a beaker, the elimination rate constant for the parent drug could be the minimum value rate-defining process for all subsequent metabolic steps. For example, if the first step in a metabolic elimination process is very slow, the observed rate constant for the subsequent metabolic steps will be that initial rate constant for the metabolism of the parent drug…. The critical aspect of our approach is that only rate-defining processes can be combined to determine the overall rate constant for elimination or clearance following Kirchhoff’s Laws. Passive permeability, no matter how slow, cannot be a rate-defining process for elimination…, clearance and elimination rate will never be equal to passive permeability. When hepatic basolateral transporters affect permeability and active influx is greater than active efflux, this can be a rate-defining process, but not when active efflux is greater than active influx. That is, clearance can never be defined singly as active efflux minus smaller active influx since the value is negative.” Note, inherent in this definition is the requirement that under some conditions, a rate-defining step can be experimentally measured. That is, if one is deriving in vivo clearance, each rate-defining step can potentially be measured in vivo.

Application of Kirchhoff’s Laws to Derive In Vivo Hepatic Clearance Relationships and Experimental Data

Patcher et al. (2022) derived hepatic clearance equations in terms of the three rate-defining processes in series in the liver: hepatic blood flow (Q_H), hepatic basolateral transport intrinsic clearance (PS_influx – PS_efflux), and the sum of metabolic and biliary intrinsic clearances (CL_int). When deriving total drug clearance, the intrinsic clearances must be multiplied by the fraction of drug unbound in blood (f_uB). Thus, when basolateral transport is not clinically relevant, hepatic clearance (CL_H) is given by eq. 3

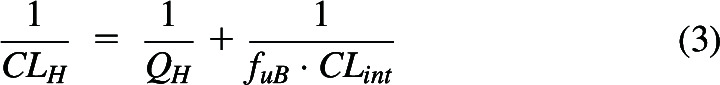which when solved, yields

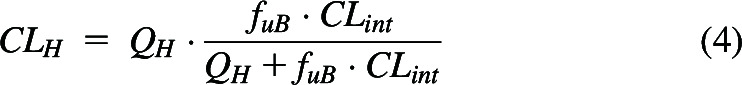Equation 4 has been believed for the past 50 years to be the well-stirred model (WSM) of hepatic elimination. However, eq. 4 was derived making no assumptions concerning the mechanism of hepatic elimination and we believe it to be the general relationship between Q_H, f_uB and CL_int when only systemic concentrations can be measured. The critical condition is “when only systemic concentrations can be measured”. Further, experimental data in isolated perfused rat liver (IPRL) studies (four high clearance drug studies with lidocaine, meperidine, and propranolol, four studies with high clearance compounds, galactose and taurocholate, and five studies in which two low clearance drugs, diazepam and diclofenac, are made high clearance by manipulating protein binding) support the generalizability of eq. 4 over the alternatively suggested hepatic disposition models, as we reported (Sodhi et al., 2020). There are no valid experimental studies that unambiguously demonstrate that the data are better fit by the parallel tube model (PTM) or dispersion models (DMs) as compared with eq. 4.

At the September 13, 2023 International Society for the Study of Xenobiotics symposium, “50 Years of CL Prediction,” we were surprised when both Rowland and Sugiyama displayed versions of Fig. 1A as the only experimental data they presented in support of alternate mechanistic models of hepatic elimination, especially since the methodology used in these studies was an indirect approach to test model discrimination, combining IPRL studies with in vitro-in vivo extrapolation (IVIVE) approaches. Rowland cited the publications of Rane et al. (1977) and Roberts and Rowland (1986) and Sugiyama cited the publication from his laboratory (Iwatsubo et al., 1996), which added additional data points to the previous analyses. In these studies, recreated in Fig. 1A, the y-axis values are published hepatic availability (F_H) measures, experimentally determined from ex-vivo IPRL studies. However, the x-axis values are calculated efficiency numbers (f_u ⋅ CL_int/Q_H) that are determined by combining the experimentally used Q_H and f_u values from the IPRL study with a predicted in vivo CL_int that is based on IVIVE extrapolation of in vitro CL_int measures from a different study. Notably, the calculated in vivo CL_int values assume that IVIVE has no error, and that the in vitro CL_int value may accurately predict the in vivo CL_int. In the last century, it may have been believed that IVIVE would give quantitatively accurate values, but we know today from multiple studies that this is not true and that throughout the field, as presently employed, IVIVE consistently underpredicts the in vivo measured experimental clearance values (Sodhi and Benet, 2021). At the time that Fig. 1A was originally presented, the authors understandably may not have appreciated this difference. However, subsequently, both speakers have published with their colleagues that they recognize that the previous assumption of the accuracy of IVIVE is incorrect (Chiba et al., 2009), and as Rowland and Pang (2018) wrote, “IVIVE tends to underpredict the estimated in vivo hepatic clearance (Hallifax et al., 2010) for poorly understood reasons.” This is the reason why we were surprised that both Rowland and Sugiyama referred to Fig. 1A, in 2023, as evidence supporting alternate hepatic disposition models.

Fig. 1.

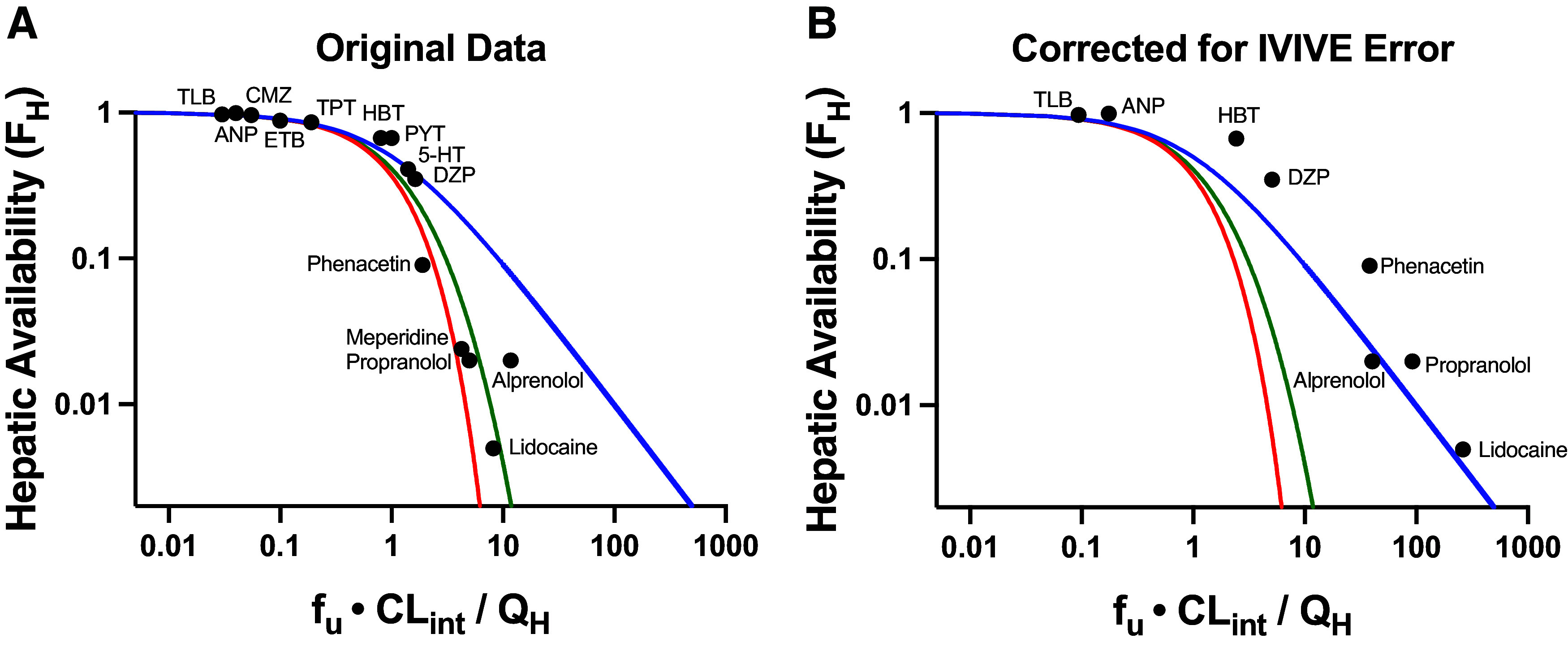
Plots of hepatic availability (F_H) vs. efficiency number (f_u·CL_int/Q_H) based on (A) originally published analysis, and (B) further corrected for in vitro-in vivo underprediction error. The theoretical clearance relationships are represented with lines in blue (the eq. 4 relationship; previously regarded as WSM), red (parallel tube model), and green (dispersion model). (A) Data points assuming no error in IVIVE prediction are depicted, based on original analysis from Roberts and Rowland (1986) and Iwatsubo et al. (1996). (B) Original data are corrected for degree of observed IVIVE underprediction error, based on human liver microsomal IVIVE data reported by Wood et al. (2017) in the Supplemental Data of that paper. The five high extraction ratio compounds included in this analysis (alprenolol, lidocaine, meperidine, phenacetin and propranolol) are labeled. Additional compounds (low and moderate extraction ratio) are labeled with the following abbreviations: 5-HT, 5-hydroxytryptamine; ANP, antipyrine; CMZ, carbamazepine; DZP, diazepam; ETB, ethoxybenzamide; HBT, hexobarbitone; PYT, phenytoin; TLB, tolbutamide; TPT, thiopental.

In Fig. 1B, using the degree of IVIVE underprediction for human microsome experiments, as reported by Wood et al. (2017), we replotted the x-values for all of the data points where IVIVE error data were available (i.e., the plotted values in Fig. 1B use the measured microsomal intrinsic clearance values of Wood et al.). It is striking that when the IVIVE underprediction is accounted for, all of the data appear to be best described by eq. 4 (blue line), previously regarded as the WSM. Thus, we continue to maintain that although the field believes that the WSM is unphysiologic and that the PTM and DMs are more representative of liver elimination for high clearance drugs, there are no quality experimental studies available demonstrating that data are best described by the PTM and DMs.

Application of Kirchhoff’s Laws to Explain Previously-Considered Anomalous Experimental Data Following Slow Drug Input Processes

Historically, for first-order processes, pharmacokinetics was based on differential equations as employed in chemistry to describe rates of reaction in terms of measurable systemic drug concentrations. These equations were then integrated over all time to define the relationship between systemic exposure (AUC_0→∞), available dose, and clearance. Thus, for an intravenous bolus dose

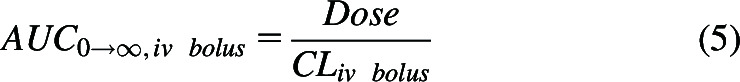For an orally administered dose, the numerator is the product of the systemic bioavailability (F) and dose.

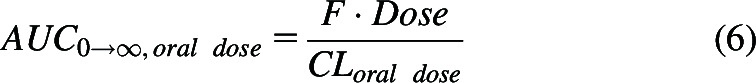All teaching of pharmacokinetics for the past 100 years and every pharmacokinetic textbook assumes for drugs following linear pharmacokinetics where there is no change in the elimination or distribution rate constants, then $\mathit{C}{\mathit{L}}_{\mathit{oral} \mathit{dose}}=\mathit{C}{\mathit{L}}_{\mathit{i}\mathit{v} \mathit{bolus}}$ with the implication that the input process (the rate of absorption from the gastrointestinal tract) has no effect on area under the curve (AUC) and thus F may be calculated from the dose corrected ratio of areas oral/intravenous bolus over all time.

However, it is quite simple to demonstrate that these universally believed assumptions may not always be true. All textbooks of pharmacokinetics describe the so-called “flip-flop” model, as we previously reviewed (Garrison et al., 2015), for which the absorption rate constant from the gastrointestinal tract is much slower than the rate constant for elimination from the systemic circulation and, therefore, the elimination from the systemic fluids will be rate limited by the slow absorption. Thus, by always assuming that for linear systems $\mathit{C}{\mathit{L}}_{\mathit{oral} \mathit{dose}}\hspace{0.17em}=\mathit{C}{\mathit{L}}_{\mathit{i}\mathit{v} \mathit{bolus}}$, our field for the past 100 years has paradoxically both (1) recognized that the elimination rate from the systemic circulation can be rate-limited by the slow gastrointestinal absorption rate constant, but assumes that (2) slow drug clearance from the gastrointestinal absorption site does not affect systemic clearance. Yet, as we described in the Introduction, our field recognizes that if a drug undergoes sequential metabolism (metabolic in series steps; e.g., Drug to Metabolite 1 to Metabolite 2 to Metabolite 3) and the clearance of Drug to Metabolite 1 is very slow, then following dosing of the Drug, the measured clearance of Metabolite 1 to Metabolite 2 (and Metabolite 2 to Metabolite 3) will be rate-limited by clearance of the Drug, even when it is known that if we dosed Metabolite 2 (or Metabolite 3) their measured clearance values would be much higher than the clearance of the Drug itself (Houston and Taylor, 1984). Thus, we pose the question for an analogous scenario, what is the basis for believing that slow clearance from the gastrointestinal tract would not affect the measured systemic AUC following oral dosing?

Recognizing that for linear systems $\mathit{C}{\mathit{L}}_{\mathit{oral} \mathit{dose}}$ may not always be equal to $\mathit{C}{\mathit{L}}_{\mathit{i}\mathit{v} \mathit{bolus}}$ provides the explanation for appreciable published pharmacokinetic results considered previously to be anomalous. In Wakuda et al. (2024), we cite in humans (1) examples where measures of systemic bioavailability are statistically significantly greater than 1 (i.e., cimetidine, levetiracetam, ofloxacin, and probably additionally treprostinil sodium); (2) human studies following slow oral and subcutaneous drug administration where renal clearance is statistically significantly lower than renal clearance following intravenous dosing (i.e., 1-deamino-8-arginine vasopressin, sodium fluoride, cimetidine, and hydroxyurea), and (3) studies where bioavailability in humans calculated using systemic concentrations is statistically significantly greater than bioavailability calculated using measures of unchanged drug in urine within the same study (i.e., cilazapril and cimetidine). None of these outcomes are possible if $\mathit{C}{\mathit{L}}_{\mathit{oral} \mathit{dose} \left(\mathit{o}\mathit{r} \mathit{SubQ}\right)}\hspace{0.17em}=\mathit{C}{\mathit{L}}_{\mathit{i}\mathit{v} \mathit{bolus}}$ is invariably true for linear systems. These measured outcomes result from a very slow absorption process that increases the measured systemic AUC, analogous to the sequential metabolism example above where slow metabolic clearance of Drug to Metabolite 1 results in increased AUC of Metabolite 2 or Metabolite 3.

The experimental results cited above may be predicted using Kirchhoff’s Laws for in series rate-defining process in a manner similar to that used to derive eq. 3, where:

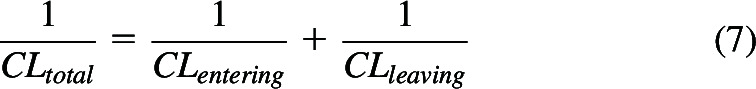In deriving hepatic clearance (eq. 3), CL_entering was Q_H, while CL_leaving was f_uB·CL_int. For oral absorption processes, CL_entering will be CL_gut, clearance from the intestine, a parameter not previously considered in pharmacokinetics but can be simply considered as the product of the first order rate constant for absorption multiplied by the volume of distribution of drug in the gut, a parameter that has no more physiologic relevance than volume of distribution at steady-state (V_ss, but will certainly not be equal to V_ss, as we previously described (Benet and Sodhi, 2023; Wakuda et al., 2024), while CL_leaving will be the clearance following an intravenous bolus dose of the drug, CL_{iv bolus}. Thus, for in-series first-order oral dosing processes from Kirchhoff’s Laws

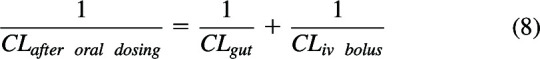Solving eq. 8 gives

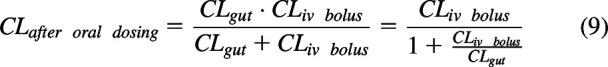Reviewing eq. 9 shows that if $\mathit{C}{\mathit{L}}_{\mathit{gut}}\gg \mathit{C}{\mathit{L}}_{\mathit{i}\mathit{v} \mathit{bolus}}$, the ratio in the denominator approaches zero and then $\mathit{C}{\mathit{L}}_{\mathit{after} \mathit{oral} \mathit{dosing}}\hspace{0.17em}=\mathit{C}{\mathit{L}}_{\mathit{i}\mathit{v} \mathit{bolus}.}$ This is often the case, especially when the CL_{iv bolus} is a small value. However, when clearance from the gut or any input site is slow, as is true for drugs exhibiting flip-flop kinetics, then the ratio in the denominator is not negligible and the slow gut clearance affects the measured systemic clearance, especially for high clearance drugs. These conditions, $\mathit{C}{\mathit{L}}_{\mathit{after} \mathit{oral} \mathit{dosing}}<\mathit{C}{\mathit{L}}_{\mathit{i}\mathit{v} \mathit{bolus}}$, explain the anomalous data tabulated by Wakuda et al. (2024). As previously explained in detail (Benet and Sodhi, 2023; Wakuda et al., 2024), eq. 9 cannot be derived using differential equations, the approach traditionally used by the field to derive pharmacokinetic relationships borrowed from the field of Chemistry. This is because what are measured in pharmacokinetic studies are concentrations, but differential equations are derived based on amounts, then converted to a concentration-based equation by dividing by a single volume of distribution. That is, the amount versus time equation can only be changed into a concentration versus time equation by dividing by a single volume term, the systemic volume of distribution. This causes no difficulties when deriving clearance following intravenous bolus dosing. However, when an input site with its own volume of distribution is included in the derivation the error is introduced, since CL_gut, as stated above, will be the product of the rate constant for absorption and the gut volume of distribution, a hypothetical volume that will have no more physiologic relevance than the systemic volume of distribution but will notably not equal the systemic volume of distribution. It was only through the recognition that Kirchhoff’s Laws could be employed to derive clearance relationships that led to eq. 9.

The Papers Challenging the Validity of the Kirchhoff’s Laws Approach Never Consider Published Experimental Pharmacokinetic Data, Never Consider the Limitations of the Derivations of the Mechanistic Models of Hepatic Elimination, Nor Do They Address Clinically Relevant Pharmacokinetic Concepts

Since our first paper proposing the application of Kirchhoff’s Laws to deriving pharmacokinetic and chemistry linear rates of reaction (Patcher et al., 2022), three peer reviewed publications have challenged the validity of our approach (Korzekwa and Nagar, 2023; Rowland et al., 2023; Siegel, 2024). What is most telling in these three publications is that none of them address or allude to published experimental pharmacokinetic data.

Korzekwa and Nagar (2023) questioned our Kirchhoff’s Laws approach in that it could not be used following intravenous bolus dosing to derive the clearance of a drug into different hypothetical multicompartment models when considering intercompartmental diffusional clearances with elimination occurring from different compartments. This is an excellent example of the false relevance of differential equation derivations that do not consider experimental pharmacokinetic data. For all of the models in the Korzekwa and Nagar publication, the clearance will be the same, as we have shown (Benet et al., 2021), since clearance may only be defined as the amount eliminated divided by the exposure driving that elimination. That is, for an intravenous bolus dose into any multicompartment model, $\mathit{C}{\mathit{L}}_{\mathit{i}\mathit{v} \mathit{bolus}}\hspace{0.17em}=\hspace{0.17em}\frac{\mathit{Dose}}{\mathit{A}\mathit{U}{\mathit{C}}_{0\to \infty }}.$ Clinically, in terms of clearance, it is impossible to differentiate any of the Korzekwa and Nagar models from each other and model discernment is only accomplished by differential equation simulations that cannot be differentiated experimentally. Furthermore, to prove that Kirchhoff’s laws were not applicable to their models, Korzekwa and Nagar tried to derive overall clearance in terms of diffusional clearances between compartments. However, as we indicated earlier, Kirchhoff’s Laws allows the relevant parameters of clearance to be derived only in terms of rate-defining processes (eq. 3). Passive intercompartmental clearances will never be a rate-defining process (i.e., total clearance can never be equal to a passive diffusion process). A good portion of the Siegel (2024) manuscript also relates to derivations including intercompartmental diffusional clearances in predicting total clearance and that publication also does not include any relationship to experimentally measurable drug concentrations in the analyses.

The inclusion of intercompartmental clearances in the Siegel derivations lead to some very strange conclusions in terms of mean residence time concepts, which again points out the liability of not considering experimental data. For multicompartment systems following iv bolus dosing, no matter the number of interconnected compartments and the site of drug elimination from the model, CL is determined as Dose/AUC_0→∞, V_ss is determined as $\frac{\mathit{Dose}\cdot \mathit{AUM}{\mathit{C}}_{0\to \infty }}{\mathit{A}\mathit{U}{\mathit{C}}_{0\to \infty }^2}$ and mean residence time of the system is the ratio of $\frac{{\mathit{V}}_{\mathit{s}\mathit{s}}}{\mathit{C}\mathit{L}}$, where AUMC is the area under the moment curve, as we first showed (Benet and Galeazzi, 1979), assuming for the V_ss and mean residence time calculations that elimination occurs from the measured compartment (but no assumption is made for the CL determination) since it is impossible to experimentally determine the site of elimination. Consistent with the above, the Siegel (2024) approach results in different mean residence times for the different compartment models he proposes, which clinically would be impossible to determine when dosing drugs and measuring systemic concentrations.

Then by including intercompartmental diffusion clearances in the derivation, Siegel (2024) concludes that an additional term, volume of distribution of drug in the gut (V_gut) divided by the intravenous bolus clearance must be included in the equation describing mean residence time of drug in the body following oral dosing where k_e is the inverse of the drug mean residence time following intravenous bolus dosing:

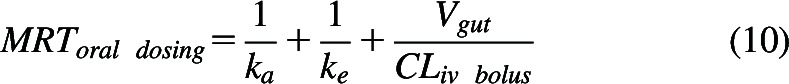The manuscript suggests that the ratio will most often be small and have little effect on the sum. The Siegel analyses appear to be confounded by the introduction of the terms ‘relay processes’ versus ‘in series processes’. Siegel (2024) attributes a relay process to be a sequence of processes that occur one after another (with no reversible steps) and provides a swimming relay race as an example. The manuscript attributes the first two terms on the right hand side of eq. 10 as the mean residence time that would occur for this relay process crediting Yamaoka et al. (1979). If drug can pass back into the intestine from the systemic circulation, then according to Siegel (2024), this is the in series process and MRT_{oral dosing} must include the third term on the right hand side of eq. 10. Again, it is telling that the manuscript includes no simulations, together with no experimental data. The major error is the assumption that drug may diffuse back from the systemic circulation into the gut following oral dosing but does not allow diffusion into the gut following intravenous dosing. For first order processes, if drug passes from the systemic fluids to the gut following oral dosing, then it must also pass from the systemic fluids to the gut following intravenous dosing. There is no justification for the Siegel (2024) assumption that drug does not pass into the gut following intravenous dosing. Just like k_e, which is independent of how many reversible compartments and exits there are in the disposition model, where the inverse of k_e is the mean residence time following an intravenous bolus dose, k_a is independent of how many compartments are in the gut model and whether there is a reverse process from the systemic circulation or not and the inverse of k_a is the mean absorption time. There is no validity to eq. 10, and there is no relevance to the differentiation of relay and in series processes with respect to determination of the absorption rate constant. A simple simulation, as presented in the Supplemental Material using LaPlace transform input and disposition functions (Nakashima and Benet, 1988), can easily demonstrate that mean absorption time is the inverse of k_a, regardless of whether there is passage of drug from the systemic circulation back into the intestinal tract.

Rowland et al. (2023) take a different approach to questioning the Kirchhoff’s Laws derivations, concentrating on the idea that the WSM and our derivation of eq. 4 assumes “that each of the three aqueous spaces of the liver-vascular space, interstitial space, and intracellular water space, is well-stirred” and that this is not true for the PTM and DMs. Not only have Rowland et al. (2023) ignored the experimental data as we detailed above, they have also ignored their own simple mass balance derivations that serve as the basis for the WSM, PTM, and DMs, in that all hepatic models are derived based on assuming a single average steady-state concentration (not changing or considering different concentrations in the various liver aqueous spaces). The initially proposed mass balance derivations—Rowland et al. (1973) for the WSM, Pang and Rowland (1977) for the PTM, and Roberts and Rowland (1986) for DMs— that serve today and for the past 50 years as the basis for the hepatic clearance–intrinsic clearance relationship for the WSM, PTM, and DMs, as well as for the characterization of hepatic elimination in physiologic based pharmacokinetic models at steady-state, is:

where C_Blood is the steady-state concentration of total drug in the blood, CL_Blood is blood clearance, C_in and C_out are the blood concentrations of total drug (unbound plus bound) entering and leaving the liver, respectively, and C_H,u is the average concentration of unbound drug within the liver, as recently reviewed by Li and Jusko (2022). When eq. 11 is used to derive the WSM, the far right hand side of eq. 11 becomes $\mathit{C}{\mathit{L}}_{\mathit{int}\mathit{WSM}}\cdot {\mathit{C}}_{\mathit{out}u}$; when eq. 11 is used to derive the PTM, the far right hand side of eq. 11 becomes $\mathit{C}{\mathit{L}}_{\mathit{int},\mathit{PTM}}\cdot \frac{{\mathit{C}}_{\mathit{i}\mathit{n}\mathit{u}}-{\mathit{C}}_{\mathit{out}\mathit{u}}}{ln\frac{{\mathit{C}}_{\mathit{i}\mathit{n}\mathit{u}}}{{\mathit{C}}_{\mathit{out}\mathit{u}}}}$; when eq. 11 is used to derive the DMs, the far right hand side of eq. 11 becomes $\mathit{C}{\mathit{L}}_{\mathit{int},\mathit{D}\mathit{M}}\cdot {\mathit{C}}_{\mathit{avg}\mathit{u}}$, where ${\mathit{C}}_{\mathit{avg}\mathit{u}}$ is a very complicated equation for the average unbound liver concentration for the DMs depending upon the dispersion number. That is, the derivation of each of the mechanistic models of hepatic elimination is based on a single average steady-state unbound concentration within the liver that takes no account of the three aqueous spaces of the liver. The supporters of PTM and DMs then claim that although the derivations of the models do not consider the changing concentrations as the drug traverses the liver, they can use the models to simulate the changing concentrations. If one ignores the finding that there are no valid experimental studies where one can unambiguously show that the data are better fit by the PTM or DMs as compared with eq. 4 (Sodhi et al., 2020), including the data presented in Fig. 1, and the admission of Pang et al. (2019) that most experimental data are best described by eq. 4, we recognize that the two sides of the argument between our laboratory and those supporting PTM and DMs are theoretical. We believe our most recent publication (Benet and Sodhi, 2024), described in the next section, does provide a differentiator that will be recognized by the general scientific community. However, here we first address other points raised in Rowland et al. (2023).

Rowland et al. (2023) ask, why was f_uB·CL_int chosen in eq. 4, and not just CL_int? They attribute the answer to a characteristic of the WSM but the answer is much simpler. If one solved for unbound systemic clearance in eq. 4, then f_uB is not included in the solution. However, eq. 4 solves for total clearance, thus the unbound CL_int term must be multiplied by f_uB. Rowland et al. (2023) then raise their favorite justification for the validity of their approach, mass balance. However, all of the Kirchhoff’s Laws derivations also maintain mass balance.

The primary question that we raised in our first questioning of the WSM derivation approach (Benet et al., 2018) was why is the mass balance relationship in eq. 11 set equal to $\mathit{C}{\mathit{L}}_{\mathit{int}}\cdot {\mathit{C}}_{\mathit{H}\mathit{u}}$? It appears that Rowland and colleagues do not fully appreciate the reason for our questioning of the WSM derivation. This relationship was first used in the 1973 Rowland et al. publication, in which Dr. Benet was a coauthor (Rowland et al., 1973). However, we now ask why is the correct mass balance relationship not equal to $\mathit{C}{\mathit{L}}_{\mathit{H}\mathit{u}}\cdot {\mathit{C}}_{\mathit{H}\mathit{u}}$, where CL_H,u is the clearance of unbound drug in the liver, rather than assuming it is the intrinsic clearance? If the drug clearance in the blood is rate limited by hepatic blood flow, should the drug clearance in the liver not also be rate limited by hepatic blood flow? Rowland et al. (2023) also misinterpret our use of in vivo parallel and in series processes, believing they relate to anatomical locations. Rather, parallel clearance processes are two clearances that do not affect each other. That is, the clearance value of biliary clearance in the liver has no effect on the measured metabolic liver clearance value and vice versa. Thus, liver clearance is the sum of these two parallel clearance processes, although anatomically biliary excretion occurs at the apical hepatic border after the metabolic process. In series processes are characterized by sequential processes, in which the measured clearance value of a first process may potentially have an effect on the measured clearance value of subsequent processes, as in our Drug to Metabolite 1 to Metabolite 2 to Metabolite 3 scenario referenced twice above.

Equation 11 and Its Use in Deriving the WSM, PTM, and DMs Leads to Unsupportable Conclusions When Determining Steady-State Unbound Liver to Unbound Systemic Concentration Ratios (Kp_uu)

As indicated above, if one chooses to ignore all experimental results, then the difference between our laboratory and those questioning our new Kirchhoff’s Laws approach to deriving clearance is theoretical. Previously, we have detailed our position that the mechanistic models of hepatic elimination are not useful in defining clearance relationships for drugs when only systemic concentrations are measured (Benet et al., 2018; Benet and Sodhi, 2020; Benet et al., 2021; Benet and Sodhi, 2022; Patcher et al., 2022; Benet and Sodhi, 2023). In our most recent publication (Benet and Sodhi, 2024), we focus on the crux of our position, that the eq. 11 relationship is inherently incorrect, and that utilizing this equality as the basis of subsequent derivation of various hepatic disposition models is invalid and is responsible for significant errors in hypothetical analysis of pharmacokinetic relationships by our field for the past 50 years. Our field’s present analysis accepts eq. 11, which leads directly to unbelievable relationships between $\mathit{K}{\mathit{p}}_{\mathit{u}\mathit{u}}$ (the ratio of unbound steady-state concentration in the liver to the unbound steady-state systemic concentration, for any route of administration) and measures of ${\mathit{F}}_{\mathit{H} }$(the first pass hepatic bioavailability following an oral dose). We have shown (Benet and Sodhi, 2024) that for the WSM, without including transporter activity, eq. 11 leads to $\mathit{K}{\mathit{p}}_{\mathit{u}\mathit{u}}={\mathit{F}}_{\mathit{H}}$ with an outcome that $\mathit{K}{\mathit{p}}_{\mathit{u}\mathit{u}}$ can never exceed unity. An equally unhelpful outcome is found using the potential Li and Jusko (2022) definition of $\mathit{K}{\mathit{p}}_{\mathit{u}\mathit{u}}$, which relates unbound steady-state hepatic concentrations to unbound steady-state concentrations in the hepatic vein following any route of administration. Under that condition for the WSM relationship, $\mathit{K}{\mathit{p}}_{\mathit{u}\mathit{u}}\hspace{0.17em}=\hspace{0.17em}1.0$ for all drugs, as the WSM assumes ${\mathit{C}}_{\mathit{H},\mathit{u}}\hspace{0.17em}=\hspace{0.17em}{\mathit{C}}_{\mathit{out},\mathit{u}}$. Based on eq. 11, we also derived the relationship between $\mathit{K}{\mathit{p}}_{\mathit{u}\mathit{u}}$ and ${\mathit{F}}_{\mathit{H}}$ for the PTM with outcomes that we believe no pharmaceutical scientist will accept. That is, $\mathit{K}{\mathit{p}}_{\mathit{u}\mathit{u}}$ is a function of ${\mathit{F}}_{\mathit{H}}$ and whether the drug is a low or high extraction ratio (ER) compound, independent of any structural molecule characteristics, and we suggest that pharmaceutical scientists will also concur that such relationships are unlikely to be valid. We did not analyze the much more complicated DMs; the results would be numerically different than the PTM analysis depending on the dispersion number chosen, but the outcome will be the same; $\mathit{K}{\mathit{p}}_{\mathit{u}\mathit{u}}$ will be a function of ${\mathit{F}}_{\mathit{H}}$ with values intermediate to those for the WSM and PTM.

We also derived Kp_uu and F_H for the extended clearance model of hepatic clearance, where hepatic basolateral transporters can be rate limiting, as shown in the usual form of the equation for clearance when hepatic blood flow is assumed to be much greater and not included as given in eq. 12.

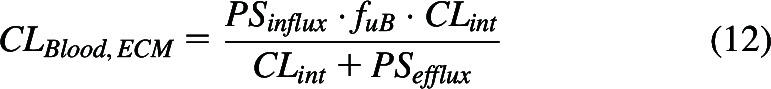where PS_influx and PS_efflux are the total hepatic (active plus passive) intrinsic basolateral influx and efflux clearances, respectively. We showed that when hepatic basolateral transport is rate limiting, not only is Kp_uu,ECM always less than 1.0, but Kp_uu,ECM is always less than F_H. Thus, in all cases detailed above for the WSM and PTM, whether (1) hepatic basolateral transport is not relevant or (2) when basolateral hepatic uptake is the rate limiting step for hepatic clearance, then $\mathit{K}{\mathit{p}}_{\mathit{u}\mathit{u}}\le {\mathit{F}}_{\mathit{H}}$, based on the eq. 11 assumption and the usual definition of in vivo $K{p}_{uu}$ (Di et al., 2021). As a result, the value of $\mathit{K}{\mathit{p}}_{\mathit{u}\mathit{u}}$ can never exceed unity. We think that no pharmaceutical scientist would believe any of the outcomes above showing a relationship between $\mathit{K}{\mathit{p}}_{\mathit{u}\mathit{u}}$ and ${\mathit{F}}_{\mathit{H}}$. Benet and Sodhi (2024) further detail the eq. 11 error in assuming that $\mathit{C}{\mathit{L}}_{\mathit{Blood}}\cdot {\mathit{C}}_{\mathit{Blood}}\hspace{0.17em}=\hspace{0.17em}\mathit{C}{\mathit{L}}_{\mathit{int}}\cdot {\mathit{C}}_{\mathit{H},\mathit{u}}$ rather than the proposed $C{L}_{\mathit{Blood}}\cdot C_{\mathit{Blood}}\hspace{0.17em}=\hspace{0.17em}C{L}_{H,u}\cdot C_{H,u}$ as discussed above, where the latter leads to the more likely outcome of no relationship between Kp_uu and F_H.

The Inclusion of Hepatic Basolateral Transporters in Deriving Hepatic Clearance

A major concern described in Korzekwa and Nagar (2023), Rowland et al. (2023) and Siegel (2024) is the equations we propose (Patcher et al., 2022) using Kirchhoff’s Laws when hepatic basolateral transporter clearances are relevant, but Q_H is much larger and therefore not included (eq. 13)

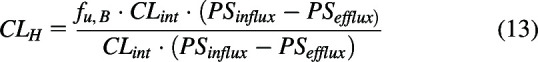They ask what is the result if PS_efflux is greater than PS_influx? The answer is that, as we described above, Kirchhoff’s Laws are only applicable for rate-defining processes. If $(\mathit{P}{\mathit{S}}_{\mathit{influx}}-\mathit{P}{\mathit{S}}_{\mathit{efflux}})$ is negative, hepatic basolateral transport cannot be a rate defining process since CL_H cannot equal a negative value and hepatic basolateral transporters should not have been considered in the derivation, and therefore the resulting clearance relationship would be eq. 4 in such a scenario. This is analogous to why passive permeability is not included.

Comparing the extended clearance model relationships of eq. 13 with eq. 12, we note that eq. 12 is derived based on eq. 11, which we argue is not valid. Furthermore, for hepatic basolateral transport to be valid as a rate limiting step in eq. 12, PS_efflux must be zero or very small so that CL_int in the numerator and denominator may cancel. And finally, for eq. 12 there is no possibility for hepatic basolateral transport to be relevant yet still have CL_int be the rate limiting step. As we have asked previously (Patcher at al., 2022; Benet and Sodhi, 2023), why should PS_efflux have to be negligible to have basolateral hepatic transport be rate limiting, only that the positive difference between influx and efflux clearances be much smaller than CL_int? Like we demonstrated above for gut clearance and intravenous bolus clearance, rearranging eq. 13 shows the relative importance of the two rate-defining processes, transport and hepatic elimination, when both are considered.

In the Rowland et al. (2023) Appendix part 2, the authors question our transporter equations by inserting the hepatic basolateral transporter difference into eq. 11. We believe that our recent Kp_uu and F_H analysis (Benet and Sodhi, 2024) convincingly demonstrates that any analysis based on eq. 11 is highly questionable, and thus the Appendix part 2 derivations are not valid. Similarly, derivations based on eq. 11 in Siegel (2024) and Li and Jusko (2022) are questionable.

Physics and Electrical Circuits versus Pharmacokinetics and In Vivo Clinical Pharmacology

Each of the three papers criticizing our approach (Siegel, 2024; Korzekwa and Nagar, 2023; Rowland et al., 2023), and particularly Siegel (2024), raise questions concerning our transforming electrical circuit theory into pharmacokinetic derivations of clearances and rate constants, and they have a point. We made advancements on Kirchhoff’s Laws of parallel and in series processes to indicate that when applied to pharmacologic systems only rate-defining processes should be included in the derivation, a distinction that Kirchhoff did not have to make. Furthermore, although Kirchhoff considered electrical process going forward and backward, he did not consider that these processes could be happening simultaneously (as for hepatic basolateral transporter clearances), and certainly, neither Kirchhoff nor any other physicist or chemist considered that although these parallel and in series processes would be solvable in physics and chemistry where all of the reactions occur in a single fixed volume (i.e., for rate constants), they would need to be solvable in vivo where different processes will occur in different volumes of distribution and drug dosing decisions are made based on clearance measurements, not rate constant measurements.

Therefore, perhaps we should not have titled our methodology as the application of “Kirchhoff’s Laws”, but rather the application of “Benet and Sodhi Rules” to deriving clearance and overall rate constants for parallel and in series processes, or maybe some nonpersonal title, such as “Series/Parallel Rules”. We would not object to any such name change; we chose “Kirchhoff’s Laws” since the prominent criteria in solving clearance equations are for parallel and in series processes as given in eqs. 1 and 2.

Conclusions

We return to the questions of Popper (1962) concerning theory as a proposed solution to a set of problems. Does it solve the problem? Yes, the Kirchhoff’s Laws approach explains why all of the experimental IPRL data concerning liver clearance appear to fit eq. 4, which was previously regarded as the WSM. In addition, the Kirchoff’s Laws approach explains why for linear pharmacokinetic systems systemic bioavailability determinations can be greater than 1, why renal clearance can be a function of drug input processes, and why statistically different bioavailability measures may be found for urinary excretion versus systemic concentration measurements. Does it solve it better than other theories? Yes, the present pharmacokinetic theory cannot explain any of the experimental findings listed in the response to the previous question, and also leads to unbelievable relationships between Kp_uu and F_H. Has it merely shifted the problem? No, the Kirchhoff’s Laws approach is applicable to all pharmacokinetic analyses of experimental data, those that were previously adequately explained with present pharmacokinetic theory, and those that were not. Is the solution simple?Yes, clearance and rate constant equations characterizing pharmacokinetic experimental data may be simply derived using eqs. 1 and 2, not requiring differential equation derivations. Is it fruitful? Certainly. We have proposed a simple approach that is consistent with all experimental data (including changing clearance with continuous zero order infusions, in vivo nonlinear pharmacokinetic processes and why increased pharmacodynamic response may be seen with extended-release dosage forms compared with comparable dose immediate-release formulations, which will be the subjects of future publications).

Abbreviations

AUC

area under the curve

C _Blood

steady-state concentration of drug in the blood

C _H,u

average concentration of unbound drug within the liver

C _in

concentration of total drug in blood entering the liver

C _out

concentration of total drug in blood leaving the liver

CL

clearance

CL _entering

entering clearance

CL _gut

clearance from the intestine

CL _H

hepatic clearance

CL _H,u

hepatic clearance of unbound drug

CL _int

intrinsic clearance

CL _leaving

leaving clearance

DM

dispersion model

ER

extraction ratio

F _H

first pass hepatic bioavailability

f _uB

fraction unbound in blood

IPRL

isolated perfused rat liver

IVIVE

in vitro-in vivo extrapolation

k _a

absorption rate constant

k _e

elimination rate constant

Kp _uu

the ratio of unbound steady-state liver to unbound systemic concentrations

PS _efflux

hepatic basolateral efflux transport intrinsic clearance

PS _influx

hepatic basolateral influx transport intrinsic clearance

PTM

parallel tube model

Q _H

hepatic blood flow

V _gut

volume of distribution in the gut

V _ss

volume of distribution at steady-state

WSM

well-stirred model

Authorship Contributions

Performed data analysis: Benet, Sodhi.

Wrote or contributed to the writing of the manuscript: Benet, Sodhi.