ABSTRACT
Introduction
Computational head injury models are promising tools for understanding and predicting traumatic brain injuries. However, most available head injury models are “average” models that employ a single set of head geometry (e.g., 50th-percentile U.S. male) without considering variability in these parameters across the human population. A significant variability of head shapes exists in U.S. Army soldiers, evident from the Anthropometric Survey of U.S. Army Personnel (ANSUR II). The objective of this study is to elucidate the effects of head shape on the predicted risk of traumatic brain injury from computational head injury models.
Materials and Methods
Magnetic resonance imaging scans of 25 human subjects are collected. These images are registered to the standard MNI152 brain atlas, and the resulting transformation matrix components (called head shape parameters) are used to quantify head shapes of the subjects. A generative machine learning model is used to generate 25 additional head shape parameter datasets to augment our database. Head injury models are developed for these head shapes, and a rapid injurious head rotation event is simulated to obtain several brain injury predictor variables (BIPVs): Peak cumulative maximum principal strain (CMPS), average CMPS, and the volume fraction of brain exceeding an injurious CMPS threshold. A Gaussian process regression model is trained between head shape parameters and BIPVs, which is then used to study the relative sensitivity of the various BIPVs on individual head shape parameters. We distinguish head shape parameters into 2 types: Scaling components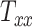 
, 
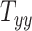, and 
that capture the breadth, length, and height of the head, respectively, and shearing components (
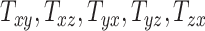, and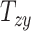 
) that capture the relative skewness of the head shape.
Results
An overall positive correlation is evident between scaling components and BIPVs. Notably, a very high, positive correlation is seen between the BIPVs and the head volume. As an example, a 57% increase in peak CMPS was noted between the smallest and the largest investigated head volume parameters. The variation in shearing components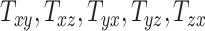 
, and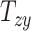 
on average does not cause notable changes in the BIPVs. From the Gaussian process regression model, all 3 BIPVs showed an increasing trend with each of the 3 scaling components, but the BIPVs are found to be most sensitive to the height dimension of the head. From the Sobol sensitivity analysis, the 
scaling parameter contributes nearly 60% to the total variance in peak and average CMPS;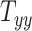 
contributes approximately 20%, whereas 
contributes less than 5%. The remaining contribution is from the 6 shearing components. Unlike peak and average CMPS, the VF-CMPS BIPV is associated with relatively evenly distributed Sobol indices across the 3 scaling parameters. Furthermore, the contribution of shearing components on the total variance in this case is negligible.
Conclusions
Head shape has a considerable influence on the injury predictions of computational head injury models. Available “average” head injury models based on a 50th-percentile U.S. male are likely associated with considerable uncertainty. In general, larger head sizes correspond to greater BIPV magnitudes, which point to potentially a greater injury risk under rapid neck rotation for people with larger heads.
INTRODUCTION
Traumatic brain injury (TBI) is a leading cause of death and disability in the U.S. Military. More than 450,000 TBI cases in the military were reported between 2000 and 2022.1 Non-penetrating mild TBI (mTBI) forms most of these cases (i.e., ∼82%), commonly occurring because of rapid head movement or application of forces and pressures on soldiers’ heads during training and combat. Termed a silent epidemic, mTBI can cause long-term cognitive defects such as impaired memory, slowed processing speed, and issues with multitasking.2
In vitro and in vivo brain injury studies across length scales (neuron level to full-head level) suggest a strong correlation between brain tissue deformation (i.e., strain) during injury and the resulting neuropathology.3–5 Owing to this biomechanical origin, computational head injury models, which can simulate the brain’s mechanical response to rapid movements or force loading, have emerged as potential tools to understand and predict the risk of TBI.6 Several strain-based brain injury predictor variables (BIPVs) have been proposed in the literature, providing a quantitative estimate of TBI risk when compared to available strain-based injury thresholds and risk functions.7
Despite their promising aspects, most available computational head injury models suffer from a major limitation: They are “average” models that employ a single set of head geometry (e.g., of a 50th-percentile U.S. male) and brain tissue mechanical properties without considering their variability across the human population.8–10 As an example of head shape variability in the context of the U.S. Military, the Anthropometric Survey of U.S. Army Personnel (ANSUR II) that contains head shape measurements from 4,082 male and 1,986 female U.S. Army soldiers reports a wide range of head circumferences: From approximately 510 mm to 640 mm for male soldiers and from 500 mm to 635 mm for female soldiers.11 A natural question thus arises: How does head geometry affect the injury predictor variables resulting from computational brain injury simulations? A quantitative investigation into this question is a crucial step toward understanding the uncertainty in the injury risk predictions of existing models and can provide critical insights into the relative risk of injury among different soldiers.
Prior studies point to a potentially considerable influence of head geometry on the brain’s biomechanical response during injury. For example, Ommaya et al.12 conducted whiplash experiments on rhesus monkeys and related their injury tolerances to humans via dimensional scaling analysis. They concluded that larger heads have a lower tolerance to injury. Among computational studies, Li et al.13 simulated rapid head acceleration using finite element-based human head injury models and showed that a smaller intracranial volume is generally associated with smaller brain strains. Teferra et al.14 studied the influence of head volume on computationally simulated intracranial pressure (ICP) under blast loading. They showed that the peak ICP can vary by more than 30% because of head morphological variability. Iliopoulos et al.15 reported a qualitative influence of head breadth and length on the predicted ICP field via a reduced-order head model. Although helpful in highlighting the overall effect of head morphology on brain biomechanics, these studies fail to quantitatively capture the individual effects of different morphological features such as head length, breadth, height, circumference, skewness, etc. As significantly different head shapes can have the same head size/volume, a detailed investigation of the effect of individual head morphological features on brain biomechanics is needed to discover subject-specific differences in brain injury tolerance and the uncertainty in the injury prediction of “average” head models. Another limitation of these computational studies is that they utilize either linear or quasi-linear viscoelastic constitutive models to capture brain tissue response, which are known to cause errors in predictions compared to fully nonlinear visco-hyperelastic models.16,17
Thus, this study aims to elucidate the quantitative relationships between human head shape features and the risk of TBI because of rapid head accelerations using high-fidelity computer models based on a fully nonlinear visco-hyperelastic constitutive framework.
MATERIALS AND METHODS
A detailed framework of this study is shown in Figure 1. It consists of 4 steps: Biomedical imaging of healthy human subjects and quantification of their head shapes using a standard brain atlas; probabilistic modeling and generation of additional head shape features from the available data via generative machine learning (ML); construction of head injury models for each head shape and simulations of an injurious, rapid head rotation to obtain various BIPVs; and Gaussian process regression (GPR)–based data-driven modeling and sensitivity analysis to discover the statistical relationship between head shape features and the BIPVs. These individual steps will now be explained in greater detail.
FIGURE 1.
A flowchart of the 4-step framework of this study. (A) Step 1: Biomedical imaging and head shape quantification, where MRI scans of 25 human subjects are acquired and their head shape parameters are quantified as components of the affine transformation matrix matrices (with respect to the MNI152 brain atlas). (B) Step 2: Probabilistic modeling and additional data generation, where a generative ML method is used to quantify the joint probability distribution of head shape parameters and generate additional datasets. (C) Step 3: Head injury modeling and simulations, where head injury models of the 50 head shape parameters are generated by scaling a standard MNI152 head model, and an injurious, rapid head rotation event is simulated using these models to obtain brain injury predictor variables (BIPVs). (D) Step 4: Gaussian process regression (GPR) and sensitivity analysis, where a GPR mapping between head shape parameters and BIPVs is learned and the effect of individual parameters on BIPVs is quantified via sensitivity analysis.
Biomedical Imaging and Head Shape Quantification
Anatomical brain images of 25 healthy volunteers (age: 21-49 years, 12 males and 13 females) are acquired using T1-weighted MRI. Data acquisition, subject recruitment, and study approval details are provided elsewhere.18,19 These images are affinely registered to the standard MNI152 (Montreal Neurological Institute) brain atlas20 using the Advanced Normalization Toolkit,21 as depicted in Figure 1A. MNI152 is a standard brain template that is used extensively in biomedical research.22 For a given pair of images, an affine transformation linearly maps homogeneous coordinates from one image,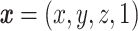 
, to the corresponding coordinates on the target image, 
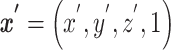, via a transformation matrix, 
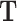, such that
 |
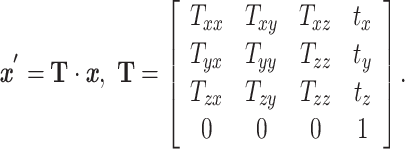(1) |
From Equation 1, the transformation matrix components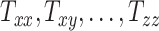 
capture image scaling and shear, whereas the components 
, 
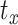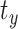, and 
capture image translation along the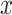 
, 
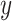, and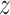 
directions, respectively. Affine registration of our magnetic resonance (MR) images to the MNI152 brain atlas provided these 12 components for each subject-specific MRI scan. Note, in the coordinate system of our MR images, the positive x-axis represents the right–left direction, the positive y-axis represents the anterior–posterior direction, and the positive z-axis represents the inferior–superior direction. The 9 scaling and shearing components (
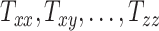) of these matrices capture the differences in the subjects’ head shape with respect to the MNI152 brain atlas. Specifically, the 3 scaling components 
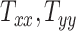, and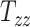 
quantify the relative breath, length, and height of a subject’s head relative to the MNI152 atlas; the 6 shearing components 
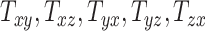, and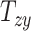 
quantify the relative skewness of a subject’s head relative to the MNI152 atlas. These 9 parameters represent the quantitative head shape features of human subjects in this study and will hereafter be referred to as “head shape parameters.”
Probabilistic Modeling of Head Shape Features and the Generation of Additional Data
Once multiple head shape parameter sets are generated, the goal is to generate computational models with these head geometries, simulate an injurious head rotation event, and study the influence of individual head shape parameters on the predicted BIPVs via GPR. Given the small number of available datasets from MRI scanning and registration, there is expected to be significant epistemic uncertainty in the resulting GPR model caused by a lack of injury prediction for a considerable range of inputs.23 To minimize this uncertainty, we employ a generative ML method introduced by Soize and Ghanem24 to discover the joint probability distribution of head shape parameters from the available 25 datasets and then predict new, realistic head shape parameters via statistical sampling (Fig. 1B). Briefly, this method utilizes multidimensional Gaussian kernel-density estimation to obtain the joint probability distribution of scaled and normalized data, followed by an application of diffusion maps to reveal the underlying local geometric structure of the data. Finally, Markov Chain Monte Carlo based on Itô stochastic differential equations is utilized to sample realizations of the random vector (in our case, the random vector of head shape parameters). In this work, we generated 25 additional sets of head shape parameters to create a total dataset of 50 head shape parameters, which are used to build head injury models for further analysis.
Development of Head Injury Models and Simulations
Computational head injury models are created for each set of head shape parameters by scaling a head injury model of the MNI152 brain atlas. To create the MNI152 head model, a framework recently proposed by the authors is used.16,19 Briefly, the MNI152 brain image is resampled to 1.5 mm isotropic resolution, skull-stripped, and segmented into different anatomical substructures using a multi-atlas segmentation and cortical reconstruction algorithm.25 The segmented substructures are deep gray matter, cortical gray matter, cerebral white matter (composed of the corpus callosum and corona radiata), cerebellar gray matter, cerebellar white matter, brainstem, ventricles, and cerebrospinal fluid (CSF). From these segmented images, the subarachnoid space is identified using a method described in Alshareef et al.19 The falx and tentorium are reconstructed using a fast-marching multi-atlas-based segmentation method.26 The corpus callosum is delineated from cerebral white matter using the ITK-SNAP segmentation software.27 Finally, the MONSTR tool28 is used for skull stripping to obtain a brain mask, which is dilated to generate an artificial skull. The fully constructed 3D MNI152 head model geometry and its section views highlighting different brain regions are shown in Figure 1C. This model is inversely transformed (Equation 1) using the transformation matrices corresponding to each set of head shape parameters in our dataset (note, the translational components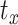 
, 
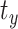, and 
are set to zero at this stage) and then resampled to 1.5 mm isotropic resolution to obtain the 50 head injury models for injury risk analysis.
In all 50 computational head models that feature different head shapes, the same material properties are used for the various brain tissue substructures. Specifically, the Ogden–Upadhyay–Subhash–Spearot (O–USS) nonlinear visco-hyperelastic constitutive model is calibrated for the 7 parenchymal brain substructures (deep gray matter, cortical gray matter, corpus callosum, corona radiata, cerebellar gray matter, cerebellar white matter, and brainstem) using experimental ex vivo stress–strain data from the literature.29,30 A summary of these ex vivo studies is provided in Section SM1 of the Supplementary Material. For a detailed description of the O–USS model, its calibration, and numerical implementation, the reader is referred to Upadhyay et al.16,17 This model assumes an additive decomposition of total stress into hyperelastic and viscous-dissipation components: A 2-parameter Ogden strain energy density function31 is used to capture the hyperelastic part, whereas the 3-parameter Upadhyay–Subhash–Spearot viscous-dissipation potential17 is used for the viscous part. The model comprises the following material properties: Long-term shear modulus (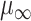
), nonlinearity parameter (
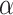), linear and nonlinear rate sensitivity control parameters (
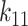and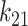 
), rate sensitivity index (
), the bulk modulus (
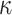), and density (
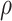). A complete list of O–USS model parameters of different brain substructures is provided in Section SM2 of the Supplementary Material. The material properties of minor, nonparenchymal brain regions are provided in Section SM3 of the Supplementary material. The following constitutive models are considered for these regions: 1-branch Generalized Maxwell linear viscoelastic model for the subarachnoid space; linear elastic model for falx, tentorium, and skull; and a viscous fluid model for the ventricles and CSF. Our recent work16 showed that applying the O–USS model in computational head simulations leads to improved accuracy of strain field prediction when compared to hereditary integral-based models (e.g., linear viscoelasticity and quasi-linear viscoelasticity).
Using our head models, we numerically simulated an injury-causing rapid head rotation event via the material point method32 in the Uintah software (for details of our material point method simulations, the reader is referred to Upadhyay et al.16). Figure 1C shows the angular velocity profile (sinusoidal) of time-period 20 ms and a peak amplitude of 42.87 rad/s, which is applied to the skull for head rotation about the inferior–superior axis passing through the foramen (i.e., the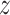 
-axis). The applied peak angular velocity corresponds to a 50% probability of Abbreviated Injury Scale 4+ anatomic brain injuries as per the BrIC brain injury criteria.9 The head injury simulations yield time-varying full-field maps of the Green–Lagrange strain at a 1.5 mm spatial resolution and a 2 ms temporal resolution for 40 ms, which are then used to compute time-varying MPS fields as the first eigenvalue of the Green–Lagrange strain. Finally, the MPS fields are post-processed to obtain full-field cumulative maximum principal strain (CMPS). Cumulative maximum principal strain at a given brain voxel is the peak value of MPS over the entire simulation duration. Using the CMPS fields, the following BIPVs are computed7,33–35: Peak CMPS (evaluated at 95th-percentile level), average CMPS (evaluated at 50th-percentile level), and brain volume fraction exceeding the CMPS threshold value of 0.20 (denoted by VF-CMPS). From Zhao et al.,7 CMPS of 0.20 corresponds to a 50% concussion probability. Overall, our head injury simulations generate 50 sets of these 3 BIPVs (peak CMPS, average CMPS, and VF-CMPS), one from each simulation, that correspond to the 50 sets of 9 head shape parameters (
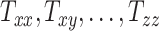). These data are used to train a GPR model that is described next.
Gaussian Process Regression and Sensitivity Analysis
Gaussian process regression is employed in this work to discover a statistical mapping between head shape parameters and the resulting BIPVs. Gaussian process regression provides a nonparametric model for a response function given an input training dataset through a Bayesian update involving an assumed prior distribution and a likelihood tying the posterior distribution to observed data.36 As shown in Figure 1D, our training dataset comprises an input of the head shape parameter dataset (dimension: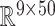 
)—represented by a random vector 
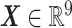—and an output of the corresponding predicted BIPVs from head injury simulations (dimension: 
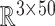)—represented by a random vector 
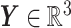. The GPR mapping (
) has the following mathematical formulation33,36:
 |
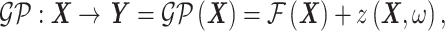(2) |
where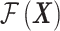 
represents the mean value of the Gaussian process (assumed constant in this study) and 
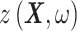represents a zero-mean, stationary Gaussian process in the underlying probability space 
defined in terms of a correlation function. Training a GPR model involves calibrating the hyperparameters of this correlation function. In this work, a Gaussian correlation function is selected. Once trained, our GPR model can predict BIPVs corresponding to arbitrary head shape parameter input sets. We use the leave-one-out cross-validation method to assess the performance of the trained GPR model in terms of the coefficient of determination (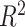
) accuracy metric.
To elucidate the effects of individual head shape parameters on BIPVs, we conducted local and global sensitivity analyses. In our local sensitivity analysis, the GPR model was employed to predict BIPVs when only 1 of the head shape parameters is varied, whereas the others are fixed to their mean values (across all 50 datasets). Global sensitivity analysis was performed using the Sobol’s method.37 Briefly, the Sobol’s method decomposes the variance of the model output (in our case, the BIPVs) into fractions attributed to different input parameters or sets of input parameters (via interaction effects). This results in 2 measures of sensitivity: (1) First-order sensitivity index, which measures the proportion of the output variance that can be attributed to the variability in a single input parameter, independently of the other parameters, and (2) total-order index, which measures the proportion of the output variance attributable to both the direct impact of a parameter and its interactions with other parameters.
All calculations presented in this work are performed in Python. For ML tasks, the Scikit-learn38 package is used; for sensitivity analysis, the SALib39 package is used.
RESULTS AND DISCUSSION
Head Shape Features
As explained previously, in this work, biomedical imaging of 25 healthy human subjects followed by image registration to the MNI152 brain atlas provided the head shape parameters that capture the relative scaling and shear in the subjects’ heads with respect to the MNI152 head. Using this initial dataset, a generative ML framework was applied to obtain 25 additional head shape features. Figures 2A and B show the pairwise correlation plots of all scaling and 3 representative shearing components (for brevity) of these parameters, respectively, along with the normalized histograms to reveal the distributions of individual parameters. The observed data from real subjects are shown as red datapoints, whereas the ML-generated data are shown as blue datapoints.
FIGURE 2.
Pairwise correlation plots and normalized histograms of head shape parameters. (A) The 3 scaling components of the head shape parameters, and (B) 3 representative shearing components of the head shape parameters. The available data from MRI of real subjects is shown in red, and the head shape parameters artificially generated via generative ML is shown in blue.
From Figure 2A, the observed datapoints reveal a significant variability in scaling components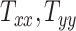 
, and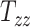 
across the test subject population. Specifically, 
, which represents the breadth scaling factor between a subject’s brain image and the MNI152 atlas, has a standard deviation of 0.04. For 
(the length scaling factor) and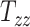 
(the height scaling factor), the standard deviations are 0.04 and 0.03, respectively. From Figure 2B, there is a relatively small variation and overall minimal values in the case of shearing components. The average standard deviation across all the shearing components is 0.02. Finally, from both plots, the generated data (in blue) closely follow the original data distribution (in red). This shows that the generative ML framework applied in this work accurately models the joint probability distribution of head shape parameters and can artificially create head shapes that are statistically equivalent to the head shapes of actual human subjects.
Head Injury Simulation Results: Effect of the Overall Head Size on TBI Risk
Our 50 head injury simulations with models of different head geometries provided a corresponding set of BIPVs. Figures 3A to I show the evolution of the different BIPVs with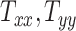 
, and 
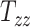. The corresponding Pearson correlation coefficients (denoted by 
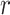) are also indicated on the plots. An overall positive correlation is evident between scaling components and BIPVs. Among the 3 scaling components, 
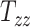resulted in the highest correlation coefficient, followed by 
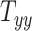and 
. Note that the high noise in these plots is because all head shape parameters are varied simultaneously in the different head injury simulations—so, for example, a relatively large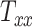 
can be associated with an overall small head if the other two scaling parameters are small.
FIGURE 3.
The evolution of brain injury predictor variables with different head shape features from our head injury simulations. (A, D, G, J, and M): Peak cumulative maximum principal strain (CMPS) versus 
, 
, 
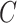(head circumference parameter), and 
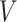(head volume parameter), respectively. (B, E, H, K, and N): Average CMPS versus 
, 
, 
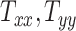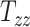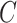, and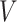 
, respectively. (C, F, I, L, and O): VF-CMPS (brain volume fraction exceeding a 0.20 CMPS threshold) versus 
, 
, 
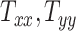, and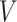 
, respectively.
To better capture the effect of the overall head shape and size on the BIPVs, we define 2 parameters that qualitatively capture the relative head circumference and head volume from subject-specific MRI scans.
Head circumference parameter:
 |
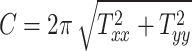(3a) |
Head volume parameter:
 |
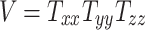(3b) |
Figures 3J to O plot the evolution of the BIPVs with the above-defined head circumference and volume parameters. A very high, positive correlation can be seen, especially in the case of the head volume parameter. As an example of the overall effect of head volume on injury predictors, a 57% increase in peak CMPS was noted between the smallest and the largest investigated head volume parameters. These results show that brain injury risk because of rapid rotational head accelerations increases with the overall head size.
Finally, our results showed that variation in shearing components 
, and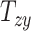 
on average does not cause notable changes in the BIPVs. The representative peak CMPS versus shearing components plots are provided in Section SM4 of the Supplementary Material. Owing to their small effect on the brain’s biomechanical response and tiny values that may stem from imaging artifacts, the shearing components are not considered for further analysis.
Gaussian Process Regression Results: Effect of Individual Head Shape Parameters on TBI Risk
As described before, a GPR model was trained using the input data of head shape parameters and the corresponding output data of BIPVs from head injury simulations. The hyperparameter calibration of the Gaussian correlation function resulted in an optimized kernel length scale value of 0.10. Leave-one-out cross-validation resulted in an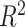 
= 0.99 ± 0.02, indicating an excellent model prediction accuracy. The trained GPR model can predict BIPVs for arbitrary values of head shape parameters.
The GPR model is approximately a million times faster than standard computational head injury simulation, which allows for sensitivity analysis. Figures 4A to C show the results of our local sensitivity analysis, which explain the effect of changing 1 scaling component (say, 
) on the 3 BIPVs when the rest of the 8 head shape parameters are fixed to their mean values (across the 50 available datasets). In general, all 3 BIPVs show an increasing trend with each of the 3 scaling components. Across the investigated range of scaling components, the peak and average CMPS are most sensitive to changes in the height dimension of the head (captured by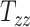 
), followed by the length dimension (captured by 
) and then the breadth dimension (captured by 
). Interestingly, it is seen that peak CMPS is nearly insensitive to changes in the breadth of the head model. In the case of VF-CMPS, the BIPV is most sensitive to changes in the length and breadth dimensions and slightly less sensitive to changes in the height of the head.
FIGURE 4.
The sensitivity of brain injury predictor variables (BIPVs) on the different scaling components of head shape parameters. (A–C) Local sensitivity of peak cumulative maximum principal strain (CMPS), average CMPS, and VF-CMPS (brain volume fraction exceeding a 0.20 CMPS threshold) with respect to the 3 scaling components, respectively. In each case, all but 1 scaling component is varied, and the corresponding BIPVs are calculated using the trained Gaussian process regression model. (D–F) Global sensitivity of peak CMPS, average CMPS, and VF-CMPS with respect to the 3 scaling components, respectively. Each bar graph shows the first-order sensitivity index (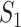
) and the total-order sensitivity index (
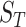) of the 3 scaling components for that BIPV.
The results of the global sensitivity analysis are shown in Figures 4D to F, which plot the first-order sensitivity and total-order indices of the 3 scaling components corresponding to peak CMPS, average CMPS, and VF-CMPS, respectively. These sensitivity indices were obtained from 8,192 (i.e., 213) GPR model predictions of BIPVs for randomly sampled head shape parameters and capture the relative contribution (out of 1) of each head shape parameter on the total variance of these BIPVs. In all 3 plots, the first-order sensitivity and total-order indices have similar magnitudes, indicating a negligible interaction effect between the 3 scaling components. From Figures 4D and E, the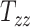 
scaling parameter contributes nearly 60% to the total variance in peak and average CMPS. On the other hand, 
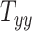contributes approximately 20%, whereas 
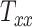contributes less than 5% to the variance of these BIPVs. The remaining contribution to the variance stems from the 6 shearing components. Unlike peak and average CMPS, the VF-CMPS BIPV is associated with relatively evenly distributed Sobol’s indices across the 3 scaling parameters. Furthermore, the contribution of shearing components to the total variance in this case is negligible.
CONCLUSION
The present study is the first to investigate the correlation between individual head shape features and the risk of mTBI using an anatomically detailed head injury model based on a nonlinear visco-hyperelastic constitutive framework. Our results show that head shape has a considerable influence on the injury predictions of computational head injury models. As most available head models are based on the “average” head of a 50th-percentile U.S. male, applying these models for brain injury prediction will be associated with considerable uncertainty. Our simulations specifically show that given a set of fixed brain tissue material properties and external loading conditions, larger head sizes correspond to greater BIPV magnitudes. This points to potentially a greater injury risk under rapid neck rotation for people with larger heads. The application of GPR in this work allowed for deeper insights into the individual effect of different head shape features on the predicted injury risk. It is observed that BIPVs are more sensitive to scaling components of the head shape parameters, which capture the breadth, length, and height of the head model, than the shearing components that capture the skewness of the head model (with respect to the MNI152 head). Overall, BIPVs are found to be most sensitive to the height dimension of the head.
The present study is a key step toward understanding subject-specific differences in mTBI risk among U.S. Military soldiers. Such insights can lead to safer military training programs, combat duty assignments, and the development of next-generation personalized protective devices, thus enhancing warfighter combat readiness. However, there are some limitations of this study. First, mTBI in the military can be caused by rapid momentum transfer to the head (e.g., rapid head rotation) or because of shock waves from blasts; however, this study only considers the former mechanism and does not capture the effect of head shape on the risk of primary blast-induced TBI. Approximately one-third of all TBI cases in the military result from a blast event.40 Second, this study focuses solely on mTBI, the most seen type of TBI in the military.1 As a result, its conclusions do not apply to moderate, severe, and penetrating TBI, which comprise approximately 11%, 1%, and 1% of the total TBI cases in the military, respectively.1 Third, the linear affine transformation used in this work to obtain subject-specific head injury models focuses on outer head geometry and neglects any subject-specific differences in individual brain substructure morphologies (e.g., white matter volume) and mechanical properties. Our future work will employ nonaffine transformations to address finer brain substructure morphological differences and their effect on the simulated brain deformation and pressure fields under blunt impact and blast loading, respectively. We note that large-scale observational studies on the head morphology of military personnel who suffered TBI would be critical to building confidence in and validating the conclusions of computational TBI studies.
Supplementary Material
ACKNOWLEDGMENTS
None declared.
Contributor Information
Kshitiz Upadhyay, Department of Mechanical and Industrial Engineering, Louisiana State University, Baton Rouge, LA 70803, USA.
Roshan Jagani, Department of Mechanical Engineering, Johns Hopkins University, Baltimore, MD 21218, USA.
Dimitris G Giovanis, Department of Civil and Systems Engineering, Johns Hopkins University, Baltimore, MD 21218, USA.
Ahmed Alshareef, Department of Mechanical Engineering, University of South Carolina, Columbia, SC 29208, USA.
Andrew K Knutsen, Center for Neuroscience and Regenerative Medicine, Henry M. Jackson Foundation, Bethesda, MD 20817, USA.
Curtis L Johnson, Department of Biomedical Engineering, University of Delaware, Newark, DE 19713, USA.
Aaron Carass, Department of Electrical and Computer Engineering, Johns Hopkins University, Baltimore, MD 21218, USA.
Philip V Bayly, Mechanical Engineering and Materials Science, Washington University in St. Louis, St. Louis, MO 63130, USA.
Michael D Shields, Department of Civil and Systems Engineering, Johns Hopkins University, Baltimore, MD 21218, USA.
K T Ramesh, Department of Mechanical Engineering, Johns Hopkins University, Baltimore, MD 21218, USA.
CLINICAL TRIAL REGISTRATION
Not applicable.
INSTITUTIONAL REVIEW BOARD (HUMAN SUBJECTS)
Not applicable.
INSTITUTIONAL ANIMAL CARE AND USE COMMITTEE (IACUC)
Not applicable.
INDIVIDUAL AUTHOR CONTRIBUTION STATEMENT
K.U.: Conceptualization, data curation, formal analysis, investigation, methodology, software, validation, visualization, writing—original draft, writing—review and editing; R.J.: Formal analysis, investigation, writing—review and editing; D.G.G.: Methodology, software, writing—review and editing; A.A.: Data curation, investigation, writing—review and editing; A.K.K.: Data curation, investigation, writing—review and editing; C.L.J.: Funding acquisition, investigation, supervision, writing—review and editing; A.C.: Data curation, investigation, writing—review and editing; P.V.B.: Funding acquisition, project administration, supervision, writing—review and editing; M.D.S.: Methodology, software, writing—review and editing; K.T.R.: Conceptualization, funding acquisition, project administration, resources, supervision, writing—review and editing.
INSTITUTIONAL CLEARANCE
Not applicable.
SUPPLEMENTARY MATERIAL
Supplementary material is available at Military Medicine online.
FUNDING
This research was supported by the National Institute of Neurological Disorders and Stroke of the NIH under Grant No. U01 NS112120.
SUPPLEMENT SPONSORSHIP
This article appears as part of the supplement “Proceedings of the 2023 Military Health System Research Symposium,” sponsored by Assistant Secretary of Defense for Health Affairs.
CONFLICT OF INTEREST STATEMENT
None declared.
DATA AVAILABILITY
The data underlying this article will be shared on reasonable request to the corresponding author.
REFERENCES
- 1. Annual Report 2022: Traumatic Brain Injury Center of Excellence, 2022. Available at https://health.mil/Military-Health-Topics/Centers-of-Excellence/Traumatic-Brain-Injury-Center-of-Excellence; accessed April 21, 2023.
- 2. Pavlovic D, Pekic S, Stojanovic M, Popovic V: Traumatic brain injury: neuropathological, neurocognitive and neurobehavioral sequelae. Pituitary 2019; 22(3): 270–82.doi: 10.1007/s11102-019-00957-9 [DOI] [PubMed] [Google Scholar]
- 3. Donat CK, Yanez Lopez M, Sastre M, et al. : From biomechanics to pathology: predicting axonal injury from patterns of strain after traumatic brain injury. Brain 2021; 144(1): 70–91.doi: 10.1093/brain/awaa336 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Xiong Y, Mahmood A, Chopp M: Animal models of traumatic brain injury. Nat Rev Neurosci 2013; 14(2): 128–42.doi: 10.1038/nrn3407 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Bar-Kochba E, Scimone MT, Estrada JB, Franck C: Strain and rate-dependent neuronal injury in a 3D in vitro compression model of traumatic brain injury. Sci Rep 2016; 6(1): 30550.doi: 10.1038/srep30550 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Ji S: Biomechanical modeling of traumatic brain injury. In: Jaeger D and Jung R eds. Encyclopedia of Computational Neuroscience. Springer New York; 2018: 1–4. [Google Scholar]
- 7. Zhao W, Cai Y, Li Z, Ji S: Injury prediction and vulnerability assessment using strain and susceptibility measures of the deep white matter. Biomech Model Mechanobiol 2017; 16(5): 1709–27.doi: 10.1007/s10237-017-0915-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Wu T, Alshareef A, Giudice JS, Panzer MB: Explicit modeling of white matter axonal fiber tracts in a finite element brain model. Ann Biomed Eng 2019; 47(9): 1908–22.doi: 10.1007/s10439-019-02239-8 [DOI] [PubMed] [Google Scholar]
- 9. Takhounts EG, Craig MJ, Moorhouse K, McFadden J, Hasija V: Development of Brain Injury Criteria (BrIC). Stapp Car Crash J 2013; 57: 243–66.doi: 10.4271/2013-22-0010 [DOI] [PubMed] [Google Scholar]
- 10. Ghazi K, Wu S, Zhao W, Ji S: Instantaneous whole-brain strain estimation in dynamic head impact. J Neurotrauma 2021; 38(8): 1023–35.doi: 10.1089/neu.2020.7281 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Gordon CC, Blackwell CL, Bradtmiller B, et al. : 2012 Anthropometric Survey of U.S. Army Personnel: Methods and Summary Statistics. NATICK/TR-15/007. U.S. Army Natick Soldier Research, Development and Engineering Center, 2014.
- 12. Ommaya AK, Yarnell P, Hirsch AE, Harris EH: Scaling of experimental data on cerebral concussion in sub-human primates to concussion threshold for man. SAE Technical Papers; 1967.
- 13. Li X, Zhou Z, Kleiven S: An anatomically detailed and personalizable head injury model: significance of brain and white matter tract morphological variability on strain. Biomech Model Mechanobiol 2021; 20(2): 403–31.doi: 10.1007/s10237-020-01391-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Teferra K, Tan XG, Iliopoulos A, Michopoulos J, Qidwai S: Effect of human head morphological variability on the mechanical response of blast overpressure loading. Int J Numer Method Biomed Eng 2018; 34(9): 1–18.doi: 10.1002/cnm.3109 [DOI] [PubMed] [Google Scholar]
- 15. Iliopoulos AP, Michopoulos JG, Avery P, Farhat C, Teferra K, Qidwai S: Towards Model Order Reduction for uncertainty propagation in blast-induced traumatic brain injury. In: American Society of Mechanical Engineers. Volume 1: 37th Computers and Information in Engineering Conference. Cleveland, Ohio, USA; 2017: 1–12.doi: 10.1115/DETC2017-67556. [DOI] [Google Scholar]
- 16. Upadhyay K, Alshareef A, Knutsen AK, et al. : Development and validation of subject-specific 3D human head models based on a nonlinear visco-hyperelastic constitutive framework. J R Soc Interface 2022; 19(195): 1–27.doi: 10.1098/rsif.2022.0561 [DOI] [Google Scholar]
- 17. Upadhyay K, Subhash G, Spearot D: Visco-hyperelastic constitutive modeling of strain rate sensitive soft materials. J Mech Phys Solids 2020; 135: 103777.doi: 10.1016/j.jmps.2019.103777 [DOI] [Google Scholar]
- 18. Bayly PV, Alshareef A, Knutsen AK, et al. : MR imaging of human brain mechanics in vivo: new measurements to facilitate the development of computational models of brain injury. Ann Biomed Eng 2021; 49(10): 2677–92.doi: 10.1007/s10439-021-02820-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Alshareef A, Knutsen AK, Johnson CL, et al. : Integrating material properties from magnetic resonance elastography into subject-specific computational models for the human brain. Brain Multiphysics 2021; 2: 100038.doi: 10.1016/j.brain.2021.100038 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Fonov V, Evans A, McKinstry R, Almli C, Collins D: Unbiased nonlinear average age-appropriate brain templates from birth to adulthood. Neuroimage 2009; 47:S102.doi: 10.1016/S1053-8119(09)70884-5 [DOI] [Google Scholar]
- 21. Avants BB, Tustison NJ, Stauffer M, Song G, Wu B, Gee JC: The Insight ToolKit image registration framework. Front Neuroinf 2014; 8: 44.doi: 10.3389/fninf.2014.00044 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Mandal PK, Mahajan R, Dinov ID: Structural brain atlases: design, rationale, and applications in normal and pathological cohorts. J Alzheimer’s Dis 2012; 31(SUPPL. 3): S169–88.doi: 10.3233/JAD-2012-120412 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Olivier A, Shields MD, Graham-Brady L: Bayesian neural networks for uncertainty quantification in data-driven materials modeling. Comput Methods Appl Mech Eng 2021; 386: 114079.doi: 10.1016/j.cma.2021.114079 [DOI] [Google Scholar]
- 24. Soize C, Ghanem R: Data-driven probability concentration and sampling on manifold. J Comput Phys 2016; 321(September 2015): 242–58.doi: 10.1016/j.jcp.2016.05.044 [DOI] [Google Scholar]
- 25. Huo Y, Plassard AJ, Carass A, et al. : Consistent cortical reconstruction and multi-atlas brain segmentation. Neuroimage 2016; 138: 197–210.doi: 10.1016/j.neuroimage.2016.05.030 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Glaister J, Carass A, Pham DL, Butman JA, Prince JL: Falx cerebri segmentation via multi-atlas boundary fusion. Med Image Comput Comput Assist Interv 2017; 10433: 92–9.doi: 10.1007/978-3-319-66182-7_11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Yushkevich PA, Piven J, Hazlett HC, et al. : User-guided 3D active contour segmentation of anatomical structures: significantly improved efficiency and reliability. Neuroimage 2006; 31(3): 1116–28.doi: 10.1016/j.neuroimage.2006.01.015 [DOI] [PubMed] [Google Scholar]
- 28. Roy S, Butman JA, Pham DL: Robust skull stripping using multiple MR image contrasts insensitive to pathology. Neuroimage 2017; 146: 132–47.doi: 10.1016/j.neuroimage.2016.11.017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Jin X, Zhu F, Mao H, Shen M, Yang KH: A comprehensive experimental study on material properties of human brain tissue. J Biomech 2013; 46(16): 2795–801.doi: 10.1016/j.jbiomech.2013.09.001 [DOI] [PubMed] [Google Scholar]
- 30. Li Z, Ji C, Li D, Luo R, Wang G, Jiang J: A comprehensive study on the mechanical properties of different regions of 8-week-old pediatric porcine brain under tension, shear, and compression at various strain rates. J Biomech 2020; 98: 109380.doi: 10.1016/j.jbiomech.2019.109380 [DOI] [PubMed] [Google Scholar]
- 31. Ogden RW: Large deformation isotropic elasticity—on the correlation of theory and experiment for incompressible rubberlike solids. Proc R Soc London A Math Phys Sci 1972; 326(1567): 565–84.doi: 10.1098/rspa.1972.0026 [DOI] [Google Scholar]
- 32. Sulsky D, Chen Z, Schreyer HL: A particle method for history-dependent materials. Comput Methods Appl Mech Eng 1994; 118(1–2): 179–96.doi: 10.1016/0045-7825(94)90112-0 [DOI] [Google Scholar]
- 33. Upadhyay K, Giovanis DG, Alshareef A, et al. : Data-driven uncertainty quantification in computational human head models. Comput Methods Appl Mech Eng 2022; 398: 115108.doi: 10.1016/j.cma.2022.115108 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Carlsen RW, Fawzi AL, Wan Y, Kesari H, Franck C: A quantitative relationship between rotational head kinematics and brain tissue strain from a 2-D parametric finite element analysis. Brain Multiphysics 2021; 2: 100024.doi: 10.1016/j.brain.2021.100024 [DOI] [Google Scholar]
- 35. Gabler LF, Crandall JR, Panzer MB: Development of a metric for predicting brain strain responses using head kinematics. Ann Biomed Eng 2018; 46(7): 972–85.doi: 10.1007/s10439-018-2015-9 [DOI] [PubMed] [Google Scholar]
- 36. Williams C, Rasmussen C: Gaussian Processes for Regression. In: Touretzky D, Mozer MC and Hasselmo M eds. Advances in Neural Information Processing Systems. Vol. 8. MIT Press; 1995. [Google Scholar]
- 37. Sobol′ I: Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates. Math Comput Simul 2001; 55(1–3): 271–80.doi: 10.1016/S0378-4754(00)00270-6 [DOI] [Google Scholar]
- 38. Pedregosa F, Varoquaux G, Gramfort A, et al. : Scikit-learn: machine learning in Python. J Mach Learn Res 2011; 12: 2825–30. [Google Scholar]
- 39. Herman J, Usher W: SALib: An open-source Python library for sensitivity analysis. J Open Source Softw. 2017; 2(9): 97.doi: 10.21105/joss.00097. [DOI] [Google Scholar]
- 40. Bryden DW, Tilghman JI, Hinds SR: Blast-related traumatic brain injury: current concepts and research considerations. J Exp Neurosci. 2019; 13: 1–11.doi: 10.1177/1179069519872213 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The data underlying this article will be shared on reasonable request to the corresponding author.