Abstract
River channel migration often occurs inside the floodplain areas of the river. The structural changes occurring in rivers within floodplain zones serve as a significant ecological signal of their tremendous impact on both ecological and human survival. The aim of the research is to assess the spatial and temporal fluctuations of the Meghna River's bankline from 1990 to 2020 (for 30 years), and to predict the future bankline position. The Landsat imageries from USGS were used for this study. The bankline was extracted from satellite imageries (Landsat) using Modified Normalized Difference Water Index (MNDWI) indices. The variations in bankline dynamics were assessed through the application of Net Shoreline Movement (NSM) and End Point Rate (EPR) analyses using the Digital Shoreline Analysis System (DSAS). Predictive modeling was conducted utilizing the Modified EPR Model, with validation performed via the Root Mean Square Error (RMSE) technique. Adjustment of errors was achieved by employing error coefficients tailored to each individual transect. Over the past three decades, the cumulative river erosion in Chandpur Sadar amounted to 18.03 square kilometers, with the highest Net Shoreline Movement (NSM) recorded at −1979.62 m during the study period. The forecasted maximum Net Shoreline Movement (NSM) is anticipated to be −495.79 m, signifying that the transect is associated with erosion, resulting in landward movement. Conversely, the minimum NSM is projected to be −1.01 m. The most significant movement is expected to occur in Puran Bazar, while the least movement is foreseen in Bakharpur. On average, the NSM across all transects is predicted to be −76.25 m. This study presents a cost-effective approach for evaluating the changes in river erosion over time. This technique may be valuable for policymakers in developing effective plans to reduce the negative impacts of erosion-related risks.
Keywords: DSAS, River Erosion, Accretion, Bankline Prediction, End Point Rate
1. Introduction
In many regions of the world, riverbank erosion is the most significant geomorphological processes and natural disasters [1]. From a socioeconomic standpoint, riverbank erosion is particularly noteworthy since it results in the loss of agricultural land next to the river channel [[2], [3], [4]]. River erosion is the process by which the riverbed and bank are diminished over time. A variety of elements have been found to influence riverbank erosion, including temperature conditions, precipitation, flow conditions, soil moisture content, composition of the soil, and snowmelt dynamics for glacial rivers [5,6]. Human interventions such as channelization, embankment construction, and dredging alter the natural flow patterns of rivers, leading to increased erosion forces on riverbanks. Channel straightening and embankment construction can accelerate water flow velocities, resulting in higher rates of bank erosion. Similarly, dredging activities disturb sediment dynamics, destabilizing riverbanks and increasing susceptibility to erosion. Unsustainable sand mining and quarrying activities along riverbanks alter sediment transport dynamics, leading to bank instability and erosion. The extraction of sand and gravel from riverbeds disrupts sediment balance, resulting in channel incision and bank collapse. The dynamic interplay between erosional and depositional processes within floodplain environments can induce notable alterations in channel position along the longitudinal course of the river [7,8]. Rivers exhibit dynamic characteristics as they perpetually modify their course in accordance with varying flow conditions [9]. Two fundamental processes that influence river morphology—the study of the shape, form, and structure of rivers and their channels—are erosion and accretion [10].
Bangladesh is recognized as a riverine country that frequently encounters river erosion where seven hundred (700) rivers flow through Bangladesh from the northern parts to the south, and these are Bangladesh's blessing and a curse [11]. River erosion occurs annually in Bangladesh, displaying unpredictable patterns [12]. Every year, more than one million people are affected by river erosion [13,14]. It forces people to migrate through displacement from their origin to an unknown destination, causing the loss of agricultural lands, homesteads, and urban poverty [[15], [16], [17]]. The bankline change rate for Bangladesh's major river systems (the Padma, Meghna, and Jamuna) was calculated, where the amount of land lost over the last three decades was estimated to be around 0.1 million hectares, leaving over 0.8 million people landless. The rate of riverbank erosion may vary depending on space and time [18,19]. Furthermore, over 7 % of its total land area is encompassed by diverse river systems [20]. The occurrence of this geomorphological phenomenon is frequently observed in the dynamic deltas, as noted by Ref. [21]. During the monsoon season, the flow of water through rivers becomes more forceful, leading to widespread erosion of river banks [22]. River erosion in Bangladesh is a significant natural disaster that occurs regularly and has severe consequences [[21], [22], [23]]. According to Ref. [23], a total of 51 out of 64 districts are identified as being prone to erosion. According to Ref. [24] river erosion affects approximately 2000–3000 km of riverbank on an annual basis.
Many studies have been conducted around the world in the last few decades that are related to either direct erosion detection or exploration of the consequences of erosion, riverbank movement using GIS-RS [[25], [26], [27], [28], [29], [30], [31], [32], [33], [34]]. Several studies have been conducted so far on the bank dynamics of major rivers in Bangladesh [27,[35], [36], [37], [38], [39], [40], [41], [42], [43], [44], [45], [46], [47], [48]] and in India [[49], [50], [51], [52], [53], [54]]. The utilization of remote sensing and GIS techniques for detecting spatio-temporal changes is widely prevalent, particularly in relation to the extensive and highly dynamic river systems. The investigation into bankline changes has been conducted in Vilavancode and Kalkulam taluks over a decade spanning from 2009 to 2019, utilizing multitemporal satellite data from Landsat 7 ETM+ and Sentinel platforms. The alterations in the planform of the Brahmaputra River were analyzed employing the GIS-based Digital Shoreline Analysis System (DSAS) [[55], [56], [57], [58], [59]]. A study was conducted to examine the shifting pattern of the eastern bank of the Padma River in Shibganj Upazila of Chapai Nawabganj district, Bangladesh. The study was done using Satellite Imageries and a recent morphological map [39]. The volume of erosion and deposition in the channel was also calculated. The estimation of erosion and accretion areas on both banks was conducted for the entire reach by creating a new polygon through the spatial union of two consecutive river polygons (specifically, those from 1973 to 1977) within a segment [42].
Satellite data serves as a robust tool for indicating data at both large and small scales. The monitoring of river bankline changes in the Mediterranean basin was conducted using satellite data [60]. The tracking of river bankline change can be effectively accomplished through the utilization of ArcGIS and the Digital Shoreline Analysis System (DSAS) software. The Digital Shoreline Analysis System (DSAS), developed by the United States Geological Survey (USGS), constitutes a prevalent computerized methodology utilized for quantifying shoreline or river bankline alteration rates across diverse coastal locales. This freely available tool is seamlessly integrated with the ArcGIS software platform, facilitating its widespread adoption. DSAS systematically contrasts shoreline or bankline positions across temporal intervals, yielding a range of statistical metrics to assess changes. Leveraging discrete assessments of both right and left banks, the DSAS methodology is extensively applied to ascertain channel migration rates [61,62]. Several researchers utilized DSAS as a geoprocessing tool that was integrated within the ArcGIS environment for the purpose of measuring, quantifying, and monitoring bankline changes. The DSAS extension is a freely accessible add-on that is integrated with the ArcGIS environment [60]. The utilization of DSAS by researchers facilitated the documentation of bankline dynamics for historical records [[63], [64], [65], [66], [67], [68], [69]].
However, there is a notable scarcity of scientific research focusing on changes in riverbank morphology of the Meghna River, with previous studies failing to quantify the rate of bank erosion or forecast future bankline positions. To bridge this knowledge gap, the present investigation employs a methodological approach utilizing the application of modified end point rate (mEPR). Additionally, DSAS-based statistical models are utilized to project the anticipated location of the bankline in 2025 and 2030. Transect-based methodologies have been conventionally employed in shoreline or bankline analysis to compute shoreline or bankline change statistics, yet they have typically overlooked the orientation of the transects. In this study, however, a modified End Point Rate (mEPR) model is introduced, which specifically accounts for the orientation of the transects. This enhancement leads to a more refined prediction of bankline positions, thus improving the accuracy and reliability of the analysis. The findings of this study hold promise for informing policymakers tasked with devising strategies to mitigate the socioeconomic impacts stemming from shifts in bankline positions, particularly concerning local economies and food security.
2. The study area
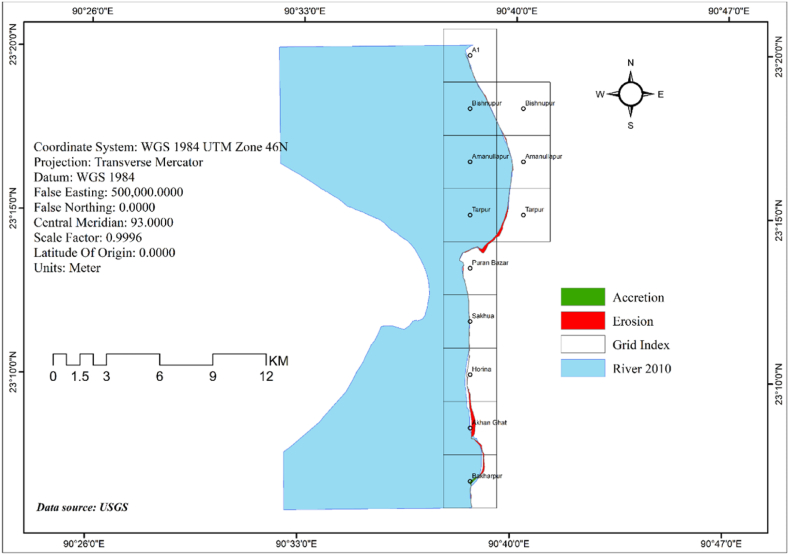
Chandpur Sadar is located within the Chandpur district, which falls under the Chattogram (Previously spelled as Chittagong) Division of Bangladesh. The site is situated at the confluence of the Meghna and Dakatia Rivers. The area spanning from the upper reach (Matlab Upazila) to the lower reach (Haimchar Upazila), is situated within the latitudes 23° 12′ 50.04″ N and 90° 38′ 9.96″ E (Fig. 1: a-c). The research work has exclusively focused on the right bank of the entire river. The length of the right bank adjacent to the study area measures approximately 28 km in total distance. The primary factor influencing the choice of the appropriate bank is the occurrence of substantial erosion on the right bank of the Meghna River [70]. The Chandpur Sadar region spans around 308.77 square kilometers, with 66.13 square kilometers consisting of riverine regions. As per the 2011 Bangladesh census data, the Chandpur Sadar Upazila recorded a total of 98,109 households and a population of 465,919 individuals [71]. The elevation of Chandpur Sadar ranges from −18m to 41m from the mean sea level, and the highest mean annual Rainfall of Chandpur Sadar is 2170 mm. The hydro-morphological equilibrium in Chandpur is disrupted by various factors, including wave action, tidal influence, and the convergence of the Dakatia River [72]. Chandpur's lower Meghna has been eroded continuously for the last 73 years [73].
Fig. 1.
Study area map (a) Bangladesh (b) chandpur district (c) chandpur sadar.
3. Materials and methods
3.1. Data collection and processing
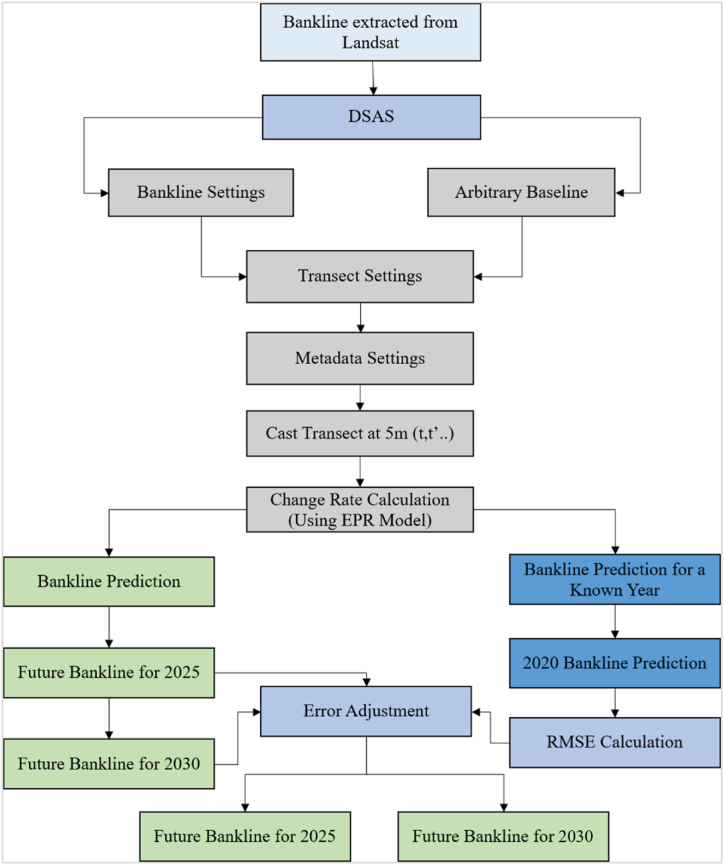
RS (Remote Sensing) and GIS (Geographic Information Systems) are advanced tools that facilitate the integration of climate data with its spatio-temporal framework. This integration enables the visualization and analysis of potential changes that may arise because of climate change. The Digital Shoreline Analysis System (DSAS) is a significant tool utilized for the purpose of monitoring and forecasting alterations in bankline conditions. This study utilizes remote sensing (RS) and geographic information systems (GIS) in conjunction with the Digital Shoreline Analysis System (DSAS) tool to observe and track alterations in the bankline of the Meghna river from 1990 to 2020. In the current decade, several high-resolution satellite data are available. However, this study uses Landsat data because it offers cross-calibrated earth observation free data of more than four decades, and is invaluable to detect changes of various geographic features of the world. It should be noted that this study has used satellite images from 1990 to 2020 at a 10-year interval. The high-resolution satellite images are not available for the months of 1990, 2000 and 2010 that we considered in this study. The resolution of satellite imagery used for bankline analysis is relatively coarse (the higher resolution images are not freely available), potentially limiting the ability to accurately detect small-scale changes in bank morphology. This could lead to an underestimation or overestimation of erosion and accretion rates, particularly in areas with subtle bankline features. The availability of satellite imagery may be limited to specific time periods, resulting in gaps in the temporal coverage of bankline changes. This could introduce biases in trend analysis, especially if significant erosion or accretion events occurred outside the available time frame. Despite advancements in remote sensing technology, inaccuracies in satellite imagery, such as cloud cover, atmospheric distortion, and sensor noise, can affect the reliability of bankline measurements. Additionally, errors in georeferencing and image registration may impact the spatial accuracy of the data. The methodology employed in this study is depicted in Fig. 2, which presents a flow chart.
Fig. 2.
Flow chart of methodology.
3.2. Method used for bankline delineation
The modification of the water index NDWI was documented by Ref. [74]. The water index NDWI was modified by substituting bands, such as band 5 for TM sensors. The Modified Normalized Difference Water Index (MNDWI) is a technique that can effectively enhance open water features while simultaneously suppressing and removing noise from built-up land, vegetation, and soil. The current algorithm overestimates the area of the extracted water feature. In this scenario, the Modified Normalized Difference Water Index (MNDWI) can be utilized to augment the data pertaining to the identified water feature within a region predominantly characterized by built-up land areas. According to Ref. [74] the MNDWI is expressed as follows:
Where SWIR is a middle infrared band such as TM band 5.
After completing the MNDWI analysis, the Reclassify tool was used to extract the river body from the raster image. Higher values of MNDWI were grouped into a single class, while all other values were grouped into another class. Once the Reclassify operation was executed, the raster image was converted into vector format using the Raster to Polygon tool from the Arc Toolbox. Subsequently, the river shape was selected by initiating the editing process, and it was exported to proceed with further work.
The Clip tool was employed to intersect one feature class with another feature class, acting as a “cookie-cutter” to create a new feature class, often referred to as a study area or Region of Interest (ROI), which contains a geographic subset of the features present in another, larger feature class. Following the clipping of the ROI, the river shape was extracted using an analysis tool, and subsequently, the extracted shape of the river body was edited to remove unnecessary portions of water bodies. Vector editing techniques were applied to omit sandbars, thereby facilitating more precise and efficient erosion and accretion calculations. Upon completion of the vector editing process, the final river body shape for two consecutive years was utilized to compute erosion and accretion using overlay tools.
3.3. DSAS input preparation for transect based analysis
The prerequisite for conducting analysis in DSAS involves ensuring that the input files are in the appropriate format and possess the necessary field attributes required for accurately computing rate statistics of bankline change. Here is a concise overview of the methodology employed in DSAS.
3.3.1. Geodatabase creation
The initial step in conducting DSAS analysis involves creating a personal geodatabase. All input data must be imported exclusively from the personal geodatabase created. It is important to note that the personal geodatabase serves as the storage location for transects and their associated statistics generated by the program. The database must adhere to the meter units in the UTM coordinate system. To conduct a DSAS analysis, both the baseline and all extracted shoreline/bankline data must be stored within the same geodatabase. If certain conditions are not met, a warning message will be displayed on the screen, and the calculation of the change rate will not be performed.
3.3.2. Bankline
Storing banklines in a personal geodatabase requires converting them into shapefiles. To incorporate the banklines, they must be either appended or merged into a unified file. This consolidated file can then be imported into a geodatabase using ArcCatalog. As previously mentioned, all inputs must be in meter units within the projected coordinate system. The bankline dataset needs to include the following attribute fields to facilitate accurate analysis.
Bankline Requirements Checklist.
-
⁃
The creation of the feature class is required to be done on a personal geodatabase.
-
⁃
A bankline date can be either a single line or a collection of segments.
-
⁃
The user is required to meet the “Bankline Attribute Field Requirements."
3.3.3. Bankline Attribute Field Requirements
Bankline data must adhere to specific attribute requirements to be compatible with DSAS. It is essential to ensure that the bankline dataset includes these attributes with their respective data types to facilitate accurate analysis within DSAS. Table 1 outlines the necessary field names and their corresponding data types.
Table 1.
Bankline attribute field requirements for digital shoreline analysis system (DSAS).
| Field Name | Data Type | Attribute Addition | DSAS Requirement |
|---|---|---|---|
| OBJECTID | Object identifier | Auto generated | Required |
| SHAPE | Geometry | Auto-generated | Required |
| SHAPE_Length | Double | Auto-generated | Required |
| DATE_ (DSAS_date) * | Text (Length = 10 OR Length = 20) |
User-created* | Required |
| UNCERTAINTY (DSAS_uncy) * | Any numeric field | User-created* | Required |
| SHORELINE_TYPE (DSAS_type) * | Text | User-created* | Optional (unless dataset includes the proxy-datum bias, then this field is required) |
3.3.4. Baseline creation
The next prerequisite input for DSAS analysis is the baseline. DSAS utilizes the baseline method to compute change statistics over a series of time intervals [75]. The user is responsible for creating the baseline, which must be stored in the designated personal geodatabase. Serving as the reference point for all measurements, the baseline is pivotal in calculating bankline change rates. The baseline must include the following attribute fields in Table 2, Table 3 [76].
Table 2.
Descriptions of baseline attribute fields for digital shoreline analysis system (DSAS).
| Field Name | Data Type | Attribute Addition | DSAS Requirement |
|---|---|---|---|
| OBJECTID | Object identifier | Autogenerated | Required |
| SHAPE (alias: Shape) | Geometry | Autogenerated | Required |
| SHAPE_Length (alias: Shape_Length) | Double | Autogenerated | Required |
| ID | Long Integer | User-created | Required |
| Group (DSAS_group) | Long Integer | User-created | Optional |
| Search_Distance (DSAS_search) | Double | User-created | Optional |
Table 3.
Baseline attribute field requirements in the digital shoreline analysis system.
| Attribute field | Description |
|---|---|
| DATE_ | It is not name specific. The date field is required. It can be named DATE_ or DSAS_date. The dates are needed to be formatted as mm/dd/yyyy. Note: The computer's date format must be set to English mm/dd/yyyy. |
| UNCERTAINTY | It can be written as UNCERTAINTY or DSAS_uncy or as per the user-defined name. This field is required for the attribute of shapefiles |
| BANKLINE_TYPE | This field is usually used to clarify the datum the bankline is referenced. One thing that should be kept in mind is that it does not name specific. It is a required field as part of the proxy-datum bias (PDB) correction when proxy-based and datum-based Banklines are combined to compute Bankline change rates. |
3.3.5. Cast transects
Once default parameters have been established, the process of generating transects is initiated. To create a new transect feature class, the user must input a file name in the designated space. Additionally, the user is required to input transect parameters, including defining the maximum search distance, transect spacing, and smoothing distance. The smoothing value specified by the user facilitates the creation of an orthogonal transect/shoreline intersect. This is achieved by generating a supplementary baseline, which is not visible to the user, at the specified smoothing length. The transect location is then positioned at the midpoint of this baseline [76]. In this study, transects were delineated at 150m intervals, and they are always perpendicular to the baseline.
3.4. Modified EPR model
The objective of this research is to propose river management planning techniques that can be readily implemented by local stakeholders, ensuring the long-term sustainability of river management in the study area. Therefore, the authors aimed to forecast forthcoming changes in bankline dynamics by leveraging findings from our comprehensive riverbank baseline investigation. The End Point Rate (EPR) formula has been employed for forecasting forthcoming alterations in bankline [[77], [78], [79], [80], [81], [82], [83], [84]], as it can be applied without requiring additional knowledge about sediment transport or wave interference, as all long-term processes are accounted for in the creation of the time series [84]. The EPR rates have demonstrated the best results for calculating future bankline positions [85]. In this study, EPR rates were utilized by extending the last bankline, i.e., of the year 2020, along transects. Points were generated for each transect according to the following equations:
| (1) |
| (2) |
Where,
Ix = x-coordinate of the predicted bankline point.
Iy = y-coordinate of the predicted bankline point
x = x-coordinate of the intersection of the transect with the most recent bankline (2020).
y = y-coordinate of the intersection of the transect with the most recent bankline (2020).
r = Rate of change of bankline (EPR or LRR in m/y).
ΔT = Time difference (in the year) between the year for which prediction is needed and the last year (most recent bankline) 2020.
The angle θt can be calculated from the x- and y-coordinates of the intersection points of any two banklines (say Sn and Sn-1) with the transect t. The coordinates of the predicted point p after time ΔT can thus be written as [86].
| (3) |
| (4) |
Where,
| (5) |
(Sy, t) n = y-coordinate of the intersection of the transect with the first bankline (2000).
(Sx, t) n = x-coordinate of the intersection of the transect with the first bankline (2000).
Fig. 3 illustrates the rationale behind formulating equations (3), (4)). The blue color represents the most recent bankline of 2020, while the red-colored line depicts a transect perpendicular to the black baseline. When determining the future position, e.g., after 5 or 10 years, points A, B, C, D, and E need to be considered. The measurement of erosion and accretion along each transect may introduce errors. Therefore, it is essential to incorporate the angle created with the UTM grid into the calculation.
Fig. 3.
Illustration of modified transect based EPR model.
Adding the distance RtΔT to the x-coordinate of A, the y-coordinate of A, or both the x- and y-coordinates of A would result in erroneous predictions for points D, B, or C, respectively, as Rt is calculated along the transect. The correct point to consider is E, as the distance was measured along the transect. Point E is located at the intersection of the circle passing through points B and C with point A and the transect.
Here, rΔT (NSM) represents the radius of the circle. The cosine and sine values should be taken from the transect's angle concerning the grid's x-axis. If the slope of the transect is denoted as m, then the equation can be represented as the intersection with the oldest bankline and the transect as the origin.
| (6) |
The equation presented above in slope-intercept form represents a general equation of a straight line. Here, the intersection is considered the origin, and in this specific case, the intercept (c) is zero. In this equation, y represents the y-coordinate of the intersection of the transect with the most recent bankline (2020), and x represents the x-coordinate of the intersection of the transect with the most recent bankline (2020).
Similarly, for the oldest bankline and transect, the y-coordinate (y0) can be expressed as the function of x-coordinate (x0) as follows:
| (7) |
As both equations (6), (7) indicate, the same straight line, i.e., transect the value of m, remains the same. Now, by subtracting equation (7) from equation (6), we can rewrite as:
| (8) |
| (9) |
Concerning transect the equation in terms of angle with x-axis as
| (10) |
The calculation can be performed as
| (11) |
Subsequently, the obtained angle of the transect with the x-axis, expressed in terms of x and y coordinates, is multiplied by NSM (rΔT) and then added to the coordinates of the most recent or last bankline. The points corresponding to each transect are then added using the ‘Add XY’ function within the ArcGIS window. Next, these points are exported to be further processed. The points are then converted into lines using the ‘Feature to Line’ tool from the Arc Toolbox.
To ensure methodological rigor and accuracy in forecasting future bankline positions, careful consideration was given to the selection of predictive models and parameters. The choice of predictive models, such as the Modified End Point Rate (EPR) Model and DSAS-based statistical models, was based on their established effectiveness in previous research and their compatibility with the study objectives. The Modified EPR Model was selected for its ability to incorporate the orientation of transects particularly relevant in riverine environments characterized by complex geomorphic features, thereby improving the accuracy of bankline predictions. By considering the directionality of erosion and accretion processes, the Modified EPR Model provides more refined predictions of bankline positions compared to traditional EPR models. The errors are reduced by up to 20 % when using the modified EPR Model compared to the conventional EPR model [87]. Similarly, DSAS-based statistical models were chosen for their robustness in analyzing bankline changes over time and projecting future bankline positions. The parameters used in predictive models, such as the error coefficient adjustment in the Modified EPR Model and the cross-validation method using Root Mean Square Error (RMSE), were selected based on their ability to optimize model performance and minimize prediction errors. The error coefficient adjustment accounts for variations in erosion rates along different transects, ensuring that predictions are tailored to specific geomorphic conditions. Likewise, RMSE-based cross-validation provides a robust measure of model accuracy by quantifying the difference between predicted and observed bankline positions.
3.5. Validation of the model
The primary concern of any prediction model lies in its validation. The typical method employed in model validation compares the actual bankline with the predicted bankline, with predictions made using previous data. Initially, the bankline is predicted for a known year. Subsequently, the positional error of the predicted bankline is estimated by calculating the Root Mean Square Error (RMSE). RMSE is widely utilized for validating the prediction of banklines [79,81,82,84]. In this study, the most recent historical bankline of 2020 has been utilized for predicting the future position of the bankline. The comparison, validation, and estimation of the error of the predicted bankline can be conducted using the following equation:
Where Xp and Yp are coordinates of the predicted bankline, and Xa and Ya denote the measured or observed coordinates of the bankline sample points [86]. Furthermore, n denotes the total number of transects delineated. After performing the RMSE calculation, the error can be adjusted, and the future position of the bankline can be predicted.
3.6. Error adjustment
No model provides a hundred percent accuracy. Like other models, the Modified EPR model also requires error correction [88]. The correction of the predicted X and Y coordinates can be defined as:
| (12) |
| (13) |
Where Xp and Yp are coordinates of the predicted bankline, and Xa and Ya denote the measured or observed coordinates at all transects.
The time between the last bankline (most recent bankline) and the predicted bankline is a time interval. Using the above correction rate, the predicted position of the bankline needs to be adjusted. The adjustment equation can be expressed as:
| (14) |
| (15) |
Here, , denotes the corrected coordinate of the predicted bankline.
4. Results
4.1. Overall insight of erosion dynamics (1990–2020)
The present study employed remote sensing (RS), geographic information system (GIS), and statistical methodologies to evaluate the rate of change in the bankline. The rate of shoreline/bankline change was assessed by quantifying the magnitude of shift along each transect. Alterations in the bankline of Chandpur Sadar were investigated through the analysis of multi-date satellite imagery spanning a period of 30 years, utilizing the DSAS methodology. In terms of the baseline, movement of the bankline towards the river was considered as a positive value, indicating accretion, while movement away from the river was regarded as a negative value, indicating erosion.
The study area of Chandpur Sadar was partitioned into twelve discrete grids measuring 3 km × 3 km each, using the ‘Grid Feature Index’ tool from Arc Toolbox. The objective of grid segmentation was to delineate areas within the study region that are more susceptible to erosion. This facilitates a comprehensive understanding and informed decision-making regarding riverbank protection measures by relevant authorities. Given Bangladesh's limited economic resources, it is impractical to implement protective measures across all river areas. Therefore, it is essential to identify specific regions prone to erosion that necessitate significant protection efforts.
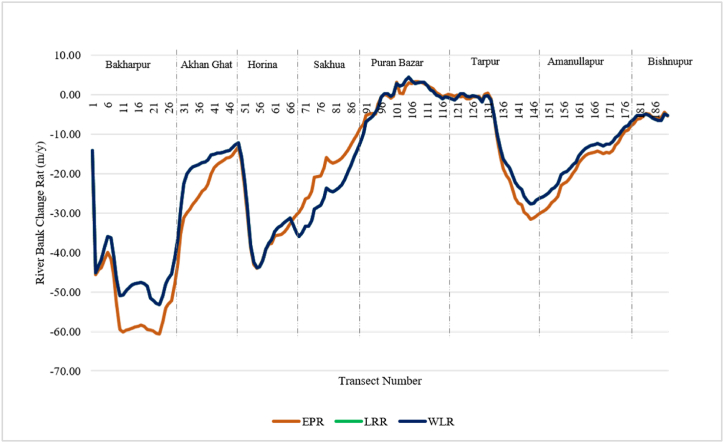
Fig. 4 depicts the spatial distribution of End Point Rate (EPR), Linear Regression Rate (LRR), and Weighted Linear Regression (WLR) along a transect spanning the River in Chandpur Sadar from 1990 to 2020. The figure illustrates the fluctuating movement of the bankline along Chandpur Sadar, highlighting a prevalent trend of erosion. The validity of the zonation was confirmed by comparing it with Net Shoreline Movement (NSM) and Shoreline Change Envelope (SCE). NSM exhibited a similar pattern to that observed in LRR, EPR, and WLR, while SCE identified a contrasting pattern compared to NSM (Fig. 5).
Fig. 4.
Bankline change rate in EPR, LRR, and WLR at chandpur sadar.
Fig. 5.
Bankline change rate in NSM and SCE at chandpur sadar.
Based on the movement of the bankline, the zones were classified into four categories (Table 4): Very High Erosion (−1824.89m to −1303.15m), High Erosion (−1303.15m to −751.87m), Low Erosion (−751.87m to −100.47m), and Moderate Accretion (+1m to +100m). According to the data analysis in the DSAS window, Fig. 4 indicates that all zones, except Puran Bazar and Tarpur, experienced land loss due to the shift of the riverbank. This diagram illustrates the overarching pattern observed over the past three decades.
Table 4.
Zone wise bankline change statistics of chandpur sadar.
| Grid and Location | Statistical Parameters | No. of Transect | Mean | Minimum | Maximum | Average R2 |
Remarks |
|---|---|---|---|---|---|---|---|
| 1 | SCE | 14 | 202.25 | 158.48 | 295.54 | 0.70 | Low erosion |
| NSM | −182.38 | −142.32 | −267.70 | ||||
| EPR | −6.06 | −4.73 | −8.90 | ||||
| LRR | −5.86 | −4.95 | −7.81 | ||||
| WLR | −5.86 | −4.95 | −7.81 | ||||
| 2–3 Bishnupur |
SCE | 36 | 490.06 | 261.37 | 691.32 | 0.62 | High Erosion |
| NSM | −478.50 | −241.84 | −691.32 | ||||
| EPR | −15.90 | −8.04 | −22.97 | ||||
| LRR | −13.98 | −6.90 | −20.28 | ||||
| WLR | −13.98 | −6.90 | −20.28 | ||||
| 4–5 Amanullapur |
SCE | 38 | 806 | 331.08 | 956.81 | 0.63 | High Erosion |
| NSM | −795.90 | −314.86 | −948.19 | ||||
| EPR | −26.45 | −10.46 | −31.51 | ||||
| LRR | −23.09 | −9.44 | −27.74 | ||||
| WLR | −23.09 | −9.44 | −27.74 | ||||
| 6–7 Tarpur |
SCE | 31 | 150.85 | 34.95 | 241.76 | 0.13 | Low erosion |
| NSM | 9.39 | 99.87 | −198.40 | ||||
| EPR | 0.31 | 3.32 | −5.60 | ||||
| LRR | 0.05 | 3.25 | −27.74 | ||||
| WLR | 0.05 | 3.25 | −27.74 | ||||
| 8 Puran Bazar |
SCE | 27 | 245.75 | 31.61 | 656.94 | 0.39 | Low erosion |
| NSM | −87.58 | 99.87 | −454.06 | ||||
| EPR | −2.91 | 3.32 | −15.09 | ||||
| LRR | −3.91 | 4.43 | −21.36 | ||||
| WLR | −3.91 | 4.43 | −21.36 | ||||
| 9 Sakhua |
SCE | 22 | 848.31 | 656.94 | 1064.36 | 0.73 | High Erosion |
| NSM | −724.11 | −454.06 | −1064.36 | ||||
| EPR | −24.06 | −15.09 | −35.37 | ||||
| LRR | −29.20 | −21.36 | −35.84 | ||||
| WLR | −29.20 | −21.36 | −35.84 | ||||
| 10 Horina |
SCE | 20 | 896.47 | 397.13 | 1322.16 | 0.78 | High Erosion |
| NSM | −896.47 | −397.13 | −1322.16 | ||||
| EPR | −27.79 | −13.20 | −43.93 | ||||
| LRR | −28.64 | −12.10 | −43.81 | ||||
| WLR | −28.64 | −12.10 | −43.81 | ||||
| 11 Akhan Ghat |
SCE | 21 | 1101.27 | 517.96 | 1824.27 | 0.52 | High Erosion |
| NSM | −1029.93 | −517.96 | −1824.27 | ||||
| EPR | −34.22 | −17.21 | −60.62 | ||||
| LRR | −27.52 | −14.75 | −53.14 | ||||
| WLR | −27.52 | −14.75 | −53.14 | ||||
| 12 Bakharpur |
SCE | 27 | 1619.79 | 231.25 | 1903.93 | 0.63 | Very High Erosion |
| NSM | −1575.24 | −231.25 | −1824.27 | ||||
| EPR | −52.63 | −15.34 | −60.62 | ||||
| LRR | −45.60 | −14.12 | −53.14 | ||||
| WLR | −45.60 | −14.12 | −53.14 |
The extent of land loss was most pronounced at Bakharpur, followed by Horina and then Amanullapur. Over the past three decades, land has been gained in Grids 05, 07, 08, 10, 11, and 12, while the remaining grids exhibited erosion dominance. Specifically, in Zone/Grid 01, there was a net loss of land amounting to −0.534 square kilometers, where the negative sign indicates that the quantity of lost land exceeds the amount gained. Similarly, in Grid 02, the net change in land area resulted in a loss of 1.350 square kilometers, while in Grid 03, it was determined to be a loss of 0.138 square kilometers. In Grid 04, the loss was identified as 0.300 square kilometers, and in Grid 05, it was assessed as 1.926 square kilometers.
The discrepancies for Grids 07, 08, 09, 10, 11, and 12 were as follows: 0.202, −0.400, −2.183, −2.228, −2.453, and −4.348 square kilometers, respectively. Conversely, the discrepancy in Grid 06 amounted to 0.006 square kilometers, where the presence of a positive sign implies that the amount of land acquired in the past 30 years exceeds the amount lost as a result of bankline displacement.
Cumulatively, erosion in Grid 01 over the past 30 years amounted to a negative value of 0.553 square kilometers. The total erosion in grid cells 02, 03, 04, 05, 06, 07, 08, 09, 10, 11, and 12 between 1990 and 2020 was calculated as follows: 1.3499, −0.1468, −0.3000, −1.9629, −0.1139, −0.3517, −0.6708, −2.5449, −2.5145, −2.928, and −4.5945 square kilometers, respectively.
4.2. Future prediction of bankline for 2025 and 2030 in Chandpur Sadar
Determining the future position of the bankline was crucial to improve decision-making regarding riverbank management. Bangladesh has long recognized river erosion as a significant natural hazard. Human intervention cannot alter natural processes, but it can direct efforts towards mitigating their consequences. To address these consequences effectively, it is crucial to integrate natural hazard considerations into planning frameworks. In this study, the author endeavored to forecast the future position of the bankline using a modified End Point Rate (mEPR) model.
The utilization of the modified EPR model resulted in a reduction of errors by up to 20 % compared to the conventional EPR model. This modification incorporated slope considerations; a factor absent in the traditional EPR model. Predictions for the bankline's future position in 2020 were based on statistical analyses derived from bankline data spanning 2000, 2005, 2010, and 2015. Utilizing DSAS version 5.0, the rate of bankline movement was calculated at 5-m intervals across 5656 sample transects. Initially, the bankline for 2020 was predicted using the 2015 bankline as the baseline. Subsequently, the predicted bankline for 2020 and observed bankline data extracted from satellite images were compared using Root Mean Square Error (RMSE) analysis. The RMSE ranged from 0.04 m to 0.092 m, with a mean RMSE of 0.115 m. Notably, 89.05 % of data points fell within one standard deviation, indicating the model's reliability for predicting future bankline positions.
Error coefficients were determined using equations (12), (13)), and positional errors against each transect were adjusted accordingly for (x, y) coordinates using equations (14), (15)). Following error adjustment, the positional error was nullified, resulting in an RMSE of 0. Future positions of the bankline were then predicted using corrected coordinates for 2025 and 2030. Error correction procedures were applied for both 2025 and 2030, and the corrected points were plotted in ArcGIS (Fig. 6). Despite predictions indicating downstream movement of the bankline, it is important to note that these projections were based on past erosion trends. Considering ongoing government interventions, such as the Protection Works project, it is expected that certain areas, such as Puran Bazar (Grid No. 08) and Horina (Grid No. 10), may experience minimal movement. Conversely, increased erosion is anticipated in upstream regions, particularly at Tarpur and Akhan Ghat (Grid No. 11), highlighting the dynamic nature of riverbank dynamics and the need for adaptive management strategies.
Fig. 6.
Prediction of bankline for 2030 at chandpur sadar.
4.3. Land loss or gain during 2020–2030
The land gains or losses anticipated for the years 2020 and 2025 are depicted in Fig. 7. During this period, an estimated 1.092 sq. km of land is projected to erode, while the total accretion is expected to be 0.114 sq. km. Consequently, the net land loss is forecasted to be 0.978 sq. km. Notably, the most significant erosion is forecasted to occur in Grid 11, specifically at Akhan Ghat, resulting in a loss of approximately 0.370 sq. km.
Fig. 7.
River erosion accretion during 2020 and 2025 at chandpur sadar.
Conversely, the least erosion is expected in Grid 03, identified as Bishnupur. Additionally, the maximum accretion is anticipated in Grid 12, known as Bakharpur, with an estimated gain of 0.057 sq. km of land. On the other hand, the minimum land accretion is projected for Grid 03, Bishnupur, with an anticipated gain of approximately 0.002 sq. km. This analysis offers crucial insights into the anticipated land loss or gains resulting from riverbank movements during the 2020–2025 period.
Fig. 8 illustrates the erosion and accretion trends between 2025 and 2030. The erosion and accretion rates are expected to increase significantly compared to the preceding period from 2020 to 2025. The total area affected by erosion and accretion is estimated to be 1.126 sq. km and 0.122 sq. km, respectively. Grid No. 11 is anticipated to experience the most substantial erosion during this phase, consistent with previous observations. The erosion rate in this grid is projected to increase by 0.27 % compared to the previous period.
Fig. 8.
River erosion accretion during 2025 and 2030 at chandpur sadar.
Conversely, Grid No. 03 is expected to exhibit minimal erosion, remaining relatively stable with no significant changes anticipated. Table 5 highlights the dominance of erosion across all grids, with particular attention warranted for Tarpur and Akhan Ghat due to the substantial erosion predicted in these areas. Notably, 32.94 % of the total erosion between 2025 and 2030 is projected to occur in Grid No. 11, while Tarpur is expected to contribute 16.16 % to the overall erosion during this period.
Table 5.
Land loss or gain during 2020 and 2030 at Chandpur Sadar.
| Grid | 2020–2025 |
2025–2030 |
||
|---|---|---|---|---|
| Accretion Sq.km | Erosion Sq.km | Erosion Sq.km | Accretion Sq.km | |
| 1 | 0.013 | 0.011 | 0.011 | 0.018 |
| 2 | 0.007 | 0.023 | 0.023 | 0.008 |
| 3 | 0.002 | 0.009 | 0.009 | 0.002 |
| 5 | 0.014 | 0.035 | 0.034 | 0.014 |
| 6 | 0.000 | 0.047 | 0.028 | 0.000 |
| 7 | 0.008 | 0.168 | 0.182 | 0.008 |
| 8 | 0.009 | 0.190 | 0.224 | 0.009 |
| 9 | 0.000 | 0.050 | 0.049 | 0.000 |
| 10 | 0.000 | 0.082 | 0.081 | 0.000 |
| 11 | 0.003 | 0.370 | 0.371 | 0.004 |
| 12 | 0.057 | 0.107 | 0.115 | 0.060 |
| Total | 0.114 | 1.092 | 1.126 | 0.122 |
4.4. Statistics of future prediction (2020–2030)
The Net Shoreline Movement (NSM) and End Point Rate (EPR) provide insights into the dynamics of riverbank movement in Chandpur Sadar over the period spanning from 2020 to 2030, as depicted in Fig. 9, Fig. 10. Predictive modeling reveals that the maximum NSM is anticipated to reach −495.79 m, indicating an erosive trend along the transect. Conversely, the minimum NSM is projected to be −1.01 m, signifying relatively minimal erosion activity. Notably, the most significant movement is expected in Puran Bazar, while Bakharpur is anticipated to experience the least movement. The mean NSM is estimated at −76.25 m, providing a comprehensive overview of the average shoreline dynamics within the study area.
Fig. 9.
Bankline change rate in NSM and SCE at chandpur sadar.
Fig. 10.
Bankline change rate in EPR and LRR at chandpur sadar.
In Table 6, an overview of the comprehensive change statistics pertaining to bankline movement, encompassing EPR, Linear Regression Rate (LRR), Shoreline Change Envelope (SCE), and NSM, is presented. The statistical analysis includes calculations of mean, minimum, and maximum values for each zone or grid, facilitating categorization into five distinct groups based on the direction and magnitude of bankline movement.
Table 6.
Statistical change of bankline during 2020 and 2030 at chandpur sadar.
| Grid and Location | Statistical Parameters | No. of Transect | Mean | Minimum | Maximum | Remarks |
|---|---|---|---|---|---|---|
| 1 | SCE | 13 | 30.52 | 3.04 | 63.23 | Moderate Accretion |
| NSM | 10.46 | −48.26 | 63.23 | |||
| EPR | 1.045 | −4.83 | 6.320 | |||
| LRR | 1.05 | −4.83 | ||||
| 2–3 Bishnupur |
SCE | 30 | 22.90 | 0.27 | 76.09 | Low Erosion |
| NSM | −11.76 | 27.92 | −76.09 | |||
| EPR | −1.176 | 2.7 | −7.6 | |||
| LRR | −1.18 | 2.79 | −7.69 | |||
| 4–5 Amanullapur |
SCE | 22 | 31.44 | 1.45 | 82.07 | Low Erosion |
| NSM | −12.07 | 46.39 | −82.07 | |||
| EPR | −1.20 | 4.64 | −8.21 | |||
| LRR | −1.21 | 4.64 | −8.21 | |||
| 6–7 Tarpur |
SCE | 27 | 139.60 | 15.53 | 297.17 | High Erosion |
| NSM | −130.73 | 23.70 | −294.17 | |||
| EPR | −13.07 | 2.37 | −29.42 | |||
| LRR | −13.07 | 2.37 | −29.42 | |||
| 8 Puran Bazar |
SCE | 27 | 129.75 | 15.14 | 495.79 | High Erosion |
| NSM | −125.10 | 32.79 | −495.79 | |||
| EPR | −12.10 | 3.28 | −49.58 | |||
| LRR | −12.51 | 3.28 | −49.58 | |||
| 9 Sakhua |
SCE | 21 | 33.14 | 12.61 | 50.15 | Moderate Erosion |
| NSM | −33.14 | −12.61 | −50.15 | |||
| EPR | −3.32 | −1.26 | −5.02 | |||
| LRR | −3.31 | −1.26 | −5.02 | |||
| 10 Horina |
SCE | 20 | 53.77 | 2.97 | 141.53 | Moderate Erosion |
| NSM | −53.77 | −2.97 | −141.53 | |||
| EPR | −5.378 | −0.300 | −14.15 | |||
| LRR | −5.38 | −0.30 | −14.15 | |||
| 11 Akhan Ghat |
SCE | 21 | 240.62 | 39.22 | 426.48 | Very High Erosion |
| NSM | −236.88 | 39.22 | −426.48 | |||
| EPR | −23.68 | 3.92 | −42.65 | |||
| LRR | −23.63 | 3.92 | −42.65 | |||
| 12 Bakharpur |
SCE | 22 | 113.74 | 1.01 | 239.10 | Moderate Erosion |
| NSM | −65.73 | −196.13 | 239.10 | |||
| EPR | −6.57 | −19.610 | 23.910 | |||
| LRR | −6.57 | −19.610 | 23.910 |
4.4.1. Future zonation mapping
The author prepared zonation map for Chandpur Sadar, basing them on the movement of banklines, quantified as Net Shoreline Movement (NSM). Fig. 11illustrates the zonation of the erosion trend, which is based on the movement of the bankline between 2020 and 2030. We classified the erosion trend using the Natural Break (Jenks) method in ArcGIS, based on NSM data. The NSM −497.36 to −266.94m marked as Very High Erosion, High Erosion (−266.93 to −102.79m), Moderate Erosion (−102.78m to −1m), Moderate Accretion (+1m to 150m), and High Accretion (150m to 246m). According to NSM, Akhan Ghat and a portion of Tarpur will be the dominant erosion locations.
Fig. 11.
Erosion zonation based on NSM at Chandpur Sadar.
The implications of this research in terms of urban planning, understanding the dynamics of river erosion is crucial for designing resilient infrastructure, implementing effective land-use zoning strategies, and ensuring the safety of communities living in flood-prone areas. By incorporating these research findings into urban planning initiatives, policymakers can make informed decisions to mitigate the risks associated with river erosion and enhance the resilience of urban landscapes. From an ecological sustainability standpoint, it can contribute to the conservation and restoration of riparian habitats, preservation of biodiversity, and maintenance of ecosystem services provided by rivers. By identifying areas prone to erosion and understanding the factors driving erosion processes, conservationists and environmental policymakers can prioritize conservation efforts and implement measures to protect vulnerable ecosystems. The predictive model for projecting the future location of the bankline suggests that the bankline will continue to move farther away. Utilizing multi-temporal satellite imagery and the DSAS model, mapping, monitoring, and predicting alterations in the bankline along the Meghna River can play a pivotal role in developing effective mitigation policies and regulations. The outcomes of this analysis offer valuable insights into the historical transformations that the bankline has experienced and its future outlook.
5. Discussion
Wave action, tidal effects, and the presence of Dakatia confluence cause the hydro-morphological condition at Chandpur to be out of balance [72]. Chandpur's lower Meghna has been eroded continuously for the last 73 years [73]. The rate of erosion and the location of erosion have changed from year to year. Ref. [70] has studied the rate of erosion for the period from 1980 to 2010 and found an erosion rate of 495.03 square meters per year. From 1980 to 1990, the erosion was high in Chandpur. In the decade 2002–2010, the accretion rate was comparatively higher than the erosion rate. In the last 30 years (1980–2010), the total erosion of Meghna at Chandpur was 14851 square meters, and the total deposition was 10940 square meters [70]. The lower section of the Meghna River exhibits constant and substantial channel migration, with high rates of erosion and deposition occurring along its riverbanks every year. Therefore, the buffer regions of the river undergo ongoing modifications throughout time. The research's results demonstrate a distinct pattern of erosion and accretion in the Meghna River study region, with the left bank exhibiting significant erosion. These trends are expected to continue based on the forecasts generated using the DSAS model. Furthermore, our findings emphasize that the lower section of the Meghna River is the most active channel, marked by frequent movement.
Over the last 30 years, the erosion trend has been downward. The total eroded land area was 18.03 sq. km in 1990–2020, and the amount of accreted land was 1.97 sq. km. The area of erosion was 13.32 sq. km in 1990–2000; the area of erosion significantly decreased to 4.29 sq. km in 2000–2010; and the area of erosion further decreased to 0.42 sq. km in 2010–2020. The area of accretion was 0.88 sq. km in 1990–2000; it decreased to 0.43 sq. km in 2000–2010; and it increased slightly to 0.66 sq. km in 2010–2020. Over the past three decades, there has been a clear decrease in erosion in Chandpur. The erosion decreased from 13.32 sq km in 1990–2000 to just 0.42 sq km in 2010–2020. Accretion saw a slight decrease from 0.88 sq. km in 1990–2000 to 0.43 sq. km in 2000–2010. In 2010–2020, there was a modest increase in accretion to 0.66 sq km. Chandpur has experienced a substantial reduction in erosion over the past three decades, accompanied by a minor fluctuation in accretion rates, with a slight increase in the most recent period.
The significant consequences of these alterations in the channels are apparent in the displacement of residences, agricultural areas, infrastructure, and other vital resources experienced by the local community. This highlights the tangible effects of riverbank erosion on the populations living in the research location. In 2010 and 2012, the total number of families displaced, i.e., those who became homeless due to Chandpur's erosion, was 200 families and 100 families, respectively. The extent of the population's vulnerability and economic loss as a result of bank erosion has significantly risen in recent years in Chandpur Sadar. The loss of homestead land, dwellings, animals, crops, trees, and household furnishings are the main effects of land loss [89,90]. About 35 families lost their homes in 2019, and Chandpur's protection works and nearly 200 m of land suffered erosion [91]. A cyclone shelter at Rajrajeshwar Union (a project of Tk 2 crore and 29 lakh) was destroyed in 2020, which was 3 km away from the River [92,93]. Moreover, 500 houses were washed away in this union in 2020 [94].
Prior research has shown conflicting viewpoints about the effectiveness of traditional EPR and LRR in analyzing shoreline change. Ref. [95] did not see any significant difference between EPR and LRR and Ref. [96] expressed a preference for LRR over EPR. While various statistical methods are available for analyzing shoreline change, the authors of this article strongly advocate for the use of modified End-Point Rate for long-term shoreline analysis. This method is preferred due to its high accuracy in predicting changes, consistency in results, straightforward calculation procedure, and ease of communication and understanding. Despite using just, the initial and final shoreline position data, the results of modified EPR are quite satisfactory. By including trigonometric elements into the prediction of future shoreline points, the potential mistakes that may arise from EPR-based forecasts (as well as those based on other statistics, such as LRR) are minimized. The authors assert that the equations provided in this study are more accurate both in terms of conceptual understanding and the precision of the acquired findings. They argue that excluding these trigonometric elements will result in incorrect outcomes. Although these words have not been widely used in prior literature, this study suggests and advocates for the usage of these corrective terms in future research. To ensure robustness and precision in forecasting forthcoming bankline positions, meticulous attention was devoted to the selection of predictive models and associated parameters. The decision to employ predictive models, such as the Modified End Point Rate (EPR) Model and DSAS-based statistical models, was predicated on their demonstrated efficacy in prior studies and their alignment with the study's objectives. The Modified EPR Model was chosen owing to its capacity to integrate the orientation of transects, particularly pertinent in riverine settings typified by intricate geomorphic characteristics, thus enhancing the precision of bankline forecasts. By incorporating the directional aspects of erosion and accretion processes, the Modified EPR Model yields more nuanced prognostications of bankline positions relative to traditional EPR models. The adoption of the modified EPR Model resulted in a reduction of errors by up to 20 % compared to the conventional EPR model, underscoring its enhanced predictive capability.
The bankline is highly dynamic, undergoing continual shifts and changes over time. Therefore, accurately delineating the bankline is crucial for various applications such as coastal management and environmental monitoring. High-resolution satellite data offers higher accuracy in shoreline delineation compared to medium-resolution satellite data. This is primarily because high-resolution imagery provides finer spatial details and greater clarity, enabling more precise identification and mapping of bankline features and changes. As a result, high-resolution satellite data is preferred for tasks requiring accurate and detailed bankline delineation, especially in areas experiencing rapid bankline changes or where precise bankline information is essential for decision-making processes.
6. Conclusion
River erosion is a significant and often overlooked disaster that poses a severe threat to communities living along rivers. The path of the river often changes over time, making it challenging to resist the forces of nature. Like other natural disasters, river erosion often fails to receive the necessary attention from the relevant authorities. The ability to withstand and recover from natural disasters, namely floods and riverbank erosion, is of utmost significance for developing countries such as Bangladesh. The nation has seen frequent occurrences of flash floods and river erosion, which have greatly hindered attempts to improve infrastructure. The scarcity of on-site observations restricts our understanding of river monitoring, requiring the use of other approaches to collect vital data for disaster planning and response. This research focused exclusively on the Meghna River to evaluate the overall extent of land loss on the Chandpur Sadar side caused by riverbank erosion. The present work utilized an artificial computer environment (DSAS v.5) to assess the past and future movement of banklines. This tool is capable of precisely measuring and forecasting erosion and deposition. The planned and actual banklines were utilized for assessing the level of precision. During the study period, Chandpur's maximum NSM was −1979.62 m where the land eroded 18.03 sq. km. The maximum NSM is predicted to be −495.79m. The minimum NSM is predicted to be −1.01m. The maximum movement will occur in Puran Bazar, and the minimum movement will take place in Bakharpur. The RMSE varies from 0.04 m to 0.092 m. We found the overall mean RMSE to be 0.115 m. We calculated the standard deviation and checked how many data values fell within one standard deviation. We found that the 89.05 % value falls within one standard deviation. Therefore, this model can be used to predict future bankline positions.
This research did not investigate the reasons for the bankline alterations, although natural processes, human activities, and climate change are driving landward bankline shift. With a geographical and temporal erosion trend in bankline alterations predicted, follow-up studies in coastal locations with considerable bankline retreat and coastal risk management strategies that account for this fact are needed.
Data availability statement
Data will be made available on request.
CRediT authorship contribution statement
Jahid Hasan: Writing – review & editing, Writing – original draft, Visualization, Conceptualization. Md Alif Uz Zaman: Validation, Software, Formal analysis. Mst Ilme Faridatul: Writing – review & editing, Supervision, Resources, Methodology.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgment
The author would like to thank the Department of Urban & Regional Planning, Rajshahi University of Engineering &Technology, Bangladesh.
Contributor Information
Jahid Hasan, Email: jahid@urp.ruet.ac.bd.
Md Alif Uz Zaman, Email: alifuzzamanemon@gmail.com.
Mst Ilme Faridatul, Email: mifaridatul@urp.ruet.ac.bd.
References
- 1.Langat P.K., Kumar L., Koech R. Monitoring river channel dynamics using remote sensing and GIS techniques. Geomorphology. 2019;325:92–102. [Google Scholar]
- 2.Das T.K., et al. River bank erosion induced human displacement and its consequences. Living Reviews in Landscape Research. 2014;8(3):1–35. [Google Scholar]
- 3.Sarif M.N., et al. Challenges of Disasters in Asia: Vulnerability, Adaptation and Resilience. Springer; 2022. Household-based approach to assess the impact of river bank erosion on the socio-economic condition of people: a case study of Lower Ganga Plain; pp. 73–101. [Google Scholar]
- 4.Baki A.B.M., Gan T.Y. Riverbank migration and island dynamics of the braided Jamuna River of the Ganges–Brahmaputra basin using multi-temporal Landsat images. Quat. Int. 2012;263:148–161. [Google Scholar]
- 5.Wright J.M. The University of Tennessee; Knoxville: 2008. Floodplain Management: Principles and Current Practices. [Google Scholar]
- 6.Longoni L., et al. Monitoring riverbank erosion in mountain catchments using terrestrial laser scanning. Rem. Sens. 2016;8(3):241. [Google Scholar]
- 7.Yao Z., et al. Bank erosion and accretion along the ningxia–inner Mongolia reaches of the yellow river from 1958 to 2008. Geomorphology. 2011;127(1–2):99–106. [Google Scholar]
- 8.Rakhal B., et al. Assessment of channel shifting of Karnali Megafan in Nepal using remote sensing and GIS. Spatial Sci. 2021;27(2):177–188. [Google Scholar]
- 9.Shu A., et al. An experimental study on mechanisms for sediment transformation due to riverbank collapse. Water. 2019;11(3):529. [Google Scholar]
- 10.Saleem A., et al. Spatial and temporal variations of erosion and accretion: a case of a large tropical river. Earth Systems and Environment. 2020;4:167–181. [Google Scholar]
- 11.Islam M.F., Rashid A.B. Riverbank erosion displacees in Bangladesh: need for institutional response and policy intervention. Bangladesh J. Bioeth. 2011;2(2):4–19. [Google Scholar]
- 12.James H., Bangladesh W. Robert. Washington: GPO for the Library of Congress. 1989. A country study. available on. [Google Scholar]
- 13.Sarker M. University of Nottingham; 2009. Morphological Response of the Brahmaputra-Padma- Lower Meghna River System to the Assam Earthquake of 1950. [Google Scholar]
- 14.Elahi K.M., Rogge J. 1990. Riverbank Erosion, Flood, and Population Displacement in Bangladesh. [Google Scholar]
- 15.Lawler D. A new technique for the automatic monitoring of erosion and deposition rates. Water Resour. Res. 1991;27(8):2125–2128. [Google Scholar]
- 16.Larsen E.W., Premier A.K., Greco S.E. Cumulative effective stream power and bank erosion on the sacramento river, California, USA 1. JAWRA Journal of the American Water Resources Association. 2006;42(4):1077–1097. [Google Scholar]
- 17.Mukherjee R., et al. Bank erosion and accretion dynamics explored by GIS techniques in lower Ramganga river, Western Uttar Pradesh, India. Spatial Information Research. 2017;25(1):23–38. [Google Scholar]
- 18.Lawler D., et al. Downstream change in river bank erosion rates in the Swale–Ouse system, northern England. Hydrol. Process. 1999;13(7):977–992. [Google Scholar]
- 19.Hooke J.M. Magnitude and distribution of rates of river bank erosion. Earth Surf. Process. 1980;5(2):143–157. [Google Scholar]
- 20.Hossain M.M., Baki A., Ahmad S. 4th International Symposium on Flood Defense. Managing flood Risk, Reliability and vulnerability; Toronto, Ontario, Canada: 2008. The flood problem and mitigation methods in Bangladesh. [Google Scholar]
- 21.Hassan M.S. Quantification of river bank erosion and bar deposition in chowhali Upazila, sirajganj district of Bangladesh: a remote sensing study. J. Geosci. Environ. Protect. 2015;4(1):50–57. [Google Scholar]
- 22.Babar M. The Financial Express. 2018. River erosion: the silent destroyer. [Google Scholar]
- 23.Munna T.I. The Daily Sun. 2019. River erosion: a silent disaster in Bangladesh. [Google Scholar]
- 24.Islam M., Islam A. A brief account of bank erosion, model studies and bank protective works in Bangladesh. REIS Newsletter. 1985;2:11–13. [Google Scholar]
- 25.Fuller I.C., Large A.R., Milan D.J. Quantifying channel development and sediment transfer following chute cutoff in a wandering gravel-bed river. Geomorphology. 2003;54(3–4):307–323. [Google Scholar]
- 26.Kotoky P., et al. Nature of bank erosion along the Brahmaputra river channel, Assam, India. Curr. Sci. 2005:634–640. [Google Scholar]
- 27.Kummu M., et al. Riverbank changes along the mekong river: remote sensing detection in the vientiane–nong khai area. Quat. Int. 2008;186(1):100–112. [Google Scholar]
- 28.Lawler D.M. The measurement of river bank erosion and lateral channel change: a review. Earth Surf. Process. Landforms. 1993;18(9):777–821. [Google Scholar]
- 29.Li L., Lu X., Chen Z. River channel change during the last 50 years in the middle Yangtze River, the Jianli reach. Geomorphology. 2007;85(3–4):185–196. [Google Scholar]
- 30.Muller E., Décamps H., Dobson M.K. Contribution of space remote sensing to river studies. Freshw. Biol. 1993;29(2):301–312. [Google Scholar]
- 31.Rinaldi M. Recent channel adjustments in alluvial rivers of Tuscany, Central Italy. Earth Surf. Process. Landforms: The Journal of the British Geomorphological Research Group. 2003;28(6):587–608. [Google Scholar]
- 32.Surian N. Channel changes due to river regulation: the case of the Piave River, Italy. Earth Surf. Process. Landforms: The Journal of the British Geomorphological Research Group. 1999;24(12):1135–1151. [Google Scholar]
- 33.Yang X. Satellite monitoring of the dynamic environmental change of the active yellow river delta, China. International Archives of Photogrammetry and Remote Sensing. 1996;31:801–806. [Google Scholar]
- 34.Yang X., Damen M.C., Van Zuidam R.A. Satellite remote sensing and GIS for the analysis of channel migration changes in the active Yellow River Delta, China. Int. J. Appl. Earth Obs. Geoinf. 1999;1(2):146–157. [Google Scholar]
- 35.Elahi K., Ahmed K., Mafizuddin M. Jahangirnagar University; Dhaka: 1991. Riverbank Erosion, Flood and Population Displacement in Bangladesh, Riverbank Erosion Impact Study. Savar. [Google Scholar]
- 36.Kalam M., Hoque N. Erosion trend study of the Ganges river course using remote sensing techniques. Asia Pacific Remote Sensing Journal. 1995;8(1):43–50. [Google Scholar]
- 37.Rahman M., Ashrafuzzaman A. River geometry and bankline movement of the Ganges river in Bangladesh. Jounal of NOAMI. 2004;21(2):19–31. [Google Scholar]
- 38.Sarker M.H. The Ganges Water Diversion: Environmental Effects and Implications. Springer; 2004. Impact of upstream human interventions on the morphology of the Ganges-Gorai system; pp. 49–80. [Google Scholar]
- 39.Yeasmin S., Kabir S., Asaduzzaman A. Shifting of the Padma River in Shibganj Upazila of Chapai Nawabganj district, Bangladesh. J. Geol. Soc. India. 2007;70(5):793. [Google Scholar]
- 40.Thakur P.K., Laha C., Aggarwal S. River bank erosion hazard study of river Ganga, upstream of Farakka barrage using remote sensing and GIS. Nat. Hazards. 2012;61(3):967–987. [Google Scholar]
- 41.Hossain M.A., Gan T.Y., Baki A.B.M. Assessing morphological changes of the Ganges River using satellite images. Quat. Int. 2013;304:142–155. [Google Scholar]
- 42.Dewan A., et al. Assessing channel changes of the Ganges-Padma River system in Bangladesh using Landsat and hydrological data. Geomorphology. 2017;276:257–279. [Google Scholar]
- 43.Mannan A., Sheikh A. vol. 12. Rajshahi Univ. Stud. Part B; 1984. pp. 61–79. (The Shifting of the Ganges River (The Padma) and its Morphological Effect within the Rajshahi District). [Google Scholar]
- 44.Kalam M., Jabbar M. REIS-JU; Dhaka: 1991. River Course Monitoring of the Ganges At Godagari, Rajshahi Using Remote Sensing Techniques. Riverbank Erosion, Flood and Population Displacement in Bangladesh; pp. 73–85. [Google Scholar]
- 45.Klassen G., Vermeer K. International Conference on River Regime. Hydraulics Research Limited; Wallingford, Oxon UK: 1988. Channel characteristics of the braiding Jamuna river, Bangladesh; pp. 173–189. 16 fig, 1 tab, 13 ref. 1988. [Google Scholar]
- 46.Gilvear D., Bryant R., Hardy T. Remote sensing of channel morphology and in-stream fluvial processes. Prog. Environ. Sci. 1999;1:257–284. [Google Scholar]
- 47.Bhakal L., Dubey B., Sarma A.K. Estimation of bank erosion in the river Brahmaputra near Agyathuri by using geographic information system. Journal of the Indian Society of Remote Sensing. 2005;33(1):81–84. [Google Scholar]
- 48.Das J., Saraf A. Remote sensing in the mapping of the Brahmaputra/Jamuna River channel patterns and its relation to various landforms and tectonic environment. Int. J. Rem. Sens. 2007;28(16):3619–3631. [Google Scholar]
- 49.Philip G., Gupta R., Bhattacharya A. Channel migration studies in the middle Ganga basin, India, using remote sensing data. Int. J. Rem. Sens. 1989;10(6):1141–1149. [Google Scholar]
- 50.Paura R.K. Journal of the Institution of Engineers. Civil Engineering Division; India: 2002. Fluvial geomorphology of the river Ganga around Farakka; pp. 193–196. 82(FEV) [Google Scholar]
- 51.Harijan N., et al. Course of river Ganga over a century near Kanpur city based on remote sensing data. Journal of the Indian Society of Remote Sensing. 2003;31(1):1–2. [Google Scholar]
- 52.Pati J.K., et al. Spatio-temporal shift of western bank of the Ganga river, Allahabad city and its implications. Journal of the Indian Society of Remote Sensing. 2008;36(3):289–297. [Google Scholar]
- 53.Sinha R., Ghosh S. Understanding dynamics of large rivers aided by satellite remote sensing: a case study from Lower Ganga plains, India. Geocarto Int. 2012;27(3):207–219. [Google Scholar]
- 54.Gupta N., Atkinson P.M., Carling P.A. Decadal length changes in the fluvial planform of the River Ganga: bringing a mega-river to life with Landsat archives. Remote sensing letters. 2013;4(1):1–9. [Google Scholar]
- 55.Debnath J., et al. Modelling on assessment of flood risk susceptibility at the Jia Bharali River basin in Eastern Himalayas by integrating multicollinearity tests and geospatial techniques. Modeling Earth Systems and Environment. 2023 [Google Scholar]
- 56.Ahmed I., et al. Erosion induced channel migration and its impact on dwellers in the lower Gumti River, Tripura, India. Spatial Information Research. 2018;26(5):537–549. [Google Scholar]
- 57.Debnath J., et al. Assessing the impacts of current and future changes of the planforms of river Brahmaputra on its land use-land cover. Geosci. Front. 2023;14(4) [Google Scholar]
- 58.Debnath J., et al. Geospatial modeling to assess the past and future land use-land cover changes in the Brahmaputra Valley, NE India, for sustainable land resource management. Environ. Sci. Pollut. Control Ser. 2023;30(49):106997–107020. doi: 10.1007/s11356-022-24248-2. [DOI] [PubMed] [Google Scholar]
- 59.Debnath J., Das N., Sahariah D. Impacts of temperature–rainfall and land use/land cover changes on the hydrological regime in the Muhuri River basin, Northeast India. Sustainable Water Resources Management. 2022;8(5):153. [Google Scholar]
- 60.Thieler E.R., et al. US Geological Survey; 2009. The Digital Shoreline Analysis System (DSAS) Version 4.0-an ArcGIS Extension for Calculating Shoreline Change. [Google Scholar]
- 61.Jana S. An automated approach in estimation and prediction of riverbank shifting for flood-prone middle-lower course of the Subarnarekha river, India. Int. J. River Basin Manag. 2021;19(3):359–377. [Google Scholar]
- 62.Suhaimi H., Jamal M., Ahmad A. IOP Conference Series: Earth and Environmental Science. IOP Publishing; 2018. Assessment of river bank erosion at Kilim River, Langkawi using geospatial technique. [Google Scholar]
- 63.Carrasco A.R., et al. Natural and human-induced coastal dynamics at a back-barrier beach. Geomorphology. 2012;159:30–36. [Google Scholar]
- 64.Jabaloy-Sánchez A., et al. Six thousand years of coastline evolution in the Guadalfeo deltaic system (southern Iberian Peninsula) Geomorphology. 2014;206:374–391. [Google Scholar]
- 65.Chrisben Sam S., Gurugnanam B. End point rate analysis and estimation along the southwest coast of Kanyakumari, Tamil Nadu, using geospatial techniques. Int. J. Environ. Sci. Technol. 2023;20(7):7463–7476. [Google Scholar]
- 66.Basheer Ahammed K., Pandey A.C. Shoreline morphology changes along the Eastern Coast of India, Andhra Pradesh by using geospatial technology. J. Coast Conserv. 2019;23:331–353. [Google Scholar]
- 67.Basheer Ahammed K., Pandey A.C. Assessment and prediction of shoreline change using multi-temporal satellite data and geostatistics: a case study on the eastern coast of India. Journal of Water and Climate Change. 2022;13(3):1477–1493. [Google Scholar]
- 68.Anam B., Khan J.A., Munir B.A. Assessment of river evolution and channel migration rates in the fluvial regime of Punjab province of Pakistan. J. Spacecraft Technol. 2015;5(1) [Google Scholar]
- 69.Hasanuzzaman M., et al. BEHI, and REBVI Models: Evidence from the Lower Ganga River in India. 2021. Estimation and prediction of riverbank erosion susceptibility and shifting rate using DSAS. [Google Scholar]
- 70.Nath B., Naznin S.N., Alak P. Trends analysis of river bank erosion at Chandpur, Bangladesh: a remote sensing and GIS approach. Int. J. Geomatics Geosci. 2013;3(3):454–463. [Google Scholar]
- 71.BBS . Bangladesh Bureau of Statistics (BBS); Bangladesh: 2013. District Statistics 2011,Chandpur. [Google Scholar]
- 72.Ahmed N. BUET; Dhaka: 1989. Study Of Some Bank Protective Works in Bangladesh. Unpublished M. Sc. Thesis, Dept. Of Water Resource Engineering. [Google Scholar]
- 73.Siddique K. Unpublished MS Thesis, Dept. Of Water Resources Engineering. BUET; Dhaka: 2004. Evaluation of Chandpur town protection. [Google Scholar]
- 74.Xu H. Modification of normalised difference water index (NDWI) to enhance open water features in remotely sensed imagery. Int. J. Rem. Sens. 2006;27(14):3025–3033. [Google Scholar]
- 75.Leatherman S., Clow B. UMD shoreline mapping project. IEEE Geoscience and Remote Sensing Society Newsletter. 1983;22(3):5–8. [Google Scholar]
- 76.USGS . 2018. Digital Shoreline Analysis System (DSAS) Version 5.0 User Guide. [Google Scholar]
- 77.Mukhopadhyay A., et al. Automatic shoreline detection and future prediction: a case study on Puri Coast, Bay of Bengal, India. European Journal of Remote Sensing. 2012;45(1):201–213. [Google Scholar]
- 78.Cenci L., et al. Geomatics for integrated coastal zone management: multitemporal shoreline analysis and future regional perspective for the Portuguese central region. J. Coast Res. 2013;(65):1349–1354. [Google Scholar]
- 79.Kuleli T. Quantitative analysis of shoreline changes at the Mediterranean Coast in Turkey. Environ. Monit. Assess. 2010;167(1–4):387–397. doi: 10.1007/s10661-009-1057-8. [DOI] [PubMed] [Google Scholar]
- 80.Prukpitikul S., et al. Shoreline change prediction model for coastal zone management in Thailand. J. Shipp. Ocean Eng. 2012;2(4):238. [Google Scholar]
- 81.Deepika B., Avinash K., Jayappa K. Shoreline change rate estimation and its forecast: remote sensing, geographical information system and statistics-based approach. Int. J. Environ. Sci. Technol. 2014;11(2):395–416. [Google Scholar]
- 82.Hegde A.V., Akshaya B. Shoreline transformation study of Karnataka coast: geospatial approach. Aquatic Procedia. 2015;4(2015):151–156. [Google Scholar]
- 83.Li R., Liu J.-K., Felus Y. Spatial modeling and analysis for shoreline change detection and coastal erosion monitoring. Mar. Geodesy. 2001;24(1):1–12. [Google Scholar]
- 84.Barman N.K., Chatterjee S., Khan A. Trends of shoreline position: an approach to future prediction for balasore shoreline, Odisha, India. Open J. Mar. Sci. 2014;5(1):13. [Google Scholar]
- 85.Stancioff C., et al. Predicting coastal erosion in St. Kitts: collaborating for nature and culture. Ocean Coast Manag. 2018;156:156–169. [Google Scholar]
- 86.Ghosh P., Mukhopadhyay A. EGUGA; 2018. A Modified Equation to Calculate the Potential Future Shoreline Position Using Transects; p. 3982. [Google Scholar]
- 87.Mukhopadhyay A., et al. Threats to coastal communities of Mahanadi delta due to imminent consequences of erosion – present and near future. Sci. Total Environ. 2018;637–638:717–729. doi: 10.1016/j.scitotenv.2018.05.076. [DOI] [PubMed] [Google Scholar]
- 88.Basiouny M., et al. Shoreline change rate detеction and futurе prediction using rеmote sensing and GIS tеchniques: a case study of ras EL-hekma, north western coast, Egypt. Journal of Geography, Environment and Earth Science International. 2017;9(3):1–14. [Google Scholar]
- 89.Star T.D. The Daily Star. 2010. Erosion makes hundreds homeless in Chandpur. The Daily Star: Dhaka, Bangladesh. [Google Scholar]
- 90.Star T.D. The Daily Star. 2012. Erosion in Chandpur renders over 100 families homeless. The Daily Star: Dhaka, Bangladesh. [Google Scholar]
- 91.Rony I. Dhaka Tribune. 2019. Meghna erosion wreaks havoc in Chandpur. Dhaka, Bangladesh. [Google Scholar]
- 92.Rony I. Dhaka Tribune. Dhaka Tribune; Dhaka, Bangladesh: 2020. Padma River erosion claims Tk2 crore cyclone shelter in Chandpur. [Google Scholar]
- 93.Times C. In: Rajarajeshwar Omar Ali High School Cum Cyclone Center Washed Away. Times Chandpur., editor. Chandpur Times; Chandpur, BAngladesh: 2020. [Google Scholar]
- 94.Times C. In: In Chandpur People Loses Their Homestead Due to Erosion of Padma. Times Chandpur., editor. Chandpur Times; Chandpur, BAngladesh: 2020. [Google Scholar]
- 95.Sutikno S. Integrated remote sensing and GIS for calculating shoreline change in rokan estuary. KnE Engineering. 2016 [Google Scholar]
- 96.Dean R.G., Malakar S.B. Projected flood hazard zones in Florida. J. Coast Res. 1999:85–94. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data will be made available on request.