Quantifying brain-functional dynamics using deep dynamical systems: Technical considerations

Summary

Both mental health and mental illness unfold in complex and unpredictable ways. Novel artificial intelligence approaches from the area of dynamical systems reconstruction can characterize such dynamics and help understand the underlying brain mechanisms, which can also be used as potential biomarkers. However, applying deep learning to model dynamical systems at the individual level must overcome numerous computational challenges to be reproducible and clinically useful. In this study, we performed an extensive analysis of these challenges using generative modeling of brain dynamics from fMRI data as an example and demonstrated their impact on classifying patients with schizophrenia and major depression. This study highlights the tendency of deep learning models to identify functionally unique solutions during parameter optimization, which severely impacts the reproducibility of downstream predictions. We hope this study guides the future development of individual-level generative models and similar machine learning approaches aimed at identifying reproducible biomarkers of mental illness.

Graphical abstract

Highlights

• •Reconstructed dynamical systems underlying fMRI data via machine learning approach
• •Extracted dynamical features that reflect the properties of the dynamics
• •Characterized the computational challenges during training/extraction pipeline
• •Explored two ways to make individual-level features useable for downstream prediction

Psychiatry; Artificial intelligence

Introduction

The use of advanced machine learning (ML) tools is widely considered to provide deeper insight into the biology of mental illness and support precision medicine.^1,2 The application of machine learning tools has focused on a broad spectrum of data types, including neuroimaging,^3,4,5 multi-omics,⁶ electrophysiological,^7,8 speech,^9,10,11 or medical record data.¹² In most cases, the principal aim has been the identification of illness-related patterns present across patients with a given diagnosis (or subgroups thereof), in order to allow prediction at the individual level. Rarely, however, have ML approaches been applied to characterize the longitudinally changing, dynamic nature of data potentially relevant for mental illness. As the behavior of most biological and higher-order (e.g., cognition and behavior) systems is dynamic by nature, there is a rapidly growing body of work in the field of psychiatry that has focused on the use of dynamical systems theory (DST) for their quantitative analysis.^13,14,15,16 DST offers a powerful theoretical framework for studying such complex systems and may have utility as a unified mathematical language for describing functional characteristic of psychiatric conditions and the links between behavior and brain activity at different scales.^{16,17,18,19,20,21}

However, until recently, there were no computational approaches available to extract generative dynamical systems (DS) models directly from data. Although there is a long history of methods for characterizing signatures of nonlinear system dynamics in experimental data, such as Lyapunov exponent,²² as well as mainly linear methods such as dynamic causal modelling (DCM) for capturing functional interactions,^23,24 truly “generative” models that recreate the attractors and long-term statistics of an observed system is a fairly recent development.^14,25 These rely on the ability of the underlying models to serve as general (non-linear) function approximators, as well as recent advances in training techniques for dynamical systems. Such generative models have been demonstrated to accurately capture the ground truth of a given dynamical system.^14,25 Machine learning model types for such an analysis include the so-called “recurrent neural networks” (RNNs). These belong to the class of deep neural networks and comprise “recurrent” connections, which allow the model to act as a dynamical system itself and thus to emulate a generative surrogate model of brain dynamics. The inherent alignment of mathematical principles between RNNs and DST enables RNNs to characterize the dynamical system properties underlying the observed time series of e.g., functional MRI data.^14,26 Interesting dynamical system properties that can be extracted from RNN models include, for example, the number and geometry of attractors, or bifurcations the system undergoes, and can be quantified at the individual participant level.^27,28 This makes such properties potentially useful predictors for downstream analysis, as has been explored in a preliminary study on amyotrophic lateral sclerosis using resting-state functional magnetic resonance imaging (rs-fMRI) data.²⁹ In the field of neuroscience, RNNs and DST have previously been integrated as a framework to study neurophysiological functions and neural computations. This approach allows researchers to peek inside the “black box” by interpreting RNN models trained using experimental neurophysiological data.³⁰ These data-driven studies have been widely used to explore topics such as synaptic mechanisms, sequence propagation, neural circuits, interactions among brain areas, and the relationship between neural and behavioral variables.^14,30 Many of these data-driven RNNs can be considered generative models, as they can generate new data with similar statistical properties to the training data. However, this does not imply that these RNN models are generative in the context of DST. For this, a far stricter definition is required: the inferred model must converge to the same attractor states when run independently and, at least locally, it must have a similar vector field topology as the true DS underlying the training data.¹⁴ To achieve this goal, specially designed model architectures, training algorithms, optimization goals, and evaluation metrics are essential.¹⁴ Therefore, the “generative model” in this study refers to the generative model in the DS context.

While RNN-based generative models are powerful tools to characterize dynamical systems behavior, and algorithms for such data-driven analysis exist,²⁸ there are major challenges relevant for their application on brain dynamics, and psychiatry-relevant data, in general. The power of RNN models comes with substantial model complexity. Neural networks in general, and deep learning models in particular, are prone to converge to saddle regions or local model minima in training.^31,32 Moreover, different dynamical systems formulations may only be compatible with a limited sample of time series measurements. Therefore, a central question is whether the solutions obtained by a given model correspond to the “true” dynamical system. In supervised machine learning, where a set of features is used for the prediction of an (e.g., clinical) outcome, an intrinsic assumption is that the feature values measured at the individual subject level relate to the same underlying “population.” When using features extracted from deep learning models, such assumptions may not hold, if these relate to different local minima associated with different parameter sets. For dynamical systems modeling, this is particularly important, since models are usually trained independently for the data from each individual, and it may be challenging (if not impossible) to a priori guarantee that repeatedly trained models consistently yield the same parameter estimates. Consequently, machine learning tools applied downstream would not be able to detect consistent signatures of dynamical system properties and lack predictive power.

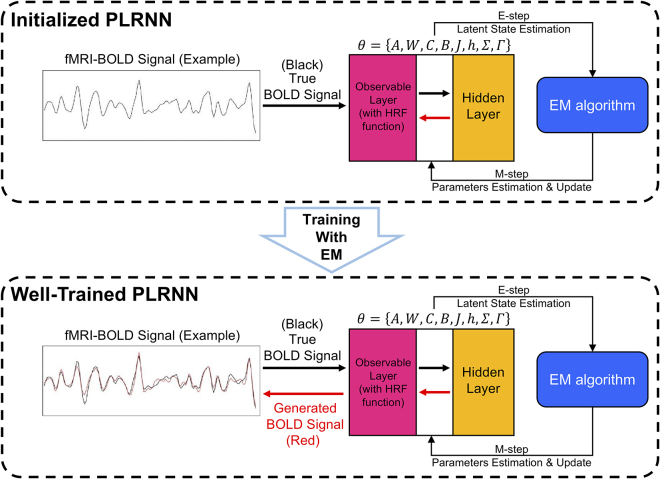
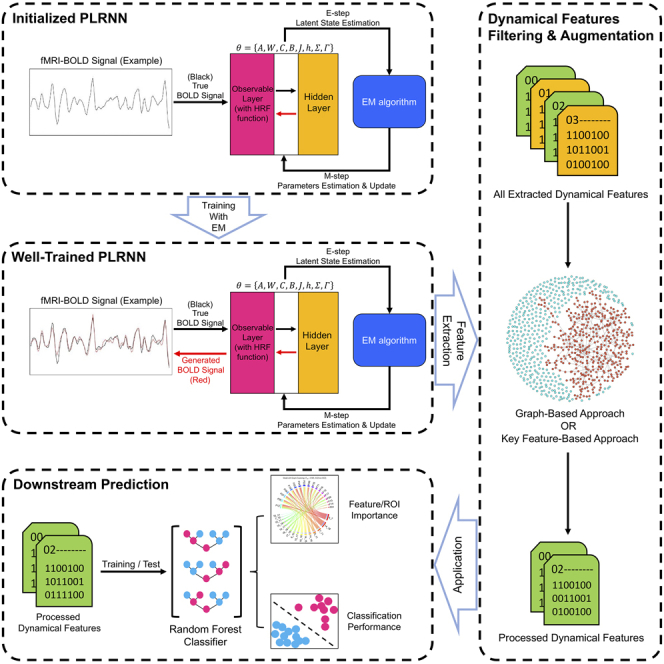
To explore this, we used the piecewise linear recurrent neural networks (PLRNNs) model^27,33,34 to reconstruct the dynamical system underlying the input resting-state fMRI data and to extract 18 features (F01–F18, see Table S3 for details) at the individual level. These features have been designed and proven in previous studies^27,33,34 to reflect the general properties of the reconstructed dynamics in state space, such as the count of stable fixed points, unstable fixed points, and cycles of the reconstructed system. The PLRNN model consists of two parts: the latent layer, which learns and reconstructs the temporal evolution of the dynamical states based on signals from the observable layer, and the observable layer is responsible for mapping between the observable input signals and the latent dynamical states. The expectation-maximization (EM) algorithm was used for the training process. Figure 1 presents a simplified illustration of the PLRNN model and its training process. The resting-state fMRI dataset used in this study includes 132 participants: 46 with schizophrenia (SCZ), 44 with major depressive disorder (MDD), and 42 healthy controls (HCs). Multiple models were inferred independently from the time series data of each individual, in order to evaluate the consistency of the extracted dynamical features. We used the random forest (RF) model to predict the diagnosis of each individual based on these extracted dynamical features. In addition, we proposed and implemented both (1) a non-hypothesis-driven, graph-based approach and (2) a hypothesis-driven approach to identify features from comparable model solutions. This study thus highlights practical aspects of using RNN models to capture dynamical system properties from direct analysis of neural time-series data, and the use of the extracted dynamical features for machine learning and personalized medicine approaches.

Figure 1.

A simplified illustration of the PLRNN model architecture and the training process

Results

A PLRNN pipeline for individual-level prediction using dynamical system features

A PLRNN pipeline was implemented for (1) modeling of the time-series data from resting state fMRI individually for each participant using 19 pre-defined regions of interest (ROI) parcellated based on the Harvard-Oxford Atlas³⁵ (2 mm cortical probabilistic masks thresholded at 25 percent, as distributed with FSL—FMRIB software library), (2) extracting 18 dynamical features²⁹ from each model, and (3) using the extracted dynamical features for diagnostic classification based on RFs. To test basic properties of the pipeline, we first focused on data from patients with SCZ and HCs, only.

An important question for the first step, the modeling of the rs-fMRI data, is its brain-regional focus. Since dynamical systems may differ at different regional granularity, we first modeled all 19 ROIs simultaneously (see Tables S2 and S3). Subsequently, we focused on all respective pairs of the 19 ROIs within the default mode network^36,37,38 (DMN) and salience network^39,40,41 (SN), in order to test whether this increased granularity had an impact on classification performance.

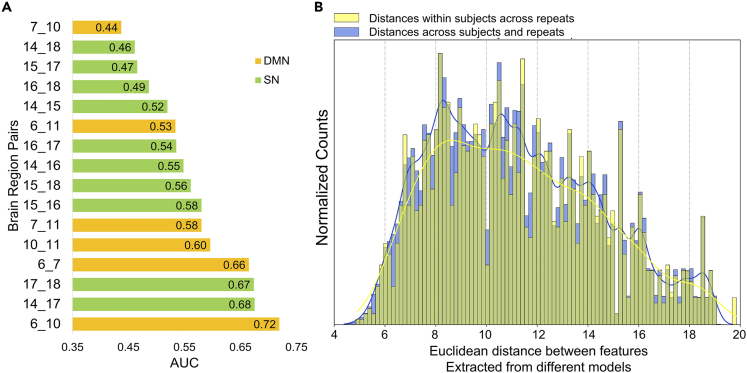
For the combined ROI analysis, the RF classifier yielded a low ROC-AUC (area under the receiver operating characteristic curve) of 0.54 in 5-fold cross validation (CV), indicating that the extracted dynamical features could not differentiate between patients with SCZ and HCs (Table S4 shows that similar results were obtained for classifiers other than RF). For the analysis of ROI pairs within the DMN and SN, AUC values between 0.44 and 0.72 were observed (Figure 2A), indicating at least partially independent information could be extracted from the region pairs. However, concatenating these features in a single RF model also resulted in a low AUC of 0.58 (p = 0.22), suggesting integration of more granular dynamical system features did not enhance classification performance.

Figure 2.

Performance of RF classifiers using features from different brain regions and demonstration of weak feature robustness

(A) Average AUC scores of RF classifiers for the SCZ/HC classification task in 5-fold cross validation using features extracted from region pairs belonging to the DMN (yellow) and SN (green). The complete results can be found in the Table S5. The full list of region indices/names can be found in Table S2.

(B) The distribution of the Euclidean distances between features extracted from different PLRNN models (blue: distance across participants and repeats; yellow: distance within participants across repeats).

Stability of dynamical systems features

The use of dynamical systems features in machine learning critically depends on the ability of the PLRNN to consistently identify solutions associated with the true dynamical system. As repeatedly trained deep learning models, such as the PLRNN, may always converge on different model parameters (here, primarily due to the initialization of the EM procedure), the robustness of the extracted dynamical features, which represent “meta-statistics” related to the model parameters, is an essential question. To quantify this robustness and its impact on classification performance, for each individual in the dataset, due to computational resource constraints, six RNN models were selected after only six independent training repetitions. We first calculated the Spearman’s correlation between the dynamical features extracted from all participants and modeling repeat combinations. The median correlation was very low at 0.1 (range 0.09–0.12, Table S6), indicating a substantial inconsistency of the extracted features. An interesting question was whether this feature robustness could be increased by averaging feature values from multiple repetitions. However, the overall correlation between the averaged features of the first three repetitions and those of the last three repetitions was still only 0.12. We also applied these new generated features to the RF model, but the overall classification performance during 5-fold CV showed no significant difference compared to the baseline model (see Tables S7 and S8 for further details).

Another useful indicator of feature robustness is the comparison of the distance between the features obtained repeatedly from the same versus different individuals. Reproducible models should yield substantially lower distances for features repeatedly determined from the same individuals. However, Figure 2B shows that across all possible within- versus between-individual comparison, the obtained distribution of distances were highly overlapping, and not statistically different (p = 0.20). These results further support the notion that the PLRNN models did not yield comparable dynamical systems features, even when repeatedly trained on the same individuals.

However, we hypothesized that the model solutions were not entirely individual-specific. In other words, we aimed to explore whether we could identify models that were comparable across repeats and individuals, and test whether such models would allow improved classification. For this purpose, we first employed a non-hypothesis-driven approach that employed graph clustering to identify comparable features. Second, we conducted a hypothesis-driven manual selection based on three critical properties of the dynamical systems.

Hypothesis-free, graph-based identification of comparable RNN models

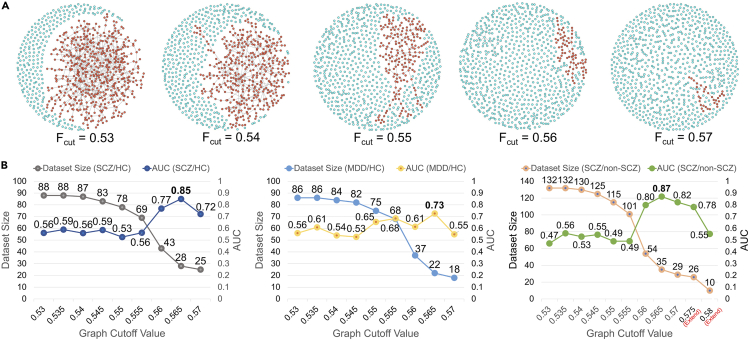
For the non-hypothesis-driven approach, we estimated the pairwise similarity between all individuals and repeats, based on the extracted features. We assumed that similar solutions would lead to the formation of clusters in the resulting similarity graph, as demonstrated in Figure 3A, and we only used the features within the same cluster for downstream analysis. To identify such clusters, graph links reflecting similarity estimates below a given cutoff value $F_{cut}$ were gradually removed from the graph. In each graph with different cutoff value, we excluded all feature records in the nodes outside the largest cluster (marked in red), averaged the remaining features for each participant and region pair, and repeated the classification using a nested leave-one-out cross validation (LOOCV). This procedure incorporated “bagging” to increase the stability of the model’s predictions, as well as feature selection to retain only the most predictive features for classification.

Figure 3.

Graph clustering approach and impact on classification performance

(A) Illustration of graph-filtering cut-off ($F_{cut}$) on the graph where each node represents an individual per model building repeat. The largest cluster is highlighted in red, while other nodes or smaller clusters are marked in cyan.

(B) The LOOCV performances of the RF classifiers using the graph clustering method in the SCZ/HC, MDD/HC, and SCZ/non-SCZ (HC + MDD) classification tasks. The detail of model performance can be found in the Table S9.

Figure 3B displays the performance of RF models using features selected by the graph-clustering method. For schizophrenia versus control classification (SCZ/HC), it demonstrates that once the graph filtering surpassed a certain threshold ($F_{cut}$ = 0.56), the classification AUC score increased to 0.77 (p = 0.001) for a subset of 43 individuals (49% of the entire dataset), and to 0.85 (p = 0.0009) with 28 individuals (32%) remaining in the dataset. This represented a significant improvement compared to the AUC = 0.58 achieved by baseline model.

We further tested depression versus control classification (MDD/HC) to explore the effect of the graph clustering method. Figure 3B shows a similar performance trend, where the RF model also achieved its best AUC = 0.73 (p = 0.007) at $F_{cut}$ = 0.565, albeit with an overall lower classification performance compared to the SCZ/HC classification. Next, we compared the combined MDD and HC groups (i.e., HC + MDD) against SCZ, and observed that the RF model achieved an even higher maximum AUC of 0.87 (p = 3.80e−05, Figure 3B). For further details, please refer to the Table S9.

In addition, to assess the diagnostic specificity of classification models, we utilized the MDD/HC model to predict SCZ subgroup and the SCZ/HC model to predict MDD subgroup (using dynamical features from the optimal graph-clustering setting). For the MDD/HC model, 32% of patients with SCZ were misclassified as MDD. For the SCZ/HC model, 29% of individuals with MDD were misclassified as SCZ. As a reference, the baseline model without using graph clustering had misclassification rates of 45% and 42% on the SCZ and MDD sets, respectively. The higher specificity achieved with classifiers using dynamical features optimized by graph clustering suggests that these features captured specific dynamical system properties of the respective selected patient subgroups.

Hypothesis-driven identification of comparable RNN models

The graph-based approach aimed to identify comparable dynamical systems across individuals. It is possible that such an approach will miss illness-relevant differences, as it focuses on a relatively small, more homogeneous subset of patients and controls. Thus, as an alternative approach, we focused on three dynamical features that reflect the general geometric properties of the system in state space. These features are likely to play a critical role in identifying comparable dynamical systems and their corresponding features^16,26,27,42: the count of stable fixed points, unstable fixed points, and cycles of the reconstructed system. Among the six models corresponding to each participant, we used only those related to the most consistent values of the three features described previously for further analysis. The dynamical features extracted from these models were averaged and the remaining models discarded. In contrast to the graph clustering approach, this method considers all participants for analysis, and may retain dynamical system properties that are fundamentally different between patients and controls. For the SZC/HC classification, this approach resulted in an AUC = 0.69 (p = 0.0009). For the SCZ/(HC + MDD) classification, there was no improvement in performance (AUC = 0.59; p = 0.048). For the MDD/HC classification, the AUC was even lower than the baseline model (AUC = 0.66, p = 0.006) at AUC = 0.56 (p = 0.347), indicating that the selection based on key dynamical system properties could not improve classification performance. For further details, please see Table S10. The diagnostic specificity of the MDD/HC and SCZ/HC models for the SCZ and MDD subgroups was low, with misclassification rates of 59.13% and 53.98%, respectively.

Feature contributions during classification using RF

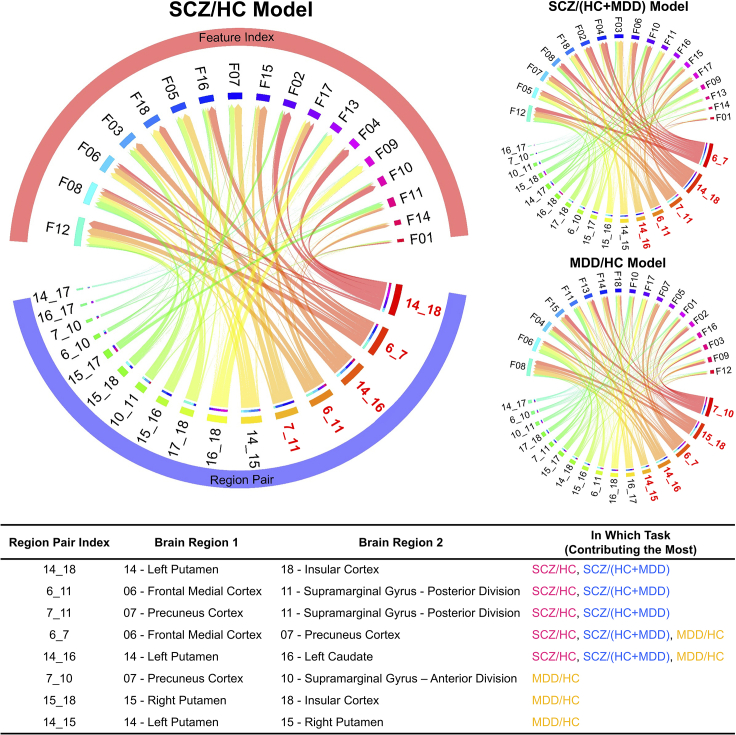
To quantify which features and region pairs contributed to classification, we recorded their selection frequency and importance for the RF models. Figure 4 shows which region pairs and dynamical systems features were most frequently selected in the three classification tasks (marked in red) and their respective relationships. The table in Figure 4 further illustrates the detailed information about the brain regions related to these pairs. The name list of all 19 brain regions can be found in Table S2.

Figure 4.

Feature and region pair importance for classification

The chord plots demonstrate which region pairs and dynamical features were most frequently selected in the three classification tasks (SCZ/HC, SCZ/(MDD+HC), and MDD/HC) and their corresponding relationships. All region pairs and feature indices are ordered clockwise based on frequencies. The top 5 region pairs are marked in red, with detailed information listed in the following table. The full list of feature and region names can be found in Tables S2 and S3.

Focusing on the feature sets used by the models selected through graph-clustering, we observed a consistent set of region pairs that was most frequently selected in the SCZ/HC and SCZ/(HC + MDD) classification tasks (please refer to the table in Figure 4). This pair set was only partially overlapping with that found for the MDD/HC classification, consistent with the observed diagnostic specificity of the respective models. In terms of dynamical features (see Table S3 for details and “method details” section for equations), F05/06/07 (variance of parameters in the both/regularized/non-regularized part of the transition matrix A and weight matrix W in Equation 1), F08 (average of the regularized part of bias vector h in Equation 1), F11/12 (mean of the regularized/non-regularized part of weight matrix W), and F17/18 (mean/variance of regression coefficient matrix B in Equation 2) exhibited a high selection frequency across all three classification tasks. Among these features, F05/06/07 relate to the general stability of network activity and dynamical modes.^29,43 F08 reflects the mean activity level of the system; F11/12 is related to weight matrix W, characterizing how balanced or biased the connectivity and connection strengths are; and F17/18 reflects whether state information is distributed evenly or unevenly across observation signals.²⁹

Discussion

The aim of this study was to characterize computational challenges associated with the application of deep learning for the modeling of individual-level brain dynamics, and the downstream use of model parameters as potential biomarkers for mental health and mental illnesses such as SCZ and MDD.

We observed that PLRNN models were highly prone to identify solutions with heterogeneity during parameter optimization. This may be attributed to a well-known issue where deep learning algorithms identify only local minima, or even just saddle regions, in parameter space.^32,44 Alternatively, these heterogeneous solutions may also equally explain the data well, as these resulted in models with an overall similar quality of fit, it was not possible to filter out solutions prior to parameter extraction and downstream machine learning classification of SCZ and MDD. This eventually prohibits the direct usage of model parameters for downstream classification. We here therefore focused on “meta-statistics” of the model related to dynamical systems features of the underlying system. But even these may be subject to uncertainties in parameter initialization, in the training process itself, or due to the fact that potentially different dynamical models explain the finite experimental data equally well. In fact, we observed that models showed a substantial variability between repetitions in the same participant, which was comparable to the variation observed across individuals. Consequently, patients with both diagnoses could not be differentiated from controls with an accuracy above chance. This issue also did not be improve after averaging multiple individual models in attempt to increase the signal-to-noise ratio related to the dynamical system of a given participant. This suggests that the identified models did not capture comparable dynamical system properties across participants, which is an intrinsic assumption of machine learning models to work well for the downstream prediction using the extracted model parameters.

Based on the hypothesis that solutions to dynamical systems with similar features across subjects are likely to better capture “average” brain dynamics and should thus be more predictive of diagnosis, we employed a graph-based selection process of comparable models. This resulted in a substantial increase in classification performance for SCZ and for MDD, but required the removal of a large fraction of participants from the analysis. More specifically, approximately 70% of participants had to be excluded from analysis for models to achieve maximum performance. It should be noted, however, that the performance estimates obtained here likely do not reflect generalizable estimates when tested in independent data, as these relate to a data-driven subgroup analysis. Furthermore, cut-offs for filtering the graph were not chosen using nested cross validation, due to the limited sample size and time constraints, and likely inflating the obtained performance measure. Despite this, the identified models showed significant differential diagnostic specificity and were related to different features in partially overlapping brain regions. For SCZ, these regions involved particularly the left putamen, insular and frontal medial cortex, as well as the precuneus. For depression, these regions included the precuneus, the insular cortex, as well as the right putamen.

This study has important implications for machine learning studies using models built on the individual participant level, such as deep learning models of time series deployed here. In particular, with complex models that are likely to identify local optima of the parameter solutions, or with limited single subject data equally compatible with different dynamical models, it is vital to explore the similarity of such solutions across multiple training repetitions. Otherwise, in data with small sample sizes especially, derived signatures may appear predictive, but will likely not be generalizable.

However, the current clustering method is still not ideal, as a large fraction of the data had to be discarded for classification to reach statistically significant performance estimates. Therefore, our future works may focus on approaches that first aim at identifying parameter solutions that are shared among individuals before fine-tuning such models to the time series obtained for individual participants. Alternatively, computationally efficient training procedures that allow to repeatedly infer a high number of models, could be leveraged to identify similar (more robust) features within subjects. Also, if features are to be extracted from such models as input for downstream prediction, as has been performed here for features describing dynamical system properties, such features could be filtered a priori to include only those with less sensitivity to local parameter optima.

Another promising strategy would be to define such features in a data-driven manner, in order to improve their predictive value for a given outcome of interest. Such data driven optimization may also be relevant for the identification of the specific data the analysis is applied on. Here, we utilized ROI pairs and showed that the resulting system features are different from those obtained on the entire brain, supporting a degree of brain-regional specificity. However, it is unclear whether this degree of aggregation is optimal in terms of capturing the true underlying dynamical system properties, as well as in terms of maximizing predictive performance. Currently, the limited computational scalability of the deployed deep learning approaches prevented a more comprehensive analysis of a broader, data-driven selection of regions for dynamical system modeling. In the future, addressing this critical bottleneck will also aid in facilitating such analyses on data from multiple, larger cohorts, which will allow further exploring the properties and reproducibility of dynamical system features.

In conclusion, we here provided an in-depth analysis of deep learning for the modeling of dynamical systems in fMRI time-series data, and its downstream application for classification of SCZ and MDD. We highlighted the utility of such approaches for classification if comparable parameter solutions can be obtained. However, identifying such comparable models is challenging, and we outlined several approaches to support the reproducibility and feasibility of future applications of similar modeling approaches. These, in turn, are important further steps to harness the potential of artificial intelligence in understanding and predicting human behavior.

Limitations of the study

This study has several limitations that need to be considered and addressed in future research. First, although using the graph clustering approach to filter the dynamical features significantly improved the results of downstream prediction, a large fraction of the data had to be discarded during this process, which may affect the generalizability of these features. Second, due to limited computational power, we only extracted dynamical features from six independent training repetitions and only trained three models independently for each participant in each repetition. Future studies could benefit from implementing more computationally efficient training algorithms that allow us to train a larger number of models to identify more robust features for each participant. Third, the graph clustering approach we used in this study is a similarity-based affinity graph. Although it allows us to control the filtering results using various manually chosen thresholds, it is still worth exploring other novel unsupervised clustering algorithms to determine whether replacing our current method with these unsupervised methods could bring additional benefits for the dynamical features. Finally, the 18 dynamical features used to describe the dynamical system properties in this study were still manually designed. Future research should investigate whether these features can be pre-filtered to include only those that are less sensitive to local parameter optima.

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Software and algorithms
MATLAB	https://www.mathworks.com/	8.5.0 R2015a
Python	https://www.python.org/	Version 3.8
R	https://www.r-project.org/	Version 4.2.3
Scikit-learn	https://scikit-learn.org/	Version 1.1.2
igraph	https://igraph.org/	Version 1.4.1
PLRNN model	https://github.com/DurstewitzLab/PLRNN_SSM	Koppe et al.33
Feature Extraction	https://github.com/JanineT-oss/ALS_PLRNN_classification	Thome et al.29

Resource availability

Lead contact

Further information and requests for resources and reagents should be directed to and will be fulfilled by the lead contact, Prof. Emanuel Schwarz. E-mail: emanuel.schwarz@zi-mannheim.de.

Materials availability

This study did not involve/generate any unique reagents.

Data and code availability

• •The fMRI data used in this study cannot be deposited in a public repository as this would not be consistent with the consent signed by all participants. Therefore, any requests for data must be submitted to the lead contact first.
• •The original code for PLRNN model training and feature extraction were kindly provided by Koppe et al., and has been deposited at online GitHub repository (feature extraction: https://github.com/JanineT-oss/ALS_PLRNN_classification and PLRNN model: https://github.com/DurstewitzLab/PLRNN_SSM). All other packages or software used in this study can be found online with the following versions: All PLRNN models were trained and evaluated in a MATLAB 8.5.0 R2015a environment. Data preprocessing and result analysis were performed in a Python 3.8 environment. All experiments described in section “stability of dynamical systems features” were conducted in a Python environment using the machine learning framework Scikit-learn 1.1.2. Experiments presented in section “hypothesis-free, graph-based identification of comparable RNN models” and section “hypothesis-driven identification of comparable RNN models” were implemented in the R 4.2.3 environment using igraph package (version 1.4.1) to build the graph used to identify comparable RNN models.
• •Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.

Experimental model and study participant details

All experiments in this study were performed in silico. No additional data were collected from participants. No new participants were recruited for this study. No human, animal, in vitro, or genetic experiments were conducted in this study. No additional approval from the local ethics committee was required. The dataset used in this study contain 132 records (after preprocessing), including 46 participants with SCZ (28 male, 18 female, mean age 38.2 years, standard deviation 11.3), 44 participants with MDD (19 male, 25 female, mean age 35.5 years, standard deviation 11.2), and 42 healthy participants (22 male, 20 female, mean age 36.5 years, standard deviation 12.5). Demographic details can be found in Table S1. The use of these data in this project is consistent with the intended use for which they were permitted and consented to during collection. All participants were informed about the study procedures and potential risks associated with the fMRI scan both orally and in writing before providing written informed consent. All participants were free to withdraw from the study at any time. The Medical Faculty Mannheim (Medical Ethics Committee II) at the Ruprecht-Karls-University of Heidelberg approved the study (Approval Number: 2019-733N).

Method details

Dataset for pipeline implementation and evaluation

In this study, we used resting-state fMRI data to build a pipeline for individual level dynamical feature extraction via RNNs and evaluate the performance of the extracted dynamical features in a diagnostic prediction task. The dataset originally contained resting-state fMRI data from 147 individuals. The raw data (blood-oxygen-level-dependent fMRI with an echo-planar-imaging sequence) for each participant was collected using the 3 Tesla Siemens Prisma^fit scanner with a 64-channel head coil (Siemens). The scanning parameters were set as follows: multiband acceleration factor 6, echo time (TE) 38.2ms, 60 oblique slices per volume, voxel dimensions 2.4 × 2.4 × 2.4mm³, repetition time (TR) 800ms, 31° flip angle, 204mm field of view and 64 × 64 in-plane resolution. During the scan, participants were instructed to keep their eyes open, relax, and refrain from engaging in any specific mental activity. The task duration was 7 min and 8 s, comprising 525 whole-brain scans, while a gray background with a fixation cross was presented. We then parcellated and extracted BOLD signals from 19 predefined ROIs based on the Harvard-Oxford Atlas³⁵ (2mm cortical probabilistic masks thresholded at 25 percent, as distributed with FSL), with each ROI having a BOLD signal dimension of 525 × 1. Further preprocessing steps were performed using fMRIprep package,⁴⁵ including skull-stripping, co-registration, slice-time correction, resampling, head-motion correction, realignment, normalization, and smoothing with a 6mm FWHM filter. Inconsistent data were also removed during this pipeline. Of the remaining 132 records, 46 were patients with SCZ, 44 patients with MDD, and 42 HCs. The remaining data were then processed using a down-sampling method to accelerate the training speed. (See “data down-sampling and model tuning” section). Apart from the above methods, no additional aggregation or windowing methods were performed. Demographic details can be found in Table S1. The details of the 19 ROIs investigated in the present study are listed in Table S2.

Piecewise Linear Recurrent Neural Networks model for dynamics reconstruction and feature extraction

In this study, the PLRNN model^27,33,34 was applied to reconstruct and analyze the dynamical system properties of fMRI data and to extract features that describe properties of the dynamical systems.

The architecture of the vanilla PLRNN model can be divided into two parts, the latent layer (state space model) and the observable layer (observation model). The latent layer is designed to learn and reconstruct the temporal evolution of the dynamical states based on the signals passed to it by the observable layer. The observable layer is responsible for mapping the latent dynamics in the model’s state space to the observed signals, and thus also enabling the unsupervised inference of the former from the latter.³³ A standard hidden layer can be defined by the following Equation:

$$z_t=A{z}_{t-1}+W\varphi \left(z_{t-1}\right)+C{s}_t+h+{\epsilon }_t$$ (Equation 1)

where z_t and z_t−1 represent latent state vectors at time t and t−1, respectively, each of size M × 1. The value of M corresponds to the dimension of the latent space, which is considered as a hyperparameter and needs to be set by the user. Matrix A (M × M) is a diagonal auto-regression weights matrix and matrix W (M × M) is an off-diagonal connection weights matrix. ϕ(x) denotes the nonlinear activation function ReLU(x) = max(0,x). C (M×K) is the coefficient matrix used to modulate s_t (K × 1), a time-dependent external signal vector with K channels at time t (if available). This external signal typically represents external stimuli presented during a cognitive task. h (M × 1) represents a constant bias vector and ε_t (M × 1) is a white Gaussian noise vector with 0 mean and covariance matrix Σ (ε_t ∼ N(0,Σ)).³³ On the other hand, we used a modified version of the observable layer proposed by Koppe et al.,^29,33 defined as:

$$x_t=B(hrf\ast z_{\tau :t})+J{r}_t+{\eta }_t$$ (Equation 2)

where x_t represents the generated temporal signal vector at time point t, with a size of N × 1, where N is the number of channels equal to the observed temporal signal used for training. Matrix B (N×M) denotes regression coefficients responsible for mapping the convolved latent states from latent space to observable space. hrf ∗ z_τ:t denotes convolution between time-lagged latent states z_τ:t (latent states in several previous time steps) with the Hemodynamic Response Function (HRF). In addition, artifact data with R channels (e.g., motion/physiological artifact data) are also considered in this layer as vector r_t (R × 1) along with the corresponding learnable weight matrix J (N × R). η_t is a noise vector at the observable layer that follows a normal distribution with a mean of 0 and a covariance matrix Γ (η_t ∼ N(0,Γ)).^29,33

In this study, we employed the PLRNN model implemented on the MATLAB platform.²⁹ The optimization (training) process is based on the EM algorithm, which iterates between an expectation steps, in which states are estimated given a fixed set of parameter estimates, and a maximization step, in which model parameters are updated, until convergence. Additional information and derivations of the EM algorithm for PLRNN training have been provided in previous study (e.g., see ref.³³).

Our primary focus in this study was to acquire robust individual-level dynamical features by applying two feature aggregation methods to dynamical features extracted from six independent training repetitions. To ensure that the quality of the final aggregated features was not contaminated by possible low-quality source features from each repetition, we implemented a pre-selection step in each training repetition. During each training repetition, we independently trained three models in parallel for each participant in the dataset. The decision to train only three models, rather than more, was based on time constraints and the limitations of computing power. From three models trained for each participant, we filtered out poorly converged models and retained only one model for future downstream analysis.

In this project, we followed the same approach as taken by previous studies, which use three metrics to evaluate the reconstruction (training) quality of the PLRNN model: Mean Square Error (MSE), Power Spectrum Correlation (PSC), and Kullback-Leibler Divergence (KLX). The details and effectiveness of these metrics have already been demonstrated in previous studies.^27,29,33 For MSE, we calculated the mean squared error between the 20-steps ahead generated signals by PLRNN model and the ground truth signals. The PSE evaluates the similarity between the generated signals and the observed signals in the frequency domain by computing the correlation coefficient of their power spectrum. A higher correlation indicates that the signals generated by the model are more similar to the real signals in the frequency domain. For KLX, it directly evaluates whether important properties of the generated dynamical system (e.g., attractors) match the real system in terms of geometry in state space. It provides a way to assess how well the hidden layer captures long-term dynamical features of the real system when run in ‘generative’ mode (without receiving information about the actual observations).^27,29,33 Since there are a large number of models waiting to be evaluated, manual case-by-case analysis and selection are not feasible. Therefore, we used a simple and direct overall score, which is the combination of all three metric scores (KLX + MSE + (1 - PSC), to rank and select the models in batches.

The MATLAB code for extracting these features has already been made available by Koppe et al. in a previous study.²⁹ Each dynamical system feature is calculated based on the internal parameter matrices of both the latent and observable parts of the model, corresponding to a numerical value that represents a certain feature of the reconstructed dynamics. For example, features such as F01, F02, and F10 quantify the presence of stable/unstable fixed points and cycles within the dynamics. In the dynamical state space, fixed points and cycles are examples of crucial dynamic phenomena such as attractors (if stable), repellors (if unstable), or saddles (if half-stable). Consequently, they offer valuable global insights into the states within the reconstructed dynamics. Additionally, features such as F03 and F04, which are computed based on the eigenvalues of the transition matrix around the fixed points, quantify the type and stability of the fixed points (i.e., whether they are attractors, repellors, saddles, or spiral points, for instance).

Data down-sampling and model tuning

We faced several challenges while constructing the pipeline since the PLRNN model was originally designed for a different fMRI dataset with different settings during data collection (e.g., scanning time, repetition time, etc.) and preprocessing methods (e.g., utilizing a different atlas and noise reduction methods) compared to the INDICATE dataset used in this study.

Our first challenge was the long duration of the training process, which is mainly due to two reasons: 1) The EM algorithm used for PLRNN is a second-order method, which can numerically provide a more precise solution but has higher computational cost. 2) The inclusion of the HRF function further increases the time required to estimate the state covariance matrices. These factors significantly prolong the training process, especially when using fMRI data with a low TR. For example, training with the demo data (TR = 3.0s) from the previous PLRNN project,²⁹ which has a similar data structure as the INDICATE dataset, took only about 10–15 min per participant. However, when training with our INDICATE data (TR = 0.8s), it took approximately 10–25 h per participant. Therefore, we decided to address this problem with down-sampling techniques to reduce the size of the data matrix. Among the three down-sampling approaches, uniform sampling, max pooling, and average pooling, we chose average pooling. In average pooling, each signal is divided into non-overlapping regions (based on the step size) in the temporal dimension. The average value of the signal within each region is then considered as the down-sampled value for that region. However, down-sampling always leads to information loss. To reduce training time while maintaining reconstruction quality, we tested down-sampling the data with step sizes of 2, 3, and 4, corresponding to equivalent TR values of 1.6s, 2.4s, and 3.2s, respectively. We ultimately selected the down-sampled data with a step size of 3 (equivalent TR of 2.4s, with dimension of 175 × 1 per ROI) as the default setting for the next phase since it resulted in fewer models that did not converge and outperformed the other two options in terms of the three metrics. Second, in order to speed up the convergence speed of the model during the training process, we referred to previous studies on the PLRNN model and performed standardization of the data before feeding them into the model for training.

Finally, the PLRNN model, like other machine learning models, requires a process for hyperparameter tuning. In the current MATLAB version of PLRNN, there are two important hyperparameters that need to be tuned: the λ value to control regularization during training and the dimension of the dynamical state space Z (hidden space). Referring to previous studies on the application of PLRNN models,^27,29,33 we determined the search space for these two hyperparameters as $\lambda \in \left\{0,10,{10}^2,{10}^3,{10}^4,{10}^5\right\}$ and $\mathrm{Z}\in \left\{6,7,8,9,10,11,12\right\}$. In the end, based on the grid search experiment and overall metric scores, we selected the combination of M = 7 and λ = ${10}^4$ as the default hyperparameter setting in this study.

Quantification and statistical analysis

In this study, we used MSE, PSC, and Kullback-Leibler Divergence (KLX) to evaluate the quality of the PLRNN model. The detailed definitions of these three metrics can be found in the referenced literature.^27,29,33 We used the ROC-AUC (area under the curve) score as the main metric to evaluate the performance of the machine learning classifiers (RF). Additionally, the statistical significance of the classification results was evaluated using the two-sided Fisher’s Exact Test, with p < 0.05 indicating a statistically significant difference. Table S1 lists the demographic details of the fMRI dataset used in this study, and the statistical significance of the participants’ age and sex in the dataset was evaluated using ANOVA and the chi-square test, respectively. All calculations were conducted using MATLAB 8.5.0 R2015a, R 4.2.3, and Python 3.8 environments.

Published: July 22, 2024