IRIME: Mitigating exploitation-exploration imbalance in RIME optimization for feature selection

Jinpeng Huang; Yi Chen; Ali Asghar Heidari; Lei Liu; Huiling Chen; Guoxi Liang

doi:10.1016/j.isci.2024.110561

. 2024 Jul 22;27(8):110561. doi: 10.1016/j.isci.2024.110561

IRIME: Mitigating exploitation-exploration imbalance in RIME optimization for feature selection

Jinpeng Huang ¹, Yi Chen ^1,^∗, Ali Asghar Heidari ², Lei Liu ³, Huiling Chen ^1,^5,^∗∗, Guoxi Liang ^4,^∗∗∗

PMCID: PMC11334803 PMID: 39165845

Summary

Rime optimization algorithm (RIME) encounters issues such as an imbalance between exploitation and exploration, susceptibility to local optima, and low convergence accuracy when handling problems. This paper introduces a variant of RIME called IRIME to address these drawbacks. IRIME integrates the soft besiege (SB) and composite mutation strategy (CMS) and restart strategy (RS). To comprehensively validate IRIME’s performance, IEEE CEC 2017 benchmark tests were conducted, comparing it against many advanced algorithms. The results indicate that the performance of IRIME is the best. In addition, applying IRIME in four engineering problems reflects the performance of IRIME in solving practical problems. Finally, the paper proposes a binary version, bIRIME, that can be applied to feature selection problems. bIRIMR performs well on 12 low-dimensional datasets and 24 high-dimensional datasets. It outperforms other advanced algorithms in terms of the number of feature subsets and classification accuracy. In conclusion, bIRIME has great potential in feature selection.

Subject areas: Computing methodology, Artificial intelligence, Engineering

Graphical abstract

Highlights

•
This study introduces the SB and CMS-RS into RIME, named IRIME
•
IRIME addresses the drawbacks of balance between exploration and exploitation
•
IRIME performs well in benchmark functions and real-world engineering problems
•
IRIME has outstanding performance in feature selection

Computing methodology; Artificial intelligence; Engineering

Introduction

In engineering design optimization problems, balancing resource allocation and constraint conditions is often challenging.¹ When facing real-world problems, the optimization process frequently involves multiple variables and diverse constraints, significantly increasing the difficulty of optimization.² Engineering optimization also often considers factors such as performance and cost, leading to complex problems with multiple variables and objectives. Among optimization problems, feature selection is a problem widely investigated by scholars, especially in today’s era of rapid information growth, where data abundance leads to issues like data redundancy, high computational costs, and weakened model generalization abilities. Feature selection plays a crucial role in reducing computational expenses, simplifying models, and enhancing their generalization capabilities. Commonly used feature selection methods include filter, wrapper, and embedded methods.³^,⁴^,⁵^,⁶ Filter methods primarily determine the importance of features to the target variable based on statistical properties between features or the relationship between feature variables and target variables. While filter methods can be independently analyzed without involving machine learning, they overlook other connections between features. Embedded methods, although capable of uncovering complex relationships between features, require consideration of intricate parameters and structures and are influenced by the machine learning model. Meanwhile, wrapper methods, favored by many researchers because of their straightforward nature and ease of implementation, face a challenge when dealing with an n-dimensional feature dataset, resulting in possible combinations of features.⁷^,⁸ Faced with such complex computations, researchers have started using metaheuristic algorithms as a feasible solution for wrapper methods.

Heuristics are problem-solving strategies that use basic principles or shortcuts to quickly uncover approximate answers, generally valuing speed above accuracy.⁹^,¹⁰^,¹¹^,¹²^,¹³ Metaheuristics, on the other hand, work at a higher abstraction level, directing the search of solution spaces.¹⁴ They enable the search of optimum or nearly optimal solutions across several issue domains by continually refining and adapting heuristic techniques, so overcoming the constraints of individual problem settings.¹⁵ Metaheuristic algorithms represent advanced optimization techniques that simulate certain biological or physical phenomena found in nature. These algorithms can generally be categorized into physics-based, swarm intelligence-based, and evolution-inspired. Physics-based metaheuristic algorithms, such as the sine cosine algorithm (SCA),¹⁶ RUNge Kutta optimizer (RUN),¹⁷ weighted mean of vectors (INFO),¹⁸ simulated annealing (SA),¹⁹ gravitational search algorithm (GSA),²⁰ and rime optimization algorithm (RIME),²¹ draw inspiration from different natural entities. SCA is inspired by trigonometric functions like sine and cosine, simulating their properties for the search process. SA is inspired by material cooling from high temperatures to a stable state, involving the probabilistic selection of optimal solutions. Newton’s law of universal gravitation inspires GSA. The algorithm is modeled based on this concept, with individual fitness values treated as mass in the gravitational formula. An adaptive gravitational constant is introduced into GSA. RIME simulates the growth of rime-ice in nature, modeling both soft-rime and hard-rime and eventually incorporating a greedy selection strategy. Swarm intelligence-based metaheuristic algorithms have seen rapid development, featuring algorithms like particle swarm optimizer (PSO),²² water cycle algorithm (WCA),²³ gray wolf optimizer (GWO),²⁴ hunger games search (HGS),²⁵ slime mold algorithm (SMA),²⁶^,²⁷ Harris hawks optimizer (HHO),²⁸ moth-flame optimization (MFO),²⁹ liver cancer algorithm (LCA),³⁰ parrot optimizer (PO),³¹ colony predation algorithm (CPA),³² among others. SMA draws inspiration from the foraging process of slime mold, including aspects like capturing, encircling, and approaching food. HHO mathematically models the soft besiege (SB) and hard besiege processes of Harris hawks. MFO involves the mathematical modeling of moths’ attraction to flames. In MFO, the number of flames is adjusted based on the iteration count, and flames are selected according to their fitness values. The author models moths’ spiraling flight behavior when they are close to flames. Evolution-inspired metaheuristic algorithms primarily include differential evolution (DE),³³ genetic algorithm (GA),³⁴ and biogeography-based optimization (BBO).³⁵ DE operates through mutation, crossover, and selection operations, guiding individuals toward potentially better solutions. GA treats each individual as a chromosome, facilitating genetic operations among chromosomes to achieve search outcomes. BBO models migration and mutation in biogeography, relying on migration probability for population updates. These algorithms possess robust optimization capabilities and are expected to demonstrate superior performance in various applications such as fault identification,³⁶ vehicle communication,³⁷ text privacy,³⁸ hemodialysis prediction,³⁹ target tracking,⁴⁰ economic emission,⁴¹^,⁴² and intrusion detection.⁴³

As scholars delve into the study of metaheuristic algorithms, numerous outstanding variants have emerged and been successfully applied in various domains.⁴⁴^,⁴⁵^,⁴⁶^,⁴⁷ Ozsoydan et al.⁴⁸ modified the mutation mechanism of elite wolves, proposing a new variant of GWO that effectively tackled multiple combinatorial problems and the 0–1 knapsack problem. Dhargupta et al.⁴⁹ utilized spearman’s rank correlation coefficient to determine whether wolf packs engage in opposition learning, enhancing the convergence speed and capability of populations within GWO. Deng et al.⁵⁰ divided the SMA into two populations dynamically, adjusting population sizes to balance the algorithm’s exploitation and exploration capabilities and successfully applying it to real-world engineering problems. Samantaray et al.⁵¹ combined SMA with PSO, successfully applying this hybrid approach to predict flood flow rates. Tan et al.⁵² combined the whale optimization algorithm (WOA) with the equilibrium optimizer, validating its performance on benchmark test sets. Wang et al.⁵³ enhanced population diversity in WOA by reducing intra-population similarity, ultimately applying it to multi-threshold image segmentation tasks. Kumar et al.⁵⁴ augmented the global search capability of HHO through opposition learning, successfully addressing multi-objective hydrothermal power generation scheduling problems. Tian et al.⁵⁵ proposed a novel initialization method, incorporating elite opposition learning to improve HHO populations, ultimately applying it to engineering problems. Tiwari et al.⁵⁶ addressed issues such as poor population diversity and inadequate exploration capabilities in DE. They improved DE by incorporating ideas from PSO to enhance its global search ability. Additionally, they changed the crossover rate of DE, proposing a new crossover rate, and introduced a new selection method to further promote DE’s convergence capabilities, successfully applied to engineering design optimization problems. Pham et al.⁵⁷ proposed a strategy of opposition learning and roulette selection to improve the global optimization capability of SCA. The enhanced SCA maintains a balanced exploration and exploitation similar to the original SCA but with increased stability, ideal for challenging real-world optimization problems. Huang et al.⁵⁸ combined various strategies, including Nelder-Mead simplex, opposition learning, and spiral strategy, to enhance beluga whale optimization (BWO). Combining different strategies at different algorithm stages improved BWO’s performance, successfully applied it to engineering design problems, and tested it on the CEC benchmark dataset. Gomes et al.⁵⁹ proposed and compared a hybrid algorithm with GA. They applied metaheuristic algorithms to channel parameter estimation and successfully demonstrated GA’s advantages over the hybrid algorithm in channel parameter estimation. Gundogdu et al.⁶⁰ successfully applied an improved GWO to photovoltaic systems. They improved GWO to escape local optima, enhancing performance in photovoltaic system applications. Yu et al.⁶¹ improved the teaching-learning-based optimization algorithm (TLBO) using reinforcement learning to enhance TLBO’s update phase, successfully applied to wind farm data problems. Moustafa et al.⁶² applied mantis search algorithm (MSA) to economic dispatch in combined heat and power systems, drawing inspiration from collective intelligence of mantises. Al-Areeq et al.⁶³ utilized a hybrid two-population intelligence algorithm for flood hazard assessment. Tu et al.⁶⁴ combined GWO and HHO into HGWO, improving collective search ability, convergence speed, and accuracy compared to GWO, applied to real-world engineering problems. Combining optimization algorithms is a crucial approach to improving metaheuristic algorithms. Silva et al.⁶⁵ combined ant colony optimization (ACO) and GA, enhancing ACO’s convergence capability and mitigating the algorithm’s tendency to get stuck in local optima, applied to sustainable solution problems. Moreover, metaheuristic algorithms have found extensive applications in the domain of feature selection.

Peng et al.⁶⁶ adopted hierarchical strategies to enhance HHO, conducting feature selection on both low and high-dimensional datasets. Yu et al.⁶⁷ improved WOA using various strategies, including sine initialization and employed a kernel extreme learning machine as a classifier for feature selection. AbdelAty et al.⁶⁸ utilized chaos theory to boost the convergence capability of the hunter-prey optimization algorithm, successfully applying it to feature selection. Al-Khatib et al.⁶⁹ enhanced lemurs optimization by integrating local search strategies and opposition learning, evaluating feature selection performance on UCI datasets. Zaimoglu et al.⁷⁰ employed different chaos learning methods to improve the herd optimization algorithm and conducted feature selection tests across multiple classifiers. Chhabra et al.⁷¹ improved bald eagle search by incorporating three distinct enhancement strategies at different stages of algorithm execution, successfully applying them to feature selection. Pan et al.⁷² improved the initialization strategy of GWO and enhanced GWO using differential and competition-guided strategies for feature selection in high-dimensional data. Askr et al.⁷³ used various strategies to enhance the exploration and exploitation capabilities of the golden jackal optimization (GJO) algorithm. They proposed a binary form of GJO and tested it for feature selection on multiple high-dimensional datasets. Wang et al.⁷⁴ made improvements to the transfer function, introducing a new function specifically targeting the deficiencies of the GWO in handling feature selection problems. They applied different enhancement methods to elite and ordinary wolves within the population to enhance the balance between exploration and exploitation in GWO. Ye et al.⁷⁵ enhanced the optimization capability of the hybrid breeding optimization using the elite opposition mechanism and Levy flight strategy. They combined different classifiers for intrusion detection feature selection problems. Yang et al.⁷⁶ focused on feature space, dividing it into regions and proposing a new initialization strategy. They successfully applied the golden eagle optimizer to solve feature selection problems in medium to small-dimensional spaces. Chakraborty et al.⁷⁷ improved the WOA using a horizontal crossing strategy and collaborative hunting. They introduced a binary version of WOA and combined it with the K-nearest neighbor for feature selection on UCI datasets. Abdelrazek et al.⁷⁸ incorporated different chaotic mappings into the dwarf mongoose optimization algorithm (DMO), enabling DMO to better adapt to wrapper-based feature selection methods. The improved algorithm was validated on various UCI datasets, demonstrating competitive performance compared to other metaheuristic algorithms. Mostafa et al.⁷⁹ used spider wasp optimization to enhance DE, improving DE’s problem-solving capabilities and incorporating methods to enhance solution quality, specifically applied to feature selection. As per the no free lunch (NFL)⁸⁰ theorem, no single algorithm can address all feature selection tasks, especially in complex optimization environments, where RIME tends to get stuck in local optima and encounter slow convergence issues. Hence, this paper develops a variant of RIME to enhance its performance in complex optimization environments and with intricate datasets. RIME, a new algorithm proposed by Su in 2023,²¹ has seen limited use in feature selection studies.

Research and application of RIME is underway. Yu et al.⁸¹ combined the triangular game search strategy and random follower search strategy to improve RIME, enhancing its global search capability and inter-population information exchange capabilities. The enhanced RIME was then applied in the diagnostic process of pulmonary hypertension. Yang et al.⁸² applied the improved RIME in photovoltaic systems to maintain temperature stability. Zhong et al.⁸³ improved RIME by utilizing Latin hypercube sampling and distance-based selection mechanisms and enhanced the hard-rime process, ultimately applying the improved RIME to engineering design problems. Zhu et al.⁸⁴ improved RIME using the Gaussian diffusion and interactive mechanism strategy, which effectively solved multi-threshold image segmentation problems. Li et al.⁸⁵ also applied the improved RIME in multi-threshold image segmentation.

In this paper, to further enhance the capability of RIME in feature selection applications, we introduced SB, composite mutation strategy, and restart strategy (CMS-RS) into RIME, naming it IRIME. SB expands the search space of RIME, increases population diversity in the early stage, and effectively prevents the problem of local optima caused by greedy strategies. Additionally, CMS encourages more in-depth exploitation at the current position of RIME, to some extent, enhancing RIME’s exploitation abilities. RS keeps an eye on whether RIME falls into local optima and restarts when it does. The combination of these mechanisms involves adaptive parameters and does not run in a singular form like classical PSO and DE, but instead has multiple optimization methods. In sum, the combination of these approaches balances the exploration and exploitation abilities of RIME. To validate IRIME’s performance, this study conducted tests on the IEEE CEC 2017 benchmark tests and compared them with other advanced algorithms, demonstrating significant advantages for IRIME. In addition, IRIME’s performance in engineering design problems also reflects its ability to solve practical problems. Finally, it applied to feature selection in low-dimensional and high-dimensional datasets. In summary, this paper’s primary contributions encompass.

•
Proposed a variant of RIME named IRIME.
•
This paper effectively enhances the population diversity of RIME by using SB, expands the search space, and enhances the exploratory ability.
•
This paper integrates CMS-RS to improve the exploitation capacity of RIME and explores new solutions when stuck in a local optimum.
•
IRIME has demonstrated excellent performance in IEEE CEC 2017 benchmark functions and demonstrated the ability to solve practical problems in engineering design.
•
The paper proposes a binary version of IRIME applied to feature selection problems, which respectively achieves good results on high- and low-dimensional datasets.

Results and discussion

Experimental design and analysis of results

A series of systematic experiments were conducted in this study to validate the efficacy of the RIME variant. The IEEE CEC 2017 benchmark functions were utilized,⁸⁶ comprising functions categorized into four types: simple unimodal (F1-F3), simple multimodal (F4-F10), hybrid (F11-F20), and composite functions (F21-F30),⁸⁷ as shown in Table 1. The IEEE CEC 2017 benchmark functions were a set of standard functions used during the 2017 IEEE congress on evolutionary computation for evaluating the performance of evolutionary algorithms and other optimization algorithms.⁸⁸^,⁸⁹ These functions are designed to test different optimization problem settings and have undergone extensive research and validation to ensure that they pose a certain level of complexity and diversity, effectively evaluating the performance of optimization algorithms. The experiments involved historical trajectory analysis, balance and diversity analyses of IRIME, stability analysis, and ablation studies. A comparison was made against 13 conventional algorithms and 11 advanced algorithms. In addition, apply IRIME to 4 practical engineering problems to verify its ability to solve engineering problems. Finally, it was applied to 12 low-dimensional and 24 high-dimensional datasets to validate its performance in feature selection. To ensure statistical significance in the experimental results, non-parametric statistical tests such as the Wilcoxon signed-rank test⁹⁰ were employed, with a significance level set at 0.05. Additionally, average (AVG) and standard deviation (STD) analyses were used, and ranking was conducted using the Friedman test.⁹¹ In testing the IEEE CEC 2017 benchmark function, all experiments referred to previous research to minimize bias as much as possible.

Table 1.

IEEE CEC 2017 benchmark functions (Search Range: ${[- 100, 100]}^{D}$ )

Class	No.	Functions	Optimum
Unimodal	F1	Shifted and Rotated Bent Cigar Function	100
	F2	Shifted and Rotated Bent Sum of Different Power Function	200
	F3	Shifted Rotated Zakharov Function	300
Multimodal	F4	Shifted and Rotated Rosenbrock’s Function	400
	F5	Shifted and Rotated Rastrigin’s Function	500
	F6	Shifted and Rotated Expanded Scaffer’s F6 Function	600
	F7	Shifted and Rotated Lunacek Bi_Rastrigin’s Function	700
	F8	Shifted and Rotated Non-Continuous Rastrigin’s Function	800
	F9	Shifted and Rotated Levy Function	900
	F10	Shifted and Rotated Schwefel’s Function	1000
Hybrid	F11	Hybrid Function 1 (N = 3)	1100
	F12	Hybrid Function 2 (N = 3)	1200
	F13	Hybrid Function 3 (N = 3)	1300
	F14	Hybrid Function 4 (N = 4)	1400
	F15	Hybrid Function 5 (N = 4)	1500
	F16	Hybrid Function 6 (N = 4)	1600
	F17	Hybrid Function 6 (N = 5)	1700
	F18	Hybrid Function 6 (N = 5)	1800
	F19	Hybrid Function 6 (N = 5)	1900
	F20	Hybrid Function 6 (N = 6)	2000
Composition	F21	Composition Function 1 (N = 3)	2100
	F22	Composition Function 2 (N = 3)	2200
	F23	Composition Function 3 (N = 4)	2300
	F24	Composition Function 4 (N = 4)	2400
	F25	Composition Function 5 (N = 5)	2500
	F26	Composition Function 6 (N = 5)	2600
	F27	Composition Function 7 (N = 6)	2700
	F28	Composition Function 8 (N = 6)	2800
	F29	Composition Function 9 (N = 3)	2900
	F30	Composition Function 10 (N = 3)	3000

Open in a new tab

The experiments in this study were conducted using MATLAB R2020a on a system running the Windows 11 operating system, powered by an Intel(R) Core(TM) i5-12400 12th generation processor clocked at 2.50 GHz. The relevant parameters for the algorithms tested alongside IRIME are listed in Table 2.

Table 2.

The parameters of the algorithm involved

Algorithm	Parameters
RIME	$w = 5$ , $E = \sqrt{t / T}$
SCA	$c_{1} = r a n d$ , $c_{2} = r a n d$ , $l = 2$
WOA	$b = 1$ , $r_{1} = r a n d$ , $r_{2} = r a n d$
DE	$b e t a \in [0.2, 0.8]$ , $p c r = 0.2$
SSA	$c_{1} = r a n d$ , $c_{2} = r a n d$ , $l = 2$
PSO	$w_{\max} = 0.9$ , $w_{\min} = 0.2$ , $c_{1} = c_{2} = 2$
MFO	$b = 1$ , $a = - 1 + F E s (- 1 / M a x F E s)$ , $t = (a - 1) r a n d + 1$
GWO	$r_{1} = r a n d$ , $r_{2} = r a n d$ , $a = 2 - F E s (2 / M a x F E s)$
BA	$Q_{\min} = 0$ , $Q_{\max} = 2$
CS	$b e t a = 1.5$ , $p a = 0.25$
FA	$α = 0.5$ , $b e t a_{\min} = 0.2$
CPA	$a = \exp (9 - 18 F E s / M a x F E s)$ , $S 0 = a (1 - F E s / M a x F E s)$
HHO	$c = 2 (1 - (F E s / M a x F E s))$ , $E s c a p i n g_E n e r g y = c (2 r a n d - 1)$
EBOwithCMAR	$m e m o r y s i z e = 6$
LSHADE_cnEpSi	$p b = 0.4$ , $p s = 0.5$
ALCPSO	$w = 0.4$ , $c_{1} = 2$ , $c_{2} = 2$ , $T = 2$
CLPSO	$c = 1.49445$
LSHADE	$p_b e s t_r a t e = 0.11$ , $\max_p o p s i z e = p o p s i z e$
SADE	$n u m s t = 4$
JADE	$c = 0.1$ , $c r m = 0.5$ , $f m = 0.5$
RCBA	$Q_{\min} = 0$ , $Q_{\max} = 2$
EPSO	$n s i z e = 3$ , $L P = 50$
CBA	$Q_{\min} = 0$ , $Q_{\max} = 2$
LWOA	$b = 1$ , $b e t a = 1.5$

Open in a new tab

Qualitative analysis of IRIME

Analysis of historical search trajectories

In Figure 1, F1 represents a unimodal function. Observing Figures 1B and 1D, it is apparent that IRIME converges to smaller fitness values. Moreover, the sudden increase in the average fitness of all agents in later iterations is due to the CMS-RS initiating a restart upon identifying local optima, thereby exploring new solutions and enhancing the possibility of discovering potential solutions. In Figure 1A, the red dots indicate the positions where the best solution has been found so far, while the black dots represent the trajectory points during the search. Initially, individuals are randomly distributed in the solution space, but with IRIME iterations, they gradually approach the peak of the unimodal function. In Figure 1C, the one-dimensional trajectory also shows that IRIME has a broader search space in both the initial and final stages than RIME. In the middle stage of IRIME, there is a bias toward exploitation: initially influenced by SB and later influenced by RS, with CMS contributing more to exploitation in the middle stage. For functions F4-F10, representing simple multimodal functions, Figure 1A shows that IRIME’s individuals are distributed across each peak at the onset. Gradually, IRIME discovers better peaks and exploits them. In Figures 1B and 1D, IRIME consistently achieves better fitness values than RIME. When IRIME gets stuck in local optima, the CMS-RS opens up new spaces. Figure 1C also indicates that IRIME initially explores multiple peaks and gradually converges to a better peak, which is evident in the selected region, which shows better fitness values than RIME. Similarly, in composite functions F21 and F22, IRIME initially exhibits a larger search space than RIME and converges to better fitness values later, discovering regions where RIME fails to reach.

The history trajectory analysis for IRIME

(A) The search trajectory of IRIME, (B) Average fitness of IRIME, (C) One-dimensional trajectory of IRIME, (D) convergence curves for IRIME (red) and RIME (blue).

Balance and diversity analysis

This section utilizes the IEEE CEC 2017 benchmark functions to evaluate the balance and diversity of IRIME and RIME. As depicted in Figures 2 and 3, the blue line represents the algorithm in an exploitation phase, the red line illustrates the algorithm in an exploration phase, and the green line indicates an increasing trend when the exploration outweighs the exploitation or a decreasing trend otherwise. As shown in the graphs for unimodal functions F2 and F3, the variant of RIME proposed in this paper, IRIME, tends to be explored more extensively in the early stages. This appropriate increase in the exploration phase expedites the algorithm’s convergence and mitigates the susceptibility to local optima. In contrast, RIME spends less time exploring F2 and F3, particularly with only 1.6321% in F2. This results in slow convergence of the algorithm in unimodal functions. However, the integration of SB effectively enhances IRIME’s exploratory capability, accelerating convergence. As observed in the diversity graph, IRIME’s individuals are initially distributed across a broader space due to SB’s influence, leading to higher diversity than RIME. During the mid-phase, extensive exploitation occurs, and a sudden rise in diversity toward the end is attributed to CMS-RS’s role, which detects the algorithm’s local entrapment and enhances IRIME’s precision. In the case of simple multimodal functions F8 and F10, RIME exhibits minimal exploration, especially in F10. This starkly contrasts IRIME, where the exploration capability exceeds 20%, while RIME’s exploration capability is only around 2%. Consequently, RIME is highly prone to local optima, only developing around specific peaks and failing to explore potentially more fruitful regions. The diversity curve further demonstrates that IRIME possesses greater initial population diversity and engages in substantial exploitation in the mid-phase, and after exploitation stagnation, IRIME attempts to break out of local optima to find better solutions. For hybrid functions F13, F15, and F20, RIME only explores about 1%, whereas IRIME explores more extensively. Additionally, the population’s diversity increases. CMS-RS also plays a role in discovering better solutions in the later phase. A similar pattern emerges for functions F21, F23, and F29, where RS and CMS-RS balance the exploration and exploitation capabilities of the original RIME, increasing population diversity and enhancing convergence accuracy. This also empowers IRIME to escape local optima. In conclusion, the combination of SB and CMS-RS equips IRIME with superior balance and diversity, allowing it to escape local optima more effectively.

Algorithm diversity analysis for IRIME and RIME

Parameter sensitivity experiment

The selection of parameters critically influences algorithm’s performance; therefore, conducting a parameter sensitivity analysis is essential.⁹² This analysis evaluates how different parameter values affect the performance of the algorithm, thereby optimizing algorithm efficiency and ensuring robustness under various conditions.⁹³^,⁹⁴ In this paper, most parameters used in IRIME are supported by theoretical or empirical justifications from original papers. The only point of contention is the threshold at which the restart strategy in CMS-RS begins to execute. As mentioned earlier, the threshold is set at 50. To verify the appropriateness of this threshold, this paper conducted experiments at threshold values of 30, 50, and 100, represented as IRIME30, IRIME50, and IRIME100, respectively.

The experimental results are shown in Table 3. The symbols “+/ = /-” represent whether IRIME performs significantly better, equal to, or worse than other algorithms in this experiment on the Wilcoxon signed-rank test. From the table, it can be seen that the choice of threshold affects the overall performance of IRIME. However, the differences are not pronounced for most functions. As per the results, the performance difference between IRIME30 and IRIME50 is insignificant in 19 functions, while between IRIME100 and IRIME50, the difference is insignificant in 18 functions. On the whole, the overall performance of the IRIME algorithm is better when the threshold is set at 50. As shown in the table, the average ranking of IRIME50 is smaller, with a final score of 1.7.

Table 3.

Comparison results between IRIME and IRIMEs

Overall Rank
Algorithm	Rank	+/ = /-	Avg
IRIME50	1	∼	1.7
IRME30	3	10/19/1	2.4
IRIME100	2	7/18/5	1.866667

Open in a new tab

The influence of SB and CMS-RS

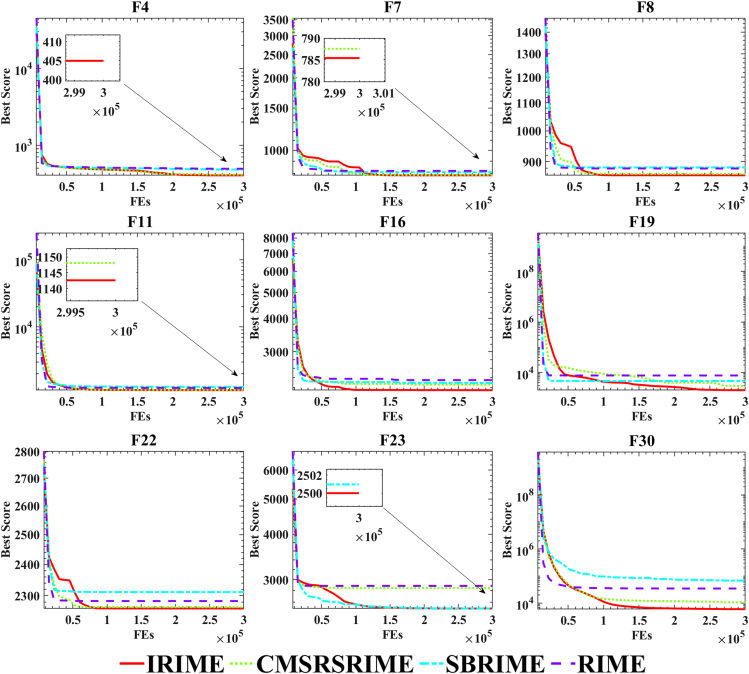
In this section, we specifically examine the precise impact of SB and CMS-RS on RIME using the IEEE CEC 2017 benchmark functions. In this experiment, the population size was set to 30, problem dimensionality was set to 30, and the maximum iteration count was 300,000. To eliminate potential incidental influences, each algorithm ran independently 30 times. SBRIME represents RIME integrated with SB, while CMSRSRIME denotes RIME integrated with CMS-RS. The symbols "+/ = /-" represent whether IRIME performs significantly better, equal to, or worse than other algorithms in this experiment on the Wilcoxon signed-rank test.

Table 4 shows that the average ranking of IRIME is 1.43333, securing the top position. This indicates that combining these two methods improves RIME in various aspects. Compared to the original RIME, 28 out of 30 benchmark functions perform better, while two functions converge to the same outcome. This suggests that the incorporation of SB and CMS-RS has not adversely affected RIME. We conducted a Friedman ranking, as depicted in Figure 4. From the Friedman ranking, it is evident that IRIME ranks first, and the algorithm’s performance improves with each additional mechanism integrated.

Table 4.

Comparison results between IRIME and RIMEs

Overall Rank
Algorithm	Rank	+/ = /-	Avg
IRIME	1	∼	1.433333
SBRIME	3	23/4/3	3.133333
CMSRSRIME	2	9/18/3	2.066667
RIME	4	28/2/0	3.366667

Open in a new tab

Table 5 presents specific comparative data of the algorithms, with bold text highlighting the best results obtained among all algorithms. It also includes convergence graphs, as depicted in Figure 5. The graph and the table show that solely incorporating SB or CMS-RS does not lead the algorithm to perform optimally. Solely adding SB enhances population diversity, boosting RIME’s exploratory capability. This improvement is evident in RIME’s performance on composite functions like F22 and F23. However, it does not manifest advantages in unimodal functions like F3 or multimodal functions like F8. Solely incorporating CMS-RS strengthens the algorithm’s performance on unimodal functions such as F1, multimodal functions like F4 and F5, and hybrid functions like F11 and F12. However, CMS-RS does not demonstrate significant effects on composite functions, mainly because it effectively improves RIME’s convergence capability, meeting the requirements for local exploitation and, to some extent, providing the ability to escape local optima. Yet, it offers less in terms of population diversity and weaker exploratory capabilities. Only through the comprehensive integration of SB and CMS-RS can IRIME achieve the top-ranking position. Additionally, Table 6 provides the algorithm’s p-values. From a statistical perspective, IRIME holds a dominant position across most functions.

Table 5.

Comparison of IRIME with RIMEs

	F1		F2		F3
	AVG	STD	AVG	STD	AVG	STD
IRIME	1.000000E+02	4.341879E-07	1.208397E+04	1.692978E+04	3.000675E+02	6.544860E-02
CMSRSRIME	1.000000E+02	6.787999E-07	9.608267E+03	2.901084E+04	3.000137E+02	1.440701E-02
SBRIME	6.912754E+03	3.342332E+03	1.903663E+04	3.287184E+04	3.019264E+02	7.738878E-01
RIME	6.740600E+03	4.683236E+03	1.725470E+04	4.617363E+04	3.016142E+02	7.393312E-01

	F4		F5		F6
	AVG	STD	AVG	STD	AVG	STD
IRIME	4.049188E+02	1.660907E+01	5.612429E+02	1.547367E+01	6.000036E+02	1.901825E-03
CMSRSRIME	4.119034E+02	2.428008E+01	5.592430E+02	1.695952E+01	6.000025E+02	1.635151E-03
SBRIME	4.822844E+02	2.432146E+01	5.940733E+02	2.538615E+01	6.008424E+02	7.132176E-01
RIME	4.934413E+02	3.982441E+01	5.792156E+02	2.035945E+01	6.003355E+02	3.274886E-01

	F7		F8		F9
	AVG	STD	AVG	STD	AVG	STD
IRIME	7.854226E+02	1.459656E+01	8.592915E+02	1.276500E+01	9.000000E+02	1.360593E-11
CMSRSRIME	7.875552E+02	1.590540E+01	8.632096E+02	1.265242E+01	9.031533E+02	9.154477E+00
SBRIME	8.092856E+02	2.294600E+01	8.825459E+02	2.181813E+01	1.832479E+03	8.498307E+02
RIME	8.196870E+02	2.584547E+01	8.795674E+02	2.032560E+01	1.300574E+03	5.075069E+02

	F10		F11		F12
	AVG	STD	AVG	STD	AVG	STD
IRIME	3.370405E+03	6.680517E+02	1.142597E+03	2.458383E+01	3.778128E+03	1.308558E+03
CMSRSRIME	3.527053E+03	4.907452E+02	1.148122E+03	2.141947E+01	3.759469E+03	1.719976E+03
SBRIME	3.618576E+03	5.236817E+02	1.276824E+03	7.583414E+01	6.747955E+06	3.731713E+06
RIME	3.402741E+03	6.191174E+02	1.231434E+03	6.460259E+01	4.432634E+06	2.177431E+06

	F13		F14		F15
	AVG	STD	AVG	STD	AVG	STD
IRIME	1.334285E+03	8.006018E+00	1.444883E+03	1.161457E+01	1.559461E+03	2.867685E+01
CMSRSRIME	1.338540E+03	9.647202E+00	1.449102E+03	1.254535E+01	1.569876E+03	3.745820E+01
SBRIME	4.021342E+03	3.087106E+03	1.564542E+03	8.300780E+01	4.034866E+03	3.706339E+03
RIME	4.693434E+03	2.467541E+03	1.504226E+03	3.706804E+01	6.473199E+03	4.852897E+03

	F16		F17		F18
	AVG	STD	AVG	STD	AVG	STD
IRIME	2.153008E+03	2.439803E+02	1.937497E+03	8.960966E+01	1.363427E+04	8.005798E+03
CMSRSRIME	2.256912E+03	2.333114E+02	1.999397E+03	1.131100E+02	1.223189E+04	1.042454E+04
SBRIME	2.290189E+03	2.808756E+02	2.041873E+03	8.707292E+01	7.422992E+04	5.051162E+04
RIME	2.348066E+03	2.163382E+02	2.026551E+03	1.694096E+02	1.018748E+05	7.327155E+04

	F19		F20		F21
	AVG	STD	AVG	STD	AVG	STD
IRIME	2.014868E+03	2.572843E+02	2.189910E+03	8.610377E+01	2.134962E+03	3.507469E+01
CMSRSRIME	2.925334E+03	3.347182E+03	2.181714E+03	9.010563E+01	2.125485E+03	3.190956E+01
SBRIME	4.612865E+03	4.464702E+03	2.361028E+03	1.289487E+02	2.207251E+03	3.255049E+01
RIME	7.662323E+03	6.550908E+03	2.290457E+03	1.005639E+02	2.214770E+03	3.275008E+01

	F22		F23		F24
	AVG	STD	AVG	STD	AVG	STD
IRIME	2.259745E+03	1.569471E+01	2.500000E+03	8.301258E-06	2.600000E+03	1.888236E-13
CMSRSRIME	2.263672E+03	1.606741E+01	2.845609E+03	1.510916E+01	3.394899E+03	1.332673E+01
SBRIME	2.311125E+03	3.239709E+01	2.500972E+03	8.935810E-01	2.600053E+03	5.355676E-02
RIME	2.282943E+03	2.054662E+01	2.884192E+03	3.074977E+01	3.360063E+03	1.826656E+02

	F25		F26		F27
	AVG	STD	AVG	STD	AVG	STD
IRIME	2.707120E+03	3.899517E+01	2.800000E+03	7.208242E-10	2.920793E+03	1.138842E+02
CMSRSRIME	2.918437E+03	2.484449E+01	5.090513E+03	1.921404E+02	3.437174E+03	3.633907E+01
SBRIME	2.700552E+03	3.402318E-01	2.800529E+03	4.689096E-01	2.902733E+03	9.562687E-01
RIME	2.965889E+03	4.976697E+01	4.887692E+03	9.898190E+02	3.547105E+03	7.414412E+01

	F28		F29		F30
	AVG	STD	AVG	STD	AVG	STD
IRIME	3.031860E+03	7.474622E+01	3.255024E+03	1.067390E+02	5.978167E+03	3.490858E+03
CMSRSRIME	4.714342E+03	8.194617E+02	3.418242E+03	1.152990E+02	1.069414E+04	4.913513E+03
SBRIME	3.000791E+03	6.112466E-01	3.109261E+03	4.379583E+00	6.810517E+04	8.243885E+04
RIME	3.350192E+03	3.439794E+02	3.545178E+03	1.500152E+02	3.456162E+04	2.103248E+04

Open in a new tab

Convergence curves of IRIME and RIMEs at IEEE CEC 2017

Table 6.

p−value of Wilcoxon signed−rank test between IRIME and other RIMEs

	F1	F2	F3	F4	F5	F6
CMSRSRIME	2.9574621307E-03	1.0746884002E-01	3.4052567233E-05	4.7794743855E-01	4.7794743855E-01	6.0350064738E-03
SBRIME	1.7343976283E-06	4.1653380739E-01	1.7343976283E-06	1.9209211049E-06	2.1630223984E-05	1.7343976283E-06
RIME	1.7343976283E-06	3.4934556237E-01	1.7343976283E-06	1.7343976283E-06	3.3788544377E-03	1.7343976283E-06

	F7	F8	F9	F10	F11	F12
CMSRSRIME	7.3432529144E-01	2.5364409755E-01	1.6367234818E-01	4.0483472216E-01	1.1092566513E-01	4.6528258188E-01
SBRIME	3.5888445045E-04	1.2505680433E-04	1.7343976283E-06	9.3675596532E-02	1.7343976283E-06	1.7343976283E-06
RIME	4.0715116266E-05	7.1570338462E-04	1.7343976283E-06	7.0356369987E-01	2.3534209951E-06	1.7343976283E-06

	F13	F14	F15	F16	F17	F18
CMSRSRIME	1.2543823903E-01	4.7794743855E-01	2.8947707171E-01	6.8713630797E-02	8.7296677536E-03	3.3885615525E-01
SBRIME	1.7343976283E-06	1.9209211049E-06	1.7343976283E-06	5.4462503972E-02	2.2248266458E-04	1.7343976283E-06
RIME	1.7343976283E-06	2.1266360107E-06	1.7343976283E-06	2.1052603409E-03	2.8485956185E-02	1.7343976283E-06

	F19	F20	F21	F22	F23	F24
CMSRSRIME	3.0861485053E-01	7.0356369987E-01	1.5885549929E-01	1.6502656562E-01	1.7343976283E-06	1.7343976283E-06
SBRIME	2.3534209951E-06	4.8602606067E-05	2.3534209951E-06	4.7292023374E-06	1.7343976283E-06	1.7343976283E-06
RIME	1.7343976283E-06	4.1955098606E-04	1.7343976283E-06	8.1877534396E-05	1.7343976283E-06	1.7343976283E-06

	F25	F26	F27	F28	F29	F30
CMSRSRIME	1.9209211049E-06	1.7343976283E-06	1.9209211049E-06	1.7333066442E-06	1.9729484516E-05	1.6046383717E-04
SBRIME	3.1123151154E-05	1.7343976283E-06	3.1123151154E-05	5.7096495243E-02	4.7292023374E-06	3.1816794110E-06
RIME	1.7343976283E-06	1.7343976283E-06	1.9209211049E-06	1.7343976283E-06	1.9209211049E-06	1.9209211049E-06

Open in a new tab

Stability testing of IRIME

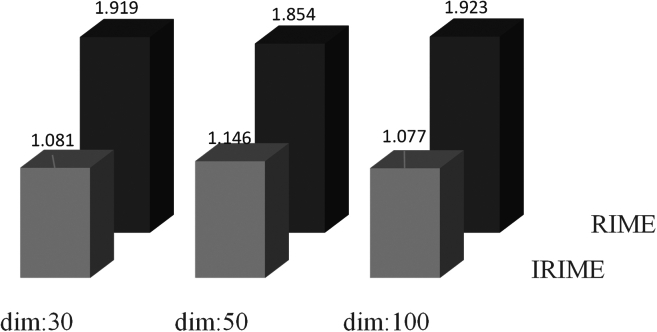
Stability experiments were conducted in this section to validate the stability of IRIME. The parameter settings remained mostly similar to the previous experiments, except for variations in dimensions (30, 50, and 100). The specific experimental data is shown in Table 7. The table shows that IRIME outperforms RIME in 30, 29, and 29 benchmark functions across different dimensions, demonstrating significantly better stability than RIME. Particularly on functions like F6 and F26, as the dimensions increase, RIME’s convergence to the optimal value also grows, but IRIME maintains convergence at similarly low optimal values. A Friedman ranking was computed, as shown in Figure 6, demonstrating IRIME’s significant advantage as the dimensionality increases. In summary, with changing problem dimensions, IRIME sustains its competitiveness, showcasing remarkable stability and maintaining strong performance.

Table 7.

Stability testing of IRIME and RIME

Metric	30		50		100
Metric	IRIME	RIME	IRIME	RIME	IRIME	RIME
AVG	1.000000E+02	1.028739E+04	8.150018E+03	3.498054E+04	3.587010E+04	5.599304E+05
STD	6.624418E-07	1.822468E+04	1.360977E+04	1.030577E+04	2.748387E+04	1.181859E+05
AVG	6.779600E+03	3.152160E+04	3.707965E+13	8.353509E+13	9.181274E+56	1.820439E+80
STD	8.247370E+03	6.815905E+04	1.077243E+14	2.980378E+14	3.252605E+57	9.948538E+80
AVG	3.000804E+02	3.017968E+02	9.127787E+02	5.914656E+02	9.806014E+04	9.242816E+04
STD	8.807603E-02	7.545155E-01	3.786835E+02	1.216696E+02	1.448744E+04	1.933928E+04
AVG	4.161644E+02	4.904783E+02	4.920837E+02	5.228727E+02	6.357680E+02	6.980471E+02
STD	2.870048E+01	3.720042E+01	1.411291E+01	4.746566E+01	4.853969E+01	4.424859E+01
AVG	5.619552E+02	5.836654E+02	6.267921E+02	6.818772E+02	8.695937E+02	9.965034E+02
STD	1.790301E+01	1.722221E+01	2.854613E+01	3.959170E+01	6.564103E+01	8.890611E+01
AVG	6.000026E+02	6.002950E+02	6.000213E+02	6.027180E+02	6.002694E+02	6.182405E+02
STD	1.369855E-03	2.141152E-01	8.625810E-03	1.841028E+00	1.523005E-01	4.611132E+00
AVG	7.840374E+02	8.168247E+02	8.740425E+02	9.318452E+02	1.181254E+03	1.294812E+03
STD	1.300727E+01	2.777899E+01	1.874723E+01	4.792427E+01	6.421225E+01	9.746528E+01
AVG	8.621855E+02	8.839896E+02	9.318084E+02	9.770503E+02	1.184238E+03	1.324732E+03
STD	1.320405E+01	1.835873E+01	2.928632E+01	3.136398E+01	6.472031E+01	8.014492E+01
AVG	9.000181E+02	1.124300E+03	9.045256E+02	3.715535E+03	1.520706E+03	1.770827E+04
STD	8.398819E-02	2.651242E+02	8.449065E+00	1.840252E+03	7.826171E+02	7.679602E+03
AVG	3.403375E+03	3.318342E+03	6.472167E+03	6.607002E+03	1.483534E+04	1.553603E+04
STD	5.195037E+02	4.690800E+02	7.651949E+02	7.082011E+02	1.171622E+03	1.278887E+03
AVG	1.144627E+03	1.235619E+03	1.213375E+03	1.566197E+03	1.639799E+03	2.527533E+03
STD	1.801979E+01	7.120005E+01	2.596203E+01	1.123408E+02	1.378813E+02	2.185059E+02
AVG	3.259220E+03	3.185041E+06	6.215314E+03	8.247759E+06	2.146365E+04	9.556442E+07
STD	9.613443E+02	2.533263E+06	2.619565E+03	3.820874E+06	9.818197E+03	3.444275E+07
AVG	1.339929E+03	3.903406E+03	1.038753E+04	5.893687E+04	2.624556E+04	2.400604E+05
STD	1.078343E+01	3.101797E+03	7.408806E+03	4.089735E+04	1.241422E+04	8.196934E+04
AVG	1.443579E+03	1.497542E+03	1.466908E+03	1.651542E+03	1.532119E+03	1.599748E+04
STD	9.549785E+00	2.906395E+01	1.731724E+01	5.900106E+01	2.628161E+01	7.791170E+03
AVG	1.560320E+03	7.576501E+03	2.017887E+03	4.234476E+03	8.630684E+03	5.690617E+04
STD	3.352494E+01	6.640569E+03	7.957409E+02	2.180854E+03	9.731233E+03	2.010337E+04
AVG	2.189042E+03	2.341539E+03	2.641367E+03	2.967189E+03	5.169371E+03	5.974952E+03
STD	2.485710E+02	3.008552E+02	3.246147E+02	4.208589E+02	6.400325E+02	5.933374E+02
AVG	1.932272E+03	2.019690E+03	2.303726E+03	2.577466E+03	4.363901E+03	4.793590E+03
STD	1.219315E+02	1.098334E+02	2.243114E+02	2.717036E+02	4.906362E+02	5.352419E+02
AVG	1.321118E+04	1.282609E+05	1.076984E+05	6.718929E+05	8.873835E+05	2.215444E+06
STD	1.040334E+04	9.873021E+04	4.224163E+04	4.070633E+05	4.590897E+05	7.540629E+05
AVG	1.996303E+03	8.668593E+03	9.349882E+03	1.402825E+04	6.842005E+03	4.190986E+04
STD	2.888304E+02	7.195163E+03	1.038581E+04	1.488471E+04	3.688717E+03	2.169956E+04
AVG	2.171758E+03	2.261173E+03	2.579609E+03	2.792553E+03	4.184473E+03	4.741982E+03
STD	7.861606E+01	9.435565E+01	2.374063E+02	2.490740E+02	4.799121E+02	4.920016E+02
AVG	2.129702E+03	2.194063E+03	2.212182E+03	2.270509E+03	2.250000E+03	2.250002E+03
STD	3.233579E+01	2.859524E+01	3.470840E+01	3.920999E+01	1.705788E-06	1.661872E-04
AVG	2.261555E+03	2.278551E+03	2.339057E+03	2.389399E+03	2.350000E+03	2.350000E+03
STD	1.980115E+01	1.982225E+01	2.854209E+01	4.896348E+01	8.275093E-09	9.695178E-06
AVG	2.500000E+03	2.877338E+03	2.522419E+03	3.249900E+03	2.500380E+03	3.959631E+03
STD	9.799078E-06	2.785766E+01	1.227458E+02	5.579856E+01	3.389571E-01	8.897769E+01
AVG	2.600000E+03	3.299834E+03	2.600000E+03	3.829701E+03	2.600019E+03	5.362005E+03
STD	2.533334E-13	2.579968E+02	4.619013E-06	6.618639E+01	2.013730E-02	9.411192E+01
AVG	2.707120E+03	2.973604E+03	2.881642E+03	3.051111E+03	2.700225E+03	3.340697E+03
STD	3.899625E+01	5.501906E+01	1.531719E+02	2.489686E+01	2.330694E-01	6.969830E+01
AVG	2.800000E+03	5.014069E+03	2.800000E+03	7.360208E+03	2.800134E+03	1.570043E+04
STD	4.776900E-13	9.979314E+02	2.963824E-05	1.592764E+03	1.101589E-01	1.136894E+03
AVG	2.918219E+03	3.594628E+03	2.971923E+03	3.994026E+03	3.097434E+03	5.449449E+03
STD	9.978696E+01	8.565568E+01	2.188521E+02	1.697183E+02	5.004242E+02	3.176788E+02
AVG	3.023799E+03	3.412600E+03	3.275639E+03	3.342462E+03	3.000172E+03	3.407231E+03
STD	7.300070E+01	4.842390E+02	1.299708E+02	3.360505E+01	1.083659E-01	4.757740E+01
AVG	3.240401E+03	3.560112E+03	3.569520E+03	4.500026E+03	5.375933E+03	6.954458E+03
STD	6.760153E+01	1.833220E+02	2.907660E+02	3.105699E+02	4.990865E+02	5.511103E+02
AVG	6.144891E+03	4.017941E+04	2.279465E+04	7.241399E+05	9.420026E+03	6.578093E+06
STD	3.632263E+03	2.698645E+04	1.915455E+03	4.691778E+05	2.867600E+03	2.615942E+06

Open in a new tab

Friedman ranking of IRIME in different dimensions

Comparison with conventional algorithms

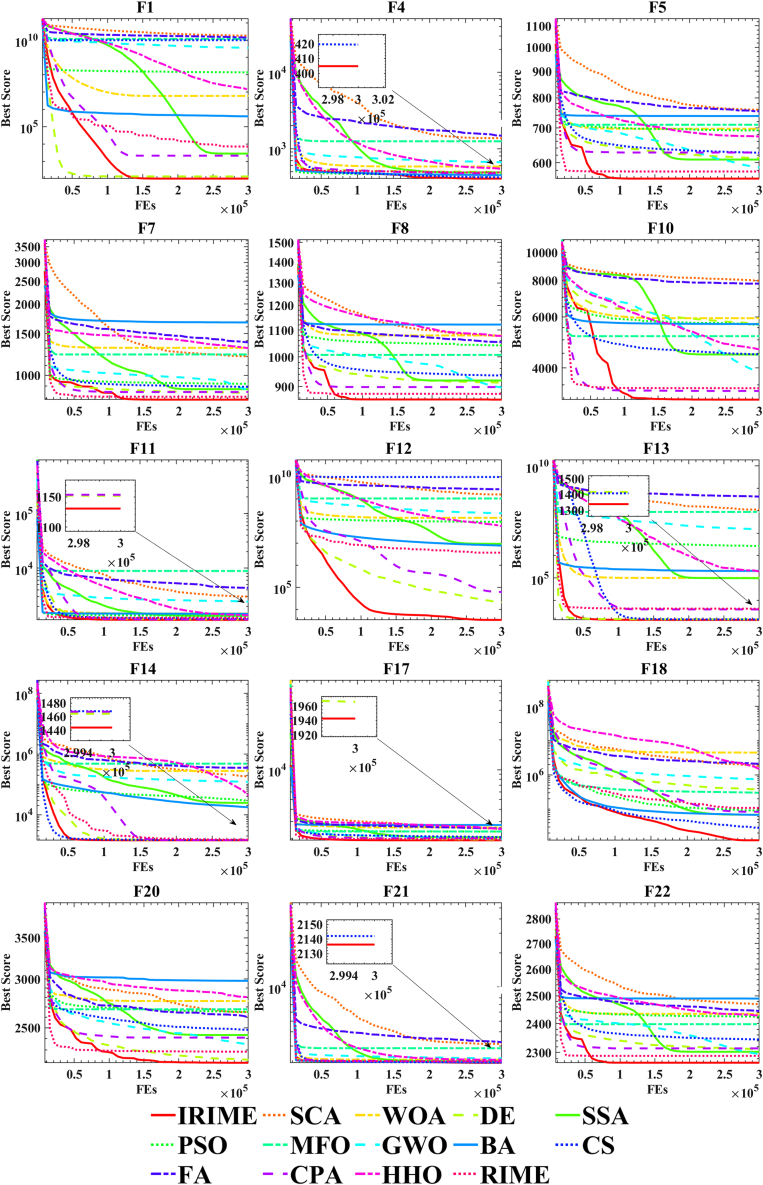
In this section, IRIME was primarily compared against 13 conventional algorithms: RIME,²¹ SCA,¹⁶ WOA,⁹⁵ DE,³³ SSA,⁹⁶ PSO,⁹⁷ MFO,²⁹ GWO,⁹⁸ BA,⁹⁹ CS,⁹¹ FA,¹⁰⁰ CPA³² and HHO.²⁸ Table 8 illustrates that IRIME achieves an average ranking of 1.733333, indicating its exceptional performance across all 30 benchmark test functions. Detailed experimental data is provided in Table 9. Upon careful comparison with SCA, WOA, DE, PSO, MFO, GWO, FA, and RIME, IRIME does not exhibit noticeably poorer performance than these algorithms. Furthermore, compared to other algorithms such as CPA, HHO, etc., there are many cases where IRIME is significantly superior. For a visual representation of IRIME’s performance, convergence curve plots were generated, as depicted in Figure 7. These curves demonstrate IRIME’s distinctive characteristics compared to RIME, especially evident in simple unimodal functions F1, multimodal functions F4, F5, F7, F8 and F10, hybrid functions F11, F12, F13, F14, F17, and F18, and composite functions F21 and F22. This notable performance is primarily attributed to balancing RIME’s exploration and exploitation abilities by SB and CMS-RS, enabling IRIME’s ability to escape local optima. Moreover, the Friedman ranking chart in Figure 8 positions IRIME at the top. To indicate the statistical significance of IRIME’s superiority over other algorithms, a table presenting p-values of the Wilcoxon signed-rank test is included in Table10.

Table 8.

Comparison results between IRIME and conventional algorithms

Overall Rank
Algorithm	Rank	+/ = /-	Avg
IRIME	1	∼	1.733333
SCA	13	30/0/0	12.2
WOA	11	27/3/0	10.3
DE	3	25/2/3	5
SSA	6	29/0/1	5.833333
PSO	9	30/0/0	8.366667
MFO	12	30/0/0	10.93333
GWO	8	28/2/0	7.566667
BA	10	28/1/1	9.366667
CS	5	27/2/1	5.766667
FA	14	30/0/0	12.3
CPA	2	18/4/8	3.333333
HHO	7	22/2/6	6.9
RIME	3	29/1/0	5

Open in a new tab

Table 9.

Comparison of IRIME with conventional algorithms

	F1		F2		F3
	AVG	STD	AVG	STD	AVG	STD
IRIME	1.000000E+02	8.228886E-07	1.092587E+04	2.557057E+04	3.000768E+02	8.230567E-02
SCA	1.841382E+10	3.722769E+09	7.136067E+32	1.990604E+33	3.706668E+04	4.666736E+03
WOA	6.004626E+06	6.340405E+06	2.066092E+29	1.113738E+30	1.338299E+04	5.360271E+03
DE	1.333382E+02	1.663241E+02	1.983923E+25	3.478891E+25	1.996025E+04	3.770712E+03
SSA	2.792499E+03	3.017484E+03	4.056705E+06	2.112276E+07	3.000000E+02	8.818389E-09
PSO	1.389773E+08	1.936371E+07	2.561524E+12	2.515226E+12	6.259001E+02	3.466948E+01
MFO	1.178499E+10	5.277154E+09	4.606288E+38	2.268979E+39	1.139089E+05	5.365509E+04
GWO	3.656408E+09	2.680374E+09	8.477831E+28	2.813243E+29	3.158195E+04	9.978276E+03
BA	3.979009E+05	1.875329E+05	2.001667E+02	9.128709E-01	3.000746E+02	4.876542E-02
CS	1.000000E+10	0.000000E+00	1.000000E+10	0.000000E+00	1.185032E+04	2.895928E+03
FA	1.422799E+10	1.490877E+09	2.637550E+34	2.817855E+34	5.846299E+04	8.407209E+03
CPA	2.114254E+03	2.746738E+03	1.107555E+05	5.629322E+05	3.000000E+02	1.708056E-07
HHO	1.397816E+07	2.883833E+06	2.473100E+12	7.349195E+12	2.801396E+03	1.243863E+03
RIME	7.124393E+03	4.505485E+03	2.058783E+04	5.563495E+04	3.016689E+02	7.524137E-01

	F4		F5		F6
	AVG	STD	AVG	STD	AVG	STD
IRIME	4.047558E+02	1.615793E+01	5.592333E+02	1.350497E+01	6.000030E+02	2.016607E-03
SCA	1.374591E+03	2.771825E+02	7.588440E+02	1.443074E+01	6.417769E+02	5.229569E+00
WOA	5.840244E+02	5.335661E+01	6.972605E+02	4.197744E+01	6.644217E+02	1.299889E+01
DE	4.901688E+02	3.989320E+01	6.123099E+02	1.004958E+01	6.000000E+02	0.000000E+00
SSA	4.880627E+02	3.685931E+01	6.083748E+02	3.205830E+01	6.293176E+02	1.206613E+01
PSO	4.559716E+02	3.206651E+01	6.922583E+02	2.502204E+01	6.343293E+02	1.113896E+01
MFO	1.249248E+03	7.468984E+02	7.099112E+02	3.925173E+01	6.444544E+02	9.505611E+00
GWO	6.646073E+02	1.181156E+02	5.870130E+02	2.823283E+01	6.064975E+02	3.413389E+00
BA	4.492754E+02	5.335580E+01	7.378640E+02	4.005934E+01	6.715805E+02	1.149586E+01
CS	4.193988E+02	2.958199E+01	6.269874E+02	2.190149E+01	6.269248E+02	8.245281E+00
FA	1.482195E+03	1.539432E+02	7.535040E+02	1.239110E+01	6.437613E+02	3.892201E+00
CPA	4.741417E+02	4.920473E+01	6.277521E+02	2.556818E+01	6.000000E+02	1.993686E-07
HHO	5.452018E+02	3.950364E+01	6.738793E+02	1.994907E+01	6.526138E+02	3.710877E+00
RIME	4.869630E+02	2.962177E+01	5.771337E+02	1.783255E+01	6.003665E+02	2.821859E-01

	F7		F8		F9
	AVG	STD	AVG	STD	AVG	STD
IRIME	7.883173E+02	1.821927E+01	8.592822E+02	1.301643E+01	9.000454E+02	1.386272E-01
SCA	1.203477E+03	5.847467E+01	1.077141E+03	2.148756E+01	7.055291E+03	1.483905E+03
WOA	1.305250E+03	1.357140E+02	1.079100E+03	5.445599E+01	9.026235E+03	3.453609E+03
DE	8.431410E+02	9.738404E+00	9.123994E+02	6.583571E+00	9.000000E+02	2.985563E-14
SSA	8.727399E+02	4.585326E+01	9.195604E+02	3.175260E+01	3.902221E+03	1.700013E+03
PSO	9.195953E+02	1.906608E+01	1.041707E+03	3.675778E+01	6.310334E+03	2.485837E+03
MFO	1.223923E+03	2.587419E+02	1.007102E+03	4.956693E+01	8.133813E+03	2.578392E+03
GWO	8.687501E+02	5.299589E+01	8.966145E+02	2.657562E+01	2.549040E+03	8.862296E+02
BA	1.672298E+03	2.052284E+02	1.121454E+03	5.642799E+01	1.596200E+04	4.562495E+03
CS	8.931793E+02	2.914000E+01	9.358801E+02	2.485981E+01	5.137085E+03	1.624264E+03
FA	1.378286E+03	4.499559E+01	1.053642E+03	1.212715E+01	5.904095E+03	5.642448E+02
CPA	8.489678E+02	3.506446E+01	8.985005E+02	2.920458E+01	3.316187E+03	7.771718E+02
HHO	1.302266E+03	9.362298E+01	1.076979E+03	4.260311E+01	7.620443E+03	1.098960E+03
RIME	8.108969E+02	2.663949E+01	8.771250E+02	1.542515E+01	1.282633E+03	7.780124E+02

	F10		F11		F12
	AVG	STD	AVG	STD	AVG	STD
IRIME	3.113983E+03	4.683815E+02	1.130403E+03	1.468068E+01	3.319172E+03	7.705038E+02
SCA	7.981345E+03	3.150563E+02	3.022295E+03	6.445754E+02	1.574493E+09	3.979278E+08
WOA	5.934370E+03	7.789161E+02	1.481984E+03	8.519552E+01	1.382265E+08	7.101250E+07
DE	5.672989E+03	2.624536E+02	1.152053E+03	8.966502E+00	2.025299E+04	4.813425E+04
SSA	4.452536E+03	7.094846E+02	1.344872E+03	7.211084E+01	9.182351E+06	5.040467E+06
PSO	5.643005E+03	5.073707E+02	1.347653E+03	5.680875E+01	8.995054E+07	3.766610E+07
MFO	5.147688E+03	8.203648E+02	8.873480E+03	7.933486E+03	1.033950E+09	1.367383E+09
GWO	3.885633E+03	9.366685E+02	2.439886E+03	1.375237E+03	2.211911E+08	5.231662E+08
BA	5.665602E+03	6.360143E+02	1.463662E+03	1.486178E+02	7.653362E+06	7.277742E+06
CS	4.458374E+03	2.296132E+02	1.185109E+03	1.742362E+01	9.666740E+09	1.825338E+09
FA	7.802109E+03	2.450349E+02	4.351898E+03	6.829350E+02	2.681007E+09	3.497603E+08
CPA	3.335836E+03	4.680002E+02	1.153764E+03	2.469058E+01	6.094811E+04	5.596317E+04
HHO	4.635003E+03	5.314861E+02	1.373707E+03	9.325560E+01	5.779730E+07	3.642617E+07
RIME	3.409716E+03	5.427260E+02	1.236769E+03	6.668725E+01	3.654135E+06	2.400589E+06

	F13		F14		F15
	AVG	STD	AVG	STD	AVG	STD
IRIME	1.336538E+03	8.473889E+00	1.443824E+03	8.556915E+00	1.553682E+03	2.436474E+01
SCA	1.135809E+08	3.597453E+07	1.857652E+05	8.431296E+04	4.841776E+06	2.356802E+06
WOA	1.000657E+05	7.298211E+04	2.780113E+05	1.802183E+05	5.291920E+04	8.617273E+04
DE	1.412306E+03	3.210871E+02	1.464071E+03	7.837059E+00	1.550860E+03	1.334677E+01
SSA	9.785285E+04	1.030243E+05	2.465348E+04	2.001924E+04	3.396406E+04	1.937665E+04
PSO	2.672529E+06	6.920589E+05	2.900206E+04	1.903076E+04	3.161740E+05	1.329552E+05
MFO	8.890284E+07	2.019387E+08	4.818146E+05	1.166317E+06	4.578076E+04	4.589563E+04
GWO	1.493141E+07	2.605109E+07	1.207818E+05	1.325602E+05	2.080886E+06	1.127817E+07
BA	2.056385E+05	1.475900E+05	1.764583E+04	8.026951E+03	9.857857E+04	9.742760E+04
CS	1.403952E+03	2.910464E+01	1.467773E+03	8.666795E+00	1.566742E+03	1.286895E+01
FA	4.300832E+08	1.161389E+08	3.545473E+05	1.403319E+05	5.339371E+07	1.919045E+07
CPA	3.945263E+03	2.400788E+03	1.467093E+03	3.012936E+01	7.282572E+03	4.871670E+03
HHO	1.949828E+05	8.419094E+04	4.341608E+04	3.603063E+04	3.486027E+04	1.511152E+04
RIME	4.237048E+03	2.386911E+03	1.521076E+03	4.668063E+01	7.385270E+03	4.797001E+03

	F16		F17		F18
	AVG	STD	AVG	STD	AVG	STD
IRIME	2.157519E+03	2.319810E+02	1.942563E+03	8.414615E+01	1.227806E+04	8.274997E+03
SCA	3.297912E+03	2.433252E+02	2.544122E+03	1.996151E+02	1.843845E+06	9.558486E+05
WOA	3.325774E+03	4.574786E+02	2.621453E+03	3.052444E+02	4.481267E+06	3.637390E+06
DE	2.025687E+03	1.610609E+02	1.965870E+03	4.022178E+01	3.533861E+05	1.845308E+05
SSA	2.392214E+03	2.408053E+02	2.084263E+03	1.671643E+02	6.859217E+04	5.922140E+04
PSO	2.668135E+03	2.316809E+02	2.379098E+03	2.458484E+02	8.997152E+04	4.816071E+04
MFO	3.191869E+03	4.313203E+02	2.382983E+03	2.636714E+02	2.996153E+05	6.695035E+05
GWO	2.252737E+03	2.427924E+02	1.984203E+03	1.120046E+02	7.415711E+05	1.403432E+06
BA	3.490398E+03	5.264603E+02	2.771914E+03	3.374694E+02	6.745901E+04	2.947320E+04
CS	2.458258E+03	1.646827E+02	2.093107E+03	8.895653E+01	2.839660E+04	8.739249E+03
FA	3.171391E+03	1.900067E+02	2.556076E+03	1.239653E+02	2.123477E+06	7.703717E+05
CPA	2.638873E+03	3.589458E+02	2.035829E+03	1.520298E+02	8.337727E+04	5.771694E+04
HHO	2.853986E+03	4.348123E+02	2.518518E+03	2.613917E+02	1.479073E+06	1.536378E+06
RIME	2.361515E+03	2.358123E+02	1.997354E+03	1.314076E+02	1.082342E+05	6.657172E+04

	F19		F20		F21
	AVG	STD	AVG	STD	AVG	STD
IRIME	2.332181E+03	1.864812E+03	2.192876E+03	9.492175E+01	2.136135E+03	3.352597E+01
SCA	2.168794E+07	1.687208E+07	2.650003E+03	1.360133E+02	3.142386E+03	2.110077E+02
WOA	7.039075E+05	7.090756E+05	2.762562E+03	1.563571E+02	2.275860E+03	3.276134E+01
DE	4.947694E+03	2.473822E+03	2.216929E+03	4.611997E+01	2.187477E+03	1.809598E+01
SSA	1.667896E+05	1.140472E+05	2.432897E+03	1.772135E+02	2.203093E+03	3.248284E+01
PSO	3.430261E+05	1.514502E+05	2.653687E+03	1.678977E+02	2.177850E+03	3.668529E+01
MFO	3.757899E+05	1.837212E+06	2.678688E+03	2.917192E+02	2.874566E+03	8.105786E+02
GWO	5.753903E+04	6.494282E+04	2.350499E+03	1.051505E+02	2.337764E+03	7.529951E+01
BA	2.695612E+05	1.461260E+05	2.978931E+03	2.096352E+02	2.161001E+03	4.171884E+01
CS	1.931255E+03	5.385502E+00	2.480485E+03	8.794099E+01	2.141894E+03	3.215894E+01
FA	3.416584E+07	1.587037E+07	2.599760E+03	9.585333E+01	3.244746E+03	1.713522E+02
CPA	4.131226E+03	2.932877E+03	2.409347E+03	1.245356E+02	2.192308E+03	2.812837E+01
HHO	1.482658E+05	9.248775E+04	2.802366E+03	2.084324E+02	2.264632E+03	2.386389E+01
RIME	8.102371E+03	6.772024E+03	2.285830E+03	1.169991E+02	2.197692E+03	3.982284E+01

	F22		F23		F24
	AVG	STD	AVG	STD	AVG	STD
IRIME	2.265552E+03	1.375038E+01	2.500000E+03	2.412039E-05	2.600000E+03	2.234190E-13
SCA	2.469766E+03	1.862005E+01	3.280074E+03	5.293000E+01	3.860830E+03	7.261677E+01
WOA	2.434663E+03	4.591771E+01	3.152556E+03	1.486188E+02	2.826444E+03	4.640745E+02
DE	2.312139E+03	9.803931E+00	2.873856E+03	1.165131E+01	3.396319E+03	7.143519E+00
SSA	2.302442E+03	2.696481E+01	2.899683E+03	4.591268E+01	2.600461E+03	1.754068E+00
PSO	2.424424E+03	2.981972E+01	4.664458E+03	5.424066E+02	2.667356E+03	4.579105E+00
MFO	2.397898E+03	4.542225E+01	2.955630E+03	3.010570E+01	3.492602E+03	4.045296E+01
GWO	2.294783E+03	2.927255E+01	2.885035E+03	4.101812E+01	3.028401E+03	3.720900E+02
BA	2.490033E+03	5.712484E+01	3.541796E+03	2.055549E+02	2.846532E+03	4.871311E+02
CS	2.344756E+03	2.801735E+01	2.913872E+03	2.132308E+01	2.869770E+03	2.713068E+02
FA	2.445136E+03	1.294870E+01	3.103677E+03	1.621235E+01	3.691747E+03	1.601300E+01
CPA	2.313971E+03	2.535603E+01	2.500000E+03	0.000000E+00	2.600000E+03	0.000000E+00
HHO	2.428248E+03	2.689161E+01	2.500000E+03	0.000000E+00	2.600000E+03	0.000000E+00
RIME	2.288698E+03	1.933506E+01	2.875461E+03	1.894064E+01	3.218714E+03	3.332643E+02

	F25		F26		F27
	AVG	STD	AVG	STD	AVG	STD
IRIME	2.700000E+03	3.014049E-06	2.800000E+03	7.966475E-13	2.917703E+03	9.696226E+01
SCA	3.620928E+03	1.263230E+02	7.789088E+03	1.025837E+03	4.061770E+03	1.175104E+02
WOA	2.717575E+03	9.626031E+01	3.542405E+03	1.941872E+03	3.968988E+03	2.352272E+02
DE	2.912818E+03	4.515466E+00	5.310729E+03	3.259103E+02	3.440492E+03	2.054747E+01
SSA	2.956126E+03	4.508026E+01	2.803337E+03	1.825686E+01	3.603933E+03	8.474287E+01
PSO	2.953735E+03	3.770860E+01	3.409442E+03	3.172684E+01	5.031577E+03	7.931823E+02
MFO	3.699591E+03	7.905559E+02	6.711784E+03	5.120422E+02	3.590907E+03	6.526928E+01
GWO	3.212052E+03	1.861504E+02	4.866584E+03	9.148374E+02	3.681051E+03	9.477657E+01
BA	3.013904E+03	8.224810E+01	5.309482E+03	3.576900E+03	3.906917E+03	1.275351E+02
CS	2.907161E+03	8.298785E+00	3.789000E+03	1.166225E+03	3.509616E+03	7.246362E+01
FA	4.108952E+03	1.520293E+02	7.293080E+03	1.459334E+02	3.902377E+03	8.965520E+01
CPA	2.700000E+03	0.000000E+00	2.800000E+03	0.000000E+00	2.900000E+03	0.000000E+00
HHO	2.700000E+03	0.000000E+00	2.800000E+03	0.000000E+00	2.900000E+03	0.000000E+00
RIME	2.956893E+03	4.093764E+01	5.213364E+03	8.405995E+02	3.566066E+03	7.106036E+01

	F28		F29		F30
	AVG	STD	AVG	STD	AVG	STD
IRIME	3.034850E+03	8.227287E+01	3.279330E+03	8.123477E+01	5.583571E+03	2.871580E+03
SCA	5.650824E+03	5.471978E+02	4.271864E+03	2.801958E+02	7.855927E+06	1.863115E+07
WOA	3.308537E+03	6.514672E+02	4.361104E+03	4.091531E+02	1.826287E+06	1.767812E+06
DE	3.941911E+03	6.995067E+02	3.466897E+03	8.981603E+01	6.628119E+04	2.352216E+04
SSA	3.305292E+03	3.583736E+02	3.771022E+03	1.643812E+02	1.179055E+06	1.017255E+06
PSO	3.311009E+03	1.132244E+02	4.050026E+03	2.446224E+02	2.561684E+06	1.127760E+06
MFO	4.866595E+03	7.300049E+02	4.138832E+03	2.317888E+02	1.941961E+06	2.782699E+06
GWO	3.705572E+03	2.929996E+02	3.524327E+03	1.794326E+02	1.259130E+06	4.317675E+06
BA	3.415627E+03	5.750275E+02	4.654428E+03	4.556327E+02	1.054830E+06	6.501027E+05
CS	3.228935E+03	4.607668E+01	3.677880E+03	1.126906E+02	7.589453E+03	1.446341E+03
FA	4.068826E+03	1.044341E+02	4.559695E+03	1.650738E+02	1.171501E+08	3.086506E+07
CPA	3.000000E+03	0.000000E+00	3.100000E+03	0.000000E+00	3.200000E+03	0.000000E+00
HHO	3.000000E+03	0.000000E+00	3.100000E+03	0.000000E+00	3.200000E+03	0.000000E+00
RIME	3.549195E+03	6.610575E+02	3.609103E+03	1.811955E+02	3.838771E+04	2.085730E+04

Open in a new tab

Convergence curves of IRIME and conventional algorithms at IEEE CEC 2017

The Friedman ranking of IRIME and conventional algorithms

Table 10.

p−value of Wilcoxon signed−rank test between IRIME and conventional algorithms

	F1	F2	F3	F4	F5	F6
SCA	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06
WOA	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06
DE	5.7516532694E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06
SSA	1.7343976283E-06	1.3594767037E-04	1.7343976283E-06	2.8785992194E-06	3.5152372790E-06	1.7343976283E-06
PSO	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.9209211049E-06	1.7343976283E-06	1.7343976283E-06
MFO	1.7343976283E-06	1.7343976283E-06	1.9209211049E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06
GWO	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	2.1630223984E-05	1.7343976283E-06
BA	1.7343976283E-06	9.3385961710E-06	5.9993592817E-01	1.4772761749E-04	1.7343976283E-06	1.7343976283E-06
CS	4.3204630578E-08	1.7126865599E-06	1.7343976283E-06	5.4462503972E-02	1.9209211049E-06	1.7343976283E-06
FA	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06
CPA	1.7343976283E-06	5.5774268620E-01	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06
HHO	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06
RIME	1.7343976283E-06	7.3432529144E-01	1.7343976283E-06	2.1266360107E-06	6.1564062070E-04	1.7343976283E-06

	F7	F8	F9	F10	F11	F12
SCA	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06
WOA	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06
DE	1.7343976283E-06	1.7343976283E-06	1.6976242501E-06	1.7343976283E-06	2.1630223984E-05	1.7343976283E-06
SSA	1.7343976283E-06	3.1816794110E-06	1.7343976283E-06	1.9209211049E-06	1.7343976283E-06	1.7343976283E-06
PSO	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06
MFO	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06
GWO	2.6033283895E-06	3.5152372790E-06	1.7343976283E-06	8.9187274245E-05	1.7343976283E-06	1.7343976283E-06
BA	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06
CS	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.9209211049E-06	1.7343976283E-06
FA	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06
CPA	1.9209211049E-06	4.7292023374E-06	1.7343976283E-06	2.0588822306E-01	4.5335631776E-04	1.7343976283E-06
HHO	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06
RIME	1.1973382000E-03	4.8602606067E-05	1.7343976283E-06	1.3974564120E-02	3.1816794110E-06	1.7343976283E-06

	F13	F14	F15	F16	F17	F18
SCA	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06
WOA	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.9209211049E-06	1.7343976283E-06	1.7343976283E-06
DE	3.5008956820E-02	1.7343976283E-06	8.6121251974E-01	3.6826128416E-02	4.2766688017E-02	1.7343976283E-06
SSA	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	4.5335631776E-04	8.9443006475E-04	1.7343976283E-06
PSO	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	3.8821823861E-06	2.1266360107E-06	1.7343976283E-06
MFO	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	2.1266360107E-06	1.7343976283E-06	1.9209211049E-06
GWO	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	6.8713630797E-02	1.8462187723E-01	1.7343976283E-06
BA	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.9209211049E-06	1.7343976283E-06	1.7343976283E-06
CS	1.7343976283E-06	2.8785992194E-06	1.7518393580E-02	4.4493372835E-05	1.6394463017E-05	2.3534209951E-06
FA	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06
CPA	1.7343976283E-06	3.5888445045E-04	1.9209211049E-06	2.8434237746E-05	6.4242118722E-03	4.2856858692E-06
HHO	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	6.3391355731E-06	1.7343976283E-06	1.7343976283E-06
RIME	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	3.3788544377E-03	4.4918903765E-02	1.7343976283E-06

	F19	F20	F21	F22	F23	F24
SCA	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06
WOA	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	3.1250000000E-02
DE	2.3704477026E-05	1.8462187723E-01	1.7343976283E-06	1.9209211049E-06	1.7343976283E-06	1.7343976283E-06
SSA	1.7343976283E-06	8.4660816904E-06	2.1266360107E-06	6.3391355731E-06	1.7343976283E-06	1.7343976283E-06
PSO	1.7343976283E-06	1.9209211049E-06	4.9915540124E-03	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06
MFO	8.4660816904E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06
GWO	1.7343976283E-06	2.5967125848E-05	1.7343976283E-06	6.8922902968E-05	1.7343976283E-06	1.3183388898E-04
BA	1.7343976283E-06	1.7343976283E-06	4.9915540124E-03	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06
CS	4.4918903765E-02	1.9209211049E-06	8.5895825870E-02	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06
FA	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06
CPA	5.3069919381E-05	2.3704477026E-05	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.0000000000E+00
HHO	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.0000000000E+00
RIME	3.4052567233E-05	2.9574621307E-03	6.9837831475E-06	1.1499217544E-04	1.7343976283E-06	1.7343976283E-06

	F25	F26	F27	F28	F29	F30
SCA	1.7343976283E-06	2.5630832507E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06
WOA	5.3710937500E-02	1.2500000000E-01	1.7343976283E-06	4.1652148500E-01	1.7343976283E-06	2.3534209951E-06
DE	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	2.1266360107E-06	1.7343976283E-06
SSA	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06
PSO	1.7343976283E-06	1.7343976283E-06	1.9209211049E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06
MFO	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7300371293E-06	1.7343976283E-06	1.7343976283E-06
GWO	2.5630832507E-06	8.2980993064E-06	1.7343976283E-06	1.7343976283E-06	5.2164934470E-06	1.7343976283E-06
BA	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	2.3534209951E-06	1.7343976283E-06	1.7343976283E-06
CS	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	3.8821823861E-06	1.7343976283E-06	9.6265892907E-04
FA	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06
CPA	1.9531250000E-03	1.0000000000E+00	1.7343976283E-06	1.7191759139E-06	1.7343976283E-06	1.7343976283E-06
HHO	1.9531250000E-03	1.0000000000E+00	1.7343976283E-06	1.7191759139E-06	1.7343976283E-06	1.7343976283E-06
RIME	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	2.1266360107E-06

Open in a new tab

Comparison with advanced algorithms

To further validate IRIME’s performance, this study compared it with some advanced algorithms using the IEEE CEC 2017 benchmark test suite. These algorithms include EBOwithCMAR,¹⁰¹ LSHADE_cnEpSi,⁸⁶ ALCPSO,¹⁰² CLPSO,¹⁰³ LSHADE,¹⁰⁴ SADE,¹⁰⁵ JADE,¹⁰⁶ RCBA,¹⁰⁷ EPSO,¹⁰⁸ CBA,¹⁰⁹ and LWOA,¹¹⁰ The specific experimental data is detailed in Table 11. The results in the table highlight that IRIME, alongside some advanced algorithms, achieves performance near the theoretical optimum in functions such as F1, F3, F6, and F9. Compared to exceptional variants of DE like JADE and SADE, IRIME demonstrates some drawbacks in multimodal functions (F4, F5, F7, and F10) and hybrid functions (F12, F16, F17, and F18). This can be attributed to the limitations of SB and CMS-RS in improving convergence accuracy. Nevertheless, these limitations do not significantly impact IRIME’s overall performance. IRIME can also find very good results on multimodal functions F7 and F8, indicating that IRIME is not uniformly poor on multimodal functions. In addition, the hybrid functions F11, F13, F14, and F15 can also reflect excellent results, demonstrating that the disadvantage of IRIME on hybrid functions is not significant. Particularly in composite functions (F23, F24, F25, F26, F27, F28 and F29), IRIME exhibits advantages that aren’t present in these advanced algorithms, such as EBOwithCMAR, LSHADE_cnEpSi, ALCPSO, and CLPSO. When compared to other successful improvements in swarm intelligence algorithms like RCBA, CBA, and LWOA, IRIME outperforms them in convergence capability, especially in simple unimodal functions such as F1 and F2. Despite potential shortcomings in convergence accuracy, IRIME’s strong exploration abilities and the balance between exploration and exploitation elevate its average ranking to the top among these algorithms, as depicted in Table 12.

Table 11.

Comparison of IRIME with advanced algorithms

	F1		F2		F3
	AVG	STD	AVG	STD	AVG	STD
IRIME	1.000000E+02	6.154959E-07	1.010703E+04	1.303957E+04	3.000649E+02	5.911368E-02
EBOwithCMAR	1.000000E+02	7.463907E-15	2.456040E+21	1.345229E+22	2.400802E+04	3.386547E+04
LSHADE_cnEpSi	1.000000E+02	1.355622E-09	2.409411E+21	9.065340E+21	3.000060E+02	1.496863E-02
ALCPSO	1.090225E+03	1.626553E+03	1.080386E+19	4.265054E+19	2.652894E+04	4.688938E+03
CLPSO	1.064836E+02	1.516141E+01	6.521139E+13	1.787106E+14	8.761694E+03	2.317848E+03
LSHADE	1.000000E+02	3.369109E-14	3.545959E+12	1.851603E+13	5.041967E+03	1.485133E+04
SADE	1.000000E+02	4.856153E-06	2.000000E+02	0.000000E+00	3.224915E+02	1.121460E+02
JADE	1.000000E+02	2.447205E-14	4.353151E+11	2.250183E+12	2.152864E+03	4.413241E+03
RCBA	1.865639E+04	6.844783E+03	2.203667E+02	2.627767E+01	3.005611E+02	1.705823E-01
EPSO	6.291322E+02	8.551875E+02	1.672571E+13	6.510333E+13	5.967043E+03	1.583147E+03
CBA	1.418221E+05	7.288431E+05	1.079177E+04	1.420128E+04	3.142839E+02	5.455682E+00
LWOA	5.842765E+05	1.266102E+05	5.940121E+05	8.651440E+05	3.226856E+02	7.158850E+00

	F4		F5		F6
	AVG	STD	AVG	STD	AVG	STD
IRIME	4.073550E+02	2.050446E+01	5.660927E+02	1.848911E+01	6.000037E+02	1.694265E-03
EBOwithCMAR	4.002521E+02	8.386622E-01	5.236547E+02	6.702270E+00	6.001585E+02	2.583089E-01
LSHADE_cnEpSi	4.055120E+02	1.717506E+01	5.380104E+02	1.063740E+01	6.017437E+02	1.478015E+00
ALCPSO	5.308335E+02	5.904290E+01	6.161281E+02	2.700655E+01	6.053601E+02	5.947913E+00
CLPSO	4.711778E+02	2.235273E+01	5.533829E+02	9.235232E+00	6.000000E+02	7.313105E-14
LSHADE	4.045201E+02	1.653684E+01	5.353546E+02	9.099230E+00	6.002333E+02	2.393252E-01
SADE	4.329790E+02	3.720693E+01	5.492836E+02	1.048001E+01	6.000063E+02	3.290097E-02
JADE	4.042788E+02	1.628497E+01	5.336508E+02	8.884047E+00	6.000000E+02	0.000000E+00
RCBA	4.743177E+02	3.834853E+01	7.518372E+02	5.131458E+01	6.655776E+02	1.003048E+01
EPSO	4.548814E+02	5.265618E+01	6.600886E+02	2.641726E+01	6.000003E+02	5.045327E-04
CBA	5.134138E+02	3.745535E+01	7.559000E+02	5.956804E+01	6.661605E+02	1.013116E+01
LWOA	5.100688E+02	4.313991E+01	7.240533E+02	4.400702E+01	6.517513E+02	9.359289E+00

	F7		F8		F9
	AVG	STD	AVG	STD	AVG	STD
IRIME	7.870448E+02	1.584953E+01	8.597845E+02	1.429043E+01	9.000000E+02	1.461630E-11
EBOwithCMAR	7.617788E+02	1.086112E+01	8.241612E+02	6.468610E+00	1.010946E+03	1.865535E+02
LSHADE_cnEpSi	7.834569E+02	1.377100E+01	8.383194E+02	9.682021E+00	1.216868E+03	3.280355E+02
ALCPSO	8.599645E+02	3.415210E+01	8.992732E+02	3.062454E+01	1.812602E+03	6.849134E+02
CLPSO	7.839056E+02	6.953906E+00	8.472955E+02	7.448280E+00	9.157469E+02	7.964412E+00
LSHADE	7.815275E+02	1.571445E+01	8.335645E+02	9.503744E+00	9.902918E+02	7.764578E+01
SADE	7.749352E+02	1.226535E+01	8.473600E+02	9.523944E+00	9.273077E+02	3.178418E+01
JADE	7.650131E+02	8.822871E+00	8.336426E+02	7.420753E+00	9.052861E+02	1.104424E+01
RCBA	2.010604E+03	2.965324E+02	1.136632E+03	6.332926E+01	9.032123E+03	2.911425E+03
EPSO	9.549782E+02	1.501968E+01	9.418434E+02	4.081173E+01	9.061145E+02	7.897042E+00
CBA	2.101250E+03	3.264006E+02	1.133645E+03	4.797118E+01	9.231007E+03	2.672835E+03
LWOA	1.120801E+03	8.984370E+01	1.063691E+03	5.696527E+01	8.045517E+03	2.647910E+03

	F10		F11		F12
	AVG	STD	AVG	STD	AVG	STD
IRIME	3.605941E+03	4.881660E+02	1.139898E+03	1.331120E+01	3.089471E+03	8.489044E+02
EBOwithCMAR	2.525258E+03	3.088550E+02	1.286875E+03	9.828048E+01	2.880533E+03	4.158699E+02
LSHADE_cnEpSi	2.624054E+03	2.002851E+02	1.318372E+03	8.695477E+01	2.866196E+03	4.327095E+02
ALCPSO	3.954499E+03	6.489345E+02	1.229450E+03	7.662722E+01	1.033384E+04	1.464053E+04
CLPSO	2.880675E+03	2.651593E+02	1.142415E+03	1.084536E+01	9.469498E+05	1.654078E+06
LSHADE	2.752554E+03	4.173304E+02	1.270254E+03	6.932573E+01	2.949696E+03	4.558499E+02
SADE	2.879776E+03	3.917646E+02	1.200905E+03	4.515427E+01	4.726730E+03	2.647403E+03
JADE	2.623302E+03	2.383964E+02	1.212654E+03	7.928624E+01	2.766356E+03	3.864192E+02
RCBA	5.680930E+03	9.100438E+02	1.398023E+03	1.096345E+02	3.280932E+06	1.606840E+06
EPSO	6.247404E+03	5.886293E+02	1.167354E+03	3.521652E+01	7.818073E+03	1.446235E+04
CBA	5.949017E+03	7.647499E+02	1.484663E+03	1.029935E+02	4.628344E+07	2.003444E+07
LWOA	4.946551E+03	7.285654E+02	1.335759E+03	6.241386E+01	2.401700E+07	1.462717E+07

	F13		F14		F15
	AVG	STD	AVG	STD	AVG	STD
IRIME	1.337193E+03	1.082334E+01	1.446440E+03	1.111946E+01	1.573745E+03	6.698064E+01
EBOwithCMAR	2.309903E+03	6.775576E+02	1.700054E+03	1.581119E+02	1.608253E+03	5.932891E+01
LSHADE_cnEpSi	3.344365E+03	7.163644E+02	1.759389E+03	1.762675E+02	1.636242E+03	6.554775E+01
ALCPSO	2.184079E+03	1.462129E+03	1.544889E+03	7.325523E+01	1.647693E+03	1.043166E+02
CLPSO	1.395122E+03	6.029177E+01	2.709409E+03	1.346364E+03	1.591891E+03	4.846005E+01
LSHADE	1.638179E+03	4.617010E+02	1.632836E+03	1.126944E+02	1.603103E+03	6.605244E+01
SADE	1.407279E+03	6.616253E+01	1.557814E+03	7.421909E+01	1.676438E+03	2.594247E+02
JADE	1.348047E+03	3.333131E+01	1.582810E+03	1.344301E+02	1.609297E+03	7.385639E+01
RCBA	7.265341E+04	6.402215E+04	4.696516E+03	2.785539E+03	5.711193E+04	4.796568E+04
EPSO	3.093509E+03	1.468986E+03	2.316170E+03	7.585056E+02	4.753825E+03	2.553358E+03
CBA	9.975372E+04	8.820378E+04	3.683850E+04	2.700027E+04	1.212623E+05	9.118596E+04
LWOA	1.022851E+05	8.880648E+04	6.616154E+03	4.192332E+03	5.954205E+04	5.615821E+04

	F16		F17		F18
	AVG	STD	AVG	STD	AVG	STD
IRIME	2.188709E+03	2.197289E+02	1.961515E+03	8.368609E+01	1.701529E+04	1.205528E+04
EBOwithCMAR	1.993310E+03	1.574016E+02	1.868368E+03	5.873619E+01	1.060575E+04	3.319645E+04
LSHADE_cnEpSi	2.006091E+03	1.640479E+02	1.900019E+03	1.040879E+02	2.028030E+03	7.770539E+01
ALCPSO	2.375960E+03	2.883184E+02	2.135919E+03	1.673665E+02	3.233300E+05	3.245044E+05
CLPSO	2.064265E+03	1.272278E+02	1.909224E+03	3.344437E+01	1.218734E+05	8.742301E+04
LSHADE	2.053002E+03	2.111169E+02	1.876846E+03	6.557391E+01	1.997827E+03	7.261495E+01
SADE	2.026547E+03	1.726456E+02	1.808450E+03	3.439651E+01	1.079344E+04	6.893049E+03
JADE	1.948349E+03	1.473068E+02	1.853893E+03	8.751333E+01	1.589941E+04	5.056289E+04
RCBA	3.142629E+03	4.326378E+02	2.802676E+03	3.220768E+02	7.429505E+04	5.466366E+04
EPSO	2.041652E+03	2.649307E+02	1.931363E+03	7.198191E+01	1.677313E+05	7.516923E+04
CBA	3.304683E+03	5.172750E+02	3.035659E+03	3.673759E+02	1.371818E+05	1.114421E+05
LWOA	2.845689E+03	3.162336E+02	2.368900E+03	1.988964E+02	3.029696E+05	2.802489E+05

	F19		F20		F21
	AVG	STD	AVG	STD	AVG	STD
IRIME	1.959884E+03	6.476027E+01	2.155432E+03	5.634312E+01	2.135293E+03	3.274789E+01
EBOwithCMAR	2.027494E+03	5.613013E+01	2.191757E+03	7.615655E+01	2.100907E+03	1.563620E+00
LSHADE_cnEpSi	2.099848E+03	7.203404E+01	2.181353E+03	7.953380E+01	2.126027E+03	3.902697E+01
ALCPSO	7.603640E+03	6.793607E+03	2.447291E+03	1.420227E+02	2.202135E+03	3.840544E+01
CLPSO	1.955767E+03	2.567386E+01	2.196185E+03	6.826542E+01	2.175023E+03	1.811541E+01
LSHADE	2.040357E+03	7.342819E+01	2.205063E+03	8.215525E+01	2.112883E+03	2.853235E+01
SADE	2.255521E+03	4.320845E+02	2.107392E+03	5.241777E+01	2.173371E+03	2.708825E+01
JADE	2.136178E+03	4.362812E+02	2.150406E+03	5.833396E+01	2.120825E+03	3.842830E+01
RCBA	7.723117E+03	4.296416E+03	2.964025E+03	2.131662E+02	2.188202E+03	2.425089E+01
EPSO	4.506391E+03	3.811221E+03	2.311569E+03	1.462999E+02	2.181575E+03	2.455679E+01
CBA	4.467737E+05	3.324954E+05	2.944890E+03	2.356614E+02	2.227517E+03	3.350044E+01
LWOA	9.466100E+04	6.146595E+04	2.609928E+03	2.214594E+02	2.215128E+03	3.341065E+01

	F22		F23		F24
	AVG	STD	AVG	STD	AVG	STD
IRIME	2.259506E+03	1.682965E+01	2.500000E+03	1.948270E-05	2.600000E+03	2.234190E-13
EBOwithCMAR	2.227091E+03	7.221436E+00	2.832506E+03	1.693732E+01	2.601079E+03	5.909505E+00
LSHADE_cnEpSi	2.246370E+03	1.094491E+01	2.906475E+03	5.638362E+01	2.826014E+03	3.289360E+02
ALCPSO	2.302378E+03	2.860447E+01	3.068606E+03	2.059907E+02	3.123298E+03	4.347163E+02
CLPSO	2.253704E+03	7.132959E+00	2.841313E+03	8.614610E+00	2.636610E+03	1.413640E+02
LSHADE	2.239367E+03	1.035199E+01	2.837869E+03	1.690434E+01	3.322111E+03	2.046145E+02
SADE	2.252534E+03	1.170676E+01	2.839123E+03	2.000302E+01	2.600000E+03	0.000000E+00
JADE	2.236709E+03	6.770296E+00	2.826564E+03	1.041841E+01	2.889271E+03	3.212827E+02
RCBA	2.497327E+03	6.821186E+01	3.666152E+03	3.324807E+02	2.963443E+03	6.156478E+02
EPSO	2.326335E+03	4.395933E+01	2.842157E+03	1.645687E+01	2.600237E+03	1.299120E+00
CBA	2.508071E+03	7.161797E+01	3.530369E+03	2.816484E+02	2.823170E+03	5.107849E+02
LWOA	2.437273E+03	5.166642E+01	3.091381E+03	9.601964E+01	2.740857E+03	3.580514E+02

	F25		F26		F27
	AVG	STD	AVG	STD	AVG	STD
IRIME	2.707107E+03	3.892667E+01	2.800000E+03	8.775726E-13	2.918588E+03	1.018113E+02
EBOwithCMAR	2.964937E+03	4.444758E+01	2.867373E+03	1.035210E+02	3.630655E+03	9.660895E+01
LSHADE_cnEpSi	2.988170E+03	5.291435E+01	4.396978E+03	1.077869E+03	3.733814E+03	1.371558E+02
ALCPSO	2.979627E+03	4.998191E+01	5.062450E+03	1.458940E+03	3.817345E+03	2.051964E+02
CLPSO	2.906255E+03	8.572836E+00	3.874735E+03	8.128199E+02	3.509834E+03	2.967095E+01
LSHADE	2.927482E+03	3.570898E+01	4.835357E+03	3.439051E+02	3.534700E+03	6.625671E+01
SADE	3.022715E+03	4.584665E+01	2.800000E+03	3.377779E-13	3.474498E+03	3.861081E+01
JADE	2.934809E+03	3.928321E+01	4.005817E+03	9.835249E+02	3.535885E+03	7.435108E+01
RCBA	2.998403E+03	1.137192E+02	6.186807E+03	3.541301E+03	3.886796E+03	1.714723E+02
EPSO	2.971111E+03	5.719272E+01	3.387140E+03	9.647026E+02	3.544143E+03	9.782839E+01
CBA	3.019975E+03	1.188225E+02	5.897695E+03	3.939380E+03	3.908455E+03	1.994220E+02
LWOA	2.754015E+03	1.012658E+02	4.201834E+03	2.352678E+03	3.835631E+03	1.280903E+02

	F28		F29		F30
	AVG	STD	AVG	STD	AVG	STD
IRIME	3.005807E+03	3.180635E+01	3.264609E+03	7.599340E+01	5.323413E+03	2.519083E+03
EBOwithCMAR	3.220699E+03	5.279574E+01	3.314116E+03	8.246615E+01	6.601682E+03	4.179781E+03
LSHADE_cnEpSi	3.278647E+03	5.287670E+01	3.400352E+03	1.112338E+02	4.480632E+03	4.524749E+02
ALCPSO	3.419074E+03	4.964794E+02	3.767528E+03	2.488379E+02	9.323689E+04	1.782215E+05
CLPSO	3.280910E+03	1.712080E+01	3.358882E+03	6.498981E+01	1.531679E+04	6.821514E+03
LSHADE	3.273343E+03	6.553523E+01	3.396029E+03	1.152126E+02	4.770491E+03	2.514803E+03
SADE	3.273393E+03	3.954162E+01	3.269617E+03	4.273034E+01	8.067340E+03	2.739648E+03
JADE	3.273310E+03	3.944772E+01	3.368281E+03	9.272310E+01	5.674743E+03	7.892053E+03
RCBA	3.405828E+03	4.996942E+02	4.703163E+03	3.687816E+02	3.265553E+05	2.072308E+05
EPSO	3.282789E+03	3.920240E+01	3.322935E+03	8.698164E+01	5.535669E+03	2.114442E+03
CBA	3.609872E+03	8.361012E+02	4.929752E+03	4.003558E+02	1.991735E+06	1.063884E+06
LWOA	3.362448E+03	6.242544E+02	3.872058E+03	3.305692E+02	1.342063E+06	6.054879E+05

Open in a new tab

Table 12.

Comparison results between IRIME and advanced algorithms

Overall Rank
Algorithm	Rank	+/ = /-	Avg
IRIME	1	∼	3.533333
EBOwithCMAR	3	15/4/11	4.066667
LSHADE_cnEpSi	6	15/5/10	5.6
ALCPSO	9	29/1/0	8.8
CLPSO	7	20/4/6	5.666667
LSHADE	5	16/3/11	4.766667
SADE	4	15/6/9	4.5
JADE	2	14/3/13	3.6
RCBA	11	29/0/1	9.933333
EPSO	8	26/2/2	7
CBA	12	29/1/0	10.9
LWOA	10	30/0/0	9.5

Open in a new tab

To provide a clear visual representation of IRIME’s performance, this study developed convergence curve graphs, in Figure 9. From the graph, it is evident that IRIME does not exhibit outstanding convergence speed. The red curve initially positions relatively higher among numerous algorithms. However, unlike other algorithms that directly converge near a local optimum and struggle to escape, IRIME demonstrates more excellent exploitation capabilities. Despite its slower initial convergence, IRIME and CMS-RS effectively explore and break away from local optima. This ability enables IRIME to converge to better positions in functions such as F9, F13, and F27. Likewise, to assess whether IRIME statistically outperforms these advanced algorithms, a Friedman ranking graph was generated in Figure 10. It is evident from the graph that IRIME secures the top rank among these algorithms, with a value of 3.71. JADE is still a strong algorithm, and IRIME has a slight advantage over JADE. Variations of other DEs, such as SADE and SHADE, also rank closely behind IRIME and JADE, demonstrating excellent performance. It is worth mentioning that EBOwithCMAR also achieves results similar to DE variants and ranks fourth, even more competitive than SHADE. Specific p-values are available in Table 13. From the p-value of the Wilcoxon signed-rank test, it can be seen that IRIME is significantly superior to other algorithms in most cases.

Convergence curves of IRIME and advanced algorithms at IEEE CEC 2017

The Friedman ranking of IRIME and advanced algorithms

Table 13.

p−value of Wilcoxon signed−rank test between IRIME and advanced algorithms

	F1	F2	F3	F4	F5	F6
EBOwithCMAR	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.4772761749E-04	1.7343976283E-06	6.8922902968E-05
LSHADE_cnEpSi	1.7343976283E-06	1.9209211049E-06	1.0246327833E-05	5.7096495243E-02	8.4660816904E-06	1.7343976283E-06
ALCPSO	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	3.5152372790E-06	1.7343976283E-06
CLPSO	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	2.4147041360E-03	1.7343976283E-06
LSHADE	1.7343976283E-06	2.3534209951E-06	2.7652741970E-03	1.9645813713E-03	1.0246327833E-05	2.3534209951E-06
SADE	3.1123151154E-05	5.6061165275E-06	1.0201069525E-01	3.8811142877E-04	8.1877534396E-05	5.3069919381E-05
JADE	1.7343976283E-06	5.3069919381E-05	5.7096495243E-02	2.5967125848E-05	2.1266360107E-06	1.7343976283E-06
RCBA	1.7343976283E-06	3.1816794110E-06	1.7343976283E-06	3.8821823861E-06	1.7343976283E-06	1.7343976283E-06
EPSO	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.8909720230E-04	1.7343976283E-06	1.9209211049E-06
CBA	1.7343976283E-06	9.5899017214E-01	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06
LWOA	1.7343976283E-06	9.3156585911E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06

	F7	F8	F9	F10	F11	F12
EBOwithCMAR	1.2380795615E-05	1.7343976283E-06	1.7343976283E-06	2.1266360107E-06	1.7343976283E-06	3.1849060258E-01
LSHADE_cnEpSi	3.7093530785E-01	1.6394463017E-05	1.7343976283E-06	3.5152372790E-06	1.7343976283E-06	5.7164578367E-01
ALCPSO	1.7343976283E-06	3.4052567233E-05	1.7343976283E-06	5.4462503972E-02	2.6033283895E-06	4.2856858692E-06
CLPSO	3.7093530785E-01	3.3172583108E-04	1.7343976283E-06	7.6908593028E-06	3.8203416302E-01	1.7343976283E-06
LSHADE	1.9861020995E-01	4.7292023374E-06	1.7343976283E-06	3.8821823861E-06	1.7343976283E-06	7.8126371015E-01
SADE	2.7652741970E-03	4.5335631776E-04	1.7343976283E-06	1.6394463017E-05	2.6033283895E-06	6.1564062070E-04
JADE	1.9729484516E-05	1.7343976283E-06	1.3601107968E-05	2.3534209951E-06	4.8602606067E-05	2.7029156618E-02
RCBA	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06
EPSO	1.7343976283E-06	3.1816794110E-06	1.7343976283E-06	1.7343976283E-06	8.9443006475E-04	5.7924461898E-05
CBA	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06
LWOA	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	3.8821823861E-06	1.7343976283E-06	1.7343976283E-06

	F13	F14	F15	F16	F17	F18
EBOwithCMAR	1.7343976283E-06	1.7343976283E-06	3.1617649367E-03	8.9443006475E-04	2.6134309227E-04	3.5888445045E-04
LSHADE_cnEpSi	1.7343976283E-06	1.7343976283E-06	3.3172583108E-04	2.2551238908E-03	1.1748106348E-02	1.7343976283E-06
ALCPSO	1.7343976283E-06	1.7343976283E-06	4.4493372835E-05	6.4242118722E-03	4.0715116266E-05	1.7343976283E-06
CLPSO	1.7343976283E-06	1.7343976283E-06	2.0671113567E-02	1.6565526979E-02	6.8358564253E-03	1.9209211049E-06
LSHADE	1.7343976283E-06	1.7343976283E-06	3.1617649367E-03	2.8485956185E-02	4.5335631776E-04	1.7343976283E-06
SADE	3.4052567233E-05	1.7343976283E-06	2.4519030932E-01	1.8325799472E-03	1.7343976283E-06	1.1748106348E-02
JADE	1.6502656562E-01	6.8922902968E-05	2.7029156618E-02	7.5136622549E-05	4.8969007053E-04	6.1564062070E-04
RCBA	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.9209211049E-06	1.7343976283E-06	2.1266360107E-06
EPSO	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	2.1826721596E-02	1.7790738330E-01	1.7343976283E-06
CBA	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06
LWOA	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	4.2856858692E-06	3.1816794110E-06	1.7343976283E-06

	F19	F20	F21	F22	F23	F24
EBOwithCMAR	2.2248266458E-04	6.2682812500E-02	1.7343976283E-06	1.9209211049E-06	1.7343976283E-06	1.0000000000E+00
LSHADE_cnEpSi	1.3601107968E-05	1.3059163494E-01	2.8021440811E-01	2.9574621307E-03	1.7343976283E-06	1.8712393203E-06
ALCPSO	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	3.1816794110E-06	1.7343976283E-06	5.4553418355E-06
CLPSO	3.8203416302E-01	3.1617649367E-03	6.3197567644E-05	2.4519030932E-01	1.7343976283E-06	1.7343976283E-06
LSHADE	2.6134309227E-04	6.5641143410E-02	1.5927015021E-03	4.8602606067E-05	1.7343976283E-06	1.7333066442E-06
SADE	7.6908593028E-06	6.4242118722E-03	1.2505680433E-04	8.5895825870E-02	1.7343976283E-06	1.0000000000E+00
JADE	1.0569503498E-04	7.8126371015E-01	3.8723026479E-02	1.9729484516E-05	1.7343976283E-06	1.2062023719E-04
RCBA	1.7343976283E-06	1.7343976283E-06	3.5152372790E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06
EPSO	1.0246327833E-05	8.1877534396E-05	9.3156585911E-06	1.0246327833E-05	1.7343976283E-06	5.3372636003E-07
CBA	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06
LWOA	1.7343976283E-06	1.7343976283E-06	1.9209211049E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06

	F25	F26	F27	F28	F29	F30
EBOwithCMAR	1.9209211049E-06	2.4414062500E-04	1.7343976283E-06	1.7333066442E-06	3.0009891313E-02	1.5885549929E-01
LSHADE_cnEpSi	1.7343976283E-06	3.6947913156E-06	1.7343976283E-06	1.7343976283E-06	6.3391355731E-06	4.9498046028E-02
ALCPSO	1.7343976283E-06	1.6741785257E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.9209211049E-06
CLPSO	1.9209211049E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	2.8434237746E-05	1.7343976283E-06
LSHADE	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	2.8434237746E-05	2.1826721596E-02
SADE	1.7343976283E-06	1.2500000000E-01	1.7343976283E-06	1.7343976283E-06	6.8835929823E-01	1.8909720230E-04
JADE	1.7343976283E-06	3.9632291146E-05	1.7343976283E-06	1.7300371293E-06	3.3172583108E-04	6.8358564253E-03
RCBA	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06
EPSO	1.7343976283E-06	2.1320754352E-04	1.7343976283E-06	1.7343976283E-06	2.0671113567E-02	4.2843002855E-01
CBA	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06
LWOA	2.1630223984E-05	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06	1.7343976283E-06

Open in a new tab

The experiments for engineering design

To further validate the performance of IRIME in practical applications, this paper applies IRIME to five real-world engineering problems, including the tension compression string problem (TCSP), cantilever beam problem (CBP), I-beam problem (IBP), and Belleville spring problem (BSP). It compares it with some algorithms that perform excellently in engineering design. The maximum number of iterations in the engineering problems is set to 2000, and the population size is 50. The purpose of this setup is to follow the original RIME²¹ paper.

TCSP

The TCSP¹¹¹ is an optimization problem involving three variables: the number of effective coils (N), average coil diameter (D), and wire diameter (d). As shown in Figure 11, the TCSP problem can be formulated as follows:

\begin{array}{c} C o n s i d e r & \vec{x} = [x_{1} x_{2} x_{3}] = [d D N] \end{array}

\begin{array}{c} O b j e c t i v e f u n c t i o n & f {(\vec{x})}_{\min} = x_{1}^{2} x_{2} x_{3} + 2 x_{1}^{2} x_{2} \end{array}

\begin{array}{c} S u b j e c t t o & h_{1} (\vec{x}) = 1 - \frac{x_{2}^{3} x_{3}}{71785 x_{1}^{4}} \leq 0, \\ h_{2} (\vec{x}) = \frac{4 x_{2}^{2} - x_{1} x_{2}}{12566 (x_{2} x_{1}^{3} - x_{1}^{4})} + \frac{1}{5180 x_{1}^{2}} - 1 \leq 0, \\ h_{3} (\vec{x}) = 1 - \frac{140.45 x_{1}}{x_{2}^{3} x_{3}} \leq 0, \\ h_{4} (\vec{x}) = \frac{x_{1} + x_{2}}{1.5} - 1 \leq 0, \end{array}

\begin{array}{c} V a r i a a b l e r a n g e s & 0.05 \leq x_{1} \leq 2.00, \\ 0.25 \leq x_{2} \leq 1.30, \\ 2.00 \leq x_{3} \leq 15.0 \end{array}

As shown in Table 14, compared with the other five excellent algorithms, IRIME can achieve better results, with the final optimal value being 0.012665.

Table 14.

Comparison of IRIME optimization results with literature for the TCSP

Methods	Optimal values for variables			Optimum result
Methods	d	D	N	Optimum result
IRIME	0.051694	0.356844	11.28156	0.012665
CPSO¹¹²	0.015728	0.357644	11.244543	0.0126747
ES¹¹³	0.051989	0.363965	10.890522	0.012681
GA¹¹⁴	0.05148	0.351661	11.632201	0.0127048
IHS¹¹⁵	0.051154	0.349871	12.076432	0.0126706
EWOA¹¹⁶	0.051961	0.363306	10.91296	0.012667

Open in a new tab

CBP

In CBP,¹¹⁷ the goal is to optimize the performance of the beam while minimizing its weight. There are five variables representing the height of the cross-section, as shown in Figure 12. The mathematical expression of this problem is as follows:

\begin{array}{l} C o n s i d e r & \vec{z} = [z_{1} z_{2} z_{3} z_{4} z_{5}] \\ O b j e c t i v e f u n c t i o n & f {(\vec{z})}_{\min} = 0.6224 (z_{1} + z_{2} + z_{3} + z_{4} + z_{5}) \\ S u b j e c t t o & g (\vec{z}) = \frac{61}{z_{1}^{2}} + \frac{27}{z_{2}^{2}} + \frac{19}{z_{3}^{2}} + \frac{7}{z_{4}^{2}} + \frac{1}{z_{5}^{2}} - 1 \leq 0 \\ V a r i a b l e r a n g e & 0.01 \leq z_{1}, z_{2}, z_{3}, z_{4}, z_{5} \leq 100 \end{array}

Table 15 shows that IRIME can ultimately achieve 1.339957, which is unattainable by the other four algorithms compared in CBP.

Table 15.

Comparison of IRIME optimization results with literature for the CBP

Methods	Optimal values for variables					Optimum result
Methods	$z_{1}$	$z_{2}$	$z_{3}$	$z_{4}$	$z_{5}$	Optimum result
IRIME	6.01674	5.310676	4.49418	3.499961	2.152106	1.339957
CMHHO¹¹⁷	6.012090792	5.308024726	4.492675534	3.50272647	2.158177954	1.33996575
CS⁹¹	6.0089	5.3049	4.5023	3.5077	2.1504	1.33999
GCA_I¹¹⁸	6.01000	5.3000	4.49000	3.49000	2.15000	1.34
MFO¹¹⁹	5.984871773	5.316726924	4.497332586	3.513616468	2.161620293	1.339988086

Open in a new tab

IBP

IBP ¹²⁰ is about reducing vertical displacement in the design process of I-beam. This problem involves four variables as shown in Figure 13. The specific expression of IBP is as follows:

\begin{array}{l} C o n s i d e r & \vec{x} = [x_{1} x_{2} x_{3} x_{4}] \\ O b j e c t i v e f u n c t i o n & f {(\vec{x})}_{\min} = \frac{5000}{\frac{x_{3} (x_{2} - 2 x_{4})}{12} + \frac{x_{1} x_{4}^{3}}{6} + 2 x_{1} x_{4} {(\frac{x_{2} - x_{4}}{2})}^{2}} \\ S u b j e c t t o & g (\vec{x}) = 2 x_{1} x_{3} + x_{3} (x_{2} - 2 x_{4}) \end{array}

\begin{array}{c} V a r i a b l e r a n g e & 10 \leq x_{1} \leq 50 \\ 10 \leq x_{2} \leq 80 \\ 0.9 \leq x_{3} \leq 5 \\ 0.9 \leq x_{4} \leq 5 \end{array}

From Table 16, it can be seen that under the same running environment as RIME, IRIME will have better results. Compared with the other algorithms, IRIME can also achieve very good results, and ultimately IRIME can get 0.013074.

Table 16.

Comparison of IRIME optimization results with literature for the IBP

Methods	Optimal values for variables				Optimum result
Methods	$x_{1}$	$x_{2}$	$x_{3}$	$x_{4}$	Optimum result
IRIME	50	80	0.9	2.321792	0.013074
RIME²¹	50	80	0.9	2.321676	0.01308
SOS¹²¹	50	80	0.9	2.3218	0.131
ARSM¹²⁰	37.05	80	1.71	2.31	0.0157
CS¹¹⁹	50	80	0.9	2.3217	0.131

Open in a new tab

BSP

BSP¹²² involves four variables to make the Belleville spring’s mass as small as possible while satisfying constraints. This problem involves four variables, as shown in Figure 14. Its mathematical expression is as follows:

\begin{array}{c} C o n s i d e r & \vec{x} = [x_{1} x_{2} x_{3} x_{4}] = [D_{e} D_{i} t h] \end{array}

\begin{array}{c} O b j e c t i v e f u n c t i o n & f {(\vec{x})}_{\min} = 0.07075 t π (D_{e}^{2} - D_{i}^{2}) \\ K = \frac{D_{e}}{D_{i}}, P_{\max} = 5400, α = {(\frac{K - 1}{K})}^{2} \frac{6}{π \ln K}, a = \frac{t}{h}, \\ β = (\frac{K - 1}{\ln K} - 1) \frac{6}{π \ln K}, γ = (\frac{K - 1}{2}) \frac{6}{π \ln K}, E = 30 e 6 P s i \\ μ = 0.3, δ_{\max} = 0.2, S = 200 K P s i, D_{\max} = 12.01, H = 2, δ_{l} = h f (a) \end{array}

\begin{array}{c} S u b j e c t t o & h_{1} (\vec{x}) = \frac{4 E δ_{\max}}{α D_{e}^{2} (1 - μ^{2})} [γ t + β (h - \frac{δ_{\max}}{2})] - S \leq 0, \\ h_{2} (\vec{x}) = P_{\max} - \frac{4 E δ_{\max}}{α D_{e}^{2} (1 - μ^{2})} [t (h - δ_{\max}) (h - \frac{δ_{\max}}{2}) + t^{3}] \leq 0, \\ h_{3} (\vec{x}) = δ_{\max} - δ_{l} \leq 0, \\ h_{4} (\vec{x}) = t + h - H \leq 0, \\ h_{5} (\vec{x}) = D_{e} - D_{\max} \leq 0, \\ h_{6} (\vec{x}) = D_{i} - D_{e} \leq 0, \\ h_{7} (\vec{x}) = \frac{h}{D_{e} - D_{i}} - 0.3 \leq 0, \end{array}

\begin{array}{c} V a r i a a b l e r a n g e s & 1 \leq R, R_{0}, Q \leq 16, \\ 1 e - 6 \leq μ \leq 16 e - 6, \end{array}

As shown in Table 17, in the BSP, IRIME can achieve excellent results with 1.979675.

Table 17.

Comparison of IRIME optimization results with literature for the BSP

Methods	Optimal values for variables				Optimum result
Methods	$x_{1}$	$x_{2}$	$x_{3}$	$x_{4}$	Optimum result
IRIME	12.01	10.03047	0.204143	0.2	1.979675
AGOA¹²³	12.0019	10.02024	0204158	0.20013	1.980342
Gene AS I¹²⁴	11.627	9.354	0.205	0.201	2.018070
Gene AS II¹²⁴	11.499	9.268	0.210	0.204	2.162560

Open in a new tab

The experiments for feature selection

In this section, a variant form of IRIME, called bIRIME, was introduced. bIRIME was tested for feature selection using a K-nearest neighbor classifier. The results indicate that bIRIME outperforms IRIME in both low-dimensional and high-dimensional datasets. This superiority is primarily observed in having fewer feature subsets while maintaining higher accuracy levels. To reduce bias in the experiment, this paper follows the same experiment steps and validation methods as those researchers.¹²⁵^,¹²⁶

Simulation experiments

In this study, we conducted experiments using both UCI datasets¹²⁷ and the SBCB machine learning library microarray datasets.¹²⁸ Tables 18, 19, and 20 demonstrate our selection of 12 high-dimensional datasets and 12 low-dimensional datasets from the UCI dataset collection. Among the low-dimensional datasets, the categories range from 2-class to 7-class classifications. The features vary from 11 to 326, and the sample sizes range from 73 to 6598. The high-dimensional datasets primarily consist of medical gene expression data such as Colon, Leukemia, and Lung_Cancer. These datasets typically exhibit numerous features with relatively fewer samples. Due to the high feature count, noise and filtration often lead to insufficient classification accuracy, making feature selection critical. To further demonstrate bIRIME’s performance in high-dimensional datasets, we utilized SBCB microarray data and selected 12 high-dimensional data. These datasets possess a substantial number of features, ranging from 22,277 to 54,675. To comprehensively display bIRIME’s performance, it was compared against bMFO,¹²⁹ bGWO,¹³⁰ bSMA,¹³¹ bALO,¹³² BBA,¹³³ BSSA,¹³⁴ bWOA,¹³⁵ and bHHO.¹³⁶ The dimension size depends on the dataset’s dimensionality, and the population size is set to 20. The parameters involved in these algorithms are detailed in Table 21.

Table 18.

Characteristics of UCI low dimensional datasets

Datasets	Samples	Features	Classes	Datasets	Samples	Features	Classes
WineEW	178	13	3	segment	2310	19	7
BreastEW	569	30	2	penglungEW	73	326	7
clean1	476	166	2	JPNdata	152	11	2
clean2	6598	166	2	semeion	1593	25	2
Dermatology	358	34	7	wdbc	569	30	2
IonosphereEW	351	34	2	DLBCL	267	22	2

Open in a new tab

Table 19.

Characteristics of UCI high dimensional datasets

Datasets	Samples	Features	Classes	Datasets	Samples	Features	Classes
Colon	62	2000	2	Prostate_Tumor	102	10509	2
Leukemia2	72	11225	3	Leukemia	72	7130	2
Lung_Cancer	203	12600	3	Brain_Tumor1	90	5920	5
Tumors_9	60	5726	9	Brain_Tumor2	50	10367	4
Tumors_11	174	12533	11	CNS	60	7129	2
Leukemia1	72	5327	3	DLBCL	77	5469	4

Open in a new tab

Table 20.

Characteristics of SBCB high dimensional datasets

Datasets	Samples	Features	Classes	Datasets	Samples	Features	Classes
Brain_GSE50161	130	54675	5	Leukemia_GSE9476	64	22283	5
Brain_GSE15824	37	54675	4	Leukemia_GSE28497	281	22283	7
Breast_GSE10797	66	22277	3	Liver_GSE14520_U133_2	41	22277	2
Breast_GSE22820	139	33579	2	Liver_GSE14520_U133A	357	22277	2
Colorectal_GSE44861	105	22277	2	Lung_GSE7670	51	22283	2
Colorectal_GSE77953	55	22283	4	Lung_GSE63459	65	24526	2

Open in a new tab

Table 21.

Parameters of competing algorithms

Algorithm
bMFO	a = 2; b = 1
bGWO	a = [0,2]
bSMA	z = 0.03
bALO	–
BBA	a = 0.5; r = 0.5
BSSA	–
bWOA	a = [0,2]; b = 1
bHHO	c = [0,2]

Open in a new tab

Figure 15 vividly illustrates the feature selection process. Data preprocessing is conducted, and necessary preparations are made for cross-validation. Subsequently, bIRIME is employed to update the population and select pertinent features. Finally, the chosen features are utilized for classification, and the average of the best results from the 10-fold cross-validation is taken as the evaluation metric (average fitness value, average error rate, and average number of selected features).

IRIME for feature selection block diagram

The average of fitness is specifically shown in Table 22, the average number of selected feature subsets is in Table 23, and the average error rate is in Table 24. It’s evident from the data in the tables that bIRIME outperforms all other algorithms across all 36 datasets. When observed closely, the average number of selected feature subsets is the smallest on each dataset, accompanied by the lowest average classification error rate—achieving first place in all rankings. On the low-dimensional datasets, bIRIME exhibits outstanding performance. Based on the fitness values, bIRIME yields exceptional results, especially on medical datasets like wdbc and Dermatology. bIRIME can select an average of 4.2 and 6.7 features, with the fewest selected features and remarkably low error rates—outperforming all other algorithms. Some datasets even achieve 100% accuracy, such as Dermatology, IonosphereEW, JPNdata, and penglungEW. Additionally, the STD of bIRIME is extremely low, indicating its stability. To visualize the performance of bIRIME, convergence curves are plotted in Figure 16. These curves indicate that bIRIME converges to better results across the 12 low-dimensional datasets. Furthermore, several high-dimensional microarray medical datasets, such as Leukemia, Brain_Tumor1, and Brain_Tumor2 were considered for an in-depth analysis of high-dimensional data. Even with thousands of features, bIRIME can reduce these datasets to two-digit figures, while other algorithms stay around 4,000 to 5,000 features. The best-performing bGWO still has significantly more features than bIRIME, and bIRIME maintains low classification error rates. For instance, in Tumors_9 and Tumors_11, which are multi-classification problems, bIRIME reduces the dataset features to around 611.8 and 1310, respectively, while maintaining error rates at approximately 0.05 and 0.02. Corresponding convergence curve graphs are presented in Figure 17, highlighting bIRIME’s superior fitness values compared to other algorithms, demonstrating its competitive edge. To further demonstrate the algorithm’s performance on high-dimensional medical microarray gene expression datasets, 12 datasets from SBCB were selected, ranging from dimensions 22277 to 54675. bIRIME drastically reduces the dataset features, decreasing from over ten thousand features, while other algorithms struggle, to just a few dozen features. Particularly in low-sample, binary classification problems such as Liver_GSE14520_U133_2 and Lung_GSE7670, Lung_GSE63459, bIRIME achieves an outstanding error rate of 0. Moreover, the convergence curve graph in Figure 18 vividly illustrates bIRIME’s significantly superior performance compared to other algorithms. IRIME’s relatively balanced exploration and exploitation capabilities enhance its performance, making it more suitable for complex feature selection problems and particularly prominent in high-dimensional feature selection. Additionally, combining the binary version of IRIME in wrapper-based feature selection, the wrapper-based feature selection method can select a feature set that maximizes model performance by comprehensively considering the interrelationships between features and optimizing the final predictive model. This ultimately leads to improved model performance.¹³⁷^,¹³⁸ In conclusion, bIRIME demonstrates excellent results across 12 low-dimensional datasets and 24 high-dimensional medical gene expression datasets, ranking first among the compared algorithms. It significantly reduces the number of features while maintaining algorithm accuracy. Overall, bIRIME exhibits excellent performance in feature selection.

Table 22.

Average fitness value of IRIME and other algorithms

Datasets	Metric	bRLRUN	bMFO	bGWO	bSMA	bALO	BBA	BSSA	bWOA	bHHO
BreastEW	STD	7.9815E-03	2.5737E-02	1.3499E-02	1.2733E-02	8.1784E-03	1.8250E-02	8.9557E-03	1.7751E-02	1.2013E-02
BreastEW	AVG	1.4000E-02	4.6885E-02	1.7667E-02	3.5473E-02	2.5089E-02	6.3953E-02	4.0835E-02	3.3167E-02	3.3696E-02
clean1	STD	8.0113E-03	3.0677E-02	1.3548E-02	2.7793E-02	1.4896E-02	4.3625E-02	4.2877E-02	2.6929E-02	2.3570E-02
clean1	AVG	9.1950E-03	8.7581E-02	1.1962E-02	6.8613E-02	3.8623E-02	1.0669E-01	6.9863E-02	6.7017E-02	5.6441E-02
clean2	STD	2.0256E-03	6.5742E-03	5.8958E-03	5.9095E-03	7.1673E-03	8.0765E-03	5.6477E-03	5.4483E-03	2.1300E-02
clean2	AVG	9.6195E-03	5.9140E-02	1.4324E-02	5.1541E-02	3.4053E-02	5.4659E-02	4.5573E-02	4.8422E-02	4.3298E-02
Dermatology	STD	1.5579E-03	3.2107E-03	7.8873E-03	3.9944E-03	3.0847E-03	2.3074E-02	2.7730E-03	5.4674E-03	9.6025E-03
Dermatology	AVG	9.8529E-03	2.5147E-02	1.2492E-02	1.9706E-02	1.2059E-02	3.6433E-02	2.3529E-02	2.1471E-02	2.0874E-02
IonosphereEW	STD	1.6695E-03	2.5263E-02	8.3861E-03	1.8966E-02	2.5900E-02	2.1877E-02	2.2691E-02	1.0195E-02	1.7295E-02
IonosphereEW	AVG	7.6471E-03	6.7648E-02	1.1244E-02	3.5408E-02	2.4673E-02	7.9065E-02	5.1711E-02	4.0904E-02	2.7185E-02
JPNdata	STD	4.1973E-02	3.9584E-02	4.1074E-02	3.2128E-02	3.2662E-02	3.3562E-02	4.4824E-02	4.7941E-02	3.5860E-02
JPNdata	AVG	2.7208E-02	6.1307E-02	5.4042E-02	3.4104E-02	4.6771E-02	1.0361E-01	4.6979E-02	4.8625E-02	4.1342E-02
penglungEW	STD	3.6117E-04	9.0751E-02	4.9428E-04	6.6442E-02	6.6761E-02	8.5537E-02	6.0959E-02	5.6188E-02	5.8670E-02
penglungEW	AVG	9.5385E-04	7.2404E-02	1.7077E-03	7.1400E-02	6.6839E-02	7.9025E-02	3.8278E-02	4.2958E-02	4.3981E-02
WineEW	STD	2.5960E-03	3.7157E-03	2.5641E-03	4.0744E-03	3.1404E-03	1.6826E-02	4.9488E-03	4.2327E-03	3.3677E-03
WineEW	AVG	1.0385E-02	1.6923E-02	1.1538E-02	1.4231E-02	1.1538E-02	2.6432E-02	1.5000E-02	1.5769E-02	1.1923E-02
segment	STD	4.0264E-03	7.6491E-03	6.8076E-03	5.9976E-03	5.5373E-03	6.3285E-03	5.6081E-03	6.4091E-03	7.8559E-03
segment	AVG	2.3472E-02	3.7996E-02	2.3999E-02	3.2470E-02	2.6318E-02	4.5317E-02	3.7174E-02	3.2552E-02	3.2667E-02
semeion	STD	1.1349E-03	9.1866E-03	2.7014E-03	5.0273E-03	3.2573E-03	8.9377E-03	6.9273E-03	3.7990E-03	6.0018E-03
semeion	AVG	7.5849E-03	3.6688E-02	8.8553E-03	2.9001E-02	2.4024E-02	3.4877E-02	3.2268E-02	2.8356E-02	2.5773E-02
SpectEW	STD	2.5801E-02	5.0296E-02	2.3642E-02	3.7956E-02	3.1472E-02	5.7054E-02	3.8109E-02	4.2316E-02	3.4303E-02
SpectEW	AVG	6.4373E-02	9.8474E-02	6.8878E-02	9.3054E-02	7.0309E-02	1.3453E-01	9.1260E-02	9.0159E-02	9.0684E-02
wdbc	STD	8.4911E-03	1.1968E-02	7.7347E-03	1.3064E-02	1.1282E-02	1.7392E-02	1.2655E-02	1.0739E-02	1.0621E-02
wdbc	AVG	8.6667E-03	3.1167E-02	1.2971E-02	2.3393E-02	1.4000E-02	3.7089E-02	2.6863E-02	2.4530E-02	2.1060E-02
Brain_GSE15824	STD	7.5101E-02	2.2845E-01	1.6307E-01	2.2375E-01	2.2070E-01	2.3333E-01	2.2150E-01	2.3873E-01	1.7940E-01
Brain_GSE15824	AVG	2.3760E-02	2.7655E-01	2.5446E-01	3.0016E-01	2.2860E-01	3.0551E-01	2.6169E-01	2.3637E-01	2.3515E-01
Brain_GSE50161	STD	7.9444E-04	1.0133E-01	1.3569E-01	1.3112E-01	1.2586E-01	1.5356E-01	1.3274E-01	1.3839E-01	1.4238E-01
Brain_GSE50161	AVG	6.0062E-04	2.9848E-01	2.2520E-01	2.8648E-01	2.9762E-01	2.9273E-01	2.7187E-01	2.6971E-01	2.0587E-01
Brain_Tumor1	STD	5.1502E-04	5.2538E-02	4.7623E-02	8.0800E-02	5.4370E-02	6.8528E-02	6.6492E-02	6.6683E-02	6.6470E-02
Brain_Tumor1	AVG	7.5000E-04	8.7679E-02	3.4915E-02	8.2239E-02	7.4680E-02	9.1747E-02	6.8237E-02	7.5196E-02	6.0576E-02
Brain_Tumor2	STD	6.7161E-04	9.9264E-02	9.0702E-02	9.7213E-02	1.2296E-01	1.2498E-01	6.9413E-02	1.0473E-01	9.0844E-02
Brain_Tumor2	AVG	4.5722E-04	1.3717E-01	4.8412E-02	1.1624E-01	1.1373E-01	1.1387E-01	4.1818E-02	7.6558E-02	6.4574E-02
Breast_GSE10797	STD	6.2274E-02	1.4917E-01	1.2966E-01	8.6308E-02	1.4945E-01	1.4455E-01	1.7530E-01	2.0822E-01	1.6484E-01
Breast_GSE10797	AVG	2.9855E-02	2.7758E-01	1.7319E-01	2.7517E-01	2.9292E-01	2.9566E-01	2.5801E-01	2.6357E-01	2.1799E-01
Breast_GSE22820	STD	4.2233E-06	9.6618E-05	2.1338E-04	8.5628E-05	6.9469E-05	2.8593E-03	9.0516E-03	2.5629E-03	8.0285E-04
Breast_GSE22820	AVG	6.8495E-06	2.4786E-02	5.7423E-03	2.4585E-02	2.4083E-02	1.8268E-02	8.8250E-03	1.1224E-02	5.5063E-03
CNS	STD	3.0828E-04	1.1663E-01	2.5095E-04	1.1950E-01	7.6410E-02	1.0827E-01	1.1331E-01	5.1080E-02	1.0908E-01
CNS	AVG	4.4887E-04	2.0079E-01	5.9616E-03	1.4978E-01	7.1066E-02	2.0477E-01	1.1291E-01	1.6154E-01	8.6624E-02
Colon	STD	1.3375E-04	2.3220E-01	7.9046E-02	1.6408E-01	1.2419E-01	1.6361E-01	1.1769E-01	1.5715E-01	1.0511E-01
Colon	AVG	2.2000E-04	2.1891E-01	6.4971E-02	2.1131E-01	1.7304E-01	2.0421E-01	1.4447E-01	1.5245E-01	1.1528E-01
Colorectal_GSE44861	STD	4.7573E-02	1.3523E-01	8.4068E-02	1.0603E-01	8.8658E-02	1.1494E-01	8.8834E-02	1.1544E-01	1.4981E-01
Colorectal_GSE44861	AVG	5.5397E-02	2.1172E-01	1.6615E-01	2.0507E-01	2.0234E-01	2.2692E-01	1.9172E-01	1.9228E-01	1.8551E-01
Colorectal_GSE77953	STD	9.8112E-05	1.4855E-01	6.9790E-02	1.7012E-01	1.1539E-01	1.3445E-01	1.1875E-01	1.1285E-01	1.3783E-01
Colorectal_GSE77953	AVG	8.8857E-05	1.6819E-01	3.8405E-02	1.1959E-01	1.2529E-01	1.8073E-01	9.1832E-02	1.3292E-01	1.0747E-01
DLBCL	STD	6.7466E-05	4.2949E-02	3.7536E-02	3.7527E-02	3.7584E-02	5.5531E-02	4.8047E-03	5.4671E-02	3.6925E-02
DLBCL	AVG	1.0697E-04	3.8334E-02	1.7209E-02	3.5939E-02	3.4550E-02	4.4220E-02	5.0622E-03	3.8731E-02	1.9087E-02
Leukemia_GSE9476	STD	1.7988E-05	7.1088E-02	6.2127E-02	9.4898E-02	7.3056E-02	7.3603E-02	8.0684E-02	7.1131E-02	5.7598E-02
Leukemia_GSE9476	AVG	3.7248E-05	6.8578E-02	3.5054E-02	7.8771E-02	6.9155E-02	7.4000E-02	6.7760E-02	5.5499E-02	3.3527E-02
Leukemia_GSE28497	STD	4.0929E-02	7.0408E-02	4.7071E-02	3.3890E-02	6.7803E-02	4.6150E-02	7.7667E-02	5.0513E-02	6.8309E-02
Leukemia_GSE28497	AVG	5.4689E-02	1.8486E-01	9.5053E-02	1.7731E-01	1.6724E-01	1.8078E-01	1.5189E-01	1.5928E-01	1.3127E-01
Leukemia1	STD	8.7998E-04	3.6799E-03	3.4717E-04	4.2325E-04	2.0229E-04	5.2337E-02	5.2211E-03	3.7791E-03	2.9042E-03
Leukemia1	AVG	5.6786E-04	2.6291E-02	5.2431E-03	2.4129E-02	2.2738E-02	4.2726E-02	5.6796E-03	1.5124E-02	7.3925E-03
Leukemia2	STD	1.2603E-04	5.7290E-02	2.1923E-04	4.2902E-02	2.5406E-04	6.8639E-02	4.8773E-02	4.3369E-02	4.4738E-03
Leukemia2	AVG	1.4477E-04	5.1794E-02	5.4552E-03	3.7868E-02	2.3536E-02	6.1354E-02	2.2450E-02	2.5908E-02	7.7639E-03
Liver_GSE14520_U133_2	STD	1.5149E-06	7.5132E-02	7.5081E-02	7.5093E-02	7.5094E-02	1.2344E-01	1.0897E-01	7.4785E-02	9.0972E-02
Liver_GSE14520_U133_2	AVG	3.8156E-06	4.8469E-02	2.9365E-02	4.8297E-02	4.7669E-02	9.0935E-02	5.5549E-02	3.5035E-02	4.7669E-02
Liver_GSE14520_U133A	STD	1.9078E-02	2.1906E-02	1.5255E-02	4.3383E-02	2.1969E-02	3.9167E-02	2.5007E-02	3.3678E-02	3.3828E-02
Liver_GSE14520_U133A	AVG	1.1138E-02	6.2681E-02	3.5134E-02	6.1369E-02	6.0968E-02	5.6843E-02	5.3275E-02	5.1179E-02	4.0948E-02
Lung_Cancer	STD	1.4101E-03	3.0019E-02	2.4070E-02	3.3055E-02	3.2334E-02	3.6533E-02	3.0129E-02	2.7963E-02	3.2113E-02
Lung_Cancer	AVG	1.6659E-03	5.8019E-02	2.4535E-02	5.2618E-02	4.2477E-02	5.4925E-02	4.2002E-02	3.6842E-02	2.2758E-02
Lung_GSE7670	STD	6.3289E-06	1.2490E-01	1.0692E-01	8.7083E-02	8.5529E-02	8.1515E-02	9.2001E-02	8.7004E-02	1.3341E-01
Lung_GSE7670	AVG	8.5267E-06	7.8513E-02	5.3048E-02	7.8280E-02	6.3476E-02	6.9025E-02	6.9140E-02	6.4658E-02	8.1411E-02
Lung_GSE63459	STD	4.2794E-02	1.4580E-01	1.5776E-01	1.2649E-01	1.9248E-01	1.2000E-01	1.4982E-01	1.9898E-01	1.2405E-01
Lung_GSE63459	AVG	1.3940E-02	3.4092E-01	1.8239E-01	3.0298E-01	2.7123E-01	3.5521E-01	2.3901E-01	2.4614E-01	2.5828E-01
Prostate_Tumor	STD	5.1841E-04	7.2804E-02	3.0095E-02	6.5441E-02	8.4864E-02	6.9476E-02	4.0830E-02	6.8358E-02	4.9091E-02
Prostate_Tumor	AVG	5.9663E-04	1.0209E-01	1.5606E-02	7.9993E-02	6.8506E-02	1.2328E-01	3.6777E-02	6.5066E-02	4.8100E-02
Tumors_9	STD	5.4431E-02	8.4402E-02	8.8788E-02	1.2171E-01	1.3037E-01	1.5507E-01	1.4641E-01	9.0359E-02	1.2999E-01
Tumors_9	AVG	3.0789E-02	6.6583E-02	5.9178E-02	1.8182E-01	1.5710E-01	2.4602E-01	1.6895E-01	1.6403E-01	1.3934E-01
Tumors_11	STD	2.2165E-02	5.4079E-02	2.3720E-02	5.8568E-02	4.5486E-02	5.2819E-02	6.3385E-02	4.9406E-02	5.8841E-02
Tumors_11	AVG	1.5782E-02	9.2876E-02	1.7671E-02	8.4907E-02	7.0923E-02	1.1335E-01	8.6000E-02	7.7339E-02	6.4372E-02
Leukemia	STD	2.0834E-04	2.7844E-03	3.3545E-04	1.7732E-04	2.7192E-04	4.1094E-03	2.8667E-03	3.1979E-03	1.7701E-03
Leukemia	AVG	1.3324E-04	2.5518E-02	5.4369E-03	2.4106E-02	2.2933E-02	1.7079E-02	3.6950E-03	1.3627E-02	6.6115E-03
	AVG	1	7.97	2.46	6.51	4.86	8.31	4.94	5.09	3.83
	Rank	1	8	2	7	4	9	5	6	3

Open in a new tab

Table 23.

Average number of features obtained by IRIME and other algorithms

Datasets	Metric	bIRIMR	bMFO	bGWO	bSMA	bALO	BBA	BSSA	bWOA	bHHO
BreastEW	STD	1.5776	2.5734	2.0656	2.4967	3.1972	2.8983	2.6352	2.9981	3.4254
BreastEW	AVG	6.4	17.2	6.6	13.3	9	13.2	16.5	14.9	13.2
clean1	STD	5.1088	6.8508	3.5277	6.9769	8.4781	5.4985	23.3771	14.1221	21.9396
clean1	AVG	17.1	111.4	20	81.7	62.1	69.7	93.4	90.1	61.7
clean2	STD	2.8597	15.8328	4.2426	6.6072	6.168	5.9861	26.1621	20.0544	17.9679
clean2	AVG	26.2	90.7	27	77.9	68.6	63.5	44.7	64.2	44.8
Dermatology	STD	1.0593	2.1833	1.8288	2.7162	2.0976	2.9814	1.8856	3.7178	2.8363
Dermatology	AVG	6.7	17.1	6.7	13.4	8.2	14	16	14.6	12.4
IonosphereEW	STD	1.1353	1.8288	1.3166	2.9059	1.3499	2.9515	5.2239	3.9285	4.383
IonosphereEW	AVG	5.2	18.3	5.8	13	7.6	13.6	16.8	13.1	11.1
JPNdata	STD	0.78881	1.1595	0.73786	0.73786	0.73786	1.2293	1.1595	1.075	1.1972
JPNdata	AVG	1.8	3.7	2.1	3.1	3.1	3.2	3.3	2.6	3.1
penglungEW	STD	2.3476	5.9479	3.2128	7.3907	6.0452	20.0832	51.8739	32.2897	21.5726
penglungEW	AVG	6.2	148.4	11.1	138.2	106.1	123	68.7	102.8	52.6
WineEW	STD	0.67495	0.96609	0.66667	1.0593	0.8165	1.9692	1.2867	1.1005	0.8756
WineEW	AVG	2.7	4.4	3	3.7	3	5.9	3.9	4.1	3.1
segment	STD	0.67495	1.5811	1.1005	1.1738	0.94281	2.8363	1.2693	1.5239	1.792
segment	AVG	4.7	8.5	4.9	6.4	5	7.4	8.5	6.9	7.1
semeion	STD	6.0148	22.1883	3.7476	7.2793	9.7502	6.4842	40.8799	19.3509	15.3148
semeion	AVG	40.2	143.9	40.6	122.1	105.2	110.4	123.5	118.7	82.9
SpectEW	STD	1.1353	1.8856	2.1187	1.5811	1.5492	2.1731	3.8586	2.0656	3.5917
SpectEW	AVG	4.8	12	5.4	9.5	5.8	7.5	9	9.6	8.7
wdbc	STD	2.2998	1.6364	1.9322	1.8257	1.7764	2.3664	4.4083	3.199	3.0623
wdbc	AVG	4.2	13.7	4.8	11	6.4	12.4	13.1	9.7	9.6
Brain_GSE15824	STD	11.6065	65.3031	153.118	117.1173	112.1333	1007.2227	10851.9124	3637.7805	3019.6378
Brain_GSE15824	AVG	10.4	27118.6	6424.7	26962.3	26629.1	21879.3	12600.6	12613.1	6085.6
Brain_GSE50161	STD	353.9549	70.7041	85.5706	78.8799	52.6081	484.9491	3973.6415	1191.9019	858.0189
Brain_GSE50161	AVG	267.6	11042.8	2581.1	10937.4	10661.5	9041.4	6445.4	5282.2	3038.7
Brain_Tumor1	STD	60.9787	448.2748	57.8624	39.2458	53.3912	158.3239	742.5944	579.1508	936.8074
Brain_Tumor1	AVG	88.8	3132.5	634.5	2863.3	2718.2	2343.3	955.5	1779.5	1298.2
Brain_Tumor2	STD	139.251	85.9613	53.1882	55.7838	59.9941	205.6697	1105.0287	766.008	626.9682
Brain_Tumor2	AVG	94.8	5131.7	1173.9	5060.5	4868.8	4238.6	2104.8	2742	1570.4
Breast_GSE10797	STD	121.6189	932.2376	117.3364	105.8715	38.6586	319.2611	2425.964	936.5835	569.7187
Breast_GSE10797	AVG	147.5	8388.1	1903.5	8043.9	7783.6	6852.1	2274.7	4538.3	2057.1
Breast_GSE22820	STD	2.8363	64.8867	143.2994	57.506	46.6543	1912.4869	6078.8883	1721.1711	539.1781
Breast_GSE22820	AVG	4.6	16645.5	3856.4	16510.5	16173.8	13633.8	5926.7	7538.1	3697.9
CNS	STD	43.9545	536.9503	35.7802	46.8686	38.8829	208.6891	1449.3973	523.8594	579.0644
CNS	AVG	64	3795.5	850	3489	3360.1	2945.4	2424.8	2586.4	1385.7
Colon	STD	5.35	33.8633	9.6609	17.9938	18.2589	45.6172	301.1333	213.3695	84.6493
Colon	AVG	8.8	975.5	156	943	859.5	802.6	259.8	579.1	268.2
Colorectal_GSE44861	STD	100.6106	1663.5714	103.2098	88.8525	70.9926	586.2611	1695.3644	1609.8696	1227.7201
Colorectal_GSE44861	AVG	55.4	11795.4	2585.4	10947.9	10692.2	9420.6	3714.3	5634.7	3001.1
Colorectal_GSE77953	STD	43.7244	76.2848	82.6169	93.6872	67.4105	600.6082	3477.4347	2159.3564	1118.6136
Colorectal_GSE77953	AVG	39.6	11045.4	2600	10957.8	10677.2	8947	3830	5913.6	2734
DLBCL	STD	7.3794	43.2904	32.3495	27.2334	15.943	361.8856	525.5336	358.0402	274.3796
DLBCL	AVG	11.7	2708.5	583.4	2632.1	2480.2	2195.1	553.7	1453.1	788.8
Leukemia_GSE9476	STD	8.0166	1230.3573	76.3036	65.7115	68.4297	346.9749	4050.7056	1775.9559	1037.8521
Leukemia_GSE9476	AVG	16.6	11409.7	2517.7	10912	10658.8	9040.7	3988.7	5580.7	2845
Leukemia_GSE28497	STD	453.0615	2093.6994	100.9667	152.4565	86.8179	412.9731	4868.3445	2632.1426	1536.9839
Leukemia_GSE28497	AVG	1385.7	12364.7	2884.6	11031.1	10761.7	9353.9	7078.2	7723.1	4167.8
Leukemia1	STD	93.7529	392.0516	36.9871	45.0926	21.5523	302.6517	556.252	402.6275	309.4131
Leukemia1	AVG	60.5	2801	558.6	2570.7	2422.5	2072.6	605.1	1611.3	787.6
Leukemia2	STD	28.2931	32.7102	49.2162	41.1183	57.0369	206.3349	1892.2037	583.1634	1004.3603
Leukemia2	AVG	32.5	5534.2	1224.7	5454.6	5283.9	4651.1	1993.3	2769.6	1743
Liver_GSE14520_U133_2	STD	0.67495	35.2844	78.3579	58.6402	23.9372	534.9238	4079.327	1012.2107	302.7592
Liver_GSE14520_U133_2	AVG	1.7	11013.1	2501.8	10936.7	10656.9	8792.2	3586.1	5027.9	2191.7
Liver_GSE14520_U133A	STD	84.0806	1238.4951	198.1242	55.69	56.9928	1228.6671	3153.1031	1583.0377	1396.8465
Liver_GSE14520_U133A	AVG	125	11396	2617.9	10945.6	10666.2	8725.3	3614.3	6274.7	2892.4
Lung_Cancer	STD	355.3536	727.6364	94.772	74.8031	47.5904	213.324	3748.5934	1691.9311	484.3701
Lung_Cancer	AVG	419.8	6463.9	1508.8	6185.8	5967.2	5040	3497.6	4478.9	2126.8
Lung_GSE7670	STD	2.8206	51.8112	57.2539	20.6669	33.1678	578.7427	4161.6603	1142.9429	628.1154
Lung_GSE7670	AVG	3.8	10998.8	2472.7	10894.7	10648.1	9097.7	4704.6	4824.2	2411.3
Lung_GSE63459	STD	225.7063	1871.412	105.4702	283.9564	62.5372	527.5762	4625.5503	1503.2684	1285.2096
Lung_GSE63459	AVG	180.7	13004.6	2923.2	12149.1	11831.7	10319	4344.3	6457.6	3537.9
Prostate_Tumor	STD	108.9589	1067.7715	48.8653	91.198	61.3753	173.2097	2300.4042	1161.1786	585.1257
Prostate_Tumor	AVG	125.4	6029.1	1283.4	5195.8	4959.6	4401.4	1921.1	3873.5	2122.9
Tumors_9	STD	288.3897	516.3061	83.0793	81.4777	48.7785	335.6235	1163.4018	724.2532	406.3999
Tumors_9	AVG	611.8	3092	689.8	2818.8	2669.7	2230.5	2174.7	2492	1399.7
Tumors_11	STD	512.3098	1115.9752	89.4884	81.3853	77.025	317.9088	2373.6164	821.3965	1469.4393
Tumors_11	AVG	1310	7279.1	1618.2	6214.7	5987.2	5091	5200.9	5493.2	3587.2
Leukemia	STD	29.7097	397.0611	47.8355	25.2861	38.7751	222.0476	408.7861	456.0148	252.4211
Leukemia	AVG	19	3638.8	775.3	3437.5	3270.2	2832.7	526.9	1943.2	942.8
	AVG	1	8.94	2.14	7.31	5.92	5.94	4.81	5.36	3.39
	Rank	1	9	2	8	6	7	4	5	3

Open in a new tab

Table 24.

Classification error rate of IRIME and other algorithms

Datasets	Metric	bRLRUN	bMFO	bGWO	bSMA	bALO	BBA	BSSA	bWOA	bHHO
BreastEW	STD	7.3971E-03	2.7868E-02	1.2267E-02	1.3837E-02	9.1414E-03	3.7780E-02	7.4011E-03	1.7050E-02	1.4456E-02
BreastEW	AVG	3.5088E-03	1.9177E-02	7.0175E-03	1.4007E-02	1.0620E-02	7.0243E-02	1.4037E-02	8.7719E-03	1.2312E-02
clean1	STD	8.9776E-03	3.3100E-02	1.4061E-02	2.9450E-02	1.3891E-02	4.4568E-02	4.5523E-02	2.7819E-02	2.4970E-02
clean1	AVG	4.2572E-03	5.6871E-02	6.2500E-03	4.6321E-02	2.0966E-02	1.4685E-01	4.3927E-02	4.1977E-02	3.9849E-02
clean2	STD	1.9951E-03	8.2843E-03	5.6298E-03	6.6392E-03	5.6738E-03	9.0642E-03	1.0893E-02	5.4336E-03	6.6965E-03
clean2	AVG	1.8189E-03	3.3495E-02	6.5172E-03	2.9555E-02	1.4095E-02	4.5766E-02	3.3800E-02	3.0616E-02	3.1372E-02
Dermatology	STD	0.0000E+00	0.0000E+00	8.7841E-03	0.0000E+00	0.0000E+00	6.9606E-02	0.0000E+00	0.0000E+00	8.7841E-03
Dermatology	AVG	0.0000E+00	0.0000E+00	2.7778E-03	0.0000E+00	0.0000E+00	7.2036E-02	0.0000E+00	0.0000E+00	2.7778E-03
IonosphereEW	STD	0.0000E+00	2.7619E-02	9.0351E-03	1.9984E-02	2.7722E-02	3.7861E-02	2.6593E-02	1.2007E-02	1.4765E-02
IonosphereEW	AVG	0.0000E+00	4.2880E-02	2.8571E-03	1.7148E-02	1.4206E-02	8.5420E-02	2.8427E-02	2.2778E-02	1.1433E-02
JPNdata	STD	4.2682E-02	4.2930E-02	4.4618E-02	3.1553E-02	3.4719E-02	1.1073E-01	4.4879E-02	5.2705E-02	3.5206E-02
JPNdata	AVG	1.9167E-02	4.5060E-02	4.5833E-02	1.9583E-02	3.2917E-02	2.2673E-01	3.2083E-02	3.7500E-02	2.7202E-02
penglungEW	STD	0.0000E+00	9.2854E-02	0.0000E+00	6.9537E-02	7.0397E-02	1.0462E-01	6.2268E-02	7.0722E-02	6.3115E-02
penglungEW	AVG	0.0000E+00	9.1468E-02	0.0000E+00	5.2778E-02	5.3175E-02	9.1071E-02	2.9167E-02	6.6468E-02	3.7778E-02
WineEW	STD	0.0000E+00	0.0000E+00	0.0000E+00	0.0000E+00	0.0000E+00	5.7457E-02	0.0000E+00	0.0000E+00	0.0000E+00
WineEW	AVG	0.0000E+00	0.0000E+00	0.0000E+00	0.0000E+00	0.0000E+00	4.4771E-02	0.0000E+00	0.0000E+00	0.0000E+00
segment	STD	4.1069E-03	7.8508E-03	8.1756E-03	5.6994E-03	5.6994E-03	5.8501E-02	3.0269E-03	5.8615E-03	5.8437E-03
segment	AVG	1.1688E-02	1.6450E-02	1.1688E-02	1.6450E-02	1.3853E-02	6.5801E-02	1.5584E-02	1.5152E-02	1.4719E-02
semeion	STD	0.0000E+00	7.3437E-03	2.6518E-03	5.9204E-03	3.0327E-03	1.1005E-02	9.5200E-03	5.1139E-03	5.9432E-03
semeion	AVG	0.0000E+00	1.0039E-02	1.2579E-03	6.2775E-03	4.3947E-03	2.5095E-02	9.4381E-03	6.2736E-03	1.0664E-02
SpectEW	STD	2.6996E-02	5.3540E-02	9.1270E-02	4.0268E-02	3.2490E-02	6.1361E-02	3.8675E-02	4.2238E-02	3.8752E-02
SpectEW	AVG	5.6278E-02	7.4949E-02	5.9585E-02	7.5224E-02	6.0134E-02	2.2498E-01	7.4532E-02	7.1937E-02	7.4644E-02
wdbc	STD	5.5479E-03	1.2405E-02	8.4262E-03	1.2017E-02	1.1096E-02	3.6333E-02	1.1878E-02	1.2430E-02	8.5758E-03
wdbc	AVG	1.7544E-03	8.7719E-03	5.2329E-03	5.3258E-03	3.5088E-03	4.9373E-02	5.2945E-03	8.8033E-03	5.3258E-03
Brain_GSE15824	STD	7.9057E-02	2.3100E-01	1.7160E-01	2.3560E-01	2.3233E-01	2.4417E-01	2.3528E-01	2.4930E-01	1.9023E-01
Brain_GSE15824	AVG	2.5000E-02	3.1500E-01	2.6167E-01	2.9000E-01	2.1500E-01	3.0333E-01	2.6333E-01	3.3667E-01	2.4167E-01
Brain_GSE50161	STD	0.0000E+00	1.0675E-01	1.4288E-01	1.3798E-01	1.3254E-01	1.8059E-01	1.3659E-01	1.4686E-01	1.5008E-01
Brain_GSE50161	AVG	0.0000E+00	2.8810E-01	2.3095E-01	2.7571E-01	2.8810E-01	3.3524E-01	2.7095E-01	2.7143E-01	2.0952E-01
Brain_Tumor1	STD	0.0000E+00	5.2326E-02	5.0185E-02	8.4984E-02	5.7485E-02	1.2373E-01	7.2208E-02	6.6882E-02	7.2587E-02
Brain_Tumor1	AVG	0.0000E+00	7.5556E-02	3.1111E-02	6.1111E-02	5.4444E-02	1.4111E-01	6.3333E-02	8.8333E-02	5.2222E-02
Brain_Tumor2	STD	0.0000E+00	1.0436E-01	9.5598E-02	1.0238E-01	1.2959E-01	1.9487E-01	7.0273E-02	1.1434E-01	9.6609E-02
Brain_Tumor2	AVG	0.0000E+00	1.1833E-01	4.5000E-02	9.6667E-02	9.5000E-02	2.9333E-01	3.3333E-02	8.6667E-02	6.0000E-02
Breast_GSE10797	STD	6.5494E-02	1.5685E-01	1.3664E-01	9.0690E-02	1.5732E-01	1.8436E-01	1.8492E-01	2.1991E-01	1.7343E-01
Breast_GSE10797	AVG	3.0952E-02	2.6524E-01	1.7619E-01	2.6381E-01	2.8333E-01	3.5238E-01	2.6429E-01	2.6286E-01	2.2286E-01
Breast_GSE22820	STD	0.0000E+00	0.0000E+00	0.0000E+00	0.0000E+00	0.0000E+00	2.2588E-02	0.0000E+00	0.0000E+00	0.0000E+00
Breast_GSE22820	AVG	0.0000E+00	0.0000E+00	0.0000E+00	0.0000E+00	0.0000E+00	7.1429E-03	0.0000E+00	0.0000E+00	0.0000E+00
CNS	STD	0.0000E+00	1.2298E-01	0.0000E+00	1.2565E-01	8.0508E-02	1.8829E-01	1.1793E-01	5.4758E-02	1.1621E-01
CNS	AVG	0.0000E+00	1.8333E-01	0.0000E+00	1.3190E-01	5.0000E-02	3.3286E-01	1.0095E-01	1.5095E-01	8.0952E-02
Colon	STD	0.0000E+00	2.4467E-01	8.3277E-02	1.7281E-01	1.3043E-01	1.7368E-01	1.2267E-01	1.6551E-01	1.1156E-01
Colon	AVG	0.0000E+00	2.0476E-01	6.4286E-02	1.9762E-01	1.5952E-01	2.1190E-01	1.4524E-01	1.4524E-01	1.1429E-01
Colorectal_GSE44861	STD	5.0197E-02	1.4438E-01	8.8567E-02	1.1162E-01	9.3352E-02	1.3306E-01	9.5036E-02	1.2315E-01	1.5787E-01
Colorectal_GSE44861	AVG	5.8182E-02	1.9500E-01	1.6879E-01	1.9000E-01	1.8773E-01	2.3909E-01	1.9303E-01	1.8909E-01	1.8818E-01
Colorectal_GSE77953	STD	0.0000E+00	1.5646E-01	7.3525E-02	1.7916E-01	1.2151E-01	1.3572E-01	1.2236E-01	1.2062E-01	1.4470E-01
Colorectal_GSE77953	AVG	0.0000E+00	1.5095E-01	3.4286E-02	1.0000E-01	1.0667E-01	2.1357E-01	8.7619E-02	1.2595E-01	1.0667E-01
DLBCL	STD	0.0000E+00	4.5175E-02	3.9528E-02	3.9528E-02	3.9528E-02	9.6806E-02	0.0000E+00	5.6626E-02	3.9528E-02
DLBCL	AVG	0.0000E+00	1.4286E-02	1.2500E-02	1.2500E-02	1.2500E-02	8.0357E-02	0.0000E+00	2.6786E-02	1.2500E-02
Leukemia_GSE9476	STD	0.0000E+00	7.3128E-02	6.5494E-02	9.9887E-02	7.6947E-02	8.0781E-02	8.0312E-02	7.3128E-02	6.0234E-02
Leukemia_GSE9476	AVG	0.0000E+00	4.5238E-02	3.0952E-02	5.7143E-02	4.7619E-02	7.6190E-02	6.1905E-02	4.5238E-02	2.8571E-02
Leukemia_GSE28497	STD	4.3607E-02	7.3975E-02	4.9652E-02	3.5586E-02	7.1267E-02	7.5138E-02	7.8860E-02	5.2083E-02	7.1357E-02
Leukemia_GSE28497	AVG	5.4295E-02	1.6539E-01	9.3242E-02	1.6058E-01	1.5062E-01	2.0426E-01	1.4316E-01	1.4942E-01	1.2834E-01
Leukemia1	STD	0.0000E+00	0.0000E+00	0.0000E+00	0.0000E+00	0.0000E+00	1.0623E-01	0.0000E+00	0.0000E+00	0.0000E+00
Leukemia1	AVG	0.0000E+00	0.0000E+00	0.0000E+00	0.0000E+00	0.0000E+00	6.2500E-02	0.0000E+00	0.0000E+00	0.0000E+00
Leukemia2	STD	0.0000E+00	6.0234E-02	0.0000E+00	4.5175E-02	0.0000E+00	1.0773E-01	4.5175E-02	4.5175E-02	0.0000E+00
Leukemia2	AVG	0.0000E+00	2.8571E-02	0.0000E+00	1.4286E-02	0.0000E+00	1.1131E-01	1.4286E-02	1.4286E-02	0.0000E+00
Liver_GSE14520_U133_2	STD	0.0000E+00	7.9057E-02	7.9057E-02	7.9057E-02	7.9057E-02	1.3006E-01	1.0541E-01	7.9057E-02	9.5598E-02
Liver_GSE14520_U133_2	AVG	0.0000E+00	2.5000E-02	2.5000E-02	2.5000E-02	2.5000E-02	7.8333E-02	5.0000E-02	2.5000E-02	4.5000E-02
Liver_GSE14520_U133A	STD	1.9977E-02	2.3361E-02	1.6042E-02	4.5679E-02	2.3189E-02	4.3890E-02	2.3007E-02	3.5082E-02	3.4871E-02
Liver_GSE14520_U133A	AVG	1.1429E-02	3.9056E-02	3.0798E-02	3.8739E-02	3.8977E-02	4.4700E-02	4.7540E-02	3.9048E-02	3.6270E-02
Lung_Cancer	STD	0.0000E+00	3.2547E-02	2.5218E-02	3.4707E-02	3.4035E-02	4.5504E-02	2.5589E-02	2.5986E-02	3.4761E-02
Lung_Cancer	AVG	0.0000E+00	3.4073E-02	1.9524E-02	2.9549E-02	1.9787E-02	8.3358E-02	2.9603E-02	2.0072E-02	1.5072E-02
Lung_GSE7670	STD	0.0000E+00	1.3152E-01	1.1249E-01	9.1692E-02	9.0010E-02	8.6353E-02	1.0124E-01	9.1692E-02	1.3984E-01
Lung_GSE7670	AVG	0.0000E+00	5.6667E-02	5.0000E-02	5.6667E-02	4.1667E-02	5.3333E-02	6.1667E-02	5.6667E-02	8.0000E-02
Lung_GSE63459	STD	4.5175E-02	1.5520E-01	1.6602E-01	1.3330E-01	2.0265E-01	1.0966E-01	1.5199E-01	2.0970E-01	1.3159E-01
Lung_GSE63459	AVG	1.4286E-02	3.3095E-01	1.8571E-01	2.9286E-01	2.6012E-01	4.0238E-01	2.4226E-01	2.4524E-01	2.6429E-01
Prostate_Tumor	STD	0.0000E+00	7.5727E-02	3.1623E-02	6.8862E-02	8.9463E-02	1.3870E-01	4.6906E-02	7.0052E-02	5.1640E-02
Prostate_Tumor	AVG	0.0000E+00	7.7273E-02	1.0000E-02	5.8182E-02	4.7273E-02	2.0818E-01	2.9091E-02	4.9091E-02	4.0000E-02
Tumors_9	STD	5.6626E-02	2.7035E-01	9.3914E-02	1.2790E-01	1.3735E-01	2.0722E-01	1.5429E-01	9.2272E-02	1.3791E-01
Tumors_9	AVG	2.6786E-02	3.2750E-01	5.5952E-02	1.6548E-01	1.4083E-01	5.0810E-01	1.5786E-01	1.4976E-01	1.3381E-01
Tumors_11	STD	2.3424E-02	8.7234E-02	2.4942E-02	6.1668E-02	4.7832E-02	4.7091E-02	6.2645E-02	5.3297E-02	6.3592E-02
Tumors_11	AVG	1.1111E-02	9.3989E-02	1.1806E-02	6.3278E-02	4.9513E-02	1.3793E-01	6.8685E-02	5.8342E-02	5.2696E-02
Leukemia	STD	0.0000E+00	0.0000E+00	0.0000E+00	0.0000E+00	0.0000E+00	7.5190E-02	0.0000E+00	0.0000E+00	0.0000E+00
Leukemia	AVG	0.0000E+00	0.0000E+00	0.0000E+00	0.0000E+00	0.0000E+00	5.7738E-02	0.0000E+00	0.0000E+00	0.0000E+00
	AVG	1	6.39	2.33	4.92	3.64	8.75	4.78	4.78	3.81
	Rank	1	8	2	7	3	9	5	5	4

Open in a new tab

Convergence curves of bIRIME and other algorithms for UCI low dimensional datasets

Convergence curves of bIRIME and other algorithms for UCI high dimensional datasets

Convergence curves of bIRIME and other algorithms for SBCB high dimensional datasets

Time cost

Figure 19 shows the time each algorithm takes with low-dimensional data, from which it can be seen that bIRIME takes slightly more time, primarily due to the additional computation of fitness values, increasing the algorithm’s time, but from the figure, it can be observed that the time increase is not very noticeable. Figure 20 displays the time each algorithm takes with high-dimensional data, from which it is discernible that bIRIME has a higher time cost, with a significant difference. It is worth mentioning that Figures 17 and 18 show that bIRIME can converge at the 2/5 mark of the convergence curve in almost all high-dimensional datasets, such as Colon, Leukemia2, Lung_Cancer, Tumors_9, Tumors_11, and Leukemia1. This indicates that when bIRIME achieves peak performance, the time difference with other algorithms is not as extensive as indicated in Figure 20. To sum it up, while bIRIME does come with a time cost, it indeed manages to enhance performance.

The time cost of bIRIME and other algorithms on high dimensional datasets

Conclusions and future directions

RIME is an emerging metaheuristic algorithm that suffers from issues like imbalanced exploration and exploitation, making it prone to local optima. To address these limitations, this paper introduces a variant of RIME, incorporating SB to facilitate inter-population information exchange, enhancing population diversity and subsequently bolstering exploration capabilities. The addition of composite mutation strategy and restart strategy further amplifies RIME’s exploitation ability and equips it with the capability to escape local optima. To evaluate IRIME’s performance, the study utilizes the IEEE CEC 2017 benchmark functions. In the initial analysis of historical trajectories, the search process of IRIME can be preliminarily obtained. The average fitness value shows that the function of CMS-RS allows RIME to reach a better fitness value quickly, and in the late stage of the population, IRIME can jump out of the local optimal situation. The convergence curve can initially show that IRIME is superior to RIME, and it can also be seen from the one-dimensional trajectory analysis that IRIME will have a broader search in the early and late stages compared to RIME. From the balance analysis, it can be seen that IRIME has an advantage over RIME in terms of balance. IRIME has solved the problem of the weak exploration ability of RIME. From the diversity analysis, it can be seen that the population diversity of IRIME is more abundant, allowing IRIME to explore a broader space and providing the ability to jump out locally. This is also the role that SB plays in it. The stability analysis shows that IRIME expands to more dimensions, and its stability is better than that of RIME. When compared with conventional algorithms, IRIME has significant advantages. In addition, when compared with advanced algorithms, which include EBOwithCMAR, LSHADE_cnEpSi, LSHADE, SADE, and JADE, which performed outstandingly in IEEE CEC 2017, IRIME also has an advantage. For functions like F1, IRIME can converge around the optimal theoretical value, and IRIME also has an advantage in composite functions. However, compared to excellent algorithms such as JADE and EBOwithCMAR, IRIME shows some disadvantages in multimodal and hybrid functions, which is a direction for future improvement. Nevertheless, the overall performance of IRIME is still the first to be compared to these advanced algorithms. To verify the performance of IRIME in practical applications, IRIME was applied to four engineering problems: TCSP, IBP, BSP, and CBP. This demonstrated that IRIME also has good application potential and performance in practical engineering directions. Additionally, the paper introduces bIRIME, a binary version validated across 12 UCI low-dimensional datasets and 24 high-dimensional medical datasets. The validation underscores bIRIME’s substantial potential in addressing feature selection problems, notably in high-dimensional datasets, where it significantly reduces feature numbers and improves KNN classification accuracy.

Moving forward, the focus remains on refining the algorithm IRIME and exploring its application in various domains, including engineering optimization, multi-objective optimization, and image segmentation. There are many engineering design problems with complex conditions that need to be optimized, including multi-objective engineering design problems. Moreover, the multi-objective problem is also a problem studied by many researchers, which includes some workshop scheduling and other economic problems. In addition, medical image segmentation is also a focal point of research. While solving the existing problems of IRIME, such as poor performance on multimodal functions, the potential application of IRIME to these problems will be explored. In addition, we urgently need to verify the potential of IRIME in real-time applications.

Limitations of the study

Of course, the current IRME still has some limitations. First, on the IEEE CEC 2017 test functions, despite reaching first place compared to many algorithms, both convergence accuracy and the capability of multimodal functions need to be improved. Second, for engineering design problems, there exist some unstable situations where it does not always converge to the best value. Third, in feature selection issues, the binary conversion method only tested one, and other conversion functions need to be tested. Moreover, only one type of classifier was used on the classifier, and no tests were conducted on other classifiers. Fourth, in feature selection, its running time would be longer than that of other algorithms because the added mechanism would increase the complexity of RIME. In summary, when applying IRIME to practical problems in situations with different classifiers, IRIME may encounter worse situations than KNN, and there might be an occurrence of overfitting. In addition, the selection of significance level is also an important factor affecting the experiment in this article.

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Software and algorithms

RIME	Ali Asgher Heidari	https://aliasgharheidari.com/RIME.html
IRIME	This paper	https://github.com/TingJin0/IRIME.git

Deposited data

UCI dataset	UCI Repository	https://archive.ics.uci.edu/
SBCB dataset	SBCB Lab	https://sbcb.inf.ufrgs.br/

Open in a new tab

Resource availability

Lead contact

For further inquiries for information, please direct them to the lead contact, Huiling Chen, who will handle them accordingly. You can reach him via email at chenhuiling.jlu@gmail.com.

Materials availability

This study did not generate new materials.

Data and code availability

•
The dataset for this study is publicly accessible online and can be shared by the primary contact upon request. Links to the code and DOIs are included in the resources table.
•
The data presented in this paper will be made available through the primary contact upon request.
•
The paper does not include the original code directly, but it can be accessed from the designated contact upon request for reanalysis purposes.

Method details

The proposed method primarily comprises RIME, SB, and CMS-RS, along with the relevant theories and content regarding feature selection.

RIME

RIME is a new physics-based metaheuristic algorithm whose main idea is to simulate the growth process of rice-ice. Its modeling process is divided into three parts: soft-time, hard-rime, and greedy selection.

Soft-rime

Due to relatively low wind forces, rime-ice primarily grows outward from the center of the frost during the initial stages of rime-ice formation. This growth process does not continue indefinitely but gradually reaches a stable state. Expressed mathematically, it can be represented as follows:

X_{i, j}^{n e w} = X_{j}^{b} + 2 \times (h_{1} - 0.5) \times \cos θ \times β \times (h_{2} \times (u b_{j} - l b_{j}) + l b_{j}), r_{1} < E

(Equation 1)

θ = t π / 10 T

(Equation 2)

β = 1 - [t w / T] / w

(Equation 3)

E = \sqrt{t / T}

(Equation 4)

where, $X_{i, j}^{n e w}$ represents the generated new candidate solution, i and j denote the i-th particle and the j-th dimension, respectively. $X_{j}^{b}$ signifies the value of the optimal solution's j-th dimension discovered thus far. $h_{1}$ , $h_{2}$ and $r_{1}$ are uniformly distributed random numbers between [0, 1]. $u b_{j}$ and $l b_{j}$ represent the upper and lower bounds in j-th dimension. $[\cdot]$ denotes rounding, while t and T depict the present iteration number and the total iteration count, respectively. In the original paper, $w$ is set to 5, and this paper follows the original setting. A visual representation of soft-rime is depicted in Figure S1.

Hard-rime

In high wind conditions, rime-ice tends to grow in the same direction and exhibits crossing phenomena. According to the inspiration, the authors proposed the rime puncture mechanism, represented mathematically as follows:

X_{i, j}^{n e w} = X_{j}^{b}, r_{2} < N (F_{i})

(Equation 5)

where $X_{i, j}^{n e w}$ represents the generated new candidate solution, $r_{2}$ is a random number uniformly distributed from 0 to 1. $F_{i}$ represents the fitness value of the i-th individual, and $N (F_{i})$ is the Z-score standardized value of $F_{i}$ . A schematic diagram of hard-rime puncture is shown in Figure S2.

Greedy selection

After generating a new candidate solution, its fitness value is computed to ensure its reliability. If the fitness value is less than (all problems considered in this paper are minimization problems) the fitness value of the current solution, the algorithm replaces the original individual with the generated candidate solution. The pseudocode of RIME is shown in Algorithm 1.

Algorithm 1. Pseudo-code for RIME.

1. Initialization: population $X$ , $X^{b}$ , $T$ , $F_{i}$ , $E$

2. While t<T

3. if $r_{1}$ <E

4. soft-rime: update $X_{i}^{n e w}$ by Equations 1, 2, 3, and 4

5. end if

6. if $r_{2}$ < $N (F_{i})$

7. hard-rime: update $X_{i}^{n e w}$ by Equation 5

8. end if

9. if fitness of ( $X_{i}^{n e w}$ )< $F_{i}$

10. greedy selection: $X_{i} = X_{i}^{n e w}$

11. end if

12. update t, $F_{i}$ , $X^{b}$

13. end while

14. return $X^{b}$

After reviewing the entire algorithm during the soft-rime process, although it can move towards the newly generated rime particles, increasing the population's diversity as described in Equation 1, it only searches around the optimal point. Its influence on population diversity is limited, and RIME lacks effective communication among individuals, affecting its ability to discover potential optimal solutions among them. Additionally, in the hard-rime phase, higher fitness values tend to assign better values to certain dimensions after Z-score normalization. Coupled with greedy selection, although it somewhat enhances RIME's exploitation capability, it severely diminishes its exploration ability. This tendency makes RIME prone to falling into local optima when dealing with complex problems. Therefore, suitable methods are needed to solve the problems that exist in RIME.

The proposed IRIME

RIME lacks interaction among individuals, quickly falling into local optima and experiencing low convergence accuracy, mainly when dealing with complex problems like feature selection. The main reason for choosing SB is its potential to enhance RIME's global capabilities. SB is inspired by HHO, which has strong global search abilities. Integrating SB aims to enhance RIME's global capabilities and exploration abilities. The main reason for selecting CMS-RS is because it strengthens population communication abilities and can also break out of local optima. CMS-RS is inspired by CoDE, and enhancing population information exchange through individual differential operations enables new spaces to be explored through restart mechanisms. Including SB and CMS-RS enables effective individual communication, expands RIME's search space, and enhances its convergence accuracy. When RIME gets trapped in local optima, a restart strategy can be initiated to explore the problem further. Let us delve into detailed explanations of SB and CMS-RS.

SB

The concept of SB is primarily derived from HHO.²⁸ Hawks, while hunting, hover in the air to observe the positions of other individuals and prey, aiming to find the optimal attack position. The specific mathematical expression for this concept is given in Equation 6:

X_{i, j}^{n e w} = \begin{array}{c} {\begin{array}{c} X_{A} - k_{1} | X_{B} - 2 k_{2} X_{i} |, p \geq 0.5 \\ X^{b} - X^{m} - k_{3} (k_{4} (u b_{j} - l b_{j}) + l b_{j}), p < 0.5 \end{array} & | E_{0} | > 1 \end{array}

(Equation 6)

where $X_{i}^{n e w}$ represents the newly generated candidate solution, $X_{A}$ and $X_{B}$ denote two distinct individuals within the population. $k_{1}$ , $k_{2}$ , $k_{3}$ , $k_{4}$ , and p are uniformly distributed random numbers within the interval [0, 1]. $X^{m}$ signifies the mean of all individuals, and $X_{i}$ denotes the i-th individual. $u b_{j}$ and $l b_{j}$ represent the upper and lower bounds in j-th dimension, respectively. $| \cdot |$ indicates the absolute value. It can be observed that SB updates the newly generated candidate solution with equal probability. This method involves multiple individuals, making full use of information within the population, and its randomness contributes to increasing population diversity. $E_{0}$ as Equation 7:

E_{0} = (a - 1) \times 2 (1 - t / T)

(Equation 7)

where t represents the current iteration number, T denotes the total iteration count, and a stands for a uniformly distributed random number within the interval [0, 2].

CMS-RS

The inclusion of CMS-RS is primarily derived from the CoDE,¹³⁹ which has been further explored by other researchers as well.¹⁴⁰ CMS-RS can significantly enhance the precision of RIME. When RIME gets stuck in a local optimum, CMS-RS can assist in restarting RIME to explore other dimensions within the solution space. Firstly, CMS enhances information exchange between individuals through three different differentiation methods. The specific mathematical model is as follows:

X 1_{j} = {\begin{array}{c} \begin{array}{c} X_{r 1, j} + F_{1} (X_{r 2, j} - X_{r 3, j}) i f & r a n d < C_{r 1} o r j = j_{r a n d} \end{array} \\ \begin{array}{c} X_{i, j} & e l s e \end{array} \end{array}

(Equation 8)

where $X 1_{j}$ represents the newly generated solution's value in dimension j, where r1, r2, and r3 are three different integers ranging from 1 to N, with N being the population size. $X_{r 1, j}$ , $X_{r 2, j}$ , and $X_{r 3, j}$ denote the values in the j-th dimension for three distinct individuals within the population. $X_{i, j}$ signifies the value of the i-th individual in the j-th dimension. In this section, the subsequent $X_{i, j}$ represents the same concept. rand refers to a uniformly distributed random number between 0 and 1. The value for $C_{r 1}$ is 0.1, and $F_{1}$ is 1. j represents the j-th dimension, while $j_{r a n d}$ is an integer ranging from 1 to D. D signifies the problem's dimension.

X 2_{j} = {\begin{array}{c} \begin{array}{c} X_{r 4, j} + F_{2} (X_{r 5, j} - X_{r 6, j}) + F_{2} (X_{r 7, j} - X_{r 8, j}) i f & r a n d < C_{r 2} o r j = j_{r a n d} \end{array} \\ \begin{array}{c} X_{i, j} & e l s e \end{array} \end{array}

(Equation 9)

where $X 2_{j}$ represents the newly generated solution's value in dimension j. r4-r8 are four distinct integers ranging between 1 and N, with N being the population size. $X_{r 4, j}$ - $X_{r 8, j}$ respectively denote the values in the j-th dimension for four distinct individuals within the population. rand refers to a uniformly distributed random number within the range of 0 to 1. Here, the value for $C_{r 2}$ is 0.2, which is an increased probability compared to $C_{r 1}$ , providing a greater chance for differentiation. Similarly, the number of individuals selected for differentiation has increased from three to four, fully utilizing the information within the population. Here, $F_{2}$ is valued at 0.8. j represents the j-th dimension, while $j_{r a n d}$ is an integer ranging from 1 to D. D signifies the problem's dimension.

X 3_{j} = {\begin{array}{c} \begin{array}{c} X_{i, j} + r a n d (X_{r 9, j} - X_{i, j}) + F_{3} (X_{r 10, j} - X_{r 11, j}) i f & r a n d < C_{r 3} o r j = j_{r a n d} \end{array} \\ \begin{array}{c} X_{i, j} & e l s e \end{array} \end{array}

(Equation 10)

where, $X 3_{j}$ represents the newly generated solution's value in dimension j. r9-r11 are three distinct integers ranging between 1 and N, with N being the population size. $X_{r 9, j}$ , $X_{r 10, j}$ , and $X_{r 11, j}$ respectively denote the values in the j-th dimension for three distinct individuals within the population. rand refers to a uniformly distributed random number within the range of 0 to 1. Here, the value for $C_{r 3}$ is 0.9, indicating an increased probability for differentiation compared to the previous two differential mechanisms, aiming to enhance population diversity. $F_{3}$ is valued at 1. j represents the j-th dimension, while $j_{r a n d}$ is a random integer ranging from 1 to D. D signifies the problem's dimension. After the completion of CMS, the optimal individual selected is denoted as $X_{i}^{n e w}$ . The subsequent section pertains to the restart strategy, outlined as follows.

During the entire operation of RIME, we employed a variable count(i) to track how long each individual had gone without further updating its fitness value and the duration since the CMS result had not outperformed the current fitness value. Here, i represents an integer within the range of [1, N], denoting the i-th individual. Upon exceeding a certain threshold, set at 50 in this study, we initiate RS. There are two specific RS strategies, with the first one being random restart, as depicted in Equation 11:

Y 1_{j} = r a n d (u b_{j} - l b_{j}) + l b_{j}

(Equation 11)

where $Y 1_{j}$ represents the newly generated solution's value in dimension j, rand is a uniformly distributed random number within [0, 1], and $u b_{j}$ and $l b_{j}$ represent the upper and lower bounds in j-th dimension. The second strategy involves opposition restart, as illustrated in Equation 12:

Y 2_{j} = r a n d (u b_{j} + l b_{j}) - X_{i, j}

(Equation 12)

where $Y 2_{j}$ represents the newly generated solution's value in dimension j, rand is a uniformly distributed random number within [0,1], and $u b_{j}$ and $l b_{j}$ represent the upper and lower bounds in j-th dimension. Upon the completion of the restart strategy, the best-performing individual is selected as $X_{i}^{n e w}$ .

Framework of proposed IRIME

During the execution of IRIME, the population's update is determined by $E_{0}$ . $E_{0}$ determines whether the population is updated through SB or according to the original RIME method. Based on the nature of $E_{0}$ , the algorithm is more likely to update the population using the SB method in the initial stages. Indeed, this form is not found in algorithms like PSO and DE. DE works on a simple concept of differential and mutation, and PSO operates on the singular idea of swarm intelligence. Both of these methods have a straightforward optimization process. As iterations progress, the probability of executing SB decreases gradually until it reaches zero. This approach facilitates extensive information exchange within the population, allowing RIME's convergence capability to prevail in the later stages. Following each population update, CMS is employed to leverage the information within the population further and explore potential solutions among individuals. The best-performing individual is greedily selected based on fitness; if it surpasses the current individual, a replacement strategy is performed. When the algorithm becomes trapped in local optima, an RS restarts and replaces individuals within the population. RS is not present in simple DE and PSO, which is why they are particularly prone to falling into local optima in the later stages. However, the RS in this paper can constantly monitor the running state of IRIME. When an individual falls into a local optimum, it performs a restart. In summary, the combination of these mechanisms is not straightforward and does indeed differ from classical algorithms such as DE and PSO. The specific pseudocode is provided in Algorithm 2, and the process flow is depicted in Figure S3.

Algorithm 2. Pseudo-code for IRIME.

1. Initialization: population $X$ , $X^{b}$ , $T$ , $F_{i}$ , $E$ , count(i)

2. While t<T

3. if $| E_{0} |$ >1

4. SB: update $X_{i}^{n e w}$ by Equation 6

5. else

6. if $r_{1}$ <E

7. soft-rime: update $X_{i}^{n e w}$ by Equations 1, 2, 3, and 4

8. end if

9. if $r_{2}$ < $N (F_{i})$

10. hard-rime: update $X_{i}^{n e w}$ by Equation 5

11. end if

12. end if

13. if fitness of ( $X_{i}^{n e w}$ )< $F_{i}$

14. greedy selection: $X_{i} = X_{i}^{n e w}$

15. else

16. count(i)=count(i)+1

17. end if

18. CMS: Choose best position in X1 X2 and X3 as $X_{i}^{n e w}$

19. if fitness of ( $X_{i}^{n e w}$ )< $F_{i}$

20. $X_{i} = X_{i}^{n e w}$

21. else

22. count(i)=count(i)+1

23. end if

24. if count(i)>50

25. RS: Choose best position in Y1 and Y2 as $X_{i}$

26. count(i)=0

27. end if

28. update t, $F_{i}$ , $X^{b}$

29. end while

30. return $X^{b}$

Computational complexity analysis

Computational complexity is a critical metric for assessing the efficiency of an algorithm.¹⁴¹^,¹⁴² If the dimension of the problem is D, the population size is N, and the maximum number of iterations is T, the main processes of IRIME include population initialization, fitness value calculation, and position updating. The complexity of initialization is O(D×N), and the complexity of fitness value calculation is O(T×N×F) + O(log(T)×N×3F+T×N/50×2F) where F is the complexity of calculating fitness values. The complexity of position updating is O(T×N×D). Therefore, the overall complexity of the algorithm is O(T×N×D + T×N×F + log(T)×N×3F+T×N/50×2F + D×N). It is worth noting that compared to RIME, IRIME primarily increases the complexity of the CMS-RS calculation, which is O(log(T)×N×3F+T×N/50×2F).

K-nearest neighbor classifier

The K-nearest neighbor classifier (KNN)¹⁴³ is a commonly used classification method. Its main concept involves finding the K nearest individuals in proximity to a given point, which then defines its class as the one most frequently present among these neighbors. For proximity measurement, this study adopts the Euclidean distance, expressed by the specific formula:

D i s (X, Y) = \sqrt{\sum_{k = 1}^{n} {(X_{k} - Y_{k})}^{2}}

(Equation 13)

where X represents the training samples, Y represents the test samples, and n denotes the number of samples.

Binary IRIME

The feature selection problem can be regarded as a discrete combinatorial optimization problem, where we use “0” or “1” to represent not selecting or selecting a particular feature. In this manner, algorithms need to be adjusted to handle binary problems. The following equation provides the specific transformation function:

T (x) = \frac{1}{1 + e^{- 10 (x - 0.5)}}

(Equation 14)

where x represents the value of an individual on a certain dimension. It is noteworthy that Equation 14 was proposed in bGWO.¹³⁰ For the sake of experimental rigor, a 10-fold cross-validation was employed during the experimentation process. The specific transformation process is detailed in Equation 15:

X_{i, j} (t + 1) = {\begin{array}{c} \begin{array}{c} 1 \\ 0 \end{array} & \begin{array}{c} r a n d < T (x) \\ r a n d > T (x) \end{array} \end{array}

(Equation 15)

where t represents the current iteration count, i and j denote the i-th individual within the population, and the j-th dimension of an individual respectively. rand stands for a uniformly distributed random number within the interval [0,1]. This paper treats the feature selection problem as a single-objective problem,¹⁴⁴ where the objective function is defined as follows:

F i t n e s s = α * e r r + (1 - α) * \frac{N}{M}

(Equation 16)

where, $α$ takes a value of 0.95, err represents the error rate, M stands for the dimensionality of the dataset, and N denotes the dimensionality after feature selection. It is evident from the formula that the error rate of Fitness is related to the size of the selected feature subset. Additionally, the smaller the Fitness, the better the algorithm performs in feature selection applications.

Acknowledgments

This work was supported in part by the Natural Science Foundation of Zhejiang Province (LZ22F020005), National Natural Science Foundation of China (62076185, 62301367). We acknowledge the comments of the reviewers.

Author contributions

H.J.P.: Writing – Original Draft, Writing – Review and Editing, Software, Visualization, and Investigation. C.Y.: Writing – Original Draft, Writing – Review and Editing, Software, Visualization, Investigation, Conceptualization, Methodology, and Formal Analysis. A.A.H.: Writing – Review and Editing, Software, Visualization, and Investigation. L.L.: Writing – Original Draft, Writing – Review and Editing, Software, Visualization, and Investigation. C.H.L.: Conceptualization, Methodology, Formal Analysis, Investigation, Writing – Review and Editing, Funding Acquisition, Supervision, and Project administration. L.G.X.: Conceptualization, Methodology, Formal Analysis, Investigation, Writing – Review and Editing, Funding Acquisition, Supervision, and Project administration.

Declaration of interests

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Declaration of generative AI and AI-assisted technologies in the writing process

During the preparation of this work the authors didn’t use generative AI and AI-assisted technologies in the writing process.

Published: July 22, 2024

Footnotes

Supplemental information can be found online at https://doi.org/10.1016/j.isci.2024.110561.

Contributor Information

Yi Chen, Email: kenyoncy2016@gmail.com.

Huiling Chen, Email: chenhuiling.jlu@gmail.com.

Guoxi Liang, Email: guoxiliang2017@gmail.com.

Supplemental information

Document S1. Figures S1–S3

mmc1.pdf^{(371.2KB, pdf)}

References

1.Cao B., Zhao J., Yang P., Gu Y., Muhammad K., Rodrigues J.J.P.C., de Albuquerque V.H.C. Multiobjective 3-D Topology Optimization of Next-Generation Wireless Data Center Network. IEEE Trans. Ind. Inf. 2020;16:3597–3605. doi: 10.1109/TII.2019.2952565. [DOI] [Google Scholar]
2.Xiao Z., Shu J., Jiang H., Lui J.C.S., Min G., Liu J., Dustdar S. Multi-Objective Parallel Task Offloading and Content Caching in D2D-Aided MEC Networks. IEEE Trans. Mob. Comput. 2022;22:1–16. doi: 10.1109/TMC.2022.3199876. [DOI] [Google Scholar]
3.Chandrashekar G., Sahin F. A survey on feature selection methods. Comput. Electr. Eng. 2014;40:16–28. doi: 10.1016/j.compeleceng.2013.11.024. [DOI] [Google Scholar]
4.Chen J., Xu M., Xu W., Li D., Peng W., Xu H. A Flow Feedback Traffic Prediction Based on Visual Quantified Features. IEEE Trans. Intell. Transp. Syst. 2023;24:10067–10075. doi: 10.1109/TITS.2023.3269794. [DOI] [Google Scholar]
5.Wang J., Dong Y. An interpretable deep learning multi-dimensional integration framework for exchange rate forecasting based on deep and shallow feature selection and snapshot ensemble technology. Eng. Appl. Artif. Intell. 2024;133 doi: 10.1016/j.engappai.2024.108282. [DOI] [Google Scholar]
6.Babalik A., Babadag A. A binary sparrow search algorithm for feature selection on classification of X-ray security images. Appl. Soft Comput. 2024;158 doi: 10.1016/j.asoc.2024.111546. [DOI] [Google Scholar]
7.Wang P., Xue B., Liang J., Zhang M. Differential Evolution-Based Feature Selection: A Niching-Based Multiobjective Approach. IEEE Trans. Evol. Comput. 2023;27:296–310. doi: 10.1109/TEVC.2022.3168052. [DOI] [Google Scholar]
8.Tang Q., Li G. Sparse L0-norm least squares support vector machine with feature selection. Inf. Sci. 2024;670 doi: 10.1016/j.ins.2024.120591. [DOI] [Google Scholar]
9.Xie Y., Wang X.Y., Shen Z.J., Sheng Y.H., Wu G.X. A Two-Stage Estimation of Distribution Algorithm With Heuristics for Energy-Aware Cloud Workflow Scheduling. IEEE Trans. Serv. Comput. 2023;16:4183–4197. doi: 10.1109/TSC.2023.3311785. [DOI] [Google Scholar]
10.Sun G., Zhu G., Liao D., Yu H., Du X., Guizani M. Cost-efficient service function chain orchestration for low-latency applications in NFV networks. IEEE Syst. J. 2019;13:3877–3888. doi: 10.1109/JSYST.2018.2879883. [DOI] [Google Scholar]
11.Das S.R., Mishra A.K., Sahoo A.K., Hota A.P., Viriyasitavat W., Alghamdi N.S., Dhiman G. Fuzzy Controller Designed Based Multilevel Inverter for Power Quality Enhancement. IEEE Trans. Consum. Electron. 2024:1. doi: 10.1109/TCE.2024.3389687. [DOI] [Google Scholar]
12.Alferaidi A., Yadav K., Yasmeen S., Alharbi Y., Viriyasitavat W., Dhiman G., Kaur A. Node Multi-Attribute Network Community Healthcare Detection Based on Graphical Matrix Factorization. J. Circ. Syst. Comput. 2023;33 doi: 10.1142/S0218126624500804. [DOI] [Google Scholar]
13.Zhang C., Fan W., Li H., Chen C. Multi-level graph regularized robust multi-modal feature selection for Alzheimer’s disease classification. Knowl. Base Syst. 2024;293 doi: 10.1016/j.knosys.2024.111676. [DOI] [Google Scholar]
14.Yu F., Lu C., Zhou J., Yin L., Wang K. A knowledge-guided bi-population evolutionary algorithm for energy-efficient scheduling of distributed flexible job shop problem. Eng. Appl. Artif. Intell. 2024;128 doi: 10.1016/j.engappai.2023.107458. [DOI] [Google Scholar]
15.Lu C., Gao R., Yin L., Zhang B. Human–Robot Collaborative Scheduling in Energy-Efficient Welding Shop. IEEE Trans. Ind. Inf. 2024;20:963–971. doi: 10.1109/TII.2023.3271749. [DOI] [Google Scholar]
16.Mirjalili S. SCA: A Sine Cosine Algorithm for solving optimization problems. Knowl. Base Syst. 2016;96:120–133. doi: 10.1016/j.knosys.2015.12.022. [DOI] [Google Scholar]
17.Ahmadianfar I., Heidari A.A., Gandomi A.H., Chu X., Chen H. RUN beyond the metaphor: An efficient optimization algorithm based on Runge Kutta method. Expert Syst. Appl. 2021;181 doi: 10.1016/j.eswa.2021.115079. [DOI] [Google Scholar]
18.Ahmadianfar I., Heidari A.A., Noshadian S., Chen H., Gandomi A.H. INFO: An Efficient Optimization Algorithm based on Weighted Mean of Vectors. Expert Syst. Appl. 2022;195 doi: 10.1016/j.eswa.2022.116516. [DOI] [Google Scholar]
19.Kirkpatrick S., Gelatt C.D., Vecchi M.P. Optimization by Simulated Annealing. Science. 1983;220:671–680. doi: 10.1126/science.220.4598.671. [DOI] [PubMed] [Google Scholar]
20.Rashedi E., Nezamabadi-pour H., Saryazdi S. GSA: A Gravitational Search Algorithm. Inf. Sci. 2009;179:2232–2248. doi: 10.1016/j.ins.2009.03.004. [DOI] [Google Scholar]
21.Su H., Zhao D., Heidari A.A., Liu L., Zhang X., Mafarja M., Chen H. RIME: A physics-based optimization. Neurocomputing. 2023;532:183–214. doi: 10.1016/j.neucom.2023.02.010. [DOI] [Google Scholar]
22.Cao B., Gu Y., Lv Z., Yang S., Zhao J., Li Y. RFID reader anticollision based on distributed parallel particle swarm optimization. IEEE Internet Things J. 2021;8:3099–3107. doi: 10.1109/JIOT.2020.3033473. [DOI] [Google Scholar]
23.Hu J., Zou Y., Soltanov N. A multilevel optimization approach for daily scheduling of combined heat and power units with integrated electrical and thermal storage. Expert Syst. Appl. 2024;250 doi: 10.1016/j.eswa.2024.123729. [DOI] [Google Scholar]
24.Yin L., Zhuang M., Jia J., Wang H. Energy saving in flow-shop scheduling management: an improved multiobjective model based on grey wolf optimization algorithm. Math. Probl Eng. 2020;2020:1–14. doi: 10.1155/2020/9462048. [DOI] [Google Scholar]
25.Yang Y., Chen H., Heidari A.A., Gandomi A.H. Hunger games search: Visions, conception, implementation, deep analysis, perspectives, and towards performance shifts. Expert Syst. Appl. 2021;177 doi: 10.1016/j.eswa.2021.114864. [DOI] [Google Scholar]
26.Chen H., Li C., Mafarja M., Heidari A.A., Chen Y., Cai Z. Slime mould algorithm: a comprehensive review of recent variants and applications. Int. J. Syst. Sci. 2022;54:204–235. doi: 10.1080/00207721.2022.2153635. [DOI] [Google Scholar]
27.Li S., Chen H., Wang M., Heidari A.A., Mirjalili S. Slime mould algorithm: A new method for stochastic optimization. Future Generat. Comput. Syst. 2020;111:300–323. doi: 10.1016/j.future.2020.03.055. [DOI] [Google Scholar]
28.Heidari A.A., Mirjalili S., Faris H., Aljarah I., Mafarja M., Chen H. Harris hawks optimization: Algorithm and applications. Future Generat. Comput. Syst. 2019;97:849–872. doi: 10.1016/j.future.2019.02.028. [DOI] [Google Scholar]
29.Mirjalili S. Moth-flame optimization algorithm: A novel nature-inspired heuristic paradigm. Knowl. Base Syst. 2015;89:228–249. doi: 10.1016/j.knosys.2015.07.006. [DOI] [Google Scholar]
30.Houssein E.H., Oliva D., Samee N.A., Mahmoud N.F., Emam M.M. Liver Cancer Algorithm: A novel bio-inspired optimizer. Comput. Biol. Med. 2023;165 doi: 10.1016/j.compbiomed.2023.107389. [DOI] [PubMed] [Google Scholar]
31.Lian J., Hui G., Ma L., Zhu T., Wu X., Heidari A.A., Chen Y., Chen H. Parrot optimizer: Algorithm and applications to medical problems. Comput. Biol. Med. 2024;172 doi: 10.1016/j.compbiomed.2024.108064. [DOI] [PubMed] [Google Scholar]
32.Tu J., Chen H., Wang M., Gandomi A.H. The Colony Predation Algorithm. J. Bionic Eng. 2021;18:674–710. doi: 10.1007/s42235-021-0050-y. [DOI] [Google Scholar]
33.Storn R., Price K. Differential Evolution – A Simple and Efficient Heuristic for global Optimization over Continuous Spaces. J. Glob. Optim. 1997;11:341–359. doi: 10.1023/A:1008202821328. [DOI] [Google Scholar]
34.Mou J., Gao K., Duan P., Li J., Garg A., Sharma R. A Machine Learning Approach for Energy-Efficient Intelligent Transportation Scheduling Problem in a Real-World Dynamic Circumstances. IEEE Trans. Intell. Transp. Syst. 2023;24:15527–15539. doi: 10.1109/TITS.2022.3183215. [DOI] [Google Scholar]
35.Simon D. Biogeography-Based Optimization. IEEE Trans. Evol. Comput. 2008;12:702–713. doi: 10.1109/TEVC.2008.919004. [DOI] [Google Scholar]
36.Wang S., Xiang J., Zhong Y., Zhou Y. Convolutional neural network-based hidden Markov models for rolling element bearing fault identification. Knowl. Base Syst. 2018;144:65–76. doi: 10.1016/j.knosys.2017.12.027. [DOI] [Google Scholar]
37.Qiu B., Xiao H. A Non-Stationary Geometry-Based Cooperative Scattering Channel Model for MIMO Vehicle-to-Vehicle Communication Systems. KSII Trans. Internet Inf. Syst. 2019;13:2838–2858. doi: 10.3837/tiis.2019.06.004. [DOI] [Google Scholar]
38.Wu Z., Shen S., Lian X., Su X., Chen E. A dummy-based user privacy protection approach for text information retrieval. Knowl. Base Syst. 2020;195 doi: 10.1016/j.knosys.2020.105679. [DOI] [Google Scholar]
39.Liu Y.-S., Yang C.-Y., Chiu P.-F., Lin H.-C., Lo C.-C., Lai A.S.-H., Chang C.-C., Lee O.K.-S. Machine Learning Analysis of Time-Dependent Features for Predicting Adverse Events During Hemodialysis Therapy: Model Development and Validation Study. J. Med. Internet Res. 2021;23 doi: 10.2196/27098. [DOI] [PMC free article] [PubMed] [Google Scholar]
40.Chen H., Cao L., Yue Y. TDOA/AOA Hybrid Localization Based on Improved Dandelion Optimization Algorithm for Mobile Location Estimation Under NLOS Simulation Environment. Wirel. Pers. Commun. 2023;131:2747–2772. doi: 10.1007/s11277-023-10578-y. [DOI] [Google Scholar]
41.Dong R., Liu Y., Wang S., Heidari A.A., Wang M., Chen Y., Wang S., Chen H., Zhang Y. Multi-strategy enhanced kernel search optimization and its application in economic emission dispatch problems. J. Comput. Des. Eng. 2023;11:135–172. doi: 10.1093/jcde/qwad110. [DOI] [Google Scholar]
42.Dong R., Sun L., Ma L., Heidari A.A., Zhou X., Chen H. Boosting Kernel Search Optimizer with Slime Mould Foraging Behavior for Combined Economic Emission Dispatch Problems. J. Bionic Eng. 2023;20:2863–2895. doi: 10.1007/s42235-023-00408-z. [DOI] [Google Scholar]
43.Huang J.C., Zeng G.Q., Geng G.G., Weng J., Lu K.D., Zhang Y. Differential evolution-based convolutional neural networks: An automatic architecture design method for intrusion detection in industrial control systems. Comput. Secur. 2023;132 doi: 10.1016/j.cose.2023.103310. [DOI] [Google Scholar]
44.Peng L., Li X., Yu L., Heidari A.A., Chen H., Liang G. Q-learning guided mutational Harris hawk optimizer for high-dimensional gene data feature selection. Appl. Soft Comput. 2024;161 doi: 10.1016/j.asoc.2024.111734. [DOI] [Google Scholar]
45.Zhang K., Liu Y., Wang X., Mei F., Kang H., Sun G. IBMRFO: Improved binary manta ray foraging optimization with chaotic tent map and adaptive somersault factor for feature selection. Expert Syst. Appl. 2024;251 doi: 10.1016/j.eswa.2024.123977. [DOI] [Google Scholar]
46.Jiang H., Yang Y., Wan Q., Dong Y. Feature selection based on dynamic crow search algorithm for high-dimensional data classification. Expert Syst. Appl. 2024;250 doi: 10.1016/j.eswa.2024.123871. [DOI] [Google Scholar]
47.Van L.N., Tran V.N., Nguyen G.V., Yeon M., Do M.T.-T., Lee G. Enhancing wildfire mapping accuracy using mono-temporal Sentinel-2 data: A novel approach through qualitative and quantitative feature selection with explainable AI. Ecol. Inf. 2024;81 doi: 10.1016/j.ecoinf.2024.102601. [DOI] [Google Scholar]
48.Ozsoydan F.B. Effects of dominant wolves in grey wolf optimization algorithm. Appl. Soft Comput. 2019;83 doi: 10.1016/j.asoc.2019.105658. [DOI] [Google Scholar]
49.Dhargupta S., Ghosh M., Mirjalili S., Sarkar R. Selective Opposition based Grey Wolf Optimization. Expert Syst. Appl. 2020;151 doi: 10.1016/j.eswa.2020.113389. [DOI] [Google Scholar]
50.Deng L., Liu S. An enhanced slime mould algorithm based on adaptive grouping technique for global optimization. Expert Syst. Appl. 2023;222 doi: 10.1016/j.eswa.2023.119877. [DOI] [Google Scholar]
51.Samantaray S., Sahoo P., Sahoo A., Satapathy D.P. Flood discharge prediction using improved ANFIS model combined with hybrid particle swarm optimisation and slime mould algorithm. Environ. Sci. Pollut. Res. 2023;30:83845–83872. doi: 10.1007/s11356-023-27844-y. [DOI] [PubMed] [Google Scholar]
52.Tan W.-H., Mohamad-Saleh J. A hybrid whale optimization algorithm based on equilibrium concept. Alex. Eng. J. 2023;68:763–786. doi: 10.1016/j.aej.2022.12.019. [DOI] [Google Scholar]
53.Wang J., Bei J., Song H., Zhang H., Zhang P. A whale optimization algorithm with combined mutation and removing similarity for global optimization and multilevel thresholding image segmentation. Appl. Soft Comput. 2023;137 doi: 10.1016/j.asoc.2023.110130. [DOI] [Google Scholar]
54.Kumar A., Dhillon J.S. Enhanced Harris hawk optimizer for hydrothermal generation scheduling with cascaded reservoirs. Expert Syst. Appl. 2023;226 doi: 10.1016/j.eswa.2023.120270. [DOI] [Google Scholar]
55.Tian F., Wang J., Chu F. Improved Multi-Strategy Harris Hawks Optimization and Its Application in Engineering Problems. Mathematics. 2023;11:1525. doi: 10.3390/math11061525. [DOI] [Google Scholar]
56.Tiwari P., Mishra V.N., Parouha R.P. Developments and Design of Differential Evolution Algorithm for Non-linear/Non-convex Engineering Optimization. Arch. Comput. Methods Eng. 2024;31:2227–2263. doi: 10.1007/s11831-023-10036-9. [DOI] [Google Scholar]
57.Pham V.H.S., Nguyen Dang N.T., Nguyen V.N. Enhancing engineering optimization using hybrid sine cosine algorithm with Roulette wheel selection and opposition-based learning. Sci. Rep. 2024;14:694. doi: 10.1038/s41598-024-51343-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
58.Huang J., Hu H. Hybrid beluga whale optimization algorithm with multi-strategy for functions and engineering optimization problems. J. Big Data. 2024;11:3. doi: 10.1186/s40537-023-00864-8. [DOI] [Google Scholar]
59.Gomes S.B.F., Simmons N., Sofotasios P.C., Yacoub M.D., Cotton S.L. Channel Parameter Estimation in Millimeter-Wave Propagation Environments Using Genetic Algorithm. IEEE Antennas Wirel. Propag. Lett. 2024;23:24–28. doi: 10.1109/LAWP.2023.3315422. [DOI] [Google Scholar]
60.Gundogdu H., Demirci A., Tercan S.M., Cali U. A Novel Improved Grey Wolf Algorithm Based Global Maximum Power Point Tracker Method Considering Partial Shading. IEEE Access. 2024;12:6148–6159. doi: 10.1109/ACCESS.2024.3350269. [DOI] [Google Scholar]
61.Yu X., Zhang W. A teaching-learning-based optimization algorithm with reinforcement learning to address wind farm layout optimization problem. Appl. Soft Comput. 2024;151 doi: 10.1016/j.asoc.2023.111135. [DOI] [Google Scholar]
62.Moustafa G., Alnami H., Hakmi S.H., Shaheen A.M., Ginidi A.R., Elshahed M.A., Mansour H.S.E. A Novel Mantis Search Algorithm for Economic Dispatch in Combined Heat and Power Systems. IEEE Access. 2024;12:2674–2689. doi: 10.1109/ACCESS.2023.3344679. [DOI] [Google Scholar]
63.Al-Areeq A.M., Saleh R.A.A., Ghanim A.A.J., Ghaleb M., Al‑Areeq N.M., Al-Wajih E. Flood hazard assessment in Yemen using a novel hybrid approach of Grey Wolf and Levenberg Marquardt optimizers. Geocarto Int. 2023;38 doi: 10.1080/10106049.2023.2243884. [DOI] [Google Scholar]
64.Tu B., Wang F., Huo Y., Wang X. A hybrid algorithm of grey wolf optimizer and harris hawks optimization for solving global optimization problems with improved convergence performance. Sci. Rep. 2023;13 doi: 10.1038/s41598-023-49754-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
65.Silva B.N., Khan M., Wijesinghe R.E., Wijenayake U. Meta-heuristic optimization based cost efficient demand-side management for sustainable smart communities. Energy Build. 2024;303 doi: 10.1016/j.enbuild.2023.113599. [DOI] [Google Scholar]
66.Peng L., Cai Z., Heidari A.A., Zhang L., Chen H. Hierarchical Harris hawks optimizer for feature selection. J. Adv. Res. 2023;53:261–278. doi: 10.1016/j.jare.2023.01.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
67.Yu H., Zhao Z., Heidari A.A., Ma L., Hamdi M., Mansour R.F., Chen H. An accelerated sine mapping whale optimizer for feature selection. iScience. 2023;26 doi: 10.1016/j.isci.2023.107896. [DOI] [PMC free article] [PubMed] [Google Scholar]
68.Mabrouk A., Yousri D., Aaaa S., Alduailij M., Elsayed Abd Elaziz M. Fractional order adaptive hunter-prey optimizer for feature selection. Alex. Eng. J. 2023;75:531–547. doi: 10.1016/j.aej.2023.05.092. [DOI] [Google Scholar]
69.Al-Khatib R.M., Al-qudah N.E.A., Jawarneh M.S., Al-Khateeb A. A novel improved lemurs optimization algorithm for feature selection problems. J. King Saud Univ. Comput. Inf. Sci. 2023;35 doi: 10.1016/j.jksuci.2023.101704. [DOI] [Google Scholar]
70.Zaimoğlu E.A., Yurtay N., Demirci H., Yurtay Y. A binary chaotic horse herd optimization algorithm for feature selection. Eng. Sci. Technol. 2023;44 doi: 10.1016/j.jestch.2023.101453. [DOI] [Google Scholar]
71.Chhabra A., Hussien A.G., Hashim F.A. Improved bald eagle search algorithm for global optimization and feature selection. Alex. Eng. J. 2023;68:141–180. doi: 10.1016/j.aej.2022.12.045. [DOI] [Google Scholar]
72.Pan H., Chen S., Xiong H. A high-dimensional feature selection method based on modified Gray Wolf Optimization. Appl. Soft Comput. 2023;135 doi: 10.1016/j.asoc.2023.110031. [DOI] [Google Scholar]
73.Askr H., Abdel-Salam M., Hassanien A.E. Copula entropy-based golden jackal optimization algorithm for high-dimensional feature selection problems. Expert Syst. Appl. 2024;238 doi: 10.1016/j.eswa.2023.121582. [DOI] [Google Scholar]
74.Wang Y., Ran S., Wang G.-G. Role-oriented binary grey wolf optimizer using foraging-following and Lévy flight for feature selection. Appl. Math. Model. 2024;126:310–326. doi: 10.1016/j.apm.2023.08.043. [DOI] [Google Scholar]
75.ye Z., Luo J., Zhou W., Wang M., He Q. An ensemble framework with improved hybrid breeding optimization-based feature selection for intrusion detection. Future Generat. Comput. Syst. 2024;151:124–136. doi: 10.1016/j.future.2023.09.035. [DOI] [Google Scholar]
76.Yang X., Zhen L., Li Z. Binary golden eagle optimizer combined with initialization of feature number subspace for feature selection. Knowl. Base Syst. 2023;282 doi: 10.1016/j.knosys.2023.111109. [DOI] [Google Scholar]
77.Chakraborty S., Saha A.K., Ezugwu A.E., Chakraborty R., Saha A. Horizontal crossover and co-operative hunting-based Whale Optimization Algorithm for feature selection. Knowl. Base Syst. 2023;282 doi: 10.1016/j.knosys.2023.111108. [DOI] [Google Scholar]
78.Abdelrazek M., Abd Elaziz M., El-Baz A.H. CDMO: Chaotic Dwarf Mongoose Optimization Algorithm for feature selection. Sci. Rep. 2024;14:701. doi: 10.1038/s41598-023-50959-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
79.Mostafa R.R., Khedr A.M., Al Aghbari Z., Afyouni I., Kamel I., Ahmed N. An adaptive hybrid mutated differential evolution feature selection method for low and high-dimensional medical datasets. Knowl. Base Syst. 2024;283 doi: 10.1016/j.knosys.2023.111218. [DOI] [Google Scholar]
80.Wolpert D.H., Macready W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997;1:67–82. doi: 10.1109/4235.585893. [DOI] [Google Scholar]
81.Yu X., Qin W., Lin X., Shan Z., Huang L., Shao Q., Wang L., Chen M. Synergizing the enhanced RIME with fuzzy K-nearest neighbor for diagnose of pulmonary hypertension. Comput. Biol. Med. 2023;165 doi: 10.1016/j.compbiomed.2023.107408. [DOI] [PubMed] [Google Scholar]
82.Yang B., Wang J., Su S., Li Y., Wu P., Yang Z., Fan H., Li W., Li J. Mismatch losses mitigation of PV-TEG hybrid system via improved RIME algorithm: Design and hardware validation. J. Clean. Prod. 2024;434 doi: 10.1016/j.jclepro.2023.139957. [DOI] [Google Scholar]
83.Zhong R., Yu J., Zhang C., Munetomo M. SRIME: A strengthened RIME with Latin hypercube sampling and embedded distance-based selection for engineering optimization problems. Neural Comput. Appl. 2024;36:6721–6740. doi: 10.1007/s00521-024-09424-4. [DOI] [Google Scholar]
84.Zhu W., Fang L., Ye X., Medani M., Escorcia-Gutierrez J. IDRM: Brain tumor image segmentation with boosted RIME optimization. Comput. Biol. Med. 2023;166 doi: 10.1016/j.compbiomed.2023.107551. [DOI] [PubMed] [Google Scholar]
85.Li Y., Zhao D., Ma C., Escorcia-Gutierrez J., Aljehane N.O., Ye X. CDRIME-MTIS: An enhanced rime optimization-driven multi-threshold segmentation for COVID-19 X-ray images. Comput. Biol. Med. 2024;169 doi: 10.1016/j.compbiomed.2023.107838. [DOI] [PubMed] [Google Scholar]
86.Awad N.H., Ali M.Z., Suganthan P.N. 2017 IEEE Congress on Evolutionary Computation (CEC) Donostia; 2017. Ensemble sinusoidal differential covariance matrix adaptation with Euclidean neighborhood for solving CEC2017 benchmark problems; pp. 372–379. [DOI] [Google Scholar]
87.LaTorre A., Peña J.M. 2017 IEEE Congress on Evolutionary Computation (CEC) Donostia; 2017. A comparison of three large-scale global optimizers on the CEC 2017 single objective real parameter numerical optimization benchmark; pp. 1063–1070. [DOI] [Google Scholar]
88.Liu X., Huang H., Xiang J. A personalized diagnosis method to detect faults in gears using numerical simulation and extreme learning machine. Knowl. Base Syst. 2020;195 doi: 10.1016/j.knosys.2020.105653. [DOI] [Google Scholar]
89.Li J., Lin J. A probability distribution detection based hybrid ensemble QoS prediction approach. Inf. Sci. 2020;519:289–305. doi: 10.1016/j.ins.2020.01.046. [DOI] [Google Scholar]
90.Liu K., Ke F., Huang X., Yu R., Lin F., Wu Y., Ng D.W.K. DeepBAN: A Temporal Convolution-Based Communication Framework for Dynamic WBANs. IEEE Trans. Commun. 2021;69:6675–6690. doi: 10.1109/TCOMM.2021.3094581. [DOI] [Google Scholar]
91.Yang X.S., Suash D. 2009 World Congress on Nature & Biologically Inspired Computing (NaBIC) 2009. Cuckoo Search via Lévy flights; pp. 210–214. [DOI] [Google Scholar]
92.Ahmed S., Groenli T.-M., Lakhan A., Chen Y., Liang G. A reinforcement federated learning based strategy for urinary disease dataset processing. Comput. Biol. Med. 2023;163 doi: 10.1016/j.compbiomed.2023.107210. [DOI] [PubMed] [Google Scholar]
93.Pan X., Zhang G., Lin A., Guan X., Chen P., Ge Y., Chen X. An evaluation model for children’s foot & ankle deformity severity using sparse multi-objective feature selection algorithm. Comput. Biol. Med. 2022;151 doi: 10.1016/j.compbiomed.2022.106229. [DOI] [PubMed] [Google Scholar]
94.Zhou P., Chen J., Fan M., Du L., Shen Y.D., Li X. Unsupervised feature selection for balanced clustering. Knowl. Base Syst. 2020;193 doi: 10.1016/j.knosys.2019.105417. [DOI] [Google Scholar]
95.Mirjalili S., Lewis A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016;95:51–67. doi: 10.1016/j.advengsoft.2016.01.008. [DOI] [Google Scholar]
96.Mirjalili S., Gandomi A.H., Mirjalili S.Z., Saremi S., Faris H., Mirjalili S.M. Salp Swarm Algorithm: A bio-inspired optimizer for engineering design problems. Adv. Eng. Softw. 2017;114:163–191. doi: 10.1016/j.advengsoft.2017.07.002. [DOI] [Google Scholar]
97.Kennedy J., Eberhart R. Vol. 4. 1995. Particle swarm optimization; pp. 1942–1948. (Proceedings of ICNN'95 - International Conference on Neural Networks). [DOI] [Google Scholar]
98.Mirjalili S., Mirjalili S.M., Lewis A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014;69:46–61. doi: 10.1016/j.advengsoft.2013.12.007. [DOI] [Google Scholar]
99.Yang X.S., Hossein Gandomi A. Bat algorithm: A novel approach for global engineering optimization. Eng. Comput. 2012;29:464–483. doi: 10.1108/02644401211235834. [DOI] [Google Scholar]
100.Emary E., Zawbaa H.M., Ghany K.K.A., Hassanien A.E., Parv B. Proceedings of the 7th Balkan Conference on Informatics Conference. 2015. Firefly Optimization Algorithm for Feature Selection. [DOI] [Google Scholar]
101.Kumar A., Misra R.K., Singh D. 2017 IEEE Congress on Evolutionary Computation (CEC) Donostia; 2017. Improving the local search capability of Effective Butterfly Optimizer using Covariance Matrix Adapted Retreat Phase; pp. 1835–1842. [DOI] [Google Scholar]
102.Chen W.N., Zhang J., Lin Y., Chen N., Zhan Z.H., Chung H.S.H., Li Y., Shi Y.H. Particle Swarm Optimization With an Aging Leader and Challengers. IEEE Trans. Evol. Comput. 2013;17:241–258. doi: 10.1109/TEVC.2011.2173577. [DOI] [Google Scholar]
103.Liang J.J., Qin A.K., Suganthan P.N., Baskar S. Comprehensive learning particle swarm optimizer for global optimization of multimodal functions. IEEE Trans. Evol. Comput. 2006;10:281–295. doi: 10.1109/TEVC.2005.857610. [DOI] [Google Scholar]
104.Tanabe R., Fukunaga A.S. 2014 IEEE Congress on Evolutionary Computation (CEC) 2014. Improving the search performance of SHADE using linear population size reduction; pp. 1658–1665. [DOI] [Google Scholar]
105.Qin A.K., Huang V.L., Suganthan P.N. Differential Evolution Algorithm With Strategy Adaptation for Global Numerical Optimization. IEEE Trans. Evol. Comput. 2009;13:398–417. doi: 10.1109/TEVC.2008.927706. [DOI] [Google Scholar]
106.Zhang J., Sanderson A.C. JADE: Adaptive Differential Evolution With Optional External Archive. IEEE Trans. Evol. Comput. 2009;13:945–958. doi: 10.1109/TEVC.2009.2014613. [DOI] [Google Scholar]
107.Liang H., Liu Y., Shen Y., Li F., Man Y. A Hybrid Bat Algorithm for Economic Dispatch With Random Wind Power. IEEE Trans. Power Syst. 2018;33:5052–5061. doi: 10.1109/TPWRS.2018.2812711. [DOI] [Google Scholar]
108.Lynn N., Suganthan P.N. Ensemble particle swarm optimizer. Appl. Soft Comput. 2017;55:533–548. doi: 10.1016/j.asoc.2017.02.007. [DOI] [Google Scholar]
109.Gandomi A.H., Yang X.-S. Chaotic bat algorithm. J. Comput. Sci. 2014;5:224–232. doi: 10.1016/j.jocs.2013.10.002. [DOI] [Google Scholar]
110.Ling Y., Zhou Y., Luo Q. Lévy Flight Trajectory-Based Whale Optimization Algorithm for Global Optimization. IEEE Access. 2017;5:6168–6186. doi: 10.1109/ACCESS.2017.2695498. [DOI] [Google Scholar]
111.Yu H., Zhao Z., Zhou J., Heidari A.A., Chen H. Sine cosine algorithm with communication and quality enhancement: Performance design for engineering problems. J. Comput. Des. Eng. 2023;10:1868–1891. doi: 10.1093/jcde/qwad073. [DOI] [Google Scholar]
112.Ben Guedria N. Improved accelerated PSO algorithm for mechanical engineering optimization problems. Appl. Soft Comput. 2016;40:455–467. doi: 10.1016/j.asoc.2015.10.048. [DOI] [Google Scholar]
113.Mezura-Montes E., Coello C.A.C. An empirical study about the usefulness of evolution strategies to solve constrained optimization problems. Int. J. Gen. Syst. 2008;37:443–473. doi: 10.1080/03081070701303470. [DOI] [Google Scholar]
114.Coello Coello C.A. Use of a self-adaptive penalty approach for engineering optimization problems. Comput. Ind. 2000;41:113–127. doi: 10.1016/S0166-3615(99)00046-9. [DOI] [Google Scholar]
115.Mahdavi M., Fesanghary M., Damangir E. An improved harmony search algorithm for solving optimization problems. Appl. Math. Comput. 2007;188:1567–1579. doi: 10.1016/j.amc.2006.11.033. [DOI] [Google Scholar]
116.Tu J., Chen H., Liu J., Heidari A.A., Zhang X., Wang M., Ruby R., Pham Q.-V. Evolutionary biogeography-based whale optimization methods with communication structure: Towards measuring the balance. Knowl. Base Syst. 2021;212 doi: 10.1016/j.knosys.2020.106642. [DOI] [Google Scholar]
117.Shan W., He X., Liu H., Heidari A.A., Wang M., Cai Z., Chen H. Cauchy mutation boosted Harris hawk algorithm: Optimal performance design and engineering applications. J. Comput. Des. Eng. 2023;10:503–526. doi: 10.1093/jcde/qwad002. [DOI] [Google Scholar]
118.Chickermane H., Gea H.C. Structural optimization using a new local approximation method. Int. J. Numer. Methods Eng. 1996;39:829–846. doi: 10.1002/(SICI)1097-0207(19960315)39:5<829::AID-NME884>3.0.CO;2-U. [DOI] [Google Scholar]
119.Gandomi A.H., Yang X.-S., Alavi A.H. Cuckoo search algorithm: a metaheuristic approach to solve structural optimization problems. Eng. Comput. 2013;29:17–35. doi: 10.1007/s00366-011-0241-y. [DOI] [Google Scholar]
120.Wang G.G. Adaptive Response Surface Method Using Inherited Latin Hypercube Design Points. J. Mech. Des. 2003;125:210–220. doi: 10.1115/1.1561044. [DOI] [Google Scholar]
121.Cheng M.-Y., Prayogo D. Symbiotic Organisms Search: A new metaheuristic optimization algorithm. Comput. Struct. 2014;139:98–112. doi: 10.1016/j.compstruc.2014.03.007. [DOI] [Google Scholar]
122.Li X., Lin Z., Lv H., Yu L., Heidari A.A., Zhang Y., Chen H., Liang G. Advanced slime mould algorithm incorporating differential evolution and Powell mechanism for engineering design. iScience. 2023;26 doi: 10.1016/j.isci.2023.107736. [DOI] [PMC free article] [PubMed] [Google Scholar]
123.Wang G., Heidari A.A., Wang M., Kuang F., Zhu W., Chen H. Chaotic Arc Adaptive Grasshopper Optimization. IEEE Access. 2021;9:17672–17706. doi: 10.1109/ACCESS.2021.3052800. [DOI] [Google Scholar]
124.Deb K., Goyal M. 1997. Optimizing Engineering Designs Using a Com Bined Genetic Search. [Google Scholar]
125.Zhang M., Chen H., Heidari A.A., Cai Z., Aljehane N.O., Mansour R.F. OCRUN: An oppositional Runge Kutta optimizer with cuckoo search for global optimization and feature selection. Appl. Soft Comput. 2023;146 doi: 10.1016/j.asoc.2023.110664. [DOI] [Google Scholar]
126.Zhou X., Gui W., Heidari A.A., Cai Z., Liang G., Chen H. Random following ant colony optimization: Continuous and binary variants for global optimization and feature selection. Appl. Soft Comput. 2023;144 doi: 10.1016/j.asoc.2023.110513. [DOI] [Google Scholar]
127.Oliveira D.A.B., Ferreira R.S., Silva R., Brazil E.V. Improving Seismic Data Resolution With Deep Generative Networks. Geosci. Rem. Sens. Lett. IEEE. 2019;16:1929–1933. doi: 10.1109/LGRS.2019.2913593. [DOI] [Google Scholar]
128.Feltes B.C., Chandelier E.B., Grisci B.I., Dorn M. CuMiDa: An Extensively Curated Microarray Database for Benchmarking and Testing of Machine Learning Approaches in Cancer Research. J. Comput. Biol. 2019;26:376–386. doi: 10.1089/cmb.2018.0238. [DOI] [PubMed] [Google Scholar]
129.Tumar I., Hassouneh Y., Turabieh H., Thaher T. Enhanced Binary Moth Flame Optimization as a Feature Selection Algorithm to Predict Software Fault Prediction. IEEE Access. 2020;8:8041–8055. doi: 10.1109/ACCESS.2020.2964321. [DOI] [Google Scholar]
130.Emary E., Zawbaa H.M., Hassanien A.E. Binary grey wolf optimization approaches for feature selection. Neurocomputing. 2016;172:371–381. doi: 10.1016/j.neucom.2015.06.083. [DOI] [Google Scholar]
131.Abdel-Basset M., Mohamed R., Sallam K.M., Chakrabortty R.K., Ryan M.J. BSMA: A novel metaheuristic algorithm for multi-dimensional knapsack problems: Method and comprehensive analysis. Comput. Ind. Eng. 2021;159 doi: 10.1016/j.cie.2021.107469. [DOI] [Google Scholar]
132.Emary E., Zawbaa H.M., Hassanien A.E. Binary ant lion approaches for feature selection. Neurocomputing. 2016;213:54–65. doi: 10.1016/j.neucom.2016.03.101. [DOI] [Google Scholar]
133.Mirjalili S., Mirjalili S.M., Yang X.-S. Binary bat algorithm. Neural Comput. Appl. 2014;25:663–681. doi: 10.1007/s00521-013-1525-5. [DOI] [Google Scholar]
134.Faris H., Mafarja M.M., Heidari A.A., Aljarah I., Al-Zoubi A.M., Mirjalili S., Fujita H. An efficient binary Salp Swarm Algorithm with crossover scheme for feature selection problems. Knowl. Base Syst. 2018;154:43–67. doi: 10.1016/j.knosys.2018.05.009. [DOI] [Google Scholar]
135.Mafarja M., Mirjalili S. Whale optimization approaches for wrapper feature selection. Appl. Soft Comput. 2018;62:441–453. doi: 10.1016/j.asoc.2017.11.006. [DOI] [Google Scholar]
136.Thaher T., Heidari A.A., Mafarja M., Dong J.S., Mirjalili S. Evolutionary Machine Learning Techniques: Algorithms and Applications. Springer; 2020. Binary Harris Hawks Optimizer for High-Dimensional, Low Sample Size Feature Selection; pp. 251–272. [DOI] [Google Scholar]
137.Ganesh N., Shankar R., Čep R., Chakraborty S., Kalita K. Efficient Feature Selection Using Weighted Superposition Attraction Optimization Algorithm. Appl. Sci. 2023;13:3223. doi: 10.3390/app13053223. [DOI] [Google Scholar]
138.Priyadarshini J., Premalatha M., Čep R., Jayasudha M., Kalita K. Analyzing Physics-Inspired Metaheuristic Algorithms in Feature Selection with K-Nearest-Neighbor. Appl. Sci. 2023;13:906. doi: 10.3390/app13020906. [DOI] [Google Scholar]
139.Wang Y., Cai Z., Zhang Q. Differential Evolution With Composite Trial Vector Generation Strategies and Control Parameters. IEEE Trans. Evol. Comput. 2011;15:55–66. doi: 10.1109/TEVC.2010.2087271. [DOI] [Google Scholar]
140.Zhang H., Wang Z., Chen W., Heidari A.A., Wang M., Zhao X., Liang G., Chen H., Zhang X. Ensemble mutation-driven salp swarm algorithm with restart mechanism: Framework and fundamental analysis. Expert Syst. Appl. 2021;165 doi: 10.1016/j.eswa.2020.113897. [DOI] [Google Scholar]
141.Gao R., Tao J., Zhang J., Ma L., Xu M. NSGA-III-SD based Fuzzy energy management system optimization for lithium battery/supercapacitor HEV. Appl. Soft Comput. 2023;142 doi: 10.1016/j.asoc.2023.110280. [DOI] [Google Scholar]
142.Li Y., Liu Y., Guo Y.Z., Liao X.F., Hu B., Yu T. Spatio-Temporal-Spectral Hierarchical Graph Convolutional Network With Semisupervised Active Learning for Patient-Specific Seizure Prediction. IEEE Trans. Cybern. 2022;52:12189–12204. doi: 10.1109/TCYB.2021.3071860. [DOI] [PubMed] [Google Scholar]
143.Govindarajan M., Chandrasekaran R.M. Evaluation of k-Nearest Neighbor classifier performance for direct marketing. Expert Syst. Appl. 2010;37:253–258. doi: 10.1016/j.eswa.2009.04.055. [DOI] [Google Scholar]
144.Hu P., Pan J.-S., Chu S.-C. Improved Binary Grey Wolf Optimizer and Its application for feature selection. Knowl. Base Syst. 2020;195 doi: 10.1016/j.knosys.2020.105746. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Document S1. Figures S1–S3

mmc1.pdf^{(371.2KB, pdf)}

Data Availability Statement

•
The dataset for this study is publicly accessible online and can be shared by the primary contact upon request. Links to the code and DOIs are included in the resources table.
•
The data presented in this paper will be made available through the primary contact upon request.
•
The paper does not include the original code directly, but it can be accessed from the designated contact upon request for reanalysis purposes.

[bib1] 1.Cao B., Zhao J., Yang P., Gu Y., Muhammad K., Rodrigues J.J.P.C., de Albuquerque V.H.C. Multiobjective 3-D Topology Optimization of Next-Generation Wireless Data Center Network. IEEE Trans. Ind. Inf. 2020;16:3597–3605. doi: 10.1109/TII.2019.2952565. [DOI] [Google Scholar]

[bib2] 2.Xiao Z., Shu J., Jiang H., Lui J.C.S., Min G., Liu J., Dustdar S. Multi-Objective Parallel Task Offloading and Content Caching in D2D-Aided MEC Networks. IEEE Trans. Mob. Comput. 2022;22:1–16. doi: 10.1109/TMC.2022.3199876. [DOI] [Google Scholar]

[bib3] 3.Chandrashekar G., Sahin F. A survey on feature selection methods. Comput. Electr. Eng. 2014;40:16–28. doi: 10.1016/j.compeleceng.2013.11.024. [DOI] [Google Scholar]

[bib4] 4.Chen J., Xu M., Xu W., Li D., Peng W., Xu H. A Flow Feedback Traffic Prediction Based on Visual Quantified Features. IEEE Trans. Intell. Transp. Syst. 2023;24:10067–10075. doi: 10.1109/TITS.2023.3269794. [DOI] [Google Scholar]

[bib5] 5.Wang J., Dong Y. An interpretable deep learning multi-dimensional integration framework for exchange rate forecasting based on deep and shallow feature selection and snapshot ensemble technology. Eng. Appl. Artif. Intell. 2024;133 doi: 10.1016/j.engappai.2024.108282. [DOI] [Google Scholar]

[bib6] 6.Babalik A., Babadag A. A binary sparrow search algorithm for feature selection on classification of X-ray security images. Appl. Soft Comput. 2024;158 doi: 10.1016/j.asoc.2024.111546. [DOI] [Google Scholar]

[bib7] 7.Wang P., Xue B., Liang J., Zhang M. Differential Evolution-Based Feature Selection: A Niching-Based Multiobjective Approach. IEEE Trans. Evol. Comput. 2023;27:296–310. doi: 10.1109/TEVC.2022.3168052. [DOI] [Google Scholar]

[bib8] 8.Tang Q., Li G. Sparse L0-norm least squares support vector machine with feature selection. Inf. Sci. 2024;670 doi: 10.1016/j.ins.2024.120591. [DOI] [Google Scholar]

[bib9] 9.Xie Y., Wang X.Y., Shen Z.J., Sheng Y.H., Wu G.X. A Two-Stage Estimation of Distribution Algorithm With Heuristics for Energy-Aware Cloud Workflow Scheduling. IEEE Trans. Serv. Comput. 2023;16:4183–4197. doi: 10.1109/TSC.2023.3311785. [DOI] [Google Scholar]

[bib10] 10.Sun G., Zhu G., Liao D., Yu H., Du X., Guizani M. Cost-efficient service function chain orchestration for low-latency applications in NFV networks. IEEE Syst. J. 2019;13:3877–3888. doi: 10.1109/JSYST.2018.2879883. [DOI] [Google Scholar]

[bib11] 11.Das S.R., Mishra A.K., Sahoo A.K., Hota A.P., Viriyasitavat W., Alghamdi N.S., Dhiman G. Fuzzy Controller Designed Based Multilevel Inverter for Power Quality Enhancement. IEEE Trans. Consum. Electron. 2024:1. doi: 10.1109/TCE.2024.3389687. [DOI] [Google Scholar]

[bib12] 12.Alferaidi A., Yadav K., Yasmeen S., Alharbi Y., Viriyasitavat W., Dhiman G., Kaur A. Node Multi-Attribute Network Community Healthcare Detection Based on Graphical Matrix Factorization. J. Circ. Syst. Comput. 2023;33 doi: 10.1142/S0218126624500804. [DOI] [Google Scholar]

[bib13] 13.Zhang C., Fan W., Li H., Chen C. Multi-level graph regularized robust multi-modal feature selection for Alzheimer’s disease classification. Knowl. Base Syst. 2024;293 doi: 10.1016/j.knosys.2024.111676. [DOI] [Google Scholar]

[bib14] 14.Yu F., Lu C., Zhou J., Yin L., Wang K. A knowledge-guided bi-population evolutionary algorithm for energy-efficient scheduling of distributed flexible job shop problem. Eng. Appl. Artif. Intell. 2024;128 doi: 10.1016/j.engappai.2023.107458. [DOI] [Google Scholar]

[bib15] 15.Lu C., Gao R., Yin L., Zhang B. Human–Robot Collaborative Scheduling in Energy-Efficient Welding Shop. IEEE Trans. Ind. Inf. 2024;20:963–971. doi: 10.1109/TII.2023.3271749. [DOI] [Google Scholar]

[bib16] 16.Mirjalili S. SCA: A Sine Cosine Algorithm for solving optimization problems. Knowl. Base Syst. 2016;96:120–133. doi: 10.1016/j.knosys.2015.12.022. [DOI] [Google Scholar]

[bib17] 17.Ahmadianfar I., Heidari A.A., Gandomi A.H., Chu X., Chen H. RUN beyond the metaphor: An efficient optimization algorithm based on Runge Kutta method. Expert Syst. Appl. 2021;181 doi: 10.1016/j.eswa.2021.115079. [DOI] [Google Scholar]

[bib18] 18.Ahmadianfar I., Heidari A.A., Noshadian S., Chen H., Gandomi A.H. INFO: An Efficient Optimization Algorithm based on Weighted Mean of Vectors. Expert Syst. Appl. 2022;195 doi: 10.1016/j.eswa.2022.116516. [DOI] [Google Scholar]

[bib19] 19.Kirkpatrick S., Gelatt C.D., Vecchi M.P. Optimization by Simulated Annealing. Science. 1983;220:671–680. doi: 10.1126/science.220.4598.671. [DOI] [PubMed] [Google Scholar]

[bib20] 20.Rashedi E., Nezamabadi-pour H., Saryazdi S. GSA: A Gravitational Search Algorithm. Inf. Sci. 2009;179:2232–2248. doi: 10.1016/j.ins.2009.03.004. [DOI] [Google Scholar]

[bib21] 21.Su H., Zhao D., Heidari A.A., Liu L., Zhang X., Mafarja M., Chen H. RIME: A physics-based optimization. Neurocomputing. 2023;532:183–214. doi: 10.1016/j.neucom.2023.02.010. [DOI] [Google Scholar]

[bib22] 22.Cao B., Gu Y., Lv Z., Yang S., Zhao J., Li Y. RFID reader anticollision based on distributed parallel particle swarm optimization. IEEE Internet Things J. 2021;8:3099–3107. doi: 10.1109/JIOT.2020.3033473. [DOI] [Google Scholar]

[bib23] 23.Hu J., Zou Y., Soltanov N. A multilevel optimization approach for daily scheduling of combined heat and power units with integrated electrical and thermal storage. Expert Syst. Appl. 2024;250 doi: 10.1016/j.eswa.2024.123729. [DOI] [Google Scholar]

[bib24] 24.Yin L., Zhuang M., Jia J., Wang H. Energy saving in flow-shop scheduling management: an improved multiobjective model based on grey wolf optimization algorithm. Math. Probl Eng. 2020;2020:1–14. doi: 10.1155/2020/9462048. [DOI] [Google Scholar]

[bib25] 25.Yang Y., Chen H., Heidari A.A., Gandomi A.H. Hunger games search: Visions, conception, implementation, deep analysis, perspectives, and towards performance shifts. Expert Syst. Appl. 2021;177 doi: 10.1016/j.eswa.2021.114864. [DOI] [Google Scholar]

[bib26] 26.Chen H., Li C., Mafarja M., Heidari A.A., Chen Y., Cai Z. Slime mould algorithm: a comprehensive review of recent variants and applications. Int. J. Syst. Sci. 2022;54:204–235. doi: 10.1080/00207721.2022.2153635. [DOI] [Google Scholar]

[bib27] 27.Li S., Chen H., Wang M., Heidari A.A., Mirjalili S. Slime mould algorithm: A new method for stochastic optimization. Future Generat. Comput. Syst. 2020;111:300–323. doi: 10.1016/j.future.2020.03.055. [DOI] [Google Scholar]

[bib28] 28.Heidari A.A., Mirjalili S., Faris H., Aljarah I., Mafarja M., Chen H. Harris hawks optimization: Algorithm and applications. Future Generat. Comput. Syst. 2019;97:849–872. doi: 10.1016/j.future.2019.02.028. [DOI] [Google Scholar]

[bib29] 29.Mirjalili S. Moth-flame optimization algorithm: A novel nature-inspired heuristic paradigm. Knowl. Base Syst. 2015;89:228–249. doi: 10.1016/j.knosys.2015.07.006. [DOI] [Google Scholar]

[bib30] 30.Houssein E.H., Oliva D., Samee N.A., Mahmoud N.F., Emam M.M. Liver Cancer Algorithm: A novel bio-inspired optimizer. Comput. Biol. Med. 2023;165 doi: 10.1016/j.compbiomed.2023.107389. [DOI] [PubMed] [Google Scholar]

[bib31] 31.Lian J., Hui G., Ma L., Zhu T., Wu X., Heidari A.A., Chen Y., Chen H. Parrot optimizer: Algorithm and applications to medical problems. Comput. Biol. Med. 2024;172 doi: 10.1016/j.compbiomed.2024.108064. [DOI] [PubMed] [Google Scholar]

[bib32] 32.Tu J., Chen H., Wang M., Gandomi A.H. The Colony Predation Algorithm. J. Bionic Eng. 2021;18:674–710. doi: 10.1007/s42235-021-0050-y. [DOI] [Google Scholar]

[bib33] 33.Storn R., Price K. Differential Evolution – A Simple and Efficient Heuristic for global Optimization over Continuous Spaces. J. Glob. Optim. 1997;11:341–359. doi: 10.1023/A:1008202821328. [DOI] [Google Scholar]

[bib34] 34.Mou J., Gao K., Duan P., Li J., Garg A., Sharma R. A Machine Learning Approach for Energy-Efficient Intelligent Transportation Scheduling Problem in a Real-World Dynamic Circumstances. IEEE Trans. Intell. Transp. Syst. 2023;24:15527–15539. doi: 10.1109/TITS.2022.3183215. [DOI] [Google Scholar]

[bib35] 35.Simon D. Biogeography-Based Optimization. IEEE Trans. Evol. Comput. 2008;12:702–713. doi: 10.1109/TEVC.2008.919004. [DOI] [Google Scholar]

[bib36] 36.Wang S., Xiang J., Zhong Y., Zhou Y. Convolutional neural network-based hidden Markov models for rolling element bearing fault identification. Knowl. Base Syst. 2018;144:65–76. doi: 10.1016/j.knosys.2017.12.027. [DOI] [Google Scholar]

[bib37] 37.Qiu B., Xiao H. A Non-Stationary Geometry-Based Cooperative Scattering Channel Model for MIMO Vehicle-to-Vehicle Communication Systems. KSII Trans. Internet Inf. Syst. 2019;13:2838–2858. doi: 10.3837/tiis.2019.06.004. [DOI] [Google Scholar]

[bib38] 38.Wu Z., Shen S., Lian X., Su X., Chen E. A dummy-based user privacy protection approach for text information retrieval. Knowl. Base Syst. 2020;195 doi: 10.1016/j.knosys.2020.105679. [DOI] [Google Scholar]

[bib39] 39.Liu Y.-S., Yang C.-Y., Chiu P.-F., Lin H.-C., Lo C.-C., Lai A.S.-H., Chang C.-C., Lee O.K.-S. Machine Learning Analysis of Time-Dependent Features for Predicting Adverse Events During Hemodialysis Therapy: Model Development and Validation Study. J. Med. Internet Res. 2021;23 doi: 10.2196/27098. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib40] 40.Chen H., Cao L., Yue Y. TDOA/AOA Hybrid Localization Based on Improved Dandelion Optimization Algorithm for Mobile Location Estimation Under NLOS Simulation Environment. Wirel. Pers. Commun. 2023;131:2747–2772. doi: 10.1007/s11277-023-10578-y. [DOI] [Google Scholar]

[bib41] 41.Dong R., Liu Y., Wang S., Heidari A.A., Wang M., Chen Y., Wang S., Chen H., Zhang Y. Multi-strategy enhanced kernel search optimization and its application in economic emission dispatch problems. J. Comput. Des. Eng. 2023;11:135–172. doi: 10.1093/jcde/qwad110. [DOI] [Google Scholar]

[bib42] 42.Dong R., Sun L., Ma L., Heidari A.A., Zhou X., Chen H. Boosting Kernel Search Optimizer with Slime Mould Foraging Behavior for Combined Economic Emission Dispatch Problems. J. Bionic Eng. 2023;20:2863–2895. doi: 10.1007/s42235-023-00408-z. [DOI] [Google Scholar]

[bib43] 43.Huang J.C., Zeng G.Q., Geng G.G., Weng J., Lu K.D., Zhang Y. Differential evolution-based convolutional neural networks: An automatic architecture design method for intrusion detection in industrial control systems. Comput. Secur. 2023;132 doi: 10.1016/j.cose.2023.103310. [DOI] [Google Scholar]

[bib44] 44.Peng L., Li X., Yu L., Heidari A.A., Chen H., Liang G. Q-learning guided mutational Harris hawk optimizer for high-dimensional gene data feature selection. Appl. Soft Comput. 2024;161 doi: 10.1016/j.asoc.2024.111734. [DOI] [Google Scholar]

[bib45] 45.Zhang K., Liu Y., Wang X., Mei F., Kang H., Sun G. IBMRFO: Improved binary manta ray foraging optimization with chaotic tent map and adaptive somersault factor for feature selection. Expert Syst. Appl. 2024;251 doi: 10.1016/j.eswa.2024.123977. [DOI] [Google Scholar]

[bib46] 46.Jiang H., Yang Y., Wan Q., Dong Y. Feature selection based on dynamic crow search algorithm for high-dimensional data classification. Expert Syst. Appl. 2024;250 doi: 10.1016/j.eswa.2024.123871. [DOI] [Google Scholar]

[bib47] 47.Van L.N., Tran V.N., Nguyen G.V., Yeon M., Do M.T.-T., Lee G. Enhancing wildfire mapping accuracy using mono-temporal Sentinel-2 data: A novel approach through qualitative and quantitative feature selection with explainable AI. Ecol. Inf. 2024;81 doi: 10.1016/j.ecoinf.2024.102601. [DOI] [Google Scholar]

[bib48] 48.Ozsoydan F.B. Effects of dominant wolves in grey wolf optimization algorithm. Appl. Soft Comput. 2019;83 doi: 10.1016/j.asoc.2019.105658. [DOI] [Google Scholar]

[bib49] 49.Dhargupta S., Ghosh M., Mirjalili S., Sarkar R. Selective Opposition based Grey Wolf Optimization. Expert Syst. Appl. 2020;151 doi: 10.1016/j.eswa.2020.113389. [DOI] [Google Scholar]

[bib50] 50.Deng L., Liu S. An enhanced slime mould algorithm based on adaptive grouping technique for global optimization. Expert Syst. Appl. 2023;222 doi: 10.1016/j.eswa.2023.119877. [DOI] [Google Scholar]

[bib51] 51.Samantaray S., Sahoo P., Sahoo A., Satapathy D.P. Flood discharge prediction using improved ANFIS model combined with hybrid particle swarm optimisation and slime mould algorithm. Environ. Sci. Pollut. Res. 2023;30:83845–83872. doi: 10.1007/s11356-023-27844-y. [DOI] [PubMed] [Google Scholar]

[bib52] 52.Tan W.-H., Mohamad-Saleh J. A hybrid whale optimization algorithm based on equilibrium concept. Alex. Eng. J. 2023;68:763–786. doi: 10.1016/j.aej.2022.12.019. [DOI] [Google Scholar]

[bib53] 53.Wang J., Bei J., Song H., Zhang H., Zhang P. A whale optimization algorithm with combined mutation and removing similarity for global optimization and multilevel thresholding image segmentation. Appl. Soft Comput. 2023;137 doi: 10.1016/j.asoc.2023.110130. [DOI] [Google Scholar]

[bib54] 54.Kumar A., Dhillon J.S. Enhanced Harris hawk optimizer for hydrothermal generation scheduling with cascaded reservoirs. Expert Syst. Appl. 2023;226 doi: 10.1016/j.eswa.2023.120270. [DOI] [Google Scholar]

[bib55] 55.Tian F., Wang J., Chu F. Improved Multi-Strategy Harris Hawks Optimization and Its Application in Engineering Problems. Mathematics. 2023;11:1525. doi: 10.3390/math11061525. [DOI] [Google Scholar]

[bib56] 56.Tiwari P., Mishra V.N., Parouha R.P. Developments and Design of Differential Evolution Algorithm for Non-linear/Non-convex Engineering Optimization. Arch. Comput. Methods Eng. 2024;31:2227–2263. doi: 10.1007/s11831-023-10036-9. [DOI] [Google Scholar]

[bib57] 57.Pham V.H.S., Nguyen Dang N.T., Nguyen V.N. Enhancing engineering optimization using hybrid sine cosine algorithm with Roulette wheel selection and opposition-based learning. Sci. Rep. 2024;14:694. doi: 10.1038/s41598-024-51343-w. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib58] 58.Huang J., Hu H. Hybrid beluga whale optimization algorithm with multi-strategy for functions and engineering optimization problems. J. Big Data. 2024;11:3. doi: 10.1186/s40537-023-00864-8. [DOI] [Google Scholar]

[bib59] 59.Gomes S.B.F., Simmons N., Sofotasios P.C., Yacoub M.D., Cotton S.L. Channel Parameter Estimation in Millimeter-Wave Propagation Environments Using Genetic Algorithm. IEEE Antennas Wirel. Propag. Lett. 2024;23:24–28. doi: 10.1109/LAWP.2023.3315422. [DOI] [Google Scholar]

[bib60] 60.Gundogdu H., Demirci A., Tercan S.M., Cali U. A Novel Improved Grey Wolf Algorithm Based Global Maximum Power Point Tracker Method Considering Partial Shading. IEEE Access. 2024;12:6148–6159. doi: 10.1109/ACCESS.2024.3350269. [DOI] [Google Scholar]

[bib61] 61.Yu X., Zhang W. A teaching-learning-based optimization algorithm with reinforcement learning to address wind farm layout optimization problem. Appl. Soft Comput. 2024;151 doi: 10.1016/j.asoc.2023.111135. [DOI] [Google Scholar]

[bib62] 62.Moustafa G., Alnami H., Hakmi S.H., Shaheen A.M., Ginidi A.R., Elshahed M.A., Mansour H.S.E. A Novel Mantis Search Algorithm for Economic Dispatch in Combined Heat and Power Systems. IEEE Access. 2024;12:2674–2689. doi: 10.1109/ACCESS.2023.3344679. [DOI] [Google Scholar]

[bib63] 63.Al-Areeq A.M., Saleh R.A.A., Ghanim A.A.J., Ghaleb M., Al‑Areeq N.M., Al-Wajih E. Flood hazard assessment in Yemen using a novel hybrid approach of Grey Wolf and Levenberg Marquardt optimizers. Geocarto Int. 2023;38 doi: 10.1080/10106049.2023.2243884. [DOI] [Google Scholar]

[bib64] 64.Tu B., Wang F., Huo Y., Wang X. A hybrid algorithm of grey wolf optimizer and harris hawks optimization for solving global optimization problems with improved convergence performance. Sci. Rep. 2023;13 doi: 10.1038/s41598-023-49754-2. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib65] 65.Silva B.N., Khan M., Wijesinghe R.E., Wijenayake U. Meta-heuristic optimization based cost efficient demand-side management for sustainable smart communities. Energy Build. 2024;303 doi: 10.1016/j.enbuild.2023.113599. [DOI] [Google Scholar]

[bib66] 66.Peng L., Cai Z., Heidari A.A., Zhang L., Chen H. Hierarchical Harris hawks optimizer for feature selection. J. Adv. Res. 2023;53:261–278. doi: 10.1016/j.jare.2023.01.014. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib67] 67.Yu H., Zhao Z., Heidari A.A., Ma L., Hamdi M., Mansour R.F., Chen H. An accelerated sine mapping whale optimizer for feature selection. iScience. 2023;26 doi: 10.1016/j.isci.2023.107896. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib68] 68.Mabrouk A., Yousri D., Aaaa S., Alduailij M., Elsayed Abd Elaziz M. Fractional order adaptive hunter-prey optimizer for feature selection. Alex. Eng. J. 2023;75:531–547. doi: 10.1016/j.aej.2023.05.092. [DOI] [Google Scholar]

[bib69] 69.Al-Khatib R.M., Al-qudah N.E.A., Jawarneh M.S., Al-Khateeb A. A novel improved lemurs optimization algorithm for feature selection problems. J. King Saud Univ. Comput. Inf. Sci. 2023;35 doi: 10.1016/j.jksuci.2023.101704. [DOI] [Google Scholar]

[bib70] 70.Zaimoğlu E.A., Yurtay N., Demirci H., Yurtay Y. A binary chaotic horse herd optimization algorithm for feature selection. Eng. Sci. Technol. 2023;44 doi: 10.1016/j.jestch.2023.101453. [DOI] [Google Scholar]

[bib71] 71.Chhabra A., Hussien A.G., Hashim F.A. Improved bald eagle search algorithm for global optimization and feature selection. Alex. Eng. J. 2023;68:141–180. doi: 10.1016/j.aej.2022.12.045. [DOI] [Google Scholar]

[bib72] 72.Pan H., Chen S., Xiong H. A high-dimensional feature selection method based on modified Gray Wolf Optimization. Appl. Soft Comput. 2023;135 doi: 10.1016/j.asoc.2023.110031. [DOI] [Google Scholar]

[bib73] 73.Askr H., Abdel-Salam M., Hassanien A.E. Copula entropy-based golden jackal optimization algorithm for high-dimensional feature selection problems. Expert Syst. Appl. 2024;238 doi: 10.1016/j.eswa.2023.121582. [DOI] [Google Scholar]

[bib74] 74.Wang Y., Ran S., Wang G.-G. Role-oriented binary grey wolf optimizer using foraging-following and Lévy flight for feature selection. Appl. Math. Model. 2024;126:310–326. doi: 10.1016/j.apm.2023.08.043. [DOI] [Google Scholar]

[bib75] 75.ye Z., Luo J., Zhou W., Wang M., He Q. An ensemble framework with improved hybrid breeding optimization-based feature selection for intrusion detection. Future Generat. Comput. Syst. 2024;151:124–136. doi: 10.1016/j.future.2023.09.035. [DOI] [Google Scholar]

[bib76] 76.Yang X., Zhen L., Li Z. Binary golden eagle optimizer combined with initialization of feature number subspace for feature selection. Knowl. Base Syst. 2023;282 doi: 10.1016/j.knosys.2023.111109. [DOI] [Google Scholar]

[bib77] 77.Chakraborty S., Saha A.K., Ezugwu A.E., Chakraborty R., Saha A. Horizontal crossover and co-operative hunting-based Whale Optimization Algorithm for feature selection. Knowl. Base Syst. 2023;282 doi: 10.1016/j.knosys.2023.111108. [DOI] [Google Scholar]

[bib78] 78.Abdelrazek M., Abd Elaziz M., El-Baz A.H. CDMO: Chaotic Dwarf Mongoose Optimization Algorithm for feature selection. Sci. Rep. 2024;14:701. doi: 10.1038/s41598-023-50959-8. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib79] 79.Mostafa R.R., Khedr A.M., Al Aghbari Z., Afyouni I., Kamel I., Ahmed N. An adaptive hybrid mutated differential evolution feature selection method for low and high-dimensional medical datasets. Knowl. Base Syst. 2024;283 doi: 10.1016/j.knosys.2023.111218. [DOI] [Google Scholar]

[bib80] 80.Wolpert D.H., Macready W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997;1:67–82. doi: 10.1109/4235.585893. [DOI] [Google Scholar]

[bib81] 81.Yu X., Qin W., Lin X., Shan Z., Huang L., Shao Q., Wang L., Chen M. Synergizing the enhanced RIME with fuzzy K-nearest neighbor for diagnose of pulmonary hypertension. Comput. Biol. Med. 2023;165 doi: 10.1016/j.compbiomed.2023.107408. [DOI] [PubMed] [Google Scholar]

[bib82] 82.Yang B., Wang J., Su S., Li Y., Wu P., Yang Z., Fan H., Li W., Li J. Mismatch losses mitigation of PV-TEG hybrid system via improved RIME algorithm: Design and hardware validation. J. Clean. Prod. 2024;434 doi: 10.1016/j.jclepro.2023.139957. [DOI] [Google Scholar]

[bib83] 83.Zhong R., Yu J., Zhang C., Munetomo M. SRIME: A strengthened RIME with Latin hypercube sampling and embedded distance-based selection for engineering optimization problems. Neural Comput. Appl. 2024;36:6721–6740. doi: 10.1007/s00521-024-09424-4. [DOI] [Google Scholar]

[bib84] 84.Zhu W., Fang L., Ye X., Medani M., Escorcia-Gutierrez J. IDRM: Brain tumor image segmentation with boosted RIME optimization. Comput. Biol. Med. 2023;166 doi: 10.1016/j.compbiomed.2023.107551. [DOI] [PubMed] [Google Scholar]

[bib85] 85.Li Y., Zhao D., Ma C., Escorcia-Gutierrez J., Aljehane N.O., Ye X. CDRIME-MTIS: An enhanced rime optimization-driven multi-threshold segmentation for COVID-19 X-ray images. Comput. Biol. Med. 2024;169 doi: 10.1016/j.compbiomed.2023.107838. [DOI] [PubMed] [Google Scholar]

[bib86] 86.Awad N.H., Ali M.Z., Suganthan P.N. 2017 IEEE Congress on Evolutionary Computation (CEC) Donostia; 2017. Ensemble sinusoidal differential covariance matrix adaptation with Euclidean neighborhood for solving CEC2017 benchmark problems; pp. 372–379. [DOI] [Google Scholar]

[bib87] 87.LaTorre A., Peña J.M. 2017 IEEE Congress on Evolutionary Computation (CEC) Donostia; 2017. A comparison of three large-scale global optimizers on the CEC 2017 single objective real parameter numerical optimization benchmark; pp. 1063–1070. [DOI] [Google Scholar]

[bib88] 88.Liu X., Huang H., Xiang J. A personalized diagnosis method to detect faults in gears using numerical simulation and extreme learning machine. Knowl. Base Syst. 2020;195 doi: 10.1016/j.knosys.2020.105653. [DOI] [Google Scholar]

[bib89] 89.Li J., Lin J. A probability distribution detection based hybrid ensemble QoS prediction approach. Inf. Sci. 2020;519:289–305. doi: 10.1016/j.ins.2020.01.046. [DOI] [Google Scholar]

[bib90] 90.Liu K., Ke F., Huang X., Yu R., Lin F., Wu Y., Ng D.W.K. DeepBAN: A Temporal Convolution-Based Communication Framework for Dynamic WBANs. IEEE Trans. Commun. 2021;69:6675–6690. doi: 10.1109/TCOMM.2021.3094581. [DOI] [Google Scholar]

[bib91] 91.Yang X.S., Suash D. 2009 World Congress on Nature & Biologically Inspired Computing (NaBIC) 2009. Cuckoo Search via Lévy flights; pp. 210–214. [DOI] [Google Scholar]

[bib92] 92.Ahmed S., Groenli T.-M., Lakhan A., Chen Y., Liang G. A reinforcement federated learning based strategy for urinary disease dataset processing. Comput. Biol. Med. 2023;163 doi: 10.1016/j.compbiomed.2023.107210. [DOI] [PubMed] [Google Scholar]

[bib93] 93.Pan X., Zhang G., Lin A., Guan X., Chen P., Ge Y., Chen X. An evaluation model for children’s foot & ankle deformity severity using sparse multi-objective feature selection algorithm. Comput. Biol. Med. 2022;151 doi: 10.1016/j.compbiomed.2022.106229. [DOI] [PubMed] [Google Scholar]

[bib94] 94.Zhou P., Chen J., Fan M., Du L., Shen Y.D., Li X. Unsupervised feature selection for balanced clustering. Knowl. Base Syst. 2020;193 doi: 10.1016/j.knosys.2019.105417. [DOI] [Google Scholar]

[bib95] 95.Mirjalili S., Lewis A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016;95:51–67. doi: 10.1016/j.advengsoft.2016.01.008. [DOI] [Google Scholar]

[bib96] 96.Mirjalili S., Gandomi A.H., Mirjalili S.Z., Saremi S., Faris H., Mirjalili S.M. Salp Swarm Algorithm: A bio-inspired optimizer for engineering design problems. Adv. Eng. Softw. 2017;114:163–191. doi: 10.1016/j.advengsoft.2017.07.002. [DOI] [Google Scholar]

[bib97] 97.Kennedy J., Eberhart R. Vol. 4. 1995. Particle swarm optimization; pp. 1942–1948. (Proceedings of ICNN'95 - International Conference on Neural Networks). [DOI] [Google Scholar]

[bib98] 98.Mirjalili S., Mirjalili S.M., Lewis A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014;69:46–61. doi: 10.1016/j.advengsoft.2013.12.007. [DOI] [Google Scholar]

[bib99] 99.Yang X.S., Hossein Gandomi A. Bat algorithm: A novel approach for global engineering optimization. Eng. Comput. 2012;29:464–483. doi: 10.1108/02644401211235834. [DOI] [Google Scholar]

[bib100] 100.Emary E., Zawbaa H.M., Ghany K.K.A., Hassanien A.E., Parv B. Proceedings of the 7th Balkan Conference on Informatics Conference. 2015. Firefly Optimization Algorithm for Feature Selection. [DOI] [Google Scholar]

[bib101] 101.Kumar A., Misra R.K., Singh D. 2017 IEEE Congress on Evolutionary Computation (CEC) Donostia; 2017. Improving the local search capability of Effective Butterfly Optimizer using Covariance Matrix Adapted Retreat Phase; pp. 1835–1842. [DOI] [Google Scholar]

[bib102] 102.Chen W.N., Zhang J., Lin Y., Chen N., Zhan Z.H., Chung H.S.H., Li Y., Shi Y.H. Particle Swarm Optimization With an Aging Leader and Challengers. IEEE Trans. Evol. Comput. 2013;17:241–258. doi: 10.1109/TEVC.2011.2173577. [DOI] [Google Scholar]

[bib103] 103.Liang J.J., Qin A.K., Suganthan P.N., Baskar S. Comprehensive learning particle swarm optimizer for global optimization of multimodal functions. IEEE Trans. Evol. Comput. 2006;10:281–295. doi: 10.1109/TEVC.2005.857610. [DOI] [Google Scholar]

[bib104] 104.Tanabe R., Fukunaga A.S. 2014 IEEE Congress on Evolutionary Computation (CEC) 2014. Improving the search performance of SHADE using linear population size reduction; pp. 1658–1665. [DOI] [Google Scholar]

[bib105] 105.Qin A.K., Huang V.L., Suganthan P.N. Differential Evolution Algorithm With Strategy Adaptation for Global Numerical Optimization. IEEE Trans. Evol. Comput. 2009;13:398–417. doi: 10.1109/TEVC.2008.927706. [DOI] [Google Scholar]

[bib106] 106.Zhang J., Sanderson A.C. JADE: Adaptive Differential Evolution With Optional External Archive. IEEE Trans. Evol. Comput. 2009;13:945–958. doi: 10.1109/TEVC.2009.2014613. [DOI] [Google Scholar]

[bib107] 107.Liang H., Liu Y., Shen Y., Li F., Man Y. A Hybrid Bat Algorithm for Economic Dispatch With Random Wind Power. IEEE Trans. Power Syst. 2018;33:5052–5061. doi: 10.1109/TPWRS.2018.2812711. [DOI] [Google Scholar]

[bib108] 108.Lynn N., Suganthan P.N. Ensemble particle swarm optimizer. Appl. Soft Comput. 2017;55:533–548. doi: 10.1016/j.asoc.2017.02.007. [DOI] [Google Scholar]

[bib109] 109.Gandomi A.H., Yang X.-S. Chaotic bat algorithm. J. Comput. Sci. 2014;5:224–232. doi: 10.1016/j.jocs.2013.10.002. [DOI] [Google Scholar]

[bib110] 110.Ling Y., Zhou Y., Luo Q. Lévy Flight Trajectory-Based Whale Optimization Algorithm for Global Optimization. IEEE Access. 2017;5:6168–6186. doi: 10.1109/ACCESS.2017.2695498. [DOI] [Google Scholar]

[bib111] 111.Yu H., Zhao Z., Zhou J., Heidari A.A., Chen H. Sine cosine algorithm with communication and quality enhancement: Performance design for engineering problems. J. Comput. Des. Eng. 2023;10:1868–1891. doi: 10.1093/jcde/qwad073. [DOI] [Google Scholar]

[bib129] 112.Ben Guedria N. Improved accelerated PSO algorithm for mechanical engineering optimization problems. Appl. Soft Comput. 2016;40:455–467. doi: 10.1016/j.asoc.2015.10.048. [DOI] [Google Scholar]

[bib130] 113.Mezura-Montes E., Coello C.A.C. An empirical study about the usefulness of evolution strategies to solve constrained optimization problems. Int. J. Gen. Syst. 2008;37:443–473. doi: 10.1080/03081070701303470. [DOI] [Google Scholar]

[bib131] 114.Coello Coello C.A. Use of a self-adaptive penalty approach for engineering optimization problems. Comput. Ind. 2000;41:113–127. doi: 10.1016/S0166-3615(99)00046-9. [DOI] [Google Scholar]

[bib132] 115.Mahdavi M., Fesanghary M., Damangir E. An improved harmony search algorithm for solving optimization problems. Appl. Math. Comput. 2007;188:1567–1579. doi: 10.1016/j.amc.2006.11.033. [DOI] [Google Scholar]

[bib133] 116.Tu J., Chen H., Liu J., Heidari A.A., Zhang X., Wang M., Ruby R., Pham Q.-V. Evolutionary biogeography-based whale optimization methods with communication structure: Towards measuring the balance. Knowl. Base Syst. 2021;212 doi: 10.1016/j.knosys.2020.106642. [DOI] [Google Scholar]

[bib112] 117.Shan W., He X., Liu H., Heidari A.A., Wang M., Cai Z., Chen H. Cauchy mutation boosted Harris hawk algorithm: Optimal performance design and engineering applications. J. Comput. Des. Eng. 2023;10:503–526. doi: 10.1093/jcde/qwad002. [DOI] [Google Scholar]

[bib134] 118.Chickermane H., Gea H.C. Structural optimization using a new local approximation method. Int. J. Numer. Methods Eng. 1996;39:829–846. doi: 10.1002/(SICI)1097-0207(19960315)39:5<829::AID-NME884>3.0.CO;2-U. [DOI] [Google Scholar]

[bib135] 119.Gandomi A.H., Yang X.-S., Alavi A.H. Cuckoo search algorithm: a metaheuristic approach to solve structural optimization problems. Eng. Comput. 2013;29:17–35. doi: 10.1007/s00366-011-0241-y. [DOI] [Google Scholar]

[bib113] 120.Wang G.G. Adaptive Response Surface Method Using Inherited Latin Hypercube Design Points. J. Mech. Des. 2003;125:210–220. doi: 10.1115/1.1561044. [DOI] [Google Scholar]

[bib136] 121.Cheng M.-Y., Prayogo D. Symbiotic Organisms Search: A new metaheuristic optimization algorithm. Comput. Struct. 2014;139:98–112. doi: 10.1016/j.compstruc.2014.03.007. [DOI] [Google Scholar]

[bib114] 122.Li X., Lin Z., Lv H., Yu L., Heidari A.A., Zhang Y., Chen H., Liang G. Advanced slime mould algorithm incorporating differential evolution and Powell mechanism for engineering design. iScience. 2023;26 doi: 10.1016/j.isci.2023.107736. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib137] 123.Wang G., Heidari A.A., Wang M., Kuang F., Zhu W., Chen H. Chaotic Arc Adaptive Grasshopper Optimization. IEEE Access. 2021;9:17672–17706. doi: 10.1109/ACCESS.2021.3052800. [DOI] [Google Scholar]

[bib138] 124.Deb K., Goyal M. 1997. Optimizing Engineering Designs Using a Com Bined Genetic Search. [Google Scholar]

[bib115] 125.Zhang M., Chen H., Heidari A.A., Cai Z., Aljehane N.O., Mansour R.F. OCRUN: An oppositional Runge Kutta optimizer with cuckoo search for global optimization and feature selection. Appl. Soft Comput. 2023;146 doi: 10.1016/j.asoc.2023.110664. [DOI] [Google Scholar]

[bib116] 126.Zhou X., Gui W., Heidari A.A., Cai Z., Liang G., Chen H. Random following ant colony optimization: Continuous and binary variants for global optimization and feature selection. Appl. Soft Comput. 2023;144 doi: 10.1016/j.asoc.2023.110513. [DOI] [Google Scholar]

[bib117] 127.Oliveira D.A.B., Ferreira R.S., Silva R., Brazil E.V. Improving Seismic Data Resolution With Deep Generative Networks. Geosci. Rem. Sens. Lett. IEEE. 2019;16:1929–1933. doi: 10.1109/LGRS.2019.2913593. [DOI] [Google Scholar]

[bib118] 128.Feltes B.C., Chandelier E.B., Grisci B.I., Dorn M. CuMiDa: An Extensively Curated Microarray Database for Benchmarking and Testing of Machine Learning Approaches in Cancer Research. J. Comput. Biol. 2019;26:376–386. doi: 10.1089/cmb.2018.0238. [DOI] [PubMed] [Google Scholar]

[bib119] 129.Tumar I., Hassouneh Y., Turabieh H., Thaher T. Enhanced Binary Moth Flame Optimization as a Feature Selection Algorithm to Predict Software Fault Prediction. IEEE Access. 2020;8:8041–8055. doi: 10.1109/ACCESS.2020.2964321. [DOI] [Google Scholar]

[bib120] 130.Emary E., Zawbaa H.M., Hassanien A.E. Binary grey wolf optimization approaches for feature selection. Neurocomputing. 2016;172:371–381. doi: 10.1016/j.neucom.2015.06.083. [DOI] [Google Scholar]

[bib121] 131.Abdel-Basset M., Mohamed R., Sallam K.M., Chakrabortty R.K., Ryan M.J. BSMA: A novel metaheuristic algorithm for multi-dimensional knapsack problems: Method and comprehensive analysis. Comput. Ind. Eng. 2021;159 doi: 10.1016/j.cie.2021.107469. [DOI] [Google Scholar]

[bib122] 132.Emary E., Zawbaa H.M., Hassanien A.E. Binary ant lion approaches for feature selection. Neurocomputing. 2016;213:54–65. doi: 10.1016/j.neucom.2016.03.101. [DOI] [Google Scholar]

[bib123] 133.Mirjalili S., Mirjalili S.M., Yang X.-S. Binary bat algorithm. Neural Comput. Appl. 2014;25:663–681. doi: 10.1007/s00521-013-1525-5. [DOI] [Google Scholar]

[bib124] 134.Faris H., Mafarja M.M., Heidari A.A., Aljarah I., Al-Zoubi A.M., Mirjalili S., Fujita H. An efficient binary Salp Swarm Algorithm with crossover scheme for feature selection problems. Knowl. Base Syst. 2018;154:43–67. doi: 10.1016/j.knosys.2018.05.009. [DOI] [Google Scholar]

[bib125] 135.Mafarja M., Mirjalili S. Whale optimization approaches for wrapper feature selection. Appl. Soft Comput. 2018;62:441–453. doi: 10.1016/j.asoc.2017.11.006. [DOI] [Google Scholar]

[bib126] 136.Thaher T., Heidari A.A., Mafarja M., Dong J.S., Mirjalili S. Evolutionary Machine Learning Techniques: Algorithms and Applications. Springer; 2020. Binary Harris Hawks Optimizer for High-Dimensional, Low Sample Size Feature Selection; pp. 251–272. [DOI] [Google Scholar]

[bib127] 137.Ganesh N., Shankar R., Čep R., Chakraborty S., Kalita K. Efficient Feature Selection Using Weighted Superposition Attraction Optimization Algorithm. Appl. Sci. 2023;13:3223. doi: 10.3390/app13053223. [DOI] [Google Scholar]

[bib128] 138.Priyadarshini J., Premalatha M., Čep R., Jayasudha M., Kalita K. Analyzing Physics-Inspired Metaheuristic Algorithms in Feature Selection with K-Nearest-Neighbor. Appl. Sci. 2023;13:906. doi: 10.3390/app13020906. [DOI] [Google Scholar]

[bib139] 139.Wang Y., Cai Z., Zhang Q. Differential Evolution With Composite Trial Vector Generation Strategies and Control Parameters. IEEE Trans. Evol. Comput. 2011;15:55–66. doi: 10.1109/TEVC.2010.2087271. [DOI] [Google Scholar]

[bib140] 140.Zhang H., Wang Z., Chen W., Heidari A.A., Wang M., Zhao X., Liang G., Chen H., Zhang X. Ensemble mutation-driven salp swarm algorithm with restart mechanism: Framework and fundamental analysis. Expert Syst. Appl. 2021;165 doi: 10.1016/j.eswa.2020.113897. [DOI] [Google Scholar]

[bib141] 141.Gao R., Tao J., Zhang J., Ma L., Xu M. NSGA-III-SD based Fuzzy energy management system optimization for lithium battery/supercapacitor HEV. Appl. Soft Comput. 2023;142 doi: 10.1016/j.asoc.2023.110280. [DOI] [Google Scholar]

[bib142] 142.Li Y., Liu Y., Guo Y.Z., Liao X.F., Hu B., Yu T. Spatio-Temporal-Spectral Hierarchical Graph Convolutional Network With Semisupervised Active Learning for Patient-Specific Seizure Prediction. IEEE Trans. Cybern. 2022;52:12189–12204. doi: 10.1109/TCYB.2021.3071860. [DOI] [PubMed] [Google Scholar]

[bib143] 143.Govindarajan M., Chandrasekaran R.M. Evaluation of k-Nearest Neighbor classifier performance for direct marketing. Expert Syst. Appl. 2010;37:253–258. doi: 10.1016/j.eswa.2009.04.055. [DOI] [Google Scholar]

[bib144] 144.Hu P., Pan J.-S., Chu S.-C. Improved Binary Grey Wolf Optimizer and Its application for feature selection. Knowl. Base Syst. 2020;195 doi: 10.1016/j.knosys.2020.105746. [DOI] [Google Scholar]

PERMALINK

IRIME: Mitigating exploitation-exploration imbalance in RIME optimization for feature selection

Jinpeng Huang

Yi Chen

Ali Asghar Heidari

Lei Liu

Huiling Chen

Guoxi Liang

Summary

Graphical abstract

Highlights

Introduction

Results and discussion

Experimental design and analysis of results

Table 1.

Table 2.

Qualitative analysis of IRIME

Analysis of historical search trajectories

Figure 1.

Balance and diversity analysis

Figure 2.

Figure 3.

Parameter sensitivity experiment

Table 3.

The influence of SB and CMS-RS

Table 4.

Figure 4.

Table 5.

Figure 5.

Table 6.

Stability testing of IRIME

Table 7.

Figure 6.

Comparison with conventional algorithms

Table 8.

Table 9.

Figure 7.

Figure 8.

Table 10.

Comparison with advanced algorithms

Table 11.

Table 12.

Figure 9.

Figure 10.

Table 13.

The experiments for engineering design

TCSP

Figure 11.

Table 14.

CBP

Figure 12.

Table 15.

IBP

Figure 13.

Table 16.

BSP

Figure 14.

Table 17.

The experiments for feature selection

Simulation experiments

Table 18.

Table 19.

Table 20.

Table 21.

Figure 15.

Table 22.

Table 23.

Table 24.

Figure 16.

Figure 17.

Figure 18.

Time cost

Figure 19.

Figure 20.

Conclusions and future directions

Limitations of the study

STAR★Methods

Key resources table

Resource availability

Lead contact