Improving the thermal performance of vertical ground heat exchanger by modifying spiral tube geometry: A numerical study

Abstract

Ground heat exchanger (GHE) is the most crucial element of a ground source heat pump (GSHP) system for building cooling and heating by the utilization of geothermal energy. Therefore, intending to enhance the performance of GHE, the present study conducts a computational investigation of the thermal performance of modified spiral tube vertical GHEs. Several modifications of uniform-pitched spiral GHE are made to increase its thermal performance. Some modifications are introduced as variable-pitched spiral tube GHE where spiral inlet pipes are densified in the lower part of GHEs by reducing pitch distance. Conversely, in some modifications, the position of the outlet straight pipe is changed. Water is considered as the working fluid and the inlet temperature of the water is maintained fixed at 300.15 K. After extensive analysis, it is evident that, when the outlet pipe is placed outside of the spiral coil, there is a 7.67 % enhancement in the thermal performance than a traditional uniform-pitched spiral tube GHE. However, modifications like variable-pitched spiral tube GHEs are not significant to improve the thermal performance due to the quick saturation of the ground soil temperature around the GHE pipes. To have a balance between heat transfer rate and pressure drop, thermal performance capability (TPC) and coefficient of performance improvement (COP_imprvt) criterion were evaluated and it is found that the uniform-pitched spiral tube GHE along with the outlet pipe at the outside of the spiral provides maximum thermal performance with a maximum TPC value of 1.062 and provides the positive value of COP_imprvt criterion. The positive values of COP_imprvt indicate that the spiral tube GHEs are energy efficient based on heat transfer and pressure drop. Moreover, spiral GHE with high-density polyethylene (HDPE), concrete pile, and sandy clay outperform the other materials for pipe, backfill, and soil, respectively. Specifically, HDPE pipe, concrete backfill, and sandy clay as soil offer around 7 %, 5 %, and 7.8 % higher thermal performance compared to polyethylene, sand silica, and clay, respectively.

Highlights

• •Several modifications of vertical spiral-tube ground heat exchangers (GHE) are introduced.
• •The effects of altering spiral pitch and flow rate on the performance are investigated.
• •Dimensionless parameters of heat transfer effectiveness and thermal performance capability are determined for optimization.
• •The effect of using different materials on the thermal performance of GHE is evaluated.
• •Adjusting the outlet pipe position offers up to 7.56 % improvement of thermal performance than traditional configuration.

1. Introduction

Energy demand is rapidly growing worldwide each year due to steady population growth, rapid industrial development, and the need to maintain a standard of living, making energy a critical issue for all nations [1,2]. Currently, global energy need is primarily supplied by traditional fossil fuels [3,4]. Since the global energy demand is growing, the burning of fossil fuels is releasing a huge amount of greenhouse gases (GHGs) into the atmosphere which is responsible for global warming [5] and consequently promotes global environmental issues such as climate change [6]. Approximately 40 % of global energy is consumed in the building sector [7] which is responsible for the world's CO₂ emissions more than 36 % [8]. Due to the uncertainty of fossil fuel prices, and depletion of conventional energy resources [9], attention should be provided to potential uses of renewable energy sources as these sources are endless, clean, and will grow soon due to the advancement of new technology [10,11]. To overcome GHG emissions, the exploration of alternative sources such as solar, wind, hydro, tidal, biomass, and geothermal is a pollution-free solution [12,13]. However, due to the irregular availability of some renewable energy sources such as solar, wind, and tidal [14], geothermal energy offers significant advantages for continuous energy supply [15], and can be considered a substitute for conventional fossil energy sources [16] for building space heating and cooling with low or no emissions [12].

The ground temperature beyond a certain depth (5–10 m) becomes steady throughout the year [17]. Therefore, geothermal energy is regarded as a more stable thermal energy source and sink [18], and this source is utilized by the ground source heat pump (GSHP) system [19]. GSHP is gaining popularity in countries and regions such as the USA, Europe, Australia, Korea, Japan, Canada, and China [20,21]. GSHP system is used for transforming geothermal energy into useable heat energy to warm and chill building spaces by integrating a ground heat exchanger (GHE) [22]. There are two types of GHEs to extract or reject thermal energy from/to the ground, which are embedded in horizontal trenches or vertical boreholes [23]. The horizontal GHEs are the most frequent choice and more cost-effective to install compared to vertical GHEs [24]. Conversely, vertical placement requires a modest land area of installation and provides notably enhanced thermal performance than horizontal placement [25]. The heat transfer capability of any kind of heat exchanger is of great importance for an efficient heat transfer system [[26], [27], [28]]. Therefore, performance optimization of GHEs is required to decrease excessive installation costs due to oversizing or reduced energy transfer due to under-sizing and to increase the overall performance of the GSHP system [29].

Performance enhancement of GHEs is vital for enhancing the efficiency of GSHP systems for utilization in building heating and cooling applications [30]. Numerous studies were conducted to investigate the impacts of density, thermal conduction coefficient, specific heat capacity of both fluid and soil, pipe diameter, fluid velocity, and different heat exchanger configurations on the overall output of GHE. The thermal performance of several spiral tube GHEs having uniformly distributed coil pitches was numerically investigated by Jalaluddin and Miyara [24]. The reduced-pitched spiral tube GHE was found to have greater thermal performance with a higher pressure drop. Moreover, Ali and Miyara [31] computationally investigated the heat transfer efficiency of the slinky GHE. Several measures were taken to improve thermal performance. To enhance the utilization of soil heat energy around GHEs, the slinky GHEs with variable loop pitch intervals were installed. Loop pitch intervals gradually decreased from leading to trailing loops. In most of their modifications, the average heat transfer rate was improved. Al-Kbodi et al. [32] conducted comparative three-dimensional transient numerical analyses for enhancing the performance of a novel U-tube GHE with distinct hollow-finned shapes. They concluded that, among the considered arrangements, the Y-shaped hollow-finned U-tube GHE offers higher heat transfer performance, with a 52.64 % improvement in heat transfer rate per unit length compared to the typical circular U-tube GHE. In addition, these designs reduced thermal resistance and boring costs. Dehghan [33] studied different vertical spiral GHE configurations to optimize the performance. Their findings revealed that, even though greater vertical length improved thermal performance, it also increased the drilling expenses. Saeidi et al. [34] investigated the impacts of alteration of flow rate, pitch distance, thermal conduction coefficient, and specific heat capacity of boreholes and soil substances on the thermal performance of spiral GHE. Liang et al. [35] investigated the impacts of fluid velocity and different borehole substances on the heat transfer of a vertical spiral GHE. They concluded that higher heat transfer was achieved when the Reynolds number was maintained at 5000. Rajeh et al. [36] performed a detailed computational investigation on oval-shaped coaxial GHEs against traditional circular-shaped coaxial GHEs for GSHP systems to reduce environmental impact and cost. They concluded that oval-shaped ones outperformed traditional circle-shaped GHEs by significantly lowering life cycle energy consumption, cost, and CO₂ emissions. Moreover, the utilization of HDPE as intake pipes and steel as exit pipes in oval-CGHEs significantly improved thermal performance. Chicco and Mandrone [37] studied vertical borehole heat exchangers considering four types of backfill material with different thermal conductivities to investigate and compare thermal performance. Their outcomes indicated that the borehole substance with a higher thermal conduction coefficient ensured better performance. Similarly, Javadi et al. [38] numerically studied eight different kinds of helical GHEs. The heat transfer surface area of all the GHE models under consideration was the same. Their findings indicated that the triple helix GHE provided a maximum heat transfer rate. Serageldin et al. [39] performed a novel three-dimensional, transient study of double spiral GHE utilizing the finite volume method to decrease installation costs and improve heat transfer performance. They found that the double spiral GHE yielded a 44.1 % higher thermal performance compared to U-tube GHE. However, Zarrella et al. [40], considered the weather state and axial heat transfer impact on the thermal performance of spiral GHE and noticed that the weather state had a notable effect, while the pitch between turns had little effect on the performance of spiral GHE. Wang et al. [41] investigated how the heat transfer rate of a spiral tube GHE is affected by the groundwater flow. Their results demonstrated improved heat transfer and reduced temperature elevation when groundwater flow was present.

Zhao et al. [42,43], Luo et al. [44], and Carotenuto et al. [45] comprehensively investigated the performance of various kinds of vertical GHEs, such as single, double, and triple U-tube, W, and spiral-shaped configurations. All of them found that the spiral-shaped GHE outperformed the other types concerning heat transfer rate. Additionally, Dehghan [46] numerically examined the combined performance of multiple spiral GHEs, finding that a configuration with nine spiral GHEs achieved the highest thermal performance. Wang et al. [47], Leroy and Bernier [48] developed novel methods to study the heat transfer capability of spiral GHEs. Ahmadi [49] studied a double-tube heat exchanger using a spiral turbulator, varying the spiral pitch and radius. The conclusions indicated that enhanced fluid mixing at low-pitch dimensions resulted in higher heat transfer. Moreover, corrugated tubes improved the thermal performance of any type of heat exchanger rather than smooth the tubes [50]. Table 1 presents crucial information about significant prior studies concerning different types of vertical spiral tube GHEs.

Table 1.

Pertinent information on different types of GHEs.

Author(s)	Methods	Spiral pitch dimension (m)	Spiral pitch distance Variable pitched GHE	Optimization of GHE materials	Remarks
Jalaluddin and Miyara [24]	Numerical	0.05, 0.1, 0.2	Uniform	No	Spiral tube GHEs were examined and compared to U-tube GHE. The smaller-pitched spiral GHEs exhibited the maximum heat transfer and pressure drop.
Zhao et al. [42]	Numerical	0.25, 0.5, 1, 2	Uniform	Yes	The impact of spiral pitch variation on the thermal performance of spiral GHEs was investigated, revealing enhanced performance at smaller pitch values.
Dehghan [46]	Numerical	0.1	Uniform	Yes	The combined performance of nine spiral tube GHEs was investigated. Thermal performance improved with longer vertical lengths, despite the higher construction costs.
Wang et al. [47]	Numerical	1	Uniform	No	Analytical approach employing the Laplacian method was developed to investigate spiral GHEs.
Zhao et al. [43]	Experimental and numerical	0.25	Uniform	No	A comparative study of the performances of U-shaped, W-shaped, and spiral-shaped GHEs was conducted, with the spiral-shaped GHE offering the best performance under identical conditions.
Leroy et al. [48]	Numerical	0.4	Uniform	No	An innovative helical coil GHE model was proposed to account for axial heat transfer effects.
Luo et al. [44]	Experimental	0.3	Uniform	No	Double-U, triple-U, double-W, and spiral tube GHEs were studied. The spiral configuration demonstrated 15 % better performance than the W configuration.
Carotenuto et al. [45]	Numerical	0.1, 0.25, 0.5, 0.7	Uniform	No	The performance of single, double, and triple U-tube and spiral GHEs was investigated. Spiral GHEs with excessively small pitch resulted in increased pressure drop.
Dehghan [33]	Experimental and numerical	0.1	Uniform	No	Various combinations of uniformly pitched spiral GHEs were studied. The configuration comprising nine spiral GHEs demonstrated the highest heat transfer rate.
Ahmadi [49]	Numerical	0.05, 0.1, 0.25, 0.5	Uniform	No	Different configurations of spiral GHEs were investigated by varying the spiral pitch and spiral radius. A decrease in pitch resulted in enhanced heat transfer due to improved fluid mixing.
Present study	Numerical	0.10, 0.11, 0.17, 0.19, 0.20, 0.25, 0.29, 0.45	Variable	Yes	Variable-pitched spiral GHEs are used to optimize the performance. Additionally, the position of the exit straight tube is adjusted to minimize thermal interference with the inlet spiral tube. Various parameters such as GHE pipe material, backfill, and ground soil material are optimized to enhance performance. Finally, the impact of varying flow rates on thermal performnace and pressure drop are investigated.

From the detailed literature review above, it is evident that prior studies investigated the thermal performance of spiral/coiled-type vertical GHEs where coils were uniformly distributed (see Table 1). Since the thermal gradient amid GHE working fluid and ground soil around the spiral GHE is higher in the initial part (leading turns) than in subsequent parts (trailing turns), hence heat exchange capability diminishes progressively from the leading turns to subsequent ones [12]. Therefore, measures are taken to modify the uniform-pitched spiral GHE by increasing the number of turns in the lower part of the inlet spiral pipe to ensure maximum use of available ground heat energy. Also, the position of the outlet straight pipe is modified to reduce the thermal interference effect between the inlet and outlet pipes. The redistribution of spiral turns and repositioning of the outlet straight pipe may improve the thermal performance of the vertical spiral tube GHEs. Subsequently, the performances of modified GHEs are compared with a traditional spiral GHE regarding outlet temperature, heat transfer rate, and pressure drop to decide the best configuration. After that, the best configuration is considered to study the impact of the tube, borehole, and ground materials along with the variation flow rate on the thermal performance. Thus, the current study can contribute to proper GHE designing by optimizing the configuration of vertical spiral GHEs to enhance heat exchange efficiency and reduce thermal interference, leading to improved thermal performance. Consequently, it can drive the GSHP system by increasing energy efficiency.

2. Physical model

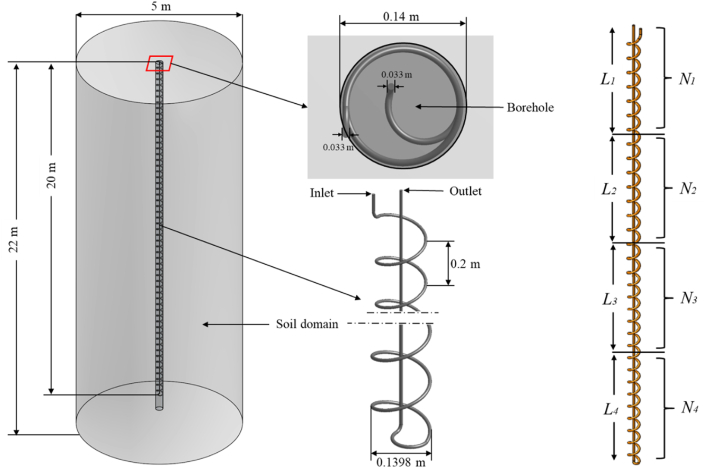
The physical model of the present numerical study comprises a vertical spiral tube GHE along with a borehole and neighboring ground soil as depicted in Fig. 1. Total height of the GHE is considered H = 20 m in this study. The total height of the spiral GHE is divided into four segments, with the topmost part denoted as L₁ and the other parts as L₂, L_3, and L₄ from top to bottom correspondingly (see Fig. 1). The number of turns for the topmost portion is represented as N₁ and other parts are by N₂, N_3, and N₄ from top to bottom correspondingly. Table 2 describes the different arrangements of modified spiral GHEs in detail.

Fig. 1.

Potrayal of the physical domain includes a spiral tube GHE along with a borehole and soil area.

Table 2.

Different arrangements and configurations of the spiral GHEs.

Case	GHE pipe length	Spiral turn number				Outlet pipe position
	L1 = L2 = L3 = L4 (m)	N1	N2	N3	N4
Case1	5	25	25	25	25	Inside spiral
Case 2	5	20	20	30	30	Inside spiral
Case 3	5	11	17	27	45	Inside spiral
Case 4	5	25	25	25	25	Outside spiral
Case 5	5	11	17	27	45	Outside spiral
Case 6	5	50	50	50	50	Inside spiral

The visual representation of different GHE configurations considered in this study is presented in Fig. 2. Each GHE has a spiral diameter of D_T = 0.1398 m and is placed inside a borehole of 20 m depth. The soil domain surrounding the borehole is modeled as 5 m in diameter and 22 m in depth. In all configurations, the outer and inner diameters of the GHE pipe are taken as 0.033 m and 0.026 m, respectively. For all the modifications, the inlet and outlet pipes of GHE are spiral and straight, respectively. The equivalent straight length of the spiral inlet is 48.26 m from Case 1 to Case 5. Whereas, for Case 6, the equivalent straight length of the spiral inlet coil is 90.09 m. In addition, the outlet straight pipe length is 20 m for all the Cases. A brief description of each GHE configuration is provided below.

• •Case 1: The spiral inlet is uniform-pitched with a total number of turns is100. The outlet pipe is placed inside the spiral coil.
• •Case 2: The top two parts (L₁ and L₂) have 20 turns each. Conversely, the bottom two parts (L₃ and L₄) have 30 turns each. The outlet pipe is placed inside the spiral coil.
• •Case 3: The topmost part (L₁) has 11 turns. The other parts (L₂, L₃, and L₄) contain 17, 27, and 45 turns, respectively. The outlet pipe is placed inside the spiral coil.
• •Case 4: The spiral inlet is uniform-pitched with a total number of turns of 100. The outlet pipe is placed outside the spiral coil.
• •Case 5: The topmost part (L₁) has 11 turns. The other parts (L₂, L₃, and L₄) contain 17, 27 and 45 turns respectively. The outlet pipe is placed outside the spiral coil.
• •Case 6: The spiral inlet is uniform-pitched with a total turn number of 200. The outlet pipe is placed inside the spiral coil.

Fig. 2.

Portrayal of different spiral pitch arrangements of GHE set-ups considered in this study.

Typically, the rate of heat transfer of spiral GHE is higher in the leading part from the inlet and progressively reduces towards the trailing part [31]. This is because of the elevated thermal gradient between the soil and the working fluid inside the leading part compared to the trailing part during the operational period. To ensure equal utilization of the available ground heat around the GHE, modifications are made in Cases 2, 3, and 5 which involve increasing the number of turns in the lower section of the spiral pipe (inlet), resulting in a larger pipe contact area between GHE pipe and ground soil in the trailing part. The thermal interference between the inlet and outlet tubes can be reduced by increasing the space between them. In Cases 4 and 5, modifications are made by placing the outlet straight pipe on the outside of the spiral coil. This change is implemented to minimize thermal interference between the inlet and exit tubes. Furthermore, to increase the total heat transfer area, the total number of turns is increased in Case 6.

At first, all of these GHEs are simulated with a flow rate of 2 L/min employing polyethylene as the GHE pipe material, sand silica as the backfill material, and clay as the ground soil material. Subsequently, the effect of using different materials for GHE pipe including high-density polyethylene (HDPE), low-density polyethylene (LDPE), and polyvinyl chloride (PVC), on heat transfer rate is investigated using the optimized configuration. Among these materials, the best-performing material has been selected and further simulations are conducted in which the borehole is considered as a concrete pile and sand-silica. Furthermore, the impact of distinct soil materials, such as clay and sandy clay, on thermal performance is studied. Finally, the impact of varying fluid flow rates is investigated using optimal configuration and materials. The thermo-physical properties of the material employed in the current investigation are listed in Table 3.

Table 3.

Thermophysical properties of materials employed in the current investigation [24].

Material	Density (kg/m3)	Specific heat (J/kg.K)	Thermal conductivity (W/m.K)
Polyethylene	920	2300	0.35
HDPE	950	2300	0.45
LDPE	920	3400	0.34
PVC	1380	960	0.15
Sand-silica	2210	750	1.4
Concrete pile	2200	1000	1.65
Clay	1700	1800	1.2
Sandy-clay	1960	1200	2.1
Water	998.2	4182	0.6

3. Mathematical modeling

In this study, ANSYS FLUENT software is employed for the numerical analysis. The following assumptions are made in the present numerical investigations [[51], [52], [53], [54]].

• •The working fluid (water) is considered to be incompressible fluid with constant thermo-physical properties.
• •The thermophysical properties of all parts of the GHE are regarded as homogeneous, isotropic, and unaffected by temperature fluctuations.
• •The radiation effect is ignored.
• •Radiative, convective, and evaporative thermal losses/gains in the upper surface of the soil are neglected.
• •Advection of groundwater flow is neglected.
• •Thermal contacts among different components of the GHE are considered perfect for conjugate heat transfer.

While these assumptions simplify the numerical modeling process, they may influence the simulation results. For instance, neglecting thermal losses/gains from soil surfaces might affect temperature distributions and system efficiency. Furthermore, excluding considerations like groundwater advection, and variations in surface temperature due to solar radiation may introduce inaccuracies in predicting the performance of GHE across various environmental conditions. Although the above assumptions may affect the accuracy of the result, the heat transfer rate in the GHE system is often governed by the lower thermal conduction coefficient of ground soil. Therefore, the above-mentioned assumptions simplify modeling with negligible error. The heat and fluid flow of the working fluid inside the tubes are governed by classical Navier-Strokes (continuity and momentum equations) and thermal energy conservation equations. Under the given assumptions, ANSYS FLUENT solves the mathematical models that govern the fluid flow and heat transfer inside the computational domain, which can be presented as follows [[55], [56], [57], [58]]:

The conservation of mass or continuity equation:

$${\rho }_f\nabla .\mathit{u}=0\text{,}$$ (1)

Momentum conservation:

$${\rho }_f\frac{\partial \mathit{u}}{\partial t}+\rho \left(\mathit{u}.\nabla \right)\mathit{u}=\nabla .(-PI+\mu \left(\nabla \mathit{u}\right)+\left(\nabla {\mathit{u}}^T\right)+F\text{,}$$ (2)

Thermal energy conservation:

$${\rho }_f{C}_{p,f}{A}_p\frac{\partial T}{\partial t}+{\rho }_f{C}_{p,f}{A}_p\mathit{u}.\nabla T=A_p{k}_f\nabla .\nabla T+f_D{A}_p\frac{{\rho }_f}{2d_h}\left|u\right|u^2+Q_{wall}\text{.}$$ (3)

Here, ρ, u, P, I, μ, T, t, F, A_p, k, f_d, d_h, and Q_wall denote density in kg/m³, the velocity of the working fluid in m/s, pressure in Pa, identity matrix, dynamic viscosity in Pa.s, temperature in K, time in second, body (volume) force commence from numerous sources including gravitational acceleration in N/m³, cross-sectional area of the pipe in m², thermal conduction coefficient in W/(m.K), coefficient of friction, hydraulic diameter of the pipe in m and the amount of heat transfer along tube surface to the neighboring soil in W/m, respectively. The subscript f and p represent fluid and pipe material, respectively. The term Q_wall can be calculated as follows:

$$Q_{wall}=hz\left(T_p-T_f\right)\text{,}$$ (4)

$$hz=\frac{2\mathrm{\pi }}{\frac{1}{r_{po}{h}_{\mathrm{int}}}+\frac{\ln \left(\frac{r_{po}}{r_{pi}}\right)}{k_p}}\text{,}$$ (5)

where z, h, T_p, h_int, r_po, and r_pi represent the wetted perimeter of the tube in m, overall heat transfer coefficient in W/(m²K), wall temperature of the pipe in K, convective heat transfer coefficient in W/(m²K), and outer and inner radius of the tube in m, respectively. The following equation is used to account for the heat transmission through the borehole and soil material:

$${\rho }_s{C}_{p,s}\frac{\partial T}{\partial t}=k_s\nabla .\Delta T\text{,}$$ (6)

where ρ_s and k_s represent the densities in kg/m³ and the thermal conduction coefficient of the borehole and soil materials in W/(m.K).

4. Simulation procedure and boundary conditions

4.1. 4.1procedure and simulation set-up

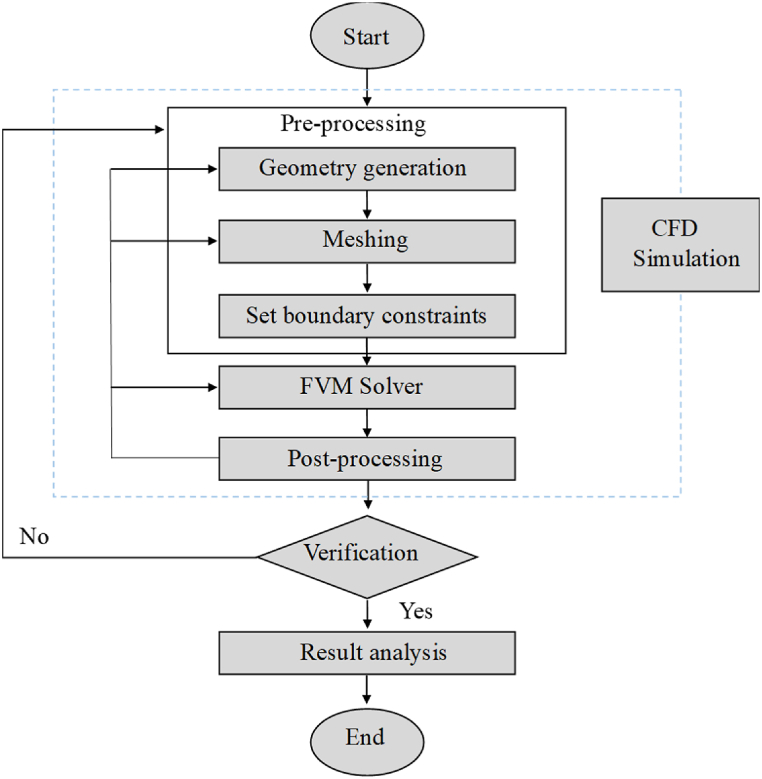
In the current study, computational fluid dynamics software ANSYS FLUENT is used for a three-dimensional unsteady numerical analysis. The software solves the problem by the finite volume method using governing equations (1), (2), (3), (6). This technique involves discretizing the integral form of the conservation equations directly in the physical space. The computational domain is divided into numerous contiguous control volumes, each ensuring the exact conservation of relevant properties. Variables are computed at the centroid of these control volumes. To express the variable values at the control volume surfaces, interpolation is used, and quadrature formulas approximate the surface and volume integrals. This results in an algebraic equation for each control volume, which includes values from neighboring nodes. Unlike methods that operate at grid intersection points, the finite volume method uses control volumes, allowing it to support various grid types. In this research, unstructured grids are favored over structured grids, offering flexibility in defining control volume shapes and locations. Because the grid specifies only the control volume boundaries, the method maintains conservation as long as the surface integrals employed at these boundaries match those of the adjacent control volumes. The SIMPLE scheme is employed to couple pressure and velocity, while the second-order upwind approach is employed for the spatial discretization of the governing equations. However, a first-order implicit technique is employed to model the unsteady characteristics of the flowing fluid. Additionally, under-relaxation factors are applied, with a value of 0.3 for pressure, 1 for both density and body force term, and 0.7 for momentum. The convergence criteria are established at 10⁻⁵ for both continuity and momentum and 10⁻⁶ for the energy equation. Furthermore, a fixed time step size of 60 s with a total number of 4320 timesteps (3 days) is employed for the current transient problem. Moreover, in ANSYS FLUENT, the multigrid method is employed to minimize errors and enhance the convergence of numerical solutions [57]. This technique solves the problem across a sequence of grids with varying levels of refinement, aiming to speed up convergence by tackling errors at different spatial scales. In this study, among various multigrid cycle types, V-cycle and Flexible cycle types are used for pressure and momentum, respectively. The detailed sequential computational procedure employed in the current study is shown in Fig. 3.

Fig. 3.

Detailed sequential numerical process employing finite volume method.

4.2. Boundary conditions

In the present problem, a consistent flow rate of 2 lit/min is maintained under laminar flow conditions, with the fluid entering at a temperature of 300.15 K. The boundary conditions include a velocity inlet and a pressure outlet. While mass flow inlet condition is typically recommended for compressible flows, it is not necessary for incompressible flows [58]. Additionally, although a pressure inlet can be utilized, the known inlet velocity and the assumption of incompressible water justify the use of a velocity inlet condition [58]. At the outlet, for an unknown outlet flow condition (whether it is fully developed or not), a pressure outlet boundary condition is applied to ensure a better and rapid convergence rate [58]. Initially, the temperature of all parts of the computational domain is assumed of 290.86 K. Moreover, the top, side, and bottom walls are considered to be in isothermal condition.

4.3. Grid refinement test and model validation

The CFD software ANSYS Fluent employs the finite volume approach to solve the governing equations along with their corresponding auxiliary conditions. This finite volume method involves dividing the computational region into a definite quantity of triangular and quadrilateral elements, using linear basis functions for all unknown entities. Dense mesh generation is applied near the boundaries to inhibit the creation of singularity, accurately grasp rapid changes in unknown entities, and accelerate the precision of the solution. Specifically, to decrease the total quantity of elements and improve precision, finer mesh generation surrounding and within the GHE pipe is employed, while the mesh dimension apart from the GHE pipe is progressively widened. The same approach of meshing is used for the rest of the cases. To determine the optimal mesh size, a grid refinement analysis is conducted, assessing the accuracy of various computational grid sizes for a 0.2 m uniform-pitched GHE at a flow rate of 2 lit/min over 72 h of continuous operation. The mean heat transfer rate after 72 h is evaluated for several mesh element numbers (N_E) at the time of the mesh independence test. The iterative process stabilizes, indicating an optimal solution has been achieved. Following the grid refinement assessment, the optimal element size is determined to be N_E = 11, 470, 933, as illustrated in Fig. 4. This mesh setting offers a balanced trade-off between computational duration and precision. Fig. 5 presents the optimal mesh arrangement configuration following the grid refinement test. For all cases, the same approach of meshing is employed.

Fig. 4.

Grid independence test using a 0.2 m uniform-pitched GHE at a flow rate of 2 L/min over 72 h of continuous operation.

Fig. 5.

Finite volume mesh generation within the computational domain: (a) isometric view, (b) top view, and (c) magnified view around the borehole.

To validate the precision of the employed computational approach, the findings obtained by the same model must be validated with prior published works under identical conditions. The current model is verified through a comparison with the findings obtained by the numerical study of Jalaluddin and Miyara [24]. They computationally examined the thermal performance of a traditional spiral tube GHE with a uniform spiral pitch of 0.2 m and grout height of 20 m. Fig. 6(a) compares the outlet temperature variations of water after 24, 48, and 72 h of continuous operation at a flow rate of 2 lit/min. The results show reasonable agreement between the current and published data. The error between the present model and the published study [24] (see Fig. 6(a)) is determined by employing the expression: Error (%) = |Outlet T_c − Outlet T_p| × 100/Outlet T_p. Here, the subscripts ‘c’ and ‘p’ present the current model and published outcome, respectively. Additionally, Fig. 6(b) illustrates the mean heat transfer rate per meter borehole of 72 h of continuous operation for uniform-pitched (0.1 m and 0.2 m) spiral tube GHEs. It is seen that the obtained heat transfer rate from the present simulation model and Jalaluddin and Miyara [24] are almost identical with 0.8 % and 3.2 % deviation for spiral pitch 0.1m and 0.2 m, respectively. The nearly identical outcomes validate the current numerical approach.

Fig. 6.

Verification of the current model with the findings of Jalaluddin and Miyara [24] using identical boundary conditions and physical configuration: (a) distribution of exit temperature and (b) average heat transfer rate per meter borehole for 72 h of continuous operation.

Furthermore, Jalaluddin et al. [59] performed an experimental study on a spiral tube GHE with a flow rate of 3.6 lit/min and an inlet water temperature of 35 °C. Fig. 7 illustrates a comparison of the variation of the exit water temperature derived from the current simulation and the experimental outcomes of Jalaluddin et al. [59]. The trends observed in these plots align reasonably well with the published data, thereby further validating the present computational model. However, discrepancies noted in Fig. 7 are attributed to inherent uncertainties and variations in experimental conditions, which may differ between the current model and the original experimental setup.

Fig. 7.

Validation of the present model with the outcomes of Jalaluddin et al. [59], showing outlet water temperature from 17:00 to 18:00 at a flow rate of 3.6 L/min and an inlet temperature of 35 °C.

5. Results and discussion

The present investigation numerically studies the thermal performance of traditional and modified spiral tube GHEs. Moreover, the impacts of different materials and variations in flow rates on thermal performance and pressure drop are also studied. Outlet water temperature (OWT), heat transfer rate, pressure drop, effectiveness, thermal performance capability, and coefficient of performance improvement criterion are evaluated to assess the performance of GHEs. The performance of the GHE is evaluated for 72 h in a continuous cooling operation mode with an inlet water temperature (IWT) of 300.15 K.

5.1. Comparison of outlet water temperature (OWT)

The temperature difference between IWT and OWT should be as large as possible to achieve a elevated heat transfer rate. Table 4 presents the OWT after 24, 48, and 72 h of continuous operation for all cases. At the beginning of the operation, the water inside GHE ejects a large quantity of heat to the neighboring ground soil during the cooling operation, thus lower OWT is achieved. As the operational time increases, the OWT gradually increases. This happens because of GHEs’ operational period extends, the water inside the GHE ejects lower heat into the neighboring soil, and the thermal gradient amid the water and the soil lessens. As a result, OWT increases with operational time for all cases (see Table 4). OWT denotes the effect of GHE thermal response.

Table 4.

Outlet water temperature for all the cases after 24, 48, and 72 h of continuous operation.

Case	Outlet water temperature (K)
	After 24 h	After 48 h	After 72 h
Case 1	296.76	297.06	297.21
Case 2	296.86	297.15	297.30
Case 3	296.88	297.17	297.32
Case 4	296.49	296.82	296.99
Case 5	296.45	296.81	296.98
Case 6	296.39	296.77	296.96

5.2. Thermal performance analysis

The heat transfer rate (Q) is determined by employing the equation below:

$$Q=\stackrel{•}{m}Cp\Delta T\text{,}$$ (7)

where $\stackrel{•}{m}$ and ΔT denote the mass flow rate and thermal gradient between inlet and outlet circulating water, respectively.

Fig. 8 shows the GHEs' heat transfer rate with the operation time. The heat transfer rate is higher at the beginning of the operation and gradually decreases with operation time. Approximately, after 30 h of operational time, the heat transfer rate approaches a steady value since heat builds up inside the ground soil neighboring GHEs as shown in Fig. 8. In Cases 2, 3, and 5, pitch intervals are increased in the leading parts, and are densified in the tailing parts to ensure more evenly utilization of soil's heat energy around GHEs. The heat transfer rate for Cases 2 and 3 is lower compared to a uniform distribution of spiral turns. In most cases, Hasan et al. [31] applied the same type of modification for slinky-type horizontal GHE and achieved better thermal performance. In their research, the loop diameter was 1 m. However, in this study, the loop or spiral diameter is 0.1398 m, which is too small. As a result, the ground soil around GHEs becomes saturated quickly, and these modifications do not improve thermal performance as illustrated in Fig. 9.

Fig. 8.

Variation of heat transfer rate with the operational time.

Fig. 9.

Variation of average heat transfer rate for all cases after 72 h of continuous operation.

The thermal interference inside the spiral coil of the inlet pipe has a major influence on heat transfer along the outlet tube. To decrease this impact, the outlet straight pipe is positioned outside of the spiral coil in Cases 4 and 5. Fig. 10 shows the heat transfer rate after 72 h of continuous operation through the inlet and exit tubes. Heat transfer along the inlet pipe is higher than the outlet pipe. In Case 5, where the outlet straight pipe is taken outside of the spiral coil, heat transfer in the outlet straight pipe increases significantly. By inserting the straight pipe at the outside of the spiral inlet pipe, thermal interference between the inlet spiral pipe and the exit straight tube is be reduced. As a result, the heat transfer rate has increased. In Case 6, having the lowest pitch distance causes the heat transport rate along the outlet pipe to be negative. This is due to the inlet spiral pipe thermal interference effects on heat transfer through the outlet pipe.

Fig. 10.

Heat transfer rate of inlet and exit tubes after 72 h of continuous operation.

5.3. Pressure drop analysis

The pressure drop (ΔP) due to the fluid flow through the GHE pipe is calculated as follows:

$$\Delta P=P_i-P_o\text{.}$$ (8)

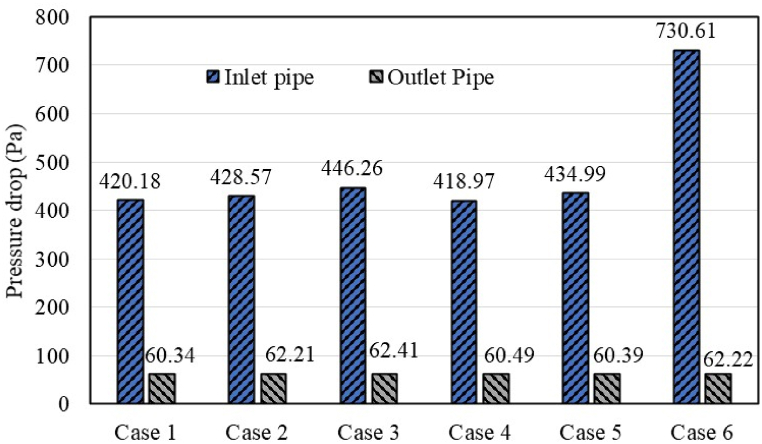
where P_i, and P_o denote pressure at inlet and exit, respectively. The pressure drop between the inlet and exit pipes of a GHE is depicted in Fig. 11. Pressure drops are almost similar for all the Cases rather than Case 6. As the turn numbers of the spiral tube increased (Case 6), the pressure drops of the working fluid along the pipe increased while the height remained constant. This is because the total equivalent straight length of the pipe increases at a higher number of turns (Case 6), and the fluid encounters more resistance to flow, resulting in a higher pressure drop. Fig. 12 depicts the pressure drop through the inlet and exit tubes. The pressure drop through an outlet straight tube is nearly the same in all cases, but the pressure drop of spiral inlet tubes increases for Case 6 since the turn number increases. Furthermore, the spiral geometry of pipes causes an increase in pipe length per meter of the borehole, consequent in a greater pressure drop than straight outlet pipe. For instance, the contour for pressure distribution along the GHE tube for Case 1 is depicted in Fig. 13. The pressure of the working fluid is much higher at the leading part of the inlet spiral pipe. However, as the fluid flows through the tube, the pressure gradually decreases due to flow resistance caused by pipe roughness. Therefore, the pressure at the fluid exit is lower than at the fluid inlet, as illustrated in Fig. 13.

Fig. 11.

Total pressure drop through the GHEs.

Fig. 12.

Pressure drop through the inlet and exit tubes of GHEs.

Fig. 13.

Visualization of pressure distribution along GHE in Case 1.

5.4. Heat transfer effectiveness

The effectiveness coefficient of heat transport (E) can be employed [38] to determine the efficiency of GHE which can be expressed as follows:

$$E=\frac{Q_{actual}}{Q_{\max imum}}=\frac{\stackrel{•}{m}{C}_p\left(T_i-T_o\right)}{\stackrel{•}{m}{C}_p\left(T_i-T_g\right)}\text{,}$$ (9)

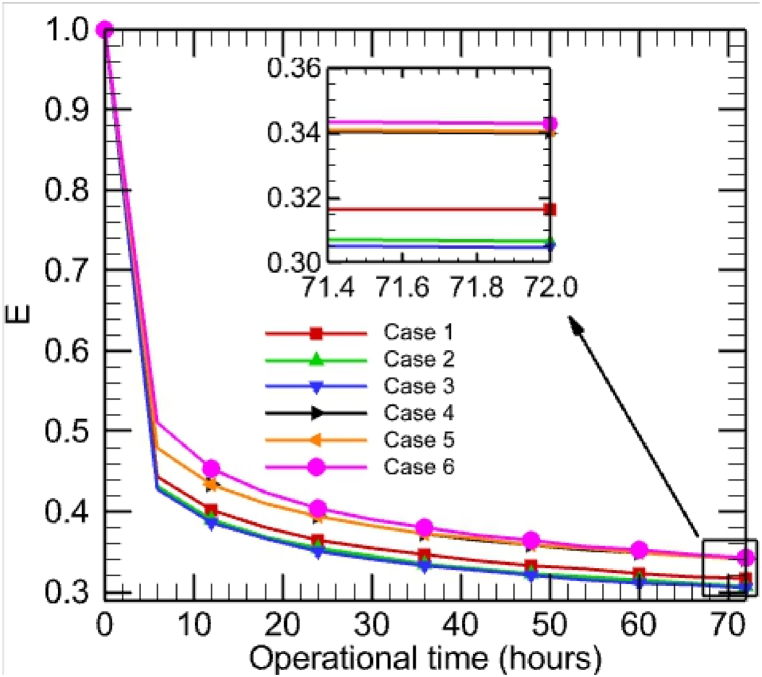
where Q_actual, Q_maximum, T_i, T_o, and T_g represent the actual capacity and utmost attainable GHE heat transfer capability, inlet and exit temperature of the working fluid, and initial soil temperature, respectively. Furthermore, E is the non-dimensional parameter that denotes the capability of the GHE to obtain the lowest exit temperature in summer and the highest exit temperature in winter [38]. Fig. 14 demonstrates changes in the effectiveness of different GHEs over time. During the cooling mode of a GHE, heat is transmitted from the water to the ground soil. However, over time, heat builds up around the ground soil, which increases its temperature and reduces the thermal gradient between the working fluid and the soil. This results in a reduction in the actual heat transfer capacity of the GHE and a decrease in its effectiveness with the increases of time. Among all GHEs shown in Fig. 14, Case 6 has the highest effectiveness due to its larger heat transfer area. While Cases 1 to 5 have the same heat transfer area, the effectiveness improves in Cases 4 and 5 but decreases in Cases 2 and 3 compared to Case 1. The improvement in effectiveness in Cases 4 and 5 is due to a reduction in thermal interference amid the inlet and exit tubes.

Fig. 14.

Variation of heat transfer effectiveness of different GHEs concerning operational time.

5.5. Thermal performance capability

To achieve a balance between heat transport and pressure drop, Javedi et al. [38] proposed a parameter known as thermal performance capability (TPC). This parameter is defined as the proportion of heat transfer to pressure drop. The following equation presents TPC [38]:

$$TPC=\frac{E/E_o}{{\left(f/f_o\right)}^{1/3}}\text{,}$$ (10)

where E_o and f_o denote the effectiveness and friction factor, respectively of traditional spiral tube GHE (Case 1), and E and f denote the effectiveness and friction factor, respectively for modified spiral tube GHE. The following equation determines f [38]:

$$f=\frac{2d_h\Delta P}{p{u}_f^2{L}_p}\text{,}$$ (11)

where d_h and L_p represent the hydraulic diameter of the pipe and the total equivalent straight length of a spiral tube which is determined as follows [38,60]:

$$L_p=n(\sqrt{p^2+{\left(\mathrm{\pi }D\right)}^2}\text{,}$$ (12)

where p is the spiral pitch, n denotes the turn number in the spiral tube and D_T is the spiral diameter. TPC has a proportional relationship with effectiveness and an inverse relationship with pressure drop. With higher TPC signifying greater thermal performance of the GHE [38]. Fig. 15 depicts the variation of TPC for different GHE configurations compared to the traditional spiral GHE. Case 4 has the highest TPC with a value of 1.062, indicating the highest heat transport rate and the highest pressure drop among the other GHEs. From Fig. 8, it is evident that the maximum heat transfer rate is obtained for Case 6. Even though Case 6 offers an augmented heat exchange than Case 4, by balancing between heat transfer and pressure drop, Case 4 having the highest TPC indicates that it has an optimal performance. Thus, this GHE configuration of Case 4 is suitable to install which will reduce the operational pumping cost.

Fig. 15.

Comparison of thermal performance criterion among various GHEs.

5.6. Coefficient of performance improvement criterion

It is found that the mean heat transfer rate can be increased by modifying the spiral coil arrangement as evident from Fig. 9, Fig. 11. On the other hand, pressure drop increases at a higher rate than increases in heat transfer rate. Therefore, the pressure drop and heat exchange rate must be taken into consideration when assessing the system's energy efficiency. Jalaluddin and Miyara [24] proposed a new approach to balance between heat transfer rate and pressure drop, known as the coefficient of performance improvement (COP_imprvt) criterion. The criterion of COP_imprvt is determined as follows [24]:

$$\frac{Q_H^{\prime }}{Q_H}-\frac{V_f\Delta P\Delta P^{\prime }}{Q_H\Delta P}>0\text{.}$$ (13)

where Q_H, denotes the heating rate (W/m), Qʹ_H denotes the augmentation in heating rate (W/m), V_f represents the flow rate (m³/s), and ΔPʹ represents the pressure drop increment. Moreover, in the current investigation, the COP_imprvt criterion is employed to assess the performance of different modified spiral tube GHEs (Cases 2 to 6), based on a traditional spiral tube GHE (Case 1). The findings are tabulated in Table 5, where positive and negative values indicate an improvement and reduction in net COP, respectively. The analysis of the results reveals that the net COP is enhanced in the Cases 4, 5, and 6, while it is decreased in the Cases 2 and 3.

Table 5.

Variation of COP improvement criterion for different GHE configurations.

Case	Qcase1 = QH (W/m)	QH−C (W/m)	${\mathit{Q}}_{\mathit{H}}^{\prime }$ (W/m)	V (m3/s)<	ΔPcase1 = ΔP (Pa/m)	ΔPc (Pa/m)	$\mathbf{\Delta }{\mathit{P}}^{\prime }$ (Pa/m)	COPimprvt criterion from Eq (13)
Case 2	23.61	22.9265	−0.6835	3.33 × 10−5	24.026	24.539	0.513	−0.029
Case 3	23.61	22.7475	−0.8625	3.33 × 10−5	24.026	25.4335	1.4075	−0.037
Case 4	23.61	25.3795	1.7695	3.33 × 10−5	24.026	23.973	−0.053	0.075
Case 5	23.61	25.4215	1.8115	3.33 × 10−5	24.026	24.769	0.743	0.077
Case 6	23.61	26.2595	2.6495	3.33 × 10−5	24.026	39.6415	15.6155	0.112

5.7. Effect of using different materials

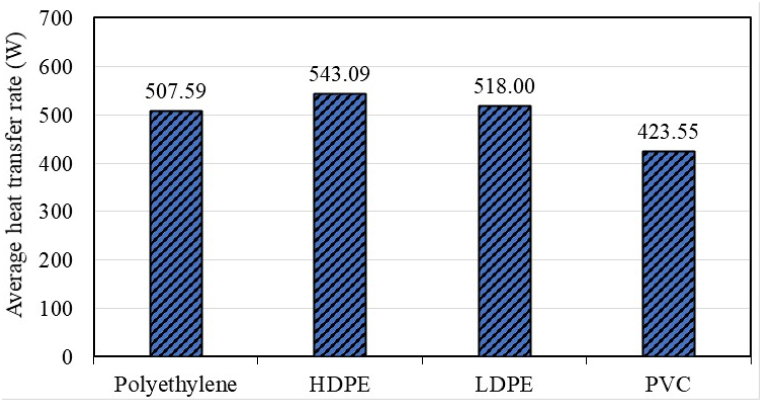
Since Case 4 is the optimal model as determined based on TPC (See Fig. 15), it is used for analyzing the influence of distinct materials on the heat transport through GHE. Distinct tube materials including HDPE, LDPE, and PVC are employed to observe the impact of pipe materials on thermal performance. Among these pipe materials, HDPE has the maximum heat transfer as depicted in Fig. 16. Compared to polyethylene, HDPE provides about 7 % augmentation of the heat transfer rate. This happens because of its high thermal conductivity, which is 28.6 % greater than polyethylene. Because of the low thermal conductivity of PVC, which significantly affects thermal performance when used as a pipe material. LDPE outperforms polyethylene and PVC while being slightly less effective than HDPE.

Fig. 16.

Variation of average heat transfer rate concerning alterations in pipe material.

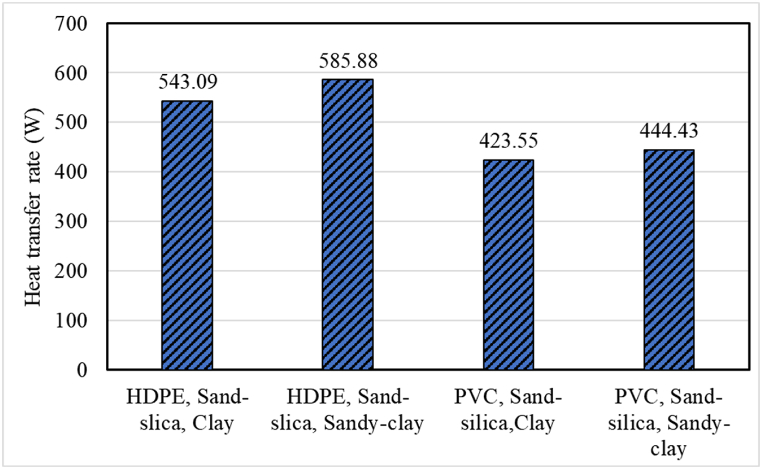
The effect of various backfilled materials while keeping the pipe and soil materials as HDPE and clay, respectively, is depicted in Fig. 17. When the concrete pile is used as backfill material, it performs around 5 % better than sand-silica. This can be attributed to the greater thermal conduction coefficient and specific heat of concrete, so it can quickly transfer heat and store more heat per unit mass. Fig. 18 depicts the influence of different soil materials on the heat transmission of GHEs. As a soil material, sandy clay performs 7.88 % better than clay for GHEs when HDPE and sand-silica are employed as pipe and backfill materials, respectively. On the other hand, when sandy clay is utilized as a soil material, it provides around 5 % better performance than clay when pipe and backfill materials are PVC and sand-silica, respectively. Sandy clay outperforms clay in terms of thermal performance because its thermal conductivity is 1.75 times higher than clay.

Fig. 17.

The influence of distinct backfill materials on heat transfer rate.

Fig. 18.

Variation of the mean heat transfer rate for different soil materials.

5.8. The impact of flow rate variation

For the investigation of the impact of modifying the mass flow rate of the working fluid on heat transmission and pressure drop, the combination of best materials for GHE is considered. Case 4 offered the best results, with HDPE, sand-silica, and sandy-clay functioning as pipe, backfill, and soil materials, respectively, at a flow rate of 2 lit/min (see Fig. 16, Fig. 17, Fig. 18). Fig. 19 shows variations in the average heat transfer rate and pressure drop through the GHE for different sets of flow rates.

Fig. 19.

Variation of average heat transfer rate and pressure drop along the GHE for distinct sets of flow rates.

When the flow rate is doubled from 2 to 4 lit/min, the heat transfer rate augments by 20.23 %, and the pressure drop increases by 2.86 times. However, raising the flow rate again by two times, from 4 to 8 L per minute, results in only a small improvement in heat transfer rate, the pressure drop increases 4.6 times. The increases in pressure drop also need higher pumping power to overcome the pressure drop during operation. Pumping power (P_pump) can be presented as the product of volumetric flow rate (V_f) and pressure drop (ΔP). The following equation determines the pumping power [24]:

$$P_{pump}=V_f\Delta P\text{.}$$ (14)

Pumping power is directly proportional to pressure drop. At a higher flow rate, pressure drop increases significantly. Thus, in cases of higher flow rates, pumping power requirements will increase significantly. Therefore, it can be suggested that it is better to operate the GHE with a reasonably lower flow rate.

5.9. Analysis of temperature distribution

The temperature distribution along the YZ plane in the mid-section of the GHE for Cases 1, 2, 4, and 6 after 72 h of continuous operation is illustrated in Fig. 20. In Cases 1, 4, and 6, the GHEs feature a uniform-pitched spiral coil arrangement, meaning the turns are evenly distributed along the length of the GHE. Consequently, the temperature progressively degrades from the leading turns to the trailing turns, as depicted in Fig. 20(a), (c), and (d), respectively. In these cases, the temperature degradation is significantly higher in the leading turns compared to the trailing turns, which can be attributed to the greater heat load in the leading turns. This occurs due to a higher thermal gradient between the working fluid and the neighboring soil. As the working fluid flows from the leading part to the trailing part, it dissipates heat, resulting in heat accumulation in the neighboring soil and a reduced heat load in the subsequent turns. In contrast, Case 2 employs denser turns toward the trailing part of the GHE to distribute the available heat energy more evenly within the neighboring soil. Thus, the heat load is higher in the trailing turns compared to the leading turns, facilitating the easier flow of thermal energy into the surrounding soil. Consequently, temperature degradation is significantly higher in the trailing turns compared to the leading turns, as shown in Fig. 20(b). Moreover, in Case 4, thermal interference between the spiral inlet tube and the straight outlet tube is minimized due to the positioning of the outlet pipe at the outside of the spiral inlet pipe, as depicted in Fig. 20(c). This arrangement enhances the heat transfer rate, as evident from the quantitative findings presented in previous sections. Additionally, the increased number of turns in Case 6, which indicates a larger heat transfer area, results in a higher heat load in the leading turns compared to Cases 1 and 4 (see Fig. 20(a) and (c)). This leads to greater heat dissipation in the leading portion of the GHE to the surrounding soil, as demonstrated in Fig. 20(d).

Fig. 20.

Temperature distribution along the YZ plane in the mid-section of the GHEs.

5.10. Comparison of significant outcomes with prior studies

A comparative study between significant prior studies and the present study has been conducted. Key findings and technical information about different research studies are summarized in Table 6. Among the studies, Jalaluddin and Miyara [24] concluded that a spiral GHE with a 0.2 m pitch had 22.86 W per meter borehole which is 33.6 % higher performance compared to a single U-tube GHE under identical operating conditions. Interestingly, Saeidi et al. [34] undertook a novel modification by incorporating an aluminum fin on the pipe. After 48 h of continuous operation, they reported a 12 W/m heat transfer rate for 0.2 m pitched spiral GHE with a 0.2 m/s velocity of the working fluid. Jalaluddin et al. [61] and Wang et al. [62] obtained nearly identical outcomes for U-tube heat exchangers with heat transfer rates ranging from 20 to 23.1 W per meter borehole. In the present study, the GHE with variable pitch and an external position of the outlet straight pipe (Case 5) demonstrated optimal performance with a heat transfer rate of 25.42 W per meter borehole length which is higher than the study conducted by Ref. [24]. However, the GHE with a smaller pitch of 0.1 m (Case 6) showed the maximum thermal performance despite its excessive pressure drop, as evident from previous analysis (see Fig. 9).

Table 6.

Comparison of thermal performance between prior studies and the present investigation.

Author(s)	GHEs type	System's technical description							Heat transfer rate per meter borehole (W/m)
		Grout depth (m)	Pipe material	Pitch (m)	Spiral tube diameter (m)	Mass flow rate (kg/s)	Operation time (hrs.)	Straight outlet pipe placement concerning spiral pipe
Jalaluddin and Miyara [24]	U-tube	20	Polyethylene	–	–	0.033	72	–	17.11
	Spiral-tube	20	Polyethylene	0.2	0.1398	0.033	72	Inside	22.86
Saeidi et al. [34]	Finned Spiral-tube	10	–	0.2	1	0.2	48	Inside	12
Jalaluddin et al. [61]	U-tube	20	Crosslinked Polyethylene	–	–	0.033	18	–	23.1
Wang et al. [62]	U-tube	80	HDPE	–	–	0.2	96	–	20
Present study	Spiral-tube (Case 1)	20	Polyethylene	0.2	0.1398	0.033	72	Inside	23.61
	Spiral-tube (Case 2)	20	Polyethylene	0.25, 0.17	0.1398	0.033	72	Inside	22.93
	Spiral-tube (Case 3)	20	Polyethylene	0.45, 0.29, 0.19, 0.11	0.1398	0.033	72	Inside	22.75
	Spiral-tube (Case 4)	20	Polyethylene	0.20	0.1398	0.033	72	Outside	25.38
	Spiral-tube (Case 5)	20	Polyethylene	0.45, 0.29, 0.19, 0.11	0.1398	0.033	72	Outside	25.42
	Spiral-tube (Case 6)	20	Polyethylene	0.10	0.1398	0.033	72	Inside	26.26

6. Conclusion

The thermal performance and pressure drop of different spiral tube GHE configurations are numerically investigated to improve thermal performance. The main findings of this study can be summarized as follows.

• •The heat transfer rate increases by 7.5 % and 7.67 %, when the outlet pipe of modified GHEs is placed outside of the spiral coil (Cases 4 and 5) in comparison to a traditional and uniformly pitched spiral GHE (Case 1), respectively, due to the reduction of the thermal interference effect between the inlet and the exit tubes. However, these configurations result in almost similar pressure drops.
• •In the case of variable-pitched spiral GHEs (Cases 2 and 3), there is no noticeable augmentation in heat transmission in comparison to a traditional and uniformly pitched spiral GHE due to the small spiral diameter resulting in the soil around the GHEs becoming saturated quickly.
• •The heat transfer rate increases by 11.2 % when the turn numbers are doubled in a traditional spiral GHE. However, the pressure drop increases by 65 %. The longer length of the pipe and the spiral design are the main causes of the increased pressure drop, which requires more pumping power.
• •Among all GHE configurations with the same heat transfer area, Case 4 offers the maximum effectiveness.
• •Cases 4, 5, and 6 show improved thermal performance over traditional spiral GHE based on their COP improvement criteria, while Case 6 has the highest improvement. Cases 2 and 3, on the other hand, show worse thermal performance with negative COP improvement criteria
• •Among different pipe materials, HDPE and LDPE provide 7 % and 2.1 % better thermal performance than polyethylene, respectively. However, thermal performance drops by 16.56 % in the case of PVC.
• •Among various backfill materials, concrete offers 5 % higher thermal performance compared to sand silica. In contrast, among different soil materials, sandy clay results in 7.88 % greater thermal performance than clay. Moreover, increasing the flow rate does not greatly enhance thermal performance, but it significantly rises the pressure drop.
• •Ultimately, Case 4 achieves the optimal balance between heat transfer and pressure drop. Furthermore, among various materials, HDPE, concrete piles, and sandy soil offer the maximum thermal performance.

Due to certain limitations, several areas in this study remain unexplored. Future research could address the following aspects and conditions.

• •Utilize GHEs with larger spiral diameters: To mitigate rapid soil saturation around the GHE, employing a GHE with larger spiral diameters is recommended.
• •Assessing different pipe materials: Investigating the use of different materials for the inlet and outlet pipes within a single GHE could yield beneficial results. For instance, utilizing HDPE for the inlet pipe and PVC for the outlet pipe may enhance performance.
• •Adopt intermittent operation modes: Shifting from continuous to discontinuous operation modes might offer new insights and improve the overall efficiency of GHEs.
• •Examine the impact of tube thickness: Analyzing how variations in tube thickness affect the performance of GHEs could provide valuable information for optimizing their design and functionality.

Nomenclature

Abbreviation
COP	Coefficient of Performance
GHE	Ground Heat Exchangers
GSHP	Ground Source Heat Pump
HDPE	High-Density Polyethylene
IWT	Inlet Water Temperature
LDPE	Low-Density Polyethylene
OWT	Outlet Water Temperature
PVC	Polyvinyl Chloride
TPC	Thermal Performance Capability
Symbolic
Ap	cross-sectional area (m2)
Cp	specific heat (J/kg.K)
DT	spiral diameter (m)
dh	hydraulic diameter (m)
E	effectiveness coefficient
F	body (volume) force (N/m3)
f	friction coefficient
H	height of the borehole (m)
P	pressure (Pa)
p	spiral pitch (m)
Ppump	pumping power (W)
Qwall	wall heat transfer rate (W/m)
Re	Reynolds number
rpi	inner radius of the tube (m)
rpo	outer radius of the tube (m)
T	temperature (K)
t	time (s)
Vf	volumetric flow rate (m3/s)
z	Wetted perimeter (m)
Q	Heat transfer rate (W)
h	heat transfer coefficient (W/m2K)
hint	convective heat coefficient (W/m2K)
I	identity matrix
k	thermal conductivity (W/m.K)
L	vertical tube height (m)
Lp	total length of a spiral tube (m)
$\stackrel{·}{m}$	mass flow rate (kg/m3)
N	number of turns
NE	mesh element counts
Greek symbols
u	velocity (m/s)
μ	dynamic viscosity (Pa.s)
ρ	density (kg/m3)
Δ	difference
Subscripts
b	borehole
f	fluid
g	ground
imprvt	improvement
i	inlet
o	outlet
s	soil, borehole material
p	pipe material

Data availability statement

The data that has been used of this study are available within the article.

Funding

This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.

CRediT authorship contribution statement

Nahid Hasan: Writing – review & editing, Writing – original draft, Visualization, Validation, Methodology, Investigation, Formal analysis, Data curation, Conceptualization. Md Hasan Ali: Writing – review & editing, Writing – original draft, Visualization, Validation, Supervision, Software, Resources, Methodology, Investigation, Funding acquisition, Formal analysis, Data curation, Conceptualization. Nahyan Ahnaf Pratik: Writing – review & editing, Writing – original draft, Visualization, Validation, Methodology, Investigation, Formal analysis, Data curation, Conceptualization. Nafisa Lubaba: Writing – review & editing, Writing – original draft, Visualization, Validation, Methodology, Investigation, Formal analysis, Data curation, Conceptualization. Akio Miyara: Writing – review & editing, Visualization, Supervision, Software, Resources, Methodology, Investigation, Funding acquisition, Conceptualization.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.