Abstract
With the rapid development of information technology, high-speed digital optical signal transmission technology has become the core of modern communication networks. However, the increase in transmission rates brings challenges such as noise, distortion, and interference, which affect the accuracy of clock recovery. To address these issues, this study proposes a clock recovery algorithm based on the eye diagram opening area to improve the accuracy and efficiency of high-speed digital optical signal jitter measurement. The proposed method extracts clock information from the signal using the opening area and curvature characteristics of the eye diagram for jitter measurement. Experimental results demonstrate that the clock recovery algorithm based on the eye diagram opening area can stably reconstruct the signal eye diagram and obtain jitter parameters under different optical power conditions. At optical powers of −7.2 dBm, −12.2 dBm, and −17.2 dBm, the Q-factors were 8.8, 7.6, and 4.3, respectively, and the RMS jitter values were 12.2 ps, 13.4 ps, and 21.2 ps, respectively. At optical powers of −2.3 dBm, 0.1 dBm, 2.4 dBm, 4.6 dBm, and 6.0 dBm, the Q-factors were 9.1, 9.3, 9.5, 9.7, and 10.0, respectively, and the average jitter values were 8.9 ps, 8.5 ps, 8.0 ps, 7.5 ps, and 7.0 ps. These results indicate that the proposed algorithm performs excellently under low optical power conditions and maintains high recovery accuracy even when jitter increases at higher optical powers. The clock recovery algorithm based on the eye diagram opening area significantly improves the accuracy and stability of high-speed digital optical signal jitter measurement, enriches the theoretical research of clock recovery algorithms, and shows significant advantages in improving signal transmission quality, reducing bit error rate, and enhancing communication link reliability. The research outcomes provide key technical support for the optimization of modern high-speed optical communication systems.
Keywords: High-speed digital optical signal, Jitter evaluation, Clock synchronization, Eye diagram opening area, Noise interference, Bit error rate
1. Introduction
With the rapid development of information technology, high-speed digital optical signal transmission technology has become a core component of modern communication networks. This technology is widely used in fields such as telecommunications, mobile communications, and computer networks due to its advantages of high speed, large capacity, and long-distance transmission [1]. However, as transmission rates continue to increase, issues such as noise, distortion, and interference encountered during transmission have become more severe, leading to decreased accuracy in clock recovery, which in turn affects the performance of the entire communication system [2]. Clock recovery technology is crucial for ensuring correct signal decoding and reducing transmission errors, highlighting its undeniable importance. Currently, significant progress has been made internationally in the research of high-speed digital optical signal transmission technology, particularly in the area of optical device technology. The bandwidth and sampling rate of key components such as high-speed optical receivers and high-speed ADCs have been continuously improved, significantly enhancing the rate and distance of high-speed digital optical signal transmission [3]. However, the limitations of traditional clock recovery algorithms when handling high-speed signals have gradually become apparent, especially in aspects of jitter measurement and signal quality evaluation [4]. Therefore, developing an algorithm that can improve the accuracy and stability of clock recovery has become an urgent research need. This study aims to propose a clock recovery algorithm based on eye diagram opening area to enhance the accuracy and efficiency of jitter measurement in high-speed digital optical signals, providing theoretical support and technical assurance for optimizing communication system performance.
Currently, research on clock recovery techniques primarily focuses on interpolation algorithms and filtering algorithms. Interpolation algorithms estimate the clock information of the signal by inserting a reference clock into the received signal. Lin et al. (2021) summarized commonly used interpolation methods, including linear interpolation, polynomial interpolation, and spline interpolation, and systematically analyzed the advantages and disadvantages of these methods [5]. Although interpolation algorithms improve the accuracy of clock recovery to a certain extent, their effectiveness is limited by the choice of interpolation function and the number of interpolation points. On the other hand, filtering algorithms extract clock information from the signal by designing specific filters, such as bandpass filters, notch filters, and all-pass filters. However, Altay and Kremlev (2021) pointed out that filtering algorithms face significant challenges in design and implementation, as well as poor real-time performance in practical applications [6]. Additionally, both methods primarily focus on the amplitude variations of the signal in jitter measurement, neglecting the phase information. This oversight leads to poor recovery performance and stability issues when dealing with high-speed digital optical signal transmission.
To address these issues, this study proposes a clock recovery algorithm based on the eye diagram opening area. By analyzing the opening area of the eye diagram, the clock information of the signal is extracted. Compared to traditional methods, this study offers significant contributions in the following aspects: (1) By using the well-continuous eye diagram opening area as an evaluation criterion, the stability and accuracy of clock recovery are improved, avoiding the poor recovery performance caused by the discreteness of traditional interpolation and filtering algorithms when processing high-speed signals; (2) Curvature characteristics: By analyzing the curvature characteristics of the eye diagram opening area, the phase information of the signal can be more accurately captured, allowing the clock recovery to consider both amplitude and phase variations, thereby enhancing the comprehensiveness and accuracy of jitter measurement; (3) Noise interference: This study employs high-speed digital optical signal processing technology to achieve high-precision and rapid measurement of the signal, improving measurement resolution and speed while significantly reducing noise interference. The results of this study not only enrich the theoretical research on clock recovery algorithms but also provide important guidance for practical engineering applications.
The structure of this paper is as follows: The first section introduces the research background, research questions, and research objectives. The second section is a literature review, which organizes existing studies in the relevant field, identifies research gaps, and highlights the significance of this research. The third section describes the research methodology, detailing the theoretical basis and implementation steps of the clock recovery algorithm based on the eye diagram opening area. The fourth section presents the experimental results and analysis, validating the effectiveness and superiority of the algorithm through experiments. The fifth section is a discussion, providing an in-depth analysis of the research results and exploring their theoretical and practical implications. The sixth section concludes the paper, summarizing the findings, noting the limitations of the study, and suggesting directions for future research.
2. Literature review
2.1. Clock recovery techniques for high-speed digital optical signals
The role of the clock recovery circuit is to accurately extract a clock signal from the demodulated data stream at the receiving end that is perfectly synchronized with the clock at the transmitting end. This ensures that data can be correctly sampled and demodulated, enabling reliable and efficient information transmission [7].
Traditional clock recovery techniques mainly encompass two categories: phase detection-based switching techniques and interpolation algorithm-based non-coherent sampling techniques. The switching technique utilizes phase detection and control loops to compare the phase difference between the received data and the local clock, and then calibrates the local clock through the control circuitry [8]. The non-coherent interpolation technique, on the other hand, does not rely on phase detection loops but reconstructs the clock signal by interpolating and resampling the received data stream [9].
With the continuous increase in communication rates, the precision requirements for clock recovery have also risen, rendering traditional analog and digital logic circuits increasingly inadequate. This has spurred ongoing innovation in novel clock recovery technologies. For orbital angular momentum (OAM) mode-division multiplexed optical wireless communication, Li et al. [10] proposed an improved digital feedback clock recovery algorithm, achieving high-precision channel synchronization. Their 60Gbps three-mode multiplexing link experiment demonstrated low bit error rates and excellent clock recovery performance. Kumar and Raganna [11] presented a digital clock and data recovery (CDR) circuit design for high-speed passive wireless data transmission in SerDes applications, reducing power consumption. Sun et al. [12] and Li et al. [13] respectively proposed new clock recovery algorithms characterized by low latency, low jitter, and low complexity for bandwidth-limited PAM-4 systems and non-integer oversampling systems. Xiang et al. [14] achieved full optical broadband chaotic synchronization and clock recovery in a semiconductor laser mutual injection chaotic optical communication system, supporting high-speed OOK/QPSK signal encryption transmission. Hu et al. [15] applied clock recovery technology to optical switching data center networks, proposing an equalizer state caching scheme that significantly reduced adaptive latency in 56Gbaud PAM-4 systems. Beyond these innovations, researchers have continued to optimize the operational range of existing clock recovery circuits. Li et al. [16] designed an HDB3 clock recovery module that expanded the operational frequency range to 64Kb/s-32.768 Mb/s, achieving a balance between performance and time cost.
2.2. Jitter measurement techniques for high-speed digital optical signals
Jitter measurement technology is crucial for assessing the quality of high-speed digital optical signals. Jitter in the signal can severely impact the accuracy of clock recovery, leading to data errors and transmission faults [17]. Currently, commonly used jitter measurement techniques are classified into time-domain and frequency-domain measurements. Time-domain measurement methods, primarily based on eye diagram analysis and histogram analysis, can directly measure time displacement [[18], [19], [20]]. In contrast, frequency-domain measurement obtains phase noise information through spectrum analysis, thereby deriving the corresponding jitter amount [21,22].
In recent years, novel measurement techniques based on optical sampling have garnered widespread attention from researchers due to their exceptionally high temporal resolution and bandwidth advantages, offering new solutions for precise jitter measurement in high-speed signals. Jitter components in signals can severely impact signal quality in modern digital video transmission and analog-to-digital conversion systems. Zidan et al. [23] investigated the thermal lens effect in cadmium selenide quantum dots prepared using the dual-beam Z-scan technique. Additionally, they extracted specific parameters of the cadmium selenide quantum dot solution, providing a reference for the further development of semiconductor optical devices. Liu et al. [24] proposed a jitter measurement method for high-speed serial digital interface (SDI) signals based on an improved dual-Dirac model, enabling accurate analysis of different jitter components in SDI signals through time-domain measurement techniques. Addressing the clock jitter issue in analog-to-digital converters (ADCs), Zhang et al. [25] designed a measurement scheme based on a simple coherent sampling algorithm, capable of precisely measuring the distribution sequence of clock jitter. These works provide powerful tools for jitter analysis in digital signal systems. Optical sampling technology leverages the high-speed characteristics of narrow pulse light to achieve isochronous sampling of high-speed electrical signals, thus overcoming the bandwidth limitations of electronic measurements. Jiang et al. [26] proposed a method for measuring electrical signal jitter based on photonic time stretch, achieving femtosecond-level high-resolution measurement by amplifying the jitter signal in the optical domain. Sośnicki et al. [27] demonstrated radio frequency (RF) waveform noise measurement technology based on electro-optic sampling, measuring the minute timing jitter of high-frequency single-tone signals and optically generated pulses. These techniques provide extremely high measurement accuracy for time jitter analysis in high-speed signal systems. Real-time jitter monitoring of high-speed optoelectronic signals is crucial for status evaluation and fault diagnosis in communication systems. Yang et al. [28] introduced a new technique for analyzing jitter components using bit error rate (BER) eye diagram analysis, which can quickly extract and analyze various jitter components with high measurement accuracy and low cost. Huang et al. [29] designed a real-time eye diagram monitoring method based on optical sampling, capable of accurately measuring key parameters such as temporal jitter and Q-factor of high-speed optical signals over a wide dynamic range. These technologies provide efficient and reliable means for real-time performance monitoring of high-speed communication signals.
2.3. Signal quality evaluation based on eye diagram analysis and its application in clock recovery
An eye diagram is a graphical representation used to assess the quality of digital signals, where the horizontal axis represents time and the vertical axis represents voltage amplitude. In an eye diagram, the waveforms of each symbol overlap, creating a shape that resembles an eye. The opening area, known as the eye opening, is closely related to the signal's clock recovery performance [30]. Eye diagram analysis is an effective method for evaluating digital signal quality; by analyzing the overlapping patterns of the signal on the time and voltage axes, issues such as jitter and distortion that affect signal integrity can be visually identified [31]. In recent years, signal quality evaluation techniques based on eye diagrams have made significant progress, encompassing both traditional feature extraction methods [32] and emerging machine learning approaches [33,34]. Additionally, several other innovative techniques have been applied to eye diagram analysis, including random matrix theory [35], time-frequency analysis [36], and digital signal processing techniques [37].
Clock recovery is a critical technology in high-speed digital communication systems, aimed at extracting a clock signal at the receiver that is synchronized with the transmitter. Eye diagram analysis can provide essential foundational information for clock recovery. Traditional clock recovery algorithms, mainly based on linear or nonlinear data interpolation, have limited jitter tolerance [38]. In recent years, researchers have applied eye diagram analysis techniques to clock recovery, with research covering aspects from software analysis and machine learning applications to real-time monitoring. Park et al. [39] proposed an accelerated statistical eye diagram estimation method, significantly reducing eye diagram acquisition time by optimizing voltage step size and improving convolution operations. Usama and Chang [40] developed the PyEye software package, which integrates advanced algorithms and visualization techniques, providing researchers with a powerful analytical tool. The introduction of machine learning has opened new avenues. Weiyang et al. [41] explored the application of convolutional neural networks in eye diagram recognition, while Lee et al. [42] demonstrated the effectiveness of the AGSI-GAN method in high-bandwidth memory interconnect design. In simulation technology, Zhou et al. [43] proposed a fast eye diagram simulation algorithm that enhances simulation speed and stability. Cortiula et al. [44] developed a time-domain numerical modeling framework that deepens the understanding of jitter phenomena in high-speed serial interfaces. Real-time monitoring and uncertainty assessment have also seen progress. Huang et al. [45] introduced a real-time eye diagram monitoring method based on optical sampling, improving the immediacy and accuracy of monitoring. Telescu et al. [46] developed a stochastic time-domain mapping method, providing a new approach for reliability assessment in high-speed links.
2.4. Research summary
High-speed digital optical signal processing technology has made significant strides in recent years, with breakthroughs in key areas such as high-speed optical devices, high-precision clock recovery algorithms, and high-resolution jitter measurement methods. However, current technologies still face numerous challenges when handling ultra-high-speed digital optical signals.
In terms of clock recovery algorithms, traditional interpolation and filtering methods primarily focus on amplitude variations of the signal, neglecting the importance of phase information. Consequently, these methods exhibit poor recovery accuracy and stability when dealing with high-speed digital optical signals. Some novel algorithms have introduced mechanisms such as phase-locked loops to enhance accuracy, but these approaches increase hardware complexity and still do not fully address the issue of phase information.
In terms of jitter measurement technology, although novel techniques based on optical sampling provide extremely high temporal resolution and bandwidth for measuring jitter in high-speed signals, most methods are still limited to offline measurement and post-processing analysis. Few approaches can achieve real-time, online jitter monitoring for high-speed signals. Additionally, the measurement accuracy and anti-interference capability in noisy environments still need improvement.
In terms of signal quality assessment, existing eye diagram-based evaluation methods either rely on empirical parameter extraction, which lacks generality, or depend on machine learning algorithms, which suffer from black-box issues and make it difficult to physically interpret eye diagram features. Consequently, their ability to comprehensively evaluate the quality of high-speed digital signals is limited.
To address the aforementioned issues, this paper proposes a novel clock recovery algorithm based on the curvature characteristics of the eye opening area. Unlike existing methods, this algorithm can simultaneously obtain and comprehensively analyze both amplitude and phase information of the signal. More importantly, by analyzing the physical significance of the eye opening curvature, it establishes a mathematical analytical model relating clock frequency and other parameters to curvature characteristics, thereby achieving high-precision clock recovery both theoretically and methodologically. Compared to existing methods, this algorithm has three main innovations:1)Comprehensive Utilization of Amplitude and Phase Information: It evaluates the quality of high-speed digital signals more comprehensively by leveraging both amplitude and phase information. 2)Theoretical Accuracy and Stability Improvement: Based on a mathematical analytical model rather than empirical approximations, it theoretically enhances the accuracy and stability of clock recovery. 3)Real-time Efficient Measurement: Utilizing advanced high-speed optical sampling technology, it supports real-time and efficient measurements, eliminating the limitations of offline post-processing in traditional methods.
3. Methodology
3.1. Overall technical solution
This study proposes a jitter measurement technique for high-speed digital optical signals based on an eye diagram opening area clock recovery algorithm, as illustrated in Fig. 1.
Fig. 1.
Schematic diagram of the high-speed digital optical signal jitter measurement technique based on eye diagram opening area clock recovery algorithm.
The overall scheme includes the control center, optical signal input interface, optical sampling and quantization, and eye diagram and jitter measurement components. The control center's functions encompass power management, input optical signal access control, optical sampling control, quantization control, and measurement system monitoring. The function of the optical signal input interface is to adjust polarization by monitoring optical power to achieve optimal input. The role of optical sampling is to sample the optical signal. The quantization function is to convert the optical signal into an electrical signal. The eye diagram and jitter measurement functions involve data reconstruction, clock recovery, eye diagram restoration, and jitter measurement.
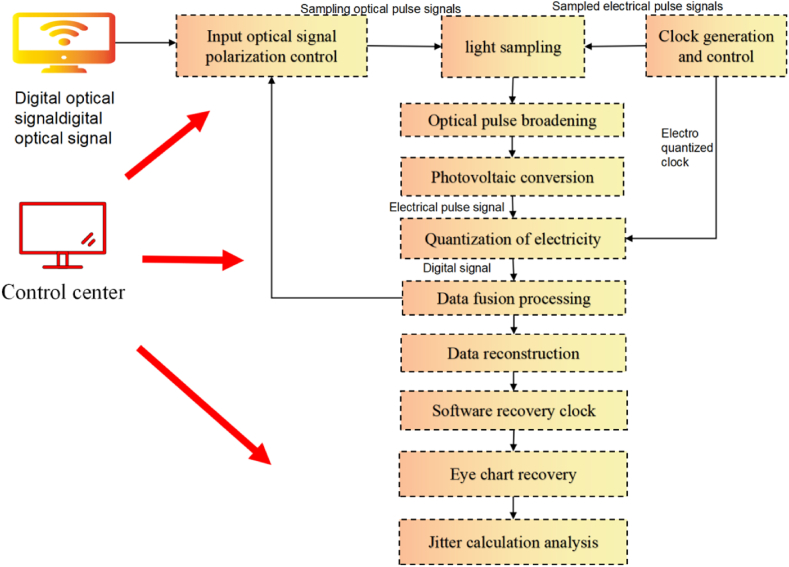
The specific principle is as follows: First, the digital optical signal is injected into the optical interface, ensuring that the polarization state is optimized. Then, the sampling electric pulse signal controls the sampling of the input digital optical signal, obtaining the sampled optical pulse signal. Next, the optical pulse signal is broadened and converted into an electrical signal by a photodetector. This electrical signal is then quantized by the quantization module. After quantization, the data undergoes software-based data reconstruction, clock recovery, and eye diagram restoration, ultimately yielding the jitter measurement results of the digital optical signal. The workflow is shown in Fig. 2.
Fig. 2.
Detailed workflow of high-speed digital optical signal jitter measurement.
3.2. Random equivalent sampling data processing and reconstruction
Based on the optical sampling and quantization module, the data stream of the digital optical signal can be further obtained through the random equivalent sampling method. Fig. 3 illustrates the complete data processing workflow. The specific steps are as follows: First, extract the collected data and transfer it to the data table. During this process, rearrange and reconstruct the signal data according to the expected digital signal period and the known random sampling times. Next, accurately recover the clock frequency and signal period of the digital signal. Using the precise clock period, reconstruct the digital signal at periodic time positions to obtain the eye diagram. Finally, by analyzing the eye diagram of the digital signal, calculate the jitter characteristics and output the results.
Fig. 3.
Steps for eye diagram reconstruction.
To accurately reconstruct the actual state of the digital signal, it is necessary to rebuild the discrete data obtained from random equivalent sampling. Random equivalent sampling relies on the repeatability of the digital signal, which alternates between "0″ and "1″ states in a periodic manner. In a complete digital signal, the probabilities of "0″ and "1″ are each 50 %. Signal reconstruction requires determining two key elements: the expected signal clock period and the sampling clock period. Once these two periods are known, interpolation can be used to obtain the phase information corresponding to the number of samples, thereby reconstructing one or more periods of the digital signal. The eye diagram of the digital signal is restored through multiple interpolation reconstructions, which allows for faster equivalent sampling indirectly through this interpolation method.
Given the known sampling clock period and signal clock period, digital signals can be reconstructed step by step. In practical sampling, the rates of SDH digital signals and Ethernet data streams are usually known, such as 622 Mb/s, 2.5 Gb/s, 10 Gb/s for SDH data or 1.25 Gb/s for gigabit Ethernet data. However, the clock periods corresponding to these rates are not precise and are only approximate values. To obtain accurate values, precise calculations or algorithmic reconstructions are necessary. Therefore, the reconstruction of digital signals is based on the predicted original clock period information. First, the clock period must be accurately reconstructed. Given the sampling rate of the optical sampling and electrical quantization system, the equivalent sampling time period , which is the time difference between the previous and the next sampling, can be derived as shown in Equation (1):
| (1) |
Given the digital signal rate, with a period interval of Tx and a sampling interval of TS, the nnn-th sampling time is located at nTS. The corresponding position within one signal period is Δt, where Δt is the remainder of nTS divided by TX, i.e.:
| (2) |
The period of the 2.5 Gb/s NRZ digital signal is TX = 400ps, with a sampling time of TS = 420ps (sampling rate≈2.38 Gb/s). Through random equivalent sampling, 20 sampling data points were obtained, corresponding to time positions within one period of the digital signal. Based on the relative time positions in Table 1, the sampling points can be shifted into a range with a period time of 400 ps and rearranged accordingly to reconstruct the eye diagram.
Table 1.
Random equivalent sampling list.
| Index | Signal Period (ps) | Sampling Period (ps) | Relative Position (ps) | Index | Signal Period (ps) | Sampling Period (ps) | Relative Position (ps) |
|---|---|---|---|---|---|---|---|
| 1 | 400 | 420 | 20 | 11 | 4400 | 4620 | 220 |
| 2 | 800 | 840 | 40 | 12 | 4800 | 5040 | 240 |
| 3 | 1200 | 1260 | 60 | 13 | 5200 | 4560 | 260 |
| 4 | 1600 | 1680 | 80 | 14 | 5600 | 5880 | 280 |
| 5 | 2000 | 2100 | 100 | 15 | 6000 | 6300 | 300 |
| 6 | 2400 | 2520 | 120 | 16 | 6400 | 6720 | 320 |
| 7 | 2800 | 2940 | 140 | 17 | 6800 | 7140 | 340 |
| 8 | 3200 | 3360 | 160 | 18 | 7200 | 7560 | 360 |
| 9 | 3600 | 3718 | 180 | 19 | 7600 | 7980 | 380 |
| 10 | 4000 | 4200 | 200 | 20 | 8000 | 8400 | 400 |
In fiber optic transmission systems, digital optical signals do not carry specific clock parameters, necessitating the reconstruction of the clock signal to obtain accurate clock period information. The data reconstruction process utilizes the expected clock time to acquire preliminary characteristics of the digital signal, but this accuracy is insufficient to meet jitter measurement requirements [47]. To achieve precise data reconstruction and eye diagram recovery, it is essential to accurately reconstruct the clock signal, extracting and reconstructing accurate clock information from the initially reconstructed digital signal.
3.3. Digital optical signal clock and eye diagram recovery
Based on the characteristics of the eye diagram, an iterative algorithm using the eye height and width has been proposed to accurately calculate the period time of digital signals. When the eye height and eye width of the eye diagram reach their maximum values, the eye diagram timing is closest to the actual state. The eye diagram contains two clock periods, with the eye height representing the signal amplitude and the eye width representing the signal clock period. The shaded area in the left eye diagram indicates the degree of eye opening; the larger this area, the closer the reconstructed eye diagram clock period TX is to the actual clock period of the digital signal. Solving for TX involves maximizing the shaded area [48].
Based on the above principles, a synchronization algorithm and its implementation plan have been developed. The formula for calculating the shaded area is as follows:
| (3) |
After reconstructing the image using a digital grid, the image area is divided into multiple strips, each with a width and height of and , respectively. The area of the shaded portion can be calculated. To recover the clock frequency fX (or the period TX) of the digital signal, the following algorithmic steps need to be performed:
The periodic time TX needs to be calculated according to the following algorithmic steps.
-
(1)
Determine the expected periodic time TX based on the digital signal transmission rate.
-
(2)
Recover the digital signal and determine the shaded areas , , and of the eye diagram. Then, perform the summation calculation according to equation (3) to initially obtain a value that can be defined as .
-
(3)
Increase TX by nΔt and repeat step (2) to obtain .
-
(4)
Set n = 1 and follow step (2) to obtain S1. Calculate . If Y > 0, proceed to the next step; if Y<0, go directly to step (6); if Y = 0, the clock period can be directly determined based on the current periodic time.
-
(5)
Then, let n = n+1, and refer to step (2) to obtain S2. Continue repeating this operation and compare Sn and Sn+1. Calculate . If Y > 0, keep increasing n and repeat the current step until the condition (Sn/256) > Y>(-Sn/256)is satisfied. The resulting period time(TX + nΔt)is the clock period, and its reciprocal is the digital signal rate.
-
(6)
Set n = −1, and refer to step (2) to obtain S-1. Calculate . If Y > 0, then set n = n-1 and refer to step (2) to obtain S-2, comparing Sn and Sn-1. Calculate . If Y > 0, continue decreasing n and return to step (6), repeating the loop until the condition (Sn/256) > Y>(-Sn/256) is satisfied. All other steps are the same as in step (5).
According to the SDH fiber optic communication standard specifications, the nominal transmission rate for the STM-16 optical digital signal is set at 2488.320 GHz, corresponding to a clock period of 401.877 ps. This serves as the basic data for random equivalent sampling reconstruction of digital signals and eye diagrams. The SDH reference clock accuracy is set at 1 × 10−11, the SDH transit node is set at 5 × 10−9, the SDH terminal node is set at 1 × 10−7, and the SDH network element clock accuracy is 4.6 × 10−6. Therefore, the maximum clock error for STM-16 is 11.446 MHz, corresponding to a clock frequency range of 2476.873 MHz–2499.766 MHz, and a clock period range of 403.734 ps–400.037 ps. The relationship between the period time and the clock frequency and its variations is expressed as:
| (4) |
In the equation, f and Δf represent the frequency and its variation, respectively, while T and ΔT represent the period and its variation, respectively. When Δf is 1 MHz, the corresponding ΔT is 0.16ps. From this, the period variation for other frequency changes can be derived.
Based on this characteristic, this study designed an optimized random equivalent sampling method. The corresponding parameter settings are shown in Table 2, and the detailed process is illustrated in Fig. 4.
Table 2.
Key parameters for optimizing the random equivalent sampling method.
| Parameter Standard | Data Information |
|---|---|
| Nominal SDH Rate Initial Value | 2488.320 Mb/s |
| Time Period | 401.877 ps |
| Scanning Method | Frequency step scanning from high to low at 100 kHz, 10 kHz, and 1 kHz |
| Sampling Point Processing (1 MHz) | 10000 sampling data points |
| Sampling Point Processing(100 kHz) | 50000 sampling data points |
| Sampling Point Processing(10 kHz) | 250000 sampling data points |
| Sampling Point Processing(1 kHz) | 524288 sampling data points |
Fig. 4.
Flowchart of the random equivalent sampling method.
By utilizing the random equivalent sampling method, the phase and time positions of different samples can be obtained. Based on multiple samplings, the signal can be reconstructed, and the accurate clock can be restored. This enables the synchronized display of the digital signal's eye diagram. The specific algorithm for the eye diagram recovery procedure is as follows.
| # (1) Read sampling and quantized data data = np.random.rand(1000) # Replace with actual data clock_frequency = 1e9 # 1 GHz, replace with actual value sample_rate = 10e9 # 10 GHz, replace with actual value # (2) Determine the number of data points and scan frequency step num_data_points = len(data) scan_freq_step = 1e6 # 1 MHz, replace with actual value time_per_sample = 1/sample_rate # (3) Establish coordinate system and rearrange sampling points by new phase time_axis = np.arange(num_data_points) * time_per_sample quantized_amplitude = data new_phase = np.mod(time_axis, 1/clock_frequency) sorted_indices = np.argsort(new_phase) sorted_time_axis = time_axis[sorted_indices] sorted_quantized_amplitude = quantized_amplitude[sorted_indices] # (4) Divide the coordinate system into N × M squares time_interval = 0.1e-12 # 0.1 ps amplitude_interval = 2 # Quantized amplitude change is 2 num_time_bins = int((max(sorted_time_axis) - min(sorted_time_axis))/time_interval) + 1 num_amplitude_bins = int((max(sorted_quantized_amplitude) - min(sorted_quantized_amplitude))/amplitude_interval) + 1 # (5) Count the number of squares without sampling points, i.e., area S0 histogram, xedges, yedges = np.histogram2d(sorted_time_axis, sorted_quantized_amplitude, bins = [num_time_bins, num_amplitude_bins]) S0 = np.sum(histogram = = 0) # (6) Calculate the signal clock frequency # This step is a placeholder as actual calculation logic depends on the specific application # (7) Reassign data points and scan frequency steps, iterate from step (3) if needed # This step is omitted for simplicity, assuming all scans are completed # (8) Generate the eye diagram |
The corresponding eye diagram recovery process is shown in Fig. 5.
Fig. 5.
Eye diagram recovery process.
The aforementioned algorithm restores eye diagrams through software, tested on a 2.5 Gb/s NRZ digital signal of an SDH system. The nominal clock frequency is 2488.320 MHz, with a clock period of 401.877 ps. The system sampling rate is 1.5 GS/s, with a sampling period of 666.667 ps. A total of 524,288 samples were taken, corresponding to a time period of 349.525 μs. Fig. 6 demonstrates the eye diagram recovery performance over 2 cycles (Fig. 6a) and 4 cycles (Fig. 6b), validating the algorithm's effectiveness in recovering digital signal eye diagrams.
Fig. 6.
Eye diagrams over multiple cycles: (a) 2 cycles; (b) 4 cycles.
3.4. Extraction and measurement analysis of jitter parameters
In optical fiber communication systems, the processing and transmission of high-speed digital optical signals are primary contributors to jitter. Total jitter (TJ) can be categorized into deterministic jitter (DJ) and random jitter (RJ) based on its causes. Assuming total jitter is repeatable, random jitter can be described using a Gaussian or normal distribution, while deterministic jitter has finite or bounded characteristics and can be represented by two impulse functions. For high-speed digital optical signals, jitter parameters can be extracted from the dual-Dirac model, which primarily relies on the statistical probability distribution function (PDF) domain [49]. The total jitter probability distribution function (TJ-PDF) for digital optical signals can be described as the convolution of the random jitter probability distribution function (RJ-PDF) and the deterministic jitter probability distribution function (DJ-PDF):
| (5) |
where represents the statistical probability distribution function of the total jitter for digital optical signals, represents the statistical probability distribution function of random jitter for digital optical signals, and represents the statistical probability distribution function of deterministic jitter. Random jitter, being an unbounded phenomenon, follows a Gaussian or normal distribution and can be expressed as:
| (6) |
where represents the standard deviation of the normal distribution function.
Deterministic jitter, being a bounded phenomenon, is typically represented as the sum of two impulse functions or Dirac delta functions:
| (7) |
where represents the impulse function or Dirac delta function, and are the deterministic time positions. The expression for deterministic jitter in the time domain is given as .
By substituting equations (6), (7) into equation (5), the statistical probability distribution function of the total jitter for digital optical signals can be obtained as follows:
| (8) |
where and represent the standard deviations of the normal distribution functions at the two deterministic positions. In the time domain, random jitter is represented as .
In the time domain, the expression for the total jitter of digital optical signals is as follows:
| (9) |
The process for generating jitter distribution histograms based on eye diagram reconstruction is as follows.
-
(1)
Determine the cross point location. Identify the cross point near the half-height of the eye diagram, which corresponds to the area with the highest occurrence probability, and define this as the central time point.
-
(2)
Determine the boundaries of the time points. The horizontal axis of the cross point should traverse all data. If the number of sampling points is zero for two consecutive time intervals, it is considered that the left and right boundaries of the jitter have been determined.
-
(3)
Plot the histogram. The horizontal axis represents the unit time, while the vertical axis represents the number of sampling points in the cross point region corresponding to that time.
-
(4)
Calculate basic jitter parameters based on the jitter histogram. This includes calculating the peak-to-peak value, mean value, and root mean square (RMS) value of the jitter.
The Bit Error Rate (BER) is used to evaluate the performance of digital optical receivers and is defined as the dimensionless parameter Q:
| (10) |
Where and are the photocurrents corresponding to the "0″ and "1″ bits, respectively, and and are the noise variances corresponding to the "0″ and "1″ bits, respectively. The BER calculation expression is given by:
| (11) |
From Equation (10), the BER variation curve for different Q parameters can be derived, as shown in Fig. 7. As illustrated in the figure, when Q > 6, the BER is less than 10−9, which meets the error rate requirements of standard optical fiber communication systems. Furthermore, when Q > 7, the BER is less than 10−12, satisfying the error rate requirements for high-performance systems.
Fig. 7.
Bit Error Rate (BER) versus Q parameter.
The process for obtaining the Q parameter and BER of a digital signal is as follows.
-
(1)
Determine the decision center point. Identify the positions of two adjacent crossing points in the eye diagram and draw a line connecting these two points. The midpoint of this line is the center point of the eye diagram.
-
(2)
Expand outward half a period from the center point. Calculate the average values I1 and I0 corresponding to the "1″ and "0″ levels in this region, as well as the noise levels and .
-
(3)
Calculate the Q parameter and BER.
4. Experimental results
4.1. Design of jitter measurement equipment
To evaluate the jitter characteristics of high-speed digital optical signals, we designed and constructed a high-precision jitter measurement system. The overall structure of this system is shown in Fig. 8, consisting of an upper computer and a lower computer. Upon powering on, the lower computer utilizes the main control chip and RS422, RS232 serial interfaces to control various components, thereby achieving functions such as control, detection, data transmission, and display.
Fig. 8.
Architecture design of the test prototype.
The key equipment parameters and specifications for the jitter measurement experiment in this study are detailed in Table 3 below.
Table 3.
Specifications of the jitter measurement equipment.
| Equipment Name | Model | Manufacturer |
|---|---|---|
| Optical Signal Source | TE100-AT-1550 | TE Connectivity |
| Optical Module | 2.5G-SFP-GE-LH40-SM1550 | Various |
| Optical Attenuator | JDSU MTS-6000 | Viavi Solutions |
| Polarization Controller | Agiltron OPC-100 | Agiltron |
| Photon-Induced Near-field detector (PIN) | Newport 818-BB-21A | Newport Corporation |
| Transimpedance Amplifier (TIA) | Femto HCA-200M-50K–C | Femto Messtechnik GmbH |
| Real-time Oscilloscope | Teledyne Lecroy SDA820Zi-B | Teledyne LeCroy |
| Data Processing Computer | Dell Precision 7920 | Dell Inc. |
| Main Control Chip and Interfaces | Microcontroller Unit (MCU) | Various |
The specific functionalities of key components for jitter measurement are as follows.
-
(1)
Optical Signal Source
Utilizes the TE100 Channel Tester (Model: TE100-AT-1550) to generate pseudo-random digital optical signals with NRZ encoding. It operates in 23-bit pseudo-random code mode at SDH 2.5 Gb/s NRZ coding to output a 2.5 Gb/s digital optical signal. The 2.5G-SFP-GE-LH40-SM1550 optical module is selected and integrated into the TE100 Channel Tester.
-
(2)
Optical Attenuator
Employs the JDSU MTS-6000 optical attenuator to adjust the power of the digital optical signal input to the jitter tester, effectively simulating diverse transmission conditions and optical power levels.
-
(3)
Polarization Controller
Uses the Agiltron OPC-100 polarization controller to regulate the polarization state of the digital optical signal, ensuring uniform polarization across optical interfaces in other jitter testers.
-
(4)
Jitter Tester Host
Hosted in a 19-inch 3U chassis, the front panel features a power switch, USB serial data interface, optical input APC/FC interface, and LCD touch screen. The rear panel includes a 220V AC input socket. The mainboard is structured into three blocks with a dual-layer design: the rear block houses electrical and data output modules, interconnected with the front panel's data interface. The left block's upper layer employs an MCU as the main control module, with the DC power module linked to various functional modules via twisted pair cables. The lower layer connects to the rear panel's 220V AC power module via cables, while output power is routed to the upper DC power module via additional cabling. The upper layer of the right-side module supplies essential clock signal sources for the prototype, transmitted to various modules via high-frequency cables. Clock generation facilitates the production of sampling pulse signals, amplified and directed to the lower optical sampling module to generate optical sampling pulse signals. The lower layer includes slope control circuits for the optical sampling module, alongside circuits for optical pulse widening and photoelectric conversion.
-
(5)
Data Processing Computer
Utilizes the Dell Precision 7920 workstation to analyze eye diagram data and extract information on digital signal jitter, essential for comprehensive analysis and evaluation in optical signal processing.
The main functions of the main control and power module in the digital optical signal jitter measurement system include providing stable DC power to each functional module, implementing timed power on/off controls, and closely monitoring the system's operational status throughout its runtime, as illustrated in Fig. 9.
Fig. 9.
Architecture of the main control and power supply module.
4.2. Jitter measurement equipment testing and analysis
-
(1)
Digital Optical Signal
The measurement system comprises five main components: a channel tester, an optical attenuator, a polarization controller, the jitter tester host, and a data processing computer. The channel tester, a TE100 channel tester, is used to generate pseudo-random digital optical signals with NRZ coding. The optical attenuator is an adjustable optical attenuator that regulates the power of the digital optical signal input to the jitter tester. The polarization controller adjusts the polarization state of the digital optical signal to ensure consistency with the optical interface in other jitter testing equipment. The data processing computer analyzes eye diagram data to extract information such as digital signal jitter.
A 2.5G-SFP-GE-LH40-SM1550 optical module is selected and inserted into the TE100 channel tester. The TE100 is set to operate in the 23-bit pseudo-random code mode at an SDH rate of 2.5 Gb/s with NRZ coding to output a 2.5 Gb/s digital optical signal. The digital optical signal is input to the photodetector and converted into an electrical signal. The electrical signal is tested in real-time using an oscilloscope (Teledyne Lecroy SDA820Zi-B) with a sampling rate of 80 GS/s and an operational bandwidth of 20 GHz. During this measurement, the bias voltage range of the MZM modulator is set from [-5V, 5V], with a step size of 0.1V. The bias voltage is gradually adjusted, and the changes in the eye diagram are observed. The optimal bias voltage is determined to be −0.5V, at which point the eye opening area is maximized and jitter is minimized. Based on this, the digital signal shown in Fig. 10 is obtained.
Fig. 10.
Output signal of the 2.5G-SFP-GE-LH40-SM1550 optical module measured by the real-time oscilloscope.
As shown in Fig. 10, the output digital signal of the 2.5G-SFP-GE-LH40-SM1550 optical module is a random non-return-to-zero (NRZ) digital signal. The period of this digital signal is approximately 401.5 ps, with a 10%–90 % rise time of about 140 ps and a 90%–10 % fall time of about 90 ps.
-
(2)
Sampled Optical Pulses and Pulse Broadening
As illustrated in Fig. 11, the waveforms of the optical pulse and the broadened optical pulse are displayed on the real-time oscilloscope. Fig. 11(a) and (c) show the recorded waveforms of the optical pulses with measurement times of 200 ns and 4 ns, respectively. Fig. 11(b) and (d) show the recorded waveforms of the broadened optical pulses with the same respective measurement times.
Fig. 11.
Optical Pulse Waveforms Measured by the Real-Time Oscilloscope(a) Optical sampling pulse after the MZM modulator, with a recording time of 200 ns.(b) Broadened optical sampling pulse, with a recording time of 200 ns.(c) Optical sampling pulse after the MZM modulator, with a recording time of 4 ns.(d) Broadened optical sampling pulse, with a recording time of 4 ns.
Experimental results indicate that the sampling period of the optical pulses remains the same before and after broadening, both being 667.7 ps. The pulse width before broadening is approximately 83.5 ps, and after broadening, it is about 227 ps.
-
(3)
Actual Process of Optical Sampling
After the broadened optical sampling pulse signal is quantized, the equivalent sampling data is obtained. By applying the eye diagram recovery method proposed in this paper, the grid image shown in Fig. 12a is obtained. Measurements indicate that the signal period is approximately 401.8 ps, consistent with previous experimental results. Simultaneously, after the digital optical signal is converted to an electrical signal, it is measured in real-time using an oscilloscope (Teledyne Lecroy SDA820Zi-B), resulting in the eye diagram of the digital optical signal shown in Fig. 12b. The signal period is approximately 401.8 ps, consistent with the experimental results from the jitter tester developed in this study. Furthermore, the grid patterns measured by the research equipment and the commercial real-time oscilloscope show a high degree of consistency in the details of the rising and falling edges, further validating the accuracy of the eye diagram test results.
Fig. 12.
Eye Diagram Test Results from the Jitter Tester (a) Test results from the prototype jitter tester.(b) Test results from the real-time oscilloscope.
Using the dual-Dirac model-based method, the fitting results obtained from fitting the jitter histogram are as follows:
| (13) |
The fitting coefficient (R2) is 0.9869. The fitting results indicate that the deterministic jitter components of the measured digital optical signal are located at 7.974 ps and −5.243 ps, respectively, with a deterministic jitter time of 13.20 ps. The standard deviations of the normal distribution functions corresponding to different deterministic jitter positions are 7.378/2°.5≈5.2ps and 9.157/2°.5≈6.5ps, respectively, which suggests that the measured random jitter time of the digital optical signal is (5.2 + 6.5)/2 = 5.85ps. Therefore, the total jitter of the digital optical signal is the sum of the deterministic jitter time and the random jitter time, i.e., 13.2 + 5.85 = 19.05 ps.
Additionally, the digital optical signal testing power range of the jitter tester was evaluated, and the results indicated that the testing power range exceeds 10 dB. Table 4 lists the Q-values and jitter parameters of the digital optical signals at different optical powers. The test results show that when the optical power of the digital optical signal is −7.2 dBm, −12.2 dBm, and −17.2 dBm, the Q-values are 8.8, 7.6, and 4.3, respectively, with RMS jitter values of 12.2 ps, 13.4 ps, and 21.2 ps, respectively. This indicates that as the optical power decreases (or the fiber transmission distance increases), the quality of the digital optical signal degrades.
Table 4.
Q-parameter and jitter of digital optical signals at different optical powers.
| No. | Optical Signal Power (dBm) | Q-Parameter | Peak Jitter (ps) | RMS Jitter (ps) | Mean Jitter (ps) |
|---|---|---|---|---|---|
| 1 | −7.2 | 8.8 | 39.0 | 12.2 | 9.8 |
| 2 | −12.2 | 7.6 | 55.0 | 13.4 | 10.8 |
| 3 | −17.2 | 4.3 | 74.0 | 21.2 | 16.7 |
| 4 | −2.3 | 9.1 | 36 | 11.5 | 8.9 |
| 5 | 0.1 | 9.3 | 34.5 | 11 | 8.5 |
| 6 | 2.4 | 9.5 | 33 | 10.5 | 8 |
| 7 | 4.6 | 9.7 | 31.5 | 10 | 7.5 |
| 8 | 6 | 10 | 30 | 9.5 | 7 |
In further tests, this study selected multiple optical power levels of −2.3 dBm, 0.1 dBm, 2.4 dBm, 4.6 dBm, and 6.0 dBm for in-depth analysis. The results show that as the optical power increases, the Q-parameter of the digital optical signal improves, but the jitter parameters also increase. At −2.3 dBm, 0.1 dBm, 2.4 dBm, 4.6 dBm, and 6.0 dBm, the Q-values are 9.1, 9.3, 9.5, 9.7, and 10.0, respectively, while the corresponding mean jitter values are 8.9 ps, 8.5 ps, 8.0 ps, 7.5 ps, and 7.0 ps, respectively. The results indicate that although the Q-parameter of the digital optical signal improves at higher powers, the increase in jitter may negatively affect signal quality. Specifically, at 6.0 dBm, despite the Q-parameter reaching 10.0, the jitter increased to 7.0 ps. This indicates that at higher power levels, nonlinear effects significantly increase, affecting signal stability.
After validating the eye diagram and jitter testing capabilities, it was found that the device can accurately reconstruct the eye diagram of digital optical signals and obtain jitter parameters. Comparing the results with those from commercial real-time oscilloscopes shows that the device's test results are equally accurate and reliable. Additionally, this method also demonstrated that the optical power bandwidth of the digital optical signal exceeds 10 dB. In summary, the prototype performs excellently, achieving the expected testing goals. At a high power of 6.0 dBm, although the algorithm maintains high stability, ensuring stable signal quality output.
-
(4)
Time Error Analysis
During random sampling, the stability of the sampling clock inevitably leads to measurement errors. The following analysis addresses the errors caused by the stability of the sampling clock in the measurement system. Let TX and TS represent the signal period and the sampling clock period, respectively. The stability of the sampling clock frequency is defined as δ (ppm), which physically represents the ratio of the maximum frequency drift per unit time (per second) to the center frequency. This ratio is given by:
| (13) |
We can calculate the time error over a specific measurement interval based on the stability parameters of common crystal oscillators. The relationship between the sampling frequency and the sampling period is:
| (14) |
Differentiating Equation (14) yields the relationship between sampling frequency error and time error:
| (15) |
By further substituting Equation (13) into the calculation, we obtain Equation (16):
| (16) |
The time error corresponding to the unit period time obtained from Equation (16) is given by:
| (17) |
At a sampling rate of 1.5 GS/s, specific to the SDH fixed frame length of 125 μs and the maximum frame length of 1518 bytes for Gigabit Ethernet (corresponding to 12,144 cycles, with Gigabit Ethernet using 8B10B encoding and an actual transmission rate of 1.25 Gb/s, resulting in an actual frame time length of 12,144 ns), the time error due to crystal oscillator stability and measurement time can be calculated, as detailed in Table 5.
Table 5.
Time error ΔTS of the crystal oscillator (ps).
| 100 | 10 | 1 | 0.1 | 0.01 | |
|---|---|---|---|---|---|
| 12.144 | 8.1 × 10−1 | 8.1 × 10−2 | 8.1 × 10−3 | 8.1 × 10−4 | 8.1 × 10−5 |
| 100 | 6.7 | 6.7 × 10−1 | 6.7 × 10−2 | 6.7 × 10−3 | 6.7 × 10−4 |
| 125 | 8.3 | 8.3 × 10−1 | 8.3 × 10−2 | 8.3 × 10−3 | 8.3 × 10−4 |
| 1000 | 6.7 × 10 | 6.7 | 6.7 × 10−1 | 6.7 × 10−2 | 6.7 × 10−3 |
| 10000 | 6.7 × 102 | 6.7 × 10 | 6.7 | 6.7 × 10−1 | 6.7 × 10−2 |
Thus, it can be seen that the jitter measurement system generally requires the crystal oscillator stability to be in the range of 1–10 ppm, which can meet the requirements for digital signal jitter measurement.
The process from optical sampling to electrical conversion proposed in this paper includes the following three main stages: optical sampling, optical pulse broadening, and optoelectronic conversion and electrification. During the optical signal processing, the noise mainly originates from the intensity noise of the optical signal source, the extinction ratio noise of the sampling optical switch, the white noise introduced by the optoelectronic conversion amplifier, thermal noise, and amplifier noise. The sampled optical pulse signal is divided into two signals, each passing through different optical delay paths: the pulse optical signal passes through a photodetector (PIN), a transimpedance amplifier (TIA), an electric coupler, and a linear amplifier (LA), ultimately reaching the electrical quantization module. Components such as the front-end light source, MZM modulator, PIN, TIA, and LA all introduce noise. According to the thermal noise theory, the main noise in the optoelectronic conversion system comes from the photodetector and the transimpedance amplifier. The total optoelectronic conversion noise is as follows:
| (18) |
The signal-to-noise ratio (SNR) of the detected optical signal at this time is:
| (19) |
Where q is the electron charge, k is the Boltzmann constant, T is the absolute temperature, RL is the load resistance, F1 is the noise figure of the TIA, Δf is the equivalent noise bandwidth, p is the detected optical power, R is the responsivity of the PIN detector, RIN is the relative intensity noise coefficient, and ΔP is the noise power caused by the extinction ratio. The first term in the noise equation represents white noise , which is the noise power caused by the randomness of electrons generated during optoelectronic conversion. The second term represents thermal noise, which is the noise power caused by the thermal motion of carriers. The third term represents intensity noise, which is the noise power introduced by the power stability of the semiconductor laser. The fourth term represents the noise power introduced by the switch extinction ratio of the modulator, which is also a unique characteristic of the system.
Analysis shows that the average optical power reaching the photodetector in the test system is generally less than −10 dBm. At this point, the thermal noise is much greater than the white noise and the laser intensity noise, denoted as . After simplification, the formula is:
| (20) |
Given the Boltzmann constant , , , , , the thermal noise power can be calculated as 3.2 × 10−12 A2. The responsivity R of the photodetector is 0.9A/W, and the input optical power is −10 dBm. With an optical switch extinction ratio of 30 dB, the second term, representing the switch leakage noise power, is 0.8 × 10−14 A2. Therefore, thermal noise is the primary noise source. However, when the extinction ratio decreases to 20 dB, the thermal noise and the noise introduced by the extinction ratio become comparable, significantly reducing the signal-to-noise ratio (SNR) of the photodetector and affecting the dynamic range and accuracy of eye diagram measurements. The impact of thermal noise is unavoidable during the measurement process. Thus, improving the extinction ratio to reduce the impact of leakage noise is crucial for enhancing measurement performance. After machine screening, bias control, and drive voltage amplitude control, the extinction ratio of the test equipment can be stabilized at above 30 dB.
5. Discussion
This study addresses the issues of accuracy and stability deficiencies in existing clock recovery algorithms for high-speed digital optical signal processing by proposing a novel clock recovery algorithm based on eye-opening area for jitter measurement of high-speed digital optical signals. This algorithm demonstrates exceptional performance in various aspects and maintains high recovery accuracy even in complex scenarios, which is crucial for the stability of practical communication systems. The algorithm achieves simultaneous utilization of both amplitude and phase information of the signal, theoretically overcoming the performance bottlenecks of traditional algorithms that focus solely on amplitude or suffer from discreteness issues. This significantly enhances the accuracy and stability of clock recovery. The research not only enriches the theoretical foundation of clock recovery algorithms but also provides key technical support for optimizing the overall performance of high-speed digital optical communication systems. It holds significant importance for improving signal transmission quality, reducing bit error rates, and enhancing the reliability of communication links.
Unlike existing clock recovery algorithms based on interpolation or filtering, this study's algorithm uses the curvature characteristics of the eye diagram opening area as an evaluation criterion, avoiding the poor recovery accuracy and stability caused by discreteness when processing high-speed signals with traditional algorithms. The research by Ben-Hamida and D'Amours [50] focuses on optimizing wavelength resource utilization, which affects the precision of clock recovery. Huang et al. [51] proposed a real-time eye diagram monitoring method based on optical sampling, which, while having high time resolution, fails to utilize phase information and has deficiencies in noise resistance. Yang et al. [52]'s bit error rate eye diagram analysis method overlooks the deterministic components of jitter. In contrast, this study's algorithm captures signal phase changes through mathematical modeling, theoretically improving the accuracy and robustness of clock recovery, providing a new solution for the quality evaluation of high-speed digital optical signals.
Theoretically, this study expands the research scope of clock recovery algorithms by introducing the analysis of the eye diagram opening area, providing a new high-accuracy, high-stability clock recovery method, enriching the theoretical system of high-speed digital optical signal processing. Practically, the findings of this study have important guiding significance for the design and optimization of high-speed communication systems. It is recommended that the clock recovery algorithm based on the eye diagram opening area be adopted in practical engineering applications to improve signal transmission quality and system stability. Additionally, communication equipment manufacturers should enhance the research and application of eye diagram analysis technology, developing more advanced signal processors and clock recovery circuits to meet the increasing demands for communication speed and quality.
Despite the positive progress, there are still some limitations in the current algorithm due to experimental conditions. Firstly, in high-noise environments, the characteristics of the eye diagram opening area curvature may be affected, leading to reduced clock recovery accuracy. Therefore, it is necessary to further optimize the algorithm's noise resistance. Secondly, this study mainly targets digital optical signals, and the clock recovery capability for other types of signals (such as analog signals) remains to be verified. Future research should expand the algorithm's applicability to achieve broader applications. Additionally, with the continuous development of communication technology, the complexity and diversity of high-speed signal transmission are also increasing. Future research should further explore various algorithm combinations based on eye diagram analysis to address the complex signal processing needs in different application scenarios.
6. Conclusion
This study proposes a novel clock recovery algorithm based on the curvature characteristics of the eye-opening area, aiming to address existing issues in high-speed digital optical signal processing. Experimental results demonstrate that this algorithm exhibits significant advantages in several key aspects.
-
(1)
Performance Stability: The algorithm consistently reconstructs signal eye diagrams and accurately retrieves jitter parameters across a wide optical power range from −17.2 dBm to 6.0 dBm. Notably, even under low optical power conditions (−17.2 dBm), the Q factor remains at 4.3, indicating excellent performance.
-
(2)
Noise Immunity: Utilizing high-speed digital optical signal processing technology, the algorithm significantly reduces noise interference, ensuring the precision and stability of clock recovery, particularly in high-noise environments.
-
(3)
Accuracy Validation: The signal period obtained using the random equivalent sampling method (approximately 401.8 ps) aligns with the actual transmission rate, confirming the algorithm's effectiveness for SDH 2.5 Gb/s NRZ-coded digital signals. The measured eye diagrams closely match those obtained from commercial real-time oscilloscopes, further verifying the accuracy of the tests.
This research not only theoretically enhances clock recovery and jitter measurement algorithms but also provides a high-precision, high-efficiency, and noise-resistant technical solution for practical applications. It holds significant implications for optimizing modern high-speed optical communication systems. Future research will explore the potential applications of this algorithm in higher data rates and more complex modulation formats.
Data availability
The research data of this study have not been provided in a public database. Considering the innovativeness of this study and data protection requirements, the data have not been made publicly available at this time. Some data are included in the article and its supplementary materials, or referenced within the article.
CRediT authorship contribution statement
Suping Liu: Writing – original draft.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- 1.Liu X. Enabling optical network technologies for 5G and beyond. J. Lightwave Technol. 2021;40:358–367. doi: 10.1109/jlt.2021.3099726. [DOI] [Google Scholar]
- 2.Ding J., Xu T., Zhang Y., Liu Z., Jin C., Zhao J., Liu T. vol. 11891. SPIE; 2021. Influence of equalization enhanced phase noise on digital nonlinearity compensation in Nyquist-spaced superchannel transmission systems; pp. 38–45. (Semiconductor Lasers and Applications XI). [DOI] [Google Scholar]
- 3.Karar A.S., Falou A.R.E., Barakat J.M.H., Gürkan Z.N., Zhong K. Recent advances in coherent optical communications for short-reach. Phase retrieval methods. In Photonics. 2023, March;10(3):308. doi: 10.3390/photonics10030308. MDPI. [DOI] [Google Scholar]
- 4.Tang J., Chen H., Cui S., Chen Y., Dai L., Zhou K., Liu D. High receiver skew-tolerant and hardware-efficient clock recovery for short-reach coherent transmission. Opt Express. 2022;30(15):27064–27079. doi: 10.1364/oe.461105. [DOI] [PubMed] [Google Scholar]
- 5.Lin S.C., Chuang K., Chang C.W., Chen J.H. Efficient interpolation method for wireless communications and signal processing applications. IEEE Trans. Microw. Theor. Tech. 2021;69(5):2753–2761. doi: 10.1109/TMTT.2021.3061563. [DOI] [Google Scholar]
- 6.Altay Y., Kremlev A. 2021 IEEE Conference of Russian Young Researchers in Electrical and Electronic Engineering (ElConRus) 2021. Signal-to-Noise ratio and mean square error improving algorithms based on Newton filters for measurement ECG data processing; pp. 1590–1595. [DOI] [Google Scholar]
- 7.Kazi I., Reynaert P., Dehaene W. 2022 20th IEEE Interregional NEWCAS Conference (NEWCAS) 2022. Clock recovery circuit using a transmission line as a delay element from a 100Gb/s bit stream; pp. 261–264. [DOI] [Google Scholar]
- 8.Souliotis G., Tsimpos A., Vlassis S. Phase interpolator-based clock and data recovery with jitter optimization. IEEE Open Journal of Circuits and Systems. 2023;4:203–217. doi: 10.1109/OJCAS.2023.3295649. [DOI] [Google Scholar]
- 9.Park H., Sim J., Choi Y., Choi J., Kwon Y., Kim C. A 2.4–8 GHz phase rotator delay-locked loop using cascading structure for direct input–output phase detection. IEEE Transactions on Circuits and Systems II: Express Briefs. 2021;69(3):794–798. doi: 10.1109/TCSII.2021.3113926. [DOI] [Google Scholar]
- 10.Li J., Yuan Y., Cai Y. High-precision clock date recovery for optical wireless communications using orbital-angular-momentum-based mode division multiplexing. Opt Lett. 2023 doi: 10.1364/ol.492859. [DOI] [PubMed] [Google Scholar]
- 11.Kumar K.J., Raganna A. Implementation of low-power high-speed clock and data recovery. Cognitive Informatics and Soft Computing. 2021 doi: 10.1007/978-981-16-1056-1_27. [DOI] [Google Scholar]
- 12.Sun L., Xiao J., Cai Y., Shen G., Liu N., Lu C. Low-latency and efficient retiming and equalizing scheme for a 112-Gbps bandwidth-limited optical PAM-4 system. Opt Express. 2022 doi: 10.1364/oe.457998. [DOI] [PubMed] [Google Scholar]
- 13.Li C., Cui S., Liu J., Chen Y., Dai L., Zhou K., Tang M.B. Time-domain low-complexity clock recovery for non-integer oversampled Nyquist signals with a small roll-off factor. Opt Express. 2023 doi: 10.1364/oe.489594. [DOI] [PubMed] [Google Scholar]
- 14.Xiang S., Yang M., Wang J. Chaotic optical communications of 12.5-Gbaud OOK and 10-Gbaud QPSK signals based on mutual injection of semiconductor lasers. Opt Lett. 2022 doi: 10.1364/ol.457625. [DOI] [PubMed] [Google Scholar]
- 15.Hu Z., Zhou Z., Chan C., Liu Z. Equalizer state caching for fast data recovery in optically-switched data center networks. J. Lightwave Technol. 2021 doi: 10.1109/JLT.2021.3089684. [DOI] [Google Scholar]
- 16.Li H., Lu S., Zhao Z. 2023 IEEE 2nd International Conference on Electrical Engineering, Big Data and Algorithms (EEBDA) 2023. Design and implementation of HDB3 clock recovery module with large frequency range. [DOI] [Google Scholar]
- 17.Zhu Y., Yang T., Wang M., Hong H., Zhang Y., Wang L., Rao Q., Zhu Y., Yang T., Wang M., Hong H., Zhang Y., Wang L., Rao Q. Jitter detection method based on sequence CMOS images captured by rolling shutter mode for high-resolution remote sensing satellite. Rem. Sens. 2022;14(2):342. doi: 10.3390/rs14020342. [DOI] [Google Scholar]
- 18.Cortiula A., Menin D., Bandiziol A., Grollitsch W., Nonis R., Palestri P. A time-domain simulation framework for the modeling of jitter in high-speed serial interfaces. IEEE Transactions on Circuits and Systems I: Regular Papers. 2022;70(2):940–951. doi: 10.1109/TCSI.2022.3226320. [DOI] [Google Scholar]
- 19.Jiang T., Wang L., Li J. High-resolution timing jitter measurement based on the photonics time stretch technique. Opt Express. 2023;31(4):6722–6729. doi: 10.1364/oe.479124. [DOI] [PubMed] [Google Scholar]
- 20.Yang W., Tian S., Dai Z. 2023 IEEE 16th International Conference on Electronic Measurement & Instruments (ICEMI) IEEE; 2023, August. High-speed signal jitter measurement method based on bit error rate eye diagram; pp. 71–77. [DOI] [Google Scholar]
- 21.Tschapek P., Körner G., Hofmann A., Carlowitz C., Vossiek M. Phase noise spectral density measurement of broadband frequency-modulated radar signals. IEEE Trans. Microw. Theor. Tech. 2022;70(4):2370–2379. doi: 10.1109/TMTT.2022.3148311. [DOI] [Google Scholar]
- 22.Liu X., Lu H., He Y., Wu F., Zhang C., Wang X. Analysis on the effect of phase noise on the performance of satellite communication and measurement system. Symmetry. 2023;15(11):2053. doi: 10.3390/sym15112053. [DOI] [Google Scholar]
- 23.Zidan M.D., Allahham A., Ghanem A., Mousa N., Abdallah B., Al Salman A. Thermal lens investigation of the CdSe quantum dots using dual beam z-scan technique. Results in Optics. 2024;16 [Google Scholar]
- 24.Liu D., He C., Wang L., Gao H., Wu Z. A jitter measurement technique for digital ultra-high-definition-video signals. J. Mod. Opt. 2021;65(6):3–8. doi: 10.12338/J.ISSN.2096-9015.2020.9039. [DOI] [Google Scholar]
- 25.Zhang S., Sun Q., Chen X., Wang B., Li Y. ADC clock jitter measurement based on simple coherent sampling algorithm. J. Phys. Conf. 2022, November;2366(1) doi: 10.1088/1742-6596/2366/1/012045. IOP Publishing. [DOI] [Google Scholar]
- 26.Jiang T., Wang L., Li J. High-resolution timing jitter measurement based on the photonics time stretch technique. Opt Express. 2023;31(4):6722–6729. doi: 10.1364/oe.479124. [DOI] [PubMed] [Google Scholar]
- 27.Sośnicki F., Golestani A., Karpiński M. 2023 48th International Conference on Infrared, Millimeter, and Terahertz Waves (IRMMW-THz) IEEE; 2023, September. RF waveform noise measurement by electro-optic sampling; pp. 1–2. [DOI] [Google Scholar]
- 28.Yang W., Tian S., Dai Z. 2023 IEEE 16th International Conference on Electronic Measurement & Instruments (ICEMI) IEEE; 2023, August. High-speed signal jitter measurement method based on bit error rate eye diagram; pp. 71–77. [DOI] [Google Scholar]
- 29.Huang T., Fan Z., Su J., Qiu Q. Real-time eye diagram monitoring for optical signals based on optical sampling. Appl. Sci. 2023;13(3):1363. doi: 10.3390/app13031363. [DOI] [Google Scholar]
- 30.Zhou Y., Shi B., Zhao Y., Schutt-Ainé J.E. 2022 IEEE Electrical Design of Advanced Packaging and Systems (EDAPS) IEEE; 2022, December. Fast eye diagram simulation based on latency insertion method; pp. 1–3. [DOI] [Google Scholar]
- 31.Yang W., Tian S., Dai Z. 2023 IEEE 16th International Conference on Electronic Measurement & Instruments (ICEMI) IEEE; 2023, August. High-speed signal jitter measurement method based on bit error rate eye diagram; pp. 71–77. [DOI] [Google Scholar]
- 32.Li C., Cui S., Liu J., Chen Y., Dai L., Zhou K., Tang M. Time-domain low-complexity clock recovery for non-integer oversampled Nyquist signals with a small roll-off factor. Opt Express. 2023;31 11:18599–18612. doi: 10.1364/oe.489594. [DOI] [PubMed] [Google Scholar]
- 33.Kozdrowski S., Cichosz P., Sujecki S. 2022 International Conference on Software, Telecommunications and Computer Networks (SoftCOM) 2022. Machine learning application to transmission quality assessment in optical networks; pp. 1–3. [DOI] [Google Scholar]
- 34.Weiyang M., Tan C., Rotaru M. 2022 IEEE 24th Electronics Packaging Technology Conference (EPTC) 2022. Eye diagram analysis with deep neural networks for signal integrity applications; pp. 212–217. [DOI] [Google Scholar]
- 35.Chu X., Guo W., Wang J., Wu F., Luo Y., Li Y. Fast and accurate estimation of statistical eye diagram for nonlinear high-speed links. IEEE Trans. Very Large Scale Integr. Syst. 2021;29(7):1370–1378. doi: 10.1109/TVLSI.2021.3082208. [DOI] [Google Scholar]
- 36.Huang T., Fan Z., Su J., Qiu Q. Real-time eye diagram monitoring for optical signals based on optical sampling. Appl. Sci. 2023;13(3):1363. doi: 10.3390/app13031363. [DOI] [Google Scholar]
- 37.Usama M., Chang D. 2023 IEEE International Conference on Consumer Electronics-Asia (ICCE-Asia) 2023. PyEye: an integrated approach for signal integrity assessment and eye diagram generation; pp. 1–3. [DOI] [Google Scholar]
- 38.Souliotis G., Tsimpos A., Vlassis S. Phase interpolator-based clock and data recovery with jitter optimization. IEEE Open Journal of Circuits and Systems. 2023;4:203–217. doi: 10.1109/OJCAS.2023.3295649. [DOI] [Google Scholar]
- 39.Park J., Kim Y., Kim D. Accelerated statistical eye diagram estimation method for efficient signal integrity analysis. IEEE Access. 2023;11:132699–132707. doi: 10.1109/ACCESS.2023.3336568. [DOI] [Google Scholar]
- 40.Usama M., Chang D.E. 2023 IEEE International Conference on Consumer Electronics-Asia (ICCE-Asia) 2023. PyEye: an integrated approach for signal integrity assessment and eye diagram generation. [DOI] [Google Scholar]
- 41.Weiyang M., Tan C.S., Rotaru M.D. 2022 IEEE 24th Electronics Packaging Technology Conference (EPTC) IEEE; 2022, December. Eye diagram analysis with deep neural networks for signal integrity applications; pp. 212–217. [DOI] [Google Scholar]
- 42.Lee J., Choi S., Son S., Park J., Kim H., Kim K., Shin T., Sim B., Hong J., Yoon J., Kim J.-K., Kim J. 2023 IEEE 32nd Conference on Electrical Performance of Electronic Packaging and Systems (EPEPS) IEEE; 2023. Adaptive gramian-angular-field segmentation integration based generative adversarial network (AGSI-GAN) for eye diagram estimation of high bandwidth memory (hbm) interposer; pp. 1–3. [DOI] [Google Scholar]
- 43.Zhou Y., Shi B., Zhao Y., Schutt-Ainé J.E. 2022 IEEE Electrical Design of Advanced Packaging and Systems (EDAPS) IEEE; 2022, December. Fast eye diagram simulation based on latency insertion method; pp. 1–3. [DOI] [Google Scholar]
- 44.Cortiula A., Menin D., Bandiziol A., Grollitsch W., Nonis R., Palestri P. A time-domain simulation framework for the modeling of jitter in high-speed serial interfaces. IEEE Transactions on Circuits and Systems I: Regular Papers. 2022;70(2):940–951. doi: 10.1109/TCSI.2022.3226320. [DOI] [Google Scholar]
- 45.Huang T., Fan Z., Su J., Qiu Q. Real-time eye diagram monitoring for optical signals based on optical sampling. Appl. Sci. 2023;13(3):1363. doi: 10.3390/app13031363. [DOI] [Google Scholar]
- 46.Telescu M., Trinchero R., Soleimani N., Tanguy N., Stievano I. Stochastic time-domain mapping for comprehensive uncertainty assessment in eye diagrams. IEEE Trans. Electromagn C. 2023;65(6):1930–1938. doi: 10.1109/TEMC.2023.3317974. [DOI] [Google Scholar]
- 47.Wang K., Wei W., Wang D., Wang P., Xie W., Dong Y. Time-stable receiving system with local digitization based on a dithered sample clock. IEEE Photon. J. 2022;15(1):1–6. doi: 10.1109/JPHOT.2022.3227054. [DOI] [Google Scholar]
- 48.Lee S., Kang B., Rhee W., Jeong D.K. A 0.061-pj/b/dB 28-Gb/s gradient-based maximum eye tracking CDR with 2-tap DFE adaptation in 28-nm CMOS. IEEE Transactions on Circuits and Systems II: Express Briefs. 2023;70(11):3998–4002. doi: 10.1109/TCSII.2023.3277838. [DOI] [Google Scholar]
- 49.Huang T., Fan Z., Su J., Qiu Q. Time jitter analysis of an optical signal based on gated on-off optical sampling and dual-Dirac modeling. Electronics. 2023;12(3):633. doi: 10.3390/electronics12030633. [DOI] [Google Scholar]
- 50.Abdo A., Aouini S., Riaz B., Ben-Hamida N., D'Amours C. Adaptive coherent receiver settings for optimum channel spacing in gridless optical networks. Future Internet. 2019;11(10):206. [Google Scholar]
- 51.Huang T., Fan Z., Su J., Qiu Q. Real-time eye diagram monitoring for optical signals based on optical sampling. Appl. Sci. 2023;13(3):1363. doi: 10.3390/app13031363. [DOI] [Google Scholar]
- 52.Yang W., Tian S., Dai Z. 2023 IEEE 16th International Conference on Electronic Measurement & Instruments (ICEMI) 2023. High-speed signal jitter measurement method based on bit error rate eye diagram; pp. 71–77. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The research data of this study have not been provided in a public database. Considering the innovativeness of this study and data protection requirements, the data have not been made publicly available at this time. Some data are included in the article and its supplementary materials, or referenced within the article.